When to help juveniles, adults, or both: analyzing the evolutionary models of stage-structured mutualism

Mutualism is common in nature and is crucial for population dynamics, community structure, and ecosystem functioning. Studies have recently pointed out that life-history stage structure (e.g., juveniles and adults) is a key factor to better understand the ecological consequences of mutualism (termed stage-structured mutualism). Despite the potential importance, little is known about what kinds of stage-structured mutualism can evolve and when it is likely to occur. Here, we theoretically investigated how a mutualistic partner species should allocate efforts of mutualistic associations for different life-history stages of its host species to maximize its fitness. We assessed the partner’s optimal strategy by using a one host–one partner model with the host’s juvenile-adult stage structure. The results showed that different forms of stage-structured mutualism can evolve, such as juvenile-specialized association, adult-specialized association, and inter-stage partner sharing (i.e., the partner associates with both the juvenile and adult stages of the host) depending on the shape of association trade-off, i.e., how much association with one stage is weakened when the partner strengthens its association with the other stage. In general, stage-specialized association (either juvenile-specialized or adult-specialized association) tends to evolve when being associated with that stage is relatively beneficial. Meanwhile, when the association trade-off is weak, inter-stage partner sharing can occur if the mutualistic benefits of juvenile-specific and adult-specific associations are sufficiently large. We also found that when the association trade-off is strong, alternative stable states occur in which either juvenile-specialized or adult-specialized associations evolve depending on the initial trait value. These results suggest that pairwise interspecific mutualism is more complicated than previously thought, implying that we may under-or overestimate the strength of mutualistic interactions when looking at only certain life-history stages. This study provides a conceptual basis for better understanding the mechanisms underlying ontogenetic shifts of mutualistic partners and more complex mutualistic networks mediated by the life-history stages of organisms and their stage-structured interactions.

1. Introduction

Mutualism, a cooperative association between different species, is one of the major interaction types in nature and is crucial for ecological dynamics and evolutionary processes (Bascompte and Jordano, 2014; Bronstein, 2015). It also plays an important role in applied ecological fields of biodiversity conservation and agricultural management (Gianinazzi et al., 2010; Albrecht et al., 2014). For understanding how mutualism works in nature, it is crucial to accurately describe the network structure of mutualistic association and identify key mechanisms underlying it. In mutualistic networks, there is a process called partner choice that has been extensively studied (Bshary and Grutter, 2002; Simms and Taylor, 2002; Biedermann and Kaltenpoth, 2014; Werner and Kiers, 2015; Chomicki et al., 2016; Younginger and Friesen, 2019). This process involves selecting one or more association partners from a group of potential candidates, with the goal of maximizing one’s own fitness. Partner choice is a significant factor in determining the overall structure of mutualistic relationships.

Another important factor determining the structure of mutualistic relationships is stage structure (including age-and body size-structure; Skelton et al., 2014, 2016; Thomas et al., 2016; Ke and Nakazawa, 2018; Nakazawa, 2020; Nakazawa and Katayama, 2020). The concept of “stage-structured mutualism” is that the nature of pairwise interspecific mutualism changes qualitatively and quantitatively during the ontogenetic development of individuals. Indeed, many studies have reported that species are often associated with different mutualistic partners at different life-history stages (termed ontogenetic partner shifts; Nakazawa, 2020). Examples are abundant including nutritional mutualism between microbes and plants (Baudoin et al., 2002; Husband et al., 2002; Mougel et al., 2006; Houlden et al., 2008; Micallef et al., 2009; Chaparro et al., 2014; Sugiyama et al., 2014; Horton, 2015; Oono et al., 2015), nutritional mutualism between microbes and insects (Koga et al., 2003; Dillon et al., 2010; Stoll et al., 2010; Duguma et al., 2015; Johnston and Rolff, 2015; Shukla et al., 2016; Ali et al., 2019), defensive mutualism between ants and plants (Heil and McKey, 2003; Palmer et al., 2010; Quintero et al., 2013; Heil, 2015), and cleaning mutualism between cleaner and recipient animals (Skelton et al., 2014, 2016; Thomas et al., 2016; Vaughan et al., 2017; Quimbayo et al., 2018). These examples indicate that partner choice is a stage-specific process (see Nakazawa, 2020 and references therein for details). At present, however, little is known about how partner choice can form stage-structured mutualism, because previous studies of partner choice have typically considered that mutualism occurs between homogeneous species without stage structure (Bascompte and Jordano, 2014; Bronstein, 2015).

Suppose that one species has a life-history stage structure (e.g., juvenile and adult stages) due to a larger body size and a longer lifespan than the other species in a pairwise interspecific mutualism while the other smaller and shorter-lived species does not have it; hereafter we call them host and partner, respectively, for convenience. In their stage-structured relationship, the non-structured partner would allocate mutualistic association efforts, i.e., any forms of costs incurred to maintain the mutualistic relationship (e.g., nutrient provision by microbes to host plants), for different life-history stages of the host. One may intuitively expect that the partner would allocate more association efforts for more beneficial stages of the host. However, it is uncertain whether the partner should allocate all association efforts for the most beneficial stage or more evenly allocate association efforts for multiple stages depending on their relative benefits because indirect mutualistic benefits may arise due to dynamic changes in stage distribution. It is important to study such an issue because it provides a mechanistic basis to describe mutualistic networks mediated by the life-history stages of organisms and their stage-structured associations. If the partner allocates all association efforts only for the most beneficial stage of the host, it can lead to an ontogenetic change in their mutualistic relationship. By contrast, if the partner allocates association efforts for multiple stages of the host, it obscures their stage-structured relationship (termed ontogenetic partner sharing; Nakazawa, 2020). Considering the common occurrence of ontogenetic partner shifts (see above), we are particularly concerned with the former situation.

In this study, we analyze a mathematical model to assess the optimal effort allocation of the mutualistic partner in stage-structured mutualism from the evolutionary viewpoint. As an initial study, we consider the simplest situation, that is, a pairwise mutualistic relationship in which one species (host) has a juvenile-adult stage structure and the other species (partner) associates with the juvenile and/or adult stages of its host species. As such, the partner species determines which or both of life-history stages of the host to associate with and how strongly to do it. We then investigate under what condition stage-specific association can evolve. The model is simple but potentially applicable to a wide range of stage-structured mutualisms (e.g., nutritional mutualism between microbes and insects; see above for other examples) while providing a mechanistic basis to better understand the mechanisms underlying ontogenetic partner shits and more complex mutualistic network mediated by the life-history stages of organisms and their stage-structured interactions.

2. Methods

We consider a one host–one partner system in which the host species has a juvenile–adult stage structure and the partner species is non-structured and improves juvenile maturation (growth) and/or adult reproduction of the stage-structured host (Figure 1A). While we are interested in adaptive evolution of mutualistic association effort allocation in the partner species, we start with developing an ecological model to describe the host-partner population dynamics rather than assuming static population abundances because the partner’s adaptive strategy can affect the host’s stage distribution via ontogenetic development on the ecological time scale which may in turn feedback on the partner’s evolution. The ecological model is formulated as follows:

$\begin{array}{l}\frac{{\mathrm{dH}}_{\mathrm{J}}}{\mathrm{dt}}=\left({\mathrm{r}}_{\mathrm{A}}+{\mathrm{B}}_{\mathrm{AP}}{\mathrm{X}}_{\mathrm{A}}\mathrm{P}\right){\mathrm{H}}_{\mathrm{A}}-\left({\mathrm{r}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{JP}}{\mathrm{X}}_{\mathrm{J}}\mathrm{P}\right){\mathrm{H}}_{\mathrm{J}}\\ -\left({\mathrm{d}}_{\mathrm{JJ}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{d}}_{\mathrm{AJ}}{\mathrm{H}}_{\mathrm{A}}\right){\mathrm{H}}_{\mathrm{J}}\end{array}$

$\frac{{\mathrm{dH}}_{\mathrm{A}}}{\mathrm{dt}}=\left({\mathrm{r}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{JP}}{\mathrm{X}}_{\mathrm{J}}\mathrm{P}\right){\mathrm{H}}_{\mathrm{J}}-\left({\mathrm{d}}_{\mathrm{JA}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{d}}_{\mathrm{AA}}{\mathrm{H}}_{\mathrm{A}}\right){\mathrm{H}}_{\mathrm{A}}$

$\frac{\mathrm{dP}}{\mathrm{dt}}=\left({\mathrm{r}}_{\mathrm{P}}+{\mathrm{B}}_{\mathrm{PJ}}{\mathrm{X}}_{\mathrm{J}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{PA}}{\mathrm{X}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}-{\mathrm{d}}_{\mathrm{P}}\mathrm{P}\right)\mathrm{P}$

where H_i and P are the abundances of the juvenile (i = J) or adult (i = A) host and non-structured partner, respectively. The parameter r_i is the host’s basic maturation (i = J) or reproduction (i = A) rate (Nakazawa, 2020; Nakazawa and Katayama, 2020), which increases by B_iP (i = J, A) because of its association with the partner. Meanwhile, the partner has an intrinsic population growth rate r_P, which increases by B_Pi (i = J, A) because of its association with the juvenile and/or adult host. The host and partners are facultative when r_i or r_p is positive, and obligate when it is zero. When it is positive, the model assumes that the host and partner are supported by other species not explicitly considered in the model, and their abundances are largely constant independent of the focal system. Note that B_iP and B_Pi are the net benefits after accounting for the costs of mutualism. For simplicity, we formulate B_Pi = α_iB_iP (i.e., the benefits for the partner are proportional to those for the host), where α_i is the scaling coefficient. The partner allocates association efforts X_J and X_A for the juvenile and adult host, respectively. More specifically, we assume that an increase in the association of the partner with the juvenile host decreases its association with the adult host as X_A = (1 − X_J)^q, where the parameter q determines the shape of the trade-off between stage-specific associations (Figure 1B). When q < 1, the juvenile-specific association decreases the adult-specific association slightly, which biologically means that the partner can provide sufficient rewards to both stages. In other words, the inter-stage competition for rewards provided by the partner (termed mutualistic niches; Peay, 2016) is weak within the host species. Conversely, when q > 1, the juvenile-specific association decreases the adult-specific association substantially, which means that the partner cannot provide sufficient rewards to both stages because the inter-stage competition for rewards provided by the partner is strong within the host species. We a priori assume that both juvenile-and adult-specific associations are positive or neutral (i.e., X_i ≥ 0), as we are interested in allocating mutualistic association efforts (see Nakazawa and Katayama, 2020 for stage-specific parasitism). We do not consider the situation where there is no relationship between the host and partner species (i.e., X_J = X_A = 0) because the situation is out of the scope. The partner species exhibits logistic growth in the absence of the host due to limited amounts of resources. Thus, the partner has the density-dependent death rate and its carrying capacity in the absence of the host is r_P/d_P. Likewise, juvenile and adult hosts also compete for limited resources, and thus they have density-dependent death rates d_ij (i, j = J or A). High values of d_ij indicate that the stage i has a strong negative effect on the stage j. It is natural to assume that the adult stage is more competitive than the juvenile stage (i.e., d_JA < d_ii < d_AJ). The default parameter values are r_i = 1, r_P = 0 (i.e., the mutualistic partner cannot persist without the host species), d_ii = d_P = 0.05, d_JA = 0.01, d_AJ = 0.1, and α_i = 1 (i = J, A).

FIGURE 1

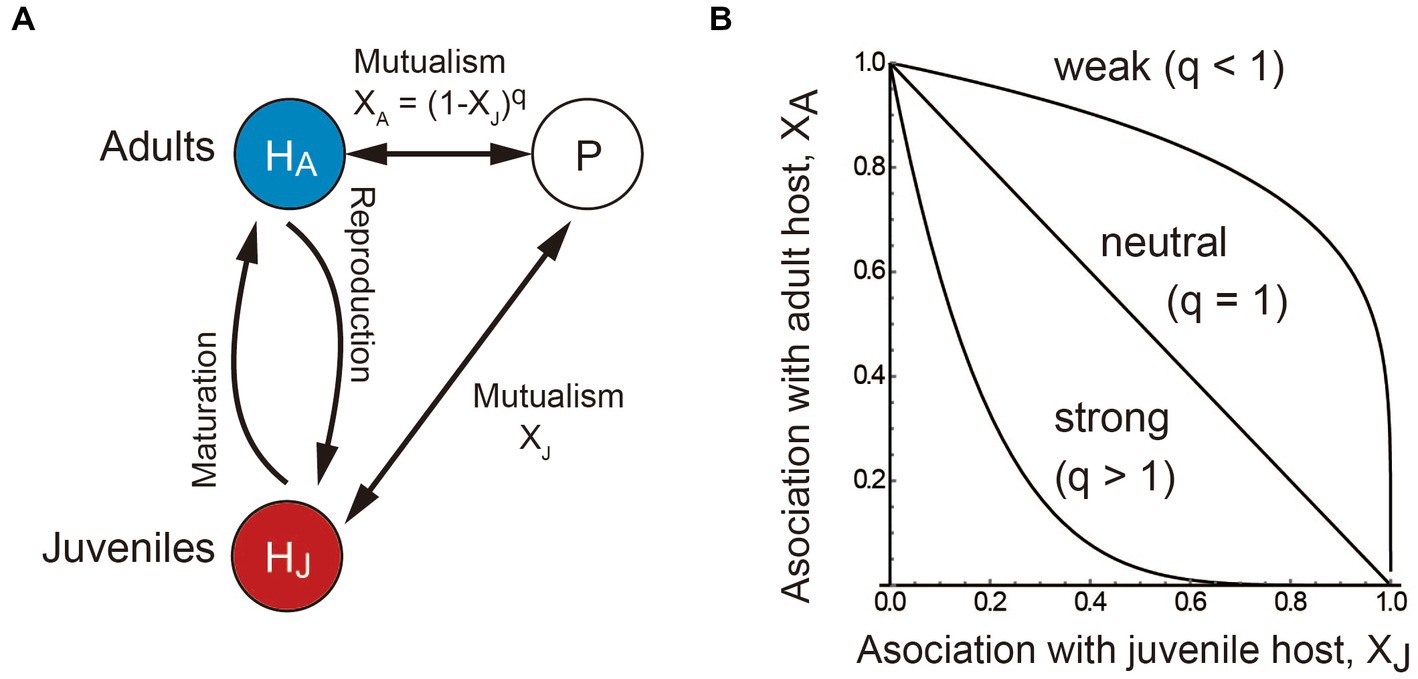
Figure 1. Conceptual illustration of the model. (A) The host species has a juvenile–adult stage structure (H_J and H_A) and the partner species P increases the maturation and reproduction rates of the host. (B) The adult-specific association effect X_A is a decreasing function of the juvenile-specific association effort X_J. The more the partner associates with the juvenile host, the weaker the association with the adult host. The parameter q determines the shape of the trade-off between stage-specific associations. The association trade-off is weak (concave) when q < 1, neutral (linear) when q = 1, and strong (convex) when q > 1. For presentation, q = 0.2 (concave), 1 (linear), and 5 (convex) in (B).

Next, we consider the evolutionary dynamics of the stage-specific association effort X_i based on the ecological model developed above. To obtain robust predictions on the optimal mutualistic association X_i^*, we use two analytical tools of evolutionary ecology, that can be applied along with population dynamics models: (a) quantitative genetic approach (Abrams, 2001; Yamamichi et al., 2019), and (b) evolutionary invasion analysis (Metz et al., 1992; Geritz et al., 1998). The two approaches differ mainly in their assumptions regarding the time scales of ecological processes and adaptive evolution as well as the possibility of evolutionary branching (Abrams, 2001; Nowak and Sigmund, 2004). The former approach considers that population dynamics and evolutionary dynamics occur in the same time scale where the stage-specific allocation X_i dynamically evolves with the host-partner population dynamics. Meanwhile, the latter approach generally considers that population dynamics is much faster than slow evolutionary dynamics. To further evaluate the robustness of predictions, we also perform sensitivity analysis by varying one parameter while fixing the others to the default values for both analytical approaches.

3. Results

3.1. Quantitative genetic approach

Another formula is added to the above ecological model to describe the evolutionary dynamics of the juvenile-specific association X_J:

$\frac{{\mathrm{dX}}_{\mathrm{J}}}{\mathrm{dt}}={\mathrm{wX}}_{\mathrm{J}}\left(1-{\mathrm{X}}_{\mathrm{J}}\right)\frac{\partial }{\partial {\mathrm{X}}_{\mathrm{J}}}\left(\frac{1}{\mathrm{P}}\frac{\mathrm{dP}}{\mathrm{dt}}\right)$

where the parameter w is the adaptation rate. X_J (1 − X_J) measures the additive genetic variance of juvenile-specific association X_J, as well as ensuring that the trait value is constrained between zero and one (Yamamichi et al., 2019). The equation intuitively means that the partner will increase juvenile-specific association X_J if it increases the fitness (i.e., the per-capita population growth rate). The initial population abundances are H_i (0) = P (0) = 1 and the initial trait value X_J (0) was set at random between zero and one. The simulation was run until t = 2 × 10⁴.

The numerical results showed that if the association trade-off is weak (q < 1), the partner tends to associate only with the juvenile host (i.e., X_J = 1) when the benefits of juvenile mutualism are relatively large (red region in Figure 2A). On the other hand, the partner tends to associate only with the adult host (i.e., X_J = 0) when the benefits of adult mutualism are relatively large (blue region in Figure 2A). We term the situation as juvenile-specialized (or adult-specialized) association. When the mutualistic benefits of both juvenile-specific and adult-specific associations are sufficiently large, the partner associates with both the juvenile and adult stages of the host (i.e., inter-stage partner sharing; green and yellow regions in Figure 2A). Figure 3A shows the convergent dynamics of X_J to the intermediate optima when the association trade-off is weak. If the association trade-off is neutral (q = 1), the parameter space for inter-stage partner sharing shrinks and juvenile-specialized (or adult specialized) association occur when it is relatively beneficial (Figure 2B). Note that the adult-specialized association can evolve (i.e., X_J = 0) even when the juvenile-specific association is more beneficial (B_PJ > B_PA). This would be because the partner can gain indirect mutualistic benefits by promoting adult reproduction. If the association trade-off is strong (q > 1), alternative stable states occur in which either juvenile-specialized or adult-specialized associations emerge depending on the initial trait value (mottled pattern in Figure 2C). There seems to be a tendency for juvenile-specific mutualism to evolve (X_J = 1) when it is relatively beneficial, and for adult-specific mutualism to evolve (X_J = 0) when it is relatively beneficial (Figure 2C). However, this is not always the case, as juvenile-specific mutualism can also evolve when adult-specific mutualism is relatively beneficial, and vice versa. This could be because the initial trait value X_J (0) is close to zero or one. Indeed, Figure 3B shows the divergent dynamics of X_J to zero or one depending on the initial trait value. The adaptation rate w does not affect the equilibrium state, although it affects the time it takes for the evolutionary dynamics to converge to the equilibrium (not shown). Sensitivity analysis confirmed that these results are generally robust to changes in the parameters (Supplementary Information A).

FIGURE 2

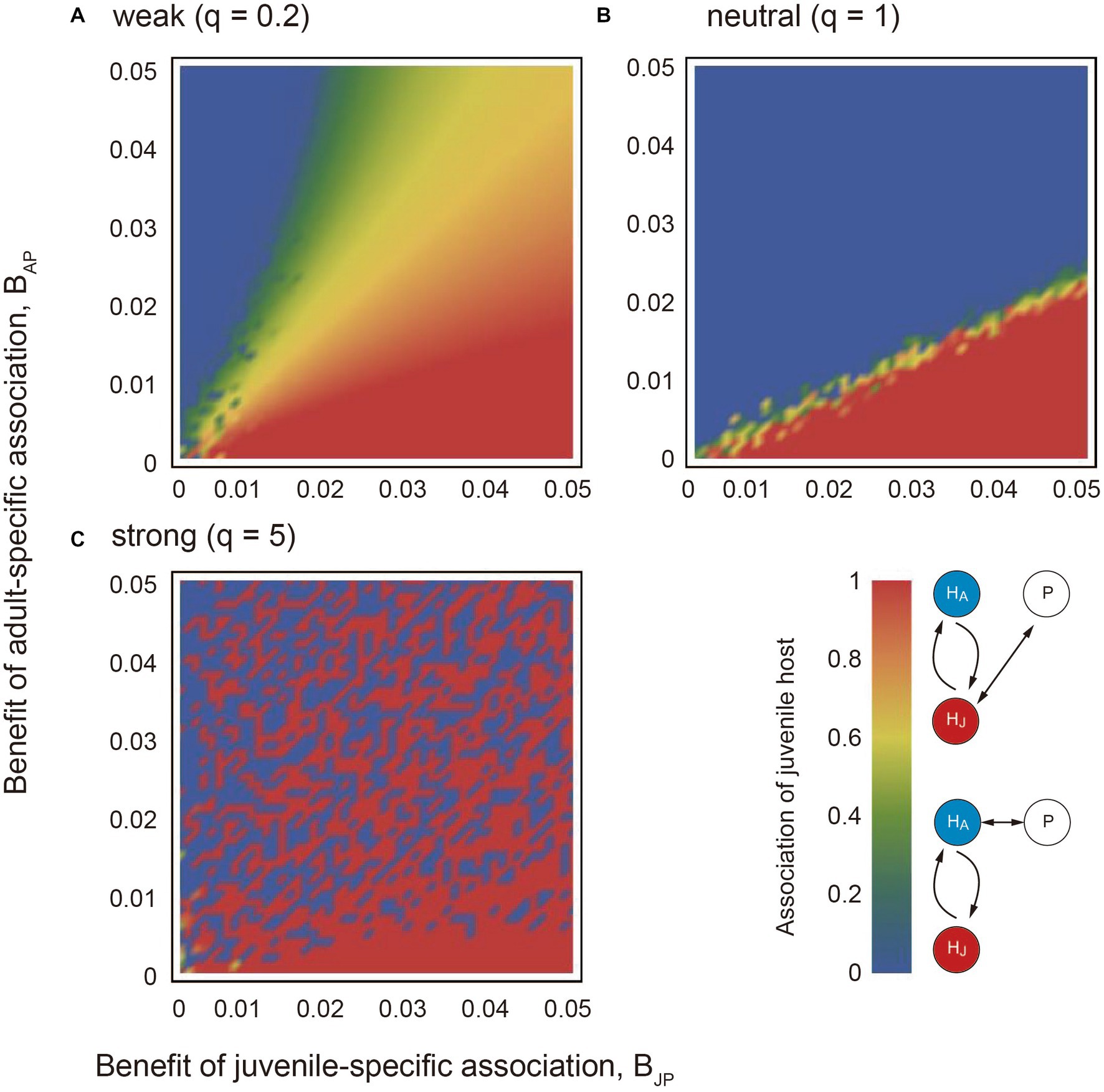
Figure 2. The results of applying the quantitative genetic approach to the model. The association trade-off is (A) weak (q = 0.2), (B) neutral (q = 1), and (C) strong (q = 5). In each panel, the x and y axes indicate the mutualistic benefit of juvenile-specific and adult-specific associations (B_PJ and B_PA), respectively. The red and blue colors indicate strong and weak associations with the juvenile host at the steady state, respectively. The adaptation rate w = 0.01. Other parameter values are described in the main text.

FIGURE 3

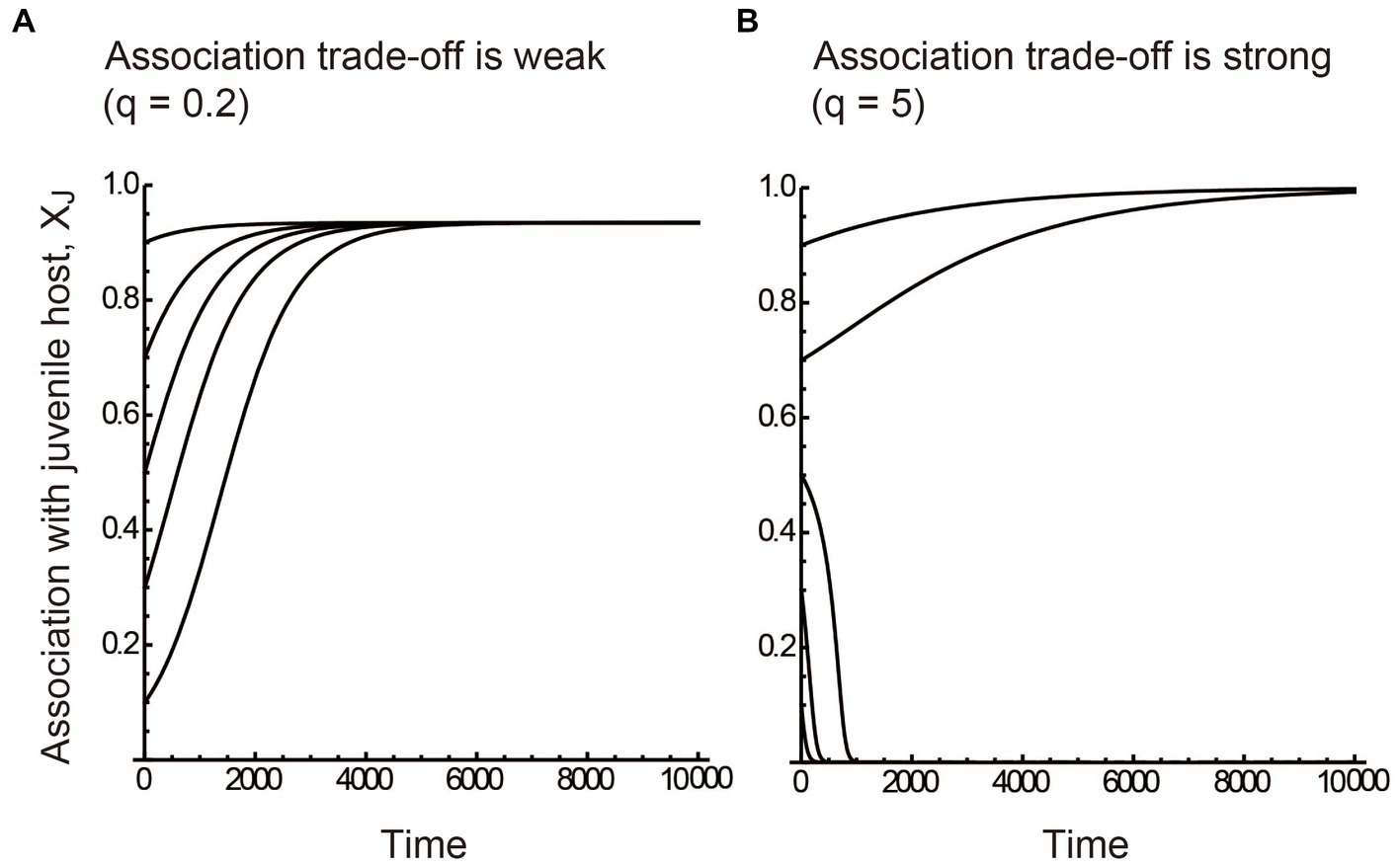
Figure 3. Evolutionary dynamics described by the quantitative genetics approach. (A) The juvenile-specific association X_J converges to the intermediate optima (i.e., inter-stage partner sharing) when the association trade-off is weak (q = 0.2). (B) X_J diverges to either zero (adult-specialized association) or one (juvenile-specialized association) depending on the initial trait value when the association trade-off is strong (q = 5). The benefits of stage-specific mutualisms are relatively large at (A) the juvenile stage (B_PJ = 0.04 and B_PA = 0.01) and (B) the adult stage (B_PJ = 0.01 and B_PA = 0.04). The five alternative dynamics in each panel were simulated using five initial trait values X_J (0) = 0.1, 0.3, 0.5, 0.7, and 0.9, respectively. The adaptation rate w = 0.01. Other parameter values are described in the main text.

3.2. Evolutionary invasion analysis

Next, we consider that the partner species has a resident (major) and mutant (rare) type, and their population dynamics are described separately. Thus, the original model is re-formulated to include four variables as follows:

$\begin{array}{c}\frac{{\mathrm{dH}}_{\mathrm{J}}}{\mathrm{dt}}=\left[{\mathrm{r}}_{\mathrm{A}}+{\mathrm{B}}_{\mathrm{AP}}\left({\mathrm{X}}_{\mathrm{A},\mathrm{r}}{\mathrm{P}}_{\mathrm{r}}+{\mathrm{X}}_{\mathrm{A},\mathrm{m}}{\mathrm{P}}_{\mathrm{m}}\right)\right]{\mathrm{H}}_{\mathrm{A}}\\ -\left[{\mathrm{r}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{JP}}\left({\mathrm{X}}_{\mathrm{J},\mathrm{r}}{\mathrm{P}}_{\mathrm{r}}+{\mathrm{X}}_{\mathrm{J},\mathrm{m}}{\mathrm{P}}_{\mathrm{m}}\right)\right]{\mathrm{H}}_{\mathrm{J}}\\ -\left({\mathrm{d}}_{\mathrm{JJ}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{d}}_{\mathrm{AJ}}{\mathrm{H}}_{\mathrm{A}}\right){\mathrm{H}}_{\mathrm{J}}\end{array}$

$\frac{{\mathrm{dH}}_{\mathrm{A}}}{\mathrm{dt}}=\left[{\mathrm{r}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{JP}}\left({\mathrm{X}}_{\mathrm{J},\mathrm{r}}{\mathrm{P}}_{\mathrm{r}}+{\mathrm{X}}_{\mathrm{J},\mathrm{m}}{\mathrm{P}}_{\mathrm{m}}\right)\right]{\mathrm{H}}_{\mathrm{J}}-\left({\mathrm{d}}_{\mathrm{JA}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{d}}_{\mathrm{AA}}{\mathrm{H}}_{\mathrm{A}}\right){\mathrm{H}}_{\mathrm{A}}$

$\frac{{\mathrm{dP}}_{\mathrm{r}}}{\mathrm{dt}}=\left[{\mathrm{r}}_{\mathrm{P}}+{\mathrm{B}}_{\mathrm{PJ}}{\mathrm{X}}_{\mathrm{J},\mathrm{r}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{PA}}{\mathrm{X}}_{\mathrm{A},\mathrm{r}}{\mathrm{H}}_{\mathrm{A}}-{\mathrm{d}}_{\mathrm{P}}\left({\mathrm{P}}_{\mathrm{r}}+{\mathrm{P}}_{\mathrm{m}}\right)\right]{\mathrm{P}}_{\mathrm{r}}$

$\frac{{\mathrm{dP}}_{\mathrm{m}}}{\mathrm{dt}}=\left[{\mathrm{r}}_{\mathrm{P}}+{\mathrm{B}}_{\mathrm{PJ}}{\mathrm{X}}_{\mathrm{J},\mathrm{m}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{PA}}{\mathrm{X}}_{\mathrm{A},\mathrm{m}}{\mathrm{H}}_{\mathrm{A}}-{\mathrm{d}}_{\mathrm{P}}\left({\mathrm{P}}_{\mathrm{r}}+{\mathrm{P}}_{\mathrm{m}}\right)\right]{\mathrm{P}}_{\mathrm{m}}$

where P_k is the abundance of the resident (k = r) and mutant (k = m) partners, respectively. They are different only in stage-specific association as X_A,k = (1 − X_J,k)^q. First, we simulate the model without the mutant until the dynamics reach the equilibrium (H_i = H_i^* and P_r = P_r^*). Thereafter, we identify the evolutionary stable strategy by assessing the potential for the mutant type to invade the resident population based on whether the per-capita population growth rate of the mutant type is positive at the resident equilibrium (Metz et al., 1992; Geritz et al., 1998):

${\frac{1}{{\mathrm{P}}_{\mathrm{m}}}\frac{{\mathrm{dP}}_{\mathrm{m}}}{\mathrm{dt}}|}_{{\mathrm{H}}_{\mathrm{i}}={\mathrm{H}}_{\mathrm{i}}^{\ast },{\mathrm{P}}_{\mathrm{r}}={\mathrm{P}}_{\mathrm{r}}^{\ast },{\mathrm{P}}_{\mathrm{m}}=0}>0$

We then summarized the outcome of intraspecific competition in so-called pairwise invasibility plots wherein whether the mutant type can invade the resident population or not is shown for different combinations of X_J,r and X_J,m values (Figure 4).

FIGURE 4

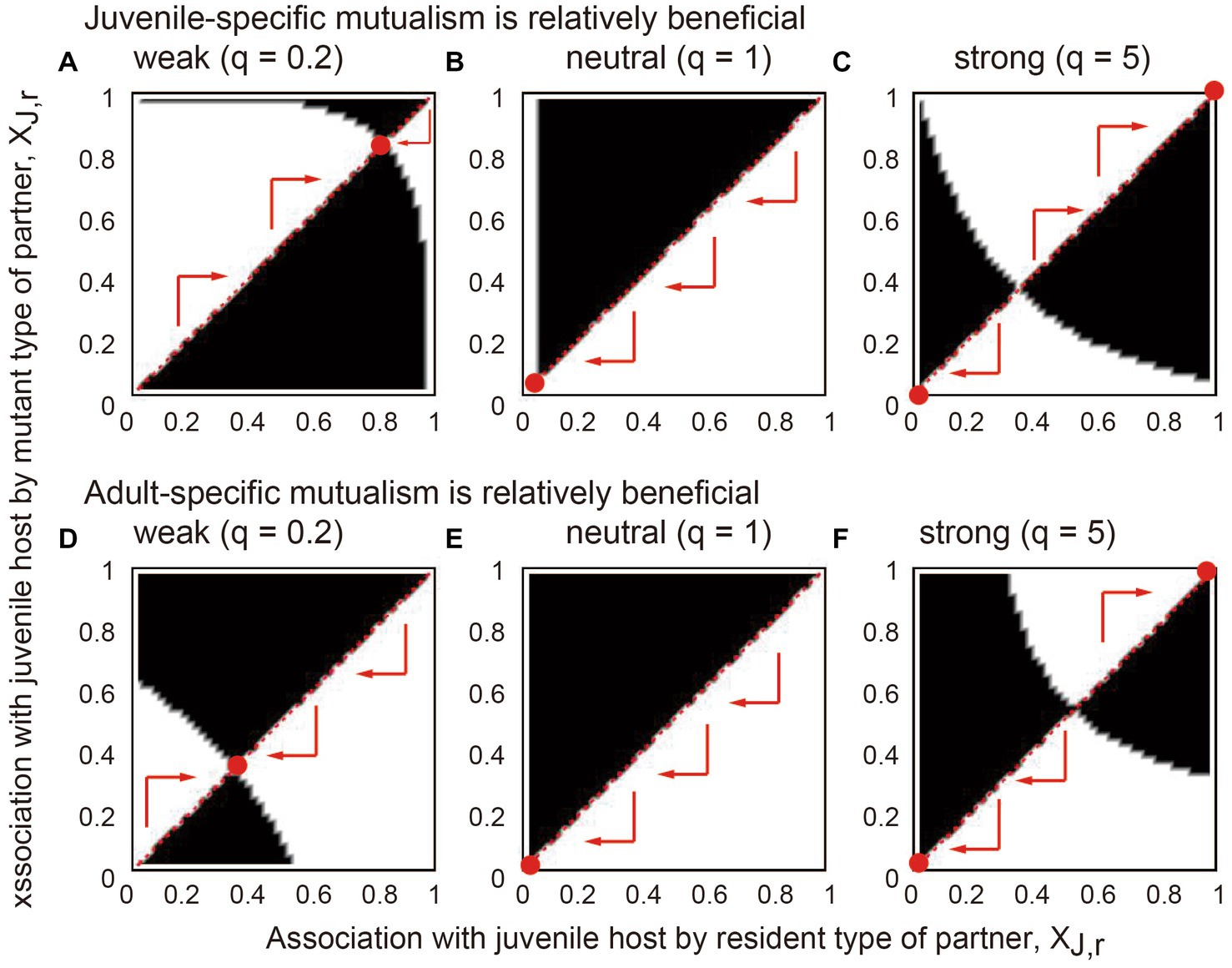
Figure 4. The results of applying evolutionary invasion analysis to the model. In each panel, the x and y axes indicate the juvenile-specific association of the resident and mutant partners (X_J,r and X_J,m), respectively. The white regions indicate the parameter space where the mutant can invade the resident equilibrium, and in the black regions, the invasion of the mutant is not possible. The arrows indicate possible evolutionary trajectories following competitive replacement. The red points are evolutionary and convergent stable strategies where any mutant type cannot invade. The benefits of stage-specific mutualisms are relatively large at (A–C) the juvenile stage (B_PJ = 0.04 and B_PA = 0.02) and (D–F) the adult stage (B_PJ = 0.02 and B_PA = 0.04). The association trade-off is (A,D) weak (q = 0.2), (B,E) neutral (q = 1), and (C,F) strong (q = 5). Other parameter values are described in the main text.

The results showed that if the association trade-off is weak (q < 1), inter-stage partner sharing occurs (Figures 4A,D). Meanwhile, the partner evolves a stronger association with the juvenile host when the juvenile-specific association is more beneficial (compare Figures 4A,D). If the association trade-off is neutral (q = 1), the adult-specialized association occurs (Figures 4B,E), although the evolutionary outcome is variable depending on the parameter values (Supplementary Information B). If the association trade-off is strong (q > 1), alternative stable states occur in which either the juvenile-specialized or adult-specialized association emerges depending on the initial trait value (Figures 4C,F). Furthermore, juvenile-specific mutualism is more likely to evolve, i.e., a divergent threshold becomes smaller when juvenile-specific mutualism is relatively beneficial (compare Figures 4C,F). Conversely, adult-specific mutualism is more likely to evolve when the benefits of adult mutualism are relatively large, resulting in a larger divergent threshold. Sensitivity analysis confirmed that these results are generally robust to changes in the parameters (Supplementary Information B).

4. Discussion

We showed that different forms of stage-structured mutualism can evolve between two species, such as juvenile-specialized association, adult-specialized association, and inter-stage partner sharing. Further, alternative stable states can also occur in which juvenile-specific or adult-specific association evolves depending on the initial trait value. These results suggest that pairwise interspecific mutualism can exhibit diverse patterns of relationships, which implies that we may overlook mutualistic (or neutral) interactions when looking at only certain life-history stages; therefore, the strength of mutualism may be over-or underestimated and the ecological dynamics can be inaccurately described unless life cycles of organisms are appropriately considered.

Our results are mainly threefold. Firstly, juvenile-specialized (or adult-specialized) association tends to evolve when it is relatively beneficial, irrespective of the shape of the association trade-off. Secondly, if the association trade-off is weak, the partner can associate with both the juvenile and adult stages of the host (i.e., inter-stage partner sharing) when the mutualistic benefits of both juvenile-and adult-specific associations are sufficiently large. Thirdly, when the association trade-off is strong, the partner evolves either juvenile-or adult-specialized association depending on the initial trait value. These results give some answers to the question of when the partner should allocate all association efforts only for the more beneficial stage (i.e., stage-specific association) or more evenly allocate association efforts for both stages depending on the relative benefits (i.e., inter-stage partner sharing).

We also emphasize that similar parameter conditions were identified for the structural diversity of stage-structured mutualism in the two analytical approaches; i.e., the quantitative genetics approach and evolutionary invasion analysis (Figures 2, 4). While this consistency suggests that our findings are highly robust, it implies that their different assumptions regarding the time scales of ecological processes and adaptive evolution would not matter to the evolution of stage-structured mutualism. Based on the results, we infer that the evolution of stage-structured mutualism could be simply understood without describing the ecological (population) dynamics. To discuss it, we apply the geometrical fitness set approach by Levins (1962). Here, suppose the following per-capita population growth rate (i.e., fitness) of the partner:

$\frac{1}{\mathrm{P}}\frac{\mathrm{dP}}{\mathrm{dt}}={\mathrm{r}}_{\mathrm{P}}+{\mathrm{B}}_{\mathrm{PJ}}{\mathrm{X}}_{\mathrm{J}}{\mathrm{H}}_{\mathrm{J}}+{\mathrm{B}}_{\mathrm{PA}}{\mathrm{X}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}-{\mathrm{d}}_{\mathrm{P}}\mathrm{P}$

We plotted different shapes of the association trade-off along with fitness contours on the two-dimensional plane of the stage-specific associations X_J and X_A (Figure 5), which graphically illustrate how the partner would evolve the stage-specific association X_i depending on the relative benefits of stage-specific mutualism B_Pi and the juvenile-adult stage distribution H_i. The results showed that inter-stage partner sharing occurs (i.e., X_J converge to the intermediate optima) when the association trade-off is weak while juvenile-specialized or adult-specialized association occurs (i.e., X_J diverges to either zero or one depending on the initial trait value) when the association trade-off is strong (Figure 5; see Rueffler et al., 2013 for similar examples). Further, the optimal X_J is relatively high for weak association trade-offs or X_J is likely to converge to one (i.e., a divergent threshold is relatively small) for strong association trade-offs when the juvenile host is more abundant (e.g., compare Figures 5A,C) or when the juvenile-specific mutualism is more beneficial (e.g., compare Figures 5A,D). These patterns are generally consistent with the results of the quantitative genetics approach (Figure 2) and evolutionary invasion analysis (Figure 4).

FIGURE 5

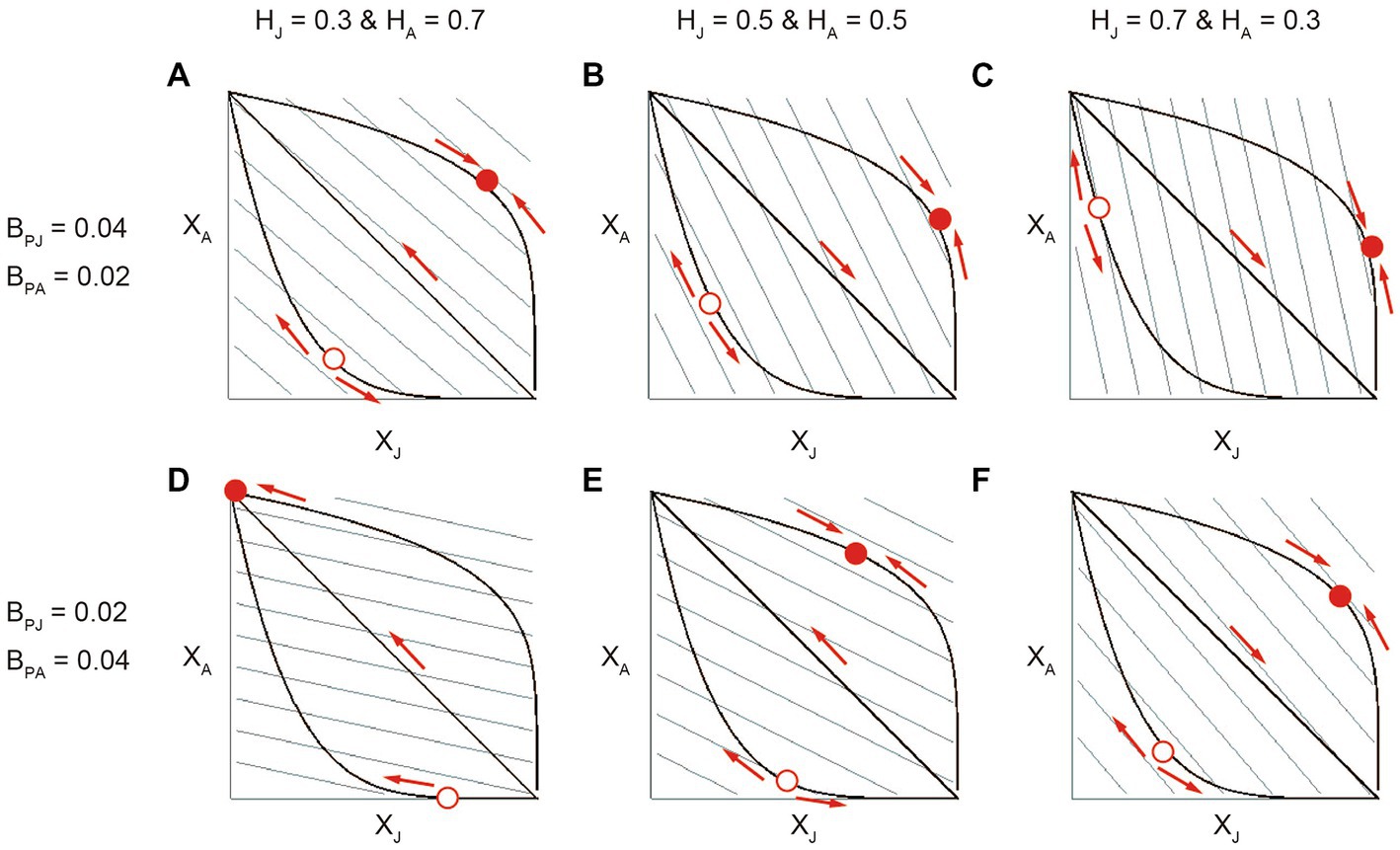
Figure 5. The results of applying the geometrical fitness set approach to the model. In each panel, thick lines correspond to weak, neutral and strong association trade-offs between X_J and X_A. For presentation, q = 0.2 (concave), 1 (linear), and 5 (convex). The grey parallel lines represent contour lines of the fixed fitness landscape, which increases with both X_J and X_A. The evolution occurs so as to increase the fitness along the trade-off curve and changes the combination of trait values as indicated by the arrows. The sold and open circles are fitness maxima and minima, respectively. The mutualistic benefits of stage-specific associations are (B_PJ, B_PA) = (A–C; 0.04, 0.02) and (D-F; 0.02, 0.04). The abundances of the juvenile and adult host are (H_J, H_A) = (A,D; 0.3, 0.7), (B,E; 0.5, 0.5), and (C,F; 0.7, 0.3).

Our results illustrate the importance of quantifying intraspecific (dis)similarity of mutualistic niches (Peay, 2016) between different life-history stages since the functional form of the trade-off between juvenile-and adult-specialized associations can critically affect the evolutionary dynamics of stage-structured mutualism. Nutritional mutualism between plants and microbes provides a suitable system for empirically testing our predictions (Chamberlain et al., 2014). In particular, woody and herbaceous plants may be compared, as their adult body sizes are completely different implying that inter-stage differences in nutritional requirements would be qualitatively different and more apparent in woody plants (Meinzer et al., 2011; Mediavilla et al., 2014). Our models predicted that inter-stage partner sharing or stage-specialized association occurs depending on the shape of the association trade-off. Specifically, if the association trade-off is relatively weak, inter-stage partner sharing would be likely to occur because the partner can readily meet requirements of both stages. On the other hand, the association trade-off is strong, stage-specialized association would be more likely to occur. Based on the prediction, we hypothesize that if the adult stage of woody plants competes with their juvenile (e.g., germination and seedling) stage relatively weakly for nutrients, woody plants may have similar mutualistic microbes across their life-history stages. On the other hand, if the adult stage of herbaceous plants competes with their juvenile stage relatively strongly, herbaceous plants may have dissimilar mutualistic microbes across their life-history stages. Note that this hypothesis was made from the viewpoint of microbial partner choice. If plants choose microbial partners (Werner and Kiers, 2015), woody plants may exhibit more pronounced ontogenetic shifts in microbial compositions than herbaceous plants due to distinct body sizes and nutrient requirements across stages. Apparently supporting our predictions, many studies have reported dynamic changes in microbial composition during the development of herbaceous plants (Baudoin et al., 2002; Mougel et al., 2006; Houlden et al., 2008; Micallef et al., 2009; Chaparro et al., 2014; Sugiyama et al., 2014), while the evidence is still limited for woody plants (Husband et al., 2002; Oono et al., 2015). Meta-analytical approaches are required to explicitly test it by integrating both woody and herbaceous plants. At the same time, the present pairwise mutualism model needs to be extended to consider multiple mutualistic partners and ontogenetic partner shifts (see below for details).

Experimental approaches are also warranted to mechanistically validate our model assumptions and predictions. We are particularly interested in quantifying the association trade-off within a partner species (or inter-stage competition for mutualistic niches within a host species). To do it, we may compare the relative microbial biomass at plant roots when the plants are inoculated with nutritional microbes in the presence and absence of a neighboring plant with different life-history stages. If the microbial biomass is reduced in the presence of a neighboring plant, it suggests the existence of the association trade-off. Further, the reduction of the microbial biomass may depend on the life-history stage of the neighboring plant. It is also necessary to quantify the relative biomass of microbial partners across different life-history stages of a plant and assess stage-specific benefits to the microbes. Together, we can test whether the stage-specific association or inter-stage partner sharing is developed depending on the association trade-off. Not only plant–microbe nutritional mutualism but also other mutualisms (see Introduction) would also be worthwhile to perform such experiments.

We also encourage the development of more complex models in future studies. We envision three approaches. First, while we have explored the minimum situation where the host has a two life-history stages following previous studies on stage-structured mutualism (Ke and Nakazawa, 2018; Nakazawa, 2020; Nakazawa and Katayama, 2020), it may be more appropriate for some species to consider more than two stages or continuous size structure by employing, for example, integral projection models (Ellner et al., 2016) or partial differential equations (Tuljapurkar and Caswell, 1997). Second, the present pairwise model needs to be extended to include more than two mutualistic partners (Nakazawa et al., in preparation). This is particularly important, because the optimal effort allocation of a mutualistic partner can be affected by competition with other mutualistic partners (i.e., inter-partner competition), and also because other mutualistic partners affect the host performance, which in turn may mediate the optimal effort allocation of the focal partner (i.e., indirect effects through the host’s ontogeny). Finally, the host species may also have the capability of choosing more beneficial partners in the presence of multiple mutualistic partners (Kiers et al., 2011; Heath and Stinchcombe, 2014; Fields and Friman, 2022; i.e., coevolution). From a theoretical viewpoint, it is inappropriate to apply the quantitative genetics approach to the stage-structured host species because stage-specific adaptation does not reflect lifetime fitness in stage-structured population, whereas it is technically difficult to apply evolutionary invasion analysis to the coevolutionary trait dynamics of multiple partners. Therefore, we propose the application of the quantitative genetic approach and evolutionary invasion analysis in non-structured partners and stage-structured host species, respectively, with the assumption that the evolutionary dynamics of the host are much slower than the host-partner population dynamics and the evolutionary dynamics of the partners. Along with well-designed experiments (see above), such theoretical efforts will contribute to a better understanding of the development and maintenance of complex mutualistic networks mediated by the ontogenetic development of organisms and their stage-structured interactions.

In conclusion, we analyzed the evolutionary model of stage-structured mutualism. The model presented testable hypotheses regarding the context dependence of stage-structured mutualism, which highlights the primary role of the association trade-off (or inter-stage competition for mutualistic niches within the host). In addition, this study provides a conceptual basis for more complex situations, which may consider multiple life-history stages, multiple mutualistic partners, and host–partner coevolution. Further research efforts are needed in both theoretical and empirical approaches to better understand ecological and evolutionary aspects of stage-structured mutualism.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TN conceived the idea, analyzed the models, and wrote the draft. NK, AY, and SU helped finalizing the manuscript. MY supervised the study and finalized the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by National Science and Technology Council grant number (MOST 110-2628-B-006-024), Taiwan.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1138138/full#supplementary-material

References

Abrams, P. A. (2001). Modelling the adaptive dynamics of traits involved in inter-and intraspecific interactions: an assessment of three methods. Ecol. Lett. 4, 166–175. doi: 10.1046/j.1461-0248.2001.00199.x

CrossRef Full Text | Google Scholar

Albrecht, J., Gertrud Berens, D., Jaroszewicz, B., Selva, N., Brandl, R., and Farwig, N. (2014). Correlated loss of ecosystem services in coupled mutualistic networks. Nat. Commun. 5:3810. doi: 10.1038/ncomms4810

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, H., Muhammad, A., Sanda, N. B., Huang, Y., and Hou, Y. (2019). Pyrosequencing uncovers a shift in bacterial communities across life stages of Octodonta nipae (Coleoptera: Chrysomelidae). Front. Microbiol. 10:466. doi: 10.3389/fmicb.2019.00466

PubMed Abstract | CrossRef Full Text | Google Scholar

Bascompte, J., and Jordano, P. (2014). Mutualistic networks. Princeton, USA: Princeton Univ. Press.

Google Scholar

Baudoin, E., Benizri, E., and Guckert, A. (2002). Impact of growth stage on the bacterial community structure along maize roots, as determined by metabolic and genetic fingerprinting. Appl. Soil Ecol. 19, 135–145. doi: 10.1016/S0929-1393(01)00185-8

CrossRef Full Text | Google Scholar

Biedermann, P. H., and Kaltenpoth, M. (2014). New synthesis: the chemistry of partner choice in insect-microbe mutualisms. J. Chem. Ecol. 40:99. doi: 10.1007/s10886-014-0382-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bronstein, J. L. (2015). Mutualism. Oxford, UK: Oxford Univ. Press.

Google Scholar

Bshary, R., and Grutter, A. S. (2002). Experimental evidence that partner choice is a driving force in the payoff distribution among cooperators or mutualists: the cleaner fish case. Ecol. Lett. 5, 130–136. doi: 10.1046/j.1461-0248.2002.00295.x

CrossRef Full Text | Google Scholar

Chamberlain, S. A., Bronstein, J. L., and Rudgers, J. A. (2014). How context dependent are species interactions? Ecol. Lett. 17, 881–890. doi: 10.1111/ele.12279

CrossRef Full Text | Google Scholar

Chaparro, J. M., Badri, D. V., and Vivanco, J. M. (2014). Rhizosphere microbiome assemblage is affected by plant development. ISME J. 8, 790–803. doi: 10.1038/ismej.2013.196

PubMed Abstract | CrossRef Full Text | Google Scholar

Chomicki, G., Staedler, Y. M., Schönenberger, J., and Renner, S. S. (2016). Partner choice through concealed floral sugar rewards evolved with the specialization of ant–plant mutualisms. New Phytol. 211, 1358–1370. doi: 10.1111/nph.13990

PubMed Abstract | CrossRef Full Text | Google Scholar

Dillon, R. J., Webster, G., Weightman, A. J., and Keith Charnley, A. (2010). Diversity of gut microbiota increases with aging and starvation in the desert locust. Antonie Van Leeuwenhoek 97, 69–77. doi: 10.1007/s10482-009-9389-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Duguma, D., Hall, M. W., Rugman-Jones, P., Stouthamer, R., Terenius, O., Neufeld, J. D., et al. (2015). Developmental succession of the microbiome of Culex mosquitoes. BMC Microbiol. 15:140. doi: 10.1186/s12866-015-0475-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellner, S. P., Childs, D. Z., and Rees, M. (2016). Data-driven modelling of structured populations. Switzerland: Springer.

Google Scholar

Fields, B., and Friman, V. P. (2022). Microbial eco-evolutionary dynamics in the plant rhizosphere. Curr. Opin. Microbiol. 68:102153. doi: 10.1016/j.mib.2022.102153

PubMed Abstract | CrossRef Full Text | Google Scholar

Geritz, S. A., Kisdi, E.´., Mesze´NA, G., and Metz, J. A. J. (1998). Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 12, 35–57. doi: 10.1023/A:1006554906681

CrossRef Full Text | Google Scholar

Gianinazzi, S., Gollotte, A., Binet, M. N., van Tuinen, D., Redecker, D., and Wipf, D. (2010). Agroecology: the key role of arbuscular mycorrhizas in ecosystem services. Mycorrhiza 20, 519–530. doi: 10.1007/s00572-010-0333-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Heath, K. D., and Stinchcombe, J. R. (2014). Explaining mutualism variation: a new evolutionary paradox? Evolution 68, 309–317. doi: 10.1111/evo.12292

PubMed Abstract | CrossRef Full Text | Google Scholar

Heil, M. (2015). Extrafloral nectar at the plant–insect interface: a spotlight on chemical ecology, phenotypic plasticity and food webs. Annu. Rev. Entomol. 60, 213–232. doi: 10.1146/annurev-ento-010814-020753

PubMed Abstract | CrossRef Full Text | Google Scholar

Heil, M., and McKey, D. (2003). Protective ant–plant interactions as model systems in ecological and evolutionary research. Annu. Rev. Ecol. Evol. Syst. 34, 425–553. doi: 10.1146/annurev.ecolsys.34.011802.132410

CrossRef Full Text | Google Scholar

Horton, T. R. (2015). Mycorrhizal networks. Dordrecht, the Netherlands: Springer.

Google Scholar

Houlden, A., Timms-Wilson, T. M., Day, M. J., and Bailey, M. J. (2008). Influence of plant developmental stage on microbial community structure and activity in the rhizosphere of three field crops. FEMS Microbiol. Ecol. 65, 193–201. doi: 10.1111/j.1574-6941.2008.00535.x

CrossRef Full Text | Google Scholar

Husband, R., Herre, E. A., Turner, S. L., Gallery, R., and Young, J. P. W. (2002). Molecular diversity of arbuscular mycorrhizal fungi and patterns of host association over time and space in a tropical forest. Mol. Ecol. 11, 2669–2678. doi: 10.1046/j.1365-294X.2002.01647.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, P. R., and Rolff, J. (2015). Host and symbiont jointly control gut microbiota during complete metamorphosis. PLoS Pathog. 11:e1005246. doi: 10.1371/journal.ppat.1005246

PubMed Abstract | CrossRef Full Text | Google Scholar

Ke, P. J., and Nakazawa, T. (2018). Ontogenetic antagonism–mutualism coupling: perspectives on resilience of stage-structured communities. Oikos 127, 353–363. doi: 10.1111/oik.04702

CrossRef Full Text | Google Scholar

Kiers, E. T., Duhamel, M., Beesetty, Y., Mensah, J. A., Franken, O., Verbruggen, E., et al. (2011). Reciprocal rewards stabilize cooperation in the mycorrhizal symbiosis. Science 333, 880–882. doi: 10.1126/science.1208473

PubMed Abstract | CrossRef Full Text | Google Scholar

Koga, R., Tsuchida, T., and Fukatsu, T. (2003). Changing partners in an obligate symbiosis: a facultative endosymbiont can compensate for loss of the essential endosymbiont Buchnera in an aphid. Proc. R. Soc. B 270, 2543–2550. doi: 10.1098/rspb.2003.2537

PubMed Abstract | CrossRef Full Text | Google Scholar

Levins, R. (1962). Theory of fitness in a heterogeneous environment. I. the fitness set and adaptive function. Am. Nat. 96, 361–373. doi: 10.1086/282245

CrossRef Full Text | Google Scholar

Mediavilla, S., García-Iglesias, J., González-Zurdo, P., and Escudero, A. (2014). Nitrogen resorption efficiency in mature trees and seedlings of four tree species co-occurring in a Mediterranean environment. Plant Soil 385, 205–215. doi: 10.1007/s11104-014-2230-6

CrossRef Full Text | Google Scholar

Meinzer, F. C., Lachenbruch, B., and Dawson, T. E. (2011). Size-and age-related changes in tree structure and function. Dordrecht, the Netherlands: Springer.

Google Scholar

Metz, J. A., Nisbet, R. M., and Geritz, S. A. (1992). How should we define ‘fitness’ for general ecological scenarios? Trends Ecol. Evol. 7, 198–202. doi: 10.1016/0169-5347(92)90073-K

PubMed Abstract | CrossRef Full Text | Google Scholar

Micallef, S. A., Channer, S., Shiaris, M. P., and Colón-Carmona, A. (2009). Plant age and genotype impact the progression of bacterial community succession in the Arabidopsis rhizosphere. Plant Signal. Behav. 4, 777–780. doi: 10.4161/psb.4.8.9229

PubMed Abstract | CrossRef Full Text | Google Scholar

Mougel, C., Offre, P., Ranjard, L., Corberand, T., Gamalero, E., Robin, C., et al. (2006). Dynamic of the genetic structure of bacterial and fungal communities at different developmental stages of Medicago truncatula Gaertn. cv. Jemalong line J5. New Phytol. 170, 165–175. doi: 10.1111/j.1469-8137.2006.01650.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakazawa, T. (2020). A perspective on stage-structured mutualism and its community consequences. Oikos 129, 297–310. doi: 10.1111/oik.06653

CrossRef Full Text | Google Scholar

Nakazawa, T., and Katayama, N. (2020). Stage-specific parasitism by a mutualistic partner can increase the host abundance. Front. Ecol. Evol. 8:602675. doi: 10.3389/fevo.2020.602675

CrossRef Full Text | Google Scholar

Nowak, M. A., and Sigmund, K. (2004). Evolutionary dynamics of biological games. Science 303, 793–799. doi: 10.1126/science.1093411

CrossRef Full Text | Google Scholar

Oono, R., Lefèvre, E., Simha, A., and Lutzoni, F. (2015). A comparison of the community diversity of foliar fungal endophytes between seedling and adult loblolly pines (Pinus taeda). Fungal Biol. 119, 917–928. doi: 10.1016/j.funbio.2015.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Palmer, T. M., Doak, D. F., Stanton, M. L., Bronstein, J. L., Kiers, E. T., Young, T. P., et al. (2010). The synergy of multiple partners, including freeloaders, increases host fitness in a multispecies mutualism. Proc. Natl. Acad. Sci. U. S. A. 107, 17234–17239. doi: 10.1073/pnas.1006872107

PubMed Abstract | CrossRef Full Text | Google Scholar

Peay, K. G. (2016). The mutualistic niche: mycorrhizal symbiosis and community dynamics. Annu. Rev. Ecol. Evol. Syst. 47, 143–164. doi: 10.1146/annurev-ecolsys-121415-032100

CrossRef Full Text | Google Scholar

Quimbayo, J. P., Cantor, M., Dias, M. S., Grutter, A. S., Gingins, S., Becker, J. H. A., et al. (2018). The global structure of marine cleaning mutualistic networks. Glob. Ecol. Biogeogr. 27, 1238–1250. doi: 10.1111/geb.12780

CrossRef Full Text | Google Scholar

Quintero, C., Barton, K. E., and Boege, K. (2013). The ontogeny of plant indirect defenses. Perspect. Plant Ecol. Evol. Syst. 15, 245–254. doi: 10.1016/j.ppees.2013.08.003

CrossRef Full Text | Google Scholar

Rueffler, C., Metz, J. A. J., and van Dooren, T. J. M. (2013). What life cycle graphs can tell about the evolution of life histories. J. Math. Biol. 66, 225–279. doi: 10.1007/s00285-012-0509-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shukla, S. P., Sanders, J. G., Byrne, M. J., and Pierce, N. E. (2016). The gut microbiota of dung beetles correspond to dietary specializations of adults and larvae. Mol. Ecol. 25, 6092–6106. doi: 10.1111/mec.13901

PubMed Abstract | CrossRef Full Text | Google Scholar

Simms, E. L., and Taylor, D. L. (2002). Partner choice in nitrogen-fixation mutualisms of legumes and rhizobia. Integr. Comp. Biol. 42, 369–380. doi: 10.1093/icb/42.2.369

PubMed Abstract | CrossRef Full Text | Google Scholar

Skelton, J., Creed, R. P., and Brown, B. L. (2014). Ontogenetic shift in host tolerance controls initiation of a cleaning symbiosis. Oikos 123, 677–686. doi: 10.1111/j.1600-0706.2013.00963.x

CrossRef Full Text | Google Scholar

Skelton, J., Doak, S., Leonard, M., Creed, R. P., and Brown, B. L. (2016). The rules for symbiont community assembly change along a mutualism–parasitism continuum. J. Anim. Ecol. 85, 843–853. doi: 10.1111/1365-2656.12498

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoll, S., Feldhaar, H., Fraunholz, M. J., and Gross, R. (2010). Bacteriocyte dynamics during development of a holometabolous insect, the carpenter ant Camponotus floridanus. BMC Microbiol. 10:308. doi: 10.1186/1471-2180-10-308

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugiyama, A., Ueda, Y., Zushi, T., Takase, H., and Yazaki, K. (2014). Changes in the bacterial community of soybean rhizospheres during growth in the field. PLoS One 9:e100709. doi: 10.1371/journal.pone.0100709

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, M. J., Creed, R. P., Skelton, J., and Brown, B. L. (2016). Ontogenetic shifts in a freshwater cleaning symbiosis: consequences for hosts and their symbionts. Ecology 97, 1507–1517. doi: 10.1890/15-1443.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Tuljapurkar, S., and Caswell, H. (1997). Structured-population models in marine, terrestrial, and freshwater systems. Chapman and Hall, New York, USA: Springer.

Google Scholar

Vaughan, D. B., Grutter, A. S., Costello, M. J., and Hutson, K. S. (2017). Cleaner fishes and shrimp diversity and a re-evaluation of cleaning symbioses. Fish Fish. 18, 698–716. doi: 10.1111/faf.12198

CrossRef Full Text | Google Scholar

Werner, G. D., and Kiers, E. T. (2015). Partner selection in the mycorrhizal mutualism. New Phytol. 205, 1437–1442. doi: 10.1111/nph.13113

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamamichi, M., Klauschies, T., Miner, B. E., and van Velzen, E. (2019). Modelling inducible defences in predator–prey interactions: assumptions and dynamical consequences of three distinct approaches. Ecol. Lett. 22, 390–404. doi: 10.1111/ele.13183

PubMed Abstract | CrossRef Full Text | Google Scholar

Younginger, B. S., and Friesen, M. L. (2019). Connecting signals and benefits through partner choice in plant–microbe interactions. FEMS Microbiol. Lett. 366:fnz217. doi: 10.1093/femsle/fnz217

PubMed Abstract | CrossRef Full Text | Google Scholar