Kin selection in interactions between gametes: Gamete competition, gamete limitation, and sex allocation

Kin selection on one hand, and gamete interactions in post-ejaculatory sexual selection on the other are two major research themes that have risen to prominence over the past half century and have simultaneously developed into central fields of research in evolutionary biology. There is a natural connection between the two: when gametes interact with each other, very commonly many of them originate from the same parent and are thus siblings. For example, sperm competition will almost always involve competition between sibling gametes even if the interacting parents are not related to each other. If parents are related to each other, the relatedness between gametes increases further. Here we discuss the relation between kin selection on one hand, and gamete competition, gamete limitation, local gamete competition, and the evolution of sex allocation on the other. To illustrate these topics, we present a novel model on sex allocation in simultaneous hermaphrodites under sperm limitation and limited, costly dispersal. We find that sperm limitation can significantly increase allocation into male function, but limited dispersal (and thus increased relatedness) does not alter sex allocation regardless of the presence of sperm limitation.

1. Introduction

The 1960s and 1970s saw the emergence of two research topics within evolutionary biology that could be described as revolutions. Kin selection provided an explanation for the evolution of altruistic traits and more generally for the evolution of social behavior (Hamilton, 1963, 1964a,b). Meanwhile, post-copulatory sexual selection extended the scope of sexual selection from Darwin’s view of pre-copulatory sexual selection (Darwin, 1871) to selection taking place after copulation, or more generally, after ejaculation, with consequences that rival those of pre-copulatory sexual selection (Parker, 2020). A key form of post-ejaculatory sexual selection is sperm competition (Parker, 1970), with far-reaching consequences for the evolution of both gametic and organismal traits (Parker, 2020). Kin selection and sperm competition have both since become central research areas within evolutionary biology (Gardner et al., 2011; Lehtonen, 2020a; Parker, 2020). Whilst the intersection of sexual selection, sexual conflict, and kin selection has been the focus of considerable theoretical attention in recent years (e.g., Rankin, 2011; Wild et al., 2011; Faria et al., 2015, 2020), there has been relatively little theoretical work focusing explicitly on the intersection of sperm competition and kin selection. In this article, we discuss ways in which the two fields intersect, and how sperm competition, as well as the related topics of local sperm competition, sperm limitation, and sex allocation can be viewed from a kin selection perspective. We focus on an overview of these broad themes, taking a theoretical evolutionary ecology perspective (for a detailed discussion of ‘sperm sociality’ (see, e.g., Pizzari and Foster, 2008; Higginson and Pitnick, 2011). We then derive a novel model of sex allocation in simultaneous hermaphrodites that makes use of and illuminates all these topics.

2. Why is kin selection relevant in models of sperm competition? Sperm relatedness, and the question of control

In kin selection theory, fitness effects on genetic relatives are explicitly accounted for: individuals acting on their relatives indirectly affect the propagation of copies of their own genes (Hamilton, 1964a). An individual can increase its inclusive fitness by increasing either its direct fitness effect by its own reproductive success or its indirect fitness by increasing the reproductive success of its genetic relatives (Hamilton, 1964a). A central aspect of kin selection theory is the relatedness coefficient that measuress the relative quality of individuals as propagators of the focal individual’s genes. When related individuals interact, the evolution of altruistic traits can be promoted, and the evolution of selfish traits can be restricted to the extent that it maximises the overall propagation of the focal individual’s genes into future generations, via its own offspring (direct fitness) as well as those of other, related individuals (indirect fitness).

Considering relatedness from the gametic perspective, Trivers expressed the question: ‘If close degrees of relatedness predispose individuals to altruism, why not search for such examples in sex cells, specifically sperm?’ (Trivers, 1985), justifying the question with the fact that sperm from a single male are related to each other by a relatedness coefficient of ½ (under outbreeding). This quote illustrates the reason why kin selection is relevant and useful in thinking about sperm competition. Kin selection is important in interactions between organisms when related individuals, such as siblings interact. By similar logic, kin selection is relevant in interactions between male gametes even when the sperm descend from the same male. Therefore, as the quote by Trivers suggests, in competition between gametes such kin interactions are almost inevitable. From such considerations follows our central message: if we shift our perspective to gametes as analogues of interacting individuals, sperm competition models can typically be interpreted as kin selection models. Furthermore, a kin selection perspective can bring with it a unified structure across models that is readily extendable to situations where competing gametes are related beyond a simple sibling relationship. An example of this kind of scenario is the sex allocation model we present in this paper, where relatedness between competing gametes depends on the rate and cost of dispersal in the population.

Trivers’ quote above seems to attribute control of the sperm phenotype to the haploid genotype. The extent of haploid control in gametes is an active area of ongoing research, and the view that haploid transcription is insignificant in animals has in recent years been challenged and at least partially overturned (Immler, 2019). However, current evidence still shows that haploid expression is much more extensive in plants than it is in animals (Immler, 2019) and the prevailing view seems to be that sperm form and function is mainly under diploid control (e.g., Higginson and Pitnick, 2011). Thus, whilst its importance remains debated, the evidence is clear that haploid gene expression does exist and that there is a continuum of expression levels.

The theoretical predictions of sperm competition theory depend crucially on whether the evolution of sperm behavior is controlled completely by the male (diploid control: Parker, 1993) or by the male and the sperm, the sperm having sufficiently strong haploid gene expression. Haploid control (sperm phenotype driven by the spermatozoon itself) has been modelled by Parker and Begon (1993). Under haploid control, there is potential for conflict between the evolutionary interests of the parent and gamete, because there is competition both within and between ejaculates, whilst under diploid (parental) control there is competition only between ejaculates from different males. The magnitude of this conflict decreases as the magnitude of inter-ejaculate competition increases (Parker and Begon, 1993). Typically, the term ‘sperm competition’ refers to inter-ejaculate competition, and this default meaning is advocated by Parker and Begon (1993), whilst ‘inter-ejaculate’ and ‘intra-ejaculate’ sperm competition can be used where necessary to differentiate evolution under haploid expressed sperm competition.

This can also be seen from a kin selection perspective: the appropriate kin selection relatedness coefficient depends on the ‘control individual’ (Taylor, 1988a). If control lies with the gamete (haploid control), then the coefficient of ½ between sibling gametes in Trivers’ quote is correct: from a focal gamete’s perspective it measures how likely a sibling gamete is to transmit a copy of the same allele as the focal does, and under outbreeding this probability is ½. It is essentially a measure of the similarity of the sibling gamete to the focal gamete. However, if the parent has control, the relevant relatedness coefficient is instead a measure of the relative similarity of the two gametes to the control individual (Taylor, 1988a), and this relatedness coefficient equals 1: from the parent’s perspective, one of its own gametes is not any better than its sibling as a propagator of genes. Therefore, sperm cells should be predisposed to altruism as Trivers suggests, but under the typical assumption of diploid control this is due to a relatedness coefficient of 1, rather than a relatedness coefficient ½. We should therefore be careful in directly comparing the evolution of cooperation between gametes to, e.g., that between siblings. Pizzari and Foster (2008) remark that if only one male has mated with a female, from the perspective of the diploid genome of the male parent all sperm competing for fertilisation are equally valuable, whilst different sperm haplotypes from the same male are in evolutionary conflict with each other. As noted above, under haploid control, the conflict between the evolutionary interests of the parent and gamete decreases as inter-ejaculate sperm competition increases (Parker and Begon, 1993). A kin selection interpretation of this effect is that as the number of individuals contributing to sperm competition increases, the relatedness of a focal spermatozoon to a random competitor spermatozoon decreases, regardless of whether control lies with the parent or gamete: the fraction of unrelated competitors increases in both cases. However, conflict does not necessarily disappear entirely even under extremely high sperm competition (Parker and Begon, 1993). The kin selection explanation for this is that whilst relatedness between sperm competing for fertilisations may approach 0 under intense sperm competition, we must additionally consider relatedness between spermatozoa competing for resources, and these are still sibling gametes regardless of the level of sperm competition. Regardless of the intensity of sperm competition, it may pay off for mutant sperm under haploid control to sap resources from non-mutant sperm of the same parent (with relatedness ½ between sibling gametes), whilst under diploid control (with relatedness 1 from the parent’s perspective) this does not pay off.

The above applies to situations where the parent individuals are not necessarily related to each other. However, the parent individuals can of course also be related to each other, and modelling suggests that sperm expenditure decreases with increasing relatedness between males in sperm competition (Parker, 2000). This is a very intuitive outcome: it does not pay off (or at least is not as valuable) to invest into competition with individuals who are likely to pass on copies of the focal individual’s genes anyway. Empirical tests of this theory have, however, so far not found clear evidence for this prediction (e.g., Thomas and Simmons, 2008). On the theoretical side, Parker and Pizzari (2010) note that Parker’s (2000) models may have implicitly assumed that the population had low viscosity (i.e., high dispersal). It may be worth pursuing these relatively understudied questions further in future work, accounting explicitly for factors such as dispersal rate.

3. Gamete limitation, kin selection, and secondary effects

Sperm competition refers to competition between sperm for eggs, typically assuming that the total number of fertilisations is fixed and limited only by the number of eggs. However, the fertilisation success of eggs may depend on the number or density of spermatozoa, and this problem may be particularly acute in marine broadcast spawner settings (Levitan and Petersen, 1995; Yund, 2000). This concept of sperm limitation (or more generally, gamete limitation) can be described mathematically using fertilisation functions (an early example can be found in Rothschild and Swann, 1951, and for reviews see Lehtonen and Dardare, 2019, and Crimaldi and Zimmer, 2014 for more complex physical settings).

Sperm limitation can interact with sperm competition, together driving sperm and ejaculate evolution (Ball and Parker, 1996). Similarly, it has been argued that gamete limitation can drive the evolution of anisogamy (i.e., the ancestral divergence of the sexes), either by itself (Iyer and Roughgarden, 2008; Roughgarden and Iyer, 2011) or in conjunction with gamete competition (Lehtonen and Kokko, 2011; Lehtonen and Parker, 2014). The latter models unify the proposed evolutionary pressures of gamete competition and gamete limitation in a common framework, and in these models local spawning group size modulates the relative evolutionary pressure via gamete competition and gamete limitation. This can again be viewed through a kin selection lens: group size influences the relatedness of gametes within the group, and the average relatedness of a parent to those gametes. Consider an extreme case of a group of one adult spawning individual. Then, all gametes within the group will be siblings, and the parent will be maximally related to the gametes in the group. Then again, in very large groups, or in panmictic populations with no group structure, the vast majority of gamete interactions occur between unrelated individuals. The relative importance of gamete limitation as a selective pressure becomes emphasised in small groups whilst that of gamete competition becomes reduced (Parker and Lehtonen, 2014). Taking a step further, it has been suggested that more generally and beyond the group size effect, relatedness within groups modulates the selective effects of gamete competition and gamete limitation (Lehtonen, 2016).

However, this last argument comes with a caveat not mentioned in the article (Lehtonen, 2016). Beyond group size, the simplest and most likely source of increased relatedness in a mating group is limited dispersal between groups: if some offspring remain in their natal patch to breed in the next generation, relatedness within the patch increases. However, classic studies in the kin selection literature show that under such circumstances, there is limited scope for increased relatedness to promote the evolution of altruistic traits. The reason for this is the secondary effect of increased competition between relatives: if one individual helps a related individual make more offspring, and some of those offspring remain within the natal patch, they increase competition for reproductive opportunities within the patch. Under many circumstances, these effects cancel each other exactly (Taylor, 1992a,b). Similarly, in models of sex ratio evolution in organisms with separate sexes, the effect of increased relatedness and increased competition (both due to limited dispersal) tend to cancel each other out (Bulmer, 1986; Frank, 1986; Taylor, 1988b), so that relatedness has no effect on the stable sex ratio. It therefore seems plausible that a similar effect might arise, at least in some circumstances, with gamete limitation. An example of this will be seen in the model of hermaphrodite sex ratio evolution we present later.

4. Local gamete competition

A model of sex allocation in simultaneously hermaphroditic organisms (Charnov, 1980) predicted that a larger fraction of reproductive resources should be invested in egg production (and conversely, less in sperm production) when the mating group size is small. Conversely, with increasing mating group size sex allocation becomes less female gamete biassed, approaching a 1:1 sex allocation ratio in large groups. Fischer (1981) derived a similar conclusion, apparently independent from (Charnov, 1980; see also West, 2009, p. 83 and references therein).

At its core this model is built on gamete interactions, including sperm competition. In accordance with the central message stated above, the logic of these models is analogous to models of sex ratio evolution under local mate competition in gonochoristic species (Hamilton, 1967; West, 2009). The main difference is that the ‘local competition’ for fertilisations happens on the level of gametes in simultaneous hermaphrodites, instead of the level of adult organisms in organisms with separate sexes. Due to the analogy, Schärer (2009) has proposed the term ‘local sperm competition’ (LSC) to describe such situations in hermaphrodites.

From a broader, kin selection perspective, in simultaneous hermaphrodites female-biassed sex allocation arises when competition occurs between related sperm for the fertilisation of ova of the mating partner (Schärer, 2009), emphasising the fact that the sperm need not be siblings and instead it suffices that they are related (Schärer, 2009). Relatedness between sperm in an ejaculate is thus analogous to the relatedness between gonochoristic brothers, but other factors may also increase relatedness – in particular limited dispersal of zygotes or adult individuals after fertilisation. However, it is again uncertain how this effect would interact with the secondary effects of increased local competition for breeding spots that must be taken into account (see previous section). The model on hermaphrodite sex ratio evolution that follows shows that in a manner similar to separate sexes, primary and secondary effects tend to cancel out, so that local competition between related gametes need not influence the sex ratio, beyond the effect driven by group size alone.

In some sense, local sperm competition can be thought to be the inverse of sperm competition (Singh and Schärer, 2022): under selfing (or in the absence of selfing, in mating groups of two individuals), there is no sperm competition and maximally strong LSC; in slightly larger mating groups, there is weak sperm competition and weak LSC; and in large mating group size, there is strong sperm competition and no LSC (Schärer, 2009). Thus, increasing mating group size, that is, increasing the number of unrelated sperm competing to fertilise the eggs, increases sperm competition between unrelated ejaculates and increases the investment to sperm (Charnov, 1980).

5. Putting it all together: Kin selection, sperm competition, local sperm competition, sperm limitation, and secondary effects meet in a model of sex allocation evolution in simultaneous hermaphrodites

We now present a novel model combining kin selection theory with several classical features of the theory of gametic interactions: gamete competition, local gamete competition, gamete limitation, and allocation between male and female gametes.

Consider simultaneous hermaphrodites reproducing in numerous patches of n individuals. This could correspond to either internal fertilisers where one individual transfers sperm to another (e.g., many species of barnacles which informed the model of Charnov, 1980) or broadcast spawners or spermcasters, where either one type or both types of gametes are released into the water column (common modes of fertilisation in hermaphrodites: Strathmann et al., 1984; Henshaw et al., 2014; Parker et al., 2018). Reproduction via obligate outcrossing and possible self-fertilisation are considered separately. A fraction f of eggs in a patch are fertilised, and this fraction may depend on the density of spermatozoa available for fertilisation (in other words, f corresponds to a ‘fertilisation function’ Lehtonen and Dardare, 2019). After fertilisation but prior to reproducing themselves, a fraction d of zygotes disperse to a different, random patch, whilst a fraction (1-d) remain in their natal patch. Dispersal incurs a cost, so that a fraction c of the dispersers perish. After this partial dispersal event, the mature individuals in each patch compete for n breeding spots, so that each patch is again culled to n individuals. Fertilisation amongst these n individuals takes place and the life cycle restarts.

This scenario differs from and expands upon the classic model of Charnov (1980) in numerous ways, but contains it as a special case where fertilisation is internal, there is no selfing, all gametes are fertilised (f = 1), and all individuals disperse after fertilisation (d = 1). Internal vs. external fertilisation does not significantly change the model and altering the possibility of selfing is relatively straightforward (see Appendix). However, the combined additions of sperm limitation (with f < 1 and dependent on sperm density) and limited, costly dispersal bring with them new challenges which we address in the model that follows.

Taking a kin selection approach, the model could be constructed in two equivalent ways: direct fitness or inclusive fitness (Taylor et al., 2007). Here we present a direct fitness derivation of the random fertilisation scenario where both outbreeding and selfing are possible, and an outcrossing-only model is presented in the Appendix. With the direct fitness approach, we consider fitness via male and female gametes of a focal parent, accounting for all the effects on those gametes due to the sex ratio strategy of the focal parent itself, due to those of everyone else in their local group, and to those of the population as a whole. For clarity of exposition, we construct the model in sequential steps and eventually pull all those pieces together in a single direct fitness function. The notation is presented in Table 1.

TABLE 1

Table 1. Model notation and definitions.

We begin with the reproductive output of a focal individual in its focal patch:

$\begin{array}{ll}{w}_p=\left(1-x\right)M/m_{e}f\left(y\right)+\frac{xM/m_s}{nyM/m_s}n\left(1-y\right)M/m_{e}f\left(y\right)& (1)\end{array}$

For transparency, we have included variables which cancel out in the final expression. The logic of equation (1) is as follows: Each individual has a total gametic resource budget of M units which it can allocate into female and male gametes. Variables x and y denote the sex allocation trait (fraction of resources allocated into male gametes) of the focal individual, and its mean value in the focal patch, respectively. The focal individual thus allocates $\left(1-x\right)M$ uwnits of resources into female gametes, making a total of $\left(1-x\right)M/m_e$ gametes of size $m_e$ . Total egg production in the patch is $n\left(1-y\right)M/m_e$ , and a fraction f(y) of all eggs are fertilised, potentially dependent on mean sperm production in the patch (y). The focal individual makes $xM/m_s$ sperm of size m_s, and under fair raffle sperm competition (Parker and Pizzari, 2010) they gain a fraction $\frac{xM/m_s}{nyM/m_s}$ of all fertilised eggs in the patch.

The reproductive output in its focal patch (w_p) only accounts for the success of the focal individual’s gametes in its patch prior to dispersal. However, this by itself is not sufficient. Dispersing offspring are additionally affected by the cost of dispersal. Furthermore, both non-dispersers and surviving dispersers must additionally make it through population regulation in the patch they settle in, where the probability of survival for a non-disperser is

$\begin{array}{ll}{s}_1=\frac{n}{n\left[\left(1-d\right)\left(1-y\right)f\left(y\right)+d\left(1-c\right)\left(1-z\right)f\left(z\right)\right]\left(M/m_e\right)}& (2)\end{array}$

Here z indicates the mean value of the sex allocation trait over the whole population. The symbol n in the denominator indicates the number of breeding spots being competed over, whilst the denominator indicates the total number of individuals competing in the natal patch, including both non-dispersers and surviving dispersers from other patches. For a disperser who has already made it through the dispersal stage, the probability of surviving through population regulation is

$\begin{array}{ll}{s}_2=\frac{n}{n\left[\left(1-d\right)\left(1-z\right)f\left(z\right)+d\left(1-c\right)\left(1-z\right)f\left(z\right)\right]\left(M/m_e\right)}& (3)\end{array}$

Combining these fitness components and simplifying, we find that many constants cancel out, and we are left with

$\begin{array}{l}w=w_p\left[\left(1-d\right)s_1+d\left(1-c\right)s_2\right]=\left[\left(1-x\right)+x\frac{\left(1-y\right)}{y}\right]f\left(y\right)\\ \left[\frac{1-d}{\left(1-d\right)\left(1-y\right)f\left(y\right)+d\left(1-c\right)\left(1-z\right)f\left(z\right)}+\frac{d\left(1-c\right)}{\left(1-cd\right)\left(1-z\right)f\left(z\right)}\right]\end{array}\text{ (4)}$

At this point we can perform a brief check by calculating fitness in a neutral population. Setting (x = y = z) and simplifying, we find w = 2, as it should be: in a population regulated at stable size and where all individuals are identical, in each generation a parent must on average achieve one unit of fitness via its female gametes and one via its male gametes.

To find the stable sex ratio based on this fitness function, we then need to infer how the fitness of the focal parent, achieved via its own male and female gametes, is influenced by a small change in sex allocation of the focal individual, and by a small change in the average allocation strategy in the focal group, weighted by the appropriate relatedness coefficients. The fitness effects are the partial derivatives ${\frac{\partial w}{\partial x}|}_{x=y=z}$ and ${\frac{\partial w}{\partial y}|}_{x=y=z}$ (Taylor and Frank, 1996). Then, if the relatedness of the focal individual to its own gametes is r_o and the expected relatedness of the focal individual to a randomly picked gamete in its patch is r_p, we can find the candidate ESS sex ratio by solving the equation

$\begin{array}{ll}{\frac{\partial w}{\partial x}|}_{x=y=z}{r}_o+{\frac{\partial w}{\partial y}|}_{x=y=z}{r}_p=0& (5)\end{array}$

or equivalently,

$\begin{array}{ll}{\frac{\partial w}{\partial x}|}_{x=y=z}+{\frac{\partial w}{\partial y}|}_{x=y=z}R=0& (6)\end{array}$

where R = r_p/r_o is the relatedness of a random gamete relative to the relatedness to own gametes, from the perspective of the focal parent (who controls the phenotype, but gains fitness only via the gametes). This relatedness coefficient in turn is equal to the consanguinity (Bulmer, 1994) of the parent with a random gamete relative to the consanguinity of the parent with one of its own gametes, p_p/p_o. A random haploid gamete represents an allele picked randomly from the parental population, so that p_p must be equal to the consanguinity p_rg between two random gametes in the same generation. Similarly, a haploid gamete of the parent itself represents an allele picked randomly from the parent, so that p_o must be equal to the consanguinity p_sg between two random sibling gametes (i.e., gametes from the same parent).

Therefore, to find R it suffices to find the ratio R = p_rg/p_sg, which can be computed using the recursion

$\begin{array}{ll}{p}_{rg}=\frac{1}{n}{p}_{sg}+\frac{n-1}{n}{k}^2{p}_{rg}& (7)\end{array}$

where $\frac{1}{n}$ is the probability that two random gametes have the same parent, and k is the probability that the parents of two randomly picked gametes originate from the focal patch, i.e., $k=\frac{1-d}{1-d+\left(1-c\right)d}=\frac{1-d}{1-cd}$ . Dividing through by p_sg we have

$\begin{array}{ll}R=\frac{1}{n}+\frac{n-1}{n}{k}^{2}R& (8)\end{array}$

from which we can solve

$\begin{array}{ll}R=\frac{1}{k^2+n-k^{2}n}\mathrm{or}R=\frac{{(cd-1)}^2}{1-2d+d^2-2cdn+c{d}^{2}n+2dn-d^{2}n}& (9)\end{array}$

Similar equations have been derived for various biological scenarios. For example, equation (13) in Taylor (1988a) for the relatedness between two mated diploid females on the same patch is identical in form to equation (9) above.

The partial derivatives ${\frac{\partial w}{\partial x}|}_{x=y=z}$ and ${\frac{\partial w}{\partial y}|}_{x=y=z}$ are relatively complex, but nevertheless straightforward to calculate using standard rules of differentiation (e.g., with computer software such as Mathematica). Putting everything together and simplifying, we find that the necessary ESS condition is

$\begin{array}{l}{\frac{\partial w}{\partial x}|}_{x=y=z}+{\frac{\partial w}{\partial y}|}_{x=y=z}R\\ =\left[f\left(z\right)+n\left(2z-1\right)f\left(z\right)+2\left(z-1\right)z{f}^{\prime }\left(z\right)\right]q=0\end{array}\text{ (10)}$

where $q=\frac{\left(c-1\right)d\left(d+cd-2\right)}{\left(1-2d\left(1+\left(c-1\right)n\right)+d^2\left(1+\left(c^2-1\right)n\right)\right)\left(z-1\right)zf\left(z\right)}$ . Clearly, any solutions to the equation with respect to z are determined solely by the factor in square brackets, so it is sufficient to solve

$\begin{array}{ll}f\left(z\right)+n\left(2z-1\right)f\left(z\right)+2\left(z-1\right)z{f}^{\prime }\left(z\right)=0& (11)\end{array}$

or equivalently,

$\begin{array}{ll}1+n\left(2z-1\right)=2\left(1-z\right)z\frac{f^{\prime }\left(z\right)}{f\left(z\right)}& (12)\end{array}$

where $\frac{f^{\prime }\left(z\right)}{f\left(z\right)}$ could alternatively be written as $\frac{d}{dz}\ln \left(f\left(z\right)\right)$ .

When fertilisation is limited by sperm abundance, the derivative on the right side of equation (12) is positive (i.e. an increase in sperm concentration increases fertilisation success). Sperm limitation $f^{\prime }\left(z\right)>0$ promotes less female-biased sex allocation (Figure 1), thus increasing investment into sperm and improving the fertilisation prospects of eggs. This result is analogous to that of Lehtonen and Schwanz (2018) for sex allocation under mate limitation and local mate competition, but with full dispersal (i.e. d = 1) in organisms with separate sexes. This has biological relevance particularly for broadcast spawning and spermcasting simultaneous hermaphrodites, given the relative prevalence of gamete limitation in the sea (Levitan and Petersen, 1995; Yund, 2000).

FIGURE 1

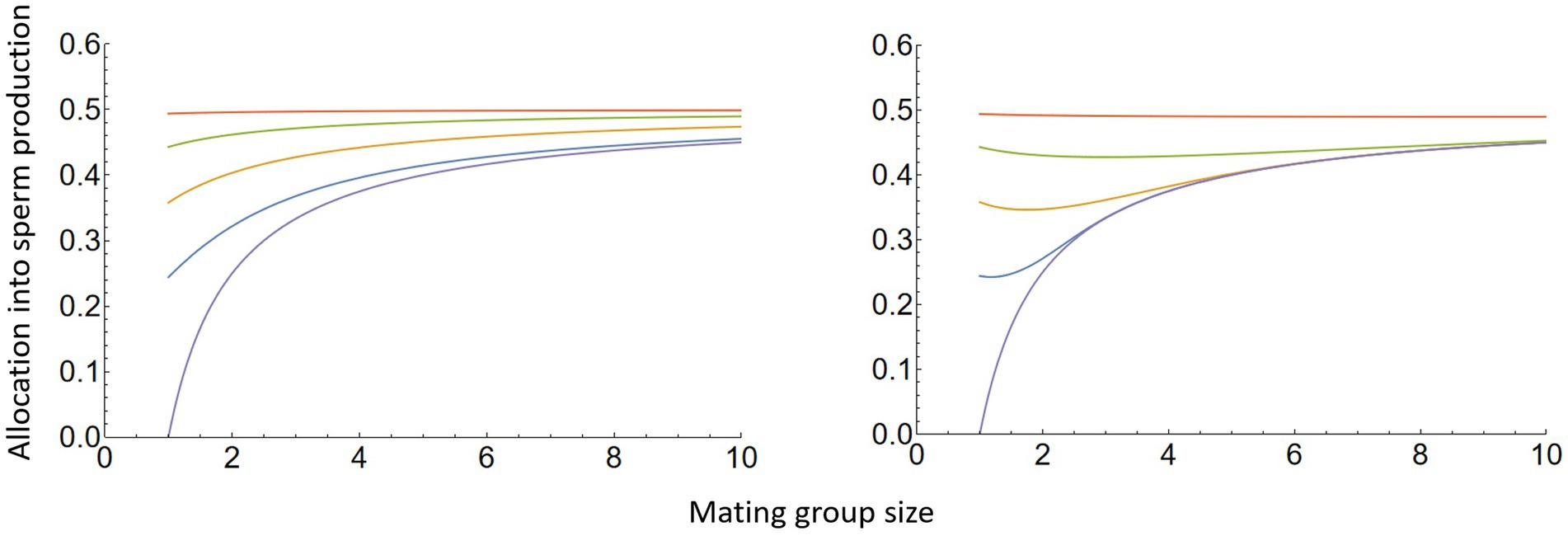
Figure 1. The influence of mating group size, sperm limitation, and dispersal (implicitly) on sex allocation in simultaneous hermaphrodites under random mating (i.e., inbreeding allowed). Note that although the figures are based on a model that accounts for variation in dispersal and the cost of dispersal, these factors do not influence the outcome. Sperm limitation has a strong effect, with sex allocation pushed towards 0.5 as sperm limitation increases: in each panel the lowest curve is with no sperm limitation (i.e., the classical result), and sperm limitation increases moving up from the lowest curve. Under some circumstances, sex allocation can even become less female-biased as group size increases: see the 2^nd and 3^rd curves from the top in the rightmost panel. On the left, we have assumed that gamete density is dependent only on the sex allocation strategy, but not on group size. On the right side, we additionally account for increasing gamete density with group size: this could happen if external fertilisers aggregate in patches of physically identical size, so that groups of several individuals have a higher density of individuals and gametes than those with fewer individuals. The figure is based on equation (12), with the fertilisation function f(z) = 1 − e^−az (left panel) or f(x) = 1 − e^−anz (right panel). Values of the parameter a are, from top to bottom: 0.1, 1, 3, 8, ∞. This fertilisation function originates in Rothschild and Swann (1951), see Lehtonen and Dardare (2019) for a review.

Whilst the effect of gamete limitation is interesting, it is equally interesting to note that c and d are both absent from equations (11, 12). Limited dispersal and increased cost of dispersal increase the relatedness of gametes within a patch, and one might expect relatedness in turn to influence the stable sex ratio. Yet no such effect is seen in the result. This is an example of the cancellation effect of increased relatedness vs. increased competition for reproductive spots amongst related females, noted in studies of sex ratio evolution in organisms with separate sexes and no sperm limitation or mate limitation (Bulmer, 1986; Frank, 1986; Taylor, 1988b). Our results show that the cancellation effect extends to simultaneous hermaphrodites, even under sperm limited conditions. Lehtonen (2016) argued that relatedness determines the relative importance of gamete limitation and gamete competition as selective forces. However, our analysis shows that the question is more nuanced when relatedness is modulated by dispersal. Whilst it is true that the effect of sperm limitation is modulated by relatedness, in the present model this effect is cancelled by secondary, competitive effects in the manner described above.

In the absence of sperm limitation (i.e. f’(z)=0) equation (12) reduces to 1 + n(2z − 1) = 0, with the solution

$\begin{array}{ll}z=\frac{n-1}{2n},& (13)\end{array}$

the classic result of sex allocation in hermaphrodites under local sperm competition when both selfing and outcrossing are allowed. We have shown that the result is not altered by increased relatedness under limited dispersal, analogous to the classic result in sex ratio evolution in organisms with separate sexes (e.g., Taylor, 1988b).

Under strict outcrossing (Appendix) we find the solution

$\begin{array}{ll}z=\frac{n-2}{2n-3}& (14)\end{array}$

in the absence of sperm limitation, and similarly find that it is independent of dispersal and of mortality under dispersal, and that sperm limitation drives a less female-biassed sex allocation (see Appendix). Note that equation (14) is equivalent to Charnov’s (1980) result: where we denote the total number of individuals in the patch with n, Charnov instead uses k to denote the number of competitors in the patch, aside from the focal individual itself. Therefore, $k=n-1$ and substituting $n=k+1$ into equation (14) we recover $\frac{k-1}{2k-1}$ as was found by Charnov.

6. Conclusion

Kin selection is a cornerstone of modern evolutionary theory and provides arguably the most powerful set of tools we have for the theoretical investigation of adaptation under long-term evolution when genetically related individuals interact. Whilst it is most commonly used in models on interactions between organisms, we have argued that kin selection can be an equally powerful tool in understanding the evolutionary consequences of interactions at the gametic level. Interactions between related gametes are ubiquitous and do not require spatial structure in the adult population if fertilisation is internal or gametes otherwise do not fully disperse after release.

We have discussed how kin selection relates to some central themes in gamete evolution and interactions: sperm competition, sperm limitation, local sperm competition, and sex allocation. All of these themes converge in the model we have presented. We draw two main conclusions from the model.

First, neither limited dispersal nor costly dispersal influence the outcome of sex ratio evolution in simultaneous hermaphrodites. Whilst the evolution of sex allocation in simultaneous hermaphrodites can be characterised in terms of ‘local sperm competition’ (LSC), i.e., sperm competition between related sperm, our results show that the effect of relatedness should be taken with caution, just as it should in models of sex allocation under ‘local mate competition’ (LMC) with separate sexes: limited dispersal is perhaps the simplest way for relatedness to arise between interacting individuals, and likely very common in nature, yet dispersal rate and dispersal cost do not affect sex allocation in our models.

Second, sperm limitation does influence the evolution of sex allocation in simultaneous hermaphrodites. This may be particularly important for understanding sex allocation evolution in broadcast spawning or spermcasting marine hermaphrodites, where sperm limitation is a real risk. We show examples of sex allocation outcomes with a specific, well-known mathematical formulation of sperm limitation in Figure 1. Under sperm-limited conditions the influence of mating/spawning group size on the sex ratio is significantly reduced, and the group size effect disappears entirely under extremely sperm limited conditions. We should therefore not necessarily expect simultaneous hermaphrodites under sperm-limited conditions to conform to the predictions of classic sex ratio models.

Whilst there are novel aspects to the model, there are also several clear parallels to earlier models. First, classic theoretical results for sex allocation in simultaneous hermaphrodites (e.g., Charnov, 1980; see Charnov, 1982; West, 2009 for reviews) are contained as a special case. Second, we have shown that the cancellation of increased relatedness and increased competition due to limited dispersal – widely studied in sex allocation theory for separate sexes (Bulmer, 1986; Frank, 1986; Taylor, 1988b) – applies equally to simultaneous hermaphrodites, with implications for the ‘local sperm competition’ effect as described above. Third, analogous to theoretical studies of sex allocation under mate limitation in organisms with separate sexes (e.g., Nagelkerke and Hardy, 1994; Lehtonen and Schwanz, 2018), we have shown that sperm limitation has a significant effect on sex allocation: strong sperm limitation is compensated by increased allocation into male function. The novel aspect of this model is the combination of phenomena it addresses. For example, whilst previous models have explored the analogous effect of mate limitation on sex allocation, we are not aware of any model analysing the effect of mate limitation or sperm limitation under limited dispersal, and therefore under increased relatedness. Without a model examining this combination, the possibility of an interaction between these factors remains. Superficially, the importance of sperm limitation as an evolutionary pressure is expected to increase with increasing relatedness (Lehtonen, 2016). However, our model shows that whilst sperm limitation does strongly influence sex allocation, here too the cancellation effect holds.

What do our results say about the importance of considering kin selection in such models? Playing the devil’s advocate, one could argue that we have shown kin selection to be unimportant after all, at least in this model. However, our view is the opposite: the scenario we have modelled would be extremely difficult to analyse and understand without carefully considering kin selection effects. Whilst the final result might suggest that relatedness plays no role in the evolution of sex allocation, we would not know this without a formal model, and might even be misled to predict that limited, costly dispersal should (via increased relatedness) modulate sex allocation. Kin selection does play a central role in the model: its various effects at different stages of the life cycle happen to cancel each other exactly, but seeing this requires computing those effects, as well as the relatedness coefficient that arises due to the combined effect of limited patch size, limited dispersal, and mortality during dispersal. All three factors appear in the relatedness coefficient (equation 9), but only the first appears in the equilibrium sex ratio.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

LM and JL contributed to the literature review, to planning the article, and writing the manuscript. JL contributed the mathematical model. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the Academy of Finland (grant number 340130, awarded to JL).

Acknowledgments

We would like to thank Jeremy Van Cleve and John Fitzpatrick for very helpful and constructive comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ball, M. A., and Parker, G. A. (1996). Sperm competition games: external fertilization and “adaptive” infertility. J. Theor. Biol. 180, 141–150. doi: 10.1006/jtbi.1996.0090

PubMed Abstract | CrossRef Full Text | Google Scholar

Bulmer, M. (1986). Sex ratio theory in geographically structured populations. Heredity 56, 69–73. doi: 10.1038/hdy.1986.10

PubMed Abstract | CrossRef Full Text | Google Scholar

Bulmer, M. G. (1994). Theoretical Evolutionary Ecology. Sunderland, Massachusetts: Sinauer Associates.

Google Scholar

Charnov, E. L. (1980). Sex allocation and local mate competition in barnacles. Marine. Biol. Lett. 1, 269–272.

Google Scholar

Charnov, E. L. (1982). The theory of sex allocation. Monogr. Popul. Biol. 18, 1–355.

Google Scholar

Crimaldi, J. P., and Zimmer, R. K. (2014). The physics of broadcast spawning in benthic invertebrates. Annu. Rev. Mar. Sci. 6, 141–165. doi: 10.1146/annurev-marine-010213-135119

PubMed Abstract | CrossRef Full Text | Google Scholar

Darwin, C. R. (1871). The Descent of Man, and Selection in Relation to Sex. London: J. Murray.

Google Scholar

Faria, G. S., Gardner, A., and Carazo, P. (2020). Kin discrimination and demography modulate patterns of sexual conflict. Nat. Ecol. Evol. 4, 1141–1148. doi: 10.1038/s41559-020-1214-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Faria, G. S., Varela, S. A., and Gardner, A. (2015). Sex-biased dispersal, kin selection and the evolution of sexual conflict. J. Evol. Biol. 28, 1901–1910. doi: 10.1111/jeb.12697

PubMed Abstract | CrossRef Full Text | Google Scholar

Fischer, E. A. (1981). Sexual allocation in a simultaneously hermaphroditic coral reef fish. Am. Nat. 117, 64–82. doi: 10.1086/283686

CrossRef Full Text | Google Scholar

Frank, S. A. (1986). The genetic value of sons and daughters. Heredity 56, 351–354. doi: 10.1038/hdy.1986.56

CrossRef Full Text | Google Scholar

Gardner, A., West, S. A., and Wild, G. (2011). The genetical theory of kin selection. J. Evol. Biol. 24, 1020–1043. doi: 10.1111/j.1420-9101.2011.02236.x

CrossRef Full Text | Google Scholar

Hamilton, W. D. (1963). The evolution of altruistic behavior. Am. Nat. 97, 354–356. doi: 10.1086/497114

CrossRef Full Text | Google Scholar

Hamilton, W. D. (1964a). Genetical evolution of social behaviour. I. J. Theor. Biol. 7, 1–16. doi: 10.1016/0022-5193(64)90038-4

CrossRef Full Text | Google Scholar

Hamilton, W. D. (1964b). Genetical evolution of social behaviour. II. J. Theor. Biol. 7, 17–52. doi: 10.1016/0022-5193(64)90039-6

CrossRef Full Text | Google Scholar

Hamilton, W. D. (1967). Extraordinary sex ratios. Science 156, 477–488. doi: 10.1126/science.156.3774.477

CrossRef Full Text | Google Scholar

Henshaw, J. M., Marshall, D. J., Jennions, M. D., and Kokko, H. (2014). Local gamete competition explains sex allocation and fertilization strategies in the sea. Am. Nat. 184, E32–E49. doi: 10.1086/676641

PubMed Abstract | CrossRef Full Text | Google Scholar

Higginson, D. M., and Pitnick, S. (2011). Evolution of intra-ejaculate sperm interactions: do sperm cooperate? Biol. Rev. 86, 249–270. doi: 10.1111/j.1469-185X.2010.00147.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Immler, S. (2019). Haploid selection in “diploid” organisms. Annu. Rev. Ecol. Evol. Syst. 50, 219–236. doi: 10.1146/annurev-ecolsys-110218-024709

CrossRef Full Text | Google Scholar

Iyer, P., and Roughgarden, J. (2008). Gametic conflict versus contact in the evolution of anisogamy. Theor. Popul. Biol. 73, 461–472. doi: 10.1016/j.tpb.2008.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehtonen, J. (2016). Multilevel selection in kin selection language. Trends Ecol. Evol. 31, 752–762. doi: 10.1016/j.tree.2016.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehtonen, J. (2020a). “Kin selection” in Encyclopedia of Evolutionary Psychological Science. eds. T. K. Shackelford and V. A. Weekes-Shackelford (Cham: Springer International Publishing), 1–10.

Google Scholar

Lehtonen, J. (2020b). The Price equation and the unity of social evolution theory. Philosophical Transactions of the Royal Society B: Biological Sciences 375:20190362.

Google Scholar

Lehtonen, J., and Dardare, L. (2019). Mathematical models of fertilization—an eco-evolutionary perspective. Q. Rev. Biol. 94, 177–208. doi: 10.1086/703633

CrossRef Full Text | Google Scholar

Lehtonen, J., and Kokko, H. (2011). Two roads to two sexes: unifying gamete competition and gamete limitation in a single model of anisogamy evolution. Behav. Ecol. Sociobiol. 65, 445–459. doi: 10.1007/s00265-010-1116-8

CrossRef Full Text | Google Scholar

Lehtonen, J., and Parker, G. A. (2014). Gamete competition, gamete limitation, and the evolution of the two sexes. Mol. Hum. Reprod. 20, 1161–1168. doi: 10.1093/molehr/gau068

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehtonen, J., and Schwanz, L. E. (2018). Mate limitation and sex ratio evolution. R. Soc. Open Sci. 5:171135. doi: 10.1098/rsos.171135

PubMed Abstract | CrossRef Full Text | Google Scholar

Levitan, D. R., and Petersen, C. (1995). Sperm limitation in the sea. Trends Ecol. Evol. 10, 228–231. doi: 10.1016/S0169-5347(00)89071-0

CrossRef Full Text | Google Scholar

Nagelkerke, C. J., and Hardy, I. C. W. (1994). The influence of developmental mortality on optimal sex allocation under local mate competition. Behav. Ecol. 5, 401–411. doi: 10.1093/beheco/5.4.401

CrossRef Full Text | Google Scholar

Parker, G. A. (1970). Sperm competition and its evolutionary consequences in the insects. Biol. Rev. 45, 525–567. doi: 10.1111/j.1469-185X.1970.tb01176.x

CrossRef Full Text | Google Scholar

Parker, G. (1993). Sperm competition games: sperm size and sperm number under adult control. Proc. R. Soc. Lond. B Biol. Sci. 253, 245–254.

Google Scholar

Parker, G. (2000). Sperm competition games between related males. Proc. R. Soc. Lond. Ser. B Biol. Sci. 267, 1027–1032.

Google Scholar

Parker, G. A. (2020). Conceptual developments in sperm competition: a very brief synopsis. Philos. Trans. R. Soc. B 375:20200061. doi: 10.1098/rstb.2020.0061

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, G. A., and Begon, M. E. (1993). Sperm competition games: sperm size and number under Gametic control. Proc. Biol. Sci. 253, 255–262. doi: 10.1098/rspb.1993.0111

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, G. A., and Lehtonen, J. (2014). Gamete evolution and sperm numbers: sperm competition versus sperm limitation. Proc. R. Soc. B Biol. Sci. 281:20140836. doi: 10.1098/rspb.2014.0836

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, G. A., and Pizzari, T. (2010). Sperm competition and ejaculate economics. Biol. Rev. 85, 897–934. doi: 10.1111/j.1469-185X.2010.00140.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, G. A., Ramm, S. A., Lehtonen, J., and Henshaw, J. M. (2018). The evolution of gonad expenditure and gonadosomatic index (GSI) in male and female broadcast-spawning invertebrates. Biol. Rev. 93, 693–753. doi: 10.1111/brv.12363

PubMed Abstract | CrossRef Full Text | Google Scholar

Pepper, J. W. (2000). Relatedness in trait group models of social evolution. J. Theor. Biol. 206, 355–368.

Google Scholar

Pizzari, T., and Foster, K. R. (2008). Sperm sociality: cooperation, altruism, and spite. PLoS Biol. 6:e130. doi: 10.1371/journal.pbio.0060130

PubMed Abstract | CrossRef Full Text | Google Scholar

Rankin, D. J. (2011). Kin selection and the evolution of sexual conflict. J. Evol. Biol. 24, 71–81. doi: 10.1111/j.1420-9101.2010.02143.x

CrossRef Full Text | Google Scholar

Rothschild, L., and Swann, M. M. (1951). The fertilization reaction in the sea-urchin the probability of a successful sperm-egg collision. J. Exp. Biol. 28, 403–416. doi: 10.1242/jeb.28.3.403

CrossRef Full Text | Google Scholar

Roughgarden, J., and Iyer, P. (2011). “Contact, not conflict, causes the evolution of anisogamy” in The Evolution of Anisogamy. eds. T. Togashi and P. Cox (Cambridge: Cambridge University Press), 96–110.

Google Scholar

Schärer, L. (2009). Tests of sex allocation theory in simultaneously hermaphroditic animals. Evolution 63, 1377–1405. doi: 10.1111/j.1558-5646.2009.00669.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, P., and Schärer, L. (2022). Evolution of sex allocation plasticity in a hermaphroditic flatworm genus. J. Evol. Biol. 35, 817–830. doi: 10.1111/jeb.14020

PubMed Abstract | CrossRef Full Text | Google Scholar

Strathmann, R. R., Strathmann, M. F., and Emson, R. H. (1984). Does limited brood capacity link adult size, brooding, and simultaneous hermaphroditism? A test with the starfish Asterina phylactica. Am. Nat. 123, 796–818. doi: 10.1086/284240

CrossRef Full Text | Google Scholar

Taylor, P. D. (1988a). An inclusive fitness model for dispersal of offspring. J. Theor. Biol. 130, 363–378. doi: 10.1016/S0022-5193(88)80035-3

CrossRef Full Text | Google Scholar

Taylor, P. D. (1988b). Inclusive fitness models with two sexes. Theor. Popul. Biol. 34, 145–168. doi: 10.1016/0040-5809(88)90039-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, P. D. (1992a). Altruism in viscous populations — an inclusive fitness model. Evol. Ecol. 6, 352–356. doi: 10.1007/BF02270971

CrossRef Full Text | Google Scholar

Taylor, P. D. (1992b). Inclusive fitness in a homogeneous environment. Proc. R. Soc. Lond. Ser. B Biol. Sci. 249, 299–302. doi: 10.1098/rspb.1992.0118

CrossRef Full Text | Google Scholar

Taylor, P. D., and Frank, S. A. (1996). How to make a kin selection model. J. Theor. Biol. 180, 27–37. doi: 10.1006/jtbi.1996.0075

CrossRef Full Text | Google Scholar

Taylor, P., Wild, G., and Gardner, A. (2007). Direct fitness or inclusive fitness: how shall we model kin selection? J. Evol. Biol. 20, 301–309. doi: 10.1111/j.1420-9101.2006.01196.x

CrossRef Full Text | Google Scholar

Thomas, M. L., and Simmons, L. W. (2008). Rival male relatedness does not affect ejaculate allocation as predicted by sperm competition theory. PLoS One 3:e2151. doi: 10.1371/journal.pone.0002151

PubMed Abstract | CrossRef Full Text | Google Scholar

Trivers, R. (1985). Social Evolution. Menlo Park, California: Benjamin/Cummings Publishing Company.

Google Scholar

West, S. A. (2009). Sex Allocation. Princeton: Princeton University Press.

Google Scholar

Wild, G., Pizzari, T., and West, S. A. (2011). Sexual conflict in viscous populations: the effect of the timing of dispersal. Theor. Popul. Biol. 80, 298–316. doi: 10.1016/j.tpb.2011.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Yund, P. O. (2000). How severe is sperm limitation in natural populations of marine free-spawners? Trends Ecol. Evol. 15, 10–13. doi: 10.1016/S0169-5347(99)01744-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix A

Model of sex allocation evolution in hermaphrodites under obligate outbreeding

In the main text we computed the relatedness coefficient using the recursion equation

$\begin{array}{ll}R=\frac{1}{n}+\frac{n-1}{n}{k}^{2}R& (1)\end{array}$

with the solution

$\begin{array}{ll}R=\frac{1}{k^2+n-k^{2}n}.& (2)\end{array}$

The same recursion equation in fact applies to the outbreeding model: the coefficients of consanguinity $p_{sg}$ and $p_{rg}$ are not the same in the two models, but their ratio, the coefficient $R=p_{rg/}{p}_{sg}$ is. However, $R$ is a whole-group relatedness coefficient which is appropriate for the random mating model. For the outbreeding model we need a so-called ‘others-only’ relatedness coefficient (see e.g., Pepper, 2000; Gardner et al., 2011; Lehtonen, 2016; Lehtonen, 2020b for the distinction between the two). In this case, as is apparent from the structure of (A1), the other-only relatedness coefficient is simply

$\begin{array}{ll}\tilde{R}=k^{2}R=\frac{k^2}{k^2+n-k^{2}n}.& (3)\end{array}$

We can now construct an outbreeding model, otherwise analogous to the random mating model of the main text.

$\begin{array}{l}{w}_p=\left(1-x\right)M/m_{e}f\left(y\right)+\frac{xM/m_s}{\left(x+\left(n-2\right)y\right)M/m_s}\\ \left(n-1\right)\left(1-y\right)M/m_{e}f\left(\left(x+\left(n-2\right)y\right)/\left(n-1\right)\right)\end{array}\text{ (A4)}$

Note that here $y$ is the phenotypic value of other individuals in the group (excluding the focal), whereas in the random mating model $y$ denoted the average value of everyone in the group. $\left(x+\left(n-2\right)y\right)/\left(n-1\right)$ is the average phenotypic value of those able to fertilise the eggs of a given non-focal individual (due to outbreeding one cannot fertilise their own eggs).

The probabilities of winning a breeding spot in a patch are (for a non-disperser and surviving disperser respectively)

$s_1=\frac{n}{\left[\begin{array}{l}\left(1-d\right)\left(1-x\right)f\left(y\right)+\left(1-d\right)\left(n-1\right)\left(1-y\right)f\left(\left(x+\left(n-2\right)y\right)/\left(n-1\right)\right)+\\ nd\left(1-c\right)\left(1-z\right)f\left(z\right)\end{array}\right]\left(M/m_e\right)}$

$\begin{array}{ll}{s}_2=\frac{n}{n\left[\left(1-d\right)\left(1-z\right)f\left(z\right)+d\left(1-c\right)\left(1-z\right)f\left(z\right)\right]\left(M/m_e\right)}& (6)\end{array}$

Again, total fitness is

$\begin{array}{ll}w=w_p\left[\left(1-d\right)s_1+d\left(1-c\right)s_2\right].& (7)\end{array}$

We can find the stable sex ratio by solving an equation analogous to that in the main text:

$\begin{array}{ll}{\frac{\partial w}{\partial x}|}_{x=y=z}+{\frac{\partial w}{\partial y}|}_{x=y=z}\tilde{R}=0& (8)\end{array}$

but note that the equation is not identical to that of the main text: the partial derivatives, as well as the relatedness coefficient are different. The computations are again tedious, but equation (A8) simplifies to

$\begin{array}{ll}\left[\left(2-3z+n\left(2z-1\right)\right)f\left(z\right)+\left(z-1\right)z{f}^{\prime }\left(z\right)\right]q=0& (9)\end{array}$

where

$q=\frac{\left(c-1\right)d\left(d+cd-2\right)n}{\left(n-1\right)\left(1-2d\left(1+\left(c-1\right)n\right)+d^2\left(1+\left(c^2-1\right)n\right)\right)\left(z-1\right)zf\left(\left(n-1\right)z\right)}$

Analogous to equation (12) in the main text, the stable sex ratio is the solution to the equation

$\begin{array}{ll}2-3z+n\left(2z-1\right)=\left(1-z\right)z\frac{f^{\prime }\left(z\right)}{f\left(z\right)}& (10)\end{array}$

which does not depend on d or c, but does depend on $f^{\prime }\left(z\right)$ . In other words, relatedness does not influence the sex ratio, but gamete limitation does. In the absence of sperm limitation, (A10) becomes

$\begin{array}{ll}2-3z+n\left(2z-1\right)=0& (11)\end{array}$

with the solution

$\begin{array}{ll}z=\frac{n-2}{2n-3}& (12)\end{array}$

which is equation (14) in the main text.