Decomposition rate as an emergent property of optimal microbial foraging

Decomposition kinetics are fundamental for quantifying carbon and nutrient cycling in terrestrial and aquatic ecosystems. Several theories have been proposed to construct process-based kinetics laws, but most of these theories do not consider that microbial decomposers can adapt to environmental conditions, thereby modulating decomposition. Starting from the assumption that a homogeneous microbial community maximizes its growth rate over the period of decomposition, we formalize decomposition as an optimal control problem where the decomposition rate is a control variable. When maintenance respiration is negligible, we find that the optimal decomposition kinetics scale as the square root of the substrate concentration, resulting in growth kinetics following a Hill function with exponent 1/2 (rather than the Monod growth function). When maintenance respiration is important, optimal decomposition is a more complex function of substrate concentration, which does not decrease to zero as the substrate is depleted. With this optimality-based formulation, a trade-off emerges between microbial carbon-use efficiency (ratio of growth rate over substrate uptake rate) and decomposition rate at the beginning of decomposition. In environments where carbon substrates are easily lost due to abiotic or biotic factors, microbes with higher uptake capacity and lower efficiency are selected, compared to environments where substrates remain available. The proposed optimization framework provides an alternative to purely empirical or process-based formulations for decomposition, allowing exploration of the effects of microbial adaptation on element cycling.

1. Introduction

Organic matter decomposition and its subsequent mineralization by microbial decomposers regulate the flow of carbon and nutrients in both terrestrial and aquatic systems. Two different sets of assumptions have been proposed to describe the kinetics of decomposition in mathematical models. First, based on the observation that the relative mass loss is nearly constant, first-order decay models were initially proposed (Salter and Green, 1933; Olson, 1963). The same concept has been adopted in numerous later biogeochemical models (Manzoni and Porporato, 2009). Second, more recent developments acknowledged the role of microbial biomass as a driver of decomposition and accounted for extra-cellular enzymes in the reaction kinetics. These works assume that the degradation of soil organic matter can be treated as an enzymatic reaction that follows Michaelis–Menten (Michaelis and Menten, 1913) or other nonlinear kinetics laws involving both substrate and enzyme concentrations (Wang and Post, 2013; Tang and Riley, 2019). Even without describing enzymatic reactions per se, nonlinear decomposition models inspired by Monod’s results (formally similar to Michaelis–Menten kinetics), or other nonlinear functions, have often been used to include microbial biomass as a driver of decomposition (Monod, 1949; Wutzler and Reichstein, 2008; Manzoni and Porporato, 2009; Abramoff et al., 2018). Despite their differences and contexts of application, linear and nonlinear approaches rely on some a priori assumption on the mathematical form of the decomposition kinetics.

Biogeochemical reactions in soils are complicated by chemical and spatial heterogeneities and by the diversity of microbial metabolic strategies. Hence, it is difficult to achieve a theoretically sound representation of macro-scale kinetics laws to interpret experimental data at the field scale, and in ecosystem models at even larger scales. Therefore, one could question whether the underlying kinetics laws should be imposed (as currently done) or regarded as emerging properties of the soil system, and derived based on some physical constrain or ecological consideration. In this contribution, we follow the latter approach by formulating a decomposition model from an optimization perspective, assuming that decomposition should proceed so that decomposers maximize their cumulative growth over the duration of decomposition.

Optimization principles are commonly used in ecology and plant science (Rosen, 1967; Harrison et al., 2021). Their underlying assumption is that evolution leads to optimally-adapted phenotypes by selecting the fittest organisms. The objectives of such evolutionary optimization are typically the maximization of reproductive effort, resource use, or net growth rate. An optimal strategy often exists because resources are limited and therefore need to be used or allocated in particular and timely manners. Moreover, physiological trade-offs and enzymatic capacity constrain the range of possible resource use strategies (Gudelj et al., 2010; Allison, 2012; Waldherr et al., 2015). For example, carbon use efficiency (i.e., the ratio of growth rate over uptake rate) tends to be lower in fast growing organisms (Lipson, 2015; Muscarella et al., 2020). Mathematically, given the optimization objective (fitness maximization) and constraints (resources are limited; physiological trade-offs), and assuming that some traits can be varied thanks to selective pressures, it is possible to formulate organism growth as an optimal control problem.

This is also the case for microbial decomposers, which exploit resources accumulated in organic matter (in soil, litter, sediments, or water) that are not only limited, but also subject to consumption by competing organisms and loss due to physical processes. Therefore, microbes face an inherent dilemma. On the one hand, resources could be consumed rapidly to ensure maximal use, but high rates of consumption are generally achieved over a short period and with low efficiency of conversion to biomass. On the other end, some microbes could aim at consuming resources slowly and efficiently, but in such a case, resources could be lost before they are consumed, because of abiotic processes or other organisms. Finding the optimal foraging strategy and the decomposition kinetics emerging as outcomes of this optimization problem frames the scope of this contribution.

Specifically, we ask:

1. Is there an optimal decomposition rate that maximizes total microbial growth for a given substrate amount?

2. Are the optimal decomposition kinetics consistent with established empirical or theoretical decomposition kinetics?

3. How does the optimal decomposition rate vary with microbial traits?

4. Are any trade-offs between growth rate and carbon-use efficiency emerging from the optimal decomposition strategy?

These questions are addressed by interpreting organic matter decomposition as an optimal control problem, which is solved analytically. The problem is set up in a general way, so that the derived equations can be applied to different decomposition systems, but we illustrate results for terrestrial litter decomposition as a case study.

2. Methods

A simple carbon (C) cycling model with a single substrate mass balance is presented first (Section 2.1), followed by the optimality conditions and the boundary conditions for the optimization (Sections 2.2 and 2.3). The equations describing microbial physiology are presented next (Section 2.4). The following Sections 2.5 and 2.6 detail the derivation of the analytical solution. Finally, the efficiency of the decomposition system is defined in Section 2.7. The model schematic is shown in Figure 1 and the symbols are explained in Table 1.

FIGURE 1

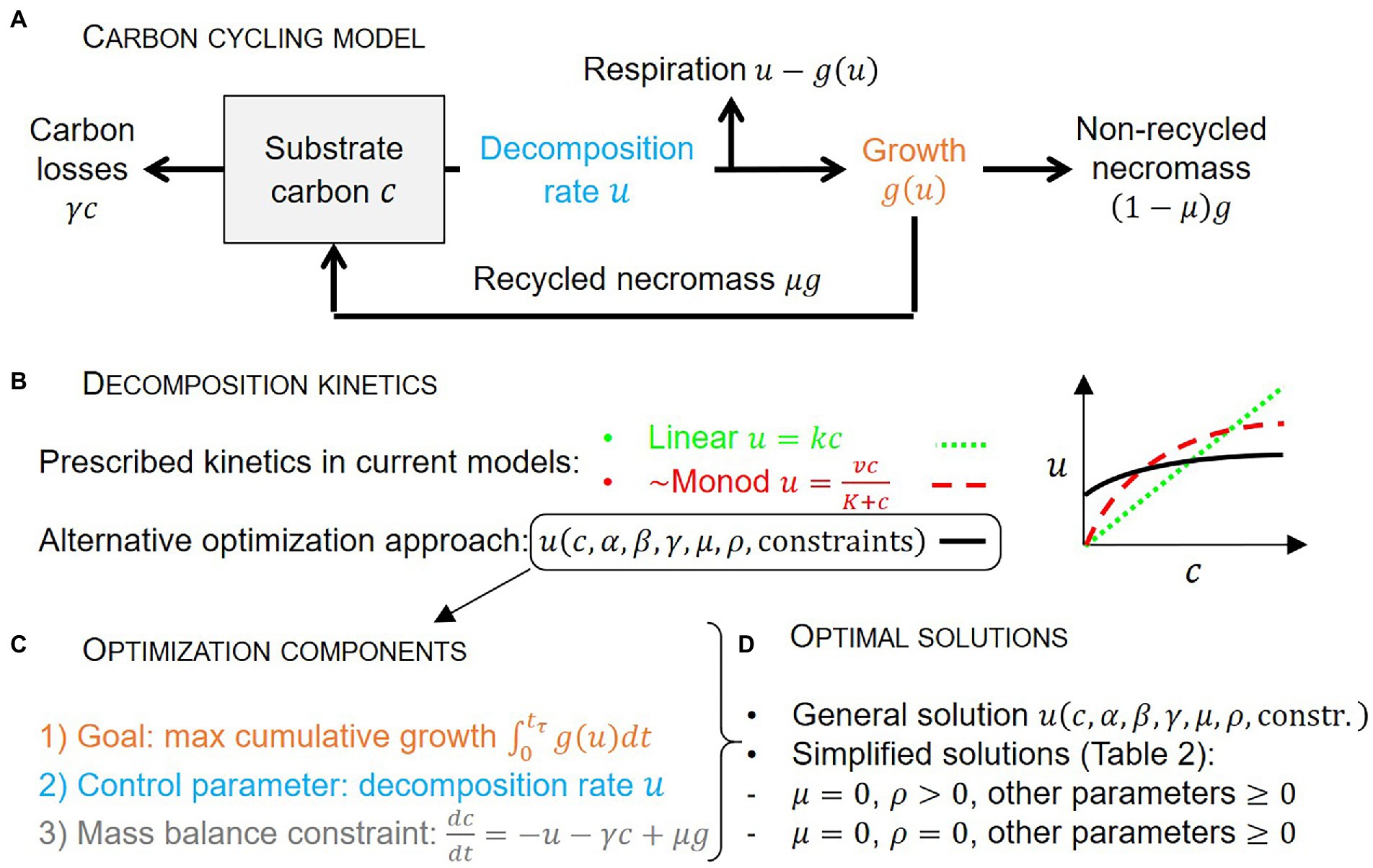
Figure 1. Schematic of the carbon cycling model (A), approaches to describe decomposition kinetics (B), main components of the microbial growth optimization problem (C), and optimal solutions (D). Symbols are defined in panel (A) and Table 1.

TABLE 1

Table 1. Symbols and units.

2.1. Carbon cycling model

We start from the premise that microbial decomposers aim at maximizing their growth rate (g) over a time interval $t_{\tau }$ that is not prescribed, but allowed to emerge as a result of the optimization. Growth is achieved by assimilating organic C, which we assume is the main limiting substrate and energy provider (Figure 1). A single cohort of organic C is denoted by c (expressed as mass of C in the system), and its mass loss during decomposition is described. The C compartment is assumed chemically homogeneous for simplicity (well-mixed approximation). Mass loss is caused by microbial-driven decomposition at rate $u$, which is not specified a priori as typically done in biogeochemical models, but is instead derived as a result of the optimization. We assume that all decomposed C is taken up, so that decomposition and uptake rates are equal to u. Physical processes such as leaching and adsorption, or uptake by other organisms, also contribute to the depletion of substrate C, following first-order kinetics (with rate constant $\gamma$). The parameter $\gamma$ is thus a measure of substrate C availability – higher $\gamma$ implies faster losses due to abiotic or biotic factors that cannot be controlled by the microbial biomass. Microbial biomass is assumed in quasi-equilibrium, so that mortality equals growth. A fraction $\mu$ of microbial necromass production is assumed to be recycled in the substrate compartment. Building on these assumptions, the mass balance equation of the organic matter cohort can thus be written as,

$\begin{array}{ll}\frac{dc}{dt}=-u-\gamma c+\mu g,c\left(0\right)=c_0.& (1)\end{array}$

2.2. Microbial growth as an optimal control problem

The microbial growth optimization problem can be formulated as the maximization of

$\begin{array}{ll}J=\underset{0}{\overset{t_{\tau }}{{\displaystyle \int }}}g\left(u\right)dt,& (2)\end{array}$

with free terminal time $t_{\tau }$ and no terminal gain, and subject to the mass-balance constraint in Equation (1). This constitutes an optimal control problem with control u bound to be larger than zero.

Necessary conditions for the optimization can be expressed in terms of the Hamiltonian (H) and a Lagrange multiplier ($\lambda$) as (Kirk, 1970; Lenhart and Workman, 2007)

$\begin{array}{ll}H=g+\lambda \frac{dc}{dt}=g+\lambda \left(-u-\gamma c+\mu g\right),& (3)\end{array}$

$\begin{array}{ll}0=\frac{\partial H}{\partial u}=g^{\prime }+\lambda \left(-1+\mu g^{\prime }\right),& (4)\end{array}$

$\begin{array}{ll}-\frac{d\lambda }{dt}=\frac{\partial H}{\partial c}=-\gamma \lambda ,& (5)\end{array}$

where we use the prime notation exclusively for derivatives with respect to u (e.g., $g^{\prime }=\partial g/\partial u$, $g^{″}={\partial }^{2}g/\partial u^2$) and continue with the Leibniz notation for other derivatives.

These necessary conditions are usually referred to as the Pontryagin Maximum Principle, in honor of the man who first proved the theorem in 1956. While the proof of the theorem is quite theoretical (Kirk, 1970), the basic idea is related to optimization in multivariable calculus. If a point $x^{\ast }$ in n-dimensional space maximizes a function $g\left(x\right)$ subject to the constraint $f\left(x\right)=0$, the Lagrange multiplier rule says that there exists a number $\lambda$such that $\nabla g=\lambda \nabla f$ (where $\nabla$ indicates the gradient of the n-dimensional functions g and f). This can be recast as a statement that $x^{\ast }$ maximizes the so-called Hamiltonian function $H=g+\lambda f$ (Equation (3)) for some $\lambda$. The simplest proof of the version of the maximum principle we are using is based on elementary calculus (Lenhart and Workman, 2007). Assuming the control variable u is the maximizer of the functional $J\left[u\right]$ (Equation (2)), we can choose any allowable variation v and assert that the function value $ϵ=0$ is the maximizer of the function $J\left[u+ϵv\right]$. The conditions (4) and (5) follow from this maximization.

In Equations (4) and (5), the first equalities are the general necessary conditions for optimization, and the second equalities represent the optimization conditions specific to this model. The downward concavity of g(u) (Section 2.4) guarantees that the solution is the maximum of J.

Independent of the specifics of g(u), the temporal evolution of the Lagrange multiplier can be obtained by solving Equation (5),

$\begin{array}{ll}\lambda \left(t\right)={\lambda }_0{e}^{\gamma t},& (6)\end{array}$

where ${\lambda }_0$ represents the initial condition, to be determined from the boundary conditions of the optimization problem, as described in the following section.

2.3. Boundary conditions for the optimization problem

Equations (4) and (6) provide two conditions to determine the four unknowns c(t), u(t), ${\lambda }_0$, and $t_{\tau }$. Therefore, two additional conditions are required to mathematically close the problem. These conditions are specified at the terminal time $t_{\tau }$. Because the terminal time is free, one of the conditions is given by setting the Hamiltonian to zero at $t=t_{\tau }$. Moreover, at the terminal time, we assume that the C compartment is completely depleted. Taking $c\left(t_{\tau }\right)=0$ into $H\left(t_{\tau }\right)=0$ yields

$\begin{array}{ll}{g}_{\tau }={\lambda }_{\tau }\left(u_{\tau }-\mu g_{\tau }\right),& (7)\end{array}$

where subscript $\tau$ indicates evaluation at the terminal time, so that $u_{\tau }=u\left(t_{\tau }\right)$, $g_{\tau }=g\left(u\left(t_{\tau }\right)\right)$, etc. Next,${\lambda }_{\tau }$ in Equation (7) can be eliminated by using Equation (4) in the form,

$\begin{array}{ll}\lambda =\frac{g^{\prime }}{1-\mu g^{\prime }}.& (8)\end{array}$

Then after evaluating at the terminal time and simplifying we find,

$\begin{array}{ll}{g}_{\tau }=u_{\tau }{g}_{\tau }^{\prime }.& (9)\end{array}$

2.4. Growth model

The growth rate is expressed as a saturating function of the uptake rate, which as explained above equals the decomposition rate,

$\begin{array}{ll}g\left(u\right)=\alpha \frac{u-\rho }{\beta +u},& (10)\end{array}$

where $\alpha$ is the maximum growth rate, $\beta$ is the half-saturation constant, and $\rho$ the rate of substrate uptake used for cellular maintenance. Because growth rate is by definition equal to the uptake rate times the microbial carbon use efficiency (CUE: ratio of growth rate over uptake rate), and $\mathrm{CUE}\le e_{\max }<1$, the values of the half-saturation constant and the maximum growth rates must be constrained to satisfy these limits. Specifically, we assume that the slope of the g(u) relation at small u (and for negligible $\rho$) equals $e_{\max }$, so that$\alpha =\beta e_{\max }$. The function g(u) is shown in Figures 2A,B for various parameter combinations.

FIGURE 2

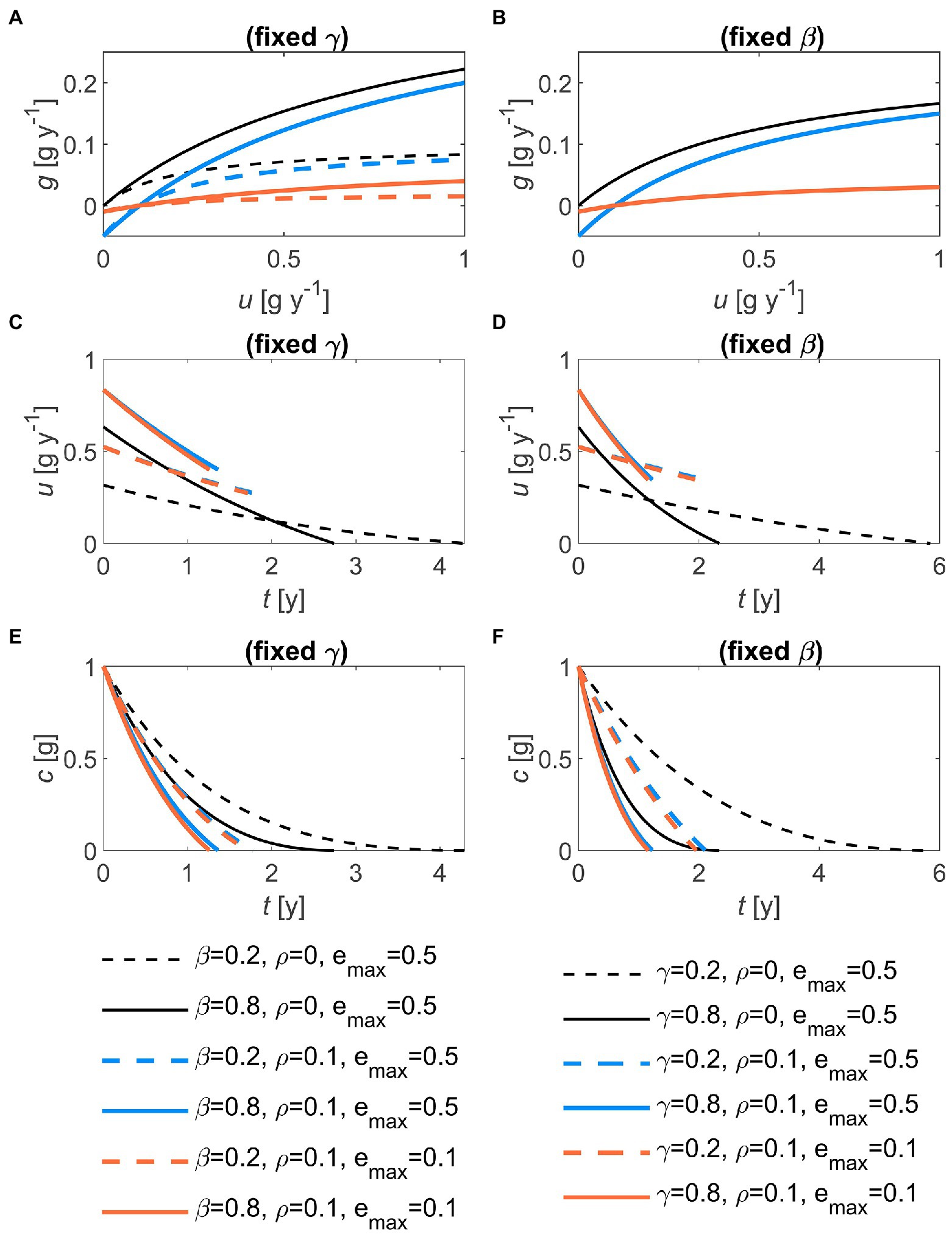
Figure 2. Effects of the half saturation constant of the microbial growth rate ($\beta$, left panels) and of the first-order decay constant ($\gamma$, right panels), for two values of maintenance respiration ($\rho$) and maximum growth efficiency ($e_{\max }$) on: (A,B) the relation between growth rate and decomposition rate, g(u); (C,D) the temporal trajectory of the optimal decomposition rate, u(t); and (E,F) the temporal trajectory of the substrate carbon, c(t). In all panels: $c_0=$1 g, $\mu =$0.5. In (B), curves with the same $\gamma$value overlap, because g(u) does not depend on $\gamma$. Parameter units are as in Table 1.

The concave shape of the g(u) relation implies declining CUE as the decomposition rate u increases. This decline can be caused by different factors that are not included in this model, but that are surrogated by the g(u) relation: (i) The marginal return on investment in extra-cellular enzymes decreases with increasing u because enzyme synthesis is energetically costly (del Giorgio and Cole, 1998) and hydrogen peroxide required for oxidative enzyme functioning may cause cell damage, thereby reducing CUE (Manzoni et al., 2021). (ii) When the microbial population reaches a steady state, the rate of growth will become limited by the enzymatic capacity in the cell and on cell walls (Waldherr et al., 2015). (iii) At high rates of enzyme release, the substrate binding sites may become saturated (Tang and Riley, 2013). (iv) Diffusion of the reaction products eventually becomes limiting (Vetter et al., 1998). (v) In the case of nitrogen-poor substrates, fast decomposition requires intense nitrogen immobilization, and when inorganic nitrogen sources are unavailable either microbial metabolism slows down due to nutrient limitation, or overflow respiration increases (Manzoni et al., 2021). In all these cases, net growth is expected to stabilize around a maximum value that allows cells to grow within their stoichiometric constraints.

With growth described by Equation (10), we can also define the microbial CUE as,

$\begin{array}{ll}\mathrm{CUE}=\frac{g}{u}=e_{\max }\frac{\beta \left(u-\rho \right)}{u\left(\beta +u\right)}.& (11)\end{array}$

Higher values of maintenance respiration $\rho$ decrease CUE, potentially causing it to become negative when $u<\rho$. At high values of u compared to $\rho$ and $\beta$ (plentiful resources), $\mathrm{CUE}\approx e_{\max }\beta /u$. In general, the maximum CUE is attained at intermediate values of u, but it remains below $e_{\max }$.

2.5. Nondimensionalization

Before beginning the analysis, it is helpful to nondimensionalize the problem, which reduces the number of parameters by two. To that end, we define dimensionless variables (see also Table 1):

$C=\frac{\gamma c}{\beta }(\text{and initial condition }{C}_0=\frac{\gamma c_0}{\beta })$,

$U=\frac{u}{\beta },$

$T=\gamma t(\text{and terminal time }{T}_{\tau }=\gamma t_{\tau })$,

$\begin{array}{ll}\Lambda =\frac{\beta \lambda }{\alpha }\left(\mathrm{and\; initial\; condition}{\Lambda }_0=\frac{\beta {\lambda }_0}{\alpha }\right),& (12)\end{array}$

growth rate.

$\begin{array}{ll}G=\frac{g}{\alpha }\left(\mathrm{and}\mathrm{its}\mathrm{derivative}{G}^{\prime }=\frac{\beta }{\alpha }{g}^{\prime }\right),& (13)\end{array}$

and parameters

${\rm P}=\frac{\rho }{\beta },$

$\begin{array}{ll}{\rm M}=\frac{\alpha \mu }{\beta },& (14)\end{array}$

With these changes, the problem consists of an initial value problem in the nondimensional substrate concentration C (from Equation (1))

$\begin{array}{ll}\frac{dC}{dT}+C=-U+{\rm M}G,C\left(0\right)=C_0,& (15)\end{array}$

an optimality condition (from Equation (4))

$\begin{array}{ll}{G}^{\prime }+\Lambda \left(-1+{\rm M}{G}^{\prime }\right)=0,& (16)\end{array}$

and terminal conditions (from Equation (9))

$G_{\tau }=U_{\tau }{G}_{\tau }^{\prime },$

$\begin{array}{ll}C\left(T_{\tau }\right)=0,& (17)\end{array}$

where the subscript $\tau$ indicates the terminal time as before. We also define the nondimensional growth rate (from Equation (10)) and its derivative with respect to U,

$G\left(U\right)=\frac{U-{\rm P}}{1+U},$

$\begin{array}{ll}{G}^{\prime }\left(U\right)=\frac{1+{\rm P}}{{\left(1+U\right)}^2},& (18)\end{array}$

and the nondimensional Lagrange multiplier (from Equation (6))

$\begin{array}{ll}\Lambda \left(T\right)={\Lambda }_0{e}^T.& (19)\end{array}$

The problem must be solved for parameters $U_{\tau }$, ${\Lambda }_0$, and $T_{\tau }$ and the variables U and C, after which the dimensional variables and functions can be determined from Equations (12)–(14).

2.6. Analytical solution

We start by substituting the formulas for G and $G^{\prime }$ (Equation (18)) into the boundary condition in Equation (17) to obtain an equation for decomposition rate at the terminal time,

$\begin{array}{ll}{U}_{\tau }=\frac{G_{\tau }}{G_{\tau }^{\prime }}=\frac{\left(U_{\tau }-{\rm P}\right)\left(1+U_{\tau }\right)}{1+{\rm P}}.& (20)\end{array}$

Solving for $U_{\tau }$ we obtain

$\begin{array}{ll}{U}_{\tau }={\rm P}+\sqrt{{\rm P}+{{\rm P}}^2},& (21)\end{array}$

$\begin{array}{ll}{G}_{\tau }^{\prime }=\frac{1+{\rm P}}{{\left(1+U_{\tau }\right)}^2}.& (22)\end{array}$

The terminal (nondimensional) decomposition rate is therefore only a function of the maintenance respiration rate, and $U_{\tau }=0$ when maintenance respiration is negligible. The result $U_{\tau }>P$ is somewhat surprising, as it means that G does not approach 0 at the end of the decomposition process. This will be a noteworthy feature in graphs of the results. In the subsequent analysis, it is helpful to define an additional function V = 1 + U and parameter $m=\sqrt{{\rm M}\left(1+P\right)}$. Substituting V into Equation (22) yields the slightly simpler formula

$\begin{array}{ll}{G}_{\tau }^{\prime }=\frac{1+{\rm P}}{V_{\tau }^2},& (23)\end{array}$

where $V_{\tau }$ is found from the definition of V and Equation (21) as,

$\begin{array}{ll}{V}_{\tau }=\sqrt{1+P}\left(\sqrt{1+P}+\sqrt{P}\right).& (24)\end{array}$

To find ${\Lambda }_0$, we combine the optimality condition of Equation (16) with the solution for $\Lambda$ of Equation (19), and evaluate at the terminal time,

$\begin{array}{ll}{\Lambda }_0=\frac{G_{\tau }^{\prime }}{1-{\rm M}{G}_{\tau }^{\prime }}{e}^{-T_{\tau }}=\frac{1+{\rm P}}{V_{\tau }^2-m^2}{e}^{-T_{\tau }}.& (25)\end{array}$

We now turn to the quantities that are functions of time: $G^{\prime }$, V, U, and C in turn. These quantities are best understood in reverse time, defined by

$\begin{array}{ll}S=T_{\tau }-T.& (26)\end{array}$

$G^{\prime }$ follows from the optimality condition of Equation (16), since $\Lambda$ is fully known. After clearing the fractions, we obtain

$\begin{array}{ll}{G}^{\prime }=\frac{1+{\rm P}}{\left(V_{\tau }^2-m^2\right)e^S+m^2}.& (27)\end{array}$

The definition of $G^{\prime }$ (Equation (18)) then yields

$\begin{array}{ll}{V}^2=\left(V_{\tau }^2-m^2\right)e^S+m^2,& (28)\end{array}$

$\begin{array}{ll}U=\sqrt{\left(V_{\tau }^2-m^2\right)e^S+m^2}-1.& (29)\end{array}$

To obtain the time trajectory of C, we first write the differential equation in reverse time, along with the reverse time initial condition (i.e., applied at $S=0$, corresponding to $T=T_{\tau }$). Substituting V for U and simplifying, we have

$\begin{array}{ll}\frac{dC}{dS}=C+V-\left(1+{\rm M}\right)+\frac{m^2}{V},C\left(0\right)=0.& (30)\end{array}$

This initial value problem has the surprisingly simple solution

$\begin{array}{ll}C=\frac{V^2}{1+{\rm P}}-2V+1.& (31)\end{array}$

which can be obtained using the integrating factor method and can be confirmed directly from the differential equation by applying the chain rule $\frac{dC}{dS}=\frac{dC}{dV}\frac{dV}{dS}$, with $\frac{dV}{dS}$ from Equation (28).

At this point, we still do not know the terminal time $T_{\tau }$ or the initial value of the decomposition rate $U_0$. By substituting V = 1 + U into the last result, we can obtain solutions for U and G in turn as functions of C,

$\begin{array}{ll}U={\rm P}+\sqrt{\left(1+{\rm P}\right)\left(C+{\rm P}\right)},& (32)\end{array}$

$\begin{array}{ll}G=\frac{\sqrt{C+{\rm P}}}{\sqrt{1+{\rm P}}+\sqrt{C+{\rm P}}}.& (33)\end{array}$

From the first of these, we obtain the value of initial U,

$\begin{array}{ll}{U}_0={\rm P}+\sqrt{\left(1+{\rm P}\right)\left(C_0+{\rm P}\right)}.& (34)\end{array}$

and the corresponding $V_0=U_0+1$,

$\begin{array}{ll}{V}_0=\sqrt{1+P}\left(\sqrt{1+P}+\sqrt{C_0+P}\right).& (35)\end{array}$

Equations (32)–(35) show that the (nondimensional) decomposition rate can be expressed as a function of substrate C and maintenance respiration rate only.

Next, $V_{\tau }$ (Equation (24)) and $V_0$ (Equation (35)) are substituted into Equation (28), evaluated at $S=T_{\tau }$, to obtain

$\begin{array}{ll}{e}^{T_{\tau }}=\frac{C_0+2U_0+1-{\rm M}}{2U_{\tau }+1-{\rm M}}.& (36)\end{array}$

Taking the logarithm yields the terminal time

$\begin{array}{ll}{T}_{\tau }=\ln \left(\frac{C_0+2U_0+1-{\rm M}}{2U_{\tau }+1-{\rm M}}\right).& (37)\end{array}$

Particularly compact solutions are found when ${\rm M}=0$ and/or ${\rm P}=0$ (Table 2).

TABLE 2

Table 2. Analytical solutions of the optimal decomposition problem when ${\rm M}=0$ or ${\rm M}={\rm P}=0$.

2.7. Efficiency of the decomposition system

We define the overall efficiency of the decomposition system as the fraction of initial substrate C that is transferred to other compartments in the form of necromass. This definition is motivated by the argument that stabilized soil organic C is largely composed of microbial necromass (Liang et al., 2017), so that decomposition is efficient from the point of view of C storage when it results in a large net export of necromass. Accordingly, we define

$\begin{array}{ll}\eta =\frac{\left(1-\mu \right)J}{c_0}=\frac{e_{\max }\left(1-\mu \right)}{C_0}\underset{0}{\overset{T_{\tau }}{{\displaystyle \int }}}G\left(U\left(T\right)\right)dT,& (38)\end{array}$

where J is the cumulative growth rate, which is maximized in the optimization problem (Equation (2)). Using this definition, we find

$\begin{array}{ll}\eta =\frac{e_{\max }\left(1-\mu \right)}{C_0}\left\{T_{\tau }-2\frac{1+{\rm P}}{m}\ln \left[\frac{V_{\tau }+m}{\sqrt{V_{\tau }^2-m^2\left(1-e^{-T_{\tau }}\right)}+m{e}^{-\frac{T_{\tau }}{2}}}\right]\right\}.& (39)\end{array}$

More compact formulas for $\eta$ are reported in Table 2 for the simpler cases with ${\rm M}=0$ and/or ${\rm P}=0$.

2.8. Model parameters

The model is meant to represent a generic system where decomposers forage on a single cohort of a chemically homogeneous substrate in the absence of additional C inputs. For illustration, we chose parameter values broadly representing the decomposition of 1 g C of plant litter by microbial saprotrophs (for conciseness, in the following we do not specify ‘C’ in the units).

We expect that litter is decomposed over time scales of years, so that $0<\gamma \le 1$ y⁻¹ (when studying CUE-growth trade-offs, we allow $\gamma$ to reach as high as 10⁴ y⁻¹ for illustration). Consistent with these characteristic timescales and initial substrate C values, $\beta$ is allowed to vary in the range $0<\beta \le 1$ g y⁻¹. The maximum growth efficiency is set to $e_{\max }=$0.5, but we also consider values within the plausible range 0$<e_{\max }\le$0.8 (Manzoni et al., 2017). The maintenance respiration rate is varied in the range $0\le \rho \le 0.4$ g y⁻¹. There is no consensus on the fraction of decomposer necromass that is recycled as a substrate. Depending on the specific microorganism and environmental context, necromass can be labile or recalcitrant, but can also be stabilized via adsorption and occlusion within soil aggregates. For labile necromass that is re-used as substrate, $\mu =1$, whereas for recalcitrant or otherwise not bioavailable necromass, $\mu =0$. Therefore, we explore the full range $0\le \mu \le 1$.

Empirical and optimization models for decomposition were compared using a litterbag decomposition time series. To meet the model assumptions, we selected litter of Swida controversa, which is characterized by relatively low lignin content (to ensure a relatively homogeneous substrate) and high initial nitrogen content (to avoid nutrient limitation), and that was almost completely degraded by the end of the field incubation (data from “upper site” in Osono and Takeda, 2005). Linear ($u=kc$), Monod-type ($u=\frac{vc}{K+c}$), and optimization-based kinetics were used to fit the time series of remaining litter C. The three models shared the same structure (including respiration and necromass recycling, as in Figure 1A), and only varied by their decomposition kinetics. Parameters k (linear model), v and K (Monod model), and $\beta$ and $\rho$ (optimization model) were estimated by nonlinear least square fitting. For all models, we set $\gamma =0.8$ y⁻¹, $e_{\max }=$0.5, $\mu =$0.5.

3. Results

In the Results section, the solutions are shown in dimensional form for ease of interpretation, and to illustrate the role of individual parameters on optimal u, and corresponding g and c, during the decomposition process. We start by presenting solutions as a function of time and remaining substrate C (Section 3.1). Next, we illustrate variations in initial decomposition rate and terminal time as microbial traits encoded in model parameters are changed (Section 3.2). Last, we present evidence of CUE-growth rate trade-offs and describe patterns in system efficiency when microbes face increasingly large abiotic C losses (Section 3.3).

3.1. Optimal decomposition kinetics and substrate C trajectories

The optimal decomposition rate decreases through time, but it reaches zero at the terminal time only if maintenance respiration is set to zero (Figures 2C,D). Increasing the rate of uncontrolled losses $\gamma$ or the half saturation constant$\beta$ (proportional to the maximum growth rate) increases the initial values of u (from dashed to solid lines in Figure 2). However, this more rapid initial depletion of the substrate causes u to decrease faster at higher $\gamma$ or $\beta$. As a direct consequence of the patterns in u in combination with the uncontrolled losses, substrate C decreases faster with higher values of $\gamma$ or $\beta$ (Figures 2E,F). Decomposition is also faster at any time point when maintenance respiration is larger than zero, because decomposition is promoted to compensate for maintenance C costs, compared to a scenario without maintenance respiration (compare colored and black lines in Figures 2C,D). Lower maximum growth efficiency ($e_{\max }$) slows down microbial growth, but marginally affects u and substrate C decline (orange vs. blue curves in Figure 2). Notably, necromass recycling does not affect u (Equation (32)), but slightly delays the decline in substrate C thanks to the partial recycling of C that would be otherwise lost from the system (not shown).

The shape of the optimal decomposition kinetics is best illustrated by plotting u as a function of substrate C (with time progressing as c is depleted). The u(c) function is concave downward, scaling approximately as $c^{1/2}$ with an intercept larger than zero at c = 0 when maintenance respiration is present (Figures 3A,B). This means that the optimal decomposition rate does not reach zero at the terminal time. Consistent with the time trajectories in Figure 2, increasing $\gamma$ or $\beta$ shifts the u(c) curves upwards. The optimal growth rate broadly follows the patterns of u, but the decline of g near c = 0 is delayed compared to u (Figures 3C,D). As a result, the CUE increases during decomposition (i.e., with decreasing c) in the absence of maintenance costs, while it remains approximately stable otherwise (Figures 3E,F). Lower $e_{\max }$ decreases both g and CUE (orange vs. blue curves in Figure 3).

FIGURE 3

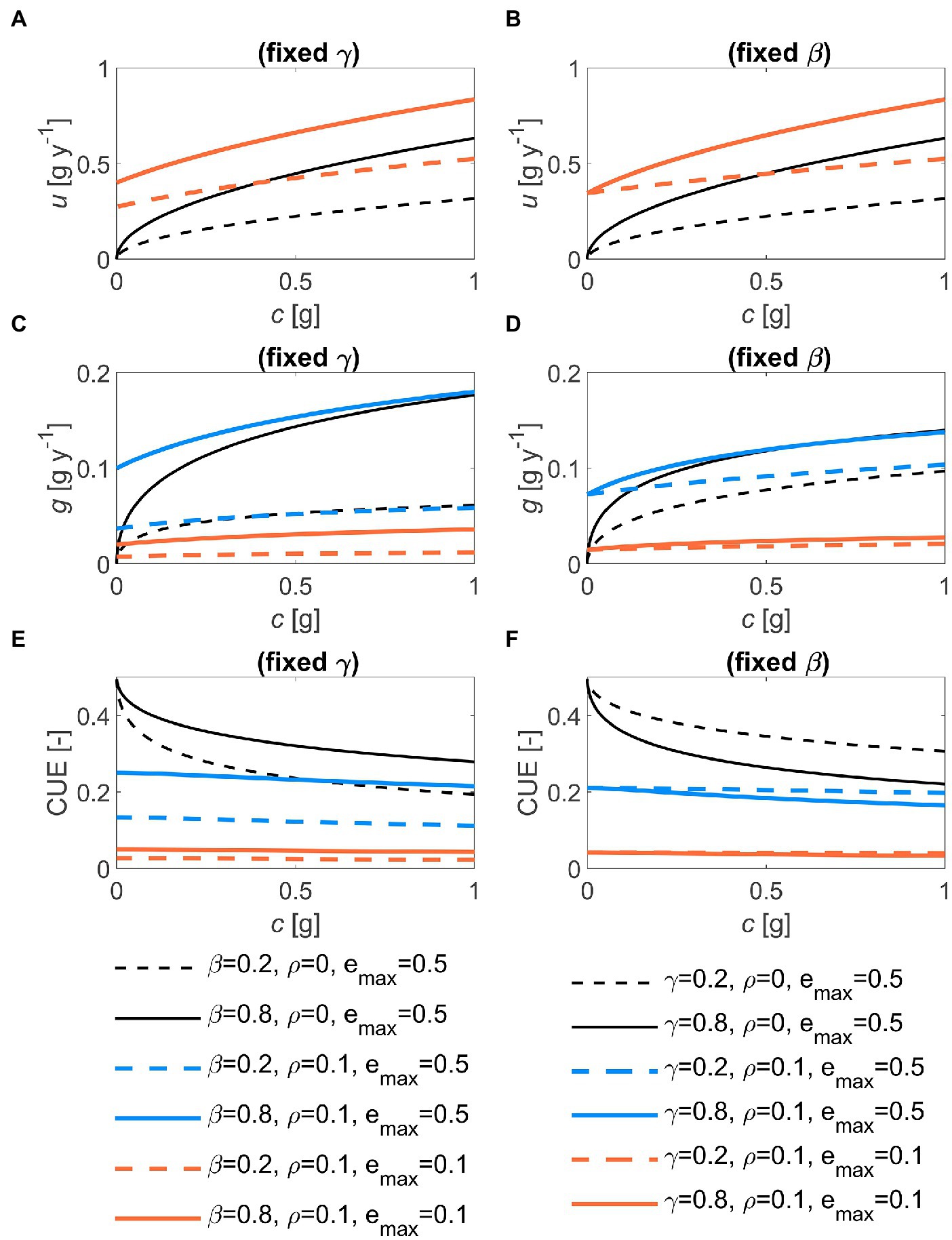
Figure 3. Effects of the half saturation constant of the microbial growth rate ($\beta$, left panels) and of the first-order decay constant ($\gamma$, right panels), for two values of maintenance respiration ($\rho$) and maximum growth efficiency ($e_{\max }$) on: (A,B) the relation between optimal decomposition rate and substrate carbon, u(c); (C,D) the relation between optimal growth rate and c, g(c); and (E,F) the relation between microbial C-use efficiency (CUE) and c. In all panels: $c_0=$1 g, $\mu =$0.5. Parameter units are as in Table 1.

3.2. Initial decomposition rate and terminal time

The initial u increases with $\gamma$ and $\beta$, whereas it is independent of $e_{\max }$ and $\mu$ (Figures 4A–C). The terminal time $t_{\tau }$ also depends on $\gamma$ and $\beta$, showing inverse trends compared to u because faster decomposition implies shorter $t_{\tau }$ (Figures 4D–F). When necromass is recycled, the time to consume all the substrate increases (blue vs. black curves in Figures 4D,F). Similarly, higher values of $e_{\max }$ – by promoting C retention in the system – lengthen the decomposition process, although this effect appears only when $\mu >0$ (Figure 4F).

FIGURE 4

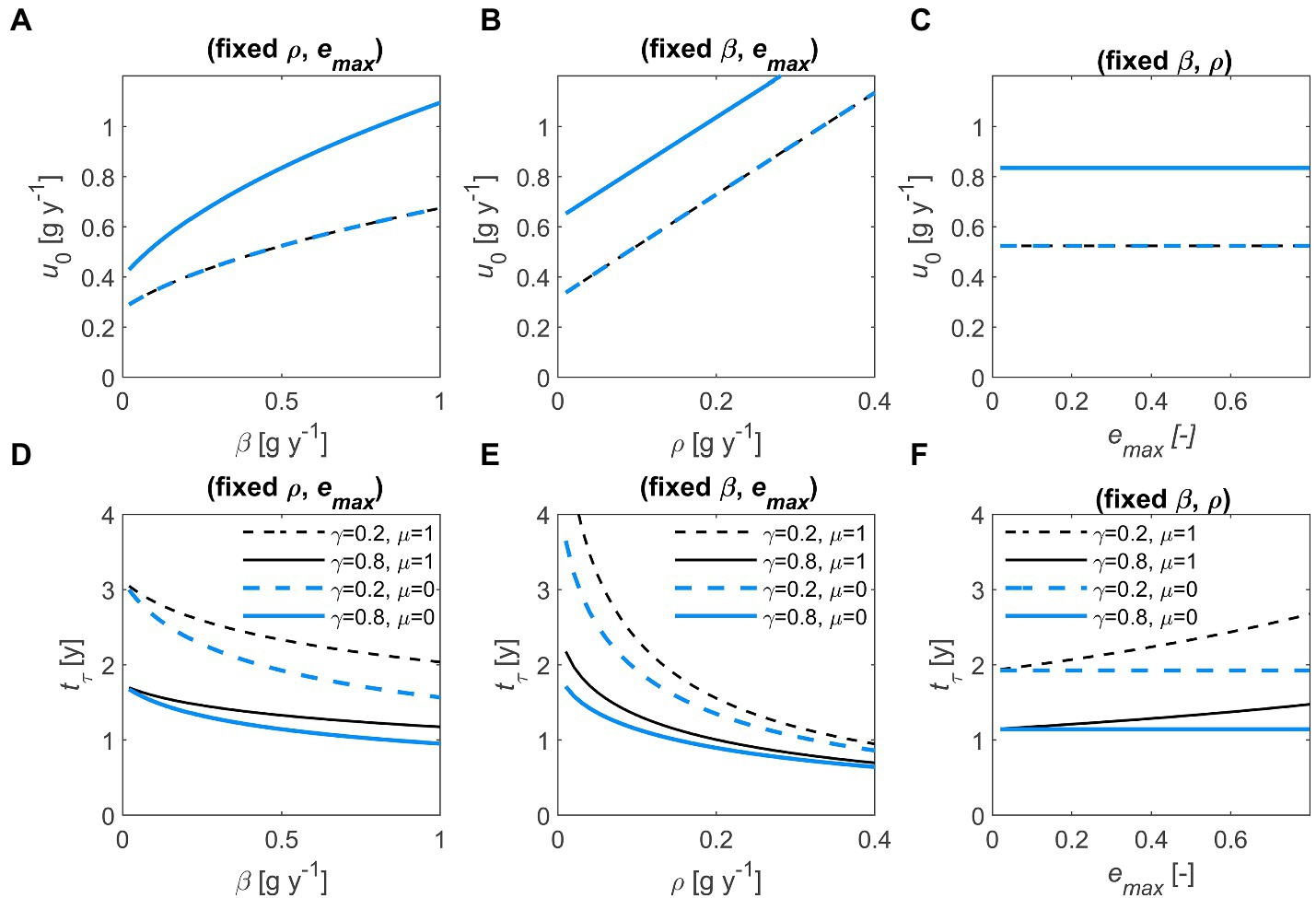
Figure 4. Effect of half saturation constant ($\beta$, left column), maintenance respiration rate ($\rho$, central column), and maximum microbial growth efficiency ($e_{\max }$, right column) on initial optimal decomposition rate ($u_0$, top row) and terminal time ($t_{\tau }$, bottom row), for two values of the first-order decay constant ($\gamma$, dashed vs. solid) and the necromass recycling fraction ($\mu$, black vs. blue). Other parameters: $c_0=$1 g (all panels), $\rho$ = 0.1 g y⁻¹ (A,C,D,F), $\beta$ = 0.5 g y⁻¹ (B,C,E,F), $e_{\max }=$0.5 (A,B,D,E). In (A–C), lines with different values of $\mu$ overlap because $u_0$ is independent of $\mu$. In all panels: $c_0=$1 g. Parameter units are as in Table 1.

3.3. C-use efficiency-growth trade-offs and system efficiency

Varying the rate of C losses $\gamma$ drives changes in the initial decomposition rate, growth rate, and CUE. As both these rates increase, initial CUE decreases (Figure 5 shows the relation between CUE and growth rate), implying a rate-efficiency trade-off along environmental gradients where resource losses vary. The trade-off is stronger when $\rho =0$ (black curves in Figure 5), because maintenance respiration tends to reduce variations in CUE (Figures 3E,F). Moreover, decreasing $e_{\max }$ shifts the trade-off relations towards lower CUE values and lower initial growth rates (orange vs. blue curves in Figure 5).

FIGURE 5

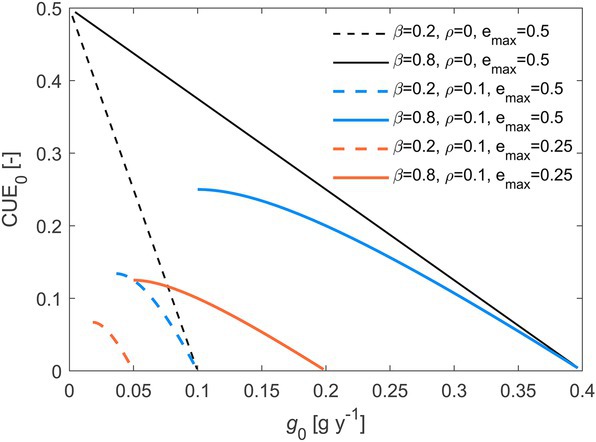
Figure 5. Trade-off between initial microbial C-use efficiency (${\mathrm{CUE}}_0$) and initial growth rate ($g_0$), when varying the C loss rate constant ($\gamma$, increasing from 10⁻⁴ to 10⁴ y⁻¹ left to right along the curves). Line styles refer to different combinations of the half saturation constant ($\beta$), maintenance respiration rate ($\rho$), and maximum microbial growth efficiency ($e_{\max }$). Other parameters: $c_0=$ 1 g, $\mu =$0.5. Parameter units are as in Table 1.

The overall system efficiency ($\eta$), decreases as substrate C losses increase (Figure 6). Such a decrease can be compensated by a lower fraction of necromass recycled (dashed vs. solid lines), a lower rate of maintenance respiration (black vs. colored lines), or a higher $e_{\max }$ (blue vs. orange curves in Figure 6). The strong effect of necromass recycling is explained by our definition of system efficiency as the fraction of initial C that is transferred to stabilized forms (i.e., that is not recycled as a labile substrate). The latter two parameters ($\rho$, $e_{\max }$) instead regulate C retention in biomass, and thus how much of the C that microbes take up can be eventually stabilized.

FIGURE 6

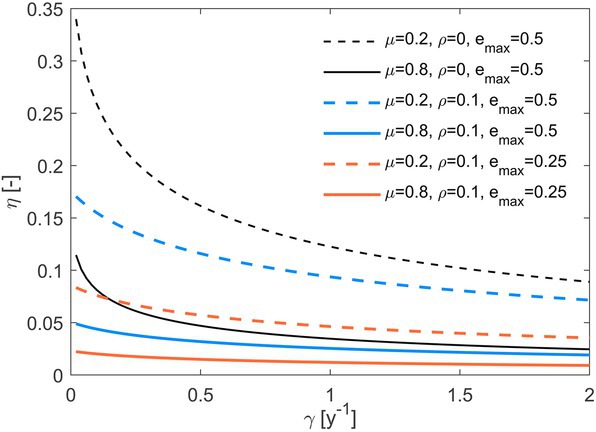
Figure 6. Whole system efficiency ($\gamma$) as a function of the C loss rate constant ($\gamma$). Line styles refer to different combinations of the fraction of necromass recycled ($\mu$), maintenance respiration rate ($\rho$), and maximum microbial growth efficiency ($e_{\max }$). Other parameters:$c_0=$1 g, $\beta =$0.5 g y⁻¹. Parameter units are as in Table 1.

4. Discussion

We proposed an optimization approach to define decomposition kinetics, based on the idea that decomposition is an emergent property of complex microbial dynamics that might be difficult to capture with prescribed kinetics. In our approach, maximum growth is attained by balancing C gains from substrate uptake and C costs for substrate acquisition, maintenance, and growth. This simple principle has already been applied to describe various aspects of decomposition (see a short review of the literature in Section 4.1), but not to our knowledge to define the shape of the decomposition kinetics or changes in decomposition rate through time. The advantage in doing so is that the optimal kinetics structurally account for environmental conditions (resource limitation setting constraints on the optimization) and physiological trade-offs. In contrast, models with prescribed kinetics can only account for these effects through time invariant parameter which might not offer sufficient flexibility to capture microbial adaptations. This advantage might prove particularly important when studying microbial responses to combined climate and land use changes, which challenge microbial communities in ways difficult to replicate in experiments.

4.1. Is there an optimal decomposition rate that maximizes total microbial growth for a given substrate amount?

Describing the decomposition process as an optimal control problem allows for determining the decomposition rate that maximizes microbial growth over the decomposition period. This approach builds on the Darwinian principle that organisms able to maximize their fitness (reproductive success, which translates into biomass growth for soil microbes) should be selected by evolutionary processes (Harrison et al., 2021). This idea has been exploited in previous theoretical works. For example, enzyme synthesis for competing cellular processes (Baloo and Ramkrishna, 1991), cell wall transporter abundance (Casey and Follows, 2020), internal cell composition (Franklin et al., 2011; Maitra and Dill, 2015), allocation to extra-cellular enzymes (Vetter et al., 1998; Averill, 2014; Wutzler et al., 2017; Calabrese et al., 2022), rates of specific metabolic reactions (Vallino et al., 1996), or allocation of C to growth vs. respiratory processes (Manzoni et al., 2017) can be optimized. However, in most of these approaches, the growth rate was maximized at a given time and for given conditions, neglecting an essential feature of decomposition systems – the limiting resources are finite and maximizing growth or consumption rates can lead to a rapid, and suboptimal, resource depletion. Here we approach the problem from the alternative perspective of optimal decomposition rate constrained by limited resource availability.

We found that there is indeed an optimal decomposition rate that allows microbes to effectively ‘compete’ with biotic or abiotic processes that remove C substrate from the system. Decomposition rates higher than the optimal would result in faster growth, but for a shorter time and at a relatively lower CUE. In contrast, slower rates would leave more substrate to the competitors or to abiotic processes removing resources from the system, leading to lower growth over the whole decomposition period. As substrate losses decrease (lower $\gamma$), the optimal decomposition rate is reduced while decomposition time (i.e., terminal time) increases, maximizing the cumulative growth. Notably, the optimal decomposition rate tends to zero in the absence of substrate losses ($\gamma =0$). This mathematical result suggests that microbes invest energy and nutrients in the production of extra-cellular enzymes as long as there is an evolutionary pressure to do so – if the substrate always remained available through time, microbes would not evolve costly acquisition strategies.

An optimal balance between resource use and time to deplete the resource emerges also in other ecological contexts. For example, plant transpiration rate can be optimized (via regulation of stomatal conductance) to maximize plant net C assimilation. This problem has been formulated – as for decomposition models – as an instantaneous maximization problem (e.g., Bassiouni and Vico, 2021 and references therein) or an optimal control problem including the constraint that soil water is limited (Manzoni et al., 2022). The advantage of formulating resource consumption problems by formally accounting for resource availability constraints (limited substrate C, or soil water in the case of plant growth) is that the optimal solution naturally captures the consumption rate-time trade-off that is inherent in these problems. Approaches based instead on instantaneous maximization can lead to sub-optimal solutions (Feng et al., 2022).

4.2. Are the optimal decomposition kinetics consistent with established empirical or theoretical decomposition kinetics?

Most optimization approaches focused on finding optimal model parameter values for prescribed kinetics of decomposition (Baloo and Ramkrishna, 1991; Averill, 2014; Wutzler et al., 2017; Casey and Follows, 2020; Calabrese et al., 2022). Here instead we do not prescribe any specific kinetics of decomposition, but let that emerge from the optimization. The optimal decomposition rate is in fact obtained analytically as a function of C availability during decomposition.

The optimal kinetics of decomposition scale as the square root of substrate C (Figures 3A,B; Table 2). As a consequence, the optimal growth rate resembles the Monod-type decomposition functions often used in models of microbial growth in cultures (Monod, 1949) and then re-purposed for soil C cycling models (see Manzoni and Porporato, 2009 for a review), although in our optimal solution substrate C appears under square root. The Monod form emerges from the combination of transport and uptake limitations or competing chemical reactions and physical processes (Liu, 2007; Tang and Riley, 2019). In contrast, here the curvature of the optimal decomposition rate vs. C concentration relation is due to two factors: decreasing returns at high decomposition rates (Equation (10)) and higher rates required to compete with other processes removing substrate C from the system.

It is noteworthy that even without prescribing specific mechanisms of C release from the substrate (enzymatic reaction kinetics, extra-cellular enzyme synthesis) and transport from the site of decomposition to the cells (diffusion, advection), we obtain optimal kinetics that have similar downward concavity as previously proposed kinetics laws. This similarity is apparent when fitting empirical and optimal kinetics to the same litter decomposition dataset (Figure 7). The optimal kinetics perform as well as linear or Monod-type kinetics, at least in the case study of a relatively homogeneous and labile litter we selected for illustration (Figure 7A). The optimal and Monod-type u(c) and g(c) relations share some qualitative similarities – e.g., downward concavity and convergence to u ~ 0 at low c. However, they both differ from the simpler linear kinetics that do not saturate at high values of c.

FIGURE 7

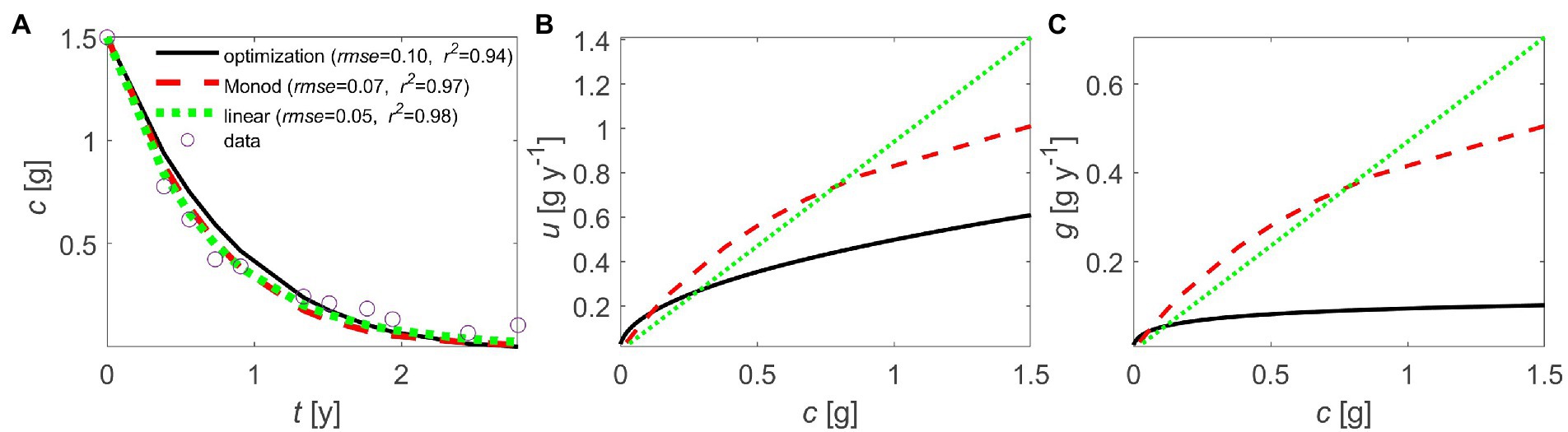
Figure 7. Comparison of linear ($u=kc$), Monod-type ($u=\frac{vc}{K+c}$), and optimal decomposition kinetics to describe litter C mass loss: (A) temporal trajectory of litter C (c) and model fitting performance (RMSE: root mean square error; R²: coefficient of determination), (B) decomposition rate as a function of litter C (u(c)), and (C) microbial growth rate as a function of litter C (g(c)). Data are from Osono and Takeda (2005); see details on model fitting in Section 2.8 (linear model parameter: k = 0.94 y⁻¹; Monod model parameters: v = 1.68 g y⁻¹, K = 1.00 g; optimization model parameters: $\beta =$0.3 g y⁻¹, $\rho =$ 0.002 g y⁻¹).

In contrast to Monod-type relations, as the substrate concentration decreases, the optimal kinetics tend to zero only when maintenance respiration is negligible, whereas in general they converge to a value larger than zero, and for small values of maintenance respiration, $u~\sqrt{\rho }$. This behavior is due to the presence of maintenance costs that require fast decomposition at low substrate to maintain positive growth even at the end of the decomposition process. This result can be contextualized by recalling that our model describes dynamics in homogeneous conditions. We can then consider a collection of homogeneous litter (or soil) patches that are internally homogeneous, but that differ in initial C or environmental conditions. The terminal times in each of these patches will differ, resulting in the superposition of patch-scale u(c) curves that could cause a tapering off of the C decay trajectory at the macroscopic scale when some patches have very long terminal times. Other processes not included here, such as dormancy, could also lengthen the decomposition process. We speculate that these effects could explain why empirical kinetics reach zero at low substrate concentrations and thus appear to be sub-optimal.

Moreover, different from classical microbial growth kinetics, the optimal decomposition rate increases with increasing rate of resource loss. While there is a clear ecological explanation for this effect (Section 4.1), we can also interpret $\gamma$ from a physical perspective for the case study of terrestrial litter decomposition. Leaching of organic C could be modelled as the product of the medium hydraulic conductance and C concentration, so that $\gamma$ is interpreted as hydraulic conductivity for a given litter layer thickness. In turn, soil hydraulic conductivity scales as medium water content to a power typically higher than 10 for soils (Rodriguez-Iturbe and Porporato, 2004), suggesting a strong nonlinear control of water content on C losses in moist conditions. Because optimal decomposition scales as the square root of $\gamma$, we can expect it to also scale as water content to a power ~ 5. This result suggests that decomposition rates in wet – but still oxic – environments should have evolved in such a way as to increase more than linearly with water content just to contrast hydrological-driven C losses.

The similarities of the optimal and empirical kinetics suggest that the proposed equations could be tested in soil C cycling models as an alternative to currently employed kinetics (Figure 1B). There are major differences between the idealized model structure we adopted and the multi-compartment structures of most C cycling models, and the parameters in our formulation (e.g., $\beta$ and $\rho$) are not widely available, hindering a direct application of our solutions in C cycling models. However, it would be interesting to test if kinetics with the same functional form as the optimal solution, but with parameters to be calibrated, perform well once included in the more complex C cycling models. This approach rests on the assumption that each compartment of these models behaves like one substrate-microbial biomass pair as conceptualized here. An application of this approach is illustrated in Figure 7 for a relatively homogeneous litter type.

4.3. How does the optimal decomposition rate vary with microbial traits?

Microbial traits encoded in model parameters affect the optimal decomposition rate mostly via the half saturation constant of the growth function ($\beta$) and the rate of maintenance respiration ($\rho$). Higher maximum microbial CUE and the fraction of recycled necromass increase the terminal time of decomposition because they promote C retention in the system, but they do not affect the optimal decomposition rate per se (Figure 4).

The effect of $\beta$ can be explained by recalling first that growth is also rescaled by $\beta$ to ensure that CUE remains lower than one. This means that $\beta$ also regulates the maximum growth rate. Therefore, microbes with higher growth capacity should evolve a matching decomposition capacity, even if the relation between these two traits is predicted to be nonlinear, with decomposition rate scaling as the square root of $\beta$ (Table 2). Higher maintenance costs require an increased decomposition rate to ensure positive net growth (Section 4.2), so increasing $\rho$ promotes faster decomposition (Figure 4B; Table 2), even though microbial CUE is decreased. Moreover, if both $\beta$ and $\rho$ exhibit similar sensitivities to environmental conditions, that sensitivity will be retained in the decomposition rate, because u scales linearly with $\rho$ and $\sqrt{\beta \rho }$ (Table 2). For example, physiological responses to warming in terms of changes in $\rho$ and $\beta$ should be reflected by similar temperature dependence of the overall decomposition rate.

4.4. Are any trade-offs between growth rate and CUE emerging from the optimal decomposition strategy?

It has been hypothesized that CUE could exhibit an inverse relation with decomposition or growth rate when comparing different microbial resource use strategies, due to increasing inefficiencies at high rates (Roller and Schmidt, 2015). The occurrence of such a relation is debated – there is both supporting (Muscarella et al., 2020) and contrasting (Calabrese et al., 2021) evidence of CUE-growth rate trade-offs across isolates grown in laboratory studies. However, this trade-off can occur in whole soil microbial communities (Lipson et al., 2009) that have adapted to a range of competition pressures (Lipson, 2015). High CUE and low resource acquisition are expected to be selected in high-resource environments (high yield strategy, ‘Y’), while high resource acquisition and low CUE would be selected in low-resource and highly competitive conditions (acquisition strategy, ‘A’) (Malik et al., 2020). Consistent with this conceptual understanding, we found that microbial CUE decreases with increasing optimal decomposition or growth rate when the risk of losing C is higher (increasing $\gamma$; Figure 5) or when initial C is lower (results not shown) – i.e., when the long-term resource availability decreases.

The tradeoff we found is also consistent with results from another optimization approach, where the allocation of resources to growth (equivalent to our CUE) was the control variable (Frank, 2010). In that framework, microbial populations with lower CUE were selected when the expected survival time of the population was shorter, suggesting that environments with high rate of resource loss (high $\gamma$) or subjected to frequent disturbances should select strains with fast, but inefficient, growth.

The shape of the CUE-growth trade-off varies with $\rho$. Higher maintenance costs, by promoting high optimal decomposition rates, also keep microbes far from the high-efficiency growth that would occur at low decomposition rate and $\rho$ = 0. As a result, the CUE-rate inverse relation flattens as $\rho$ is increased. This result is qualitatively consistent with empirical evidence that the CUE-growth rate relation is negative in microbes with high efficiency (low maintenance costs) and relatively flat in microbes with low efficiency (high maintenance costs) (Muscarella et al., 2020).

4.5. Model limitations and extensions

The proposed model, with a single substrate pool and a single microbial pool, is relatively simple to analyze, allowing full analytical tractability. While this ‘minimal’ model offers clear insights on the optimal kinetics and their consequences on the substrate C balance, it misses potentially important biological, biochemical, and ecological factors. From a biological perspective, we did not study how specific metabolic processes might be optimized, but focused on the macroscopic effect of such processes on decomposition capacity (expressed through the control variable u). As a first step towards improved biological realism, maintenance respiration could be coupled to decomposition capacity by assuming that higher capacity is possible thanks to higher respiratory costs for synthesizing enzymes (as in Calabrese et al., 2022, but in a temporally dynamic context). As an alternative, complex metabolic networks have been analyzed using optimization methods to predict biomass growth and substrate consumption rates (Vallino, 2010; Waldherr et al., 2015; Giordano et al., 2016). While less mechanistic, our approach shows the kinetics of decomposition that would emerge had the decomposers been optimally adapted.

Perhaps the main limitation of our approach is that it postulates that the whole microbial community adapts in the same way. Clearly, competition, mutualism, and predation shape microbial community dynamics (Allison, 2014; Abs et al., 2020; Sokol et al., 2022), providing evolutionary pressures to exploit different niches. However, one could argue that as a first approximation, the (optimal) behavior of a representative organism in the community could be identified and used to characterize the average system dynamics. Studying the aggregated dynamics instead of letting it emerge from the underlying interactions is prone to aggregation errors (Chakrawal et al., 2020), but at least it allows identifying the main controlling factors in a transparent way. For example, CUE at community level varies along nutrient availability gradients as predicted by a community level optimality criterion (Manzoni et al., 2017). In plant communities, most species exhibit traits converging towards the community weighted mean, also suggesting some degree of coordination in the way plants within the community acclimate and adapt (Muscarella and Uriarte, 2016). This evidence supports our assumption that – as a first approximation – optimality criteria can be applied at the community level.

This interpretation, however, can be problematic when investigating long-term processes such as decomposition. In fact, as litter is decomposed, the microbial community undergoes successional dynamics (Berg and McClaugherty, 2003). We incorporated shifts in community composition from low-efficiency, fast-growing organisms (r-strategists) to high-efficiency, slow-growing ones (K-strategists) through the shape of the g(u) relation. Therefore, rather than predicting the outcome of succession, our model is constrained by its occurrence in terms of varying CUE. The optimal u we obtain should then be interpreted as the realized decomposition rate that maximizes the community-level growth over the decomposition process, regardless of the specific actors involved at any particular time during the process.

Previous contributions have explored optimal allocation to enzymes targeting different compounds (Averill, 2014; Wutzler et al., 2017), but not in a dynamic context where the goal function is cumulative biomass growth, as done here. Other efforts focused on the selection process per se, by modelling interacting microbial taxa (Allison, 2014; Abs et al., 2020), but translating those results into easily applicable kinetics laws is difficult. Including multiple substrate pools and enzymes targeting specific substrates in our optimal control framework would thus complement these previous works. Moreover, microbial biomass dynamics could be explicitly represented by an additional mass balance constraint. Along these lines, considering also different microbial functional groups would allow addressing the current limitation that optimization is performed at the community level, but would also raise additional questions – should all groups behave optimally given the presence of the other groups? Or should we postulate an ‘ecosystem level’ optimality criterion (Dewar, 2010)?

5. Conclusion

Starting from the assumption that the decomposition rate is optimized to maximize microbial growth, we have developed an analytical model of organic matter decomposition. When neglecting maintenance respiration, the optimal decomposition kinetics scale as the square root of the substrate C content, so that the growth rate follows a Hill function with exponent ½. In a more general case, including maintenance respiration, optimal kinetics diverge from typical Hill functions, for example by prescribing high decomposition rates even when substrates are nearly exhausted. The evolutionary pressure for performing rapid decomposition is provided here by the risk of losing resources to abiotic processes or other organisms. When such a risk increases, the optimal microbial foraging strategy shifts from high efficiency growth and slow decomposition rates to low efficiency growth and fast rates. Therefore, a growth efficiency-rate trade-off emerges along gradients of increasing pressure to use limiting resources.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

SM designed the study, constructed the model, and drafted the manuscript. AC contributed to the model design and numerical solution. GL derived the analytical solution of the model. All authors contributed to the article and approved the submitted version.

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement no 101001608).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1094269/full#supplementary-material

References

Abramoff, R., Xu, X. F., Hartman, M., O’Brien, S., Feng, W. T., Davidson, E., et al. (2018). The millennial model: in search of measurable pools and transformations for modeling soil carbon in the new century. Biogeochemistry 137, 51–71. doi: 10.1007/s10533-017-0409-7

CrossRef Full Text | Google Scholar

Abs, E., Leman, H., and Ferriere, R. (2020). A multi-scale eco-evolutionary model of cooperation reveals how microbial adaptation influences soil decomposition. Commun. Biol. 3:520. doi: 10.1038/s42003-020-01198-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Allison, S. D. (2012). A trait-based approach for modelling microbial litter decomposition. Ecol. Lett. 15, 1058–1070. doi: 10.1111/j.1461-0248.2012.01807.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Allison, S. D. (2014). Modeling adaptation of carbon use efficiency in microbial communities. Front. Microbiol. 5, 1–9. doi: 10.3389/fmicb.2014.00571

PubMed Abstract | CrossRef Full Text | Google Scholar

Averill, C. (2014). Divergence in plant and microbial allocation strategies explains continental patterns in microbial allocation and biogeochemical fluxes. Ecol. Lett. 17, 1202–1210. doi: 10.1111/ele.12324

PubMed Abstract | CrossRef Full Text | Google Scholar

Baloo, S., and Ramkrishna, D. (1991). Metabolic-regulation in bacterial continuous cultures. 1. Biotechnol. Bioeng. 38, 1337–1352. doi: 10.1002/bit.260381112

CrossRef Full Text | Google Scholar

Bassiouni, M., and Vico, G. (2021). Parsimony vs predictive and functional performance of three stomatal optimization principles in a big-leaf framework. New Phytol. 231, 586–600. doi: 10.1111/nph.17392

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, B., and McClaugherty, C. A. (2003). Plant Litter. Decomposition, Humus Formation, Carbon Sequestration. Berlin: Springer.

Google Scholar

Calabrese, S., Chakrawal, A., Manzoni, S., and Van Cappellen, P. (2021). Energetic scaling in microbial growth. Proc. Natl. Acad. Sci. 118:e2107668118. doi: 10.1073/pnas.2107668118

PubMed Abstract | CrossRef Full Text | Google Scholar

Calabrese, S., Mohanty, B., and Malik, A. (2022). Soil microorganisms regulate extracellular enzyme production to maximize their growth rate. Biogeochemistry 158, 303–312. doi: 10.1007/s10533-022-00899-8

CrossRef Full Text | Google Scholar

Casey, J., and Follows, M. (2020). A steady-state model of microbial acclimation to substrate limitation. PLoS Comput. Biol. 16:e1008140. doi: 10.1371/journal.pcbi.1008140

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakrawal, A., Herrmann, A. M., Koestel, J., Jarsjo, J., Nunan, N., Kätterer, T., et al. (2020). Dynamic upscaling of decomposition kinetics for carbon cycling models. Geosci. Model Dev. 13, 1399–1429. doi: 10.5194/gmd-2019-133

CrossRef Full Text | Google Scholar

del Giorgio, P. A., and Cole, J. J. (1998). Bacterial growth efficiency in natural aquatic systems. Annu. Rev. Ecol. Syst. 29, 503–541. doi: 10.1146/annurev.ecolsys.29.1.503

CrossRef Full Text | Google Scholar

Dewar, R. C. (2010). Maximum entropy production and plant optimization theories. Philos. Trans. R. Soc. B. Biol. Sci. 365, 1429–1435. doi: 10.1098/rstb.2009.0293

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, X., Lu, Y., Jiang, M., Katul, G. G., Manzoni, S., Mrad, A., et al. (2022). Instantaneous stomatal optimization results in suboptimal carbon gain due to legacy effects. Plant Cell Environ. 45, 3189–3204. doi: 10.1111/pce.14427

PubMed Abstract | CrossRef Full Text | Google Scholar

Frank, S. A. (2010). The trade-off between rate and yield in the design of microbial metabolism. J. Evol. Biol. 23, 609–613. doi: 10.1111/j.1420-9101.2010.01930.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Franklin, O., Hall, E. K., Kaiser, C., Battin, T. J., and Richter, A. (2011). Optimization of biomass composition explains microbial growth-stoichiometry relationships. Am. Nat. 177, E29–E42. doi: 10.1086/657684

PubMed Abstract | CrossRef Full Text | Google Scholar

Giordano, N., Mairet, F., Gouze, J. L., Geiselmann, J., and de Jong, H. (2016). Dynamical allocation of cellular resources as an optimal control problem: novel insights into microbial growth strategies. PLoS Comput. Biol. 12:e1004802. doi: 10.1371/journal.pcbi.1004802

PubMed Abstract | CrossRef Full Text | Google Scholar

Gudelj, I., Weitz, J. S., Ferenci, T., Horner-Devine, M. C., Marx, C. J., Meyer, J. R., et al. (2010). An integrative approach to understanding microbial diversity: from intracellular mechanisms to community structure. Ecol. Lett. 13, 1073–1084. doi: 10.1111/j.1461-0248.2010.01507.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison, S. P., Cramer, W., Franklin, O., Prentice, I. C., Wang, H., Brännström, Å., et al. (2021). Eco-evolutionary optimality as a means to improve vegetation and land-surface models. New Phytol. 231, 2125–2141. doi: 10.1111/nph.17558

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, D. E. (1970). Optimal Control Theory. An Introduction. Englewood Cliffs, NJ: Prentice-Hall Inc.

Google Scholar

Lenhart, S., and Workman, J. T. (2007). Optimal Control Applied to Biological Problems. New York, NY: Chapman & Hall/CRC.

Google Scholar

Liang, C., Schimel, J. P., and Jastrow, J. D. (2017). The importance of anabolism in microbial control over soil carbon storage. Nat. Microbiol. 2:17105. doi: 10.1038/nmicrobiol.2017.105

PubMed Abstract | CrossRef Full Text | Google Scholar

Lipson, D. A. (2015). The complex relationship between microbial growth rate and yield and its implications for ecosystem processes. Front. Microbiol. 6:615. doi: 10.3389/fmicb.2015.00615

PubMed Abstract | CrossRef Full Text | Google Scholar

Lipson, D. A., Monson, R. K., Schmidt, S. K., and Weintraub, M. N. (2009). The trade-off between growth rate and yield in microbial communities and the consequences for under-snow soil respiration in a high elevation coniferous forest. Biogeochemistry 95, 23–35. doi: 10.1007/s10533-008-9252-1

CrossRef Full Text | Google Scholar

Liu, Y. (2007). Overview of some theoretical approaches for derivation of the Monod equation. Appl. Microbiol. Biotechnol. 73, 1241–1250. doi: 10.1007/s00253-006-0717-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Maitra, A., and Dill, K. A. (2015). Bacterial growth laws reflect the evolutionary importance of energy efficiency. Proc. Natl. Acad. Sci. 112, 406–411. doi: 10.1073/pnas.1421138111

PubMed Abstract | CrossRef Full Text | Google Scholar

Malik, A. A., Martiny, J. B. H., Brodie, E. L., Martiny, A. C., Treseder, K. K., and Allison, S. D. (2020). Defining trait-based microbial strategies with consequences for soil carbon cycling under climate change. ISME J. 14, 1–9. doi: 10.1038/s41396-019-0510-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzoni, S., Čapek, P., Mooshammer, M., Lindahl, B. D., Richter, A., and Šantrůčková, H. (2017). Optimal metabolic regulation along resource stoichiometry gradients. Ecol. Lett. 20, 1182–1191. doi: 10.1111/ele.12815

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzoni, S., Chakrawal, A., Spohn, M., and Lindahl, B. D. (2021). Modeling microbial adaptations to nutrient limitation during litter decomposition. Front. For. Glob. Change 4:686945. doi: 10.3389/ffgc.2021.686945

CrossRef Full Text | Google Scholar

Manzoni, S., Fatichi, S., Feng, X., Katul, G. G., Way, D., and Vico, G. (2022). Consistent responses of vegetation gas exchange to elevated atmospheric CO2 emerge from heuristic and optimization models. Biogeosciences 19, 4387–4414. doi: 10.5194/bg-19-4387-2022

CrossRef Full Text | Google Scholar

Manzoni, S., and Porporato, A. (2009). Soil carbon and nitrogen mineralization: theory and models across scales. Soil Biol. Biochem. 41, 1355–1379. doi: 10.1016/j.soilbio.2009.02.031

CrossRef Full Text | Google Scholar

Michaelis, L., and Menten, M. L. (1913). Die kinetik der invertinwirkung (translated by Goody R.S., and K.A. Johnson). Biochem. Z. 49, 333–369.

Google Scholar

Monod, J. (1949). The growth of bacterial cultures. Annu. Rev. Microbiol. 3, 371–394. doi: 10.1146/annurev.mi.03.100149.002103

CrossRef Full Text | Google Scholar

Muscarella, M. E., Howey, X. M., and Lennon, J. T. (2020). Trait-based approach to bacterial growth efficiency. Environ. Microbiol. 22, 3494–3504. doi: 10.1111/1462-2920.15120

PubMed Abstract | CrossRef Full Text | Google Scholar

Muscarella, R., and Uriarte, M. (2016). Do community-weighted mean functional traits reflect optimal strategies? Proc. R. Soc. B. Biol. Sci. 283:20152434. doi: 10.1098/rspb.2015.2434

PubMed Abstract | CrossRef Full Text | Google Scholar

Olson, J. S. (1963). Energy storage and the balance of producer and decomposers in ecological systems. Ecology 44, 322–331. doi: 10.2307/1932179

CrossRef Full Text | Google Scholar

Osono, T., and Takeda, H. (2005). Decomposition of organic chemical components in relation to nitrogen dynamics in leaf litter of 14 tree species in a cool temperate forest. Ecol. Res. 20, 41–49. doi: 10.1007/s11284-004-0002-0

CrossRef Full Text | Google Scholar

Rodriguez-Iturbe, I., and Porporato, A. (2004). Ecohydrology of Water-Controlled Ecosystems. Soil Moisture and Plant Dynamics. Cambridge: Cambridge University Press.

Google Scholar

Roller, B. R. K., and Schmidt, T. M. (2015). The physiology and ecological implications of efficient growth. ISME J. 9, 1481–1487. doi: 10.1038/ismej.2014.235

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosen, R. (1967). Optimality Principles in Biology. New York: Springer.

Google Scholar

Salter, R. M., and Green, T. C. (1933). Factors affecting the accumulation and loss of nitrogen and organic carbon in cropped soils. J. Am. Soc. Agron. 25, 622–630. doi: 10.2134/agronj1933.00021962002500090010x

CrossRef Full Text | Google Scholar

Sokol, N. W., Slessarev, E., Marschmann, G. L., Nicolas, A., Blazewicz, S. J., Brodie, E. L., et al. (2022). Life and death in the soil microbiome: how ecological processes influence biogeochemistry. Nat. Rev. Microbiol. 20, 415–430. doi: 10.1038/s41579-022-00695-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, J. Y., and Riley, W. J. (2013). A total quasi-steady-state formulation of substrate uptake kinetics in complex networks and an example application to microbial litter decomposition. Biogeosciences 10, 8329–8351. doi: 10.5194/bg-10-8329-2013

CrossRef Full Text | Google Scholar

Tang, J. Y., and Riley, W. J. (2019). A theory of effective microbial substrate affinity parameters in variably saturated soils and an example application to aerobic soil heterotrophic respiration. J. Geophys. Res. Biogeosci. 124, 918–940. doi: 10.1029/2018jg004779

CrossRef Full Text | Google Scholar

Vallino, J. J. (2010). Ecosystem biogeochemistry considered as a distributed metabolic network ordered by maximum entropy production. Philos. Trans. R. Soc. B. Biol. Sci. 365, 1417–1427. doi: 10.1098/rstb.2009.0272

PubMed Abstract | CrossRef Full Text | Google Scholar

Vallino, J. J., Hopkinson, C. S., and Hobbie, J. E. (1996). Modeling bacterial utilization of dissolved organic matter: optimization replaces Monod growth kinetics. Limnol. Oceanogr. 41, 1591–1609. doi: 10.4319/lo.1996.41.8.1591

CrossRef Full Text | Google Scholar

Vetter, Y. A., Deming, J. W., Jumars, P. A., and Krieger-Brockett, B. B. (1998). A predictive model of bacterial foraging by means of freely released extracellular enzymes. Microb. Ecol. 36, 75–92. doi: 10.1007/s002489900095

PubMed Abstract | CrossRef Full Text | Google Scholar

Waldherr, S., Oyarzun, D. A., and Bockmayr, A. (2015). Dynamic optimization of metabolic networks coupled with gene expression. J. Theor. Biol. 365, 469–485. doi: 10.1016/j.jtbi.2014.10.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, G., and Post, W. M. (2013). A note on the reverse Michaelis–Menten kinetics. Soil Biol. Biochem. 57, 946–949. doi: 10.1016/j.soilbio.2012.08.028

CrossRef Full Text | Google Scholar

Wutzler, T., and Reichstein, M. (2008). Colimitation of decomposition by substrate and decomposers - a comparison of model formulations. Biogeosciences 5, 749–759. doi: 10.5194/bg-5-749-2008

CrossRef Full Text | Google Scholar

Wutzler, T., Zaehle, S., Schrumpf, M., Ahrens, B., and Reichstein, M. (2017). Adaptation of microbial resource allocation affects modelled long term soil organic matter and nutrient cycling. Soil Biol. Biochem. 115, 322–336. doi: 10.1016/j.soilbio.2017.08.031

CrossRef Full Text | Google Scholar