Host competence, interspecific competition and vector preference interact to determine the vector-borne infection ecology

Understanding how ecological interactions affect vector-borne disease dynamics is crucial in the context of rapid biodiversity loss and increased emerging vector-borne diseases. Although there have been many studies on the impact of interspecific competition and host competence on disease dynamics, few of them have addressed the case of a vector-borne disease. Using a simple compartment model with two competing host species and one vector, we investigated the combined effects of vector preference, host competence, and interspecific competition on disease risk in a vector-borne system. Our research demonstrated that disease transmission dynamics in multi-host communities are more complex than anticipated. Vector preference and differences in host competence shifted the direction of the effect of competition on community disease risk, yet interspecific competition quantitatively but not qualitatively changed the effect of vector preference on disease risk. Our work also identified the conditions of the dilution effect and amplification effect in frequency-dependent transmission mode, and we discovered that adding vector preference and interspecific competition into a simple two-host-one-vector model altered the outcomes of how increasing species richness affects disease risk. Our work explains some of the variation in outcomes in previous empirical and theoretical studies on the dilution effect.

Introduction

Vector-borne diseases refer to the infectious diseases that are transmitted by blood-sucking arthropods such as mosquitoes, fleas, lice, ticks, etc. Most vector-borne diseases are zoonosis, they pose a great threat to human health and wildlife conservation. According to estimates, more than 1.5 million people die from vector-borne diseases worldwide each year, which accounts for 3/4 of the newly emerging infectious diseases in recent years (World Health Organization [WHO], 2004). The effective prevention and management of vector-borne diseases remains one of the main challenges of current scientific research.

There is an increased likelihood that host diversity and total disease risk are inversely related, i.e., the dilution effect hypothesis (Keesing et al., 2006, 2010; Ostfeld and Keesing, 2012). Ecologists have recently confirmed that the dilution effect does exist in some systems through the study of Lyme disease (Ostfeld and Keesing, 2000; LoGiudice et al., 2003), West Nile virus (Kilpatrick et al., 2006), amphibian trematodes (Johnson et al., 2013), and leaf fungal diseases (Mitchell et al., 2002; Liu et al., 2016). They have also come to the following conclusion about the underlying mechanism of the dilution effect: the order of community (dis)assembly is non-random, the most competent host species (the hosts’ ability to obtain and transmit pathogens) have the lowest probability of extinction (Halliday et al., 2019, 2020). As host diversity increases, a large number of low-competent or non-competent hosts (a host can become infected but is unable to transmit pathogens) are added to the community, which decreases the contact rate between highly competent hosts and vectors, a dilution effect occurs (Johnson et al., 2013). If this result holds, then the disease risk is highest when the community contains only the most competent host. However, some studies have questioned the universality of the dilution effect by demonstrating that the highest disease risk occurs when the community consists of several host species (Ostfeld and LoGiudice, 2003; Simpson et al., 2012; Costa et al., 2021). Additionally, several researchers have suggested that amplification and no effects also exist in the natural world (Wood et al., 2014; Halliday et al., 2017; Rohr et al., 2019; Vadell et al., 2019). These debates imply that a variety of ecological factors may affect disease risk, and different factors may play different or even perhaps opposite roles in different systems. Exploring how interspecific interactions (resource competition, transmission between species, and vector-host contact rate) affect vector-borne infection is critical not only for theoretical analysis, but also for vector-borne disease prevention and management.

Most vector-borne diseases are transmitted among a variety of hosts, but each host has its own ability to attract vectors, a phenomenon known as the vector preference (Rivera et al., 2020). Several empirical studies supported the existence of vector feeding preferences. For example, Anopheles gambiae, the vector of malaria, prefers to bite humans over cattle (Tirados et al., 2006). Triatoma bugs that transmit Chagas disease have a strong feeding preference for dogs over chickens and cats (Gürtler et al., 2009). Vector preference is an important ecological factor contributing to the heterogeneity in contact rates between hosts and vectors (Simpson et al., 2012). Both theoretical and experimental studies have found that vector preference not only affects the likelihood of disease outbreak and prevalence, but also interacts with other factors to influence disease dynamics (Kilpatrick et al., 2006; Simpson et al., 2012; Zeilinger and Daugherty, 2014).

Interspecific competition can alter the host’s behavior, abundance, living habits, fitness, etc., which can directly or indirectly increase disease risk. For instance, while increased rodent richness facilitates disease transmission between individuals, it can also result in increased interspecific competition, allowing for a decrease in host density, leading to an overall decrease in the prevalence of Sin Nombre Hantavirus (Cortez and Duffy, 2021). Importantly, accounting for interspecific competition may qualitatively alter predictions of diversity-disease relationships. For example, using a mathematical model of infection dynamics and a high-resolution multisite dataset, Luis et al. (2018) found that the prevalence of hantavirus decreased as small mammal diversity increases. However, competition effects, which cause hosts (deer mice) to congregate in refuges far from their main competitors, leading to increased host-to-host contact and thus increased incidence. Therefore, species diversity concurrently dilutes and amplifies disease transmission through competing mechanisms. Similarly, Strauss et al. (2015) used a general trait-based model and found that varying the relationship between the host’s ability to compete and its potential to transmit disease could produced three different outcomes: a dilution effect, an amplification effect, and no significant effect. These findings highlight the need for a better understanding of how interspecific competition affects disease ecology in multi-host communities. Although there have been several studies on the effect of host competition on disease transmission, to the best of our knowledge, few research has examined the situation of a vector-borne system (but see Marini et al., 2017).

The purpose of this paper is twofold. On the one hand, to investigate the combined effects of vector feeding preference and host interspecific competition on vector-borne infection ecology. On the other hand, to explore the exact conditions under which diversity amplification or dilution occurs. To this end, we developed a simple compartment model with two competing host species and one vector, based on the SIS framework, to describe the transmission dynamics of a vector-borne system. The basic reproduction number R₀ is used to quantify disease risk, which has been used to identify the conditions under which disease risk would increase or decrease in a multi-host community (Roberts and Heesterbeek, 2013; O’Regan et al., 2015). We found that the conversion of a disease from being extinct to becoming endemic can be made possible by changing the intensity of competition, and that the direction of the effect of competition on disease risk (increasing or decreasing) can be shifted by a combination of vector preference and host competence. Importantly, incorporating vector preference and interspecific competition into a simple model changes the outcomes of how increasing species richness affects disease risk. These findings underscore the importance of linking vector preference, interspecific competition, and host competence in describing vector-borne infection ecology.

Materials and methods

Model description

Mathematical models have been widely used to study complicated ecological processes. Many previous studies have used SIS or SIR compartmental models as a theoretical framework to analyze transmission dynamics in multi-host systems (Dobson, 2004; O’Regan et al., 2015). Similar to the models proposed by Lord et al. (1996) and Simpson et al. (2012), we constructed a simple compartment model with two hosts and one vector, both of which were classified according to whether they are susceptible S or infected I. We refer to host species 1 as the focal host that is a permanent community resident and host species 2 as the introduced host. Assuming that host species 1 and species 2 can compete with each other for resources (Kambatuku et al., 2010), and pathogens can only be transmitted indirectly through the vector, not directly through host-to-host transmission. Vectors feed on both host species, but with different feeding preferences. To simplify the model formulation and analysis, we assumed that infected hosts could die from disease or recover as susceptible individuals, but the vector could not recover from infection.

To model interspecific competition between two host species, as in O’Regan et al. (2015) and Marini et al. (2017), we assumed that the growth of both host species follows Lotka–Volterra dynamics. The following set of differential equations can be used to illustrate the model:

$\begin{array}{c}\frac{d{N}_1}{dt}=r_1{N}_1\left(1-\frac{N_1+c_{12}{N}_2}{K_1}\right)-{\mathrm{\mu }}_1{I}_1\hfill \\ \frac{d{N}_2}{dt}=r_2{N}_2\left(1-\frac{N_2+c_{21}{N}_1}{K_2}\right)-{\mathrm{\mu }}_2{I}_2\hfill \\ \frac{d{N}_v}{dt}=r_v{N}_v-{\mathrm{\mu }}_v{I}_v\hfill \\ \frac{d{I}_1}{dt}=\frac{P_{v_1}{b}_1{I}_v{S}_1}{N_1}-d_1{I}_1-{\mathrm{\delta }}_1{I}_1-{\mathrm{\mu }}_1{I}_1\hfill \\ \frac{d{I}_2}{dt}=\frac{P_{v_2}{b}_2{I}_v{S}_2}{N_2}-d_2{I}_2-{\mathrm{\delta }}_2{I}_2-{\mathrm{\mu }}_2{I}_2\hfill \\ \frac{d{I}_v}{dt}=\frac{P_{1v}{b}_1{I}_1}{N_1}{S}_v+\frac{P_{2v}{b}_2{I}_2}{N_2}{S}_v-d_v{I}_v-{\mathrm{\mu }}_v{I}_v\hfill \end{array}.(1)$

Where S_i and I_i represent the number of susceptible and infected individuals of species i, respectively, and N_irepresents the total population size of species i,N_i = S_i + I_i (i = 1, 2, v). c_ij represents the competition coefficient of species j on species i. K₁ and K₂ denote the carrying capacities of hosts 1 and 2, respectively. Previous studies have suggested that the transmission of pathogens in vector-borne systems follows a frequency-dependent mode. That is, the total number of bites per unit time by a single vector is independent of the host density (Dobson, 2004; Cortez and Duffy, 2021), therefore the incidence $\frac{P_{vi}{b}_i{I}_v{S}_i}{N_i}$ and $\frac{P_{iv}{b}_i{I}_i{S}_v}{N_i}$ denote the number of infected individuals per unit time for host species i and vector, respectively. To simplify notation, we let Γ_i = d_i + δ_i + μ_i and Γ_v = d_v + μ_v, which denote the per capita removal rate from the I_i class and I_v class, respectively. All parameters and definitions are listed in Table 1.

TABLE 1

Table 1. Parameters and definitions.

Model analysis

As mentioned above, we used the basic reproduction number R₀ as a measure of disease risk. It identifies the number of secondary infections induced by an infected host individual during the disease duration and the lifespan of the vector (Roberts and Heesterbeek, 2013). If R₀ < 1, the disease eventually disappears, otherwise, the disease will break out and become endemic. The basic reproduction number R₀ of system (1) is calculated by using the next-generation matrix approach, which involves linearizing the system at the disease-free equilibrium $(N_1^{{}^{*}},N_2^{{}^{*}},N_v^{{}^{*}})$ and decomposing the resulting Jacobian matrix into two matrices, F and V, which describe the disease transmission and transitions out of the infection state, respectively. The dominant eigenvalue of the next-generation matrix is the basic reproduction number R₀ (Diekmann et al., 2009; Roberts and Heesterbeek, 2013).

The disease-free non-trivial equilibrium point can be found by setting the first three equations of system (1) to 0:

$N_1^{{}^{*}}={\displaystyle \frac{K_1-c_{12}{K}_2}{1-c_{12}{c}_{21}}},N_2^{{}^{*}}={\displaystyle \frac{K_2-c_{21}{K}_1}{1-c_{12}{c}_{21}}},N_v^{{}^{*}}=K_v.$

Specifically, if there is no host interspecific competition, i.e., c₁₂ = c₂₁ = 0, then $N_1^{{}^{*}}=K_1,N_2^{{}^{*}}=K_2,N_v^{{}^{*}}=K_v$.

Here the epidemiological transmission matrix F at the disease-free equilibrium point $(N_1^{{}^{*}},N_2^{{}^{*}},N_v^{{}^{*}})$ is,

$F=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill P_{v1}{b}_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill P_{v2}{b}_2\hfill \\ \hfill {\displaystyle \frac{P_{1v}{b}_1{N}_v^{{}^{*}}}{N_1^{{}^{*}}}}\hfill & \hfill {\displaystyle \frac{P_{2v}{b}_2{N}_v^{{}^{*}}}{N_2^{{}^{*}}}}\hfill & \hfill 0\hfill \end{array}\right),$

and the epidemiological transition matrix V is,

$V=\left(\begin{array}{ccc}{d}_1+{\mathrm{\delta }}_1+{\mathrm{\mu }}_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ 0\hfill & \hfill d_2+{\mathrm{\delta }}_2+{\mathrm{\mu }}_2\hfill & \hfill 0\hfill \\ 0\hfill & \hfill 0\hfill & \hfill d_v+{\mathrm{\mu }}_v\hfill \end{array}\right)=\left(\begin{array}{ccc}{\mathrm{\Gamma }}_1\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\mathrm{\Gamma }}_2\hfill & 0\hfill \\ 0\hfill & 0\hfill & {\mathrm{\Gamma }}_v\hfill \end{array}\right)$

Therefore, the next-generation matrix M is,

$M=F{V}^{-1}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill {\displaystyle \frac{P_{v1}{b}_1}{{\mathrm{\Gamma }}_v}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\displaystyle \frac{P_{v2}{b}_2}{{\mathrm{\Gamma }}_v}}\hfill \\ \hfill {\displaystyle \frac{P_{1v}{b}_1{N}_v^{{}^{*}}}{N_1^{{}^{*}}{\mathrm{\Gamma }}_1}}\hfill & \hfill {\displaystyle \frac{P_{2v}{b}_2{N}_v^{{}^{*}}}{N_2^{{}^{*}}{\mathrm{\Gamma }}_2}}\hfill & \hfill 0\hfill \end{array}\right).$

The dominant eigenvalue of M is the basic reproduction number R₀ of system (1),

$R_0=\sqrt{\frac{P_{v1}{P}_{1v}{b}_1^2{N}_v^{{}^{*}}}{N_1^{{}^{*}}{\mathrm{\Gamma }}_1{\mathrm{\Gamma }}_v}+\frac{P_{v2}{P}_{2v}{b}_2^2{N}_v^{{}^{*}}}{N_2^{{}^{*}}{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_v}}.(2)$

Let $g_i=\frac{p_{vi}p_v{}_i}{{\mathrm{\Gamma }}_i}$ (i = 1, 2), according to Table 1, this parameter characterizes the transmission efficiency that an infected host species i successfully infects a conspecific individual (p_vip_iv) via the vector during its disease duration (1/Γ_i), thus representing the competence of host species i. The higher the g_i, the greater the ability of host species i to transmit disease. Substitute g_i into Eq. 2, it can be simplified to

$R_0=\sqrt{\frac{g_1{b}_1^2{N}_v^{{}^{*}}}{N_1^{{}^{*}}{\mathrm{\Gamma }}_v}+\frac{g_2{b}_2^2{N}_v^{{}^{*}}}{N_2^{{}^{*}}{\mathrm{\Gamma }}_v}}.(3)$

As shown in Eq. 3, one of the key factors to determining disease transmission potential and how R₀ varies with species richness is how the bites are divided between the two host species, b₁ and b₂, representing the biting rates of the vector to species 1 and 2, respectively. Assuming that host density is high enough not to limit the biting rate of the vector so that the vector has a fixed daily biting rate b_max (Rogers, 1988). If a vector has no preference for any hosts, then the biting rate of the vector for a specific host is determined by the density of the host (Marini et al., 2017), therefore $b_i=b_{\max }\cdot \frac{N_i}{N_1+N_2},i=1,2$. However, if host species i is preferred, i.e., $\frac{b_i}{b_{\max }}>\frac{N_i}{N_1+N_2}$, as in Simpson et al. (2012) and Miller and Huppert (2013), we introduced a preference parameter α to represent the feeding preference of the vector, which represents the feeding preference of the vector for host species 1 relative to species 2. From this, the biting rate becomes

$b_1=b_{\max }\cdot \frac{\mathrm{\alpha }{N}_1}{\mathrm{\alpha }{N}_1+N_2},b_2=b_{\max }\cdot \frac{N_2}{\mathrm{\alpha }{N}_1+N_2}.$

Note that when α = 1, the vector has no preference for any host and when α > 1, the vector prefers host 1, and vice versa.

Substituted b₁,b₂ into Eq. 3, it becomes

$R_0=\frac{b_{\max }}{{\mathrm{\alpha }}^2{N}_1^{{}^{*}}+N_2^{{}^{*}}}\sqrt{\frac{({\mathrm{\alpha }}^2{g}_1{N}_1^{{}^{*}}+g_2{N}_2^{{}^{*}})N_v^{{}^{*}}}{{\mathrm{\Gamma }}_v}}.(4)$

By analyzing and numerically simulating Eq. 4, we can figure out how vector preference and host interspecific competition affect disease risk in vector-borne systems.

Another major purpose of this study is to explore the exact conditions under which diversity amplification or dilution occurs. Analytical results of the effect of host species richness on disease risk were obtained via a single- and two-host species community comparison. To this end, we calculated the basic reproduction number $R_0^1$ of a community composed of a single host species (focal host) and compared it to the community composed of focal and alternative host species. The calculation of $R_0^1$ is similar to the process of calculating R₀ (see Supplementary material), and we obtained

$R_0^1=\sqrt{{\displaystyle \frac{g_1{b}_{\max }^2{N}_v^{{}^{*}}}{N_1^{{}^{*}}{\mathrm{\Gamma }}_v}}}.$

To explore the conditions under which the dilution effect occurs, we need to find the conditions in which disease risk is reduced in a community consisting of a focal and introduced host species compared to a community with only the focal host species, i.e., $R_0<R_0^1$. If this inequality holds, it is equivalent to

$\frac{g_1{b}_1^2{N}_v^{{}^{*}}}{N_1^{{}^{*}}{\mathrm{\Gamma }}_v}+\frac{g_2{b}_2^2{N}_v^{{}^{*}}}{N_2^{{}^{*}}{\mathrm{\Gamma }}_v}<\frac{g_1{b}_{\max }^2{N}_v^{{}^{*}}}{N_1^{{}^{*}}{\mathrm{\Gamma }}_v}(5)$

When Eq. 5 holds, the dilution effect will occur. Otherwise, there will be an amplification effect.

To simplify Eq. 5, a dimensionless parameter γ = g₁/g₂ is introduced to measure the host competence of species 1 relative to 2, which we define as the transmission ratio. When γ = 1, the two hosts were comparable in their ability to transmit disease, and when γ > 1 or 0 < γ < 1, the more competent host is species 1 or 2, respectively.

Next, we will find out the conditions that satisfy Eq. 5 under each of the four combinations with or without vector preference and with or without host interspecific competition. (i) When the vector has no preference for any host (α = 1) and there is no interspecific competition between hosts (c₁₂ = c₂₁ = 0), the non-trivial disease-free equilibrium point is $N_1^{{}^{*}}=K_1,N_2^{{}^{*}}=K_2,N_v^{{}^{*}}=K_v,$, and the biting rate $b_i=b_{\max }\cdot \frac{K_i}{K_1+K_2}$, substitute these parameters into Eq. 5, it is equivalent to $g_2<g_1(2+\frac{K_2}{K_1})$. Since γ = g₁/g₂, the expression becomes $\mathrm{\gamma }>\frac{K_1}{2K_1+K_2}$. That is, when there is no vector preference and no interspecific competition, as long as $\mathrm{\gamma }>\frac{K_1}{2K_1+K_2}$ holds, the dilution effect can occur. (ii) When there is both vector preference and host interspecific competition (i.e., α≠1,c₁₂,c₂₁ > 0), then

$N_1^{{}^{*}}={\displaystyle \frac{K_1-c_{12}{K}_2}{1-c_{12}{c}_{21}}},N_2^{{}^{*}}={\displaystyle \frac{K_2-c_{21}{K}_1}{1-c_{12}{c}_{21}}},N_v^{{}^{*}}=K_v,$

and $b_1=b_{\max }\cdot \frac{\mathrm{\alpha }{N}_1}{\mathrm{\alpha }{N}_1+N_2},b_2=b_{\max }\cdot \frac{N_2}{\mathrm{\alpha }{N}_1+N_2}$.

In the same way, by substituting these parameters into Eq. 5, it is possible to derive the following criteria for the occurrence of the dilution effect:

$\mathrm{\gamma }>{\displaystyle \frac{K_1-c_{12}{K}_2}{2\mathrm{\alpha }(K_1-c_{12}{K}_2)+K_2-c_{21}{K}_1}}.$

Note that in this scenario, if interspecific competition is symmetric (c₁₂ = c₂₁) and both hosts have the same carrying capacity (K₁ = K₂), the above inequality is simplified to $\mathrm{\gamma }>\frac{1}{2\mathrm{\alpha }+1}$, i.e., whether dilution or amplification occurs in this case is only related to vector preference α and transmission ratio γ. The calculation of the conditions for the dilution effect in the other two scenarios (with preference, without competition, or without preference, with competition) is similar to the above. Table 2 provides a summary of the analytical conditions for the model parameters for which Eq. 5 is valid.

TABLE 2

Table 2. The analytical conditions for the criterion of $R_0<R_0^1$ in four different cases.

Results

The effects of host interspecific competition on R₀

To exclude the impact of the presence of other factors on the outcomes, focusing on how interspecific competition affect R₀, we first investigated the situation where there is no vector preference and both hosts have the same ability to transmit disease. We assumed that the vector bites hosts based on their density, with a daily biting rate b_max = 0.3 and the disease transmission ratio γ = 1. As seen in Figure 1A (left panel), the maximum R₀ occurs when both the competition coefficient c₁₂ and c₂₁ are high (top right), whereas the minimum R₀ occurs when both c₁₂ and c₂₁ are very low (bottom left). For a fixed value of c_ij, an increase in c_ji will increase R₀. Moreover, we also found that even when all other parameters are held constant, a change in c₁₂ and c₂₁ will make R₀ changes from less than 1 to larger than 1 (R₀ ranges from 0.85 to 1.18). That is, by changing the intensity of competition, the disease may change from extinction to endemic. Secondly, we relaxed the restrictions to consider the scenarios where there is vector preference and differences in host competence. To do this, we simulated the following parameter combinations of γ,α ∈ {0.5,1,2}×{0.5,1,2} (Supplementary Figure 1). In each subplot of Supplementary Figure 1, when the competition coefficients c₁₂ and c₂₁ are large, R₀ is large, and vice versa. For a fixed value of c_ij, R₀ increases with the increase of c_ji(i, j = 1, 2), these findings were consistent with the results in Figure 1. In addition, we found that for the constant values of c₁₂and c₂₁, the larger γ is, the larger R₀ is, especially when the preferred host is the highly competent one (see Supplementary Figure 1).

FIGURE 1

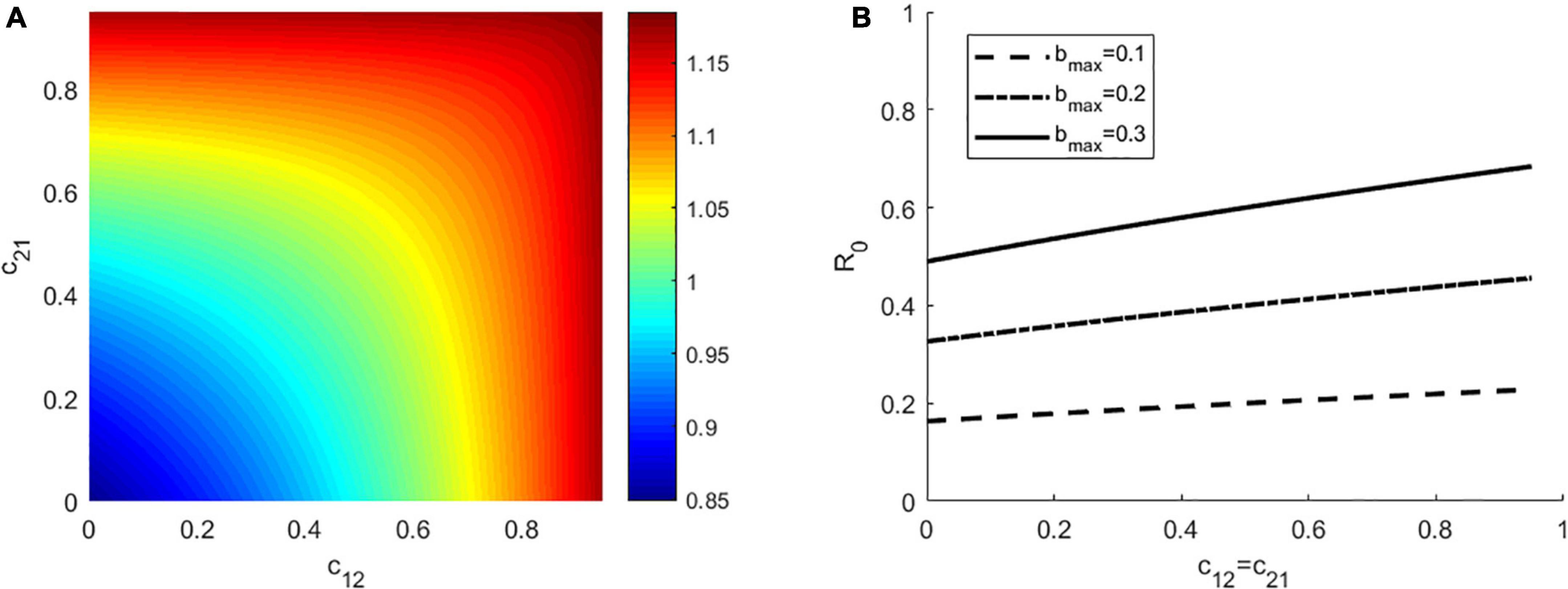
Figure 1. (A) The effect of interspecific competition on R₀. (B) The effect of interspecific competition (only for c₁₂ = c₂₁) on R₀at three different values of b_max = 0.1, 0.2, 0.3, respectively. In panel (A), b_max = 0.3, the other parameters in the two panels have the same values as: α = 1, γ = 1, K₁ = K₂ = 1000, K_v = 4000, Γ_v = 0.1, g₁ = g₂ = 0.4.

In Figure 1B (right panel), we showed how the effect of interspecific competition on R₀ is influenced by the biting rate, which we set b_max = 0.1, 0.2, 0.3, respectively. We found that for a fixed interspecific competition coefficient, the larger b_max is, the larger R₀ is. At each value of b_max, R₀ increases linearly with c₁₂ = c₂₁. Since there is no significant difference in the results for any of the three values of b_max, we only consider the case of b_max = 0.3 in the following study.

Next, we investigated how interspecific competition coefficient c₁₂ affects R₀ in the presence of vector preference and differences in host competence (i.e.,α≠1,γ≠1) (Figure 2). The horizontal axis represents the competition effect of host species 2 on species 1 (i.e., c₁₂), and the vertical axis represents R₀. As can be seen from Figure 2, for a fixed c₁₂, the larger the transmission ratio γ, the larger the R₀, especially when the preferred host is a highly competent one. As c₁₂increases, R₀ shows a non-linear trend, increasing or decreasing depending on the combined effect of transmission ratio γ and vector preference α, suggesting that vector feeding preference and differences in host competence may shift the direction of the effect of interspecific competition on R₀.

FIGURE 2

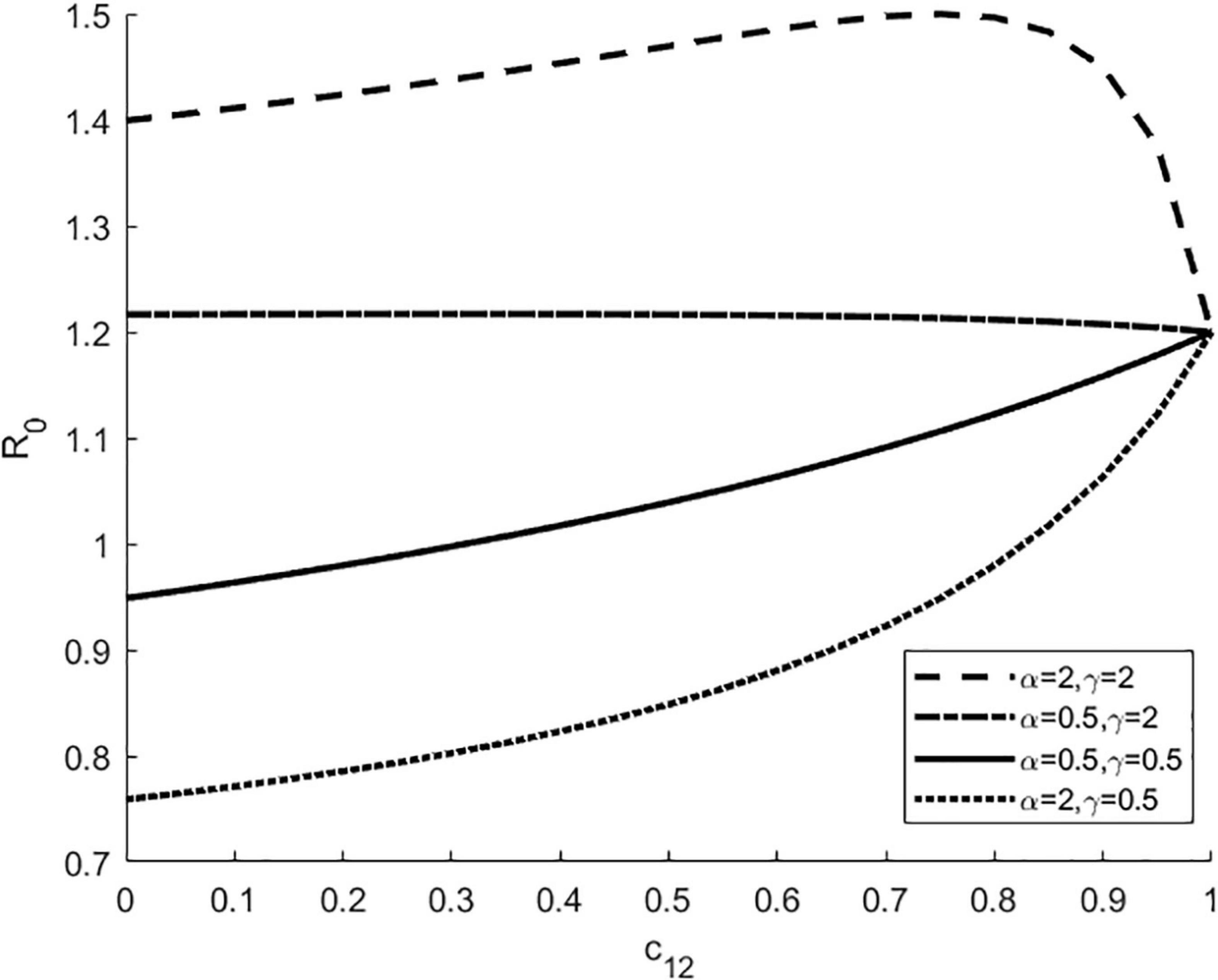
Figure 2. R₀ according to interspecific competition coefficient c₁₂ in the presence of vector preference and differences in host competence. The four lines represent four different combinations of vector preferences α and transmission ratios γ. Here c₂₁ = 0.5, b_max = 0.3, K₁ = K₂ = 1000, K_v = 4000, Γ_v = 0.1, g₂ = 0.4.

The effects of vector preference on R₀

Vector feeding preferences can lead to heterogeneity in host-vector contact, which may affect disease dynamics. To understand the effect of vector preference on disease transmission potential, we first assumed that there was no interspecific competition between hosts. In Figure 3, the horizontal axis represents the feeding preference index α, which ranges from 0 to 2, and the vertical axis represents R₀. It can be seen from Figure 1 that as α increases, R₀may increase, decrease, or vary slightly, depending on the host transmission ratio γ. If species 1 is the more competent host at this time (γ > 1), then R₀increases with the increase of α. On the contrary, if species 1 is the lower competent host, then R₀decreases as αincreases. When the two hosts are comparable in their competence (γ = 1), R₀varies within a small range as α increases. In fact, in this case, when we narrow the range of the vertical axis (the inset graph of Figure 3), we find that R₀ first decreases and then increases as α increases, and when the vector has no preference for any hosts (α = 1), R₀ takes the minimum value.

FIGURE 3

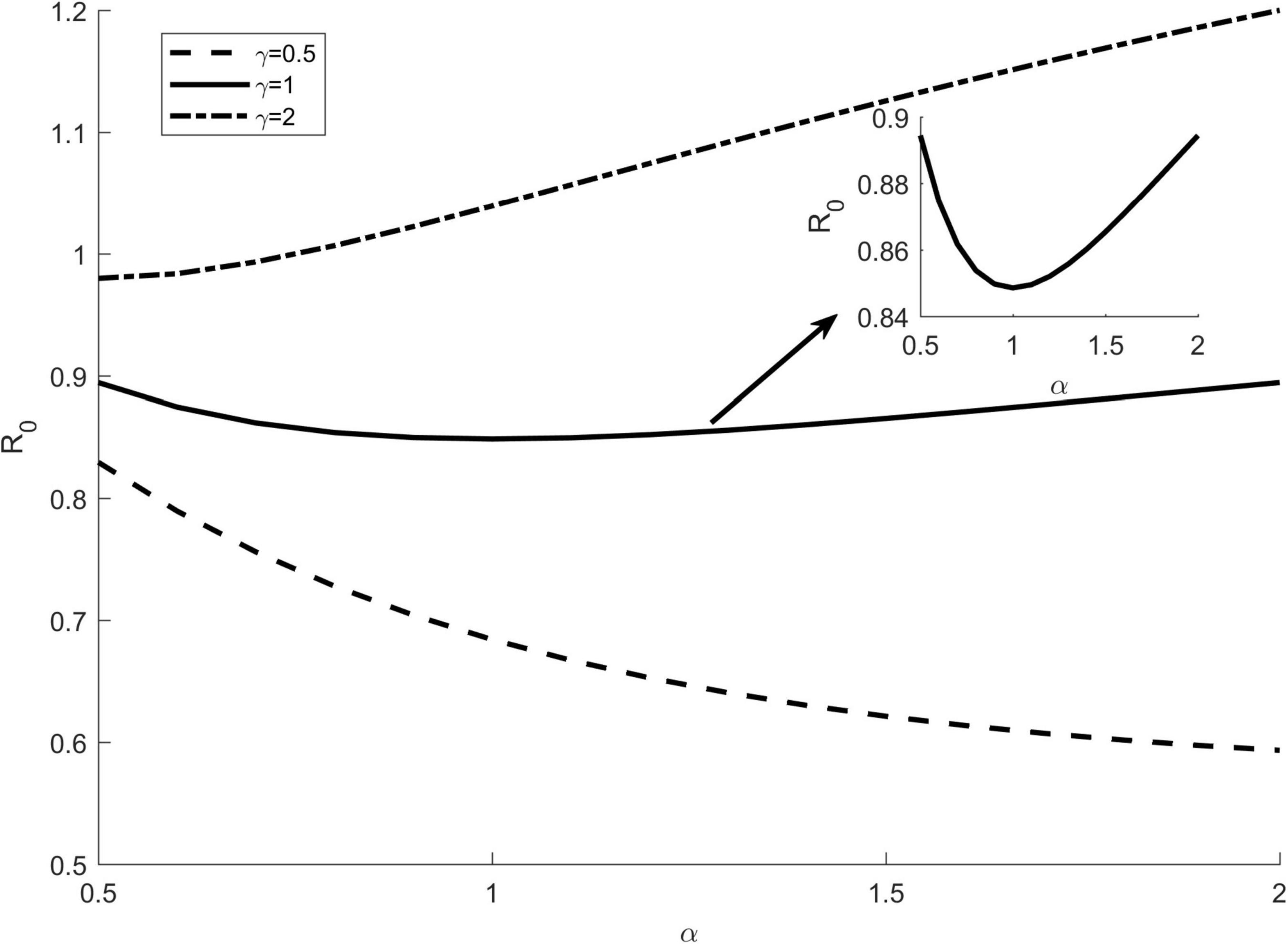
Figure 3. The effect of vector preference α on R₀ without host interspecific competition. Different lines represent the results of different values of the transmission ratio γ. The inset of figure shows the case of γ = 1 when narrowing the vertical axis. The other parameters are: c₁₂ = c₂₁ = 0, b_max = 0.3, K₁ = K₂ = 1000, K_v = 4000, Γ_v = 0.1, g₂ = 0.4.

Secondly, we considered the effect of vector preference α on R₀ in the presence of interspecific competition by simulating different competition coefficient combinations (Supplementary Figure 2). Different panels of Figure 2 refer to different values of (c₁₂,c₂₁)that assume the values of 0.1, 0.5, 0.9. It was found that there is no qualitative difference with the results in Figure 3, except that when species 1 is a less competent host or the two hosts are comparable in their competence. As α increases, the magnitude of the decrease of R₀ is lower than that in the absence of interspecific competition (Figure 3). All these results indicate that the presence or absence of interspecific competition quantitatively but not qualitatively changes the effect of vector preference on R₀.

Dilution effect versus amplification effect

Table 2 summarizes the analytical conditions that are satisfied $R_0<R_0^1$ under each of the four combinations with or without vector preference and with or without host interspecific competition (see section “Materials and methods”). In this section, we focused on how interspecific competition, vector preference, and host competence affect the occurrence of dilution effects. According to Table 2, when both interspecific competition and vector preference exist, a dilution effect can occur when

$\mathrm{\gamma }>{\displaystyle \frac{K_1-c_{12}{K}_2}{2\mathrm{\alpha }(K_1-c_{12}{K}_2)+K_2-c_{21}{K}_1}}.$

Conditions for $\mathrm{\gamma }=\frac{K_1-c_{12}{K}_2}{2\mathrm{\alpha }(K_1-c_{12}{K}_2)+K_2-c_{21}{K}_1}$(i.e., $R_0=R_0^1$) were represented by a linear configuration of vector preference α and the transmission ratio γ, the line divided α-γ parameter space into disjoint regions for which dilution and amplification effects were exhibited (Figure 4). Different lines represent different competition intensities of c₁₂, which are taken as 0.1, 0.5, and 0.9, respectively. On the upper right side of each line, it shows the parameter area where the dilution effect happens (symbol DE). On the lower left side of each line, it shows the parameter area where the amplification effect happens (symbol AE).

FIGURE 4

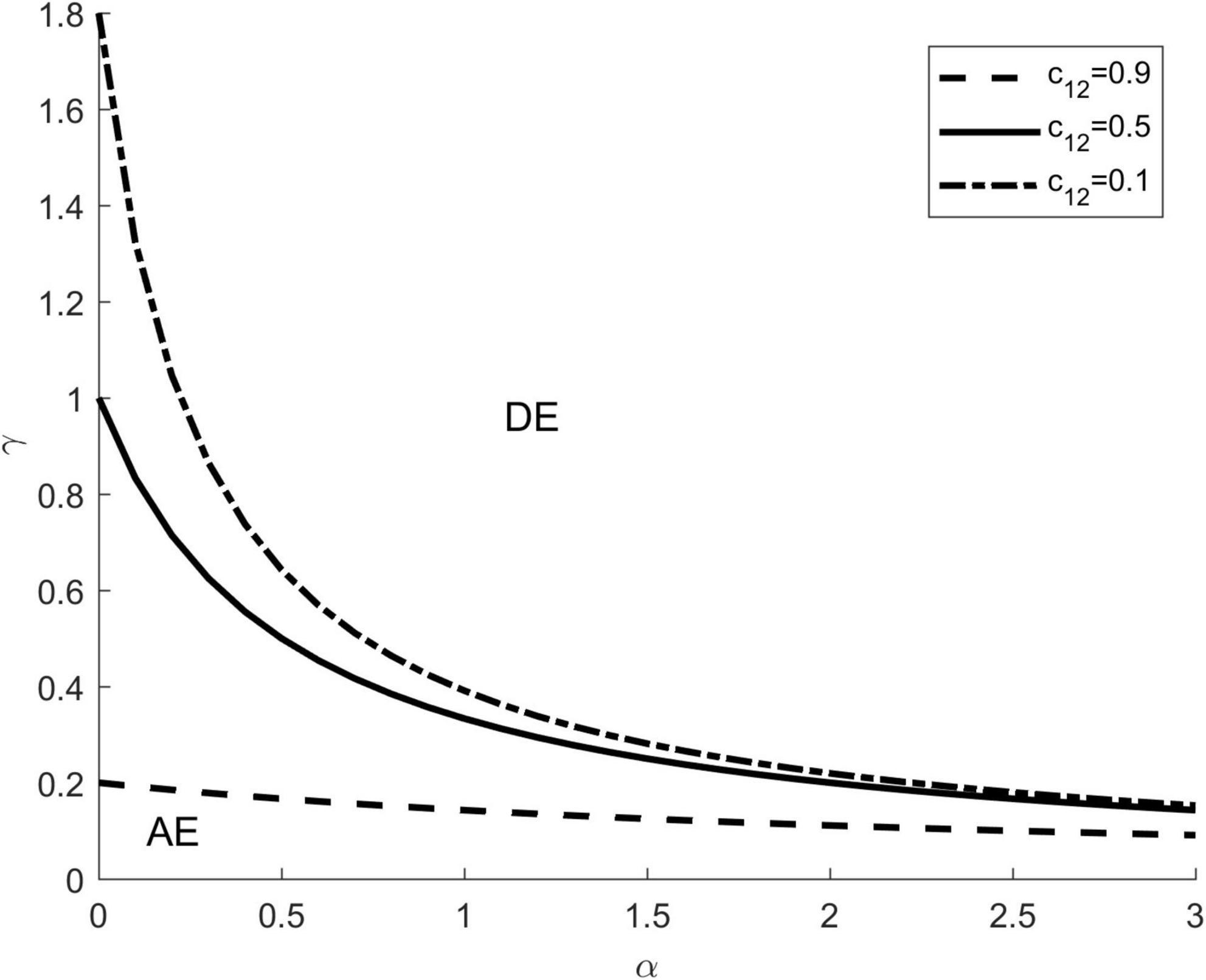
Figure 4. Analytical relationships for combinations of interspecific competition, vector preference and transmission ratio. The dotted and solid lines represent parameter sets (α,γ) for which $R_0=R_0^1$ under different competition intensity c₁₂. These lines divided α−−γ parameter space into disjoint regions where dilution and amplification effects were exhibited. The upper right of each line represents parameter pairs for which a dilution effect occurs (symbol DE), whereas the lower left of each line represents parameter pairs for which an amplification effect occurs (symbol AE). The other parameters are: K₁ = K₂ = 1000, c₂₁ = 0.5.

As shown in Figure 4, adding new species to a community can lead to both a dilution effect and an amplification effect, depending on the values of α and γ. When the focal species (species 1) is a highly competent host and the vector prefers the focal species, the addition of the introduced species (species 2) dilutes the proportion of the focal species and reduces the effective contact between the focal species and the vector, resulting in a dilution effect ($R_0<R_0^1$) (the upper right area of Figure 4). Conversely, when the introduced species is a highly competent host and the vector prefers the introduced species, the addition of the introduced species results in a higher disease risk compared to the community containing only the focal host, and thus an amplification effect occurs ($R_0>R_0^1$) (the lower left part of Figure 4). In addition, for a fixed value of c₂₁, the larger the c₁₂, the larger the parameter area where the dilution effect can occur, and vice versa.

Discussion

Understanding how ecological interactions and significant ecological factors affect vector-borne disease dynamics is crucial given the rapid loss of biodiversity and the rise in newly emerging vector-borne diseases (Rivera et al., 2020). In this study, we constructed a simple compartment model with two competing host species and one vector, in which the vector has different preferences for the hosts, to study the combined impact of vector feeding preferences and host interspecific competition on vector-borne infection ecology. Furthermore, we investigated the relationship between host species richness and disease risk by comparing disease risk R₀ in single- and two-host communities. We demonstrated that disease transmission dynamics in multi-host communities are more complex than anticipated, highlighting the significance of linking vector preference, interspecific competition, and host competence in describing vector-borne infection ecology. More specifically, we found that vector preference and differences in host competence shifted the direction of the effect of competition on R₀, yet interspecific competition quantitatively but not qualitatively changed the effect of vector preference on R₀. Furthermore, this study quantified the conditions of dilution effect and amplification effect, and clarified that incorporating vector preference and interspecific competition into a simple two-host-one-vector model changes the outcomes of how increasing species richness affects disease risk R₀.

For vector-borne diseases, the dynamics of pathogen transmission depend on the ability of host species to maintain and transmit disease and on ecological factors such as interspecific competition and contact rate between hosts and vectors (Simpson et al., 2012). Interspecific competition can either increase R₀ by increasing the vector/host ratio or decrease R₀ by decreasing the density of the host population (Marini et al., 2017), the general pattern of the effect of competition on R₀ is hard to predict, and whether competition has a positive or negative effect on R₀ depends largely on host preferences and host competence. We also found that R₀ is strongly influenced by vector feeding preference. R₀ increases with the increase of vector preference, as long as the preferred host is a highly competent host. The reason for this phenomenon may be that vector preference allows a large number of bites to be concentrated on the preferred host, increasing the effective contact between the vector and highly competent hosts, thereby increasing the efficiency of disease transmission. In fact, these findings have been confirmed in some field experiments and theoretical studies. For example, if all individuals in the community have the same ability to transmit disease, vector-host contact heterogeneity owing to vector preference can increase the risk of disease outbreak (Woolhouse et al., 1997; Miller and Huppert, 2013). These facts tell us that it is important to be scientific and rational in developing disease control strategies, and that if the control measures are not appropriate, they may be counterproductive. For example, for a population with identical individuals, selective use of insect repellent will result in a higher concentration of vectors on the unprotected individuals, which is equivalent to the vector feeding preference, the disease risk R₀ may rise rather than fall (Miller and Huppert, 2013).

Whether increased host species richness results in greater or lower disease risk has been controversial in the literature, leading to calls for theoretical studies on what conditions promote amplification versus dilution (Buhnerkempe et al., 2015; Halsey, 2018). Many previous studies on the biodiversity-diseases risk relationship have demonstrated that when diseases are transmitted in a frequency-dependent mode, an increase in species richness decreases the community R₀ (Dobson, 2004; Rudolf and Antonovics, 2005; Rohr et al., 2019). However, an interesting finding of this study is that, even in frequency-dependent transmission mode, the introduction of new species to a community may increase or decrease disease risk if interspecific competition and contact heterogeneity due to vector preference are taken into account, which is in contrast to the results of previous studies. The reason for this phenomenon can be understood from the mechanism of the dilution effect. Keesing et al. (2006) constructed a general mathematical model framework and proposed five mechanisms by which dilution effects occur. Among them, encounter reduction and susceptible host regulation have been confirmed in many empirical studies (Allan et al., 2009; Johnson and Thieltges, 2010). In a vector-borne disease system, encounter reduction refers to the presence of additional species that affects host behavior, reduces the probability of contact between vector and host, or influences vector behavior, decreasing the likelihood that susceptible individuals will become infected individuals (Clay et al., 2009). Susceptible host regulation refers to the fact that the addition of new host species to a community regulates susceptible host numbers through interspecific interactions such as competition or predation (Keesing et al., 2006). If the above assumptions are satisfied, an increase in species richness may lead to a dilution effect. Conversely, if the introduced host is a highly competent host or one that the vector prefers to feed on, or if the introduced host has strong interspecific competition ability, which reduces the frequency of low competent hosts through interspecific competition, then an increase in species richness will increase the communityR₀, whereby an amplification effect occurs. This explains, to some extent, why an amplification effect can occur in the frequency-dependent transmission mode. Our study emphasizes the need to focus not only on the transmission mode of disease, but also on interspecific interactions (interspecific competition and vector-host contact rate) and host competence (Cortez and Duffy, 2021; Su et al., 2022).

Although mathematical models have been widely used to study complex ecological phenomena, explaining and validating many empirical studies, there are still several limitations (O’Regan et al., 2015). In fact, the two-host-one-vector Lotka–Volterra competition model used in this study is very simplistic compared to the complexity of real community ecology. For example, we only compared disease risk R₀ when pathogen was transmitted in single- and two-host communities, despite the fact that natural communities can have dozens of host species. We focused only on the effect of interspecific competition on disease risk, ignoring the possible effect of intraspecific competition. Moreover, we used the basic reproduction number R₀ as a measure of community disease risk, which is challenging to estimate in field and empirical studies and does not allow for comparisons between studies (Roberts and Heesterbeek, 2018; Cortez and Duffy, 2021). In addition, we ignored some ecological factors that could affect the potential of outbreaks, including the seasonal variation in vector feeding preference (Burkett-Cadena et al., 2012; Marini et al., 2017) and demographic stochasticity (Dizney and Ruedas, 2009). However, we believe that this study of a simplified scenario provides a theoretical framework for incorporating interspecific competition, vector preference and host competence into vector-borne systems. Our work emphasizes the significance of ecological interactions in determining infection dynamics in a multi-host vector system, and contributes to explaining some of the variation in outcomes in previous empirical and theoretical studies on the dilution effect.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LC and SC designed the study and analyzed the model. LC and PK performed the software. LC and LZ drafted the manuscript. All authors have read and approved the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (31700466 and 82072228), the Foundation of National Key R&D Program of China (2020YFC2008700), the Foundation of Shanghai Municipal Commission of Economy and Informatization (202001007), and the Special Project of Health Shanghai Action (2022–2024).

Acknowledgments

We are grateful to the editor and the reviewers for their constructive comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.993844/full#supplementary-material

References

Allan, B. F., Langerhans, R. B., Ryberg, W. A., Landesman, W. J., Griffin, N. W., Katz, R. S., et al. (2009). Ecological correlates of risk and incidence of West Nile virus in the United States. Oecologia 158, 699–708. doi: 10.1007/s00442-008-1169-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Buhnerkempe, M. G., Roberts, M. G., Dobson, A. P., Heesterbeek, H., Hudson, P. J., and Lloyd-Smith, J. O. (2015). Eight challenges in modelling disease ecology in multi-host, multi-agent systems. Epidemics 10, 26–30. doi: 10.1016/j.epidem.2014.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Burkett-Cadena, N. D., Hassan, H. K., Eubanks, M. D., Cupp, E. W., and Unnasch, T. R. (2012). Winter severity predicts the timing of host shifts in the mosquito Culex erraticus. Biol. Lett. 8, 567–569. doi: 10.1098/rsbl.2012.0075

PubMed Abstract | CrossRef Full Text | Google Scholar

Clay, C. A., Lehmer, E. M., Jeor, S. S., and Dearing, M. D. (2009). Testing mechanisms of the dilution effect: Deer mice encounter rates, Sin Nombre virus prevalence and species diversity. EcoHealth 6, 250–259. doi: 10.1007/s10393-009-0240-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Cortez, M. H., and Duffy, M. A. (2021). The context-dependent effects of host competence, competition, and pathogen transmission mode on disease prevalence. Am. Nat. 198, 179–194. doi: 10.1086/715110

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, S. V., Hibberts, S. J., Olive, D. A., Budd, K., Long, A., Meiling, S. S., et al. (2021). Diversity and disease: The effects of coral diversity on prevalence and impacts of stony coral tissue loss disease in Saint Thomas, U.S. Virgin Islands. Front. Mar. Sci. 8:682688. doi: 10.3389/fmars.2021.682688

CrossRef Full Text | Google Scholar

Diekmann, O., Heesterbeek, J. A. P., and Roberts, M. G. (2009). The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7, 873–885. doi: 10.1098/rsif.2009.0386

PubMed Abstract | CrossRef Full Text | Google Scholar

Dizney, L. J., and Ruedas, L. A. (2009). Increased host species diversity and decreased prevalence of Sin Nombre virus. Emerg. Infect. Dis. 15, 1012–1018. doi: 10.3201/eid1507.081083

CrossRef Full Text | Google Scholar

Dobson, A. (2004). Population dynamics of pathogens with multiple host species. Am. Nat. 164, S64–S78. doi: 10.1086/424681

PubMed Abstract | CrossRef Full Text | Google Scholar

Gürtler, R. E., Ceballos, L. A., Ordóñez-Krasnowski, P., Lanati, L., Stariolo, R., and Kitron, U. (2009). Strong host-feeding preferences of the vector Triatoma infestans modified by vector density: Implications for the epidemiology of chagas disease. PLoS Negl. Trop. Dis. 3:e447. doi: 10.1371/journal.pntd.0000447

PubMed Abstract | CrossRef Full Text | Google Scholar

Halliday, F. W., Heckman, R. W., Wilfahrt, P. A., and Mitchell, C. E. (2017). A multivariate test of disease risk reveals conditions leading to disease amplification. Proc. R. Soc. B Biol. Sci. 284:20171340. doi: 10.1098/rspb.2017.1340

PubMed Abstract | CrossRef Full Text | Google Scholar

Halliday, F. W., Heckman, R. W., Wilfahrt, P. A., and Mitchell, C. E. (2019). Past is prologue: Host community assembly and the risk of infectious disease over time. Ecol. Lett. 22, 138–148. doi: 10.1111/ele.13176

PubMed Abstract | CrossRef Full Text | Google Scholar

Halliday, F. W., Rohr, J. R., and Laine, A. L. (2020). Biodiversity loss underlies the dilution effect of biodiversity. Ecol. Lett. 23, 1611–1622. doi: 10.1111/ele.13590

PubMed Abstract | CrossRef Full Text | Google Scholar

Halsey, S. J. (2018). Defuse the dilution effect debate. Nat. Ecol. Evol. 3, 145–146. doi: 10.1038/s41559-018-0764-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, P., and Thieltges, D. (2010). Diversity, decoys and the dilution effect: How ecological communities affect disease risk. J. Exp. Biol. 213, 961–970. doi: 10.1242/jeb.037721

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, P. T., Preston, D. L., Hoverman, J. T., and Richgels, K. L. (2013). Biodiversity decreases disease through predictable changes in host community competence. Nature 494, 230–233. doi: 10.1038/nature11883

PubMed Abstract | CrossRef Full Text | Google Scholar

Kambatuku, J. R., Cramer, M. D., and Ward, D. (2010). Intraspecific competition between shrubs in a semi-arid Savanna. Plant Ecol. 212, 701–713. doi: 10.1007/s11258-010-9856-0

CrossRef Full Text | Google Scholar

Keesing, F., Belden, L. K., Daszak, P., Dobson, A., Harvell, C. D., Holt, R. D., et al. (2010). Impacts of biodiversity on the emergence and transmission of infectious diseases. Nature 468, 647–652. doi: 10.1038/nature09575

PubMed Abstract | CrossRef Full Text | Google Scholar

Keesing, F., Holt, R. D., and Ostfeld, R. S. (2006). Effects of species diversity on disease risk. Ecol. Lett. 9, 485–498. doi: 10.1111/j.1461-0248.2006.00885.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kilpatrick, A. M., Daszak, P., Jones, M. J., Marra, P. P., and Kramer, L. D. (2006). Host heterogeneity dominates West Nile virus transmission. Proc. R. Soc. B Biol. Sci. 273, 2327–2333. doi: 10.1098/rspb.2006.3575

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Lyu, S., Zhou, S., and Bradshaw, C. J. (2016). Warming and fertilization alter the dilution effect of host diversity on disease severity. Ecology 97, 1680–1689. doi: 10.1890/15-1784.1

CrossRef Full Text | Google Scholar

LoGiudice, K., Ostfeld, R. S., Schmidt, K. A., and Keesing, F. (2003). The ecology of infectious disease: Effects of host diversity and community composition on Lyme disease risk. Proc. Natl. Acad. Sci. U.S.A. 100, 567–571. doi: 10.1073/pnas.0233733100

PubMed Abstract | CrossRef Full Text | Google Scholar

Lord, C. C., Woolhouse, M. E. J., Heesterbeek, J. A. P., and Mellor, P. S. (1996). Vector-borne diseases and the basic reproduction number: A case study of African horse sickness. Med. Vet. Entomol. 10, 19–28. doi: 10.1111/j.1365-2915.1996.tb00077.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Luis, A. D., Kuenzi, A. J., and Mills, J. N. (2018). Species diversity concurrently dilutes and amplifies transmission in a zoonotic host–pathogen system through competing mechanisms. Proc. Natl. Acad. Sci. U.S.A. 115, 7979–7984. doi: 10.1073/pnas.1807106115

PubMed Abstract | CrossRef Full Text | Google Scholar

Marini, G., Rosá, R., Pugliese, A., and Heesterbeek, H. (2017). Exploring vector-borne infection ecology in multi-host communities: A case study of West Nile virus. J. Theor. Biol. 415, 58–69. doi: 10.1016/j.jtbi.2016.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, E., and Huppert, A. (2013). The effects of host diversity on vector-borne disease: The conditions under which diversity will amplify or dilute the disease risk. PLoS One 8:e80279. doi: 10.1371/journal.pone.0080279

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, C. E., Tilman, D., and Groth, J. V. (2002). Effects of grassland plant species diversity, abundance, and composition on foliar fungal disease. Ecology 83, 1713–1726. doi: 10.1890/0012-9658(2002)083[1713:EOGPSD]2.0.CO;2

CrossRef Full Text | Google Scholar

O’Regan, S. M., Vinson, J. E., and Park, A. W. (2015). Interspecific contact and competition may affect the strength and direction of disease-diversity relationships for directly transmitted microparasites. Am. Nat. 186, 480–494. doi: 10.1086/682721

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostfeld, R. S., and Keesing, F. (2000). Biodiversity series: The function of biodiversity in the ecology of vector-borne zoonotic diseases. Can. J. Zool. 78, 2061–2078. doi: 10.1139/z00-172

CrossRef Full Text | Google Scholar

Ostfeld, R. S., and Keesing, F. (2012). Effects of host diversity on infectious disease. Annu. Rev. Ecol. Evol. Sci. 43, 157–182. doi: 10.1146/annurev-ecolsys-102710-145022

CrossRef Full Text | Google Scholar

Ostfeld, R. S., and LoGiudice, K. (2003). Community disassembly, biodiversity loss, and the erosion of an ecosystem service. Ecology 84, 1421–1427. doi: 10.1890/02-3125

CrossRef Full Text | Google Scholar

Rivera, R. M. C., Bilal, S., and Michael, E. (2020). The relation between host competence and vector-feeding preference in a multi-host model: Chagas and Cutaneous leishmaniasis. Math. Biosci. Eng. 17, 5561–5583. doi: 10.3934/mbe.2020299

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, M. G., and Heesterbeek, J. (2013). Characterizing the next-generation matrix and basic reproduction number in ecological epidemiology. J. Math. Biol. 66, 1045–1064. doi: 10.1007/s00285-012-0602-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, M. G., and Heesterbeek, J. A. P. (2018). Quantifying the dilution effect for models in ecological epidemiology. J. R. Soc. Interface 15:20170791. doi: 10.1098/rsif.2017.0791

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, D. J. (1988). The dynamics of vector-transmitted diseases in human communities. Philos. Trans. R. Soc. B Biol. Sci. 321, 513–539. doi: 10.1098/rstb.1988.0106

PubMed Abstract | CrossRef Full Text | Google Scholar

Rohr, J. R., Civitello, D. J., Halliday, F. W., Hudson, P. J., Lafferty, K. D., Wood, C. L., et al. (2019). Towards common ground in the biodiversity–disease debate. Nat. Ecol. Evol. 4, 24–33. doi: 10.1038/s41559-019-1060-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudolf, V. H., and Antonovics, J. (2005). Species coexistence and pathogens with frequency-dependent transmission. Am. Nat. 166, 112–118. doi: 10.1086/430674

PubMed Abstract | CrossRef Full Text | Google Scholar

Simpson, J. E., Hurtado, P. J., Medlock, J., Molaei, G., Andreadis, T. G., Galvani, A. P., et al. (2012). Vector host-feeding preferences drive transmission of multi-host pathogens: West Nile virus as a model system. Proc. R. Soc. B Biol. Sci. 279, 925–933. doi: 10.1098/rspb.2011.1282

PubMed Abstract | CrossRef Full Text | Google Scholar

Strauss, A. T., Civitello, D. J., Cáceres, C. E., and Hall, S. R. (2015). Success, failure and ambiguity of the dilution effect among competitors. Ecol. Lett. 18, 916–926. doi: 10.1111/ele.12468

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, M., Jiang, Z., and Hui, C. (2022). How multiple interaction types affect disease spread and dilution in ecological networks. Front. Ecol. Evol. 10:862986. doi: 10.3389/fevo.2022.862986

CrossRef Full Text | Google Scholar

Tirados, I., Costantini, C., Gibson, G., and Torr, S. J. (2006). Blood-feeding behaviour of the malarial mosquito Anopheles arabiensis: Implications for vector control. Med. Vet. Entomol. 20, 425–437. doi: 10.1111/j.1365-2915.2006.652.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vadell, M. V., Gómez Villafañe, I. E., and Carbajo, A. E. (2019). Hantavirus infection and biodiversity in the Americas. Oecologia 192, 169–177. doi: 10.1007/s00442-019-04564-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wood, C. L., Lafferty, K. D., DeLeo, G., Young, H. S., Hudson, P. J., and Kuris, A. M. (2014). Does biodiversity protect humans against infectious disease? Ecology 95, 817–832. doi: 10.1890/13-1041.1

CrossRef Full Text | Google Scholar

Woolhouse, M. E. J., Dye, C., Etard, J. F., Smith, T. J., Charlwood, J. D., Garnett, G. P., et al. (1997). Heterogeneities in the transmission of infectious agents: Implications for the design of control programs. Proc. Natl. Acad. Sci. U.S.A. 94, 338–342. doi: 10.1073/pnas.94.1.338

PubMed Abstract | CrossRef Full Text | Google Scholar

World Health Organization [WHO] (2004). Global strategic framework for integrated vector management. Geneva: WHO.

Google Scholar

Zeilinger, A. R., and Daugherty, M. P. (2014). Vector preference and host defense against infection interact to determine disease dynamics. Oikos 123, 613–622. doi: 10.1111/j.1600-0706.2013.01074.x

CrossRef Full Text | Google Scholar