Quantifying population and clone-specific non-linear reaction norms to food gradients in Daphnia magna

Phenotypic plasticity is normally quantified as a reaction norm which details how trait expression changes across an environmental gradient. Sometime reaction norms are linear, but often reaction norms are assumed to be linear because plasticity is typically quantified as the difference in trait expression measured in two environments. This simplification limits how plastic responses vary between genotypes and may also bias the predictions of models investigating how plasticity influences a population’s ability to adapt to a changing environment. Consequently, there is a pressing need to characterize the real shape of reaction norms and their genetic variability across ecologically relevant environmental gradients. To address this knowledge gap we measured the multi-trait plastic response of 7 Daphnia magna clones from the same population across a broad resource gradient. We used a Random Regression Mixed Model approach to characterize and quantify average and clone-specific responses to resource variation. Our results demonstrate that non-linear models outperformed a linear model for all 4 of the life-history traits we measured. The plastic reaction norms of all 4 traits were similar in shape and were often best described by a non-linear asymptotic model. Clonal variation in non-linear plastic responses was detectable for 3 out of the 4 traits that we measured although the nature and magnitude of variation across the resource gradient was trait-specific. We interpret our findings with respect to the impact that plasticity has on the evolutionary potential of a population in different resource environments.

Introduction

The concept of phenotypic plasticity, the ability of a single genotype to produce a range of phenotypes in response to variable environmental conditions (Via et al., 1995), is a key feature of evolutionary biology (Bradshaw, 1965; West-Eberhard, 2003; Wund, 2012). Ubiquitous in nature, plasticity is an important evolutionary strategy (Bradshaw, 1965), central in promoting adaptation and persistence at both the individual and population level (Chevin and Lande, 2010). Life history traits, those which dictate key life decisions such as growth, maturation, and fecundity, are often highly plastic (Nussey et al., 2007), allowing organisms to maximize fitness across a range of environments (Liefting et al., 2009) and persist in rapidly changing conditions (Vedder et al., 2013). Phenotypic plasticity will facilitate rapid adaptation if it creates more opportunity for selection by increasing genetic variation in traits under selection in a particular environment. However, the reverse is true if phenotypic plasticity reduces the genetic variation in fitness in an environment (Gienapp and Brommer, 2014). Phenotypic plasticity can also support rapid adaptation to novel and changing environments (Vedder et al., 2013), allowing persistence and therefore buying time for selection to act on the genotype (Pigliucci, 2005). Better understanding of the mechanics of plasticity with regards to rapid adaptation could improve knowledge of an organism’s capability to adapt to new environments (Morrissey and Liefting, 2016), an especially relevant topic given the prevalence of species range shifts as a response to human-induced environmental instability (Chen et al., 2011).

Plasticity is often modeled using the reaction norm concept, the plotted function that describes the change in a phenotypic character in response to changes in environmental condition (de Jong, 1990). Despite both the phenotypic trait values and the environmental gradient being more often than not continuous variables (Gavrilets and Scheiner, 1993), reaction norms are currently modeled using only two points along an environmental axis (Murren et al., 2014; Arnold et al., 2019). This forces a linear relationship between trait and environmental change, as such reaction norms are modeled almost exclusively using linear regression (Chevin and Hoffmann, 2017). The original intention of such a simplifying approach was to create a model that was easily replicable but still captured the essential pattern of the data (Rocha and Klaczko, 2012). The linear parameters of slope and intercept also made for easy comparison between reaction norms of different genetic units (Morrissey and Liefting, 2016). However, the decision to utilize only two experimental environments rather than a continuous range is often done for the sake of simplicity (Moreteau et al., 1997) rather than for any real scientific merit of the linear model. So far, little attention has been given to how good an approximation of reality the linear model really is (Scheiner, 1993).

While some reaction norms really are linear in nature (Charmantier et al., 2008), scientific understanding of physiological limits suggests that when measured over a sufficiently broad scale most reaction norms will be non-linear (Arnold et al., 2019). The current “two-point” linear approach to modeling reaction norms may be unrealistic to the natural setting as it often fails to account for environmental extremes (Stinchcombe et al., 2012). Extreme conditions are often excluded because they are more difficult to recreate experimentally, resulting in a poor understanding of plastic responses to these environments (Chevin and Hoffmann, 2017). This is especially true in the case of life history assays, where poor environmental conditions such as low temperature or nutrition prolong the length of the experiment due to their negative effects on growth and development. However, extreme conditions are increasingly common in the wild, with climate change exposing organisms to an increasingly wide environmental gradient on a regular basis (Easterling et al., 2000).

The assumption of linear reaction norms may obscure important aspects of plasticity leading to inaccurate estimations of the degree of heritable phenotypic variation in populations (Schlichting, 2008). For example, models that assume that reaction norms are linear necessarily predict that additive genetic variance increases in extreme environments (Chevin and Hoffmann, 2017) leading to the conclusion that plasticity plays an important role in facilitating adaptation to extreme environments (Chevin and Lande, 2011). However, plastic responses to extreme environments are unlikely to be linear because physiological constraints will generate non-linear reaction norms (Day and Rowe, 2002; Nussey et al., 2007) that are often not accounted for in models of phenotypic plasticity. This incorporation of the biology of the trait into its reaction norm creates a more realistic representation of the plastic phenotypic variation generated by genotypes within a population. Models based on realistic reaction norm shapes would vastly improve our understanding of the effects of environmental change on phenotypic expression (Nussey et al., 2007). It may also reveal more about a population’s potential for rapid adaptation, and how the plastic response itself can be shaped by selection (Via and Lande, 1985). By imposing the linear assumption and ignoring extreme environmental conditions, current reaction norm studies limit the inferences that can be made regarding the evolution of plasticity (Murren et al., 2014). The study of genetic variation in plastic responses (genotype by environment interactions, or GxE), is almost entirely defined in the context of linear reaction norms (Rocha and Klaczko, 2012). Moreover, studies of multivariate plasticity are also invariably linear in approach.

Information on the true shape of reaction norms is sparse (Gavrilets and Scheiner, 1993; Gibert et al., 1998). Beyond studies investigating thermal plasticity in Drosophila (David et al., 1997; Moreteau et al., 1997; Gibert et al., 1998), threshold traits (West-Eberhard, 2003; Chevin and Lande, 2013) and performance curves (Huey and Kingsolver, 1989; Izem and Kingsolver, 2005) a more general assessment of reaction norm non-linearity has only begun recently (Rocha and Klaczko, 2012, 2014; Murren et al., 2014; Morrissey and Liefting, 2016; Gomulkiewicz et al., 2018). When reaction norms are non-linear, the slope of the reaction norm changes across certain environments, becoming steeper or shallower as conditions change (as described in Rocha and Klaczko, 2014). This may impact the range of phenotypic targets available for selection to act upon under certain environmental conditions and alter patterns of trait co-variation. The expression of genetic variation and a population’s capacity to adapt is a pressing concern, especially in extreme environments (Chevin and Hoffmann, 2017). Improved understanding of plasticity and species’ adaptive capacity may have important environmental and economic implications, with ramifications for species conservation (Heino and Dieckmann, 2008), invasive species management (Davidson et al., 2011), and even crop production (Ly et al., 2018).

Understanding the evolution of extant species and their adaptive capacity therefore requires an accurate representation of reaction norm shape (Arnold et al., 2019). To begin to address this problem we measured the multi-trait plastic response of 7 Daphnia magna clones from the same population across a broad resource gradient. Daphnia population densities often vary by orders of magnitude across a season, demonstrating exponential population growth early in the season followed by one or more density-dependent declines due to food shortage later in the season (Ebert, 2005). As a result, Daphnia populations typically experience extreme resource fluctuations each year. We used a Random Regression Mixed Model approach (Arnold et al., 2019) to characterize and quantify population-level and clone-specific responses to resource variation over a broad environmental gradient and correlation matrices to examine how phenotypic correlations change across an environmental gradient. We demonstrate that when phenotypes are measured over a sufficiently broad range of environments, linear models cannot adequately describe plastic responses to a resource gradient. We discuss the implications of our findings for understanding how plasticity influences the likelihood of observing rapid adaptation in Daphnia populations.

Materials and methods

Experimental procedure

All Daphnia magna used were taken from laboratory lines hatched from resting eggs collected from Brown Moss Nature Reserve (52°57’01.2”N, 2°39’05.6”W) in 2016. Daphnia were conditioned at 21°C for two generations (parental and F1 generations) in the lab before the experiment to reduce any potential maternal effects (Plaistow and Collin, 2014; Plaistow et al., 2015). The offspring from the second F1 clutch were then used for experimentation.

Six concentrations of the algal food solution (spp. Chlorella vulgaris) were used to form the nutritional gradient along which Daphnia life history data was recorded. A preliminary assay was used to determine the nutritional treatments pertinent to reaction norm shape including curve inflection points, asymptotic values, and extreme high and low food concentrations. Concentrations of 10,000, 40,000, 90,000, 145,000, 200,000, and 300,000 cells mL^–1 were chosen, forming a continuous environmental gradient. Seven Daphnia clones were used, with four replicates reared at each food level. All Daphnia were kept under controlled conditions of 21^°C and a 14:10 light: dark photoperiod. Daphnia were housed individually in glass jars containing 150 mL of artificial pond water (ASTM) enriched with Marinure, a seaweed solution that provided necessary base nutrients. All individuals were fed their respective food treatment once per day, and individuals were moved to fresh jars every other day to prevent build-up of algae along the base of the jar and to make sure that food levels remained constant. Life history observations were collected until individuals released their first clutch of neonates (rather than the 3rd clutch) to minimize the time taken to collect life-history data from each clone in each environment All replicates were photographed at birth and maturity [determined as the day when eggs appeared in the Daphnia’s brood pouch (Harney et al., 2015)] using a Canon EOS 350D digital camera connected to a Leica MZ6 dissecting microscope at 2.5 × magnification, and the images were measured using the software ImageJ (Rasband, 1997). Neonate and maturity size was measured in millimeters, age was measured in days and first clutch abundance was measured as number of neonates released. Growth rate was determined as $\frac{sizeatmaturity-neonatesize}{ageatmaturity}$. Thus, four life-history traits were collected for each replicate: size at maturity, age at maturity, juvenile growth rate, and first clutch abundance.

Statistical analyses

Modeling population-level reaction norms

All statistics were performed in RStudio Team (2020). The traits of size at maturity, age at maturity, juvenile growth rate, and first clutch abundance were modeled individually to determine the best fit model for their actual reaction norm shape. For each trait, data was initially plotted graphically to give a rough estimate of the reaction norm shape, thus allowing the data itself to guide the modeling process. Each trait was modeled at the population level using the linear model, as is currently favored by reaction norm analyses:

$y=\mathit{cx}+b(1)$

in which c represents the gradient, and b the response value when the environmental gradient is at zero (the intercept). The data was also modeled using the quadratic equation:

$y=\mathit{cx}+{\mathit{cx}}^2+b(2)$

for which the parameters b and c are the same as in equation (1). The inclusion of the x² variable notates the curvature of the reaction norm. Finally, the three-parameter asymptotic exponential function was modeled:

$y=a+\left(b-a\right)*\exp \left(-\exp \left(c\right)*x\right)(3)$

in which a, b, and c are parameters representing the horizontal asymptote, the response when the input is zero (intercept), and the natural logarithm of the rate constant (slope), respectively.

Models (2) and (3) were chosen based on the shape of the raw data and preliminary model fitting, while model (1) was used to allow comparisons of goodness of fit between the currently used linear model and non-linear reaction norm models. Each iteration of the model was tested for goodness of fit by comparing Akaike Information Criterion (AIC) values, which balance the fit of each model against its complexity (Crawley, 2007). AIC values are only comparative between models of the same trait. Models were plotted using ggplot of the ggplot2 package.

Modeling clonal variability

Each trait was tested for clonal variability by expanding the best fit population-level model via the inclusion of clonal-level random effects. Following (Morrissey and Liefting, 2016), this was achieved by fitting random regression mixed models (RRMM) to the data. These models allow the fit of an overall population-level reaction norm to the data, while allowing for the addition of increased complexity in the form of clonal-level variation for each model coefficient. RRMMs were run using the nlmer function of the lme4 package. The nutritional gradient was included as a fixed effect and was mean-centered to address potential biases introduced by non-linear terms (Arnold et al., 2019). Clone was fitted as a random effect for each coefficient separately and in combination. AIC values were again generated to determine the best fit model, and models were again plotted using ggplot.

Phenotypic correlations across a resource gradient

7 clones is not sufficient to quantify how genetic correlations change across an environmental gradient. Instead we used phenotypic correlations as a tentative proxy for genetic correlations (Cheverud, 1988). Phenotypic correlations between all traits were analyzed separately for subsets of the data representing extreme low resource environments (10,000 cells mL^–1), medium resource environments (145,000 cells mL^–1) and extreme high resource environments (300,000 cells mL^–1) using the corrplot package in R (Wei and Simko, 2021).

Results

Are reaction norms linear or non-linear?

At the population level, the reaction norms for all four traits of age at maturity, size at maturity, juvenile growth rate, and first clutch abundance were each best fit by the three-parameter asymptotic regression model [model (3) above, see Figure 1]. For the traits of size at maturity and first clutch abundance the difference between the quadratic and asymptotic models was only slight, while the difference in fit was much more pronounced for age at maturity and juvenile growth rate. For all four traits, the fit of the asymptotic model was significantly better than that of the linear model (Table 1).

FIGURE 1

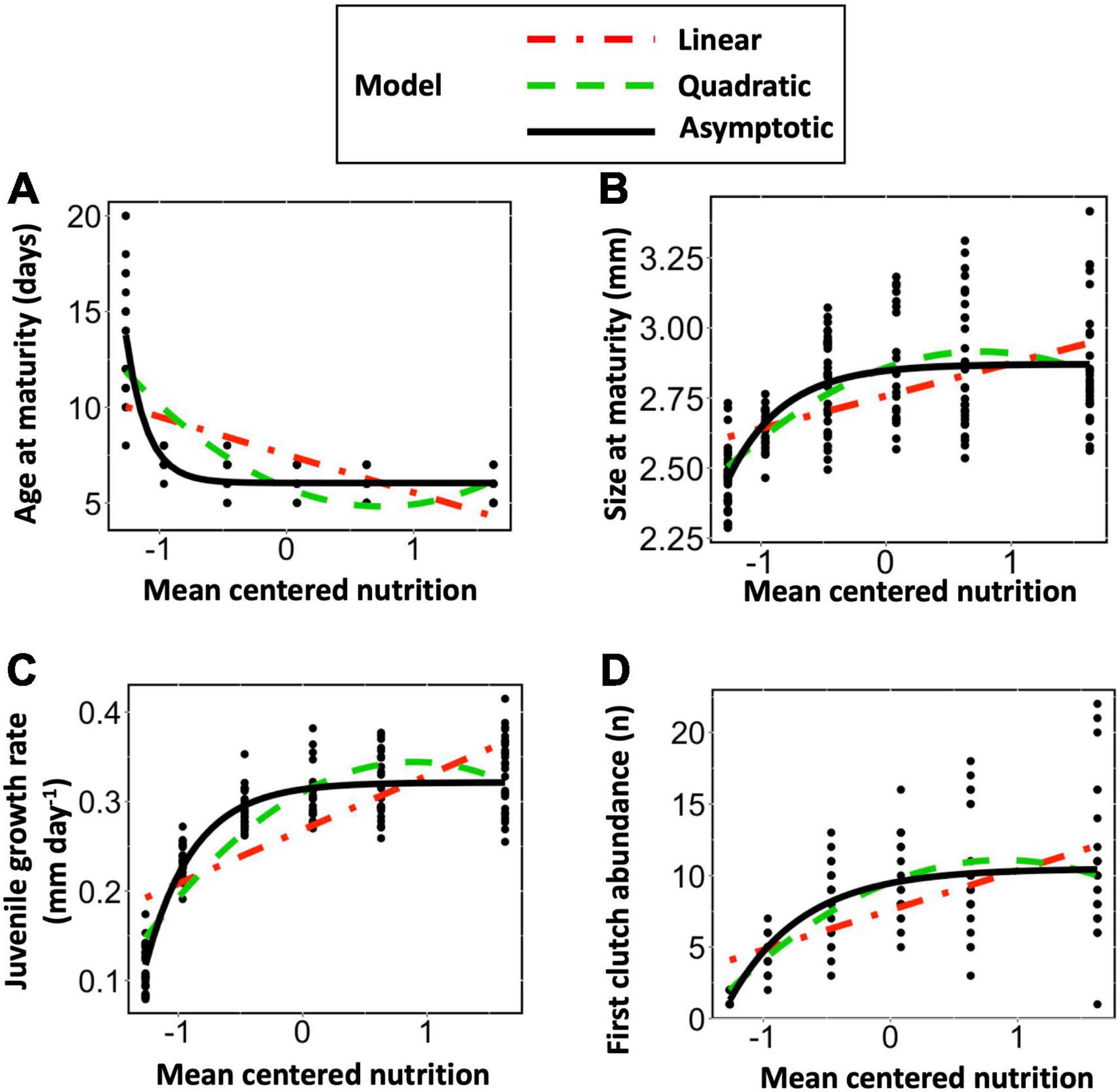
Figure 1. Population-level reaction norms for (A) Age at maturity, (B) Size at maturity, (C) Juvenile growth rate and (D) First clutch abundance modeled using either a linear, quadratic, or three parameter asymptotic exponential function. Mean-centered nutritional gradient, spanning from 10,000 to 300,000 cells mL^–1 was fitted as a fixed factor.

TABLE 1

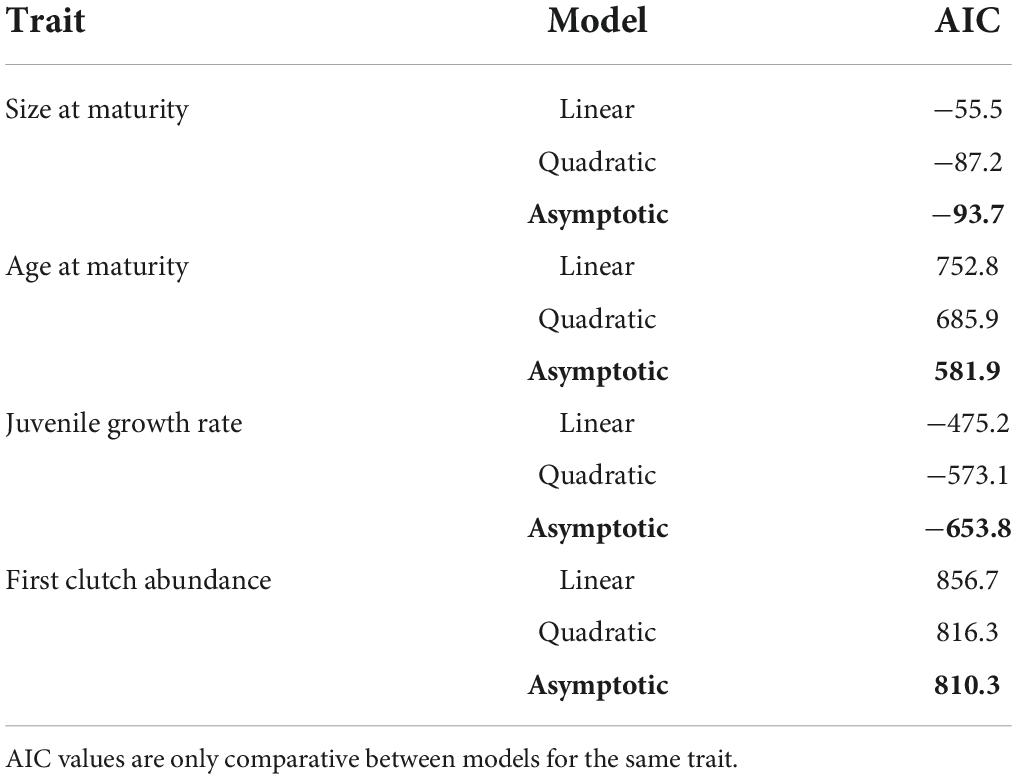
Table 1. Measures of goodness of fit for each of the three population-level reaction norms modeled for each life history trait. Best fit models are distinguished by their low AIC values and highlighted in bold.

Random regression mixed models

Age at maturity

As resource increases age at maturity sharply decreases to an asymptote where further increases in resource no longer generate decreases in age at maturity. The two best fitting models were asymptotic mixed effect models that included clonal variation in model parameters fitted as random effects (Table 2). The model with the lowest AIC value was an asymptotic mixed effect model with clonal variation in slope fitted as a random effect (Figure 2A and Table 2, Model no. 4).

TABLE 2

Table 2. Age at maturity reaction norm models, fitted using random regression mixed models (RRMM).

FIGURE 2

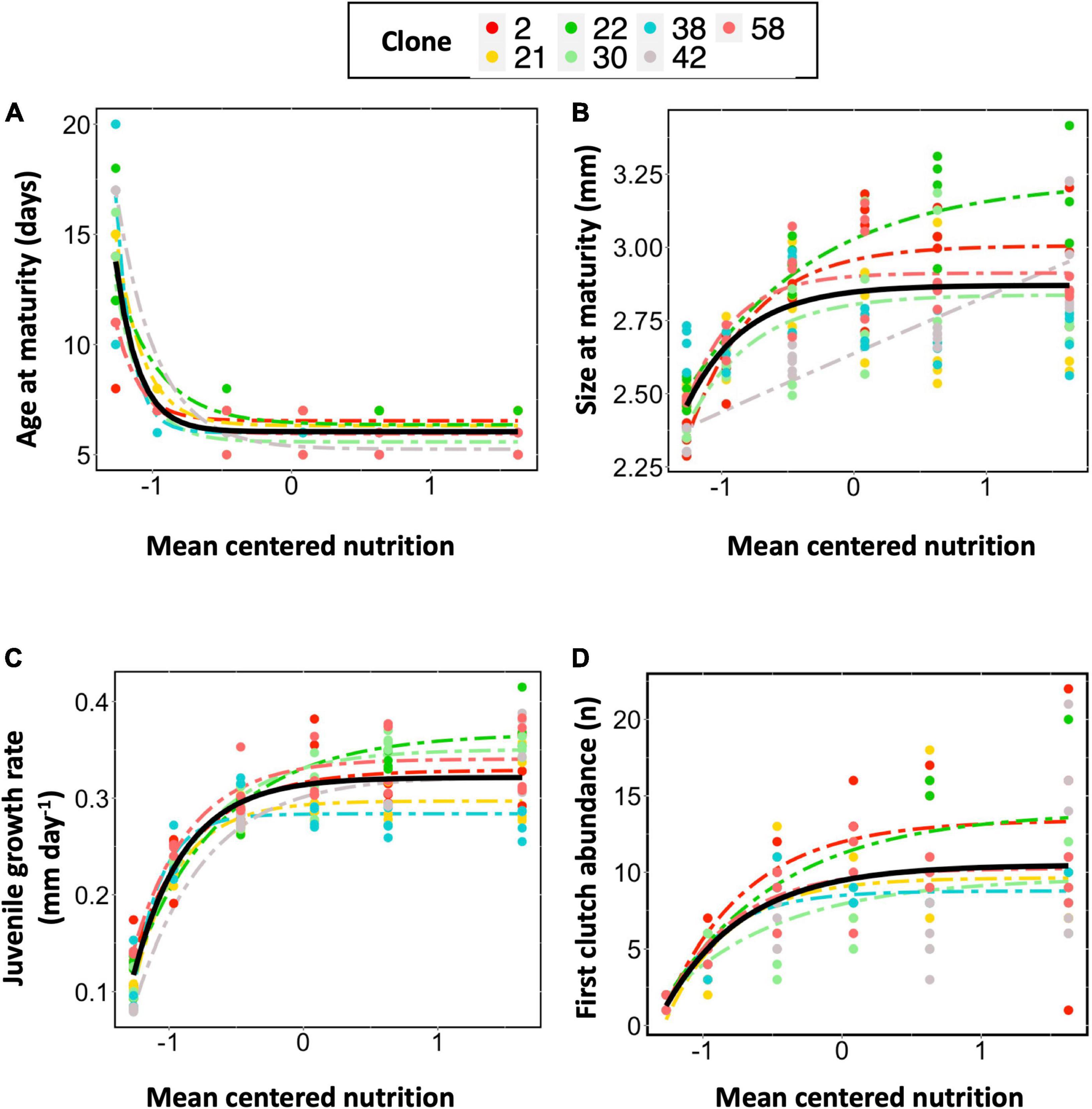
Figure 2. Population-level and clonal-level reaction norms for (A) Age at maturity, (B) Size at maturity, (C) Juvenile growth rate and (D) First clutch abundance. For each trait we utilized the best fitting model from the RRMM analysis. Mean-centered food was included as a fixed effect. Clonal variation in model parameters were included as a random effect. The solid black line shows the model fit for the population. The colored dots show the raw data for each clone and the colored dashed lines show the model fit for each clone. For age at maturity the best fitting model included a clone-specific slope term whereas for all other traits the best fitting model included clone-specific intercept and asymptotes. Clone 21 and 38 did not conform with the asymptotic model for size at maturity and clone 42 did not conform with the asymptotic model for first clutch abundance so these clones were not included in the plots visualizing clone-specific fits for these traits.

Size at maturity

As resource increases size at maturity sharply increases to an asymptote where further increases in resource no longer generates increases in size at maturity. The best fitting random regression model included clonal variation in the asymptote and intercept coefficients (Figure 2B and Table 3, Model no. 5).

TABLE 3

Table 3. Size at maturity reaction norm models, fitted using random regression mixed models (RRMM).

Juvenile growth rate

As resource increases juvenile growth rate sharply increases to an asymptote where further increases in resource no longer generates increases in juvenile growth rate. The best fitting random regression model included clonal variation in the asymptote and intercept coefficients (Figure 2C and Table 4, Model no. 8).

TABLE 4

Table 4. Juvenile growth rate reaction norm models, fitted using random regression mixed models (RRMM).

First clutch abundance

As resource increased first clutch abundance sharply increased to an asymptote where further increases in resource no longer generated increases in the number of neonates in the first clutch. The best fitting model for the first clutch abundance reaction norm was also an asymptotic mixed effect model with clone-specific asymptotes and intercepts fitted as a random term (Figure 2D and Table 5, Model no. 8).

TABLE 5

Table 5. First clutch abundance reaction norm models, fitted using random regression mixed models (RRMM).

Phenotypic correlations across a resource gradient

The non-linear reaction norms observed result in changes in both the strength and direction of phenotypic correlations between traits in different environments (see Figure 3). Neonate size was positively correlated with size and age at maturity in low resource environments but became negative in medium and high resource environments. Size at maturity was uncorrelated with other traits in low resource environments but became strongly positively correlated with age at maturity and first clutch abundance in medium and high food environments. In low resources environments, individuals that grew fast matured quicker, but this effect weakened as resources increased. First clutch abundance was not strongly correlated with any trait in low resource environments, but it became positively correlated with age and size at maturity as resources increased (see Figure 3).

FIGURE 3

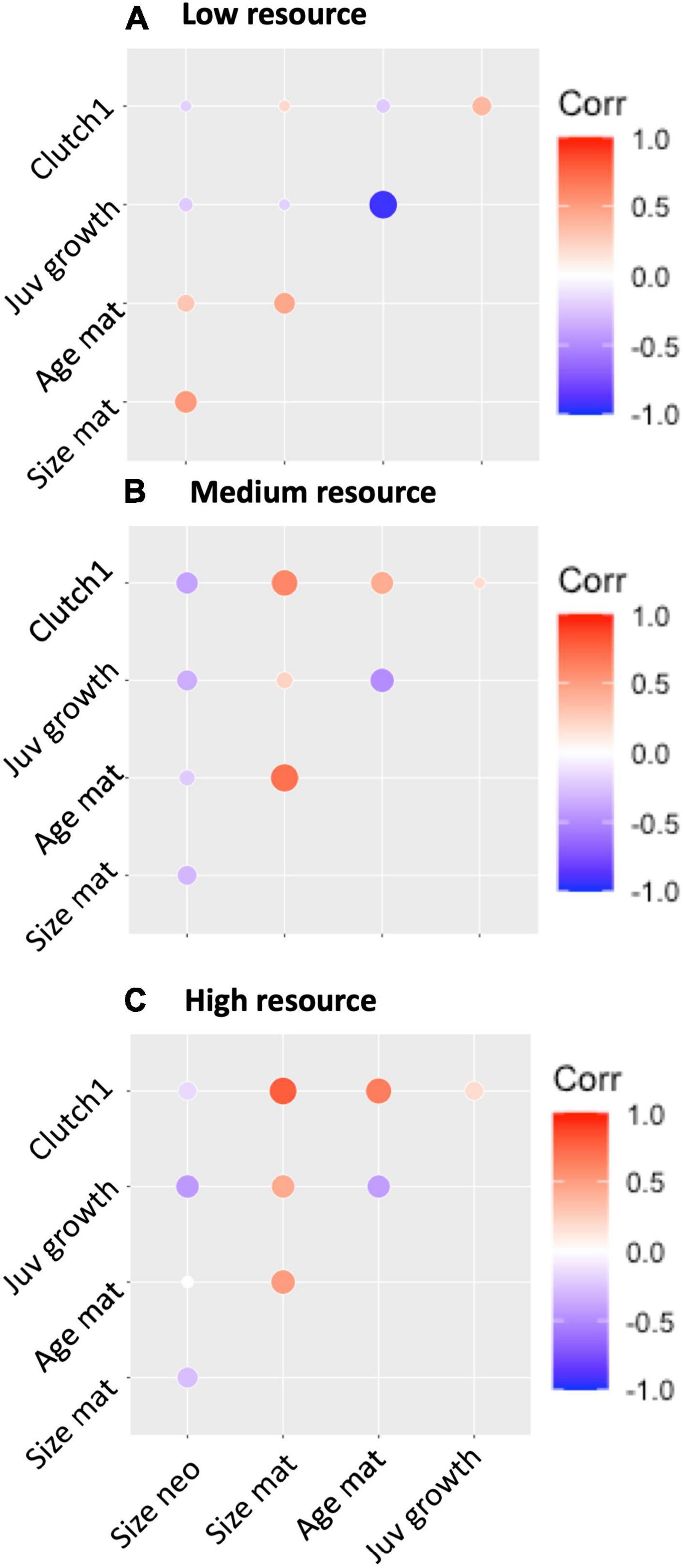
Figure 3. Correlation matrices demonstrating the direction and strength of phenotypic correlations between all traits in (A) Low resource environments (10,000 cells Chlorella vulgaris mL^–1), (B) Medium resource environments (145,000 cells C. vulgaris mL^–1) and (C) High resource environments (300,000 cells C. vulgaris mL^–1).

Discussion

Reaction norm shapes are often assumed rather than measured. As a result, there is a pressing need for empirical studies that quantify reaction norm shape and compare it to the predictions of models that assume reaction norm shape (Stinchcombe et al., 2012; Arnold et al., 2019). We measured the multi-trait plastic response of 7 Daphnia magna clones across a broad resource gradient. For each of the investigated life history traits of size at maturity, age at maturity, juvenile growth rate, and first clutch abundance, a non-linear asymptotic model provided a better fit to the data than the currently assumed linear alternative confirming that when a broad enough environmental gradient is used, reaction norm shape is not adequately described by linear models. We observed clonal variation in non-linear plastic responses for all 4 traits that we measured, demonstrating that non-linear random mixed models are useful for studying how plasticity influences the adaptive capacity of populations over broad environmental gradients.

At the population level, all four of the traits investigated in this study were best fit by asymptotic curves. Juvenile growth rate, size at maturity, and first clutch abundance all increased linearly whereas age at maturity decreased linearly as resources increased. However, at a certain point, trait responses leveled off until increases in resource no longer produced increases or decreases in traits. In other words, there was a limit to how much trait plasticity could respond to environmental change. For age at maturity clonal variation in slopes was observed, meaning that although there was no difference in the minimum number of days it took a clone to mature on high food there was clonal variation in how quickly low resource levels started to delay maturation. In Daphnia, age and size at maturity is determined by a maturation threshold (Ebert, 1994) which is already known to vary between clones (Harney et al., 2013). For size at maturity, juvenile growth rate and first clutch abundance the best fitting models included clonal variation in intercept and asymptote, resulting in clonal variation in the maximum juvenile growth rate and size at maturity achieved at high resources levels. A strong non-linear reaction norm in response to varying resource environments might not be surprising in a filter feeding organism such as Daphnia, where consumption rate increases linearly with food abundance up to a threshold level at which it remains constant (Type 1 functional response) (Jeschke et al., 2004; Chevin and Hoffmann, 2017). Thus, although demonstrations of non-linear reaction norms are currently still rare (Rocha and Klaczko, 2012; Arnold et al., 2019) we expect them to be widespread.

Fitting non-linear reaction norms requires more work than studying linear reaction norms, but identifying the real shape of reaction norms and how genetically variable they are (G × E interaction) is important for understanding how plasticity influences an organism’s capacity to adapt to new environments (Morrissey and Liefting, 2016; Arnold et al., 2019). The random regression mixed model framework (Morrissey and Liefting, 2016; Arnold et al., 2019) used in this study showcases the relative ease with which non-linearity can be incorporated into plasticity research and used to quantify population-level responses and the variation between genotypes in this response. Being able to select a function that best reflects how reaction norm shape changes across an environmental gradient greatly improves model fit and provides a much better representation of reaction norm shape than a straight line. Moreover, the random regression mixed model framework allows estimates and inferences about genetic variation in non-linear reaction norms to be obtained using a standard and relatively familiar statistical approach (Morrissey and Liefting, 2016; Arnold et al., 2019). However, this approach assumes that all genotypes in a population have the same basic reaction norm shape. This may not always be true. In our study, size at maturity could not be modeled using a non-linear asymptotic model for two clones even though this was the best fitting model at the population level. Moreover, any fixed function may still be a simplification of the real reaction norm shape that only fits the data well across some parts of the environment, or the fit in one environment may have a large and unwanted impact on the fit in other parts of the environmental gradient (Schluter, 1988; Meyer and Kirkpatrick, 2005). One way around this problem is to fit more complex non-linear models, such as GAMs, that can incorporate spline functions that captures less conventional reaction norm shapes better (Hinners et al., 2017; Arnold et al., 2019). Splines may even be fitted before selecting models to get a better understanding of the shape of population-level reaction norms (Gibert et al., 1998).

Reaction norm non-linearity has implications for understanding the evolutionary potential of a population. The shape of the reaction norm is critical for determining how phenotypic plasticity influences genetic variation in different environments. For example, models assuming linear reaction norms predict that additive genetic variation increases in extreme environments, facilitating adaptation to extreme environments (Chevin and Lande, 2011). Yet, in our study, heritable variation in trait expression (in our case—clonal variation) leveled off above a certain resource threshold suggesting that plasticity will not continue to generate increased genetic variation in traits as environments become more extreme as linear models predict. However, the response to selection doesn’t depend on how much heritable phenotypic variation is available, it depends on the proportion of phenotypic variation attributable to additive genetic variance (or clonal variation in this case) (Falconer, 1989). Since the extent to which plasticity influences trait expression declines to zero, phenotypic variation at high resource levels is likely to be genetic, increasing the likelihood that selection on traits results in genetic change. In contrast, in low resource environments even small differences in environment induce large plastic shifts in traits expression, increasing the likelihood that environmental heterogeneity obscures genetic differences in traits and makes a response to selection less likely. This might explain why in Daphnia populations clonal selection is sometimes only observed in populations that experience the unlimited resources that fuel rapid population growth (van Doorslaer et al., 2009) and may have broader implications for understanding eco-evolutionary dynamics (Hendry, 2017), the context-dependence of which is often not fully appreciated (Montejo-Kovacevich et al., 2020).

The fact that there is any genetic variation at all in extreme environments is important because it suggests that when plastic responses can no longer keep up with environmental change, further phenotypic change may be possible through trait evolution fuelled by standing genetic variation. A study with many more genotypes would be required to get a real understanding of the extent that rapid evolution could rescue a population in an extreme environment. However, studies often assume that evolutionary rescue takes over when limits to plasticity are reached, but there is still little empirical understanding of how the genetic and mutational variance in traits compares in extreme environments compared to common environments and whether genetic correlations between trait expression in common and extreme environments constrains any response to selection (Chevin and Hoffmann, 2017). Assuming that in our study phenotypic correlations are broadly reflective of genetic correlations (Cheverud, 1988), our study demonstrates that there are often correlations between traits that will limit the extent that any trait can evolve independently of other traits. However, we found that correlations between traits changed across the resource environment, suggesting that genetic architecture itself may be context-dependent. These findings align with several other Daphnia studies that have recently demonstrated genetic variance-covariance matrices are environment-dependent (Lind et al., 2015; Beckerman et al., 2017). Extreme environments are assumed to exert a strong selection pressure on populations because they sometimes cause high mortality but the rarity of extreme conditions and the fact that they are often stressful irrespective of genotype make it less likely that these environments contribute a lot to the evolution of reaction norms (Chevin and Hoffmann, 2017). Extreme environments are also not always stressful. In our study, the environment most likely to result in genetic change in the population is a benign high food environment in which small genetic differences in phenotype may translate into significant variation in fitness (Bruijning et al., 2018). Ultimately, more empirical work is required to understand how extreme environments contribute to the evolution of reaction norms. However, our demonstration that reaction norms are often extremely non-linear at least makes it clear that the contribution of plasticity and genetic adaptation to phenotypic evolution will often be quite different at different points along an environmental gradient.

Linear reaction norms have sufficed so far in plasticity research as their parameters of intercept and mean slope are informative enough to provide a general understanding of plasticity and its role in evolution (Morrissey and Liefting, 2016). However, our results confirm that the assumption of linearity is sometimes a poor reflection of the true amount of phenotypic variation expressed by genotypes. Such a misrepresentation of variation compromises the conclusions drawn from plasticity studies and can be misinformative, leading to unrealistic conclusions about species’ ability to adapt to a changing environment. Since the shape of a reaction norm is often likely to be a product of the range over which it is measured (Chevin and Hoffmann, 2017) failing to incorporate environmental extremes will often result in the wrong conclusion about the shape of reaction norms (Stinchcombe et al., 2012). Incorporating reaction norm non-linearity may improve understanding of how natural populations adapt to their environments, be it naturally occurring stressors such as heterogenous predator regimes (Carter et al., 2017), or the effects of human-induced climate change on growth and development (Ramler et al., 2014). It may also be useful in food production industries, where understanding optimal conditions for trait expression is important for crossbreeding efforts and producing higher yielding animals (Su et al., 2009) and more stress-resistant crops (Ly et al., 2018).

This paper aimed to challenge the use of linear models in reaction norm analyses, and the fundamental role they currently play in plasticity research. While the linear regression parameters of slope and intercept are informative for comparative purposes, linear models themselves may often be a poor approximation of reality. Critically, they may misrepresent the patterns of heritable phenotypic variation observed in extreme environments. Our study supports the conclusion from earlier studies (Morrissey and Liefting, 2016; Gomulkiewicz et al., 2018; Arnold et al., 2019) that non-linear random regression models provide a better way to capture true reaction norm shape and it’s likely impact on the evolvability of populations in different environments.

Data availability statement

The datasets generated and analyzed for this study can be found in the DataCat, the University of Liverpool’s open access online research data catalogue, doi: 10.17638/datacat.liverpool.ac.uk/1742.

Author contributions

SP conceptualized and obtained funding for the study, helped design the experiment, and co-wrote the original draft of the manuscript. MO’C designed the experiment, devised the methodology, carried out the investigation, the data analysis and the visualization of the results, and co-wrote the original draft of the manuscript. FB helped design the experiment and assisted with the analysis of the data and the visualization of the results. All authors reviewed and edited the final version of the manuscript.

Funding

This study was supported by a NERC Highlight (grant number: NE/N016017/1) to SP.

Acknowledgments

We thank Danny Sadler and Alan Reynolds George Rankin for help in the lab and technical support and two reviewers for comments that greatly improved an earlier version of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arnold, P. A., Kruuk, L. E. B., and Nicotra, A. B. (2019). How to analyse plant phenotypic plasticity in response to a changing climate. New Phytol. 222, 1235–1241. doi: 10.1111/nph.15656

PubMed Abstract | CrossRef Full Text | Google Scholar

Beckerman, A. P., Reger, J., Lind, M. I., and Robinson, M. R. (2017). Predation drives local adaptation of phenotypic plasticity. Nat. Ecol. Evol. 20:1.

Google Scholar

Bradshaw, A. (1965). Evolutionary significance of phenotypic plasticity in plants. Adv. Genet. 13, 115–155. doi: 10.1016/S0065-2660(08)60048-6

CrossRef Full Text | Google Scholar

Bruijning, M., Berge, A. C. M., and Jongejans, E. (2018). Population-level responses to temperature, density and clonal differences in Daphnia magna as revealed by integral projection modelling. Funct. Ecol. 32, 2407–2422. doi: 10.1111/1365-2435.13192

CrossRef Full Text | Google Scholar

Carter, M. J., Lind, M. I., Dennis, S. R., Hentley, W., and Beckerman, A. P. (2017). Evolution of a predator-induced, nonlinear reaction norm. Proc. R. Soc. B Biol. Sci. 284:20170859. doi: 10.1098/rspb.2017.0859

PubMed Abstract | CrossRef Full Text | Google Scholar

Charmantier, A., McCleery, R. H., Cole, L. R., Perrins, C., Kruuk, L. E. B., and Sheldon, B. C. (2008). Adaptive phenotypic plasticity in response to climate change in a wild bird population. Science 320, 800–803. doi: 10.1126/science.1157174

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, I.-C., Hill, J. K., Ohlemüller, R., Roy, D. B., and Thomas, C. D. (2011). Rapid range shifts of species associated with high levels of climate warming. Science 333, 1024–1026. doi: 10.1126/science.1206432

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheverud, J. M. (1988). A comparison of genetic and phenotypic correlations. Evolution 42, 958–968. doi: 10.1111/j.1558-5646.1988.tb02514.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chevin, L. M., and Hoffmann, A. A. (2017). Evolution of phenotypic plasticity in extreme environments. Philos. Trans. R. Soc. Lond. B Biol. Sci. 372:20160138. doi: 10.1098/rstb.2016.0138

PubMed Abstract | CrossRef Full Text | Google Scholar

Chevin, L. M., and Lande, R. (2010). When do adaptive plasticity and genetic evolution prevent extinction of a density-regulated population. Evolution 64, 1143–1150. doi: 10.1111/j.1558-5646.2009.00875.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chevin, L.-M., and Lande, R. (2011). Adaptation to marginal habitats by evolution of increased phenotypic plasticity. J. Evol. Biol. 24, 1462–1476. doi: 10.1111/j.1420-9101.2011.02279.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chevin, L.-M., and Lande, R. (2013). Evolution of discrete phenotypes from continuous norms of reaction. Am. Nat. 182, 13–27. doi: 10.1086/670613

PubMed Abstract | CrossRef Full Text | Google Scholar

Crawley, M. J. (2007). The R Book. Chichester: Wiley-Blackwell. doi: 10.1002/9780470515075

CrossRef Full Text | Google Scholar

David, J. R., Gibert, P., Gravot, E., Petavy, G., Morin, J.-P., Karan, D., et al. (1997). Phenotypic plasticity and developmental temperature in Drosophila: Analysis and significance of reaction norms of morphometrical traits. J. Therm. Biol. 22, 441–451. doi: 10.1023/b:gene.0000017639.62427.8b

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidson, A. M., Jennions, M., and Nicotra, A. B. (2011). Do invasive species show higher phenotypic plasticity than native species and, if so, is it adaptive? A meta-analysis. Ecol. Lett. 14, 419–431. doi: 10.1111/j.1461-0248.2011.01596.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Day, T., and Rowe, L. (2002). Developmental thresholds and the evolution of reaction norms for age and size at life-history transitions. Am. Nat. 159, 338–350. doi: 10.1086/338989

PubMed Abstract | CrossRef Full Text | Google Scholar

de Jong, G. (1990). Quantitative genetics of reaction norms. J. Evol. Biol. 3, 447–468. doi: 10.1046/j.1420-9101.1990.3050447.x

CrossRef Full Text | Google Scholar

Easterling, D. R., Meehl, G. A., Parmesan, C., Changnon, S. A., Karl, T. R., and Mearns, L. O. (2000). Climate extremes: Observations, modeling, and impacts. Science 289, 2068–2074. doi: 10.1126/science.289.5487.2068

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebert, D. (1994). A maturation size threshold and phenotypic plasticity of age and size at maturity in Daphnia magna. Oikos 69, 309–317. doi: 10.2307/3546152

CrossRef Full Text | Google Scholar

Ebert, D. (2005). Ecology, Epidemiology, and Evolution of Parasitism in Daphnia [Internet]. Bethesda, MD: National Library of Medicine (US), National Center for Biotechnology Information.

Google Scholar

Falconer, D. S. (1989). Introduction to Quantitative Genetics. New York, NY: Longman.

Google Scholar

Gavrilets, S., and Scheiner, S. M. (1993). The genetics of phenotypic plasticity. V. Evolution of reaction norm shape. J. Evol. Biol. 6, 31–48. doi: 10.1046/j.1420-9101.1993.6010031.x

CrossRef Full Text | Google Scholar

Gibert, P., Moreteau, B., David, J. R., and Scheiner, S. M. (1998). Describing the evolution of reaction norm shape: Body pigmentation in Drosophila. Evolution 52, 1501–1506. doi: 10.1111/j.1558-5646.1998.tb02032.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gienapp, P., and Brommer, J. E. (2014). “Evolutionary dynamics in response to climate change,” in Quantitative Genetics In The Wild, eds A. Charmantier, D. Garant, and L. E. B. Kruuk (Oxford, UK: Oxford University Press), 254–273. doi: 10.1093/acprof:oso/9780199674237.003.0015

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomulkiewicz, R., Kingsolver, J. G., Carter, P. A., and Heckman, N. (2018). Variation and evolution of function-valued traits. Annu. Rev. Ecol. Evol. Syst. 49, 139–164. doi: 10.1146/annurev-ecolsys-110316-022830

CrossRef Full Text | Google Scholar

Harney, E., Dooren, T. J. M. V., Paterson, S., and Plaistow, S. J. (2013). How to measure maturation: A comparison of probabilistic methods used to test for genotypic variation and plasticity in the decision to mature. Evolution 67, 525–538. doi: 10.1111/j.1558-5646.2012.01758.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Harney, E., Plaistow, S. J., and Paterson, S. (2015). Transcriptional changes during Daphnia pulex development indicate that the maturation decision resembles a rate more than a threshold. J. Evol. Biol. 28, 944–958. doi: 10.1111/jeb.12624

PubMed Abstract | CrossRef Full Text | Google Scholar

Heino, M., and Dieckmann, U. (2008). Detecting fisheries-induced life-history evolution: An overview of the reaction-norm approach. Bull. Mar. Sci. 83, 69–93.

Google Scholar

Hendry, A. P. (2017). Eco-evolutionary Dynamics. Princeton, NJ: Princeton University Press. doi: 10.1515/9781400883080

CrossRef Full Text | Google Scholar

Hinners, J., Kremp, A., and Hense, I. (2017). Evolution in temperature-dependent phytoplankton traits revealed from a sediment archive: Do reaction norms tell the whole story. Proc. R. Soc. B Biol. Sci. 284:20171888. doi: 10.1098/rspb.2017.1888

PubMed Abstract | CrossRef Full Text | Google Scholar

Huey, R. B., and Kingsolver, J. G. (1989). Evolution of thermal sensitivity of ectotherm performance. Trends Ecol. Evol. 4, 131–135. doi: 10.1016/0169-5347(89)90211-5

CrossRef Full Text | Google Scholar

Izem, R., and Kingsolver, J. G. (2005). Variation in continuous reaction norms: Quantifying directions of biological interest. Am. Nat. 166, 277–289. doi: 10.1086/431314

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeschke, J. M., Kopp, M., and Tollrian, R. (2004). Consumer-food systems: Why type I functional responses are exclusive to filter feeders. Biol. Rev. 79, 337–349. doi: 10.1017/s1464793103006286

PubMed Abstract | CrossRef Full Text | Google Scholar

Liefting, M., Hoffmann, A. A., and Ellers, J. (2009). Plasticity versus environmental canalization: Population differences in thermal responses along a latitudinal gradient in Drosophila serrata. Evolution 63, 1954–1963. doi: 10.1111/j.1558-5646.2009.00683.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lind, M. I., Yarlett, K., Reger, J., Carter, M. J., and Beckerman, A. P. (2015). The alignment between phenotypic plasticity, the major axis of genetic variation and the response to selection. Proc. Biol. Sci. R. Soc. 282:20151651. doi: 10.1098/rspb.2015.1651

PubMed Abstract | CrossRef Full Text | Google Scholar

Ly, D., Huet, S., Gauffreteau, A., Rincent, R., Touzy, G., Mini, A., et al. (2018). Whole-genome prediction of reaction norms to environmental stress in bread wheat (Triticum aestivum L.) by genomic random regression. Field Crops Res. 216, 32–41. doi: 10.1016/j.fcr.2017.08.020

CrossRef Full Text | Google Scholar

Meyer, K., and Kirkpatrick, M. (2005). Up hill, down dale: Quantitative genetics of curvaceous traits. Philos. Trans. R. Soc. B Biol. Sci. 360, 1443–1455. doi: 10.1098/rstb.2005.1681

PubMed Abstract | CrossRef Full Text | Google Scholar

Montejo-Kovacevich, G., Farkas, T., Beckerman, A., and Nosil, P. (2020). Exploring context dependency in eco-evolutionary patterns with the stick insect Timema cristinae. Ecol. Evol. 10, 8197–8209. doi: 10.1002/ece3.6526

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreteau, B., Morin, J. P., Gibert, P., Pétavy, G., and Pla, É (1997). Evolutionary changes of nonlinear reaction norms according to thermal adaptation: A comparison of two Drosophila species. C. R. Acad. Sci. Ser. III Sci. de la Vie 320, 833–841. doi: 10.1016/s0764-4469(97)85020-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrissey, M. B., and Liefting, M. (2016). Variation in reaction norms: Statistical considerations and biological interpretation. Evolution 70, 1944–1959. doi: 10.1111/evo.13003

PubMed Abstract | CrossRef Full Text | Google Scholar

Murren, C. J., Maclean, H. J., Diamond, S. E., Steiner, U. K., Heskel, M. A., Handelsman, C. A., et al. (2014). Evolutionary Change in Continuous Reaction Norms. Am. Nat. 183, 453–467. doi: 10.1086/675302

PubMed Abstract | CrossRef Full Text | Google Scholar

Nussey, D. H., Wilson, A. J., and Brommer, J. E. (2007). The evolutionary ecology of individual phenotypic plasticity in wild populations. J. Evol. Biol. 20, 831–844. doi: 10.1111/j.1420-9101.2007.01300.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pigliucci, M. (2005). Evolution of phenotypic plasticity: Where are we going now. Trends Ecol. Evol. 20, 481–486. doi: 10.1016/j.tree.2005.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Plaistow, S. J., and Collin, H. (2014). Phenotypic integration plasticity in Daphnia magna: An integral facet of G × E interactions. J. Evol. Biol. 27, 1913–1920. doi: 10.1111/jeb.12443

PubMed Abstract | CrossRef Full Text | Google Scholar

Plaistow, S. J., Shirley, C., Collin, H., Cornell, S. J., and Harney, E. D. (2015). Offspring provisioning explains clone-specific maternal age effects on life history and life span in the water flea, daphnia pulex. Am. Nat. 186, 376–389. doi: 10.1086/682277

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramler, D., Shama, L. N., Wegner, K. M., and Ahnelt, H. (2014). Nonlinear effects of temperature on body form and developmental canalization in the threespine stickleback. J. Evol. Biol. 27, 497–507. doi: 10.1111/jeb.12311

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasband, W. S. (1997). ImageJ, U. S. Bethesda, MD: National Institutes of Health.

Google Scholar

Rocha, F. B., and Klaczko, L. B. (2012). Connecting the dots of nonlinear reaction norms unravels the threads of genotype-environmental interaction in Drosophila. Evolution 66, 3404–3416. doi: 10.1111/j.1558-5646.2012.01702.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rocha, F. B., and Klaczko, L. B. (2014). Undesirable consequences of neglecting nonlinearity: Response to comments by Liefting et al. (2013) on Rocha & Klaczko (2012). Evolution 68, 1548–1551. doi: 10.1111/evo.12386

PubMed Abstract | CrossRef Full Text | Google Scholar

RStudio Team (2020). RStudio: Integrated Development for R. Boston, MA: RStudio.

Google Scholar

Scheiner, S. M. (1993). Genetics and evolution of phenotypic plasticity. Annu. Rev. Ecol. Syst. 24, 35–68. doi: 10.1146/annurev.es.24.110193.000343

CrossRef Full Text | Google Scholar

Schlichting, C. D. (2008). Hidden reaction norms, cryptic genetic variation, and evolvability. Ann. N. Y. Acad. Sci. 1133, 187–203. doi: 10.1196/annals.1438.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Schluter, D. (1988). Estimating the form of natural selection on a quantitative trait. Evolution 42, 849–861. doi: 10.1111/j.1558-5646.1988.tb02507.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stinchcombe, J. R., Function-valued Traits Working Group, and Kirkpatrick, M. (2012). Genetics and evolution of function-valued traits: Understanding environmentally responsive phenotypes. Trends Ecol. Evol. 27, 637–647. doi: 10.1016/j.tree.2012.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, G., Madsen, P., and Lund, M. S. (2009). Reaction norm model with unknown environmental covariate to analyze heterosis by environment interaction. J. Dairy Sci. 92, 2204–2213. doi: 10.3168/jds.2008-1499

PubMed Abstract | CrossRef Full Text | Google Scholar

van Doorslaer, W., Stoks, R., Duvivier, C., Bednarska, A., and De Meester, L. (2009). Population dynamics determine genetic adaptation to temperature in Daphnia. Evolution 63, 1867–1878. doi: 10.1111/j.1558-5646.2009.00679.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vedder, O., Bouwhuis, S., and Sheldon, B. C. (2013). Quantitative assessment of the importance of phenotypic plasticity in adaptation to climate change in wild bird populations. PLoS Biol. 11:e1001605. doi: 10.1371/journal.pbio.1001605

PubMed Abstract | CrossRef Full Text | Google Scholar

Via, S., and Lande, R. (1985). Genotype-environment interaction and the evolution of phenotypic plasticity. Evolution 39, 505–522. doi: 10.1111/j.1558-5646.1985.tb00391.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Via, S., Gomulkiewicz, R., Jong, G. D., and Scheiner, S. M. (1995). Adaptive phenotypic plasticity: Consensus and controversy. Trends Ecol. Evol. 10, 212–217. doi: 10.1016/S0169-5347(00)89061-8

CrossRef Full Text | Google Scholar

Wei, T., and Simko, V. R. (2021). Package ‘corrplot’: Visualization of a Correlation Matrix. (Version 0.92).

Google Scholar

West-Eberhard, M. J. (2003). Developmental Plasticity And Evolution. Oxford: Oxford University Press. doi: 10.1093/oso/9780195122343.001.0001

PubMed Abstract | CrossRef Full Text | Google Scholar

Wund, M. A. (2012). Assessing the impacts of phenotypic plasticity on evolution. Integr. Comp. Biol. 52, 5–15. doi: 10.1093/icb/ics050

PubMed Abstract | CrossRef Full Text | Google Scholar