- 1Laboratory of Biological Control and Ecosystem Services, Department of Crop Protection, Instituto Murciano de Investigación y Desarrollo Agrario y Medioambiental (IMIDA), Murcia, Spain
- 2Pacific Agri-Food Research Centre, Agriculture and Agri-Food Canada, Agassiz, BC, Canada
The ability to locate suitable food resources affects fitness in animals. Therefore, movements are necessary to optimize foraging in habitats where food is distributed in patches of different qualities. The aim of this work was to investigate the dispersal and distribution of females and males of the omnivorous mirid D. hesperus in mesocosms composed by food patches of different values in terms of fitness. In agreement with the Marginal Value Theorem (MVT) and the Ideal Free Distribution (IFD), individuals were expected to aggregate in the highest quality patches. Besides, the proportion of individuals in patches was predicted to be proportional to fitness, and interference among individuals was expected to rise as the density of individuals increased. Emigration rates were predicted to be higher for low- than for high-quality patches, while the opposite was predicted for immigration. Three types of habitats each with different combinations of food resources were tested: (1) habitat including patches of tomato plants with no-prey, and patches infested with either mite or whitefly; (2) with no-prey and whitefly; (3) with no-prey and mites. Each type of habitat was set up in a tomato greenhouse compartment and replicated four times. Individuals were tracked by mark-recapture methods using luminous paintings. The number of females and males in whitefly patches was significantly higher than in mite and no-prey patches, but a significant interaction sex*habitat and sex*patch was found. In habitats with only one type of prey, D. hesperus adults fitted the IFD, while in mixed prey habitats their distribution diverged from IFD. Interference was found to be significant, with female fitness decreasing as their density increased. Emigration rates were significantly lower for whitefly patches with a significant interaction patch*sex; the opposite was found for immigration. This research shows that it is unlikely that D. hesperus forage according to the omniscient principle of IFD and MVT; in contrast, it strongly suggests that it uses some simple rules to make decisions about inter-patch movement, and emigration from habitats and patches.
Introduction
The movements of animals in relation to food resources and patch exploitation is a key topic in behavioral and evolutionary ecology (Stephens and Krebs, 1986; Ravigné et al., 2009; Van Moorter et al., 2013). An animal’s ability to locate suitable food resource determines its survival and reproduction, and therefore, its contribution to population growth and the genetic pool (Wajnberg et al., 1999; Wajnberg, 2004; Gaillard et al., 2010). Food resources are generally scattered through the environment in patches of different quality and abundance, and movements are necessary to optimize foraging due to the dynamic quality of patches within habitats. Foraging theory predicts that animals chose food patches within habitats in order to maximize their fitness (Fretwell and Lucas, 1970; Milinski and Parker, 1991; Sutherland and Parker, 1992; Tregenza, 1994). The Marginal Value Theorem (MVT) (Charnov, 1976) and the Ideal Free Distribution (IFD) (Fretwell and Lucas, 1970) are two of the best-known classical models dealing with the exploitation of patches and the distribution of animals competing for resources in patchy environments. Patch departure rules in the MVT model assume several conditions from which it follows that a forager should remain in a patch as long as the instantaneous (i.e., “marginal”) rate of net energy gain is above the overall rate for the habitat (Charnov, 1976; Pyke, 1984). The IFD theory is based on the premise that animals are “ideal,” and are assumed to have a perfect knowledge of the distribution and quality of food resources in the environment; besides, they are “free” and they incur no cost when moving among patches within the environment (Fretwell and Lucas, 1970). Two additional assumptions in the IDF are that individuals settle in the most suitable habitat and that all individuals within a habitat have the same success rates; therefore, they are expected to locate themselves in patches within habitats in such a way that fitness cannot be improved by changing their distribution (Fretwell and Lucas, 1970; Milinski and Parker, 1991; Sutherland and Parker, 1992). However, in the real world the distribution of predators in patches is not only influenced by prey density, but also by the density of conspecific and heterospecific individuals competing for the same food resources. Interference may increase with the density of competitors, thereby reducing intake rates in the best quality patches to the same levels that can be achieved in poorer ones (Sutherland and Parker, 1992; Tregenza, 1994). In addition, internal factors such as sex and mating status are known to influence the dispersal propensity in predators and parasitoids (Nakashima and Hirose, 2003; Bowler and Benton, 2005; Schellhorn et al., 2014).
The MVT and IFD models have been criticized for being based on simplistic and unrealistic assumptions unlikely to be matched in nature (Sutherland, 1996; Nonacs, 2001; Wajnberg, 2006). It is not likely that any animal exploiting resources in a given habitat will have real-time information about the abundance and quality of resources in other patches, especially when these patches may be occupied and being depleted by an unknown number of other competitors. However, individuals could estimate the quality of food resources in a patch by resource contribution to fitness, which could be measured by the contribution of individuals to population growth (Mcgraw and Caswell, 1996; Coulson et al., 2006). In addition, individuals could estimate the contribution of nutritional resources to fitness from their physiological state (e.g., hunger) (Nakashima et al., 2002). Handling times, prey encounters, resources of prey, and traveling times between patches could also provide foragers with additional information about the quality of patches and habitats (Williams and Flaxman, 2012; Foo et al., 2016). On the other hand, animals are sensitive to prey quality as a function of net energy intake, that is, energy intake per unit of foraging effort (Charnov, 1976). Since prey of different species may contribute differently to reproductive potential, generalist predators are expected to make decisions about patch exploitation based on the energy content of prey (i.e., offspring produced per prey), which will necessarily be limited by net energy intake as described by Charnov (1976). Patches may not only provide prey but also useful information about the quality of the overall habitat, upon which natural enemies may base their decisions (Wajnberg, 2006).
Generalist arthropod predators can be important in the regulation of herbivore populations in natural systems and are often key pest antagonists in biological control (Symondson et al., 2002). In the latter case, predators are generally managed with the intention of reducing numbers of a particular pest. Nonetheless, they must forage in a landscape that may contain many potential prey species. The understanding of “generalist” is that the predator may eat many different species of prey; however, the available prey species may provide very different contributions toward survival, growth and reproduction (McGregor et al., 1999; Colares et al., 2015; Mirhosseini et al., 2015; Puchalska and Kozak, 2016). Therefore, it is quite likely that predators evaluate prey patches in habitats according to their contribution to fitness. In natural and managed ecosystems, generalist predators may forage in landscapes in which patches containing different prey species are independent (i.e., prey are not encountered simultaneously), and are distributed differently on the landscape. In addition, they encounter prey species other than the focus or target species, so it is important to understand how the predator makes decisions with respect to patch exploitation and abandonment. On discovery of a patch of potential prey, predators must decide whether to exploit the patch or abandon it in favor of searching for a better one. These decisions can be innate (i.e., based on evolved expectations of prey quality and distribution), or can be based on information acquired through exploring the habitat directly, or through remote detection of potential prey patches by sensory cues (i.e., olfactory or visual) (Bowler and Benton, 2005). The ultimate distribution of individual predators in a landscape should be a consequence of dispersal and exploitation decisions. Nonetheless, the investigation of the whole dispersal process has rarely been carried out. Much of research on this field is theoretical and has been developed based on simplistic assumptions about dispersal, which it has been summarized into a single parameter, in spite of dispersal being a process composed by three interrelated components which includes emigration, immigration and inter-patch movements (Bowler and Benton, 2005).
Many hemipterans are omnivores that feed on a wide range of animal prey and plant resources (Wheeler, 2001). For instance, different prey and plant species offered ad libitum are known to contribute in a variable degree to the survival, development, and reproduction of several omnivorous hemipterans such as Dicyphus hesperus Knight (Hemiptera: Miridae), Macrolophus pygmaeus Rambur (Hemiptera: Miridae), Podisus maculiventris (Say) (Hemiptera: Pentatomidae), and Geocoris punctipes (Say) (Hemiptera: Geocoridae) (Valicente and O’Neil, 1995; McGregor et al., 1999; Eubanks and Denno, 2000; Perdikis and Lykouressis, 2000, 2002; Sanchez et al., 2004). Dicyphus hesperus is a generalist predator that is known to complete development and reproduce feeding on several species of small, soft-bodied arthropod prey and also on some plant species (McGregor et al., 1999; Sanchez et al., 2004). Dicyphus Hesperus use flying and walking as a way of displacement, with males having a higher tendency to fly than females, especially when they are gravid with many eggs. The contribution to fitness varies as a function of the type of food. For instance, D. hesperus nymphs fed from hatch to adult on a diet of spider mites take longer to complete development and have a lower survival rate than individuals fed on a diet of whitefly nymphs (McGregor et al., 1999). In addition, lifetime egg production is lower on a mite than on whitefly diet (Gillespie, D.R., unpublished data). On the other hand, the contribution of plant feeding to fitness in D. hesperus varies with the host plant species; for example, they develop on mullein but not on tomato plants (Sanchez et al., 2004). However, even for the most suitable plant species, reproduction is lower, mortality is higher and development time is longer than for individual provided with animal prey (Sanchez et al., 2004). In this regard, D. hesperus represents a good candidate to test some of the predictions of foraging theory and to study the dispersal in habitats characterized by patches offering food resources of different values.
The aim of this work was to investigate the dispersal and distribution of D. hesperus females and males in habitats providing food patches of different values in terms of fitness. Most of the studies dealing with the distribution of organisms in relation to food resources use models or have been carried out in small arenas in the laboratory (Mills and Heimpel, 2018). In this research, a more realistic approach was adopted, working with mesocosms of similar characteristics to those where D. hesperus is released as a biocontrol agent. The food patches herein tested had no prey (i.e., only tomato plants), or mite and whitefly as prey. The habitats tested were a combination of patches with the three types of food resources, or with one type of prey (mites or whiteflies) and no-prey patches and individuals were tracked by mark-recapture methods. In agreement with both the predictions of IFD and MVT, an aggregation of individuals in the highest quality patches was expected. In addition, it was predicted that the distribution of D. hesperus in habitats would fit to an IFD model, with the number of individuals in patches being proportional to the assumed fitness realized from exploiting each particular patch. Moreover, interference was predicted to rise as the density of individuals in patches increased. At the habitat level, it was also hypothesized that habitats composed of high-quality patches would host higher abundances of D. hesperus than habitats composed of low-quality patches. Emigration rates were predicted to be higher for low- than for high- quality patches. In contrast, immigration was expected to be higher to high- than to low-quality patches. The inter patch movements were hypothesized to be a function of the quality of both patch of origin and patch of departure. Finally, our experimental setting allowed predators to abandon the habitat entirely and it was predicted that predators exploring low quality habitats (i.e., containing only patches of low quality) should abandon those habitats at a higher rate than habitats with higher quality food resources.
Materials and methods
Insect collection and rearing
The laboratory colony of Dicyphus hesperus was originally collected in 1998, from a population in Summerland, British Columbia (49°34′N, 109°39′W) on catnip Nepeta cataria L. (Lamiaceae) and mullein Verbascum thapsus L. (Scrophulariaceae) (McGregor et al., 1999). This colony was maintained on tobacco plants, Nicotiana tabacum L. (Solanaceae) supplemented with eggs of Ephestia kuehniella Zeller (Lepidoptera: Pyralidae) ad libitum. A colony of Trialeurodes vaporariorum (Westwood) (Hemiptera: Aleyrodidae) was maintained on tobacco plants; also, a colony of Tetranychus urticae Koch (Acari: Tetranychidae) was multiplied on Phaseolus vulgaris L. (Fabaceae). Whitefly and spider mites were initially provided by Applied Bionomics Ltd. (Sidney, BC). All the insect colonies were maintained in independent climatic chambers at 22°C under fluorescent lamps with a 16 h light: 8 h dark photoperiod.
Experimental setting
The experiment was conducted in two glasshouses 12 × 6 m divided transversally into three compartments of 4 × 6 m by suspended plastic, Visqueen® curtains (British Polythene Industries Ltd., Greenock, UK). The microperphorated fabric allowed airflow between the compartments, thereby providing similar climatic conditions within compartments, but restricted the movement of insects across compartments. Each of the compartments had 20 tomato plants, Solanum lycopersicum L. (Solanaceae), cv. Rhapsody, in pots arranged in four rows of five plants each. The first repeat of the experiment was carried between April 27th and June 18th, and the second between June 21st and August 20th, 2001. On both repeats, the two glasshouses hosted two of the four replicates of the experiment. Each of the three compartments in each glasshouse simulated habitats with patches of different food quality. The three compartments of each glasshouse had different combinations of patches with and without prey: (1) mixed-prey habitats had a row with five tomato plants infested with whitefly, T. vaporariorum, one row infested with spider mites, Tetranychus urticae Koch (Acari: Tetranychidae), and two rows with no prey; (2) whitefly habitats had two rows with whitefly and two rows with no prey; (3) and mite habitats had two rows with spider mites plus other two with no prey. The arrangement of rows in compartments and the disposition of compartments within glasshouses were assigned by generating random numbers in each replicate.
Prior to each run of the experiment, 30 tomato plants different from those to be used in the experiment were introduced in a temperature-controlled chamber (approx. 23°C), and one leaf of Ph. vulgaris highly infested with spider mites was placed on each of the plants. Once spider mites had multiplied and tomato plants were fully covered with mites, the plants were cut and each plant was used to infest a tomato plant in the spider mite patches of the experiment.
For each run of the experiment, 120, 6-week old tomato plants, were transplanted to four-gallon (17.5 l) pots. One week after transplanting, 30 of the plants were placed in a temperature-controlled chamber (approx. 23°C). These plants were arranged in two rows of 15 plants each, and infested with 2,000 adults of T. vaporariorum which were allowed to oviposit during 4 days and then removed. For the release, 2,000 whitefly adults were supplied in 20 vials of 100 individuals each, which were evenly distributed on the two rows of 15 tomato plants. All tomato plants were then transferred to their respective compartments and rows. The tomato plants previously infested with spider mites were cut and placed on top of the tomato plants in the corresponding spider mite patches. The original mite colony plants were left in contact with the ones to be infested until they had dried out and all the spider mites had moved away. The setting of the plants was done on May 21st and July 23rd 2001 in the first and second run of the experiment, respectively. Tomato plants were approximately 50 cm high when they were placed in the glasshouses. Within each compartment (habitat), plants within rows (patches) were separated by 50 cm and touched each other. Plants in adjacent rows were 1 m apart and did not touch each other. Every row of 5 plants of the same category (whitefly-, mite-infested and no-prey plants) and with plants touching each other was considered as a single patch and used as such in IFD and dispersal analyses. In all other analyses, single plants were used as sampling units. Inter-dependency of sampled plants within the same row was accounted for in these analyses by using plant ID, replicate and repeat as nested random variable.
Temperature and relative humidity (RH) were registered using a HOBO T/RH Loggers (Onset Computer, Bourne, MA, USA) placed in the middle of each compartment. In the first repeat, the average daily temperature over the period of the experiment was 23.7°C, and the average of the minimum and maximum temperature were 29.4 and 20.3°C, respectively. In the second repeat, the average daily temperature was 23.8°C, and the average of the minimum and maximum temperature were 29.3 and 19.8°C, respectively.
Marking and sampling
To estimate the movement of D. hesperus adults (females and males) among patches and their permanence in habitats a mark-recapture approach was followed (Hagler and Jackson, 2001). Two females and males of D. hesperus (7–10 day-old) from the rearing colonies were released per plant 4 days after the placement of the tomato plants in the glasshouses (first repeat of the experiment: 25 May 2001; second repeat: 27 Jul 2001). In total, 4 adults (2 females+2 males)*5 plants per row*4 rows ( = 80 individuals) were released per compartment in each of the four replicates of the experiment. Prior to their release, all the individuals were marked on the pronotum with a luminous paint spot (BioQuip, Rancho Dominguez, CA), using a flat pin. A different color (yellow, blue, white and red) was used for each of the four rows (patches) of each compartment (habitat).
Females and males of D. hesperus were recaptured twice during the experiment: 5 and 10 days after the date of their first release. In the first recapture, five plants selected at random from each type of patch in a habitat were carefully inspected; females and males of D. hesperus were collected using a manual aspirator and placed individually in single glass vials, which were labeled with the code of the glasshouse, compartment and plant of origin. The D. hesperus adults were cooled to 4°C to be sexed and exposed to ultra-violet light to reveal the color of the luminous mark on the pronotum under a stereomicroscope. After observation all the individuals were released on the same plant from which they had been collected. On the second recapture, all D. hesperus adults were collected from all the plants in each compartment and the same labeling and inspection procedure described above was followed. Adults were not released following the second recapture. The nymphs of D. hesperus were counted once they started to emerge, at days 21 and 28 after the introduction of the plants in the glasshouses, in five plants selected at random from each patch type in each habitat.
Whiteflies and mites were counted 3 days after the introduction of tomato plants in the glasshouses, prior to the first release of D. hesperus. Thereafter, whiteflies and mites were counted at 9, 14, 21, and 28 days after the introduction of the plants in the glasshouses. For whitefly counts, five plants were selected at random from each patch type in each compartment; a single leaf from the middle section of the plant (tenth leaf from the top), was bagged individually and taken to the laboratory, and nymphs counted under a stereomicroscope. A single leaf from the top of the same plants was bagged and taken to the laboratory for the counting of spider mites.
Analysis of the data
Abundance and distribution of Dicyphus hesperus
Linear mixed models (LMMs) using the “lmer” function (“lme4” package) (Bates et al., 2015) were used to test for the effect of type of patch, habitat, sex and date of recapture, as fixed factors, on the number of adults of D. hesperus recaptured per plant 5 and 10 days after their release. Repeat, replicate, and plant ID were treated as nested random factors. The ID of each tomato plant was unique and was built by combining the number of the repeat, replicate, greenhouse, compartment, and row. The fixed factors and interactions without a significant effect (α = 0.05) were dropped out of the definitive models, which were compared with previous versions of the models by Akaike’s Information (AIC) and Bayesian Information Criteria (BIC). The goodness of fit of the normal distribution to the experimental data was also assessed by AIC and BIC using the “fit” function in the R “fitdistrplus” package. The χ2- and p-values for the fixed factors were obtained by the Wald test using the “Anova” function in the R “car” package (R-Development-Core-Team, 2017). Post hoc pairwise multiple comparisons was obtained using the estimated marginal means (“emmeans” package) with the function “glht” (“multcomp” package) in R (Hothorn et al., 2006). For this and all the following statistical analyses, the significance level was established at α = 0.05.
The assessment of IFD in D. hesperus adults in the three types of habitats according to their fitness on the different patches was done with a Friedman’s test using the function “friedman.test” (“stats” Package) (R-Development-Core-Team, 2017). These analyses were carried out using only the data from the second recapture. The fitness of D. hesperus feeding on whitefly, mites and tomato plants was estimated by the nymph performance index (NPI = survival/development time), which is known to be correlated to the offspring produced by females (Sanchez et al., 2004). NPI was calculated using the development and survival values provided by Sanchez et al. (2004) for D. hesperus nymphs feeding on tomato plants, and by McGregor et al. (1999) for T. vaporariorum and T. urticae also with tomato as host plant. This yielded the following NPI: 0.0392 for whiteflies, 0.0304 for mites and 0.0149 for tomato plants. The expected number of D. hesperus on each of the four patches in mixed-prey, whitefly and mite habitats were calculated as E[Ni] = φ⋅NPIi⋅N, where NPIi is the nymph performance index according to the type of patch, , and N is the total number of individuals collected in a given habitat. This was done independently for each of the four replicates. Thereafter, the residuals (i.e., observed minus expected values) were calculated for each patch within each habitat for each of the four replicates, and the probability that the residuals equals zero was assessed with the Friedman’s test for each of the three types of habitats. The null hypothesis, and thus IFD, was rejected when P < 0.05.
Offspring and interference
LMMs using the “lmer” function (“lme4” package) (Bates et al., 2015) was used to test for the effect of type of patch, habitat and date of sampling (21 or 28 days after the setting of the plants in the greenhouses), as fixed factors, on the number of nymphs per plant. Repeat, replicate and plant ID were set as nested random factors. The data were transformed by the natural logarithm of x+1 to account for normality and heteroscedasticity. The goodness of fit of the normal distribution to the log-transformed data was assessed by AIC and BIC using “fit” function in R. The above-explained procedure for the abundance of females and males was also followed to obtain χ2-, p-values and the post hoc pairwise comparison.
Fitness of D. hesperus females was expressed as the per capita offspring (sensu Falconer, 1989). It was estimated independently for the two last dates of sampling by dividing the number of D. hesperus nymphs per plant by the average number of females per plant during the 10 days that elapsed between their release and the second recapture, that is the average among the number of females released (i.e., two per plant) and those found in the first and second capture. The relationship between fitness (Wi) and the density of consumers (ni) in patch i was expressed as an interference model (Parker and Sutherland, 1986): Wi = Qni –m where Q is profitability and m is the coefficient of interference. In our case, Q will be the expected number of offspring produced by a female when the average density of D. hesperus females is 1 per plant. Through natural logarithms in the two terms, this expression can be transformed into ln Wi = ln Q – m ln ni. The correlation between fitness of females, estimated at 21 and 28 days, and the density of consumers per plant was tested independently for females and males. The degree of correlation, and the parameters Q and m were estimated by linear regression using the function “lm” (“stats” package) in R. The differences between the slopes at times 21 and 28 days was tested using the function “lstrends” in the “lsmeans” package (R-Development-Core-Team, 2017).
Dispersal movements
LMMs using the “lmer” function in the “lme4” package (Bates et al., 2015), were also used to test for the effect of sex, type of habitat, patch and date of recapture, as fixed factors, on emigration, and immigration rates of D. hesperus adults following the procedure explained at the section “Abundance and distribution of Dicyphus hesperus.” Repeat and replicate were treated as nested random factors. The rates were transformed by the arcsin of the square root, to account for the deviation from normality. The goodness of fit for the transformed data was assessed by AIC and BIC as explained for the previous statistical analyses. Emigration includes mortality, and the individuals moving to other patches or leaving the habitat entirely. This was calculated as one minus the number of females or males remaining in a given patch divided by the number of individuals released in that patch. Immigration rates were calculated as the number of females or males arriving to a given patch divided by the number of individuals released on the other patches. LMMs using the “lmer” function were also used to test for the effect of sex, habitat, patch of origin, patch of arrival and date of recapture, as fixed factors, on the proportion of adults moving between patches of a different kind. Repeat and replicate were treated as nested random factors. The interpatch movement rates were calculated as the number of individuals moving from a patch of a given type to a patch of different kind divided by the number of individuals released in the former patch. Finally, LMMs using the “lmer” function and the above explained procedure were run to test for the effect of type of habitat, sex and date of recapture in the rate of persistence of D. hesperus adults in habitats. Persistence rates were calculated for the first and second recaptures as the number of females and males collected in a given habitat divided by the number of individuals released in all the sampled plants.
Prey abundance
In mixed-prey and whitefly habitats, the abundance of whitefly along the 4 weeks of the experiment was compared among patches by LMMs using the “lmer” function. Abundance, as a dependent variable, was expressed as the number of whitefly scales (nymphs+pupae) per leaf transformed by the ln of x+1 to account for normality and heteroscedasticity. The goodness of fit for the transformed data was assessed by AIC and BIC as explained above. Date of sampling was treated as a fixed factor. Repeat and replicate were introduced in the models as nested random factors. χ2-, p-values and the post hoc pairwise comparison were obtained following the above-explained procedure. The same approach was followed for the comparison of the number of mites per leaf among patches in mixed-prey and mite habitats.
Results
Distribution of Dicyphus hesperus females and males in patches with different food resources
The abundance of D. hesperus adults in tomato plants was significantly influenced by sex (χ2 = 25.9; df = 1; P < 0.001), type of patch (χ2 = 164.0; df = 2; P < 0.001) and habitat (χ2 = 7.9; df = 2; P = 0.019). The interactions sex*habitat (χ2 = 11.8; df = 2; P = 0.003) and sex*patch (χ2 = 29.6; df = 2; P < 0.001) were also significant. The date of recapture was found to be non-significant (χ2 = 1.21; df = 1; P = 0.271). The abundance of both females and males in whitefly patches differed significantly from that in mite and no-prey patches (P < 0.001), but no significant differences were found between mite and no-prey patches neither for females (P = 0.204) nor for males (P = 0.762). In relation to the interaction between sex and patch, the number of females per plant was significantly higher than that of males in whitefly (P < 0.001) and mite patches (P = 0.041), but similar in no-prey patches (P = 1). The number of females per plant in mixed-prey habitats was significantly higher than in whitefly (P = 0.030) and mite habitats (P = 0.001), but no significant differences were found between whitefly and mite habitats (P = 0.657). In contrast, no significant differences in the abundance of males was found between mite and whitefly (P = 0.124), mite and mixed-prey (P = 0.135) and whitefly mixed-prey (P = 0.922) habitats. In addition, the number of females per plant was significantly higher than that of males in mixed-prey (P < 0.001) and in habitats with whitefly as the only prey (P = 0.013), but similar in mite habitats (P = 0.179).
In mixed-prey habitats, the number of D. hesperus females in the first recapture (that is, 5 days after their release) ranged from 0.25 ± 0.13 females per plant in no-prey patches to 2.00 ± 0.39 of females per plant in whitefly patches (Figure 1). In habitats with whitefly as the only prey, 1.55 ± 0.22 and 0.15 ± 0.99 females of D. hesperus per plant were found in whitefly and no-prey patches, respectively (Figure 1). In habitats with mites as the only prey, 0.60 ± 0.22 and 0.05 ± 0.05 females per plant were found in mite and no-prey patches, respectively (Figure 1). In the second recapture (i.e., 10 days after their release), D. hesperus females were distributed in a similar way to that 5 days earlier, but their numbers had decreased in most of the patches in all the habitats, especially in whitefly and mite patches (Figure 1). Males were distributed in a similar way as females, but their abundances were lower. The abundance of males ranged between 0.45 ± 0.17 and 0.90 ± 0.17 individuals per plant in whitefly patches; in mite patches the abundance of males ranged between 0.05 ± 0.05 and 0.33 ± 0.10, and between 0.15 ± 0.10 and 0.42 ± 0.17 individuals per plant in no-prey patches (Figure 1).
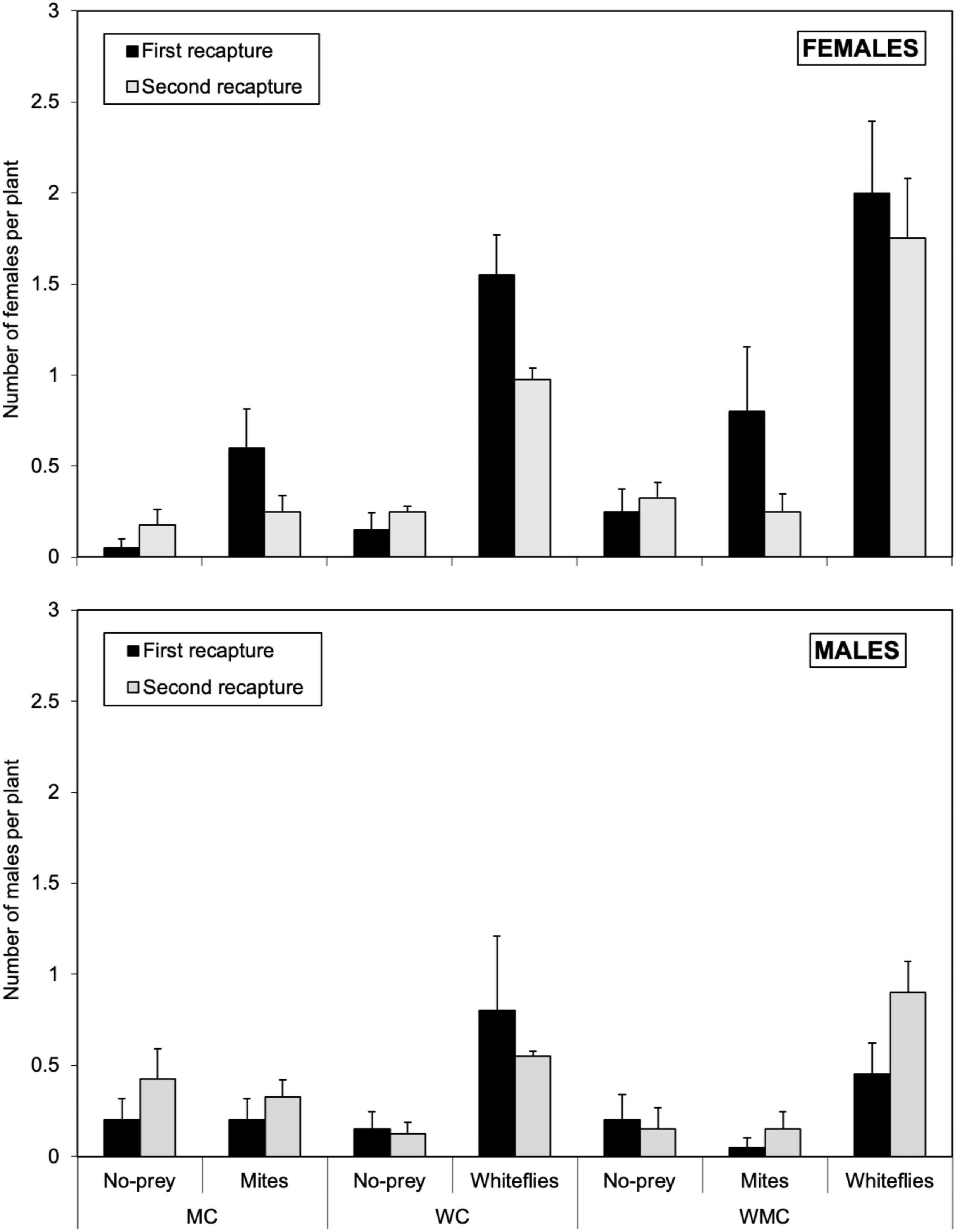
Figure 1. Average of females (upper graph) and males (lower graph) of D. hesperus per plant with standard errors in the first (5 days after the release) and second recapture (10 days after the release), in three habitats (MC, WC, and WMC) composed by patches with different food resources (No prey- C-, mites- M-, whiteflies-W-).
The distribution of D. hesperus adults was in accordance with the IFD in mite (χ2 = 4.14; df = 4; P = 0.247) and whitefly habitats (χ2 = 2.85; df = 2; P = 0.416), but not in mixed-prey habitats (χ2 = 9.77; df = 2; P = 0.021).
Offspring (fitness) and interference
The number of D. hesperus nymphs was significantly influenced by patch (χ2 = 88.1; df = 2; P < 0.001) and habitat (χ2 = 13.4; df = 2; P = 0.001) type and week of sampling (χ2 = 303.1; df = 1; P < 0.001). Significant differences were found in the number of nymphs per plant among whitefly and both mite and no-prey patches (P < 0.001), but not between no-prey and mite patches (P = 0.167). Mixed-prey (P = 0.018) and whitefly (P = 0.001) habitats had a significantly higher number of nymphs than mite habitats, but no significant differences were found between the Mixed-prey and whitefly habitats (P = 0.339). In whitefly patches, in mixed-prey habitats the number of D. hesperus nymphs increased from 10.6 ± 6.4 individuals per plant in the third week to 50.6 ± 16.7 in the fourth week; similar abundances were found in whitefly habitats (third week: 17.5 ± 5.1; fourth week: 46.1 ± 5.7 nymphs per plant) (Figure 2). In mite patches, a very similar number of nymphs were seen in habitat with mites as the only prey (third week: 2.6 ± 0.9; fourth week: 14.7 ± 3.8 nymphs per plant) and mixed-prey habitats (third week: 2.7 ± 0.7; fourth week: 13.9 ± 4.6 nymphs per plant) (Figure 2). In the patches without prey, in the third week, the number of nymphs per plant ranged from 1.7 ± 1.0 in mite habitats to 3.3 ± 1.0 in mixed-prey habitats; in the fourth week, the number of nymphs per plant in these patches ranged from 10.1 ± 4.2 in mite habitats to 19.4 ± 7.2 in mixed-prey habitats (Figure 2).
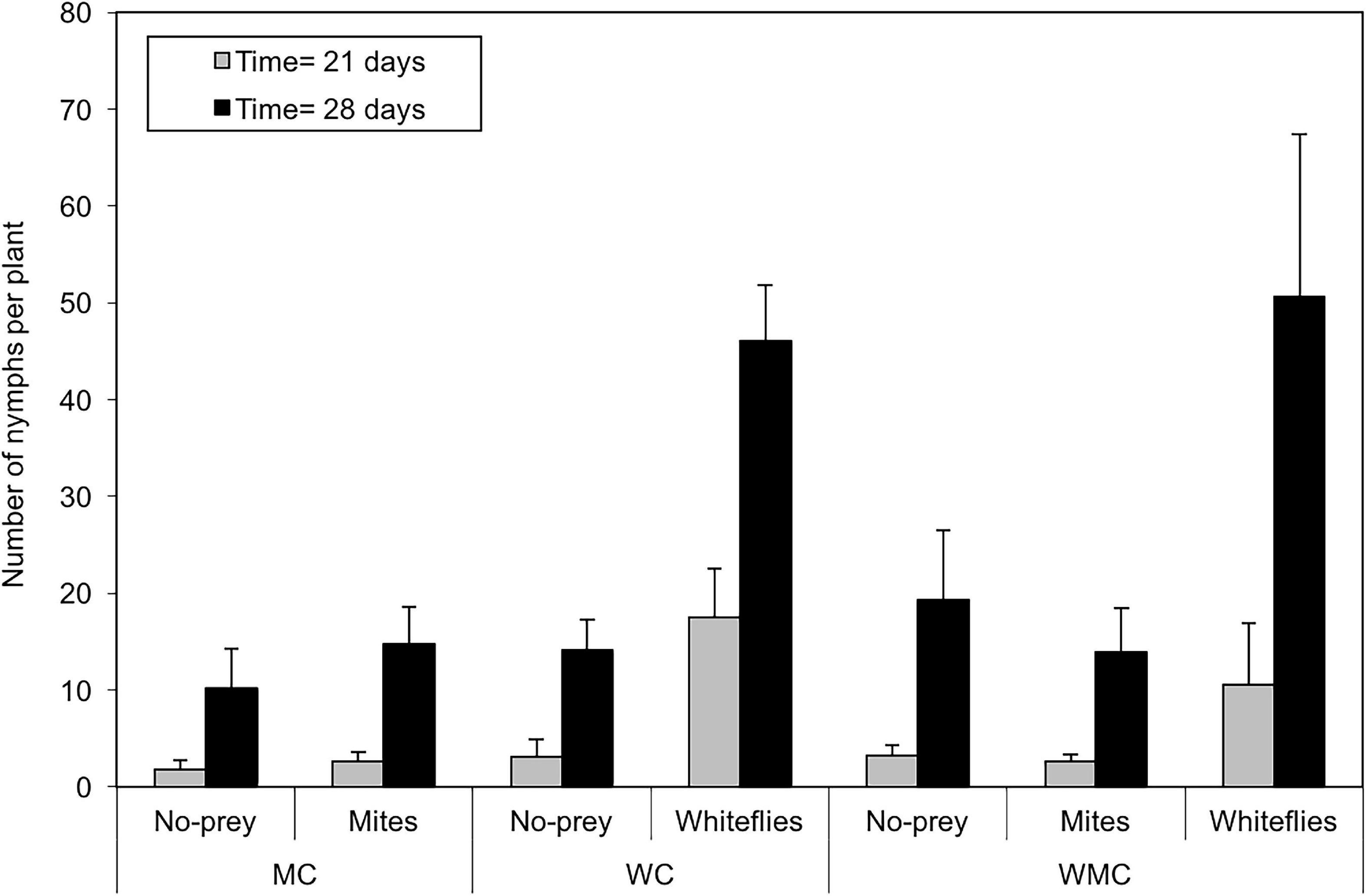
Figure 2. Fitness of D. hesperus females (offspring per female) vs. the number of females per plant as observed in the third and fourth weeks since the introduction of tomato plants in the glasshouses).
A significant correlation was found between the fitness of females (Wi), estimated using the number of nymphs counted in the third week, vs. the number of females per plant (F = 2.61; df = 1, 26; P = 0.015), and also when using the number of nymphs counted in the fourth week (F = 12.7; df = 1, 26; P = 0.001) (Figure 3). The fitted models were as it follows: ln Wi = –0.547 ln ni +1.709 in the third week (R2 = 0.177; F = 6.79; df = 1, 26; P = 0.015), and ln Wi = –0.609 ln ni +3.400 in the fourth week (R2 = 0.329; F = 12.7; df = 1, 26; P = 0.001). From this, the interference coefficient (m) was estimated to be 0.547 (95% confidence interval –CI: 0.255–0.839) and 0.609 (95% CI: 0.317–0.900) for the third and the fourth week, respectively. However, the values of m for the third and fourth weeks overlapped and were not significantly different (t = –0.301; df = 52; P = 0.765). The maximum offspring per D. hesperus female (Q), was estimated as 5.5 (95% CI: 3.4–9.1) and 28.8 (95% CI: 21.7–40.9) nymphs per female for the third and fourth week, respectively. No significant correlation was found between female fitness and the abundance of males neither in the third (F = 0.019; df = 1, 24; P = 0.890) nor in the fourth week (F = 0.290; df = 1, 22; P = 0.596) (Figure 4).
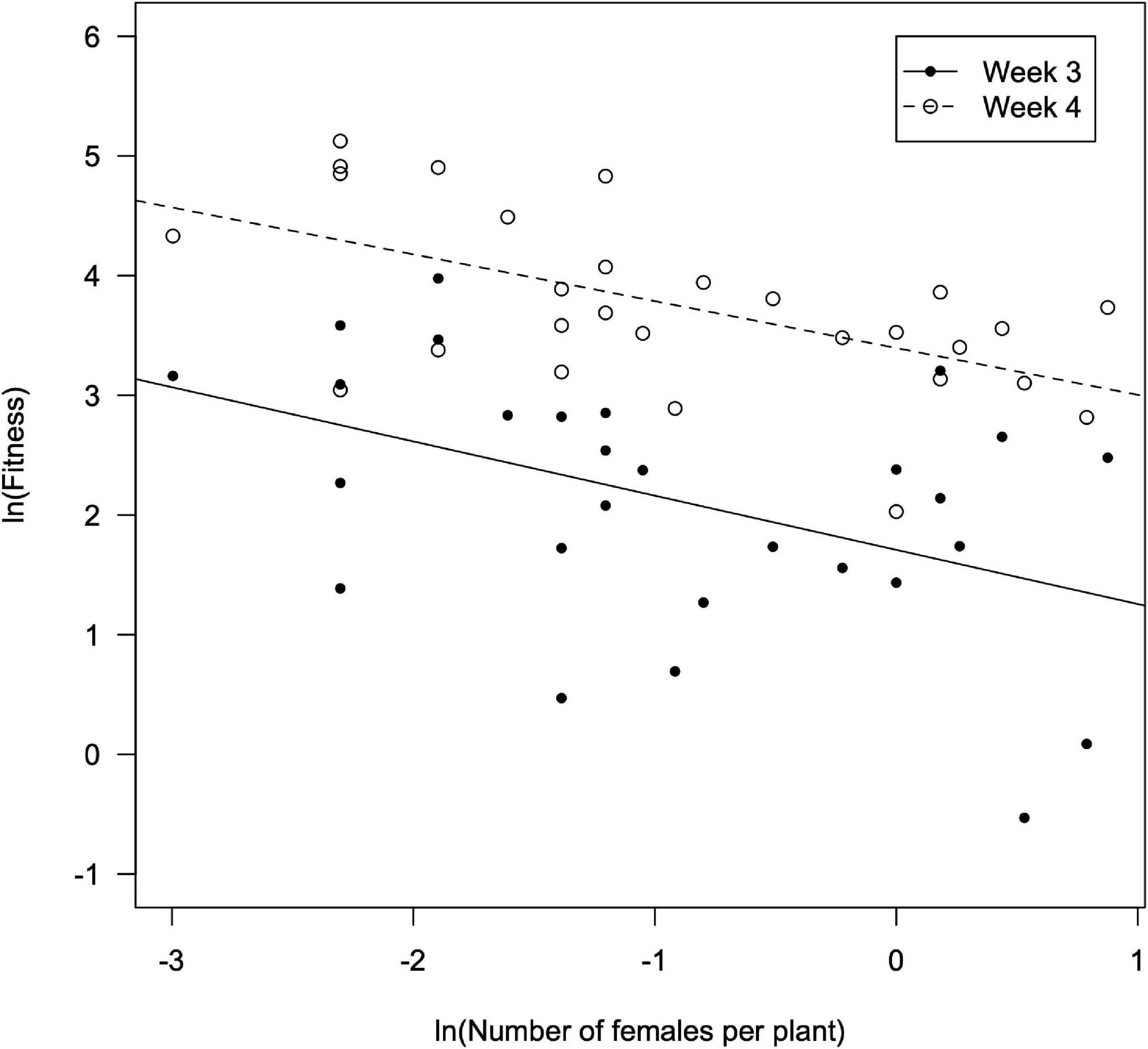
Figure 3. Average of D. hesperus nymphs per tomato plant with standard errors (21 and 28 days after the introduction of tomato plants with prey in the glasshouses) in three habitats (MC, WC, and WMC) composed by patches with different food resources (No prey- C-, mites- M-, whiteflies-W-).
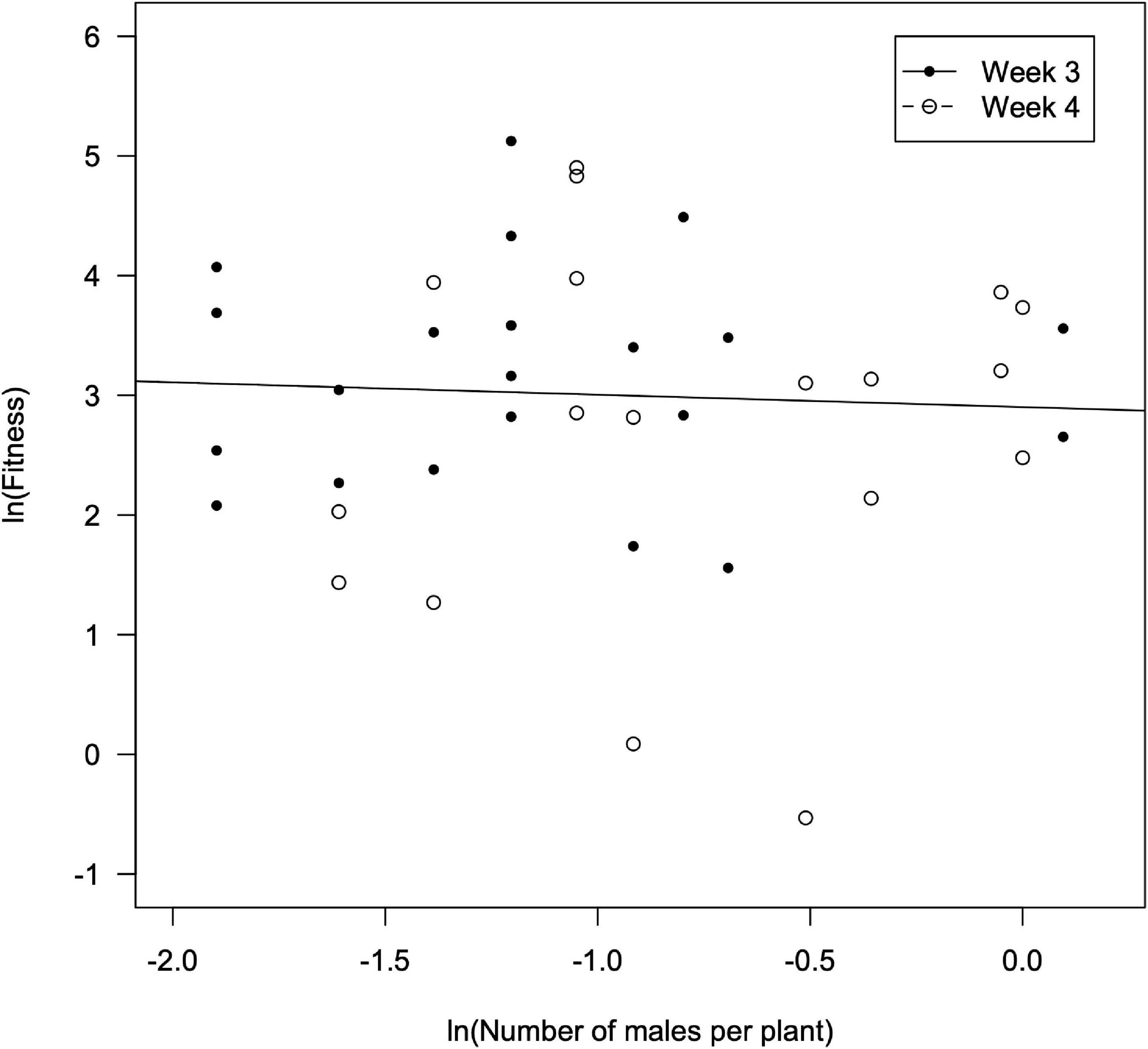
Figure 4. Fitness of D. hesperus females (offspring per female) vs. the number of males per plant as observed in the third and fourth weeks since the introduction of tomato plants in the glasshouses).
Emigration, immigration, interpatch movements, and persistence in habitats
The emigration rates were significantly influenced by the type of patch (χ2 = 41.8; df = 2; P < 0.001) and sex (χ2 = 24.6; df = 1; P < 0.001), but neither by habitat type (χ2 = 0.870; df = 2; P = 0.640) nor by date of recapture (χ2 = 3.51; df = 1; P = 0.061). In addition, the interactions patch*sex (χ2 = 6.89; df = 2; P = 0.032) and habitat*sex (χ2 = 6.18; df = 2; P = 0.046) were found to be significant. Both, females and males had significantly lower emigration rates in whitefly than in no-prey and mite patches (P < 0.05), but there were no significant differences between no-prey and mite patches for any of the sexes (P > 0.05). However, females had lower emigration rates than males in whitefly and mite patches (P < 0.001), but similar emigration rates in control patches (P = 0.194). In relation to habitat, females had significantly lower emigration rates than males in mixed-prey and whitefly habitats (P < 0.001), but no significant differences were found between sexes in habitats with mite as the only (P = 0.595). The proportion of emigrant D. hesperus females ranged from 0.500 ± 0.168 in whitefly patches in mixed-prey habitats to one in no-prey patches in habitats with mites as the only prey (Figure 5). The emigration rates of males were higher than those of females and ranged from 0.900 ± 0.070 in mite patches (mite habitats) to one in both no-prey (whitefly habitats) and mite (mixed-prey habitats) patches. The emigration rates increased generally between the first and the second recapture, both in males and females (Figure 5).
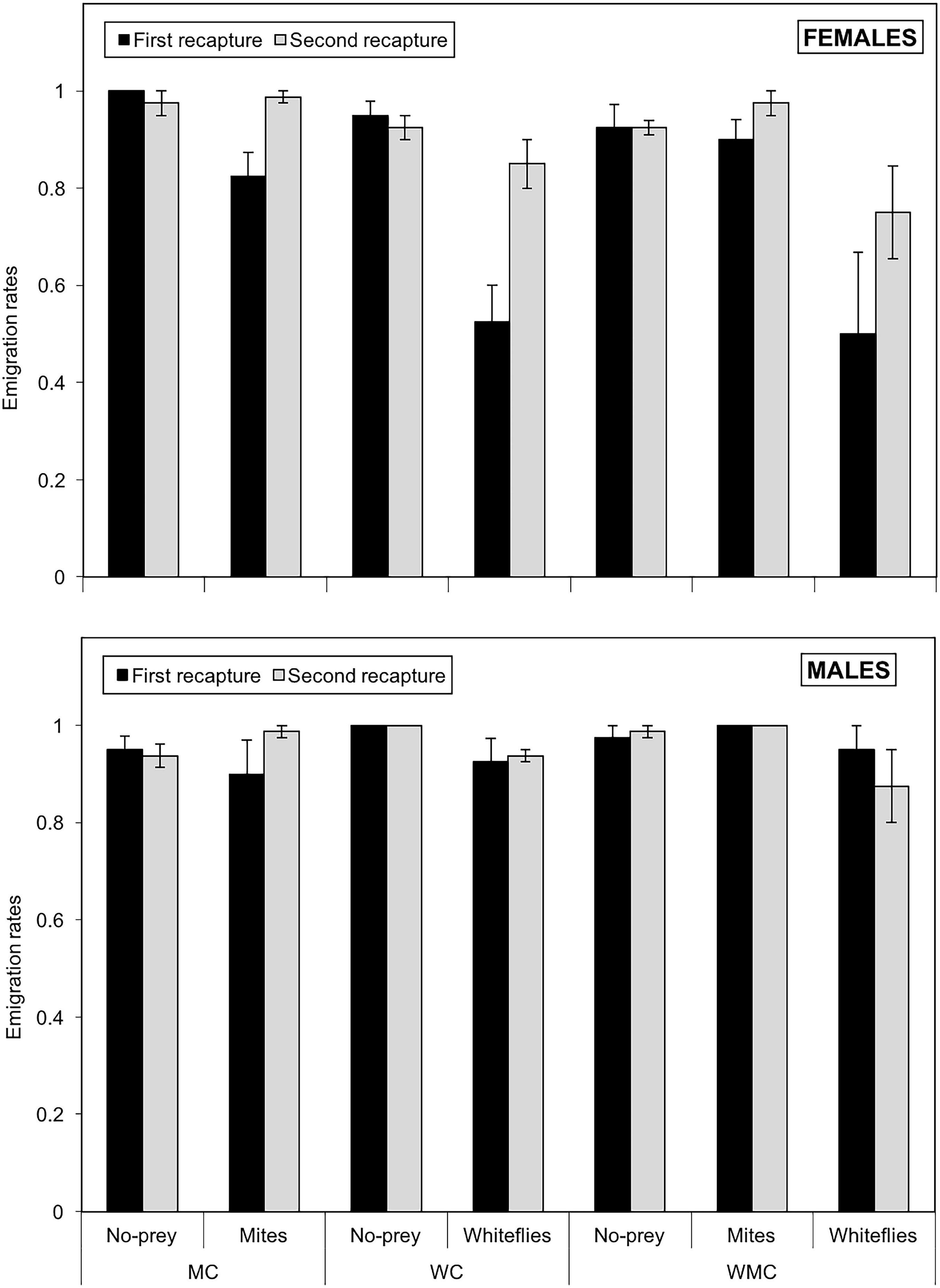
Figure 5. Emigration rates of females (upper graph) and males (lower graph) of D. hesperus per plant with standard errors, in three habitats (MC, WC, and WMC) composed by patches with different food resources (No prey- C-, mites- M-, whiteflies-W-).
The immigration rates were significantly influenced by the type of patch (χ2 = 69.2; df = 2; P < 0.001), while habitat type was found to have a marginal effect (χ2 = 5.95; df = 2; P = 0.051) and the effect of date of recapture was not significant (χ2 = 0.335; df = 1; P = 0.562). The effect of sex (χ2 = 0.069; df = 1; P = 0.792) was not significant, but the interactions patch*sex was found to be significant (χ2 = 11.5; df = 2; P = 0.003). In females, significant differences were found in immigration rates among the three types of patches (P < 0.05); in contrast, in males, immigration in whitefly patches was significantly higher than in control (P = 0.008) and mite (P = 0.0082) patches, but no significant differences were found between no-prey and mite patches (P = 0.977). Besides, females and males showed significantly different immigration rates in whitefly (P = 0.03) and no-prey (P = 0.01) patches, but not in mite patches (P = 0.604). The highest rate of immigration in females (0.250 ± 0.065) was in whitefly patches from mixed-prey habitats in the second recapture; lower immigration rates ranging from zero to 0.075 ± 0.048 were seen in mite and control patches, respectively (Figure 6). Males had generally lower immigration rates than females, ranging from 0.025 ± 0.025 in mite and no-prey patches to 0.200 ± 0.091 in whitefly patches from whitefly habitats. Little variation was observed in the immigration rates between the first and second recapture (Figure 6).
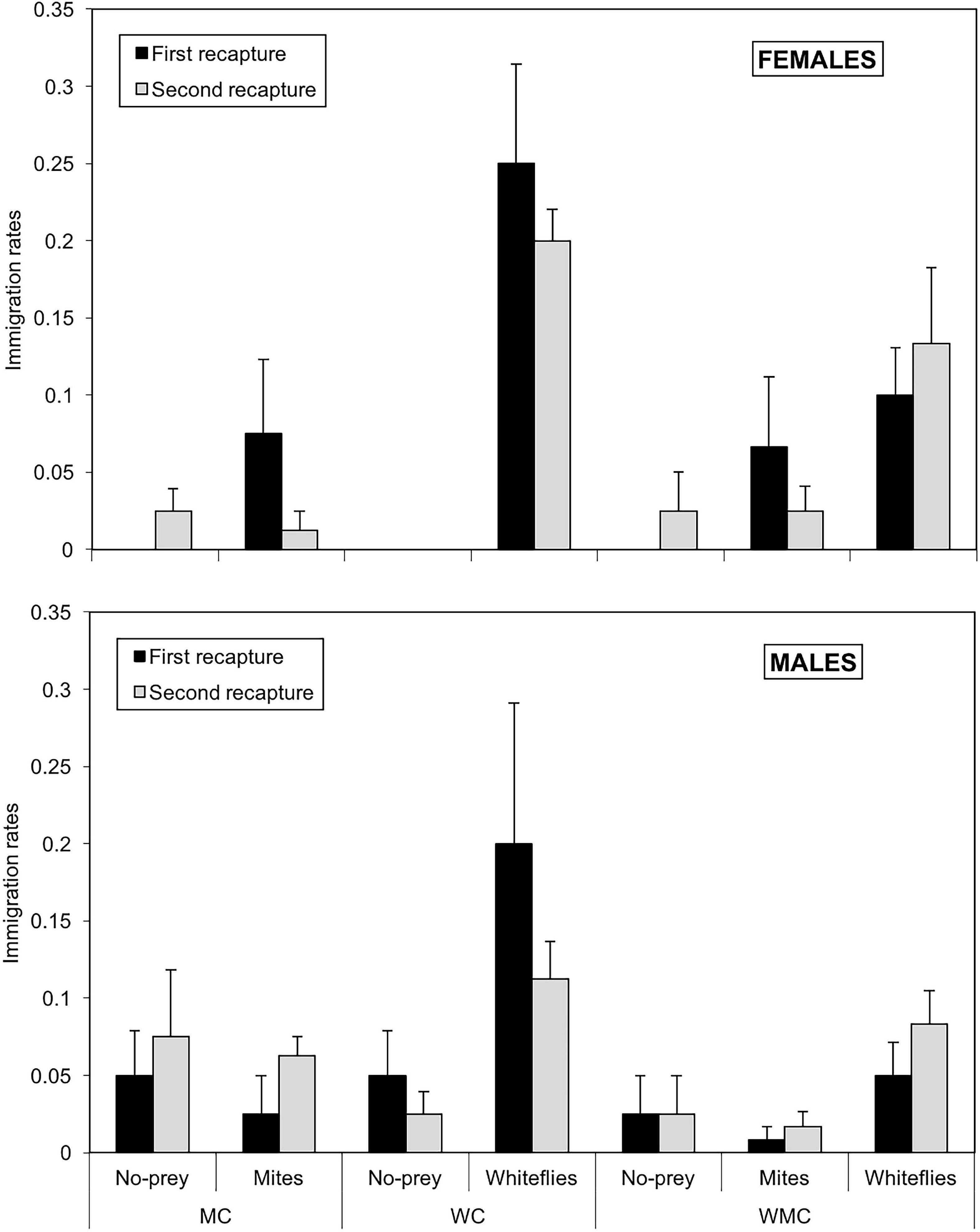
Figure 6. Immigration rates of females (upper graph) and males (lower graph) of D. hesperus per plant with standard errors, in three habitats (MC, WC, and WMC) composed by patches with different food resources (No prey- C-, mites- M-, whiteflies-W-).
The rates of interpatch movements were significantly influenced by the patch of arrival (χ2 = 37.8; df = 2; P < 0.001) and the patch of origin (χ2 = 11.2; df = 2; P = 0.003), with a significant interaction between these two variables (χ2 = 7.18; df = 2; P = 0.007). The effect of sex (χ2 = 0.683; df = 2; P = 0.409), habitat (χ2 = 3.53; df = 2; P = 0.172) and date of recapture (χ2 = 0.687; df = 2; P = 0.407) were found to be not significant. The rate of dispersal from no-prey and mite to whitefly patches was higher than the movement rates between any other pair of patches (P < 0.05), with the exception of that between no-prey to mite patches (P = 0.055) (Figure 7). The highest rates of interpatch movements were found from no-prey to whitefly patches, both in whitefly and mixed-prey habitats for females (whitefly habitats: 0.250 ± 0.065; mixed-prey habitats: 0.175 ± 0.075) and males (whitefly habitats: 0.200 ± 0.091; mixed-prey habitats: 0.150 ± 0.065). The lowest interpatch rates were found from whitefly to control and mite patches (range: 0–0.050 ± 0.029) (Figure 7). The proportion of individuals moving from control to mite patches was generally low, with the exceptional high rate for females in one of the replicate that increased the average value (Figure 7).
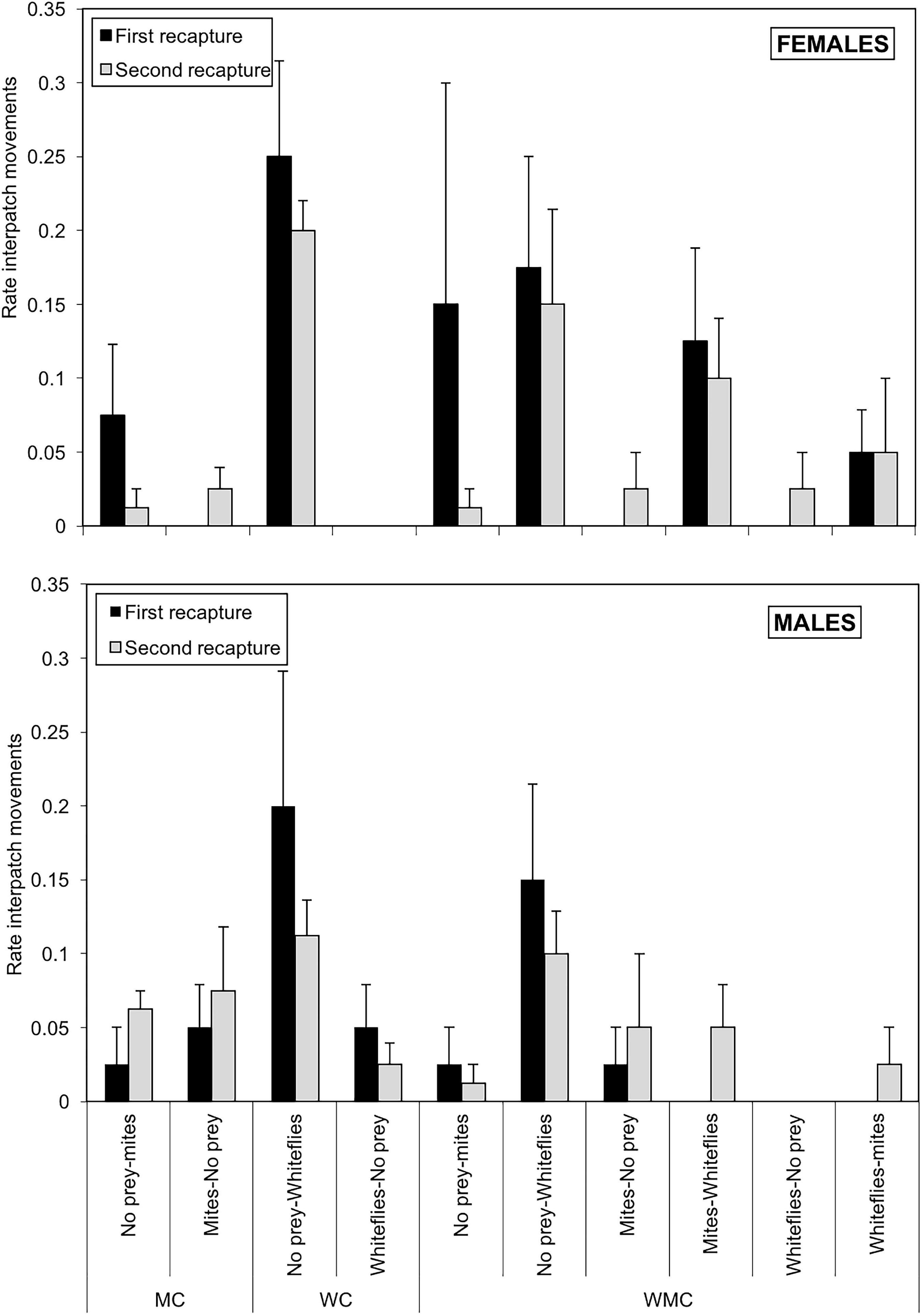
Figure 7. Interpatch movement rates of females (upper graph) and males (lower graph) of D. hesperus per plant with standard errors, in three habitats (MC, WC, and WMC) composed by patches with different food resources (No prey- C-, mites- M-, whiteflies-W-).
Type of habitat (χ2 = 13.5; df = 2; P = 0.001) and sex (χ2 = 12.2; df = 1; P < 0.001) had a significant influence on the proportion of D. hesperus adults persisting in habitats, with a significant interaction habitat*sex (χ2 = 11.9; df = 2; P = 0.003). The date of recapture did not have a significant effect (χ2 = 1.52; df = 1; P = 0.218). The persistence of females in mixed-prey and whitefly habitats was significantly higher than in habitats with mites as the only prey (P < 0.001). Females had significantly higher persistence rates than males in mixed-prey and whitefly habitat (P < 0.01), but similar in mite habitats (P = 0.443). In the first recapture, the proportion of females staying in habitats ranged from 0.125 ± 0.043 in habitats with mites as the only prey to 0.392 ± 0.086 in mixed-prey habitats (Figure 8). In the second recapture, female persistence in the three types of habitats was lower than in the first one (Figure 8). In the first recapture, the persistence of males ranged from 0.092 ± 0.037 in mixed-prey habitats to 0.163 ± 0.080 in habitat with whitefly as the only prey. These rates experienced little variation in the second recapture (Figure 8).
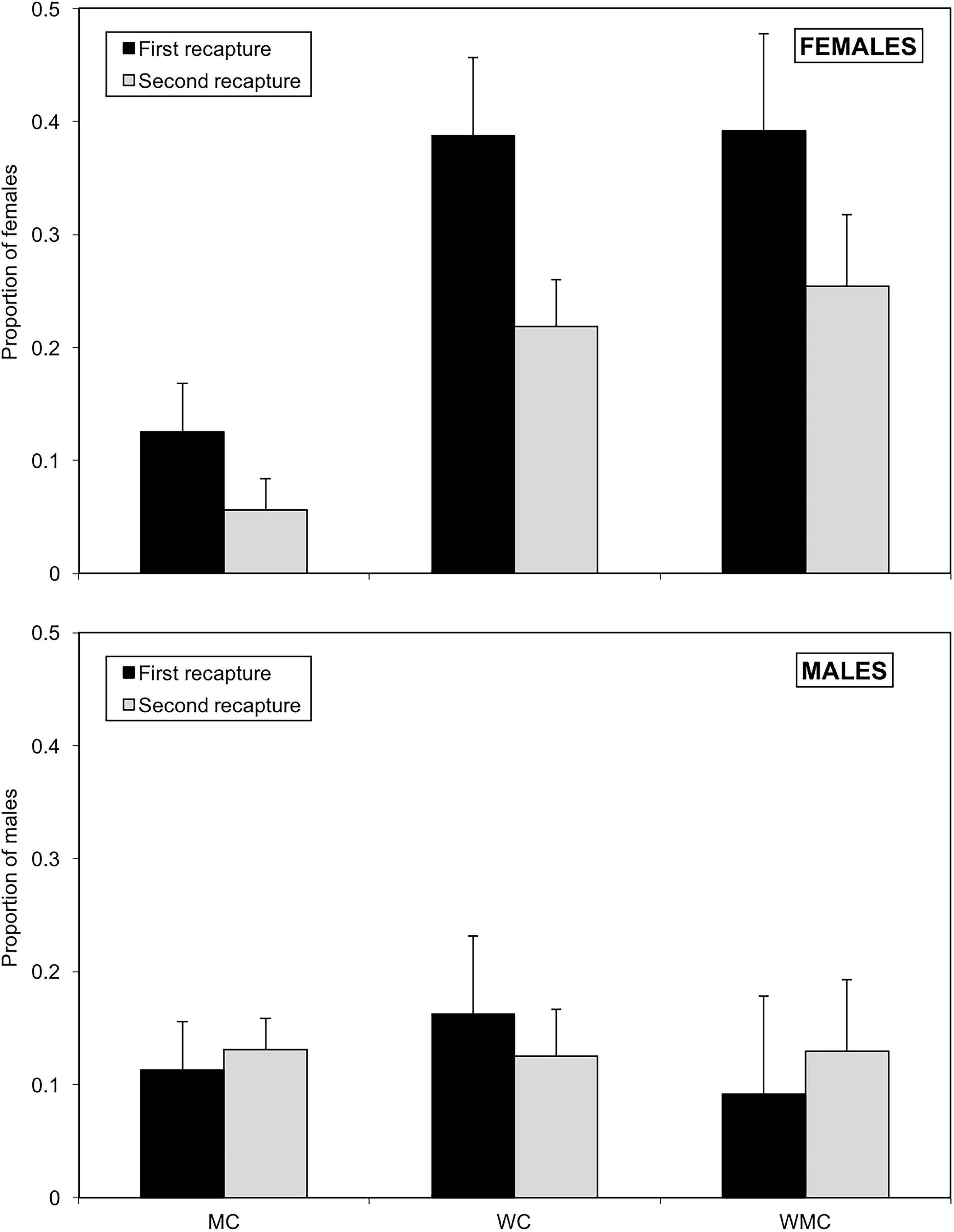
Figure 8. Proportions with standard errors of females (upper graph) and males (lower graph) of D. hesperus persisting in three habitats (MC, WC, and WMC) composed by patches with different food resources (No prey- C-, mites- M-, whiteflies-W-).
Population dynamics of whitefly and mites in patches
The prey patches maintained their initial high densities of whiteflies and mites until the second recapture of D. hesperus (Figures 9, 10). In mixed-prey habitats, significant differences were found in the number of whitefly scales (nymphs+pupae) per leaf among the different prey patches (χ2 = 251.4; d.f. = 2; P < 0.001), the abundance of scales being higher in whitefly than in mite and no-prey patches (P < 0.001). Date of sampling was not found to be significant (χ2 = 7.77; d.f. = 3; P = 0.190). Whitefly patches had 192.8 ± 26.5 and 124.0 ± 36.6 scales per leaf in the third and ninth days after the introduction of the tomato plants in the glasshouses, respectively. The number of whitefly scales was greatly reduced at day 14 with a slight increase in the following 2 weeks (Figure 9A). In mite and no-prey patches, the number of whiteflies was less than 1.5 scales per leaf until the third week of the experiment, with a slightly increase in the following 2 weeks (Figure 9A). The population dynamics of whiteflies in the habitats with whitefly as the only prey was similar to that in mixed-prey habitats (Figure 9B), the number of scales being significantly higher in plants infested with whiteflies than in non-infested plants (χ2 = 50.0; df = 1; P < 0.001). Date of sampling was not found to be significant (χ2 = 2.64; d.f. = 3; P = 0.450).
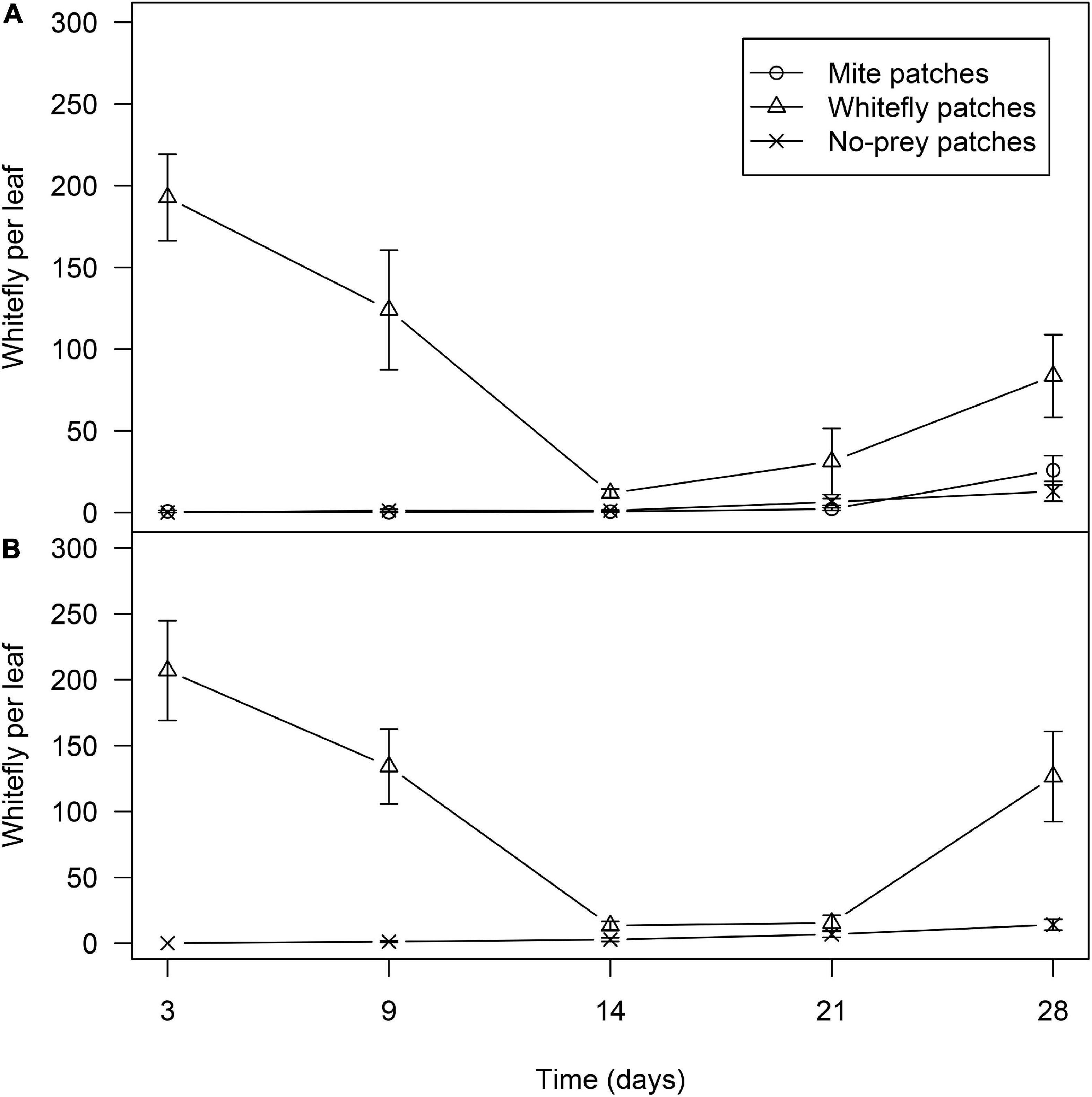
Figure 9. Average of whitefly scales (nymphs+pupae) with standard error in no-prey, mite and whitefly patches in mixed-prey (A) and whitefly habitats (B).
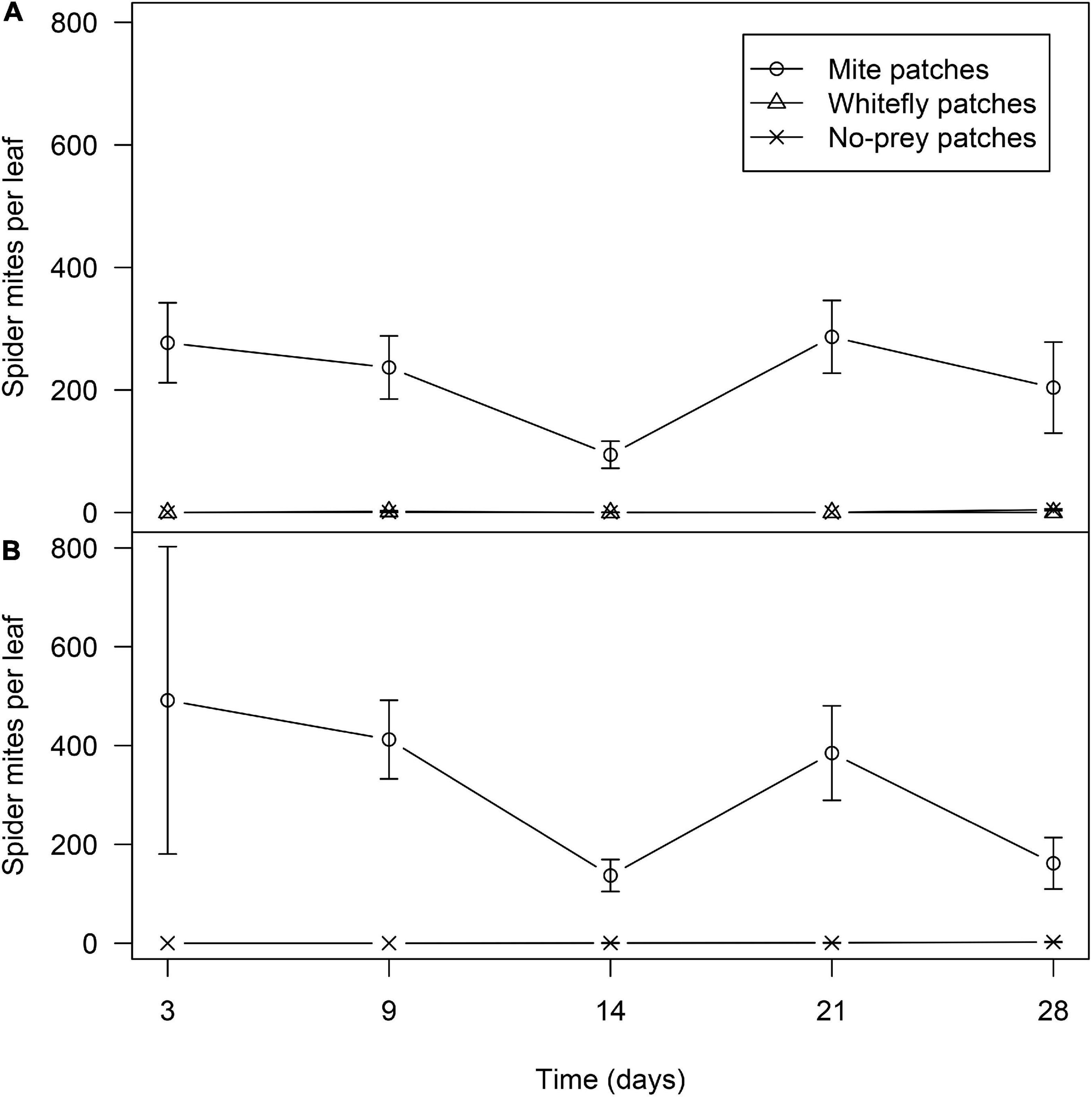
Figure 10. Average of spider mites and standard error in no-prey, mite and whitefly patches in mixed-prey (A) and whitefly habitats (B).
In the mixed-prey habitats, significant differences were found in the number of mites per leaf among patches (χ2 = 1195.2; df = 2; P < 0.01), the abundance of mites being significantly higher in the mite-infested plants than in both whitefly-infested and non-infested plants (P < 0.001). Date of sampling was not found to be significant (χ2 = 7.39; d.f. = 3; P = 0.060). The number of mites in the infested plants along the 4 weeks of the experiment ranged between 277.0 ± 65.2 and 94.3 ± 22.2 per leaf (Figure 10A). In the whitefly and no-prey patches the abundance of mites was very low; the highest abundance (1.5 mites per leaf) was seen in whitefly patches. In habitats with mites as the only prey, the population dynamics of mites was very similar to mites in mixed-prey habitats (Figure 10A), with significant differences between mite-infested and non-infested plants (χ2 = 437.6; df = 1; P < 0.01). Date of sampling was not found to be significant (χ2 = 2.86; d.f. = 3; P = 0.414). Overall, whiteflies and mites were essentially restricted to the patches on which they were released and their abundances were similar during the first 2 weeks in which the distribution and dispersal of D. hesperus females and males were assessed.
Discussion
The results of our study on movement of D. hesperus in relation to the quality of food resources in habitats, and the distribution of those resources within habitats, strongly suggest that this generalist predator uses some simple rules to make decisions about inter-patch movement, and emigration from habitats and patches. The analysis of dispersal patterns showed that it is very likely that many of the individuals in the populations had a limited direct knowledge about the abundance and the quality of the resources in complex habitats and, thus, it is unlikely that they forage according to the omniscient principle of IFD and MVT. The deviation of D. hesperus from IFD in mixed-prey habitats was probably due to the aggregation of individuals in whitefly patches, in contrast to the low and similar abundances in mite and no-prey patches, in spite of the fitness gained by feeding on whiteflies and mites not differing to a great extent according to laboratory studies (McGregor et al., 1999; Sanchez et al., 2004). This aggregation may have resulted in a response to the concentration of high quality resources and to a low interference among individuals. Interference IFD models predict a distribution of consumers in patches according to the positive effect of food resources and the negative effect of competition (Mills and Heimpel, 2018). The interference coefficient m increases with the strength of the negative interaction and, for most empirical studies, it has been reported in the range 0 < m < 1 (Hassell, 1978; Sutherland and Parker, 1992). For m = 1, a perfect matching between resources in patches and the distribution of consumers is expected; in contrast, overmatching (that is, the aggregation of consumers in the best patches) is predicted for weak interferences (m < 1), and undermatching (that is, scarce number of consumers in best patches) for strong interferences (m > 1) (Mills and Heimpel, 2018). In the present research, the coefficient of interference for the females was estimated to be around 0.6 and, thus, aggregation is expected to take place in the highest quality patches. This value is within the range of variation reported for insect predators and parasitoids (Hassell, 1978; Williams et al., 2013). Interference among the individuals may reduce fitness by reducing searching time, lower the number of eggs laid by females, and increase direct or indirect competition for resources, among others (Hassell, 1978; Sutherland and Parker, 1992; van der Hammen et al., 2012).
In the present research, the fitness of D. hesperus females was estimated from the number of offspring, which implies the risk of interference being confounded with negative interactions among nymphs. For example, cannibalism is known in omnivorous mirids (Laycock et al., 2006). However, there were no significant differences in the slope of the relationship between fitness and the abundance of females per plant (that is, minus m) when the number of nymphs per plant was low (third week, maximum offspring -Q = 5.5 nymphs per female) or high (fourth week, Q = 28.8 nymphs per female), which suggests that the estimated interference was mainly due to the interaction among the adults and not to cannibalism. Cannibalism is a form of density-dependent mortality (Mitchell and Walls, 2008) and, therefore, the interference coefficient m should have increased between the third and fourth week in the case of a significant effect.
The distribution of organisms in ecosystems is the result of dispersal movements that include emigration, immigration and interpatch switching (Turchin, 1998; Bowler and Benton, 2005). In the present research, it was found that those movements were influenced by the type of patch, while the type of habitat was found to have just a marginal effect. The aggregation of D. hesperus adults in whitefly patches was the result of the low emigration rates of the individuals released on these patches and the immigration of individuals from the low quality patches within the habitat. According to our working hypothesis, D. hesperus females and males emigrated at a higher rate from low than from high quality patches, while the opposite trend was found for immigration. The dispersal of animals is known to be influenced by many factors including the density of conspecifics and heterospecific antagonists, availability of food, internal state (e.g., sex, mating status), avoidance of inbreeding, and physical factors (e.g., temperature) (Bowler and Benton, 2005; Schellhorn et al., 2014). In our study, increasing population density was found to reduce fitness in D. hesperus females and could become a force for dispersal through exploitative (reduction of per capita resources) and interference competition. However, the fact that the higher emigration and lower immigration rates were observed in the low quality patches, which hosted the lower number of individuals, suggests that the dispersal of D. hesperus was most likely driven by the quality of food resources than by competitive interactions. Food is known to be a limited resource for many animal species and dispersal has been found to be correlated with its availability (Bowler and Benton, 2005). In the present research, it was found that, in general, males had significantly higher emigration rates than females. In the absence of prey, both females and males have similar patch emigration rates, which points to food resources as the major factor driving dispersal in both sexes. In contrast, in patches with prey, males showed higher dispersal rates than females, which suggest that other factors could influence the dispersal of the two sexes in different ways. Inbreeding avoidance and asymmetries in intrasexual competition have been found to affect sex-biased dispersal in animals (Matter and Roland, 2002). The dispersal of males may reduce inbreeding and contribute to increase the genetic flow among populations (Doums et al., 2002).
One of the most important questions in ecology is what strategies consumers use to achieve their distribution in habitats (Milinski and Parker, 1991; Turchin, 1998). In the present research, about half of the D. hesperus adults in whitefly patches were collected in the same patch where they were released, and it is most likely that many of these individuals had never left the patch of origin, which means that they had limited first-hand knowledge about the abundance and quality of the resources in other patches of the habitat. In the absence of omniscience, it is not logical to suppose that D. hesperus will leave patches when their profitability falls below the average gain rate of the whole habitat, as predicted by the MVT (Charnov, 1976). For the same reason, it is also unlikely that individuals disperse in order to equally balance gain among patches, as predicted by the IFD models (Fretwell and Lucas, 1970). Predatory insects may get cues, such as plant volatiles, that evidence the presence of prey in other patches (Dicke and van Loon, 2000; Ingegno et al., 2013), but, in the case of D. hesperus it is unrealistic to think that these cues provide information about the precise quality and amount of food resources in the presence of multiple resource patches within a habitat. Simple patch-leaving rules have also been proposed to explain the foraging behavior of consumers (Hassell and Southwood, 1978; Wajnberg, 2006). The Gibb (1962) fixed number rule is not expected to be adopted by D. hesperus because predators using this strategy will spend more time, and thus aggregate, in low quality patches as they will need more time to capture a fixed number of prey in poor than in rich patches, which is against the results of the present research. Krebs (1973) fixed time rule also does not fit our experimental findings because it results in an even distribution of consumers in patches. The fixed giving-up time (GUT) rule assumes that a predator should remain in a patch if the time of the last attack does not exceed some fixed time (Hassell and May, 1974; Murdoch and Oaten, 1975). This last strategy could explain the distribution of D. hesperus because optimum prey is encountered at a high rate in high- than in poor-quality patches and, thus, individuals will be expected to leave rich patches at a lower rate than poor ones. This strategy has been argued to be in agreement with the predictions of both MVT and IFD (Wajnberg, 2006). It has also to be taken into account that not only the number of prey encounters matters, but also the quality of the prey. For instance, predators encountering suboptimal prey may adopt lower GUT than those encountering more profitable prey. Besides, the knowledge of the resources in habitats is not expected to be the same for all the individuals of the population and could depend on the individual’s past experience. Patch leaving decision in natural enemies have been found to be influenced by intra-patch experience (Wajnberg, 2006; Roitberg and Gillespie, 2014). In this regard, D. hesperus adults landing in poor patches will be more prone to leave these patches and to explore the habitat than those landing in a rich patch, and that should confer a better knowledge of the habitat in the former situation. Several authors have suggested that female parasitoids may use the information gathered while foraging on patches to form an idea on goodness of the environment (Bernstein et al., 1988; Wajnberg, 2006). In our study, the marginal effect of habitat on dispersal suggests that D. hesperus could adopt foraging strategies mainly based on the quality of resources in patches and to a lesser degree on the composition of habitats. This is in contrast with the strong impact of habitat type observed in other species, and probably reflects the effect of the landscape scale (Bowler and Benton, 2005; Roitberg and Gillespie, 2014). Habitat structure has been found to be a strong effect on inter patch movements at large landscape scale (Roland et al., 2000; Ricketts, 2001; Schellhorn et al., 2014). Ours were small habitats in which structure probably had a small effect in comparison to that of patches.
Patch leaving may be related to the consumer’s ranking of food resources. High and similar emigration rates were found in both mite and no-prey patches, even when fitness gained by D. hesperus preying on mites was found to be close to that preying on whitefly (just 22.4% lower) but double that gained from feeding on tomato plants (McGregor et al., 1999; Sanchez et al., 2004). The ranking of patches by D. hesperus is apparently not linear, which suggests the existence of a threshold below which it is not profitable to exploit a patch. The ranking of prey could be based on the nutritional values of prey, but also on other parameters such as encounter rates and handling times (McGregor et al., 1999; Brommit, 2007). For example, handling times are a little higher for T. vaporariorum pupae than for T. urticae, but the disparity in prey size means that the value or benefit per unit of handling time is much smaller for T. urticae than for T. vaporariorum; in addition, encounter rates are higher for T. vaporariorum than for T. urticae (Brommit, 2007). In that case, the choice that maximizes fitness could depend on whether the mean rate of gain is above or below this threshold (Pyke, 1984). Animals should opt for being risk adverse when the mean gain rate is above the threshold. In contrast, they should opt for higher variance (i.e., be risk prone) when gain is below the threshold (Pyke, 1984). The higher tendency of D. hesperus to stay in high quality patches and to leave low- and medium-quality patches suggest that D. hesperus may adopt a different foraging strategy depending on the quality of the food resources, being risk adverse in rich patches and risk prone in suboptimal food patches.
The dispersal and distribution of natural enemies in habitats has a great impact on the regulation of pest populations (Sutherland and Parker, 1992; Schellhorn et al., 2014; Mills and Heimpel, 2018). In the present research, it was found that D. hesperus aggregated in whitefly patches at high numbers compared to no-prey and mite patches. This had an evident impact on the pest population dynamics, and while the density of whiteflies decreased through time, the density of mites remained almost the same during all 4 weeks. IFD models predict that density-dependent aggregation of natural enemies foraging optimally leads to a greater temporal reduction of prey density (Mills and Heimpel, 2018). The findings of the present research are in agreement with Sutherland and Parker (1992) who predicted that for m < 1, an aggregation of predators and higher predator-prey ratios in the sites of the highest quality, which will in turn produce density-dependent prey mortality. This is probably the most desirable response for natural enemies foraging on a single prey, but it may not be so ideal when they are foraging on several prey species of different quality because they will aggregate on patches of the highest quality prey, leaving lower quality prey free to grow.
Conclusion
In conclusion, the study of movements and testing of IFD models in insect natural enemies has been limited (Schellhorn et al., 2014; Mills and Heimpel, 2018). Ours is one of the few studies where the movements of individual predatory insects have been tracked, using mark-recapture techniques, in habitats of a realistic size containing food patches of different qualities. Dicyphus hesperus females and males aggregated in the highest quality patches and their distribution fit most of the times to an IFD. Deviations from the IFD were found in the complex habitats offering two prey types of different quality. This could be explained by the aggregation of females and males in the most profitable patches due to low interference and/or by the adoption of patch leaving rules based upon a leaving threshold. The findings of this study suggest that D. hesperus could adopt a risk-averse or risk-prone foraging strategy depending on the quality of the resources patch. The dispersal of D. hesperus in habitats suggest that it could acquire some information about the composition of habitats while foraging, however, it is unrealistic to think that they are omniscient about the resources in habitats. Therefore, it is not realistic to assume that generalist predators such as D. hesperus forage according to the principles of MVT and IFD models. Instead, simple foraging rules are more likely to be adopted. Our research shows the importance of understanding the foraging strategies of generalist predators in order to predict their population dynamics and impacts on prey populations in complex environments.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
JS: experimental design, investigation, analyses of data, and writing of the manuscript. DG: experimental design, investigation, review and editing of the manuscript, and funding acquisition. Both authors contributed to the article and approved the submitted version.
Funding
This work was supported by the Greenhouse Vegetable Growers Research Council, the British Columbia Investment Agriculture Foundation, the Matching Investment Initiatives of Agriculture and Agri-food Canada, Koppert BV, Biobest Inc., Applied Bionomics Ltd., Natures Alternatives International. JS was awarded grants by the Dirección General de Enseñanza Superior e Investigación Científica (Ministerio de Educación y Ciencia -Spain-).
Acknowledgments
We thank D. Quiring, Z. Klassen, L. Hoey, and C. Point Sitting-Eagle for technical assistance, and the greenhouse staff at the Pacific Agri-Food Research Centre for production and maintenance of the experimental plants.
Conflict of interest
The authors declare that this study received funding from Koppert BV, Biobest Inc., Applied Bionomics Ltd., and Natures Alternatives International. The funders were not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bates, D., Mächler, M., Bolker, B. M., and Walker, S. C. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48. doi: 10.18637/jss.v067.i01
Bernstein, C., Kacelnik, A., and Krebs, J. R. (1988). Individual decisions and the distribution of predators in a patchy environment. J. Anim. Ecol. 57, 1007–1026.
Bowler, D. E., and Benton, T. G. (2005). Causes and consequences of animal dispersal strategies: Relating individual behaviour to spatial dynamics. Biol. Rev. Camb. Philos. Soc. 80, 205–225. doi: 10.1017/S1464793104006645
Brommit, A. G. (2007). Behavioural responses of an intraguild predator: The effects of intraguild predation on population dynamics. Ph.D. thesis. Windsor, ON: University of Windsor.
Charnov, E. L. (1976). Optimal foraging, the marginal value theorem. Theor. Popul. Biol. 9, 129–136.
Colares, F., Michaud, J. P., Bain, C. L., and Torres, J. B. (2015). Indigenous aphid predators show high levels of preadaptation to a novel prey, Melanaphis sacchari (Hemiptera: Aphididae). J. Econ. Entomol. 108, 2546–2555. doi: 10.1093/jee/tov235
Coulson, T., Benton, T. G., Lundberg, P., Dall, S. R. X., Kendall, B. E., and Gaillard, J. M. (2006). Estimating individual contributions to population growth: Evolutionary fitness in ecological time. Proc. R. Soc. B: Biol. Sci. 273, 547–555. doi: 10.1098/rspb.2005.3357
Dicke, M., and van Loon, J. A. (2000). Multitrophic effects of herbive-induced plant volatile in an evolutionary context. Entomol. Exp. Appl. 97, 237–249. doi: 10.1046/j.1570-7458.2000.00736.x
Doums, C., Cabrera, H., and Peeters, C. (2002). Population genetic structure and male-biased dispersal in the queenless ant Diacamma cyaneiventre. Mol. Ecol. 11, 2251–2264. doi: 10.1046/j.1365-294x.2002.01619.x
Eubanks, M. D., and Denno, R. F. (2000). Health food versus fast food: The effects of prey quality and mobility on prey selection by a generalist predator and indirect interactions among prey species. Ecol. Entomol. 25, 140–146.
Falconer, D. S. (1989). Introduction to quantitative genetic-DS Falconer.pdf. Third edit. New York, NY: John Wiley & Sons, Inc.
Foo, D., Semmens, J. M., Arnould, J. P. Y., Dorville, N., Hoskins, A. J., Abernathy, K., et al. (2016). Testing optimal foraging theory models on benthic divers. Anim. Behav. 112, 127–138. doi: 10.1016/j.anbehav.2015.11.028
Fretwell, S. D., and Lucas, H. L. (1970). On territorial behaviour and other factors influencing habitat distribution in birds. Acta Biotheor. Acta Biotheor. 19, 16–36.
Gaillard, J. M., Hebblewhite, M., Loison, A., Fuller, M., Powell, R., Basille, M., et al. (2010). Habitat-performance relationships: Finding the right metric at a given spatial scale. Philos. Trans. R. Soc. B Biol. Sci. 365, 2255–2265. doi: 10.1098/rstb.2010.0085
Gibb, J. A. (1962). L. Tinbergen’s hypothesis of the role of specific search images. Ibis 104, 106–111. doi: 10.1111/j.1474-919X.1962.tb08633.x
Hagler, J. R., and Jackson, C. G. (2001). Methods for marking insects: Current techniques and future prospects. Annu. Rev. Entomol. 46, 511–543. doi: 10.1146/annurev.ento.46.1.511
Hassell, M. P. (1978). The dynamics of arthropod predator- prey systems. New Jersey, NJ: Princeton University Press.
Hassell, M. P., and May, R. M. (1974). Aggregation of Predators and Insect Parasites. J. Anim. Ecol. 43, 567–594.
Hassell, M. P., and Southwood, T. R. E. (1978). Foraging Strategies of Insects. Annu. Rev. Ecol. Syst. 9, 75–98. doi: 10.1146/annurev.es.09.110178.000451
Hothorn, T., Hornik, K., and Zeileis, A. (2006). Unbiased Recursive Partitioning: A Conditional Inference Framework. J. Comput. Graph. Stat. 15, 651–674. doi: 10.1198/106186006X133933
Ingegno, B. L., Ferracini, C., Gallinotti, D., Alma, A., and Tavella, L. (2013). Evaluation of the effectiveness of Dicyphus errans (Wolff) as predator of Tuta absoluta (Meyrick). Biol. Control 67, 246–252. doi: 10.1016/j.biocontrol.2013.08.002
Krebs, J. R. (1973). “Behavioral aspects of predation,” in Perspectives in ethology, eds P. P. G. Bateson and P. H. Klopfer (New York, NY: Plenum).
Laycock, A., Camm, E., Van Laerhoven, S., and Gillespie, D. (2006). Cannibalism in a zoophytophagous omnivore is mediated by prey availability and plant substrate. J. Insect Behav. 19, 219–229. doi: 10.1007/s10905-006-9020-9
Matter, S. F., and Roland, J. (2002). An experimental examination of the effects of habitat quality on the dispersal and local abundance of the butterfly Parnassius smintheus. Ecol. Entomol. 27, 308–316. doi: 10.1046/j.1365-2311.2002.00407.x
Mcgraw, J. B., and Caswell, H. (1996). Estimation of individual fitness from life-history data. Am. Nat. 147, 47–64. doi: 10.1086/285839
McGregor, R. R., Gillespie, D. R., Quiring, D. J. M., and Foisy, M. R. J. (1999). Potential use of Dicyphus hesperus Knight (Heteroptera: Miridae) for biological control of pests of greenhouse tomatoes. Biol. Control 16, 104–110.
Milinski, M., and Parker, G. A. (1991). “Competition for resources,” in Behavioural ecology: An evolutionary approach, eds J. R. Krebs and N. B. Davies (Oxford: Blackwell), 137–168.
Mills, N. J., and Heimpel, G. E. (2018). Could increased understanding of foraging behavior help to predict the success of biological control? Curr. Opin. Insect Sci. 27, 26–31. doi: 10.1016/j.cois.2018.02.013
Mirhosseini, M. A., Hosseini, M. R., and Jalali, M. A. (2015). Effects of diet on development and reproductive fitness of two predatory coccinellids (Coleoptera: Coccinellidae). Eur. J. Entomol. 112, 446–452. doi: 10.14411/eje.2015.051
Murdoch, W. W., and Oaten, A. (1975). Predation and population stability. Adv. Ecol. Res. 9, 1–131. doi: 10.1016/S0065-2504(08)60288-3
Nakashima, Y., and Hirose, Y. (2003). Sex differences in foraging behaviour and oviposition site preference in an insect predator, Orius sauteri. Entomol. Exp. Et Appl. 106, 79–86.
Nakashima, Y., Teshiba, M., and Hirose, Y. (2002). Flexible use of patch marks in an insect predator: Effect of sex, hunger state, and patch quality. Ecol. Entomol. 27, 581–587. doi: 10.1046/j.1365-2311.2002.00442.x
Nonacs, P. (2001). State dependent behavior and the Marginal Value Theorem. Behav. Ecol. 12, 71–83. doi: 10.1093/oxfordjournals.beheco.a000381
Parker, G. A., and Sutherland, W. J. (1986). Ideal free distributions when individuals differ in competitive ability: Phenotype-limited ideal free models. Anim. Behav. 34, 1222–1242. doi: 10.1016/S0003-3472(86)80182-8
Perdikis, D. C., and Lykouressis, D. P. (2002). Life table and biological characteristics of Macrolophus pygmaeus when feeding on Myzus persicae and Trialeurodes vaporariorum. Entomol. Exp. Appl. 102, 261–272.
Perdikis, D., and Lykouressis, D. (2000). Effects of Various Items, Host Plants, and Temperatures on the Development and Survival of Macrolophus pygmaeus Rambur (Hemiptera: Miridae). Biol. Control 17, 55–60. doi: 10.1006/bcon.1999.0774
Puchalska, E. K., and Kozak, M. (2016). Typhlodromus pyri and Euseius finlandicus (Acari: Phytoseiidae) as potential biocontrol agents against spider mites (Acari: Tetranychidae) inhabiting willows: Laboratory studies on predator development and reproduction on four diets. Exp. Appl. Acarol. 68, 39–53. doi: 10.1007/s10493-015-9973-5
Pyke, G. H. (1984). Optimal foraging theory: A critical review. Annu. Rev. Ecol. Syst. 15, 523–575. doi: 10.1146/annurev.es.15.110184.002515
R-Development-Core-Team (2017). A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing.
Ravigné, V., Dieckmann, U., and Olivieri, I. (2009). Live where you thrive: Joint evolution of habitat choice and local adaptation facilitates specialization and promotes diversity. Am. Nat. 174, E141–E169. doi: 10.1086/605369
Ricketts, T. H. (2001). The matrix matters: Effective isolation in fragmented landscapes. Am. Nat. 158, 87–99.
Roitberg, B. D., and Gillespie, D. R. (2014). Natural enemies on the landscape - Integrating life-history theory and landscapes. Biol. Control 75, 39–47. doi: 10.1016/j.biocontrol.2014.02.002
Roland, J., Keyghobadi, N., and Fownes, S. (2000). Alpine Parnassius butterfly dispersal: Effects of landscape and population size. Ecology 81, 1642–1653.
Sanchez, J. A., Gillespie, D. R., and McGregor, R. R. (2004). Plant preference in relation to life history traits in the zoophytophagous predator Dicyphus hesperus. Entomol. Exp. Appl. 112, 7–19. doi: 10.1111/j.0013-8703.2004.00174.x
Schellhorn, N. A., Bianchi, F. J. J. A., and Hsu, C. L. (2014). Movement of entomophagous arthropods in agricultural landscapes: Links to pest suppression. Annu. Rev. Entomol. 59, 559–581. doi: 10.1146/annurev-ento-011613-161952
Stephens, D. V., and Krebs, J. R. (1986). Foraging theory. Princeton, NJ: Princeton University Press.
Sutherland, W. J. (1996). From individual behaviour to population ecology. Oxford: Oxford University Press.
Sutherland, W. J., and Parker, G. A. (1992). The relationship between continuous input and interference models of ideal free distributions with unequal competitors. Anim. Behav. 44, 345–355. doi: 10.1016/0003-3472(92)90040-G
Symondson, W. O. C., Sunderland, K. D., and Greenstone, M. H. (2002). Can generalist predators be effective biocontrol agents? Annu. Rev. Entomol. 47, 561–594.
Tregenza, T. (1994). Common misconceptions in applying the ideal free distribution. Anim. Behav. 47, 485–487. doi: 10.1006/anbe.1994.1068
Turchin, P. (1998). Quantitative analysis of movement: Measuring and modeling population redistribution in animals and plants. Sunderland, MA: Sinauer.
Valicente, F. H., and O’Neil, R. J. (1995). Effects of host plants and feeding regimes on selected life history characteristics of Podisus maculiventris (Say) (Heteroptera: Pentatomidae). Biol. Control 5, 449–461.
van der Hammen, T., Montserrat, M., Sabelis, M. W., de Roos, A. M., and Janssen, A. (2012). Whether ideal free or not, predatory mites distribute so as to maximize reproduction. Oecologia 169, 95–104. doi: 10.1007/s00442-011-2190-y
Van Moorter, B., Bunnefeld, N., Panzacchi, M., Rolandsen, C. M., Solberg, E. J., and Sæther, B. E. (2013). Understanding scales of movement: Animals ride waves and ripples of environmental change. J. Anim. Ecol. 82, 770–780. doi: 10.1111/1365-2656.12045
Wajnberg, É (2004). “Measuring genetic variation in natural enemies used for biological control: why and how?,” in Genetics, evolution and biological control, eds L. Ehler, R. Sforza, and T. Mateille (Wallingford: CAB International), 19–37.
Wajnberg, É (2006). Time allocation strategies in insect parasitoids: From ultimate predictions to proximate behavioral mechanisms. Behav. Ecol. Sociobiol. 60, 589–611. doi: 10.1007/s00265-006-0198-9
Wajnberg, E., Rosi, M. C., and Colazza, S. (1999). Genetic variation in patch time allocation in a parasitic wasp. J. Anim. Ecol. 68, 121–133. doi: 10.1046/j.1365-2656.1999.00270.x
Wheeler, A. G. (2001). Biology of the plant bugs (Hemiptera: Miridae). Ithaca, NY: Cornell University Press.
Williams, A. C., and Flaxman, S. M. (2012). Can predators assess the quality of their prey’s resource? Anim. Behav. 83, 883–890. doi: 10.1016/j.anbehav.2012.01.008
Keywords: foraging, Marginal Value Theorem (MVT), Ideal Free Distribution (IFD), omnivorous hemipterans, mirids, dispersal, patch, mark-recapture
Citation: Sanchez JA and Gillespie DR (2022) Dispersal and distribution of a generalist predator in habitats with multiple food resources. Front. Ecol. Evol. 10:977689. doi: 10.3389/fevo.2022.977689
Received: 24 June 2022; Accepted: 05 September 2022;
Published: 04 October 2022.
Edited by:
Peter Schausberger, University of Vienna, AustriaReviewed by:
Dominiek Vangansbeke, Biobest, BelgiumGeorge Broufas, Democritus University of Thrace, Greece
Gösta Nachman, University of Copenhagen, Denmark
Copyright © 2022 Sanchez and Gillespie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Antonio Sanchez, anVhbmEuc2FuY2hlejIzQGNhcm0uZXM=
 Juan Antonio Sanchez
Juan Antonio Sanchez David R. Gillespie
David R. Gillespie