- 1Department of Agronomy, Food, Natural Resources, Animals and Environment, University of Padua, Padua, Italy
- 2Department of Agriculture, Food, Environment and Forestry (DAGRI), University of Florence, Florence, Italy
- 3Department of Sciences, Augustana Campus, University of Alberta, Camrose, AB, Canada
- 4Department of Comparative Biomedicine and Food Science – BCA, University of Padua, Padua, Italy
Complex genetic and phenotypic relationships are theorized to link different fitness components but revealing the correlations occurring among disparate traits requires large datasets of pedigreed populations. In particular, the association between traits beneficial to social dominance with health and fitness could be antagonistic, because of trade-offs, or positive, because of greater resource acquisition by dominant individuals. Studies investigating these relationships found some empirical evidence in support of both theories, mainly using multiple trait models (MTM). However, if a trait giving a social advantage is suspected to affect the expression of other traits, MTM could provide some bias, that structural equation models (SEM) could highlight. We used Aosta Chestnut-Black Pied cattle to investigate whether the fighting ability of cows (the capability of winning social dominance interactions) is genetically correlated with health and fitness traits. We ran both MTM and SEM using a Gibbs sampling algorithm to disentangle the possible causal effects of fighting ability from the genetic correlations that this trait shares with other traits: individual milk yield, somatic cells (representing mammary health), fertility, and longevity. We found antagonistic genetic correlations, similar under both approaches, for fighting ability vs. milk, somatic cells, and fertility, Accordingly, we found only a slight causal effects of fighting ability on these traits (–0.012 to 0.059 in standardized value). However, we found genetic correlations opposite in sign between fighting ability and longevity under MTM (0.237) and SEM (–0.183), suggesting a strong causal effect (0.386 standardized) of fighting ability on longevity. In other words, MTM found a positive correlation between longevity and fighting ability, while SEM found a negative correlation. The explanation could be that for economic reasons dominant cows are kept in this population for longer, thus attaining greater longevity: using MTM, the economic importance of competitions probably covers the true genetic correlation among traits. This artificially simulates a natural situation where an antagonistic genetic correlation between longevity and fighting ability appears positive under MTM due to a non-genetic advantage obtained by the best fighters. The use of SEM to properly assess the relationships among traits is suggested in both evolutionary studies and animal breeding.
Introduction
Complex relationships link all phenotypic traits of an organism, and in a number of cases they result in antagonistic correlations (Falconer et al., 1996). Adverse relationships between traits can take place when different functions compete over limited internal resources (Wikelski and Ricklefs, 2001). Genetic aspects, like pleiotropy or linkage disequilibrium, environmental causes or a combination of genes and environment may underlie these antagonistic relationships, also called genetic trade-offs (Roff, 2002). For an individual, genetic trade-offs between traits represent the costs in terms of survival, chance for reproduction or fitness occurring when a beneficial evolutionary change in one trait (or “fitness component”) is balanced by a detrimental change in another (Robinson et al., 2006; Turko et al., 2022). A well-documented example of such functional trade-off, studied at length because of its economic importance, is the adverse genetic relation between fitness and milk traits in livestock (Oltenacu and Broom, 2010).
Evolutionary studies have found that trade-offs also occur between traits conferring competitive agonistic success (display and ornaments, weaponry, fighting ability) and fitness-related traits, such as fertility, longevity, and immune function (Clutton-Brock and Huchard, 2013). Among the causes of this antagonistic relationship are the negative effects that testosterone exerts on immune functions (the variability of many traits conferring competition success is influenced by testosterone levels; Wikelski and Ricklefs, 2001). When competition occurs in females the adverse relationships with fitness can be more pronounced than in males because they directly affect individual fertility and reproduction (Clutton-Brock and Huchard, 2013). Evidence of reduced female reproductive performances due to highly competitive skills have been documented at a phenotypic level in athletic women (Wood and Stanton, 2012), and in dominant females of various animal species (Clutton-Brock and Huchard, 2013).
However, certain functional trade-offs are not straightforward to investigate, such as those involving behavioral traits, whose variability is difficult to investigate and whose influence on fitness is complex to predict (Moiron et al., 2020). A recent meta-analysis failed to find the expected antagonistic relationship between survival and reproduction effort at the phenotypic level, with resource acquisition mediating the relationship between individual fitness and behavior (Haave-Audet et al., 2021). Individuals investing more might be able to access greater resources and then increase their survival chances, creating a positive feedback loop between investment and access to resources that increases both their survival and fitness (Dehnen et al., 2021).
Accessing superior resources can be accomplished through superior fighting ability, or the capability to win the agonistic interactions that regulate competition: these dyadic agonistic interactions determine also social dominance (Strauss et al., 2022), and consequently the hierarchy within a group. In a natural social environment dominant individuals increase their condition, size, and health more than their groupmates, as their superior fighting ability grants them greater access to resources (Shackleton et al., 2005; Haave-Audet et al., 2021). Feedback and feed-forward mechanisms can additionally influence the outcomes of agonistic interactions, leading individuals that have won previous agonistic interactions to have multiple advantages in their subsequent confrontations (reviewed in Dehnen et al., 2021). Dominant individuals can therefore be expected to have equal or higher survival than subordinates, despite the adverse effects that traits conferring success in social competitions might have with traits linked to longevity, health, or reproductive success.
The relationship of traits conferring agonistic success with other key fitness components have been investigated so far at the phenotypic level, with contrasting results. Evidence was found in support both of antagonistic trade-offs between fitness components (Clutton-Brock and Huchard, 2013; Sartori et al., 2015) and of positive association mediated by resource acquisition (Haave-Audet et al., 2021), i.e., both of negative or positive relationships. However, only a few studies have investigated these theories at the genetic level. The quantitative genetic approach has been effective for estimating the variance components of traits (e.g., in Soay sheep, Ovis aries: Robinson et al., 2006; in the red deer, Cervus elaphus; Foerster et al., 2007). Nonetheless, studies on the genetic relationship of traits underlying social dominance with other traits are limited, because they require robust pedigrees and big datasets with long-term phenotypic information to perform quantitative genetic analysis (Clutton-Brock and Sheldon, 2010).
The apparent conflict between the two theories – antagonistic trade-offs and positive association mediated by resource acquisition – might be partially disentangled at the level of the statistical approach. Bivariate or multiple trait models (MTM) are typically used to investigate the common sources of variation, both genetic and phenotypic, that directly affect two or more traits. These models are the most common and widely recognized approaches in quantitative genetics studies (Wilson et al., 2010), but in some cases a different approach could be preferable, such as when direct relationships of cause and effect occur between phenotypes and may inflate the genetic correlation estimates. Structural equation models (SEM) were firstly introduced in economic studies to describe causal relationships between phenotypes (Wright, 1921). SEM use has been advocated in quantitative genetics studies (Gianola and Sorensen, 2004) to effectively disentangle the common sources of variation directly affecting two or more traits (the genetic correlation) from the causal effects that phenotypes exert on each other.
SEM have been used to study the relationship between phenotypes in various fields, including social studies, ecology, and evolutionary biology (Jöreskog, 1970; Pugesek et al., 2003; Lefcheck, 2016). The application of SEM to quantitative genetics (Gianola and Sorensen, 2004), and the consequent possibility to use this approach in animal breeding practices has provided the starting point for theoretical and applied studies analyzing the recursive relationships among traits (Gianola and Sorensen, 2004). Reviews of the methodology were provided e.g., by Rosa et al. (2011) and Rosa and Valente (2013), the latter also explaining how to apply SEM to livestock data. Following this approach, SEM has been used to investigate causal relationships between traits at the genetic level in dairy cattle, including milk quality and coagulation properties (Tiezzi et al., 2015); reproductive health disorders, clinical mastitis or somatic cells and milk yield (e.g., Wu et al., 2007; Dhakal et al., 2015, 2016); health and fertility (Heringstad et al., 2009); calving traits (de Maturana et al., 2009, 2010). Similarly, they have been used in other livestock mammal species, such as pigs (Sus scrofa, e.g., Peñagaricano et al., 2015). Finally, recently, SEM was used to investigate trade-offs at the phenotypic level between fitness components (reproductive cost and parasite load, Leivesley et al., 2019). Yet, to our knowledge no study has so far addressed the genetic relationship between traits underlying social dominance and traits linked to fitness, life history and health in livestock or wild species.
Moving from all these considerations, in the present study we aim to investigate the genetic relationships among fighting ability, a crucial measure of competitive agonistic success and fitness related traits, using both MTM and SEM. Our study subject is the Aosta Chestnut-Black Pied, a local cattle native of the West Alpine arc (Sartori and Mantovani, 2012). Cows of this breed (like of the closely-related Hérens breed) are involved in bloodless traditional competitions (Plusquellec and Bouissou, 2001; Sartori and Mantovani, 2010; Pfister et al., 2011) mimicking natural interactions for dominance occurring at pasture. We used a long-term dataset on cows’ fighting results, the routinely collected information on productive traits, and herd book data. In previous works we have identified negative genetic correlations between the competitive ability of the cows (generally referred as “fighting ability”), and fitness traits like fertility and an udder health trait (somatic cells score) in Aosta Chestnut-Black Pied, confirming the trade-off theory (Sartori et al., 2015, 2020). Notwithstanding, investigation on the genetic correlation between competition and longevity, a lifetime fitness trait, resulted in a positive correlation. We postulate that this could be a consequence of keeping the cows attaining the best performances at the traditional competitions for longer in herds, therefore the longevity strongly depends on the competitive agonistic success. This artificial situation can be considered an experimental setup, modeling a natural setting where dominant individuals gain access to additional resources that might increase their lifespan. Therefore, we used SEM to investigate the relationship that fighting ability could exert on longevity, as well as on the other fitness traits abovementioned (fertility and somatic cells score). Further, we compared results of the genetic and phenotypic correlations obtained using traditional MTM and SEM. Finally, genetic relationships and the causal effects of fighting ability on milk yield (historically the main breeding goal in dairy cattle) have been also investigated.
Materials and methods
Study species
The Aosta Chestnut and Aosta Black Pied cattle, here referred as Aosta Chestnut-Black Pied breed (ABP-Chest) are two closely related breeds of “Valdostana Cattle” (Sartori and Mantovani, 2010, 2012). These breeds are native of West Alpine Arc and managed in the same herd book, as they recently have been considered as a unique breed. Traditionally bred for the dual-purpose attitude of milk and meat, ABP-Chest has recently been assigned to a triple attitude because of the inclusion of fighting ability within the selection index. This breed of cattle is, in fact, famous for the traditional competitions called “Batailles de Reines,” a simulation of interactions for social dominance occurring at summer pasture when unfamiliar cows meet. The batailles are weekly tournaments in which pairs of cows are engaged in interactions aimed at establishing social dominance (Sartori et al., 2014). Cows’ interactions are not cruel, performed under the supervision of expert veterinarians, and display the same behavioral patterns occurring at pasture. 22 non-consecutive days of competition occur annually, and approximately 200–300 cows per competition are involved. The competition is timed around the cows’ seasonal breeding cycle, thus all participants are the same in terms of reproductive status. All cows’ performances at the tournament are recorded, with individual fighting ability scores calculated at end of each day of competition (Sartori and Mantovani, 2010, 2012). The outcome of the single interactions of a pair of cows (victory or defeat) has been also studied to investigate direct and indirect genetic components of social dominance (Sartori and Mantovani, 2013).
Traits and datasets
Herd book information for ABP-Chest was joined to a 17-years dataset of phenotypic records dating back to 2000 for fighting ability, milk yield, somatic cells, fertility, and longevity. Data were provided by the National Breeders Association (ANABoRaVa1) and by the Regional Farmer Organization (AREV2).
Competition records have been weekly collected over years by the tournament association.3 Antagonistic interactions are recreated by putting two cows in front of each other, until one of them retreats from a central grass patch. Each cow is allowed to compete in multiple days of tournament per year: within each day of tournament each cow can compete in up to seven bouts. Fighting ability, or competitive ability (FIGH), is defined as the capability of an individual to win an agonistic interaction against conspecifics, playing a role in establishing dominance relationships (Parker, 1974). This phenotype, varying in a continuous scale (1.8–4.1 points) was expressed as “Placement score” (PS; Sartori and Mantovani, 2010), that is PS = 0.1*(20+ty+d+2w), or the phenotype of a cow after a day of competition, where ty is the type of tournament (the final day of competition or not), d is a difficulty coefficient depending on tournament size and w is the number of wins achieved in a day of competition. As respect to the original formulation of Sartori and Mantovani, 2010, this score was multiplied by 0.1, as reported above in the formula.
Milk yield data were defined as the individual test-day records of milk (kg) collected during the routinely functional controls performed by the Italian Breeders Association.4 Somatic cells, measured in the same test-day milk samples as somatic cells count/ml, are considered as udder health indicator (as in, e.g., Fuerst-Waltl et al., 2016) and expressed as somatic cell score (SCS; Shook and Schutz, 1994), that is SCS = 3+(log2(SCC/100 000 cells/ml)), where SCC is the somatic cells count. This adjustment allows the trait to have a normal distribution.
Fertility was expressed in terms of calving interval (CI; in months), which is the time lag between two parities. Greater calving intervals are typical of less fertile cows, due to the possible occurrence of abortion, disease, or missed conception that may cause the loss of a reproductive season. This trait is widely used in animal breeding for evaluating fertility (Wall et al., 2003). In this study, we extracted CI from the cows’ lactations information routinely recorded by the Italian Breeders Association.
Longevity (LONG) was measured in terms of life span, as the whole productive career of each individual (years) since the birth of the cows, a common measure in the animal breeding field (VanRaden and Klaaskate, 1993). The longevity phenotype was obtained using the breed’s pedigree. The phenotype included censored records, since several cows were still alive at the time of the study and was modeled similarly to correlated longevity traits (Sartori et al., 2020). To account for the (hypothesized) effect that retaining winning cows longer in the herd could have on longevity, we fitted a fixed effect “fighting ability within herd” (five classes of percentiles) in all models for longevity. We chose to fit this effect because herd life decisions are taken at the herd level: note that we applied a similar effect also for milk production because it is also a selection criterion (Cruickshank et al., 2002; Sewalem et al., 2007).
We compiled three datasets (Data1–Data3, see details below) with the aim of detecting the causal effect of FIGH on each of the other target traits (milk, SCS, CI and longevity). Data1 was built by joining the FIGH dataset with the test-day records including milk yield and SCS. Each FIGH record, measured at a target day of competition, was merged to the closest subsequent test-day record. Only test-day information recorded within 30 days after the day of competition were retained and joined to FIGH records. Moreover, data were removed if showing calving events between a FIGH record and a test-day record. All other test-day records, as well as FIGH records not matching a test-day record, were discarded. For this reason, all individuals’ FIGH records in Data1 were associated to one subsequent test-day record. This resulted in each cow having multiple records (FIGH and associated test-day) within and between lactations. In Data2 each FIGH record was merged with calving interval information for the subsequent parity. Only the FIGH records closest to the subsequent parity were retained. The remaining CI data (not joined to a close FIGH) were discarded. All individuals’ FIGH records in Data2 were associated to one subsequent parity record, for which the CI record was known. Thus, each cow had multiple CI records between parities, none of which was censored. Finally, Data3 was built by joining the lifetime productive career of the cow (i.e., its longevity) to the lifetime best performance of the individual in competitions, under the assumption that the worth of the cow for breeders is determined by the best performance achieved during the tournaments. In this case, dataset included one single record of both types (FIGH and LONG) per cow. The number of data and cows included in each dataset is reported in Table 1. Note that all traits in each dataset have the same number of records.
Models
We computed variance components and heritability (h2) of each trait by running single-trait animal models using the following model, written in matrix notation:
where y is the target trait, b is the vector for systematic fixed effects (see further), p is the vector for individual permanent environmental component when multiple records for each cow were available (for traits included in Data1 and Data2), u was the record for the additive genetic effect and e was the random residual term. Furthermore, X, W, and Z were incidence matrices of the proper dimensions. Fixed effects of traits are reported in Table 2. Differences in the fixed effects for the same trait in different models are due to the data editing (a threshold of 2 obs./cell was applied to all the effects), and to the significance of effects in preliminary ANOVAs, but similar results for the different models were found in preliminary analyses. An inverse chi-squared distribution of the priors was used to estimate variance components. Variances components for FIGH were obtained by averaging the estimates computed from the three datasets, since the trait was included in all the datasets (with different amount of data due to data editing). Heritability was calculated as the ratio between the additive genetic variance on all the variance components for each trait. Evolvability of analyzed traits, that is the ability of a population to respond to selection, was also assessed as the ratio between the additive genetic standard deviation and the phenotypic mean, also called coefficient of additive genetic variation (CVA; Hansen and Houle, 2008).
We used bivariate animal model analyses to determine the association between fighting ability and each of the other traits: milk yield (FIGH_MY; run on Data1), SCS (FIGH_SCS; Data1), CI (FIGH_CI; Data2) and longevity (FIGH_LONG; Data3). Both multiple trait models (MTM) and structural equation models (SEM) were run on each trait pair.
The MTM was written in matrix form as follows:
where y1 and y2 were the traits considered (y1 is always FIGH, and y2 is either MY, SCS, CI, longevity); b1 and b2, p1 and p2, u1 and u2, and e1 and e2 had the same meaning of the above terms b, p, u and e, here referred for the two traits of each pair. Matrices X, W, and Z have the same meaning than above as well.
The following assumptions were considered on estimated (co)variances: Pe⭙I, G⭙A, and R⭙I, with Pe, G, and R that are 2x2 matrices including the individual permanent environmental, the additive genetic and the residual (co)variances matrices for each trait pair. The G matrix included the (co)variances σ2a1, σ2a2, σa1a2 of traits 1 and 2, Pe the individual permanent environmental (co)variances σ2pe1, σ2pe2, σpe1pe2, and R the residual (co)variances σ2e1, σ2e2 and σe1e2. Furthermore, the term ⭙ is the Kronecker product, and A and I are the additive relationships matrix and an identity matrix. Prior distributions for the Pe, G and R matrices were independent inverse Wishart (one degree of belief). Genetic correlations (ra) between trait pairs were calculated as ra = σa1a2 /(σ2a1*σ2a2)0.5, and phenotypic correlations (rP) as rP = (σa1a2+σpe1pe2+σe1e2)/((σ2a1+ σ2pe1+σ2e1)*(σ2a2+ σ2pe2+σ2e2))0.5.
The causal effect of FIGH on target traits was investigated using a SEM approach on the same datasets and analyses considered for the MTM. The SEM was written as:
The same terms as in the MTM are included, except for the structural coefficient λ2←1, which describes the magnitude of the causal effect of the first phenotype on the second, i.e., FIGH on milk, SCS, CI or longevity. The matrix of structural coefficients (Λ) is a square matrix filled with zeros, excluding specific off-diagonal elements in relation to the causal structure (Valente et al., 2010). In the present study Λ for each trait pair is:
The (co)variances matrices were the same as in the MTM except for R, being diagonal with residual covariances σe1e2 forced to be zero. This assumption confers identifiability to the structural coefficients in the likelihood function. Prior distributions for the Pe and G matrices were the same as in the MTM, whereas for R the prior distribution was an inverted chi-square (one degree of belief). Genetic and phenotypic correlations of each trait pair were calculated using the abovementioned formulas.
All analyses were run using Bayesian inference, applying the Gibbs sampling algorithm and using the program GIBBS3f90 of the BLUPF90 package (Misztal, 2008) for the single trait analyses and for the MTM, and the program thrgibbs_recur, a modification of the program THRGIBBSf90 of the BLUPF90 package (Sanchez, personal communication), for the SEM. All the analyses considered 480,000 iterations of the Gibbs sampler, with a starting burn–in that discarded 30,000 iterations. The posterior mean of 3,000 samples (one every 150 samples) was considered as parameters estimator, and the lower and upper bounds of the 95% highest posterior probability density regions (HPD95) were used as estimation error. Posterior distribution analyses were performed using the POSTGIBBSF90 program (Misztal, 2008). The convergence of the Gibbs sampling chains was checked via visual inspection.
To make the results of the bivariate SEM analyses comparable between traits pairs, the structural coefficient was standardized using the standard deviations of traits 1 and 2 (σa1 and σa2) as follows: λ2←1STD = λ2←1*σa2/σa1.
Results
Descriptive statistics
Descriptive statistics of traits are reported in Table 3. Fighting ability showed an average score of 2.35, with a coefficient of variation of 0.15. Cows showed a mean test day milk yield of 4.8 kg/day, that is low but consistent with the data editing (only milk data referred up to 30 days after a fighting event were retained, and without calving events between the fighting and the milking sampling). The whole test day milk yield dataset of the cows under study had a mean of 6.9 kg/day with a standard deviation of 2.4 kg/day. An average of 3.16 points was reported for the somatic cell score, corresponding to an average somatic cell count of 298,000 cells/ml and a median of 101,000 cells/ml. Cows showed an average calving interval of 13.6 months and an average herd life of 7.75 years.

Table 3. Descriptive statistics, variance components, and heritability ± standard error (SE) of traits reported as posterior means (Mean) of the Gibbs samples.
Variance components and heritability
Table 3 also reports variance components and heritability (h2) of traits under single trait analyses. The most heritable trait was milk (h2 = 0.242), followed by longevity. FIGH showed a h2 of 0.094, a bit higher than the h2 for SCS. The less heritable trait was fertility (calving interval), with an estimate heritability of 0.027. Milk and SCS were the most evolvable traits, with a CVA around 0.15, whereas FIGH was the less evolvable (CVA = 0.039).
Correlations and recursive effects
Genetic (Figures 1A–D) and phenotypic correlations (Figures 1E–H) between trait pairs under both SEM and MTM are shown in Table 4. Structural coefficients are reported in Table 5, and shown also in Figure 1I, under the respective traits. Under the traditional MTM model, FIGH showed a negative genetic correlation with milk yield (FIGH_MY; ra = -0.323), indicating that an increase in the FIGH produces a decrease in the genetic level for milk production. We observed only a slight negative recursive effect of FIGH on milk yield, with the structural equation coefficient λ2←1 of FIGH on milk suggesting that an increase in 1 unit of FIGH score (0.1 points) produced a decrease of just 0.106 kg of milk. The genetic correlation between FIGH and TD milk found using the SEM (ra = -0.316) was similar to the MTM estimate. The phenotypic correlation between FIGH and milk was also negative but close to zero under both MTM and SEM, and for the latter the HPD95 overlapped the zero value.
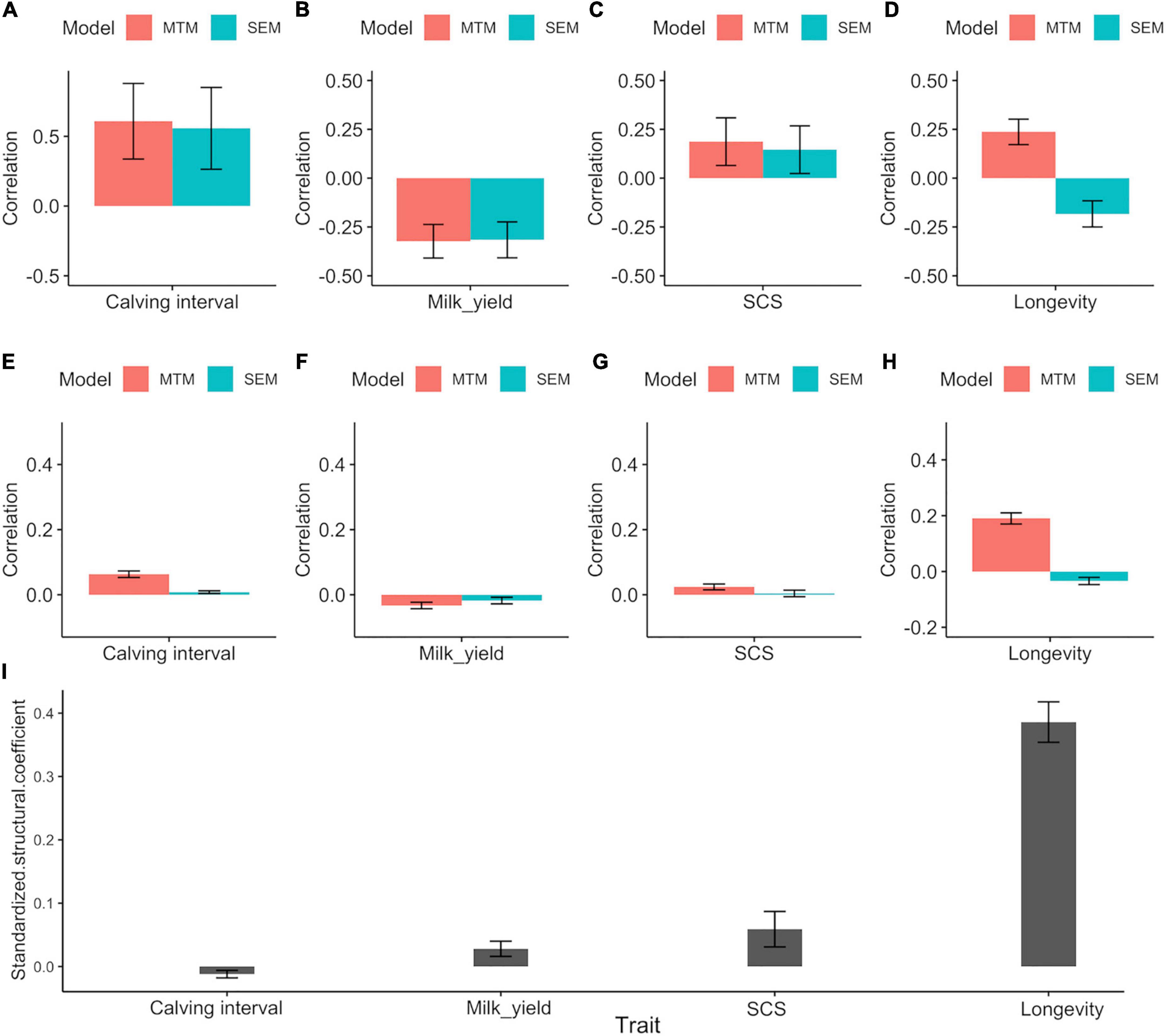
Figure 1. (A–H) Posterior means ± standard deviation (SD) for genetic and phenotypic correlations between fighting ability and the other traits under MTM and SEM. (A) Genetic correlation with calving interval. (B) Genetic correlation with milk yield. (C) Genetic correlation with SCS. (D) Genetic correlation with longevity. (E) Phenotypic correlation with calving interval. (F) Phenotypic correlation with milk yield. (G) Phenotypic correlation with SCS. (H) Phenotypic correlation with longevity. (I) Posterior means ± standard deviation (SD) for the standardized structural coefficient (λ2←1STD) obtained via SEM for the causal effect of fighting ability (FIGH) on the other traits considered.

Table 4. Posterior means ± posterior standard deviations, and 95% high posterior density regions (HPD95) for genetic and phenotypic correlations between fighting ability and the other traits under multiple trait model and structural equation model.
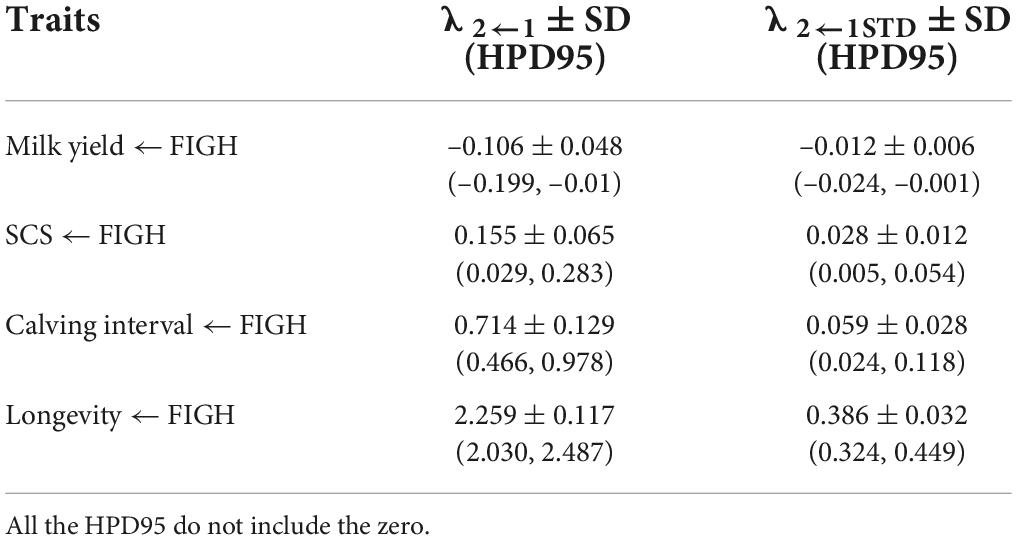
Table 5. Posterior means ± standard deviation (SD) and 95% high posterior density regions (HPD95) for the structural coefficients (λ2←1) and for the standardized structural coefficient (λ2←1STD) obtained via SEM for the causal effect of fighting ability (FIGH) on the other traits considered.
We found a moderate positive genetic correlation (ra = 0.187) between FIGH and somatic cell score (FIGH_SCS) using MTM, indicating that an increase in the combative ability is genetically associated with lower udder health. The error associated with this correlation estimate was very large, and the high posterior density region for the trait partially overlapped zero value. The SEM found a structural equation coefficient of 0.155 for the causal effect of FIGH on SCS, corresponding to an increase in the somatic cell score due to a unit of increment for FIGH. We found a similar, albeit slightly lower, genetic correlation (ra = 0.146) for the same traits under SEM, but even in this case the estimate partially overlapped zero. We found phenotypic correlations close to zero for this trait pair using both MTM and SEM.
We found a strong positive genetic correlation between fertility (calving interval) and FIGH (FIGH_CI) under both MTM and SEM (ra = 0.608 and ra = 0.557, respectively), indicating that a reduction in fertility (longer calving intervals) is associated with an intensification in FIGH. The structural equation found for this trait pair suggests that an increase of 1 unit in FIGH causes an increase of 0.71 months in the calving interval of cows. The phenotypic correlations were positive and close to zero both under MTM and SEM. None the HPD95 intervals for the correlations of FIGH_CI overlapped zero.
Overall, genetic correlations estimated using SEM for the trait pairs FIGH_MY, FIGH_SCS and FIGH_CI similar, albeit slightly lower, compared to those calculated using MTM. Interestingly, however, we found that the genetic correlation between FIGH and longevity (FIGH_LONG) turned from positive (ra = 0.237) to negative (ra = –0.183) when we analyzed it with SEM instead of MTM. We found a structural equation coefficient of 2.259 for the causal effect of FIGH on longevity, meaning that 1 unit of increment for FIGH corresponded to more than 2 years of increase in herd life. The positive phenotypic correlation between FIGH and longevity under MTM turned to close to zero negative values under SEM. All the HPD95 for these trait pair correlations did not overlap zero.
In general, all structural equation coefficients and the corresponding standardized values did not overlap zero. The standardized structural equation coefficient for the causal effect of FIGH on longevity had the greatest magnitude (λ2←1STD = 0.386), followed by the coefficient for the effect of FIGH on the calving interval (λ2←1STD = 0.059).
Discussion
In the present study we investigated the genetic correlations between fighting ability and fitness and productive traits, applying structural equation models to disentangle possible confounding relations between genetic covariances and phenotypic causation. This was made possible by the long-term dataset collected on cows’ competitive performances during the traditional competitions, together with routinely acquired cows’ productive records and calving events, which have allowed to study the genetic correlations of fighting ability with fertility and milk yield (Sartori et al., 2015), and with somatic cells and longevity (Sartori et al., 2020). We found that the phenotypic and genetic correlations obtained with MTM, and SEM were similar for fertility, milk yield and somatic cells score. However, there was a strong difference in the direction of the correlations between longevity and fighting ability, with MTM reporting a positive phenotypic and genetic correlation, while SEM revealing a negative genetic correlation.
The antagonistic genetic correlation between fighting ability and milk yield found in this study is slightly higher than the ra found with just MTM in a previous study (Sartori et al., 2015). This is most likely due to the milk record being measured as whole-lactation data in the previous study, whereas in this study we used daily milk recording. Negative genetic correlations between aggressiveness (another testosterone-related trait as fighting ability) and derived maternal milk yield (differences of calf weights after and before suckling) have been reported for heifers of the Limousine cattle breed (Phocas et al., 2006).
A moderate antagonistic genetic correlation was found also for fighting ability and SCS (first reported in Sartori et al., 2020). Differences in estimates of MTM correlation with the previous paper are mainly due to the size of the increased dataset and the specific data editing of the present study. These estimates agree with trade-off theory, predicting an antagonistic genetic relationship between immune function-related traits, such as udder health, and traits indicators of individual competition success (Roff, 2002). Ours is one of the few empirical studies providing evidence of these genetic correlations (Fedorka, 2014).
In the present study, the strong negative genetic correlation between fertility and fighting ability indicates that an increase in competition success is strongly associated to longer calving intervals and therefore to a detriment in fertility, agreeing with the theory of a trade-off between fitness components (Clutton-Brock and Huchard, 2013). Among the few empirical studies which found examples of similar genetic relations in mammals, negative genetic correlations between fertility and aggressiveness have been found in cattle (Phocas et al., 2006), and an antagonistic relationship between male competition success and the daughters’ fertility has been shown in red deer (Foerster et al., 2007).
A trade-off would also be expected for competition success and longevity, as reported in studies on male competitiveness and male or female (daughters) survival (e.g., in red deer, Foerster et al., 2007; in Soay sheep; Johnston et al., 2013). Sartori et al. (2020) provided a first example of genetic correlations between female fighting ability and longevity (expressed as productive life, strongly correlated with herd life), but found a positive genetic correlation (ra = 0.556). The reason for this was probably the economic worth of fighting ability for Aosta Chestnut-Black Pied cattle, since the most competitive cows in traditional tournaments are kept in herds longer because of their greater economic value. In the current work, the correlation between longevity and fighting ability obtained via MTM was positive (ra = 0.237) despite accounting for the effect of within-herd differences in combative ability on herd life. Indeed, a preliminary version of the longevity model without such effect, despite not presenting any difference in its estimate of heritability (h2 = 0.216), did present a higher MTM correlation with fighting ability (ra = 0.395). This indicates that, to a degree, including the correct effects in a classic MTM can help obtain slightly less inflated genetic estimates. However, a structural equation model which included the causal effect of fighting ability on herd life resulted in the discovery of a negative genetic correlation between fighting ability and longevity. The high structural equation coefficient found in this study reveals indeed that cows’ herd life is strongly dependent on their success in tournaments. This is also indicated by the drop in genetic variances observed when SEM and MTM estimates are compared. SEM allowed us to uncover that a negative genetic correlation between fighting ability and longevity indeed exists in this breed: however, due to the peculiarity of this breed’s management, it was necessary to consider that there might be a partially causal relationships among traits to properly estimate the (co)variance components. In our case this is due to the great value that breeders attribute to the best fighters: breeders allow them to live longer, “artificially” increasing their lifespan. And yet, our situation has interesting parallels with selective pressures in natural populations. In fact, while our SEM analysis showed an antagonistic genetic correlation between fighting ability and longevity, MTM showed a positive correlation. The phenotypic correlation between these traits similarly went from positive with MTM to non-existent with SEM.
The present result is interesting also because empirical evidence of the hypothesized genetic trade-off between social competitive success and longevity are scarce: evidence of the adverse genetic relationships between male competitiveness and daughters’ survival was found by Foerster et al. (2007) in their seminal work on red deer, while the present study provides the first finding of this longevity-fighting ability genetic trade-off in females.
Indeed, in natural populations individuals might be expected to face genetic trade-offs between different traits due to constraints in the allocation of resources. However, the advantages that the behavior of dominant individuals provide in terms, e.g., of acquired resources might be enough to offset their intrinsic lower quality for fitness traits, and greatly enhance their survival. Moreover, in natural populations even a phenotypic relationship between two traits might be difficult to determine due to differences in overall individual quality (McLean et al., 2019; Turko et al., 2022) and change according to feedbacks (Dehnen et al., 2021). Finally, social animals could enjoy benefits not linked to their own phenotype, but to the social composition of their group (Ligorio et al., 2020; Tuliozi et al., 2021). For all these reasons, we argue that in natural populations, wherever a genetic trade-off between fitness components is hypothesized, SEM might be more helpful to uncover it than MTM.
Correlations calculated with MTM, and SEM changed little for the other traits, indicating only a slight causal effect of fighting ability on fertility, production and SCS. In these cases, MTM is still a proper choice for the genetic estimates, although SEM approach can provide a good modeling of the complex biological relationships existing among traits.
Causal relationships between phenotypes can be mutual (simultaneous) or one-directional, that is, only one affects the other (recursive relationship; Gianola and Sorensen, 2004), and it is important to understand the complex network of causal relationships occurring among traits (Valente et al., 2010). In most situations there is a lack of prior knowledge about the possible causal dependencies among traits; therefore, it is necessary to consider all the possible causal relationships occurring among target traits. Our study was not interested in unearthing all the possible causal dependencies among traits, but in understanding whether fighting ability may have a causal effect on the other traits able to bias the (co)variance estimates if not detected. As our study involved only two traits at the same time, it was not possible to determine the causal structure in their correlation (Bello et al., 2018): again, our aim was limited to investigating how a SEM including the causal effects of fighting ability on other traits would estimate genetic and phenotypic correlations.
In this study we have shown the strong impact that the inclusion of a causal effect of fighting ability had on herd life (as well as the slight effects on milk, SCS and calving interval) and provided evidence of a trade-off between competition success and longevity in cows. This is also important information for the breed management: since the early 2000s, in the animal breeding field there has been a shift toward paying more attention to functional traits, or the characteristics related to the “good-functioning” of the organism and to individual well-being (Miglior et al., 2005). There is a keen interest in having high-productive animals that are also in good-health, and this calls for increasing consideration of the complex network of genetic and causal relationships among traits in breeding decisions (Oltenacu and Broom, 2010).
In conclusion, we have investigated the genetic correlations of fighting ability with production and fitness in the Aosta Chestnut and Aosta Black-Pied cattle. We conducted bivariate analyses between fighting ability and each of the other traits using both approaches traditional: (multiple trait modeling, MTM) and structural equation modeling (SEM). Using SEM allowed us to disentangle the possible causal effects of fighting ability on the other traits. Specifically, we found a strong causal effect of fighting ability on longevity. Most interestingly, the positive genetic correlation between fighting ability and longevity became negative when the causal component was included in the analysis. What is likely concealing from classical MTM the true genetic relationship between traits is probably that better competitors are kept longer in herds by breeders. The result agrees with theories predicting a trade-off between different fitness components such as traits related to success in competition and life history traits like longevity but suggests that to find this genetic correlation also in wild populations SEM might be more appropriate. We also found a weak causal effect of fighting ability on the other traits under study, but there was almost no influence on (co)variance components, so using MTM is still a proper solution. Our finding of an antagonistic genetic relationship between fighting ability, milk yield, fertility and somatic cells confirms the few previous quantitative studies investigating the genetic association between social competitive success and fitness or production. Our work highlights the importance of detecting true genetic relationships between traits in evolutionary and in animal breeding studies.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical review and approval was not required for the animal study because this study did not require any specific ethics permit. The cattle sampled belonged to commercial private herds and were not experimentally manipulated. Samples were collected by technicians from the National Breeders Association for Aosta Cattle (ANABoRaVa).
Author contributions
CS, FT, RM, and BT: conceptualization. CS and FT: methodology. CS and RM: formal analysis and resources. FT and RM: support to analysis. BT and CS: writing. IS, EM, NG, and RM: review and editing. All authors contributed to the article and approved the submitted version.
Funding
This work was funded by the University of Padova under: the STARS Grants programme Gentrait – Genome wide association study and pathway analysis of antagonistic traits as social dominance, production, fertility, and survival in a local cattle breed, awarded to CS; and by the Department of Agronomy, Food, Natural Resources, Animals, and Environment (DOR 2021), awarded to CS.
Acknowledgments
We greatly acknowledge the National Breeders Association for Aosta Cattle (ANABoRaVa) for providing pedigree and data.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
References
Bello, N. M., Ferreira, V. C., Gianola, D., and Rosa, G. J. (2018). Conceptual framework for investigating causal effects from observational data in livestock. J. Anim. Sci. 96, 4045–4062. doi: 10.1093/jas/sky277
Clutton-Brock, T. H., and Huchard, E. (2013). Social competition and selection in males and females. Philos. Trans. R. Soc. B Biol. Sci. 368:20130074. doi: 10.1111/jzo.12023
Clutton-Brock, T. H., and Sheldon, B. C. (2010). Individuals and populations: The role of long-term, individual-based studies of animals in ecology and evolutionary biology. Trends Ecol. Evol. 25, 562–573. doi: 10.1016/j.tree.2010.08.002
Cruickshank, J., Weigel, K. A., Dentine, M. R., and Kirkpatrick, B. W. (2002). Indirect prediction of herd life in Guernsey dairy cattle. J. Dairy Sci. 85, 1307–1313. doi: 10.3168/jds.S022-0302(02)74195-7
de Maturana, E. L., de los Campos, G., Wu, X.-L., Gianola, D., Weigel, K. A., and Rosa, G. J. M. (2010). Modeling relationships between calving traits: A comparison between standard and recursive mixed models. Genet. Sel. Evol. 42:1. doi: 10.1186/1297-9686-42-1
de Maturana, E. L., Wu, X.-L., Gianola, D., Weigel, K. A., and Rosa, G. J. M. (2009). Exploring biological relationships between calving traits in primiparous cattle with a Bayesian recursive model. Genetics 181, 277–287. doi: 10.1534/genetics.108.094888
Dehnen, T., Arbon, J. J., Farine, D. R., and Boogert, N. J. (2021). How feedback and feed-forward mechanisms link determinants of social dominance. Biol. Rev. 97, 1210–1230. doi: 10.1111/brv.12838
Dhakal, K., Tiezzi, F., Clay, J. S., and Maltecca, C. (2015). Inferring causal relationships between reproductive and metabolic health disorders and production traits in first-lactation US Holsteins using recursive models. J. Dairy Sci. 98, 2713–2726. doi: 10.3168/jds.2014-8448
Dhakal, K., Tiezzi, F., Clay, J. S., and Maltecca, C. (2016). Causal relationships between clinical mastitis events, milk yields and lactation persistency in US Holsteins. Livest. Sci. 189, 8–16. doi: 10.1016/j.livsci.2016.04.015
Falconer, D. S., Mackay, T. F., and Frankham, R. (1996). Introduction to quantitative genetics, 4th Edn. Harlow: Longmans Green.
Fedorka, K. M. (2014). “Reproductive and immune system interactions in the context of life-history and sexual selection theory,” in Eco-immunology: Evolutive aspects and future perspectives, eds E. Ottaviani and D. Malagoli (Netherland: Springer), 49–72. doi: 10.1007/978-94-017-8712-3_3
Foerster, K., Coulson, T., Sheldon, B. C., Pemberton, J. M., Clutton-Brock, T. H., and Kruuk, L. E. (2007). Sexually antagonistic genetic variation for fitness in red deer. Nature 447, 1107–1111. doi: 10.1038/nature05912
Fuerst-Waltl, B., Fuerst, C., Obritzhauser, W., and Egger-Danner, C. (2016). Sustainable breeding objectives and possible selection response: Finding the balance between economics and breeders’ preferences. J. Dairy Sci. 99, 9796–9809. doi: 10.1111/1365-2656.12575
Gianola, D., and Sorensen, D. (2004). Quantitative genetic models for describing simultaneous and recursive relationships between phenotypes. Genetics 167, 1407–1424. doi: 10.1534/genetics.103.025734
Haave-Audet, E., Besson, A. A., Nakagawa, S., and Mathot, K. J. (2021). Differences in resource acquisition, not allocation, mediate the relationship between behaviour and fitness: A systematic review and meta-analysis. Biol. Rev. 97, 708–731. doi: 10.1111/brv.12819
Hansen, T. F., and Houle, D. (2008). Measuring and comparing evolvability and constraint in multivariate characters. J. Evol. Biol. 21, 1201–1219. doi: 10.1111/j.1420-9101.2008.01573.x
Heringstad, B., Wu, X.-L., and Gianola, D. (2009). Inferring relationships between health and fertility in Norwegian Red cows using recursive models. J. Dairy Sci. 92, 1778–1784. doi: 10.3168/jds.2008-1535
Johnston, S. E., Gratten, J., Berenos, C., Pilkington, J. G., Clutton-Brock, T. H., Pemberton, J. M., et al. (2013). Life history trade-offs at a single locus maintain sexually selected genetic variation. Nature 502, 93–95. doi: 10.1038/nature12489
Jöreskog, K. G. (1970). A general method for estimating a linear structural equation system. ETS Res. Bull. Ser. 2, i–41. doi: 10.1002/j.2333-8504.1970.tb00783.x
Lefcheck, J. S. (2016). PiecewiseSEM: Piecewise structural equation modelling in R for ecology, evolution, and systematics. Met. Ecol. Evol. 7, 573–579. doi: 10.1111/2041-210X.12512
Leivesley, J. A., Bussière, L. F., Pemberton, J. M., Pilkington, J. G., Wilson, K., and Hayward, A. D. (2019). Survival costs of reproduction are mediated by parasite infection in wild Soay sheep. Ecol. Lett. 22, 1203–1213. doi: 10.1111/ele.13275
Ligorio, E., Tuliozi, B., Hoi, H., and Griggio, M. (2020). Flock-dependent exploitation of a limited resource in House Sparrow. Sci. Rep. 10, 1–11. doi: 10.1038/s41598-020-64283-y
McLean, E. M., Archie, E. A., and Alberts, S. C. (2019). Lifetime fitness in wild female baboons: Trade-offs and individual heterogeneity in quality. Am. Nat. 194, 745–759. doi: 10.1086/705810
Miglior, F., Muir, B. L., and Van Doormaal, B. J. (2005). Selection indices in Holstein cattle of various countries. J. Dairy Sci. 88, 1255–1263. doi: 10.3168/jds.S0022-0302(05)72792-2
Misztal, I. (2008). Reliable computing in estimation of variance components. J. Anim. Breed. Genet. 125, 363–370. doi: 10.1111/j.1439-0388.2008.00774.x
Moiron, M., Laskowski, K. L., and Niemelä, P. T. (2020). Individual differences in behaviour explain variation in survival: A meta-analysis. Ecol. Lett. 23, 399–408. doi: 10.1111/ele.13438
Oltenacu, P. A., and Broom, D. M. (2010). The impact of genetic selection for increased milk yield on the welfare of dairy cows. Anim. Welfare 19, 39–49.
Parker, G. A. (1974). Assessment strategy and the evolution of fighting behavior. J. Theor. Biol. 47, 223–243. doi: 10.1016/0022-5193(74)90111-8
Peñagaricano, F., Valente, B. D., Steibel, J. P., Bates, R. O., Ernst, C. W., Khatib, H., et al. (2015). Searching for causal networks involving latent variables in complex traits: Application to growth, carcass, and meat quality traits in pigs. J. Anim. Sci. 93, 4617–4623. doi: 10.2527/jas.2015-9213
Pfister, P., Kaufmann, T., Fellay, E., and Hirsbrunner, G. (2011). Erhebung von Fruchtbarkeitsdaten der Eringerrasse von 2003-2007 [Reproductive performance in Hérens cows from 2003 to 2007]. Schweiz. Arch. Tierheilk. 153, 7–13. doi: 10.1024/0036-7281/a000136
Phocas, F., Boivin, X., Sapa, J., Trillat, G., Boissy, A., and Le Neindre, P. (2006). Genetic correlations between temperament and breeding traits in Limousin heifers. Anim. Sci. 82, 805–811. doi: 10.1017/ASC200696
Plusquellec, P., and Bouissou, M. F. (2001). Behavioral characteristics of two dairy breeds of cows selected Hérens or not Brune des Alpes for fighting and dominance ability. Appl. Anim. Behav. Sci. 72, 1–21. doi: 10.1016/S0168-1591(00)00198-2
Pugesek, B. H., Tomer, A., and Von Eye, A. (2003). Structural equation modeling: Applications in ecological and evolutionary biology. Cambridge: Cambridge University Press.
Robinson, M. R., Pilkington, J. G., Clutton-Brock, T. H., Pemberton, J. M., and Kruuk, L. E. (2006). Live fast, die young: Trade-offs between fitness components and sexually antagonistic selection on weaponry in Soay sheep. Evolution 60, 2168–2181. doi: 10.1554/06-128.1
Rosa, G. J. M., and Valente, B. D. (2013). Breeding and genetics symposium: Inferring causal effects from observational data in livestock. J. Anim. Sci. 91, 553–564. doi: 10.2527/jas.2012-5840
Rosa, G. J., Valente, B. D., de los Campos, G., Wu, X.-L., Gianola, D., and Silva, M. A. (2011). Inferring causal phenotype networks using structural equation models. Genet. Sel. Evol. 43:6. doi: 10.1186/1297-9686-43-6
Sartori, C., and Mantovani, R. (2010). Genetic of fighting ability in cattle using data from the traditional battle contest of Valdostana breed. J. Anim. Sci. 88, 3206–3213. doi: 10.2527/jas.2010-2899
Sartori, C., and Mantovani, R. (2012). Effects of inbreeding on fighting ability measured in Aosta Chestnut and Aosta Black Pied cattle. J. Anim. Sci. 90, 2907–2915. doi: 10.2527/jas.2011-4010
Sartori, C., and Mantovani, R. (2013). Indirect genetic effects and the genetic bases of social dominance: Evidence from cattle. Heredity 110, 3–9. doi: 10.1038/hdy.2012.56
Sartori, C., Guzzo, N., and Mantovani, R. (2020). Genetic correlations of fighting ability with somatic cells and longevity in cattle. Animal 14, 13–21. doi: 10.1017/S175173111900168X
Sartori, C., Manser, M. B., and Mantovani, R. (2014). Relationship between number of fighting and intensity of fighting: Evidence from cow battle tournaments in Valdostana cattle. Ital. J. Anim. Sci. 13, 684–692. doi: 10.4081/ijas.2014.3286
Sartori, C., Mazza, S., Guzzo, N., and Mantovani, R. (2015). Evolution of increased competitiveness in cows trades off with reduced milk yield, fertility and more masculine morphology. Evolution 69, 2235–2245. doi: 10.1111/evo.12723
Sewalem, A., Miglior, F., Kistemaker, G. J., Sullivan, P., Huapaya, G., and Van Doormaal, B. J. (2007). Modification of genetic evaluation of herd life from a three-trait to a five-trait model in Canadian dairy cattle. J. Dairy Sci. 90, 2025–2028. doi: 10.3168/jds.2006-719
Shackleton, M. A., Jennions, M. D., and Hunt, J. (2005). Fighting success and attractiveness as predictors of male mating success in the black field cricket, Teleogryllus commodus: The effectiveness of no-choice tests. Behav. Ecol. Sociobiol. 58, 1–8. doi: 10.1007/s00265-004-0907-1
Shook, G. E., and Schutz, M. M. (1994). Selection on somatic cell score to improve resistance to mastitis in the United States. J. Dairy Sci. 77, 648–658. doi: 10.3168/jds.S0022-0302(94)76995-2
Strauss, E. D., Curley, J. P., Shizuka, D., and Hobson, E. A. (2022). The centennial of the pecking order: Current state and future prospects for the study of dominance hierarchies. Phil. Trans. R. Soc. B 377:20200432. doi: 10.1098/rstb.2020.0432
Tiezzi, F., Valente, B. D., Cassandro, M., and Maltecca, C. (2015). Causal relationships between milk quality and coagulation properties in Italian Holstein-Friesian dairy cattle. Genet. Sel. Evol. 47:45. doi: 10.1186/s12711-015-0123-7
Tuliozi, B., Camerlenghi, E., and Griggio, M. (2021). Dyadic leader-follower dynamics change across situations in captive house sparrows. Behav. Ecol. 32, 508–517. doi: 10.1093/beheco/araa148
Turko, A. J., Rossi, G. S., Blewett, T. A., Currie, S., Taylor, D. S., Wright, P. A., et al. (2022). Context-dependent relationships between swimming, terrestrial jumping and body composition in the amphibious fish Kryptolebias marmoratus. J. Exp. Biol. 225:jeb243372. doi: 10.1242/jeb.243372
Valente, B. D., Rosa, G. J., de los Campos, G., Gianola, D., and Silva, M. A. (2010). Searching for recursive causal structures in multivariate quantitative genetics mixed models. Genetics 185, 633–644. doi: 10.1534/genetics.109.112979
VanRaden, P. M., and Klaaskate, E. J. H. (1993). Genetic evaluation of length of productive life including predicted longevity of live cows. J. Dairy Sci. 76, 2758–2764. doi: 10.3168/jds.S0022-0302(93)77613-4
Wall, E., Brotherstone, S., Woolliams, J. A., Banos, G., and Coffey, M. P. (2003). Genetic evaluation of fertility using direct and correlated traits. J. Dairy Sci. 86, 4093–4102. doi: 10.3168/jds.S0022-0302(03)74023-5
Wikelski, M., and Ricklefs, R. E. (2001). The physiology of life histories. Trends Ecol. Evol. 16, 479–481. doi: 10.1016/S0169-5347(01)02279-0
Wilson, A. J., Reale, D., Clements, M. N., Morrissey, M. M., Postma, E., Walling, C. A., et al. (2010). An ecologist’s guide to the animal model. J. Anim. Ecol. 79, 13–26. doi: 10.1111/j.1365-2656.2009.01639.x
Wood, R. I., and Stanton, S. J. (2012). Testosterone and sport: Current perspectives. Horm. Behav. 61, 147–155. doi: 10.1016/j.yhbeh.2011.09.010
Keywords: fighting ability, social dominance, structural equation model – SEM, genetic correlation, antagonistic traits, cattle, fertility, longevity
Citation: Tuliozi B, Tiezzi F, Schoepf I, Mancin E, Guzzo N, Mantovani R and Sartori C (2022) Genetic correlations and causal effects of fighting ability on fitness traits in cattle reveal antagonistic trade-offs. Front. Ecol. Evol. 10:972093. doi: 10.3389/fevo.2022.972093
Received: 17 June 2022; Accepted: 12 September 2022;
Published: 30 September 2022.
Edited by:
Tom Langen, Clarkson University, United StatesReviewed by:
Yun Ma, Ningxia University, ChinaStefano Biffani, Institute of Agricultural Biology and Biotechnology (CNR), Italy
Copyright © 2022 Tuliozi, Tiezzi, Schoepf, Mancin, Guzzo, Mantovani and Sartori. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roberto Mantovani, cm9iZXJ0by5tYW50b3ZhbmlAdW5pcGQuaXQ=
 Beniamino Tuliozi
Beniamino Tuliozi Francesco Tiezzi
Francesco Tiezzi Ivana Schoepf
Ivana Schoepf Enrico Mancin
Enrico Mancin Nadia Guzzo4
Nadia Guzzo4 Roberto Mantovani
Roberto Mantovani Cristina Sartori
Cristina Sartori
