
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol. , 24 August 2022
Sec. Biogeography and Macroecology
Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.915325
This article is part of the Research Topic Integrating Multiple Scales in the Study of Species Distributions: From Habitat Fragmentation to Species Interactions View all 5 articles
Ecological niche models (ENMs) have become a practical and key mechanism for filling major gaps in spatial information for targeted conservation planning, particularly when only occurrence data are available. Nonetheless, accounting for abundance patterns in the internal structure of species’ ranges, and the role of biotic interactions in such models across broadscale, remains highly challenging. Our study gathered baseline information on abundance data of two Endangered Amazonian primates (Ateles chamek and Lagothrix lagotricha cana) to create geospatial abundance models using two spatial interpolation methods: Inverse distance weight (IDW) and Ordinary kriging (OK). The main goals were to: (i) test whether geospatial abundance models are correlated with habitat suitability derived from correlative ENMs; (ii) compare the strength of the abundance-suitability relationships between original and interpolated abundances; (iii) test whether interspecific competition between the two target taxa constrained abundance over broad spatial scales; and (iv) create ensemble models incorporating both habitat suitability and abundance to identify high-priority areas for conservation. We found a significant positive relationship between habitat suitability with observed and predicted abundances of woolly (L. l. cana) and spider (A. chamek) monkeys. Abundance-suitability correlations showed no significant differences when using original relative abundances compared to using interpolated abundances. We also found that the association between L. l. cana abundance and habitat suitability depended on the abundance of its putative competitor species, A. chamek. Our final models combining geospatial abundance information with ENMs were able to provide more realistic assessments of hotspots for conservation, especially when accounting for the important, but often neglected, role of interspecific competition in shaping species’ geographic ranges at broader scales. The framework developed here, including general trends in abundance patterns and suitability information, can be used as a surrogate to identify high-priority areas for conservation of poorly known species across their entire geographic ranges.
Ecological niche models (ENMs; also referred to as species distribution or habitat suitability models) have become a practical and important mechanism for filling major gaps in spatial information for targeted conservation planning (Zurell et al., 2021), particularly when only occurrence data are available (Phillips et al., 2006; Sillero et al., 2021; Valavi et al., 2021). ENMs relate geo-referenced species observations to environmental variables to estimate suitable habitats in a geographical space, providing hypothesis for the geographic distributions of the species (Sillero et al., 2021). Although ENMs have proven useful to adequately describe the geographic distribution of species, their capacity to inform about the abundance patterns in the internal structure of species’ ranges remains an unsolved problem (Weber et al., 2017; Dallas and Hastings, 2018; Jiménez-Valverde et al., 2021; Lee-Yaw et al., 2021). Therefore, incorporating species abundance information across broad spatial scales is a fundamental step toward effective conservation and management of species.
Abundance is not evenly distributed across space. It is expected that most species occur at low abundances in most of their range, and are highly abundant in relatively few locations (Brown et al., 1995). These patterns reflect population responses to local conditions in which the species meet its ecological requirements (de la Fuente et al., 2021). Another classical assumption of abundance distribution is that abundance variation is spatially autocorrelated, so that the probability of sites having similar abundance values is an inverse function of the distance between them (Brown et al., 1995). This is in line with the foundation of Tobler’s first law of geography (Tobler, 1970), which poses that “everything is related to everything else, but near things are more related than distant things.” This fundamental spatial dependence and autocorrelation concepts lies at the heart of methods of spatial interpolation (Li and Heap, 2008, 2011, 2014).
Spatial interpolation is the process of mapping a variable of interest at unsampled locations using the values present in a sampled set of known locations to generate spatially continuous surfaces (see Li and Heap, 2014 for topic review). Conservation scientists, policymakers and environmental managers usually require such kinds of spatially explicitly data to make effective and confident decisions over a region of conservation concern. Consequently, geostatistical techniques have been widely disseminated in different disciplines (e.g., mining engineering, soil sciences, anthropology: Li and Heap, 2008; Relethford, 2008; Li and Heap, 2014). Spatial interpolation has been used for characterizing the spatial distribution and mapping soil gradients and properties (e.g., Robinson and Metternicht, 2006; Zuquim et al., 2019), generating climate surfaces of precipitation and temperature (e.g., Tan et al., 2021), and mapping epidemic vectors and diseases (e.g., Zhou et al., 2021). In ecological studies, they have also been applied, for example, to map temporal changes in live coral cover (Walker et al., 2012), predict forest stem volume (Wallerman et al., 2002), or to characterize the spatial structure of vegetation communities (Wallace et al., 2000). However, the use of interpolation methods for spatial conservation prioritization and abundance predictions has been considerably scarcer, especially for Amazonian data-deficient species.
Black faced black spider monkeys (Ateles chamek) and the gray woolly monkeys (Lagothrix lagotricha cana) are two Endangered Amazonian primate taxa with just such abundance-data limitations, and at a number of scales (Alves et al., 2021; Cornejo et al., 2021). These two taxa are members of the subfamily Atelinae (Platyrrhini, Atelidae). They are considered to be keystone dispersers, providing invaluable ecosystem services (Peres et al., 2016; Sales et al., 2020). The extirpation of such large-bodied forest-dwelling animals from ecosystems could critically alter long-term forest dynamics and maintenance of above-ground biomass and carbon storage (Peres et al., 2016). It is estimated that Ateles spp. and Lagothrix spp. (spider and woolly monkeys, respectively) shared a common ancestor approximately 10–11 mya (Di Fiore et al., 2014). They are highly frugivorous taxa, have large home ranges that can reach up to 1,021 hectares, and are the most large-bodied genera within the Amazonian forests (Di Fiore and Campbell, 2007). Consequently, it has been suggested that a complex combination of ecological forces (e.g., regional and local variation in the degree of interspecific competition), historical biogeographical process (e.g., dispersal factors), and local hunting pressure have been shaping the current distributions of these species (Peres, 1990, 1991; Iwanaga and Ferrari, 2002; Peres et al., 2016; Rabelo et al., 2018; Cavalcante et al., 2020).
Ateles chamek has a broader distribution range that extends south, north and west of the Solimões and Japurá rivers, while L. l. cana is limited by the Guaporé River valley to an area between the Brazilian states of Mato Grosso and Rondônia (Iwanaga and Ferrari, 2002; Rabelo et al., 2018; Cavalcante et al., 2020). The geographic distribution of L. l. cana is entirely embedded within the range of A. chamek. This extensive sympatric area (1,791,200 km2) falls within the southwestern Brazilian Amazon, a region that has been called the “arc of deforestation” due to habitat loss and ongoing deforestation (Michalski et al., 2008; Trancoso, 2021). Therefore, identifying high-priority areas for conservation of these taxa across their geographic distributions can help to protect other forest-dwelling species, so reducing the rate of overall Amazonian biodiversity loss.
Our study gathered baseline information on abundance data of two Endangered Amazonian primates (Ateles chamek and Lagothrix lagotricha cana.) to create geospatial abundance models and assess abundance patterns across the entire range of each taxon. The main goals of this study were to: (i) test whether geospatial abundance models are correlated with habitat suitability derived from correlative ENMs; (ii) test whether interspecific competition between the two target taxa constrained abundance over broad spatial scales; (iii) compare the strength of the abundance-suitability relationships between original and interpolated abundances; and (iv) create ensemble models incorporating both habitat suitability and abundance to identify high-priority areas for conservation.
We hypothesized that geospatial abundance models are positively correlated with habitat suitability derived from ENMs, and that interspecific competition between our two target taxa will be an important factor in limiting their abundances across their geographic distributions. We predicted a negative correlation between A. chamek and L. l. cana abundances due to their close relatedness, comparable body sizes, specialization on ripe fruits as the principal diet component, and other similarities in their feeding ecology and ecological niche requirements (Iwanaga and Ferrari, 2001, 2002; Cavalcante et al., 2020). Finally, we expected that there would be no difference in the correlation strengths between geospatial abundance models and original abundance estimates with habitat suitability, which would support the viability of using geospatial abundance and ENMs as a surrogate to identify high-priority areas for conservation of poorly known species across their geographic distributions.
Our study area lies within the Amazon forests of Brazil, Peru and Bolivia (2°S, 55°W and 15°S, 75°W), and covers the whole geographic distribution of the two target taxa. We gathered 77 geo-referenced abundance records from the literature for the two taxa of Amazon atelins. Our abundance dataset comprises 18 different studies addressing community structure and species diversity of primates and other mammals that spanned from 1983 to 2018 across different habitat types in all three countries where both taxa occur (Figure 1 and Supplementary Table 1). To avoid bias in abundance estimation, we selected abundance data only from those studies using standard line transect surveys (see Brockelman and Ali, 1987; Peres, 1999). This standard sampling protocol documents encounter rates (sightings per 10 km surveyed), which are commonly used as indices of relative abundance for diurnal mammals (Scheel, 1993; Iwanaga and Ferrari, 2002; Gray et al., 2016). Abundance gathered from the selected studies varied from 0 (i.e., local absence) to 7.97 sightings per 10 km (mean = 0.78 ± SD 1.43), indicating that the selected studies were not biased to areas with known high primate abundance.
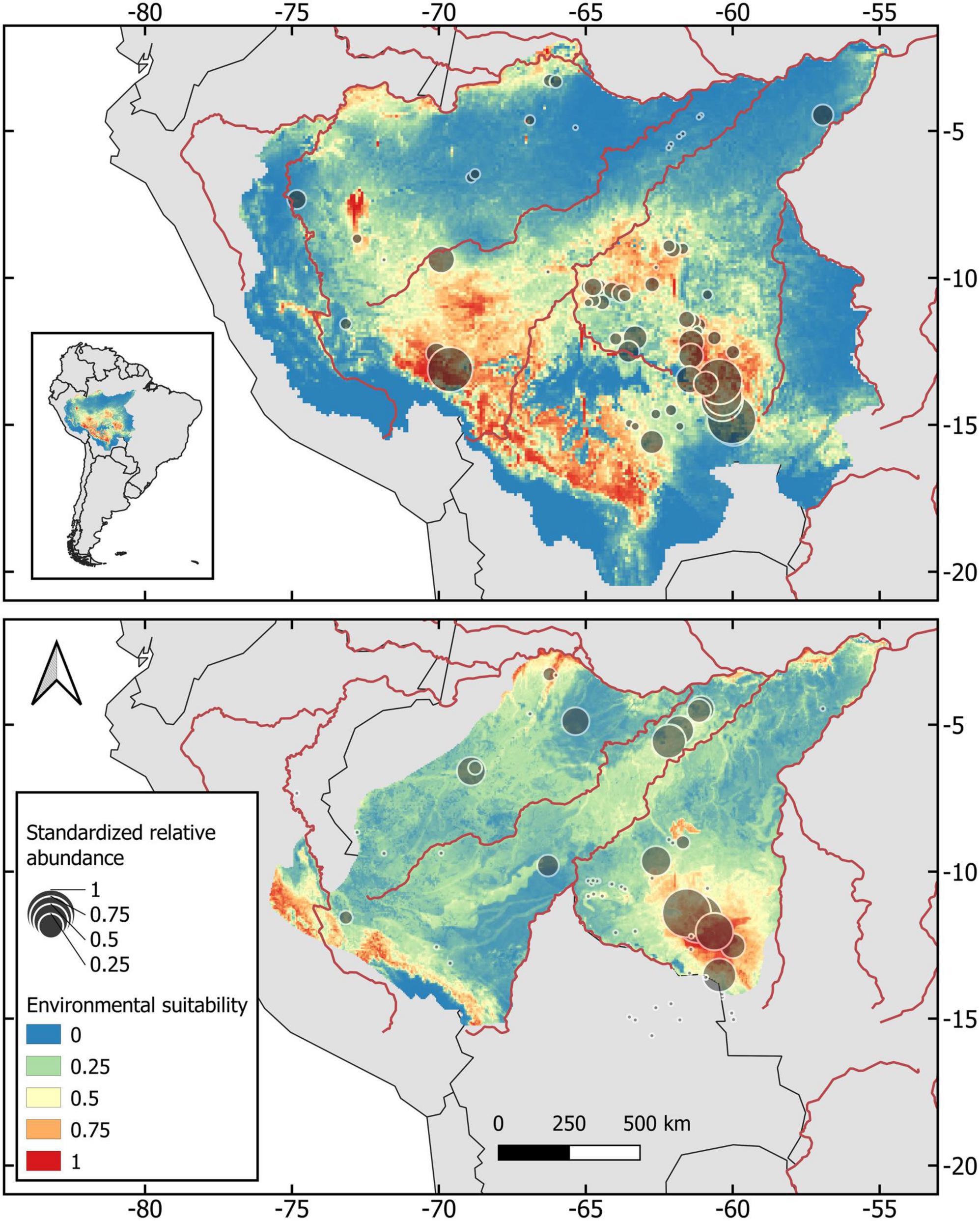
Figure 1. Habitat suitability from previously published ecological niche models (Rabelo et al., 2018; Cavalcante et al., 2020), and distribution of geo-referenced abundance records for gray woolly monkeys (Lagothrix lagotricha cana) and black-faced black spider monkeys (Ateles chamek).
Ecological niche models used in this study were previously constructed by Rabelo et al. (2018) and Cavalcante et al. (2020) using spatially explicit variables that could reasonably be expected to influence a primate species’ distribution (see Supplementary material). These variables consisted of climatic, topographic, edaphic, and vegetation layers. The estimated area of occupancy for A. chamek was 927,754 km2. Temperature seasonality, net primary productivity and potential evapotranspiration were the most important variables in the final model (Rabelo et al., 2018). Suitable habitats for the species are distributed in the Amazonas-Javary interfluvial region in Peru, and along the Lower-Jutaí and Juruá rivers in Brazil. The estimated area of occupancy for L. l. cana was 412,250 km2. The most important variables in the final model were mean annual temperature, temperature seasonality, occurrence of arenosols, and a layer of habitat suitability for A. chamek as a biotic predictor variable (Cavalcante et al., 2020). A wide area with high habitat suitability for L. l. cana is located within the southwestern Brazilian Amazonia, and also in the Amazonas-Javary interfluvial region in Peru. The two taxa show a high proportion of habitat suitability overlap (Cavalcante et al., 2020), due to similar ecological niche requirements (Iwanaga and Ferrari, 2001, 2002; Cavalcante et al., 2020).
We plotted all geo-referenced abundance records for each taxon into a GIS environment and created a polygon layer by drawing the boundaries using the previously published ENMs (Rabelo et al., 2018; Cavalcante et al., 2020). We then created a grid of 0.09° × 0.09° latitude-longitude cells to interpolate species abundance. The spatially referenced original abundance estimates data were used to interpolate the abundances across their geographic ranges, producing spatially explicit predictions of species abundance.
We created the geospatial abundance models using Inverse distance weight (IDW) and Ordinary kriging (OK). Both methods are based on the principle of spatial autocorrelation where the greater the distance, the less influence the cell has on the interpolated values, while closer cells have greater influence (Li and Heap, 2011). IDW is a simpler method which uses arbitrary exponential weighting according to distance (Watson and Philip, 1985), while OK is a more powerful and sophisticated statistical method that takes into account spatial autocorrelation of the data to assign interpolation weights based on automated variogram modeling (Pebesma et al., 2011). This later method is a reliable and highly recommended univariate method with unbiased estimates that minimize prediction errors with relatively low variances (Laslett et al., 1987; Oliver and Webster, 1990; Li and Heap, 2011). We used these two different methods because (i) they are suitable for irregularly spaced samples (Li and Heap, 2014), as in our training dataset and (ii) we intended to combine methods from different families [geostatistical (OK) and simpler non-geostatistical methodologies (IDW)] to overcome inherent biases from each individual model. Both spatial interpolation methods were implemented in ArcGIS 10.5 using the default parameter settings. Specifically, for IDW, we used a weighting power of two and for OK, we used spherical semivariogram for modeling the distance decay and infer lag, nugget and sill (Meek and Sauer, 2003; Fletcher and Fortin, 2018). More details about the OK variograms and fitted models are available in Supplementary Figure 1. Abundances predicted by the IDW and OK technique will be hereafter referred to as IDW-abundance and OK-abundance, respectively.
We tested the association between habitat suitability derived from the two previous published ENMs (Rabelo et al., 2018; Cavalcante et al., 2020) with the original relative abundance, and IDW- and OK-abundances using Pearson product-moment correlation. We aimed to determine if a significant positive relationship existed between predicted habitat suitability and predicted and original local relative abundance. Correlation methods are widely used to measure the relationship between abundance and habitat suitability derived from occurrence data (see Weber et al., 2017 for an overview). We explored other correlation coefficients that do not assume linearity (e.g., Spearman’s rs and Kendall’s tau) during data exploration but Pearson’s r provided the best fit for the correlations between abundance and suitability. We log-transformed [log(x + 1)] abundance data to match Pearson’s correlation assumptions.
We compared the ENMs to the original relative abundance data by extracting the values of predicted habitat suitability in the geo-referenced abundance points. We excluded localities with small sampling effort (i.e., <35 km of line transects surveyed, N = 11), as localities with less accurate abundance data may hide or weaken the abundance-suitability correlation (see for discussion Weber et al., 2017), especially because such possible outliers may have undesirable effects on Pearson correlation coefficient estimates (Schober et al., 2018). In case of the predicted abundances, we sampled 1,000 random points across the complete range within the extents of occurrence of both taxa to extract the values of predicted habitat suitability and predicted relative abundance for each taxon. We performed a randomization approach for spatial thinning using the “thin” function in the R package spThin (Aiello-Lammens et al., 2015) to avoid the clustering of random points in geographic space. This function returns a dataset with the maximum number of records for a given thinning distance. We used 30 km as the filter distance, following the largest control radius used in previous ENMs for the taxa of this study (Rabelo et al., 2018). The thinning process resulted in a sample of 597 random points for L. l. cana, and 751 random points for A. chamek.
We performed a set of tests of significance to compare the magnitude and strength between the correlations with the purpose of testing whether the associations differed when using original and predicted abundances. First, we compared the correlations between the original relative abundance and habitat suitability vs. the correlation between the IDW-abundance and habitat suitability. Second, we compared the same original relative abundance correlation vs. the correlation between the OK-abundance and habitat suitability. To ensure a valid and interpretable comparison, we directly contrasted the two correlations under investigation using Fisher’s z and Zou’s confidence interval (Zou, 2007) within the R package cocor, version 1.1-0 (Diedenhofen and Musch, 2015). Fisher’s z is commonly used to test the significance of the difference between two correlation coefficients, while Zou’s test considers the magnitude and precision of an estimated effect. The latter test is based on the computation of confidence intervals, which is considered to be superior to significance tests used by most of the other available approaches (Olkin and Finn, 1990; Zou, 2007; Diedenhofen and Musch, 2015). Since we expected no differences between the correlations and no a priori expectation of directionality, we used a two-tailed test of significance. Statistical difference is assigned for Fisher’s z test when P < 0.05 and Zou’s (2007) confidence intervals are considered significant different when there is no overlap with zero. A null hypothesis is retained when confidence intervals overlap zero.
To assess the role of broadscale interspecific competition, we tested if abundance variation is related to an interaction between habitat suitability and a putative interspecific competition between the two target taxa (see Braz et al., 2020; Cavalcante et al., 2020). After validating the geospatial abundance models using the tests of correlation and strength of association, we decided to use the modeled abundances to test the competition hypothesis because it was possible to make use of a large and well distributed random sample of locations within the area of sympatry of the two target taxa, providing a robust test; an approach that would not be possible using the original compiled abundance data. We used only the OK-abundances because they showed the strongest relationship with habitat suitability (see results below). For this purpose, we sampled 1,000 random points within the area of sympatry of the two target taxa. We applied the same thinning process used for the correlation tests. We extracted the values of predicted habitat suitability and predicted abundance from 607 random points to fit a generalized linear model (GLM) using the glmmTMB package (Brooks et al., 2017). To build the model, we used L. l. cana OK-abundance as the response variable, and habitat suitability and A. chamek OK-abundance extracted at the same localities as predictor variables. We decided to assess the effect of competition for only one of the two taxa because the geographic distribution of L. l. cana is entirely embedded within the range of A. chamek. Thus, the geographic distribution of L. l. cana is our main area of interest (i.e., their sympatric area).
We fitted the models with untransformed abundance data using a Tweedie error distribution with a logarithmic link function to compensate for overdispersion and to handling the zero data in our abundance models (Supplementary Figure 2; Tweedie, 1984; Dunn and Smyth, 2005). For the hypothesis testing, we compared full vs. null models using analysis of variance (ANOVA) with a chi-square test. For the full model, we used the fixed effects with an interaction term (i.e., habitat suitability*A. chamek OK-abundance). We tested the final model performance by checking residual diagnostics using the R package DHARMa (Hartig and Lohse, 2020). We used cross-sectional plots in the R package visreg (Breheny and Burchett, 2017) to visualize and identify the directionality of the interaction between habitat suitability and the abundance of the putative competitor. For this purpose, we took cross-sections at the 10, 50, and 90th percentiles of habitat suitability. Finally, given that we tested our hypothesis by comparing the full vs. null models and by testing the significance of the interaction term, we did not perform a post-hoc analysis to identify the individual effects of low, medium, and high habitat suitability.
To combine the ecological niche and geospatial abundance models, the output from each model’s predictions (i.e., habitat suitability, IDW-abundance, and OK-abundance) were united in an ensemble model, which is an effective approach to overcome any biases inherent to each individual model (Araújo and New, 2007; Anderson et al., 2017; Abrahms et al., 2019; Brodie et al., 2020). The two abundance models (IDW- and OK-abundance) were rescaled between zero and one to match the habitat suitability models. Ensemble projections were then created using the averaged index across all three models, which provides a robust consensus output of an abundance-informed ENM, where one represents greatest abundance-suitability and agreement among the models.
Finally, to identify high-priority areas for conservation of the two target taxa accounting for the broadscale interspecific competition between them, we binarized the ensemble models (L. l. cana: 0 and 1; A. chamek: 0 and 2; where 1 and 2 represent suitable-abundant areas) by setting a threshold of abundance-suitability. For this purpose, we used the threshold that has maximum sensitivity (i.e., the proportion of observed presences predicted as such) and specificity (i.e., the proportion of correctly predicted absences) in the original ENMs (Rabelo et al., 2018; Cavalcante et al., 2020), which were considered as the species’ area of occupancy (sensu IUCN: Alves et al., 2021; Cornejo et al., 2021). We then summed the binarized maps to represent how suitable-abundant areas for each taxon alone (values of 1 or 2) and coincident suitable-abundant areas (values of 3) were distributed.
Our abundance dataset based on 18 studies and 77 geo-referenced records resulted in a mean sighting rate for L. l. cana of 0.36 sightings per 10 km surveyed (SD = 0.69, range = 0–3.20). Overall, A. chamek had a higher mean sighting rate (mean = 1.19 ± SD 1.80, range = 0–7.97). The areas with higher abundances predicted by the IDW- and OK-abundance models for L. l. cana were mostly distributed in the south and northeastern Amazonia, especially in Brazil, while A. chamek had areas with higher abundances extending toward the southwestern edges of the Amazon basin (Figure 2). The IDW-abundance predicted density estimates for L. l. cana ranged from 0 to 2.99 individuals per ∼10 km2 and from 0 to 1.14 per ∼10 km2 in the OK-abundance. The mean predicted density estimated for L. l. cana by IDW were slightly smaller than OK mean estimates (mean = 0.40 ± SD 0.36 and mean = 0.42 ± SD 0.31 individuals per ∼10 km2, respectively). The IDW-abundance predicted density estimates for A. chamek ranged from 6.05 to 7.83 individuals per ∼10 km2 and from 4.54 to 4.72 per ∼10 km2 with OK-abundance. The mean predicted density estimated for A. chamek by IDW was also slightly smaller than OK mean estimates (mean = 1.24 ± SD 1.25 and mean = 1.29 ± SD 1.13 individuals per ∼10 km2, respectively).
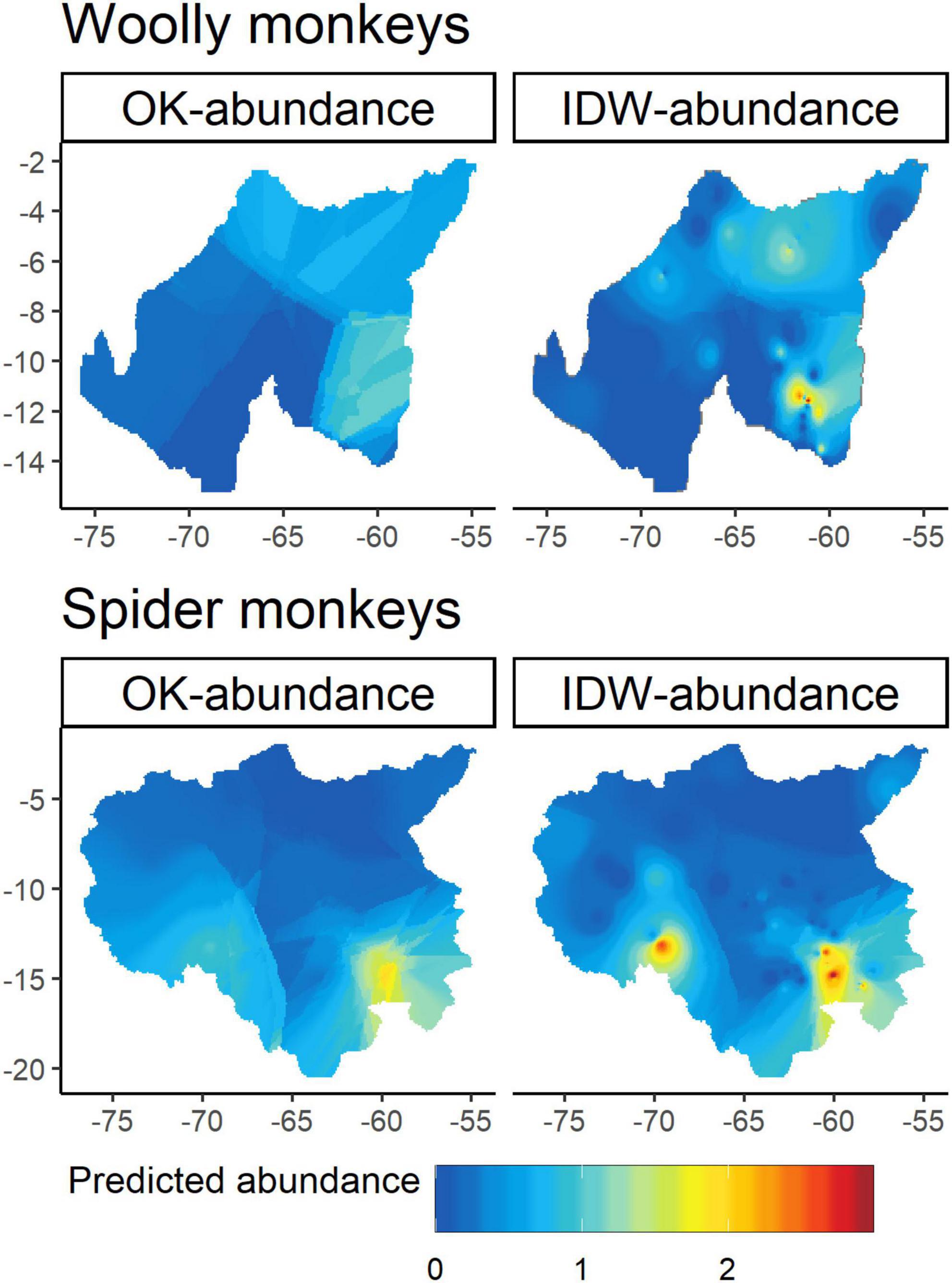
Figure 2. Predicted density estimates generated by Inverse distance weighting (IDW) and Ordinary kriging (OK) for gray woolly monkeys (Lagothrix lagotricha cana) and black-faced black spider monkeys (Ateles chamek) across their entire geographic ranges.
Regarding the abundance-suitability relationships, we found a significant positive relationship between habitat suitability and predicted and original abundances in all cases evaluated (Table 1 and Figure 3). We observed a relatively low correlation coefficient (r < 0.30) in the correlations using IDW-abundances and in the OK-abundance model for A. chamek. The strongest relationship between original relative abundance and habitat suitability was observed for L. l. cana. Between the geospatial abundance models, OK-abundances have strongest correlations with habitat suitability.

Table 1. Pearson’s correlation coefficients between habitat suitability and log-transformed abundance data for gray woolly monkeys (Lagotrhix lagotricha cana) and black-faced black spider monkeys (Ateles chamek).
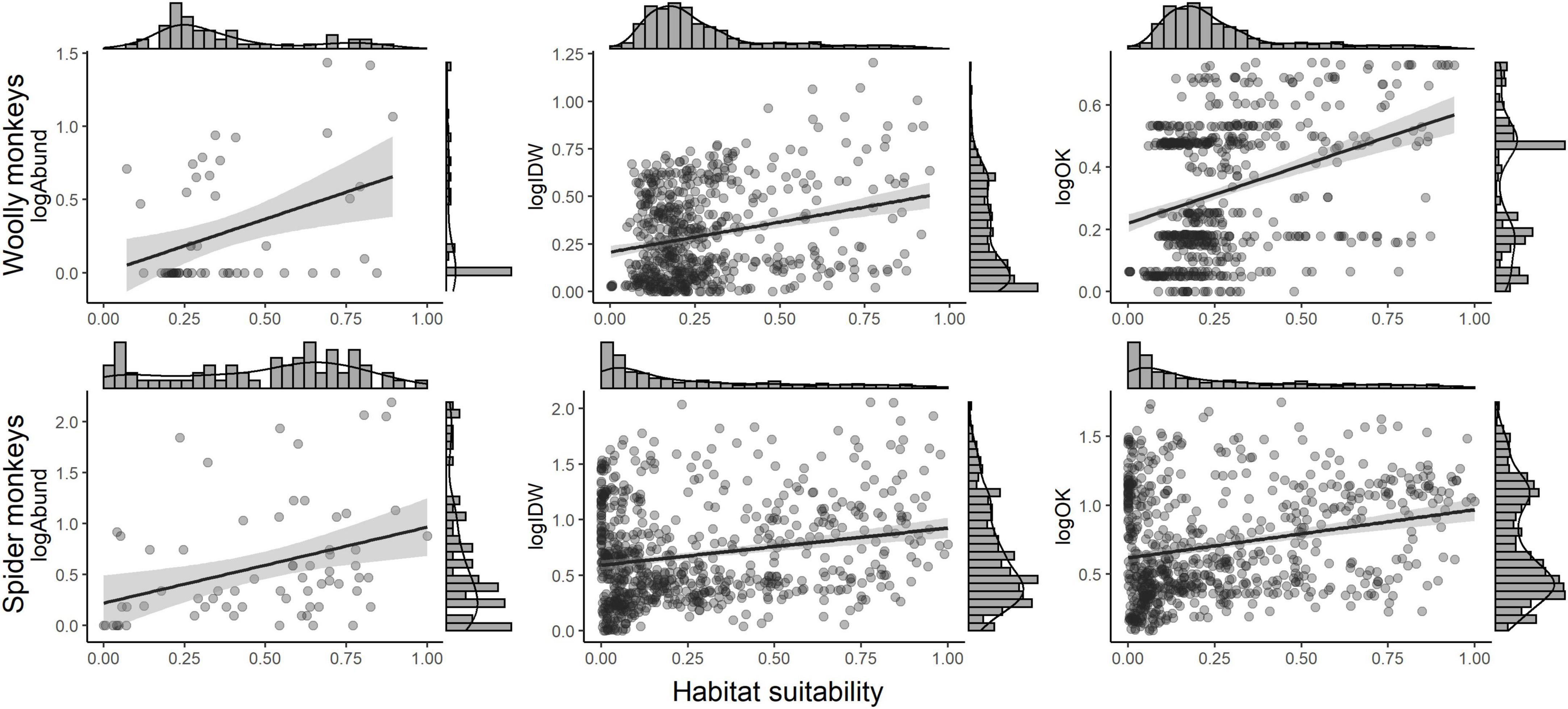
Figure 3. Relationship between habitat suitability and log-transformed observed and predicted abundances for gray woolly monkeys (Lagotrhix lagotricha cana) and black-faced black spider monkeys (Ateles chamek). Abundances were interpolated using Inverse distance weighting (IDW) and Ordinary kriging (OK).
For the differences in magnitude and significance of the relationships between the correlations, the null hypothesis was retained in all cases in the two types of tests (Fisher’s z and Zou’s test; Table 2). Therefore, we found no significant differences between the correlations of the original relative abundances and IDW- and OK-abundances. For both taxa, the abundance-informed ENMs generated more conservative values with smaller concentrated areas of greatest abundance-suitability in comparison to the original ENMs (Figure 4).
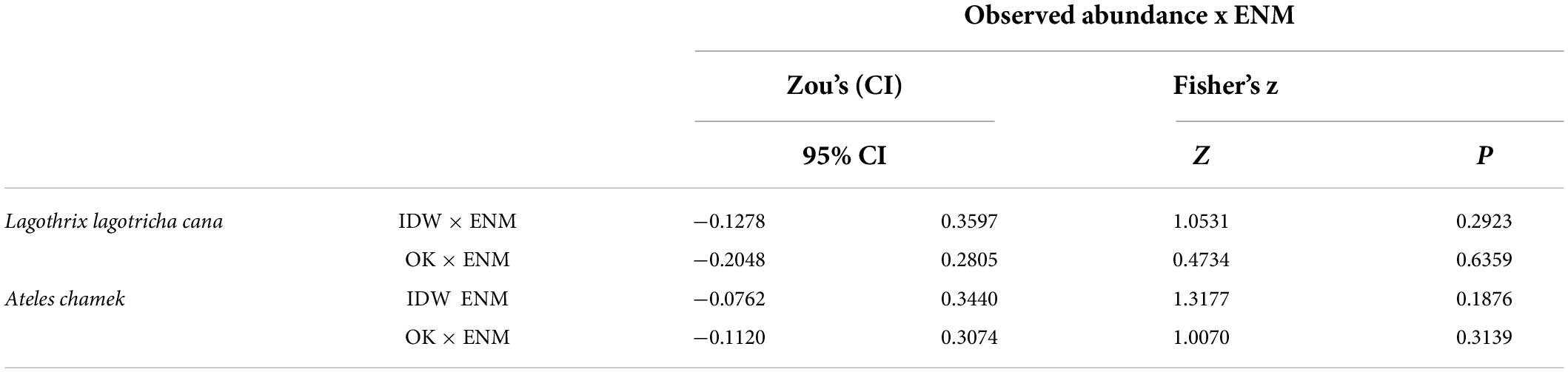
Table 2. Differences between the abundance-suitability correlations when using original relative abundances compared to using Inverse distance weighting (IDW) and Ordinary kriging (OK) for gray woolly monkeys (Lagotrhix lagotricha cana) and black-faced black spider monkeys (Ateles chamek).
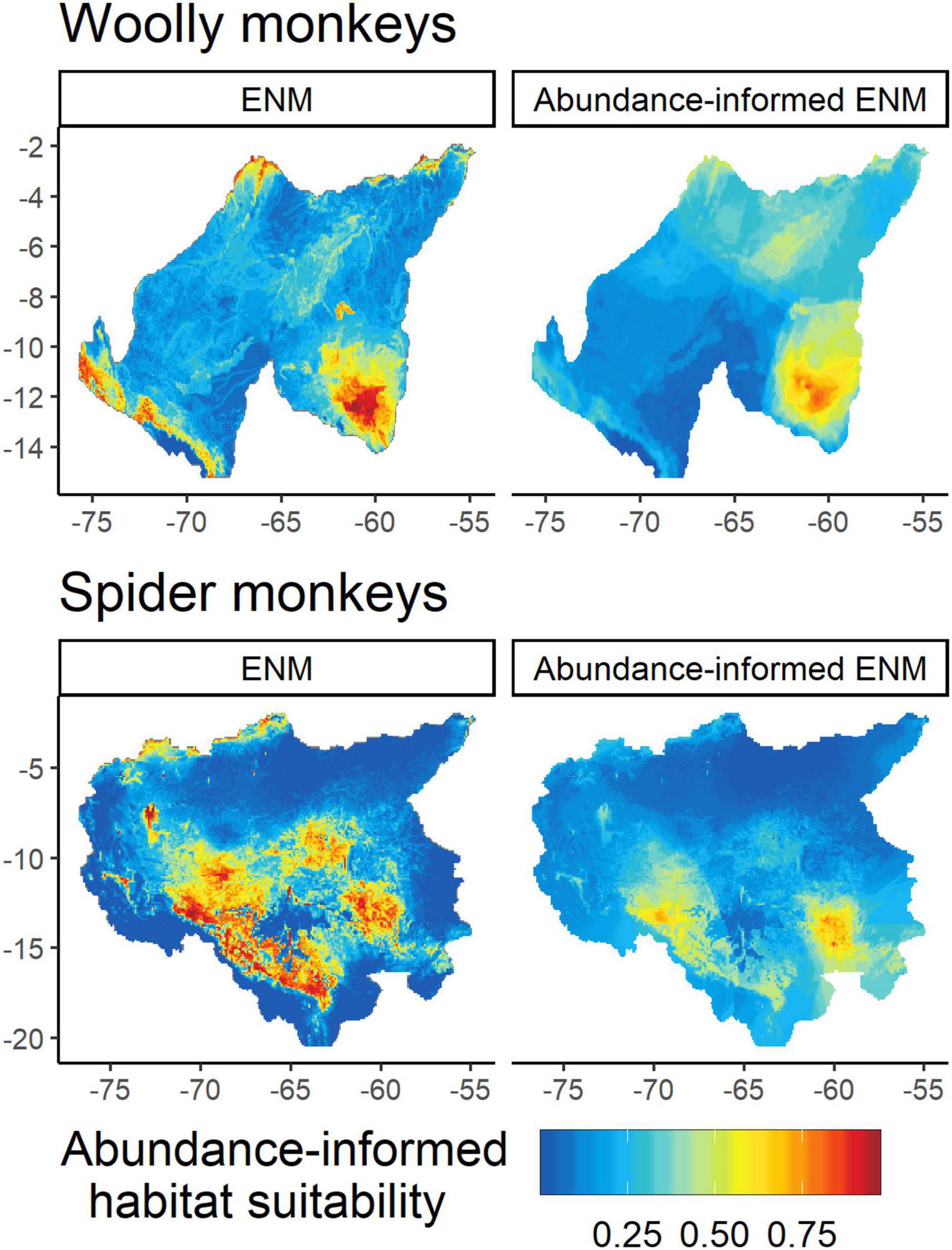
Figure 4. Ecological niche models (ENMs) and abundance-informed ENMs for gray woolly monkeys (Lagothrix lagotricha cana) and black-faced black spider monkeys (Ateles chamek). Ensemble projections were created using the averaged index across the two geospatial abundance models [Inverse distance weighting (IDW) and Ordinary kriging (OK)] and the previously published ENMs (Rabelo et al., 2018; Cavalcante et al., 2020).
We finally found that the full model (with the interaction term) predicting L. l. cana OK-abundance performed significantly better than the null model (ANOVA: χ2 = 320.45, df = 3, P < 0.005), supporting our hypothesis of broadscale interspecific competition (Figure 5). Additionally, we found a significant interaction term in the full model indicating that the association between L. l. cana abundance and habitat suitability also depends on the abundance of its putative competitor species (see Supplementary Table 2 for GLM summary statistics). Our final reclassified map also reinforces the broadscale competition hypothesis showing a pervasive pattern of spatial segregation within the area of sympatry of the two target taxa (Figure 6).
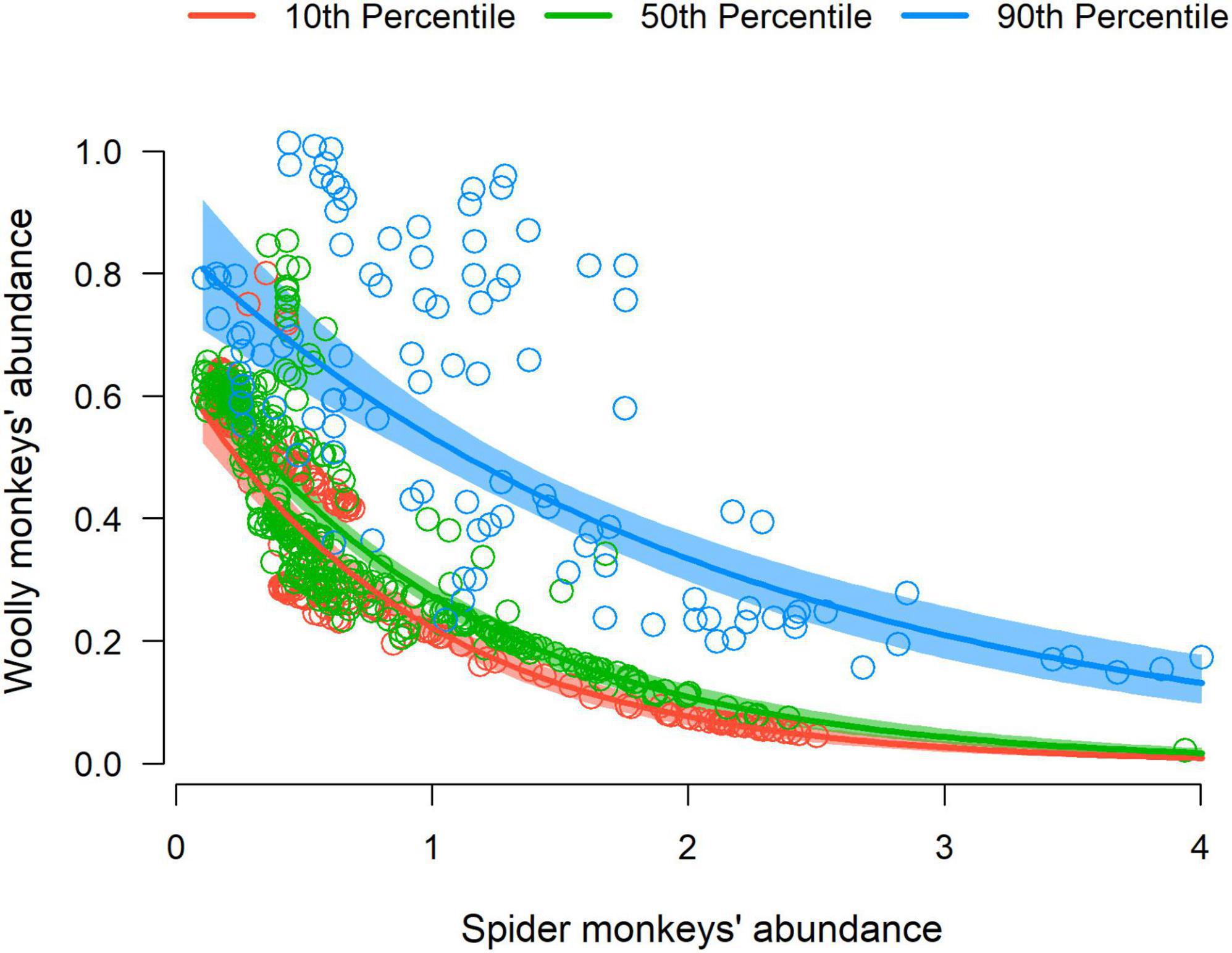
Figure 5. Relationship between modeled abundances for gray woolly monkeys (Lagothrix lagotricha cana) and black-faced black spider monkeys (Ateles chamek) in localities with low, medium, and high habitat suitability. A cross-sectional plot is shown depicting the fitted model with an interaction term between A. chamek OK-abundance and L. l. cana habitat suitability. Each point represents a random locality within the area of sympatry of the two species. The lines represent predicted means derived from the Generalized Linear Model. The overlaid red, blue, and green bands represent the 95% confidence intervals in the cross-sections at the 10, 50, and 90th percentiles of habitat suitability.
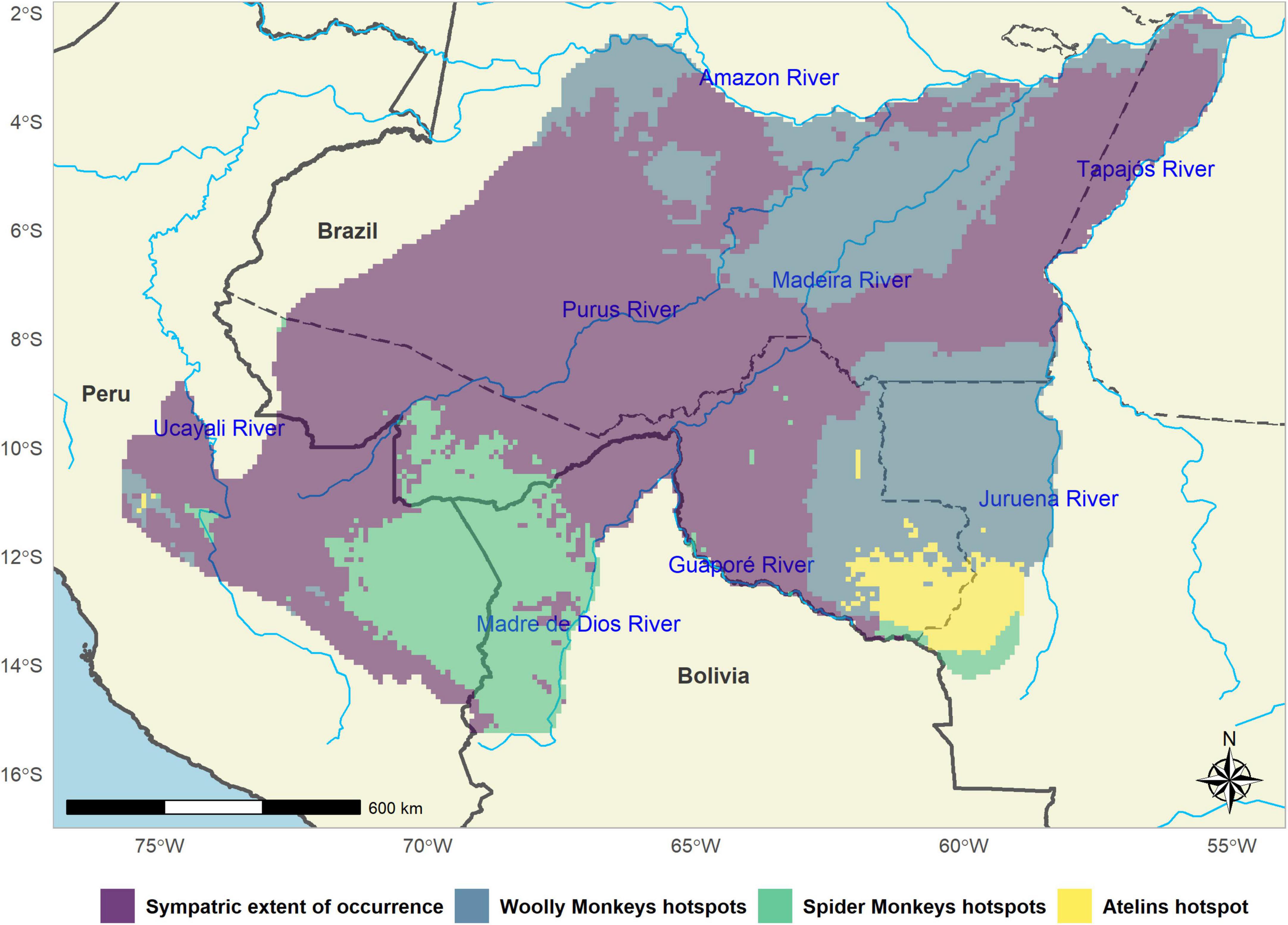
Figure 6. Hotspots for conservation of gray woolly monkeys (Lagotrhix lagotricha cana) and black-faced black spider monkeys (Ateles chamek) across their sympatric range.
This study presents an innovative approach to identify important areas for conservation taking as examples two threatened sympatric Amazonian lowland primate species. By incorporating abundance information in ENMs and, especially, accounting for the important, but often neglected, role of interspecific competition in shaping species’ geographic ranges at broader scales, our analytical framework was able to provide more realistic assessments of spatial information yielding targeted biodiversity management efforts and conservation planning at large scales.
The abundance-suitability relationship is not new to ecology and substantial efforts have been made to explore the capacity of ENMs to predict abundance patterns in the internal structure of species’ ranges (Brown et al., 1995; VanDerWal et al., 2009; Weber et al., 2017; Dallas and Hastings, 2018; de la Fuente et al., 2021; Jiménez-Valverde et al., 2021; Lee-Yaw et al., 2021). Previous studies have been corroborating a general positive trend between predicted habitat suitability from ENMs and species abundance regardless of taxonomic group and modeling methods (see Weber et al., 2017 for an overview). In our current study, we are extending these findings for abundance estimates predicted by two interpolation methods. More importantly, comparisons between abundance-suitability correlations using original and interpolated values showed no significant differences, validating the use of the two geospatial methodologies in our study case. This lack of significant differences in abundance-suitability correlations comparing original relative abundances against IDW- and OK-abundances have broad implications for conservation biology.
For instance, broadscale abundance estimates of declining species for input into ENMs are difficult to acquire, but are urgently required for conservation efforts. The geospatial models explored here, in addition to giving insightful and useful information concerning trends in abundance patterns for the two taxa, were combined with ENMs to identify high-priority areas for conservation of poorly known Amazonian species across their entire geographic range. Since recent studies are challenging the inherent capacity of ENMs to inform abundance patterns and other biological aspects of real populations (see Jiménez-Valverde et al., 2021; Lee-Yaw et al., 2021), the framework developed by this study, implicitly incorporating abundance proxies in ENMs, can be applied to a wide range of other species and with different approaches. For instance, using geospatial models as input or response variables to build ENMs and/or during modeling exercises, including setting up and interpreting results (e.g., Bahn and McGill, 2007).
Biotic interactions are important theoretical mechanisms limiting species distributions across different spatial scales, but they are frequently absent from most ENMs (Anderson et al., 2002; Guisan and Thuiller, 2005; Godsoe and Harmon, 2012). This is especially true for interspecific competition, since this type of biotic interaction is often neglected in ENMs when considering broadscale patterns (but see Braz et al., 2020; Novella-Fernandez et al., 2021 for exceptions). There is substantial evidence and previous efforts showing that interspecific competition can scale up to broad spatial scales, affecting and shaping species’ geographic ranges and abundance variation (e.g., Gotelli et al., 2010; Braz et al., 2020; Novella-Fernandez et al., 2021; Braga et al., 2022). In agreement, we found evidence for our hypothesis of broadscale interspecific competition unraveling a pervasive pattern of spatial segregation across the geographic distribution of our two target taxa.
Interspecific competition has been previously suggested to affect the local-scale patterns of coexistence between L. l. cana and A. chamek (Iwanaga and Ferrari, 2001, 2002). Also, previous studies at broader scales have identified strong similarities in the environmental niche between these taxa (Cavalcante et al., 2020). Interestingly, we found that the abundances of the two taxa are negatively related, conditional on estimated habitat suitability (Figure 5), suggesting that interspecific competition between them constrains local abundance at different strengths in low, moderate and highly suitable areas. In addition to the ecological perspective, this pattern is extremely important from a conservation standpoint since using information based only on habitat suitability could mislead efforts and affect our ability to efficiently guide resource allocation toward areas likely to be strongholds for atelins populations. For example, a previously published ENM for A. chamek (Rabelo et al., 2018) predicted that highly suitable areas would be present in the northeastern part of the species’ distribution (see Figure 4). However, the gray woolly monkey’s high density and suitability predicted by our abundance-informed ENM is liable to significantly affect spider monkey’s populations in this region. The opposite is true for gray woolly monkeys at the southwestern part of its geographic distribution. This pattern of competitive exclusion at the broadscale clearly emerged when we binarized and summed our abundance-informed ENMs, indicating a clear distinction between the eastern and western parts of the areas of sympatry for these species.
We identified priority areas for woolly and spider monkeys’ conservation in our study region as those containing highly suitable habitats with high predicted densities for each taxon. Notably, we identified an interesting high-priority area that falls within the southwestern Brazilian Amazon between the Juruena and Guaporé rivers (see Figure 6). This area holds jointly suitable habitat and high predicted densities for both taxa, in addition to some key factors and biological criteria (e.g., irreplaceability and vulnerability) that can be invoked for priority-setting purposes. First, it falls within the Rondônia center of endemism, an important component of Amazonian diversity given the high number of endemic species (Cracraft, 1985; Silva and Oren, 1996; Braga et al., 2022). Additionally, this region is located along the southern border of the Amazon rainforest in Brazil, within a region known as the arc of deforestation, where nearly half of the world’s deforestation occurs (Gascon et al., 2001; da Silva et al., 2005; Michalski et al., 2008; Silva Junior et al., 2021).
Other major threats leading to deforestation and habitat loss in this region include fire (Brando et al., 2020; Feng et al., 2021), road construction (Fearnside, 2015), mega-dam construction (Cochrane et al., 2017), and mining (Rudke et al., 2020). Our two focal taxa are part of the largest-bodied highly frugivorous clade of primates within the Amazonian forests, have large area requirements, are particularly vulnerable to habitat loss, and play major roles in ecosystem functioning (Peres, 1994; Di Fiore and Campbell, 2007; Peres et al., 2016; Rabelo et al., 2018; Cavalcante et al., 2020; Sales et al., 2020). Therefore, the identification and conservation of this high-priority area can extend protection to a large number of naturally co-occurring forest-dwelling species, reducing the rate of overall biodiversity loss and helping to stem the biodiversity crisis in the Amazonian arc of deforestation.
When comparing the interpolation techniques, we found that the resultant correlation coefficients of OK-abundances have stronger relationships with habitat suitability than IDW-abundances, which showed relatively low correlation coefficients (Table 1). Although these differences between both procedures were small, these results were expected because geostatistical methodologies (e.g., OK) are broadly considered better interpolators than simpler non-geostatistical methodologies, such as IDW (Li et al., 2011). Particularly, IDW tends to respond more strongly to discrepant values at individual data points, rather than the smoothness underlying the distance-based averaging approach in kriging methods.
Besides the interpolation techniques, the strength of the abundance-suitability relationships in our study case will also depend on distinctly factors that initially affect the ENMs and the geospatial models (e.g., the sampling distances and the density of samples in the training datasets; Li and Heap, 2008; Zarco-Perello and Simões, 2017). The sampling gaps across the taxon’s geographic distributions and a mismatch between the ENMs and geospatial models’ distribution of samples can be related to the small differences between the interpolation methods. In areas with such gaps, interpolation accuracy can significantly vary, being lower where data density is low. In this sense, our abundance predictions for the western part of the distribution of both taxa should be carefully considered and validated in situ before and alongside any conservation or management action. For these reasons we are avoiding drawing strong conclusions from our geospatial abundance models alone (e.g., estimating species populations at a geographical range scale based on spatial predictions). However, when we combined the ecological niche and geospatial abundance models using the output from each model’s predictions (i.e., habitat suitability, IDW-abundance, and OK-abundance), we are “feeding” the final models with suitability data. In other words, we are providing habitat requirements information for areas that have few or no abundance data, and these final models are the ones being used to draw the main conclusions of this study, making the case for abundance-informed ENMs as important tools for conservation purposes.
The ENMs and geospatial models exhibited similar sampling gaps across the Amazon basin. These shortfalls are intrinsically related to the lack of knowledge of species’ geographic distribution and abundance in space and time, which are often scarce and inadequate at most scales (Hortal et al., 2015). Such shortfalls notably include the highly remote regions of the Amazon basin, such as the forests of southwest Amazonia (Bush and Lovejoy, 2007; Hopkins, 2007). We expect that more sophisticated interpolation methods, which are becoming increasingly available [e.g., Euclidean distance fields in machine-learning (EDM): Behrens et al., 2018; Random forest (RF): Hengl et al., 2018], could possibly be used to partially overcome these caveats by using covariates and machine-learning methods that can improve the accuracy of the maps and the strength of the abundance-suitability relationship. Future expeditions to those remote areas are also necessary to improve geospatial models and ENMs with new field-collected abundance and occurrence records, consequently affecting the correlation coefficients of these abundance-suitability relationships.
In conclusion, the framework developed in this study can be used as a surrogate to identify high-priority areas for conservation of poorly known species across their entire geographic distributions. This procedure integrates the relationship between general trends in abundance patterns and suitability information across broader spatial scales. We confirmed a significant positive relationship between woolly (L. l. cana) and spider (A. chamek) monkeys’ habitat suitability with observed abundances and predicted abundances from geospatial abundance models. Most importantly, abundance-suitability correlations showed no significant differences when using original relative abundances against using IDW- and OK-abundances. We also found that the association between L. l. cana abundance and its habitat suitability depends on the abundance of its putative competitor species, A. chamek. Therefore, disregarding interspecific competition between our two focus taxa could affect our ability to accurately and efficiently guide resource allocation toward priority areas for conservation actions for these two large arboreal mammals that inhabit the Amazonian arc of deforestation. Finally, fundamental spatial dependence and autocorrelation concepts and principles, which lies at the heart of spatial interpolation, are pervasive in natural ecosystems and biological aspects of real populations (Koenig, 1999; Dormann, 2007). This can be seen by the widespread use of interpolation methods in several environmental disciplines (Li and Heap, 2011, 2014). We argue that the use of interpolation methods should be extended for spatial conservation prioritization since its use has been considerably scarce in conservation biology, especially for Amazonian data-deficient species, such as the two we have studied.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethical review and approval was not required for the animal study because the study is based on data gathered from the literature.
TC conceived the core ideas with important insights from MMW, gathered all data, and led the wrote of the manuscript. TC and MMW developed the overall research framework, designed the methodology, and performed all statistical analyses. All authors significantly contributed with interpretation, writing, and gave final approval for submission.
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES), Finance Code 001. TC thanks PROEX and POSGRAD 2020—Biologia (Ecologia) Edital: Resolução N. 006/2020 for the financial support for publication of this article.
We thank Simone Iwanaga for providing detailed abundance information from her previous study and Rafael M. Rabelo for providing the raster of habitat suitability for Ateles chamek. MMW thanks the Financiadora de Estudos e Projetos (FINEP) for financial support (MCT/FINEP/CT-INFRA—CAMPI REGIONAIS—01/2010). We are also thankful to Miguel Alfonso Ortega-Huerta and Eric Jason Pedersen for their valuable comments and suggestions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.915325/full#supplementary-material
Abrahms, B., Welch, H., Brodie, S., Jacox, M. G., Becker, E. A., Bograd, S. J., et al. (2019). Dynamic ensemble models to predict distributions and anthropogenic risk exposure for highly mobile species. Div. Distrib. 25, 1182–1193. doi: 10.1111/ddi.12940
Aiello-Lammens, M. E., Boria, R. A., Radosavljevic, A., Vilela, B., and Anderson, R. P. (2015). spThin: an R package for spatial thinning of species occurrence records for use in ecological niche models. Ecography 38, 541–545. doi: 10.1111/ecog.01132
Alves, S. L., Ravetta, A. L., Paim, F. P., Mittermeier, R. A., Rabelo, R. M., Wallace, R. B., et al. (2021). Ateles chamek (amended version of 2020 assessment) The IUCN Red List of Threatened Species 2021: e.T41547A191685783. Available online at: https://dx.doi.org/10.2305/IUCN.UK.2021-1.RLTS.T41547A191685783.en (Acessed on 09 May 2021).
Anderson, R. P., Peterson, A. T., and Gómez-Laverde, M. (2002). Using niche-based GIS modeling to test geographic predictions of competitive exclusion and competitive release in South American pocket mice. Oikos 98, 3–16.
Anderson, S. C., Cooper, A. B., Jensen, O. P., Minto, C., Thorson, J. T., Walsh, J. C., et al. (2017). Improving estimates of population status and trend with superensemble models. Fish Fisher. 18, 732–741. doi: 10.1111/faf.12200
Araújo, M. B., and New, M. (2007). Ensemble forecasting of species distributions. Trends Ecol. Evolut. 22, 42–47. doi: 10.1016/j.tree.2006.09.010
Bahn, V., and McGill, B. J. (2007). Can niche-based distribution models outperform spatial interpolation? Glob. Ecol. Biogeogr. 16, 733–742. doi: 10.1111/j.1466-8238.2007.00331.x
Behrens, T., Schmidt, K., Viscarra Rossel, R. A., Gries, P., Scholten, T., and MacMillan, R. A. (2018). Spatial modelling with Euclidean distance fields and machine learning. Europ. J. Soil Sci. 69, 757–770. doi: 10.1038/s41598-020-73773-y
Braga, P. L., Borges, S. H., Peres, C. A., Loiselle, B. A., Blake, J. G., Menger, J., et al. (2022). Connecting Amazonian historical biogeography and local assemblages of understorey birds: recurrent guild proportionality within areas of endemism. J. Biogeogr. 49, 324–338. doi: 10.1111/jbi.14301
Brando, P., Soares-Filho, B., Rodrigues, L., Assunção, A., Morton, D., Tuchschneider, D., et al. (2020). The gathering firestorm in southern Amazonia. Sci. Adv. 6:eaay1632. doi: 10.1126/sciadv.aay1632
Braz, A. G., Grelle, C. E. D. V., Figueiredo, M. D. S. L., and Weber, M. M. (2020). Interspecific competition constrains local abundance in highly suitable areas. Ecography 43, 1560–1570. doi: 10.1111/ecog.04898
Breheny, P., and Burchett, W. (2017). Visualization of regression models using visreg. R J. 9, 56–71. doi: 10.32614/RJ-2017-046
Brockelman, W., and Ali, R. (1987). “Methods of surveying and sampling forest primate populations,” in Primate Conservation in the Tropical Forest, eds C. W. Marsh and R. A. Mittermeier (New York: AR Liss), 23–62.
Brodie, S. J., Thorson, J. T., Carroll, G., Hazen, E. L., Bograd, S., Haltuch, M. A., et al. (2020). Trade-offs in covariate selection for species distribution models: a methodological comparison. Ecography 43, 11–24. doi: 10.1111/ecog.04707
Brooks, M. E., Kristensen, K., Van Benthem, K. J., Magnusson, A., Berg, C. W., Nielsen, A., et al. (2017). glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. R J. 9, 378–400. doi: 10.32614/RJ-2017-066
Brown, J. H., Mehlman, D. W., and Stevens, G. C. (1995). Spatial variation in abundance. Ecology 76, 2028–2043. doi: 10.2307/1941678
Bush, M. B., and Lovejoy, T. E. (2007). Amazonian conservation: pushing the limits of biogeographical knowledge. J. Biogeogr. 34, 1291–1293. doi: 10.1111/j.1365-2699.2007.01758.x
Cavalcante, T., Jesus, A. S., Rabelo, R. M., Messias, M. R., Valsecchi, J., Ferraz, D., et al. (2020). Niche overlap between two sympatric frugivorous Neotropical primates: improving ecological niche models using closely-related taxa. Biodiv. Conserv. 29, 2749–2763. doi: 10.1007/s10531-020-01997-5
Cochrane, S. M., Matricardi, E. A., Numata, I., and Lefebvre, P. A. (2017). Landsat-based analysis of mega dam flooding impacts in the Amazon compared to associated environmental impact assessments: upper Madeira River example 2006–2015. Remote Sens. Appl. 7, 1–8. doi: 10.1016/j.rsase.2017.04.005
Cornejo, F. M., Stevenson, P. R., Wallace, R. B., Ravetta, A. L., Valença-Montenegro, M. M., Rylands, A. B., et al. (2021). Lagothrix lagothricha ssp cana (amended version of 2020 assessment). The IUCN Red List of Threatened Species 2021: e.T39962A192308612. Available online at: https://dx.doi.org/10.2305/IUCN.UK.2021-1.RLTS.T39962A192308612.en (Acessed on 09 May 2021).
Cracraft, J. (1985). Historical biogeography and patterns of differentiation within the South American avifauna: areas of endemism. Ornithol. Monogr. 36, 49–84. doi: 10.2307/40168278
da Silva, J. M. C., Rylands, A. B., and da Fonseca, G. A. (2005). The fate of the Amazonian areas of endemism. Conservat. Biol. 19, 689–694. doi: 10.1017/s0031182000064751
Dallas, T. A., and Hastings, A. (2018). Habitat suitability estimated by niche models is largely unrelated to species abundance. Glob. Ecol. Biogeogr. 27, 1448–1456. doi: 10.1111/geb.12820
de la Fuente, A., Hirsch, B. T., Cernusak, L. A., and Williams, S. E. (2021). Predicting species abundance by implementing the ecological niche theory. Ecography 44, 1723–1730. doi: 10.1111/ecog.05776
Di Fiore, A., and Campbell, C. J. (2007). “The Atelines: variation in ecology, behavior and social organization,” in Primates in Perspective, eds C. J. Campbell, A. Fuentes, K. C. MacKinnon, M. Panger, and S. K. Bearder (New York: Oxford University Press), 155–185.
Di Fiore, A., Chaves, P. B., Cornejo, F. M., Schmitt, C. A., Shanee, S., Cortes-Ortiz, L., et al. (2014). The rise and fall of a genus: complete mtDNA genomes shed light on the phylogenetic position of yellow-tailed woolly monkeys, Lagothrix flavicauda, and on the evolutionary history of the family Atelidae (Primates: Platyrrhini). Mole. Phylogenet. Evol. 82, 495–510. doi: 10.1016/j.ympev.2014.03.028
Diedenhofen, B., and Musch, J. (2015). cocor: a comprehensive solution for the statistical comparison of correlations. PLoS One 10, e0121945. doi: 10.1371/journal.pone.0121945
Dormann, C. F. (2007). Effects of incorporating spatial autocorrelation into the analysis of species distribution data. Glob. Ecol. Biogeogr. 16, 129–138. doi: 10.1111/j.1466-8238.2006.00279.x
Dunn, P. K., and Smyth, G. K. (2005). Series evaluation of Tweedie exponential dispersion model densities. Statist. Comput. 15, 267–280. doi: 10.1007/s11222-005-4070-y
Fearnside, P. M. (2015). “Highway construction as a force in destruction of the Amazon forest,” in Handbook of Road Ecology, eds R. V. D. Ree, D. J. Smith, and C. Grilo (Chichester: Wiley), 414–424. doi: 10.1002/9781118568170.ch51
Feng, X., Merow, C., Liu, Z., Park, D. S., Roehrdanz, P. R., Maitner, B., et al. (2021). How deregulation, drought and increasing fire impact Amazonian biodiversity. Nature 597, 516–521. doi: 10.1038/s41586-021-03876-7
Fletcher, R., and Fortin, M.-J. (2018). “Spatial dependence and autocorrelation,” in Spatial Ecology and Conservation Modeling, eds R. Fletcher and M.-J. Fortin (Cham, Switzerland: Springer), 133–168. doi: 10.1007/978-3-030-01989-1_5
Gascon, C., Bierregaard, R. O. Jr., Laurance, W. F., and Rankin-de-Merona, J. (2001). “Deforestation and forest fragmentation in the Amazon,” in Lessons from Amazonia: the ecology and conservation of a fragmented forest, eds R. O. Bierregaard, Jr. C. Gascon, T. E. Lovejoy, and R. Mesquita (New Haven, Connecticut: Yale University Press), 22–30.
Godsoe, W., and Harmon, L. J. (2012). How do species interactions affect species distribution models? Ecography 35, 811–820. doi: 10.1111/j.1600-0587.2011.07103.x
Gotelli, N. J., Graves, G. R., and Rahbek, C. (2010). Macroecological signals of species interactions in the Danish avifauna. Proc. Natl. Acad. Sci. U.S.A. 107, 5030–5035. doi: 10.1073/pnas.0914089107
Gray, T. N., Prum, S., and Phan, C. (2016). “Density and activity patterns of the globally significant large herbivore populations of Cambodia’s Eastern Plains landscape,” in The Ecology of Large Herbivores in South and Southeast Asia, eds F. Ahrestani and M. Sankaran (Dordrecht: Springer), 207–222. doi: 10.1007/978-94-017-7570-0_9
Guisan, A., and Thuiller, W. (2005). Predicting species distribution: offering more than simple habitat models. Ecol. Lett. 8, 993–1009. doi: 10.1111/j.1461-0248.2005.00792.x
Hartig, F., and Lohse, L. (2020). Residual diagnostics for hierarchical (multilevel/mixed) regression models. R packahe version 0.3.3.0. Available online at: http://florianhartig.github.io/DHARMa/
Hengl, T., Nussbaum, M., Wright, M. N., Heuvelink, G. B., and Gräler, B. (2018). Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 6:e5518. doi: 10.7717/peerj.5518
Hopkins, M. J. (2007). Modelling the known and unknown plant biodiversity of the Amazon Basin. J. Biogeogr. 34, 1400–1411. doi: 10.1111/j.1365-2699.2007.01737.x
Hortal, J., de Bello, F., Diniz-Filho, J. A. F., Lewinsohn, T. M., Lobo, J. M., and Ladle, R. J. (2015). Seven shortfalls that beset large-scale knowledge of biodiversity. Annu. Rev. Ecol. Evolut. Systemat. 46, 523–549. doi: 10.1146/annurev-ecolsys-112414-054400
Iwanaga, S., and Ferrari, S. F. (2001). Party size and diet of syntopic atelids (Ateles chamek and Lagothrix cana) in southwestern Brazilian Amazonia. Folia Primatol. 72, 217–227. doi: 10.1159/000049941
Iwanaga, S., and Ferrari, S. F. (2002). Geographic distribution and abundance of woolly (Lagothrix cana) and spider (Ateles chamek) monkeys in southwestern Brazilian Amazonia. Am. J. Primatol. 56, 57–64. doi: 10.1002/ajp.1063
Jiménez-Valverde, A., Aragón, P., and Lobo, J. M. (2021). Deconstructing the abundance-suitability relationship in species distribution modelling. Glob. Ecol. Biogeogr. 30, 327–338. doi: 10.1111/geb.13204
Koenig, W. D. (1999). Spatial autocorrelation of ecological phenomena. Trends Ecol. Evolut. 14, 22–26. doi: 10.1016/S0169-5347(98)01533-X
Laslett, G., McBratney, A., Pahl, P. J., and Hutchinson, M. (1987). Comparison of several spatial prediction methods for soil pH. J. Soil Sci. 38, 325–341. doi: 10.1111/j.1365-2389.1987.tb02148.x
Lee-Yaw, J. A., McCune, J. L., Pironon, S., and Sheth, S. N. (2021). Species distribution models rarely predict the biology of real populations. Ecography e05877. doi: 10.1111/ecog.05877
Li, J., and Heap, A. D. (2008). A review of spatial interpolation methods for environmental scientists. Geosci. Austral. 6, 228–241. doi: 10.1016/j.ecoinf.2010.12.003
Li, J., and Heap, A. D. (2011). A review of comparative studies of spatial interpolation methods in environmental sciences: performance and impact factors. Ecol. Inform. 6, 228–241. doi: 10.1186/s12889-019-6565-z
Li, J., Heap, A. D., Potter, A., Huang, Z., and Daniell, J. J. (2011). Can we improve the spatial predictions of seabed sediments? A case study of spatial interpolation of mud content across the southwest Australian margin. Continent. Shelf Res. 31, 1365–1376. doi: 10.1016/j.csr.2011.05.015
Li, J., and Heap, A. D. (2014). Spatial interpolation methods applied in the environmental sciences: a review. Environ. Model. Softw. 53, 173–189. doi: 10.1016/j.envsoft.2013.12.008
Meek, D., and Sauer, T. (2003). “Suggestions for presenting kriging results,” in Conference on Applied Statistics in Agriculture, (Calcutta: Indian Statistical Institute). doi: 10.4148/2475-7772.1191
Michalski, F., Peres, C. A., and Lake, I. R. (2008). Deforestation dynamics in a fragmented region of southern Amazonia: evaluation and future scenarios. Environ. Conserv. 35, 93–103. doi: 10.1017/S0376892908004864
Novella-Fernandez, R., Juste, J., Ibáñez, C., Rebelo, H., Russo, D., Alberdi, A., et al. (2021). Broad-scale patterns of geographic avoidance between species emerge in the absence of fine-scale mechanisms of coexistence. Div. Distribut. 27, 1606–1618. doi: 10.1111/ddi.13375
Oliver, M. A., and Webster, R. (1990). Kriging: a method of interpolation for geographical information systems. Int. J. Geograph. Inform. System 4, 313–332. doi: 10.1080/02693799008941549
Olkin, I., and Finn, J. D. (1990). Testing correlated correlations. Psychol. Bull. 108, 330–333. doi: 10.1037/0033-2909.108.2.330
Pebesma, E., Cornford, D., Dubois, G., Heuvelink, G. B., Hristopulos, D., Pilz, J., et al. (2011). INTAMAP: the design and implementation of an interoperable automated interpolation web service. Comput. Geosci. 37, 343–352. doi: 10.1016/j.cageo.2010.03.019
Peres, C. A. (1990). Effects of hunting on western Amazonian primate communities. Biol. Conserv. 54, 47–59. doi: 10.1016/0006-3207(90)90041-M
Peres, C. A. (1991). Humboldt’s woolly monkeys decimated by hunting in Amazonia. Oryx 25, 89–95. doi: 10.1017/S0030605300035122
Peres, C. A. (1994). Which are the largest New World monkeys? J. Hum. Evolut. 26, 245–249. doi: 10.1006/jhev.1994.1014
Peres, C. A. (1999). General guidelines for standardizing line-transect surveys of tropical forest primates. Neotrop. Primates 7, 11–16.
Peres, C. A., Emilio, T., Schietti, J., Desmoulière, S. J. M., and Levi, T. (2016). Dispersal limitation induces long-term biomass collapse in overhunted Amazonian forests. Proc. Natl. Acad. Sci. U.S.A. 113, 892–897. doi: 10.1073/pnas.1516525113
Phillips, S. J., Anderson, R. P., and Schapire, R. E. (2006). Maximum entropy modeling of species geographic distributions. Ecol. Model. 190, 231–259. doi: 10.1016/j.ecolmodel.2005.03.026
Rabelo, R. M., Goncalves, J. R., Silva, F. E., Rocha, D. G., Canale, G. R., Bernardo, C. S. S., et al. (2018). Predicted distribution and habitat loss for the Endangered black-faced black spider monkey (Ateles chamek) in the Amazon. Oryx 54, 699–705. doi: 10.1017/S0030605318000522
Relethford, J. H. (2008). Geostatistics and spatial analysis in biological anthropology. Am. J. Phys. Anthropol. 136, 1–10. doi: 10.1002/ajpa.20789
Robinson, T., and Metternicht, G. (2006). Testing the performance of spatial interpolation techniques for mapping soil properties. Comput. Electr. Agricult. 50, 97–108. doi: 10.13287/j.1001-9332.202202.013
Rudke, A. P., de Souza, V. A. S., Dos Santos, A. M., Xavier, A. C. F., Rotunno Filho, O. C., and Martins, J. A. (2020). Impact of mining activities on areas of environmental protection in the southwest of the Amazon: a GIS- and remote sensing-based assessment. J. Environ. Manag. 263:110392. doi: 10.1016/j.jenvman.2020.110392
Sales, L. P., Culot, L., and Pires, M. M. (2020). Climate niche mismatch and the collapse of primate seed dispersal services in the Amazon. Biol. Conserv. 247:108628. doi: 10.1016/j.biocon.2020.108628
Scheel, D. (1993). Profitability, encounter rates, and prey choice of African lions. Behav. Ecol. 4, 90–97. doi: 10.1093/beheco/4.1.90
Schober, P., Boer, C., and Schwarte, L. A. (2018). Correlation coefficients: appropriate use and interpretation. Anesthes. Analgesia 126, 1763–1768. doi: 10.1213/ANE.0000000000002864
Sillero, N., Arenas-Castro, S., Enriquez-Urzelai, U., Vale, C. G., Sousa-Guedes, D., Martínez-Freiría, F., et al. (2021). Want to model a species niche? A step-by-step guideline on correlative ecological niche modelling. Ecol. Model. 456:109671. doi: 10.1016/j.ecolmodel.2021.109671
Silva, J. M. C. D., and Oren, D. C. (1996). Application of parsimony analysis of endemicity in Amazonian biogeography: an example with primates. Biol. J. Linnean Soc. 59, 427–437. doi: 10.1111/j.1095-8312.1996.tb01475.x
Silva Junior, C. H., Pessoa, A., Carvalho, N. S., Reis, J. B., Anderson, L. O., and Aragao, L. E. (2021). The Brazilian Amazon deforestation rate in 2020 is the greatest of the decade. Nat. Ecol. Evol. 5, 144–145. doi: 10.1038/s41559-020-01368-x
Tan, J., Xie, X., Zuo, J., Xing, X., Liu, B., Xia, Q., et al. (2021). Coupling random forest and inverse distance weighting to generate climate surfaces of precipitation and temperature with multiple-covariates. J. Hydrol. 598:126270. doi: 10.1016/j.jhydrol.2021.126270
Tobler, W. R. (1970). A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 46, 234–240. doi: 10.2307/143141
Trancoso, R. (2021). Changing Amazon deforestation patterns: urgent need to restore command and control policies and market interventions. Environ. Res. Lett. 16:041004. doi: 10.1088/1748-9326/abee4c
Tweedie, M. C. (1984). “An index which distinguishes between some important exponential families,” in Statistics: Applications and New Directions: Proc. Indian Statistical Institute Golden Jubilee Int. Conf, eds J. K. Ghosh and J. Roy (Calcutta: Indian Statistical Institute), 579–604. doi: 10.1016/j.pnpbp.2013.04.014
Valavi, R., Elith, J., Lahoz-Monfort, J. J., and Guillera-Arroita, G. (2021). Modelling species presence-only data with random forests. Ecography 44, 1731–1742. doi: 10.1111/ecog.05615
VanDerWal, J., Shoo, L. P., Johnson, C. N., and Williams, S. E. (2009). Abundance and the environmental niche: environmental suitability estimated from niche models predicts the upper limit of local abundance. Am. Natural. 174, 282–291. doi: 10.1086/600087
Walker, B. K., Larson, E. A., Moulding, A. L., and Gilliam, D. S. (2012). Small-scale mapping of indeterminate arborescent acroporid coral (Acropora cervicornis) patches. Coral Reefs 31, 885–894. doi: 10.1007/s00338-012-0910-3
Wallace, C. S. A., Watts, J. M., and Yool, S. R. (2000). Characterizing the spatial structure of vegetation communities in the Mojave Desert using geostatistical techniques. Comput. Geosci. 26, 397–410. doi: 10.1016/S0098-3004(99)00120-X
Wallerman, J., Joyce, S., Vencatasawmy, C. P., and Olsson, H. (2002). Prediction of forest stem volume using kriging adapted to detected edges. Can. J. For. Res. 32, 509–518. doi: 10.1139/x01-214
Watson, D. F., and Philip, G. (1985). A refinement of inverse distance weighted interpolation. Geo Proc. 2, 315–327.
Weber, M. M., Stevens, R. D., Diniz-Filho, J. A. F., and Grelle, C. E. V. (2017). Is there a correlation between abundance and environmental suitability derived from ecological niche modelling? a meta-analysis. Ecography 40, 817–828. doi: 10.1111/ecog.02125
Zarco-Perello, S., and Simões, N. (2017). Ordinary kriging vs inverse distance weighting: spatial interpolation of the sessile community of Madagascar reef, Gulf of Mexico. PeerJ 5:e4078. doi: 10.7717/peerj.4078
Zhou, Y., Liu, H., Leng, P., Zhu, J., Yao, S., Zhu, Y., et al. (2021). Analysis of the spatial distribution of Aedes albopictus in an urban area of Shanghai, China. Parasit. Vect. 14, 1–11. doi: 10.1186/s13071-021-05022-8
Zou, G. Y. (2007). Toward using confidence intervals to compare correlations. Psychol. Methods 12, 399–413. doi: 10.1037/1082-989X.12.4.399
Zuquim, G., Stropp, J., Moulatlet, G. M., Van Doninck, J., Quesada, C. A., Figueiredo, F. O., et al. (2019). Making the most of scarce data: mapping soil gradients in data-poor areas using species occurrence records. Methods Ecol. Evolut. 10, 788–801. doi: 10.1111/2041-210X.13178
Keywords: abundance, Ateles chamek, biotic interactions, conservation prioritization, habitat suitability, Lagothrix lagotricha cana, spatial interpolation
Citation: Cavalcante T, Weber MM and Barnett AA (2022) Combining geospatial abundance and ecological niche models to identify high-priority areas for conservation: The neglected role of broadscale interspecific competition. Front. Ecol. Evol. 10:915325. doi: 10.3389/fevo.2022.915325
Received: 07 April 2022; Accepted: 08 August 2022;
Published: 24 August 2022.
Edited by:
Frederico Mestre, University of Évora, PortugalReviewed by:
Miguel Alfonso Ortega-Huerta, National Autonomous University of Mexico, MexicoCopyright © 2022 Cavalcante, Weber and Barnett. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thiago Cavalcante, dGhpYWdvY2F2LmZlcnJlaXJhQGdtYWlsLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.