Microscopic Insights Into the Formation of Methanesulfonic Acid–Methylamine–Ammonia Particles Under Acid-Rich Conditions

Introduction

Atmospheric aerosol particles are tiny liquid and/or solid particles suspended in the air, and exist in a wide range of chemical composition and size distribution (Putaud et al., 2010). Aerosol particles can directly influence global climate by scattering and absorbing solar radiation, or indirectly by acting as cloud condensation nuclei (CCN) and ice nuclei (IN) (Merikanto et al., 2009; Myhre et al., 2013; von Schneidemesser et al., 2015; Dunne et al., 2016). They can affect atmospheric chemical processes as a heterogeneous reaction interface to change the trace component of greenhouse gases (Makkonen et al., 2012), as well as impact visibility and human health (Yu et al., 2008). Therefore, the formation of atmospheric aerosols has been attracting topic over decades around the globe (Charlson et al., 1992; Steinfeld, 1998; Kulmala, 2003; Kittelson et al., 2004; Saxon and Diaz-Sanchez, 2005; Pope and Dockery, 2006; Lelieveld et al., 2015). New particle formation (NPF), a gas-to-particle conversion process (Zhang et al., 2012; Riccobono et al., 2014), is considered to be a dominant source of atmospheric aerosol particles (Spracklen et al., 2006; Zhang et al., 2012) and has been extensively studied both experimentally and theoretically (Berndt et al., 2013; Knopf et al., 2018). Atmospheric NPF process begins as a result of collisions and favorable interactions (such as hydrogen bonding or proton transfer reactions) between gaseous vapors (Lehtinen and Kulmala, 2003; Wang et al., 2010; Zhang, 2010; Zhang et al., 2012; Kulmala et al., 2013). These newly formed stable clusters usually possess complex structures (Kulmala et al., 2014; Elm et al., 2020), multiple interactions (Sebastianelli et al., 2018), different component ratios (Chen et al., 2018; Perraud et al., 2020a), and undetectable sizes (Stolzenburg and McMurry, 1991; McMurry, 2000), which make challenging to understand the molecular-level NPF mechanisms. Therefore, we tackle these challenges here by exploring the structures, properties, chemical compositions, and stabilities of these small clusters from a microscopic perspective.

Sulfuric acid (H₂SO₄, SA) is known to be the most important driver of NPF in the atmosphere (Sipila et al., 2010; Kirkby et al., 2011; Kulmala et al., 2013), and its contribution to NPF is the most studied (Weber et al., 1995; Chan and Mozurkewich, 2001; Kuang et al., 2008; Sipila et al., 2010; Kirkby et al., 2011; Bzdek et al., 2012; Zollner et al., 2012; Almeida et al., 2013; Schobesberger et al., 2015; Elm, 2017). However, successive studies have found that pure sulfuric acid or sulfuric acid–water systems are not sufficient to explain the formation and growth of atmospheric nanoparticles (Weber et al., 1995, 1996; Kirkby et al., 2011). Subsequently, numerous experimental and theoretical studies have shown that base compounds, such as ammonia (NH₃) or amines, can significantly enhance sulfuric acid-driven particle formation (Kurten et al., 2008; Ge et al., 2011; Hanson et al., 2011; Kupiainen et al., 2012; Yu and Lee, 2012; Almeida et al., 2013; Jen et al., 2014; Olenius et al., 2017). Thereby, current studies focus on the acid–base particles with binary, ternary, or even quaternary components.

Similar to SA, methanesulfonic acid [CH₃S(O)(O)OH, MSA], another major oxidation product of dimethyl sulfide (DMS) (Glasow and Crutzen, 2004; Barnes et al., 2006), has been confirmed to be an important contributor to the NPF process in the presence of base compounds (Dawson et al., 2012, 2014; Ezell et al., 2014; Nishino et al., 2014; Chen et al., 2016; Chen and Finlayson-Pitts, 2017; Zhao et al., 2019; Perraud et al., 2020b). Finlayson-Pitts group systemically reported extensive experimental and theoretical studies based on MSA particles. They found that small alkylamines (methylamine, dimethylamine, and trimethylamine) have stronger nucleation capacity than NH₃ in MSA-driven NPF (Chen et al., 2016; Chen and Finlayson-Pitts, 2017; Perraud et al., 2020b). However, NH₃ can promote the formation of MSA–amines particles, and has a synergistic effect on particle formation and growth processes (Perraud et al., 2020b).

The cluster formation pathway, particle formation rate, and the microstructure of the critical nucleus are dependent on the molecular properties of acid and base compounds as well as environmental conditions (Chee et al., 2019, 2021). Therefore, obtaining a comprehensive understanding of atmospheric NPF process is extremely difficult task. For instance, some experimental studies have shown that acid and base molecules do not always nucleate in a simple 1:1 acid:base stoichiometric fashion (Kim et al., 2016; Lawler et al., 2016; Chen et al., 2018; Finlayson-Pitts et al., 2020; Perraud et al., 2020a). They found that although the acid has much lower concentrations than bases in the gas phase, the formed particles in small sizes are acidic, i.e., the measured acid:base ratio is larger than 1:1. Quantum chemistry is an effective method to obtain the microscopic information of nucleated clusters with different acid:base ratios. However, current theoretical studies of these small clusters mainly focus on the clusters with a same number of acid and base molecules. Hence, it is necessary to theoretically study the microstructure and reveal formation mechanism of acid–base particles under acid-rich conditions.

Here we focus on microscopic description of nanoparticles formed by the reaction of MSA with MA and NH₃ under acid-rich conditions, where the acid:base ratios correspond the detected experimental values reported by Finlayson-Pitts group (Perraud et al., 2020a). The binary (MSA)_2n-(MA)_n, (n = 1–4) and ternary (MSA)_3n-(MA)_n-(NH₃)_n, (n = 1–4) systems were investigated using computational tools. We have calculated the structures, energies, thermodynamic and dynamic stabilities, and related properties of these clusters at the level of B3LYP-D3/6-311+G(2d,2p)//B3LYP-D3/6-31G(d). The role of base synergy in acid-rich particles is also discussed.

Materials and Methods

ABCluster software (Zhang and Dolg, 2015, 2016) with the artificial bee colony algorithm (Karaboga, 2005) was employed to search local minima on the potential energy surface of the studied clusters. In the process of cluster search, molecular monomers are usually used as the basic unit to construct the initial structure. In the current study of acid-base particles, stable clusters are usually ion pairs formed by proton transfer. To more efficiently obtain reliable low-energy isomers, beside single molecules, the possible acid-base ion pairs are also considered for screening initial structures. Hence, we totally employed three classes of building block as basic units (see Scheme 1). The first class consists of single molecules and the other two classes introduce two kinds of proton transferred clusters with 1:1 and 2:1 acid:base ratios as building blocks. In our cluster search strategy, 1,000 structures were randomly generated by ABCluster program based on each building block combinations, and total of 24,000 initial structures were generated for eight systems. Due to large number of calculations, it is necessary to adopt economic calculation strategy to avoid the exhaustive and unnecessary calculations. We followed the Scheme 2 as: Firstly, 3,000 structures generated by ABCluster for each system were optimized using the PM7 semi-empirical method (Stewart, 2007; Hostaš et al., 2013). We selected the minimum structures within ΔE < 100 kcal/mol of the lowest-energy isomer, which were further optimized at the level of B3LYP/3-21G. After that we reselected the structures within ΔE < 60 kcal/mol of the lowest-energy cluster for the final optimization and vibrational frequency calculations using B3LYP functional with Grimme's dispersion correction and 6-31G(d) basis set. Finally, for conformers within ΔE < 20 kcal/mol of the lowest energy structure, the single-point energy calculations were carried out to obtain more reliable energies at the level of B3LYP-D3/6-311+G(2d,2p), and the obtained isomers with lowest Gibbs free energy were confirmed as the global minima. Previous studies have shown that B3LYP-D3 can reasonably predict the structure, energy and property of small clusters (Xantheas, 1995; Miller et al., 2007; Dawson et al., 2012; Chen et al., 2015, 2016; Perraud et al., 2020b). To verify the reliability of B3LYP-D3/6-311+G(2d,2p), we chose 2MSA-1MA as our test system and benchmarked the results against MP2/6-311+G(2d,2p). The test results showed that the lowest-energy isomers predicted by the two methods are consistent (see Supplementary Table 1, ESI†). Therefore, considering computational cost performance and complexity, B3LYP-D3/6-311+G(2d,2p) is sufficient to qualitatively predict the lowest energy isomers in this study. Normal-mode vibrational frequency analyses had confirmed that all the stable minima had positive vibrational frequencies. Natural bond orbital (NBO) analysis (Foster and Weinhold, 1980; Reed and Weinhold, 1983) was used to obtain partial charges (δ). All density functional theory (DFT) geometry optimizations and vibrational frequency calculations were performed using the Gaussian 16 program (Frisch et al., 2016).

SCHEME 1

Scheme 1. Three classes of “Building Block.”

SCHEME 2

Scheme 2. The energetic calculation strategy for searching the lowest-energy isomers.

To evaluate the dynamic stabilities of the obtained clusters, molecular dynamics simulations with semi-empirical quantum chemical potentials (PM6) (Takayanagi et al., 2008; Tosso et al., 2013; Wang et al., 2019) were carried out using the CP2K package (VandeVondele et al., 2005), on the gas-phase NVT canonical ensemble with Nose-Hover thermostats (Nosé, 1984; Hoover, 1985). In order to evaluate the reliability of PM6 for our clusters, we optimized all the lowest-energy structures at PM6 level. Test results showed that the geometries obtained at PM6 level are very close to those obtained by density functional theory. For each simulation, five trajectories were done, and each trajectory was propagated for 100 ps. The time step used here was 1 fs and the simulation temperature was at T = 300 K.

In order to explore the intermolecular interactions of acid–base clusters, we performed non-covalent interaction (NCI) analysis, which is used to describe the relationship between electron density ρ(r) and reduced density gradient (RDG) (Johnson et al., 2010). RDG(s) is calculated by Equation (1) in order to prove the deviation from the homogeneous distribution of electrons.

$\begin{array}{ll}s=\frac{1}{2{(3{\pi }^2)}^{\frac{1}{3}}}\frac{|\nabla \rho |}{{\rho }^{\frac{4}{3}}}& (1)\end{array}$

where ρ is the electron density based on B3LYP-D3/6-311+G(2d,2p)//B3LYP-D3 /6-31G(d), ∇ is the gradient operator, and |∇ρ| is the electronic density gradient mode.

The function sign(λ₂)ρ is obtained by multiplying the electron density ρ(r) by the sign of the second Hessian eigenvalue (λ₂). The RDG-sign(λ₂)ρ scatter plots and the bonding iso-surface plots were made by Multiwfn (Johnson et al., 2010; Tian and Chen, 2012) and VMD (Humphrey et al., 1996; Illinois, 2014) programs, respectively. In addition, proton transfer was evaluated by a proton-transfer parameter (ρ_PT), which is based on the extension and contraction of bonds between atoms (Kurnig and Scheiner, 1987). The specific expression of ρ_PT in this work is given in Equation (2):

$\begin{array}{ll}{\rho }_{PT}=(r_{OH}-r_{OH}^0)-(r_{H\cdots N}-r_{H\cdots N}^0)& (2)\end{array}$

where $r_{\text{OH}}^0$ and $r_{\text{H}···N}^0$ are the O-H and N-H bond distances in free MSA monomer and fully protonated MA and NH₃ $(C{H}_{3}N{H}_3^{+}andN{H}_4^{+}ion)$, respectively. Radiuses r_OH and r_H···N are those of hydrogen bond in the studied clusters.

Results

In this work, binary (MSA)_2n-(MA)_n, (n = 1–4) and ternary (MSA)_3n-(MA)_n-(NH₃)_n, (n = 1–4) clusters were used as a representative set to investigate MSA-MA-NH₃ particles under acid-rich conditions. The acid:base ratios used here were based on the experimentally detected values of small size MSA-MA-NH₃ particles (<9 nm) by Perraud et al. (2020a) Hence, we used an acid:base ratio of 2:1 for binary MSA-MA particles, and 3:2 for ternary MSA-MA-NH₃ particles. Additionally, MA:NH₃ ratio is 1:1 in ternary system. Here we will discuss the molecular structures, intermolecular interactions and dynamic stabilities of the two- and three-component clusters.

Structure Analysis

Binary (MSA)_2n-(MA)_n System

The obtained global free energy structures of the (MSA)_2n-(MA)_n, (n = 1–4) system at the level of B3LYP-D3/6-311+G(2d,2p)//B3LYP-D3/6-31G(d) are shown in Figure 1, and other high-energy isomers are shown in Supplementary Figures 1–4. For clarity, geometrical parameters for hydrogen bonds are omitted. All cluster structures in Figure 1 possess the cage-like skeletons composed of hydrogen bonds (HBs), and the number of HBs (3, 8, 11, 13) increases with the increase of n. Generally, two types of HBs were found in binary clusters. The first type is N-H···O bond (shown by the blue dash line) formed between the hydrogen atom in MA and the oxygen atom in MSA, with bond lengths ranging from 1.64 to 1.99 Å. Three hydrogen atoms in MA consist of two hydrogen atoms from the original amino group and a proton transferred from MSA. In these structures, each MA molecule obtains a proton from MSA molecule forming the ion pair [CH₃SO₃]⁻[H₃NCH₃]⁺, which is consistent with previous studies of MSA–MA clusters (Xu et al., 2017; Perraud et al., 2020b). This is also supported by the partial charge (δ) obtained using natural bond orbital (NBO) analysis. All the MA moieties have positive charges (δ = 0.86–0.89) and the deprotonated MSA moieties have negative charges (δ = −0.84 to −0.81), indicating that MA acts as the hydrogen-bond acceptor and MSA is the donor. These closed ion pairs are always located in the center of the skeleton and they increase the structure stability. The second type is the O-H···O bond (shown by the red dash line) formed between anionic and neutral MSA monomers. The length of this HB ranges from 1.37 to 1.65 Å. Those MSA molecules that do not participate in proton transfer are distributed outside of the structure, and the corresponding partial charges are δ = −0.10 to −0.04. Clearly, when MSA exhibits a strong intermolecular interaction with MA, the formed ion pairs play an important role on charge transfer, and have the major contribution to the stability of a cluster. For surrounding MSA molecules, although their contributions to charge transfer are very small, they link to ion pairs via HBs increasing the structure stability and provide more potential hydrogen binding sites for further particle growth.

FIGURE 1

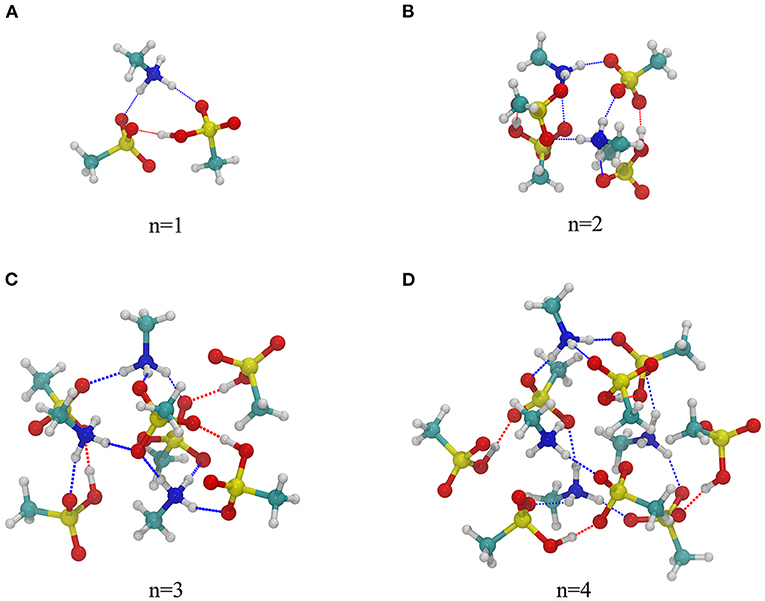
Figure 1. The most stable structures of binary (MSA)_2n-(MA)_n, (n = 1–4) clusters at the level of B3LYP-D3/6-311+G(2d,2p)//B3LYP-D3/6-31G(d). Yellow, red, blue, cyan, and white spheres represent sulfur, oxygen, nitrogen, carbon, and hydrogen atoms, respectively. Dotted lines in blue and red represent N-H···O and O-H···O hydrogen bonds, respectively.

Ternary (MSA)_3n-(MA)_n-(NH₃)_n System

Figure 2 shows the most stable structures for ternary (MSA)_3n-(MA)_n-(NH₃)_n (n = 1–4) clusters, and other obtained structures with high energy are shown in Supplementary Figures 5–8. Like the binary structures, these global minimum free energy conformers also have cage skeletons, in which ion pairs formed by proton transfer between acid and base are located in the center of the skeleton and neutral MSA molecules surround the cage structure. As Figure 2 demonstrates, both MA and NH₃ can accept a proton from MSA forming ion pairs [CH₃SO₃]⁻[H₃NCH₃]⁺ and [CH₃SO₃]⁻[H₄N]⁺, respectively. Therefore, in addition to the two kinds of HBs in binary system, there is another N-H···O hydrogen bond formed between NH₃ and MSA. The bond lengths of N-H···O hydrogen bond in ternary structures range from 1.64 to 1.99 Å and O-H···O hydrogen bonds are from 1.45 to 1.68 Å. Furthermore, NBO results show that the partial charge value (δ) of MA and NH₃ are very close (δ = 0.84–0.90). The corresponding values of MSA with and without proton transfer are δ = −0.88 to −0.79 and δ = −0.08 to −0.03, respectively. These results show that there is no significant difference in the action of the two bases with MSA under acid-rich conditions, although the basicity (both in aqueous and gas phase) of NH₃ is less than that of MA. In addition, with increasing n, the protonated NH₃ gradually replaces MA to be the inner of the cluster structure, which may be because NH₃ can form more hydrogen bonds to stabilize the structure, and the methyl group in MA has the steric hindrance effect. Similar structural effects have been found for sulfuric acid–dimethylamine–ammonia clusters (Myllys et al., 2019). In conclusion, in the presence of NH₃ and MA, more proton transfers and more HBs can be formed than in the presence of a single base. This base synergy enhances the stability of clusters and provides more sites to connect to other molecules. This is further discussed combining with stability analysis in the following section Stability Analysis.

FIGURE 2

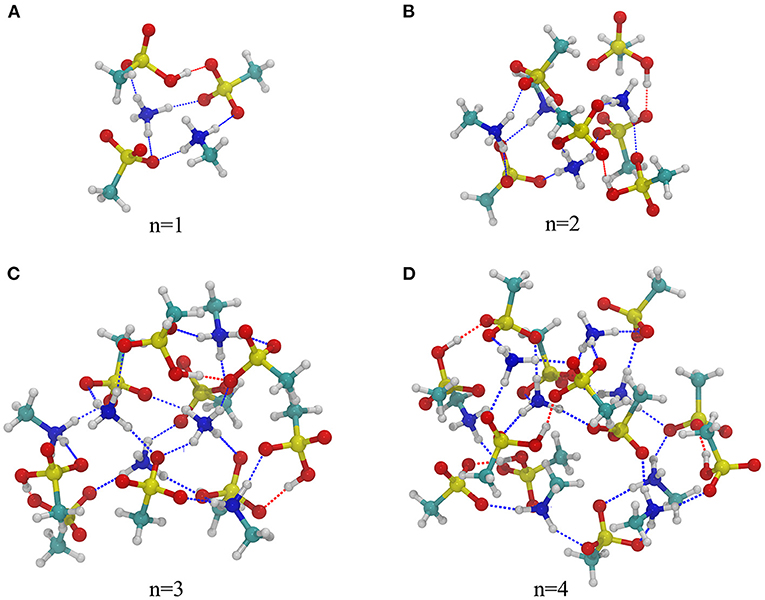
Figure 2. The most stable structures of ternary (MSA)_3n-(MA)_n-(NH₃)_n, (n = 1–4) clusters at the level of B3LYP-D3/6-311+G(2d,2p)//B3LYP-D3/6-31G(d).

Intermolecular Interactions

Intermolecular interactions in the acid–base clusters were studied using NCI index and proton transfer parameter (ρPT), respectively. The former can judge the strength of interaction by the value of sign(λ₂)ρ, and the latter can evaluate the degree of ionization of proton transfer using the distance between atoms. Both of them have been successfully used to reveal the interaction in previous reports of acid–base particles (Kurnig and Scheiner, 1987; Hunt et al., 2003; Ling et al., 2018; Zhao et al., 2020). Figures 3A,B show the scatter plot of RDG(s) vs. sign(λ₂)ρ for the smallest binary and ternary clusters (n = 1) and the corresponding bonding isosurfaces, as well as the corresponding interaction types shown in different colors (Figure 3C). For other clusters, the plots are shown in Supplementary Figures 9, 10. We found that the most stable cluster in each system has the negative sign(λ₂)ρ values indicating the presence of HBs, meanwhile, van der Waals force [sign(λ₂)ρ ~ 0] and steric hindrance [sign(λ₂)ρ > 0] can be found in each cluster. These results are also supported by the visual bonding isosurfaces, and all the HBs can completely correspond to the structures in Figures 1, 2 through the disc-like isosurface. As n increases, the values corresponding to the spike in cyan area [with small negative sign(λ₂)ρ values] gradually become larger. This is because the increased number of molecules increases the steric hindrance and weakens the strength of hydrogen bonds, which is consistent with the long bond length of HB in large system. In short, weak interactions have the major contribution in these clusters, and the abundant MSA molecules can saturate the interaction sites of the clusters.

FIGURE 3

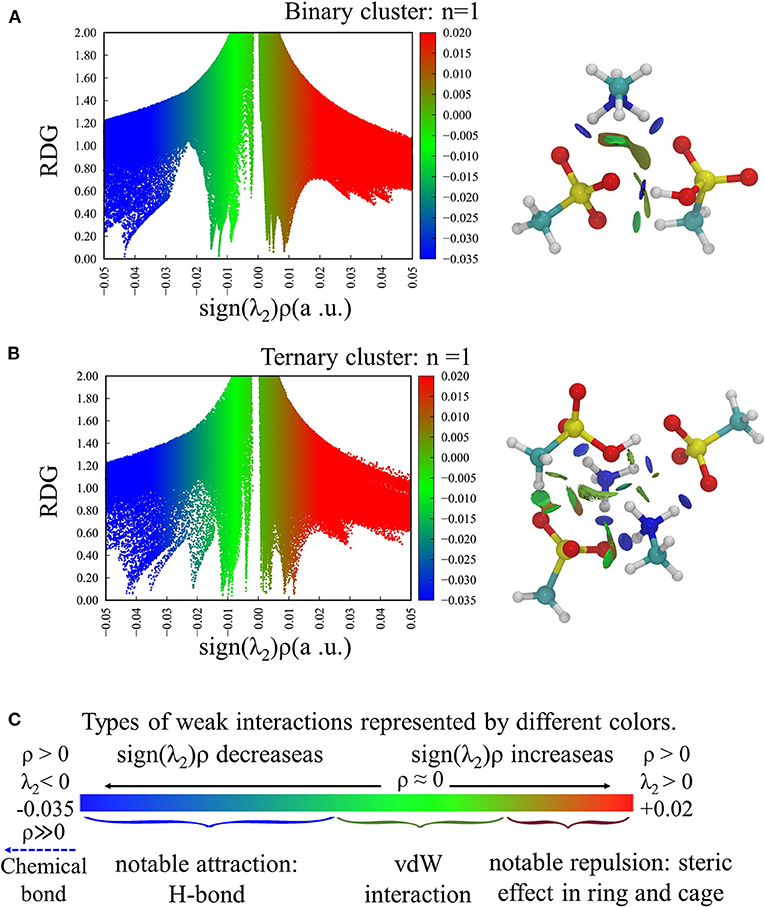
Figure 3. The plots of RDG vs. sign(λ₂)ρ function (left) and the visualized bonding isosurfaces (right) for (A) (MSA)_2n-(MA)_n (n =1), (B) (MSA)_3n-(MA)_n-(NH₃)_n (n =1). (C) The values of ρ(r) and λ₂ represented by different colors and the corresponding interaction types.

Proton transfer parameters of the smallest systems (n = 1) are listed in Table 1, and other systems can be seen in Supplementary Table 2. Based on the equation of ρ_PT, if the proton transfer fully occurs, the H-O bond on the proton donor is stretched, the second term is zero and ρPT should be positive. This means that there is a real ion pair in the cluster, and the more positive the parameter value, the stronger the proton transfer degree and ionic properties of the cluster. For all the systems we studied, the ρ_PT values are always positive, indicating the presence of proton transfer, and the number of proton transfer is equal to the total number of base molecules involved.

TABLE 1

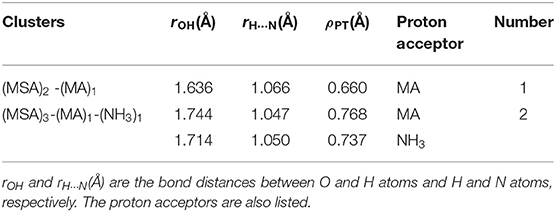
Table 1. Proton-transfer parameter (ρ_PT, in Å) and the total number of proton transfers for the smallest binary and ternary clusters (n = 1).

Stability Analysis

To study cluster stabilities, thermodynamic analysis and molecular dynamic simulations were performed. The lowest-energy structures were determined using zero-point energy corrected energies (0 K) and Gibbs free energies (298.15 K). For those isomers within 20 kcal/mol of the lowest-energy isomer, the relative energies with zero-point energy correction (ΔE + ZPE) and Gibbs free energies (ΔG) are listed in the Supplementary Tables 3–10. The thermodynamic stabilities were evaluated using three possible dissociation reactions, and ΔG of dissociation path was calculated by Equation (3). The calculated ΔG values for studied clusters were plot in Figure 4, and the exact data is listed in Supplementary Tables 11, 12. As seen in Figure 4, the ΔG values of all reaction paths are positive, indicating the studied dissociation reactions are thermodynamically unfavorable. Moreover, with the increase of n, ΔG values increase for both binary and ternary systems, which is because more HBs exist in large systems. Furthermore, the dissociation energies for ternary clusters are much larger than the corresponding binary cluster. This is partly due for the fact that studied ternary systems contain total of 5n molecules whereas corresponding binary systems contain 3n molecules, meaning that with same n ternary system is larger and have more intermolecular interactions. Additionally, a reasonable assumption would be that three-component pathway can lead to higher particle formation potential than the two-component pathways for two main reasons: (1) stronger intermolecular forces and (2) synergistic effects. (1) This is consistent with the structural discussion above that NH₃ and MSA can form ion pairs and more HBs, thus increasing the stability of cluster. (2) In these acid-rich clusters, both MA and NH₃ have an important influence on the stability of clusters and play a synergistic role on NPF, which is consistent with previous studies (Perraud et al., 2020b).

$\begin{array}{l}\Delta G={\displaystyle \sum G}\left(product\right)-{\displaystyle \sum G}\left(reactant\right)\\ ={\displaystyle \sum {\nu }_B}G\left(basicunit,B\right)-G\left(globalminima\right)\end{array}$

FIGURE 4

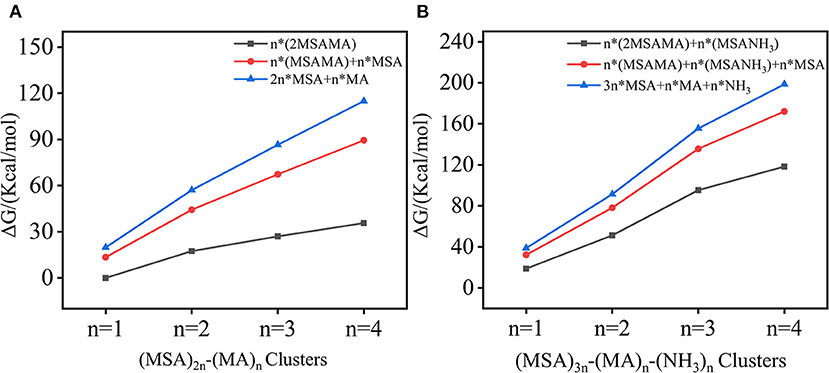
Figure 4. Dissociation free energies (ΔG, 298.15 K) of (MSA)_2n-(MA)_n and (MSA)_3n-(MA)_n -(NH₃)_n (n =1–4) clusters through three reaction paths.

The dynamic stabilities of the studied clusters were verified by molecular dynamic simulations for 100 ps at 300 K. Supplementary Figure 11 shows the energy change of each cluster during the whole simulation process, and the final structures at 100 ps are shown in Supplementary Figure 12. Throughout the simulation, the energy change is not significant and components do not evaporate from the cluster at room temperature. All the states of proton transfer remain unchanged, and the ion pairs still form cage-like skeletons with slightly different structural parameters. Therefore, we can conclude the studied binary and ternary clusters to be dynamically stable at room temperature.

Combining above structure, intermolecular interaction and stability analysis, it can be found that these acid-rich clusters possess high thermodynamic and dynamic stabilities. Hydrogen bonds and ion pairs formed by proton transfer reactions from acid to base play an important role in the formation of stable structures, and the synergistic effect between NH₃ and MA can also be detected. The excess MSA molecules enhance the stability of clusters and provide additional hydrogen binding sites for further growth.

Conclusion

In this work, we explored the microscopic formation mechanism of methanesulfonic acid–methylamine–ammonia particles under acid-rich conditions. Structures, energies, properties and stabilities of binary (MSA)_2n-(MA)_n and ternary (MSA)_3n-(MA)_n-(NH₃)_n, (n = 1–4) systems were calculated at the level of B3LYP-D3/6-311+G(2d,2p)//B3LYP-D3/6-31G(d). The most stable clusters have a cage-like skeleton, which are composed of the ion pairs formed by proton transfer from the acid to the base molecule. According to the dissociation energy and dynamic simulation at 300 K, these eight acid-rich clusters possess considerable thermodynamic and dynamic stabilities. Like in other acid–base systems, proton transfer plays an important role on charge transfer and the stability of clusters. Moreover, MA and NH₃, which are both abundant vapor molecules in many atmospheric locations, have a synergistic effect on NPF under acid-rich conditions. The excess of MSA molecules can promote the stability of clusters, and also provide potential sites for HBs to further connect with other molecules, which is favorable for particle growth. This work does not only increase the molecular-level understanding of the MSA-MA-NH₃ particle formation, but also reveals the importance of acid-rich conditions and acidic particles.

Considering the decline in sulfur dioxide (precursor of sulfuric acid in the air) associated with the burning of fossil fuels (Jefferson et al., 1998; Klimont et al., 2013; Perraud et al., 2015; Murphy et al., 2017) and higher gas concentration of MSA in coastal areas (Berresheim et al., 1993, 2013; Eisele and Tanner, 1993; Jefferson et al., 1998; Berresheim, 2002; Bardouki et al., 2003), it can be predicted that the aerosol particles produced by MSA may become more important in the future. Thus, more experimental and theoretical studies focusing on MSA-rich conditions should be conducted to estimate the climatic impact of multi-component MSA aerosol particles. Especially in the ever-changing and complex atmospheric environment, the ubiquitous water molecules and various volatile acidic compounds from natural sources, and climatic phenomena such as acid mist and acid rain caused by anthropogenic sources will all affect the formation rate of new particles. The measurement of atmospheric composition in a higher acid state and its theoretical research are essential to understand acidizing deposition and to formulate economic and effective control strategies in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

ML: conceptualization, formal analysis, investigation, methodology, data curation, visualization, and writing—original draft. NM: resources, supervision, validation, and writing—review and editing. YH: data curation and visualization. ZW: investigation and methodology. LC: funding acquisition and writing—review and editing. WL: conceptualization, funding acquisition, investigation, project administration, resources, supervision, validation, and writing—review and editing. JX: conceptualization, funding acquisition, investigation, project administration, resources, supervision, validation, and writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Zhejiang Provincial Natural Science Foundation of China (No. LQ20B030002), and the National Natural Science Foundation of China (Nos. 12075211, 11975206, and 11875236).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.875585/full#supplementary-material

References

Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., and Praplan, A. P. (2013). Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere. Nature 502, 359–363. doi: 10.1038/nature12663

PubMed Abstract | CrossRef Full Text | Google Scholar

Bardouki, H., Berresheim, H., Vrekoussis, M., Sciare, J., Kouvarakis, G., and Oikonomou, K. (2003). Gaseous (DMS, MSA, SO₂, H₂SO₄ and DMSO) and particulate (sulfate and methanesulfonate) sulfur species over the northeastern coast of Crete. Atmos. Chem. Phys. 3, 1871–1886. doi: 10.5194/acp-3-1871-2003

CrossRef Full Text | Google Scholar

Barnes, I., Hjorth, J., and Mihalopoulos, N. (2006). Dimethyl sulfide and dimethyl sulfoxide and their oxidation in the atmosphere. ChemInform 37. doi: 10.1002/chin.200624259

PubMed Abstract | CrossRef Full Text | Google Scholar

Berndt, T., Sipilä, M., Stratmann, F., Petäjä, T., Vanhanen, J., and Mikkilä, J. (2013). Enhancement of Atmospheric H2SO4/H2O Nucleation: Organic Oxidation Products vs. Amines. Gases/Laboratory Studies/Troposphere/Chemistry (chemical composition and reactions) [Preprint]. Available online at: https://doi.org/10.5194/acpd-13-16301-2013

Google Scholar

Berresheim, H. (2002). Gas-aerosol relationships of H₂SO₄, MSA, and OH: Observations in the coastal marine boundary layer at Mace Head, Ireland. J. Geophys. Res. 107:8100. doi: 10.1029/2000JD000229

CrossRef Full Text | Google Scholar

Berresheim, H., Adam, M., Monahan, C., ODowd, C., Plane, J. M. C., and Bohn, B. (2013). Missing SO₂ oxidant in the coastal atmosphere? - Evidence from high resolution measurements of OH and atmospheric sulfur compounds. Atmosp. Chem. Phys. 14, 12209–12223. doi: 10.5194/acp-14-12209-2014

CrossRef Full Text | Google Scholar

Berresheim, H., Eisele, F. L., Tanner, D. J., Mcinnes, L. M., Ramsey-Bell, D. C., and Covert, D. S. (1993). Atmospheric sulfur chemistry and cloud condensation nuclei (CCN) concentrations over the northeastern Pacific Coast. J. Geophys. Res. 98:12701. doi: 10.1029/93JD00815

CrossRef Full Text | Google Scholar

Bzdek, B. R., Zordan, C. A., Pennington, M. R., Luther, G. W., and Johnston, M. V. (2012). Quantitative assessment of the sulfuric acid contribution to new particle growth. Environ. Sci. Technol. 46, 4365–4373. doi: 10.1021/es204556c

PubMed Abstract | CrossRef Full Text | Google Scholar

Chan, T., and Mozurkewich, M. (2001). Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis. J. Aerosol Sci. 32, 321–339. doi: 10.1016/S0021-8502(00)00081-1

CrossRef Full Text | Google Scholar

Charlson, R. J., Schwartz, S. E., Hales, J. M., Cess, R. D., Coakley, J. A., and Hansen, J. E. (1992). Climate forcing by anthropogenic aerosols. Science 255, 423–430. doi: 10.1126/science.255.5043.423

PubMed Abstract | CrossRef Full Text | Google Scholar

Chee, S., Barsanti, K., Smith, J. N., and Myllys, N. (2021). A predictive model for salt nanoparticle formation using heterodimer stability calculations. Atmos. Chem. Phys. 21, 11637–11654. doi: 10.5194/acp-21-11637-2021

CrossRef Full Text | Google Scholar

Chee, S., Myllys, N., Barsanti, K. C., Wong, B. M., and Smith, J. N. (2019). An experimental and modeling study of nanoparticle formation and growth from dimethylamine and nitric acid. J. Phys. Chem. A 123, 5640–5648. doi: 10.1021/acs.jpca.9b03326

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Chee, S., Lawler, M. J., Barsanti, K. C., Wong, B. M., and Smith, J. N. (2018). Size resolved chemical composition of nanoparticles from reactions of sulfuric acid with ammonia and dimethylamine. Aerosol Sci. Technol. 52, 1120–1133. doi: 10.1080/02786826.2018.1490005

CrossRef Full Text | Google Scholar

Chen, H., Ezell, M. J., Arquero, K. D., Varner, M. E., Dawson, M. L., and Finlayson-Pitts, B. J. (2015). New particle formation and growth from methanesulfonic acid, trimethylamine and water. Phys. Chem. Chem. Phys. 17, 13699–13709. doi: 10.1039/c5cp00838g

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., and Finlayson-Pitts, B. J. (2017). New particle formation from methanesulfonic acid and amines/ammonia as a function of temperature. Environ. Sci. Technol. 51, 243–252. doi: 10.1021/acs.est.6b04173

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Varner, M. E., Gerber, R. B., and Finlayson-Pitts, B. J. (2016). Reactions of methanesulfonic acid with amines and ammonia as a source of new particles in air. J. Phys. Chem. B 120, 1526–1536. doi: 10.1021/acs.jpcb.5b07433

PubMed Abstract | CrossRef Full Text | Google Scholar

Dawson, M. L., Varner, M. E., Perraud, V., Ezell, M. J., Gerber, R. B., and Finlayson-Pitts, B. J. (2012). Simplified mechanism for new particle formation from methanesulfonic acid, amines, and water via experiments and ab initio calculations. Proc. Natl. Acad. Sci. U.S.A. 109, 18719–18724. doi: 10.1073/pnas.1211878109

PubMed Abstract | CrossRef Full Text | Google Scholar

Dawson, M. L., Varner, M. E., Perraud, V., Ezell, M. J., Wilson, J., and Zelenyuk, A. (2014). Amine–amine exchange in aminium–methanesulfonate aerosols. J. Phys. Chem. C 118, 29431–29440. doi: 10.1021/jp506560w

CrossRef Full Text | Google Scholar

Dunne, E. M., Gordon, H., Kürten, A., Almeida, J., Duplissy, J., and Williamson, C. (2016). Global atmospheric particle formation from CERN CLOUD measurements. Science 354, 1119–1124. doi: 10.1126/science.aaf2649

PubMed Abstract | CrossRef Full Text | Google Scholar

Eisele, F. L., and Tanner, D. J. (1993). Measurement of the gas phase concentration of H₂SO₄ and methane sulfonic acid and estimates of H₂SO₄ production and loss in the atmosphere. J. Geophys. Res. Atmos. 98, 9001–9010. doi: 10.1029/93JD00031

CrossRef Full Text | Google Scholar

Elm, J. (2017). Elucidating the limiting steps in sulfuric acid–base new particle formation. J. Phys. Chem. A 121, 8288–8295. doi: 10.1021/acs.jpca.7b08962

PubMed Abstract | CrossRef Full Text | Google Scholar

Elm, J., Kubečka, J., Besel, V., Jääskeläinen, M. J., Halonen, R., and Kurtén, T. (2020). Modeling the formation and growth of atmospheric molecular clusters: a review. J. Aerosol Sci. 149:105621. doi: 10.1016/j.jaerosci.2020.105621

CrossRef Full Text | Google Scholar

Ezell, M. J., Chen, H., Arquero, K. D., and Finlayson-Pitts, B. J. (2014). Aerosol fast flow reactor for laboratory studies of new particle formation. J. Aerosol Sci. 78, 30–40. doi: 10.1016/j.jaerosci.2014.08.009

CrossRef Full Text | Google Scholar

Finlayson-Pitts, B. J., Wingen, L. M., Perraud, V., and Ezell, M. J. (2020). Open questions on the chemical composition of airborne particles. Commun. Chem. 3:108. doi: 10.1038/s42004-020-00347-4

CrossRef Full Text | Google Scholar

Foster, J. P., and Weinhold, F. (1980). Natural hybrid orbitals. J. Am. Chem. Soc. 102, 7211–7218. doi: 10.1021/ja00544a007

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., and Cheeseman, J. R. (2016). Gaussian 16, Revision A.03. Wallingford, CT: Gaussian, Inc.

Google Scholar

Ge, X., Wexler, A. S., and Clegg, S. L. (2011). Atmospheric amines – Part I. A review. Atmos. Environ. 45, 524–546. doi: 10.1016/j.atmosenv.2010.10.012

CrossRef Full Text | Google Scholar

Glasow, R. V., and Crutzen, P. J. (2004). Model study of multiphase DMS oxidation with a focus on halogens. Atmos. Chem. Phys. 4, 589–608. doi: 10.5194/acp-4-589-2004

CrossRef Full Text | Google Scholar

Hanson, D. R., McMurry, P. H., Jiang, J., Tanner, D., and Huey, L. G. (2011). Ambient pressure proton transfer mass spectrometry: detection of amines and ammonia. Environ. Sci. Technol. 45, 8881–8888. doi: 10.1021/es201819a

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697. doi: 10.1103/PhysRevA.31.1695

PubMed Abstract | CrossRef Full Text | Google Scholar

Hostaš, J., Rezáč, J., and Hobza, P. (2013). On the performance of the semiempirical quantum mechanical PM6 and PM7 methods for noncovalent interactions. Chem. Phys. Lett. 568–569, 161–166. doi: 10.1016/j.cplett.2013.02.069

CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graph. 14, 33–38. doi: 10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunt, S. W., Higgins, K. J., Craddock, M. B., Brauer, C. S., and Leopold, K. R. (2003). Influence of a polar near-neighbor on incipient proton transfer in a strongly hydrogen bonded complex. J. Am. Chem. Soc. 125, 13850–13860. doi: 10.1021/ja030435x

PubMed Abstract | CrossRef Full Text | Google Scholar

Illinois, U. (2014). Visual Molecular Dynamics. Available online at: http://www.mendeley.com/research/visual-molecular-dynamics/ (accessed August 5, 2021).

Google Scholar

Jefferson, A., Tanner, D. J., Eisele, F. L., Davis, D. D., Chen, G., and Crawford, J. (1998). OH photochemistry and methane sulfonic acid formation in the coastal Antarctic boundary layer. J. Geophys. Res. Atmos. 103, 1647–1656. doi: 10.1029/97jd02376

CrossRef Full Text | Google Scholar

Jen, C. N., McMurry, P. H., and Hanson, D. R. (2014). Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine. J. Geophys. Res. 119, 7502–7514. doi: 10.1002/2014JD021592

CrossRef Full Text | Google Scholar

Johnson, E. R., Keinan, S., Mori-Sanchez, P., Contreras-Garcia, J., Cohen, A. J., and Yang, W. (2010). Revealing noncovalent interactions. J. Am. Chem. Soc. 132:6498. doi: 10.1021/ja100936w

PubMed Abstract | CrossRef Full Text | Google Scholar

Karaboga, D. (2005). An Idea Based on Honey Bee Swarm for Numerical Optimization. Available online at: http://www.researchgate.net/publication/255638348 (accessed October 5, 2009).

Google Scholar

Kim, J., Ahlm, L., Yli-Juuti, T., Lawler, M., Keskinen, H., and Tröstl, J. (2016). Hygroscopicity of nanoparticles produced from homogeneous nucleation in the CLOUD experiments. Atmos. Chem. Phys. 16, 293–304. doi: 10.5194/acp-16-293-2016

CrossRef Full Text | Google Scholar

Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., and Ehrhart, S. (2011). Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation. Nature 476, 429–433. doi: 10.1038/nature10343

PubMed Abstract | CrossRef Full Text | Google Scholar

Kittelson, D. B., Watts, W. F., and Johnson, J. P. (2004). Nanoparticle emissions on Minnesota highways. Atmos. Environ. 38, 9–19. doi: 10.1016/j.atmosenv.2003.09.037

CrossRef Full Text | Google Scholar

Klimont, Z., Smith, S. J., and Cofala, J. (2013). The last decade of global anthropogenic sulfur dioxide: 2000–2011 emissions. Environ. Res. Lett. 8:014003. doi: 10.1088/1748-9326/8/1/014003

CrossRef Full Text | Google Scholar

Knopf, D. A., Alpert, P. A., and Wang, B. (2018). The role of organic aerosol in atmospheric ice nucleation: a review. ACS Earth Space Chem. 2, 168–202. doi: 10.1021/acsearthspacechem.7b00120

CrossRef Full Text | Google Scholar

Kuang, C., McMurry, P. H., McCormick, A. V., and Eisele, F. L. (2008). Dependence of nucleation rates on sulfuric acid vapor concentration in diverse atmospheric locations. J. Geophys. Res. 113:D10209. doi: 10.1029/2007JD009253

CrossRef Full Text | Google Scholar

Kulmala, M. (2003). Atmospheric science: how particles nucleate and grow. Science 302, 1000–1001. doi: 10.1126/science.1090848

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulmala, M., Kontkanen, J., Junninen, H., Lehtipalo, K., Manninen, H. E., and Nieminen, T. (2013). Direct observations of atmospheric aerosol nucleation. Science 339, 943–946. doi: 10.1126/science.1227385

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulmala, M., Petäjä, T., Ehn, M., Thornton, J., Sipilä, M., and Worsnop, D. R. (2014). Chemistry of atmospheric nucleation: on the recent advances on precursor characterization and atmospheric cluster composition in connection with atmospheric new particle formation. Annu. Rev. Phys. Chem. 65, 21–37. doi: 10.1146/annurev-physchem-040412-110014

PubMed Abstract | CrossRef Full Text | Google Scholar

Kupiainen, O., Ortega, I. K., Kurtén, T., and Vehkamäki, H. (2012). Amine substitution into sulfuric acid – ammonia clusters. Atmos. Chem. Phys. 12, 3591–3599. doi: 10.5194/acp-12-3591-2012

CrossRef Full Text | Google Scholar

Kurnig, I. J., and Scheiner, S. (1987). Ab Initio investigation of the structure of hydrogen halide-amine complexes in the gas phase and in a polarizable medium. Int. J. Quant. Chem. 32, 47–56. doi: 10.1002/qua.560320809

CrossRef Full Text | Google Scholar

Kurten, T., Loukonen, V., Vehkamaki, H., and Kulmala, M. (2008). Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia. Atmos. Chem. Phys. 8, 4095–4103. doi: 10.5194/acp-8-4095-2008

CrossRef Full Text | Google Scholar

Lawler, M. J., Winkler, P. M., Kim, J., Ahlm, L., Tröstl, J., and Praplan, A. P. (2016). Unexpectedly acidic nanoparticles formed in dimethylamine–ammonia–sulfuric-acid nucleation experiments at CLOUD. Atmos. Chem. Phys. 16, 13601–13618. doi: 10.5194/acp-16-13601-2016

CrossRef Full Text | Google Scholar

Lehtinen, K., and Kulmala, M. (2003). Initial Steps of Particle Formation and Growth. Washington, DC: AGU Fall Meeting Abstracts.

Google Scholar

Lelieveld, J., Evans, J. S., Fnais, M., Giannadaki, D., and Pozzer, A. (2015). The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 525, 367–371. doi: 10.1038/nature15371

PubMed Abstract | CrossRef Full Text | Google Scholar

Ling, L., Li, H., Zhang, H., Zhong, J., Bai, Y., Ge, M., et al. (2018). The role of nitric acid in atmospheric new particle formation. Phys. Chem. Chem. Phys. 20, 17406–17414. doi: 10.1039/C8CP02719F

PubMed Abstract | CrossRef Full Text | Google Scholar

Makkonen, R., Asmi, A., Kerminen, V.-M., Boy, M., Arneth, A., and Hari, P. (2012). Air pollution control and decreasing new particle formation lead to strong climate warming. Atmos. Chem. Phys. 12, 1515–1524. doi: 10.5194/acp-12-1515-2012

CrossRef Full Text | Google Scholar

McMurry, P. H. (2000). A review of atmospheric aerosol measurements. Atmos. Environ. 34, 1959–1999. doi: 10.1016/S1352-2310(99)00455-0

CrossRef Full Text | Google Scholar

Merikanto, J., Spracklen, D. V., Mann, G. W., Pickering, S. J., and Carslaw, K. S. (2009). Impact of nucleation on global CCN. Atmos. Chem. Phys. 9, 8601–8616. doi: 10.5194/acp-9-8601-2009

CrossRef Full Text | Google Scholar

Miller, Y., Chaban, G. M., Jia, Z., Asmis, K. R., Neumark, D. M., and Gerber, R. B. (2007). Vibrational spectroscopy of ($S{O}_4^{2-})·{(H_{2}O)}_{\text{n}}$ clusters, n=1-5: Harmonic and anharmonic calculations and experiment. J. Chem. Phys. 127:250. doi: 10.1063/1.2764074

PubMed Abstract | CrossRef Full Text | Google Scholar

Murphy, J. G., Gregoire, P. K., Tevlin, A. G., Wentworth, G. R., Ellis, R. A., and Markovic, M. Z. (2017). Observational constraints on particle acidity using measurements and modelling of particles and gases. Faraday Discuss. 200, 379–395. doi: 10.1039/C7FD00086C

PubMed Abstract | CrossRef Full Text | Google Scholar

Myhre, G., Myhre, C. L., Samset, B., and Storelvmo, T. (2013). Aerosols and their Relation to Global Climate and Climate Sensitivity. Available online at: http://www.researchgate.net/publication/259117107_Aerosols_and_their_Relation_to_Global_Climate_and_Climate_Sensitivity

Google Scholar

Myllys, N., Chee, S., Olenius, T., Lawler, M., and Smith, J. (2019). Molecular-level understanding of synergistic effects in sulfuric acid–amine–ammonia mixed clusters. J. Phys. Chem. A 123, 2420–2425. doi: 10.1021/acs.jpca.9b00909

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishino, N., Arquero, K. D., Dawson, M. L., and Finlayson-Pitts, B. J. (2014). Infrared studies of the reaction of methanesulfonic acid with trimethylamine on surfaces. Environ. Sci. Technol. 48, 323–330. doi: 10.1021/es403845b

PubMed Abstract | CrossRef Full Text | Google Scholar

Nosé, S. (1984). A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519. doi: 10.1063/1.447334

CrossRef Full Text | Google Scholar

Olenius, T., Halonen, R., Kurtén, T., Henschel, H., Kupiainen-Määttä, O., Ortega, I. K., et al. (2017). New particle formation from sulfuric acid and amines: comparison of monomethylamine, dimethylamine, and trimethylamine. J. Geophys. Res. 122, 7103–7118. doi: 10.1002/2017JD026501

CrossRef Full Text | Google Scholar

Perraud, V., Horne, J. R., Martinez, A. S., Kalinowski, J., Meinardi, S., Dawson, M. L., et al. (2015). The future of airborne sulfur-containing particles in the absence of fossil fuel sulfur dioxide emissions. Proc. Natl. Acad. Sci. U.S.A. 112, 13514–13519. doi: 10.1073/pnas.1510743112

PubMed Abstract | CrossRef Full Text | Google Scholar

Perraud, V., Li, X., Jiang, J., Finlayson-Pitts, B. J., and Smith, J. N. (2020a). Size-resolved chemical composition of sub-20 nm particles from methanesulfonic acid reactions with methylamine and ammonia. ACS Earth Space Chem. 4, 1182–1194. doi: 10.1021/acsearthspacechem.0c00120

CrossRef Full Text | Google Scholar

Perraud, V., Xu, J., Gerber, R. B., and Finlayson-Pitts, B. J. (2020b). Integrated experimental and theoretical approach to probe the synergistic effect of ammonia in methanesulfonic acid reactions with small alkylamines. Environ. Sci. 22, 305–328. doi: 10.1039/C9EM00431A

PubMed Abstract | CrossRef Full Text | Google Scholar

Pope, C. A., and Dockery, D. W. (2006). Health effects of fine particulate air pollution: lines that connect. J. Air Waste Manage. Assoc. 56, 709–742. doi: 10.1080/10473289.2006.10464485

PubMed Abstract | CrossRef Full Text | Google Scholar

Putaud, J.-P., Van Dingenen, R., Alastuey, A., Bauer, H., Birmili, W., and Cyrys, J. (2010). A European aerosol phenomenology – 3: physical and chemical characteristics of particulate matter from 60 rural, urban, and kerbside sites across Europe. Atmos. Environ. 44, 1308–1320. doi: 10.1016/j.atmosenv.2009.12.011

CrossRef Full Text | Google Scholar

Reed, A. E., and Weinhold, F. (1983). Natural bond orbital analysis of near-Hartree–Fock water dimer. J. Chem. Phys. 78, 4066–4073. doi: 10.1063/1.445134

PubMed Abstract | CrossRef Full Text | Google Scholar

Riccobono, F., Schobesberger, S., Scott, C. E., Dommen, J., Ortega, I. K., and Rondo, L. (2014). Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles. Science 344, 717–721. doi: 10.1126/science.1243527

PubMed Abstract | CrossRef Full Text | Google Scholar

Saxon, A., and Diaz-Sanchez, D. (2005). Air pollution and allergy: you are what you breathe. Nat. Immunol. 6, 223–226. doi: 10.1038/ni0305-223

PubMed Abstract | CrossRef Full Text | Google Scholar

Schobesberger, S., Franchin, A., Bianchi, F., Rondo, L., Duplissy, J., and Kürten, A. (2015). On the composition of ammonia–sulfuric-acid ion clusters during aerosol particle formation. Atmos. Chem. Phys. 15, 55–78. doi: 10.5194/acp-15-55-2015

CrossRef Full Text | Google Scholar

Sebastianelli, P., Cometto, P. M., and Pereyra, R. G. (2018). Systematic characterization of gas phase binary pre-nucleation complexes containing H₂SO₄ + X, [X = NH₃, (CH₃)NH₂, (CH₃)₂NH, (CH₃)₃N, H₂O, (CH₃)OH, (CH₃)₂O, HF, CH₃F, PH₃, (CH₃)PH₂, (CH₃)₂PH, (CH₃)₃P, H₂S, (CH₃)SH, (CH₃)₂S, HCl, (CH₃)Cl]. A computational study. J. Phys. Chem. A 122, 2116–2128. doi: 10.1021/acs.jpca.7b10205

PubMed Abstract | CrossRef Full Text | Google Scholar

Sipila, M., Berndt, T., Petaja, T., Brus, D., Vanhanen, J., Stratmann, F., et al. (2010). The role of sulfuric acid in atmospheric nucleation. Science 327, 1243–1246. doi: 10.1126/science.1180315

PubMed Abstract | CrossRef Full Text | Google Scholar

Spracklen, D. V., Carslaw, K. S., and Kulmala, M. (2006). The contribution of boundary layer nucleation events to total particle concentrations on regional and global scales. Atmos. Chem. Phys. 6, 5631–5648. doi: 10.5194/acp-6-5631-2006

CrossRef Full Text | Google Scholar

Steinfeld, J. I. (1998). Atmospheric chemistry and physics: from air pollution to climate change. Environment 40, 26–26. doi: 10.1080/00139157.1999.10544295

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, J. (2007). Optimization of parameters for semiempirical methods V: modification of NDDO approximations and application to 70 elements. J. Mol. Model. 13, 1173–1213. doi: 10.1007/s00894-007-0233-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Stolzenburg, M. R., and McMurry, P. H. (1991). An ultrafine aerosol condensation nucleus counter. Aerosol Sci. Technol. 14, 48–65. doi: 10.1080/02786829108959470

PubMed Abstract | CrossRef Full Text | Google Scholar

Takayanagi, T., Yoshikawa, T., Kakizaki, A., Shiga, M., and Tachikawa, M. (2008). Molecular dynamics simulations of small glycine–(H₂O)_n (n=2–7) clusters on semiempirical PM6 potential energy surfaces. J. Mol. Struct. 869, 29–36. doi: 10.1016/j.theochem.2008.08.016

CrossRef Full Text | Google Scholar

Tian, L., and Chen, F. (2012). Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592. doi: 10.1002/jcc.22885

PubMed Abstract | CrossRef Full Text | Google Scholar

Tosso, R. D., Andujar, S. A., Gutierrez, L., Angelina, E., Rodríguez, R., Nogueras, M., et al. (2013). Molecular modeling study of dihydrofolate reductase inhibitors. Molecular dynamics simulations, quantum mechanical calculations, and experimental corroboration. J. Chem. Inform. Model. 53, 2018–2032. doi: 10.1021/ci400178h

PubMed Abstract | CrossRef Full Text | Google Scholar

VandeVondele, J., Krack, M., Mohamed, F., Parrinello, M., Chassaing, T., and Hutter, J. (2005). Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 167, 103–128. doi: 10.1016/j.cpc.2004.12.014

CrossRef Full Text | Google Scholar

von Schneidemesser, E., Monks, P. S., Allan, J. D., Bruhwiler, L., Forster, P., and Fowler, D. (2015). Chemistry and the linkages between air quality and climate change. Chem. Rev. 115, 3856–3897. doi: 10.1021/acs.chemrev.5b00089

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Khalizov, A. F., Zheng, J., Xu, W., Ma, Y., and Lal, V. (2010). Atmospheric nanoparticles formed from heterogeneous reactions of organics. Nat. Geosci. 3, 238–242. doi: 10.1038/ngeo778

CrossRef Full Text | Google Scholar

Wang, M., Mei, Y., and Ryde, U. (2019). Host–guest relative binding affinities at density-functional theory level from semiempirical molecular dynamics simulations. J. Chem. Theory Comput. 15, 2659–2671. doi: 10.1021/acs.jctc.8b01280

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, R. J., Marti, J. J., McMurry, P. H., Eisele, F. L., Tanner, D. J., and Jefferson, A. (1996). Measured atmospheric new particle formation rates: implications for nucleation mechanisms. Chem. Eng. Commun. 151, 53–64. doi: 10.1080/00986449608936541

CrossRef Full Text | Google Scholar

Weber, R. J., McMurry, P. H., Eisele, F. L., and Tanner, D. J. (1995). Measurement of expected nucleation precursor species and 3-500-nm diameter particles at mauna loa observatory. Hawaii. J. Atmos. Sci. 52, 2242–2257. Available online at: https://journals.ametsoc.org/view/journals/atsc/52/12/1520-0469_1995_052_2242_moenps_2_0_co_2.xml (accessed April 5, 2022).

Google Scholar

Xantheas, S. S. (1995). Ab initio studies of cyclic water clusters (H₂O)n, n=1–6. III. Comparison of density functional with MP2 results. J. Chem. Phys. 102, 4505–4517. doi: 10.1063/1.469499

CrossRef Full Text | Google Scholar

Xu, J., Finlayson-Pitts, B. J., and Gerber, R. B. (2017). Nanoparticles grown from methanesulfonic acid and methylamine: microscopic structures and formation mechanism. Phys. Chem. Chem. Phys. 19, 31949–31957. doi: 10.1039/C7CP06489F

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, F., Wang, Z., Luo, G., and Turco, R. (2008). Ion-mediated nucleation as an important global source of tropospheric aerosols. Atmos. Chem. Phys. 8, 2537–2554. doi: 10.5194/acp-8-2537-2008

CrossRef Full Text | Google Scholar

Yu, H., and Lee, S.-H. (2012). Chemical ionisation mass spectrometry for the measurement of atmospheric amines. Environ. Chem. 9:190. doi: 10.1071/EN12020

CrossRef Full Text | Google Scholar

Zhang, J., and Dolg, M. (2015). ABCluster: the artificial bee colony algorithm for cluster global optimization. Phys. Chem. Chem. Phys. 17, 24173-24181. doi: 10.1039/c5cp04060d

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., and Dolg, M. (2016). Global optimization of clusters of rigid molecules using the artificial bee colony algorithm. Phys. Chem. Chem. Phys. 18, 3003–3010. doi: 10.1039/c5cp06313b

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, R. (2010). Getting to the critical nucleus of aerosol formation. Science 328, 1366–1367. doi: 10.1126/science.1189732

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, R., Khalizov, A., Wang, L., Hu, M., and Xu, W. (2012). Nucleation and growth of nanoparticles in the atmosphere. Chem. Rev. 112, 1957–2011. doi: 10.1021/cr2001756

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, F., Feng, Y.-J., Liu, Y.-R., Jiang, S., Huang, T., and Wang, Z.-H. (2019). Enhancement of atmospheric nucleation by highly oxygenated organic molecules: a density functional theory study. J. Phys. Chem. A 123, 5367–5377. doi: 10.1021/acs.jpca.9b03142

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., Liu, Y.-R., Jiang, S., Huang, T., Wang, Z.-H., and Xu, C.-X. (2020). Volatile organic compounds enhancing sulfuric acid-based ternary homogeneous nucleation: the important role of synergistic effect. Atmos. Environ. 233:117609. doi: 10.1016/j.atmosenv.2020.117609

CrossRef Full Text | Google Scholar

Zollner, J. H., Glasoe, W. A., Panta, B., Carlson, K. K., McMurry, P. H., and Hanson, D. R. (2012). Sulfuric acid nucleation: power dependencies, variation with relative humidity, and effect of bases. Atmos. Chem. Phys. 12, 4399–4411. doi: 10.5194/acp-12-4399-2012

CrossRef Full Text | Google Scholar