Lev R. Ginzburg1*John Damuth2- 1Department of Ecology and Evolution, Stony Brook University, Stony Brook, NY, United States
- 2Department of Ecology, Evolution and Marine Biology, University of California, Santa Barbara, Santa Barbara, CA, United States
Empirical observations and an analogy with the history of ballistics illuminate the ongoing debate about the default choice for types of functional responses, based on consumer interference. The two ideal views of consumer interference are: (1) There is no direct mutual interference among consumers (“prey-dependence”), and (2) Consumers show strong mutual interference, the functional response depending on the number of prey per consumer (“ratio-dependence”). Each of these minimal-information concepts are what we refer to as “root” models, of limited accuracy in themselves, but they are the base upon which we erect complex models for specific, real-world cases. We argue that the ratio dependent view coincides more naturally with the way we model the dynamics of any population, and taken alone it is the model more consistent with empirical observations. Both root models often will give the “wrong answer” when applied directly to real world cases. Nevertheless, one root model may be “less wrong” than the other. This is not unlike developments 400 years ago in physics, when two root models competed in ballistics. Galileo’s demonstration that the default trajectory of a projectile is a parabola eventually replaced what had been the dominant root model since Aristotle. Both ballistic root models are inaccurate in the presence of air friction, but the parabolic model is, overall, less wrong. We argue that the ratio-dependent model, like the parabolic trajectory, is the “less wrong” and it is therefore a natural view from which to start thinking about consumer-resource interaction and developing more elaborate models.
Introduction
All theories are abstractions. What actually occurs in nature seldom agrees completely with the predictions of any model or theory. For example, if we want to know where a thrown ball will come to earth, we now start with the basics of Newtonian theory: direction and strength of the initial force applied to the ball, and gravity. We know that in a vacuum, the ball will travel in a parabolic trajectory. But to have a more accurate predictive model for a real situation, we also know that we need to introduce other parameters such as air resistance (friction), wind, etc. So, in most cases we take a basic model (a minimally informed theory), as a starting point, and expand the model to include adjustments that make its predictions conform more and more closely with observation.
But, what basic theory or (as we will call it) “root model” should be our starting point? And, when, if ever, should we switch to a new root model? For predator-prey systems these issues were raised, but left unresolved, in Abrams and Ginzburg (2000). We see root models as basal models that cannot be meaningfully simplified (though more complex models can be built from them). In principle, we would want the root model to represent as closely (and as simply) as possible the mechanisms known to be operating in the most typical case(s). Furthermore, we expect that it should also model causal processes in a way consistent with how the same or similar processes are modeled in other circumstances. This way, we would presumably maximize the predictive power of the root model used alone; if we knew just the minimum amount of information, we would still have a reasonably accurate guess. On the other hand, even a root model that no longer represents well our current understanding of the fundamental causal mechanisms will often still “work,” if we elaborate the model with a sufficient number of additional mechanisms. All root models are “wrong,” in the sense that their predictions, alone, are not perfect. But some root models are more wrong than others. We suggest that in comparing two root models, one should prefer the one that is “less wrong.”
Of course, in practice, ecologists studying specific cases seldom use the root model by itself to investigate empirical data. Instead, a root model is, and always has been, elaborated and augmented by adding additional variables and processes that account for details regarded as relevant to the real-world situation. For example, Holling’s (1959a; 1959b) influential and widely used models of the functional response were originally based on the assumptions of the Lotka–Volterra, prey-dependent root model (see below), but extend it in various ways; such elaborated models, and their descendants, have shown considerable predictive utility. The purpose of identifying a potential alternative root model is not to argue for a wholesale discarding of models of proven practical value and their replacement with an overly simple root model. Rather, we should think of the root model as the starting place in conceptual studies, and the foundation of more complex predictive models. The preferred root model would ordinarily be the one that most faithfully represents the mechanisms at work in nature with the least possible specification of detail.
Two Alternative Root Models of the Functional Response
Standard ecological predator-prey models take the form of a pair of population growth equations, one for the predator and one for the prey. Linking these equations are a set of terms that make up the functional response. This defines the rate at which the predator population consumes prey, and, ultimately, the rate at which the predator population can grow as a result of that consumption. There are many models of the functional response, but in current theory all derive from one of two contrasting root models. These have usually been termed prey-dependent and ratio-dependent (Arditi and Ginzburg, 1989). These two versions of predator-prey interaction refer to different points on a continuum, based on the degree to which the predators are interfering with each other’s consumption. Models using prey-dependent functional responses base the growth rate of the predator population entirely on the abundance of the prey; the size of the predator population in relation to the prey has no direct effect upon the predator’s consumption rate. In ratio-dependent models, in contrast, the growth rate of the predator population depends also on the predator population size, specifically, on the ratio between predator and prey population sizes (which represents the number of prey available to each predator, on average).
The conversation in the literature has heretofore mostly focused on a distinction between these two different theoretical starting points. But we know that nature is not likely to be precisely predicted by either one. One approach to extending the root models, which we will discuss below, is a so-called consumer-dependent model that explicitly contains a single additional parameter, m, that describes the level of mutual interference among the predators (Hassell and Varley, 1969; Arditi and Akçakaya, 1990; Arditi and Ginzburg, 2012). Other commonly used complex models incorporating varying levels of consumer interference, such as Beddington–DeAngelis (Beddington, 1975; DeAngelis et al., 1975), always have more parameters than the two root models and include both root models as special cases. See also Crowley and Martin (1989).
Consumer-dependent models can be thought of as ones where consumer population growth depends on both the numbers of prey and numbers of consumers, to varying degrees. When m = 0, these models reduce to the prey-dependent root model, and where m = 1 they become identical to the ratio-dependent one. Which one of these assumptions, 0 or 1, more closely coincides with the most typical situations? Knowing how frequent, and how strong, mutual interference (m) is in nature, we can compare the predictive performance of the two root models by themselves.
Figure 1 shows empirical m values in a large sample of natural and naturalistic experimental populations compiled by Novak and Stouffer (2021). The frequency distribution shows neither a peak near 0 (as expected from the prey-dependent model), nor a random dispersion throughout the continuum, but rather a distribution with a distinct mode near (or slightly below) 1, the value expected from the ratio-dependent model. This empirical generalization seems to be becoming the accepted view (Skalski and Gilliam, 2001; DeLong and Vasseur, 2011; Arditi and Ginzburg, 2012; Molles, 2019; Novak and Stouffer, 2021). Some level of mutual interference is now seen as an important component of functional response models (DeLong, 2021). Furthermore, a few empirical interference values greater than 1 had been noticed by DeLong and Vasseur (2011) and Arditi and Ginzburg (2012), but this larger data set of Novak and Stouffer (2021), Figure 1, confirms that we should expect to see such high values regularly (see also Tyutyunov and Titova, 2021). Novak and Stouffer (2021) caution that because of the large and varied number of uncontrolled sources of variation in the included datasets, including effects of very small sample sizes in some, the accuracy and comparability of the observed m values is less than ideal. However, the qualitative result – that m exhibits a peaked distribution with values on either side of 1 and relatively few values ≈ 0, appears to be robust. Even if a small-sample bias in our current estimation techniques proves to be present it will not change this qualitative conclusion.
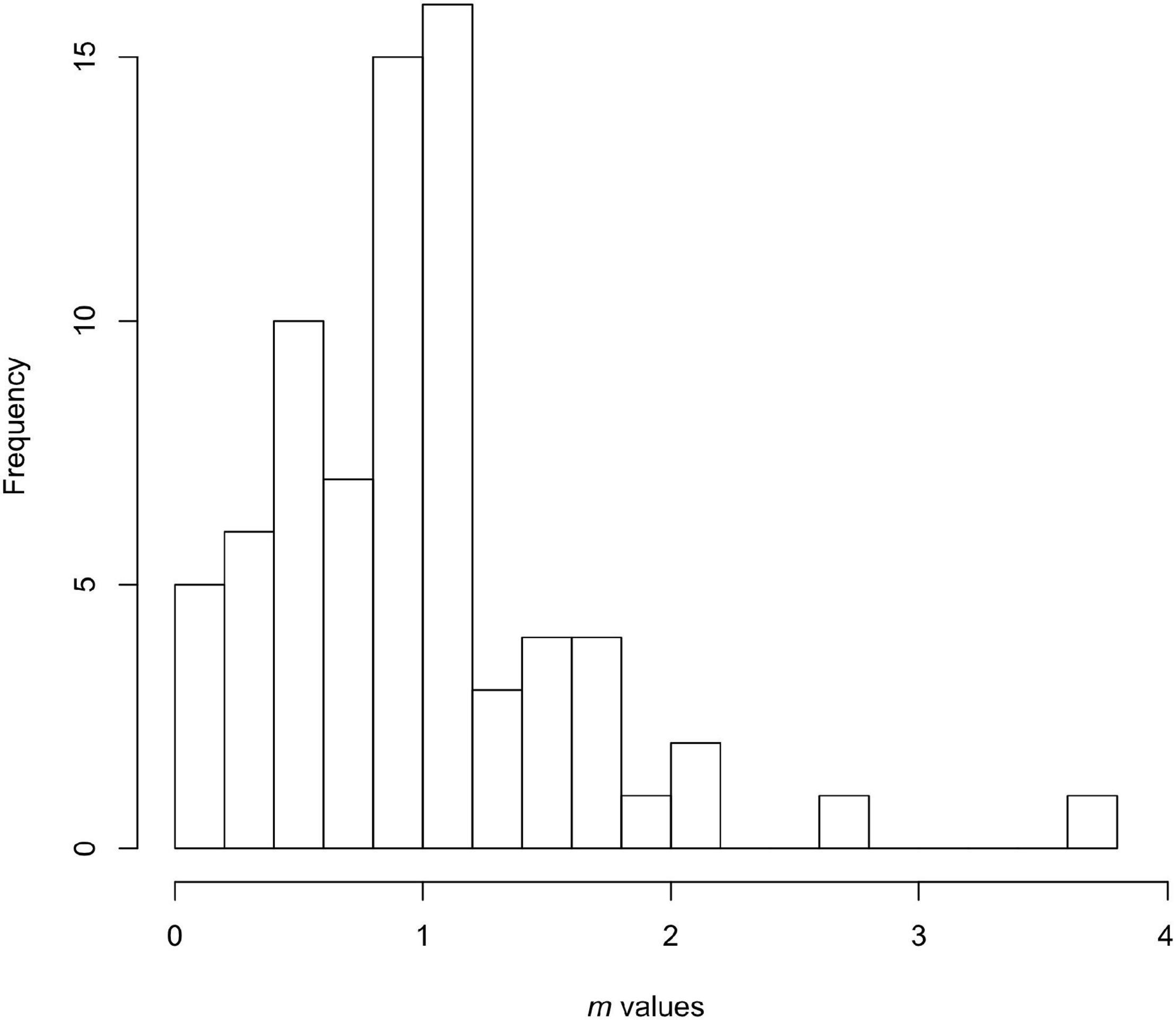
Figure 1. Values of the consumer interference parameter m estimated from the literature by Novak and Stouffer (2021), as defined by the consumer-dependent model of Arditi and Akçakaya (1990). The 75 cases range in value from 0.034 to 3.79 (two cases where the authors were unable to obtain reasonable standard errors have been omitted). The truncation at 0, positive skew, and a modal value near to but less than 1 are evident.
The empirical distribution of m suggests two things. First, since the modal value is close to the value of simple ratio-dependence, in the absence of any specific knowledge of a predator-prey system the better guess would be the ratio-dependent root model, rather than the prey-dependent one. Second, the simplest and most useful model in practice may be a consumer-dependent model that includes m and few other parameters, such as that of Arditi and Akçakaya (1990) and Arditi and Ginzburg (2012). Since the ratio-dependent root model contains the effect of mutual interactions of the predator from the beginning, and by itself corresponds closely to the empirical level of interference, why not always start conceptually with a root model that has these properties (Akçakaya et al., 1995)?
For historical reasons, though, predator-prey systems have almost exclusively been modeled as if the populations were always at the prey-dependent end of the spectrum (corresponding to m = 0). However, this extreme seems to be rare or absent in nature. In laboratory experiments it is easy to create prey dependence by using non-interfering, rarified consumers; this is not evidence for prey dependence in natural systems (Arditi et al., 2004).
The ratio-dependent root model’s rough correspondence with the mode of the distribution of m does not appear to be a coincidence. As shown by Arditi and Ginzburg (2012), stability of the predator-prey system increases as m increases from 0, up to the value of 1. Above 1, stability, for a different reason, decreases again (Arditi et al., 2004; Tyutyunov and Titova, 2021; Damuth and Ginzburg, In prep.). A value of m near 0 means that the consumer population is limited by some external factor to be extremely sparse relative to the prey; food is superabundant for the consumers and consumers don’t affect each other’s feeding. Although the prey-dependent model describes this situation well, in general prey-dependent models are unstable, and can give rise to unrealistic behavior such as the “paradox of enrichment” (Rosenzweig, 1971; Jensen and Ginzburg, 2005; Arditi and Ginzburg, 2012). The observed distribution clearly suggests processes acting to remove populations exhibiting both very low and very high values of interference. We argue elsewhere (Damuth and Ginzburg, In prep.) that two non-adaptive selection processes of the type described in Borrelli et al. (2015) guarantee that most natural predator-prey systems, after selection against the unstable extremes, will be clustered around an intermediate value of m.
Note that values of m above 1 challenge a long-standing discourse concerning prey-dependence vs. ratio-dependence. Arditi and Ginzburg (1989, 2012) treated prey- and ratio-dependence as opposite extremes of interference levels. The discussion in the literature generally followed this convention. We now think that this is an incorrect view. Prey-dependence is indeed the extreme lower limit, but ratio-dependence is not an upper limit. The pure ratio-dependent root model lies inside the range of possible interference levels, near the mode of the distribution.
Moreover, the ratio-dependent root model is also more consistent with general modeling of population dynamics than is the prey-dependent one. Under current ecological theory, we model single populations with density dependent growth, but, inconsistently, when predator and prey populations interact we depict only the prey as exhibiting density dependence due to (its own) mutual interference (Arditi and Ginzburg, 2012, pp. 148–149). So, in its predictive ability, realism, and in its consistency with related theory the ratio-dependent root model appears to be much less wrong than the prey-dependent one.
Analogy With the History of Theories of Projectile Motion
Although ballistics is a topic far from population ecology, there is a striking similarity to the current discussion in the history of a transition between two root models in physics. Beginning with Aristotle, the generally accepted view of the motion of a projectile was that it followed a roughly “triangular” trajectory (Figure 2). According to this theory, a projectile such as a cannonball traveled on an upward inclined straight line until its initial “impetus” was exhausted. It then stopped horizontal motion and fell vertically to the ground. The linear upward and horizontal movement caused by the impetus was described as “violent,” because it was initiated by the action of some agent; the vertical movement was described as “natural” because it represented the projectile returning to its natural place (on the ground).
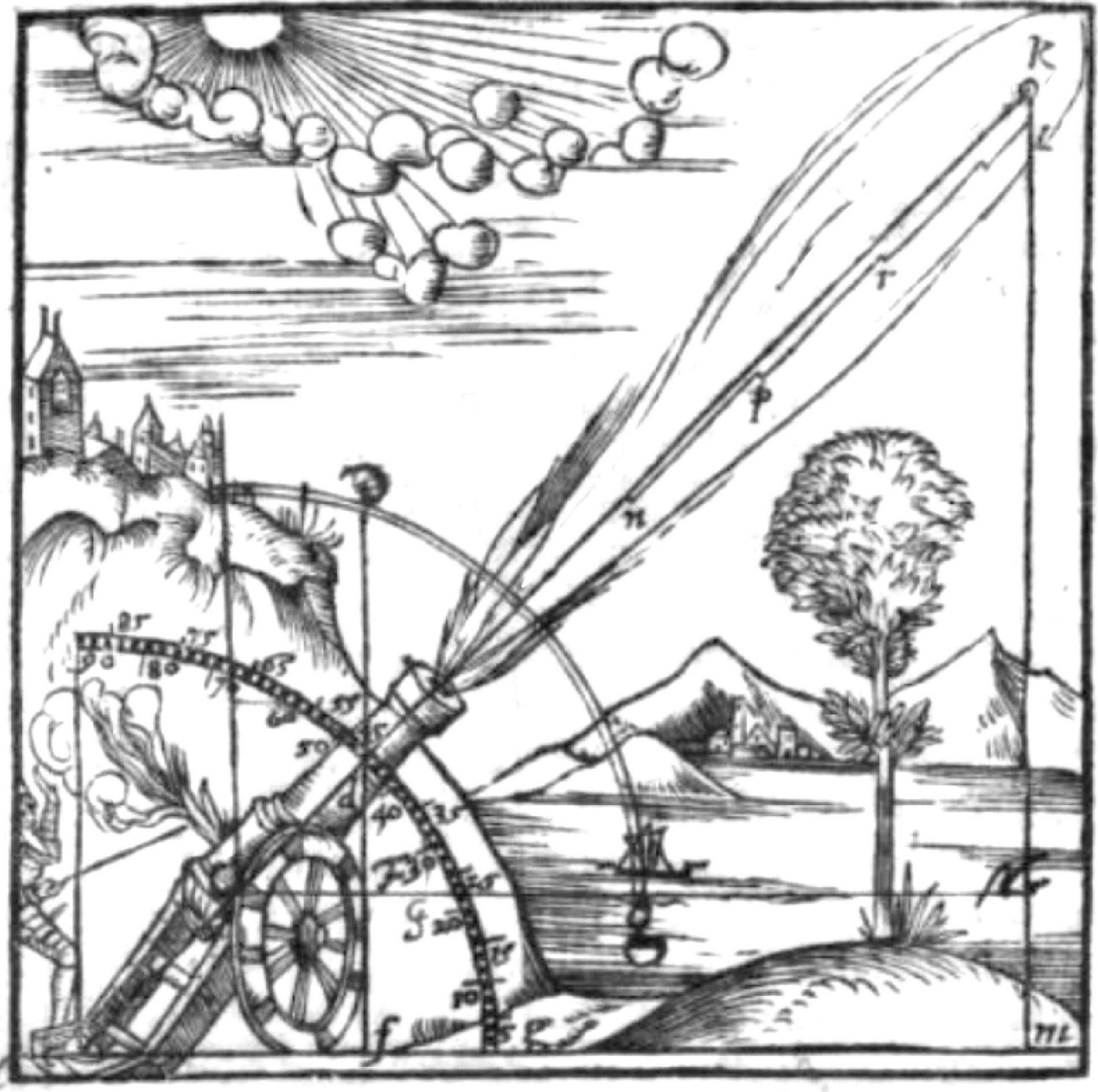
Figure 2. Santbech’s (1561, p. 212) depiction of the Aristotelian triangular theory. The cannonball flies in a straight line to k (the “violent motion”), stops, and then drops straight to the ground (k, l, m; the “natural” motion).
Over the roughly 2,000 years that this triangular root model held sway, there were attempts to correct it to make better predictions of where a projectile would land, but not by altering the basic idea of two (or more) forces that acted in sequence. Most Renaissance scholars were aware that the projectile would not stop dead in its tracks at its high point, and, following Tartaglia (1537), thought that there was a region of the trajectory where either additional forces came into play, or the effects of the two main forces “mixed” (Walley, 2018). This led to a smoothing of the upper part of the trajectory, but these adjustments did not generate a parabola, and the idea of two sequential main forces was preserved. By 1604, Galileo had demonstrated that projectiles instead followed a parabolic trajectory. He was led to this through his recognition of what we would now call inertia, and from a combination of empirical experiments and mathematical reasoning about falling objects. For Galileo, the horizontal and vertical (falling) motions were not sequential, but rather operated simultaneously throughout the projectile’s flight (Naylor, 1980). The parabolic trajectory – true only in a vacuum – is now accepted, because its basic explanatory structure, as outlined by Galileo, coincides with the simultaneous action of inertia and gravity, as found in classical Newtonian mechanics (developed more than 80 years after Galileo’s discovery).
The triangular root model was so successfully replaced by the parabolic one that by now it is entirely forgotten. However, in the real world, where forces such as air friction also intervene, a projectile will not follow either a parabolic or a triangular trajectory. Under the right real-world conditions, serviceable predictions of the landing point of the projectile might be made from the triangular root model, and the prediction could by chance even be more accurate than that yielded by the parabolic root model by itself (Stewart, 2012). But we do not regard the issue as a question of which root model alone gives us the best prediction under specific, real-world conditions, but rather a choice between which root model is “less wrong” to begin with. The parabolic theory is consistent with Newtonian mechanics and predicts better in a vacuum; to study typical cases in our experience, we now start thinking about the projectile from the parabolic (less wrong) ideal, and then add air friction, etc., if necessary, to achieve more accurate results.
One of the signs that a root model is in trouble is the way that it conflicts with more general bodies of theory concerning similar situations. In 1604, Galileo was not aware of Newton’s laws of motion (1687). However, now we can easily and naturally identify the components of Galileo’s theory as Newtonian inertia and gravity, which underlie all of classical mechanics. If we still adhered to the triangular view of projectile motion, we would expect most macroscopic objects in the universe to obey Newton’s laws, but projectiles would require a different set of special laws unique to them, which would derive from different principles. Thus the continued use of the triangular root theory would be at the cost of the isolation of ballistics from the rest of classical mechanics.
Discussion
One argument against our position could be that it is moot; there is no need for “root models.” Or, at least, that differences among them are of little consequence. This would be because the addition of supplementary mechanisms – through the incorporation of additional model parameters – might well provide sufficient accuracy when applied to specific real-world situations, regardless of the root model on which they are based. Many, if not most, ecologists are in the position of the artillerist, whose primary goal is accurate prediction or model fit to data, given a particular task. In such cases, the theoretical underpinnings of the practical model to be used may matter less than the effect of a number of different parameters specific to the situation (e.g., DeAngelis et al., 2021).
But root models are not used only as a starting place for empirical studies. Root models are akin to null models, default models and other starting points for research efforts when data are insufficient to do better, or are intentionally left unspecified. A significant use for the root model is in conceptual investigations, where the desire is to start with a model that is realistic but that makes as few specific assumptions as possible. This is not because we think the world really is that simple, but rather because the power of conceptual results often comes from limiting the number of parameters to just those that are necessary (Ginzburg and Jensen, 2004). In this kind of modeling, we often want to start by assuming as little as possible about the details of a situation, and are thus led directly in the direction of the root model itself.
In the first case (prediction), the model’s fit to data is of paramount concern, but in the second case, the realism of the root model is of primary importance.
If we had only the sketchiest data on trajectories of various actual projectiles the parabolic root model would certainly win as the best starting point for analysis of their dynamics. In the current state of ecological knowledge of predator-prey functional responses, it is clear to us that the ratio-dependent model would be the winner when the data are similarly limited. The less we know (or want to specify) the higher the value of a root model.
Root models in long use should not be discarded on a whim. There may be practical reasons for retaining approaches that have worked well in the investigation of particular situations in the past. But when a root model predicts poorly in typical circumstances and does not conform to the general conceptual landscape, we run the risk of isolating one area from the rest of the field – even if the established root model and its modifications can provide serviceable predictions. Taken alone, the ratio-dependent root model predicts the level of mutual interference better than does the prey-dependent root model (i.e., Lotka–Volterra) and yields the most stable predator-prey dynamics. Further, it is conceptually consistent with the way we model the growth and dynamics of any ecological population, incorporating density-dependence. Powerful, more specific models, supplying more detail, can be built upon the ratio-dependent root model, as they have been on the prey-dependent one (e.g., Akçakaya et al., 1995; Hossie and Murray, 2016). Compared to the ratio-dependent root model, the prey-dependent model is so much “more wrong” that the time may have come for it to be abandoned, as was the triangular ballistic trajectory in physics.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: ele13660-sup-0001-Supinfo.pdf.
Author Contributions
Both authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Resit Akçakaya, Roger Arditi, Lara Borrell, Rafael D’Andrea, Pablo Inchausti, and Yuri V. Tuytuynov for comments on earlier versions of this manuscript. We also thank Mark Novak and Daniel Stouffer for kindly providing us with their data for Figure 1.
References
Abrams, P. A., and Ginzburg, L. R. (2000). The nature of predation: prey dependent, ratio dependent or neither? Trends Ecol. Evol. 15, 337–341. doi: 10.1016/s0169-5347(00)01908-x
Akçakaya, H. R., Arditi, R., and Ginzburg, L. R. (1995). Ratio-dependent predation: an abstraction that works. Ecology 76, 995–1004. doi: 10.2307/1939362
Arditi, R., and Akçakaya, H. R. (1990). Underestimation of mutual interference of predators. Oecologia 83, 358–361. doi: 10.1007/BF00317560
Arditi, R., Callois, J.-M., Tyutyunov, Y., and Jost, C. (2004). Does mutual interference always stabilize predator–prey dynamics? A comparison of models. Comptes Rendus Biol. 327, 1037–1057. doi: 10.1016/j.crvi.2004.06.007
Arditi, R., and Ginzburg, L. R. (1989). Coupling in predator-prey dynamics: ratio-dependence. J. Theoret. Biol. 139, 311–326.
Arditi, R., and Ginzburg, L. R. (2012). How Species Interact: Altering the Standard View on Trophic ecology. Oxford: Oxford University Press.
Beddington, J. R. (1975). Mutual interference between parasites or predators and its effect on searching efficiency. J. Anim. Ecol. 44, 331–340.
Borrelli, J. J., Allesina, S., Amarasekare, P., Arditi, R., Chase, I., Damuth, J., et al. (2015). Selection on stability across ecological scales. Trends Ecol. Evol. 30, 417–425. doi: 10.1016/j.tree.2015.05.001
Crowley, P. H., and Martin, E. K. (1989). Functional responses and interference within and between year classes of a dragonfly population. J. North Am. Benthol. Soc. 8, 211–221. doi: 10.1007/BF00378720
Damuth, J., and Ginzburg, L. R. (In prep). Nonadaptive Selection: An Evolutionary Source of Ecological Laws. Chicago, IL: University of Chicago Press.
DeAngelis, D. L., Goldstein, R. A., and O’Neill, R. V. (1975). A model for trophic interaction. Ecology 56, 881–892. doi: 10.1111/1365-2656.13499
DeAngelis, D. L., Yurek, S., Tennenbaum, S., and Lee, H. W. (2021). Hierarchical functional response of a forager on a wetland landscape. Front. Ecol. Evol. 9:729236. doi: 10.3389/fevo.2021.729236
DeLong, J. P. (2021). Predator Ecology: Evolutionary Ecology of the Functional Response. Oxford: Oxford University Press.
DeLong, J. P., and Vasseur, D. A. (2011). Mutual interference is common and mostly intermediate in magnitude. BMC Ecol. 11:1. doi: 10.1186/1472-6785-11-1
Ginzburg, L. R., and Jensen, C. X. J. (2004). Rules of thumb for judging ecological theories. Trends Ecol. Evol. 19, 121–126. doi: 10.1016/j.tree.2003.11.004
Hassell, M. P., and Varley, G. C. (1969). New inductive population model for insect parasites and its bearing on biological control. Nature 223, 1133–1137. doi: 10.1038/2231133a0
Holling, C. S. (1959a). The components of predation as revealed by a study of small-mammal predatioon of the European pine sawfly. Can. Entomol. 91, 293–320.
Holling, C. S. (1959b). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398.
Hossie, T. J., and Murray, D. L. (2016). Spatial arrangement of prey affects the shape of ratio-dependent functional response in strongly antagonistic predators. Ecology 97, 834–841. doi: 10.1890/15-1535.1
Jensen, C. X. J., and Ginzburg, L. R. (2005). Paradoxes or theoretical faulures? The jury is still out. Ecol. Modell. 188, 3–14.
Molles, M. C. Jr. (2019). Ecology: Concepts and Applications. Eighth edition. New York: McGraw-Hill.
Novak, M., and Stouffer, D. B. (2021). Systematic bias in studies of consumer functional responses. Ecol. Lett. 24, 580–593. doi: 10.1111/ele.13660
Rosenzweig, M. L. (1971). Paradox of enrichment: destabilization of exploitation ecosystems in ecological time. Science 171, 385–387. doi: 10.1126/science.171.3969.385
Santbech, D. (1561). Problemata Astronomicorum et Geometricorum Sectiones Septem. Basel: Henrich Petri and Petrus Perna.
Skalski, G. T., and Gilliam, J. F. (2001). Functional responses with predator interference: viable alternatives to the Holling type II model. Ecology 82, 3083–3092.
Stewart, S. M. (2012). On the trajectories of projectiles depicted in early ballistic woodcuts. Eur. J. Phys. 33, 149–166.
Tyutyunov, Y. V., and Titova, L. I. (2021). Ratio-dependence in predator-prey systems as an edge and basic minimal model of predator interference. Front. Ecol. Evol. 9:725041. doi: 10.3389/fevo.2021.725041
Walley, S. M. (2018). Aristotle, Projectiles and Guns. Available online at: http://arxiv.org/abs/1804.00716 (accessed June 24, 2020).
Keywords: consumer interference, ratio-dependence, prey-dependence, consumer-dependence, root models, functional response
Citation: Ginzburg LR and Damuth J (2022) The Issue Isn’t Which Model of Consumer Interference Is Right, but Which One Is Least Wrong. Front. Ecol. Evol. 10:860542. doi: 10.3389/fevo.2022.860542
Received: 23 January 2022; Accepted: 22 February 2022;
Published: 18 March 2022.
Edited by:
Thomas John Hossie, Trent University, CanadaReviewed by:
John Paul DeLong, University of Nebraska–Lincoln, United StatesLeonardo Capitani, Federal University of Rio Grande do Norte, Brazil
Copyright © 2022 Ginzburg and Damuth. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lev R. Ginzburg, bGV2QHJhbWFzLmNvbQ==