Prediction of Air Pollution Interval Based on Data Preprocessing and Multi-Objective Dragonfly Optimization Algorithm

With the rapid development of global industrialization and urbanization, as well as the continuous expansion of the population, large amounts of industrial exhaust gases and automobile exhaust are released. To better sound an early warning of air pollution, researchers have proposed many pollution prediction methods. However, the traditional point prediction methods cannot effectively analyze the volatility and uncertainty of pollution. To fill this gap, we propose a combined prediction system based on fuzzy granulation, multi-objective dragonfly optimization algorithm and probability interval, which can effectively analyze the volatility and uncertainty of pollution. Experimental results show that the combined prediction system can not only effectively predict the changing trend of pollution data and analyze local characteristics but also provide strong technical support for the early warning of air pollution.

Introduction

With the continuous development of the economy and the rising living standards, the deterioration of the environment, land desertification, greenhouse effect, and other problems have begun to plague us. In addition, the United States and other developed countries have classified indoor air pollution into the five environmental factors that endanger human health. The Health Effects Institute from the US released “State of Global Air (2020),” which indicates that, at least 6.7 million people worldwide, will die from chronic exposure to air pollution in 2019 (State of Global Air, 2020).

Up to now, many studies have been conducted to study the problem of air pollution. Recently, to accurately measure the quality of air, particulate matter (PM) has become a significant and common index to be monitored (Beaulant et al., 2008). PM₂.₅ is one type of PM, which means that the particulate matter in the ambient air has an aerodynamic equivalent diameter less than or equal to 2.5 μm (van Donkelaar et al., 2006). It can be suspended in the air for a long period, and the higher the concentration of its content in the air, the more serious the air contamination. Compared with coarser atmospheric particles, PM₂.₅ has the following features: small particle size, large area, strong activity, easy adhesion, and long residence time in the atmosphere; thus, it has a greater impact on human health and the quality of the atmospheric environment (Sun and Li, 2020).

As a result, PM₂.₅ has become a worldwide problem to be solved, and many institutions have established various methods to accurately monitor PM₂.₅ concentrations (McKeen et al., 2007; Borrego et al., 2011; Air Quality Expert Group, 2012; Bergen et al., 2013; Wakamatsu et al., 2013).

Bai et al. (2019) proposed the DL-SSAE method as an autoencoder model to consider the advantages of seasonal analysis and deep feature learning to predict the hourly PM₂.₅ concentrations. Irina et al. developed the Community Multiscale Air Quality method with five different data preprocessing strategies to analyze the concentrations of PM₂.₅, and they found that the Kalman filter correction could compute the most precise results (Djalalova et al., 2015). In addition, Samia et al. (2012) combined autoregressive integrated moving average (ARIMA) and Ann to enhance predicting performance, and the results show that the proposed hybrid system could be used to efficiently forecast and provide useful air quality information. In addition, multiple linear regression have been utilized to forecast PM₂.₅ or PM₁₀ concentrations in the air to make decisions related to traffic restrictions in the future or support the control of air quality (Akyüz and Çabuk, 2009; Genc et al., 2010). Moreover, Banik et al. (2020) employed long short-term memory (LSTM) to analyze wind speed in various seasons, and they concluded that LSTM performs better than Elman and non-linear auto-regressive models. Osowski and Garanty (2007) used support vector machine (SVM) to decompose the original data and to predict the air quality of Poland based on wavelet representation. Another common method is the gray model (GM), which was employed by Pai et al. After comparing with other models for predicting the performance of PM₂.₅ and PM₁₀ concentrations of Taipei, they demonstrated that GM (1, 1) could be a useful early warning system for nearby citizens (Pai et al., 2013).

Additionally, the temporal convolutional network (TCN) is widely used to achieve more accurate performance. For instance, Zhu et al. (2020) solved the problem of long-term dependencies and performance degradation of a deep convolutional model by TCN, which shows that the power system with TCN performs better and more stably compared with others. Li et al. (2018) predicted oil consumption with various parameters according to TCN and found that the proposed model could obtain more satisfying results and help make decisions for the energy market. Wei designs a convolutional spiking neural network to deal with temporal datasets, which corrects and optimizes the historical performance, and more accurately forecasts wind speed. Also, this method could quantify the differences in predicting the performances that resulted from uncertainties (Wei et al., 2021). Chen et al. (2020) established a structure with the convolutional neural network (CNN) to forecast associated sequences and to handle more complex seasonal problems, which helps make useful decisions to assess power generation by providing more evidence. Yang W. et al. (2020) combined empirical mode decomposition (EMD) and TCN to forecast the remaining useful life and reduce the cost during the operation. Tian and Wang (2021) applied the temporal convolution networks with the quantile regression (TCNQR) method to judge the period of health and operation. In this study, we used TCN as one of the forecasting tools to obtain the results of air quality.

The recently developed approaches mainly belong to point forecasting, which includes some disadvantages and limitations (Wang J. et al., 2021). For example, Wang et al. (2022b) have pointed out that the point predicting approaches produce an unavoidable error during the operation, which might result in immense risks for an electric power system since it only depends on the accurate results. In addition, a considerable amount of time and high cost will be wasted if precise information cannot be provided, which is also a loss to the entire power system.

Unlike point prediction, which gives a “specific numerical prediction,” the interval forecast aims for a future period and gives an interval in which the predicted values are likely to occur, with a prediction interval corresponding to the expected probability. The interval forecast gives more prediction information than the point forecast, which means that we can get the value of the point forecast within a certain interval based on a certain probability, thus more scientifically characterizing the uncertainty of the model forecast.

As for data preprocessing, information granulation (IG) is a technique for studying the formation and representation of information grains and for information pre-processing. Fuzzy information granulation (FIG) is one type of IG first proposed by Zadeh (1997) to discuss how to deal with fuzzy datasets. FIG has been employed to acquire original data of fluctuating traffic and construct a traffic flow, predicting the approach with interval forecasting (Guo et al., 2018). Zhang and Na (2018) applied FIG to transform the historical agricultural price into FIG particles, and the forecasting results show that the proposed price predicting system model performs more efficiently with better accuracy. FIG could also be used in the power system. For example, the authors utilize FIG to remove the variability of the historical series of wind and solar energy, and the experimental results demonstrate that the developed approach performs efficiently and could help decision-makers stabilize the energy system (He et al., 2019b). Additionally, to forecast the actual streamflow data, FIG is combined with support vector regression (SVR) to provide more precise computation and eliminate the fluctuation of the streamflow, which means that the proposed model has a more accurate prediction interval of the hydrologic system (He et al., 2019a).

According to the existing research about PM₂.₅ concentrations and forecasting, we found that the majority of the models are combined models. Compared with the traditional single model, the combined models avoid the error of individual approaches and yield more accurate results. Therefore, more researchers have adopted combined models for prediction. For example, Wang S. et al. (2021) applied a novel wind power combined predicting system to obtain more precise performance, which supports further research in wind generation. Wang et al. (2022a) used four foundation models and optimized the weight coefficient using a multi-objective water cycle algorithm (MOWCA) to predict hourly PM₂.₅ concentrations. Details of a single model and combined models are summarized in Table 1. In Table 2 for detailed nomenclature in the article.

TABLE 1

Table 1. Summary of predicting approach types.

TABLE 2

Table 2. Nomenclature.

Based on the analyses above, this study employs a novel combined predicting system to monitor PM₂.₅ and PM₁₀. It integrates FIG, TCN, ARIMA, and LSTM to forecast PM₂.₅ and PM₁₀ concentrations, then uses a weight generation structure to compute each coefficient, and finally combines the single approaches to achieve a better result of the experiments.

The primary contributions and innovations of this study are shown as follows.

(1) To avoid the limitations of point predicting methods, this study proposes a useful interval predicting approach. This technique could deal with the fluctuation associated with the PM₂.₅ and PM₁₀ concentrations by quantifying the information of the original dataset. The performance of interval predicting is shown to be more effective than that of other point forecasting approaches.

(2) According to the decomposition and reconstruction techniques, this study applies the data pretreatment method to eliminate the negative influence of the initial data series. As a superior data preprocessing strategy, FIG is used to decrease high-frequency noise and to reconstruct the novel data sequences to acquire the significant elements of the historical data and facilitate the smooth implementation of the next phase.

(3) A combined model is developed in the predicting section to obtain the results of PM₂.₅ concentrations. It obtains more accurate prediction results when compared with the traditional PM₂.₅ and PM₁₀ concentrations of prediction approaches.

(4) The developed model could be employed in air quality monitoring. The proposed system and the predicting results are clearly improved by providing more useful information on air quality to people and analyzing and predicting PM₂.₅ and PM₁₀ concentrations even in more complicated conditions.

The rest of this article is organized as follows. Section “Forecasting System Development” touches upon the design of the forecasting system, including data fuzzy information granulation and the proposed combined forecasting system. Section “Framework of the Proposed Forecasting System and Parameter” describes the framework and parameters of the proposed prediction system. To further verify the accuracy and effectiveness of the proposed combined model from various aspects, detailed experimental results and analysis are presented in section “Experimental Results and Discussion”. Finally, section “Conclusion” concludes this research.

Forecasting System Development

This section develops an innovative combined predicting system to predict the PM₂.₅ and PM₁₀ concentrations in the air, which enhances the performance of the results by a data denoising strategy and a predicting approach.

Decomposition and Denoising Strategies

Fuzzy information granules (FIG) construct information granules by building fuzzy sets for each subsequence formed by discretizing the time series (Mencar and Fanelli, 2008). The core of fuzzy information granulation is to complete the fuzzification process after the window is created, which mainly includes window division and information fuzzification.

The window division is to convert the time series $\overline{\mathit{\text{R}}}=\{{\overline{\mathit{\text{R}}}}_1,{\overline{\mathit{\text{R}}}}_2,\mathrm{\dots },{\overline{\mathit{\text{R}}}}_{\mathrm{\gamma }}\}$ into the granular time series $\overline{\overline{\mathbf{\Theta }}}=\{{\overline{\overline{\mathbf{\Theta }}}}_1,{\overline{\overline{\mathbf{\Theta }}}}_2,\mathrm{\dots },{\overline{\overline{\mathbf{\Theta }}}}_{\varsigma }\}$ after information granulation by setting the time granularity $\stackrel{⌢}{\mathit{E}}$ to divide $\overline{\mathit{\text{R}}}=\{{\overline{\mathit{\text{R}}}}_1,{\overline{\mathit{\text{R}}}}_2,\mathrm{\dots },{\overline{\mathit{\text{R}}}}_{\mathrm{\gamma }}\}$ into $\underset{¯}{\mathit{\text{H}}}$ subseries $\overline{\overline{\mathbf{\Theta }}}=\{{\overline{\overline{\mathbf{\Theta }}}}_1,{\overline{\overline{\mathbf{\Theta }}}}_2,\mathrm{\dots },{\overline{\overline{\mathbf{\Theta }}}}_{\varsigma }\}$, where $\underset{¯}{\mathit{\text{H}}}=\frac{\mathrm{\gamma }}{\stackrel{⌢}{\mathit{E}}}$ and theηth subseries is ${\overline{\overline{\mathbf{\Theta }}}}_{\mathrm{\eta }}=[{\overline{\overline{\mathit{\text{R}}}}}_1^{\left(\mathrm{\eta }\right)},{\overline{\overline{\mathit{\text{R}}}}}_2^{\left(\mathrm{\eta }\right)},\mathrm{\dots },{\overline{\overline{\mathit{\text{R}}}}}_{\stackrel{⌢}{\mathit{E}}}^{\left(\mathrm{\eta }\right)}]$.

$\{{\overline{\mathit{R}}}_1,{\overline{\mathit{R}}}_2,\mathrm{\dots },{\overline{\mathit{R}}}_{\mathbf{\gamma }}\}\Rightarrow \{[{\overline{\overline{\mathit{R}}}}_1^{\left(1\right)},{\overline{\overline{\mathit{R}}}}_2^{\left(1\right)},\mathrm{\dots },{\overline{\overline{\mathit{R}}}}_{\stackrel{⌢}{\mathbf{E}}}^{\left(1\right)}],\mathrm{\dots },[{\overline{\overline{\mathit{R}}}}_1^{\left(\underset{¯}{\mathbf{H}}\right)},{\overline{\overline{\mathit{R}}}}_2^{\left(\underset{¯}{\mathbf{H}}\right)},\mathrm{\dots },{\overline{\overline{\mathit{R}}}}_{\stackrel{⌢}{\mathbf{E}}}^{\left(\underset{¯}{\mathbf{H}}\right)}]\}(2-1-1)$

The information granulation of the time series $\overline{\mathit{\text{R}}}=\{{\overline{\mathit{\text{R}}}}_1,{\overline{\mathit{\text{R}}}}_2,\mathrm{\dots },{\overline{\mathit{\text{R}}}}_{\mathbf{\gamma }}\}$ is to construct the information particles $\tilde{\mathbf{\Gamma }}=\{{\tilde{\mathbf{\Gamma }}}_1^{\prime },{\tilde{\mathbf{\Gamma }}}_2^{\prime },\mathrm{\dots },{\tilde{\mathbf{\Gamma }}}_{\mathbf{\varsigma }}^{\prime }\}$ using the fuzzy method for each of the $\underset{¯}{\mathbf{\text{H}}}$ subsequences $\overline{\overline{\mathbf{\Theta }}}=\{{\overline{\overline{\mathbf{\Theta }}}}_1,{\overline{\overline{\mathbf{\Theta }}}}_2,\mathrm{\dots },{\overline{\overline{\mathbf{\Theta }}}}_{\varsigma }\}$formed by the discretization operation.

Suppose that Z is a given theoretical domain, then a fuzzy subset Λ = {χ,Ω(χ)|χ ∈ Z} on Z, Ω(χ):χ→[0,1] represents the affiliation function of Λ. Two fuzzy subsets, Φ and Ξ, are equal, denoted by Φ = Ξ, if they have the same affiliation function, i.e., $\stackrel{⌢}{\mathbf{\Omega }}{}^{\prime }{}_{\mathbf{\Phi }}\left(\mathbf{\chi }\right)=\stackrel{⌢}{\mathbf{\Omega }}{}^{\prime }{}^{\prime }{}_{\mathbf{\Xi }}\left(\mathbf{\chi }\right)$.

In this study, the triangular fuzzy particles are chosen to construct the information grain and its affiliation function is as follows:

${\mathbf{\text{A}}}_{Tf}(\mathbf{x})=\{\begin{array}{c}\hfill \frac{\mathbf{x}-{\mathbf{I}}_{Tf}}{{\mathbf{K}}_{Tf}-{\mathbf{I}}_{Tf}},{\mathbf{\text{I}}}_{Tf}\le \mathbf{\text{x}}\le {\mathbf{\text{K}}}_{Tf}\hfill \\ \hfill 0,\mathbf{\text{x}}<{\mathbf{\text{I}}}_{Tf}\cup \mathbf{\text{x}}>{\mathbf{\text{N}}}_{Tf}\hfill \\ \hfill \frac{{\mathbf{N}}_{Tf}-\mathbf{x}}{{\mathbf{N}}_{Tf}-{\mathbf{K}}_{Tf}},{\mathbf{\text{K}}}_{Tf}<\mathbf{\text{x}}\le {\mathbf{\text{N}}}_{Tf}\hfill \end{array}(2-1-2),$

where x is the variable in the theoretical domain and I_Tf, K_Tf, and N_Tf are the three parameters of the triangular type fuzzy example affiliation function, which correspond to the lower boundary, average level, and upper boundary of the window after fuzzy particleization, respectively.

Fuzzy sets get rid of the either-or duality in classical set theory and extend the value domain of the affiliation function from the binary {0,1} to the multi-valued interval [0,1], which is a kind of extension of the set theory. Information fuzzification is the fuzzification of each information grain, and the fuzzification of a single sub-window, ${\overline{\overline{\mathbf{\Theta }}}}_{\mathbf{\mu }}$, generates multiple fuzzy sets ${\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu }}^{\prime }=[{\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu };1}^{″},{\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu };2}^{″},{\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu };3}^{″}]$.

Considering the single-window problem, ${\overline{\overline{\mathbf{\Theta }}}}_{\mathbf{\mu }}=[{\overline{\overline{\mathit{\text{T}}}}}_1^{\left(\mathbf{\mu }\right)},{\overline{\overline{\mathit{\text{T}}}}}_2^{\left(\mathbf{\mu }\right)},\mathrm{\dots },{\overline{\overline{\mathit{\text{T}}}}}_{\stackrel{⌢}{\mathbf{E}}}^{\left(\mathbf{\mu }\right)}]$ should first be viewed as a window for fuzzification. The task of fuzzification is to build a triangular fuzzy particle TFP on ${\overline{\overline{\mathbf{\Theta }}}}_{\mathbf{\mu }}=[{\overline{\overline{\mathit{\text{T}}}}}_1^{\left(\mathbf{\mu }\right)},{\overline{\overline{\mathit{\text{T}}}}}_2^{\left(\mathbf{\mu }\right)},\mathrm{\dots },{\overline{\overline{\mathit{\text{T}}}}}_{\stackrel{⌢}{\mathbf{E}}}^{\left(\mathbf{\mu }\right)}]$, which can reasonably explain the fuzzy concept M of ${\overline{\overline{\mathbf{\Theta }}}}_{\mathbf{\mu }}$. The fuzzy particle ${\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu }}^{\prime }=[{\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu };1}^{″}={\stackrel{⌢}{\mathit{\text{I}}}}_{Tf}^{\mathbf{\mu }},{\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu };2}^{″}={\stackrel{⌢}{\text{K}}}_{Tf}^{\mathbf{\mu }},{\tilde{\mathbf{\Gamma }}}_{\mathbf{\mu };3}^{″}={\stackrel{⌢}{\mathit{\text{N}}}}_{Tf}^{\mathbf{\mu }}]$ can be constructed by the relevant parameters in the determined affiliation function (2-1-2) of the triangular fuzzy particle.

Predicting Algorithm

In this section, the basic theory and equations of some forecasting approaches are described.

Auto-Regressive Integrated Moving Average Model

The AR(p) model means the auto-regressive approach of the p^th order, expressed as (Hamilton James, 2015):

${\text{y}}_t=\mathit{\text{c}}+{\mathit{\text{a}}}_{\mathit{1}}{y}_{t-1}+\mathrm{\cdots }+{\mathit{\text{a}}}_{\mathit{p}}{y}_{t-p}+u_t\mathit{\hspace{1em}\hspace{1em}}(2-2-1),$

where a₁, ⋯, a_p are indicators; c is a constant; and u_t is referred to as the random variable.

Besides, the MA(q) model represents the moving average model of the p^th order, which is defined as:

$y_t=\mathit{\text{a}}+u_t+{\mathit{\text{m}}}_{\mathit{1}}{u}_{t-1}+\mathrm{\cdots }+{\mathit{\text{m}}}_{\mathit{q}}{u}_{t-q}\mathit{\hspace{1em}\hspace{1em}}(2-2-2),$

where m₁, ⋯, m_q are the factors of the approach; y_t is always set as 0, and the expectation of y_t can be written as a. Also, u_t, u_t–1 and u_t–q could describe the white noise error terms of the initial series.

Then, the ARMA(p, q) combines the two approaches listed above, which is shown in the following formula:

$y_t=c+{\mathit{a}}_{\mathit{1}}{y}_{t-1}+\cdots +{\mathit{a}}_{\mathit{p}}{y}_{t-p}+u_t+{\mathit{m}}_{\mathit{1}}{u}_{t-1}+\cdots +{\mathit{m}}_{\mathit{q}}{u}_{t-q}(2-2-3)$

If these three approaches are employed in dealing with samples with non-stationarity evidence, we could consider taking various steps to decrease this limitation, which is regarded as ARIMA (p,d,q), where d is the degree of differencing.

Deep Learning Using Long Short-Term Memory Recurrent Neural Networks

Recurrent neural network (RNN) is one type of ANN, and the combinations of various samples become a directed cycle. LSTM is proposed to handle long series. Both LSTM and RNNs could employ some gates to fix the gradient problem. Some scientists have proved that RNNs are included in the hidden layer, which is one of the features of LSTM (Gers et al., 2000). The three layers of RNNs with LSTM demonstrated in Figure 1 present the memory cell functions.

$f_t=\mathrm{\sigma }(W_f•[C_{t-1},h_{t-1},x_t]+b{}_f)\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}}(2-2-4)$

$i_t=\mathrm{\sigma }(W_i•[C_{t-1},h_{t-1},x_t]+b{}_i)\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}}(2-2-5)$

$o_t=\mathrm{\sigma }(W_o•[C_t,h_{t-1},x_t]+b_o)\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}}(2-2-6)$

$C_t=f_t\times C_{t-1}+i_t\times {\tilde{C}}_t\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}(2-2-7)$

${\tilde{C}}_t=\mathit{\text{tanh}}(W_c•[h_{t-1},x_t]+b_c)\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}}(2-2-8)$

$h_t=o_t\times \mathit{\text{tanh}}(C_t)\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}}(2-2-9),$

where x_t is the input value; h_t is the output vector; C_t represents the cell state variable; W and b are indicator matrices and indicator; f_t, i_t, and o_t are forget, input, and output gate variables, respectively. In the equation, σ means the sigmoid formula and tanh refers to a rescale logistic sigmoid function belonging to (−1, 1).

FIGURE 1

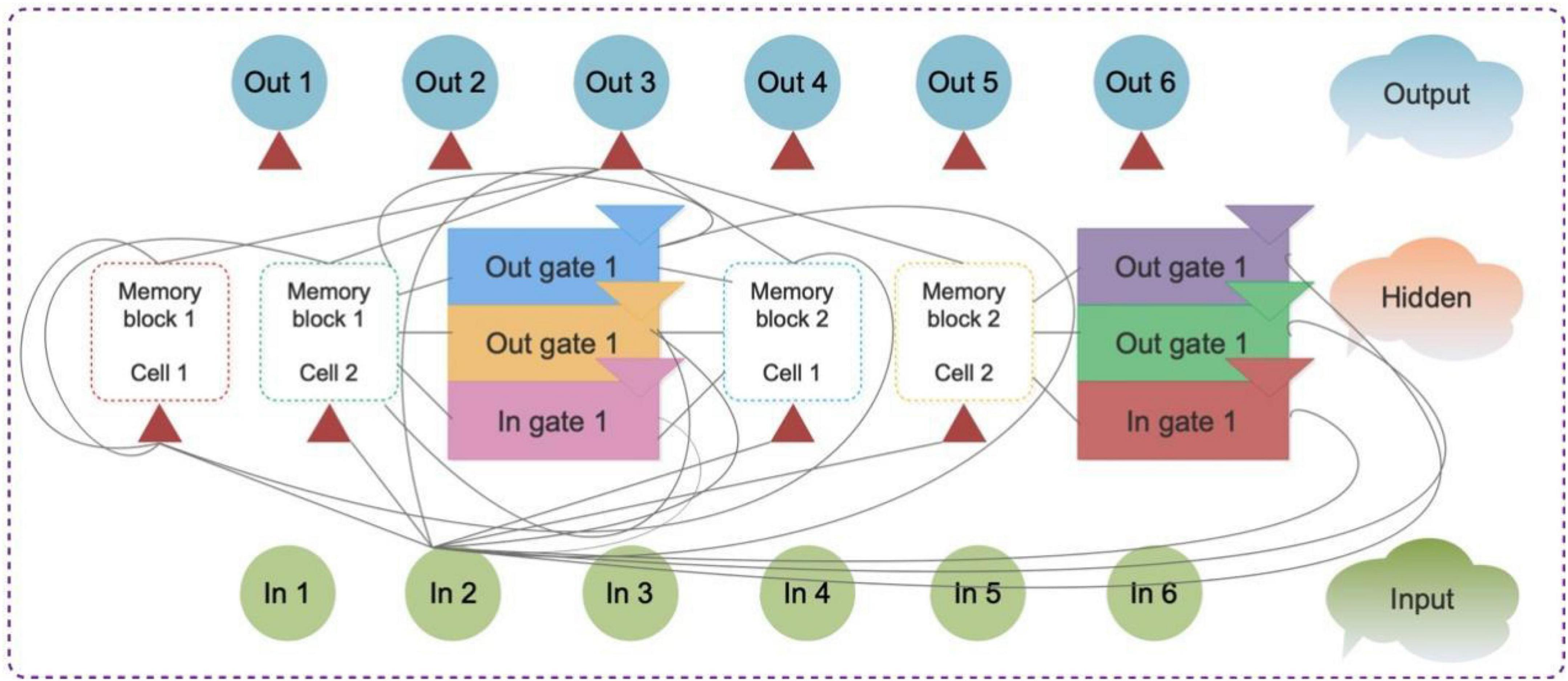
Figure 1. Three-layer long short-term memory (LSTM) of two LSTM memory blocks (Gers et al., 2000).

Temporal Convolutional Network

A TCN, an interval predicting method, is a special kind of CNN (Shelhamer et al., 2017). It includes three sections: causal convolution, dilated convolution, and residual network. The first section makes sure of the result at time β, and we assume the input value $\overleftrightarrow{\mathbf{\mu }}\in {\underrightarrow{\tilde{\mathbf{\Theta }}}}^{\text{B}}$ and a filter π : {0, …, k − 1} → $\underrightarrow{\tilde{\mathbf{\Theta }}}$. The historical convolutional layer is stated by two equations: $\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_{\mathrm{\beta }})=(\overleftrightarrow{\mathbf{\mu }}\odot \mathrm{\pi })(\mathrm{\beta })={\sum }_{j=0}^{k-1}{\mathrm{\pi }}_j{\overleftrightarrow{\mathbf{\mu }}}_{\mathrm{\beta }-j}$ and $\widetilde{\widehat{\mathit{ouse}}}=(\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_1),\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_2),\mathrm{\cdots },\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_{\text{B}}))$, where k is the size of convolutional kernel, $\widetilde{\widehat{\mathit{ouse}}}$ is the output series, and $\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}(•)$ is the process of convolution.

The second part uses a hyperparameter to jump some input values; thus, a range longer than it used to be could be accepted by the filter. In detail, if the causal convolution mixes, the m^th layer dilated convolution can be described by: $\begin{array}{c}\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_{\mathrm{\beta }})=(\overleftrightarrow{\mathbf{\mu }}\odot d_m\mathrm{\pi })(\mathrm{\beta })={\sum }_{j=0}^{k-1}{\mathrm{\pi }}_j{\overleftrightarrow{\mathbf{\mu }}}_{\mathrm{\beta }-d_{m}j}\hfill \\ \mathrm{\beta }-d_{m}j\hfill \end{array}$ and $\widetilde{\widehat{\mathit{ouse}}}=(\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_1),\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_2),\mathrm{\dots },\underleftrightarrow{\widehat{\tilde{\mathbf{\Lambda }}}}({\overleftrightarrow{\mathbf{\mu }}}_{\text{B}}))$, where d_m means the dilation indicator of the m^th layer and the range could be set to 2^m−12^m−1. Here, β−d_mj represents the historical direction. The second formula is a temporal convolutional layer, which constructs TCN in many layers.

If the layers are deep, to deal with the issue of decreased efficiency of the CNN results, a residual block is utilized. During the training procedure, we added a residual connection into the block to ensure normal operation in the deep layers. Moreover, TCN prevents the over-fitting problem by introducing the dropout layer after each dilated convolution (Srivastava et al., 2014).

Combined Model

Combining forecasts has long been recognized as an effective and a simple way to improve forecast stability, an improvement over a single model. This study proposes a new combined forecasting model that fuses ARIMA, neural networks, and the non-positive constraint theory.

The traditional forecasting combination method attempts to find the best weight of the combined models based on minimizing SSE:

$\min \mathit{\text{F}}={\mathit{\text{D}}}^T\mathit{\text{ED}}=\sum _{t=1}^T\sum _{j=1}^m\sum _{i=1}^m{d}_i{d}_j{e}_{it}{e}_{jt}\{\begin{array}{c}\hfill {\mathit{\text{R}}}^{\mathit{T}}\mathit{\text{D}}=1\hfill \\ \hfill \mathit{\text{D}}\ge 0\hfill \end{array}(2-3-1),$

where D = (d₁, d₂, …, d_m)^T is the weight vector; R = (1, 1, …, 1)^T is a column vector where all elements are 1; and E = (E = _ij)_m×m is called the error information matrix (${\mathbf{\text{E}}}_{ij}=e_i^T{e}_j$, e_i = (e_i1, e_i2, …, e_iN)).

An improvement of the traditional combination method based on the non-negative constraint theory (TCM-NNCT) and non-positive constraint theory is given as follows:

$\min \mathit{\text{J}}={\mathit{\text{D}}}^T\mathit{\text{ED}}=\sum _{t=1}^T\sum _{j=1}^m\sum _{i=1}^m{d}_i{d}_j{e}_{it}{e}_{jt}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}}(2-3-2)$

$\text{st }{\mathbf{R}}^T\mathbf{D}=1(2-3-3)$

In Eq. (2-3-1), the weight vector has no limitation in the range [0,1]. The experiment results show that the combination model can obtain desirable results if the weight vector has a value in the range of [−2,2]. This section provides a weight-determined method that will be assessed by experimental simulation rather than a theoretical proof.

Interval Prediction Based on Temporal Convolutional Network

In this section, we constructed a novel multidimensional time series CNN prediction model for air contamination forecasting and uncertainty analysis.

Interval Prediction Module

There is no need to presuppose an error distribution in an interval forecasting model that, based on a linear model, is expressed as:

$\mathbf{Y}={\tilde{\mathrm{\beta }}}_0\left(\mathrm{\theta }\right)+{\tilde{\mathrm{\beta }}}_1\left(\mathrm{\theta }\right){\mathbf{X}}_{\mathbf{1}}>+\mathrm{\cdots }+{\tilde{\mathrm{\beta }}}_n\left(\mathrm{\theta }\right){\mathbf{X}}_{\mathbf{n}}+u=\tilde{Q}(\mathrm{\theta };\mathbf{X})+\mathbf{u}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(2-4-1),$

where X is n explanatory variables, ${\tilde{\mathrm{\beta }}}_i$ is a vector that can be determined based on X and θ, and ${\tilde{\mathrm{\beta }}}_i$ is a vector that can be identified based on X and θ. Given K samples, the vector is statistically estimated: ${\tilde{\mathrm{\beta }}}_i\left(\mathrm{\theta }\right)=\arg \underset{\mathrm{\beta }}{min}{\sum }_{i=1}^{K}f\left(\mathrm{\theta }\right)[{\mathbf{\text{Y}}}_i-\tilde{Q}(\mathrm{\theta };\mathbf{X})](i=1,2,\mathrm{\dots },K)$,

where f(θ) is a piecewise linear loss function that can be defined as:

$f\left(\mathrm{\theta }\right)=\{\begin{array}{cc}\hfill \mathrm{\theta }u,\hfill & \hfill u\ge 0\hfill \\ \hfill \left(\mathrm{\theta }-1\right)u,\hfill & \hfill u<0\hfill \end{array}\mathit{\hspace{1em}\hspace{1em}}(2-4-2)$

Evaluation Index of Prediction Model and Interval Forecasting

Due to the advanced non-linear characteristics and uncertainty of air contamination data, the prediction error of a single model is usually possible. For this case, the calculation of the prediction interval, i.e., the higher and lower bounds for predicting future values, is appropriate for the prediction of air contamination data. Below the given prediction interval, the predictions are often created higher and therefore the stability of prediction can be additionally improved. Different indicators can judge the prediction results and quality of the interval prediction model, such as the following common evaluation indicators.

Prediction interval coverage probability (PICP) is the most important index to measure the quality of the prediction interval, which reflects the probability result of the observed value falling into the prediction interval, namely reliability. In other words, the greater the probability value, the more the observations covered by the prediction interval and vice versa. In general, within the established prediction interval, the calculated probability p (PICP) should be higher than the rated confidence level, namely: $p=P(f_i\in [L\left(\overline{\overline{{\mathbf{\text{X}}}_i}}\right),U\left(\overline{\overline{{\mathbf{\text{X}}}_i}}\right)])\ge \mathbf{\mu }$, i = 1, 2, …, K, where P(•) is the expressed probability; $L\left(\overline{\overline{{\mathbf{\text{X}}}_i}}\right),U\left(\overline{\overline{{\mathbf{\text{X}}}_i}}\right)$ represent the lower and upper bounds of the prediction interval predicted by $\overline{\overline{{\mathbf{\text{X}}}_i}}$, respectively; f_i is the predicted value; and μ is a given confidence level. According to Bernoulli’ law of huge numbers, ${\tilde{\mathbf{\chi }}}_{cp}$ will be expressed by the frequency that the prediction interval covers the determined value, and its likelihood converges to P, namely:

${\tilde{\mathbf{\chi }}}_{cp}=\frac{1}{D}\sum _{i=1}^D{c}_i\times 100\%\stackrel{P}{⟶}P(f_i\in [L\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right),U\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right)])(2-4-3)$

where D is the predicted sample size and C_i is a Boolean quantity.

$C_i=\{\begin{array}{c}1,\mathit{if}{f}_i\in [L\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right),U\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right)]\hfill \\ 0,\mathit{if}{f}_i\notin [L\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right),U\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right)]\hfill \end{array}\mathit{\hspace{1em}\hspace{1em}}(2-4-4)$

If ${\tilde{\mathbf{\chi }}}_{cp}\ge \mathbf{\mu }$, it indicates that the established prediction interval is valid; otherwise, it indicates that the established prediction interval is invalid, and it should be reestablished.

To decide the prediction interval more reasonably, it is necessary to depend on the prediction interval mean width percentage (PIMWP), which is the parameter basis for evaluating the prediction interval. If the forecast interval is wide enough, the coverage of the forecast interval will be on the brink of 100%. However, such a good interval cannot effectively provide the uncertainty data of the predicted value, rendering the results of the forecast interval meaningless.

If ${\tilde{\mathbf{\chi }}}_{cp}$ is larger and ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$ is smaller, the prediction interval of the model is more accurate and the performance is better.

${\overline{\tilde{\mathbf{\chi }}}}_{MWP}=\frac{1}{D}\sum _{i=1}^D\frac{U\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right)-L\left(\overline{\overline{{\mathit{\text{X}}}_i}}\right)}{{\mathit{\text{f}}}_{\mathit{i}}}\times 100\%\mathit{\hspace{1em}\hspace{0.5em}\hspace{1em}}(2-4-5)$

In addition, single high reliability and high clarity cannot reflect the performance of the interval prediction model, which is one of the biggest differences with the evaluation index of the deterministic prediction model. ${\tilde{\mathbf{\chi }}}_{cp}$The performance evaluation indexes, ${\tilde{\mathbf{\chi }}}_{cp}$ and ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, are often used to predict interval models. However, if some special situations occur, these two indicators cannot achieve a reasonable and scientific performance evaluation of the interval prediction model. For example, if the observed value is not within the prediction interval and if there is a small difference between ${\tilde{\mathbf{\chi }}}_{cp}$ and ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$ at the same time, it is impossible to measure the degree of deviation of the observed value from the prediction interval. The extent to which observations deviate from the predicted interval is immeasurable. To compensate for the shortcomings of ${\tilde{\mathbf{\chi }}}_{cp}$ and ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, this study introduces another evaluation index of the prediction interval model, namely accumulated width deviation (AWD), which can clearly measure the deviation degree of observed values outside the prediction interval. Here, ${\overline{\overline{\mathbf{\chi }}}}_{AWD}={\sum }_{i=1}^D{\mathrm{\zeta }}_i$, where ζ_i represents the degree to which the observed value deviates from the upper and lower bounds of the predicted interval.

${\mathbf{\zeta }}_i=\{\begin{array}{c}\frac{L\left(\overline{\overline{{\mathbf{X}}_i}}\right)-f_i}{f_i},\mathbf{if}{f}_i<L\left(\overline{\overline{X_i}}\right)\hfill \\ 0,\mathbf{if}{f}_i\in [L\left(\overline{\overline{X_i}}\right),U\left(\overline{\overline{X_i}}\right)]\hfill \\ \frac{f_i-U\left(\overline{\overline{X_i}}\right)}{f_i},\mathbf{if}{f}_i>U\left(\overline{\overline{X_i}}\right)\hfill \end{array}(2-4-6)$

Under the condition of the same ${\tilde{\mathbf{\chi }}}_{cp}$ and ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, the smaller the value of ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$, the higher the quality of the prediction interval.

The above three evaluation indicators, ${\tilde{\mathbf{\chi }}}_{cp}$, ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, and ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$, are independent of each other, and only a certain feature of the prediction interval is considered. However, if only one evaluation index is selected, it is not enough to explain the quality and performance of the prediction interval. A high-quality prediction interval should conform to the confidence level requirements, i.e., ${\tilde{\mathbf{\chi }}}_{cp}$ should be as high as possible while ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$ and ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$ should be as low as possible. However, the definitions of ${\tilde{\mathbf{\chi }}}_{cp}$, ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, and χ_AWD show that these three metrics are conflicting with each other: the higher the ${\tilde{\mathbf{\chi }}}_{cp}$, the higher the ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$; the lower ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, the lower ${\tilde{\mathbf{\chi }}}_{cp}$ and the higher ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$; the lower the ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$ is, the higher the ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$ is. Therefore, taking these three indicators into consideration, this study proposes a comprehensive index that can quantitatively evaluate the prediction interval, namely, prediction interval satisfaction index (PISI). It can be calculated by:

${\mathbf{\chi }}_{PISI}=\left[1-\left(1+\mathrm{\lambda }\times {\overline{\overline{\mathbf{\chi }}}}_{AWD}\right){\overline{\tilde{\mathbf{\chi }}}}_{MWP}\times \left(1+e^{-\mathrm{\eta }\left({\mathbf{\chi }}_{cp}-\mathbf{\mu }\right)}\right)\right]\times 100\%\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(2-4-7),$

where λ is the penalty factor of ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$, η is the penalty factor of ${\tilde{\mathbf{\chi }}}_{cp}$, and μ (95%) is the given confidence level. In this study, we choose λ = 0.5 and η = 50.

If ${\tilde{\mathbf{\chi }}}_{cp}$ is greater than the given confidence level μ, the curve of χ_PISI is flat and the value of χ_PISI tends to 1. At this point, χ_PISI is mainly determined by ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$ and ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$. If ${\tilde{\mathbf{\chi }}}_{cp}$ is less than the given confidence level μ, the value of χ_PISI changes according to the difference between ${\tilde{\mathbf{\chi }}}_{cp}$ and μ, and χ_PISI is mainly determined by ${\tilde{\mathbf{\chi }}}_{cp}$ at this time. Therefore, χ_PISI can further reflect the quality of the prediction interval by combining ${\tilde{\mathbf{\chi }}}_{cp}$, ${\overline{\tilde{\mathbf{\chi }}}}_{MWP}$, and ${\overline{\overline{\mathbf{\chi }}}}_{AWD}$, making the evaluation of the prediction interval more effective and accurate.

Framework of the Proposed Forecasting System and Parameter

This section presents the description of the material analyzed (section “Dataset Description”) and the entire probabilistic forecasting system applied in this study (section “Flow of the Proposed Ensemble Probabilistic Forecasting System”).

Dataset Description

This study took the PM₂.₅ and PM₁₀ pollution data of Beijing, Shanghai, and Shenzhen as the experimental data set, which are daily data from January 2020 to December 2021. From each dataset, we extracted 4,386 point values as experimental sequences and selected 80% of the total length as training sets. The remaining 20% points were divided into test sets as shown in Figure 2.

FIGURE 2

Figure 2. Information of the research areas.

Flow of the Proposed Ensemble Probabilistic Forecasting System

In accordance with the aforementioned data processing approaches and forecasting models, the proposed forecasting system includes Fuzzy information granulation, ARIMA, LSTM, TCN, multi-objective optimization, and interval prediction.

Step 1: The original three data sets were divided into a training set and a test set. A total of 4,386 pieces of data were collected. There were 3,500 pieces of data in training sets and 877 pieces of data in test sets.

Step 2: The pollution values of PM₂.₅ and PM₁₀ are reconstructed by graining Fuzzy information granulation and the data after noise reduction has been obtained.

Step 3: ARIMA, LSTM, and TCN were used for forecasting, and they were used as the comparative models of the multi-target dragonfly combination prediction results in the fourth step.

Step 4: The prediction results of ARIMA, LSTM, and TCN were combined with a multi-objective Dragonfly algorithm for optimization.

Step 5: Probabilistic forecasting module: The upper and lower bounds and the prediction interval were obtained by using interval prediction to forecast the progress of PM₂.₅ and PM₁₀ data.

By constructing the prediction interval, the probability prediction of air pollution is carried out. To determine the distribution of forecast errors resulting from point forecasts, three metrics were used: the PICP, the BW, and the PINAW. Furthermore, interval forecasts were created by combining upper and lower bounds with an optimal distribution with a design confidence level of 95%.

Model Selection and Parameter Setting

In general, a hybrid forecasting system adopts a decomposition strategy using a shallow neural network; all of the ARIMA and LSTM have satisfactory performance in solving regression problems. In DL, the TCN based on multidimensional time series is sensitive to the prediction of statistical data. Therefore, we selected the multi-objective dragonfly optimization algorithm based on the multidimensional time series for interval prediction. The model naming and argument details of the other models are presented in Table 3.

TABLE 3

Table 3. Compare the parameter settings of each model.

Evaluation Index

In this study, five evaluation indexes [such as the mean absolute percentage error (MAPE) and root mean square error (RMSE)] were used to assess the prediction system stability and accuracy, and other indicators were used to evaluate the interval prediction capability. Table 4 presents the specific equations and definitions.

TABLE 4

Table 4. Evaluation metrics applied in this study.

Experimental Results and Discussion

This section discusses in detail the fuzzy granulation strategy based on multi-dimensional time series, the multi-objective dragonfly optimization algorithm, and the simulation results of interval prediction. To further improve the prediction results, the prediction efficiency (FE) and improvement rate (IR) of the proposed combined prediction model and interval prediction, as well as sensitivity, are analyzed in the study.

Data Pre-processing: Fuzzy Information Granulation

Through fuzzy information granulation, the pollution data of PM₂.₅ and PM₁₀ are processed.

Specific steps are as follows:

(1). To confirm sample extraction and fuzzification processing, sample information needs to be extracted to a certain extent. Then, the specific size of the window can be understood through the extracted data. Later, fuzzy information granulation processing is carried out according to the formula (2-1-1).

(2). The minimum, average, and maximum values are normalized after granulation treatment. The processing formula is:

${\mathit{\text{p}}}_i=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }},$

where p_i is a variable data in the sample data; x_i is the normalized data coefficient; x_min is the minimum value of the extracted data; and x_maxis the maximum value in the sample.

In the subsequent combined prediction model, we use the granulated average R as the input for training and testing. The comparison result of fuzzy granulation with the original data is shown in Figure 3.

FIGURE 3

Figure 3. Data preprocessing flowchart.

Multi-Objective Optimization Combination Forecasting and Comparison Model

This section compares the proposed combined forecasting model with the commonly used single-point forecasting models. The single models of point prediction include ARIMA, LSTM, and T-convolutional neural network.

Experiment I: PM₂.₅ and PM₁₀ forecasting.

In this experiment, three traditional single models, ARIMA, LSTM, and TCN, are utilized to compare with the proposed system. The prediction results are shown in Tables 5, 6.

TABLE 5

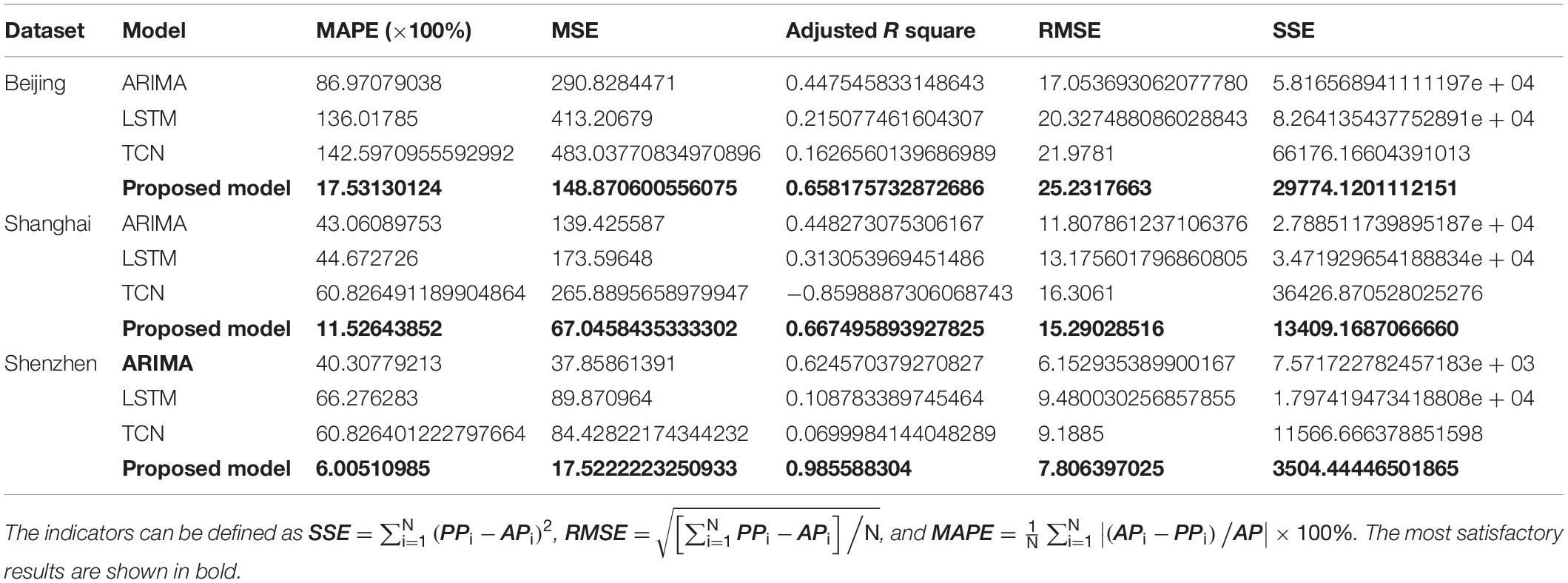
Table 5. Statistical errors of the proposed system and three traditional models for daily PM_2.5 concentrations of Beijing, Shanghai, and Shenzhen.

TABLE 6

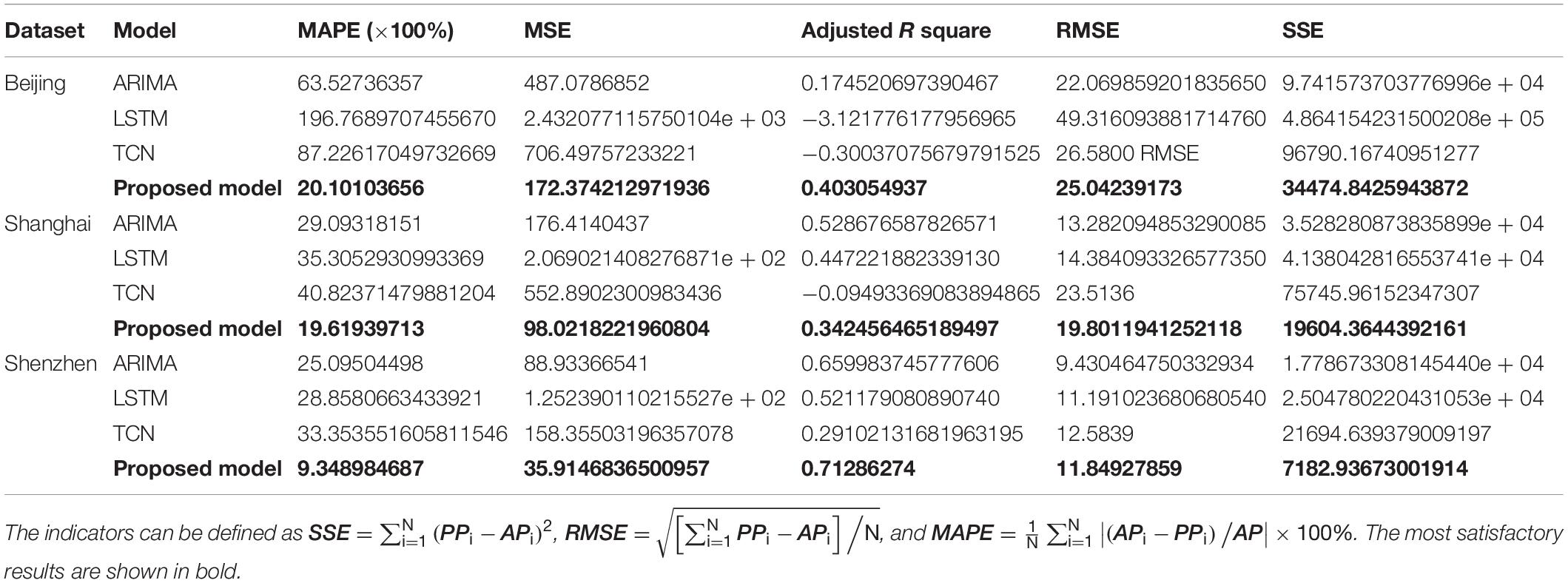
Table 6. Statistical errors of the proposed system and three traditional models for daily PM₁₀ concentrations of Beijing, Shanghai, and Shenzhen.

(a) From Tables 5, 6, we can see that the proposed model has achieved significant improvements compared with the three single models. In the forecast of PM₂.₅ daily concentration in the three cities, the MAPE (×100%) of the model in this study are 17.53130124, 11.52643852, and 6.00510985, respectively, and the MAPE of PM₁₀ are 20.10103656, 19.61939713, and 9.348984687, respectively. In addition, there are substantial improvements in other data comparisons, which demonstrate the superior predictive power of the proposed model in simulating air contamination series.

(b) MAPE and RMSE are mainly used to measure the prediction error of each model. The smaller the value, the better the model prediction performance. In addition, the R index mainly evaluates the fit consistency between the original value and the predicted value. The index values of the system are all larger than the reference model, indicating that the system has a better simulation effect on the air pollution sequence. The R value is negative, indicating that the model is not suitable for simulating the air pollution series.

Experiment II: SO2 and CO forecasting.

In Experiment I, we performed prediction experiments using PM2.5 and PM10 data, which achieved good results. To further verify the effectiveness of the prediction system, in Experiment 2, the SO₂ and CO data of three cities were used to conduct the experiment again.

Therefore, in this part, we selected the CO value and sulfur dioxide data of three cities for comparative experiments. The detailed results are shown in Table 7.

TABLE 7

Table 7. The forecasting performances of various models for SO₂ and CO in three cities.

To further explore the application of the point prediction system, this experiment used SO₂ and CO daily datasets in Beijing, Shanghai, and Shenzhen to examine the superiority and applicability of the developed system. The results showed that the model proposed in this study not only exhibits the best prediction performance, indicating that the prediction system in this study is not only suitable for the prediction of PM₂.₅ and PM₁₀, but also for the prediction of other air pollutants. Although the randomness and complexity of different datasets are different, the results show that the proposed model has strong applicability and effectiveness for the prediction of various air pollution and has potential application prospects in air pollution monitoring.

Indexes of Prediction Model and Interval Forecasting

Point forecasting only provides each forecast point for the target and does not show the probability of correct forecasting. However, in several problems, it is necessary to quantify the accuracy of estimates using countermeasures. Once the extent of uncertainty increases, the dependability of the point prediction decreases significantly. In contrast to point forecasting, prediction intervals not only provide the location in which observations are presumably made but also conjointly provide an indicator of capability known as the confidence level. Since interval forecasting is more reliable and informative than the settled point forecast, it is helpful to investigate and evaluate the data.

Experiment III: Interval forecasting and evaluation index.

To comprehensively evaluate the forecast results of the prediction model, four analysis indexes are adopted in the study, including the prediction interval coverage probability (PICP), coverage width criterion (CWC), prediction band width (PBW), and PI normalized averaged width (PINAW).

Prediction interval coverage probability is the basic evaluation index to assess the overall probability of the actual value falling into the PBW, and it is expressed as follows:

$\mathit{\text{PICP}}=\left(\frac{1}{n}\sum _{i=1}^n{\overline{\overline{\mathit{\text{C}}}}}_i\right)\times 100\%\mathit{\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.25em}}(4-3-1)$

${\overline{\overline{\mathit{\text{C}}}}}_i=\{\begin{array}{c}0{\mathit{\text{y}}}_i\notin ({\mathit{\text{L}}}_i,{\mathit{\text{U}}}_{\mathit{I}})\hfill \\ 1{\mathit{\text{y}}}_i\in ({\mathit{\text{L}}}_{\mathit{I}},{\mathit{\text{U}}}_{\mathit{I}})\hfill \end{array}\mathit{\hspace{1em}\hspace{1em}}(4-3-2),$

Where the variable y_i is the actual air contamination value. U_i and L_i represent the upper and lower bounds, respectively, and n is the number of samples.

If the PI width is sufficiently large, the PICP can easily reach 100%. Considering that the PICP meets the prediction interval nominal confidence (PINC) of the required prediction interval, the PBW should be as small as possible to guarantee the prediction effect.

Due to the contradiction between PICP and PINRW, CWC is used as a comprehensive evaluation index. In addition, because PICP is a basic evaluation indicator compared with PINAW (or PINRW) and is expected to achieve the desired nominal confidence level μ, an improved CWC design can assess the prediction effect better.

The modified CWC used in the experiment is defined as follows:

${\text{CWC}}_{proposed}=\{\begin{array}{c}{\mathrm{\eta }}_{\mathit{1}}\cdot \mathit{\text{PINAW}}(\text{PICP}\ge \mathbf{\mu })\hfill \\ (0.1+{\mathbf{\mu }}_{\mathit{1}}\cdot \mathit{\text{PINAW}})[1+\exp ({\mathrm{\eta }}_{\mathit{2}}(\mathbf{\mu }-\mathit{\text{PICP}}))]\hfill \\ (\text{PICP}<\mathbf{\mu })\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} (4-3-3)\hfill \end{array}$

PBW, PICP, PINAW, and CWC are used to assess the IP performance. The detailed forecasting results of the proposed hybrid forecasting system and the comparative models are presented in Figure 4 and Table 8.

FIGURE 4

Figure 4. A graph of interval prediction results.

TABLE 8

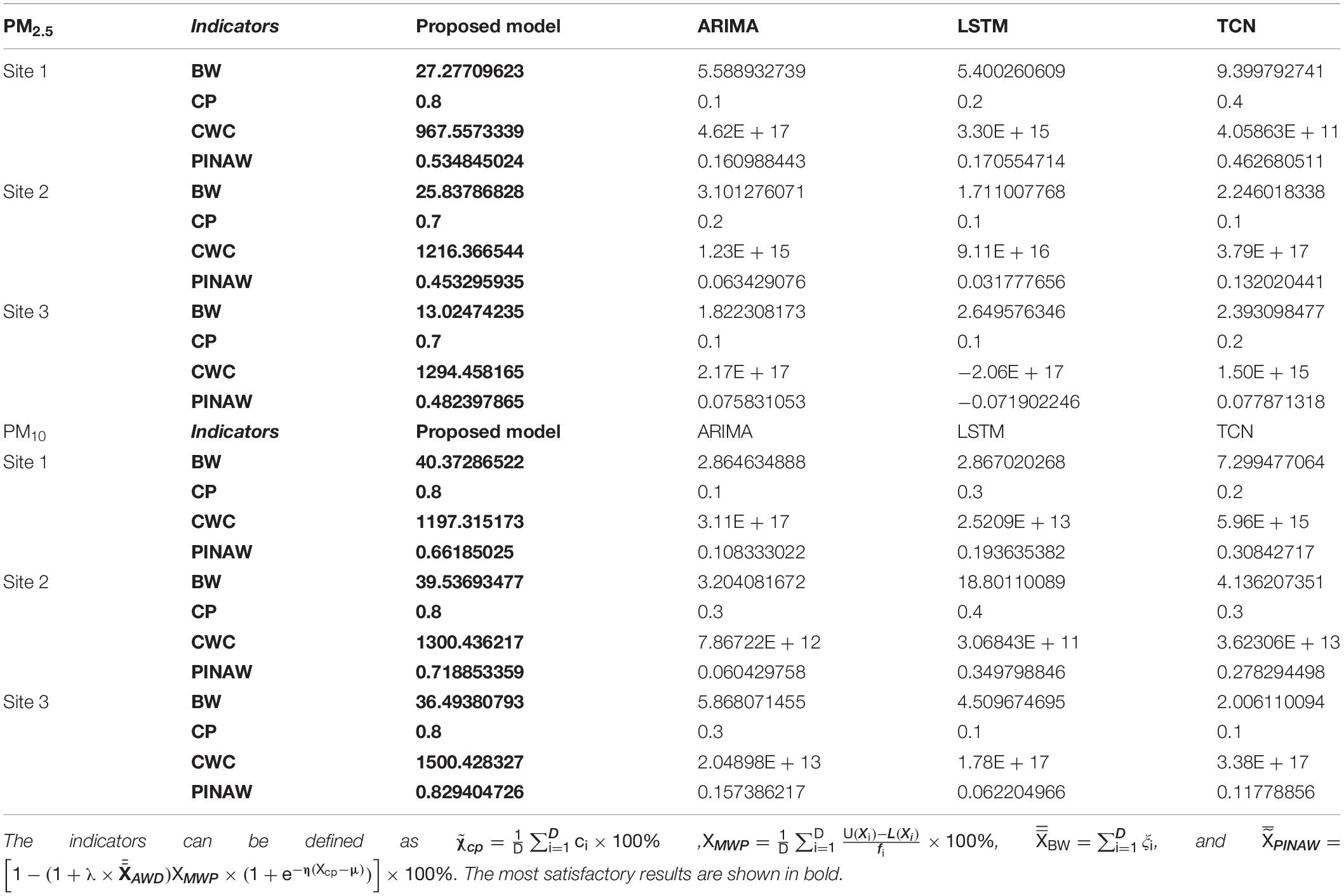
Table 8. Interval forecasting results of the proposed system for daily PM_2.5 and PM₁₀concentrations of Beijing, Shanghai, and Shenzhen.

(a) After optimization using the combined prediction algorithm, the interval prediction can estimate the upper and lower bounds of the probability prediction. Then, PICP, PINAW, and CWC indicators are selected to measure the performance of interval prediction of air pollution series. PICP mainly measures the probability of the original data entering the prediction interval, and PINAW is used to evaluate the normalized average width of the interval. This section adopts the interval prediction of PM₂.₅ and PM₁₀, and the obtained results provide a practical application for analyzing the uncertainty of air pollution.

(b) Table 8 show the daily probability prediction evaluation results of PM₂.₅ and PM₁₀ in Beijing, Shanghai, and Shenzhen. It can be seen that the results of a single model interval are not good because the result of the width is too narrow and the coverage rate is low, while the interval coverage rate of the combined forecasting system proposed in this study is higher than that of a single model and the results are more accurate.

(c) It is difficult to satisfy all the optimal conditions due to the large number of indicators that measure the performance of interval prediction. However, the higher the confidence, the greater the coverage probability and the wider the interval. Therefore, the probability forecast has a certain prediction interval, which provides a reference for the actual application of air pollution monitoring.

Discussion

In this section, we used three methods to discuss the performance of the proposed combined forecasting system: forecasting effectiveness (FE), stability analysis (SA), and improvement ratio (IR).

Forecasting Effectiveness

To verify the availability of the relevant prediction system, the finite element method (Banik et al., 2020) is adopted in this study. This may be determined using the expected result of the prediction accuracy series, that is, the deviation between the expected value and normal deviation. The indicator is explained as follows.

Count the d-th order predicting availability element ${\mathit{\text{m}}}^{\mathit{d}}={\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{\text{Q}}}_{\mathit{i}}{\mathit{\text{A}}}_{\mathit{i}}^{\mathit{d}}$, where A_i is the prediction accuracy, Q_i is the discrete probability distribution, and ${\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\text{Q}}}_{\mathit{i}}=\mathbf{1},{\mathit{\text{Q}}}_{\mathit{i}}>0$. Since we could not obtain any prior information on Q_i, it is determined as Q_i = 1/n, i = 1, 2, …, n. The other A_i is calculated using ${\mathit{\text{A}}}_{\mathit{i}}=1-\left|{\overline{\overline{\xi }}}_{\mathit{i}}\right|$, in which ${\overline{\overline{\xi }}}_i$ is expressed as:

${\overline{\overline{\xi }}}_i=\{\begin{array}{c}-1,\hfill \\ (A{P}_i-P{P}_i)\mathrm{/}A{P}_i,\hfill \\ 1,\hfill \end{array}\begin{array}{c}\hfill (A{P}_i-P{P}_i)\mathrm{/}A{P}_i<-1\\ \hfill -1\le (A{P}_i-P{P}_i)\mathrm{/}A{P}_i<1\\ \hfill (A{P}_i-P{P}_i)\mathrm{/}A{P}_i>1\end{array},(4-4-1)$

where PP_i and AP_i indicate the i-th point forecast value and observation quantitative value, respectively.

Thereafter, the continuous function $\overline{\overline{\mathit{\text{L}}}}({\mathit{\text{g}}}^1,{\mathit{\text{g}}}^2,\mathrm{\dots },{\mathit{\text{g}}}^d)$ of a d-order unit is introduced to assess the d-th order predicting availability. While there is only one variable in the equation $\overline{\overline{\mathit{\text{L}}}}\left(\mathit{z}\right)=\mathit{\text{z}}$, the first-order FE can be expressed as $\overline{\overline{\mathit{\text{L}}}}\left(g^1\right)=g^1$.

If there are two variables in this equation, for instance, $\overline{\overline{\mathit{\text{L}}}}(i,j)=i\left(1-\sqrt{j-i^2}\right)$, the second-order FE can be expressed as follows:

$\overline{\overline{\mathit{\text{L}}}}(g^1,g^2)=g^1\left(1-\sqrt{g^2-{\left(g^1\right)}^2}\right)\mathit{\hspace{1em}\hspace{1em}}(4-4-2)$

According to the FE definition, the higher the value of $\overline{\overline{\mathit{\text{L}}}}$, the better the prediction performance of the models.

Therefore, the d-th order FE is expressed as H(m¹, m², ⋯, m^k). Thus, the first-order prediction effectiveness is defined as H(m¹) = m¹. If there are two variables in the equation, the second-order FE is given by $\mathit{\text{H}}({\mathit{\text{m}}}^1,{\mathit{\text{m}}}^2)={\mathit{\text{m}}}^1\left(1-\sqrt{{\mathit{\text{m}}}^2-{\left({\mathit{\text{m}}}^1\right)}^2}\right)$.

By comparing the FE values with those of other related models, it can be easily concluded that the proposed system obtains the highest index value in both the first-order and second-order calculations, which shows that its performance in air pollution prediction exceeds that of other models. Specifically, we took Beijing PM₁₀ data as an example in one-step, ${\mathit{\text{H}}}_1^{\mathit{Beijing}}=\begin{array}{c}\hfill \mathbf{0.820324675}\end{array}$ and ${\mathit{\text{H}}}_2^{\mathit{Beijing}}=\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{0.612407931}\end{array}\end{array}$ in two orders, and the FE is much larger than that of other models. In other predictions, our proposed system exhibits the best forecast performance compared with the other models. The specific experimental results of the other models are listed in Table 9.

TABLE 9

Table 9. Forecasting effectiveness (FE) of different models (PM_2.5).

Sensitivity Analysis

In this section, the sensitivity of the proposed prediction system is analyzed experimentally. Since the weight determination method plays an important role in the final prediction, this study discusses the prediction sensitivity of the combined prediction model by adjusting the optimization parameters. In the parameter setting stage, the important parameter of the population size has a great influence on the optimization performance. Therefore, the experiment adopts the method of changing one parameter to examine its influence on the prediction result. Here, the size of the population is set to 40, 60, 80, and 100 in turn. The specific experimental results are shown in Table 10. The relevant conclusions are summarized as follows:

TABLE 10

Table 10. Experimental results of forecasting results under different population sizes.

From Table 10, it can be seen that the performance of the proposed mode is different under various parameter settings. For example, in the Shenzhen PM2.5 forecast, MAPE values range from 5.9821 to 6.4834%.

Consequently, the fluctuation range of the forecast values in the three regions is small, indicating that the forecast system is less sensitive to the two modes and has a good stability in practical applications.

Improvement Ratio

In this section, the effectiveness of the combined forecasting model system is analyzed by the percentage improvement of MAPE and MSE. We proposed an index IR_MAPE to measure the improvement in the PCFM prediction accuracy. IR_MAPE can be expressed as:

${\overline{\overline{\mathit{\text{P}}}}}_{\mathit{MAPE}}=\left[\left({\mathit{\text{MAPE}}}^{\mathit{com}}-{\mathit{\text{MAPE}}}^{\mathit{pro}}\right)\mathrm{/}{\mathit{\text{MAPE}}}^{\mathit{com}}\right]\times 100\%$

${\overline{\overline{\mathit{\text{P}}}}}_{\mathit{MSE}}=\left[\left({\mathit{\text{MSE}}}^{\mathit{com}}-{\mathit{\text{MSE}}}^{\mathit{pro}}\right)\mathrm{/}{\mathit{\text{MSE}}}^{\mathit{com}}\right]\times 100\%,$

where MAPE^com is the compared model MAPE values and MAPE^pro indicates MAPE values of the prediction system. Moreover, the three models are compared with different indicators, which shows the superiority of the combined forecasting model system. The detailed calculation results are shown in Table 11.

TABLE 11

Table 11. Improvement ratio (IR) for CO of different models (×100%).

(a) The model is improved by MAPE, which verifies the superiority of the proposed prediction system. Compared with the ARIMA model, this model improves by 35.460472%. For the LSTM model, the combined prediction system achieves a 43.412275% improvement in MAPE. The results show that the system has a good prediction effect on PM₂.₅ and PM₁₀.

(b) For the three urban datasets considering mean square error (MSE) and MAPE, the proposed prediction system still achieves a significant improvement in prediction accuracy. Experiments show that, compared with the TCN model (taking Beijing as an example), the MAPE of the combined model is improved by 56.084%.

Conclusion

Predicting air quality plays a vital role in the environment and economy of energy development, which is widely discussed worldwide. In recent years, more researchers have focused on the methods to forecast PM₂.₅ and PM₁₀ concentrations and provide useful information for the citizens in their daily lives. However, to overcome the limitations and negative effects of an individual approach, this study develops a novel combined forecasting system that takes advantage of data preprocessing, single models, and the interval predicting approach.

The developed system includes an advanced data denoising technique, three single forecasting algorithms, and an optimization approach to predict the PM₂.₅ and PM₁₀ concentrations. Based on the experiments, we concluded that the combined model has the following advantages: (1) as for data denoising strategy, the combined system computes the data series without fluctuation and uncertainty by FIG, which yields better performance compared with single models by decomposing and reconstructing the initial data. (2) In the comparative experiments, to predict the PM₂.₅ and PM₁₀ concentrations of three cities, we found that the PM₂.₅ MAPE (×100%) values of the proposed system are 17.53130124, 11.52643852, and 6.00510985, which provide more satisfying results than the ARIMA models (86.97079038, 43.06089753, and 40.30779213). (3) Consequently, MODOA is utilized as an advanced optimization algorithm to determine the weight of every single model and to obtain the forecasting values of PM₂.₅ and PM₁₀ concentrations.

The proposed early warning system has many practical applications, such as warning and guiding the public before the occurrence of harmful air pollutants and mining the characteristics of air pollutants.

(1) The fuzzy preference rough set was applied to the early warning system to determine the main pollutants suitable for different cities. Attribute selection simplifies the process of early warning systems and makes the prediction of pollutants more effective. In addition, these results can help decision-makers in relevant sectors to monitor and analyze certain polluting pollutants, which play a crucial role in formulating effective strategies for each city.

(2) In the developed early warning system, the interval forecast based on deterministic forecast provides the forecast range and the confidence level, which can be used to analyze and monitor the uncertainty information of the future value of pollutants. Air quality warning systems trigger alerts when air pollution exceeds an upper limit. According to the forecast range, different early warning levels can also be divided as a guide for daily life.

Therefore, we concluded that the proposed combined predicting system enhances the forecasting capacity and accuracy of PM₂.₅ and PM₁₀ concentrations by conducting and analyzing the experiments. Accurate forecasts not only reduce the cost and risk of dealing with air pollution systems but also help policymakers come up with effective strategies.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://www.tianqihoubao.com.

Author Contributions

ZL contributed to the conception and design of the study. JW organized the model development and the experimental analysis and wrote the first draft of the manuscript. JL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This study was supported by the Science and Technology Development Fund, FDCT, Macau SAR, under Grant 0064/2021/A2.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Air Quality Expert Group (2012). Fine particulate matter (PM2.5) in the UK. Technical report. Available online at: http://uk-air.defra.gov.uk [accessed on March 19, 2022]

Google Scholar

Akyüz, M., and Çabuk, H. (2009). Meteorological variations of PM2.5/PM10 concentrations and particle-associated polycyclic aromatic hydrocarbons in the atmospheric environment of Zonguldak, Turkey. J. Hazard. Mater. 170, 13–21. doi: 10.1016/j.jhazmat.2009.05.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Bai, Y., Li, Y., Zeng, B., Li, C., and Zhang, J. (2019). Hourly PM2.5 concentration forecast using stacked autoencoder model with emphasis on seasonality. J. Clean. Prod. 224, 739–750. doi: 10.1016/j.jclepro.2019.03.253

CrossRef Full Text | Google Scholar

Banik, A., Behera, C., Sarathkumar, T. V., and Goswami, A. K. (2020). Uncertain wind power forecasting using LSTM-based prediction interval. IET Renew. Power Gener. 14, 2657–2667. doi: 10.1049/iet-rpg.2019.1238

CrossRef Full Text | Google Scholar

Beaulant, A. L., Perron, G., Kleinpeter, J., Weber, C., Ranchin, T., and Wald, L. (2008). Adding virtual measuring stations to a network for urban air pollution mapping. Environ. Int. 34, 599–605. doi: 10.1016/j.envint.2007.12.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergen, S., Sheppard, L., Sampson, P. D., Kim, S. Y., Richards, M., Vedal, S., et al. (2013). A national prediction model for PM2.5 component exposures and measurement error-corrected health effect inference. Environ. Health Perspect. 121, 1017–1025. doi: 10.1289/ehp.1206010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bin, H., Zu, Y. X., and Zhang, C. (2014). A forecasting method of short-term electric power load based on BP neural network. Appl. Mech. Mater. 538, 247–250. doi: 10.4028/www.scientific.net/AMM.538.247

CrossRef Full Text | Google Scholar

Borrego, C., Cascão, P., Lopes, M., Amorim, J. H., Tavares, R., Rodrigues, V., et al. (2011). Impact of urban planning alternatives on air quality: URBAIR model application. WIT Trans. Ecol. Environ. 147, 13–24. doi: 10.2495/AIR110021

CrossRef Full Text | Google Scholar

Chen, Y., Kang, Y., Chen, Y., and Wang, Z. (2020). Probabilistic forecasting with temporal convolutional neural network. Neurocomputing 399, 491–501. doi: 10.1016/j.neucom.2020.03.011

CrossRef Full Text | Google Scholar

Ding, S. (2019). A novel discrete grey multivariable model and its application in forecasting the output value of China’s high-tech industries. Comput. Ind. Eng. 127, 749–760. doi: 10.1016/j.cie.2018.11.016

CrossRef Full Text | Google Scholar

Djalalova, I., Delle Monache, L., and Wilczak, J. (2015). PM2.5 analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model. Atmos. Environ. 108, 76–87. doi: 10.1016/j.atmosenv.2015.02.021

CrossRef Full Text | Google Scholar

Genc, D. D., Yesilyurt, C., and Tuncel, G. (2010). Air pollution forecasting in Ankara, Turkey using air pollution index and its relation to assimilative capacity of the atmosphere. Environ. Monit. Assess. 166, 11–27. doi: 10.1007/s10661-009-0981-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Gers, F. A., Schmidhuber, J., and Cummins, F. (2000). Learning to forget: continual prediction with LSTM. Neural Comput. 12, 2451–2471. doi: 10.1162/089976600300015015

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, J., Liu, Z., Huang, W., Wei, Y., and Cao, J. (2018). Short-term traffic flow prediction using fuzzy information granulation approach under different time intervals. IET Intell. Transp. Syst. 12, 143–150. doi: 10.1049/iet-its.2017.0144

CrossRef Full Text | Google Scholar

Hamilton James, D. (2015). Time Series Analysis. Beijing: China Renmin University Press.

Google Scholar

He, Y., Yan, Y., Wang, X., and Wang, C. (2019a). Uncertainty forecasting for streamflow based on support vector regression method with fuzzy information granulation. Energy Procedia 158, 6189–6194. doi: 10.1016/j.egypro.2019.01.489

CrossRef Full Text | Google Scholar

He, Y., Yan, Y., and Xu, Q. (2019b). Wind and solar power probability density prediction via fuzzy information granulation and support vector quantile regression. Int. J. Electr. Power Energy Syst. 113, 515–527. doi: 10.1016/j.ijepes.2019.05.075

CrossRef Full Text | Google Scholar

Li, J., Wang, R., Wang, J., and Li, Y. (2018). Analysis and forecasting of the oil consumption in China based on combination models optimized by artificial intelligence algorithms. Energy 144, 243–264. doi: 10.1016/j.energy.2017.12.042

CrossRef Full Text | Google Scholar

Liu, H., Jin, K., and Duan, Z. (2019). Air PM2.5 concentration multi-step forecasting using a new hybrid modeling method: comparing cases for four cities in China. Atmos. Pollut. Res. 10, 1588–1600. doi: 10.1016/j.apr.2019.05.007

CrossRef Full Text | Google Scholar

Liu, W., Guo, G., Chen, F., and Chen, Y. (2019). Meteorological pattern analysis assisted daily PM2.5 grades prediction using SVM optimized by PSO algorithm. Atmos. Pollut. Res. 10, 1482–1491. doi: 10.1016/j.apr.2019.04.005

CrossRef Full Text | Google Scholar

Majumder, H., and Maity, K. (2018). Application of GRNN and multivariate hybrid approach to predict and optimize WEDM responses for Ni-Ti shape memory alloy. Appl. Soft Comput. 70, 665–679. doi: 10.1016/j.asoc.2018.06.026

CrossRef Full Text | Google Scholar

McKeen, S. A., Chung, S. H., Wilczak, J., Grell, G., Djalalova, I., Peckham, S., et al. (2007). Evaluation of several PM2.5 forecast models using data collected during the ICARTT/NEAQS 2004 field study. J. Geophys. Res. Atmos 112, 1–20. doi: 10.1029/2006JD007608

CrossRef Full Text | Google Scholar

Mencar, C., and Fanelli, A. M. (2008). Interpretability constraints for fuzzy information granulation. Inf. Sci. 178, 4585–4618. doi: 10.1016/j.ins.2008.08.015

CrossRef Full Text | Google Scholar

Osowski, S., and Garanty, K. (2007). Forecasting of the daily meteorological pollution using wavelets and support vector machine. Eng. Appl. Artif. Intell. 20, 745–755. doi: 10.1016/j.engappai.2006.10.008

CrossRef Full Text | Google Scholar

Pai, T. Y., Hanaki, K., and Chiou, R. J. (2013). Forecasting hourly roadside particulate matter in taipei county of taiwan based on first-order and one-variable grey model. Clean Soil Air Water. 41, 737–742. doi: 10.1002/clen.201000402

CrossRef Full Text | Google Scholar

Samia, A., Kaouther, N., and Abdelwahed, T. (2012). A hybrid ARIMA and artificial neural networks model to forecast air quality in urban areas: case of Tunisia. Adv. Mater. Res. 518, 2969–2979. doi: 10.4028/www.scientific.net/AMR.518-523.2969

CrossRef Full Text | Google Scholar

Sfetsos, A. (2000). A comparison of various forecasting techniques applied to mean hourly wind speed time series. Renew. Energy 21, 23–35. doi: 10.1016/S0960-1481(99)00125-1

CrossRef Full Text | Google Scholar

Shelhamer, E., Long, J., and Darrell, T. (2017). Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 3431–3440. doi: 10.1109/TPAMI.2016.2572683

PubMed Abstract | CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958.

Google Scholar

State of Global Air (2020). Health Effects Institute. Available online at: https://www.stateofglobalair.org [accessed on October 22, 2020]

Google Scholar

Sun, W., and Li, Z. (2020). Hourly PM2.5 concentration forecasting based on feature extraction and stacking-driven ensemble model for the winter of the Beijing-Tianjin-Hebei area. Atmos. Pollut. Res. 11, 110–121. doi: 10.1016/j.apr.2020.02.022

CrossRef Full Text | Google Scholar

Tian, Q., and Wang, H. (2021). Predicting remaining useful life of rolling bearings based on reliable degradation indicator and temporal convolution network with the quantile regression. Appl. Sci. 11:4773. doi: 10.3390/app11114773

CrossRef Full Text | Google Scholar

van Donkelaar, A., Martin, R. V., and Park, R. J. (2006). Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing. J. Geophys. Res. Atmos 111:D21201. doi: 10.1029/2005JD006996

CrossRef Full Text | Google Scholar

Wakamatsu, S., Morikawa, T., and Ito, A. (2013). Air pollution trends in Japan between 1970 and 2012 and impact of urban air pollution countermeasures. Asian J. Atmos. Environ. 7, 177–190. doi: 10.5572/ajae.2013.7.4.177

CrossRef Full Text | Google Scholar

Wang, J., and Hu, J. (2015). A robust combination approach for short-term wind speed forecasting and analysis - Combination of the ARIMA (Autoregressive Integrated Moving Average), ELM (Extreme Learning Machine), SVM (Support Vector Machine) and LSSVM (Least Square SVM) forecasts using a GPR (Gaussian Process Regression) model. Energy 93, 41–56. doi: 10.1016/j.energy.2015.08.045

CrossRef Full Text | Google Scholar

Wang, J., Zhang, L., and Li, Z. (2022b). Interval forecasting system for electricity load based on data pre-processing strategy and multi-objective optimization algorithm. Appl. Energy 305:117911. doi: 10.1016/j.apenergy.2021.117911

CrossRef Full Text | Google Scholar

Wang, J., Wang, R., and Li, Z. (2022a). A combined forecasting system based on multi-objective optimization and feature extraction strategy for hourly PM2.5 concentration. Appl. Soft Comput. 114:108034. doi: 10.1016/j.asoc.2021.108034

CrossRef Full Text | Google Scholar

Wang, J., Zhang, L., Wang, C., and Liu, Z. (2021). A regional pretraining-classification-selection forecasting system for wind power point forecasting and interval forecasting. Appl. Soft Comput. 113:107941. doi: 10.1016/j.asoc.2021.107941

CrossRef Full Text | Google Scholar

Wang, S., Wang, J., Lu, H., and Zhao, W. (2021). A novel combined model for wind speed prediction – Combination of linear model, shallow neural networks, and deep learning approaches. Energy 234:121275. doi: 10.1016/j.energy.2021.121275

CrossRef Full Text | Google Scholar

Wang, Y., Wang, J., Zhao, G., and Dong, Y. (2012). Application of residual modification approach in seasonal ARIMA for electricity demand forecasting: a case study of China. Energy Policy 48, 284–294. doi: 10.1016/j.enpol.2012.05.026

CrossRef Full Text | Google Scholar

Wang, Z., Wang, C., and Wu, J. (2016). Wind energy potential assessment and forecasting research based on the data pre-processing technique and swarm intelligent optimization algorithms. Sustainability 8:1191. doi: 10.3390/su8111191

CrossRef Full Text | Google Scholar

Wei, D., Wang, J., Niu, X., and Li, Z. (2021). Wind speed forecasting system based on gated recurrent units and convolutional spiking neural networks. Appl. Energy 292:116842. doi: 10.1016/j.apenergy.2021.116842

CrossRef Full Text | Google Scholar

Xiao, X., Xie, W., Zhou, Y., Zhao, W., Liu, X., and Zhang, C. (2019). Prediction and analysis of energy demand of high energy density AC/DC park based on spatial static load forecasting method. J. Eng. 2019, 3388–3391. doi: 10.1049/joe.2018.8389

CrossRef Full Text | Google Scholar

Yang, H., Zhu, Z., Li, C., and Li, R. (2020). A novel combined forecasting system for air pollutants concentration based on fuzzy theory and optimization of aggregation weight. Appl. Soft Comput. J. 87:105972. doi: 10.1016/j.asoc.2019.105972

CrossRef Full Text | Google Scholar

Yang, W., Yao, Q., Ye, K., and Xu, C. Z. (2020). Empirical mode decomposition and temporal convolutional networks for remaining useful life estimation. Int. J. Parallel Program. 48, 61–79. doi: 10.1007/s10766-019-00650-1

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1997). Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 90, 111–127. doi: 10.1016/S0165-0114(97)00077-8

CrossRef Full Text | Google Scholar

Zhang, X., Wang, J., and Gao, Y. (2019). A hybrid short-term electricity price forecasting framework: cuckoo search-based feature selection with singular spectrum analysis and SVM. Energy Econ. 81, 899–913. doi: 10.1016/j.eneco.2019.05.026

CrossRef Full Text | Google Scholar

Zhang, Y., and Na, S. (2018). A novel agricultural commodity price forecasting model based on fuzzy information granulation and MEA-SVM model. Math. Probl. Eng. 2018, 1–10. doi: 10.1155/2018/2540681

CrossRef Full Text | Google Scholar

Zhu, R., Liao, W., and Wang, Y. (2020). Short-term prediction for wind power based on temporal convolutional network. Energy Rep. 6, 424–429. doi: 10.1016/j.egyr.2020.11.219

CrossRef Full Text | Google Scholar