Limited Pairwise Synergistic and Antagonistic Interactions Impart Stability to Microbial Communities

One of the central goals of ecology is to explain and predict coexistence of species. In this context, microbial communities provide a model system where community structure can be studied in environmental niches and in laboratory conditions. A community of microbial population is stabilized by interactions between participating species. However, the nature of these stabilizing interactions has remained largely unknown. Theory and experiments have suggested that communities are stabilized by antagonistic interactions between member species, and destabilized by synergistic interactions. However, experiments have also revealed that a large fraction of all the interactions between species in a community are synergistic in nature. To understand the relative significance of the two types of interactions (synergistic vs. antagonistic) between species, we perform simulations of microbial communities with a small number of participating species using two frameworks—a replicator equation and a Lotka-Volterra framework. Our results demonstrate that synergistic interactions between species play a critical role in maintaining diversity in cultures. These interactions are critical for the ability of the communities to survive perturbations and maintain diversity. We follow up the simulations with quantification of the extent to which synergistic and antagonistic interactions are present in a bacterial community present in a soil sample. Overall, our results show that community stability is largely achieved with the help of synergistic interactions between participating species. However, we perform experiments to demonstrate that antagonistic interactions, in specific circumstances, can also contribute toward community stability.

Introduction

Developing an understanding of the distribution and stable coexistence of species is a major goal of ecology. The classical view in this context states that the sum total of abiotic factors in an environment defines the niche available to species in a particular area (Hutchinson, 1978; Colwell and Rangel, 2009). An increasing body of literature now demonstrates that biotic factors can expand or contract the niche available for species to exist in an environment (Hardin, 1960; Bruno et al., 2003; Colwell and Rangel, 2009; Bulleri et al., 2016). How interactions between the biotic factors in an environment impact the coexistence and stability of species is the focus of this work.

Microbes live in complex communities. The interactions between them are important for the ecosystem from a variety of contexts (Azam and Malfatti, 2007; Lee and Hase, 2014). These assemblies comprise of large number of genomes and are engaged in a number of antagonistic and synergistic interactions between participating species (Faust and Raes, 2012; Corel et al., 2016). Via these interactions, the participating species can change the physical, chemical, and biological environment, and thus, influence the growth of all members of the environment (Andrade-Dominguez et al., 2014; Moreno-Fenoll et al., 2017). The altered environment can, in turn, also impacts the strength of interactions between species (Ratzke et al., 2020). Hence, a feedback between species and environment exists.

Interactions between species can be of two types. In the first, presence of one species aids growth of another. This form of interaction is synergistic. Alternatively, individuals of one species hinder growth of another species (Hiltunen et al., 2017). This form of interaction is termed as an antagonistic interaction. In a microbial context, the former is present when waste or a secreted metabolite of one species is used by individuals of another species for growth (Pacheco et al., 2019), and the latter, when an antibiotic released by one species, which limits growth of another species.

Which of the two types of interactions described above contributes more toward preservation of diversity in an ecological community? The nature of interactions (synergistic/antagonistic) present in a community shape how the community responds to challenges like, perturbations in composition of community, environmental shifts, migration. In this context, we study the nature of interactions and their relative effects on stability of a community comprising a small number of species.

Consider Figure 1. Species A (red) grows at rate r_A, and B (blue) grows at r_B (both constant in a given environment). Let r_A < r_B. Let P_AB be the parameter which defines how A influences growth of B (P_AB > 0, when synergistic; and P_AB < 0, when antagonistic). Similarly, let P_BA be the parameter, which defines how B influences A. Depending on the nature of interactions between the two species, several topologies are possible (Figure 1). In the parameter space of P_AB and P_BA, how do we identify regions where one species outcompetes the other; and regions where the two species stably coexist?

FIGURE 1

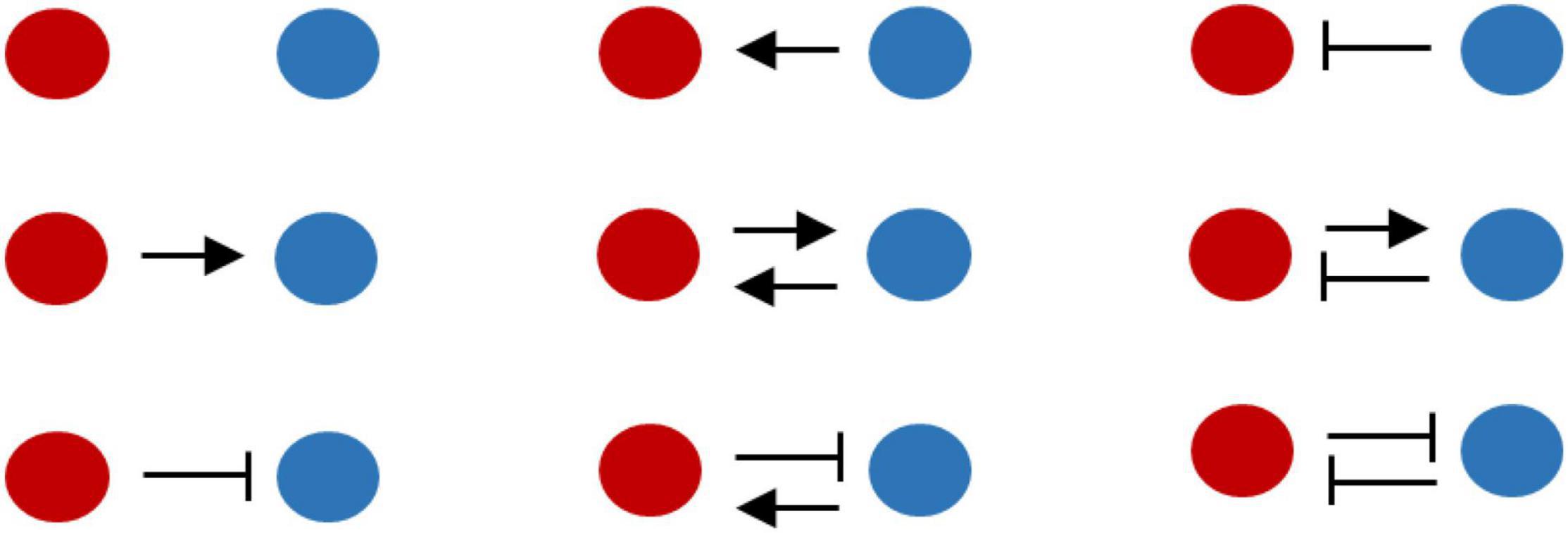
Figure 1. Nature and magnitude of interactions between species dictates criteria for stable coexistence. Two species A (red) and B (blue) in an environment can exhibit nine topologies depending on how presence of one impacts growth of the other. In this cartoon, we assume that species A (red) grows slower than B (blue), when growing in absence of any other species. Arrow represents synergistic interaction while a blunt end represents an antagonistic interaction.

In a particular environment, the number of species (n) is in several dozens, if not more (Vega and Gore, 2018) and previous work has suggested that diversity brings the challenge of stability (May, 1972; McCann, 2000; Allesina and Tang, 2012; Coyte et al., 2015; Bunin, 2017). Hence, a large number of possible topologies, describing interactions between species, exist. Each of these topologies dictates the criteria of coexistence of species, and the community’s response to perturbations. The interactions could lead to coexistence of any number of one to n of all participating species. Moreover, coexistence of species could be stable or unstable. In such a context, which interactions (synergistic or antagonistic) are more relevant for coexistence of multiple species? In other words, how the distribution of interactions shape communities is unknown (Kehe et al., 2020), and is the focus of this work. Multiple aspects of stability can be defined and examined for a multi-species community. Here, we ask the question—given an interaction network that supports coexistence, how do the different kinds of stability vary with differing degrees of connectance and fraction of interactions that are synergistic. We form this analysis for small communities, with three or four participating species.

Evidence in this context is conflicting. It has been reported that synergistic interactions between participating species are rare (Foster and Bell, 2012; Ghoul and Mitri, 2016), while others report that the fraction of interactions which are synergistic can be widespread, and depend on the precise environment in which the participating species are present (Jared Kehe et al., 2020). In addition, metabolic modeling and bioinformatics analysis also suggests strong presence of cooperation among species in an ecological context (Goldford et al., 2018; Pacheco et al., 2019). The problem with mutually positive interactions (cooperative behavior between two species) has shown to be that it leads to reduced stability of communities (May, 1972; Allesina and Tang, 2012; Coyte et al., 2015). Analytical work to study the effect of synergistic interactions on community structures has also led to the same result (Coyte et al., 2015). In general, it is thought that for highly connected networks (where, most species are interacting with each other), cooperative interactions of even small magnitude are sufficient to make the system unstable. However, while theory does not support extensive presence of cooperation and synergistic interactions in an ecological community, experimental evidence suggests that synergistic interactions can be present to a relatively large extent (Pande et al., 2014, 2016; Kehe et al., 2020).

In this context, several questions remain. How does the system react to a perturbation? How is the stability of the system dependent on the structure of the topology of the interactions in the system? Here, stability can be interpreted in a number of ways. First, stability can be defined as the ability of the community to, after a transient environmental perturbation, restore the original frequencies of species. Second, stability can also be the ability of the system to retain the remaining N - 1 species, should one of the participating species go extinct. Third, stability can also refer to the ability of the system to resist intrusion into the community from non-associated species (Case, 1990; Bascompte et al., 2006; Fontaine et al., 2011; Coyte et al., 2015; Mougi, 2016; Rouze et al., 2017). Lastly, stability can also refer to change in the species composition in a niche, when the environment changes. This facet of stability has been recently studied, and shown to have the capacity to facilitate coexistence of species (Abreu et al., 2020). However, the effect of the structure of the topology of interactions itself on the coexistence of species has not been explored. In this study, we study the structure of interactions between participating species in a small ecological community, and its impact on the stability of the community.

To answer this question, we use two modeling approaches. In the first, we use a replicator dynamic equation to model coexistence among N interacting species. In the second, we use a Lotka-Volterra representation to study coexistence among microbial species. Both these formulations, replicator (Lundh and Gerlee, 2013; Zomorrodi and Segre, 2017; Venkateswaran and Gokhale, 2019; Madec and Gjini, 2020) and Lotka-Volterra (Momeni et al., 2017; Xiao et al., 2017; Gonze et al., 2018; Kuntal et al., 2019; Mickalide and Kuehn, 2019), have been used extensively in literature to study population dynamics in a multi-species environment. However, a comparative analysis between the two modeling exercises has not been performed.

We use simulations to show that synergistic interactions play an important role in maintenance of diversity in microbial communities. We first describe our mathematical representation of a microbial community, and then analyze it for stability and co-existence of species. We study the effect of interactions between species to help stabilize the system against perturbations to the system at steady state, and also, when one of the species is removed from the system. We then use an experimental system of bacterial species isolated from soil, to quantify the relative frequency of positive and antagonistic interactions in this community.

Materials and Methods

Replicator Equation Model

Model Description

We use a system of autonomous non-linear differential equations to track the frequency of each species with time in a constant environment with a fixed interaction network. While ecological communities are large and comprise of several dozen species, we do this analysis for small communities. As the size of communities increases, the likelihood of space being a relevant variable in explaining coexistence increases. As a result, we focus on communities comprising of a small number of species. In a multi-species population, the relative number of individuals of any species can be represented as a frequency, i.e., the ratio of the number of individuals of the species (n_i) to the total population size (N), which lies between 0 and 1. In the absence of any external effects such as interactions, each species may be linked with an innate growth rate (r_i), and the change in frequency of a species is proportional to the present frequency (Nowak, 2006).

We model an environment as a chemostat, with a total population size N. Perturbations change the growth rate of the participating species or changes frequencies of the participating species. Due to species interactions, relative changes in growth rate and/or changes in community composition changes the overall structure of the population as well (Butler and O’Dwyer, 2018). Thus, for any i^th species in an N-species population, the frequency of the i^th population, x_i is,

$$x_i=\frac{n_i}{\mathrm{\Sigma }{n}_i}(1)$$

Hence,

$$\mathrm{\Sigma }{x}_i=1and\mathrm{\Sigma }{n}_i=N$$

To ensure this, we introduce a mean growth rate term (Φ), with the frequency of each species acting as the corresponding weights (Nowak, 2006).

$$\mathrm{\Phi }=\sum _{i=1}^n{r}_i{x}_i(2)$$

The population dynamics of the system can therefore be represented as,

$$\frac{d{x}_i}{dt}=r_i{x}_i-\mathrm{\Phi }{x}_i(3)$$

The replicator equation has been used extensively to study deterministic behavior of large populations (Hofbauer et al., 1979). An important feature of the model is that density limits growth rate, effectively acting as a negative feedback loop. It has also been shown, in a game theoretic framework, that a replicator equation for n strategies is equivalent to a Lotka-Volterra equation for n - 1 species (Hofbauer and Sigmund, 1988).

Interaction Effects

Let the interaction effect on species i by species j be designated as P_ij, which is positive if the interaction is synergistic, negative if the interaction is antagonistic and zero if there is no interaction. The strength of these effects is also proportional to the frequency of the species causing the interactions. Only interactions between distinct species are considered. The effect of a species’ metabolic products on its own growth are absorbed in the r_i term. This assumption, however, is violated when the system is far from steady state.

The population dynamics can then be quantified as,

$$\frac{d{x}_i}{dt}=x_i\left(r_i+P_{i1}{x}_1+P_{i2}{x}_2+\mathrm{\cdots }+P_{iN}{x}_N\right)-\mathrm{\Phi }{x}_i(4)$$

Where the mean fitness of the population is represented as,

$$\mathrm{\Phi }=\sum _{i=1}^n{x}_i(r_i+P_{i1}{x}_1+P_{i2}{x}_2+\mathrm{\cdots }+P_{iN}{x}_N)(5)$$

Steady State Analysis and Stable Coexistence

At steady state, the system of ordinary differential equations is a system of polynomial equations whose solutions represent the frequencies of all species of the population at steady state.

$$\frac{d{x}_i}{dt}=0=x_i\left(r_i+P_{i1}{x}_1+P_{i2}{x}_2+\mathrm{\cdots }+P_{iN}{x}_N\right)-\mathrm{\Phi }{x}_i(6)$$

We analyze the stability of solutions by performing a Taylor’s expansion of the governing equations in the neighborhood of the fixed points such that time derivatives of the deviations y_i from equilibrium can be written in the linear form,

$$\frac{dy}{dt}=Ay(7)$$

Where, y is a column vector of deviations from equilibrium =[y₁y₂…y_N]^T, and A is an N × N Jacobian matrix of the governing equations. An equilibrium is stable if real parts of all eigenvalues of matrix A are negative.

For a given set of innate growth rates and interaction parameters, the system is stable if there exists a stable fixed point at which frequencies of all species present in the population is non-zero.

The above formulation assumes that the population size remains constant with time. However, in an ecological setting, this is likely to be not true. Environmental perturbations are likely to lead to fluctuating population sizes over time. To mimic this, separate simulations were performed. We show that the systems found to be stable in the context as defined in (7) were also found to be stable, when perturbed due to an environmental disturbance (See Supplementary Section 1 for more details).

Generating Random Networks

Species networks were simulated using the following growth rates: three species, [0.98, 1, 1.02] time^–1; four species, [0.98, 0.99, 1.01, 1.02] time^–1; five species, [0.97, 0.98, 1, 1.02, 1.03] time^–1, and six species, [0.97, 0.98, 0.99, 1.01, 1.02, 1.03] time^–1. We study the steady state behavior of the system as a function of two parameters. First, connectance (c): the ratio of non-zero interactions to the total number of possible interactions in the system. This can take values between 0 and 1, where c = 0 signifies a system with no interaction effects while c = 1 represents a completely connected system, that is, each species directly affects growth rates of all others. In the case with c = 0, the interaction matrix P only comprises of zeros; in the case c equal to 1, all off-diagonal terms of P are non-zero. Second, the fraction of non-zero interactions in the network which are synergistic (f_c), i.e., fraction of non-zero elements of the P matrix which are positive.

For a specified pair of values of these parameters, c, and f_c, 1,000 interaction networks were randomly generated in the following manner. For a given c, non-zero interactions were selected randomly from the N(N - 1) off-diagonal terms in the P matrix. Among the designated non-zero interactions, a fraction f_c were chosen randomly to be > 0. The distribution of interaction effects among interacting species are not well-known. Hence, the magnitude of each interaction effect was sampled in two different ways. In the first, the strength of interactions were sampled from a uniform distribution ranging between 0 and 1. The distribution generated via random sampling from a uniform distribution was identical to a uniform distribution (p < 0.00001). In the second, strength of interactions were sampled from exponential distributions. The exponential distributions were so chosen such that the mean of an antagonistic interaction was 10% of the maximum innate growth rate (r_i) in the species group. The mean of synergistic interactions was 5% of the maximum innate growth rate (r_i) in the group of species whose growth is being studied.

Lotka-Volterra Model

We use the Lotka-Volterra system of equations to model the growth of an interacting multi-species microbial population. The interaction between participating species can be modeled as effects on the intrinsic growth rate of the species experiencing the interactions.

In an n-species population, the rate of change of individuals of a i^th species can be thus modeled as follows,

$$\frac{d{N}_i}{dt}=\left(r_i+P_{i{1}^{\prime }}{N}_1+P_{i{2}^{\prime }}{N}_2+\mathrm{\cdots }+P_{i{n}^{\prime }}{N}_n\right)N_i(8)$$

Where, N_i is the number of individuals of species i, r_i is the growth rate of species i, P_ij’ is the interaction effect of species j on species i. In this representation, P_ij′ > 0 signifies a cooperative interaction directed from j to i, P_ij′ < 0 signifies an antagonistic interaction, while P_ij′=0 represents the absence of any interaction effect of species j on species i. In our model, all P_ii’ terms are taken to be negative, that is, P_ii′ < 0. This is because resources are limited, and numbers of any species cannot continue to grow indefinitely (Venturelli et al., 2018). In our simulations, we take P_ii’ equal to -1 × 10^–12.

Sampling Random Matrices

We use the model above to study populations comprising three or four different species. For the three species network, r was taken as defined above. We study the behavior of the system with regard to two key variables: (a) the extent of interactions present in the community, and (b) the relative pervasiveness of cooperative and antagonistic interactions.

We call the first variable connectivity (c), and is mathematically defined as the ratio of number of non-zero interactions present to the number of possible non-zero interactions. Consider a 3-species system. The interaction matrix may be defined as,

$$P=\begin{array}{ccc}\hfill P_{11}\hfill & \hfill P_{12}\hfill & \hfill P_{13}\hfill \\ \hfill P_{21}\hfill & \hfill P_{22}\hfill & \hfill P_{23}\hfill \\ \hfill P_{31}\hfill & \hfill P_{32}\hfill & \hfill P_{33}\hfill \end{array}.(9)$$

As defined earlier, P_ii’s are all set to less than zero and are not included in the number of non-zero interactions. Thus, the number of possible non-zero interactions is six. Thus, c equals number of non-zero interactions present in a particular simulation divided by six. The second variable is fraction of interactions which are cooperative (f_c), and is defined as the ratio of number of cooperative interactions to the total number of non-zero interactions.

The interaction strengths are assumed to be exponentially distributed and the values are assigned to each element by sampling from an exponential distribution. The magnitude in case of antagonistic interactions is taken to be twice as large as in case of cooperative interactions. The mean of the exponential distribution from which the strength of cooperative interactions were sampled was 10^–9 and that of the exponential distribution from which the strength of antagonistic interactions were sampled was 2 × 10^–9. Alternatively, the magnitudes of cooperative and antagonistic interactions were sampled from a uniform distribution between magnitudes zero and 2 × 10^–9, for both cooperative and antagonistic interactions. The relative magnitude of interaction strengths in an Lotka-Volterra representation for microbial systems has been previously used (Venturelli et al., 2018).

Likelihood of Coexistence

For a population with a given number of species, we study the likelihood of the community coexisting stably as the two parameters vary. Given independent growth rates and an interaction matrix, we model the growth of each species, starting from an equal number of individuals and note the number of individuals of each species at equilibrium. The population is said to coexist if the frequency of each species (x_i) at equilibrium is non-zero.

$$x_i=\frac{N_i}{\mathrm{\Sigma }{N}_i}(10)$$

We numerically solve the ODEs mentioned above (Equation 8). We approach the equilibrium asymptotically, and the frequency of a species is taken to be zero if x_i < 10⁻⁵. For a given pair of values of c and f_c, we generate a large number (≅1,000) of matrices, and observe the equilibrium state in each instance. The likelihood of coexistence for the given parameter set is estimated as the fraction of instances in which a coexisting population is observed.

Likelihood of Coexistence After Loss of a Species

To study the ability of a community to coexist in the event of a loss of one species from the population, for a given system of species, we remove a single species from the population. The resulting P matrix does not contain the interaction effects pertaining to the species removed. The system is then simulated, and the new equilibrium recorded. We record the number of instances in which, upon removal of one species, the remaining species coexisted. We estimate the likelihood that a population having an interaction network [of a particular set of (c,f_c)] would coexist on loss of any one species, by calculating the fraction of instances when the remaining population survived after removal of a species.

Experiments With Soil Bacteria

There is limited data regarding the relative frequency of absence, antagonistic, or synergistic interactions among microbial species existing in ecological niches. One of the niches where microbial communities have been studied is soil samples. To quantify this distribution, we isolate bacterial species from a garden soil sample, and study pairwise interaction.

Isolation of Soil Bacteria

Bacterial strains used were isolated from one gram soil in the Indian Institute of Technology Bombay nursery (19 Dec 2018).

One gram of soil was suspended in 10 ml of 50 mM phosphate buffer (in 1 liter, 8 g NaCl, 0.2 g KCl, 0.2 g KH₂PO₄, 1.15 g Na₂PO₄) at pH 7.5 (adjusted with HCl). The mixed solution was diluted in the phosphate buffer by the factor of 10²–10⁶. Each dilution was spread on the LB agar media plate containing Nystatin (25 μg/ml) (Juhnke and des Jardin, 1989). The plates were then incubated for 24 h at 37°C. Following appearance of colonies, all colonies which exhibited a unique morphology and/or color were picked and steaked onto fresh LB agar plates individually to isolate pure strains. The fraction of soil bacteria which is culturable in laboratory environment is known to be extremely small (Stewart, 2012).

Glycerol stocks were prepared from the pure colony culture and stored at -80°C. The genomic DNA from all species was isolated, and the 16s RNA sequenced to identify the bacterial species. Bacterial 16S rRNA gene (1,500 bp) was amplified using polymerase chain reaction in a thermal cycler using universal primers 5′-AGAGTTTGATCCTGGCTCAG–3′ and 5′–CCGTCAATTCMTTTRAGTTT–3′ (Fredriksson et al., 2013). All the 16s RNA sequences were analyzed using NCBI BLAST sequence alignment tool. Most similar matches were taken together to construct phylogenetic trees to understand the bacterial classification.

Nutrient rich medium (LB) used [composition per liter of distilled water: peptone, 10 g; yeast extract, 5 g and sodium chloride, 10 g (Sambrook and Russell, 2000)]. Minimal media (M9) was used as per the following composition (per liter): Na₂HPO₄, 6.78 g: KH₂PO₄, 3 g: NaCl, 0.5 g; NH₄Cl, 1 g; to which filter sterile 1 M MgSO₄ and 0.1 M CaCl₂ solutions added aseptically. Bacterial cultures were supplemented with glucose, 0.2% or glycerol 0.2% or pyruvic acid or sodium acetate, 0.2% as the sole carbon and energy source. Agar (1.5%) was used to solidify the medium.

Pairwise Growth Experiments

Frozen stocks of individual species were streaked on LB agar plates, grown at 30°C for 24 h. Single colonies were picked and each species was grown separately in 2 ml LB broth for 24 h. The growth rate of each species was obtained from the resulting growth curve (Supplementary Section 2) (Sane et al., 2020). After this growth, an equal number of colony forming units (CFUs) for the two strains were transferred to the M9 media containing 2% glucose. The initial density of the culture was 0.05 OD600 nm.

After 24 h of growth, appropriate dilutions of the M9 media were plated on LB plates and the number of colonies of each of the two strains counted. Based on the count of the colonies of each kind, the species were recorded to be co-existing (if colonies of both morphologies were observed) or one specie eliminating the other (if only one morphology was observed). The individual growth rates of the two participating species were calculated from this. The growth rate, so obtained, of each species was compared with the growth rate of that species growing in a pure culture. If the growth rate in pure culture was less than the growth rate when grown with another species, the interaction was defined to be positive. Alternatively, if the growth rate in pure culture was greater or equal to that when grown with another speices, the interaction was defined to be antagonistic or absent, respectively. In this manner, a pairwise competition experiment was performed for all 190 pairs, and the number of synergistic and antagonistic interactions quantified. All experiments were performed three times independently. A minimum of 500 colonies were counted in each pairwise growth experiment.

Experiments With Bacillus haikouensis (A), Bacillus firmus (B), and Bacillus megaterium (C)

In a three species network (comprising of species A, B, and C), to test the relevance of the antagonistic interaction between A and C, the following experiment was performed. In the first experiment, co-culture of the three species, with equal CFUs of the three species, with an initial OD of 0.05 in LB broth was allowed to grow for 24 h. After this period of growth, the relative frequencies of the three species were determined by plating on LB. This was done by counting the number of colonies for the distinct morphologies of each kind.

To mimic a setting where the A to C antagonistic interaction is not present, we start the co-culture with equal number of members of the three species. The three species’ co-culture was then allowed to grow for 2 h, after which, the frequency of the three species was noted. To calculate the frequency of the three species, the co-culture was spread of LB plates, and individual colonies of each species counted. A minimum of 500 colonies was counted to estimate the frequency of each of the three species. The same frequencies were then recreated by adding A and B (spun down from their respective independent cultures) to a tube in which only species C was allowed to grow for 2 h. The premise of this exercise was that by doing do, we allow the metabolite secreted by C into the media remain in the co-culture, while the metabolite released by species A is not introduced to the culture media. The three species were then allowed to growth together for another 2 h, and the whole process was repeated. This was done because during growth for 2 h, the antagonistic metabolite released by A, would likely start interfering with growth of C. To prevent this, the community was created again using a culture of pure C, with spun down A and B added to the tube. All experiments were performed three times independently. The experiment was continued till no change in the species composition was observed. This equilibrium was achieved after eight rounds of growth for 2 h.

Results

Minimum Connectivity Needed to Preserve Diversity

We first answer if there exist bounds on the number of interactions in the population for a coexistence solution to be possible. For this purpose, we use a replicator equation representation.

For connectance, c = 0, coexistence is never possible and the species with the greatest innate growth rate (r_i) takes over the population. This indicates the existence of a lower bound on connectance, to ensure coexistence. Consider two species i and j in an N species population. The equations predicting their frequencies at steady state are,

$$x_i\left(r_i+P_{i1}{x}_1+P_{i2}{x}_2+\mathrm{\cdots }+P_{iN}{x}_N\right)-\mathrm{\Phi }{x}_i=0(11)$$

$$x_j\left(r_j+P_{j1}{x}_1+P_{j2}{x}_2+\mathrm{\cdots }+P_{jN}{x}_N\right)-\mathrm{\Phi }{x}_j=0(12)$$

Suppose i and j do not interact with any other species i.e., all P_ik and P_jk terms are zero, for all k from one to N. The equations then reduce to,

$$x_i{r}_i=\mathrm{\Phi }{x}_i,and{x}_j{r}_j=\mathrm{\Phi }{x}_j(13)$$

The two equations only hold true if r_i is equal to r_j. This suggests that for any two species with dissimilar innate growth rates, coexistence is not possible in the absence of interaction terms.

Thus, this suggests that for a larger network with N species, at least N – 1 species must be recipients of at least one non-zero interaction effect. We can evaluate a minimum connectance (c_min) necessary for any N-species population to have a coexistence solution. Each species can instigate at most N – 1 interactions, and the total number of interactions possible in an N-species network is, hence, N(N−1).

The minimum number of non-zero interactions necessary is N-1.

$$c_{min}=\frac{N-1}{N\left(N-1\right)}=\frac{1}{N}(14)$$

Additionally, the species causing these interactions must be distinct. Consider the case where the minimum required N – 1 interactions are all instigated by one species, say species N. The steady state equation for x_N then reduces to,

$$x_N=\frac{\mathrm{\Phi }-r_1}{P_{1N}}=\frac{\mathrm{\Phi }-r_2}{P_{2N}}=\mathrm{\cdots }=\frac{\mathrm{\Phi }-r_{N-1}}{P_{\left(N-1\right)N}}(15)$$

For the given innate growth rates, a solution exists only if the interaction effects are of a magnitude which precisely satisfy the Equation (15). Such a constraint is severe and infeasible. This relation between two interaction effects would arise unless the interaction effects are caused by distinct species in the population.

Thus, alongside a minimum degree of connectance c equal to 1/N, where N – 1 distinct species are recipients of interaction effects; these effects must also be instigated by distinct species, unless the interaction parameters yield to follow extremely severe constraints.

In the Lotka-Volterra formulation, the minimum degree of connectance c, which ensures coexistence is zero. In such a scenario, each species will approach a density as dictated by its innate growth rate, and the self-limiting term P_ii.

Synergistic Interactions Help Preserve the Diversity in a Microbial Community

We now attempt to uncover the precise features of these interaction networks that help a multi-species population coexist. The first aspect we study are the nature of interactions, namely, synergy and antagonism.

Consider two species (A and B) inhabiting a common constant environment, each capable of surviving in the absence of the other. In the absence of any interactions, the species whose members grow fastest (say B) takes over the population. We now let interactions develop between the species with the goal of ensuring coexistence of both. The most simple interaction networks would involve a beneficial interaction directed from B to A, and/or a detrimental one directed from A to B (Figure 2A).

FIGURE 2

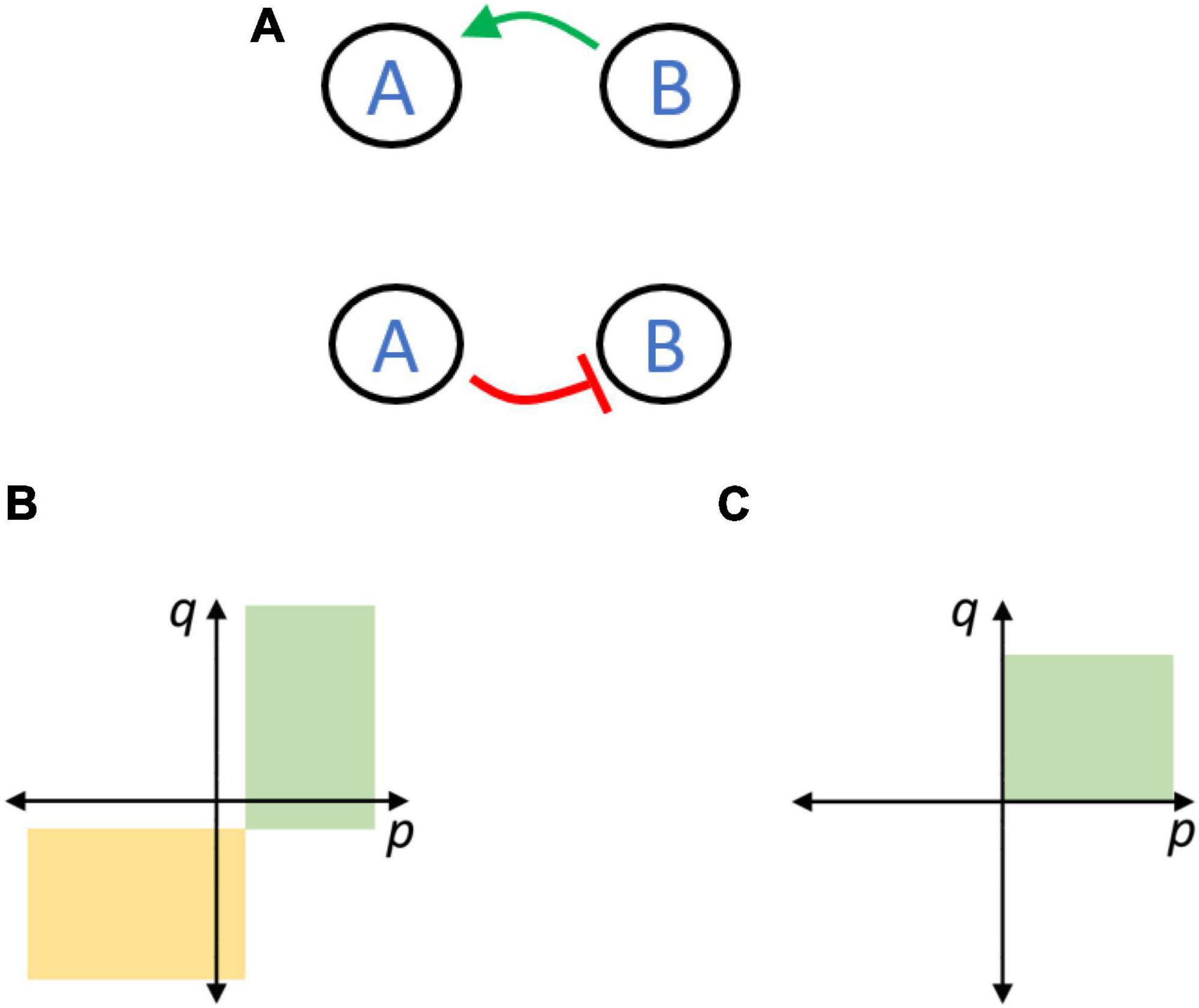
Figure 2. Coexistence in a two-species system can be facilitated via a beneficial (A top) or an antagonistic (A bottom) interaction. (B) In the replicator model, coexistence solutions were identified as non-zero solutions of the steady state of the differential equations used. For parameter values in the green and yellow regions, such coexistence solutions were possible. The stability of these solutions was determined by linearizing the equations around these fixed points, and checking the Eigen values of the Jacobian matrix obtained. The coexistence solutions determined by the green region were stable, that is, frequencies of all species were attracted toward this solution. For the yellow region, the coexistence solutions were unstable, that is, frequencies of all species were repelled away from this solution and the fate of the population was extinction of one species. (C) In the Lotka-Volterra model, stable coexistence solutions were determined by numerically solving the differential equations from a random initial condition, and observing if the population approached a point where all species coexisted. For parameter values in the green region, frequencies of both species approached a non-zero value, and hence, the coexistence solution is stable. For other parameter values, frequency of one of the species approached zero. The exact boundaries of the rectangles in panels (B,C) depend on the numerical values of the innate growth rates used in the model.

Both topologies, under appropriate interaction strengths, generate a solution where the two species coexist at steady state. However, synergy allows the solution to be stable while antagonism renders it unstable.

Consider the case presented in Figure 2A, where species A represses B. Assume that initially the species are present in the precise frequencies, which correspond to the coexistence solution. Suppose a perturbation causes a slight excess of species A. The excess individuals of A would increasingly inhibit growth of species B, which frees individuals of A to proliferate even further. This effective positive feedback for species A encoded via an antagonistic interaction would drive species B to extinction and allow individuals of A to take over the population.

Similarly, an excess of B would result in the individuals of A, whose frequency has now decreased slightly, unable to inhibit species B to a sufficient extent such that they have equal growth rates; and individuals of B would eventually occupy the entire niche.

Following similar arguments, consider the case of synergy between the two species, as represented in Figure 2A. Let us assume that the initial frequencies of the two species are such that the system is at equilibrium. A perturbation which increases the frequency of species A would diminish the beneficial interaction directed toward A, causing its numbers to consequently drop back to equilibrium. An excess of B would initially decrease the frequency of species A, but would allow it to recover, courtesy the increased benefit imparted to individuals of A by the elevated numbers of species B.

In the replicator equation formulation, while solutions that lead to coexistence (dashed lines, Figure 2B) are possible for interactions of either nature, they are stable only when the interaction is synergistic. This differing response to synergy and antagonism results in synergistic interactions being critical to preservation of species diversity while antagonistic interactions tend to lead to a loss of biodiversity in natural ecosystems.

Consider the interaction matrix:

$$\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{\text{p}}\hfill \\ \hfill \mathbf{\text{q}}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]$$

p represents the interaction effect of species B on species A, and q represents the interaction effect from A to B. On a plot of pvs.q, we can study the interaction values which enable a coexistence solution.

Both the rectangles, with boundaries enclosed by the dashed lines, represent sets of values of p and q which result in a coexistence solution. The green one, which lies largely in the first quadrant, depicts a stable solution while the solution associated with the yellow one, primarily in the third quadrant, is always unstable.

In the Lotka-Volterra formulation, the region of parameters p and q which facilitate stable coexistence are as shown in Figure 2C.

These results combined show that synergistic interactions are in a large manner responsible for coexistence of species in an ecological niche.

Interplay Between Synergy and Connectivity Dictates Steady State Behavior of System

We now explore the interplay between synergy and connectance, i.e., the nature of interactions and the density of the connections in the network of the participating species, in dictating the steady state behavior of the system.

The innate growth rates of all participating species and the interaction strengths between species i and j are sampled randomly, as described in “Materials and Methods” section. These choices give us a complete description of the network. From this, the probability of stable coexistence of all participating species was calculated. For this calculation, in the replicator equation formulation, stability against small fluctuations in the composition of the community were studied by local linearization of the coexistence solution. Negative real parts of eigenvalues of the Jacobian matrix indicate that the solution is locally stable in the face of perturbations. In Figure 3, the x-axis denotes the fraction of interactions that are synergistic, and the y-axis denotes the likelihood of a randomly sampled network ensuring stable coexistence. The different lines represent different degrees of connectance.

FIGURE 3

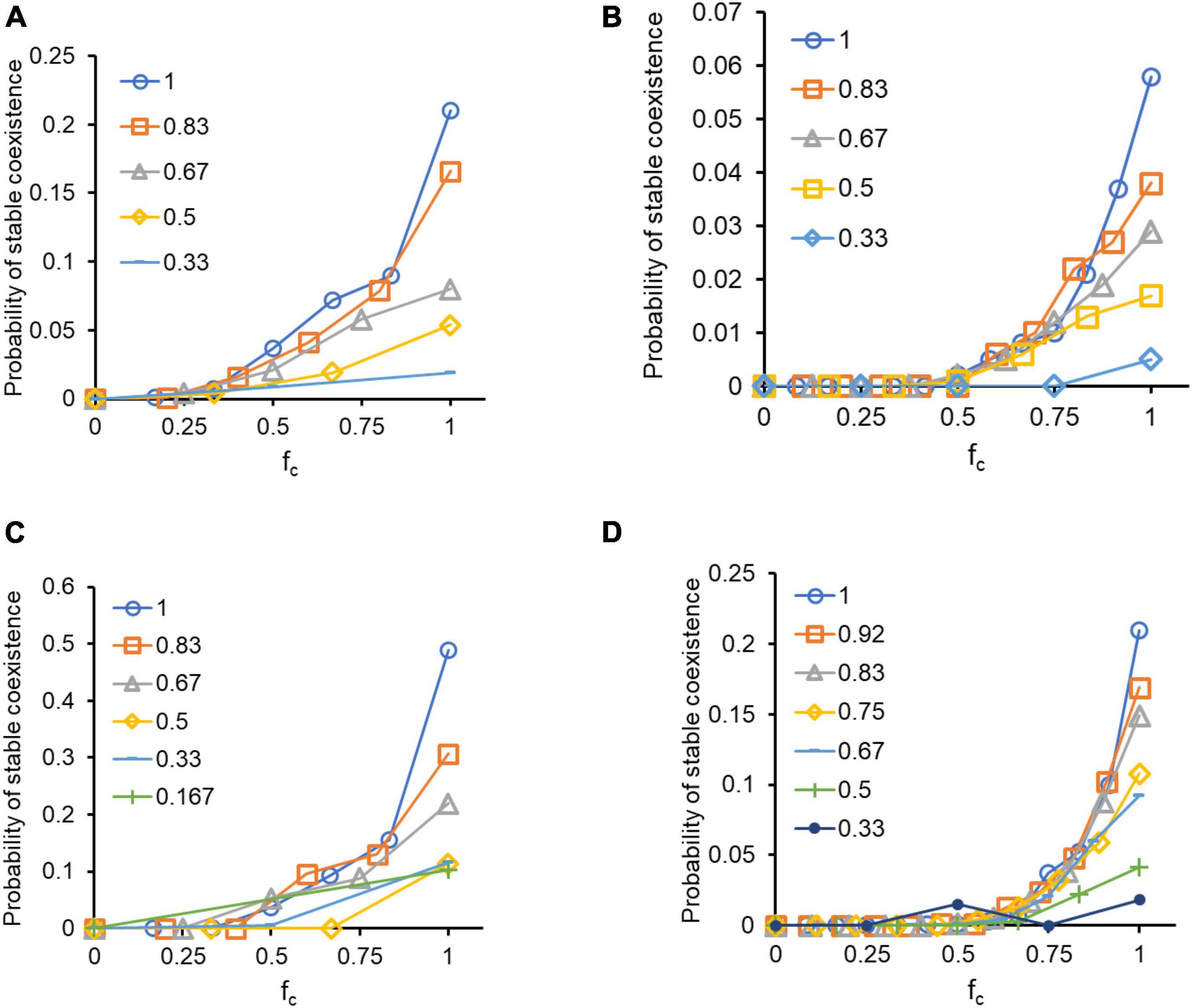
Figure 3. A higher connectance and a higher fraction of synergistic interactions, both, independently, facilitate coexistence. In the replicator formulation, three- (A) and four-species (B) systems exhibit greater likelihood of coexistence as the number of interactions which are positive increases. In the Lotka-Volterra formulation, three- (C) and four-species (D) systems exhibit greater likelihood of coexistence as the number of interactions which are positive increases. The strength of interactions in the randomized networks is chosen from an exponential distribution. Mean strength of antagonistic interactions was 0.1 and that of positive interaction was 0.05. The legend describes the value of c for each set of simulations.

For the Lotka-Volterra case, for each randomly generated network, the corresponding systems of differential equations were numerically solved (starting with a 1,000 individuals of each species) until the frequency of each species approached a constant value. If all frequencies were observed to be non-zero, the network was said to ensure stable coexistence.

The likelihood of stability of a network shows a strong positive correlation with the fraction of synergistic interactions; and appears independent of connectance for all values except at very high values of fc. We also note that the likelihood of the system reaching a stable coexisting steady state decreases as we increase the size of the network from three to four species. Both replicator equation (Figures 3A,B) and Lotka-Volterra (Figures 3C,D) formulations demonstrate this result. In this formulation, we sample the interaction strengths from an exponential distribution. The mean strength of interaction for antagonistic interactions is twice the mean strength for the cooperative interactions. The same result holds if the strength of interactions were sampled from a uniform distribution, and if the analysis is repeated for networks with size N equal to 5 or 6 (Supplementary Figure 3).

Stability

As a first measure of stability, we locate all steady state coexisting solutions for a three-species system and check for their stability, when the system is perturbed from the steady state. By perturbation, we mean a change in the frequency of species present in the community. This represents a scenario where a large fluctuation is introduced in the composition of the community, perhaps via convective flow introducing a large number of members of a particular species. Thus, after introducing a change in the composition, the ability of the system to reach the original steady state was quantified as stability of the system. For an interaction network in a 3-species system, which has a coexistence solution, the likelihood of the solution being stable (y-axis) is positively correlated to the fraction of synergistic interactions (x-axis) in the network (Figure 4). The likelihood of stability is largely independent of c. However, below a critical fc, stability is almost never achieved in a three-species network. This analysis was performed with the replicator equation representation.

FIGURE 4

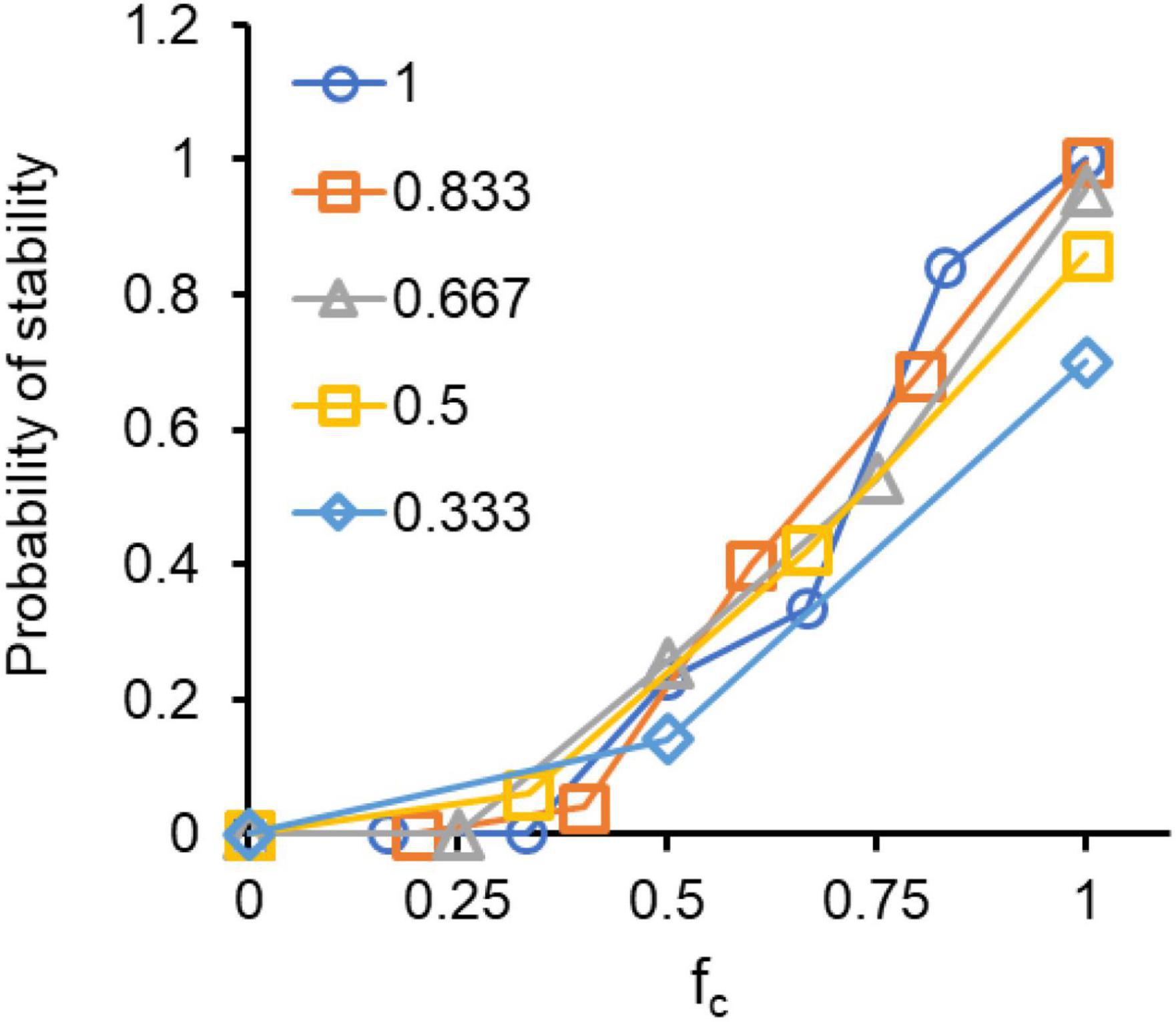
Figure 4. Synergistic interactions make the system more stable. Randomized networks, when perturbed from their steady state have a greater tendency to return to the original steady state when the fraction of interactions which are cooperative is high. Perturbations were introduced such that frequency of each species changes by at least 20%. There exists a critical threshold of fraction of interactions, which should be positive for system to exhibit stability.

The same analysis could not be performed for the Lotka-Volterra equations since, in this setup, the population could be at equilibrium with respect to the frequencies of each constituent species, but not with respect to their numbers, that is, the frequencies of each species might approach a constant value, while the number of individuals were still dynamic. Thus, analytical solutions to the system of equations dn_i/dt = 0, required for finding coexistence solutions and checking their local stability to perturbations, could not be obtained. This would be the case when $\frac{1}{n_i}.\frac{d{n}_i}{dt}=\frac{1}{n_j}.\frac{d{n}_j}{dt}\ne 0$.

We also examine stability from the context of loss of a species from a network. This was explored in the following manner—for an interaction network that had a stable coexistence solution, each of the constituent species was removed one at a time, and the remaining N – 1 species allowed to reach a new equilibrium. If the new equilibrium retained all remaining N – 1 species, then the system was characterized as stable with respect to perturbations where a species is eliminated from a niche. This was repeated for all interaction networks known to have a locally stable coexistence solution. The number of instances where the network was resilient to the loss of a species was recorded, and the likelihood that, for a given degree of connectance c, and fraction of interactions which are synergistic, f_c, a stable N-species population will be resilient to the loss of a species estimated.

As shown in Figures 5A,B, for a three- and four-species network using the replicator equation, the resilience of a population against the loss of a species shows trends similar to those observed for stability against internal perturbations in frequencies. An increasing fraction of synergistic interactions tends to lend the population stability against the loss of a species, with increasing connectance conferring minimal gains in this regard. Similar results were obtained when the process was repeated for a three- four-species network (Figures 5C,D) using the Lotka-Volterra model. Figure 5 represents results when interaction strengths for the P matrix were sampled from exponential distributions. Qualitatively similar results were observed when interactions were sampled from a uniform distribution for the two formulations (Supplementary Figure 3). In these simulations, each species was removed one at a time, for each of the 1,000 randomized matrices, and the stability thus classified for the N1000 matrices.

FIGURE 5

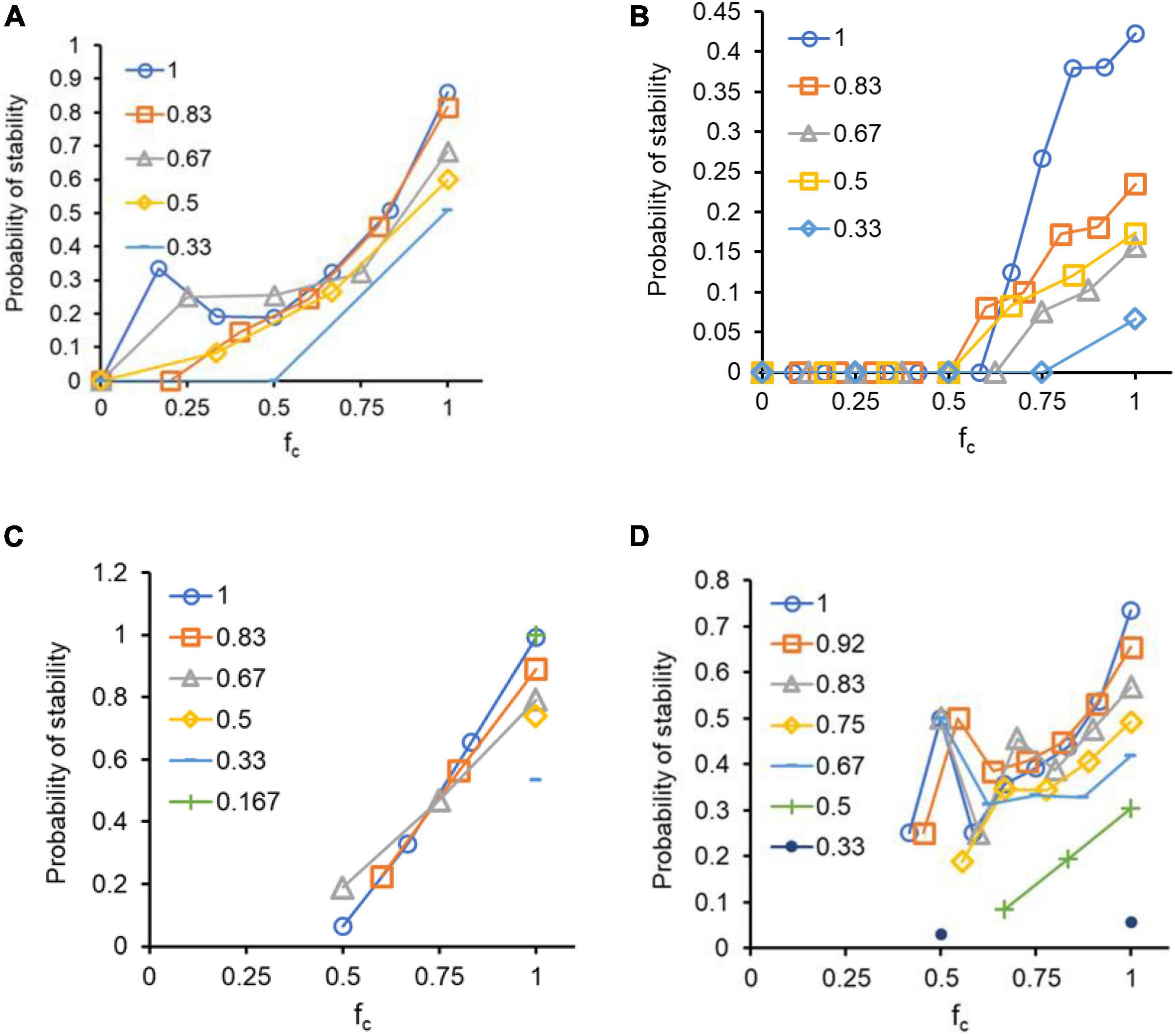
Figure 5. Cooperative interactions help the system retain diversity. Upon removal of a species from an N-sized network, the remaining N - 1 species are allowed to reach the new equilibrium. If the new steady state comprises of all N - 1 species, the system is classified as stable. (A) Three-species network, and (B) four-species network when analyzed in a replicator equation framework. (C) Three-species network, and (D) four-species network when analyzed in a Lotka-Volterra framework. All interactions are sampled from exponential distributions. The data represents data from 1,000 simulations of randomized P matrices for each pair of c and f_c. The legend describes the value of c for each set of simulations.

Connectance, c and Fraction of Interactions, Which Are Synergistic fc From Ecological Samples

While our modeling results show that the major determinant of preservation of diversity, in a small community of 3–4 participating species, is the fraction of interactions in a network that are synergistic, we still do not know of the respective values of these numbers from real systems. Toward this end, we isolated bacterial samples from a garden soil sample, and isolated bacterial species as described in “Materials and Methods” section. Twenty bacterial species were isolated from these samples.

We next performed pairwise growth cultures of all 190 pairs from this set of twenty, and on comparing their growth with cultures of single species, characterized the interaction between the pairs as cooperative or antagonistic or no change in the growth because of presence of another species. Of 380 possible interactions, in our experiments, we find 39 cooperative, and 9 antagonistic interactions. This equates to a connectance c of 0.12 and fraction of interactions, which are cooperative fc as equal to 0.81. The qualitative nature of this relative distribution, though, is likely to be strongly dependent on the system/species being studied (Adler et al., 2018).

The c value from our analysis is likely to be an underestimation of the actual interactions present in the network. This is due to the following reasons. First, we measure the impact of one species on the other by counting colonies of each species, when two species are grown together for a specific amount of time. While the technique can capture large effects, it is likely insufficient to be able to estimate small effects on fitness of the participating species. Second, the niche from where these species were isolated was a soil sample. The experiments we perform to estimate the interaction between species are in an environment where there is no spatial structure (liquid media). As a result, it is likely that interactions between species, which are associated with spatial arrangement will be missed from our analysis. Third and lastly, while we only investigate pairwise interactions in our work, it is also possible that higher order interactions exist in the community (Mickalide and Kuehn, 2019). The presence of these higher-order interactions can increase or decrease the number of pairwise interactions in the community.

While there have been few studies which have quantified the distribution of interaction effects between participating species in a network, for our system, a large number of interactions are synergistic. This result is also likely a function of physical and chemical environmental conditions in which these experiments were performed. Given the widespread distribution of synergistic interactions, our results, however, raise the following question: What is the role of antagonistic interactions in a consortium of species? Consider the following two three-species systems (A, B, and C), with innate growth rates in the order r_C > r_B > r_A.

We are merely drawing the reader’s attention to the Figure 6A. The synergistic interaction directed from C to A stabilizes the number of individuals of species A in the culture media (since A grows the slowest). The antagonistic interaction between species A and C inhibits such commensalism and establishes a negative feedback loop to maintain population diversity, by ensuring presence of species B at steady state.

FIGURE 6

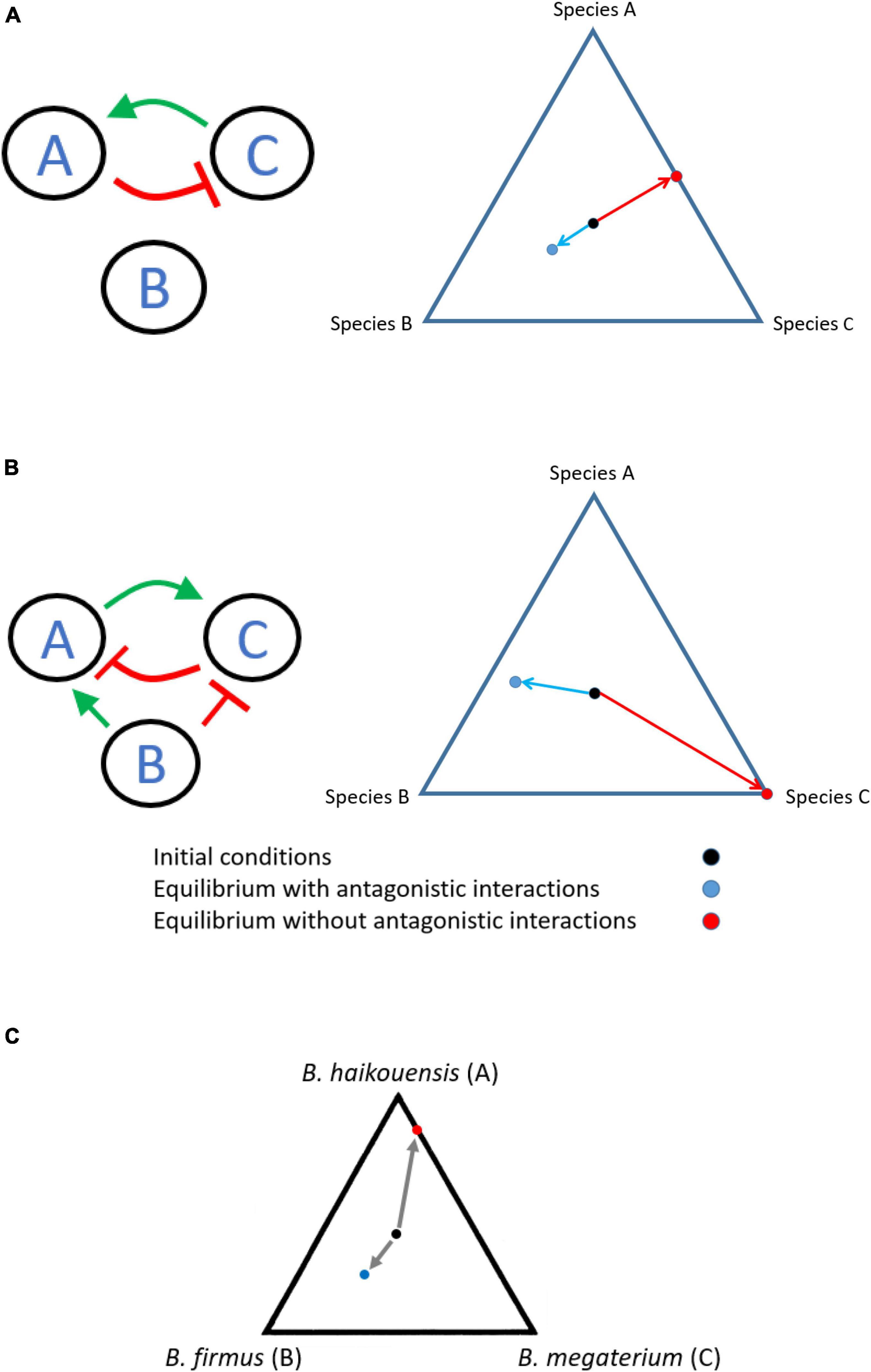
Figure 6. Possible role of antagonistic interactions in maintaining species diversity. Loss of antagonistic interactions in two different topologies (A,B) in a community leads to loss of diversity. (C) Antagonistic interaction provides stability to a three-species system. Black circle represents the starting frequencies of the three species. Blue circle represents the steady state between the three species when cooperative and antagonistic interactions between A and C were present. Red circle represents the steady state when only cooperative interaction from C to A was present; and the antagonistic interaction was absent from the system. Steady state in this experiment represents serial culturing the growth media yielded no change in the frequencies of the species present. The experiment was performed in triplicate, and the average of the three experiments is shown. The standard deviation in the frequencies for the case with all interactions present was <5% of frequency. Species B was eliminated in all three runs of the experiment, when antagonistic interaction was eliminated.

The network in Figure 6B ensures stable coexistence of the three species. Here, species C, unlike A and B, does not aid the growth of the other two species. Rather, species C and the antagonistic interaction between species B and C serve to restrain C from taking over the population. The absence of either or both antagonistic interactions would render coexistence impossible and lead to extinction of A and B.

Experimental Test of Role of Antagonistic Interactions

Topology 6A was observed between three of the species isolated from soil samples. From 16sRNA sequencing, we determined that the participating species in this three species network were Bacillus haikouensis (A), Bacillus firmus (B), and Bacillus megaterium (C), respectively (See Supplementary Section 5 for more details about the physiology of the three species).

As shown in Figure 6C, in the culture experiment, the end-point result of the experiment when all three species are allowed to grow unperturbed, stable coexistence of the three species was found. However, in the altered design, where the antagonistic interaction from A to C is eliminated, species B is lost from the system (see methods section “Experiments With Soil Bacteria” for more details). These experiments propose a likely role of antagonistic interactions, in specific contexts, toward aiding diversity in an environment. While these simple experiments suggest a possible role for antagonistic interactions in maintaining diversity in a culture, other possibilities remain. First, it is also possible that higher-order interactions between species are disrupted on removal of species C from the system. As a result, the effect on dynamics is not due to altered topology, but due to eliminating of this higher-order interaction. We also note that the experimental system in our study does not strictly represent the mathematical formulation of species growth, which is best studied in a chemostat environment. However, we present evidence that manipulating the interactions between species, as we perform the experiments, dictates the equilibrium structure of populations.

Discussion

There has been considerable interest in studying bacterial/microbial communities in recent years (Chubiz et al., 2015; Goldford et al., 2018; Vega and Gore, 2018; Pacheco and Segre, 2019). This is largely due to the fact that microbial communities (a) represent the physiology of microorganisms as they exist in their environments and (b) are relatively easy to re-create and study in a laboratory environment. The community structure includes interactions between the members of participating species. These interactions between members of same/different species can be due to changes brought about in the physical, chemical, or biological environments. In this context, the broad prevalent nature of these interactions in ecology remains an open question. While theory predicts that cooperative interactions render the system unstable (May, 1972; McCann, 2000), and hence, community interactions are largely antagonistic; experimental evidence suggests that positive interactions are widely present in bacterial communities (Kehe et al., 2020).

In this context, through simulations using two approaches and experiments, we, via simulations of small number of species networks and experiments to study nature of interactions among bacterial species in soil, present evidence that stability to microbial systems is largely conferred by synergistic interactions. These interactions provide stability against perturbations in population structure, loss of species. In an ecological context, other measures of stability exist too. These include preventing invasion by an antagonist species, or stability against environmental fluctuations. The last one is particularly relevant in an ecological context, where selection is likely to be cyclic in nature, and not time invariant (Abreu et al., 2020). The number of possible topologies increases exponentially as the size of the network increases. Hence, sampling topologies from all possibilities as the network size increases becomes a computational challenge. The analysis is made more intensive by the fact that, for each topology, many networks exist, depending on the value of the interaction strength parameters. Moreover, as number of species increases in a community, their relative arrangement in space is also likely an important factor dictating coexistence. Space, as a variable, is largely absent from studies of microbial species (Vega and Gore, 2018; Abreu et al., 2020; Ratzke et al., 2020). In a recent study, however, this aspect of microbial ecology was studied, and it was reported that different species occupy distinct niches in a spatially structured environment (Borer et al., 2018). Spatial arrangement was also shown to ensure coexistence of two species, when present in chaotic flows (Karolyi et al., 2000; Galla and Perez-Munuzuri, 2017). Second, ecological communities are often studied in synthetic media from the sub-set of species isolated from the niche (Kehe et al., 2019; Amor et al., 2020; Lax et al., 2020). Thus, our interferences are only limited to interactions between the few isolated species in the synthetic media conditions in well-mixed environments of a laboratory setting.

Conclusion

We show that in a bacterial community in soil, synergistic interactions far outnumber antagonistic interactions between the participating species. While our simulation results show that synergistic interactions are more significant for coexistence, we show that, in specific contexts, antagonistic interactions can also contribute toward coexistence of species in an environment. While our simulations are for very small networks which are not representative of the complexity of a structured environment and diversity in an ecological sample, these results provide evidence to explain the presence of extent of synergistic interactions in microbial communities, as reported recently (Kehe et al., 2020). Next steps in this direction of research would be making use of simulations and theories to design artificial communities, toward biotechnological applications.

The principles for understanding coexistence of species is important from fundamental as well as applied perspectives. No good methods exist for establishing systems where coexistence of multiple species can be studied long periods of time in a spatially structured environment. In the absence of fundamentals which help us design microbial communities, the challenge associated with instability of multi-species network has been addressed by generating auxotrophic mutants, whose existence is contingent on metabolic trade with each other (D’Souza and Kost, 2016; Giri et al., 2019). Theory has also been used to explain this coexistence because of metabolic trade and co-dependence (Dutta and Saini, 2021). Exploration of space as a variable, and metabolic cooperation/dependence will likely shed more light in explaining coexistence of microbial communities with a large number of species participants.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AM: performed the simulations, analyzed the data, and wrote the manuscript. SK: performed the experiments and wrote the manuscript. SS: conceived the study and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Anjali Mahilkar for discussions and help with the competition experiments between bacterial species. We also thank the reviewers for their comments regarding the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.648997/full#supplementary-material

References

Abreu, C. I., Andersen Woltz, V. L., Friedman, J., and Gore, J. (2020). Microbial communities display alternative stable states in a fluctuating environment. PLoS Comput. Biol. 16:e1007934. doi: 10.1371/journal.pcbi.1007934

PubMed Abstract | CrossRef Full Text | Google Scholar

Adler, P. B., Smull, D., Beard, K. H., Choi, R. T., Furniss, T., Kulmatiski, A., et al. (2018). Competition and coexistence in plant communities: intraspecific competition is stronger than interspecific competition. Ecol. Lett. 21, 1319–1329. doi: 10.1111/ele.13098

PubMed Abstract | CrossRef Full Text | Google Scholar

Allesina, S., and Tang, S. (2012). Stability criteria for complex ecosystems. Nature 483, 205–208. doi: 10.1038/nature10832

PubMed Abstract | CrossRef Full Text | Google Scholar

Amor, D. R., Ratzke, C., and Gore, J. (2020). Transient invaders can induce shifts between alternative stable states of microbial communities. Sci. Adv. 6:eaay8676. doi: 10.1126/sciadv.aay8676

PubMed Abstract | CrossRef Full Text | Google Scholar

Andrade-Dominguez, A., Salazar, E., Vargas-Lagunas Mdel, C., Kolter, R., and Encarnacion, S. (2014). Eco-evolutionary feedbacks drive species interactions. ISME J. 8, 1041–1054. doi: 10.1038/ismej.2013.208

PubMed Abstract | CrossRef Full Text | Google Scholar

Azam, F., and Malfatti, F. (2007). Microbial structuring of marine ecosystems. Nat. Rev. Microbiol. 5, 782–791. doi: 10.1038/nrmicro1747

PubMed Abstract | CrossRef Full Text | Google Scholar

Bascompte, J., Jordano, P., and Olesen, J. M. (2006). Asymmetric coevolutionary networks facilitate biodiversity maintenance. Science 312, 431–433.

Google Scholar

Borer, B., Tecon, R., and Or, D. (2018). Spatial organization of bacterial populations in response to oxygen and carbon counter-gradients in pore networks. Nat. Commun. 9:769. doi: 10.1038/s41467-018-03187-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruno, Jf, Stachowicz, J. J., and Bertness, Md (2003). Inclusion of facilitation into ecological theory. Trends Ecol. Evol. 18, 119–125. doi: 10.1016/s0169-5347(02)00045-9

CrossRef Full Text | Google Scholar

Bulleri, F., Bruno, J. F., Silliman, B. R., and Stachowicz, J. J. (2016). Facilitation and the niche: implications for coexistence, range shifts and ecosystem functioning. Funct. Ecol. 30, 70–78.

Google Scholar

Bunin, G. (2017). Ecological communities with Lotka-Volterra dynamics. Phys. Rev. E 95:042414.

Google Scholar

Butler, S., and O’Dwyer, J. P. (2018). Stability criteria for complex microbial communities. Nat. Commun. 9:2970. doi: 10.1038/s41467-018-05308-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Case, T. J. (1990). Invasion resistance arises in strongly interacting species-rich model competition communities. Proc. Natl. Acad. Sci. U.S.A. 87, 9610–9614. doi: 10.1073/pnas.87.24.9610

PubMed Abstract | CrossRef Full Text | Google Scholar

Chubiz, L. M., Granger, B. R., Segre, D., and Harcombe, W. R. (2015). Species interactions differ in their genetic robustness. Front. Microbiol. 6:271. doi: 10.3389/fmicb.2015.00271

PubMed Abstract | CrossRef Full Text | Google Scholar

Colwell, R. K., and Rangel, T. F. (2009). Hutchinson’s duality: the once and future niche. Proc. Natl. Acad. Sci. U.S.A. 106(Suppl. 2), 19651–19658. doi: 10.1073/pnas.0901650106

PubMed Abstract | CrossRef Full Text | Google Scholar

Corel, E., Lopez, P., Meheust, R., and Bapteste, E. (2016). Network-thinking: graphs to analyze microbial complexity and evolution. Trends Microbiol. 24, 224–237.

Google Scholar

Coyte, K. Z., Schluter, J., and Foster, K. R. (2015). The ecology of the microbiome: networks, competition, and stability. Science 350, 663–666. doi: 10.1126/science.aad2602

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Souza, G., and Kost, C. (2016). Experimental evolution of metabolic dependency in bacteria. PLoS Genet. 12:e1006364. doi: 10.1371/journal.pgen.1006364

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutta, D., and Saini, S. (2021). Cell growth model with stochastic gene expression helps understand the growth advantage of metabolic exchange and auxotrophy. mSystems 6:e0044821. doi: 10.1128/mSystems.00448-21

PubMed Abstract | CrossRef Full Text | Google Scholar

Faust, K., and Raes, J. (2012). Microbial interactions: from networks to models. Nat. Rev. Microbiol. 10, 538–550. doi: 10.1038/nrmicro2832

PubMed Abstract | CrossRef Full Text | Google Scholar

Fontaine, C., Guimaraes, P. R. Jr., Kefi, S., Loeuille, N., Memmott, J., Van Der Putten, W. H., et al. (2011). The ecological and evolutionary implications of merging different types of networks. Ecol. Lett. 14, 1170–1181. doi: 10.1111/j.1461-0248.2011.01688.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster, K. R., and Bell, T. (2012). Competition, not cooperation, dominates interactions among culturable microbial species. Curr. Biol. 22, 1845–1850. doi: 10.1016/j.cub.2012.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Fredriksson, N. J., Hermansson, M., and Wilen, B. M. (2013). The choice of PCR primers has great impact on assessments of bacterial community diversity and dynamics in a wastewater treatment plant. PLoS One 8:e76431. doi: 10.1371/journal.pone.0076431

PubMed Abstract | CrossRef Full Text | Google Scholar

Galla, T., and Perez-Munuzuri, V. (2017). Time scales and species coexistence in chaotic flows. EPL 117:68001. doi: 10.1073/pnas.240242797

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghoul, M., and Mitri, S. (2016). The ecology and evolution of microbial competition. Trends Microbiol. 24, 833–845. doi: 10.1016/j.tim.2016.06.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Giri, S., Waschina, S., Kaleta, C., and Kost, C. (2019). Defining division of labor in microbial communities. J. Mol. Biol. 431, 4712–4731. doi: 10.1016/j.jmb.2019.06.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldford, J. E., Lu, N., Bajic, D., Estrela, S., Tikhonov, M., Sanchez-Gorostiaga, A., et al. (2018). Emergent simplicity in microbial community assembly. Science 361, 469–474. doi: 10.1126/science.aat1168

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonze, D., Coyte, K. Z., Lahti, L., and Faust, K. (2018). Microbial communities as dynamical systems. Curr. Opin. Microbiol. 44, 41–49. doi: 10.1016/j.mib.2018.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1960). The competitive exclusion principle. Science 131, 1292–1297.

Google Scholar

Hiltunen, T., Virta, M., and Laine, A. L. (2017). Antibiotic resistance in the wild: an eco-evolutionary perspective. Philos. Trans. R. Soc. Lond. B Biol. Sci. 372:20160039. doi: 10.1098/rstb.2016.0039

PubMed Abstract | CrossRef Full Text | Google Scholar

Hofbauer, J., and Sigmund, K. (1988). The Theory of Evolution and Dynamical Systems, Mathematical Aspects of Selection. Cambridge: Cambridge University Press.

Google Scholar

Hofbauer, J., Schuster, P., and Sigmund, K. (1979). A note on evolutionary stable strategies and game dynamics. J. Theor. Biol. 81, 609–612. doi: 10.1016/0022-5193(79)90058-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutchinson, G. E. (1978). An Introduction to Population Ecology. New Haven, CT: Yale University Press.

Google Scholar

Juhnke, M. E., and des Jardin, E. (1989). Selective medium for isolation of Xanthomonas maltophilia from soil and rhizosphere environments. Appl. Environ. Microbiol. 55, 747–750. doi: 10.1128/aem.55.3.747-750.1989

PubMed Abstract | CrossRef Full Text | Google Scholar

Karolyi, G., Pentek, A., Scheuring, I., Tel, T., and Toroczkai, Z. (2000). Chaotic flow: the physics of species coexistence. Proc. Natl. Acad. Sci. U.S.A. 97, 13661–13665.

PubMed Abstract | Google Scholar

Kehe, J., Kulesa, A., Ortiz, A., Ackerman, C. M., Thakku, S. G., Sellers, D., et al. (2019). Massively parallel screening of synthetic microbial communities. Proc. Natl. Acad. Sci. U.S.A. 116, 12804–12809. doi: 10.1073/pnas.1900102116

PubMed Abstract | CrossRef Full Text | Google Scholar

Kehe, J., Ortiz, A., Kulesa, A., Gore, J., Blainey, P. C., and Friedman, J. (2020). Positive interactions are common among culturable bacteria. bioRxiv [Preprint]. doi: 10.1101/2020.06.24.169474

CrossRef Full Text | Google Scholar

Kuntal, B. K., Gadgil, C., and Mande, S. S. (2019). Web-gLV: a web based platform for lotka-volterra based modeling and simulation of microbial populations. Front. Microbiol. 10:288. doi: 10.3389/fmicb.2019.00288

PubMed Abstract | CrossRef Full Text | Google Scholar

Lax, S., Abreu, C. I., and Gore, J. (2020). Higher temperatures generically favour slower-growing bacterial species in multispecies communities. Nat. Ecol. Evol. 4, 560–567. doi: 10.1038/s41559-020-1126-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, W. J., and Hase, K. (2014). Gut microbiota-generated metabolites in animal health and disease. Nat. Chem. Biol. 10, 416–424. doi: 10.1038/nchembio.1535

PubMed Abstract | CrossRef Full Text | Google Scholar

Lundh, T., and Gerlee, P. (2013). Cross-feeding dynamics described by a series expansion of the replicator equation. Bull. Math. Biol. 75, 709–724. doi: 10.1007/s11538-013-9828-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Madec, S., and Gjini, E. (2020). Predicting N-Strain coexistence from Co-colonization Interactions: epidemiology meets ecology and the replicator equation. Bull. Math. Biol. 82:142. doi: 10.1007/s11538-020-00816-w

PubMed Abstract | CrossRef Full Text | Google Scholar

May, R. M. (1972). Will a large complex system be stable? Nature 238, 413–414.

Google Scholar

McCann, K. S. (2000). The diversity-stability debate. Nature 405, 228–233.

Google Scholar

Mickalide, H., and Kuehn, S. (2019). Higher-order interaction between species inhibits bacterial invasion of a phototroph-predator microbial community. Cell Syst. 9, 521–533.e10.^**521-533.e10 doi: 10.1016/j.cels.2019.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Momeni, B., Xie, L., and Shou, W. (2017). Lotka-Volterra pairwise modeling fails to capture diverse pairwise microbial interactions. Elife 6:e25051. doi: 10.7554/eLife.25051

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno-Fenoll, C., Cavaliere, M., Martinez-Garcia, E., and Poyatos, J. F. (2017). Eco-evolutionary feedbacks can rescue cooperation in microbial populations. Sci. Rep. 7:42561. doi: 10.1038/srep42561

PubMed Abstract | CrossRef Full Text | Google Scholar

Mougi, A. (2016). The roles of amensalistic and commensalistic interactions in large ecological network stability. Sci Rep 6, 29929. doi: 10.1038/srep29929

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak, M. A. (2006). Evolutionary Dynamics. Cambridge, MA: Harvard University Press.

Google Scholar

Pacheco, A. R., and Segre, D. (2019). A multidimensional perspective on microbial interactions. FEMS Microbiol. Lett. 366:fnz125. doi: 10.1093/femsle/fnz125

PubMed Abstract | CrossRef Full Text | Google Scholar

Pacheco, A. R., Moel, M., and Segre, D. (2019). Costless metabolic secretions as drivers of interspecies interactions in microbial ecosystems. Nat. Commun. 10:103. doi: 10.1038/s41467-018-07946-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Pande, S., Kaftan, F., Lang, S., Svatos, A., Germerodt, S., and Kost, C. (2016). Privatization of cooperative benefits stabilizes mutualistic cross-feeding interactions in spatially structured environments. ISME J. 10, 1413–1423. doi: 10.1038/ismej.2015.212

PubMed Abstract | CrossRef Full Text | Google Scholar

Pande, S., Merker, H., Bohl, K., Reichelt, M., Schuster, S., De Figueiredo, L. F., et al. (2014). Fitness and stability of obligate cross-feeding interactions that emerge upon gene loss in bacteria. ISME J. 8, 953–962. doi: 10.1038/ismej.2013.211

PubMed Abstract | CrossRef Full Text | Google Scholar

Ratzke, C., Barrere, J., and Gore, J. (2020). Strength of species interactions determines biodiversity and stability in microbial communities. Nat. Ecol. Evol. 4, 376–383. doi: 10.1038/s41559-020-1099-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Rouze, H., Leray, M., Magalon, H., Penin, L., Gelin, P., Knowlton, N., et al. (2017). Molecular characterization reveals the complexity of previously overlooked coral-exosymbiont interactions and the implications for coral-guild ecology. Sci. Rep. 7:44923.

Google Scholar

Sambrook, J., and Russell, D. W. (2000). Molecular Cloning: A Laboratory Manual, 3rd Edn. New York, NY: Cold Spring Harbor Laboratory Press.

Google Scholar

Sane, M., Diwan, G. D., Bhat, B. A., Wahl, L. M., and Agashe, D. (2020). Shifts in mutation spectra enhance access to beneficial mutations. bioRxiv [Preprint]. doi: 10.1101/2020.09.05.284158

CrossRef Full Text | Google Scholar

Stewart, E. J. (2012). Growing unculturable bacteria. J. Bacteriol. 194, 4151–4160.

Google Scholar

Vega, N. M., and Gore, J. (2018). Simple organizing principles in microbial communities. Curr. Opin. Microbiol. 45, 195–202. doi: 10.1016/j.mib.2018.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Venkateswaran, V. R., and Gokhale, C. S. (2019). Evolutionary dynamics of complex multiple games. Proc. Biol. Sci. 286:20190900. doi: 10.1098/rspb.2019.0900

PubMed Abstract | CrossRef Full Text | Google Scholar

Venturelli, O. S., Carr, A. C., Fisher, G., Hsu, R. H., Lau, R., Bowen, B. P., et al. (2018). Deciphering microbial interactions in synthetic human gut microbiome communities. Mol. Syst. Biol. 14:e8157. doi: 10.15252/msb.20178157

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, Y., Angulo, M. T., Friedman, J., Waldor, M. K., Weiss, S. T., and Liu, Y. Y. (2017). Mapping the ecological networks of microbial communities. Nat. Commun. 8:2042. doi: 10.1038/s41467-017-02090-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Zomorrodi, A. R., and Segre, D. (2017). Genome-driven evolutionary game theory helps understand the rise of metabolic interdependencies in microbial communities. Nat. Commun. 8:1563. doi: 10.1038/s41467-017-01407-5

PubMed Abstract | CrossRef Full Text | Google Scholar