Guanming Guo
Zeyu Zhang1
Helin Zhang
Jinbao Liao- 1Research Center for Theoretical Ecology, Ministry of Education’s Key Laboratory of Poyang Lake Wetland and Watershed Research, School of Geography and Environment, Jiangxi Normal University, Nanchang, China
- 2School of Mathematics, Statistics and Actuarial Sciences, University of Kent, Canterbury, United Kingdom
Intransitive competition, typically represented by the classic rock-paper-scissors game, provides an endogenous mechanism promoting species coexistence. As well known, species dispersal and interaction in nature might occur on complex patch networks, with species interacting in diverse ways. However, the effects of different interaction modes, combined with spatial heterogeneity in patch connectivities, have not been well integrated into our general understanding of how stable coexistence emerges in cyclic competition. We thus incorporate network heterogeneity into the classic rock-paper-scissors game, in order to compare ecosystem stability under two typical modes of interaction: species compete to fill empty sites, and species seize each other’s colony sites. On lattice-structured regular networks, the two interaction modes produce similar stability patterns through forming conspecific clusters to reduce interspecific competition. However, for heterogeneous networks, the interaction modes have contrasting effects on ecosystem stability. Specifically, if species compete for colony sites, increasing network heterogeneity stabilizes competitive dynamics. When species compete to fill empty sites, an increase in network heterogeneity leads to larger population fluctuations and therefore a higher risk of stochastic extinctions, in stark contrast to current knowledge. Our findings strongly suggest that particular attention should be devoted to testing which mode of interaction is more appropriate for modeling a given system.
Introduction
Understanding the mechanisms of ecosystem stability is a fundamental issue in ecology (May, 1972; Chesson, 2000; Levine and HilleRisLambers, 2009; Allesina and Levine, 2011). Many proposed mechanisms rely heavily on exogenous factors mitigating the effects of competition, such as niche differentiation (Chesson, 2000; Levine and HilleRisLambers, 2009; Chu and Adler, 2015) and intermediate disturbance hypothesis (Connell, 1978; Roxburgh et al., 2004; Liao et al., 2022). In contrast to these exogenous mechanisms, intransitive competition provides an endogenous mechanism promoting coexistence (Laird and Schamp, 2006; Allesina and Levine, 2011; Soliveres et al., 2015; Levine et al., 2017), and, in particular, the simple rock-paper-scissors game has become a typical case to explain ecosystem stability (Huisman and Weissing, 1999; Kerr et al., 2002; Reichenbach et al., 2007). The classic, cyclic game of rock-paper-scissors usually leads to species’ abundances neutrally cycling without converging to a stable equilibrium point, which is rarely observed in nature. To overcome this problem, many approaches have been proposed to explain the robust persistence of the cyclically competing system, such as higher-order interactions (Grilli et al., 2017) and spatially structured interactions (Durrett and Levin, 1997; Czárán et al., 2002; Rojas-Echenique and Allesina, 2011; Calleja-Solanas et al., 2021; Zhang et al., 2022). In particular, the latter mechanism of local structured interactions stabilizing coexistence has been documented experimentally (Kerr et al., 2002). Thus, it is widely believed that the inclusion of spatial structure, where the interactions and dispersal of individuals are local, can result in stable coexistence in rock-paper-scissors games. Yet, these conclusions are mostly drawn from lattice-based models, where each individual is assumed to only interact with its surrounding neighbors. This assumption is relatively restrictive, as species dispersal and interactions in nature might occur on complex networks with variation in patch connectivities (i.e., spatial heterogeneity in dispersal networks; Urban and Keitt, 2001; Fortuna et al., 2006; Dale and Fortin, 2010; Galpern et al., 2011; Grilli et al., 2015; Fortin et al., 2021; He et al., 2021; Li et al., 2021; Zhang et al., 2021).
There is abundant evidence that landscape structure, and other factors (e.g., patch quality; Liao et al., 2013), can result in anisotropic (i.e., directionally biased) dispersal behavior and therefore spatial heterogeneity in patch connectivities (Urban and Keitt, 2001; Fortuna et al., 2006; Dale and Fortin, 2010; Galpern et al., 2011; Grilli et al., 2015; Fortin et al., 2021; He et al., 2021). Since different patches in the landscape might be perceived differently by species (Hansbauer et al., 2010; Dondina et al., 2018), and the resulting dispersal network would display diverse patterns of patch connectivity (Yeaton and Bond, 1991; Bunn et al., 2000; Nicholson and Possingham, 2006; Fortuna et al., 2009; Bearup et al., 2013; Hirt et al., 2018; Germain et al., 2019). For instance, species dispersal between sub-reefs within the Great Barrier Reef has been characterized with scale-free networks (Kininmonth et al., 2010), while seed dispersal by birds, as opposed by winds, is better described by an irregular network than a spatially uniform network. In addition, Fortuna et al. (2006) identified a large spatial dispersal network of temporary ponds, which are used as breeding sites for amphibian species, following a power-law degree distribution. As such, there has been an increasing interest in exploring the effects of network heterogeneity on ecosystem stability using graph theory (Szabó et al., 2004; Szolnoki and Szabó, 2004; Masuda and Konno, 2006; Dale and Fortin, 2010; Schütt and Claussen, 2010; Galpern et al., 2011; Laird, 2014; Nagatani et al., 2018; Fortin et al., 2021; He et al., 2021; Zhang et al., 2021). Many studies have found that increasing network heterogeneity (i.e., increasing variation in patch connectivities) can promote stable coexistence in cyclic competition (Masuda and Konno, 2006; Schütt and Claussen, 2010; Nagatani et al., 2018).
Despite these advances, several lattice-based models (Laird and Schamp, 2008; Rojas-Echenique and Allesina, 2011; Zhang et al., 2022) have observed that local intransitive competition can reduce species coexistence compared to long-range competition, in stark contrast to current knowledge of local interactions stabilizing coexistence (Durrett and Levin, 1997; Huisman and Weissing, 1999; Czárán et al., 2002; Kerr et al., 2002; Calleja-Solanas et al., 2021). Rojas-Echenique and Allesina (2011) and Zhang et al. (2022) attributed the opposite outcomes to different interaction modes, which can induce distinct stabilizing mechanisms in lattice-structured models. Indeed, species in diverse natural ecosystems might interact in different ways. For example, there are two typical interaction modes often observed in nature: seedlings of tree species or propagules of grass species compete to fill gaps, while animal species fight directly for colony sites (Rojas-Echenique and Allesina, 2011; Calleja-Solanas et al., 2021; Zhang et al., 2022). However, the effects of these different interaction modes, in combination with spatial heterogeneity in dispersal networks mentioned above, have not been well integrated into our general understanding of how stable coexistence emerges in cyclic competition. In this study, we thus incorporate dispersal network heterogeneity into the classic rock-paper-scissors games, in order to make a comparative analysis of ecosystem stability between the two typical interaction modes.
Materials and methods
Dispersal network heterogeneity
We consider a landscape consisting of a finite number (N) of patches (so-called colony sites), with each accommodating only one individual (or a subpopulation) of a species. In the landscape, individuals can move and interact between patches only along a predefined set of dispersal pathways. This shapes a dispersal network, with patches and dispersal pathways being represented by network nodes and links, respectively. To model the effect of spatial heterogeneity in dispersal networks (with fixed average patch degree 4), we generate four typical network structures with contrasting heterogeneities (i.e., the extent of variation in patch connectivities):
(1) A lattice-structured regular network with all patches having the same degree (illustrated in Figure 1A with each patch linked to other four patches).
(2) A randomly structured network with randomly connected patches (Watts and Strogatz, 1998), yielding small variation in patch degrees (Figure 1B).
(3) An exponential network constructed based on the algorithm of random attachment (Barabási and Albert, 1999). This produces a greater variation in patch connectivities than the random network (Figure 1C).
(4) A scale-free network structured according to the algorithm of preferential attachment (Barabási and Albert, 1999), producing the highest variation in patch connectivities (Figure 1D).
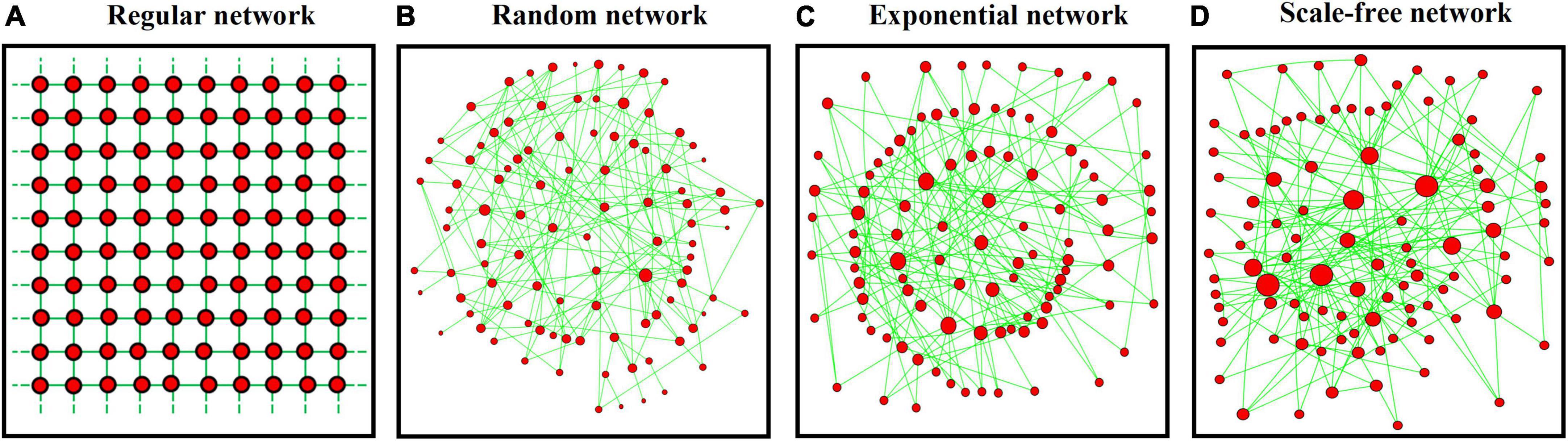
Figure 1. Four typical network structures consisting of 100 patches (red nodes) with 200 links (green lines): (A) lattice-structured regular, (B) randomly connected, (C) exponential, and (D) scale-free networks. Variation in patch degree (proportional to node size) increases from left to right panels.
In these networks, species are assumed to use dispersal links in either direction without preference (i.e., undirected dispersal).
Two typical interaction modes
We consider a system of three cyclically competing species on a landscape of size N = 10,000 patches connected by dispersal networks. Each patch can only accommodate one individual of a species. The competitive relationships between these three species (i, j, and k) follow the rock-paper-scissors game, an example of intransitive competition which usually yields species coexistence with oscillations (Grilli et al., 2017; Li et al., 2020).
To focus solely on the effect of species competition on ecosystem stability, we perform simulations as follows: (i) according to the typical assumption in previous work (Masuda and Konno, 2006; Rojas-Echenique and Allesina, 2011; Grilli et al., 2017; Nagatani et al., 2018; Calleja-Solanas et al., 2021; Zhang et al., 2022), initially all patches are populated with individuals randomly drawn from the three species; (ii) in each time step, we perform a competition event using the two interaction modes specified below; (iii) we repeat step (ii) for a long time, finding that 1,000 generations (1 generation = 10,000 time steps at N = 10,000 patches) are sufficient for the system to achieve steady state; (iv) at steady state, we record the number of individuals for each species and the spatial patterns at every generation.
In this study, we consider two interaction modes separately in the simulations.
Mode 1: Similar to Grilli et al. (2017) and Calleja-Solanas et al. (2021), in each time step, we randomly select a focal individual (with probability 1/N in the whole network) to die, and immediately choose two individuals randomly from its directly linked neighbors for pairwise competition, with the offspring of the winner occupying this empty patch. If the two individuals belong to the same species, then this species directly occupies the empty patch. If there is only one neighbor for the empty patch, then it is occupied directly by this neighbor.
Mode 2: Similar to Rojas-Echenique and Allesina (2011), in each time step, we randomly select two directly linked individuals for competition, with the offspring of the superior competitor substituting the inferior one (otherwise keeping the original state).
Under these two different interaction modes, we firstly explore how increasing network heterogeneity affects ecosystem stability in classic rock-paper-scissors games, and then test whether these outcomes are robust to varying network size.
Results
We begin our analysis by inspecting the temporal evolution of species abundances (Figure 2). When species compete to fill an empty patch (Mode 1), increasing network heterogeneity (from lattice-structured regular to scale-free networks) increases the magnitude of population fluctuations and speeds up stochastic species extinctions. In contrast, if the superior competitor directly substitutes the inferior one (Mode 2), all three species can coexist, and the magnitude of population fluctuations around the equilibrium point (≈1/3) decreases as network heterogeneity increases. In lattice-structured regular networks, both interaction modes yield similar fluctuation size (Figure 2A vs. Figure 2E with different ranges of y-axis). This is more clear when looking at their dynamic trajectories (Figure 2I vs. Figure 2M). In these dynamic trajectories (Figures 2I–P), the abundances of the species at each generation represent a point in the 3-simplex, whose vertices correspond to a monospecific population. Over time, the point follows a trajectory which will reflect the state of the system. If the system is close to the equilibrium abundances, the trajectory eventually occupies a small area near it, whilst larger fluctuations cover larger areas. Similar to Figures 2A–H, the interaction mode 1 results in greater fluctuations and ultimately monoculture in more heterogeneous networks (Figures 2I–L), as opposed to the interaction mode 2 where ecosystems are more stable in networks with higher heterogeneity.
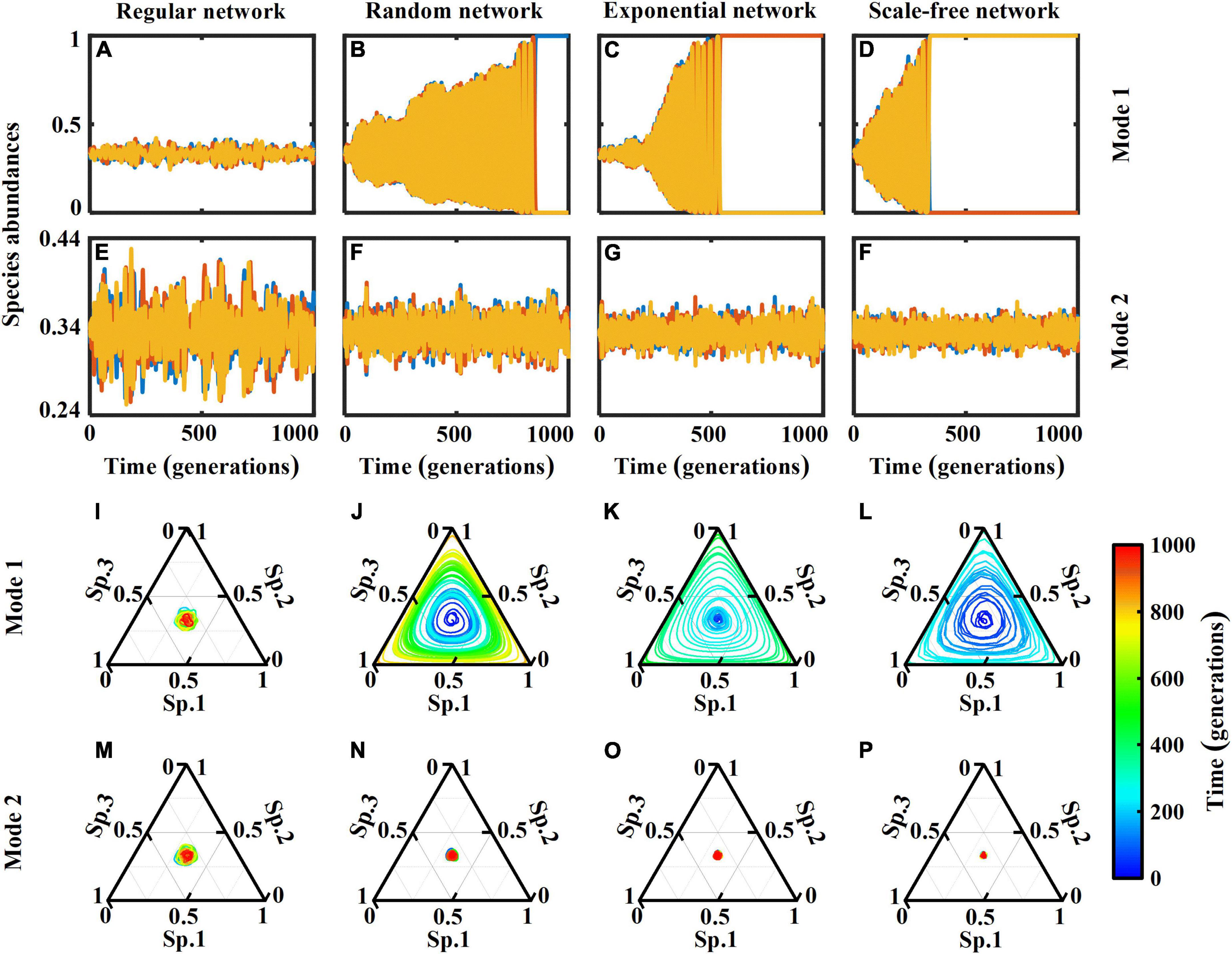
Figure 2. (A–H) Dynamics of species abundances of a rock-paper-scissors system (with 1,000 generations = 1 × 107 time steps) in complex networks of size N = 104 nodes with 2 × 104 links (average patch degree 4), including lattice-structured regular, randomly connected, exponential and scale-free networks. Two interaction modes are considered: (Mode 1) species compete to fill empty patches; and (Mode 2) species seize each other’s patches. (I–P) Trajectories in the phase space represented by the 3-simplex, corresponding to the dynamics in panels (A–H). The color bar represents time evolution (generations). Oscillations around the equilibrium point cover a smaller area, indicating a more stable ecosystem.
To test whether these outcomes are robust, we simulate 20 replicates for each case, by regenerating the dispersal network in each replicate (Figure 3). In Mode 1, three species can coexist with oscillations around the equilibrium point in the lattice-structured regular network (see Figure 2A), unlike other three heterogeneous networks where only one species ultimately dominates the system (Figure 3A). As such, the outcome in the regular network is absent in Figure 3A. In other three heterogeneous networks, we record the extinction time of the first species in each replicate, with more time required for species extinction implying more stable coexistence. As shown in Figure 3A, increasing network heterogeneity generally leads to species going extinct sooner. In Mode 2, all species can coexist with fluctuations around the equilibrium point in all dispersal networks. Thus, we use variation in fluctuations size (C.V. around the mean species abundances at steady state) to characterize ecosystem stability, with lower values of C.V. indicating more stable coexistence. As shown in Figure 3B, an increase in network heterogeneity generally results in smaller fluctuations in species abundances, yielding a more stable system. These outcomes further confirm our previous conclusions in Figure 2.
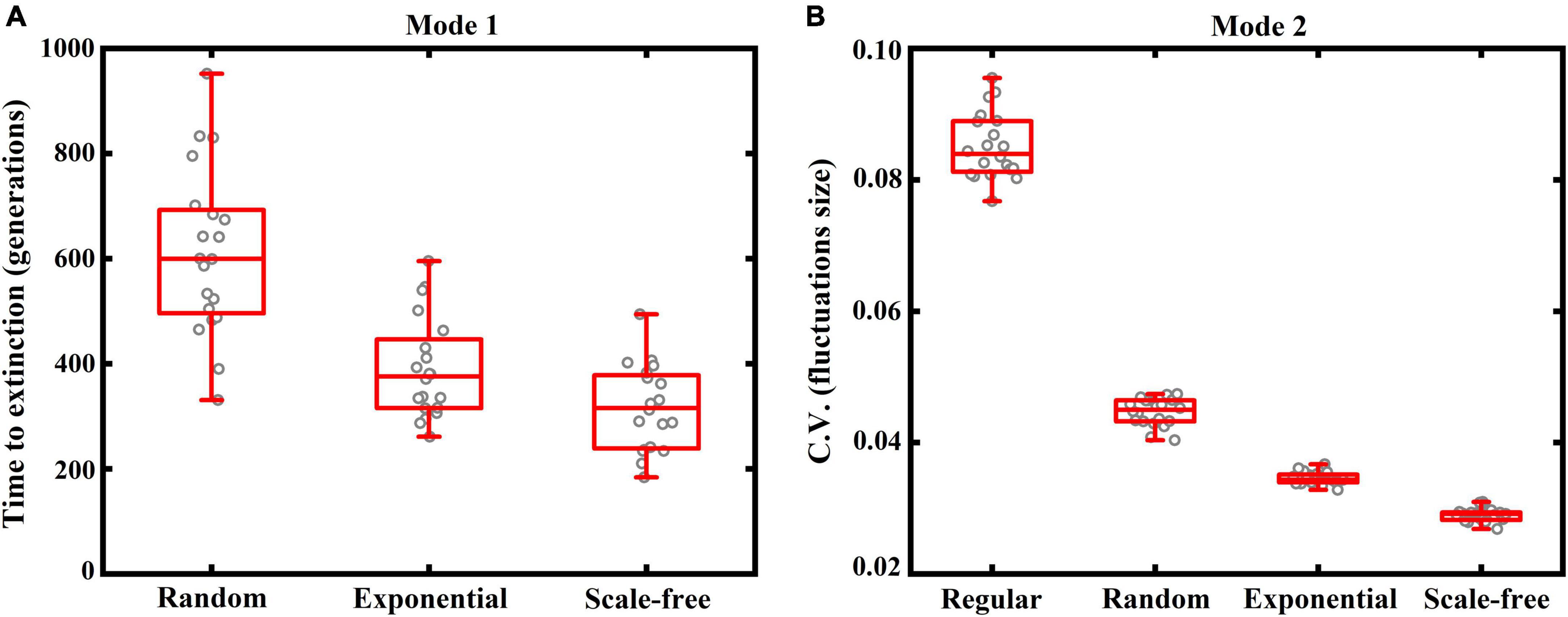
Figure 3. Box plots (red) of ecosystem stability (with 20 replicates for each case, indicated by gray cycles), characterized by panel (A: Mode 1) the time (generations) required for the first species to go extinct if stochastic extinctions occur, or (B: Mode 2) coefficient of variation in fluctuations size (C.V. around the mean species abundances at steady state) if three species can coexist. Again, four typical network structures are included: lattice-structured regular, randomly connected, exponential and scale-free networks. Note that, under Mode 1, three species can coexist in the regular network (see Figure 2A), which is thus absent in panel (A). More time required for species extinction or lower values of C.V. implies more stable coexistence. Other settings are the same as in Figure 2.
To better understand the mechanisms behind these dynamic behaviors, we display several snapshots of the spatial patterns of the three competitors in complex networks (Figure 4). In the lattice-structured regular network, both interaction modes produce similar conspecific clumping patterns (Figures 4A,B). To clearly illustrate the spatial organization in dispersal networks with contrasting heterogeneities, we take a system of N = 100 patches for example by displaying their snapshots at the 5th generation in Mode 1 and the 20th generation in Mode 2 (Figures 4C–J). In Mode 1 (Figures 4C–F), when three species have almost equal abundance in the regular network, increasing network heterogeneity which tends to increase network modularity, enlarges differences in species abundances, most likely accelerating stochastic extinctions. In Mode 2 (Figures 4G–J), if three species have unequal abundances in the regular network, dispersal network heterogeneity (i.e., network modularity) acts as a driving force to equalize their abundances, thereby stabilizing the ecosystem. We also observe that species can form self-organized conspecific clusters with the most connected patches at the core in these heterogeneous networks.
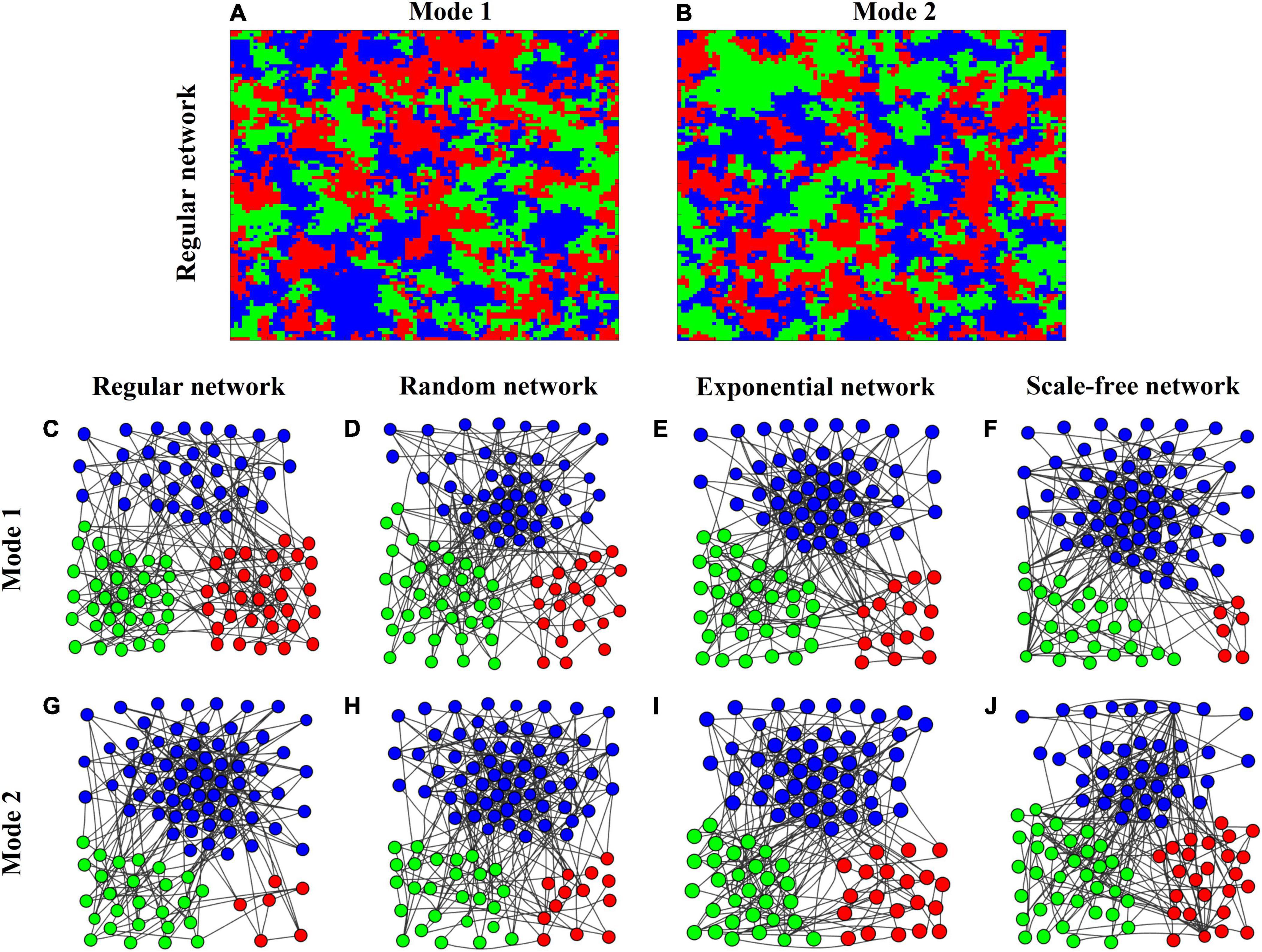
Figure 4. (A,B) Snapshots of the spatial organization of a 3-species system in rock-paper-scissors games at the 1000th generation in the lattice-structured regular network of size N = 104 patches with average degree 4 under Modes 1 & 2. Individuals of each species are painted in a different color. (C–J) Snapshots of the spatial patterns of the three species under Modes 1 & 2. (C–F) Mode 1 at the 5th generation; (G–J) Mode 2 at the 20th generation) in different networks (lattice-structured regular, randomly connected, exponential, and scale-free) of small size N = 100 patches (with 4) for clarity.
Under both interaction modes, we finally focus on how system size (i.e., increasing network size) affects fluctuations in species abundance in networks with contrasting heterogeneities (Figure 5). Intuitively, increasing network size promotes ecosystem stability, regardless of interaction mode and network heterogeneity. Specifically, stochastic extinctions in Mode 1 require more time to occur as network size increases, especially in networks with less heterogeneity (Figure 5A). This also demonstrates that increasing network heterogeneity greatly destabilizes the system. In Mode 2, the size of population fluctuation declines linearly with increasing network size (with log-log scale in Figure 5B), thereby promoting ecosystem stability. Furthermore, increasing network heterogeneity leads to smaller fluctuations, further confirming that network heterogeneity can stabilize the cyclically competing system.
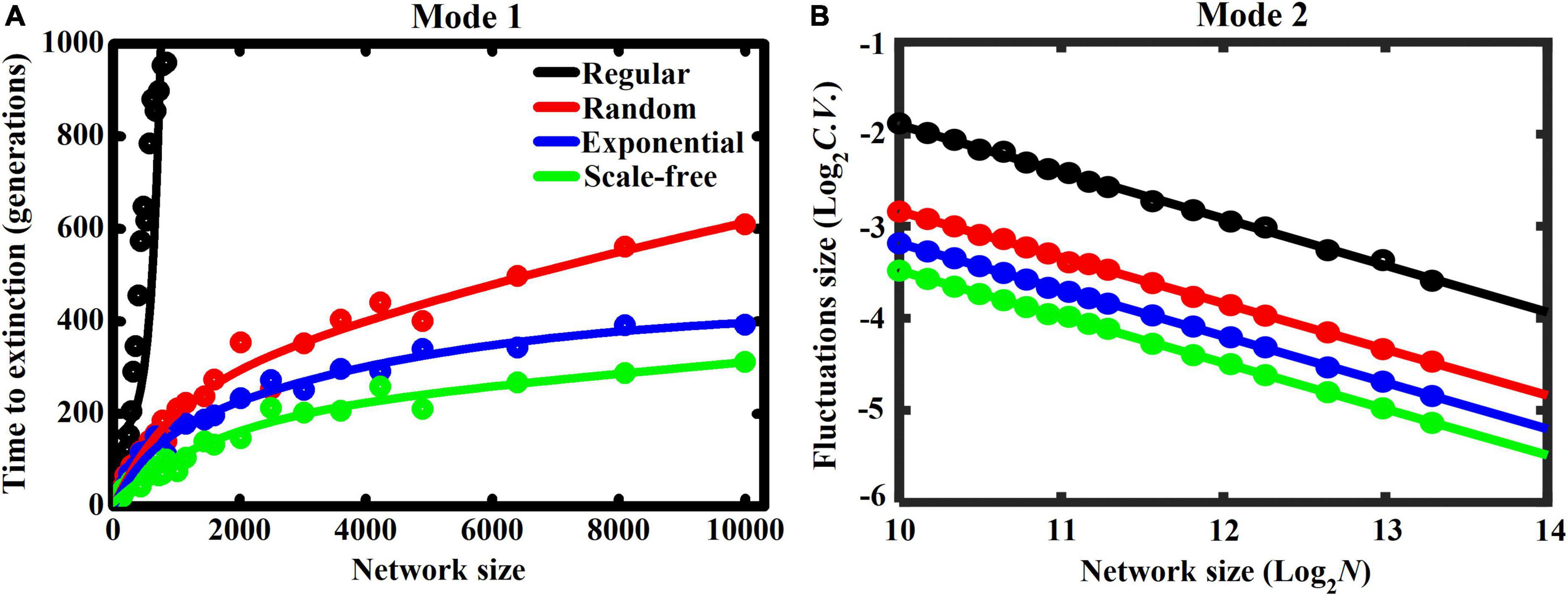
Figure 5. Effect of network size (N) on ecosystem stability under Modes 1 & 2 in networks with contrasting heterogeneities, including lattice-structured regular, randomly connected, exponential, and scale-free networks (each dot represents the mean of 20 replicates). Stability is characterized by panel (A: Mode 1) the time (generations) required for the first species going extinct, or (B: Mode 2) the coefficient of variation (C.V.) in fluctuations size around the mean species abundances at steady state. More time required for species extinction or lower values of C.V. indicates a more stable system.
Discussion
Incorporating complex networks into the classic rock-paper-scissors game, we find that whether network heterogeneity can stabilize competitive dynamics depends on the interaction mode. Specifically, if species compete directly for colony sites, increasing spatial heterogeneity in dispersal networks stabilizes the cyclically competing ecosystems, further confirming previous theoretical arguments (Masuda and Konno, 2006; Schütt and Claussen, 2010; Nagatani et al., 2018). In contrast, when species compete to fill an empty site, an increase in network heterogeneity leads to stronger population fluctuations and thus increases the risk of stochastic extinctions. Interestingly, in the lattice-structured regular network, both interaction modes display similar coexistence patterns based on the same mechanism: local interactions allow species to survive by forming conspecific clusters (via self-organization) where interspecific competition only takes place at the borders between heterospecific clusters, thereby decreasing the effective interspecific competition (by reducing interspecific encounter rate) and therefore population fluctuations (Figures 4A,B).
There exist different mechanisms between the two interaction modes that induce contrasting effects of network heterogeneity on ecosystem stability. In our model, the stabilizing role of network heterogeneity is observed when competition occurs through the superior competitor displacing the inferior one in a randomly chosen pair of neighbors. This competition mode has been commonly used and is symmetric in a cyclical way. However, increasing variation in patch connectivities implies that a few patches are highly connected while most have only few connections. A patch with more connections is more likely to be selected as a neighbor, while another neighbor can be sampled from multiple patches that might accommodate any of the three species. As such, which species can occupy this highly connected patch will change more frequently in networks with higher heterogeneity. To some extent, this prohibits the growth of self-organized conspecific clusters with the most connected patches at the core. In fact, increasing network heterogeneity breaks the symmetry in species interactions, that is, those individuals in highly connected patches have a higher chance to participate in competition than other individuals in poorly connected patches. This results in asymmetric interactions that can produce negative frequency dependence (NFD) which is absent in symmetric interactions (Rojas-Echenique and Allesina, 2011). Specifically, the NFD can decrease the average fitness of individuals when they become more common (cf. Zhang et al., 2022). Thus, the NFD, which is more significant in more heterogeneous networks, can suppress the population growth of dominant species but promote the growth of rare species, thereby increasing the frequency of oscillations and stabilizing competitive dynamics.
Network heterogeneity is destabilizing for the interaction mode where species compete for an empty site. This is because, in this mode, each species has the same probability to be selected to die, regardless of patch connectivities, so NFD cannot emerge. As such, conspecific clusters, with highly connected patches at the core, can grow (via self-organization) without restriction especially in networks with higher heterogeneity. Within these conspecific clusters, a competition event does not contribute to variation in species abundance, as local competition occurs between conspecific individuals. Thus, changes in species abundances can only take place along the borders between heterospecific clusters. However, the length of these borders increases more rapidly in more heterogeneous networks (i.e., a rapid increase in the number of “active” individuals that can change the state at the borders), promoting interspecific encounter rate and therefore interspecific competition. In addition, these heterospecific clusters can be treated as compartments dominated by different species, but there are lots of links connecting these compartments. If a superior competitor invades a compartment dominated by an inferior one, then it can colonize this compartment via the highly connected core. Ultimately, this results in larger population fluctuations and makes stochastic extinction events more likely.
This study incorporates complex networks into the rock-paper-scissors game under two commonly observed modes of interaction. In the lattice-structured regular network, both interaction modes yield similar system stability through forming conspecific clusters to reduce interspecific competition (Figure 4A vs. Figure 4B). Interestingly, we find that the inclusion of network heterogeneity can induce contrasting coexistence patterns between the two interaction modes, due to different mechanisms as explained above. This strongly suggests that particular attention should be devoted to testing, theoretically and experimentally, which mode of interaction is more appropriate for modeling a given competing system. For example, whereas the death of a tree or grass creates a gap in plant communities (i.e., Mode 1), animal species more typically fight for territory (i.e., Mode 2). Thus, these communities should be modeled with different interaction modes and so can be expected to be affected differently by the structure of the landscape they inhabit. Overall, even if these outcomes are obtained using an extremely simplified model, our findings can help identify different mechanisms to explain the role of different interaction modes in stabilizing competitive dynamics in complex networks with contrasting heterogeneities.
Data availability statement
The original contributions presented in this study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
GG, ZZ, and HZ built the model, performed simulations, and analyzed the results. JL conceived the study and wrote the manuscript. DB contributed substantially to revisions. All authors contributed to the article and approved the submitted version.
Funding
JL was supported by the National Natural Science Foundation of China (Nos. 32271548 and 31901175).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allesina, S., and Levine, J. M. (2011). A competitive network theory of species diversity. Proc. Natl. Acad. Sci. U.S.A. 108, 5638–5642. doi: 10.1073/pnas.1014428108
Barabási, A. L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512. doi: 10.1126/science.286.5439.509
Bearup, D., Petrovskii, S., Blackshaw, R. P., and Hastings, A. (2013). Synchronized dynamics of Tipula paludosa metapopulation in a southwestern Scotland agroecosystem: linking pattern to process. Am. Nat. 182, 393–409. doi: 10.1086/671162
Bunn, A. G., Urban, D. L., and Keitt, T. H. (2000). Landscape connectivity: a conservation application of graph theory. J. Environ. Manage. 59, 265–278. doi: 10.1006/jema.2000.0373
Calleja-Solanas, V., Khalil, N., Hernández-García, E., Gómez-Gardeñes, J., and Meloni, S. (2021). Structured interactions as a stabilizing mechanism for competitive ecosystems. arXiv [Preprint]. doi: 10.48550/arXiv.2012.14916
Chesson, P. (2000). Mechanisms of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343
Chu, C., and Adler, P. B. (2015). Large niche differences emerge at the recruitment stage to stabilize grassland coexistence. Ecol. Monogr. 85, 373–392. doi: 10.1890/14-1741.1
Connell, J. H. (1978). Diversity in tropical rain forests and coral reefs. Science 199, 1302–1310. doi: 10.1126/science.199.4335.1302
Czárán, T. L., Hoekstra, R. F., and Pagie, L. (2002). Chemical warfare between microbes promotes biodiversity. Proc. Natl. Acad. Sci. U.S.A. 99, 786–790. doi: 10.1073/pnas.012399899
Dale, M. R. T., and Fortin, M. J. (2010). From graphs to spatial graphs. Ann. Rev. Ecol. Evol. Syst. 41, 21–38. doi: 10.1146/annurev-ecolsys-102209-144718
Dondina, O., Orioli, V., Colli, L., Luppi, M., and Bani, L. (2018). Ecological network design from occurrence data by simulating species perception of the landscape. Landsc. Ecol. 33, 275–287. doi: 10.1007/s10980-017-0600-1
Durrett, R., and Levin, S. (1997). Allelopathy in spatially distributed populations. J. Theor. Biol. 185, 165–171. doi: 10.1006/jtbi.1996.0292
Fortin, M. J., Dale, M. R. T., and Brimacombe, C. (2021). Network ecology in dynamic landscapes. Proc. R. Soc. B 288:20201889. doi: 10.1098/rspb.2020.1889
Fortuna, M., Albaladejo, R., Fernández, L., Aparicio, A., and Bascompte, J. (2009). Networks of spatial genetic variation across species. Proc. Natl. Acad. Sci. U.S.A. 106, 19044–19049. doi: 10.1073/pnas.0907704106
Fortuna, M., Gómez-Rodríguez, C., and Bascompte, J. (2006). Spatial network structure and amphibian persistence in stochastic environments. Proc. R. Soc. B 273, 1429–1434. doi: 10.1098/rspb.2005.3448
Galpern, P., Manseau, M., and Fall, A. (2011). Patch-based graphs of landscape connectivity: a guide to construction, analysis and application for conservation. Biol. Conserv. 144, 44–55. doi: 10.1016/j.biocon.2010.09.002
Germain, R. M., Jones, N. T., and Grainger, T. N. (2019). Cryptic dispersal networks shape biodiversity in an invaded landscape. Ecology 100:e02738. doi: 10.1002/ecy.2738
Grilli, J., Barabás, G., and Allesina, S. (2015). Metapopulation persistence in random fragmented landscapes. PLoS Comput. Biol. 11:e1004251. doi: 10.1371/journal.pcbi.1004251
Grilli, J., Barabás, G., Michalska-Smith, M. J., and Allesina, S. (2017). Higher-order interactions stabilize dynamics in competitive network models. Nature 548, 210–213. doi: 10.1038/nature23273
Hansbauer, M. M., Storch, I., Knauer, F., Pilz, S., Küchenhoff, H., Végvári, Z., et al. (2010). Landscape perception by forest understory birds in the Atlantic Rainforest: black-and-white versus shades of grey. Landsc. Ecol. 25, 407–417. doi: 10.1007/s10980-009-9418-9
He, P., Montiglio, P. O., Somveille, M., Cantor, M., and Farine, D. R. (2021). The role of habitat configuration in shaping animal population processes: a framework to generate quantitative predictions. Oecologia 196, 649–665. doi: 10.1007/s00442-021-04967-y
Hirt, M. R., Grimm, V., Li, Y., Rall, B. C., Rosenbaum, B., and Brose, U. (2018). Bridging scales: allometric random walks link movement and biodiversity research. Trends Ecol. Evol. 33, 701–712. doi: 10.1016/j.tree.2018.07.003
Huisman, J., and Weissing, F. J. (1999). Biodiversity of plankton by species oscillations and chaos. Nature 402, 407–410. doi: 10.1038/46540
Kerr, B., Riley, M. A., Feldman, M. W., and Bohannan, B. J. M. (2002). Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature 418, 171–174. doi: 10.1038/nature00823
Kininmonth, S. J., De’ath, G., and Possingham, H. P. (2010). Graph theoretic topology of the great but small barrier reef world. Theor. Ecol. 3, 75–88. doi: 10.1007/s12080-009-0055-3
Laird, R. A. (2014). Population interaction structure and the coexistence of bacterial strains playing ‘rock–paper–scissors’. Oikos 123, 472–480. doi: 10.1111/j.1600-0706.2013.00879.x
Laird, R. A., and Schamp, B. S. (2006). Competitive intransitivity promotes species coexistence. Am. Nat. 168, 182–193. doi: 10.1086/506259
Laird, R. A., and Schamp, B. S. (2008). Does local competition increase the coexistence of species in intransitive networks? Ecology 89, 237–247. doi: 10.2307/27651526
Levine, J. M., Bascompte, J., Adler, P. B., and Allesina, S. (2017). Beyond pairwise mechanisms of species coexistence in complex communities. Nature 546, 56–64. doi: 10.1038/nature22898
Levine, J. M., and HilleRisLambers, J. (2009). The importance of niches for the maintenance of species diversity. Nature 461, 254–257. doi: 10.1038/nature08251
Li, C., Feng, T., Zhang, H., Chen, D., Cressman, R., Liao, J., et al. (2021). Multilayer network structure enhances the coexistence of competitive species. Phys. Rev. E 104:e024402. doi: 10.1103/PhysRevE.104.024402
Li, Y., Bearup, D., and Liao, J. (2020). Habitat loss alters effects of intransitive higher-order competition on biodiversity: a new metapopulation framework. Proc. Roy. Soc. B 287:20201571. doi: 10.1098/rspb.2020.1571
Liao, J., Barabás, G., and Bearup, D. (2022). Competition–colonization dynamics and multimodality in diversity–disturbance relationships. Ecology 103:e3672. doi: 10.1002/ecy.3672
Liao, J., Li, Z., Hiebeler, D. E., Iwasa, Y., Bogaert, J., and Nijs, I. (2013). Species persistence in landscapes with spatial variation in habitat quality: a pair approximation model. J. Theor. Biol. 335, 22–30. doi: 10.1016/j.jtbi.2013.06.015
Masuda, N., and Konno, N. (2006). Networks with dispersed degrees save stable coexistence of species in cyclic competition. Phys. Rev. E 74:e066102. doi: 10.1103/physreve.74.066102
May, R. M. (1972). Will a large complex system be stable? Nature 238, 413–414. doi: 10.1038/238413a0
Nagatani, T., Ichinose, G., and Tainaka, K. (2018). Heterogeneous network promotes species coexistence: metapopulation model for rock-paper-scissors game. Sci. Rep. 8:7094. doi: 10.1038/s41598-018-25353-4
Nicholson, E., and Possingham, H. P. (2006). Objectives for multiple-species conservation planning. Conserv. Biol. 20, 871–881. doi: 10.1111/j.1523-1739.2006.00369.x
Reichenbach, T., Mobilia, M., and Frey, E. (2007). Mobility promotes and jeopardizes biodiversity in rock-paper-scissors games. Nature 448, 1046–1049. doi: 10.1038/nature06095
Rojas-Echenique, J., and Allesina, S. (2011). Interaction rules affect species coexistence in intransitive networks. Ecology 92, 1174–1180. doi: 10.1890/10-0953.1
Roxburgh, S. H., Shea, K., and Wilson, J. B. (2004). The intermediate disturbance hypothesis: patch dynamics and mechanisms of species coexistence. Ecology 85, 359–371. doi: 10.2307/3450202
Schütt, M., and Claussen, J. C. (2010). Stabilization of biodiversity in the coevolutionary rock-paper-scissors game on complex networks. arXiv [Preprint]. doi: 10.48550/arXiv.1003.2922
Soliveres, S., Maestre, F. T., Ulrich, W., Manning, P., Boch, S., Bowker, M. A., et al. (2015). Intransitive competition is widespread in plant communities and maintains their species richness. Ecol. Lett. 18, 790–798. doi: 10.1111/ele.12456
Szabó, G., Szolnoki, A., and Izsák, R. (2004). Rock-scissors-paper game on regular small-world networks. J. Phys. A Math. Gen. 37, 2599–2609. doi: 10.1088/0305-4470/37/7/006
Szolnoki, A., and Szabó, G. (2004). Phase transitions for rock-scissors-paper game on different networks. Phys. Rev. E 70, 37102–37102. doi: 10.1103/PhysRevE.70.037102
Urban, D., and Keitt, T. (2001). Landscape connectivity: a graph-theoretic perspective. Ecology 85, 1205–1218. doi: 10.2307/2679983
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442. doi: 10.1038/30918
Yeaton, R. I., and Bond, W. J. (1991). Competition between two shrub species: dispersal differences and fire promote coexistence. Am. Nat. 138, 328–341. doi: 10.2307/2462476
Zhang, H., Bearup, D., Nijs, I., Wang, S., Barabás, G., Tao, Y., et al. (2021). Dispersal network heterogeneity promotes species coexistence in hierarchical competitive communities. Ecol. Lett. 24, 50–59. doi: 10.1111/ele.13619
Keywords: competitive intransitivity, cyclically competing ecosystems, dispersal network heterogeneity, ecosystem stability, rock-paper-scissors games
Citation: Guo G, Zhang Z, Zhang H, Bearup D and Liao J (2022) Contrasting effects of dispersal network heterogeneity on ecosystem stability in rock-paper-scissors games. Front. Ecol. Evol. 10:1068830. doi: 10.3389/fevo.2022.1068830
Received: 13 October 2022; Accepted: 28 October 2022;
Published: 10 November 2022.
Edited by:
Rui-Wu Wang, Northwestern Polytechnical University, ChinaReviewed by:
Min Su, Hefei University of Technology, ChinaXiaojie Chen, University of Electronic Science and Technology of China, China
Copyright © 2022 Guo, Zhang, Zhang, Bearup and Liao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jinbao Liao, amluYmFvbGlhb0AxNjMuY29t