Limited predictability of body length in a fish population

Recent theoretical studies have identified chaotic dynamics in eco-evolutionary models. Yet, empirical evidence for eco-evolutionary chaos in natural ecosystems is lacking. In this study, we combine analyses of empirical data and an eco-evolutionary model to uncover chaotic dynamics of body length in a fish population (northeast Arctic cod: Gadus morhua). Consistent with chaotic attractors, the largest Lyapunov exponent (LE) of empirical data is positive, and approximately matches the LE of the model calculation, thus suggesting the potential for chaotic dynamics in this fish population. We also find that the autocorrelation function (ACF) of both empirical data and eco-evolutionary model shows a similar lag of approximately 7 years. Our combined analyses of natural time series and mathematical models suggest that chaotic dynamics of a phenotypic trait may be driven by trait evolution. This finding supports a growing theory that eco-evolutionary feedbacks can produce chaotic dynamics.

Introduction

One of the main questions in evolutionary biology is how ecological interactions affect the phenotypic trait evolution of species (Thompson, 2005). Variation in phenotypic traits (e.g., body size, behavior, morphology, and physiology) are a common feature in natural populations and phenotypic traits can evolve in natural environments (Coulson et al., 2011; Hanski, 2011; Agrawal et al., 2013). Mutual adaptation induced by ecological interactions; that is, coevolution, can shape the adaptive peaks of pairs of associated species (Guimarães et al., 2017). Moreover, selection caused by ecological interactions can even affect the dynamics of whole ecological systems (Koskella and Brockhurst, 2015) and accelerate the adaptation process of natural population (Galetti et al., 2013). These ecological and evolutionary interactions are critical to the structure and functioning of biodiversity (Ehrlich and Raven, 1964; Thompson, 2005). Hence, understanding how ecological interactions shape biodiversity will determine how coevolution acts on associated species (Iwao and Rausher, 1997; Parchman and Benkman, 2002; Ridenhour, 2005; Thompson et al., 2013).

The interplay of ecological and evolutionary dynamics has been an increasingly active area of research (Schoener, 2011; Koch et al., 2014). To this end, one of the most important areas of research is the long-term predictability of evolution (Green, 1991; Kauffman and Johnsen, 1991; Ferriere and Fox, 1995), where recent theoretical work has focused on the chaotic properties of ecological and evolutionary processes (Dercole et al., 2010; Schreiber et al., 2011; Gilpin and Feldman, 2017). For example, Dercole et al. (2010) coupled an evolutionary equation to a food chain model and found that coevolution can drive the population size to oscillate at the edge of chaos. Gilpin and Feldman (2017) showed that an even simple two-species predator-prey model could give chaotic dynamics when evolution was included in the model. Schreiber et al. (2011) established an eco-evolutionary model showing how predator trait variation affects the trait value of prey, showing that rapid evolution of a polyphagous predator may generate chaotic dynamics due to eco-evolutionary feedbacks. Some researchers have also explored chaotic dynamics of multidimensional phenotypic traits and considered the effects of high-order interactions (e.g., the rate of phenotype x change with time (dx/dt) is affected by the x³ term) on the rate of traits change with time, with the aim of analyzing the unpredictability of long-term evolution under high-order coupling (Doebeli and Ispolatov, 2014; Rego-Costa et al., 2018).

It is important to note that proving if eco-evolutionary feedbacks can lead to chaotic dynamics is a daunting task, and the empirical evidence for chaos in phenotypic traits are rare. This lack of evidence may be primarily due to the absence of long time series data on phenotypic traits. Interestingly, body size–a vital phenotypic trait–is also well known to be a major player in the dynamics and stability of interactions and here some longer time series exist (De Roos et al., 2003; Rooney et al., 2010; Heckmann et al., 2012; Delong et al., 2015). For example, Delong et al. (2015) analyzed the interaction between body size and trophic cascades, and found that the loss of larger predators have greater consequences on trophic control and biomass structure than smaller predators. Rooney et al. (2010) systematically analyzed the inner property of two food webs–the Cantabrian Sea Shelf marine and the Central Plains Experimental Range (CPER) shortgrass prairie soil. They found that biomass turnover rates (Production: Biomass ratio) decrease with increasing body size and larger organisms tend to have higher trophic positions. Heckmann et al. (2012) used a bioenergetics approach to analyze the interplay of body-size structure and adaptive foraging of consumers, and they found that stronger body-size structures (i.e., species on higher trophic levels have larger body masses than species on lower levels) and faster adaptation stabilize food webs. De Roos et al. (2003) synthesized research about population dynamics and body size dependence in individual life history, and they found that body size generally leads to population cycles driven by differences in competitiveness of differently sized individuals. Given that body size has been identified as important in mediating dynamical outcomes, it is surprising that no research has investigated eco-evolutionary dynamical properties (e.g., chaos) in the body size.

All of the previously mentioned research has shown that body size affects population dynamics and food web stability. Consistent with this, recent macroecological results found that body size from aquatic ecosystems (composed of smaller body-sized organisms) were less stable (a higher coefficient of variation) than wetland and terrestrial organisms (Rip and McCann, 2011). At the same time, for freshwater fish, recent work showed that the linear correlation between community biomass and mean body mass was not significant (Hatton et al., 2015). However, due to the influence of eco-evolutionary feedbacks (Ferriere and Legendre, 2013), we speculate that there is a non-linear correlation between community biomass and body mass. One well-known mechanism for eco-evolutionary feedbacks that may play a potent role in fish population dynamics is fisheries-induced evolution, which has been significant and ubiquitous in harvested ecosystems (Olsen et al., 2004; Jørgensen et al., 2007). Empirical data of a single fish population has found that body length of different ages can yield cyclic dynamics over time (Eikeset et al., 2016), it remains unknown whether these potentially and rapidly evolution induced evolutionary feedback can have chaotic properties or not.

In practice, the Lyapunov exponent (LE) is a classical method to characterize the chaotic nature of real and model ecosystems (Li et al., 2020; Rogers et al., 2022), and two approaches have been used to compute the LE: direct estimation and Jacobian/indirect estimation. On the one hand, the direct approach uses the definition to estimate LE from the data by measuring the divergence rate of the nearest neighbors over a finite time horizon (Rosenstein et al., 1993). In ecology, this approach is mainly used to describe the results of experimental systems (Becks et al., 2005; Graham et al., 2007; Benincà et al., 2008; Kosuta et al., 2008; Becks and Arndt, 2013; Wang et al., 2019). On the other hand, the Jacobian/indirect approach requires fitting a delayed embedding model (with embedding dimension and lag) to the available time series and calculating the LE from the Jacobian matrix of the model (Nychka et al., 1992). A variety of methods may be used to estimate unknown model frameworks, such as generalized additive models (GAMs) (Benincà et al., 2015), neural networks (Ellner and Turchin, 1995), local linear regression (Sugihara, 1994), and non-linear local LE (Li and Ding, 2022). In particular, to accurately predict the model framework of empirical data, the Jacobian/indirect method usually requires the incorporation of abiotic factors (e.g., temperature) into the system, which inevitably increases the data quality requirements.

In what follows, we use a biologically plausible eco-evolutionary model to study the relationship between a phenotypic trait (body length) and population biomass. We first examine dynamical properties of body length based on the direct LE estimation to reveal evidence of underlying oscillations [via autocorrelation function (ACF)] and chaotic dynamics (via attractor reconstruction) of the phenotypic trait in a natural time series. Second, we explore a relatively simple, yet plausible, theoretical eco-evolutionary model with body length as a trait, that shows similar dynamical signatures and chaos. Our results suggest that potential for eco-evolutionary dynamics. We answer two vital problems: how phenotypic trait affects population dynamics and system stability; and whether changes in the magnitude of genetic variation in body length can drive eco-evolutionary chaos (chaotic dynamics in ecological and evolutionary processes) in fish population dynamics. Our work supports a growing theory that eco-evolutionary feedbacks can produce chaotic dynamics.

Materials and methods

Time series data

We used a previously published time series data set (Eikeset et al., 2016) on the body length of the northeast Arctic cod (Gadus morhua), to study the dynamics of a phenotypic trait. The data set consists of mean body length for different age stages (age 3–12 years) of the population from year 1946 to 2004 (Supplementary Figure 1). The original data set includes body length for all 10 age stages. For simplicity, the data set was divided into three broader age classes: age class I (age 3–5), age class II (age 6–9), and age class III (age 10–12). Each class has a different competition (compete for the shared resources) ability and reproductive (egg supply) rate per biomass. We assume that cod of the age class I has the lowest competition ability (characterized by the maximal attack rate) and reproductive rate, the age class II has a moderate level, and the age class III has a high level; we assume that three age classes have low, moderate, and high growth potential in body length (see Table 1), respectively. In each age class, means of body length were calculated. Finally, to facilitate data analysis, three time series were transformed by a square-root power transformation to suppress sharp peaks.

TABLE 1

Table 1. Parameters used in the eco-evolutionary model.

Phase space reconstruction of body length

For the empirical data, we employed a state-space reconstruction (i.e., we reconstructed the multidimensional dynamics of each body length class, using the body length time series) (Takens, 1981; Becks et al., 2005; Benincà et al., 2008; Wang et al., 2019; Dakos, 2020). To this end, the C–C method (Kim et al., 1999), which is useful for smaller data sets, was first used to calculate the time delay (τ) of each time series. Second, combined with the time delay (τ), the Grassberger–Procaccia (G–P) method was used to calculate the embedding dimension (m) (Grassberger and Procaccia, 1983). Third, by combining τ and m, the largest LE of each time series was derived (Wolf et al., 1985); moreover, in order to distinguish whether chaos is driven by external environmental noise or endogenous factors, we use wdencmp function (Donoho et al., 1995) to filter out the environmental noise of empirical data and re-calculate the largest LE of body length (see Supplementary Figure 2 and simulation codes in Supplementary material). Notably, the system has chaotic dynamics only if the Lyapunov exponent is larger than zero. The Lyapunov exponent quantifies the rate of exponential divergence (or convergence) of nearby trajectories (Strogatz, 1994), and a positive LE indicates chaos where the magnitude of LE effectively measures the system sensitivity to initial conditions.

Eco-evolutionary model

Different with the attractor reconstruction approach, we combine ecological processes (consumer-resource dynamics) with evolutionary processes (phenotypic trait dynamics) to simulate the complex dynamics in fish populations.

The time series data show that fish in the different age stages have different body lengths (Supplementary Figure 1). Different with early age-structured consumer-resource models (Schreiber and Rudolf, 2008; Nilsson et al., 2018), in this study, 10 ages are divided into three age classes (mean, body, and length), under the biologically plausible assumptions (i.e., different maximal attack rate and reproductive rate in Table 1) of each age class, the system is similar to a multi-species consumer-resource system. Here, we establish a bioenergetic consumer-resource model (McCann, 1998) to include phenotypic representations of quantitative trait evolution (Cortez, 2016, 2018; McPeek, 2017; Yamamichi and Letten, 2021). The model can be written as:

$\frac{dR}{dt}=R(r\left(S_R\right)-\mathrm{\alpha }R-\frac{x_1(S_R,S_1)C_1}{1+x_1(S_R,S_1)h_{1}R}\mathrm{\hspace{1em}}-\frac{x_2(S_R,S_2)C_2}{1+x_2(S_R,S_2)h_{2}R}-\frac{x_3(S_R,S_3)C_3}{1+x_3(S_R,S_3)h_{3}R})(1.1)$

$\frac{d{C}_i}{dt}=\left(-d_i\left(S_i\right)-{\mathrm{\delta }}_i{a}_i\right)C_i+g_i\frac{x_i(S_R,S_i)C_{i}R}{1+x_i(S_R,S_i)h_{i}R}+X_i{Y}_i(1.2)$

$\frac{d{J}_i}{dt}=b_i{C}_i-J_i\left(d_{Ji}+d_{JD}\sum _{j=1}^{n=3}{J}_j\right)(1.3)$

$\frac{d{S}_i}{dt}=V_i\left(-\frac{\partial d_i\left(S_i\right)}{\partial S_i}+g_i\frac{R\frac{\partial x_i(S_R,S_i)}{\partial S_i}}{{\left(1+x_i(S_R,S_i)h_{i}R\right)}^2}\right)(1.4)$

$\frac{d{S}_R}{dt}=V_4(\frac{\partial r\left(S_R\right)}{\partial S_R}-\frac{C_1\frac{\partial x_1(S_R,S_1)}{\partial S_R}}{1+x_1(S_R,S_1)h_{1}R}\mathrm{\hspace{1em}}-\frac{C_2\frac{\partial x_2(S_R,S_2)}{\partial S_R}}{1+x_2(S_R,S_2)h_{2}R}-\frac{C_3\frac{\partial x_3(S_R,S_3)}{\partial S_R}}{1+x_3(S_R,S_3)h_{3}R})(1.5)$

Where i = 1, 2, 3, and

$X_i=\frac{\left(W_1-W_2\right){(1-e^{-k_i{\mathrm{\tau }}_i})}^3+W_2}{W_2}(1.6)$

$Y_i=\frac{e^{-d_{Ji}{\mathrm{\tau }}_i}{\mathrm{\delta }}_i{d}_{Ji}{\sum }_{j=1}^{n=3}{J}_j}{2\left(d_{JD}\left(1-e^{-d_{Ji}{\mathrm{\tau }}_i}\right){\mathrm{\delta }}_i{\sum }_{j=1}^{n=3}{J}_j+d_{Ji}\right)}.(1.7)$

The state variable R is the resource biomass; C_i, J_i, and S_i are the biomass, egg biomass and body length of fish in age class i, respectively; S_R is the body length of the resource fish. Equations (1.1–1.3) represent biomass dynamics and Eqs (1.4, 1.5) represent trait dynamics, where $\frac{d{S}_i}{dt}=V_i\frac{\partial }{\partial S_i}\left[\frac{d{C}_i/dt}{C_i}\right]$ and $\frac{d{S}_R}{dt}=V_R\frac{\partial }{\partial S_R}\left[\frac{dR/dt}{R}\right]$. Here we assume that selection is frequency-dependent in both the resource (R) and consumers (C_i). τ_i is the maturation time for all individuals in a consumer population (McCann, 1998). Y_i is Beverton–Holt recruitment of age class i based on reproductive effort τ_i years ago and X_i is the growth of surviving recruits over τ_i, in which growth follows a Bertalanffy function (McCann, 1998). We assume the resource fish shows logistic growth: r is the intrinsic rate of increase of the resource, α is the intraspecific competition coefficient for the resource; Moreover, we use Holling type-II functional response to show predation terms: x_i and h_i are the attack rate and handling time of fish in age class i on the resource, respectively; d_i is the instantaneous rate of mortality of fish in age class i; δ_i is the instantaneous rate of reproductive energy invested into offspring for fish in age class i; a_i is the conversion costs of production of soma to gonadal tissue; g_i is the conversion efficiency of prey biomass into adult biomass; b_i is the egg supply rate of fish in age class i; d_Ji is density-independent egg mortality rate; d_JD is egg mortality related to egg density dependence; k_i is the rate of fish growth; W₁ is the asymptotic mass; and W₂ is the mass of an individual egg; both V_i and V₄ are the genetic variation of body length S_i and S_R, respectively; a higher value of the genetic variation means a faster speed of evolution. Finally, based on the relationship among resource and fish, similar to the early theoretical approach (Dercole et al., 2010), trait dependencies are modeled using the following functional forms:

$x_i=x_i(S_i,S_R)=x_{i0}\text{exp}[-{\left(\frac{S_i-w_{i0}}{e_i}\right)}^2+2l_i\frac{S_i-w_{i0}}{e_i}\cdot \frac{S_R-w_{40}}{f_i}-{\left(\frac{S_R-w_{40}}{f_i}\right)}^2](1.8)$

$r=r\left(S_R\right)=r_0\left(1-r_1{\left(S_R-w_{40}\right)}^2\right)(1.9)$

$d_i=d_i\left(S_i\right)=d_{i0}\left(1+m_i{\left(S_i-w_{i0}\right)}^2\right)(1.10)$

Where w_i0 (i = 1, 2, 3) is the optimal trait values. r₀, r₁, x_i0, e_i, l_i, f_i, d_i0, and m_i are all positive. The growth rate r is maximum at S_R = w₄₀, where the growth of the resource is best adapted to its environment. The attack rate x_i is maximum at S_i = w_i0 and S_R = w₄₀ when the body length of cod matches with the prey fish. The mortality d_i of a fish in age class i is minimum at S_i = w_i0.

For eco-evolutionary model (Thompson, 2005), most of the parameter values were derived from the previous research (McCann, 1998) while the remaining set of parameters were obtained based on the reasonable guess values from parameter space presented in Supplementary Figure 3. All parameters can be found in Table 1. Similar to early theoretical work (McPeek, 2017; Cortez, 2018), we mainly explore how the speed of evolution in terms of the magnitude of genetic variation (V_i) affects the stability of the eco-evolutionary model (Thompson, 2005). We studied the dynamical properties of the eco-evolutionary model using numerical simulation method. Bifurcation diagrams and LE spectrum can be utilized to find the conditions under which the eco-evolutionary model produced chaotic dynamics (positive LEs). Moreover, we calculated both the ACF and LE of both empirical and theoretical time series to compare model predictions with field data. All simulations were carried out using MATLAB 7.0 (MathWorks, 2004).

Results

Empirical results

The natural time series of body length suggests that chaotic dynamics may be presented in this fish species (Figure 1). First, we obtain the time delay τ = 2 (Figures 1D–F) and embedding dimension m = 11 (the rate of change of lnC(m, D) with lnD does not change with the increase of m; Figures 1G–I) for the age class I, II, and III, respectively. Then, by combining τ = 2 with m = 11, we obtain both of the LE values are greater than zero (Figures 1G–I). So, time series of the body length in the fish population exist in the chaotic region. Moreover, a similar result is obtained when the environmental noise of time series is filtered out (Supplementary Figure 2), all the LE values are larger than 0 (Supplementary Figures 2C,F,I), indicating dynamical chaos. So, the body length dynamics of the fish population present an intrinsic chaotic property.

FIGURE 1

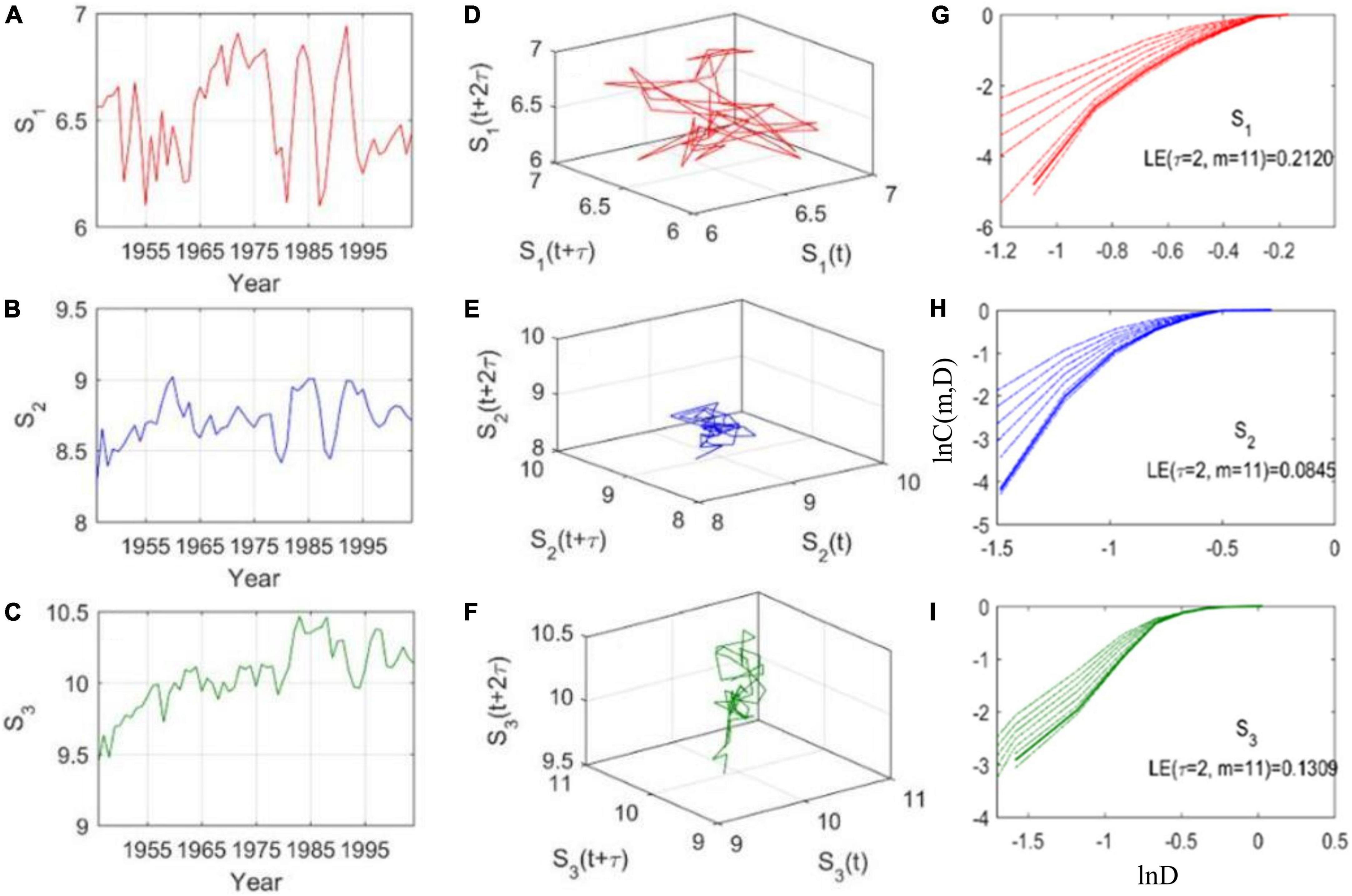
Figure 1. Phase space reconstruction of single time series of body length. (A–C) Empirical data of body length; (D–F) Attractor reconstruction (τ = 2; based on the C–C method) of empirical data with noise; (G–I) Lyapunov exponent (LE) of body length: D is the neighborhood radius, m is the embedding dimension, and C is the correlation integral, which is influenced by both D and m. In each rectangle, m varies from 5 to 12 (from top line to bottom line, m = 11 can be obtained for each case when the rate of change of lnC(m, D) with lnD does not change with the increase of m). Body length S₁ (age class I: age 3–5), S₂ (age class II: age 6–9), and S₃ (age class III: age 10–12) are the mean of each age class. The original data is shown in Supplementary Figure 1.

Theoretical predictions of eco-evolutionary model

As revealed by a theoretical simulation (Figure 2), the eco-evolutionary model can give rise to a rich set of potential dynamics. When the genetic variation of body length in the age class I, V₁, is small (V₁ = 0.03, LE = −0.0016; Figure 2A), the dynamics of body length S₁ approaches a simple, regular oscillation (period-2 oscillation). After an increase in the magnitude of genetic variation in body length S₁, V₁ (V₁ = 0.27, LE = −0.0012; Figure 2B), the dynamics of body length S₁ presents a doubling-periodic oscillation. Further, when V₁ is increased even more, the dynamics of body length S₁ appears to enter a chaotic regime (V₁ = 0.5, LE = 0.0643; Figure 2C) as suggested by the Lyapunov exponent (Figure 2F). Finally, periodic dynamics (regular oscillation) is observed when V₁ is increased even further (V₁ = 0.764, LE = −0.001; Figure 2D).

FIGURE 2

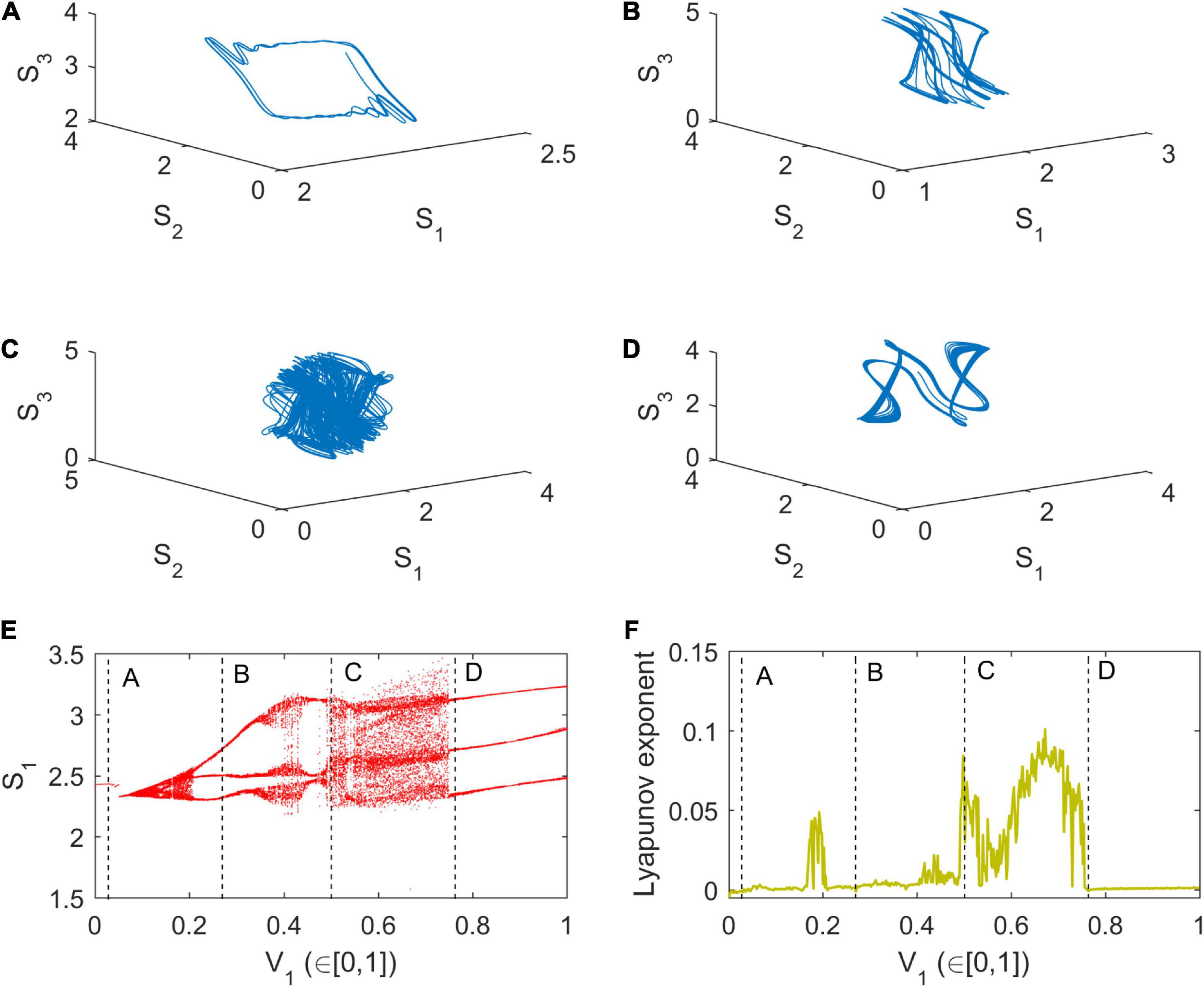
Figure 2. Eco-evolutionary dynamical simulations. (A–D) Space phase diagrams; (E) Bifurcation diagram; (F) Lyapunov exponent (LE) spectrum. Model parameters are presented in Table 1 and V₁ varies in [0, 1]: Panels (A) V₁ = 0.03, (B) V₁ = 0.27, (C) V₁ = 0.5, and (D) V₁ = 0.764. The simulation time is 1,000 and initial value of Eq. (1) is (0.1, 0.1, 0.03, 0.02, 0.03, 0.01, 0.01, 2.2, 2.4, 2.8, and 3).

Since chaos may occur purely due to ecological dynamics, we did a bifurcation analysis assuming ecological dynamics only (i.e., assuming V₁ = V₂ = V₃ = V₄ = 0). Under these purely ecological conditions, the single-parameter bifurcation shows that the ecological process may not produce chaotic dynamics (Supplementary Figure 3), and the dynamics of population biomass C₁ is merely represented as a stable equilibrium.

Comparison between theoretical predictions and empirical data

Both theoretical predictions and empirical results show that the dynamics of a phenotypic trait, such as body length, can show chaotic properties. However, if the dynamics of our theoretical model is indeed a plausible representation of the empirical data, other dynamical properties of their respective time series should also be similar.

In this regard, the ACF analysis indeed indicates dynamical similarities among natural (Figure 3A) and theoretical (Figure 3B) time series. Both theoretical data and empirical data show two major peak lags: short (about 7 years) and long periods (about 24 years). However, due to the limited length of empirical data (in total 59 data points), the long period may be not significant (Figure 3A). Moreover, a predictable period (years) of the chaotic timeseries is 1/LE(S₃) (i.e., 1/0.1309 = 7.64 years in body length S₃; Figure 1I), which is close to 7 years (calculated by the ACF). Therefore, these results illustrate the eco-evolutionary model can depict the real dynamics of body length in a single fish system.

FIGURE 3

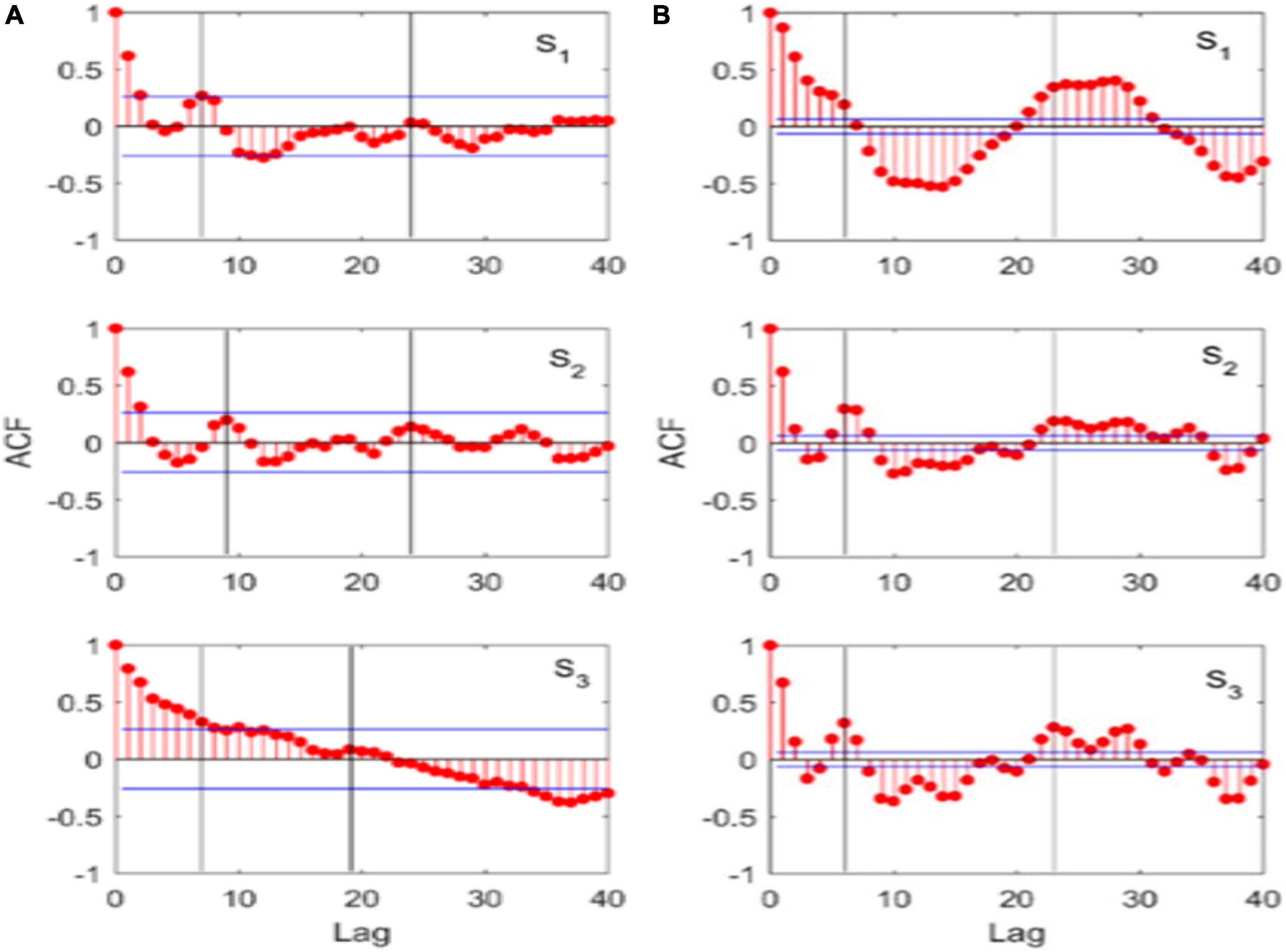
Figure 3. Chaotic dynamics is observed for the northeast Arctic cod (Gadus morhua) based on empirical data and simulation data analyzes. (A) Autocorrelation function (ACF) of empirical data; (B) ACF of simulation data; body length class I (S₁), class II (S₂), and class III (S₃). Blue line denotes significance threshold and the value in the middle of two blue lines can be considered not significantly different from 0.

Discussion

The predictability of long-term evolution has puzzled ecologists for decades (Green, 1991; Kauffman and Johnsen, 1991; Ferriere and Fox, 1995). Although recent theoretical work has analyzed the chaotic properties of eco-evolutionary dynamics (Dercole et al., 2010; Schreiber et al., 2011; Doebeli and Ispolatov, 2014; Gilpin and Feldman, 2017; Rego-Costa et al., 2018), eco-evolutionary chaos has not been shown in empirical data. In this study, we combined an eco-evolutionary model with analyzes of empirical data to uncover chaotic dynamics of body length of a single fish population. Our work may prove the eco-evolutionary chaos in the natural ecological system.

Our work may be treated as a supplementary method to study fish species. In this study, we provided a new mechanism, that is, the genetic variation of phenotypic trait determines chaotic dynamics of body length. The new mechanism revealed in our work is different from recent studies (Eikeset et al., 2016; Andersen, 2019), which showed many mechanisms could influence population dynamics (stable or oscillatory state) of fish species, such as the change of age structure, life-history parameters, and fishing. Actually, our work involved with above factors. First of all, for different study methods (attractor reconstruction and eco-evolutionary model), different age classes (age 3–12) were divided into three broader age classes, and each class has the different maximal attack rate and reproductive rate (Table 1). Moreover, life-history parameters (i.e., individual growth rate k_i and reproduction rate b_i in Table 1) indeed influence population dynamics (non-chaos in Supplementary Figure 3) of fish species when we neglected the evolutionary dynamics (V₁ = V₂ = V₃ = V₄ = 0). Finally, although we do not introduce human harvest (fishing) into the eco-evolutionary model, we infer that fishing will impact the demography and recruitment of a fish stock. Therefore, it is worth trying to analyze how each ecological parameter influence population dynamics of fish. The simulation result showed that non-chaos emerges when we do not consider phenotypic trait evolution in the mechanistic model (Supplementary Figure 3). In short, in this work, the free-equation approach (attractor reconstruction) proved chaos in trait dynamics, and then a plausible interpretation mechanism (regulating the genetic variation of phenotypic trait may result in chaotic dynamics of body length in the eco-evolutionary model) for chaos in body length of fish was suggested, that is, rapid evolution in phenotypic trait may result in chaos in both ecological (population density/biomass) and evolutionary (phenotypic trait) processes.

The road to eco-evolutionary chaos

Early theoretical work found that regulating the magnitude of genetic variation in phenotypic trait can result in periodic oscillations (McPeek, 2017; Cortez, 2018) and chaotic dynamics (Dercole et al., 2010; Gilpin and Feldman, 2017). However, empirical evidence for eco-evolutionary chaos in natural ecosystems is lacking. In this study, we first use the phase space reconstruction method to present the evidence for potential chaos in fish body length. In our eco-evolutionary model, similar to recent theoretical approaches (Cortez, 2018; Yamamichi and Letten, 2021), we only analyze how system stability varies with the genetic variation (V₁). Our results show the increase of V₁ can generate chaotic dynamics in both phenotypic trait and biomass (LE > 0; Figure 2F). However, when we do not consider trait evolution (V_i = 0) in the model, population dynamics of the fish population may not present chaos. Then the ACF of both empirical data and simulation data of the eco-evolutionary model show that the predictable period (years) of body length in fish population is about 7 years. Therefore, the eco-evolutionary model can approximately depict and predict the intrinsic dynamic behavior of empirical data.

Moreover, recent theoretical research showed that ecological process (population density/biomass) will produce population oscillation if evolutionary process (phenotypic trait) has the oscillatory dynamics (McPeek, 2017; Cortez, 2018). In our study, we first present chaotic dynamics (irregular periodic oscillation) of the body length (attractor reconstruction), while comparative analyses of the ACF reveal broadly consistent results between experimental data and theoretical models. Therefore, we infer that the eco-evolutionary chaos may be driven by body length evolution (changes in genetic variation of body length) in the cod population.

In the eco-evolutionary model, the chaotic evolutionary trajectories (LE > 0; Figure 3F) are intrinsically unpredictable, and strongly dependent on the magnitude of genetic variation in phenotypic trait (V₁). The change switches between the non-chaotic (LE < 0) and chaotic dynamics (i.e., the “edge of chaos”) was discussed in earlier work (Ferriere and Fox, 1995; Turchin and Ellner, 2000; Benincà et al., 2015), which may balance the resource-fish system near the “evolutionary sliding” (Dercole et al., 2006). This maybe provide an evolutionary explanation for chaotic dynamics in the nature (Turchin, 2003). Our work identifies eco-evolutionary chaos in a natural ecological system. This empirical finding supports the theory that eco-evolutionary feedbacks can produce chaotic dynamics.

Rapid evolution in body length of fish is limited predictability

The rapid evolution of fish population has caused widespread discussion (Olsen et al., 2004; Jørgensen et al., 2007; Eikeset et al., 2016). In this study, we infer that the change of the body length (chaotic dynamics of phenotypic trait) is due to evolution. Moreover, the body length evolution has a limited predictability due to its chaotic property.

In the cod population, we checked for chaotic dynamics (positive LE) of body length based on both empirical data and eco-evolutionary model analyses. We found the LE of empirical data [LE(S₃) = 0.1309], which means predictable periods (1/LE) of empirical data (i.e., 7.64 years in body length S₃) is also close to 7 years (calculated by the ACF). The eco-evolutionary model can approximately depict and predict the intrinsic dynamic behavior of empirical data, that is, the limited predictable period of rapid evolution (V_i > 0) in body length of fish is approach to 7 years. Fish population growth is closely bound up with our daily life, considering the effectively predictable time of body length can help us make a suitable strategy for fishery conservation.

Data availability statement

The original contributions presented in this study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LW designed the study, finished model simulations, carried out data analyses, and wrote the first draft of the manuscript. Both authors contributed substantially to revisions and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (32201259) and Doctor Start-up Fund Project of Jiangxi Normal University (12021105).

Acknowledgments

We thank Kevin McCann, Torbjörn Säterberg, Jennifer Meunier, and Xue-Qi Wang for helpful comments on the manuscript. We also thank two reviewers and editor for many useful suggestions that improved the quality of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.1064873/full#supplementary-material

References

Agrawal, A. A., Johnson, M. T., Hastings, A. P., and Maron, J. L. (2013). A field experiment demonstrating plant life-history evolution and its eco-evolutionary feedback to seed predator populations. Am. Nat. 181, S35–S45. doi: 10.1086/666727

CrossRef Full Text | Google Scholar

Andersen, K. H. (2019). Fish ecology, evolution, and exploitation: A new theoretical synthesis. Princeton, NJ: Princeton University Press. doi: 10.23943/princeton/9780691192956.001.0001

CrossRef Full Text | Google Scholar

Becks, L., and Arndt, H. (2013). Different types of synchrony in chaotic and cyclic communities. Nat. Commun. 4, 1359. doi: 10.1038/ncomms2355

PubMed Abstract | CrossRef Full Text | Google Scholar

Becks, L., Hilker, F. M., Malchow, H., Jürgens, K., and Arndt, H. (2005). Experimental demonstration of chaos in a microbial food web. Nature 435, 1226–1229. doi: 10.1038/nature03627

PubMed Abstract | CrossRef Full Text | Google Scholar

Benincà, E., Ballantine, B., Ellner, S. P., and Huisman, J. (2015). Species fluctuations sustained by a cyclic succession at the edge of chaos. Proc. Natl. Acad. Sci. U.S.A. 112, 6389–6394. doi: 10.1073/pnas.1421968112

CrossRef Full Text | Google Scholar

Benincà, E., Huisman, J., Heerkloss, R., Jöhnk, K. D., Branco, P., Van Nes, E. H., et al. (2008). Chaos in a long-term experiment with a plankton community. Nature 451, 822–825. doi: 10.1038/nature06512

PubMed Abstract | CrossRef Full Text | Google Scholar

Cortez, M. H. (2016). How the magnitude of prey genetic variation alters predator-prey eco-evolutionary dynamics. Am. Nat. 188, 329–341. doi: 10.1086/687393

CrossRef Full Text | Google Scholar

Cortez, M. H. (2018). Genetic variation determines which feedbacks drive and alter predator–prey eco-evolutionary cycles. Ecol. Monogr. 88, 353–371. doi: 10.1002/ecm.1304

CrossRef Full Text | Google Scholar

Coulson, T., MacNulty, D. R., Stahler, D. R., Wayne, R. K., and Smith, D. W. (2011). Modeling effects of environmental change on wolf population dynamics, trait evolution, and life history. Science 334, 1275–1278. doi: 10.1126/science.1209441

CrossRef Full Text | Google Scholar

Dakos, V. (2020). Nature’s dynamical complexity. Nat. Ecol. Evol. 4, 12–13. doi: 10.1038/s41559-019-1077-x

CrossRef Full Text | Google Scholar

De Roos, A. M., Persson, L., and Mccauley, E. (2003). The influence of size-dependent life-history traits on the structure and dynamics of populations and communities. Ecol. Lett. 6, 473–487. doi: 10.1046/j.1461-0248.2003.00458.x

CrossRef Full Text | Google Scholar

Delong, J. P., Gilbert, B., Shurin, J. B., Savage, V. M., Barton, B. T., Clements, C. F., et al. (2015). The body size dependence of trophic cascades. Am. Nat. 185, 354–366. doi: 10.1086/679735

CrossRef Full Text | Google Scholar

Dercole, F., Ferrière, R., Gragnani, A., and Rinaldi, S. (2006). Coevolution of slow-fast populations: Evolutionary sliding, evolutionary pseudo-equilibria and complex Red Queen dynamics. Proc. R. Soc. Lond. B Biol. Sci. 273, 983–990. doi: 10.1098/rspb.2005.3398

CrossRef Full Text | Google Scholar

Dercole, F., Ferriere, R., and Rinaldi, S. (2010). Chaotic Red Queen coevolution in three-species food chains. Proc. R. Soc. Lond. B Biol. Sci. 277, 2321–2330. doi: 10.1098/rspb.2010.0209

CrossRef Full Text | Google Scholar

Doebeli, M., and Ispolatov, I. (2014). Chaos and unpredictability in evolution. Evolution 68, 1365–1373. doi: 10.1111/evo.12354

CrossRef Full Text | Google Scholar

Donoho, D. L., Johnstone, I. M., Kerkyacharian, G., and Picard, D. (1995). Wavelet shrinkage: Asymptopia. J. R. Stat. Soc. Ser. B 57, 301–337. doi: 10.1111/j.2517-6161.1995.tb02032.x

CrossRef Full Text | Google Scholar

Ehrlich, P. R., and Raven, P. H. (1964). Butterflies and plants: A study in coevolution. Evolution 18, 586–608. doi: 10.1111/j.1558-5646.1964.tb01674.x

CrossRef Full Text | Google Scholar

Eikeset, A. M., Dunlop, E. S., Heino, M., Storvik, G., Stenseth, N. C., and Dieckmann, U. (2016). Roles of density-dependent growth and life history evolution in accounting for fisheries-induced trait changes. Proc. Natl. Acad. Sci. U.S.A. 113, 15030–15035. doi: 10.1073/pnas.1525749113

CrossRef Full Text | Google Scholar

Ellner, S., and Turchin, P. (1995). Chaos in a noisy world: New methods and evidence from time-series analysis. Am. Nat. 145, 343–375. doi: 10.1086/285744

CrossRef Full Text | Google Scholar

Ferriere, R., and Fox, G. A. (1995). Chaos and evolution. Trends Ecol. Evol. 10, 480–485. doi: 10.1016/S0169-5347(00)89194-6

CrossRef Full Text | Google Scholar

Ferriere, R., and Legendre, S. (2013). Eco-evolutionary feedbacks, adaptive dynamics and evolutionary rescue theory. Philos. Trans. R. Soc. B Biol. Sci. 368:20120081. doi: 10.1098/rstb.2012.0081

CrossRef Full Text | Google Scholar

Galetti, M., Guevara, R., Côrtes, M. C., Fadini, R., Von, M. S., Leite, A. B., et al. (2013). Functional extinction of birds drives rapid evolutionary changes in seed size. Science 340, 1086–1090. doi: 10.1126/science.1233774

CrossRef Full Text | Google Scholar

Gilpin, W., and Feldman, M. W. (2017). A phase transition induces chaos in a predator-prey ecosystem with a dynamic fitness landscape. PLoS Comput. Biol. 13:e1005644. doi: 10.1371/journal.pcbi.1005644

CrossRef Full Text | Google Scholar

Graham, D. W., Knapp, C. W., Van Vleck, E. S., Bloor, K., Lane, T. B., and Graham, C. E. (2007). Experimental demonstration of chaotic instability in biological nitrification. ISME J. 1, 385–393. doi: 10.1038/ismej.2007.45

PubMed Abstract | CrossRef Full Text | Google Scholar

Grassberger, P., and Procaccia, I. (1983). Measuring the strangeness of strange attractors. Physica D 9, 189–208. doi: 10.1016/0167-2789(83)90298-1

CrossRef Full Text | Google Scholar

Green, D. M. (1991). Chaos, fractals and nonlinear dynamics in evolution and phylogeny. Trends Ecol. Evol. 6, 333–337.

Google Scholar

Guimarães, P. R. Jr., Pires, M. M., Jordano, P., Bascompte, J., and Thompson, J. N. (2017). Indirect effects drive coevolution in mutualistic networks. Nature 550, 511–514. doi: 10.1038/nature24273

CrossRef Full Text | Google Scholar

Hanski, I. A. (2011). Eco-evolutionary spatial dynamics in the Glanville fritillary butterfly. Proc. Natl. Acad. Sci. U.S.A. 108, 14397–14404. doi: 10.1073/pnas.1110020108

CrossRef Full Text | Google Scholar

Hatton, I. A., Mccann, K. S., Fryxell, J. M., Davies, T. J., Smerlak, M., Sinclair, A. R., et al. (2015). The predator-prey power law: Biomass scaling across terrestrial and aquatic biomes. Science 349:aac6284. doi: 10.1126/science.aac6284

CrossRef Full Text | Google Scholar

Heckmann, L., Drossel, B., Brose, U., and Guill, C. (2012). Interactive effects of body-size structure and adaptive foraging on food-web stability. Ecol. Lett. 15, 243–250. doi: 10.1111/j.1461-0248.2011.01733.x

CrossRef Full Text | Google Scholar

Iwao, K., and Rausher, M. D. (1997). Evolution of plant resistance to multiple herbivores: Quantifying diffuse coevolution. Am. Nat. 149, 316–335. doi: 10.1086/285992

CrossRef Full Text | Google Scholar

Jørgensen, C., Enberg, K., Dunlop, E. S., Arlinghaus, R., Boukal, D. S., Brander, K., et al. (2007). Managing evolving fish stocks. Science 318, 1247–1248. doi: 10.1126/science.1148089

CrossRef Full Text | Google Scholar

Kauffman, S. A., and Johnsen, S. (1991). Coevolution to the edge of chaos: Coupled fitness landscapes, poised states, and coevolutionary avalanches. J. Theor. Biol. 149, 467–505. doi: 10.1016/s0022-5193(05)80094-3

CrossRef Full Text | Google Scholar

Kim, H. S., Eykholt, R., and Salas, J. D. (1999). Nonlinear dynamics, delay times, and embedding windows. Physica D 127, 48–60. doi: 10.1016/s0167-2789(98)00240-1

CrossRef Full Text | Google Scholar

Koch, H., Frickel, J., Valiadi, M., and Becks, L. (2014). Why rapid, adaptive evolution matters for community dynamics. Front. Ecol. Evol. 2:17. doi: 10.3389/fevo.2014.00017

CrossRef Full Text | Google Scholar

Koskella, B., and Brockhurst, M. A. (2015). Bacteria–phage coevolution as a driver of ecological and evolutionary processes in microbial communities. FEMS Microbiol. Rev. 38, 916–931. doi: 10.1111/1574-6976.12072

CrossRef Full Text | Google Scholar

Kosuta, S., Hazledine, S., Sun, J., Miwa, H., Morris, R. J., Downie, J. A., et al. (2008). Differential and chaotic calcium signatures in the symbiosis signaling pathway of legumes. Proc. Natl. Acad. Sci. U.S.A. 105, 9823–9828. doi: 10.1073/pnas.0803499105

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., and Ding, R. (2022). The backward nonlinear local Lyapunov exponent and its application to quantifying the local predictability of extreme high-temperature events. Clim. Dyn. 1–15. doi: 10.1007/s00382-022-06469-w

CrossRef Full Text | Google Scholar

Li, X., Ding, R., and Li, J. (2020). Quantitative study of the relative effects of initial condition and model uncertainties on local predictability in a nonlinear dynamical system. Chaos Solitons Fractals 139:110094. doi: 10.1016/j.chaos.2020.110094

CrossRef Full Text | Google Scholar

MathWorks (2004). MATLAB. Natick, MA: MathWorks.

Google Scholar

McCann, K. S. (1998). Density-dependent coexistence in fish communities. Ecology 79, 2957–2967. doi: 10.2307/176529

CrossRef Full Text | Google Scholar

McPeek, M. A. (2017). Evolutionary community ecology. Princeton, NJ: Princeton University Press.

Google Scholar

Nilsson, K. A., McCann, K. S., and Caskenette, A. L. (2018). Interaction strength and stability in stage-structured food web modules. Oikos 127, 1494–1505. doi: 10.1111/oik.05029

CrossRef Full Text | Google Scholar

Nychka, D., Ellner, S., Gallant, A. R., and McCaffrey, D. (1992). Finding chaos in noisy systems. J. R. Stat. Soc. Ser. B Methodol. 54, 399–426. doi: 10.1111/j.2517-6161.1992.tb01889.x

CrossRef Full Text | Google Scholar

Olsen, E. M., Heino, M., Lilly, G. R., Morgan, M. J., Brattey, J., Ernande, B., et al. (2004). Maturation trends indicative of rapid evolution preceded the collapse of northern cod. Nature 428, 932–935. doi: 10.1038/nature02430

CrossRef Full Text | Google Scholar

Parchman, T. L., and Benkman, C. W. (2002). Diversifying coevolution between crossbills and black spruce on Newfoundland. Evolution 56, 1663–1672. doi: 10.1554/0014-38202002056[1663:dcbcab]2.0.co;2

CrossRef Full Text | Google Scholar

Rego-Costa, A., Débarre, F., and Chevin, L. M. (2018). Chaos and the (un)predictability of evolution in a changing environment. Evolution 72, 375–385. doi: 10.1111/evo.13407

CrossRef Full Text | Google Scholar

Ridenhour, B. J. (2005). Identification of selective sources: partitioning selection based on interactions. Am. Nat. 166, 12–25. doi: 10.1086/430524

CrossRef Full Text | Google Scholar

Rip, J. M. K., and McCann, K. S. (2011). Cross-ecosystem differences in stability and the principle of energy flux. Ecol. Lett. 14, 733–740. doi: 10.1111/j.1461-0248.2011.01636.x

CrossRef Full Text | Google Scholar

Rogers, T. L., Johnson, B. J., and Munch, S. B. (2022). Chaos is not rare in natural ecosystems. Nat. Ecol. Evol. 6, 1105–1111.

Google Scholar

Rooney, N., Mccann, K. S., and Moore, J. C. (2010). A landscape theory for food web architecture. Ecol. Lett. 11, 867–881. doi: 10.1111/j.1461-0248.2008.01193.x

CrossRef Full Text | Google Scholar

Rosenstein, M. T., Collins, J. J., and De Luca, C. J. (1993). A practical method for calculating largest Lyapunov exponents from small data sets. Physica D 65, 117–134. doi: 10.1016/0167-2789(93)90009-P

CrossRef Full Text | Google Scholar

Schoener, T. W. (2011). The newest synthesis: Understanding the interplay of evolutionary and ecological dynamics. Science 331, 426–429. doi: 10.1126/science.1193954

CrossRef Full Text | Google Scholar

Schreiber, S., and Rudolf, V. (2008). Crossing habitat boundaries: Coupling dynamics of ecosystems through complex life cycles. Ecol. Lett. 11, 576–587. doi: 10.1111/j.1461-0248.2008.01171.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Schreiber, S. J., Bürger, R., and Bolnick, D. I. (2011). The community effects of phenotypic and genetic variation within a predator population. Ecology 92, 1582–1593. doi: 10.1890/10-2071.1

CrossRef Full Text | Google Scholar

Strogatz, S. H. (1994). Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering. Cambridge, MA: Perseus Books Publishing.

Google Scholar

Sugihara, G. (1994). Nonlinear forecasting for the classification of natural time series. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 348, 477–495.

Google Scholar

Takens, F. (1981). Detecting strange attractors in turbulence. Lect. Notes Math. 898, 366–381. doi: 10.1007/bfb0091924

CrossRef Full Text | Google Scholar

Thompson, J. N. (2005). The geographic mosaic of coevolution. Chicago, IL: University of Chicago Press.

Google Scholar

Thompson, J. N., Schwind, C., Guimarães, P. R. Jr., and Friberg, M. (2013). Diversification through multitrait evolution in a coevolving interaction. Proc. Natl. Acad. Sci. U.S.A. 110, 11487–11492. doi: 10.1073/pnas.1307451110

CrossRef Full Text | Google Scholar

Turchin, P. (2003). Complex population dynamics: A theoretical/empirical synthesis (MPB-35). Princeton, NJ: Princeton University Press.

Google Scholar

Turchin, P., and Ellner, S. P. (2000). Living on the edge of chaos: Population dynamics of Fennoscandian voles. Ecology 81, 3099–3116. doi: 10.2307/177404

CrossRef Full Text | Google Scholar

Wang, L., Tang, Y., Wang, R.-W., and Shang, X.-Y. (2019). Re-evaluating the ‘plankton paradox’ using an interlinked empirical data and a food web model. Ecol. Model. 407, 108721.

Google Scholar

Wolf, A., Swift, J. B., Swinney, H. L., and Vastano, J. A. (1985). Determining Lyapunov exponents from a time series. Physica D 16, 285–317. doi: 10.1016/0167-2789(85)90011-9

CrossRef Full Text | Google Scholar

Yamamichi, M., and Letten, A. D. (2021). Rapid evolution promotes fluctuation-dependent species coexistence. Ecol. Lett. 24, 812–818. doi: 10.1111/ele.13707

CrossRef Full Text | Google Scholar