The interactive effects of environmental gradient and dispersal shape spatial phylogenetic patterns

Introduction: The emergence and maintenance of biodiversity include interacting environmental conditions, organismal adaptation to such conditions, and dispersal. To understand and quantify such ecological, evolutionary, and spatial processes, observation and interpretation of phylogenetic relatedness across space (e.g., phylogenetic beta diversity) is arguably a way forward as such patterns contain signals from all the processes listed above. However, it remains challenging to extract information about complex eco-evolutionary and spatial processes from phylogenetic patterns.

Methods: We link environmental gradients and organismal dispersal with phylogenetic beta diversity using a trait-based and eco-evolutionary model of diversification along environmental gradients. The combined effect of the environment and dispersal leads to distinct phylogenetic patterns between subsets of species and across geographical distances.

Results and discussion: Steep environmental gradients combined with low dispersal lead to asymmetric phylogenies, a high phylogenetic beta diversity, and the phylogenetic diversity between communities increases linearly along the environmental gradient. High dispersal combined with a less steep environmental gradient leads to symmetric phylogenies, low phylogenetic beta diversity, and the phylogenetic diversity between communities along the gradient increases in a sigmoidal form. By disentangling the eco-evolutionary mechanisms that link such interacting environment and dispersal effects and community phylogenetic patterns, our results improve understanding of biodiversity in general and help interpretation of observed phylogenetic beta diversity.

Introduction

Community assembly is driven by environmental conditions, ecological interactions, and dispersal as well as adaptation and speciation (Rainey and Travisano, 1998; Vellend, 2010; Gillespie et al., 2020). To gain a complete understanding of such community assembly processes and the resulting biodiversity, we thus need to focus on multiple interacting processes and their relative importance. One way of improving our understanding of such complexity is to combine studies on species diversity, functional trait diversity, and phylogenetic diversity (Graham and Fine, 2008; Weinstein et al., 2014; Harmon et al., 2019). Specifically, phylogenetic analyzes provide the opportunity to extract signals from the processes listed above, across both ecological and evolutionary timescales (Webb et al., 2002; Kembel and Hubbell, 2006; Cavender-Bares et al., 2009; Harmon et al., 2019). It is also possible to incorporate spatial aspects in phylogenetic analyzes. For example, phylogenetic beta diversity (PBD) quantifies the change in phylogenetic relatedness across space, with high PBD signaling low relatedness among spatially separated subsets of species. PBD thus reflects community assembly across space and time and can be used for inference of assembly processes (Webb et al., 2002; Chave et al., 2007; Morlon et al., 2011). High PBD is commonly associated with environmental barriers (Horner-Devine and Bohannan, 2006; Kembel and Hubbell, 2006; Parmentier et al., 2014) while low PBD has been attributed to limiting similarity and competitive exclusion (Allan et al., 2013). However, the underlying mechanisms of PBD are not fully understood, ultimately constraining our ability to interpret observed patterns (Figure 1; Kembel and Hubbell, 2006; Graham and Fine, 2008; Parmentier et al., 2014).

FIGURE 1

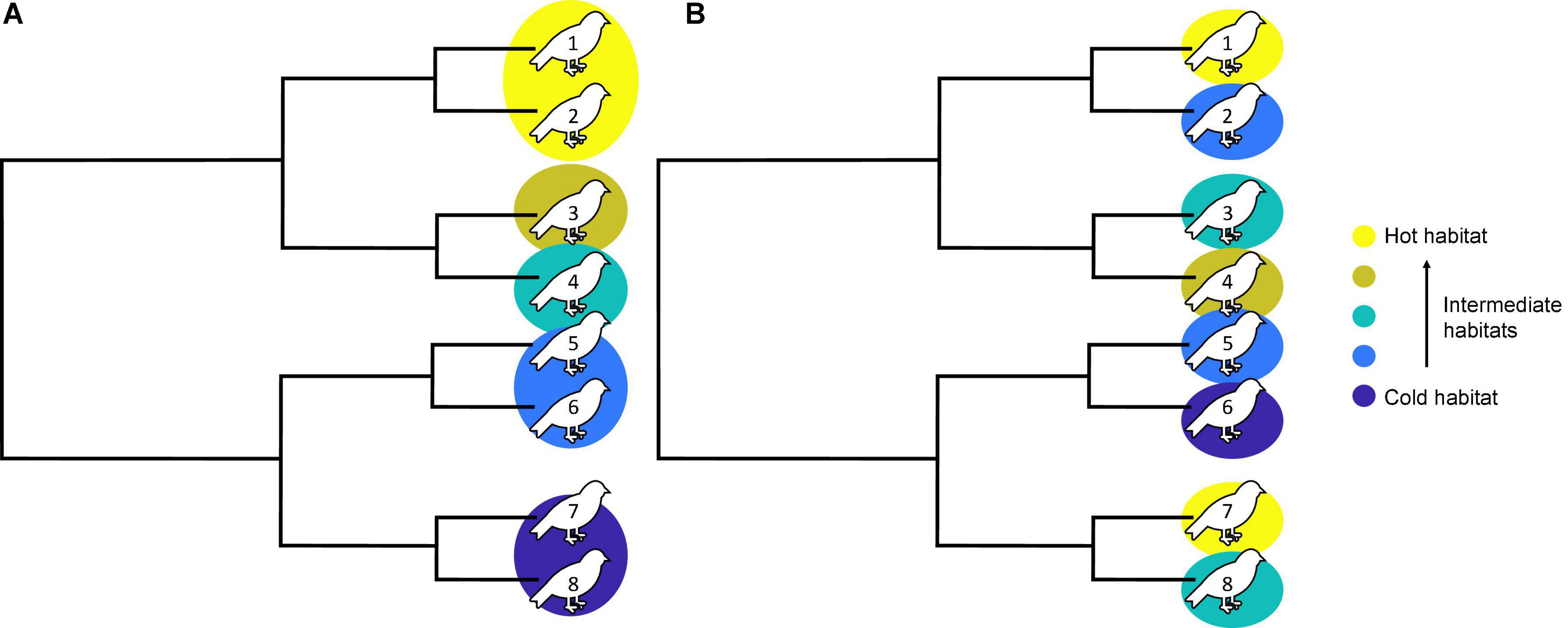
Figure 1. Illustration of two hypothetical phylogenies and species distribution in three different habitats. Eight species (numbered 1–8 on the bird sign) in the final community distribute in five habitats across an environmental gradient (e.g., temperature). For simplicity, each species can only appear in one habitat. In scenario (A), closely related species inhabit similar environment, leading to high phylogenetic beta diversity among different environments. Empirical research commonly interpreted this pattern as the presence of environmental and geographical barriers. In scenario (B), species evenly distribute across habitats with different environments, increasing the shared evolutionary history among habitats. This leads to a lower phylogenetic beta diversity across the environmental gradient. There can be multiple processes underpinning such a pattern, but without an understanding of the moderating mechanisms, it is not possible to interpret the patterns in the context of assembly processes.

Several empirical studies emphasize dispersal and environmental gradients as particularly crucial for phylogenetic patterns but consensus on the way patterns should be interpreted is somewhat lacking. Kraft et al. (2007) and Swenson et al. (2012) highlight the role of abiotic environmental filtering on Amazonian trees, whereas Kraft and Ackerly (2010) mention that dispersal can contribute to similar patterns as the abiotic environment. An integrated view including both dispersal and environmental filtering may thus be the most applicable to capture the dynamic of phylogenetic patterns in the Amazonian forest (Kraft and Ackerly, 2010). Such a notion also emphasizes the plausible interaction between dispersal and environmental gradient on community phylogenetic patterns, which has been further investigated in several systems including tropical Amazonian forests (Fine and Kembel, 2011), the woody shrublands (Morlon et al., 2011), the subterranean spider (Mammola et al., 2020), and the Hummingbirds in South America (Graham et al., 2012). Specifically, Morlon et al. (2011) propose that examining phylogenetic diversity across geographic distances provides insights into effects driven by dispersal, the environmental gradient as well as evolutionary consequences thereof. Observations in different empirical systems thus corroborate the interactive effects of environmental conditions and dispersal on generating phylogenetic diversity patterns across space, i.e., PBD (Graham and Fine, 2008). All the studies mentioned above, and the hypotheses listed within improve our general understanding of the effect of environmental conditions and dispersal on diversity patterns, but a better mechanistic understanding of phylogenetic patterns associated with dispersal and the environmental gradient is crucial for reliable conclusions. For this purpose, theoretical modeling lends itself to complex studies of interacting processes and diversity patterns.

Models can reveal the interacting effects of environmental gradients, resource gradients, and dispersal on diversification. For example, a spatially structured individual-based and eco-evolutionary model from Doebeli and Dieckmann (2003) shows that diversification is facilitated by a steep environmental gradient, especially when dispersal is limited. Similarly, Meszéna et al. (1997) analyzed a two-patch eco-evolutionary model and showed that large environmental differences between the two patches and high dispersal favor diversification. Such modeling facilitates our understanding of diversification, but the community phylogenetic structure is rarely considered, making interpretation of macro-evolutionary observations elusive. Here, we pursue the link between theoretical expectations and empirical observations on PBD. Specifically, we focus on environmental gradients and dispersal as target drivers of PBD patterns. Does PBD increase due to environmental gradient and decrease due to dispersal? Can we advance our interpretation of observed PBD patterns by disentangling the interactive effect of environmental gradient and dispersal? To answer these questions, we build on trait-based ecological modeling techniques (Dieckmann et al., 2007; Ito and Dieckmann, 2007; Pontarp and Wiens, 2017) and we utilize adaptive dynamics theory to analyze eco-evolutionary mechanisms of diversification (Metz et al., 1996; Geritz et al., 1998; Dieckmann et al., 2007; Ito and Dieckmann, 2007; Brännström et al., 2013). We simulate emerging PBD patterns as one species colonize and diversify in open niche space (i.e., assuming ecological opportunity) along an one-dimensional environmental gradient. Despite the gross simplification of the spatial dynamics, our approach allows us to isolate dominating and interacting ecological (e.g., competition for resources) and evolutionary mechanisms (e.g., selection and adaptation) that underpin diversification from the onset of evolutionary history to the end state of a spatially distributed adaptive radiation and the phylogenetic structure thereof.

Materials and methods

Given our ecological and eco-evolutionary focus on diversity patterns, we adopt a functional trait-based modeling approach. Also, as we are interested in emerging PBD patterns, we use an eco-evolutionary model of ecological diversification (i.e., adaptive radiation) in five sequentially ordered habitats with limiting resources and distinct environmental conditions (Figures 2A,B). We assume ecological opportunity at the onset of the diversification process and track the evolution of traits. Similar to several other trait-based models we use trait divergence as a proxy for speciation as the niche space is filling up (Doebeli and Dieckmann, 2000, 2003). By investigating how the emerging diversity depends on the steepness of the environmental gradient and the organismal dispersal propensity, we link dispersal-driven and environmental-driven microevolutionary mechanisms and emergent macroevolutionary patterns. Below we provide details of the ecological model, our evolutionary simulations, and subsequent analyzes of diversification and PBD.

FIGURE 2

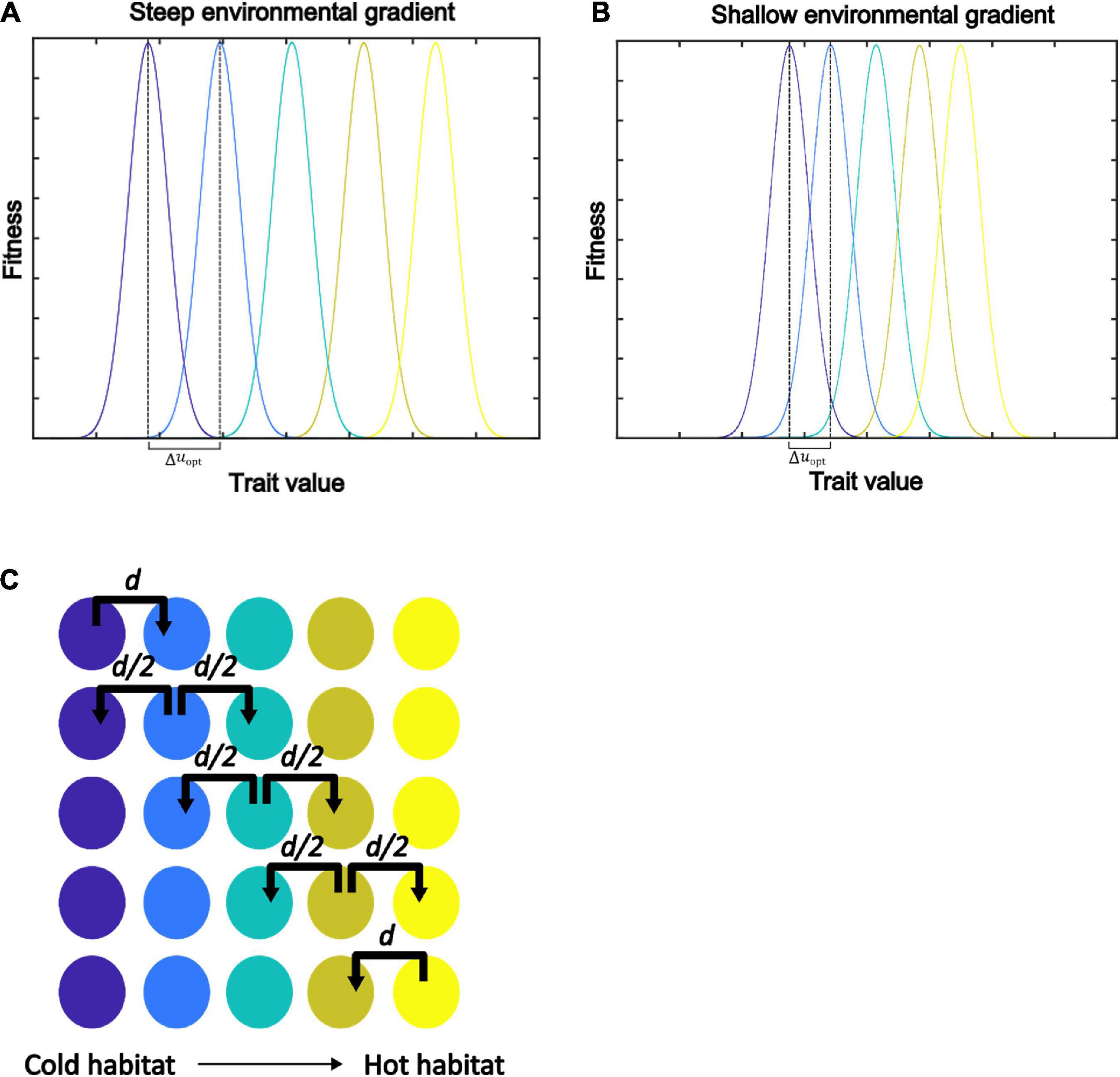
Figure 2. Illustration of the spatially explicit model with linearly spaced habitats, distinct environmental gradients (A,B), and stepping-stone dispersal (C). Panels (A,B) represent steep and shallow environmental gradients (e.g., temperature), respectively. Δu_opt denotes the difference between the mean environmental conditions in each of the habitats. (A) With a steep environmental gradient, Δu_opt is larger and species have low or zero fitness in neighboring habitats. (B) With a shallow environmental gradient, Δu_opt is smaller and species optimized in one habitat may have positive fitness in the neighboring habitat. (C) Stepping-stone dispersal allows individuals to disperse to the adjacent habitats only. For each generation, a proportion d of the residents disperse.

Ecological model

Our eco-evolutionary model combines shorter ecological and longer evolutionary timescales. Focusing on the ecological timescale for now, a species i is defined as a monomorphic population of individuals with the ecological trait u_i. The abundance of species i in habitat j changes over discrete generations depending on dispersal and the species’ realized reproductive output G(u_i,u_opt,j,N_j,t) (interpreted as the average number of offspring per individual). The realized reproductive output of a given species i in habitat j depends on how well the species’ ecological trait (u_i) matches the total abundance of species present in habitat j (N_j,t)and the mean environmental conditions (u_opt,j):

$$G(u_i,u_{\text{opt},j},N_{j,t})=R\left(N_{j,t}\right)E(u_i,u_{\text{opt},j}),(1)$$

where

$$R\left(N_{j,t}\right)=\left(1+r\left(1-\frac{N_{j,t}}{K}\right)\right),(2)$$

$$E(u_i,u_{\text{opt},j})=e^{-\frac{{\left(u_{\text{opt},j}-u_i\right)}^2}{2{\mathrm{\sigma }}_u^2}}.(3)$$

Here, R(N_j,t) models the decrease in reproductive output of any species in habitat j, where r = 1 and K = 500 represent the intrinsic growth rate and the carrying capacity of a perfectly adapted species in the absence of dispersal and competition. The potential reproductive output is thus density-dependent, and all species are competing on equal terms for the available biotic resources. In contrast, environmental effects are modeled through a trait-dependent function E(u_i,u_opt,j). The trait u_i can be viewed as a physiological trait that dictates environmental tolerance (e.g., adaptation to temperature) to an environment defined by its mean environmental condition u_opt,j. A complete matching between organismal trait u_i and the abiotic environment of habitat j (u_opt,j) maximizes Eq. 3 at a value of 1, and species i will reach its highest realized reproductive output (Eq. 1). If u_i deviates from u_opt,j, the reproductive output is decreased according to the Gaussian function (Eq. 3) with a standard deviation of σ_u. The parameter σ_u can thus be described as the abiotic environmental niche width or the environmental tolerance range of the species (Doebeli and Dieckmann, 2000; Pontarp and Wiens, 2017). The change in abundance of species i in habitat j changes over discrete generations considering both reproduction and dispersal can thus be written as:

$$N_{i,j,t+1}=G(u_i,u_{\text{opt},j},N_{j,t})N_{i,j,t}-O_{i,j,t}+I_{i,j,t},(4)$$

where N_i,j,t+1 denotes the abundance of species i in habitat j at time t + 1,N_j,t = N_1,j,t + ⋯ + N_n,j,t denotes the total abundance of individuals in patch j at time t, O_i,j,t denotes the emigration of species i from habitat j and I_i,j,t denotes the immigration of species i to habitat j. A proportion d of the offspring disperses to adjacent habitats according to a stepping-stone algorithm (Pontarp et al., 2012, 2015), as illustrated in Figure 2C. Thus, O_i,j,t = dG (u_i,u_opt,j,N_j,t)N_i,j,t and $I_{i,1,t}=\frac{O_{i,2,t}}{2}$, $I_{i,2,t}=O_{i,1,t}+\frac{O_{i,3,t}}{2}$,$I_{i,3,t}=\frac{O_{i,2,t}}{2}+\frac{O_{i,4,t}}{2}$, etc. Note that offspring born in the first and the fifth habitats (j = 1 and j = 5) can only disperse in one direction as we are modeling an environmental gradient.

Evolutionary model

We use the ecological model described above in an eco-evolutionary implementation to investigate species-specific adaptation to environmental conditions and diversification in the trait u_i. We use adaptive dynamics theory and separate ecological and evolutionary time scales. Assuming that ecological time scales are fast compared to the evolutionary ones allows us to determine the invasion fitness of possible mutations (i.e., the source of phenotypic variation) when the extant species (referred to as the residents) are at ecological equilibrium when a mutation occurs. We refer to the extant species and their abundance and distribution at ecological equilibrium as the resident environment (Metz et al., 1992; Dieckmann et al., 2007; Ito and Dieckmann, 2007) and determine invasion fitness as the initial growth rate of an initially rare mutant population in the resident environment. We assume that a mutation that happens in a resident population will result in a mutant trait close to the resident trait value. A mutant strain with positive invasion fitness in the resident environment can increase in abundance and, due to limiting similarity, typically replaces the parental resident strain from which it originated. The mutant then becomes a new and potentially better-adapted resident, forming a new resident environment with the other extant resident species. Apart from adaptation, diversification through evolutionary branching in the functional trait is also possible. Evolutionary branching occurs when selection drives a resident species toward a fitness minimum, selection becomes disruptive and two strains with similar traits can coexist (Meszéna et al., 1997; Geritz et al., 1998). The co-existing strains become new residents. Both adaptation and diversification thus emerge through sequential mutations over evolutionary time, during which populations interact and evolve. This model allows us to study adaptation and diversification across space and time, ultimately linking micro-evolutionary processes of trait evolution and phylogenetic patterns (see mathematical details and implementation below).

We initiate the simulations by seeding the first habitat with one well-adapted species (species 1), i.e., a species with a trait value equal to the mean environmental conditions of the first habitat (u₁ = u_opt,1). We solve the ecological model (Eq. 4) numerically through time until the system reaches an ecological equilibrium. For our parameterizations, the ecological equilibrium is always a fixed point, i.e., the resident environment will always reach a stable state in terms of abundance. To compute the invasion fitness of a mutant in such a resident environment, we write our model in matrix form. Since the growth rate is density dependent but not frequency dependent, it suffices to represent the resident environment with a vector N_r encompassing the total abundance of all resident species in each of the five habitats at ecological equilibrium. The potential mutant reproductive output and environmental tolerance can be written as vectors R and E according to:

$$R_j=\left(1+r\left(1-\frac{N_{r,j}}{K}\right)\right),j=1,\mathrm{\dots },\mathrm{\hspace{0.25em}5},(5)$$

$$E_j=e^{-\frac{{\left(u_{\text{opt},j}-u_{\text{m}}\right)}^2}{2{\mathrm{\sigma }}_u^2}},j=1,\mathrm{\dots },\mathrm{\hspace{0.25em}5}.$$

Here, N_r,j and u_opt,j are the resident population abundance and the environmental condition of the habitat j respectively. The realized reproductive output of a mutant strain with trait u_m in each respective habitat can therefore be described by a vector G where G_j = R_jE_j.

We also reformulate the dispersal in Eq. 4 in matrix from such that:

$$\mathbf{\text{M}}=\left[\begin{array}{ccccc}\hfill 1-d\hfill & \hfill d\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{d}{2}\hfill & \hfill 1-d\hfill & \hfill \frac{d}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{d}{2}\hfill & \hfill 1-d\hfill & \hfill \frac{d}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{d}{2}\hfill & \hfill 1-d\hfill & \hfill \frac{d}{2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d\hfill & \hfill 1-d\hfill \end{array}\right],(6)$$

where each row of M describes the distribution of the mutant after the dispersal from the corresponding habitat. Given the local growth rates of a mutant described above, the long-term growth rate of a mutant for the whole spatially structured system is determined as the dominant eigenvalue of the matrix W following Metz et al. (1992), where

$$\mathbf{\text{W}}=\left[\begin{array}{ccccc}\hfill \left(1-d\right)R_1{E}_1\hfill & \hfill d{R}_1{E}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill (d/2)R_2{E}_2\hfill & \hfill \left(1-d\right)R_2{E}_2\hfill & \hfill (d/2)R_2{E}_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill (d/2)R_3{E}_3\hfill & \hfill \left(1-d\right)R_3{E}_3\hfill & \hfill (d/2)R_3{E}_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill (d/2)R_4{E}_4\hfill & \hfill \left(1-d\right)R_4{E}_4\hfill & \hfill (d/2)R_4{E}_4\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d{R}_5{E}_5\hfill & \hfill \left(1-d\right)R_5{E}_5\hfill \end{array}\right].(7)$$

W describes the change of mutant population abundance from one generation to the next. The dominant eigenvalue of W, λ_D, in this context, is thus the invasion fitness of a mutant with the trait u_m in the spatially structured system. If the invasion fitness is larger than one, a mutant may invade and grow in abundance. From the invasion fitness, we determine the selection gradient of the i^th resident population ${\frac{d{\mathrm{\lambda }}_D}{d{u}_{\text{m}}}|}_{u_{\text{m}}=u_i}$(i = 1,…,n), which determines whether the mutants with a slightly higher or lower trait value than the resident may invade. We describe the trait evolution of the i^th resident population using the canonical equation proposed by Dieckmann and Law (1996). The canonical equation determines the rate of directional selection based on the intrinsic mutation probability (μ), the population size (N_i), and the mutation variance (${\mathrm{\sigma }}_{\mu }^2$):

$$\frac{\text{d}{u}_i}{\text{d}t}={\frac{1}{2}\mu {\mathrm{\sigma }}_{\mu }^2{N}_i\frac{\text{d}{\lambda }_{\text{D}}}{\text{d}{u}_{\text{m}}}|}_{u_{\text{m}}=u_i},i=1,\mathrm{\dots },n.(8)$$

Directional selection comes to a halt when the selection gradient vanishes. This can happen when the resident population is close to a fitness minimum and, thus, the invasion fitness of a mutant is positive on both sides of the resident trait, where $\frac{\text{d}{u}_i}{\text{d}t}\approx 0$ and ${\frac{{\text{d}}^2{\mathrm{\lambda }}_D}{\text{d}{u}_{\text{m}}^2}|}_{u_{\text{m}}=u_i}>0$. Under such conditions, any mutant strain with a slightly different trait value on either side of the resident trait can coexist with the resident. The mutant and resident then experience opposite directional selection that leads to two phenotypically distinct subpopulations. This process, through which the number of residents increases, is known as evolutionary branching (Geritz et al., 1998). We test for robustness assuming several branching criteria to ensure that final diversity patterns regarding the environmental gradient and dispersal remains unaffected (see Supplementary Appendix 1 for branching criteria). Directional selection may also cease when the resident population is close to a fitness maximum. A resident community where the selection gradient for all resident populations vanishes is known as an evolutionarily stable state (ESS), namely $\frac{{\text{du}}_{\text{i}}}{\text{d}t}\approx 0$ and ${\frac{{\text{d}}^2{\mathrm{\lambda }}_D}{\text{d}{u}_{\text{m}}^2}|}_{u_{\text{m}}=u_i}<0$ for all the i = 1,…,n. All existing resident traits are at the fitness maximum and no nearby mutant can invade. The evolutionary process hence comes to a halt. In all our simulations, the community eventually reach an ESS. We record the evolutionary trajectory and the composition of the final community until reaching the ESS for analysis.

Combined environmental gradient and dispersal scenarios

We run the eco-evolutionary model described above across 20 levels of dispersal probability and environmental gradient in a full-factorial manner, which gives us a total of 400 model realizations. More specifically, dispersal probability ranges from 10⁻⁵ (low) and 10⁻¹ (high) and is combined with a separation of the mean habitat environmental condition ranging from 0.1σ_u to σ_u. The separation of habitat optima quantifies the strength of the environmental gradient. At shallow gradients, individuals adapted to a certain habitat will still be able to survive in and thus potentially colonize the neighboring habitats, but with steep gradients, individuals adapted to one habitat will have very low fitness in adjacent habitats without adapting if they disperse there. For each scenario, we initiate the simulation by introducing the first species with a trait equal to the mean environmental conditions of the first habitat (u₁ = u_opt,1). The first species has an initial population size of five individuals across all five habitats. The initial population size is tested to be robust and does not affect the ecological equilibrium.

Phylogenetic tree and diversity indices

By assuming a one-to-one mapping between phenotype and species, i.e., using evolutionary branching as defined above as a proxy for speciation, we can follow the phylogenetic relationship between species as they differentiate in trait space through time (Pontarp and Wiens, 2017). We record each branching event and construct a pairwise distance matrix between all existing species at the end of each simulation. We construct phylogenetic trees that mirror our simulated adaptive radiation for each model realization using the “seqlinkage” function in MATLAB with the unweighted pair group method with arithmetic mean (UPGMA) algorithm and the pairwise distance matrix as the input. We then quantify phylogenetic diversity across space. First, we calculate the phylogenetic diversity (Faith, 1992) of each habitatk (PD_k) according to:

$$P{D}_k=\sum B_k,k=1,\mathrm{\dots },\mathrm{\hspace{0.17em}5}.(9)$$

B_k is the set of branches in the phylogenetic tree that corresponds to species present in habitat k.

Knowing the PD of a pair of habitats allows us to compute the PBD which is a pairwise index. PBD measures the phylogenetic dissimilarity among a pair of communities and several approaches have been proposed (Swenson, 2011; Leprieur et al., 2012). Here, we use the PhyloSor index:

$${\text{PhyloSor}}_{j,k}=\frac{2P{D}_{j,k}-P{D}_k-P{D}_j}{P{D}_k+P{D}_j}(10)$$

By defining the first habitat as the reference point, we only calculate PhyloSor_j,k where j = 1,k = 1,… 5. This gives us the PBD across increasing space from the first habitat. PD_k and PD_j consider species present in the habitat j or k, whereas PD_j,k is the phylogenetic diversity corresponds to all species that are present in either habitat j or k (PD_j,k = ∑_Bj∪Bk). Eq. 10 thus presents the proportion of phylogenetic diversity that is unique to one habitat. If two habitats have no species in common, they share no evolutionary history, leading to high PBD (PhyloSor=1). Increasing numbers of common species that are closely related will reduce the numerator of Eq. 10, hence reducing PBD between two habitats (PhyloSor<1).

Result

Selection-induced diversification

To fully understand phylogenetic beta diversity, we need to study the microevolutionary processes of diversification. Our results show that the environmental gradient acts as the main driver of diversification, which gives rise to the overall species diversity (Figure 3A). Selection toward different environments induces disruptive selection and ultimately speciation. For such disruptive selection to occur, dispersal is necessary, but dispersal can also hinder disruptive selection since mobile species have access to ecological opportunities present in other environments and are hence subjected to selection toward an intermediate strategy that allows them to inhabit wider environmental conditions. When the dispersal is high, and the environmental barrier is low enough for any trait to be sustained, disruptive selection becomes weak or even disappears. When the environmental gradient is at a higher level than dispersal, the divergent selection at each local optimum can lead to speciation. The combined effect of the environmental gradient and dispersal also dictates the temporal dynamics of the diversification (Figure 3B). Comparing simulations across levels of environmental gradient and dispersal, the ESS is reached relatively fast when a steep environmental gradient is combined with low dispersal, or when high dispersal is combined with a shallow environmental gradient. In contrast, where the dispersal and the gradient are both at intermediate levels, the divergent selection driven by the environmental gradient is reduced by the dispersal, ultimately increasing the time until ESS is reached. An explanation for a delayed time until ESS is an overall smoothened fitness landscape, i.e., the fitness difference between trait values becomes more similar. As presented in the results below, opposing effects of the environmental gradient and dispersal on diversification are further manifested in the phylogenetic diversity of the community.

FIGURE 3

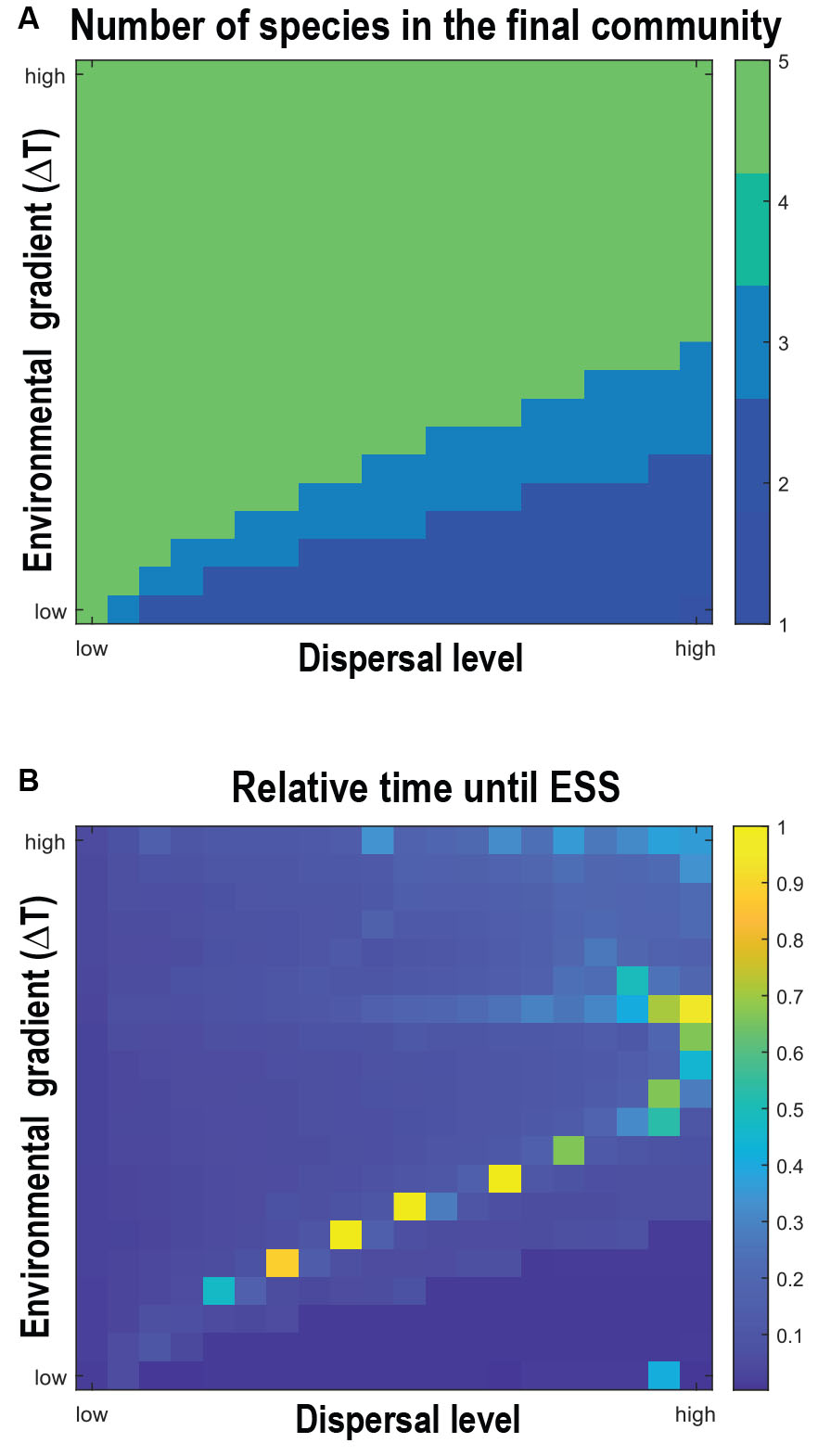
Figure 3. Simulation outputs across the parameter space of environmental gradient level (y-axis) and dispersal level (x-axis) on panel (A) number of species in the final community, and on panel (B), relative time until the evolutionary stable state. The relative time is calculated as the evolutionary time divided by the longest evolutionary time until the evolutionarily stable state. The range of environmental gradient (Δu_opt) is from 0.1σ_u to 1.0σ_u; The range of dispersal probability is from 10⁻⁵to 10⁻¹.

The pace and shape of diversification

The microevolutionary processes described in the results above affect the pace and the shape of adaptive radiation which ultimately affect phylogenetic beta diversity. When the environmental gradient is the dominating driver (steep gradient and low dispersal), the local environment induces strong directional selection toward local environmental optima. The reason is that the organisms are confined by the low dispersal ability and fitness is largely dependent on the environmental tolerance (Eq. 5). Directional selection toward different environmental optima in turn facilitates the diversification of organisms living in different habitats. Since our simulation starts from one end of the environmental gradient, stepwise colonization of habitats along the gradient takes place, followed by sequential diversification between the dispersers and the locally adapted source population (Figure 4A). This leads to increased phylogenetic diversity between two habitats with an increased environmental difference. In the extreme case where the steep environmental gradient is combined with low dispersal between habitats, five species emerge (Figures 3A, 4A). Each species is well adapted to a single environment and distributed mainly in one of the five habitats, which leads to high species richness and high phylogenetic diversity in the final community. When the environmental gradient is reduced to an intermediate level, the higher similarity between habitats allows species to colonize adjacent habitats without prior adaptation. Selection toward different environmental optima is reduced and dispersal has a strong influence on diversification. An increase in dispersal disrupts the sequential diversification and local adaptation, which leads to lower species richness and low phylogenetic diversity (Figures 3A, 4B). The mechanism connecting diversification and dispersal can be explained by analyzing the fitness landscape. Mobile species adopting an intermediate strategy (intermediate trait value between environmental optima) have the highest average fitness across various environments. Evolution thus leads to fewer species that are not perfectly adapted to any environmental optimum but reside in multiple habitats (Figures 3A, 4C).

FIGURE 4

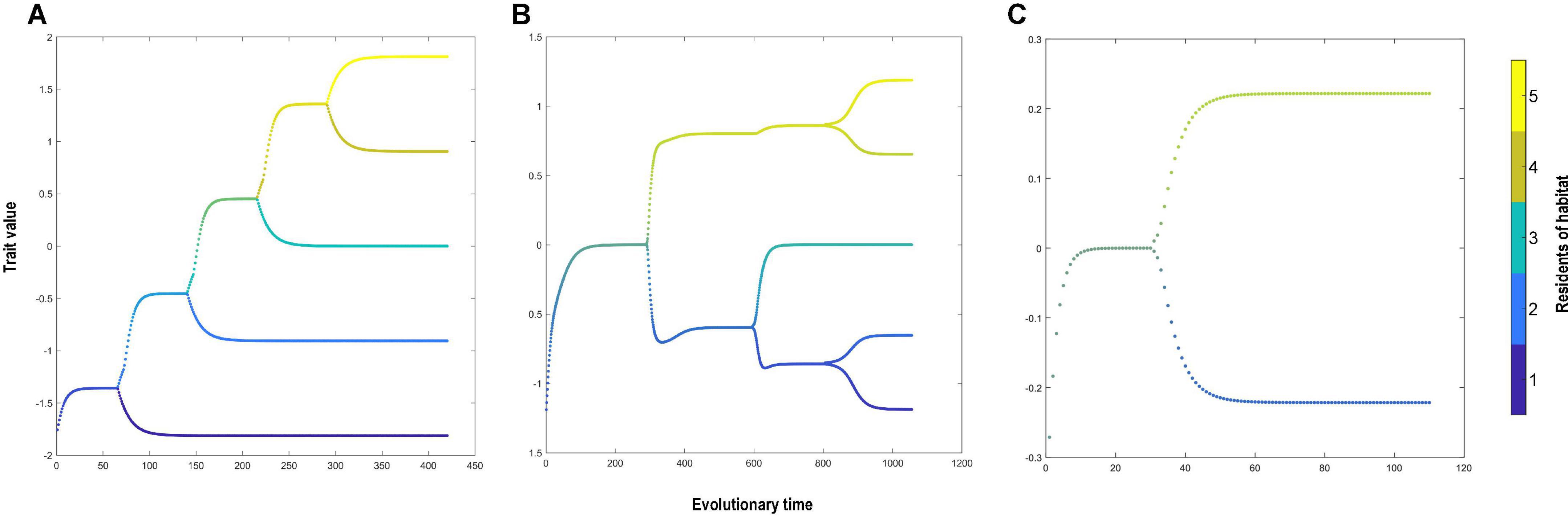
Figure 4. The evolutionary trajectory under (A) environmental gradient (Δu_opt) = 0.9σ_u with dispersal probability d = 10⁻⁵ and (B) environmental gradient (Δu_opt) = 0.6σ_u with dispersal probability d = 0.07 and (C) environmental gradient (Δu_opt) = 0.19σ_u with dispersal probability d = 0.04. The horizontal axis indicates the evolutionary time throughout the simulation, and the vertical axis indicates the population trait value. At each evolutionary time, each species is mapped as a dot with the color representing the proportional distribution among habitats.

Regarding the shape of adaptive radiation, we show that stronger dispersal contributes to a more symmetric radiation and a higher degree of shared evolutionary history between species across the environmental gradient (Figure 4B). When dispersal is high, the earliest two lineages adopt intermediate strategies (mechanisms explained above), each dominating half of the habitats across the environmental gradient. When the population approaches the carrying capacity of the habitats, increasing competition leads to increasing selective pressure toward local optima. Species that are originally distributed across multiple habitats thus go through local adaptation and become five species specializing in each of the five habitats (Figure 4B). The effect of dispersal and environmental gradient on the shape of adaptive radiation and the final species distribution either directly, or indirectly affects the phylogenetic beta diversity.

Linking microevolutionary mechanisms and phylogenetic beta diversity

The evolutionary mechanisms described above affect the progress of diversification and the spatial distribution of the population, ultimately influencing the PBD. As noted in the method section, PBD is a pairwise index and we compute the average of all the possible pairwise PBD between habitats. Focusing on the average PBD per simulation provides a general understanding of how PBD responds to the environmental gradient and dispersal (Figure 5). Mean PBD across the gradient is influenced by both the environmental gradient and dispersal, and we identify clear regions of PBD across parameter space. A steep environmental gradient combined with low dispersal leads to high PBD (Figure 5, region A), a result that is due to an asymmetric phylogeny with locally distributed species (Figure 4A). A steep environmental gradient combined with intermediate dispersal decrease PBD, ultimately driven by a smoothened fitness landscape and delayed speciation (Figure 5, region B). When the environmental gradient is intermediate to shallow, and dispersal is high, PBD is further reduced (Figure 5, regions D and E). High dispersal leads to symmetrical phylogeny with a more shared evolutionary history of the whole community. Moreover, shallow environmental gradients and high dispersal enable species to live in multiple habitats, both contributing to a low PBD.

FIGURE 5

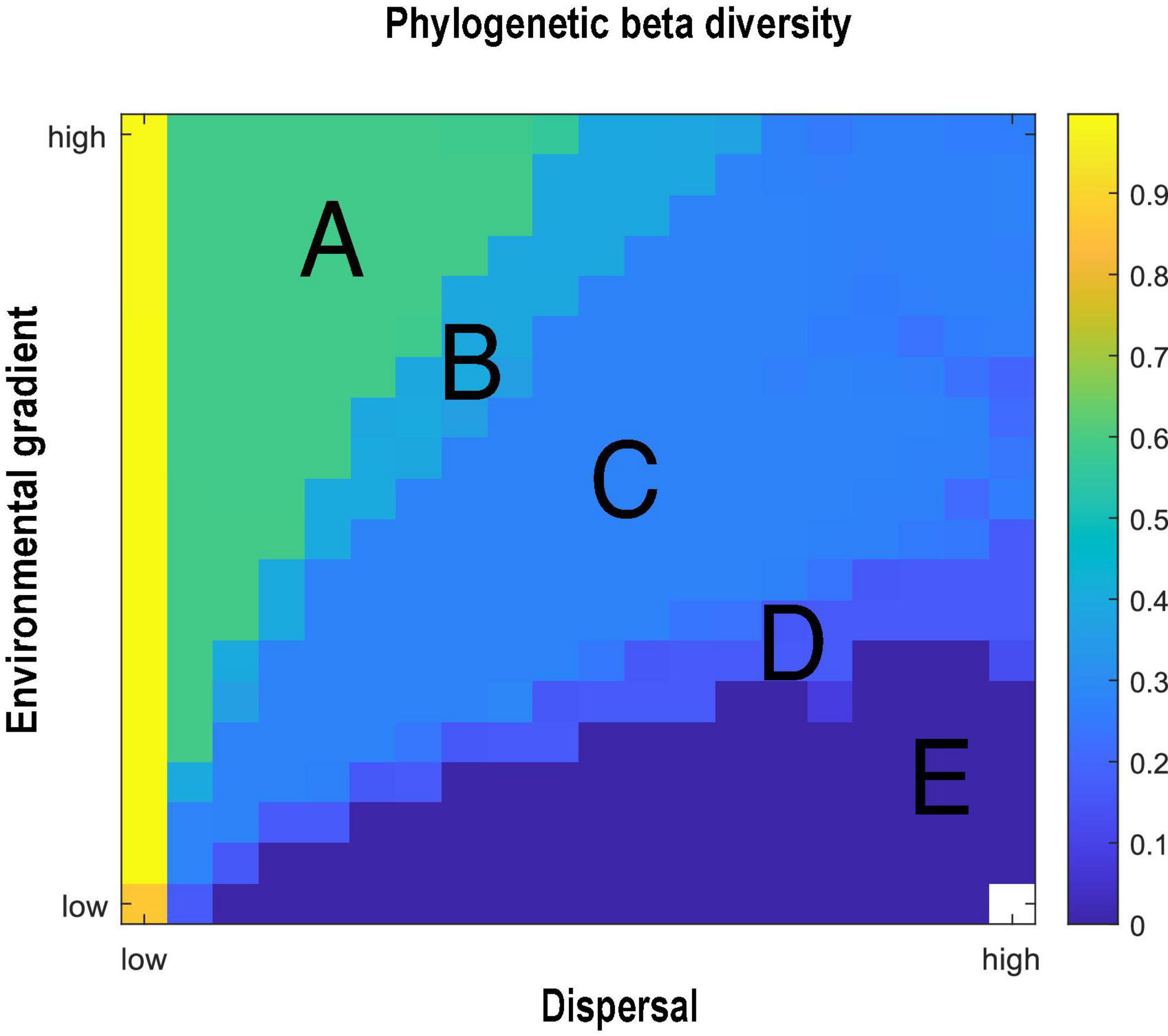
Figure 5. The phylogenetic beta diversity (PBD) reveals the interaction of the environmental gradient (y-axis) and dispersal (x-axis). Each grid indicates a simulation with a respective combination of environmental gradient and dispersal. PBD is then calculated by comparing all the possible pairwise phylogenetic relatedness between the habitats. We then take the average of the pairwise values. When PBD equals 1, there is no shared evolutionary history between species living in two compared habitats. When PBD equals 0, species living in both habitats share an identical evolutionary history. An extinction threshold of 1 is introduced to define whether a species is present or absent.

We also present PBD as a function of geographical distance from the reference habitat (Figure 6). We set the habitat at the low end of the environmental gradient as the reference habitat. We compute PBD between the reference habitat and each of the four subsequent habitats across the environmental gradient. We thus obtain four PBD values for increasing geographical distance from the reference habitat per simulation. As expected, we find a general trend of increased PBD with increasing distance to the reference habitat. Interactions between the environmental gradient and dispersal also lead to distinct responses of PBD. When a steep environmental gradient is combined with low dispersal, the PBD increases in a linear form along the environmental gradient until reaching the maximum value of 1 (Figure 6, line A). As described in the sections above, a steep environmental gradient and low dispersal lead to locally confined species with low phylogenetic relatedness even between neighboring habitats. When an intermediate environmental gradient is combined with low to intermediate dispersal, neighboring habitats may share the same species. PBD may thus remain zero between neighboring habitats and instead increase as a sigmoidal form (Figure 6, line B). When the intermediate environmental gradient is combined with an intermediate level of dispersal, PBD increases within two habitats from the reference point but remains low with increasing distance (Figure 6, line C). Such a pattern is a consequence of ancestor species with intermediate strategies that go through subsequent diversification from the center toward both ends of the environmental gradient (Figure 4B). This leads to a closer relationship between species inhabiting the intermediate environments than to the species inhabiting the two ends of the gradient. The same pattern is intensified when a shallow environmental gradient is combined with high dispersal, where PBD increases with distance until reaching a plateau at the intermediate gradient before it further increases (Figure 6, line D). High dispersal creates the plateau of PBD around the center of the gradient by increasing the similarity in species composition between central habitats. Finally, when the environmental gradient is too shallow to create divergent selections or confined species distribution, PBD remains 0 regardless of the geographical distance (Figure 6, line E).

FIGURE 6

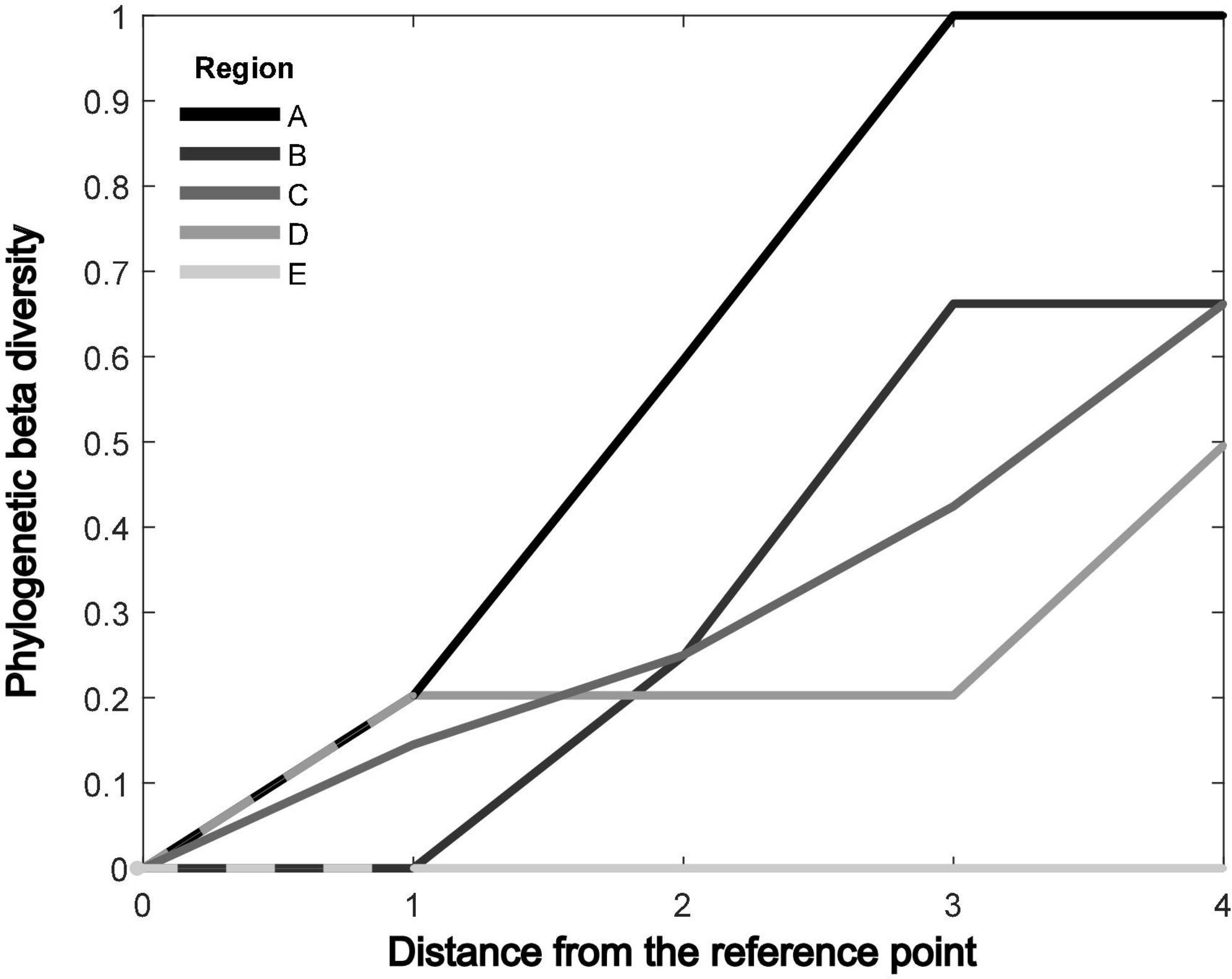
Figure 6. The interaction between the environmental gradient and dispersal affects how phylogenetic beta diversity (PBD) increases with geographical distance from the reference point. When the environmental gradient is steep and dispersal is low, PBD increases almost linearly with the geographical distance. When dispersal increases, the PBD within a short distance decreases rapidly. When the environmental gradient is low and dispersal is high, PBD does not have a linear relationship with the geographical distance. PBD is plotted with dispersal = 0.04 and across environmental gradient (A:Δu_opt = 0.95σ_u; B:Δu_opt = 0.86σ_u; C:Δu_opt = 0.52σ_u; D:Δu_opt = 0.29σ_u; E:Δu_opt = 0.19σ_u), overlapping lines are presented as dashed lines.

Discussion

Empirical research often interprets phylogenetic diversity patterns in the context of assembly processes. For example, Mammola et al. (2020) compare the phylogenetic relatedness of co-occurring subterranean spiders in different microhabitats and conclude that their habitat specialization is primarily driven by differences in environmental conditions. Similarly, Saladin et al. (2019) reveal the effect of the abiotic environment on shaping ectothermic tetrapods communities by measuring phylogenetic diversity across an environmental gradient. Others combine functional traits and phylogenetic diversity. Weinstein et al. (2014), show that geographical barriers and environmental gradients can predict hummingbird biodiversity patterns. Trait diversity and phylogenetic diversity can thus be used for inferring assembly processes (Baraloto et al., 2012; Graham et al., 2012; Swenson et al., 2012; Weinstein et al., 2014). However, limited knowledge of acting and interacting processes and emerging diversity patterns remains, ultimately hindering pattern interpretation to reach its full potential (Pausas and Verdú, 2010). Apart from various hypotheses that aim to verbally link process and pattern, quantitative analysis with mechanistic insight is needed (Pontarp et al., 2019; Pontarp, 2021). Models like the one presented here can provide explicit descriptions of the process-pattern relationship based on empirically supported assumptions. Yet, the majority of such models have been focused on diversification (Doebeli and Dieckmann, 2003; Heinz et al., 2009; Pontarp and Wiens, 2017) and less on phylogenetic community patterns (Pontarp, 2021). Here, we build on outstanding questions stemming from the empirical literature and we study diversity patterns as they emerge across evolutionary time with a mechanistic eco-evolutionary model. We specifically focus on the emergence of phylogenetic diversity across different environmental and dispersal scenarios, ultimately advancing our understanding of community assembly and the links between known processes and patterns.

It is commonly assumed that an environmental gradient can shape phylogenetic structure through the general importance of abiotic filtering on some available global pool of functional diversity (Kembel and Hubbell, 2006; Cavender-Bares et al., 2009). A steep environmental gradient may lead to distinct subsets of phenotypically unique species across the gradient. For example, distinct subsets of species across the bathymetric gradient are driven by huge differences in hydrostatic pressure and temperature in different water depths (Brown and Thatje, 2014). If the observed phenotypes are phylogenetically conserved, a steep environmental gradient will lead to closely related species inhabiting similar environmental conditions, hence leading to high PBD between different environments. Conversely, a shallow environmental gradient may allow species with similar phenotypic traits to coexist across the gradient, leading to the decreased phylogenetic difference among subsets of species, ultimately causing a low PBD across the environmental gradient. We observe the same effect of different environmental conditions on phylogenetic diversity in our model (Figure 5). We advance current knowledge of such patterns as our model combines both ecological filtering and eco-evolutionary dynamics. Our model thus reveals the mechanistic link between the environmental gradient, eco-evolutionary processes, and phylogenetic patterns. We observe the environmental-induced directional selection of the organism toward local conditions in different habitats across the gradient. Organisms living in different environments adapt and diversify. With a steep environmental gradient, the diversification happens fast and more frequently, leading to high phylogenetic diversity between sites with different environments compared to a less steep gradient, hence a high PBD. Our results suggest that environmental gradients have both ecological and evolutionary consequences, and the evolutionary signature of such a process can be observed through PBD patterns. However, to understand the full complexity of PBD patterns, we cannot view the environmental gradient in isolation from dispersal.

The pioneering review from Graham and Fine (2008) discusses several hypotheses on how PBD can be linked to both environmental gradient and dispersal. They suggest that low dispersal can lead to high PBD between sites regardless of environmental gradients and that high dispersal leads to low or random PBD. Our results confirm such hypotheses by showing that dispersal is indeed negatively related to PBD. Dispersal can thus conceal the potential effect of environmental conditions. We show that dispersal can disrupt the directional selection induced by the environment toward a local optimum and instead drive organismal adaptation to an intermediate environmental generalist strategy. Graham and Fine (2008) also propose that changes in PBD across a given region reflect environmental gradients and geographical barriers within the same region. Our results confirm the interactive effect of dispersal and the environmental gradient on trait selection and species distribution, which leads to distinct patterns of PBD across distances (Figure 6). Specifically, we show that high dispersal can reduce the directional selection imposed by the environmental gradient in the early stage of our simulation. High dispersal reduces the positive effect of local adaptation on fitness, leading to a species with intermediate trait value that can survive in multiple environments. If the environmental gradient is steep, local adaptation and trait diversification may still occur despite high dispersal, but such diversification occurs in the later stage of the macro-evolutionary trajectory. Strong competition in the late stages of the radiation due to large population size resumes selection toward local optima and PBD remains generally low across the geographical distance. Depending on the level of dispersal, the response of PBD to geographical distance under a steep environmental gradient can change from a linear form to a sigmoidal form (Figure 6). Conversely, in the case of shallow to intermediate environmental gradient, a high dispersal level can change the response of PBD to geographical distance. PBD increases with distance but reaches a plateau around the center of the gradient. The simulated patterns of PBD across geographical distance may not be directly comparable to any natural system since our model simplified the dispersal and the environmental gradient into a single dimension. Despite the limitation, our simulation shows that the environmental gradient can indeed generate phylogenetic diversity, but the final PBD pattern must be studied with the dispersal propensity of the system in mind. Moreover, we show that PBD responds distinctively across geographical distances due to the combined effects of the environmental gradient and dispersal. Our results hence suggest a possibility to unravel the interacting processes of a region from existing PBD.

Revisiting several empirical studies mentioned throughout this paper, we can observe the interactive effect of dispersal and environmental gradient in PBD patterns. As an example of high dispersal propensity, hummingbird assemblages re more phylogenetically related in harsh environments than in more benign environments (Graham et al., 2012). Such a pattern is comparable to our results showing that extreme environmental gradient can lead to high PBD despite a high dispersal level (Figure 5, region C). Nevertheless, PBD decreases drastically once the environmental gradient becomes less extreme due to such a high dispersal propensity (Figure 5, region E). In contrast, for a system with low dispersal propensity such as the tropical tree communities, closely related species appear in adjacent locations despite the absence of an environmental gradient (Swenson et al., 2012). The same pattern is observed in a recent study of mammal assemblages on oceanic islands, where low dispersal is realized through geographical barriers. High phylogenetic diversity between islands appears without a response to environmental filtering, revealing the dominant role of dispersal on the value of PBD (Si et al., 2022). These empirical examples highlight the importance of taking both dispersal and environmental gradient into account while interpreting phylogenetic diversity. Our theoretical model further enables us to interpret PBD patterns with a mechanistic understanding. However, aside from the corroboration of existing verbal hypotheses, we also expand verbal hypotheses on phylogenetic patterns to a spatial context. Our results imply that observation of PBD as a function of distance along environmental gradients can shed light on the interpretation of observed PBD patterns. For example, it remains difficult to quantitatively infer a particular process from an empirically observed pattern (Cavender-Bares et al., 2009; Harmon-Threatt and Ackerly, 2013) and similar patterns can be the result of widely different processes (Vellend, 2010). Our model also shows how the negative relationship between dispersal and PBD can conceal the potential effect of the environmental gradient on PBD. Whether a high PBD comes from strong environmental effects or low dispersal is hence difficult to infer from the PBD considering two subsets of species, because similar PBD can be recovered in different parts of parameter space. Nonetheless, our results suggest a way forward by indicating the distinct responses of PBD across geographical distances. By measuring PBD between multiple subsets of species with increasing distance, one could observe potential gradients that would otherwise be cryptic. Future implementation of a more complex spatial configuration such as a two-dimensional and continuous landscape can produce more realistic PBD patterns that might allow inferring processes from empirical patterns. Nevertheless, our study not only improves our understanding of eco-evolutionary assembly processes but also facilitates improved inferences of processes from observed PBD patterns.

Data availability statement

The original contributions presented in this study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Y-TJ and MP conceived the idea for the study. Y-TJ wrote the code for the simulation software under guidance of ÅB, analyzed the model with input from MP and ÅB, and wrote the first draft of the manuscript. All authors constructed the model and contributed to the analysis and interpretation of the material and to the writing of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.1037980/full#supplementary-material

References

Allan, E., Jenkins, T., Fergus, A. J. F., Roscher, C., Fischer, M., Petermann, J., et al. (2013). Experimental plant communities develop phylogenetically overdispersed abundance distributions during assembly. Ecology 94, 465–477. doi: 10.1890/11-2279.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Baraloto, C., Hardy, O. J., Paine, C. E. T., Dexter, K. G., Cruaud, C., Dunning, L. T., et al. (2012). Using functional traits and phylogenetic trees to examine the assembly of tropical tree communities. J. Ecol. 100, 690–701.

Google Scholar

Brännström, Å, Johansson, J., and Von Festenberg, N. (2013). The Hitchhiker’s guide to adaptive dynamics. Games 4, 304–328. doi: 10.1016/j.mito.2021.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, A., and Thatje, S. (2014). Explaining bathymetric diversity patterns in marine benthic invertebrates and demersal fishes: Physiological contributions to adaptation of life at depth. Biol. Rev. Camb. Philos. Soc. 89, 406–426. doi: 10.1111/brv.12061

PubMed Abstract | CrossRef Full Text | Google Scholar

Cavender-Bares, J., Kozak, K. H., Fine, P. V. A., and Kembel, S. W. (2009). The merging of community ecology and phylogenetic biology. Ecol. Lett. 12, 693–715.

Google Scholar

Chave, J., Chust, G., and Thébaud, C. (2007). “The importance of phylogenetic structure in biodiversity studies,” in Scaling Biodiversity, eds D. Storch, J. Brown, and P. Marquet (Cambridge: Cambridge University Press), 150–167.

Google Scholar

Dieckmann, U., and Law, R. (1996). The dynamical theory of coevolution: A derivation from stochastic ecological processes. J. Math. Biol. 34, 579–612.

Google Scholar

Dieckmann, U., Brännström, Å, HilleRisLambers, R., and Ito, H. C. (2007). “The adaptive dynamics of community structure,” in Mathematics for ecology and environmental sciences, eds Y. Takeuchi, Y. Iwasa, and K. Sato (Berlin: Springer), 145–177.

Google Scholar

Doebeli, M., and Dieckmann, U. (2000). Evolutionary branching and sympatric speciation caused by different types of ecological interactions. Am. Nat. 156, S77–S101. doi: 10.1086/303417

PubMed Abstract | CrossRef Full Text | Google Scholar

Doebeli, M., and Dieckmann, U. (2003). Speciation along environmental gradients. Nature 421, 259–264.

Google Scholar

Faith, D. P. (1992). Conservation evaluation and phylogenetic diversity. Biol. Conserv. 61, 1–10.

Google Scholar

Fine, P. V. A., and Kembel, S. W. (2011). Phylogenetic community structure and phylogenetic turnover across space and edaphic gradients in western Amazonian tree communities. Ecography 34, 552–565.

Google Scholar

Geritz, S. A. H., Kisdi, E., Mesze‘Na, G., and Metz, J. A. J. (1998). Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 12, 35–57.

Google Scholar

Gillespie, R. G., Bennett, G. M., De Meester, L., Feder, J. L., Fleischer, R. C., Harmon, L. J., et al. (2020). Comparing adaptive radiations across space, time, and taxa. J. Heredity 111, 1–20. doi: 10.1093/jhered/esz064

PubMed Abstract | CrossRef Full Text | Google Scholar

Graham, C. H., and Fine, P. V. (2008). Phylogenetic beta diversity: Linking ecological and evolutionary processes across space in time. Ecol. Lett. 11, 1265–1277. doi: 10.1111/j.1461-0248.2008.01256.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Graham, C. H., Parra, J. L., Tinoco, B. A., Stiles, F. G., and McGuire, J. A. (2012). Untangling the influence of ecological and evolutionary factors on trait variation across hummingbird assemblages. Ecology 93, S99–S111.

Google Scholar

Harmon, L. J., Andreazzi, C. S., Débarre, F., Drury, J., Goldberg, E. E., Martins, A. B., et al. (2019). Detecting the macroevolutionary signal of species interactions. J. Evol. Biol. 32, 769–782.

Google Scholar

Harmon-Threatt, A. N., and Ackerly, D. D. (2013). Filtering across spatial scales: Phylogeny, biogeography and community structure in bumble bees. PLoS One 8:e60446. doi: 10.1371/journal.pone.0060446

PubMed Abstract | CrossRef Full Text | Google Scholar

Heinz, S. K., Mazzucco, R., and Dieckmann, U. (2009). Speciation and the evolution of dispersal along environmental gradients. Evol. Ecol. 23, 53–70.

Google Scholar

Horner-Devine, M. C., and Bohannan, B. J. M. (2006). Phylogenetic clustering and overdispersion in bacterial communities. Ecology 87, S100–S108.

Google Scholar

Ito, H. C., and Dieckmann, U. (2007). A new mechanism for recurrent adaptive Radiations. Am. Nat. 170, E96–E111.

Google Scholar

Kembel, S. W., and Hubbell, S. P. (2006). The phylogenetic structure of a neotropical forest tree community. Ecology 87, S86–S99.

Google Scholar

Kraft, N. J. B., and Ackerly, D. D. (2010). Functional trait and phylogenetic tests of community assembly across spatial scales in an Amazonian forest. Ecol. Monogr. 80, 401–422.

Google Scholar

Kraft, N. J., Cornwell, W. K., Webb, C. O., and Ackerly, D. D. (2007). Trait evolution, community assembly, and the phylogenetic structure of ecological communities. Am. Nat. 170, 271–283.

Google Scholar

Leprieur, F., Albouy, C., De Bortoli, J., Cowman, P. F., Bellwood, D. R., and Mouillot, D. (2012). Quantifying phylogenetic beta diversity: Distinguishing between “true” turnover of lineages and phylogenetic diversity gradients. PLoS One 7:e42760. doi: 10.1371/journal.pone.0042760

PubMed Abstract | CrossRef Full Text | Google Scholar

Mammola, S., Arnedo, M. A., Fišer, C., Cardoso, P., Dejanaz, A. J., and Isaia, M. (2020). Environmental filtering and convergent evolution determine the ecological specialization of subterranean spiders. Funct. Ecol. 34, 1064–1077.

Google Scholar

Meszéna, G., Czibula, I., and Geritz, S. (1997). Adaptive dynamics in a 2-patch environment: A toy model for allopatric and parapatric speciation. J. Biol. Syst. 5, 265–284.

Google Scholar

Metz, J. A. J., Nisbet, R. M., and Geritz, S. A. H. (1992). How should we define ‘fitness’ for general ecological scenarios? Trends Ecol. Evol. 7, 198–202.

Google Scholar

Metz, J. A. J., Geritz, S. A., Meszéna, G., Jacobs, F. J., and Van Heerwaarden, J. (1996). “Adaptive dynamics, a geometrical study of the consequences of nearly faithful reproduction,” in Stochastic and spatial structures of dynamical systems, eds S. J. Van Strien and S. M. Verduyn Lunel (Amsterdam: North-Holland), 183–231.

Google Scholar

Morlon, H., Schwilk, D. W., Bryant, J. A., Marquet, P. A., Rebelo, A. G., Tauss, C., et al. (2011). Spatial patterns of phylogenetic diversity. Ecol. Lett. 14, 141–149.

Google Scholar

Parmentier, I., Rejou-Mechain, M., Chave, J., Vleminckx, J., Thomas, D. W., Kenfack, D., et al. (2014). Prevalence of phylogenetic clustering at multiple scales in an African rain forest tree community. J. Ecol. 102, 1008–1016.

Google Scholar

Pausas, J. G., and Verdú, M. (2010). The jungle of methods for evaluating phenotypic and phylogenetic structure of communities. BioScience 60, 614–625.

Google Scholar

Pontarp, M. (2021). Ecological opportunity and adaptive radiations reveal eco-evolutionary perspectives on community structure in competitive communities. Sci. Rep. 11:19560. doi: 10.1038/s41598-021-98842-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Pontarp, M., and Wiens, J. J. (2017). The origin of species richness patterns along environmental gradients: Uniting explanations based on time, diversification rate and carrying capacity. J. Biogeogr. 44, 722–735.

Google Scholar

Pontarp, M., Bunnefeld, L., Cabral, J. S., Etienne, R. S., Fritz, S. A., Gillespie, R., et al. (2019). The latitudinal diversity gradient: Novel understanding through mechanistic eco-evolutionary models. Trends Ecol. Evol. 34, 211–223. doi: 10.1016/j.tree.2018.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Pontarp, M., Ripa, J., and Lundberg, P. (2012). On the origin of phylogenetic structure in competitive metacommunities. Evol. Ecol. Res. 14, 269–284.

Google Scholar

Pontarp, M., Ripa, J., and Lundberg, P. (2015). The biogeography of adaptive radiations and the geographic overlap of sister species. Am. Nat. 186, 565–581. doi: 10.1086/683260

PubMed Abstract | CrossRef Full Text | Google Scholar

Rainey, P. B., and Travisano, M. (1998). Adaptive radiation in a heterogeneous environment. Nature 394, 69–72. doi: 10.1038/27900

PubMed Abstract | CrossRef Full Text | Google Scholar

Saladin, B., Thuiller, W., Graham, C. H., Lavergne, S., Maiorano, L., Salamin, N., et al. (2019). Environment and evolutionary history shape phylogenetic turnover in European tetrapods. Nat. Commun. 10:249. doi: 10.1038/s41467-018-08232-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Si, X., Cadotte, M. W., Davies, T. J., Antonelli, A., Ding, P., Svenning, J. C., et al. (2022). Phylogenetic and functional clustering illustrate the roles of adaptive radiation and dispersal filtering in jointly shaping late−Quaternary mammal assemblages on oceanic islands. Ecol. Lett. 25, 1250–1262. doi: 10.1111/ele.13997

PubMed Abstract | CrossRef Full Text | Google Scholar

Swenson, N. G. (2011). Phylogenetic beta diversity metrics, trait evolution and inferring the functional beta diversity of communities. PLoS One 6:e21264. doi: 10.1371/journal.pone.0021264

PubMed Abstract | CrossRef Full Text | Google Scholar

Swenson, N. G., Erickson, D. L., Mi, X., Bourg, N. A., Forero-Montaña, J., Ge, X., et al. (2012). Phylogenetic and functional alpha and beta diversity in temperate and tropical tree communities. Ecology 93, S112–S125. doi: 10.1007/s00248-009-9574-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Vellend, M. (2010). Conceptual synthesis in community ecology. Q. Rev. Biol. 85, 183–206.

Google Scholar

Webb, C. O., Ackerly, D. D., McPeek, M. A., and Donoghue, M. J. (2002). Phylogenies and community ecology. Annu. Rev. Ecol. Syst. 33, 475–505.

Google Scholar

Weinstein, B. G., Tinoco, B., Parra, J. L., Brown, L. M., McGuire, J. A., Gary Stiles, F., et al. (2014). Taxonomic, phylogenetic, and trait beta diversity in South American hummingbirds. Am. Nat. 184, 211–224. doi: 10.1086/676991

PubMed Abstract | CrossRef Full Text | Google Scholar