
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol. , 25 November 2022
Sec. Behavioral and Evolutionary Ecology
Volume 10 - 2022 | https://doi.org/10.3389/fevo.2022.1002475
Although mixed mating systems involving both selfing and outcrossing are fairly common in hermaphrodites, the mechanisms maintaining mixed mating are still unknown in many cases. In some species, individuals that have not yet found a mating partner delay self-fertilization for some time. This “waiting time” to selfing (WT) can exhibit heritable variation between individuals and is subject to two opposing selection pressures: waiting longer increases the density-dependent probability to encounter a mate within that time and thereby the chance to avoid inbreeding depression (ID) in offspring, but also increases the risk of dying before reproduction. It has long been hypothesized that fluctuations in population density and thus mate availability can lead to stable intermediate WTs, but to our knowledge there are so far no quantitative models that also take into account the joint evolutionary dynamics of ID. We use an individual-based model and a mathematical approximation to explore how delayed selfing evolves in response to density and density fluctuations. We find that at high density, when individuals meet often, WT evolution is dominated by genetic drift; at intermediate densities, strong ID causes WT to increase; and at low densities, ID is purged and WT approaches zero. Positive feedback loops drive the system to either complete selfing or complete outcrossing. Fluctuating density can slow down convergence to these alternative stable states. However, mixed mating, in the sense of either a stable polymorphism in WT, or stable intermediate waiting times, was never observed. Thus, additional factors need to be explored to explain the persistence of delayed selfing.
In many animal and plant species, successful reproduction requires encountering a mating partner or successful transfer of pollen, which can be difficult at low population or pollinator density. Under these conditions, having an alternative reproduction mechanism such as self-fertilization (selfing) is advantageous (Goodwillie et al., 2005; Jarne and Auld, 2006; Barrett, 2016). Facultative selfing can be realized through so-called “delayed selfing”. Here, individuals only begin to self after a certain waiting time (WT) has passed without encountering another individual to outcross with. At intermediate WT, delayed selfing leads to a mixed mating system where individuals or populations produce a proportion of offspring though selfing. Such mixed mating systems with delayed selfing are present in many animal and plant species (Goodwillie et al., 2005; Jarne and Auld, 2006). For example, Ramm et al. (2012) observed the existence of a highly variable and heritable WT in Macrostomum hystrix flatworms. Similarly, in the freshwater snail Physa acuta there is substantial heritable variation among families for age at first reproduction in isolated individuals (i.e., WT, Escobar et al., 2007). This suggests that WTs to selfing have the potential to evolve over time. Other examples of species that express such a WT to selfing are the sea slug Alderia willowi (Smolensky et al., 2009), the cestode Schistocephalus solidus (Schjørring, 2004, but see Schärer and Wedekind, 1999), the androdioecious clam shrimp Eulimnadia texana (Weeks and Zucker, 1999), and the plants Collinsia verna and Linaria cavanillesii (Kalisz et al., 2004; Voillemot et al., 2019, for a detailed list of species and taxa see Goodwillie and Weber, 2018).
Selection on WTs is thought to be density-dependent. When density is low, selfing grants reproductive assurance (Baker, 1955; Theologidis et al., 2014; Barrett, 2016), on top of its transmission advantage which arises because two gene copies are passed on to selfed offspring compared to just one for outcrossed offspring (Fisher, 1941). However, selfed offspring may suffer from inbreeding depression (ID), causing high juvenile mortality, reduced fertility and reduced lifespan; selfing avoidance may thus increase fitness when mating partners are abundant (Charlesworth and Charlesworth, 1998; Jarne et al., 2000; Ramey et al., 2000; O'Grady et al., 2006; Escobar et al., 2007; Roman and Darling, 2007; Dlugosch and Parker, 2008; Charlesworth and Willis, 2009; Ramm et al., 2012). In nature, population density and thus the availability of mating partners fluctuates over time, for example because of disturbances, predator-prey interactions or seasonality (Sassaman, 1989). Delayed selfing might be considered a “best-of-both-worlds” mechanism. On the one hand, individuals can benefit from the advantages of outcrossing if mating partners (and pollinators) are available. Examples of these benefits are the creation of new allele combinations and the protection against the consequences of recessive deleterious mutations. On the other hand, delayed selfing provides reproductive assurance when mating partners or pollinators are limiting (Goodwillie et al., 2005; Coates et al., 2006; Ramm et al., 2015; Barrett, 2016; Goodwillie and Weber, 2018). Here, we explore the hypothesis that mate or pollen limitation, and in particular an environment with variable mate or pollinator availability, can maintain stable mixed mating systems via delayed selfing (Schemske and Lande, 1985) and potentially even heritable variation among individuals in their WTs. This is a long-standing hypothesis, that, however, still lacks support (as reviewed by Goodwillie and Weber, 2018). General models for evolution under fluctuating selection pressures have shown that it can depend on the details of the ecological and evolutionary scenario whether fluctuating selection leads to a monomorphic population either for an intermediate or an extreme trait or to stable genetic polymorphism (Svardal et al., 2015; Wittmann et al., 2017; Liu et al., 2019). For example, a stable polymorphism is more likely when the environments at different times are sufficiently different and it is not possible for a genotype to perform well under all conditions (Svardal et al., 2015). For evolution of delayed selfing, this has not been explored in depth so far. Theoretical work on the topic has so far assumed either constant inbreeding depression, or abundant outcrossing opportunities. We summarize this work in the following paragraphs.
On the one hand, the effect of (variable) mate limitation on the evolution of selfing rates and selfing WTs has been studied assuming that inbreeding depression is constant over time and the same for all individuals in the population. Under these circumstances, selfing at the end of life is expected to evolve if life expectancy is predictable and delayed selfing is risk-free (Lloyd, 1979; Schoen and Brown, 1991; Morgan et al., 2005). Mixed mating systems can then still result because only those individuals (or flowers or ovules) that failed to outcross self-fertilize instead. If lifespan is not completely predictable, a trade-off emerges between the potential benefits of outcrossed offspring and the risk of dying before a mating partner is encountered (Snell and Aarssen, 2005; Goodwillie and Weber, 2018). This trade-off leads to an increase in optimal waiting time with increasing inbreeding depression, in particular when resources not used while waiting can be invested to disproportionately increase the number of future offspring (Tsitrone et al., 2003a). Alternatively, stable intermediate selfing rates can emerge when fertilization probability decreases with the number of ovules targeted for outcrossing (Huang and Burd, 2019). Similarly, fluctuations in pollen (mate) availability due to external factors such as changing environments can also lead to intermediate selfing rates (Morgan and Wilson, 2005; Cheptou and Schoen, 2007), while fluctuating mate availability due to reduced population size as a consequence of inbreeding depression appears unlikely to lead to intermediate selfing rates (Cheptou, 2004; Morgan et al., 2005). Variation in number of pollinators under a trade off between offspring quality and quantity can also lead to stable intermediate waiting times (Sakai and Ishii, 1999). However, it is currently unclear whether these findings of stable intermediate WTs in different scenarios with constant inbreeding depression persist if the dynamic feedback between selfing rates and inbreeding depression, as well as inbreeding levels differing between individuals, is taken into account.
On the other hand, models that have focused on the joint evolution of mating system and inbreeding depression tend to assume the absence of pollen or mate finding limitations. In these cases, populations will frequently evolve to be monomorphic, either exclusively outcrossing or selfing. The environmental conditions and/or coincidence determine which of these states is reached. If both mating strategies are stable and the outcome just depends on initial conditions and chance effects, we speak of alternative stable states (Lande and Schemske, 1985). The reason for a polymorphism not emerging is that when ID is determined by recessive deleterious alleles, under frequent outcrossing, genetic drift causes these alleles to rise in frequency, making selfing more and more costly, whereas under frequent selfing these alleles are purged such that the cost of selfing decreases (Lande and Schemske, 1985; Bataillon and Kirkpatrick, 2000). A reversion to outcrossing from established selfing may then occur only when ID is very strong, especially when there are advantages to selfing besides the transmission advantage (Igic and Busch, 2013), such as re-absorption of non-fertilized eggs. However, even without mate limitation, intermediate selfing rates can sometimes be stable under evolving inbreeding depression, e.g., through trade-offs between offspring quantity and quality (Goodwillie et al., 2005), local spatial structure (Ronfort and Couvet, 1995), or if inbreeding depression is due to general heterozygote advantage instead of recessive deleterious alleles (Campbell, 1986).
To our knowledge, there is so far only one study (Porcher and Lande, 2005) on the density-dependent evolution of selfing that includes both mate limitation and the dynamics of inbreeding depression through purging and accumulation of deleterious alleles. Here, stable high selfing rates (but still below 1) were achieved under a combination of pollen limitation and pollen discounting, where less pollen is exported under increased selfing (Porcher and Lande, 2005). They do however assume the degree of mate-limitation to be constant. We are not aware of any study on the joint evolution of selfing and inbreeding depression under fluctuating mate finding/pollination conditions. Thus it is still unclear whether (externally fluctuating) mate limitation can maintain mixed mating systems or even individual variation in selfing WTs when the joint dynamics of inbreeding depression are taken into account. In this study, we therefore attempt to fill this gap. An additional aspect largely missing from the literature so far, and which we therefore also sought to incorporate into our model, is that individuals with a short WT tend to reproduce early and therefore also produce grand-offspring earlier, shortening their generation time. This means that even if they have lower lifetime reproductive success, they might still leave more descendants per unit time while minimizing the risk of death before reproduction (Hallam and Levin, 1986; Kot, 2012).
To study the joint evolution of WTs and inbreeding depression under constant or fluctuating population density, we build and analyse an individual-based simulation model. This modeling approach is ideally suited to track the complex dynamics of inbreeding depression via a multi-locus model while allowing for individual variation in mating system parameters. The model is inspired by the reproductive biology of the free-living flatworm M. hystrix, but is applicable more generally to animals and plants with delayed selfing determined by a WT trait. We first study the evolution of WTs under constant density. For a simplified version of this model, we also develop an analytical approximation. We then include density fluctuations and again evaluate whether WTs evolve to extreme or intermediate values and whether heritable variation in WTs can be maintained, as observed in species such as M. hystrix (Ramm et al., 2012), P. acuta (Jarne et al., 2000), and Clarkia xantiana (Briscoe Runquist et al., 2017).
The individual-based model is stochastic and operates in discrete time with overlapping generations. Each individual has a diploid genome that determines WT to selfing and, at separate loci, may also carry recessive deleterious mutations that influence offspring viability. In each time unit, which can be interpreted as a day, first potential changes in density are executed by altering the size of the habitat. After that, the model evaluates which individuals die. Then the survivors produce eggs and encounter a mating partner with a probability that depends on the current density. After that, reproduction via outcrossing, selfing or use of stored sperm from previous matings takes place and offspring viability is determined. In the following sections, we describe each of these processes in detail.
The number of individuals, N, is variable, but is kept close to a carrying capacity of K = 200 individuals, as described below. This carrying capacity was chosen for computational efficiency, but the main results were robust against small changes in K (see Supplementary Figures 14, 15) and exploratory analyses with K = 1, 000 gave very similar results (not shown).
The habitat has no particular spatial structure and the habitat area, g2, determines the probability of encountering a mate as described below. We use g as habitat size parameter. To evaluate the effect of density and density fluctuations on the evolution of WT, we manipulate the habitat size rather than the population size, in order to keep the amount of genetic drift constant. Note that this assumption is not unrealistic for some flatworm species, whose habitat size may strongly vary with the amount of rainfall (see Sassaman, 1989). In the Supplementary material, we additionally explore a model version with fluctuating population size in a habitat of constant size (Supplementary Figure 11).
Each day, individuals die with probability d = 0.01, representing baseline mortality. Lifespan of individuals that have survived the recruitment phase (see below) is therefore geometrically distributed with mean days.
Each individual produces c = 1 eggs per day, which are stored until the next reproductive event and then released. More generally, c can also be interpreted as resources stored for future reproduction. There are three ways to fertilize eggs: (1) outcrossing with a partner, (2) using sperm from a previous selfing or outcrossing event, and (3) selfing when time since last sperm exchange (through outcrossing or selfing), or since birth for first reproduction, exceeds WT. In each reproduction phase, first each of the possible pairs of individuals independently meet with probability . Meeting events are executed in random order and an individual can mate with multiple partners. Second, all individuals who have no sperm stored and have not received sperm for longer than their individual WT, self-fertilize. Thus, individuals with longer WTs could go through phases without reproduction, even after having outcrossed or selfed before, because waiting time is reset when selfing as well as when outcrossing. Finally, individuals who have sperm stored from a previous outcrossing or selfing event use that sperm to fertilize any eggs they may have. Since the model was inspired by flatworms, we assumed that sperm only lasted for o = 10 days (Peters and Michiles, 1996; Ramm et al., 2015).
Whenever an individual has access to sperm, it releases all its stored eggs. This means other selfing or sperm usage opportunities during the same time step become obsolete, but individuals can transfer sperm and fertilize their partner's eggs in multiple outcrossing events. Sperm is always replaced by that of the most recent reproductive event. In the model this is represented by the fact that stored sperm is always replaced when outcrossing. Moreover individuals will not attempt selfing while having outcrossed sperm stored.
To model density-dependent limits on reproduction, each egg initially has the same chance of surviving, which is calculated by , where K is the carrying capacity, N the population size, and C is the total number of eggs laid by all individuals reproducing on that day. Surviving eggs are then determined via drawing survival from a Bernoulli distribution. When the population exceeds carrying capacity, no eggs survive until population size decreases below K.
Individuals are diploid, and we assume no linkage between loci. There are two types of loci: W = 5 loci that determine WT to selfing and I = 20 loci that can carry deleterious alleles and may cause ID. Sensitivity of the results to these choices is explored in Supplementary Section 11. Each offspring receives for each locus one allele from each parent (or in the case of selfing, two from the same parent, with the alleles being chosen independently).
The alleles at the waiting-time loci represent WT relative to the average life span and are encoded by positive real numbers. When an offspring is created, mutations occur. Each allele value is multiplied by a random number independently drawn from a Gamma distribution with mean 1 and standard deviation uw = 0.05 (shape = 400, scale = 0.0025). We did extensive checks to confirm that this mutation procedure introduces no bias to the trait value (Supplementary Figure 19). Assuming that the loci act additively, the average allele value across all loci represents an individual's genotypic value for WT. This genotypic value can then be converted to the actual WT by multiplying it by the expected lifespan . For example, an individual with an average allele value above 1 waits longer than an expected lifespan before starting to self.
For each inbreeding-depression locus, there are v = 10 alleles: a wild-type allele w and v−1 = 9 alleles, x1, …, x9, that are deleterious when homozygous. Mutations happen with a probability ui = 0.03 per allele copy in each new offspring and change an allele with equal probability to any of the other v−1 alleles. There are therefore four genotype classes for each inbreeding-depression locus: ww (both wildtype), wxi (wildtype and any deleterious allele), xixj (two different deleterious alleles, i≠j), and xixi (two copies of the same deleterious allele); the first three genotypes have no negative effect on fitness, while the last one affects fitness by a factor 1−s, where s = 0.8 is the selection coefficient. Biologically, this corresponds to each deleterious allele at a given locus causing a different problem, but the other allele being able to compensate for this. The loci then act multiplicatively, so that offspring survival is determined by (1−s)χ, and χ is the number of xixi-loci homozygous for a recessive deleterious mutation. Note that such a model with multiple alleles per locus at relatively few loci can also be seen as an approximation for a model with more loci with two alleles per locus that would need longer simulation run times.
The starting population consists of N0 = K = 200 individuals. Individuals start out with a time since last reproduction of zero. The number of initially stored eggs is drawn from a Poisson distribution with a mean of 10% of the average life span (i.e., 10) for each individual. For WT in the initial population, first the genotypic values, i.e., average allele values, are determined. These values are chosen to range in evenly spaced steps from 0 to 1 across individuals. For each individual, all allele values are simply set to its genotypic value. This procedure was chosen to ensure high genetic variation across individuals in the initial population. At each ID locus, each individual in the starting population carries two copies of the wildtype allele. The final “equilibrium” frequency of deleterious mutations depends on many factors such as the selfing frequency (Lande and Schemske, 1985), which results from a combination of mate availability, WTs, purging and the feedback of ID. The frequency of deleterious alleles stabilized after ca. 10,000 days, depending on density (Supplementary Figure 6).
First, we ran the model with various constant habitat sizes g in order to understand the effect of density on WT and ID. To investigate the effect of density fluctuations, we then changed habitat size g over time using a step function. This meant that habitat size alternated between two values, with each stably persisting for timescales corresponding to multiple generations at a time (i.e., hundreds or thousands of days, Supplementary Figure 1). We also checked scenarios with stochastic density patterns (Supplementary Figure 20).
Populations could in principle go extinct, but under the default conditions this was so rare that we did not observe a single case in our simulation studies. In other scenarios, such as with constant inbreeding depression (Figure 5), or random parameter conditions (Supplementary Figure 16), this happened more commonly. In these cases, we used only the surviving replicates for calculating means and standard deviations of waiting time and inbreeding depression.
The parameter values for our default scenario are given in Table 1. To assess model robustness, we ran a set of additional scenarios, with each parameter altered by ±5%. Additionally, we confirmed the robustness of our results by randomly drawing parameter values (Supplementary Table 1), and checked whether populations had approached stable intermediate WT by altering WT after 30,000 days and checking whether average WT would return to its initial state (see Supplementary Section 11, Supplementary Figures 16–18 for results).
The model was implemented in R 3.5.1 (R Core Team, 2020).
To gain a first understanding of the conditions leading to the evolution of higher or lower WTs, and specify conditions for the individual-based model, we analyzed a simplified continuous-time version of the model (Figure 1, see Supplementary Section 2 for details). Mathematical approximations were constructed with the help of Mathematica (Wolfram Research, Inc., 2021). In brief, time to first meeting TM and time to death TD are exponentially distributed with , and , where θ is the rate of meeting conspecifics (if θ is small it corresponds approximately to the probability to meet at least 1 conspecific per day), which depends on population size and habitat size, and d is the death rate. Population size N, habitat size g, and therefore density, are assumed to be constant for the mathematical approximation. We additionally assumed that individuals switch from selfing to outcrossing when meeting another individual, but never switch back to selfing after receiving outcrossed sperm. Sperm, once received, lasts for the entire lifespan of an individual. Offspring resulting from selfing are multiplied by two because of the automatic transmission advantage of selfing, but have reduced viability z < 1 due to ID, which we assumed constant. Outcrossed offspring are never affected by ID. There was no feedback from ID to population density.
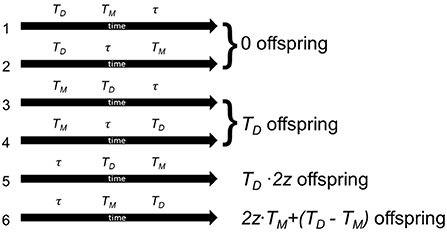
Figure 1. Possible life histories in the simplified model with their corresponding lifetime number of viable offspring. TD is the time of death, TM time to first meeting, τ is the waiting time, at which an individual will start selfing, and z the viability of selfed offspring. In the first two cases (1 and 2), an individual dies before getting the chance to reproduce. In the next two cases (3 and 4), the individual never selfed, because it met a mating partner early. It releases all of its eggs as outcrossed eggs without inbreeding depression. Case 5 represents a case where an individual selfs at time τ, and then dies before meeting a mating partner. All its offspring are affected by inbreeding depression, but it was able to lay all its eggs. Finally, in case 6, the individual started selfing after time τ, but later met a mating partner. It therefore released all its eggs until time TM as selfed progeny that suffers from inbreeding depression, but then can release the rest as outcrossed eggs that are not affected by inbreeding depression. This figure does not include the number of offspring gained from the mating partners' eggs, x.
This leads to several possible life trajectories (Figure 1): either the individual dies before reproducing (0 offspring, cases 1 and 2), or the individual outcrosses, then dies (number of offspring proportional to life span, cases 3 and 4), or the individual selfs then dies (number of offspring proportional to lifespan, but proportional loss due to inbreeding, case 5), or the individual selfs, then outcrosses and then dies (selfed portion of offspring with reduced survival due to inbreeding, case 6).
We followed an approach very similar to that by Tsitrone et al. (2003a) and integrated over all possible times of death and meeting to obtain the expected lifetime number of viable offspring (see Supplementary Section 2 for details) as a function of WT τ:
Here, x is the expected number of offspring generated via fertilizing the eggs of other individuals, which just depends on encounters but is independent of the individual's selfing WT. x does depend on average waiting time in the generation, but since we here assume that it is the same for all individuals at a given time, this will not affect the selection pressure on WT.
One main difference of our approach compared to Tsitrone et al. (2003a) is that they assume that time spent waiting affects resource allocation, growth, and future reproduction, whereas we do not assume such effects.
To study the direction of selection, we take the fitness gradient, that is, the derivative of fitness with respect to WT:
Since the exponential and WT (τ) are always positive, the direction of selection depends on θ−2z·(d+θ). These terms only depend on the set parameters and not on the state of the system, in particular not on the average waiting time. If this term is positive, i.e., if the meeting rate is above a critical value , then there is selection toward increased WTs, and WTs are expected to increase to infinity. If the meeting rate is below , selection acts to reduce WTs and WTs are expected to converge to zero. Examples of fitness gradients under different conditions can be seen in Figure 2. Note that when z>0.5 the fitness gradient will always be negative and if we let the meeting probability go to infinity, we can neglect 2z·d and the direction of selection depends on the term 1 − 2z. So we recover the classical result that selfing is favored and WT decreases if the viability of selfed offspring is above 0.5 under high density conditions. Without inbreeding depression (z = 1), the fitness gradient is always negative and waiting time would be expected to decrease to zero.
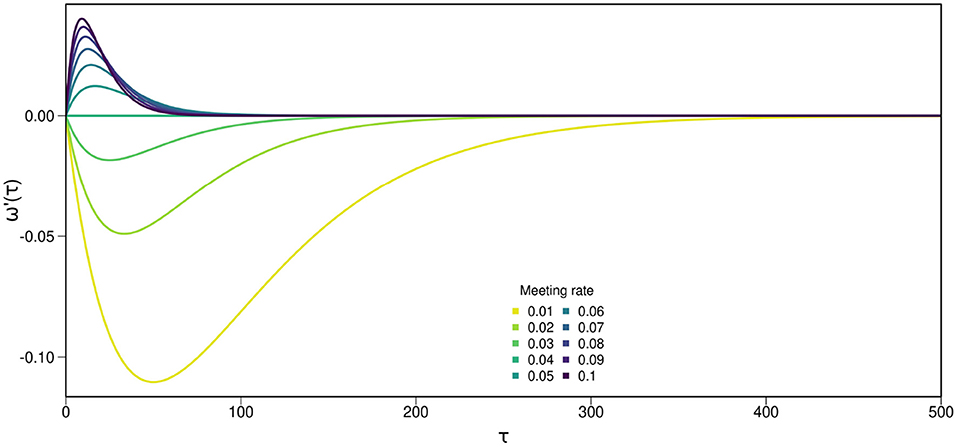
Figure 2. Results from the mathematical approximation, a simplification of the main individual-based model designed to clarify conditions which may favor long or short WTs. Effects of WT (τ) on the fitness derivative (ω′(τ)), calculated from Equation (2), under different mate encounter rates θ. This mathematical approximation illustrates that fitness ω(τ) is highest at either θ = 0 when mate availability is low or τ = ∞ at high mate availability. The critical meeting probability for the parameters we used is θ = 0.04. Assumptions are exponentially distributed time of death and time of first meeting, acquired sperm can be used for the rest of an individual's life, individuals will never self after having outcrossed, outcrossed sperm is used if present, and ID is constant. In this example, viability of selfed offspring z = 0.4 and probability of death d = 0.01.
In conclusion, if meeting rate, ID, and/or average lifespan are low, WT will evolve toward zero, and individuals will tend to immediately self. Meanwhile, high rates of meeting other individuals, strong ID or very long lifespans may lead to selfing avoidance, namely an infinite WT. In natural scenarios, this may lead to losing the ability to outcross or self, respectively. These results therefore suggest that with constant meeting rate, a population with a range of intermediate WTs to selfing cannot be explained. The simplified assumptions of the mathematical model, however, ignore several aspects of the system, such as purging, or the advantage of shorter generation times through earlier reproduction. Moreover, it does not include changes in density that cause θ to vary between being above or below the threshold. To incorporate these aspects and gain a fuller understanding of the system, including these processes, we now analyse the individual-based model.
We began by exploring how WT evolves under constant density. As in the mathematical approximation (see Section 2.8), the evolution of WT to selfing in the individual-based model depended on meeting probability, as determined by the habitat size g (Figure 3). In an alternative model run, we altered carrying capacity K instead of habitat size, so that density was determined by population size (Supplementary Figure 11) and there were potential effects of small population size such as drift, and reduced standing genetic variation. There were no qualitative differences in WT evolution between the two approaches for manipulating density. In both cases we observed three distinct scenarios at low, intermediate and high density.
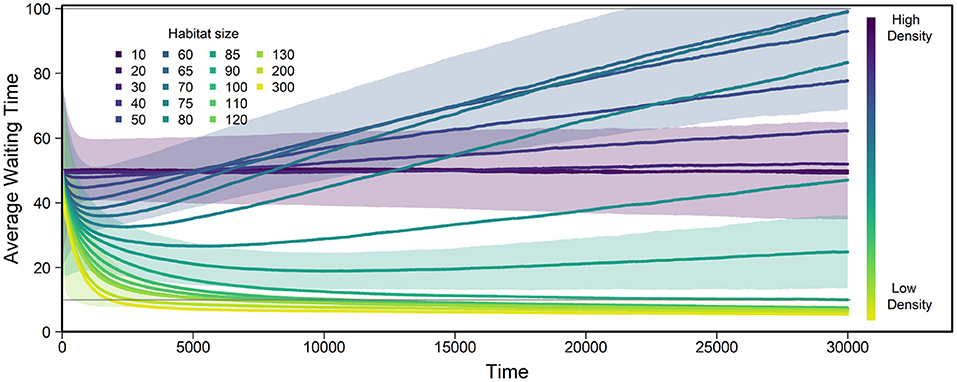
Figure 3. Evolution of average WT over all individuals and replicates using the default parameters described in Table 1 and various habitat sizes g. The color bar shows how g relates to density, e.g., lower values of g indicate higher density. Number of replicates = 1,000. Generations overlap, but average lifespan is 100 days, meaning the graph shows approximately 300 life spans. At low densities (yellow), average WT decreases, at intermediate densities (teal/blue) it increases, while it stays approximately constant on average for high densities (indigo/purple). The gray horizontal lines indicates the sperm storage duration (10), and average lifespan (100), below and above which we expect selection to weaken. Shaded areas show standard deviations across replicates for habitat sizes 10, 60, 85, and 130.
At low density, i.e., in large habitats, average WT decreases over time, converging toward zero or a small non-zero WT below the sperm storage time such that individuals start selfing as soon as they run out of stored sperm. In such large habitats, individuals are relatively unlikely to ever meet a mating partner (e.g., probability to ever encounter a potential mating partner being 0.33 for g = 200, continuous-time approximation in Supplementary Figure 2, Supplementary Equation 6). Without sperm and/or egg storage, WT always approaches zero at low density (Supplementary Figure 3).
At intermediate density, average WT increases over time. Under these conditions, individuals are likely to meet a mating partner within their lifetime (e.g., with probability 0.8 for g = 70, and 0.75 for g = 80; Supplementary Figure 2, continuous-time approximation). Importantly, in accordance with the mathematical approximation, no stable intermediate WT is reached. When WT increases above lifespan, selection decreases until average WTs drift at high values (see Supplementary Figure 5 for long-term behavior). Note that for some densities, average waiting times first decrease and then increase, but this transient behavior strongly depends on the arbitrarily chosen initial conditions.
At high density, i.e., in small habitats, WTs averaged over replicates remain constant over time. However, variation between replicates is high (as shown by areas in Figure 3), which indicates WTs being strongly driven by drift. Individuals here have essentially unlimited access to mating partners and individuals typically meet multiple potential mating partners each day. Accordingly, the proportion and number of offspring actually produced by selfing is close to zero (e.g., at g = 10, the proportion of offspring generated by selfing among all replicates over the course of the entire simulation is 1.92·10−7). Even if selection in principle favors infinite WTs, the selection pressure will be very weak because the trait itself is rarely expressed.
The rate of change in average WT varies with population density (Figure 3), which indicates that the strength of selection differs between densities. Low density affected average WT much faster than high density. The major reason for this is that while ID that leads to selfing avoidance at high densities requires the accumulation of deleterious mutations through time, a lack of mating partners is experienced immediately at low density.
Results from the robustness analysis where each parameter was varied by ±5% of its default value (Table 1) suggest that small changes in parameters cause no major changes in average WT at the end of the simulation (Supplementary Figure 14). We also checked what would happen if selfed sperm was never replaced by outcrossed sperm, or only with a 50% chance (Supplementary Figure 4). Under these alternative sperm competition scenarios results changed quantitatively, but not qualitatively.
We next examined the implications of waiting-time evolution for the frequency of deleterious alleles and thus ID. The frequency of deleterious recessive alleles declines with habitat size (Figure 4), which is expected if in large habitats there is more selfing and thus increased exposure of the ID loci to selection (Lande and Schemske, 1985). The transition from densities where deleterious alleles can spread through the population to those where strong selection effectively removes them nearly immediately is quite rapid (see also Supplementary Figure 6). Even when selection is strong, however, the total frequency of wildtype alleles only becomes 0.927 (with deleterious alleles persisting at frequency 0.073, because of mutation-selection balance; this means each deleterious allele has a frequency of 0.0081 on average).
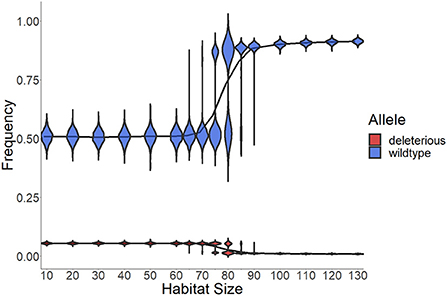
Figure 4. Frequency of wildtype and deleterious alleles at the end of the simulation. All 9 types of deleterious alleles (red) are summarized to average frequency of each mutation, therefore showing the frequency one individual mutation will have. The line should help understand the probability that a partner an individual met carries the same mutation as itself. Lines show the average frequencies of all (1,000) replicates over the entire simulation time. Violin areas indicate the distribution of allele frequencies among replicates. At low densities (large habitat size g), the frequency of wildtype alleles (blue) is high. This is because at low density selfing happens more frequently, and deleterious alleles are purged. Data from the same simulation shown in Figure 3, therefore using default parameters as shown in Table 1, and various habitat sizes g, with 1,000 replicates. The frequencies of the underlying genotypes are shown in Supplementary Figure 7, and the changes in wildtype frequency over time in Supplementary Figure 6.
In an altered model run, with only two alleles per locus determining ID (one wildtype and one deleterious rather than the nine in Figure 4), we found that the resulting allele frequency of the one deleterious allele was smaller (0.065) than the allele frequency of any specific deleterious variant in the case of 9 alleles. Thus with 9 deleterious alleles, it is less likely to find a partner with the same variant when outcrossing and the fitness difference between outcrossing and selfing was larger. In the case with just one deleterious allele, this difference was apparently not large enough for selfing avoidance to evolve (Supplementary Figure 13). To find out how strong selection against selfing needs to be in order for outcrossing to be favored, we ran additional simulations with fixed mortality rates for selfed offspring and no mortality in mated offspring (Figure 5). The fixed mortality rates for selfed offspring required to drive populations toward outcrossing, i.e., increased WTs, differs between densities and is higher than 50% for most densities shown here. In our mathematical approximation we also see a density dependence of required inbreeding depression for fixation of outcrossing, with the required inbreeding depression always above 0.5 and approaching 0.5 as θ → ∞. As we only explored a limited set of densities, there might be other densities that represent this boundary better than those chosen by us. This may explain why we could not find increasing WTs with only two variants at each locus, i.e., with just one deleterious allele (Supplementary Figure 13), as in this case even outcrossed offspring die more often with decreasing wildtype frequency and the difference in viability between outcrossed and selfed offspring is not as large as with multiple deleterious alleles per locus.
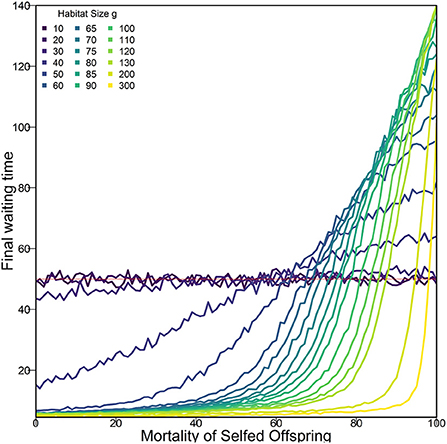
Figure 5. Average final (last day) WT with fixed mortality of selfed offspring after 30,000 days (number of days used in Figure 3). The dark (purple) lines indicate habitat size g where WT evolved due to drift alone. This line remains close to 50 (marked by red line), independently of mortality of selfed offspring. Therefore, the point where this line is crossed marks the minimum ID needed to achieve an increase in WT within this number of days for a given density. Simulations used default parameters as shown in Table 1 except offspring viability for selfing and outcrossing was not determined by genes. Each datapoint represents one set of 300 replicates (except for g =300 and Mortality = 100, where only 175 populations persisted 30,000 days) with a given habitat size g and mortality of selfed offspring.
The magnitude of variance in individual WT (Figure 6A) was largely driven by the magnitude of WT itself, which is expected because of the multiplicative mutation process. We therefore used the coefficient of variation (CV) as a more meaningful measure for comparison. The CV was calculated across the individuals within a population and then averaged over replicates. The CV is highest at intermediate densities and lowest for densities where selection favored short WTs, i.e., at large habitat sizes (Figure 6B). At high densities (small habitat size), the CV is intermediate.
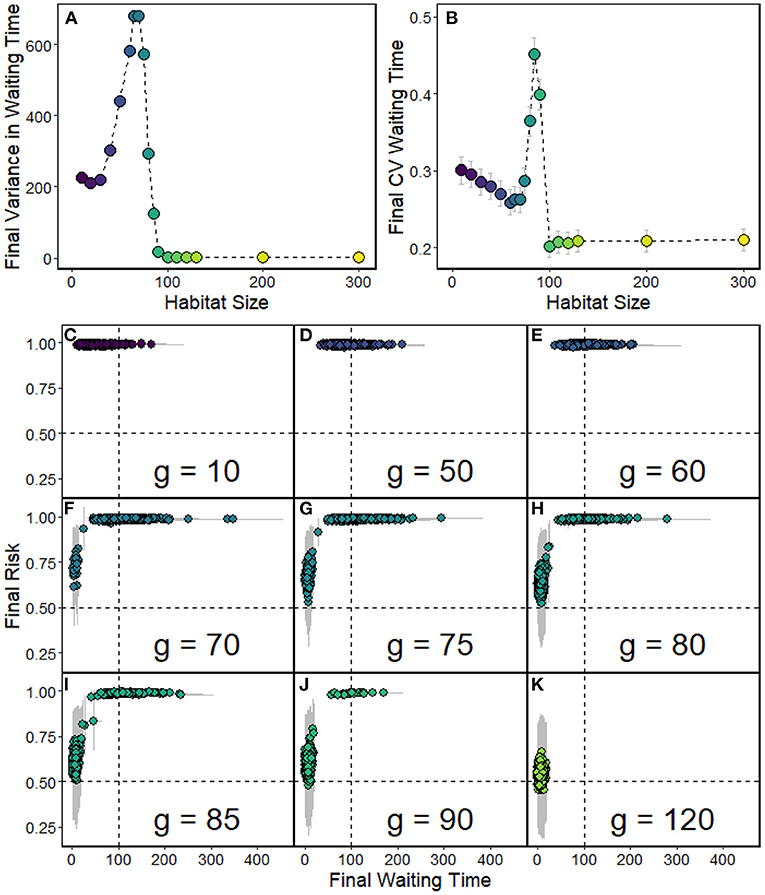
Figure 6. Variation in WT. Data from the same simulation shown in Figure 3, therefore using default parameters as shown in Table 1, and various habitat sizes g, number of replicates = 1,000. (A) Average variance in WT within replicates. (B) Average coefficient of variation (CV) in WT within replicates. (C–K) Points show the average WT in the final (last day) population plotted against average individual risk r, which is the probability for selfed offspring of an individual dying of ID. Each point represents one replicate (note that many points overlap). The gray bars represent within-replicate standard deviations for both x and y-range. Each panel shows a different habitat size g.
Populations with long final waiting times were typically characterized by a low viability of selfed offspring (Figures 6C–K). We measured this as the average individual risk r that an offspring resulting from selfing by a given parent dies due to ID:
Where nxixi is the number of loci that are homozygous for one of the deleterious mutant alleles in the parent, nxixj is the number of loci that carry two different deleterious mutations, and nwxi is the number of loci which carry one wildtype and one deleterious allele. Loci of the type xixi will always produce the genotype xixi in selfed offspring. The combination of xixj produces offspring that is homozygous for one of the deleterious alleles with probability 0.5 when selfing. For loci with genotype wxi, the probability of generating offspring with genotype xixi is 0.25 when selfing. Each homozygous deleterious locus then decreases the chance that offspring survives and acts multiplicatively with the other loci. Frequencies of genotypes can be found in Supplementary Figure 7.
At low habitat sizes, individual risk is high for almost all replicates, while WT varies across replicates (Figures 6C–K). The longest waiting times are achieved at intermediate habitat size (here, for example, g = 75, and g = 80), where selfing avoidance has evolved. At large habitat sizes, in contrast, most deleterious alleles cannot spread through the population: individual risk is therefore low, as is the WT. For a range of intermediate habitat sizes between these extremes, however, both possible outcomes occur in different replicates. Some populations evolve toward high individual risk with long WTs, whereas others exhibit low individual risk and short WT. The larger the habitat is (i.e., the lower the density), the larger the proportion of replicates that follow the latter trajectory.
The apparent increase in average WT at intermediate densities is caused by a subset of the trajectories evolving toward infinity, while those that are evolving toward the alternative stable state at zero have already reached this boundary value (Supplementary Figure 8). Accordingly, also the variance in waiting time keeps increasing in these cases, although the CV seems to level off (Supplementary Figure 9).
Finally, we explored how fluctuating density impacts the mean and variance of WT. Results for simulations with density fluctuations where g alternated between 70 (high density, chance to encounter a mating partner within lifespan is 80.4%) and 300 (low density, chance to encounter a mating partner within lifespan is 18.2%) are shown in Figure 7. In these scenarios, there are long-term trends in WT. Evolution toward zero WT appears to be faster than evolution toward long WTs (see also Figure 3). Although WT decreases under low density and increases under high density, we found no conditions with perfect balance between these. The coefficient of variation of WT becomes even smaller under fluctuating density than under constant density, as can be seen in Figure 7B. Just as for constant density, we altered all parameters by 5%, which revealed no unexpected or strong influence of any parameter (see Supplementary Figure 15). The ability to store sperm for longer made populations wait longer. Similarly, increases in parameters such as the mutation rate on inbreeding loci or number of inbreeding loci led to increased WT. Lastly, an increase in carrying capacity at a given habitat size led to larger densities and meeting probabilities and thus larger WTs.
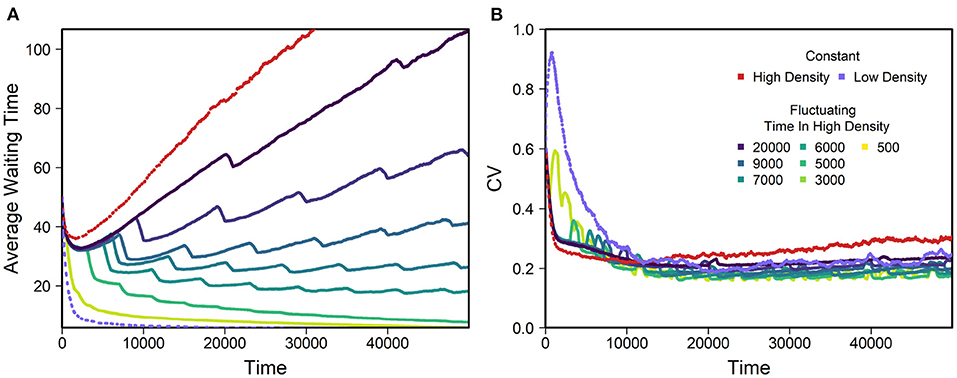
Figure 7. Example of average WT (A) and coefficient of variation (CV, B) for different patterns of density fluctuations. Average within replicate CV calculated over all replicates. The color-scaled lines show evolution for density fluctuations, while the light purple and red line show data for constant densities of g = 70 and g = 300, which were used as high and low densities. Fluctuations were assembled in a way that populations were exposed to high or low densities for a certain time, before switching to the other situation (example Supplementary Figure 1). All replicates spent 1,000 days in low density and the time in high density was as stated in the legend. All replicates began at high density. Default values as in Table 1 were used and different regimes of density fluctuations applied. We used 630 replicates per line.
In search of parameter combinations that might cause stable intermediate WTs, we ran 7,000 replicates where all parameters were randomly drawn (of which 6,577 could be evaluated, as the others went extinct). For the 10 parameter combinations where the result most strongly suggested stable intermediate WTs (for criteria see Supplementary Section 11, Supplementary Figure 16), 100 replicate simulations were run and we found that each replicate had a different WT by the end of the simulation (Supplementary Figure 17). We tested whether their final values represented a stable equilibrium value by adding or subtracting 10 days from WT after an initialization of 30,000 days and then continuing the simulation with this perturbed value to see if they would return to their state before perturbation (Supplementary Figure 18), which was not the case within the observed timeframe (20,000 days). This indicated that WT was driven by stochasticity, rather than selection. Closer inspection of these 10 scenarios revealed that the chosen parameter combinations had low mutation rates, indicating low evolvability.
We also explored the impact of fluctuations between three different densities in a regular or random pattern, but again did not observe stable variation or stable intermediate WTs (Supplementary Figure 20). In addition we set inbreeding depression to be constant, while density fluctuated. Stable variation or intermediate waiting times were not observed in this scenario (Supplementary Figure 21).
In summary, fluctuating densities may slow down the evolution of extreme WTs. However, we did not find evidence for fluctuating selection leading to stable intermediate WTs or a stable polymorphism in WTs in the long term.
Under constant density, we observed four different evolutionary scenarios but no stable polymorphisms for WT to selfing. First, at low density, WT decreases toward zero, as waiting is too risky. Second, at high density, mating opportunities are frequent and so WT is rarely expressed, such that trait changes are mostly due to genetic drift, which also explains the relatively high final variation in WT. Third, at intermediate densities, we find an increase in WT toward large values above average lifespan. Since meeting other individuals eventually is likely, waiting pays off. Finally, there are also intermediate densities at which two alternative stable states can occur: low WTs in combination with low (purged) ID, or high WTs combined with high frequency of deleterious alleles (and high ID in rare selfing events). Populations that experience the same starting conditions can potentially go either way, depending on stochasticity at the beginning of the simulation. Once a state has become established, however, it becomes hard to invade (see Figure 8). These results are consistent with classical predictions on positive feedback loops and alternative stable states in the evolution of selfing and inbreeding depression (Lande and Schemske, 1985; Kokko and Rankin, 2006; Lehtonen and Kokko, 2012).
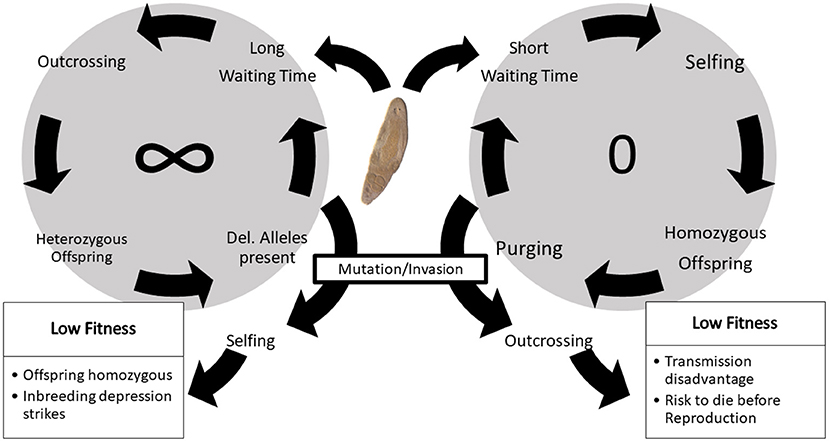
Figure 8. Positive feedback loops forming alternative stable states, and invasion scenarios. If most individuals have long WTs and reproduce mostly via outcrossing (left loop), deleterious alleles can drift to higher frequencies, making selfing more costly and leading to even higher WTs. A mutant with a short WT would have a large disadvantage in this system, as its offspring would likely be homozygous for some recessive deleterious mutations, and therefore express ID. Even an invader with a short WT and purged deleterious alleles would potentially have a disadvantage in later generations, because it might meet a resident and produce offspring with intermediate WTs and higher mutational load than the invader parent. At the other extreme, i.e., if most individuals have short WTs and self frequently (right loop), recessive deleterious mutations are purged out of the population and selfing no longer has a cost. A mutant with a long WT will then not have any advantage and only has a higher risk of death before reproduction. Moreover, it will have a transmission disadvantage because the long-waiting mutant shares the saved-up eggs with its partner, which will have already released most of its eggs in previous selfing events. The photo in the middle shows an individual of the flatworm Macrostomum hystrix. Photo by Schärer, available under: https://commons.wikimedia.org/wiki/File:Macrostomum_hystrix.jpg. licenced under https://creativecommons.org/licenses/by-sa/2.0/deed.en (CC BY-SA 2.0).
At constant density, we thus did not find evidence for a stable polymorphism of waiting times within populations. However, as long as WTs are below typical lifespans, a mixed mating system may still be observed. If mating partners are rare, some individuals will self and others will outcross, even without stable variation in WTs. The same individual might even self-fertilize and then later fertilize a mating partner's eggs. When individuals at low density occasionally meet, they will use the opportunity to outcross, even when their WT is low. In both cases, a mixed mating system is technically expressed. However, in the long run waiting time itself appears to always either approach zero or exceed the average lifespan. Natural populations might even completely lose the ability to self or outcross if there are costs to maintaining these mechanisms and they are no longer used. At relatively high densities, on the other hand, variation in WT is high through drift. This does not, however, lead to a mixed mating system, as the time between two outcrossing opportunities will be lower than any WT. We therefore conclude that in our model under constant density neither optimal intermediate WTs nor variation in WT within a population caused by anything other than stochasticity can be found. Although the population sizes we explored are relatively small, leading to a large contribution of genetic drift, we do not expect this result to change with higher values of N. With weaker genetic drift, the positive feedbacks underlying the alternative stable states of complete outcrossing or increased selfing get even stronger. Thus we would not expect any emergence of stable mixed mating systems in larger populations.
Our result that ID and density can drive a population to complete selfing or complete outcrossing supports previous work (Lande and Schemske, 1985; Jarne and Charlesworth, 1993). Furthermore, both our mathematical approximation Equations 1 and 2 and the simulations support the conclusion that ID needs to be relatively strong in order to systematically drive up WTs in the intermediate density scenarios (Supplementary Figure 5). As shown in Figure 6, at low densities the ID needed for an increase in WT is much larger than the 0.5 proposed by Lande and Schemske (1985). Critical levels of inbreeding depression above 0.5 have also been found in other models with mate or pollen limitation (Lloyd, 1979; Schoen et al., 1996). This makes sense because to favor outcrossing with mate limitation, inbreeding depression does not only need to balance out the transmission advantage of selfing but also those of reproductive assurance. Our results agrees with Tsitrone et al. (2003a) in that ID high enough to avoid selfing is hard to reach (Supplementary Figure 6, Figure 5). This effect depends on the number of deleterious alleles per locus, for example when there are only two alleles per locus, a frequency of entirely recessive lethal alleles of 50% can be purged down to 10% within three generations of selfing (Supplementary Figure 12). Charlesworth et al. (1990) describes a similar model where deleterious alleles occur as closely linked loci, which could be comparable to multiple allele variants.
A positive effect of the level of ID on WTs, where large ID is correlated with long WTs, has been shown in Physa acuta (Jarne et al., 2000; Weeks et al., 2001; Escobar et al., 2009; Noël et al., 2016, 2018), and Eulimnadia texana (Weeks et al., 1999, 2001). A recent study in plants (Brown and Kelly, 2019) has shown that ID caused by rare mutations can be severe enough to meet the criteria shown in Figure 5. It should, however, be mentioned that other studies in these species did not find links between ID and WT (Weeks et al., 1999; Escobar et al., 2007). Therefore, it is not certain whether WT was a consequence of ID or other factors, such as environmental stressors, that might potentially interact with ID (Armbruster and Reed, 2005; Cheptou and Schoen, 2007). Alternatively, density dependence of ID could lead to negative instead of positive feedback loops, as shown by Cheptou and Dieckmann (2002), who did however not include purging and mate limitation, which are driving factors for positive feedback loops in our model.
The threshold of an ID of 0.5 (Lande and Schemske, 1985) assumes that mating inflicts a cost on the egg donor, because half the offspring genes will come from the mating partner. Such a cost does not occur if reciprocal mating at the egg/ovule level is obligatory. This is because while each offspring only carries half the egg donors genes, both parents donate eggs, thereby producing twice as many descendants. Macrostromum hystrix, the species that initially inspired the model, as well as Physa acuta, and Eulimnadia texana, do not always perform obligatory reciprocal mating (Weeks and Zucker, 1999; Ramm et al., 2012; Noël et al., 2016). In practice, however, in M. hystrix, both mating partners can try to inseminate the other individual, so that mating often is reciprocal. In Physa acuta however individuals need to choose a role, often leading to conflict between mates (Noël et al., 2016). It should be noted that we do not take sex allocation and the cost of sex into account here, which could alter the results as they increase the ability to develop a selfing syndrome (Sicard and Lenhard, 2011).
Natural populations of species such as Macrostomum hystrix and Physa acuta can experience temporally strongly fluctuating environments (Sassaman, 1989; Henry et al., 2006). Density fluctuations due to changing habitat size, as in our simulation, likely also happen to natural populations, as for example ponds dry up or fill with rain water (Sassaman, 1989). Despite fluctuating density and the resulting fluctuations in selection on WT, we did not find patterns of fluctuations that would keep WTs at an intermediate level for a long time. Instead, WT evolved toward one of the two alternative endpoints, similar to the pattern described by Lande and Schemske (1985), although the approach to these endpoints took longer than under constant density (Figure 7). This was especially the case when mutation rates were low (Supplementary Figure 16). Similarly, intraspecific variation in WTs was initially lost more slowly under fluctuating density than under constant density, but in the long run fell to similar or lower values. Thus, contrary to the hypothesis that density fluctuations may promote mixed mating systems, we did not find evidence for permanently stable intermediate WTs or increased variation in WTs in our model. Our results appear to be robust to small parameter changes as well as randomly chosen combinations of parameters. Although this suggests that the absence of stable intermediate WTs and persistent variation in WTs might be a general result under our model assumptions, our parameter space was twelve-dimensional and so logistic constraints meant we could only explore a limited part of that parameter space. We did find cases of apparent stable intermediate WTs, which were, however, not repeatable (Supplementary Figure 17), or stable against perturbation (Supplementary Table 1), and therefore likely results of slow evolution (Supplementary Figure 16) and/or stochasticity. We cannot exclude the possibility that parameter combinations with stable intermediate WTs or stable variation in WTs exist somewhere in parameter space. However, if stable intermediate WTs only occurred for few very specific parameter combinations, the biological relevance in natural populations would be questionable.
We thus conclude that density fluctuations and the resulting fluctuating selection on selfing WTs are generally not a sufficient condition for the maintenance of mixed mating systems in hermaphrodites. This is opposed to the results by Sakai and Ishii (1999), Morgan and Wilson (2005), and Cheptou and Schoen (2007) who do find stable intermediate selfing rates with fluctuating pollination probabilities. However, they do not include purging and thus appear to have weaker positive feedbacks. In our model, it appears that the positive feedbacks due to the evolutionary dynamics of inbreeding depression have overpowered any negative feedbacks arising from fluctuating mate availabilities. This is similar to findings by Porcher et al. (2009) that purging and thus the feedback between selfing rates and inbreeding depression can prevent the maintenance of stable intermediate selfing rates under fluctuating selection coefficients of recessive deleterious mutations.
We speculate that sex allocation and the selfing syndrome (Noël et al., 2016) may further influence the strength of selection of WT in either direction. An alternative explanation for the maintenance of variation in WT is related to spatial structure (see also Ronfort and Couvet, 1995). In our simulations, we found different final WTs across replicates for the same density conditions. Migration between otherwise separated populations that have evolved in different directions could lead to intermediate WTs in their offspring and yield an opportunity to evolve in either direction again. In fact, flatworms collected at different sites show substantial differences in WT. While some seem to delay selfing (Ramm et al., 2012), flatworms from other locations do not (Giannakara and Ramm, 2020).
Another promising mechanism is pollen discounting or analogous mechanisms in animals, and allocation of resources toward (future) outcrossed reproduction (Gregorius, 1982; Holsinger, 1991; Tsitrone et al., 2003b; Goodwillie et al., 2005; Dlugosch and Parker, 2008; Briscoe Runquist et al., 2017; Huang and Burd, 2019; Voillemot et al., 2019). Resource allocation to future reproduction might be crucial for the emergence of intermediate WTs from a combination of density and ID (Tsitrone et al., 2003b). For example, Physa acuta uses life-history trade-offs to invest resources into growth instead of egg production (Tsitrone et al., 2003a). This mechanism leads to over-proportional gain in egg production for waiters, compared to the relatively equivalent output for waiters and non-waiters in our model. For plants, Huang and Burd (2019) similarly present an explanation for intermediate selfing rates, for the case that seed size can be adapted. Thereby offspring quality and quantity evolve in accordance with reproductive mode. Moreover, in their study, fertilization success differs between ovules. Similarly, avoiding hypodermic insemination, and the resulting cost of injury may be a reason to delay selfing (Smolensky et al., 2009). It should also be considered that a combination of multiple mechanisms can lead to a mixed mating system (Aanen and Hoekstra, 2007). All the studies mentioned here have in common that they find intermediate WTs when adding further life-history trade-offs and allocation of resources to the system. Our model in contrast was aimed specifically at the interplay of mate limitation and inbreeding depression, and therefore excluded such mechanisms.
Note that although our model is in part applicable to plants, some assumptions are specific to animals. For example, annual plants are not able to shorten their generation time through earlier reproduction. Plants may also depend on pollinators in addition to mating partners, which adds dynamics not represented in our model. Also, in our model individuals could store an indefinite number of eggs for indefinite amounts of time, and use stored sperm to fertilize eggs that are produced after mating. This is something that is not applicable to plants, as they cannot store pollen or ovules (but can potentially store resources) for an extended period, or even multiple seasons. If gametes predictably expired, or lost quality and viability over time, or if individuals could run out of physiological storage space, selfing might then be the only way to prevent wasting resources (Lloyd, 1979; Schoen and Brown, 1991; Morgan et al., 2005). Supplementary Figure 3 covers model behavior without the ability to store sperm, eggs, or both. However, also in this case, we did not observe stable mixed mating systems.
Using a stochastic individual-based simulation and mathematical approximations, we could show that WTs to selfing evolve to very small values at low density and to very large values at high density. At intermediate densities, we observed alternative stable states, but no stable polymorphism within populations. We did not find evidence that fluctuating population densities lead to maintenance of variation in WTs or stable intermediate WTs. Thus, our results question the hypothesis that density fluctuations can explain the maintenance of a mixed mating system. Variation could then only arise from either drift or variation in optimal time of reproduction. Not taking additional factors that would drive life-history evolution into account, evolution toward alternative stable states in different partially isolated subpopulations seem the most likely explanation of variation within a species.
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s. Supporting information containing further figures and simulation code files is provided as a supplement.
CB, MW, and SR designed the project and modeling framework. CB designed the computational framework, analyzed the data, and drafted the paper. SR provided insight and discussion on the empirical motivation for the project. KB improved computational efficiency of the code. MW supervised the project. All authors provided critical feedback and helped shape the research, analysis, and manuscript.
This research was partly funded by the German Research Foundation (DFG) as part of the SFB TRR 212 (NC3) - project numbers 316099922 and 396782288, who provided funds for the position of for KB. We acknowledge the financial support of the German Research Foundation (DFG) and the Open Access Publication Fund of Bielefeld University for the article processing charge.
We thank Hauke Schneider, who contributed to this work as a student assistant and the reviewers for their thoughtful comments. We would also like to thank the Theoretical Biology group, and in particular Matthias Spangenberg, for discussion and feedback on the project. Moreover, we are thankful for inspiring discussions with Hanna Kokko.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2022.1002475/full#supplementary-material
Aanen, D. K., and Hoekstra, R. F. (2007). “Why sex is good: on fungi and beyond,” in Sex in Fungi: Molecular Determination and Evolutionary Implications, eds J. Heitman, J. W. Kronstad, J. W. Taylor, and L. A. Casselton (Washington, DC: ASM Press), 527–534. doi: 10.1128/9781555815837.ch32
Armbruster, P., and Reed, D. H. (2005). Inbreeding depression in benign and stressful environments. Heredity 95, 235–242. doi: 10.1038/sj.hdy.6800721
Baker, H. G. (1955). Self-compatibility and establishment after 'long-distance' dispersal. Evolution 9, 347–349. doi: 10.1111/j.1558-5646.1955.tb01544.x
Barrett, P. H. (2016). The Works of Charles Darwin: Vol 25: The Effects of Cross and Self Fertilisation in the Vegetable Kingdom (1878). Routledge.
Bataillon, T., and Kirkpatrick, M. (2000). Inbreeding depression due to mildly deleterious mutations in finite populations: size does matter. Genet. Res. 75, 75–81. doi: 10.1017/S0016672399004048
Briscoe Runquist, R. D., Geber, M. A., Pickett-Leonard, M., and Moeller, D. A. (2017). Mating system evolution under strong pollen limitation: evidence of disruptive selection through male and female fitness in Clarkia xantiana. Am. Nat. 189, 549–563. doi: 10.1086/691192
Brown, K. E., and Kelly, J. K. (2019). Severe inbreeding depression is predicted by the “rare allele load” in Mimulus guttatus. Evolution 74, 587–596. doi: 10.1111/evo.13876
Campbell, R. (1986). The interdependence of mating structure and inbreeding depression. Theoret. Popul. Biol. 30, 232–244. doi: 10.1016/0040-5809(86)90035-3
Charlesworth, B., and Charlesworth, D. (1998). Some evolutionary consequences of deleterious mutations. Genetica 102/103, 3–19. doi: 10.1023/A:1017066304739
Charlesworth, D., Morgan, M. T., and Charlesworth, B. (1990). Inbreeding depression, genetic load and the evolution of outcrossing rates in a multilocus system with no linkage. Evolution 44, 1469–1489. doi: 10.1111/j.1558-5646.1990.tb03839.x
Charlesworth, D., and Willis, J. H. (2009). The genetics of inbreeding depression. Nat. Rev. Genet. 10, 783–796. doi: 10.1038/nrg2664
Cheptou, P.-O. (2004). Allee effect and self-fertilization in hermaphrodites: reproductive assurance in demographically stable populations. Evolution 58, 2613–2621. doi: 10.1111/j.0014-3820.2004.tb01615.x
Cheptou, P.-O., and Dieckmann, U. (2002). The evolution of self-fertilization in density-regulated populations. Proc. R. Soc. B 269, 1177–1186. doi: 10.1098/rspb.2002.1997
Cheptou, P.-O., and Schoen, D. J. (2007). Combining population genetics and demographical approaches in evolutionary studies of plant mating systems. Oikos 116, 271–279. doi: 10.1111/j.0030-1299.2007.14655.x
Coates, D. J., Tischler, G., and McComb, J. A. (2006). Genetic variation and the mating system in the rare Acacia sciophanes compared with its common sister species Acacia anfractuosa (Mimosaceae). Conserv. Genet. 7, 931–944. doi: 10.1007/s10592-006-9136-7
Dlugosch, K. M., and Parker, I. M. (2008). Invading populations of an ornamental shrub show rapid life history evolution despite genetic bottlenecks. Ecol. Lett. 11, 701–709. doi: 10.1111/j.1461-0248.2008.01181.x
Escobar, J. S., Epinat, G., Sarda, V., and David, P. (2007). No correlation between inbreeding depression and delayed selfing in the freshwater snail Physa acuta. Evolution 61, 2655–2670. doi: 10.1111/j.1558-5646.2007.00223.x
Escobar, J. S., Facon, B., Jarne, P., Goudet, J., and David, P. (2009). Correlated evolution of mating strategy and inbreeding depression within and among populations of the hermaphroditic snail Physa acuta. Evolution 63, 2790–2804. doi: 10.1111/j.1558-5646.2009.00760.x
Fisher, R. A. (1941). Average excess and average effect of a gene substitution. Ann. Eugenics 11, 53–63. doi: 10.1111/j.1469-1809.1941.tb02272.x
Giannakara, A., and Ramm, S. A. (2020). Evidence for inter-population variation in waiting times in a self-fertilizing flatworm. Invertebr. Reproduct. Dev. 16, 1–11. doi: 10.1080/07924259.2020.1732485
Goodwillie, C., Kalisz, S., and Eckert, C. G. (2005). The evolutionary enigma of mixed mating systems in plants: occurrence, theoretical explanations, and empirical evidence. Annu. Rev. Ecol. Evol. Syst. 36, 47–79. doi: 10.1146/annurev.ecolsys.36.091704.175539
Goodwillie, C., and Weber, J. J. (2018). The best of both worlds? A review of delayed selfing in flowering plants. Am. J. Bot. 105, 641–655. doi: 10.1002/ajb2.1045
Gregorius, H.-R. (1982). Selection in plant populations of effectively infinite size II. Protectedness of a biallelic polymorphism. J. Theoret. Biol. 96, 689–705. doi: 10.1016/0022-5193(82)90237-5
Hallam, T. G., and Levin, S. A., (eds.). (1986). Mathematical Ecology, Vol. 17. Berlin: Springer-Verlag. doi: 10.1007/978-3-642-69888-0
Henry, P.-Y., Vimond, L., Lenormand, T., and Jarne, P. (2006). Is delayed selfing adjusted to chemical cues of density in the freshwater snail Physa acuta? Oikos 112, 448–455. doi: 10.1111/j.0030-1299.2006.14269.x
Holsinger, K. E. (1991). Mass-action models of plant mating systems: the evolutionary stability of mixed mating systems. Am. Nat. 138, 606–622. doi: 10.1086/285237
Huang, Q., and Burd, M. (2019). The effect of pollen limitation on the evolution of mating system and seed size in hermaphroditic plants. Am. Nat. 193, 447–457. doi: 10.1086/701782
Igic, B., and Busch, J. W. (2013). Is self-fertilization an evolutionary dead end? N. Phytol. 198, 386–397. doi: 10.1111/nph.12182
Jarne, P., and Auld, J. R. (2006). Animals mix it up too: the distribution of self-fertilization among hermaphroditic animals. Evolution 60, 1816–1824. doi: 10.1111/j.0014-3820.2006.tb00525.x
Jarne, P., and Charlesworth, D. (1993). The evolution of the selfing rate in functionally hermaphrodite plants and animals. Annu. Rev. Ecol. Syst. 24, 441–466. doi: 10.1146/annurev.es.24.110193.002301
Jarne, P., Perdieu, M.-A., Pernot, A.-F., Delay, B., and David, P. (2000). The influence of self-fertilization and grouping on fitness attributes in the freshwater snail Physa acuta: population and individual inbreeding depression. J. Evol. Biol. 13, 645–655. doi: 10.1046/j.1420-9101.2000.00204.x
Kalisz, S., Vogler, D. W., and Hanley, K. M. (2004). Context-dependent autonomous self-fertilization yields reproductive assurance and mixed mating. Nature 430, 884–887. doi: 10.1038/nature02776
Kokko, H., and Rankin, D. J. (2006). Lonely hearts or sex in the city? Density-dependent effects in mating systems. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 361, 319–334. doi: 10.1098/rstb.2005.1784
Lande, R., and Schemske, D. W. (1985). The evolution of self-fertilization and inbreeding depression in plants I. Genetic models. Evolution 39, 24–40. doi: 10.1111/j.1558-5646.1985.tb04077.x
Lehtonen, J., and Kokko, H. (2012). Positive feedback and alternative stable states in inbreeding, cooperation, sex roles and other evolutionary processes. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 367, 211–221. doi: 10.1098/rstb.2011.0177
Liu, M., Rubenstein, D. R., Liu, W.-C., and Shen, S.-F. (2019). A continuum of biological adaptations to environmental fluctuation. Proceedings of the Royal Society. 286, 20191623. doi: 10.1098/rspb.2019.1623
Lloyd, D. G. (1979). Some reproductive factors affecting the selection of self-fertilization in plants. Am. Nat. 113, 67–79. doi: 10.1086/283365
Morgan, M. T., and Wilson, W. G. (2005). Self-fertilization and the escape from pollen limitation in variable pollination environments. Evolution 59, 1143–1148. doi: 10.1111/j.0014-3820.2005.tb01050.x
Morgan, M. T., Wilson, W. G., and Knight, T. M. (2005). Plant population dynamics, pollinator foraging, and the selection of self-fertilization. Am. Nat. 166, 169–183. doi: 10.1086/431317
Noël, E., Chemtob, Y., Janicke, T., Sarda, V., Pélissié, B., Jarne, P., et al. (2016). Reduced mate availability leads to evolution of self-fertilization and purging of inbreeding depression in a hermaphrodite. Evolution 70, 625–640. doi: 10.1111/evo.12886
Noël, E., Fruitet, E., Lelaurin, D., Bonel, N., Ségard, A., Sarda, V., et al. (2018). Sexual selection and inbreeding: two efficient ways to limit the accumulation of deleterious mutations. Evol. Lett. 3, 80–92. doi: 10.1002/evl3.93
O'Grady, J. J., Brook, B. W., Reed, D. H., Ballou, J. D., Tonkyn, D. W., and Frankham, R. (2006). Realistic levels of inbreeding depression strongly affect extinction risk in wild populations. Biol. Conserv. 133, 42–51. doi: 10.1016/j.biocon.2006.05.016
Peters, A., and Michiles, N. (1996). Do simultaneous hermaphrodites choose their mates? Effects of body size in a planarian flatworm. Freshw. Biol. 36, 623–630. doi: 10.1046/j.1365-2427.1996.00128.x
Porcher, E., Kelly, J. K., Cheptou, P.-O., Eckert, C. G., Johnston, M. O., and Kalisz, S. (2009). The genetic consequences of fluctuating inbreeding depression and the evolution of plant selfing rates. J. Evol. Biol. 22, 708–717. doi: 10.1111/j.1420-9101.2009.01705.x
Porcher, E., and Lande, R. (2005). The evolution of self-fertilization and inbreeding depression under pollen discounting and pollen limitation. J. Evol. Biol. 18, 497–508. doi: 10.1111/j.1420-9101.2005.00905.x,
R Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.
Ramey, R. R., Luikart, G., and Singer, F. J. (2000). Genetic bottlenecks resulting from restoration efforts: the case of bighorn sheep in badlands national park. Restorat. Ecol. 8, 85–90. doi: 10.1046/j.1526-100x.2000.80069.x
Ramm, S. A., Schlatter, A., Poirier, M., and Schärer, L. (2015). Hypodermic self-insemination as a reproductive assurance strategy. Proceedings of the Royal Society of Publishing B. 282, 1–6. doi: 10.1098/rspb.2015.0660
Ramm, S. A., Vizoso, D. B., and Schärer, L. (2012). Occurrence, costs and heritability of delayed selfing in a free-living flatworm. J. Evol. Biol. 25, 2559–2568. doi: 10.1111/jeb.12012
Roman, J., and Darling, J. A. (2007). Paradox lost: genetic diversity and the success of aquatic invasions. Trends Ecol. Evol. 22, 454–464. doi: 10.1016/j.tree.2007.07.002
Ronfort, J., and Couvet, D. (1995). A stochastic model of selection on selfing rates in structured populations. Genet. Res. 65, 209–222. doi: 10.1017/S0016672300033280
Sakai, S., and Ishii, H. S. (1999). Why be completely outcrossing? Evolutionarily stable outcrossing strategies in an environment where outcross-pollen availability is unpredictable. Evol. Ecol. Res. 1, 211–222.
Sassaman, C. (1989). Inbreeding and sex ratio variation in female-biased populations of a clam shrimp Eulimnadia texana. Bull. Mar. Sci. 45, 425–432.
Schärer, L., and Wedekind, C. (1999). Lifetime reproductive output in a hermaphrodite cestode when reproducing alone or in pairs: a time cost of pairing. Evol. Ecol. 13, 381–394. doi: 10.1023/A:1006789110502
Schemske, D. W., and Lande, R. (1985). The evolution of self-fertilization and inbreeding depression in plants II empirical observations. Evolution 39, 41–52. doi: 10.1111/j.1558-5646.1985.tb04078.x
Schjørring, S. (2004). Delayed selfing in relation to the availability of a mating partner in the cestode Schistocephalus solidusa. Evolution 58, 2591–2596. doi: 10.1111/j.0014-3820.2004.tb00887.x
Schoen, D. J., and Brown, A. H. D. (1991). Whole- and part-flower self-pollination in Glycine clandestina and G. argyrea and the evolution of autogamy. Evolution 45, 1651. doi: 10.2307/2409786
Schoen, D. J., Moran, M. T., and Bataillon, T. (1996). How does self-pollination evolve? Inferences from floral ecology and molecular genetic variation. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 351, 1281–1290. doi: 10.1098/rstb.1996.0111
Sicard, A., and Lenhard, M. (2011). The selfing syndrome: a model for studying the genetic and evolutionary basis of morphological adaptation in plants. Ann. Bot. 107, 1433–1443. doi: 10.1093/aob/mcr023
Smolensky, N., Romero, M. R., and Krug, P. J. (2009). Evidence for costs of mating and self-fertilization in a simultaneous hermaphrodite with hypodermic insemination, the opisthobranch Alderia willowi. Biol. Bull. 216, 188–199. doi: 10.1086/BBLv216n2p188
Snell, R., and Aarssen, L. W. (2005). Life history traits in selfing versus outcrossing annuals: exploring the 'time-limitation' hypothesis for the fitness benefit of self-pollination. BMC Ecol. 5, 2. doi: 10.1186/1472-6785-5-2
Svardal, H., Rueffler, C., and Hermisson, J. (2015). A general condition for adaptive genetic polymorphism in temporally and spatially heterogeneous environments. Theoret. Popul. Biol. 99, 76–97. doi: 10.1016/j.tpb.2014.11.002
Theologidis, I., Chelo, I. M., Goy, C., and Teotónio, H. (2014). “Reproductive assurance drives transitions to self-fertilization in experimental Caenorhabditis elegans,” in BMC Biology. doi: 10.1186/s12915-014-0093-1
Tsitrone, A., Duperron, S., and David, P. (2003a). Delayed selfing as an optimal mating strategy in preferentially outcrossing species: theoretical analysis of the optimal age at first reproduction in relation to mate availability. Am. Nat. 162, 318–331. doi: 10.1086/375542
Tsitrone, A., Jarne, P., and David, P. (2003b). Delayed selfing and resource reallocations in relation to mate availability in the freshwater snail Physa acuta. Am. Nat. 162, 474–488. doi: 10.1086/376889
Voillemot, M., Encinas-Viso, F., and Pannell, J. R. (2019). Data from: rapid loss of self-incompatibility in experimental populations of the perennial outcrossing plant Linaria cavanillesii. Evolution 73, 913–926. doi: 10.1111/evo.13721
Weeks, S. C., Crosser, B. R., and Gray, M. M. (2001). Relative fitness of two hermaphroditic mating types in the androdioecious clam shrimp, Eulimnadia texana. J. Evol. Biol. 14, 83–94. doi: 10.1046/j.1420-9101.2001.00251.x
Weeks, S. C., Marcus, V., and Crosser, B. R. (1999). Inbreeding depression in a self-compatible, androdiocious crustacean, Eulimnnadia texana. Evolution 53, 472–483. doi: 10.1111/j.1558-5646.1999.tb03782.x
Weeks, S. C., and Zucker, N. (1999). Rates of inbreeding in the androdioecious clam shrimp Eulimnadia texana. Can. J. Zool. 77, 1402–1408. doi: 10.1139/z99-103
Keywords: waiting time, density-dependent selection, inbreeding depression, purging, mating system, mate limitation, hermaphrodites, self-fertilization
Citation: Blüml C, Ramm SA, van Benthem KJ and Wittmann MJ (2022) Waiting for love but not forever: Modeling the evolution of waiting time to selfing in hermaphrodites. Front. Ecol. Evol. 10:1002475. doi: 10.3389/fevo.2022.1002475
Received: 25 July 2022; Accepted: 10 November 2022;
Published: 25 November 2022.
Edited by:
Francisco Garcia-Gonzalez, Doñana Biological Station (CSIC), SpainReviewed by:
Jonathan Henshaw, University of Freiburg, GermanyCopyright © 2022 Blüml, Ramm, van Benthem and Wittmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chantal Blüml, Q2hhbnRhbC5CbHVlbWxAdW5pLWJpZWxlZmVsZC5kZQ==
†ORCID: Chantal Blüml orcid.org/0000-0001-9752-2224
Steven A. Ramm orcid.org/0000-0001-7786-7364
Koen J. van Benthem orcid.org/0000-0002-3841-2110
Meike J. Wittmann orcid.org/0000-0002-7209-9172
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.