
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol. , 12 January 2022
Sec. Behavioral and Evolutionary Ecology
Volume 9 - 2021 | https://doi.org/10.3389/fevo.2021.825765
This article is part of the Research Topic Sensory Ecology of Phenotypic Plasticity: from Receptors via Modulators to Effectors View all 8 articles
Inducible defenses are a wide-spread defensive mechanism in Daphnia. For example, D. cucullata is known to form different adaptive morphologies under changing environmental conditions. In this species, predator presence elicits defensive helmets. Defended animals perform better and survive more frequently in predation attempts. Another peculiarity of D. cucullata is that they develop these defenses also in response to turbulence. The mechanisms that underly this defensive effect are so far unclear. Therefore, we investigated the three-dimensional morphology of the typical, the turbulence- and Chaoborus-exposed morph and analyzed their surface and volume alterations. We furthermore measured the swimming velocities of these morphs. With the determined shapes and the measured velocities, we simulated the drag force under different angles of attack and determined the energy necessary to move through the water. In the light of previous findings and hypotheses we here discuss biomechanical mechanisms that improve D. cucullata’s fitness in the investigated environments.
Predation is an almost omnipresent threat in ecosystems, but it varies in intensity (e.g., Volterra, 1926). Therefore, many species are phenotypically plastic and counter predators by inducible defenses (Tollrian and Harvell, 1999). Such inducible defenses are formed by many species of the genus Daphnia. Especially Daphnia cucullata, a common freshwater crustacean in European lakes, has been a textbook example of cyclomorphosis and phenotypic plasticity for decades (Woltereck, 1913; Jacobs, 1987; Lampert and Sommer, 1993; Laforsch and Tollrian, 2004c). Nowadays, the cyclomorphosis especially of helmets and crests in different Daphnia species is well-known and accepted as a phenotypically plastic trait in response to predators (Tollrian and Harvell, 1999; Weiss and Tollrian, 2018). Historically, the elicitor inducing the different morphs remained inconclusive for a long time (Wesenberg-Lund, 1900; Brooks, 1947, 1965; Jacobs, 1961, 1962). It had been hypothetically attributed to abiotic factors such as wind (and therefore water turbulence, Hrbáček, 1959) or temperature (Jacobs, 1961, 1967) and was hence thought to be a seasonal variation as observed in other species, e.g., the lepidopteran Araschnia levana with its spring and summer brood (Shapiro, 1976; Windig and Lammar, 1999).
Later publications showed that a morphological alteration could be observed in response to different independent cues, i.e., turbulence and predation. Invertebrate predators, such as the phantom midge larvae Chaoborus, induce defensive helmets increasing survival chances during predator presence (Laforsch and Tollrian, 2004c). Helmeted individuals are more frequently attacked, but evasion and escape efficiency were found strongly increased, weighing up the increased attack rate (Laforsch and Tollrian, 2004c). The protective effect of the helmet enabling prey evasion is however still unknown.
In response to fish, D. cucullata changes its morphology to a smaller and transparent body (Hrbáček, 1962). A behavioral alteration such as diel vertical migration has not been observed yet (Hrbáček, 1962; Lampert and Wolf, 1986; Tollrian, 1990; Laforsch and Tollrian, 2004c; Tollrian and Laforsch, 2006; Karpowicz et al., 2019). Intriguingly, helmets are also induced by turbulence, and also here it is still unknown why (Hrbáček, 1959; Laforsch and Tollrian, 2004b). Turbulence is discussed as an indicator of vertebrate predator presence, but also of wind as a measure for season (Laforsch and Tollrian, 2004b,c).
Different authors hypothesized that seasonal morphology, which reaches its maximum expression strength in summer and disappears in winter (Lampert and Wolf, 1986; Laforsch and Tollrian, 2004c), could also be correlated with water viscosity, as viscosity is a function of temperature (Reynolds, 1886). Hebert suggested that in higher viscosities more muscle force and accordingly more energy is necessary for locomotion (Hebert, 1978). The observed morphologies would therefore be a proxy for altered muscle position and size. He also suggested the helmets of Daphnia could be involved in gas exchange (Hebert, 1978). Jacobs moreover showed that helmeted Daphnia are more efficient swimmers than unhelmeted morphs (Jacobs, 1964).
In order to reveal the underlying mechanisms and explain the function of the observed behavioral and morphological alterations in D. cucullata, we analyzed the shape of animals exposed to turbulence and Chaoborus predation and compared them using Procrustes distance (Horstmann et al., 2018, 2021). We also examined their swimming velocities. Combining morphology and behavior, we calculated drag forces, the “friction” of D. cucullata in water, enabling to quantify their streamline properties. We calculated drag force with water impinging in the typical forward-movement angle and from beneath, resembling the sinking phases. We furthermore tested the influence of water temperature (and therefore water viscosity) on drag force. By this we approximated the costs and benefits of these alterations, governing their ecological effect.
D. cucullata clone TSBR, originating from Lake Thalersee (near Munich, Germany) were cultured in the department for several generations under laboratory conditions (16:8-h day-night cycle, 20°C ± 1°C. Animals were reared in 1 L glass beakers (J. Weck GmbH und Co. KG, Wehr-Öflingen, Germany) containing charcoal filtered tap water and were fed ad libitum with the green algae Tetradesmus obliquus. Culture beakers and beakers of the experiments were cleaned every other day and water was exchanged monthly. Chaoborus sp. larvae of the 4th instar were caught in the Botanical Gardens of the Ruhr-University Bochum and kept in 1.5 L glass beakers at 4°C in charcoal-filtered tap water.
Inductions were started with 5 female D. cucullata clone TSBR carrying offspring in the last embryonic stage, which is indicated by the occurrence of one black eye (Weiss et al., 2016), placed in 1 L glass beakers (J. Weck GmbH und Co. KG, Wehr-Öflingen, Germany). For predator exposure, we added 10 Chaoborus larvae and 100 juvenile D. cucullata TSBR and placed them into net cages prohibiting predation on the test animals (Laforsch and Tollrian, 2004b). After female mothers had released juveniles from the brood pouch, they were removed from the glass beakers.
D. cucullata was exposed to turbulence by placing individuals that bred the first clutch into 1 L glass beakers (J. Weck GmbH und Co., KG, Wehr-Öflingen, Germany). Turbulences were generated with the help of custom-made motor-driven rudders conducting three turns every 20 s (for reference see Laforsch and Tollrian, 2004b). After induction for 4 weeks, only animals that had just reached maturity were collected for analysis.
When animals reached the egg bearing instar, we determined swimming velocities in stagnant, kairmone-free medium, using a self-developed Tracking-System (Langer et al., 2021). For each treatment, we determined swimming velocities of animals (ntypical = 14, nChaoborus = 12, nturbulence = 14) over approximately 5 s at a frame rate of 30 fps (giving 150 measurements per individual) and a visual resolution of 1,920 × 1,080 pixel. The velocities per recording were pooled per animal, giving one average velocity per animal. Based on the parametric data set, we tested for statistical differences with an analysis of variance (ANOVA), and consecutively with a TukeyHSD-Post hoc-test in R (R Core Team, 2021).
Animals were fixed, stained and processed as described previously (Horstmann et al., 2018, 2021). In short, we fixed 10 animals per treatment with 4% formaldehyde diluted in PBS (pH 7.4, 0.1 M), dissected the antennae as they can be problematic during the confocal scanning, stained them with Congo red (Carl Roth GmbH + Co., KG, Karlsruhe, Germany) and scanned them with a confocal microscope (Leica TCS SP5II (Leica Microsystems, Wetzlar, Germany). We stitched image stacks of the specimens as they were often overarching the visual field of the microscope.
Three-dimensional meshes were extracted from the scans using MorphoGraphX (de Reuille et al., 2015). After projecting a grid onto the meshes using Blender (Blender, version 2.73, Blender Foundation, Blender Institute Amsterdam,1 2015), the resulting individual models consisting of comparable vertices were averaged to a single model per treatment, using an automated Matlab Script (Horstmann et al., 2018; Matlab R2014b, The Mathworks Inc., Natick, MA, 2015). With this script, we also determined displacement vectors between averaged models per treatment, i.e., vectors between respective vertices in the typical and altered morph models. We projected their length with color gradients onto the 3D surface reconstructions. Also, Wilcoxon-tests were calculated for the position of vertices in all three dimensions of space between specimens of the three treatments. To correct for error based on multiple testing with the FDR (false discovery rate)-analysis, we calculated q-values, which give a value that allows to evaluate the trustworthiness of each derived p-value (Storey and Tibshirani, 2003). These q-values are based on the false discovery rate, which is estimated based on the distribution of p-values of the conducted Wilcoxon tests. We define p-values smaller than 0.05 and q-values smaller than 0.01 at the same time as significant alteration, if q-values are larger than 0.01, we define it as statistical tendency. If p-values are larger than 0.05, we reject any statistical relevance.
The average 3D-models were used to calculate partial and full average Procrustes-distances between the treatments. Average Procrustes-distances give the sum of the distances of respective vertices after a Procrustes analysis normalized on the number of vertices. While partial Procrustes allows comparisons of form, including size effects and therefore allowing the alteration of form, full Procrustes compares shapes without influence by rotation, translation and scaling, enabling pure shape comparisons (Horstmann et al., 2021). These measures therefore enable to evaluate the degree of shape and form alterations between the morphs.
The reconstructed average body halves were then mirrored using Blender (Blender, version 2.73, Blender Foundation, Blender Institute Amsterdam, 2015; see text footnote 1) to create a full model of three morphs of the investigated species. Using GOM Inspect (GOM Software 2016, Hotfix 2, Rev. 96633, Build 2016-09-01, GOM GmbH, Braunschweig, Germany), the transitions remaining after the merging of the body halves were smoothed and holes closed, taking care not to alter the shape unnaturally.
Based on the full 3D models we also measured the surface area and the volume of the models of the respective morphs. These values can be measured in Blender using the “3D printing toolbox,”2 respectively, its “3D printing” functionality with the “Statistics” option.
In addition to this we calculated the alteration of the cross-sectional area in swimming direction, which we call the “shadow area,” measured with Photoshop (Photoshop CS6, Adobe Systems Software Ireland Limited, Dublin, Ireland) as pixel values on virtual photographs of the models taken at the same scale and at an angle of 40° (compare Scourfield, 1900). The so-called “angle of attack” is defined from 0° (water current from directly above) over 40° (from obliquely upwards and frontally) to 180° (from directly beneath), which resembles the angles during hop and sink movement.
The full models, excluding antennas, were exported as stl-files and imported in ANSYS ICEM CFD (ANSYS 2020 R1, ANSYS Inc., Canonsburg, PA, United States) to prepare a model of the animals in a virtual stream channel. For these models, a virtual fluid space was created and adjusted to the morphs’ size, making sure that it is large enough to observe water currents in front of the animals, around them and in their trailing (8 mm × 8 mm × 3 mm). Water temperature and viscosity was changed as needed. As in this approach it was only possible to simulate static objects, we did not virtually move the models through the water but rather let the water flow around them. The swimming velocities determined with the help of the 3D-Tracking System (Langer et al., 2021) were then applied on the different morphs with different angles. As angle for comparison we chose 40° (Scourfield, 1900), as this mimics a typical hop and sink movement, in which an upward and at the same time forward movement is conducted, with 5° prevalence for the upward movement. That allowed to calculate the drag in all spatial dimensions for the whole model automatically by the software.
We followed two approaches. First, we applied the velocity determined for the morph not exposed to turbulence or Chaoborus-larvae on all morphs. In a second comparison we applied the velocities determined for both treatments, respectively.
In addition to the comparison at a water temperature of 25°C, we calculated the simulations of the typical and turbulence exposed morph with a water temperature of 5°C and an accordingly higher water viscosity. In our analysis we altered the dynamic viscosity value from 0.0008899 Pa*s (25°C) to 0.0015187Pa*s (5°C). We both simulated with the swimming velocities of unexposed as well as turbulence exposed animals.
As the shape alterations of Daphnia have long been discussed as “Schwebefortsätze” (floating extensions, Woltereck, 1913; Jacobs, 1987), probably slowing down the sinking, we additionally measured the drag force while the water current impinges on the model directly from beneath (180°). For this comparison we used the velocity measured for the typical morph, as sinking is a passive movement and different velocities would render the results inconclusive.
Based on the these parameters, we calculate the drag coefficient with a typical velocity as
with the drag force FD, the density of the fluid ρ, the cross-sectional area A and the squared movement velocity v2.
We determined average velocities of 7.2 ± 5.6 mm/s for the typical morph, 3.6 ± 2.1 mm/s for the Chaoborus-defended morph and 4.7 ± 2.2 mm/s for the turbulence-exposed morph. The velocity of the Chaoborus-exposed morph was therefore reduced by 50%, the velocity of the turbulence-exposed morph reduced by 35%. We found significant differences between the swimming velocities of D. cucullata in the typical morph and the Chaoborus-exposed morph [ANOVA, nctrl = 12, nturbulence = 14, nChaoborus = 14, F(2, 37) = 3.269, p = 0.049, pairwise t-test, p = 0.047, Figure 1]. No significant differences were found between the typical and turbulence exposed morph [ANOVA, nctrl = 12, nturbulence = 14, nChaoborus = 14, F(2, 37) = 3.269, p = 0.049, pairwise t-test, p = 0.192], as well as between the two exposed morphs [ANOVA, nctrl = 12, nturbulence = 14, nChaoborus = 14, F(2, 37) = 3.269, p = 0.049, pairwise t-test, p = 0.729].
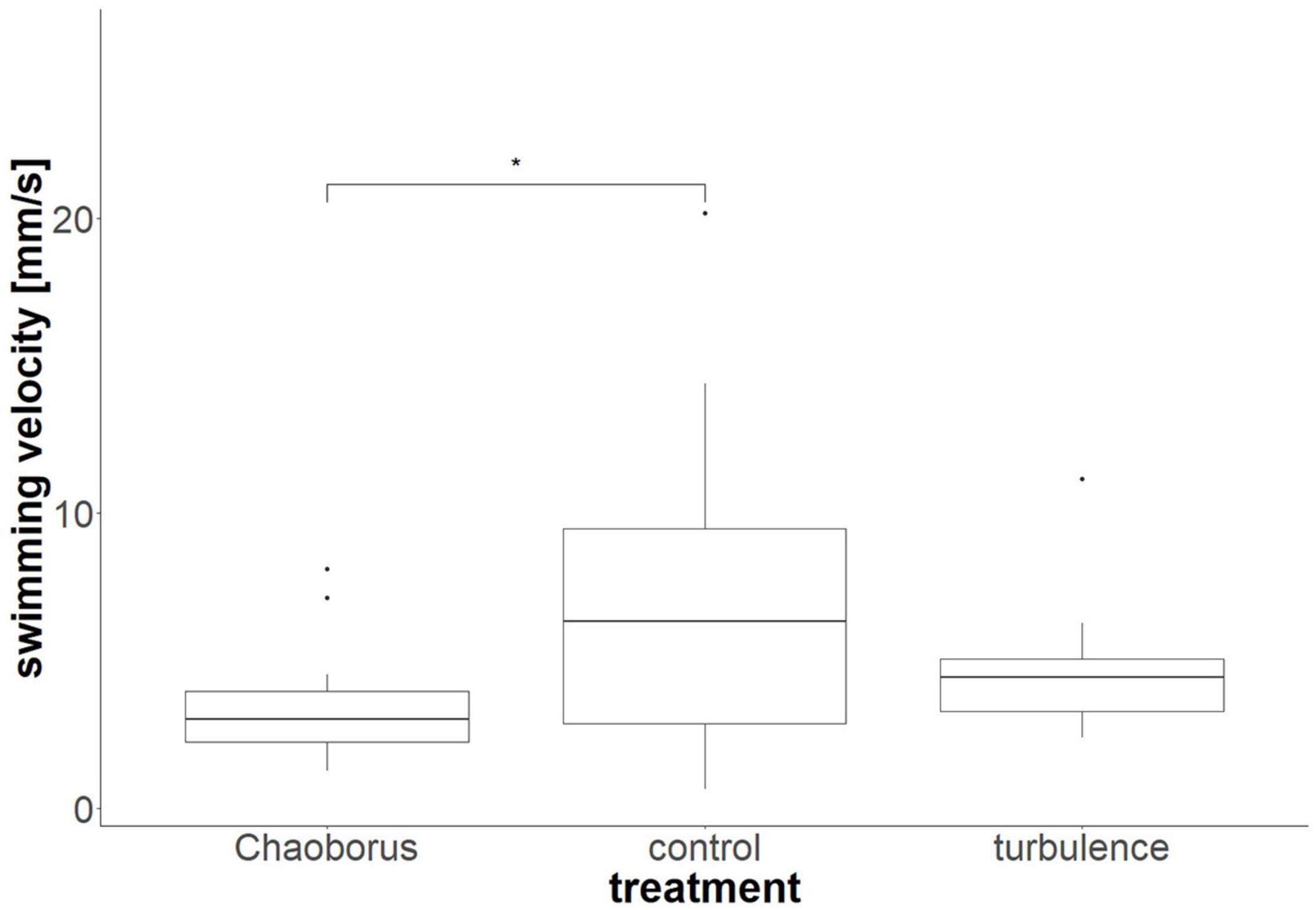
Figure 1. Swimming velocities of D. cucullata. Depicted are the swimming velocities of the typical morph, the morph in the presence of Chaoborus, as well as in the presence of turbulence. *p < 0.05.
Typically-shaped and Chaoborus-exposed animals of the species D. cucullata appear rather indifferent in most regions (Figures 2A,B), but the overall deformation plot shows differences in the helmet as well as the tail spine (Figure 2C, shades of red, > 50 μm).
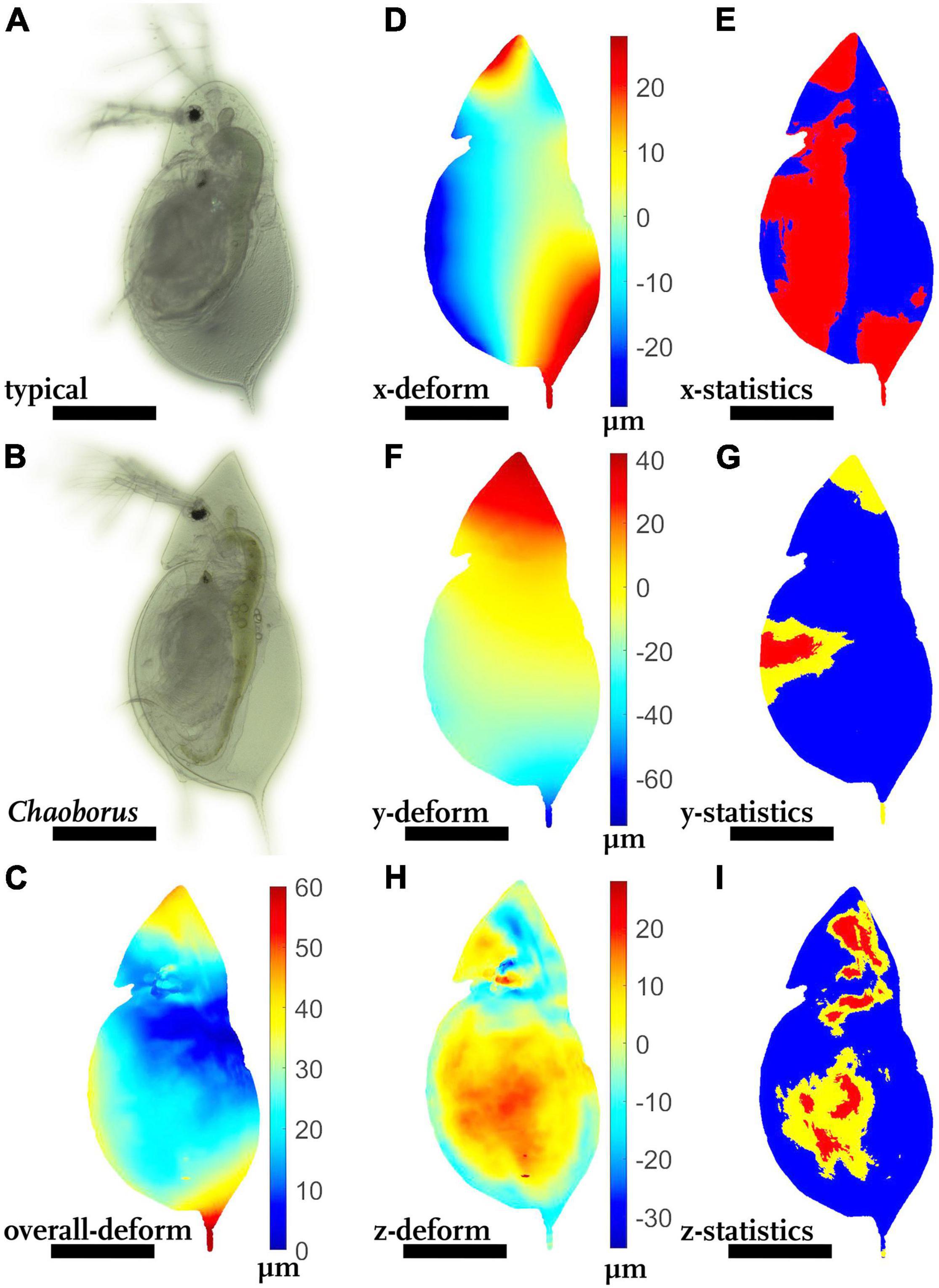
Figure 2. Morphological alterations of Chaoborus-exposed Daphnia cucullata. (A) D. cucullata, reared in the absence of Chaoborus-kairomones. (B) D. cucullata, reared in the presence of predator kairomones. (C) Overall deformation plot showing the comparison of the unexposed and Chaoborus-exposed D. cucullata model. Plotted are the vector lengths (μm) between the respective vertices on the unexposed and the Chaoborus-exposed D. cucullata model (blue 0 μm displacement, dark red 60 μm displacement). (D,F,H) Shades of blue colors represent alterations in negative direction, while shades of red display shifts in the positive direction. Shades of yellow to white indicate little or no shifts along the respective axis. (E,G,I) P-values lower than 0.05 displayed in yellow, regions supported by q-values lower than 0.05 are colored red. (D) Vertex displacements (μm) in x-(dorso-ventral) direction. (E) Wilcoxon test p-values and FDR-analysis q-values for each vertex position of the x-direction. (F) Vertex displacements in y-(longitudinal) direction (μm). (G) Wilcoxon test p-values and FDR-analysis q-values for each vertex position of the y-direction. (H) Vertex displacements in z-(lateral) direction (μm). (I) Wilcoxon test p-values and FDR-analysis q-values for each vertex position of the z-direction. nundefended = 10, ndefended = 10. All scale bars: 600 μm.
In general, animals are slightly bulkier in dorso-ventral direction (Figure 2D, shades of red at dorsal body parts, shades of blue at ventral regions), which is supported with a tendency mainly for the ventral body parts (Figure 2E, p < 0.05, q > 0.01).
In longitudinal direction, the defended morph is elongated by up to 40 μm (Figure 2F, shades of red at the head, shades of blue in the tail spine region), but statistically only supported by a tendency (Figure 2G, p < 0.05, q > 0.01). Shifts at the central ventral margin are statistically supported with a tendency as well (p < 0.05, q > 0.01).
In lateral dimension the head capsule is 10–20 μm slimmer (Figure 2H, shades of blue at the head), while the carapace is laterally 10–20 μm wider (Figure 2I, shades of red on the carapace). Both alterations of lateral width are rather diffuse instead of strong local variations and were statistically supported with a tendency (p < 0.05, q > 0.01).
In terms of Procrustes distance, the models differed on average 26.4 μm (12.6 μm, Table 1).

Table 1. Average partial and full Procrustes-distances between the different morphs of Daphnia cucullata.
Turbulence-exposed D. cucullata display an elongated helmet (Figures 3A,B). The most strongly altered region is the helmet and the rostrum (Figure 3C, shades of red, > 120 μm).
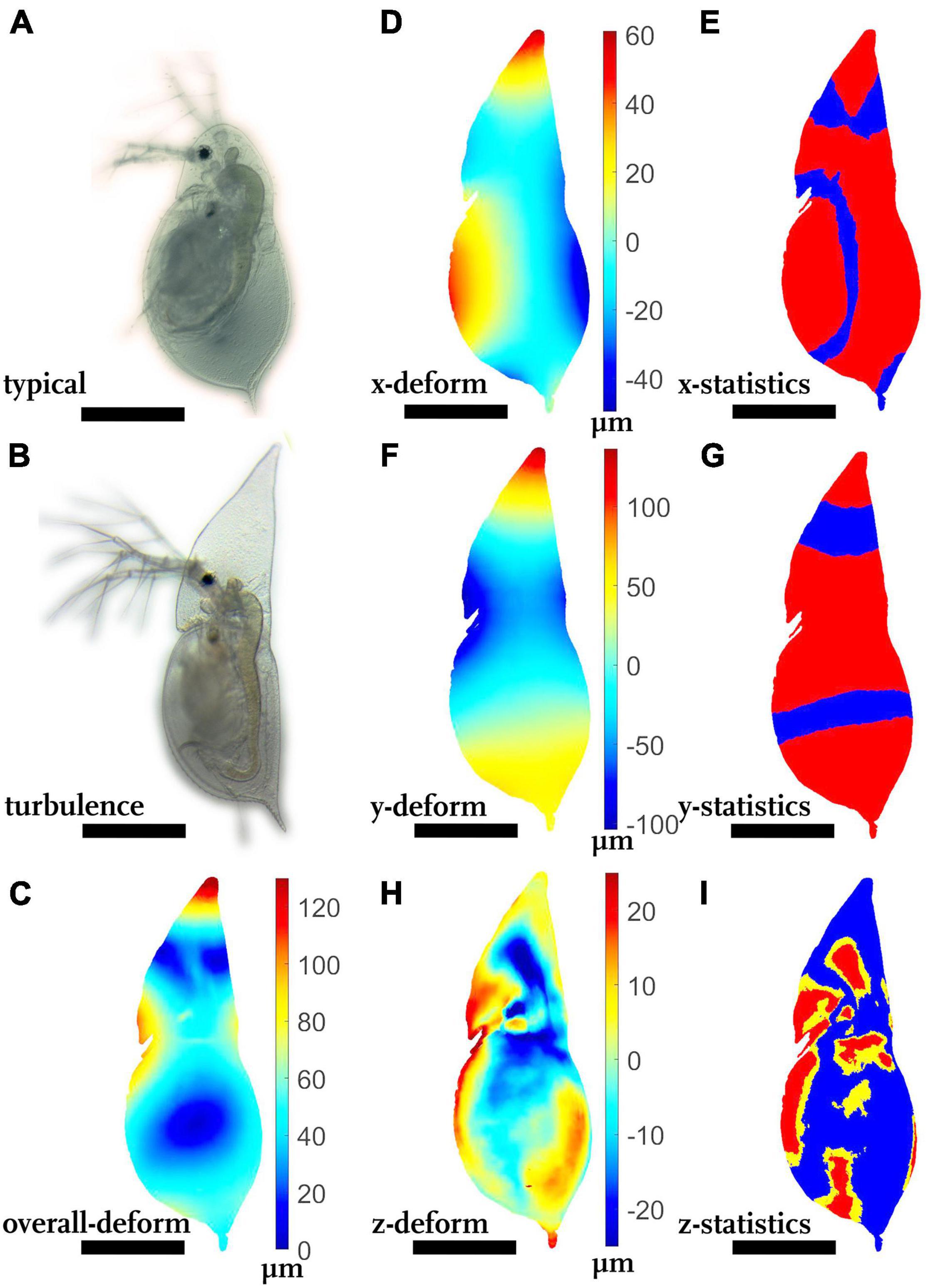
Figure 3. Morphological alterations of turbulence-exposed Daphnia cucullata. (A) D. cucullata, reared in the absence of turbulence. (B) D. cucullata, reared in the presence of turbulence. (C) Overall deformation plot showing the comparison of the unexposed and turbulence-exposed D. cucullata model. Plotted are the vector lengths (μm) between the respective vertices on the unexposed and the turbulence-exposed D. cucullata model (blue 0 μm displacement, dark red 120 μm displacement). (D,F,H) Shades of blue colors represent alterations in negative direction, while shades of red display shifts in the positive direction. Shades of yellow to white indicate little or no shifts along the respective axis. (E,G,I) p-values lower than 0.05 displayed in yellow, regions supported by q-values lower than 0.01 are colored red. (D) Vertex displacements (μm) in x-(dorso-ventral) direction. (E) Wilcoxon test p-values and FDR-analysis q-values for each vertex position of the x-direction. (F) Vertex displacements in y-(longitudinal) direction (μm). (G) Wilcoxon test p-values and FDR-analysis q-values for each vertex position of the y-direction. (H) Vertex displacements in z-(lateral) direction (μm), (I) Wilcoxon test p-values and FDR-analysis q-values for each vertex position of the z-direction. nundefended = 10, ndefended = 10. All scale bars: 600 μm.
Turbulence-exposed animals are significantly more slender by 40–50 μm at each side (Figure 3D, shades of red at the ventral body margin, shades of blue at the dorsal margin), reducing the total dorso-ventral width (>100 μm, Figure 3E, p < 0.05, q < 0.01).
In longitudinal direction turbulence-exposed D. cucullata are significantly elongated (Figures 3F,G shades of red at the tip of the helmet, > 100 μm, p < 0.05, q < 0.01).
In lateral dimension, parts of the head capsule are laterally about 20 μm more slender than the typical morph (Figure 3H, shades of blue on the head), while other parts of the head are almost unaltered or enhanced in lateral width, e.g., the rostrum region (Figure 3I, shades of red at the animals head). Similarly, carapace regions at the ventral and dorsal margin are significantly wider in the lateral dimension (Figure 3G, shades of red on the carapace, Figure 3I, p < 0.05, q < 0.01).
In terms of Procrustes distance, the unexposed and turbulence-exposed model differed on average by 49.0 μm (average partial Procrustes distance, average full Procrustes distance 46.3 μm, Table 1).
According to the average Procrustes-distances, the unexposed and Chaoborus-exposed morph are not as different as the typical and the turbulence-exposed morph. The average partial Procrustes-distances between the two altered morphs are greater than the distances between the unexposed morph and each altered morph. At the same time, the average full Procrustes distance between the changed morphs is larger than the value between unexposed and Chaoborus-exposed models, but smaller than the value between the unexposed and turbulence-exposed morph.
Animals exposed to Chaoborus-larvae or turbulence changed their shape and form and accordingly show alterations of body surface, i.e., “shadow area” and volume (Table 2).
The body surface of turbulence exposed animals decreases by 16%, as well as the volume, which decreases about 32% in relation to the typical morph. The shadow area decreases more than the body surface area (22%).
The body surface of Chaoborus-exposed animals increases by 12%, the volume is increased about 19% in comparison to the typical morph. The shadow area is larger by 13%.
Drag force depends partly on the “shadow area” and is altered in both morphs. The drag force under an angle of attack of 40° is reduced by 11.2% (11.6% at 5°C, Table 3) in the turbulence-exposed morph with the typical morph’s velocity. The drag force reduction calculated in a simulation with the respective velocity is reduced even stronger (-41.5%). The drag force of the Chaoborus-exposed morph stays almost constant with a decrease of just 0.5% simulated with the typical morph’s velocity, simulating the drag force with the treatment-respective velocity gives a drag force decrease of even 51% (Table 3 and Figures 4A,B). The drag coefficient CD for the typical morph is 23.82, for the Chaoborus-morph 20.83 and 24.81 for the turbulence induced morph.
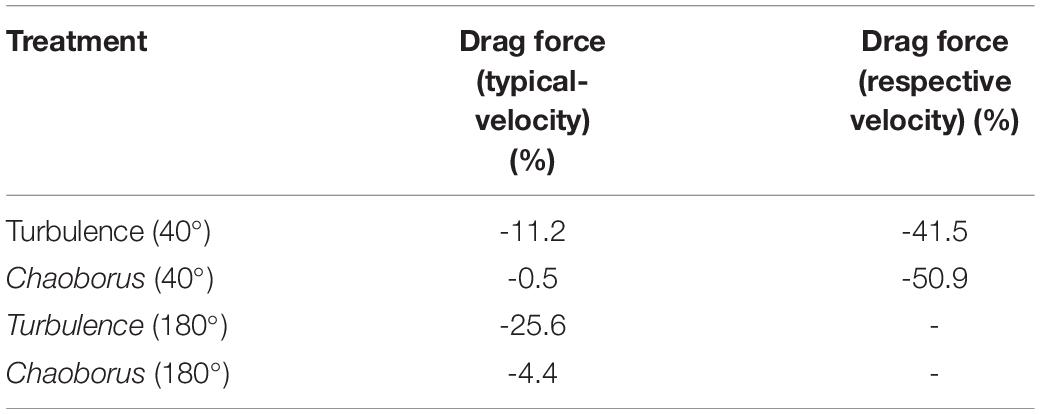
Table 3. Drag force alteration (%) of the turbulence and Chaoborus-exposed morph of D. cucullata in comparison to the typical morph at typical and respective velocities.
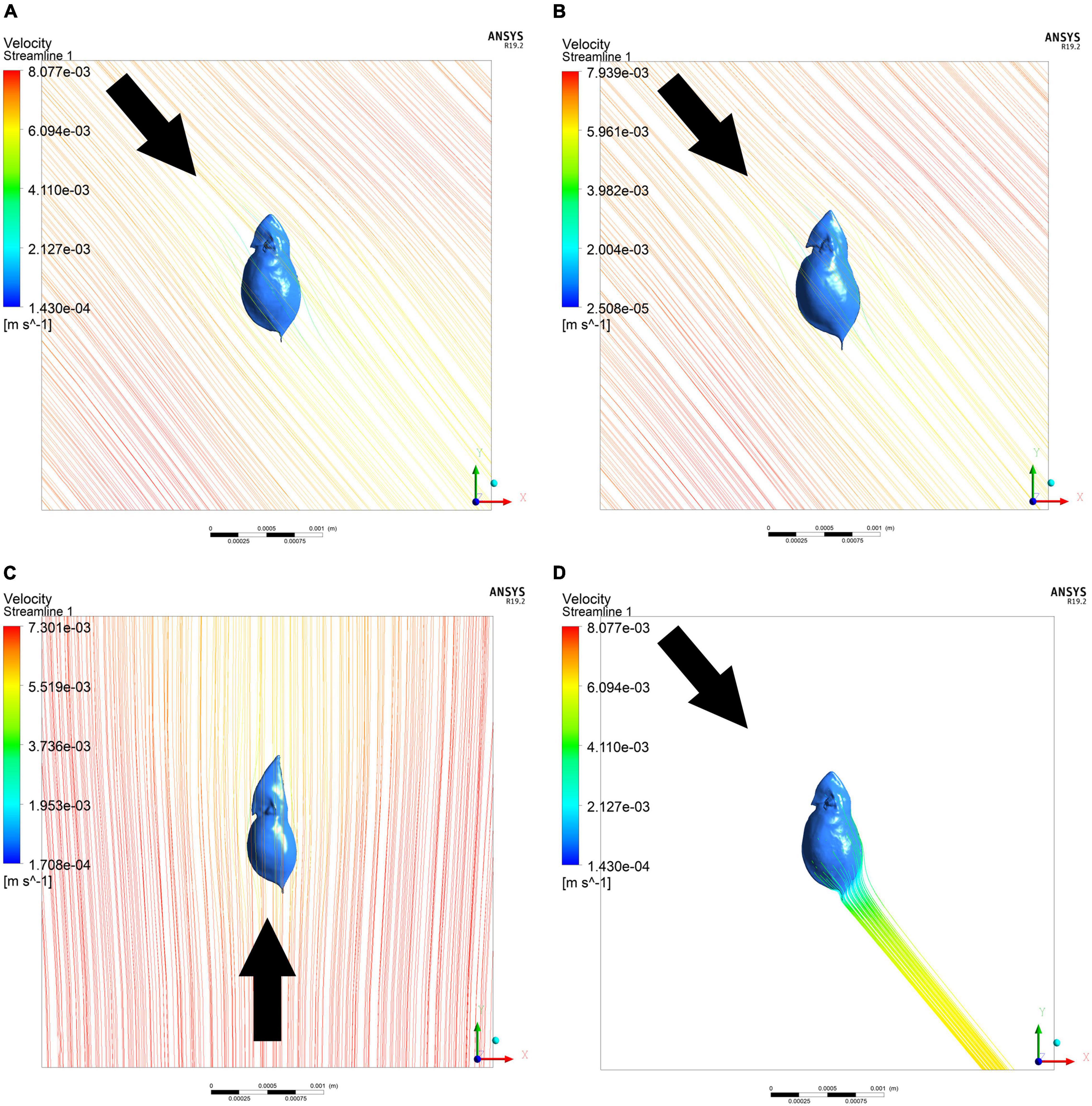
Figure 4. Exemplary 3D-simulations of streamlines around D. cucullata. Drag forces were simulated in typical (A), Chaoborus-exposed (B), and turbulence-exposed D. cucullata (C). Streamline analysis allows the simulation of different angles of attack, e.g., of 40° (A,B,D) as well as from directly beneath (180°, C). Investigating the trails of the model allows to compare differences between models (D). Arrow gives the direction of water flow.
Streamline simulations with different water temperatures at an angle of attack of 40° lead to altered drag forces in the typical and turbulence-exposed morph. The increase of viscosity with decreasing water temperature results in drag force alteration of 74.2% (typical), respectively 76.4% (turbulence), each compared to the drag force at 25°C (Table 4). Independent of the water temperature, the turbulence-exposed morph causes less drag based on its body shape.
Comparing the drag force at an angle of attack of 180°, the turbulence exposed morph shows lowest drag forces (Figure 4C). In comparison to the typical morph, drag during sinking is reduced by 26%. In the Chaoborus-exposed morph drag force is slightly reduced (4.5%). Based on the body morphology, the turbulence-exposed morph sinks the fastest, the unexposed morph sinks the slowest.
Among the morphs we investigated in this study, Chaoborus-exposed D. cucullata swam significantly slower. According to the calculation of Gerritsen and Strickler, swimming slower mathematically reduces the chances of encounter between predator and prey (Gerritsen and Strickler, 1977). A defense mechanism in the presence of Chaoborus based on swimming velocity reduction, as e.g., observed in D. magna is therefore likely (Langer et al., 2019). A behavioral defense can also manifest e.g., in swimming type or depth selection, and needs to be investigated in future studies (De Meester et al., 1999; Wickramarathna et al., 2014). Also, turbulence-exposed animals did not show a significant alteration in swimming velocity in our sample. Nevertheless, it is important to note that we here measured the swimming velocity during the typical hop and sink movement in stagnant medium, not in turbulence or during e.g., flight behavior. Under such conditions, swimming velocities may differ.
Chaoborus-defended D. cucullata are characterized by an elongated helmet and a slightly slender body in dorso-ventral direction. The head to tail spine distance is increased. Our results confirm the observations made in X and Y direction previously (Jacobs, 1987; Tollrian, 1990; Laforsch and Tollrian, 2004a). The deformation in z direction was yet unknown. We observe that the fold located in anterior-posterior direction on the head is strongly reduced laterally in defended animals. In combination with the slightly altered head morphology, this may support an anti-lock-and-key mechanism, especially as the head morphology gets more edgy (Dodson, 1974). In D. cucullata the defense is effective at the post attack level (Laforsch and Tollrian, 2004c), so that these alterations could provide protection through an anti-lock-and-key-system (Jeschke et al., 2008; Weiss et al., 2012). These alterations may be advantageous as D. cucullata thereby outgrows Chaoborus’ mouth gape (Riessen and Young, 2005) or by reducing handling efficiency, as in D. pulex (Krueger and Dodson, 1981).
Furthermore, a reduction of the wake vortexes eliciting Chaoborus’ catching movement by morphological alteration seems to be part of D. cucullata’s strategy. Our streamline analysis shows the trail to be wider in defended animals and therefore potentially less intense (Figure 4D). That way, D. cucullata may swim in a kind of ’stealth mode‘. The head capsule’s lateral width at the fornices is reduced and the carapace is laterally wider, as previously described as defense of D. pulex against Chaoborus (Horstmann et al., 2021).
The morphological reaction of D. cucullata to turbulence is not a direct reaction to a predator, but to movements in the water, speculated to be an indicator of predator presence (Hrbáček, 1959). We found that the lateral width of the head including the fornices is even stronger reduced in comparison to the Chaoborus defended morph. A more pronounced defense feature may indicate a defense against a different predator or at least a different function of the defense. Concerning the origin of the inducing effect of turbulences, it is hypothesized that the time of the year at which the turbulences naturally occur by winds (Hrbáček, 1959) correlates with high predation pressure by invertebrate or vertebrate predators. Moreover, the predators itself could not only emit chemical signals (kairomones) but also the turbulence (Lampert and Wolf, 1986; Laforsch and Tollrian, 2004b). Nevertheless, an additive effect of predator and turbulence appears unlikely at least in the case of Chaoborus, as during our induction microturbulences were present due to movements of the predators in the experimental beakers. Though, we did not observe strong defense expression. Especially as helmets were shown to be an effective protection against smaller fish (Kolar and Wahl, 1998), swarms of young fish, which elicit turbulences by swimming may be the natural cue for the observed alterations in this treatment (Lampert and Wolf, 1986; Laforsch and Tollrian, 2004b).
Furthermore, it was so far unclear, whether the morphological alterations change the hydrodynamic properties. Previously it was hypothesized that the morphological alterations lead to so far unknown benefits, e.g., through shifts in the buoyancy properties (Hrbáček, 1959; Jacobs, 1967; Laforsch and Tollrian, 2004b).
At a first glance, the morphs of D. cucullata exposed to Chaoborus and turbulence seem quite different. Considering Procrustes distance, the average partial Procrustes-values are 26 μm, respectively 49 μm, the difference between the two altered morphs is 78 μm. Therefore, the altered morphs are more different to each other than each of them is different to the typical morph, suggesting a completely different defense mechanism, confirming the hypothesis of different defenses. Though, correction for size reduces these values to 17 μm, respectively, 46 μm, the difference between the altered morphs is reduced to 35 μm (50%). The latter difference is smaller compared to the distance between the unexposed and turbulence-exposed morph. This suggests a striking effect of size. We therefore find that the turbulence morph may just be the extreme formation of the Chaoborus morph. Both morphs were already discussed as different expression strengths of a single morphological defense previously (Laforsch and Tollrian, 2004b). Though, in our experiment, we did not observe a turbulence morph in Chaoborus-exposed animals, especially not developed that fast as observed in the turbulence-exposed treatment. The different expression strengths of this alteration support the theory of an invertebrate-specific defense, as D. cucullata were naturally often found with broken tail spines, which were assessed relics of invertebrate predator attacks (Murtaugh, 1981; Pijanowska, 1990). Additionally, other studies assessed this species as not vulnerable to fish predation, due to their low conspicuity (Pijanowska, 1992). Despite these results, we assume that vulnerability is dependent on fish size. Especially swarms of young fish may indeed be a threat to D. cucullata. Nevertheless, our results support a single, adjusted defense in different size classes of D. cucullata. Such a gradual alteration is contrary to e.g., D. barbata’s defense, which is different or even oppositional confronted with its two respective predators (Herzog and Laforsch, 2013).
According to the drag equation for Reynold’s numbers > 1, drag coefficient and reference area are important factors for drag calculation (Nakayama, 1999; Batchelor, 2000).
In this term, ρ represents the fluid density, CD the drag coefficient, A the cross-sectional area and v the relative velocity between the fluid and the body.
The reference area is defined by the cross-sectional area in direction of the objects motion, while shape of the object is included in the drag coefficient. Therefore, the drag force is coupled with surface and volume via the shape. Based on our results, we calculated the drag coefficients for the three morphs. Interestingly, the Chaoborus-morph has the smallest drag coefficient (20.83), while the turbulence exposed morph has the highest value (24.81), suggesting that the small cross-sectional area is governing the low drag found in this morph, which we see in our data. In Chaoborus-exposed animals, alterations of surface and “shadow area” are less pronounced (12 and 13%), suggesting that under predation pressure the surface exposed to the water current is not under a selection toward a reduction or an increase. In comparison, “shadow area” in turbulence-exposed D. cucullata is decreased by 22% in comparison to the typical morph, while the overall surface is decreased by 15%. It can be argued, that the decrease in surface area is especially favoring the direction of movement more as the overall Daphnia shape, which is optimized for a forward movement (Zaret and Kerfoot, 1980). This is even more impressive as the volume decreases by 32%, and the accompanying surface reduction is focused mainly on the “shadow area”.
The drag force under an angle of attack of 40° and with velocity of the typical morph (7.2 mm/s), is reduced by only 11% in turbulence-exposed animals, compared to a 22% decrease in shadow area. This is a clear indication that also the body shape of D. cucullata and not only “shadow area” has, as a further parameter in the drag equation, a strong influence on the energy efficiency of swimming. As the treatments’ swimming velocities were not significantly different, these comparisons with standard velocity are most reliable. In addition, the drag force reduction with the treatment specific velocity is 42% in the turbulence-exposed treatment, as not only the shape is more streamlined, but also swimming velocity is considerably reduced (4.7 mm/s).
In general, turbulence-exposed D. cucullata experience less drag forces and are therefore more energy-saving swimmers. This could help to withstand turbulences or keep position in the water column despite turbulences are present, similar to the hypotheses of Woltereck (1913).
The drag force under an angle of attack of 40° and with the velocity of the typical morph decreased by only 0.5% in the Chaoborus-exposed morph. Using the velocity measured for this treatment in our tracking setup (Langer et al., 2021), we found the drag force decreased by 51% compared to the typical morph. The velocity of Chaoborus-defended D. cucullata was 50% lower (3.6 mm/s), which explains this clear decrease in drag force using the respective velocity. Therefore, the defense against Chaoborus does not seem to alter the body in favor of a more streamlined shape. Moreover, as more streamlined morphs of D. cucullata do not swim faster but rather slower, swimming velocity seems to be adjusted independently of morphological alteration.
As the turbulence-exposed morph was discussed to alter swimming abilities at different water temperatures (Laforsch and Tollrian, 2004b), we modeled the typical and the turbulence-exposed morph at 5°C with, respectively, altered water viscosity. In colder water (5°C), drag is highly increased, especially at low Reynold’s numbers (Reynolds, 1886; Wickramarathna et al., 2014). We observed an increase of drag force, compared to 25°C warm water, of 74% in the typical morph and an increase of 76% in the turbulence-exposed morph. In both treatments, the increase of drag force between these two treatments at 5°C compared to the simulation at 25°C was approximately 11%. Therefore, no morph has an additional advantage of shape at colder temperatures. This contradicts the assumption that high helmets are not expressed at colder temperatures to save energy (Laforsch and Tollrian, 2004b). Moreover, at 25°C the turbulence morph shows a 11.2% reduced drag force compared to the typical morph, at 5°C an even 11.6% reduced drag force, which suggests a slightly drag reducing effect of the turbulence-exposed morphology at colder temperatures.
Based on body shape, turbulence-exposed animals sink fastest and un-exposed animals slowest. Jacobs showed that additionally antennae have an important effect on sinking (Jacobs, 1967), so that morphology cannot solely predict sinking properties. He found different antennae parachutes in the winter and summer morph (Jacobs, 1967). Similarly, the Chaoborus- and turbulence morph may also have altered antennae parachutes. Nevertheless, it can be hypothesized that the typical and Chaoborus-exposed morph with its relatively high drag forces in sinking enable the maintenance of a vertical position, avoiding antennae strokes to be energetically more efficient. In winter, when food is limited and physiology slowed, the typical morphology could serve as an energy saving mechanism. The morphology in the presence of the tactile predator Chaoborus shows a 4% decreased drag force during sinking, which just slightly increases this morph’s sinking velocity. Therefore, also the Chaoborus-morph needs just very few antennae strokes to maintain vertical position, avoiding movements suspicious to this predator.
As vertebrate predators were discussed to be the natural origin of turbulence (Lampert and Wolf, 1986; Laforsch and Tollrian, 2004b), the more streamlined morphology of the turbulence-morph could help the animals to sink faster in deeper water layers in the presence of e.g., fish, especially if antennae are kept tight to the body. This migration into deeper water layers is known as diel vertical migration to avoid fish predation (Bayly, 1986; Lampert, 1993).
Summarizing these findings, the turbulence-exposed morph is slightly more efficient in the active swimming but sinks faster based on our experimental framework, in which we assumed nearly laminar flow based on previous publications on the body Reynolds number of Daphnia (Lord et al., 2006; Wickramarathna et al., 2014). The material costs of the helmet are not determined yet, but assumed to be low (Tollrian, 1991). Therefore, the fast sinking of the turbulence exposed morph combined with the necessity of more antennae strokes to keep the vertical position is possibly the only, but very relevant cost, as it increases energy investment.
In reaction to phantom-midge larvae, the assumed sinking rate based on simulated drag forces, is close to typical D. cucullata. This keeps the antennae beat frequency low, which in turn may avoid Chaoborus attacks, as they are tactile predators and sensitive for such kind of water movements. We also found the Chaoborus-morph to swim slower than the typical, reducing encounter probability (Gerritsen and Strickler, 1977). This is contradictory to previous findings, which showed helmeted morphs to be attacked more frequently than the typical morph (Laforsch and Tollrian, 2004c).
Based on our geometric morphometric analysis, the two morphs appear as different expression strengths of a single multitool response (Laforsch and Tollrian, 2004b). The swimming velocity seems independent of the morphs, as it was not increased despite drag forces were decreased, which would allow higher swimming velocities at the same energy investment.
The function of the morphological alterations remains somewhat inconclusive. Nevertheless, we can now e.g., exclude that the turbulence-exposed morph reduces the streamlining maleficently in cold water (Laforsch and Tollrian, 2004b). We can furthermore rule out the hypothesis that the helmeted morph serves as support in maintaining the vertical position in the water column, as the opposite is the case, it sinks faster. Though, the turbulence-exposed morph shows an advantage at more turbulent conditions, potentially being more maneuverable, due to lower drag. Thus, this is an advantage besides the pure defensive effect. This is in agreement with Woltereck’s hypothesis. He stated that the helmet of D. cucullata mainly serves to determine swimming direction (Woltereck, 1913). Further (simulated) investigations on the swimming with morphological alterations and potentially altered antennae parachutes in combination with predation experiments will reveal further beneficial effects of the observed alterations. In the light of the previous and current investigations it appears likely that not a single positive effect, but an accumulation of favorable effects causes the distinct changes in morphology and swimming velocity.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
MH, LW, and RT contributed to conception and design of the study and interpreted the data. MH conducted model generation, determination of swimming velocities and streamline simulations and wrote the first draft of the manuscript. MH and LW performed the statistical analysis. RT provided lab facilities. All authors read and approved the submitted version.
MH acknowledges funding by the “Studienstiftung des deutschen Volkes.” We acknowledge support by the Open Access Publication Funds of the Ruhr-Universität Bochum.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank Ulrich Witzel for years of valuable discussions and the opportunity to use the computational resources in his department. We also thank Andreas Lipphaus for technical support in simulations. Moreover, we are grateful to Hannah Skudlarek and Leonie Dierolf for their valuable help in the lab.
Bayly, I. A. E. (1986). “Aspects of diel vertical migration in zooplankton, and its enigma variations,” in Limnology in Australia, eds P. De Deckker and W. D. Williams (Dordrecht: Springer), 61.
Brooks, J. L. (1947). Turbulence as an environmental determinant of relative growth in Daphnia. Proc. Natl. Acad. Sci. U.S.A. 33, 141–148. doi: 10.1073/pnas.33.5.141
Brooks, J. L. (1965). Predation and relative helmet size in cyclomorphic Daphnia. Proc. Natl. Acad. Sci. U.S.A. 53, 119–126. doi: 10.1073/pnas.53.1.119
De Meester, L., Dawidowicz, P., Van Gool, E., and Loose, C. J. (1999). “Ecology and evolution of predator-induced behaviour of zooplankton: depth selection behaviour and diel vertical migration,” in The Ecology and Evolution of Inducible Defenses, eds R. Tollrian and C. D. Harvell (Princeton, NJ: Princeton University Press), 160–176.
de Reuille, P. B., Routier-Kierzkowska, A. L., Kierzkowski, D., Bassel, G. W., Schüpbach, T., Tauriello, G., et al. (2015). MorphoGraphX: a platform for quantifying morphogenesis in 4D. eLife 4:05864. doi: 10.7554/eLife.05864
Dodson, S. I. (1974). Adaptive change in plankton morphology in response to size-selective predation: a new hypothesis of cyclomorphosis. Limnol. Oceanogr. 19, 721–729.
Gerritsen, J., and Strickler, J. R. (1977). Encounter probabilities and community structure in zooplankton: a mathematical model. J. Fish. Res. Board Can. 34, 73–82.
Hebert, P. D. N. (1978). The adaptive significance of cyclomorphosis in Daphnia: more possibilities. Freshw. Biol. 8, 313–320.
Herzog, Q., and Laforsch, C. (2013). Modality matters for the expression of inducible defenses: introducing a concept of predator modality. BMC Biol. 11:113. doi: 10.1186/1741-7007-11-113
Horstmann, M., Ralph, T., and Weiss, L. C. (2021). Thwarting predators?? A three-dimensional perspective of morphological alterations in the freshwater crustacean Daphnia. PLoS One 16:e0254263. doi: 10.1371/journal.pone.0254263
Horstmann, M., Topham, A. T., Stamm, P., Colbourne, J. K., Tollrian, R., and Weiss, L. C. (2018). Scan, extract, wrap, compute – a 3D-method to analyse morphological shape differences. PeerJ 6:e4861. doi: 10.7717/peerj.4861
Hrbáček, J. (1959). Circulation of water as a main factor influencing the development of helmets in Daphnia cucullata sars. Hydrobiologia 13, 170–185.
Hrbáček, J. (1962). Species composition and the amount of zooplankton in relation to fish stock. Rozpr. Ces. Akad. Ved Rada Mat. Prir. Ved 72, 1–117.
Jacobs, J. (1961). Cyclomorphosis in Daphnia galeata mendotae birge, a case of environmentally controlled allometry. Arch. Hydrobiol. 58, 7–71.
Jacobs, J. (1962). Light and turbulence as co-determinants of relative growth rates in cyclomorphic Daphnia. Int. Rev. Gesamten Hydrobiol. 47, 146–156.
Jacobs, J. (1964). Hat der hohe Sommerhelm zyklomorpher Daphnien einen Anpassungswert? SIL Proc. 15, 676–683. doi: 10.1080/03680770.1962.11895590
Jacobs, J. (1967). Untersuchungen zur funktion und evolution der Zyklomorphose bei Daphnia, mit besonderer Berücksichtigung der Selektion durch Fische. Arch. Hydrobiol. 62, 467–541.
Jacobs, J. (1987). “Cyclomorphosis in Daphnia,” in Daphnia, Vol. 45, eds R. H. Peters and R. de Bernardi (Verbania Palanza: Memorie dell’Istituto Italiano di Idrobiologia), 325–352.
Jeschke, J. M., Laforsch, C., and Tollrian, R. (2008). “Animal prey defenses,” in General Ecology, eds S. E. Jorgensen and B. D. Fath (Oxford: Elsevier), 189–194.
Karpowicz, M., Ejsmont-Karabin, J., Wiȩcko, A., Górniak, A., and Cudowski, A. (2019). A place in space-the horizontal vs vertical factors that influence zooplankton (Rotifera, crustacea) communities in a mesotrophic lake. J. Limnol. 78, 243–258.
Kolar, C. S., and Wahl, D. H. (1998). Daphnid morphology deters fish predators. Oecologia 116, 556–564. doi: 10.1007/s004420050621
Krueger, D. A., and Dodson, S. I. (1981). Embryological induction and predation ecology in Daphnia pulex. Limnol. Oceanogr. 26, 219–223.
Laforsch, C., and Tollrian, R. (2004c). Inducible defenses in multipredator environments: cyclomorphosis in Daphnia cucullata. Ecology 85, 2302–2311.
Laforsch, C., and Tollrian, R. (2004a). Embryological aspects of inducible morphological defenses in Daphnia. J. Morphol. 262, 701–707. doi: 10.1002/jmor.10270
Laforsch, C., and Tollrian, R. (2004b). Extreme helmet formation in Daphnia cucullata induced by small-scale turbulence. J. Plankton Res. 26, 81–87.
Lampert, W. (1993). Ultimate causes of diel vertical migration of zooplankton: new evidence for the predator-avoidance hypothesis. Arch. Hydrobiol. Beih. Ergebn. Limnol. 39, 79–88.
Lampert, W., and Wolf, H. G. (1986). Cyclomorphosis in Daphnia cucullata: morphometric and population genetic analyses. J. Plankton Res. 8, 289–303. doi: 10.1093/plankt/8.2.289
Langer, S. M., Horstmann, M., Weiss, L. C., Junke, W., Herlitze, S., and Tollrian, R. (2021). On Daphnia’s path: a semi-automatic system to analyze three-dimensional movement patterns. Ecosphere 12:e03847. doi: 10.1002/ecs2.3847
Langer, S. M., Weiss, L. C., Ekvall, M. T., Bianco, G., Hansson, L.-A., and Tollrian, R. (2019). A three-dimensional perspective of Daphnia’s swimming behavior with and without predator cues. Limnol. Oceanogr. 64, 1515–1525. doi: 10.1002/lno.11132
Lord, H., Lagergren, R., Svensson, J. E., and Lundqvist, N. (2006). Sexual dimorphism in Bosmina: the role of morphology, drag, and swimming. Ecology 87, 788–795. doi: 10.1890/05-0082
Murtaugh, P. A. (1981). Inferring properties of mysid predation from injuries to Daphnia. Limnol. Oceanogr. 26, 811–821.
Nakayama, Y. (1999). Introduction to Fluid Mechanics, ed. R. F. Boucher (Oxford: Butterworth-Heinemann).
Pijanowska, J. (1990). Cyclomorphosis in Daphnia: an adaptation to avoid invertebrate predation. Hydrobiologia 198, 41–50.
Pijanowska, J. (1992). Anti-predator defence in three Daphnia species. Int. Rev. Gesamten Hydrobiol. 77, 153–163.
R Core Team (2021). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Reynolds, O. (1886). On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments. Proc. R. Soc. London 40, 191–203.
Riessen, H. P., and Young, J. D. (2005). Daphnia defense strategies in fishless lakes and ponds: one size does not fit all. J. Plankton Res. 27, 531–544.
Scourfield, D. J. (1900). The swimming peculiarities of Daphnia and its allies. J. Queckett. Microsc. Club 2, 217–244.
Storey, J. D., and Tibshirani, R. (2003). Statistical significance for genomewide studies. Proc. Natl. Acad. Sci. U.S.A. 100, 9440–9445. doi: 10.1073/pnas.1530509100
Tollrian, R. (1990). Predator-induced helmet formation in Daphnia cucullata (Sars). Arch. Hydrobiol. 119, 191–196.
Tollrian, R. (1991). Some aspects in the costs of cyclomorphosis in Daphnia cucullata. SIL Proc. 24, 2802–2803. doi: 10.1080/03680770.1989.11899165
Tollrian, R., and Harvell, C. D. (1999). The Ecology and Evolution of Inducible Defenses. Princeton, NJ: Princeton University Press.
Tollrian, R., and Laforsch, C. (2006). Linking predator kairomones and turbulence: synergistic effects and ultimate reasons for phenotypic plasticity in Daphnia cucullata. Arch. Hydrobiol. 167, 135–146.
Volterra, V. (1926). Fluctuations in the abundance of a species considered mathematically1. Nature 118, 558–560.
Weiss, L. C., and Tollrian, R. (2018). “Inducible defenses in Crustacea,” in The Natural History of the Crustacea, Life Histories, Vol. 5, eds T. Martin and G. A. Wellborn (Oxford: Oxford University Press).
Weiss, L. C., Heilgenberg, E., Deussen, L., Becker, S. M., Kruppert, S., and Tollrian, R. (2016). Onset of kairomone sensitivity and the development of inducible morphological defenses in Daphnia pulex. Hydrobiologia 779, 135–145.
Weiss, L. C., Laforsch, C., and Tollrian, R. (2012). “The taste of predation and the defenses of prey,” in Chemical Ecology in Aquatic Systems, ed. C. Brönmark (Oxford: Oxford University Press), 111–126.
Wesenberg-Lund, C. J. (1900). Von dem Abhängigkeitsverhältnis zwischen dem Bau der Planktonorganismen und dem spezifischen Gewicht des Süsswassers. Biol. Zbl. 20, 606–619.
Wickramarathna, L. N., Noss, C., and Lorke, A. (2014). Hydrodynamic trails produced by Daphnia: size and energetics. PLoS One 9:e92383. doi: 10.1371/journal.pone.0092383
Windig, J. J., and Lammar, P. (1999). Evolutionary genetics of seasonal polyphenism in the map butterfly Araschnia levana. Evol. Ecol. Res. 1, 875–894.
Woltereck, R. (1913). Über Funktion, Herkunft und Entstehungsursachen der sogen, Schwebe-Fortsätze“ pelagischer Cladoceren. Z. Indukt. Abstamm. Vererbungsl. 10, 475–550.
Keywords: inducible defense, streamline simulation, adaptive morphology, swimming velocity, drag force, phenotypic plasticity, Daphnia cucullata
Citation: Horstmann M, Weiss LC and Tollrian R (2022) Specific Turbulence- and Chaoborus-Induced Morphotypes Affect the Streamlining Properties of Daphnia cucullata. Front. Ecol. Evol. 9:825765. doi: 10.3389/fevo.2021.825765
Received: 30 November 2021; Accepted: 20 December 2021;
Published: 12 January 2022.
Edited by:
Mingbo Yin, Fudan University, ChinaReviewed by:
Piotr Dawidowicz, University of Warsaw, PolandCopyright © 2022 Horstmann, Weiss and Tollrian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Horstmann, bWFydGluLmhvcnN0bWFubkBydWIuZGU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.