Cheating Promotes Coexistence in a Two-Species One-Substrate Culture Model

Cheating in microbial communities is often regarded as a precursor to a “tragedy of the commons,” ultimately leading to over-exploitation by a few species and destabilization of the community. While current evidence suggests that cheaters are evolutionarily and ecologically abundant, they can also play important roles in communities, such as promoting cooperative behaviors of other species. We developed a closed culture model with two microbial species and a single, complex nutrient substrate (the metaphorical “common”). One of the organisms, an enzyme producer, degrades the substrate, releasing an essential and limiting resource that it can use both to grow and produce more enzymes, but at a cost. The second organism, a cheater, does not produce the enzyme but can access the diffused resource produced by the other species, allowing it to benefit from the public good without contributing to it. We investigated evolutionarily stable states of coexistence between the two organisms and described how enzyme production rates and resource diffusion influence organism abundances. Our model shows that, in the long-term evolutionary scale, monocultures of the producer species drive themselves extinct because selection always favors mutant invaders that invest less in enzyme production, ultimately driving down the release of resources. However, the presence of a cheater buffers this process by reducing the fitness advantage of lower enzyme production, thereby preventing runaway selection in the producer, and promoting coexistence. Resource diffusion rate controls cheater growth, preventing it from outcompeting the producer. These results show that competition from cheaters can force producers to maintain adequate enzyme production to sustain both itself and the cheater. This is similar to what is known in evolutionary game theory as a “snowdrift game” – a metaphor describing a snow shoveler and a cheater following in their clean tracks. We move further to show that cheating can stabilize communities and possibly be a precursor to cooperation, rather than extinction.

Introduction

Microorganisms in nature coexist in highly diverse communities. In these communities, not all species perform the same functions and therefore cooperative interactions can emerge that benefit not only the interacting organisms but can spill over to the whole community or population (Crespi, 2001; Smith and Schuster, 2019). These cooperative functions are usually extracellular, involving excreted products and metabolites that can be considered “public goods” because they are accessible to the entire community. However, extracellular functions, such as complex substrate degradation (e.g., cellulose), are particularly susceptible to exploitation: i.e., cheaters benefiting from a public good without contributing to it. This is because both the means (e.g., extracellular cellulase enzymes) and the products of substrate degradation (e.g., glucose) take place outside the cell (extracellular public goods) and are therefore vulnerable to cheating. The situation where cheaters emerge to exploit a shared resource was coined the “tragedy of the commons” by Hardin (1968), drawing from Lloyd’s (1833) example of unregulated cattle grazing in a common pasture. This theory describes how the emergence of cheaters leads to the inevitable demise of the whole group; the cheater either takes up too many resources or the cheating behavior propagates, leading to the same result. Cheating has been widely studied as a means of negative, competitive interaction between organisms and communities (Strassmann et al., 2000; Velicer et al., 2000; Schuster et al., 2017; De Leenheer et al., 2019). Existing studies show that cheaters should be detrimental for the system in which they emerge, because their lower fitness costs allow them to allocate additional resources to growth and reproduction, thus outcompeting other species. However, this situation shares similar characteristics and caveats with the competitive exclusion principle (Gause, 1934; Hardin, 1960) – regardless of reduced fitness costs, cheaters do not have the same access to the public good as producers (Letten et al., 2017). Hardin’s theory has attracted the attention of evolutionary biologists who sought out mechanisms though which a tragedy can be avoided. Often biological systems do not go extinct as a result of a tragedy of the commons and when they do it is often only under specific conditions (Rankin et al., 2007). Hardin’s tragedy of the commons overlooks the fact that natural biological systems are inherently reactive, and to an extent, regulate cheater abundance (Foster, 2004; Rankin et al., 2007; Ostrowski et al., 2015). Examples include regulation by host organisms (Oono et al., 2011), density-dependent metabolic costs strengthening negative frequency-dependent selection (MacLean, 2008; Morris, 2015), quorum sensing (Dandekar et al., 2012), or kin selection in heterogeneous environments (Kreft, 2004; Mitri and Foster, 2013). Indeed, the idea that any public good will always be catastrophically exploited has been heavily criticized (Dahlman, 1991; Ostrom, 1999, 2015).

Several experimental systems have shown dynamics that closely resemble a “tragedy of the commons.” However, the systems continue to persist, with no runaway exploitation taking place. Such dynamics play out in predator-prey (Jones et al., 2009; Becks et al., 2010, 2012; Blasius et al., 2020) and host-parasite models (Smith and Thieme, 2012; Frickel et al., 2016). The “tragedy of the commons” assumes that microbial cheating is a “prisoner’s dilemma” game; coexistence only depends on both players cooperating, as otherwise cheaters overwhelm the population causing the system to collapse. Instead, given the abundance of cooperative relationships between species in communities (West et al., 2007; Morris et al., 2013), the interaction between producers and cheaters possibly resembles a “snowdrift” game (Smith and Schuster, 2019). The snowdrift game model is inspired by the metaphor of a snow shoveler (producer or cooperator) who pays the cost of cleaning a path in the snow, with cheaters being able to use the already clean path without performing any work (Sugden, 2005). Under these circumstances, producers will continue to invest in public goods despite exploitation by cheaters so long as they continue to obtain sufficient benefits, e.g., partial privatization of a small amount of public goods (Gore et al., 2009). The Black Queen Hypothesis (BQH) describes a similar scenario (Morris et al., 2012). The main difference between a “snowdrift” dynamic and the BQH is that, in a BQH scenario, public good producers maintain some benefits that are not available to the cheater (Mas et al., 2016) [e.g., immediate access (Estrela et al., 2016), akin to partial privatization (Pande et al., 2015; Estrela et al., 2016)]. Contrastingly, in a “snowdrift” situation, the producer cedes any exclusive advantages to resolve the conflict (Smith, 1976). The BQH has been presented to describe the situation where, in planktonic microbial communities, selection promotes loss of extracellular functions involving public goods, allowing cheaters to emerge (Morris et al., 2012). This leads to a community where only a critical minimum of species perform a shared function, possibly allowing for dependencies and cooperative interactions to develop from the beneficiary species (Sachs and Hollowell, 2012; Morris et al., 2014; Mas et al., 2016). This raises the question of whether “snowdrift” situations are still conducive to stable coexistence.

Indeed, many studies have shown that cheaters may not only be non-destructive, but might promote biodiversity and cooperative behavior in microbial communities (Leinweber et al., 2017; Veit, 2019; García-Contreras and Loarca, 2020). In one example, wild-type Saccharomyces cerevisiae populations produce invertase that degrades sucrose into glucose. Glucose quickly diffuses from the cells, allowing for the emergence of non-producer cheaters (Gore et al., 2009). The authors showed that cheaters promoted producer species cooperation in the experimental system by keeping glucose concentrations low, thus preventing the inhibition of invertase production. The factor of diffusion is important as to whether a system can avoid a tragedy of the commons. While diffused public goods allow cheaters to emerge, producers can persist by either benefiting from their proximity and priority to the extracellular public good before diffusion or can evolve partial privatization of public goods, thus allowing coexistence (Gore et al., 2009; Smith and Schuster, 2019). Leinweber and her collaborators have also shown that cheater mutants of Pseudomonas aeruginosa act to increase intraspecific competition, promoting coexistence with Burkholderia cenocepacia, with iron as a single limiting resource (Leinweber et al., 2017). Motivated by these findings, we ask the following question: given that the emergence of cheaters is, for the most part, ecologically and evolutionarily inevitable (Strassmann et al., 2000; Ostrowski, 2019), how are public good producers and public good cheaters able to coexist? It is to be expected that to achieve coexistence, the cheater genotype must be under negative frequency dependence selection. However, this is a phenomenological description of coexistence, a fundamental property of stabilizing mechanisms, missing discussion of the deeper, underlying mechanisms that could bring about this negative frequency dependence (Chesson, 2000).

Based on these recent findings on the ecological relevance of cheaters, we examine mechanisms by which cheaters might act to stabilize producer-cheater systems, rather than destabilizing them in the classical sense. Cheaters in the model, are individuals that do not produce any amount of the public good but still benefit from it (Rankin et al., 2007). We also build on the existing literature, to show that, under certain conditions, cheaters can be crucial to the promotion and maintenance of producer cooperative behaviors and networks. To address our question, we develop a theoretical homogeneous closed coculture system model to test for evolutionarily stable states of coexistence and abundance dynamics between a producer and a cheater organism when provided with a single complex substrate resource. Choosing the scenario of a closed culture system with excess substrate available, allows us to build a model where the focus is the interaction between the two species and the parameters that influence their coexistence, without any exogenous limiting factors. We then proceed to parameterize the model with experimental data from the literature.

Model Description

Our model includes two species – an enzyme producer, N_E, and a “cheater,” N_C, growing in a common environment (Figure 1). The producer species releases exoenzymes that degrade the substrate (common good) into resources (public good) that are directly used for growth and production of exoenzymes. The cheater species does not produce the exoenzyme, thereby allowing itself to allocate more resources for growth. The cheater, however, depends on the diffusion of resources from the immediate area around the producers. Within the context of our model, we wanted to test which parameters control coexistence and how similar parameter conditions influence population abundances of producer monocultures vs. producer-cheater cocultures. Our operational definition of “cooperation” in this model is that both species must evolve toward strategies that favor stable long-term coexistence, rather than strategies that drive one or both of the species extinct.

FIGURE 1

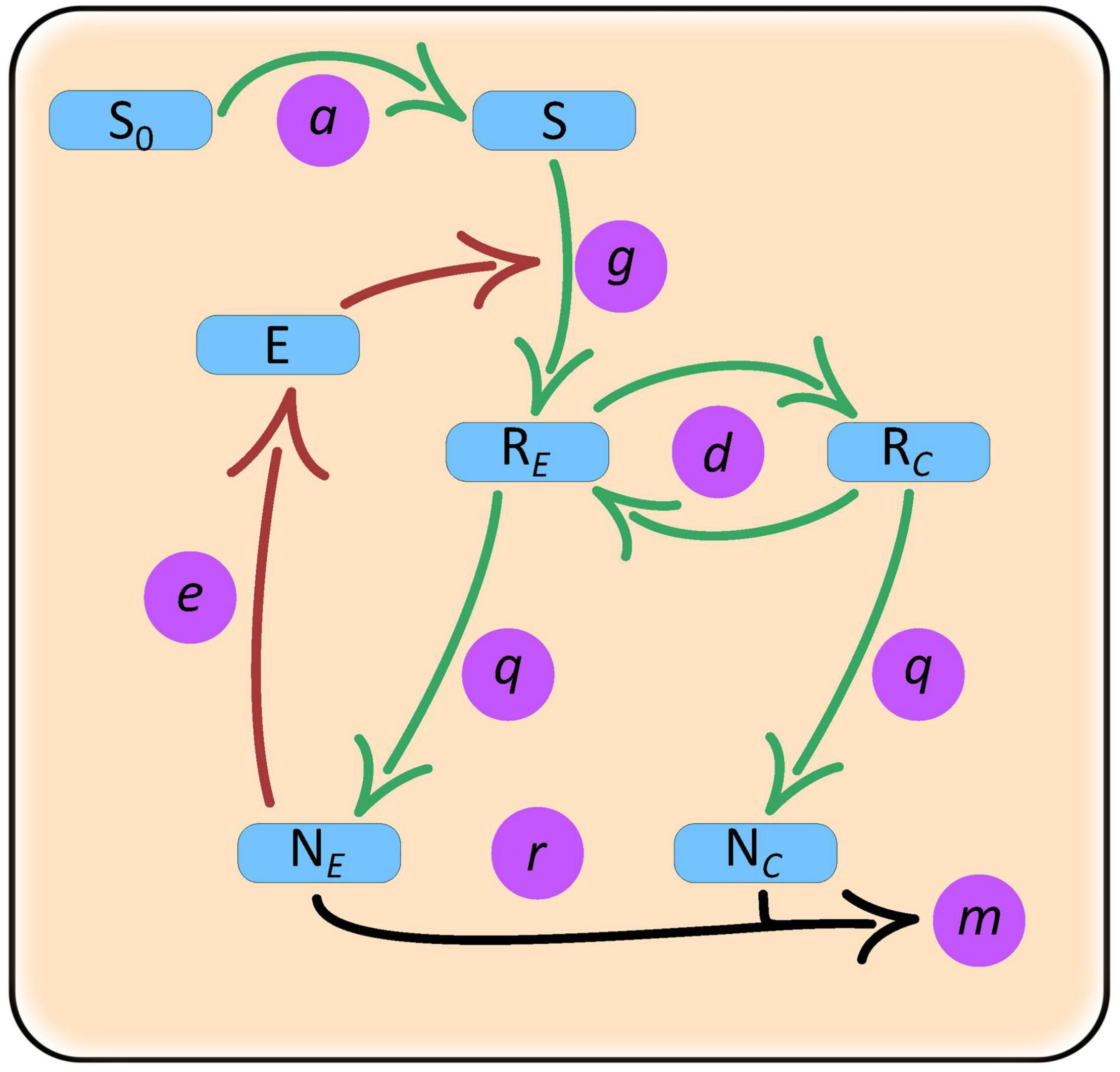
Figure 1. Schematic of a closed culture model with producer and cheater populations and a single complex substrate resource. Variables: N_E, enzyme producer population; N_C, cheater population; S, substrate; E, enzyme; R_E, enzyme producer resource; N_C, cheater resource. Parameters: a, substrate release rate; g, rate of substrate degradation by enzymes; e, enzyme production investment by the producer; d, resource diffusion rate; q, quantity of resource required for the production of species biomass; r, species growth rate; m, species mortality rate.

Other than differences in enzyme production, we assume that species share the same vital rates and requirements. It is also assumed that all species individuals have access to substrates and resources but because the producer cells release the enzymes that break down the substrate, they have first access to the resources. Once the resource concentration around the producers increases it then starts diffusing away and toward the cheaters. The model can be thought as a model of resource semi-privatization where the two species are intermixed but the conditions near each type of cell are tracked separately. Specifically, population dynamics for the enzyme producer and cheater follow:

$$\frac{d{N}_E}{dt}=\left(r{R}_E-\left(e+m\right)\right)N_E(\mathrm{1a})$$

$$\frac{d{N}_C}{dt}=\left(r{R}_C-m\right)N_C(\mathrm{1b})$$

where r is the intrinsic growth rate, m is the mortality rate, R_E and R_C are, respectively, resource concentration in the vicinity of the enzyme producer vs. the cheater, and e describes the cost of enzyme production. Thus, the enzyme producer always has a lower per-capita growth rate at any given level of resource availability.

Enzyme production is controlled by the abundance of the enzyme producer, and follows:

$$\frac{dE}{dt}=e{q}_z{N}_E-m_{z}E(2)$$

where q_z converts between the energetic cost of enzyme production to the producer vs. the rate of enzyme production, and m_z describes the rate at which the enzyme breaks down over time. Note that parameter e therefore jointly relates to the cost of enzyme production and the rate at which new enzyme is produced. Furthermore, in the absence of enzyme producers, all enzymes eventually break down and the concentration reduces to zero.

Resource dynamics in the model are controlled by the concentration of available substrate S, the concentration of enzymes that break down the substrate into usable resources, E, and the rates at which resources are taken up by species and diffuse between regions. We assume a closed system, in which new substrate, S, is released from a finite substrate source, S₀, at a rate proportional to the current concentration, and in which resources associated with dead biomass are inaccessible to the species in the system. Resource and substrate dynamics follow:

$$\frac{d{R}_E}{dt}=q_{S}gES-q{R}_{E}r{N}_E-d{R}_E+d{R}_C(\mathrm{3a})$$

$$\frac{d{R}_C}{dt}=-d{R}_C+d{R}_E-q{R}_{C}r{N}_C(\mathrm{3b})$$

$$\frac{dS}{dt}=a\left(S_0-S\right)-gES(\mathrm{3c})$$

where g describes the rate at which the enzyme breaks down the substrate, q describes the quantity of resource needed to produce a biomass unit, d is the diffusion rate governing movement of resource from the region around the enzyme producer to the region around the cheater, a describes the rate at which new substrate becomes bioavailable, and S₀ is the maximal substrate concentration in the absence of enzyme producers. While the culture system is closed, the substrate concentration S₀ is finite. The conversion rate a for S₀ to S (i.e., inaccessible substrate pool to enzyme-accessible substrate) limits the maximum achievable growth rate (i.e., if all substrate was immediately available then R_max = S₀). As an extend, species are not directly impacted by substrate concentration S, but rather, respond to changes in resource R (i.e., substrate that has been made biologically available). This way, growth rates can be modeled linearly even though the substrate is not infinite (Supplementary Figure 1). As such, growth rates are limited by resource availability, but mortality rates do not because mortality is decoupled from growth (Wang et al., 2010), allowing for the calculation of finite equilibria in our system.

At equilibrium, substrate concentration and resource concentrations in the vicinity of the enzyme producer and the cheater can be calculated as:

$$R_E^{*}=\frac{m+e}{r}if{N}_E^{*}>0,else{R}_E^{*}=0(\mathrm{4a})$$

$$R_C^{*}=\frac{m}{r}if{N}_C^{*}>0,else{R}_C^{*}=R_E^{*}(\mathrm{4b})$$

$$S^{*}=\frac{a{S}_0}{m_z}if{N}_E^{*}>0,else{S}^{*}=S_0(\mathrm{4c})$$

Because of the energetic cost of enzyme production, equilibrial resource concentrations are always higher in the vicinity of the enzyme producer. Note that these concentrations simultaneously describe the equilibrial resource concentration and the minimum resource requirement needed for positive equilibrial abundance (Tilman, 1982), meaning that the cheater is effectively a “better” competitor than the enzyme producer and, in the absence of the spatial gradient, would be able to drive it to extinction. Thus, if the diffusion rate is too high, the enzyme producer will ultimately be driven extinct, and the system will collapse.

Because enzyme and resource concentrations are primarily controlled by the enzyme producer, both the equilibrial enzyme concentration and the equilibrial abundance of the cheater can be described with relatively simple functions, based on the demographic rates and equilibrial concentration of the enzyme producer:

$$N_C^{*}=\frac{de}{mqr}(\mathrm{5a})$$

$$E^{*}=\frac{e{q}_z{N}_E^{*}}{m_z}(\mathrm{5b})$$

In contrast, the equilibrial abundance of the enzyme producer, although analytically tractable, follows a more complex set of functions, which include a monoculture equilibrium value (i.e., when N_C* = 0), a stable coexistence point where both N_E* and N_C* > 0, and an Allee point. If the population size of the enzyme producer falls below this Allee point and is held there long enough for resource and enzyme concentrations to equilibrate, the enzyme producer will ultimately be drawn toward extinction, because it is unable to counteract the diffusion gradient of resources being drawn toward the cheater. The full formulae for these three equilibria are available in the Supplementary Material R code scripts.

For the purpose of examining the model under realistic empirical conditions, we use parameter values reported in empirical studies (Supplementary Table 1). We use growth and mortality rates of Escherichia coli, a thoroughly studied model organism in experimental microbiology, with widespread relevance in biotechnology applications (Blount, 2015; Idalia and Bernardo, 2017) that can be genetically modified to produce exoenzymes such as cellulases (Gao et al., 2015). As a substrate, we identified cellulose as an appropriate carbon source. Cellulose is a complex substrate that requires specialized extracellular enzymes, cellulases, to be broken down into monosaccharides like glucose, a simple resource (public good) that can be used by most bacterial species (see Table 1 for parameter values and relevant literature). For parameter q_z, a conversion term describing the relative energy cost of enzyme production vs. biomass production, we chose units for e such that the costs to growth are equal to enzyme production rate (i.e., q_z = 1). Note that this choice does not change the generality of our results (other than complicating the interpretation of the units in which e is measured), but rather, facilitates model testing by reducing the dimensionality of our parameter space.

TABLE 1

Table 1. Term definitions.

Parameters e and d are the primary variables of interest and therefore we allow them to vary in our model, in order to find evolutionarily stable states that allow for coexistence. When diffusion rate is d = 0, all resources are privatized by the producer, causing complete exclusion of the cheater. While zero diffusion is an unlikely event, especially in a homogenized culture, it was important to verify the full range of our parameter dynamics. As d approaches infinity it is assumed that diffusion increases (e.g., producers and cheaters are mixed in a very dense culture). Similarly, we will show that varying e, the cost of enzyme production, in our model reveals maximum and minimum (non-zero) coexistence thresholds that influence both the producer monoculture and the producer-cheater mixture. Furthermore, by varying the e parameter, we can simulate the invasion of producer mutants that invest less in enzyme production. Following standard methods for quantitative genetics studies, we assume that mutations that arise which impart a fitness advantage go to fixation quickly relative to the rate of overall population dynamics (Kremer and Klausmeier, 2013).

Results

In the model, the cost of enzyme production (e) and diffusion rate (d) are the main drivers for coexistence. In the case of e, coexistence in the producer-cheater system is a product of the balance of two opposing forces; invading producer species that drive down enzyme production, and resource strain from cheaters that drives up enzyme production. These forces are at equilibrium when enzyme production investment is at the critical threshold (e*). As the investment in enzyme production increases in a producer-cheater mixture, the trade-offs between producer biomass and enzyme production reach a point where enzyme production requires too much energy and becomes unsustainable, causing the producer population to crash (indicated in Figure 2 with solid red vertical lines; e = 0.1753). However, another threshold for enzyme production investment (where e ≠ 0) exists (indicated in Figure 2 with dashed vertical lines). In monoculture, selection favors producer mutants that invest less in enzyme production (i.e., with lower e value), because these mutants can always successfully invade the producer population at equilibrium due to their higher per-capita growth rates (Figure 3A). Over time, this process reduces the production of the enzyme, which reduces the available resource, in turn reducing the population abundance of the producer. Eventually, producer abundance slowly drifts toward a critical production threshold, e* (e*_m; Figure 2A; e = 0.0004). As investment in enzyme production drifts lower than e*_m, the total population size reaches zero abundance, going extinct and causing system collapse (Figure 3C).

FIGURE 2

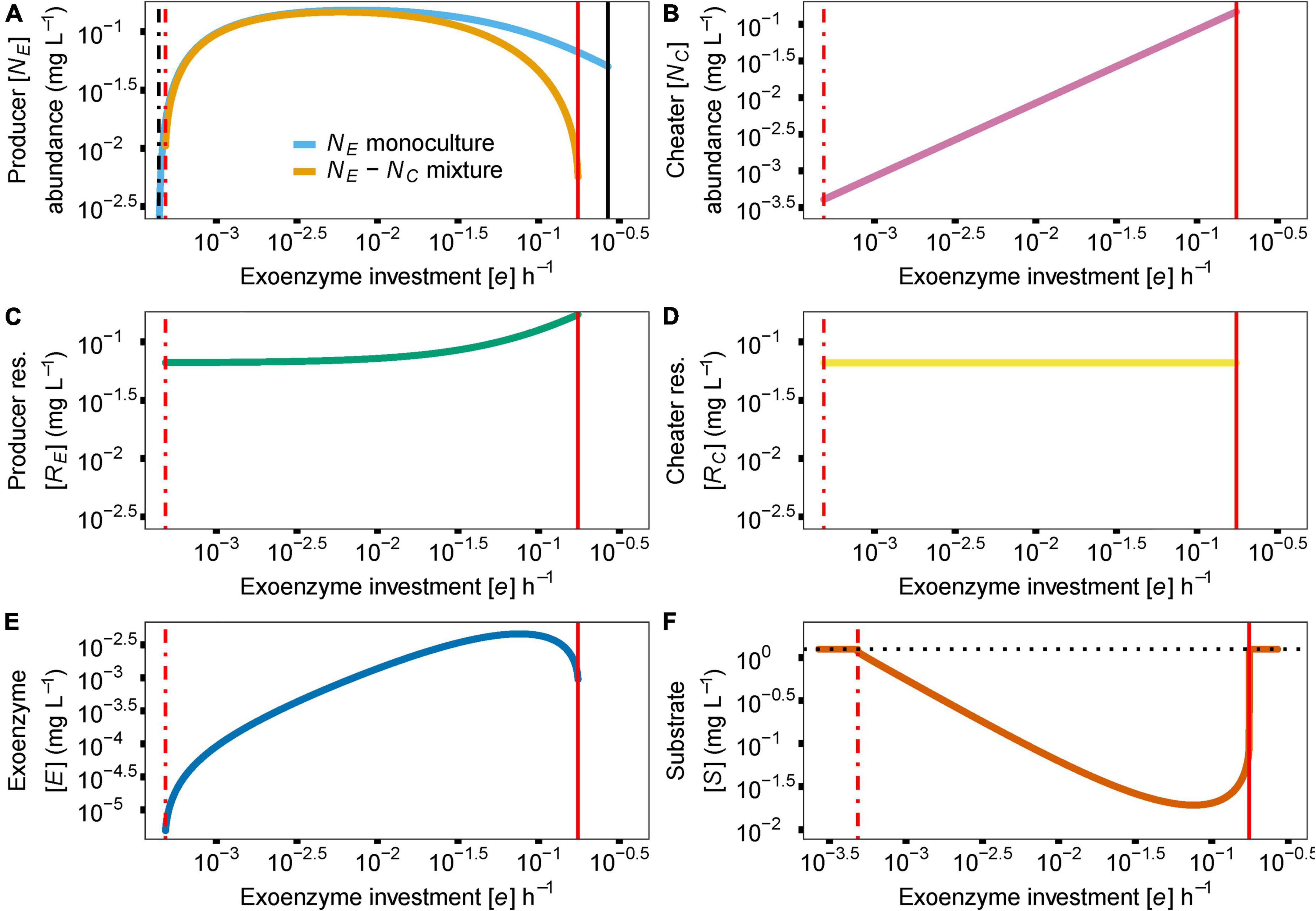
Figure 2. Effect of parameter e (cost of enzyme production) on species abundances and coexistence [y axis indicate abundance of producer (N_E) or cheater (N_C) or concentrations of enzyme (E) or substrate (S)]. The dash-dotted black vertical line indicates a critical e value creating an EES for the producer in monoculture, in the context of enzyme production investment (e*_m = 0.0004). The dash-dotted red vertical line indicates a critical e value creating an EES for the producer in mixed culture, in the context of enzyme production investment (e*_c = 0.0005). Solid vertical lines show the maximum e value before the enzyme producer population collapses due to the increased investment in enzyme production (in black for monoculture e = 0.27; in red for coculture e = 0.1753). In (A) we show the effect of the e* on the abundance of the enzyme producer (N_E) as a monoculture (blue) and in a mixture (gold). Due to the invasibility of the producer monoculture by producers with lower e, producer abundance can eventually drift to zero. On the other hand, the presence of the cheater (N_C) in the same situation creates a discontinuous shift from a positive to a negative equilibrium (e*_c = 0.0005), preventing any further invasion of lower e producers. Since cheater abundance (B), resource release (C,D) and enzyme (E) and substrate (F) concentrations are tightly linked to producer abundance, they follow similar dynamics in producer-cheater mixtures. In the absence of a producer, substrate concentration returns to baseline, indicated by the dotted black horizontal line in (F). Due to the plotting scale, e*_m and e*_c are overlapping and are both shown with a single dash-dotted red vertical line.

FIGURE 3

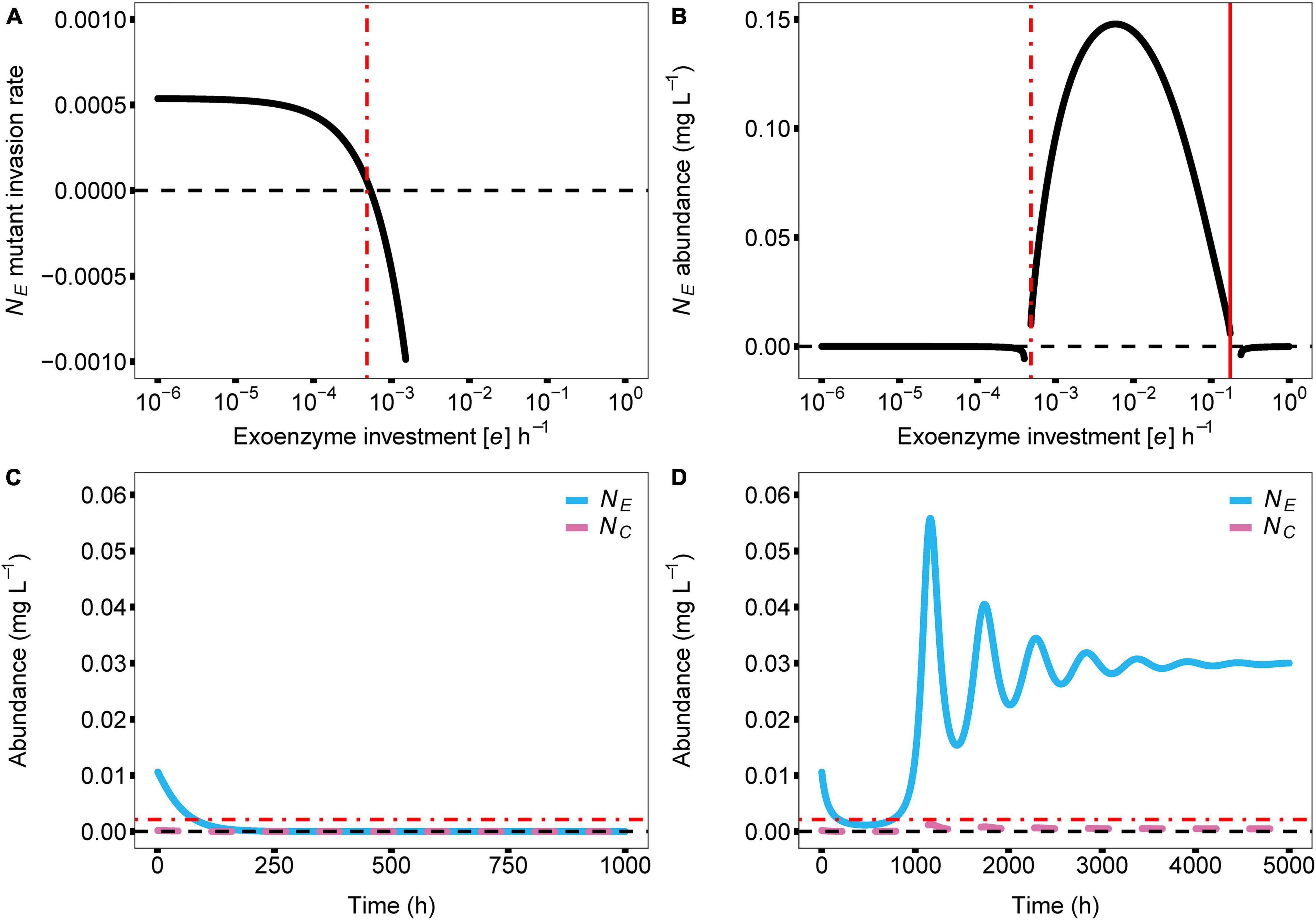
Figure 3. Dynamic relationship of parameter e (cost of enzyme production) with producer abundance (N_E) and with coculture stability and species coexistence. In all panels, the zero value for each y axis is visualised with a dashed black line. (A) Here we show the invasion rate of producers with variations in their investment in enzyme production. Producers who invest less in enzyme production have higher invasion rates and success. At the e for which the invasion success intersects with zero invasion rate, an evolutionarily stable state of the producer population emerges (e* = 0.0005). (B) Effects of model parameter e on the abundance of the enzyme producer. The solid red vertical line signifies the maximum e before negative growth occurs (max e = 0.1753) due to allocating too many resources into enzyme production and not growth. The dash-dotted red vertical line indicates the lowest possible e, a critical enzyme production investment threshold, allowed in the model before negative growth occurs for the enzyme producer, due to lack of resource release from the substrate (e* = 0.0005). This enzyme production investment threshold creates an uninvadable evolutionarily stable state — producers with lower enzyme production investment can no longer invade the producer population due to the presence of the cheater. (C,D) Show the effect of lowering the cost of enzyme production below e*. This change causes a discontinuous shift in equilibrial abundance for the enzyme producer, driving it toward extinction because it is no longer able to produce enough resources to overcome the diffusion gradient toward the cheater. If the cost of enzyme production remains below the threshold value, the enzyme producer is ultimately driven extinct (C). If the cost of enzyme production is increased back above the threshold value before resources are depleted, the enzyme producer is able to recover (D). This is possible due to residual resources in the system, allowing the producer population to recover. Parameters: a = 0.01; g = 138.01; d = 0.10; q = 0.65; m_z = 1.05; r = 1.66; m = 0.11.

In contrast, given the biologically realistic, literature-driven, parameter values we chose for the model, we observed an interesting dynamic when a cheater is present. In a producer-cheater mixture, the cheater creates a resource strain that is strong enough to prevent selection from driving producer enzyme production down to its critical limit (e*_c; Figure 3B; e = 0.0005). This strain on resources creates a discontinuous shift in equilibrium abundance, such that below a different critical threshold, e*_c, equilibrium abundance suddenly drops from positive to zero (as opposed to the slow continuous drift toward zero that occurs in producer monocultures). Moreover, in the mixed culture case where the sudden shift happens, residual resources in the system allow for the possibility of “evolutionary rescue.” In essence, the cheater shifts a continuous decline to extinction into a discreet point that cannot be pushed lower. This happens as a change in system behavior, which appears as if there are residual resources available for the producer to recover. That is, if a new producer mutant should arise with an enzyme production rate that falls above e*_c, it will be able to successfully invade the system, and will ultimately increase enzyme abundance sufficiently to stabilize the system (Figure 3D). In other words, the presence of a cheater allows for the possibility of long-term persistence of both strains, whereas a pure producer monoculture is doomed to relatively rapid extinction. Furthermore, we can observe the response of the model’s other variables to the value of e; cheater abundance (Figure 2B), producer resource (Figure 2C), cheater resource (Figure 2D), exoenzyme concentration (Figure 2E), and substrate concentration (Figure 2F) all follow the changes in enzyme investment e, including the two limits that bring upon the extinction of the producer species.

While resource diffusion does not exhibit the dual-threshold nature of enzyme production investment, it does control producer abundance in a producer-cheater system. As diffusion approaches higher values, producer access to its resource is impeded by the cheater, causing a population extinction and therefore a system collapse (Figure 4, d = 0.37). Similarly, if diffusion is too slow (Figure 4, d = 0.05), the cheater’s access to the resource is restricted, and the cheater population goes extinct, eventually causing producer abundance to drift to zero, following the producer-only evolutionary dynamics described above. Importantly, for the range of biologically realistic model parameters and literature-derived parameter values (Supplementary Table 1) that we consider here, cheaters cannot overgrow the producers. As expected, the rest of the variables in the model follow the rate of diffusing resources d and respond to the extinction of the producer species at high rates of diffusion (Figures 4B–F).

FIGURE 4

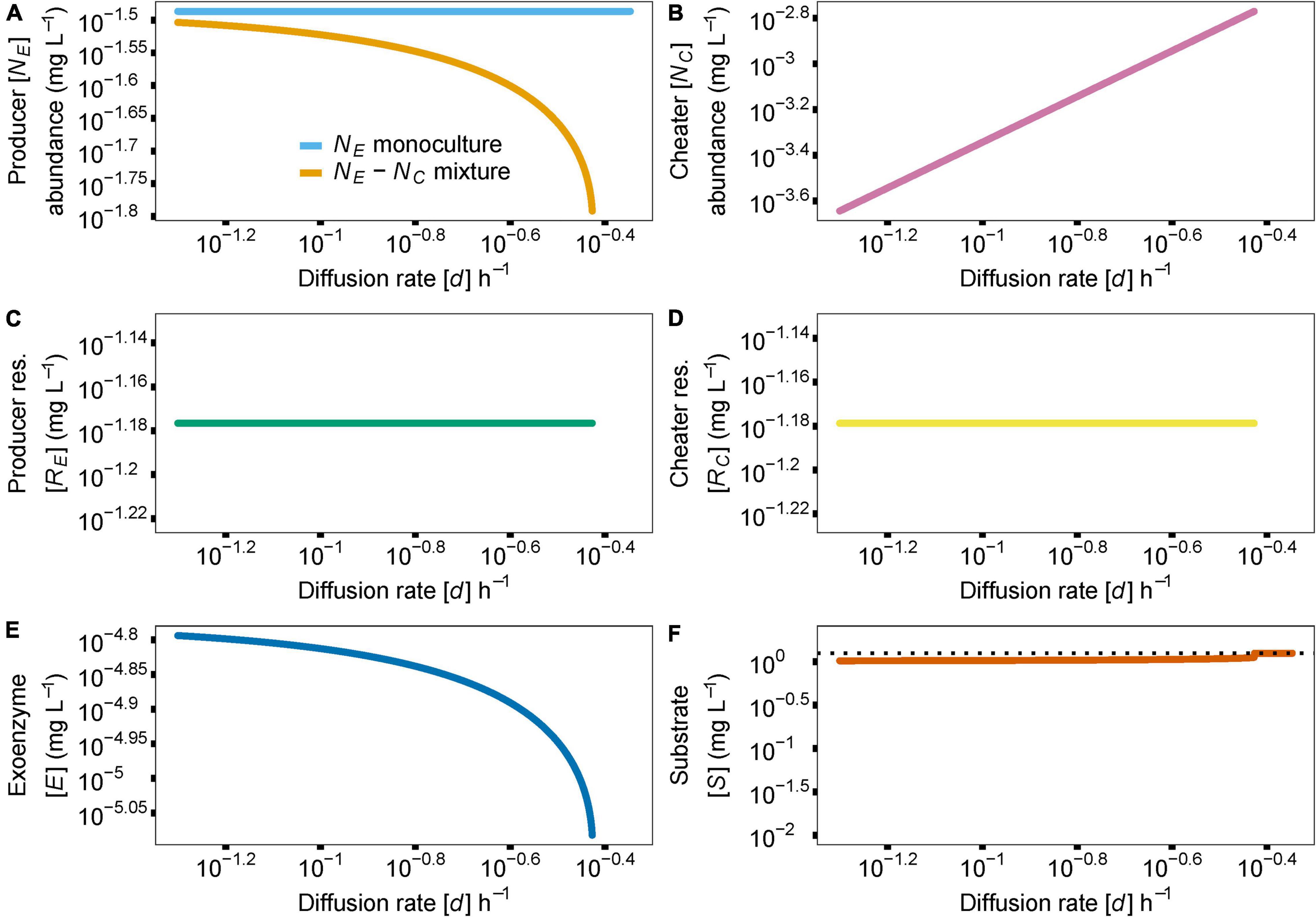
Figure 4. Similar to Figure 3, the effect of resource diffusion rate, parameter d, on species abundances and coexistence is shown (A). Increasing diffusion rate in the producer-cheater mixture [golden line in (A)] reduces resource availability to the producer, leading to extinction and system collapse. Since cheater abundance (B), resource release (C,D) and enzyme (E) and substrate (F) concentrations are tightly linked to producer abundance, the follow the trajectory of producer abundance, in producer-cheater mixtures. In the absence of a producer, substrate concentration returns to baseline, indicated by the dotted black horizontal line in (F). Y axis indicate abundance of producer (N_E) or cheater (N_C) or concentrations of enzyme (E) or substrate (S).

Discussion

Due to their important role in theoretical and experimental microbial ecology, cheaters have been widely studied in multiple systems. While in many cases, cheating is considered an eco-evolutionary prisoner’s dilemma, many have provided evidence that at least in some instances, cheating leads to coexistence as a result of a snowdrift game. We show that coexistence is stabilized by negative frequency dependence of the cheater and expand on the previous literature by showing that cheating further promotes coexistence and that it also encourages the long-term maintenance of cooperative behaviors, such as the production of extracellular public goods. While we do show that producers thrive as a monoculture, this is only in the short-term time scale. Moreover, since cheaters are abundant while cooperative behaviors continue to persist in microbial communities, we focused on evolutionarily stable states of coexistence in a producer-cheater system. Thus, we developed a model showing that the interaction between a producer and a cheater influences the production and maintenance of a public good. Using experimental data to parameterize our model, we observed a dichotomy between scenarios of a producer monoculture and a producer-cheater mixed culture, in the context of enzyme production evolution. In the producer monoculture, a population with a set enzyme investment is always invadable by producer mutants that invest less energy in enzyme production. This trend of ever-decreasing enzyme production for short-term growth benefits eventually causes the population to drift to extinction. In nature, we assume that populations of public good producers are driven by selection toward a lower production of the public good, as a result of intraspecific competition (Morris et al., 2012; Sachs and Hollowell, 2012; Lindsay et al., 2019). We propose that the evolutionarily-stable-state-e*_m effect in the producer monoculture, imposed on the enzyme producer’s abundance (Figure 2B), would not result in extinction in nature if the public good is crucial for survival and has no alternatives. Instead, under these circumstances, the population will eventually have to diverge into coexisting “wild-type” and cheater “mutant” subpopulations because the persistence of the “wild-type” producer is necessary for the survival of both subpopulations (Velicer, 2003; Allison, 2005). Divergence due to intraspecific competition has been a widely studied (Rosenzweig et al., 1994; Travisano et al., 1995; Lenski et al., 1998; Rainey and Travisano, 1998; MacLean et al., 2005; Cooper and Lenski, 2010). Indeed, a cheater like the one we use in our model would have likely emerged due to a similarly critical threshold of an eco-evolutionary process that caused the producer population to bifurcate. Importantly, our results show that in the case of the producer-cheater mixture, cheating might strengthen producer intraspecific competition, thereby leading to conditions where selection favors higher enzyme production. In our simulations, the ultimate result is an increase in the long-term persistence of the system when cheaters are present. Interspecific competition has also been shown to inhibit further adaptive population radiation, such as the emergence of lower e producer invaders in our model, by elimination the ecological opportunity for further adaptive radiation (Bailey et al., 2013). In our model, we simulate such a population divergence with the rescue scenario (Figure 3D).

To further elaborate, this is why invading producer mutants and the cheater appear to be one and the same and yet produced different effects in the model. In the model, the bifurcation event is approached from two different directions. When no cheater is present, selection drives the producer to reduce enzyme production gradually, eventually leading to a smooth shift toward an equilibrium where producer biomass equals zero. In contrast, when the simulation begins with a cheater, reductions in enzyme production by the producer are no longer favored by selection, since such reductions would lead to immediate extinction. In the language of coexistence theory, a system without cheaters is always invadable by a mutant with slightly lower allocations in enzyme production. But, given a cheater that invests nothing at all in enzyme production, no feasible other strategies for low-enzyme-producing mutants remain. Should we consider not a gradual loss of function but a producer mutant with complete loss-of-function mutation in a single step, in a producer monoculture, we would essentially have a reproduction of our system. That is, in the producer monoculture if a mutant with zero enzyme production would arise, it would stabilize the system. But if the same single step mutation took place in our producer-cheater mixture, it could potentially upset the delicate balance that allowed coexistence thus far. An additional example would be the emergence of a cheater, not on the same exoenzyme trait but in a different function. Should this result in the two cheaters interacting, coexistence would again be possible (Özkaya et al., 2018). On the other hand, the question arises as to why mutants with higher enzyme production do not invade a producer population that is gradually losing enzyme production. While the model describes resource semi-privatization, it only refers to public good priority access — a producer mutant with higher enzyme production will still not be able to keep the resource from diffusing away. This leads to higher enzyme production mutants to have lower invasion rates relative to the lower enzyme production mutants.

Such cheater-producer dynamics can either be between strains of the same species or different species (Dragoš et al., 2018). In the planktonic communities of a BQH scenario, adaptive gene loss and production of a vital public good in the microbial community are at equilibrium. Producers keep up the public good production because a reduction in public good concentration would negatively affect the entire community, including themselves. Producers also persist in the community, despite the cheaters, due to advantages inherent to the production of the public good and other cooperative interactions. For example, cheaters of one public good might be cooperators for a different function (Morris et al., 2012; Sachs and Hollowell, 2012). Cheaters could then be diverting resources, saved on one side of the metabolic scale, to the production of another public good (Trivers, 1971) possibly leading to division of labor giving the pair of species a competitive advantage over their individual populations (Morris et al., 2012; Thommes et al., 2019). This would expand the interaction horizon, from cheating, to commensalism (Morris et al., 2012). Indeed, the presence of more than one-way interactions (like cheating) in natural communities helps support the vast biodiversity we observe in nature (Bairey et al., 2016). In such cases, “cheater” would be a relative term, used to describe individual interactions rather than completely defining an organism. Multicellularity is perhaps the most profound example of microbial cooperation. The evolution of multicellularity may also be holding some clues as to the ecological role of cheaters (Rainey and Kerr, 2010; Hammerschmidt et al., 2014; Veit, 2019). Indeed, cheaters might have had a role in the emergence of multicellularity for similar reasons as to those that we explore here – in particular, our results represent yet another example of how such cooperation can arise out of selective pressures working on the level of individual organisms. An example of such altruistic behavior can be seen in protists (Fischer and Hackl, 2016). Infected protists use a virophage, intergraded in their genome, to hijack the replication of an infectious virus. This process results in the release of the defensive virophages instead of the infectious virus, protecting the protist population from further infections and yet the original protist is lysed, nonetheless.

Hardin’s (1968) article has been influencing ecological theory and research ever since, despite the efforts of critics. While most of the academic literature has moved on from the “tragedy of the commons,” the idea continues to influence human economics, politics, and policymaking (Maldonado and Moreno-Sanchez, 2016; Mattke et al., 2017; Gross and De Dreu, 2019). The industrial revolution has changed the world from a zero-sum game to a positive sum game (Clark, 2014) — resources could be created by increased productivity instead of at the expense of others. Being a cooperator frees up the beneficiaries (so-called “cheaters”) to invest more in their own development and eventually returning the benefit in another form (different public good), like in the extension of the BQH scenario. In that sense, “snowdrift” games might be the first step toward complex cooperative communities. Santos et al. (2008) modeled such diverse human social networks. Like in our model, cheaters orchestrate their own demise when they take over a network. Additionally, due to negative frequency selection brought by the increasing numbers of cheaters, they become more vulnerable to producer invasions. Successfully invaded networks remain cooperative. The authors move on to suggest that the act of cooperation is more important than the cost it incurs to the producers.

Looking ahead, our model can be modified to include resource loops where dead cells (m), denatured enzymes (m_z) are recycled back into the substrate pool (S) and an outflow parameter (a_z) is included to maintain parameter concentrations, simulating a chemostat culture. Heterogeneous, spatially structured environments have been shown to prevent (Hauert and Doebeli, 2004) or promote (Santos et al., 2006) the emergence of cooperative interactions, depending on parameters such as dynamic formation/severance of links between individuals. Adding an environmental structure parameter to the model, could inform about differences in cheating-altruism dynamics between spatially distinct environments, such as homogeneous groundwater and heterogeneous soil. In addition to different or multiple parameters, multiple traits can also be considered, instead of a single trait, like in our model.

The complexity of natural ecosystems means that they are extremely difficult to study, experimentally and computationally. Great progress has been made in recent years to study microbial interactions, such as cooperation-cheating, using multiple-trait models (reviewed in Lindsay et al., 2021). However, the outcome in these communities is not always clear, further complicated by the relative strength of interactions between multiple traits (Lindsay et al., 2018). While care should be taken as to not fall in the trap of simplistic explanations for species interactions, under the enticement of intuitive conclusions, simplified systems are still excellent for the mechanistic understanding of individual processes. Ultimately, understanding how organisms like microbes are linked to each other with more than one-way interactions can help us develop better approaches to with industrial bioreactors in biotechnology but also deal with issues in medicine, environmental management, and human socioeconomics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. The R scripts for the producer-cheater coexistence model and graph plots used in this study are available in the Supplementary Material.

Author Contributions

WSH and KK secured funding for the project. CX, ATC, and WSH designed the study and conceptualized the model. CX collected literature biological data and initiated the manuscript writing, which was finalized with substantial contributions from ATC, WSH, and KK. ATC scripted the code for the model. All authors assisted in interpreting the results.

Funding

We gratefully acknowledge the support of the German Centre for Integrative Biodiversity Research (iDiv) Halle-Jena-Leipzig funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) (DFG FZT 118, 202548816). This project has been conducted in the framework of the iDiv-Flexpool – the internal funding mechanism of iDiv. Open Access Publication Fees were funded by the Friedrich Schiller University Jena library open access fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Martin Quaas for the very helpful discussion of cheating in human economics.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.786006/full#supplementary-material

References

Allison, S. D. (2005). Cheaters, diffusion and nutrients constrain decomposition by microbial enzymes in spatially structured environments: constraints on enzymatic decomposition. Ecol. Lett. 8, 626–635. doi: 10.1111/j.1461-0248.2005.00756.x

CrossRef Full Text | Google Scholar

Bailey, S. F., Dettman, J. R., Rainey, P. B., and Kassen, R. (2013). Competition both drives and impedes diversification in a model adaptive radiation. Proc. Biol. Sci. 280:1253. doi: 10.1098/rspb.2013.1253

PubMed Abstract | CrossRef Full Text | Google Scholar

Bairey, E., Kelsic, E. D., and Kishony, R. (2016). High-order species interactions shape ecosystem diversity. Nat. Commun. 7:12285. doi: 10.1038/ncomms12285

PubMed Abstract | CrossRef Full Text | Google Scholar

Becks, L., Ellner, S. P., Jones, L. E., and Hairston, N. G. J. (2010). Reduction of adaptive genetic diversity radically alters eco-evolutionary community dynamics. Ecol. Lett. 13, 989–997. doi: 10.1111/j.1461-0248.2010.01490.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Becks, L., Ellner, S. P., Jones, L. E., and Hairston, N. G. J. (2012). The functional genomics of an eco-evolutionary feedback loop: linking gene expression, trait evolution, and community dynamics. Ecol. Lett. 15, 492–501. doi: 10.1111/j.1461-0248.2012.01763.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Blasius, B., Rudolf, L., Weithoff, G., Gaedke, U., and Fussmann, G. F. (2020). Long-term cyclic persistence in an experimental predator-prey system. Nature 577, 226–230. doi: 10.1038/s41586-019-1857-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Blount, Z. D. (2015). The unexhausted potential of E. coli. Elife 4:5826. doi: 10.7554/eLife.05826

PubMed Abstract | CrossRef Full Text | Google Scholar

Chesson, P. (2000). Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343

CrossRef Full Text | Google Scholar

Clark, G. (2014). “Chapter 5the industrial revolution,” in Handbook of Economic Growth, eds P. Aghion and S. N. Durlauf (Elsevier), 217–262. doi: 10.1016/B978-0-444-53538-2.00005-8

CrossRef Full Text | Google Scholar

Cooper, T. F., and Lenski, R. E. (2010). Experimental evolution with E. coli in diverse resource environments. I. fluctuating environments promote divergence of replicate populations. BMC Evol. Biol. 10:11. doi: 10.1186/1471-2148-10-11

PubMed Abstract | CrossRef Full Text | Google Scholar

Crespi, B. J. (2001). The evolution of social behavior in microorganisms. Trends Ecol. Evol. 16, 178–183. doi: 10.1016/s0169-5347(01)02115-2

CrossRef Full Text | Google Scholar

Dahlman, C. J. (1991). The tragedy of the commons that wasn’t: on technical solutions to the institutions game. Popul. Environ. 12, 285–296.

Google Scholar

Dandekar, A. A., Chugani, S., and Greenberg, E. P. (2012). Bacterial quorum sensing and metabolic incentives to cooperate. Science 338, 264–266. doi: 10.1126/science.1227289

PubMed Abstract | CrossRef Full Text | Google Scholar

De Leenheer, P., Schuster, M., and Smith, H. (2019). Strong cooperation or tragedy of the commons in the chemostat. Math. Biosci. Eng. 16, 139–149. doi: 10.3934/mbe.2019007

PubMed Abstract | CrossRef Full Text | Google Scholar

Dragoš, A., Kiesewalter, H., Martin, M., Hsu, C.-Y., Hartmann, R., Wechsler, T., et al. (2018). Division of labor during biofilm matrix production. Curr. Biol. 28, 1903–1913.e5. doi: 10.1016/j.cub.2018.04.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Estrela, S., Morris, J. J., and Kerr, B. (2016). Private benefits and metabolic conflicts shape the emergence of microbial interdependencies. Environ. Microbiol. 18, 1415–1427. doi: 10.1111/1462-2920.13028

PubMed Abstract | CrossRef Full Text | Google Scholar

Fischer, M. G., and Hackl, T. (2016). Host genome integration and giant virus-induced reactivation of the virophage mavirus. Nature 540, 288–291. doi: 10.1038/nature20593

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster, K. R. (2004). Diminishing returns in social evolution: the not-so-tragic commons. J. Evol. Biol. 17, 1058–1072. doi: 10.1111/j.1420-9101.2004.00747.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Frickel, J., Sieber, M., and Becks, L. (2016). Eco-evolutionary dynamics in a coevolving host-virus system. Ecol. Lett. 19, 450–459. doi: 10.1111/ele.12580

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, D., Luan, Y., Wang, Q., Liang, Q., and Qi, Q. (2015). Construction of cellulose-utilizing Escherichia coli based on a secretable cellulase. Microb. Cell Fact. 14:159. doi: 10.1186/s12934-015-0349-7

PubMed Abstract | CrossRef Full Text | Google Scholar

García-Contreras, R., and Loarca, D. (2020). The bright side of social cheaters: potential beneficial roles of “social cheaters” in microbial communities. FEMS Microbiol. Ecol. 97:fiaa239. doi: 10.1093/femsec/fiaa239

PubMed Abstract | CrossRef Full Text | Google Scholar

Gause, G. F. (1934). The Struggle for Existence. Philadelphia, PA: Williams & Wilkins.

Google Scholar

Gore, J., Youk, H., and van Oudenaarden, A. (2009). Snowdrift game dynamics and facultative cheating in yeast. Nature 459, 253–256. doi: 10.1038/nature07921

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, J., and De Dreu, C. K. W. (2019). Individual solutions to shared problems create a modern tragedy of the commons. Sci. Adv. 5:eaau7296. doi: 10.1126/sciadv.aau7296

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammerschmidt, K., Rose, C. J., Kerr, B., and Rainey, P. B. (2014). Life cycles, fitness decoupling and the evolution of multicellularity. Nature 515, 75–79. doi: 10.1038/nature13884

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1960). The competitive exclusion principle. Science 131, 1292–1297. doi: 10.1126/science.131.3409.1292

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1968). The tragedy of the commons. Science 162, 1243–1248. doi: 10.1126/science.162.3859.1243

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauert, C., and Doebeli, M. (2004). Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 428, 643–646. doi: 10.1038/nature02360

PubMed Abstract | CrossRef Full Text | Google Scholar

Idalia, V.-M. N., and Bernardo, F. (2017). “Escherichia coli as a model organism and its application in biotechnology,” in Escherichia coli, ed. A. Samie (Rijeka: IntechOpen), doi: 10.5772/67306

CrossRef Full Text | Google Scholar

Jones, L. E., Becks, L., Ellner, S. P., Hairston, N. G., Yoshida, T., and Fussmann, G. F. (2009). Rapid contemporary evolution and clonal food web dynamics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 1579–1591. doi: 10.1098/rstb.2009.0004

PubMed Abstract | CrossRef Full Text | Google Scholar

Kreft, J.-U. (2004). Biofilms promote altruism. Microbiology 150, 2751–2760. doi: 10.1099/mic.0.26829-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kremer, C. T., and Klausmeier, C. A. (2013). Coexistence in a variable environment: eco-evolutionary perspectives. J. Theor. Biol. 339, 14–25. doi: 10.1016/j.jtbi.2013.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Leinweber, A., Inglis, R. F., and Kümmerli, R. (2017). Cheating fosters species co-existence in well-mixed bacterial communities. ISME J. 11, 1179–1188. doi: 10.1038/ismej.2016.195

PubMed Abstract | CrossRef Full Text | Google Scholar

Lenski, R. E., Mongold, J. A., Sniegowski, P. D., Travisano, M., Vasi, F., Gerrish, P. J., et al. (1998). Evolution of competitive fitness in experimental populations of E. coli: what makes one genotype a better competitor than another? Antonie Van Leeuwenhoek 73, 35–47. doi: 10.1023/a:1000675521611

CrossRef Full Text | Google Scholar

Letten, A. D., Ke, P.-J., and Fukami, T. (2017). Linking modern coexistence theory and contemporary niche theory. Ecol. Monogr. 87, 161–177. doi: 10.1002/ecm.1242

CrossRef Full Text | Google Scholar

Lindsay, R. J., Jepson, A., Butt, L., Holder, P. J., Smug, B. J., and Gudelj, I. (2021). Would that it were so simple: interactions between multiple traits undermine classical single-trait-based predictions of microbial community function and evolution. Ecol. Lett. 24, 2775–2795. doi: 10.1111/ele.13861

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindsay, R. J., Pawlowska, B. J., and Gudelj, I. (2018). When increasing population density can promote the evolution of metabolic cooperation. ISME J. 12, 849–859. doi: 10.1038/s41396-017-0016-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindsay, R. J., Pawlowska, B. J., and Gudelj, I. (2019). Privatization of public goods can cause population decline. Nat. Ecol. Evol. 3, 1206–1216. doi: 10.1038/s41559-019-0944-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Lloyd, W. F. (1833). Two Lectures on the Checks to Population. Oxford: Oxford University Press.

Google Scholar

MacLean, R. C. (2008). The tragedy of the commons in microbial populations: insights from theoretical, comparative and experimental studies. Heredity 100, 471–477. doi: 10.1038/sj.hdy.6801073x

CrossRef Full Text | Google Scholar

MacLean, R. C., Dickson, A., and Bell, G. (2005). Resource competition and adaptive radiation in a microbial microcosm. Ecol. Lett. 8, 38–46. doi: 10.1111/j.1461-0248.2004.00689.x

CrossRef Full Text | Google Scholar

Maldonado, J. H., and Moreno-Sanchez, R. D. P. (2016). Exacerbating the tragedy of the commons: private inefficient outcomes and peer effect in experimental games with fishing communities. PLoS One 11:e0148403. doi: 10.1371/journal.pone.0148403

PubMed Abstract | CrossRef Full Text | Google Scholar

Mas, A., Jamshidi, S., Lagadeuc, Y., Eveillard, D., and Vandenkoornhuyse, P. (2016). Beyond the black queen hypothesis. ISME J. 10, 1–7. doi: 10.1038/ismej.2016.22

PubMed Abstract | CrossRef Full Text | Google Scholar

Mattke, S., Liu, H., Hoch, E., and Mulcahy, A. W. (2017). Avoiding the tragedy of the commons in health care: policy options for covering high-cost cures. Rand Health Q. 6:1.

Google Scholar

Mitri, S., and Foster, K. R. (2013). The genotypic view of social interactions in microbial communities. Annu. Rev. Genet. 47, 247–273. doi: 10.1146/annurev-genet-111212-133307

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, B. E. L., Henneberger, R., Huber, H., and Moissl-Eichinger, C. (2013). Microbial syntrophy: interaction for the common good. FEMS Microbiol. Rev. 37, 384–406. doi: 10.1111/1574-6976.12019

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, J. J. (2015). Black queen evolution: the role of leakiness in structuring microbial communities. Trends Genet. 31, 475–482. doi: 10.1016/j.tig.2015.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, J. J., Lenski, R. E., and Zinser, E. R. (2012). The black queen hypothesis: evolution of dependencies through adaptive gene loss. MBio 3, 1–7. doi: 10.1128/mBio.00036-12

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, J. J., Papoulis, S. E., and Lenski, R. E. (2014). Coexistence of evolving bacteria stabilized by a shared black queen function. Evolution 68, 2960–2971. doi: 10.1111/evo.12485

PubMed Abstract | CrossRef Full Text | Google Scholar

Oono, R., Anderson, C. G., and Denison, R. F. (2011). Failure to fix nitrogen by non-reproductive symbiotic rhizobia triggers host sanctions that reduce fitness of their reproductive clonemates. Proc. Biol. Sci. 278, 2698–2703. doi: 10.1098/rspb.2010.2193

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostrom, E. (1999). Coping with tragedies of the commons. Annu. Rev. Polit. Sci. 2, 493–535. doi: 10.1146/annurev.polisci.2.1.493

CrossRef Full Text | Google Scholar

Ostrom, E. (2015). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge: Cambridge University Press, doi: 10.1017/CBO9781316423936

CrossRef Full Text | Google Scholar

Ostrowski, E. A. (2019). Enforcing cooperation in the social amoebae. Curr. Biol. 29, R474–R484. doi: 10.1016/j.cub.2019.04.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostrowski, E. A., Shen, Y., Tian, X., Sucgang, R., Jiang, H., Qu, J., et al. (2015). Genomic signatures of cooperation and conflict in the social amoeba. Curr. Biol. 25, 1661–1665. doi: 10.1016/j.cub.2015.04.059

PubMed Abstract | CrossRef Full Text | Google Scholar

Özkaya, Ö, Balbontín, R., Gordo, I., and Xavier, K. B. (2018). Cheating on cheaters stabilizes cooperation in Pseudomonas aeruginosa. Curr. Biol. 28, 2070–2080.e6. doi: 10.1016/j.cub.2018.04.093

PubMed Abstract | CrossRef Full Text | Google Scholar

Pande, S., Kaftan, F., Lang, S., Svatos, A., Germerodt, S., and Kost, C. (2015). Privatization of cooperative benefits stabilizes mutualistic cross-feeding interactions in spatially structured environments. ISME J. 10, 1413–1423. doi: 10.1038/ismej.2015.212

PubMed Abstract | CrossRef Full Text | Google Scholar

Rainey, P. B., and Kerr, B. (2010). Cheats as first propagules: a new hypothesis for the evolution of individuality during the transition from single cells to multicellularity. Bioessays 32, 872–880. doi: 10.1002/bies.201000039

PubMed Abstract | CrossRef Full Text | Google Scholar

Rainey, P. B., and Travisano, M. (1998). Adaptive radiation in a heterogeneous environment. Nature 394, 69–72. doi: 10.1038/27900

PubMed Abstract | CrossRef Full Text | Google Scholar

Rankin, D. J., Bargum, K., and Kokko, H. (2007). The tragedy of the commons in evolutionary biology. Trends Ecol. Evol. 22, 643–651. doi: 10.1016/j.tree.2007.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenzweig, R. F., Sharp, R. R., Treves, D. S., and Adams, J. (1994). Microbial evolution in a simple unstructured environment: genetic differentiation in Escherichia coli. Genetics 137, 903–917.

Google Scholar

Sachs, J. L., and Hollowell, A. C. (2012). The origins of cooperative bacterial communities. MBio 3, 1–3. doi: 10.1128/mBio.00099-12

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, F. C., Pacheco, J. M., and Lenaerts, T. (2006). Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. U.S.A. 103, 3490–3494. doi: 10.1073/pnas.0508201103

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, F. C., Santos, M. D., and Pacheco, J. M. (2008). Social diversity promotes the emergence of cooperation in public goods games. Nature 454, 213–216. doi: 10.1038/nature06940

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuster, M., Foxall, E., Finch, D., Smith, H., and De Leenheer, P. (2017). Tragedy of the commons in the chemostat. PLoS One 12:e0186119. doi: 10.1371/journal.pone.0186119

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, H. L., and Thieme, H. R. (2012). Persistence of bacteria and phages in a chemostat. J. Math. Biol. 64, 951–979. doi: 10.1007/s00285-011-0434-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, J. M. (1976). Evolution and the theory of games: in situations characterized by conflict of interest, the best strategy to adopt depends on what others are doing. Am. Sci. 64, 41–45.

Google Scholar

Smith, P., and Schuster, M. (2019). Public goods and cheating in microbes. Curr. Biol. 29, R442–R447. doi: 10.1016/j.cub.2019.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Strassmann, J. E., Zhu, Y., and Queller, D. C. (2000). Altruism and social cheating in the social amoeba dictyostelium discoideum. Nature 408, 965–967. doi: 10.1038/35050087

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugden, R. (2005). The Economics of Rights, Co-Operation and Welfare. London: Palgrave Macmillan, doi: 10.1057/9780230536791

CrossRef Full Text | Google Scholar

Thommes, M., Wang, T., Zhao, Q., Paschalidis, I. C., and Segrè, D. (2019). Designing metabolic division of labor in microbial communities. mSystems 4:18. doi: 10.1128/mSystems.00263-18

PubMed Abstract | CrossRef Full Text | Google Scholar

Tilman, D. (1982). Resource competition and community structure. Monogr. Popul. Biol. 17, 1–296.

Google Scholar

Travisano, M., Vasi, F., and Lenski, R. E. (1995). Long-term experimental evolution in Escherichia coli. III. variation among replicate populations in correlated responses to novel environments. Evolution 49, 189–200. doi: 10.1111/j.1558-5646.1995.tb05970.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Trivers, R. L. (1971). The evolution of reciprocal altruism. Quart. Rev. Biol. 46, 35–57. doi: 10.1086/406755

CrossRef Full Text | Google Scholar

Veit, W. (2019). Evolution of multicellularity: cheating done right. Biol. Philos. 34:34. doi: 10.1007/s10539-019-9688-9

CrossRef Full Text | Google Scholar

Velicer, G. J. (2003). Social strife in the microbial world. Trends Microbiol. 11, 330–337. doi: 10.1016/s0966-842x(03)00152-5

CrossRef Full Text | Google Scholar

Velicer, G. J., Kroos, L., and Lenski, R. E. (2000). Developmental cheating in the social bacterium Myxococcus xanthus. Nature 404, 598–601. doi: 10.1038/35007066

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Robert, L., Pelletier, J., Dang, W. L., Taddei, F., Wright, A., et al. (2010). Robust growth of Escherichia coli. Curr. Biol. 20, 1099–1103. doi: 10.1016/j.cub.2010.04.045

PubMed Abstract | CrossRef Full Text | Google Scholar

West, S. A., Diggle, S. P., Buckling, A., Gardner, A., and Griffin, A. S. (2007). The social lives of microbes. Annu. Rev. Ecol. Evol. Syst. 38, 53–77. doi: 10.1146/annurev.ecolsys.38.091206.095740

CrossRef Full Text | Google Scholar