Discovering Ecological Relationships in Flowing Freshwater Ecosystems

Introduction

Global biodiversity has been strongly declining for many years (Butchart et al., 2010), which calls for appropriate and effective conservation measures (Pereira et al., 2010). However, despite considerable efforts, it has proven difficult to halt biodiversity decline (Mace et al., 2018). A good understanding of ecological responses to environmental change is key in designing effective conservation strategies. Experiments offer the opportunity to test specific ecological responses and relationships in randomized controlled trials. In these trials, organisms or sites are randomly assigned to a specific treatment or control group, which provides a solid basis for causal inference (Midolo et al., 2019). Knowledge obtained in controlled experiments is, however, often not directly transferable to the field situation, where additional processes are at play (Larsen et al., 2019). At the same time, controlled trials are usually impossible to conduct in large ecosystems for ethical, financial, and practical reasons (Kerr et al., 2007).

Because of these inherent limitations of controlled experiments, and facilitated by the growing availability of monitoring data, ecologists are increasingly exploring the potential of using observational data for ecological inference (Sagarin and Pauchard, 2010). While these data are relatively easy to collect across large regions, their analysis is typically challenging, for example, due to unmeasured variables that may result in spurious correlations (Larsen et al., 2019). Structural equation modeling (SEM) is a popular approach to test specific hypotheses based on observational data and explicitly allows for the modeling of latent or hidden variables (Bollen, 2005). This makes SEM a powerful tool to test and compare hypotheses that include relationships between multiple variables. SEM has a long and successful history in ecology (Grace and Pugesek, 1997; Grace and Keeley, 2006), but at the same time has its limitations. SEM typically requires detailed theoretical knowledge of a system to formulate a number of candidate models (Fan et al., 2016). This makes SEM ill-suited for analyzing complex ecological systems across large geographic extents. Causal discovery algorithms provide a means to search for invariant relationships (Spirtes et al., 2001), i.e., those relationships that have to be included in structural equation models to properly model the dependencies and independencies in the observed data. Instead of requiring the user to specify a set of candidate models, causal discovery algorithms are exploratory and consider all possible direct and indirect relationships over a given set of variables. Constraint-based causal discovery algorithms are considered to be particularly promising because of their ability to handle hidden variables (Glymour et al., 2019). These algorithms are commonly used in health care studies (Sokolova et al., 2015; Młyńczak and Krysztofiak, 2018) and gain traction in Earth system sciences (Runge et al., 2019), but, despite the huge potential, are virtually unused in ecology.

Here, we present a causal discovery algorithm designed to model the ecological relationships in streams, building upon the Fast Causal Inference (FCI) algorithm (Spirtes et al., 2001). The key innovation of our approach is that it takes into account the longitudinal hydrological connectivity that is characteristic of river networks. More specifically, we connect the variables measured at a given location to the conditions measured upstream in the river network. This approach does not only account for spatial correlations but also provides additional information for revealing ecological relationships. We apply our new approach to identify causes of reductions in the ecological integrity of fish and invertebrate assemblages in rivers in the US state of Ohio, based on a high-quality dataset consisting of measurements carried out according to a systematic and standardized protocol (Kapo et al., 2014). Further, this dataset has been analyzed in multiple previous studies (Pilière et al., 2014; Zijp et al., 2017), which offers opportunities to compare our findings with results reported previously.

Materials and Methods

Model Approach

Fast Causal Inference Algorithm

Our approach is based on the Fast Causal Inference (FCI) algorithm (Spirtes et al., 2001). The FCI algorithm is a constraint-based causal discovery algorithm that takes observational data as input and returns a causal graph as output (Figure 1). The algorithm assumes that the observational data are generated by an underlying model that can be represented by a directed acyclic graph, where acyclic means that the graph does not contain any causal cycles. It consists of two phases: the skeleton phase and the orientation phase. We explain the two phases based on an illustrative example representing a hypothetical study analyzing the relationship between the performance of two plant species, two parasite species and one butterfly species. For simplicity, we assume that the ground truth causal structure is as shown in Figure 1A. Note that water influences both plant species, yet is not included in our dataset, so it represents a hidden or latent variable.

FIGURE 1

Figure 1. Schematic illustration of the Fast Causal Inference (FCI) algorithm for a system consisting of five measured variables—the performance of two parasite species, two plant species and one butterfly species—and one hidden variable—water. (A) The true underlying causal network in which water has a causal influence on both plant species, the first parasite species influences the first plant species, the second parasite species influences the second plant species, and the second plant species has a causal effect on the butterfly species. (B) The starting network of the skeleton phase in which each node is connected to each other node. (C) The output of the skeleton phase, called the skeleton, in which nodes are connected to other nodes if and only if they cannot be separated by taking into account other variables in the model. (D) The result after the v-structure orientation rule. (E) The final output of the FCI algorithm after the orientation phase.

The starting point of the skeleton phase is a network in which each variable—in the graph also called a node—is connected by an edge with all other nodes (Figure 1B). The algorithm then consecutively tests for independence between variables by applying (conditional) independence tests. Two variables are conditionally independent if one variable is irrelevant for the other variable, given that a set of additional variables is taken into account. The algorithm performs the independence tests for pairs of variables, first taking into account no additional variables. The number of additional variables is then increased systematically. If two variables are found to be (conditionally) independent, the edge between the nodes is immediately removed from the network. This procedure is repeated until no further tests are possible. The end result (called the skeleton) is a network in which two nodes are connected if, and only if, it is impossible to separate them by conditioning upon other variables in the network. In the example, the algorithm finds that parasite 1 and parasite 2 are independent, leading to the removal of the edge between them. Likewise, the algorithm finds that parasite 1 is independent of both plant 2 and the butterfly and that parasite 2 is independent of plant 1. The algorithm then starts to take into account additional variables and finds that parasite 2 and plant 1 become independent of the butterfly if it takes into account plant 2. After that, the algorithm cannot find any more conditional independences and end up with the skeleton (Figure 1C).

The orientation phase determines the directions of the connections in the skeleton according to a set of orientation rules. Zhang (2008) showed that a set of 13 orientation rules is sufficient to find all available orientations from observational data and proved that the resulting orientations are valid given that the conditional independence tests are correct. At the start of the orientation phase, none of the edges is oriented, as expressed by circle marks at both ends of all edges in the skeleton (Figure 1C). The algorithm then applies the rules hierarchically, such that each rule starts from the results of the preceding rule(s). Each rule searches the entire skeleton for specific edge structures and combines these structures with the results of the previously carried out conditional independence tests. For example, the first orientation rule, known as the v-structure rule, searches for triples of nodes {a, b, c} where b is connected to both a and c, but a and c are not directly connected, as revealed by the conditional independence test. If this structure is found and, additionally, node b was not needed to make a and c independent, then it follows that b cannot be a cause of a or c. This enables the algorithm to orient two arrowheads in the network as a –> b <– c. In our example, the algorithm would find the triple {parasite 1, plant 1, plant 2}, where parasite 1 and plant 2 are independent without taking into account plant 1. As a result, the triple is oriented as parasite 1 o–> plant 1 <–o plant 2. Likewise, the algorithm finds another v-structure in the triple {parasite 1, plant 1, plant 2}, where the orientation rule leads to the structure plant 1 <–> plant 2 <–o parasite 2 (Figure 1D). Building upon the results of the first orientation rule, the second orientation rule searches for similar triples {a, b, c} with an arrowhead at b on the edge to a, but not on the edge to c, for which it can be shown that node b must be a cause of c. We consequently can orient the connections as a –> b –> c in the network. In our example, the algorithm would find the triple {parasite 2, plant 2, butterfly}, which can be oriented as parasite 2 o–> plant 2 –> butterfly (Figure 1E). After that, no more orientation rules apply in this example, but in general there are 13 orientation rules, as described by Zhang (2008). Per rule, orientations are made immediately and each rule is applied to all possible connections until it does not trigger anymore. Remaining circle marks indicate that from the data it was impossible to determine whether an edge mark should be an arrowhead or a tail. In Table 1, we list the types of connections that can be found during the orientation phase.

TABLE 1

Table 1. Possible relationships between two variables (here represented by A and B) and their interpretation in a causal graph.

The algorithm will produce meaningful results even in the presence of latent (hidden) variables, which is crucial as most likely not all relevant variables are included in the observational data. In our example, water is such a hidden variable. Comparing the true underlying model in the example (Figure 1A) with the output (Figure 1E), we see that the algorithm successfully detected the causal relationship between plant 2 and the butterfly, despite the presence of the hidden variable. Further, the algorithm found a bidirected edge between plant 1 and plant 2, indicating the presence of the hidden variable and its influence on plant 1 and plant 2.

In the FCI algorithm and similar causal discovery algorithms, the conditional independence test can be selected such that it fits the characteristics of the data and the presumed shape of the relationships between variables. Commonly, variables are assumed to have linear relationships and additive Gaussian errors, which is particularly easy to test by calculating partial correlations (Lawrance, 1976). While this type of test is computationally efficient, not all ecological relationships fulfill these assumptions. Therefore, in this study, we use the Kernel Conditional Independence Test (KCIT) presented in Zhang et al. (2012). In contrast to correlation-based conditional independence tests, the KCIT is able to detect both linear and non-linear relationships between variables and is hence more suited for ecological applications. The KCIT does not assume a functional form and as such can detect any type of relationship.

Adapted Algorithm

We start from a set of variables measured at different locations in a river network. The FCI algorithm is able to correctly identify connections and orientations only given that the measured data are independent and identically distributed (Spirtes et al., 2001). Because this assumption is violated in data such as ecological data sampled from a river network, we adapted the FCI algorithm (Mielke et al., 2020). In our adapted algorithm, we first divide the variables into four categories (Figure 2): (i) elements that are being transported downstream (e.g., chemical substances) hence are characterized by an upstream-downstream connection; (ii) instream characteristics that are not being transported downstream (e.g., physical habitat quality); (iii) biotic variables; and (iv) aspects describing the position of a site within the larger river network (e.g., physiographical variables and latitude/longitude). Here, we call the sets water quality (W), physical habitat quality (P), biotic variables (B), and out-of-stream (O), respectively. For the water quality variables, we assume that the Markov assumption holds, i.e., the measurements at each location are independent of all measurements further up the river network, given the measurements at locations directly upstream (Figure 2).

FIGURE 2

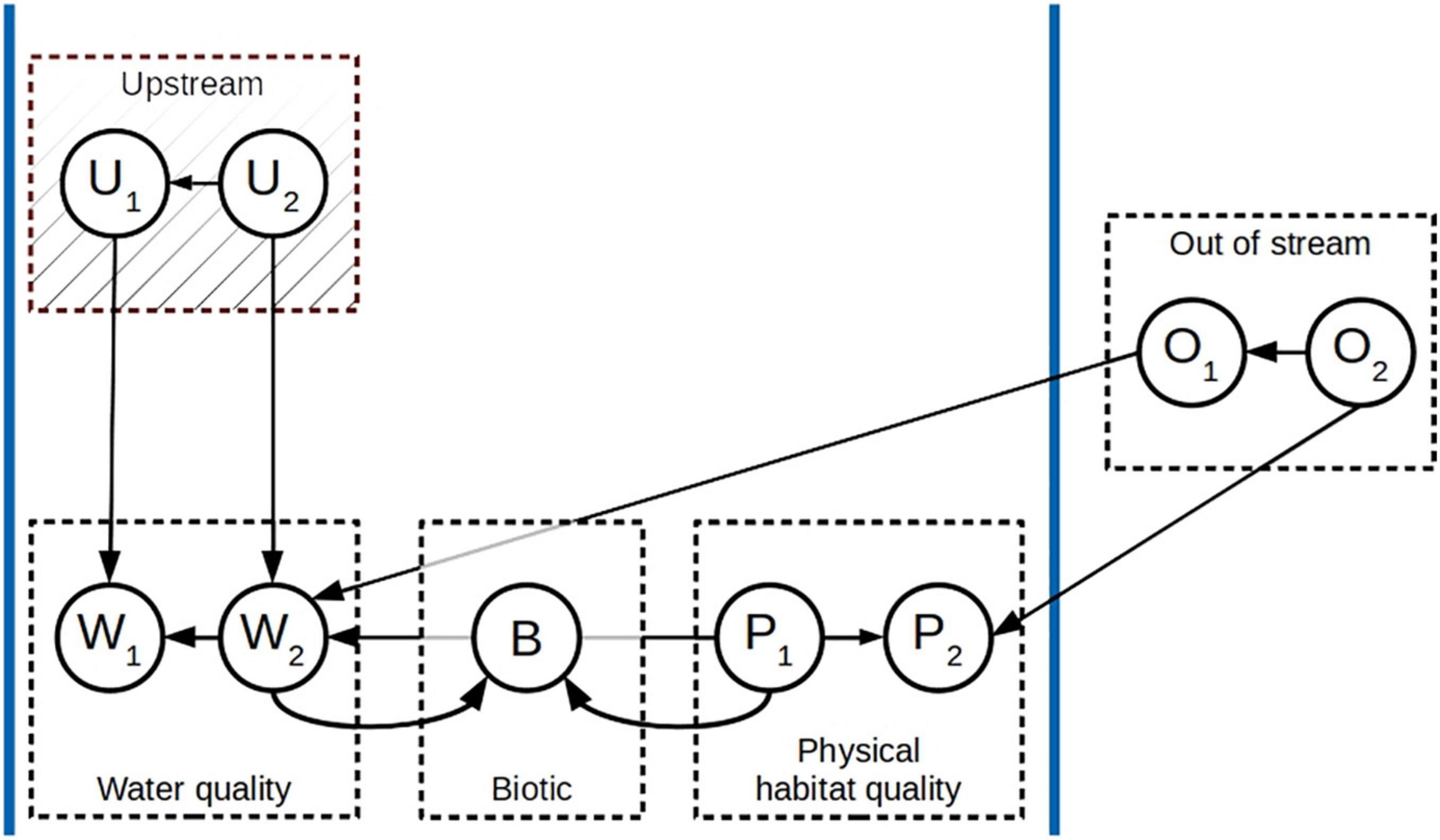
Figure 2. Exemplary schematic of a generative model of ecological relationships in flowing freshwater ecosystems, including the different groups of variables (water quality, physical habitat quality, biotic, out of stream, and upstream water quality) and their relationships. In this example, each group of variables contains two variables, indicated by their subscript, apart from the biotic variable group which consists of a single variable. The variable set U consists of the variables in the set W measured at the locations upstream.

Before applying the core part of our algorithm, we calculate for each water quality variable W_j measured at location k_i the upstream value of that variable across all the locations directly upstream. We call this set of variables U. Our algorithm includes three further important adjustments to the standard FCI algorithm. First, unnecessary independence tests are removed from the skeleton phase, i.e., we do not test for independence of pairs of downstream and upstream water quality variables, which are dependent by definition. Further, we exclude connections that are impossible or unlikely given the characteristics of the system, i.e., we exclude directed relationships from downstream to upstream locations, from water quality to out-of-stream variables, and from the biotic variables (B) to the environmental variables (W and P). Lastly, we do not perform any tests for pairs of upstream variables, but instead, impose the structure that we found for the downstream variables. These constraints ensure that we maintain the inherent logic of the dataset and reduce the computation time of the algorithm.

In our adapted FCI algorithm, we further incorporate two common FCI modifications: the conservative modification (Ramsey et al., 2012) and the stable modification (Colombo and Maathuis, 2012). The conservative modification helps to avoid incorrect orientations by performing additional tests. If there are conflicts between test results, which can occur if there is too little information in the data, edges are not oriented. The stable modification makes the algorithm independent of the order of the independence tests. In its base form, the FCI algorithm removes connections immediately after an independence is found. As a consequence, tests that are carried out later are influenced by the results of previous tests. With the stable modification, connections are removed only before the number of variables that are taken into account in the tests is increased.

In Mielke et al. (2020), we tested and compared the performance of our modified algorithm with the performance of the FCI algorithm on a simulated dataset with known ground truth. In this comparison, we found that our approach produced fewer false positives (i.e., edges that were not part of the ground truth). It also detected a larger proportion of the edge orientations and with higher accuracy.

Case Study Data

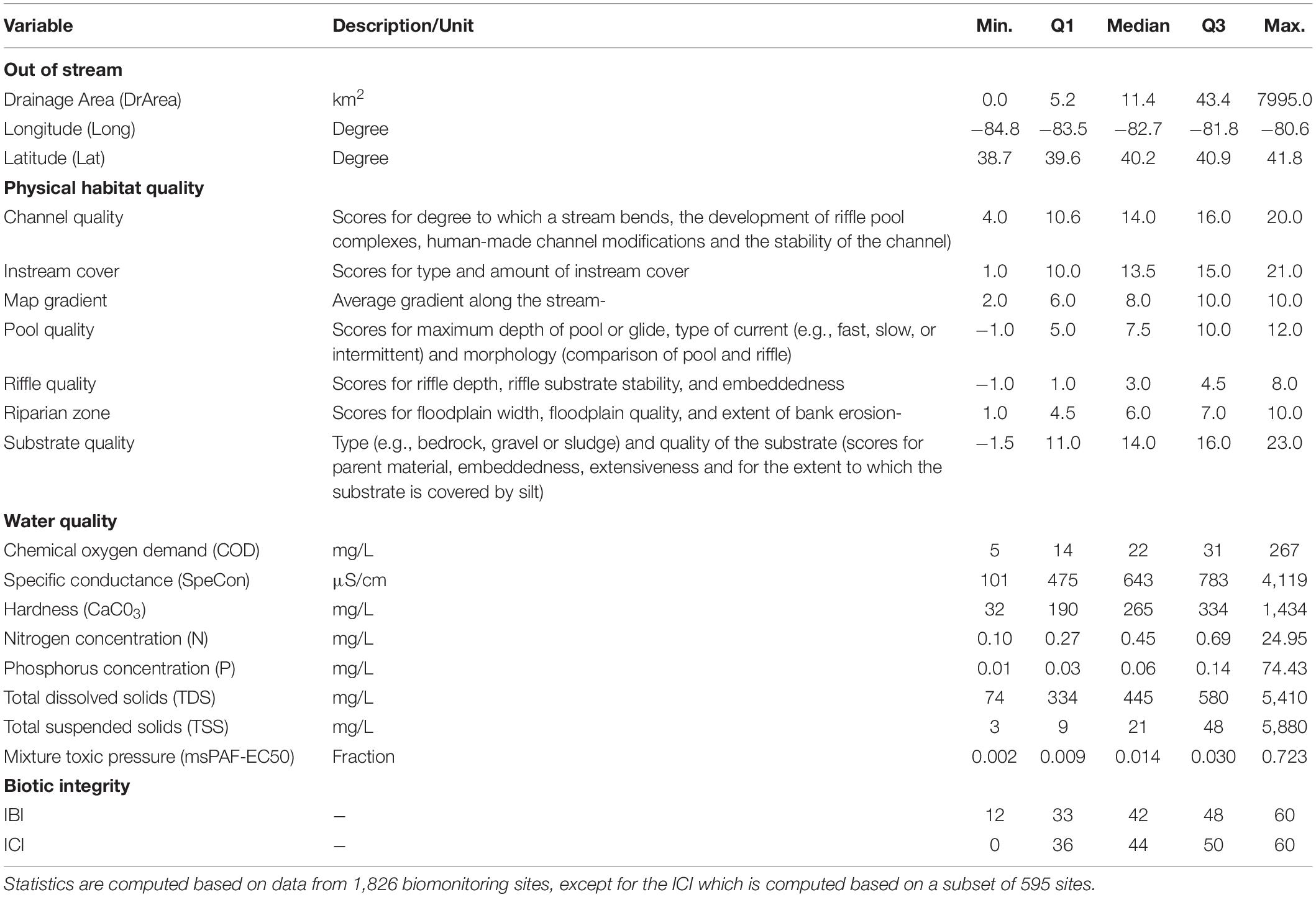
To test our approach on real-world data, we applied our causal discovery algorithm to identify potential causes of impairment of the ecological integrity of fish and invertebrate assemblages in rivers in Ohio, based on a dataset covering 1,826 biomonitoring sites sampled between 2000 and 2007 (Kapo et al., 2014; Zijp et al., 2017). We used the version of the dataset as curated and described by Zijp et al. (2017). The dataset includes presence-absence data and abundance data of fish (available for all 1,826 sites) and invertebrates (available for 595 of the sites) as well as two composite metrics of community integrity. We focused on these aggregated metrics as these collate a multitude of measured variables into overarching indicators of the ecological status of the communities, which can be used to support water quality protection, assessment, and management practices. The integrity of the fish community is captured by the Index of Biotic Integrity (IBI). The IBI is constructed by comparing the fish community at a given site to an undisturbed reference community, located in a river of similar size and in a similar region. Reference communities are obtained from sites with minimal human influence based on expert judgment. The IBI is composed of 12 sub-metrics indicative of various aspects of community integrity, including the total number of species, number of individuals, and the proportion of top predators, with each sub-metric getting a score of 1, 3, or 5. A low score represents a high deviation from the reference site (Fausch et al., 1984). Similarly, the Invertebrate Community Index (ICI) combines 10 sub-metrics including the total number of taxa and the percentage of tolerant organisms in comparison to a reference community. For the ICI, the possible scores for each sub-metric are 0, 2, 4, or 6 (Ohio Environmental Protection Agency, 1989). The IBI ranges from 12 to 60 whereas the ICI ranges from 0 to 60.

In addition to the biotic integrity metrics, the monitoring dataset contains information on physiography, physical habitat quality, and water quality (Table 2). For physiography, we considered the drainage area as well as longitude and latitude, for two reasons: (i) to check whether our approach is successful in accounting for spatial correlations in the system and (ii) as proxies of unmeasured variables, i.e., to examine whether we are missing relevant variables. If spatial correlations are well accounted for and the relevant variables underlying ecological community integrity are included, we would expect that longitude and latitude have no or only a few connections to the other variables in the network. Physical habitat quality is represented by the seven metrics that together constitute the so-called Qualitative Habitat Evaluation Index (QHEI; Ohio Environmental Protection Agency, 2006). The QHEI is an ordinal expert-based metric, with high scores indicating good habitat quality. As water quality variables we included chemical oxygen demand, conductivity, hardness, nitrogen concentration, phosphorus concentration, total dissolved solids, total suspended solids, and mixture toxic pressure. The latter is based on concentrations of chemical pollutants and 50%-effect concentrations, derived from ecotoxicity test data sets. The toxic pressure was derived from concentrations of industrial products, household products, synthetic estrogens, and pharmaceuticals (Posthuma and de Zwart, 2006) and is expressed as msPAF-EC50, a metric associated with ecological impacts (Posthuma et al., 2020).

TABLE 2

Table 2. Variables included in our models.

Application and Evaluation

Because the numbers and locations of the monitoring sites differ between the fish and invertebrate monitoring data, we built separate models for IBI and ICI. For each water quality variable, we calculate the influence from upstream by calculating a discharge-weighted mean value of the upstream measurements. We implemented the weighting to reflect that larger tributaries have more influence on the conditions downstream than smaller tributaries. We retrieved the upstream-downstream connections and the discharge data from the HydroSHEDS database (Lehner et al., 2008). We then removed the locations without any upstream locations from the subsequent analysis, resulting in datasets for IBI and ICI with 1,149 and 526 observations, respectively. Because the water quality variables showed right-skewed distributions (Table 2), we applied a log transformation before applying our algorithm. To evaluate the reliability of the connections and orientations, we performed block bootstrapping (Lahiri, 1999). First, we divided the measurement area into overlapping blocks of equal size. We then drew random blocks with replacement and added all measurement locations in the selected blocks to our bootstrap sample. We sampled blocks until, for both the IBI dataset and the ICI dataset, the dataset size equaled or exceeded the number of observations in the ICI dataset (526 observations). We kept the size of the datasets consistent between IBI and ICI to be able to compare the models. To determine the size of the bootstrapping blocks, we examined correlations between locations as a function of distance. We found that at a distance of 50 km, correlations were negligible (Supplementary Figure 1) and we used a side length of the blocks of 35 km to cover that distance.

We built 100 networks for both the IBI dataset and the ICI dataset using a significance level of 95% for the conditional independence tests. We limited our conditional independence tests to conditioning sets of size 3 as these tests are known to be unreliable for large conditioning sets (Bromberg et al., 2009). We decided to include a connection in the final network if it was part of at least 65% of all networks (Meinshausen and Bühlmann, 2010). Likewise, for an orientation to appear in the final network, it had to be oriented in the same way in at least 65% of all networks. Our algorithm does not distinguish between positive and negative relationships. To give an indication of the direction of the relationships involving the biotic endpoint variables, we calculated partial correlations after having established the networks, conditioning on the neighboring variables in the final networks. The entire workflow is illustrated in Supplementary Figure 2.

We conducted our analysis in R, version 4.0.3 (R Core Team, 2020). Our code is available at https://github.com/KoMiel/currentFCIapplication. We based our implementation of the adapted FCI algorithm on the FCI method of the R package pcalg (Kalisch et al., 2012). For the KCIT, we used the implementation available in the package RCIT (Strobl et al., 2019).

Results

Our algorithm revealed that the biotic integrity variables IBI and ICI are directly connected to the concentration of nitrogen (N) (Figures 3, 4 and Supplementary Tables 1–8). Likewise, in both models, biotic integrity is directly connected to one of the physical habitat quality variables. Specifically, IBI is directly linked to the quality of the river substrate and ICI is directly linked to the quality of the river channel. We further found a connection with latitude for IBI but not for ICI. According to the partial correlation analysis, IBI is negatively related to N (−0.28) and latitude (−0.30) and positively related to substrate quality (0.22). For ICI we found a negative relationship with N (−0.33) and a positive relationship with channel quality (0.19).

FIGURE 3

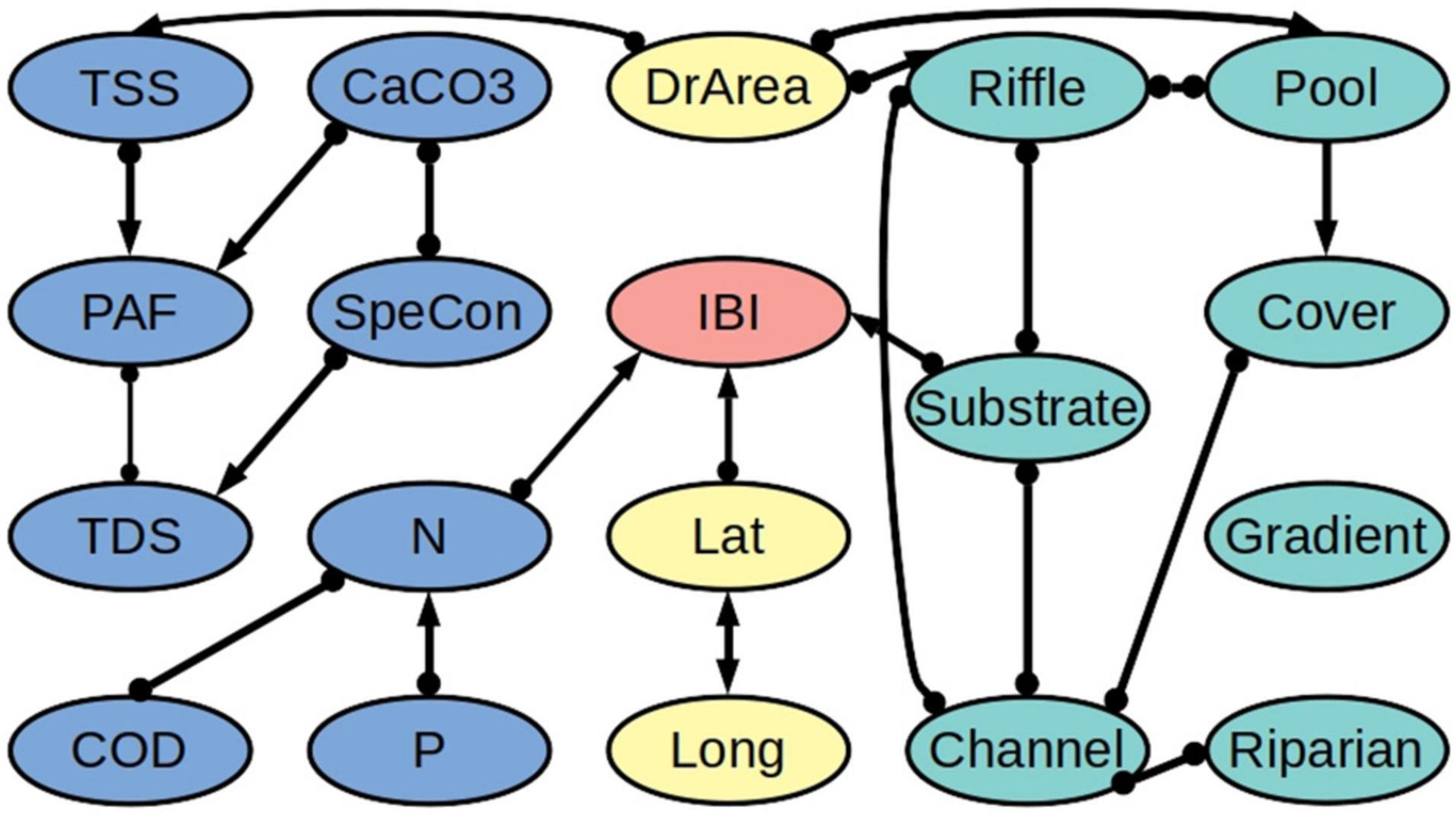
Figure 3. Network of ecological relationships for the freshwater fish assemblage Index of Biotic Integrity (IBI) in Ohio, showing the relationships among the IBI (red), the water quality variables (blue), the physical habitat quality variables (turquoise), and the out-of-stream variables (yellow). Upstream variables are mainly connected to their downstream partners and are excluded from the figure to improve readability. The thickness of a connection indicates how many of the bootstrapping samples it appeared in. The abbreviations are explained in Table 2. A summary of the bootstrapping results is provided in Supplementary Tables 1–3, 7.

FIGURE 4

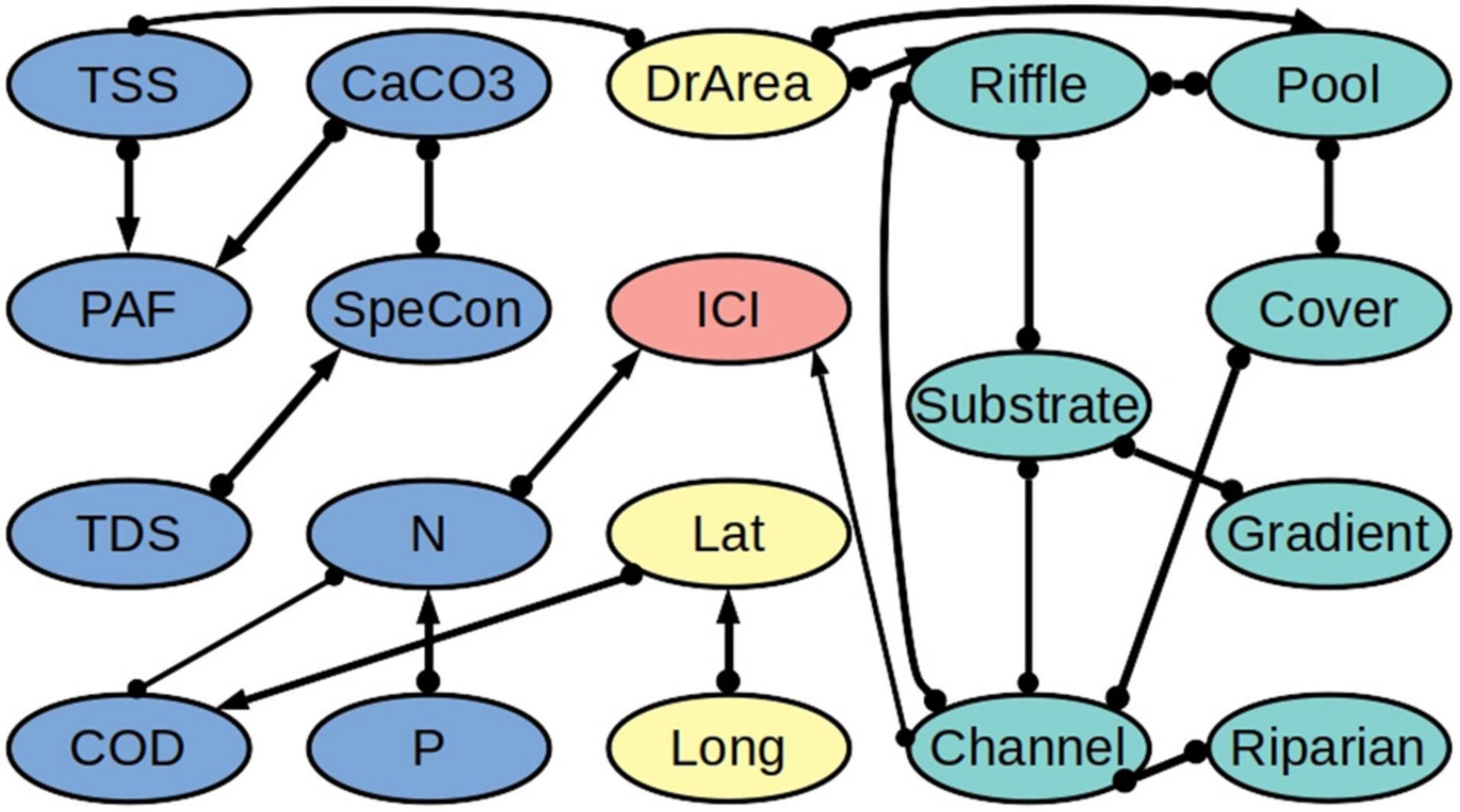
Figure 4. Network of ecological relationships for the Invertebrates Community Index (ICI) in freshwater systems in Ohio, showing the relationships among the ICI (red), the water quality variables (blue), the physical habitat quality variables (turquoise), and the out-of-stream variables (yellow). Upstream variables are mainly connected to their downstream partners and are excluded from the figure to improve readability. The thickness of a connection indicates how many of the bootstrapping samples it appeared in. The abbreviations are explained in Table 2. A summary of the bootstrapping results is provided in Supplementary Tables 4–6, 8.

We found that the water quality variables and the physical habitat quality variables are not directly linked, but only indirectly via the drainage area (DrArea). Further, while we tested for all possible relationships between downstream and upstream water quality variables (i.e., including combinations of different variables), we found that upstream water quality variables are related to their downstream counterparts only, apart from one connection to latitude. Additionally, we found relatively few connections between geographic location (latitude and longitude) and the other variables.

Due to the heterogeneity in the data and the different underlying datasets, we observed differences between the IBI and ICI models. Comparing the two models, 17 out of 20 edges are shared between the two models, and of the corresponding 34 edge marks, 26 are oriented in the same way. Likewise, the heterogeneity in the data led to variability in the direction of connections between bootstraps. Of all cause-effect relationships over all bootstrap models, 10% for the IBI dataset and 14% for the ICI dataset are relationships that are in conflict with the majority decision over all bootstraps (Supplementary Tables 1–6). With our threshold being set at 65%, this should not have a major influence on our final output.

Discussion

Case Study Results

We developed and applied a novel adaptation of the FCI causal discovery algorithm to reveal the network of ecological relationships in freshwater systems in Ohio. The results of our analysis indicate that the concentration of nitrogen is a key variable for fish and invertebrate community integrity in Ohio, likely negatively impacting both. In contrast, we did not find any direct connection between biotic integrity and the concentration of phosphorus, indicating that eutrophication impacts on fish and invertebrate community integrity in Ohio are primarily governed by nitrogen. This finding is in line with previous studies that evaluated the impact of nitrogen and phosphorus on freshwater communities, both in Ohio (Bedoya et al., 2011) and in other regions (Grizzetti et al., 2017; Lemm et al., 2021). In contrast, Pilière et al. (2014) found that phosphorus is the more important predictor of freshwater community integrity in Ohio. Further, Zijp et al. (2017) found that fish species richness in Ohio is negatively related to phosphorus rather than nitrogen. Differences between our results and these previous findings may reflect that our causal discovery approach considers all potential relationships between variables as well as the hydrological connections between data points. Moreover, by considering confounding variables, our approach has the potential to filter out spurious correlations in the data. Thus, the previously reported relationships between phosphorus and ecological integrity could be either indirect relationships or reflecting the influence of other (unmeasured) variables. While a missing link between two variables in our models does not necessarily imply that a connection does not exist, the connection is too weak to be detected in the conditional independence tests. Thus, our results at least indicate that nitrogen is more important than phosphorous in structuring freshwater fish and invertebrate assemblages in Ohio.

We further found that fish and invertebrate community integrity are each linked to a specific physical habitat quality aspect, i.e., substrate quality for fish and channel quality for invertebrates. Contrasting to our results, Pilière et al. (2014) found that riffle quality (fish) and substrate quality (invertebrates) are the most important habitat quality aspects. For most physical habitat quality metrics, however, we did not find a direct connection to the biotic integrity metrics. The lack of a direct connection may be explained by indirect relationships, for example, the instream cover of the river may be causally linked with substrate quality. Interestingly, our algorithm revealed no direct connections between the components of physical habitat quality on the one hand and water quality aspects on the other. We stress that this is a result of the application of our method rather than an assumption that we started from. This finding indicates that there are no strong relationships between the two groups of variables, although human-induced changes in physical habitat quality and water quality are often correlated (An et al., 2002).

The direct connection between IBI and latitude suggests that our dataset may miss a relevant covariate of fish community integrity. The negative sign of the partial correlation coefficient suggests that fish community integrity is, on average, lower in the north than the south of Ohio, which is in line with earlier findings (Virani and Manolakos, 2005). The reverse is true for the proportions of agricultural and urban land, which are typically larger in the north and west (Tayyebi et al., 2015). Possibly, these land uses affect aspects of water quality or habitat structure that are not fully captured by the water quality and physical habitat quality variables included in the dataset, thus resulting in a connection between IBI and latitude in our model. We further found in both the IBI and ICI model a direct connection of longitude and latitude, albeit no causal relationship. The correlation between longitude and latitude may reflect that the measurement locations are not randomly distributed, but structured along the river network. While our approach considers the upstream-downstream connectivity of the river system, it does not explicitly account for the full topology of the river network. This may result in spatial correlations not being completely removed. However, there are only few connections between geographic location and the other variables in the final models, indicating that our approach removed most of the spatial correlations from the system.

The limited size of our dataset may have restricted the possibilities to identify the directions of the ecological relationships. In fact, we could find only a single direct cause-effect relationship from pool to cover in the IBI model and no such relationship in the ICI model. To find more orientations, the study could be repeated with a larger data set. Alternatively, the FCI algorithm could be applied without the conservative modification or with a lower decision threshold. This would lead to more orientations, but potentially also more erroneous decisions (Ramsey et al., 2012). In future work, our method could also be applied to individual species or taxa. While aggregated metrics are useful to support ecological quality assessment and management practices, taxon-specific causal discovery results may help to unravel and understand the causes of biotic integrity impairment, as shown for different approaches in previous studies (Baker and King, 2010; Berger et al., 2016).

Applicability

We presented a new approach to reveal networks of relationships between biotic and abiotic variables in river systems. While it is standard practice in structural equation modeling to compare only a limited number of candidate models, our method covers all possible models that satisfy the model assumptions. More specifically, our model assumptions allow for latent variables, but we do assume acyclicity, i.e., do not consider feedback cycles. Considering a large number of candidate models has both advantages and disadvantages. We consider the approach particularly advantageous for exploratory analyses of networks of ecological relationships involving a relatively large number of variables. Further, it is computationally expensive to test all possible connections (Malinsky and Danks, 2018). The computation time depends on the number of conditional independence tests that have to be carried out. In our approach, we reduced the number of conditional independence tests by not doing tests that were unnecessary because of the spatial structure (hydrological connections) of the system. Regardless, the number of conditional independence tests increases with the number of variables included in the network. The computational cost of each test depends on the amount of data and the conditional independence test that is used. The Kernel Conditional Independence Test (KCIT) that we used in this work is slow, but powerful, due to its ability to detect non-linear relationships (Zhang et al., 2012). Strobl et al. (2019) developed approximate kernel-based conditional independence tests that are significantly faster, in particular for large datasets. For larger datasets than ours, the approximation could be a good compromise between accuracy and run time.

As our method is data-driven, different datasets may result in different networks. In our study, the ICI model was based on a subset of the measurements that were used to build the IBI model. Consequently, the final networks display a few differences. We note, however, that these differences are amplified because we implemented a threshold to summarize the bootstraps (i.e., showing only connections that appeared in at least 65 out of 100 models). As a result, a connection that is predicted to be present in one model may appear absent from the other model even though it was present in a considerable proportion of the models. For example, the connection between substrate quality and gradient was not included in the final IBI model despite being present in 27 of the bootstraps. The same is true for edge marks which are present in one model but not in the other. Removing the threshold is not an option, as this would lead to an incomprehensible graph. Overall, the relationships within the habitat quality variables and the water quality variables, respectively, are similar in both final models. Connections that are present in both networks can be interpreted with more confidence.

After the preprocessing, the data structure is similar to that of time series, with streams equaling time and locations equaling points in time. This analogy suggests that the data may also be analyzed with time series methods such as Granger causality or CCM (Sugihara et al., 2012). The number of consecutive measurement locations, however, is highly heterogeneous in our data which hinders the direct applicability of such methods.

We think that causal discovery methods, modified to reflect key characteristics of data sets (such as hydrological relationships), have great potential for application. Our adapted FCI algorithm is particularly suited for exploratory analyses of ecological relationships in rivers and diagnostic assessments of potential causes of ecological impairment. The results obtained with our algorithm can be used to formulate hypotheses or to select variables for refined follow-up analyses (Sun et al., 2015). For example, SEM could be used in a subsequent step to study and quantify specific pressure-impact relationships in more detail. Additionally, Pearl’s do-calculus (Pearl, 1994), among others, could be applied to estimate the effect strength of these relationships. Quantifying the relationships in our graphs would also allow using the networks for predictive purposes.

Data Availability Statement

Publicly available datasets were analyzed in this study. The code used to pre-process and model the data is available under doi: 10.5281/zenodo.8475. The hydroSHEDS data is available at https://www.hydrosheds.org. The biomonitoring data is archived under doi: 10.5061/dryad.dfn2z353f.

Author Contributions

TC, KM, and AS conceived the idea. TC and KM designed the methodology. MZ provided the data. KM analyzed the results with help from TC, AS, TH, and MH. KM, AS, and LP led the writing of the manuscript. All authors contributed critically to the drafts and gave their final approval for publication.

Funding

This research was partially financed by the Netherlands Organisation for Scientific Research (NWO), under project number 617.001.451.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank the editor and the two reviewers for their valuable feedback, which helped us to improve the quality of this article. Monitoring data were collected and provided by the Ohio EPA. The EPA data set was combined with other data, such as toxic pressure parameters, by Scott Dyer, Chris Holmes, Katherine Kapo, Christian Mulder, MZ, Dick de Zwart, and LP. All data providers are acknowledged for their work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.782554/full#supplementary-material

References

An, K.-G., Park, S. S., and Shin, J.-Y. (2002). An evaluation of a river health using the index of biological integrity along with relations to chemical and habitat conditions. Environ. Int. 28, 411–420. doi: 10.1016/S0160-4120(02)00066-1

CrossRef Full Text | Google Scholar

Baker, M. E., and King, R. S. (2010). A new method for detecting and interpreting biodiversity and ecological community thresholds. Methods Ecol. Evol. 1, 25–37. doi: 10.1111/j.2041-210X.2009.00007.x

CrossRef Full Text | Google Scholar

Bedoya, D., Manolakos, E. S., and Novotny, V. (2011). Characterization of biological responses under different environmental conditions: a hierarchical modeling approach. Ecol. Model. 222, 532–545. doi: 10.1016/j.ecolmodel.2010.10.007

CrossRef Full Text | Google Scholar

Berger, E., Haase, P., Oetken, M., and Sundermann, A. (2016). Field data reveal low critical chemical concentrations for river benthic invertebrates. Sci. Total Environ. 544, 864–873. doi: 10.1016/j.scitotenv.2015.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Bollen, K. A. (2005). “Structural equation models,” in Encyclopedia of Biostatistics, eds P. Armitage and T. Colton (Chichester: John Wiley & Sons, Ltd).

Google Scholar

Bromberg, F., Margaritis, D., and Honavar, V. (2009). Efficient markov network structure discovery using independence tests. jair 35, 449–484. doi: 10.1613/jair.2773

CrossRef Full Text | Google Scholar

Butchart, S. H. M., Walpole, M., Collen, B., van Strien, A., Scharlemann, J. P. W., Almond, R. E. A., et al. (2010). Global biodiversity: indicators of recent declines. Science 328, 1164–1168. doi: 10.1126/science.1187512

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombo, D., and Maathuis, M. H. (2012). Order-independent constraint-based causal structure learning. J. Mach. Learn. Res. 15, 3921–3962.

Google Scholar

Fan, Y., Chen, J., Shirkey, G., John, R., Wu, S. R., Park, H., et al. (2016). Applications of structural equation modeling (SEM) in ecological studies: an updated review. Ecol. Process. 5:19. doi: 10.1186/s13717-016-0063-3

CrossRef Full Text | Google Scholar

Fausch, K. D., Karr, J. R., and Yant, P. R. (1984). Regional application of an index of biotic integrity based on stream fish communities. Trans. Am. Fish. Soc. 113, 39–55. doi: 10.1577/1548-86591984113<39:RAOAIO<2.0.CO;2

CrossRef Full Text | Google Scholar

Glymour, C., Zhang, K., and Spirtes, P. (2019). Review of causal discovery methods based on graphical models. Front. Genet. 10:524. doi: 10.3389/fgene.2019.00524

PubMed Abstract | CrossRef Full Text | Google Scholar

Grace, J. B., and Keeley, J. E. (2006). A structural equation model analysis of postfire plant diversity in california shrublands. Ecol. Appl. 16, 503–514.

Google Scholar

Grace, J. B., and Pugesek, B. H. (1997). A structural equation model of plant species richness and its application to a coastal Wetland. Am. Nat. 149, 436–460. doi: 10.1086/285999

CrossRef Full Text | Google Scholar

Grizzetti, B., Pistocchi, A., Liquete, C., Udias, A., Bouraoui, F., and van de Bund, W. (2017). Human pressures and ecological status of European rivers. Sci. Rep. 7:205. doi: 10.1038/s41598-017-00324-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalisch, M., Mächler, M., Colombo, D., Maathuis, M. H., and Bühlmann, P. (2012). Causal inference using graphical models with the R Package pcalg. J. Stat. Soft. 47, 1–26. doi: 10.18637/jss.v047.i11

CrossRef Full Text | Google Scholar

Kapo, K. E., Holmes, C. M., Dyer, S. D., de Zwart, D., and Posthuma, L. (2014). Developing a foundation for eco-epidemiological assessment of aquatic ecological status over large geographic regions utilizing existing data resources and models. Environ. Toxicol. Chem. 33, 1665–1677. doi: 10.1002/etc.2557

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerr, J. T., Kharouba, H. M., and Currie, D. J. (2007). The macroecological contribution to global change solutions. Science 316, 1581–1584. doi: 10.1126/science.1133267

PubMed Abstract | CrossRef Full Text | Google Scholar

Lahiri, S. N. (1999). Theoretical comparisons of block bootstrap methods. Ann. Statist. 27, 386–404. doi: 10.1214/aos/1018031117

CrossRef Full Text | Google Scholar

Larsen, A. E., Meng, K., and Kendall, B. E. (2019). Causal analysis in control–impact ecological studies with observational data. Methods Ecol. Evol. 10, 924–934. doi: 10.1111/2041-210X.13190

CrossRef Full Text | Google Scholar

Lawrance, A. J. (1976). On conditional and partial correlation. Am. Statist. 30, 146–149. doi: 10.1080/00031305.1976.10479163

CrossRef Full Text | Google Scholar

Lehner, B., Verdin, K., and Jarvis, A. (2008). New global hydrography derived from spaceborne elevation data. Eos. Trans. AGU 89, 93–94. doi: 10.1029/2008EO100001

CrossRef Full Text | Google Scholar

Lemm, J. U., Venohr, M., Globevnik, L., Stefanidis, K., Panagopoulos, Y., van Gils, J., et al. (2021). Multiple stressors determine river ecological status at the European scale: towards an integrated understanding of river status deterioration. Glob. Chang Biol. 27, 1962–1975. doi: 10.1111/gcb.15504

PubMed Abstract | CrossRef Full Text | Google Scholar

Mace, G. M., Barrett, M., Burgess, N. D., Cornell, S. E., Freeman, R., Grooten, M., et al. (2018). Aiming higher to bend the curve of biodiversity loss. Nat. Sustain. 1, 448–451. doi: 10.1038/s41893-018-0130-0

CrossRef Full Text | Google Scholar

Malinsky, D., and Danks, D. (2018). Causal discovery algorithms: a practical guide. Philos. Compass 13:e12470. doi: 10.1111/phc3.12470

CrossRef Full Text | Google Scholar

Meinshausen, N., and Bühlmann, P. (2010). Stability selection. J. R. Statist. Soc. 72, 417–473. doi: 10.1111/j.1467-9868.2010.00740.x

CrossRef Full Text | Google Scholar

Midolo, G., Alkemade, R., Schipper, A. M., Benítez-López, A., Perring, M. P., and de Vries, W. (2019). Impacts of nitrogen addition on plant species richness and abundance: a global meta-analysis. Glob. Ecol. Biogeogr. 28, 398–413. doi: 10.1111/geb.12856

CrossRef Full Text | Google Scholar

Mielke, K. P., Claassen, T., Huijbregts, M. A. J., Schipper, A. M., and Heskes, T. (eds) (2020). Discovering Cause-Effect Relationships in Spatial Systems With a Known Direction Based on Observational Data. Albion, NY: MLR Press.

Google Scholar

Młyńczak, M., and Krysztofiak, H. (2018). Discovery of causal paths in cardiorespiratory parameters: a time-independent approach in elite athletes. Front. Physiol. 9:1455. doi: 10.3389/fphys.2018.01455

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohio Environmental Protection Agency (1989). Biological Criteria for the Protection of Aquatic Life. Volume III: Standardized Biological Field Sampling and Laboratory Methods for Assessing Fish and Macroinvertebrate Communities. Columbus, OH: Ohio Environmental Protection Agency.

Google Scholar

Ohio Environmental Protection Agency (2006). Methods for Assessing Habitat in Flowing Waters: Using the Qualitative Habitat Evaluation Index (QHEI). OHIO EPA Technical Bulletin. Columbus, OH: Ohio Environmental Protection Agency.

Google Scholar

Pearl, J. (1994). “A probabilistic calculus of actions,” in Uncertainty Proceedings 1994, Amsterdam: Elsevier, 454–462.

Google Scholar

Pereira, H. M., Leadley, P. W., Proença, V., Alkemade, R., Scharlemann, J. P. W., Fernandez-Manjarrés, J. F., et al. (2010). Scenarios for global biodiversity in the 21st century. Science 330, 1496–1501. doi: 10.1126/science.1196624

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilière, A., Schipper, A. M., Breure, A. M., Posthuma, L., de Zwart, D., Dyer, S. D., et al. (2014). Comparing responses of freshwater fish and invertebrate community integrity along multiple environmental gradients. Ecol. Ind. 43, 215–226. doi: 10.1016/j.ecolind.2014.02.019

CrossRef Full Text | Google Scholar

Posthuma, L., and de Zwart, D. (2006). Predicted effects of toxicant mixtures are confirmed by changes in fish species assemblages in Ohio. USA, rivers. Environ. Toxicol. Chem. 25, 1094–1105. doi: 10.1897/05-305R.1

CrossRef Full Text | Google Scholar

Posthuma, L., Zijp, M. C., de Zwart, D., van de Meent, D., Globevnik, L., Koprivsek, M., et al. (2020). Chemical pollution imposes limitations to the ecological status of European surface waters. Sci. Rep. 10:14825. doi: 10.1038/s41598-020-71537-2

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna: R Core Team.

Google Scholar

Ramsey, J., Zhang, J., and Spirtes, P. L. (2012). Adjacency-faithfulness and conservative causal inference. arXiv. [Preprint]. Avaliable online at: https://arxiv.org/abs/1206.6843 (accessed September 15, 2021).

Google Scholar

Runge, J., Bathiany, S., Bollt, E., Camps-Valls, G., Coumou, D., Deyle, E., et al. (2019). Inferring causation from time series in Earth system sciences. Nat. Commun. 10:2553. doi: 10.1038/s41467-019-10105-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Sagarin, R., and Pauchard, A. (2010). Observational approaches in ecology open new ground in a changing world. Front. Ecol. Environ. 8:379–386. doi: 10.1890/090001

CrossRef Full Text | Google Scholar

Sokolova, E., Hoogman, M., Groot, P., Claassen, T., Vasquez, A. A., Buitelaar, J. K., et al. (2015). Causal discovery in an adult ADHD data set suggests indirect link between DAT1 genetic variants and striatal brain activation during reward processing. Am. J. Med. Genet. B Neuropsychiatr. Genet. 168, 508–515. doi: 10.1002/ajmg.b.32310

PubMed Abstract | CrossRef Full Text | Google Scholar

Spirtes, P., Glymour, C., and Scheines, R. (2001). Causation, Prediction, and Search. Cambridge, MA: The MIT Press.

Google Scholar

Strobl, E. V., Zhang, K., and Visweswaran, S. (2019). Approximate kernel-based conditional independence tests for fast non-parametric causal discovery. J. Causal Inference 7:20180017. doi: 10.1515/jci-2018-0017

CrossRef Full Text | Google Scholar

Sugihara, G., May, R., Ye, H., Hsieh, C., Deyle, E., Fogarty, M., et al. (2012). Detecting causality in complex ecosystems. Science 338, 496–500. doi: 10.1126/science.1227079

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Y., Li, J., Liu, J., Chow, C., Sun, B., and Wang, R. (2015). Using causal discovery for feature selection in multivariate numerical time series. Mach. Learn. 101, 377–395. doi: 10.1007/s10994-014-5460-1

CrossRef Full Text | Google Scholar

Tayyebi, A., Pijanowski, B. C., and Pekin, B. K. (2015). Land use legacies of the Ohio River Basin: using a spatially explicit land use change model to assess past and future impacts on aquatic resources. Appl. Geogr. 57, 100–111. doi: 10.1016/j.apgeog.2014.12.020

CrossRef Full Text | Google Scholar

Virani, H., and Manolakos, E. (2005). Self Organizing Feature Maps Combined with Ecological Ordination Techniques for Effective Watershed Management. Boston, MA: Northeastern University. Tech. Report No 3 Center for Urban Environmental Studies.

Google Scholar

Zhang, J. (2008). On the completeness of orientation rules for causal discovery in the presence of latent confounders and selection bias. Artif. Intell. 172, 1873–1896. doi: 10.1016/j.artint.2008.08.001

CrossRef Full Text | Google Scholar

Zhang, K., Peters, J., Janzing, D., and Schoelkopf, B. (2012). Kernel-based conditional independence test and application in causal discovery. arXiv. [Preprint]. Avaliane online at: https://arxiv.org/abs/1202.3775 (accessed September 15, 2021).

Google Scholar

Zijp, M. C., Huijbregts, M. A. J., Schipper, A. M., Mulder, C., and Posthuma, L. (2017). Identification and ranking of environmental threats with ecosystem vulnerability distributions. Sci. Rep. 7:9298. doi: 10.1038/s41598-017-09573-8

PubMed Abstract | CrossRef Full Text | Google Scholar