The Dimensions and Units of the Population Interaction Coefficients

We discuss the interpretation and dimensions of the population dynamic parameters that are commonly used to quantify the strength of intraspecific and interspecific interactions. The concept of “interaction strength” is not unequivocal. Its theoretical formalization relies on the generalized Lotka–Volterra model. However, four different ways of parameterizing the model have been proposed in the literature, leading to four different definitions of the term “interaction strength.” In particular, the dimensions of these four definitions are not identical, some of these incorporating explicitly the dimension used to measure the population size. Using an individual-based simulation model as an illustration, we show that, in the latter case, the interaction strength depends implicitly on the habitat size. As a consequence, it is of crucial importance to quantify the population as a density rather than an absolute population abundance. We insist that the dimension of the interaction strength coefficient should not be overlooked and any quantitative estimation must be given with explicit units.

Introduction

Species interactions are at the heart of ecology. In community ecology, whether experimental or theoretical, it is often necessary to quantify the strength with which populations interact with each other. There is no universally accepted theoretical formalization of this notion of “interaction strength” but the most common definitions rely on the generalized Lotka–Volterra model (GLV):

$\frac{d{N}_i}{dt}=N_i\cdot \left(r_i-\sum _{j=1}^s{a}_{ij}{N}_j\right),i=1\mathrm{\dots }s.(1)$

Traditionally, the parameter r_i is called the “intrinsic growth rate” in the sense that it quantifies the rate with which the species i would grow (exponentially) in the absence of all interactions, whether intraspecific or interspecific. The word “intrinsic” refers to the fact that this parameter value only depends on the biological characteristics of the species i, assumed to be in low density and free from interactions with other species. Of course, r_i can still depend on general abiotic and biotic environmental conditions.

The parameter a_ij, often called the interaction coefficient, quantifies the strength with which the species j affects the population growth rate of species i. More precisely, it quantifies the per capita effect of species j on the per capita growth rate of species i. In mathematical terms, a_ij is defined as:

$a_{ij}=-\frac{\partial \left(\frac{d{N}_i}{N_{i}dt}\right)}{\partial N_j}.(2)$

The minus sign in the parentheses of Equation 1 and on the right-hand side of Equation 2 is an arbitrary convention to indicate that the effect of species j on species i is detrimental if a_ij is positive, favorable if a_ij is negative. We follow this convention here because we will mostly be interested in competitive systems. With this convention, all matrix elements, whether intraspecific or interspecific, quantify the competition strength with a positive number. It is usually assumed (although rarely said explicitly) that the coefficient a_ij only depends on the biological characteristics of the species i and j. In the same sense as r_i, it is assumed to be intrinsic to the pair of species i and j (in the given abiotic and biotic environment). From these considerations and from Equation 2, the dimension of a_ij should be unequivocal. We will show that this is far from being the case.

A look at Equation 2 shows that the matrix elements a_ij have a dimension that is the product of the reciprocals of the dimensions of the variables N_j and t. With the standard use of square brackets to designate the dimension of a variable, this can be written as:

$\left[a_{ij}\right]={\left[N_j\right]}^{-1}\cdot {\left[t\right]}^{-1}.$

For example, if N_j is a density measured in units of individuals per square meter and if the time t is measured in units of days, the units of a_ij will be m²ind⁻¹day⁻¹.

The literature about interaction coefficients is huge and we cannot possibly review it here. Instead, we refer to the very useful reviews of Berlow et al. (2004) and of Wootton and Emmerson (2005), which both rely on theoretical and empirical considerations. An earlier important reference is the paper by Bender et al. (1984), which introduces the notions of pulse and press experiments to estimate interaction strength. In both types of experiments, we have identified the dimension of the interaction coefficient as [density of i] [density of j]⁻¹. Actually, none of the cited studies considered the issue of dimensions and units. Instead, all of these reviews show that the expression “interaction strength” was used indiscriminately for different quantities, which turn out to have different dimensions. This remains true in the recent literature: for example, Carrara et al. (2015) and Novak et al. (2016) review a number of different approaches to quantify interaction strength. However, these approaches are not simply alternate methods for measuring the same quantity. They are in fact different conceptualizations of the general idea of interaction strength: different definitions with different dimensions.

Whenever numerical values are reported, they must be given with their units. Unfortunately, this is almost never done. For example, O’Gorman et al. (2010) report values of interaction strength between 0 and 0.05 with no units specified (their figure 1). Only after careful reading of Materials and Methods can the units be reconstructed as m²mg⁻¹day⁻¹. Wootton (1997) is a rare study in which care was taken to specify the units (although with some confusion of the notions of “dimension” and “unit”). Another exception is the paper by Osenberg et al. (1999) in which units are specified in their figure 2 (if corrected as m²fish⁻¹day⁻¹). In other papers, it is sometimes impossible to understand what the units are, typically when “interaction strengths” are studied with statistical models like ANOVAs or structural equation modeling.

Thus, although there exists a vast literature about the theoretical and practical aspects of interaction metrics, the issue of dimensions and units has been largely overlooked. This is unfortunate because comparisons of quantities with different dimensions are meaningless.

In this article, we will first examine four common parameterizations of the GLV model (Equation 1). In particular, we will make explicit the dimensions of the interaction coefficients in each case. For some of these parameterizations, the interaction coefficient dimension incorporates explicitly the dimension used to measure the population size, i.e., the dimension of N_i. In this case, we prove that a_ij can depend on the habitat size. Therefore, the a_ij measured in a given habitat must be used with caution in another habitat, especially if they differ in size. We will first examine this fundamental question within the logistic equation and will discuss the consequences for the four different parameterizations of the GLV. The single-species case will then be illustrated numerically, using an individual-based model.

Parameter Dimensions in the Logistic Equation

In order to expound the problem in the simplest possible way, we first restrict Equation 1 to a single population with r = r₁ and a = a₁₁:

$\frac{dN}{dt}=rN-a{N}^2$

or

$\frac{1}{N}\frac{dN}{dt}=r-aN,(3)$

which is nothing else than the well-known “logistic equation” in Verhulst’s (1838) original parameterization. It models the dynamics of a single population as Malthusian growth with the addition of a so-called “retardation force” or “friction force,” which is nowadays interpreted as intraspecific competition. The intraspecific inhibition to growth is quantified by the positive parameter a. When introduced in this way, it is implied that a, like r, is a purely demographic-biological parameter intrinsic to the species (but conditional on the given abiotic and biotic environment).

It is instructive to make a dimensional analysis of this equation (Legendre and Legendre, 2012). The dimension of the variable t is time, that is, [t] = T. Dimensional homogeneity requires that:

$\begin{array}{c}\left[r\right]={\text{T}}^{-1},\\ \left[a\right]={\left[N\right]}^{-1}{\text{T}}^{-1}.\end{array}(4)$

As for the dimension of population size N, it can depend on the system under study because the population can be measured in different ways. For example, the population of large-bodied species can be expressed as total number of individuals in the system (e.g., wolves in Isle Royale), as density per surface area (e.g., grass), or per volume (e.g., zooplankton). Equation 4 implies that the dimension of a will depend on the dimension chosen for N. Consequently, the value of the parameter a is not intrinsic to the species but also depends on the habitat size. Before illustrating this property with the use of an individual-based model, we study the dimensions of the interaction strength coefficients in four different commonly used parameterizations of the GLV.

Four Parameterizations of the Generalized Lotka–Volterra Model

The GLV model has been parameterized in several ways. In the original formulation (Equation 1), the parameter dimensions are (Table 1):

$\begin{array}{c}\left[r_i\right]={\text{T}}^{-1},\\ \left[a_{ij}\right]={\left[N_j\right]}^{-1}{\text{T}}^{-1}.\end{array}(5)$

TABLE 1

Table 1. Parameter dimensions of the generalized Lotka–Volterra model and its reparameterizations.

Assuming that r_i > 0 for all i = 1…s, the first transformation of Equation 1 makes explicit the carrying capacities K_i:

$\frac{d{N}_i}{dt}=\frac{r_i}{K_i}{N}_i\cdot \left(K_i-\sum _{j=1}^s{\tilde{a}}_{ij}{N}_j\right),i=1\mathrm{\dots }s,(6)$

where K_i is defined as r_i/a_ii and the new interaction coefficients ${\tilde{a}}_{ij}$ equal a_ij/a_ii. Note that ${\tilde{a}}_{ii}=a_{ii}/a_{ii}=1$ by definition, and that the carrying capacity K_i depends on the intrinsic growth rate r_i. As a consequence, the parameter dimensions are (Table 1):

$\begin{array}{c}\left[r_i\right]={\text{T}}^{-1},\\ \left[K_i\right]=\left[N_i\right],\\ \left[{\tilde{a}}_{ij}\right]=\left[N_i\right]{\left[N_j\right]}^{-1}.\end{array}(7)$

Note that this transformation requires that all r_i be positive (Gabriel et al., 2005). This precludes the use of Equation 6 to describe food web dynamics because the notion of carrying capacity only makes sense for basal species. This formulation can be traced back to MacArthur and Levins (1967) or even to Gause (1934, p. 47). In this parameterization, the dimensions of N_i are transferred to the carrying capacities and to the “standardized interaction coefficients” ${\tilde{a}}_{ij}$.

Still with the assumption r_i > 0, we can use the carrying capacity to normalize the species abundance, which defines the so-called “relative yield” Y_i = N_i/K_i. Relative yield is a common currency in agroecology (Vandermeer, 2012) and in the study of the biodiversity-ecosystem-functioning relationship (Cardinale et al., 2006; Fort, 2018; Parain et al., 2019). The equations for the relative yield system are obtained from the GLV Equation 1 by dividing by K_i:

$\frac{d{Y}_i}{dt}=r_i{Y}_i\cdot \left(1-\sum _{j=1}^s{\overline{a}}_{ij}{Y}_j\right),i=1\mathrm{\dots }s,(8)$

where ${\overline{a}}_{ij}=a_{ij}/a_{ii}\cdot K_j/K_i$. This leads to the following dimensions (Table 1):

$\begin{array}{c}\left[r_i\right]={\text{T}}^{-1},\\ \left[K_i\right]=\left[N_i\right],\\ Y_i\mathrm{dimensionless},\\ {\overline{a}}_{ij}\mathrm{dimensionless}.\end{array}(9)$

In this parameterization, the dimension of each N_i is transferred to the corresponding carrying capacity and consequently both the relative yield Y_i and the “relative yield interaction coefficients” ${\overline{a}}_{ij}$ are truly dimensionless.

Finally, Chesson (2000) has proposed the following parameterization:

$\frac{d{N}_i}{dt}=r_i{N}_i\cdot \left(1-\sum _{j=1}^s{\widehat{a}}_{ij}{N}_j\right),i=1\mathrm{\dots }s,(10)$

where ${\widehat{a}}_{ij}=a_{ij}/r_i$ (assuming r_i > 0). In this parameterization, the dimensions are (Table 1):

$\begin{array}{c}\left[r_i\right]={\text{T}}^{-1},\\ \left[{\widehat{a}}_{ij}\right]={\left[N_j\right]}^{-1}.\end{array}(11)$

Therefore, the reciprocal of the dimension of N_j is transferred to ${\widehat{a}}_{ij}$, called the “absolute interaction coefficient” by Chesson (2000).

Note that two of the reparameterizations of the original GLV model (Equations 6, 8) assume implicitly that the intrinsic growth rates are all positive: r_i > 0. This condition is clearly a prerequisite to properly defining the carrying capacity since K_i = r_i/a_ii (Gabriel et al., 2005; Mallet, 2012) and therefore also the relative yield. In the “absolute” parameterization (Chesson, 2000), if the species has a negative intrinsic growth rate, then the sign of ${\widehat{a}}_{ij}=a_{ij}/r_i$ follows the opposite convention to that of the GLV parameterization.

In the following, we will study the impact of habitat size on the interaction strength. As mentioned above, the dimension of the population abundance variable N can be, depending on the studied system, a total number of individuals or a density per unit surface or per unit volume. In the next section, we develop an individual-based model to illustrate this question in the case of logistic growth. Then, we will explain how this result translates in the four parameterizations of the GLV model.

An Individual-Based Model for Logistic Growth

The model incorporates a clear individual-to-individual interference mechanism such that the model simulation generates dynamics akin to logistic growth. The model is purely illustrative, with the only purpose of producing a negative correlation between the per-capita growth rate and the population density, and with no claim to biological realism.

At each time step t = 0, 1,…T_max, the population consists of N_t individuals. The population is assumed to inhabit a closed rectangular area Ω = [0, L_x] × [0, L_y]. Each individual i is located at some point (x_i, y_i) ∈ Ω. The model starts with some initial number of individuals N₀, each randomly placed in Ω. The ensuing dynamics produces a time-series of integer population numbers (N₀,…N_T) according to the following rules.

1. We suppose that each individual has a negative influence on the reproduction of conspecifics. This influence S_i declines with distance, with a normal distribution centered on the individual i:

$S_i(x,y)=\frac{1}{2\mathrm{\pi }{\mathrm{\sigma }}^2}{e}^{-\frac{{\left(x-x_i\right)}^2{\left(y-y_i\right)}^2}{2{\mathrm{\sigma }}^2}},(12)$

with standard deviation σ.

2. At each time step, each individual i replicates with probability

$b_i=\frac{b}{\left(1+c\cdot S_i^{\text{tot}}\right)},(13)$

where b is the maximum birth probability, c is a coefficient that characterizes the sensitivity to the influence of other individuals, and $S_i^{\text{tot}}$ is the total influence with which all other individuals reduce the reproduction of the individual i at position (x_i, y_i):

$S_i^{\text{tot}}=\sum _{j\ne i}{S}_j(x_i,y_i).$

According to Equation 13, the effective birth probability b_i declines hyperbolically to zero with $S_i^{\text{tot}}$.

3. Each individual can die with a constant death probability d.

4. Finally, at the end of each time step, all surviving individuals are redistributed within the habitat, at random positions (x_i, y_i) ∈ Ω.

Thus, the model runs with the six parameters σ,b, c, d, L_x, and L_y plus the initial number of individuals N₀ and the simulation time horizon T _max.

Simulation Results

The simulation algorithm was applied with the following parameter values and repeated with 25 replications: σ = 0.05, b = 0.01, c = 0.5, and d = 0.005, with an initial number N₀ = 100 and a simulation horizon T_max = 2700. The parameter values have no biological meaning other than producing the density dependence that will be displayed by Figure 1.

FIGURE 1

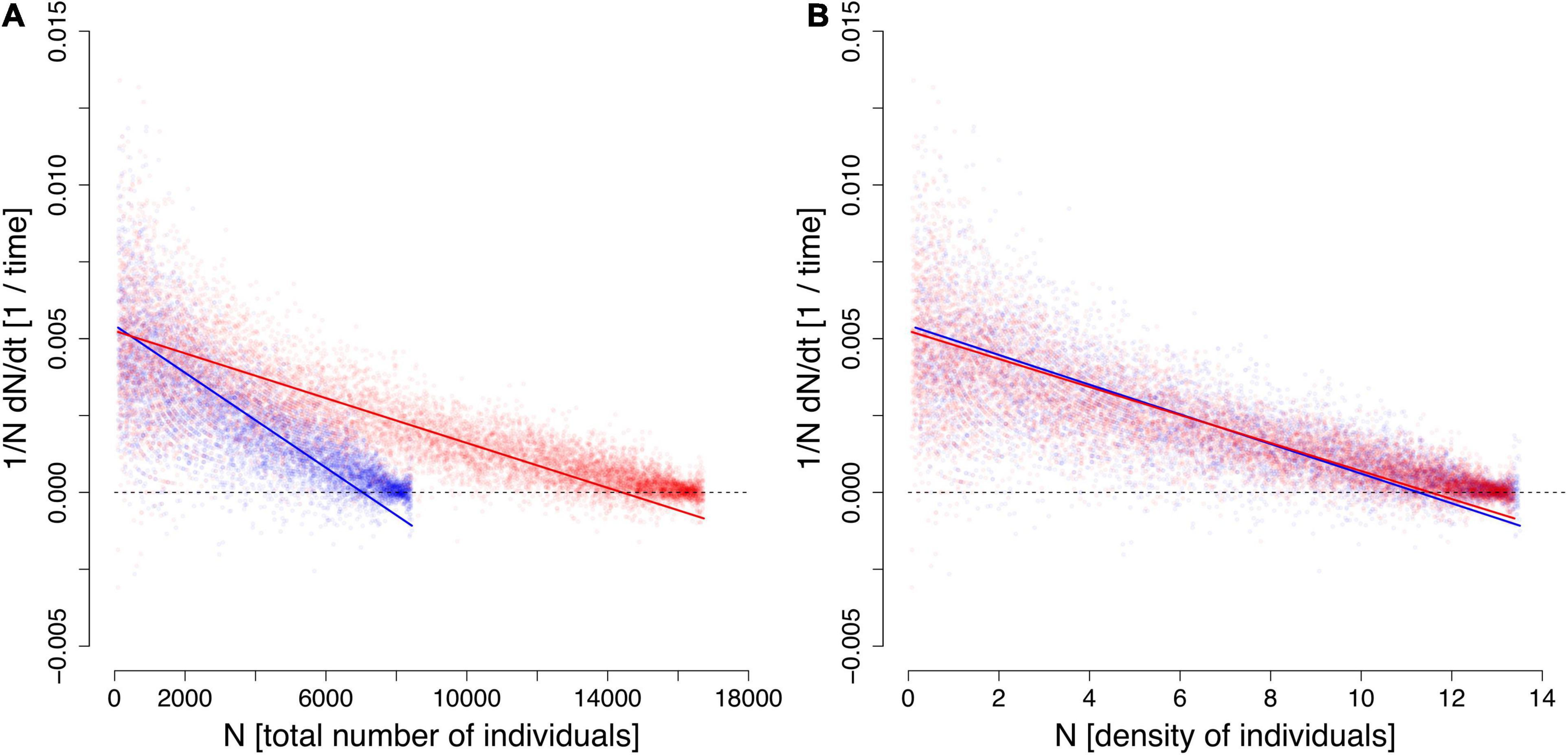
Figure 1. Simulation results of the individual-based model run in a smaller habitat (blue) and in a twice as large habitat (red). The calculated per capita growth rate (Equation 14) is expressed (A) vs. absolute population abundance and (B) vs. population density. The lines are the results of type-II regressions; the slope’s absolute value is an estimate of the interspecific competition a (Equation 3).

At each time step t, and for each replicate, we calculate the instantaneous per capita growth rate as:

$\frac{1}{N_t}\frac{d{N}_t}{dt}\approx \frac{N_{t+\mathrm{\Delta }t}-N_{t-\mathrm{\Delta }t}}{2N_t\mathrm{\Delta }t}.(14)$

Figure 1A shows the relationship of this quantity vs. N_t in two habitats of different sizes L_x × L_y: 25 × 25 (blue dots) and 25 × 50 (red dots). The lines show the best fits of the model (3) (with type-II regression). As expected, the estimates of r (y-axis intercept) are almost the same in both habitats. However, the estimates of a (slope) are different: the slope is shallower in the larger habitat, suggesting that interference is weaker. This might seem paradoxical since nothing in the individual-based reproduction algorithm refers to habitat size. However, intraspecific competition is indeed weaker in the larger habitat because, at each time step, individuals are redistributed at wider distances from one another. As shown by Figure 1B, when the variable on the abscissa is population density (number/area) rather than absolute population abundance N, both cases superimpose almost perfectly and lead to the same estimate of a. The conclusion is that model (3) only makes sense in terms of population density—not in terms of absolute population abundance. Referring to the dimensional identity (Equation 4), the proper dimension of the interference coefficient a is therefore [area][population abundance]⁻¹T⁻¹ such as, for example, m²ind⁻¹day⁻¹.

The soundness of the behavioral rules of the simulation model can be discussed at length. However, this is an unimportant question as long as the relationships displayed by Figure 1 are obtained. The simulation model is only a heuristic support for clarifying the dimensional properties of the logistic model.

Implication for the Four Generalized Lotka–Volterra Model Parameterizations

We have shown that the intraspecific interaction coefficient a depends on the habitat size when the population abundance variable N is the total number of individuals, while a is independent of the habitat size when N is the density of individuals. This result can be paraphrased as follows. By definition, the net per-capita growth rate (r−aN) has dimension T⁻¹ and the product aN also has dimension T⁻¹. Therefore, it must be independent of the habitat size. (a) If N is the total number of individuals, N will be twice larger if the habitat is twice larger; since aN needs to remain the same, a must consequently be twice smaller. (b) If N is the density, then it is independent of the habitat size and, consequently, a is also independent of the habitat size.

The same reasoning applies to the four parameterizations of the GLV model. In the original parameterization (Equation 1) as well as in Chesson’s parameterization (Equation 10), the interaction strength dimension depends on the population abundance dimension. Therefore, these two interaction coefficients behave in the same way as the intraspecific competition coefficient of logistic growth, and depend on the habitat size when N is measured as the total number of individuals.

For the other two parameterizations, which make explicit use of the carrying capacities (Equations 6, 8), the interaction coefficients are habitat-size invariant whatever dimension is used for N. This is obvious in the relative yield parameterization (Equation 8) since the interaction coefficients are truly dimensionless. In the parameterization of Equation 6, the interaction coefficients have dimension [N_i][N_j]⁻¹. Therefore, the habitat-size scaling disappears whether N_i and N_j are measured as densities or as total numbers in the same habitat (except in the situation in which N_i and N_j would be measured differently from one another).

Discussion

In Physics, it is customary to give dimensions and parameter units explicitly. As emphasized by Legendre and Legendre (2012, chapter 3), this is far from always being the case in Ecology. The four different parameterizations that we have reviewed for the interaction coefficients do not have the same dimensions. Simply speaking of “interaction strength” can be a source of confusion if the chosen parameterization is not stated explicitly. Moreover, the interaction strength coefficients are not, in general, intrinsic to the interacting species because the values of the a_ij of Equation 1 and those of the ${\widehat{a}}_{ij}$ of Equation 10 will depend on the way that N is measured. If N is the absolute population abundance, these parameters will change with the habitat size. If N is the population density, they will remain independent of the habitat size. The only two definitions that are always independent of habitat size are the ${\tilde{a}}_{ij}$ parameterization of Equation 6, with explicit use of the carrying capacities K_i (defined as r_i/a_ii), and the ${\overline{a}}_{ij}$ parameterization of Equation 8, with the relative yields Y_i. These are the only cases for which the expressions “standardized interaction strength” or “relative yield interaction strength” have sensible meanings because ${\overline{a}}_{ij}$ is truly dimensionless and ${\tilde{a}}_{ij}$ is generally dimensionless too (Cardinale et al., 2006; Fort, 2018). However, these two approaches have a cost: the intrinsic growth rates must be positive (Gabriel et al., 2005) and they require carrying capacities, which is a problematic notion (Mallet, 2012).

Laska and Wootton (1998) reviewed several definitions of interaction strength as used by empiricists. Particularly, they re-explained the famous experiments performed by Paine (1992). The latter reference illustrates the inconsistencies that can easily permeate the definition of interaction coefficients. Paine (1992) proposed an empirical measure of the interaction coefficient as:

$a_{ij}=\frac{E_i-C_i}{C_i}\cdot \frac{1}{M_j},(15)$

with C_i the density of i in absence of j, E_i the density of i in presence of j, and M_j the density of j in presence of i. The dimension of a_ij is therefore [density of j]⁻¹. This definition is valid for densities at equilibrium. Laska and Wootton (1998) show how this measure arises from the logistic equation. Thereafter, they derive from a discrete-time GLV model another definition of interaction strength when not at equilibrium. In this second definition, the dimension of the interaction coefficient is different: it is [density of j]⁻¹ [time]⁻¹. Therefore, these two definitions cannot be compared.

Adding to the confusion, some authors (e.g., Paine, 1992, in the very same paper as mentioned above) also identify the “interaction strength” with the elements of the so-called “community matrix,” as defined by May (1973) as the Jacobian at the system equilibrium:

$\frac{d{N}_i}{dt}\cong \sum _{j=1}^s{J}_{ij}\left(N_j-N_j^{*}\right),i=1\mathrm{\dots }s,(16)$

with

$J_{ij}=\frac{\partial \left(\frac{d{N}_i}{dt}\right)}{\partial N_j}(\mathrm{calculated}\mathrm{at}N=N^{*}).(17)$

Equations 16, 17 are the linear approximation of the non-linear dynamical system (Equation 1) around equilibrium. The Jacobian elements J_ij have dimension T⁻¹, which is true of none of the four parameterizations studied in the present article. It is therefore incorrect to identify the GLV interaction coefficients with the elements of the Jacobian matrix, not only because the dimensions do not match but also because they describe different phenomena, as can be seen by comparing Equation 1 with Equation 16, or Equation 2 with Equation 17. More precisely, the Jacobian element J_ij quantifies the effect of a perturbation of population abundance N_j on the net variation of population i (i.e., on dN_i/dt) while all interaction strength indicators that we have reviewed (Table 1) quantify the effect on per capita variation [i.e., on (1/N_i)dN_i/dt]. This has been a source of confusion. For example, Novak et al. (2016) wrote the Jacobian expressions (Equations 16, 17) with (1/N_i)dN_i/dt on the left-hand side instead of dN_i/dt (their Equations 6, 7). While this is mathematically possible, it is at odds with the standard use in Ecology (as introduced by May, 1973), for which local stability can be deduced from the Jacobian’s eigenvalues. Nevertheless, all expressions in Novak et al.’s Table 1 are correct and their paper is an excellent review of the various dissenting definitions of the term “community matrix.” Because this term has no unambiguous meaning, we prefer not to use it at all.

In their review, Berlow et al. (2004) discussed various metrics of interaction strength in food webs, although they defined the interaction matrix only in the GLV form a_ij, ignoring the ${\tilde{a}}_{ij}$, ${\overline{a}}_{ij},$ and ${\widehat{a}}_{ij}$ parameterizations. Bender et al. (1984) used the ${\tilde{a}}_{ij}$ parameterization only. Paine’s (1992) experiments, as re-explained by Laska and Wootton (1998), rest on the use of the ${\widehat{a}}_{ij}$ parameterization. However, in the final section of their paper, Laska and Wootton (1998) make use of the a_ij parameterization. These examples emphasize the importance of carefully defining the interaction coefficients with due consideration of their dimensions.

Finally, we should point out that the present study confirms, with additional arguments, our previous insistence on the fact that population size should preferably be measured as a density rather than an absolute abundance when intraspecific or interspecific interactions are present (Arditi et al., 2016, 2017).

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

RA, RPR, and L-FB raised the problem and conceived the approach. YuVT and LIT developed the simulation program. RPR and RA analyzed the simulation results. RA coordinated the writing of the manuscript. All authors contributed critically to the manuscript and gave final approval for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

YuVT acknowledges the state allocation no. 01201363188 to SSC RAS. RPR acknowledges the Swiss National Science Foundation grant 31003A_182386. L-FB acknowledges the Swiss National Science Foundation grant 31003A_165800.

References

Arditi, R., Bersier, L.-F., and Rohr, R. P. (2016). The perfect mixing paradox and the logistic equation: Verhulst vs. Lotka. Ecosphere 7:e01599. doi: 10.1002/ecs2.1599

CrossRef Full Text | Google Scholar

Arditi, R., Bersier, L.-F., and Rohr, R. P. (2017). The perfect mixing paradox and the logistic equation: Verhulst vs. Lotka: reply. Ecosphere 8:e01894. doi: 10.1002/ecs2.1894

CrossRef Full Text | Google Scholar

Bender, E. A., Case, T. J., and Gilpin, M. E. (1984). Perturbation experiments in community ecology: theory and practice. Ecology 65, 1–13. doi: 10.2307/1939452

CrossRef Full Text | Google Scholar

Berlow, E. L., Neutel, A.-M., Cohen, J. E., de Ruiter, P. C., Ebenman, B., Emmerson, M., et al. (2004). Interaction strengths in food webs: issues and opportunities. J. Anim. Ecol. 73, 585–598. doi: 10.1111/j.0021-8790.2004.00833.x

CrossRef Full Text | Google Scholar

Cardinale, B. J., Srivastava, D. S., Duffy, J. E., Wright, J. P., Downing, A. L., Sankaran, M., et al. (2006). Effects of biodiversity on the functioning of trophic groups and ecosystems. Nature 443, 989–992. doi: 10.1038/nature05202

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrara, F., Giometto, A., Seymour, M., Rinaldo, A., Altermatt, F., and Rees, M. (2015). Inferring species interactions in ecological communities: a comparison of methods at different levels of complexity. Methods Ecol. Evol. 6, 895–906. doi: 10.1186/s12903-021-01719-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Chesson, P. (2000). Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343

CrossRef Full Text | Google Scholar

Fort, H. (2018). On predicting species yields in multispecies communities: quantifying the accuracy of the linear Lotka-Volterra generalized model. Ecol. Modell. 387, 154–162. doi: 10.1016/j.ecolmodel.2018.09.009

CrossRef Full Text | Google Scholar

Gabriel, J.-P., Saucy, F., and Bersier, L.-F. (2005). Paradoxes in the logistic equation? Ecol. Modell. 185, 147–151. doi: 10.1016/j.ecolmodel.2004.10.009

CrossRef Full Text | Google Scholar

Gause, G. F. (1934). The Struggle for Existence. Baltimore, MD: Williams & Wilkins. doi: 10.5962/bhl.title.4489

PubMed Abstract | CrossRef Full Text | Google Scholar

Laska, M. S., and Wootton, J. T. (1998). Theoretical concepts and empirical approaches to measuring interaction strength. Ecology 79, 461–476. doi: 10.1890/0012-9658(1998)079[0461:tcaeat]2.0.co;2

CrossRef Full Text | Google Scholar

Legendre, P., and Legendre, L. (2012). Numerical Ecology. Amsterdam: Elsevier.

Google Scholar

MacArthur, R., and Levins, R. (1967). The limiting similarity, convergence, and divergence of coexisting species. Am. Nat. 101, 377–385. doi: 10.1086/282505

CrossRef Full Text | Google Scholar

Mallet, J. (2012). The struggle for existence: how the notion of carrying capacity, K, obscures the links between demography, Darwinian evolution, and speciation. Evol. Ecol. Res. 14, 627–665.

Google Scholar

May, R. M. (1973). Stability and Complexity in Model Ecosystems. Princeton, NJ: Princeton University Press.

Google Scholar

Novak, M., Yeakel, J. D., Noble, A. E., Doak, D. F., Emmerson, M., Estes, J. A., et al. (2016). Characterizing species interactions to understand press perturbations: what is the community matrix? Annu. Rev. Ecol. Evol. Syst. 47, 409–432. doi: 10.1146/annurev-ecolsys-032416-010215

CrossRef Full Text | Google Scholar

O’Gorman, E. J., Jacob, U., Jonsson, T., and Emmerson, M. C. (2010). Interaction strength, food web topology and the relative importance of species in food webs. J. Anim. Ecol. 79, 682–692. doi: 10.1111/j.1365-2656.2009.01658.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Osenberg, C. W., Sarnelle, O., Cooper, S. D., and Holt, R. D. (1999). Resolving ecological questions through meta-analysis: goals, metrics, and models. Ecology 80, 1105–1117. doi: 10.1890/0012-9658(1999)080[1105:reqtma]2.0.co;2

CrossRef Full Text | Google Scholar

Paine, R. T. (1992). Food-web analysis through field measurement of per-capita interaction strength. Nature 355, 73–75. doi: 10.1038/355073a0

CrossRef Full Text | Google Scholar

Parain, E. C., Rohr, R. P., Gray, S. M., and Bersier, L. F. (2019). Increased temperature disrupts the Biodiversity-Ecosystem-Functioning relationship. Am. Nat. 193, 227–239. doi: 10.1086/701432

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandermeer, J. H. (2012). The Ecology of Intercropping. Cambridge: Cambridge University Press.

Google Scholar

Verhulst, P.-F. (1838). Notice sur la loi que la population suit dans son accroissement. Correspondance mathématique et physique 10, 113–121.

Google Scholar

Wootton, J. T. (1997). Estimates and tests of per capita interaction strength: diet, abundance, and impact of intertidally foraging birds. Ecol. Monogr. 67, 45–64. doi: 10.1890/0012-9615(1997)067[0045:eatopc]2.0.co;2

CrossRef Full Text | Google Scholar

Wootton, J. T., and Emmerson, M. (2005). Measurement of interaction strength in nature. Annu. Rev. Ecol. Evol. Syst. 36, 419–444. doi: 10.1146/annurev.ecolsys.36.091704.175535

CrossRef Full Text | Google Scholar