Prediction of Potentially Suitable Distributions of Codonopsis pilosula in China Based on an Optimized MaxEnt Model

Species distribution models are widely used in conservation biology and invasive biology. MaxEnt models are the most widely used models among the existing modeling tools. In the MaxEnt modeling process, the default parameters are used most often to build the model. However, these models tend to be overfit. Aiming at this problem, this study uses an optimized MaxEnt model to analyze the impact of past, present and future climate on the distributions of Codonopsis pilosula, an economic species, to provide a theoretical basis for its introduction and cultivation. Based on 264 distribution records and eight environmental variables, the potential distribution areas of C. pilosula in the last interglacial, middle Holocene and current periods and 2050 and 2070 were simulated. Combined with the percentage contribution, permutation importance, and jackknife test, the environmental factors affecting the suitable distribution area of this species were discussed. The results show that the parameters of the optimal model are: the regularization multiplier is 1.5, and the feature combination is LQHP (linear, quadratic, hinge, product). The main temperature factors affecting the distribution of C. pilosula are the annual mean temperature, mean diurnal range, and isothermality. The main precipitation factors are the precipitation seasonality, precipitation in the wettest quarter, and precipitation in the driest quarter, among which the annual average temperature contributes the most to the distribution area of this species. With climate warming, the suitable area of C. pilosula exhibits a northward expansion trend. It is estimated that in 2070, the suitable area of this species will expand to its maximum, reaching 2.5108 million square kilometers. The highly suitable areas of C. pilosula are mainly in Sichuan, Gansu, Shaanxi, Shanxi, and Henan Provinces. Our findings can be used to provide theoretical support related to avoiding the blind introduction of C. pilosula.

Introduction

Based on niche theory, a species distribution model analyses the main factors affecting a species distribution and predicts its potential distribution according to the known distribution sample data and corresponding environmental factor data (Zhu et al., 2013). With the sharing of global species distribution data and the rapid development of GIS technology, the species distribution model of correlation schemes has developed rapidly (Zhu et al., 2017). The MaxEnt model, as a commonly used species distribution model, has been widely used in invasive biology (Yan et al., 2020b) and conservation biology (Yan et al., 2020a) and in evaluating the impact of global climate change on species distributions due to its short computing time, stable computing results and simple operation (Li et al., 2018). The MaxEnt model can better predict the distribution of species than other models in the case of a small sample size and can test the prediction results (Estes et al., 2013), but in the prediction of a potential distribution, it is prone to overfitting and can lead to a decline in species transfer-ability (Porfirio et al., 2014).

At present, although MaxEnt is widely used in species distribution models, most of the research methods directly use the default parameters of the MaxEnt model and do not consider the optimization of the model (Warren and Seifert, 2011). The prediction results of the unoptimized model may have serious fitting deviations, such deviations will not only lead to the wrong assessment of the species niche, but also mislead the formulation of conservation management policies. Although MaxEnt software provides some options for model optimization, there is no clear standard for the setting of these parameters (Syfert et al., 2013).

MaxEnt model optimization has four main aspects: sampling deviation correction, model complexity adjustment, selection of species distribution judgment threshold, and model performance evaluation. This article is to optimize the model complexity. The optimizations of model complexity mainly include the optimization of feature combination and regularization multiplier. These optimizations have been a hot research area in Maxent model in recent years. Maxent provides five basic feature modes, such as Linear (L), quadratic (Q), product (P), hinge (H), and threshold (T) (Elith et al., 2011). In the case of small sample sizes, the default mode of MaxEnt will limit the use of complex feature modes, the L feature is always running, the Q feature starts to run at least 10 samples, the H function requires at least 15 samples, and the P and T features require more than 80 samples. In the case of using different control multipliers, the H model and the LQH model have similar trends, and there is little difference between the model’s omission error and the AUC value (Shcheglovitova and Anderson, 2013). To balance the fit of the model, MaxEnt sets a regularization multiplier to constrain the weights of variables, so that the model does not have to accurately fit the modeling data, but sets an error bound for the modeling data, and the model is fitted according to the observation value containing the error bound. The adjustment of the regularization multiplier is essentially an adjustment of the error bound.

Although the MaxEnt is based on the default regularization multipliers set for the data of 226 species in 6 regions of the world, the impact of overfitting is greatly reduced (Phillips and Dudík, 2008), many studies have shown that it is necessary to select an individual regularization multiplier according to different species and their data structures (Elith et al., 2010, 2011; Anderson and Gonzalez, 2011; Muscarella et al., 2014; Moreno-Amat et al., 2015). A higher or lower regularization multiplier will lead to a decrease in the AUC of the modeling data and test data (Anderson and Gonzalez, 2011). The appropriate regularization multiplier is also affected by the feature model. The more feature modes, the more complex the data Gibson distribution, and the regularization multiplier should be increased accordingly (Phillips and Dudík, 2008). The regularization multiplier also implies the choice of the feature mode, for example, the regularization multiplier of some feature modes is set to zero (Elith et al., 2011). The sample size also affects the choice of the regularization multiplier. The smaller the amount of data, the narrower the estimation interval. Therefore, it is necessary to increase the regularization multiplier to increase the error bound (Phillips and Dudík, 2008). The error bound finally determined by the regularization multiplier is proportional to the standard error of the sample (Anderson and Gonzalez, 2011). This is also the reason why the regularization multiplier needs to be increased for small sample data. The most important thing is that different species have different patterns of model performance changes due to the adjustment of predictive variables, feature models, and regularization multiplier. In addition, the optimization of the model obtained by some studies may not be suitable for the target species (Shcheglovitova and Anderson, 2013), especially for the traditional Chinese medicine C. pilosula, there is almost no optimization model in this species. Therefore, it is a hot and cutting-edge issue to avoid overfitting of the MaxEnt model and to explore the possible influence of model parameters on the prediction of the Chinese medicine species.

Codonopsis pilosula is the dry root of Codonopsis pilosula (Franch.) Nannf., C. pilosula Nannf. var. modesta (Nannf.) L. T. Shen or C. tangshen Oliv. It is sweet and flat. It has the functions of strengthening the spleen, tonifying the lungs, nourishing the blood and promoting fluid production (Bi et al., 2008). Modern pharmacological research has confirmed that C. pilosula has certain effects on the digestive system and vascular systems improves blood and hematopoietic function and immune function, has anti-aging benefits and so on (Feng et al., 2012). As a less expensive substitute for ginseng, C. pilosula is also widely used in diet and health care (Gong, 2011). With the increasing market demand from Japan and South Korea, the export volume of C. pilosula continues to increase in China, with promising market prospects (Guo et al., 2017). At present, C. pilosula is mainly produced in Shanxi, Shaanxi, Gansu, and Sichuan Provinces and in other places in China, with a large amount of cultivation all over the country. Due to the scattered wild resources of this species, the quantity of commodities it can provide is extremely limited. From the perspective of production and marketing over the years, the output of wild products has been declining and cultivated products have been increasing. Therefore, cultivation of C. pilosula will still be the main source of commercial C. pilosula in the future (Zhang, 2006). At present, there are few reports on C. pilosula, and most of them focus on chemical composition (Huang et al., 2018), pharmacological activity (Liu M. X. et al., 2018), and quality evaluation (Duan et al., 2012). Some studies use the MaxEnt model to predict the potential distribution area of C. pilosula, but they do not discuss the environmental factors that restrict the distribution of this species, and they do not consider the historic distribution area of C. pilosula in the past and the potential distribution area in the future (Wu et al., 2017). To avoid the loss caused by blind introduction, explore the main environmental factors limiting geographical distribution, and grasp the change trend in the distribution pattern of C. pilosula under past and future climate change, it is particularly important to guide its introduction and cultivation scientifically.

This study aims at the current MaxEnt model’s failure to deeply discuss the impact of parameter settings on the geographical distribution of the simulated species. At the same time, combined with the problem of the scientific introduction of the current economic species C. pilosula, by setting MaxEnt different regularization multipliers and feature combinations, the simulation potential distribution area of this species under different climatic conditions in five periods (last interglacial period (LIG), middle Holocene (MHC), the current era and the projection for the periods 2041–2060 (2050), and 2061–2080 (2070), at the same time, according to the permutation feature importance, jackknife test and percentage contribution rate, this study discusses the environmental factors that affect C. pilosula, analyses the reasons for restricting the geographical spread of this species, explores the changes in the distribution pattern of C. pilosula, and provides a certain scientific basis for the resource protection and management and development of this species.

In view of the fact that the current MaxEnt model’s failure to deeply discuss the impact of parameter settings on the geographical distribution of the simulated species, the Maxent model is used to simulate the suitable distribution of C. pilosula and how this might change under different periods after parameter optimization. The specific objectives of this study were: (1) to display the influence of different parameter settings on the performance of the Maxent model; (2) to identify the main environmental variables affecting the potential suitable distribution of C. pilosula; and (3) to predict distribution of this species in different time periods.

Materials and Methods

The flowchart of this study’s contribution is shown in Figure 1. Briefly, first, the distribution record data were summarized, and environmental data were obtained. Then, these data were processed. Finally, the forecast analysis was performed.

FIGURE 1

Figure 1. The framework of this study’s contribution.

Data Source and Processing

Collection and Processing of the Geographic Data

By searching the Chinese Virtual Herbarium (CVH),¹ Global Biodiversity Information Facility (GBIF),² and National Specimen Information Infrastructure,³ 1,432 data points were obtained. Duplicate samples and samples with unclear geographic colocations were removed and cultivation records were introduced manually. The latitude and longitude information of the sampling location was obtained through the Baidu coordinate pickup system, and Google satellite maps was used to check the accuracy of the information. After removing some samples with inaccurate position coordinates, 467 data points are finally obtained. The original spatial resolution is 30 arcsec (about 1 km²), which was matched with climate data layers. To reduce the spatial autocorrelation (Fortin, 1999), only one point closest to the center in the 30 arcsec grid plots (approximately 1 km²) is selected, and 264 effective data records are obtained and converted into csv format for storage.

Screening and Processing of the Environmental Variables

Through the World Climate Database,⁴ the bioclimatic variables of the last interglacial (LIG), middle Holocene (MHC), current and future (2050, 2070) periods are downloaded. These variables (Supplementary Table 1), including 19 bioclimatic variables, were derived from a CMIP5 global circulation model, CCSM4 (Community Climate System Model version 4), generated by the National Center for Atmospheric Research (Colorado, United States). It is one of the most efficient global climate tools for the simulation of future conditions, which has been evaluated in China and successfully applied to forecast the influence of future changes on the distribution of plant species in similar circumstances (Abdelaal et al., 2019). In the 5th Assessment Report of the IPCC, four representative concentration pathways (RCPs), viz. RCP 2.6, RCP 4.5, RCP 6.0, and RCP 8.5, were defined using the total radiative forcing value in 2,100 according to the pre-industrial values of 2.6, 4.5, 6.0, and 8.5 W/m², respectively (Yan et al., 2020c). RCP 2.6 and RCP8.5 were selected to model the prospective potential distribution of C. pilosula under minimum and maximum emissions scenarios hypothesis. The resolution of these bioclimatic variables is 30 arcsec. We use Pearson correlation coefficient analysis to test the multicollinearity among climate variables was applied (Yang et al., 2013). Among a group of climate variables with high correlation (|r|0.8), only one variable closely related to species distribution or easy to explain was selected for model prediction (Kumar and Stohlgren, 2009). R program methods was used to analyze the Pearson correlation coefficients. Eight variables were selected (Supplementary Table 2), which is convenient for model interpretation: annual mean temperature (bio01), mean diurnal range (bio02), isothermality (bio03), temperature seasonality (bio04), max temperature of the warmest month (bio05), precipitation seasonality (bio15), precipitation in the wettest quarter (bio16), and precipitation in the driest quarter (bio17).

Model Setting and Selection

This study used MaxEnt v3.4.1⁵ to predict the potential geographic distribution of C. pilosula in different periods. The MaxEnt model is based on a certain algorithm to simulate a known real model with potential complexity. Its accuracy and authenticity cannot be estimated accurately. Therefore, it is necessary to take appropriate restrictive measures to reduce overfitting. Specifically, the optimal model is selected by setting the regularization multiplier (RM) and feature combination (FC). RM can affect how focused the output distribution is. A smaller RM value will result in a more localized output distribution that fits the given occurrence records better, but is more prone to overfitting (Zhu et al., 2018). Overfitted models are poorly transferable to novel environments and, thus, not appropriate to project distribution changes under environmental change. A larger RM value will produce a prediction that can be applied more widely. FC constrain the computed probability distribution. In the default parameter setting, the selection of FC is related to the number of species distribution points, and the RM value is 1 (Zhu et al., 2018). In R v3.6.3,⁶ the ENMeval data package⁷ is used for optimization. The checkerboard2 method is used to divide the distribution data, set the aggregation factor to 5, and set the RM to change from 0.5 to 4.0 with an increase by 0.5 each time. Therefore, there are eight values of RM; FC selects 7 types for testing, namely, L, LQ, H, LQH, LPQ, LQHP, LQHPT. ENMeval tests the above 56 parameter combinations, and finally, we use the corrected Akaike information criterion (AICc) (Akaike, 1998; Muscarella et al., 2014), the difference between the training and testing AUCs (AUC_DIFF) (Warren and Seifert, 2011), and the 10% training omission rate (OR₁₀) (Pearson et al., 2007), to evaluate model performance. The AICc value comprehensively reflects the goodness of fit and the complexity of the model. It is an excellent standard for measuring the performance of the model. The model with the smallest AICc value, that is, the model with delta AICc = 0, is considered the best model, and all models with delta AICc < 2 are considered to have substantial support (Burnham and Anderson, 2004; Warren and Seifert, 2011). AUC_DIFF is expected to be positively associated with the degree of model overfitting (Warren and Seifert, 2011). OR₁₀ represents the proportion of test localities with suitability values lower than that excluding the 10% of the training localities with the lowest predicted suitability. Omission rates greater than the expectation of 10% indicate model overfitting (Fielding and Bell, 1997; Peterson et al., 2011).

According to the above three evaluation indexes, the best model parameter combination is determined, and the best MaxEnt model is rebuilt with the eight selected variables. The number of best model repetitions is set to 10. The method of sampling the test samples is 10-fold cross-validation. This method divides all the current distribution records of C. pilosula into 10 subsets, each of which takes turns as the test set and the other nine subsets are as the training set, which improves the utilization ratio of the data and the persuasiveness of the results. The training data and test data of this species distribution records have three characteristics: serial number, longitude information, and latitude information.

Model Forecast Analysis

Optimized MaxEnt software is used to predict the potential geographical distribution of C. pilosula in the past, current, and future. According to the habitat suitability value of the distribution point and the normal distribution parameters _μ and _δ, the suitability of C. pilosula was divided into three levels: _0,μ–δ are unsuitable habitats, _μ–δ,μ are potential habitats and _μ,1 are high-potential habitats (Wei et al., 2019). The high-potential habitats are areas in which the ecological factors are optimal, and there are few restrictions on the growth and development of this species; the potential habitats are areas in which the ecological factors are suitable for the growth of C. pilosula, but to a certain extent, they are slightly inferior to the high-potential habitats; the unsuitable habitats are areas in which the ecological factors are severely restricted and are unfavorable for the growth of this species, and they are not suitable for cultivation and planting.

The MaxEnt model software has three functions: permutation importance, percentage contribution rate and the jackknife test, which are used to evaluate the relative importance of the environmental factors to the distribution of C. pilosula. The permutation importance value is independent of the specific algorithm path of the software and only depends on the final results of the model. The contribution degree of each environmental variable depends on the random enumerated variable values on the training point (existence point and background value) and the resulting decrease in the training AUC value. The larger the AUC decrease, the more dependent the model is on the environment variable. The percentage contribution rate depends on the specific algorithm of the maximum entropy program to obtain the optimal solution. The MaxEnt model records the contribution of the environmental variables to the adaptive model during training (Phillips, 2006). By modifying the coefficient corresponding to each eigenvalue, the model gain value will increase, and the gain value will be allocated to the environmental variables on which each eigenvalue depends; finally, the environmental contribution will be converted to the percentage output. After the jackknife test runs a single environmental factor one by one and uses all environmental factors to obtain the results, the differences between the training gain value, test gain value and AUC value are compared to understand the more important environmental factors in the distribution of C. pilosula.

The accuracy of this model was evaluated by the receiver operating characteristic (ROC) curve and the area under the ROC curve (AUC). Its value is directly proportional to the accuracy of the model prediction. When the software runs 10 times, the average training AUC is calculated automatically. The AUC is generally between 0 and 1. An AUC between 0 and 0.5 indicates that the prediction effect of the model is very poor; an AUC between 0.6 and 0.9 indicates that the prediction effect is moderate; an AUC greater than 0.9 indicates that the prediction effect of the model is very good. The closer that this value is to 1, the better the performance of the model is (Phillips et al., 2006).

Results

Model Optimization and Accuracy Evaluation

Based on 264 records of the current distribution of C. pilosula and eight layers of environmental variables, the current potential distribution habitats of this species were simulated by the MaxEnt model. The default setting of MaxEnt is FC = LQHPT, RM = 1. At this time, the delta AIC_C was 39.240 (Table 1). After ENMeval optimization, the MaxEnt model is optimized as follows: the FC is LQHP, namely, linear, quadratic, fragmented, and product, and the RM is 1.5. At this time, the delta AICc is 0, and its value is less than 2 (Figure 2A), which indicates that the complexity of the model is in an acceptable range and has high reliability. Further comparison shows that the mean AUC_DIFF and OR₁₀ of the optimized model are 0.011 (Figure 2B) and 0.118 (Figure 2C), respectively, which are 54.17 and 30.59% lower than the default setting, indicating that overfitting with the optimized parameter setting is low. Therefore, RM = 1.5 and FC = LQHP are selected as the final parameter settings. Under the condition of this parameter setting scheme, when the MaxEnt model simulates the current geographical distribution 10 times, the maximum AUC value is 0.926, the minimum AUC value is 0.846, and the average AUC value is 0.910 _± 0.009 (Figure 3B), which indicates that the prediction of the model is accurate. If the default parameters are used, the maximum AUC value is 0.878, the minimum AUC value is 0.826, and the average AUC value is 0. 865 _± 0.029 (Figure 3A). After using the optimized parameters to rebuild the model, the prediction accuracy is better than that of the default parameters.

TABLE 1

Table 1. The performance of the MaxEnt model using the default parameter settings and the optimized parameter settings.

FIGURE 2

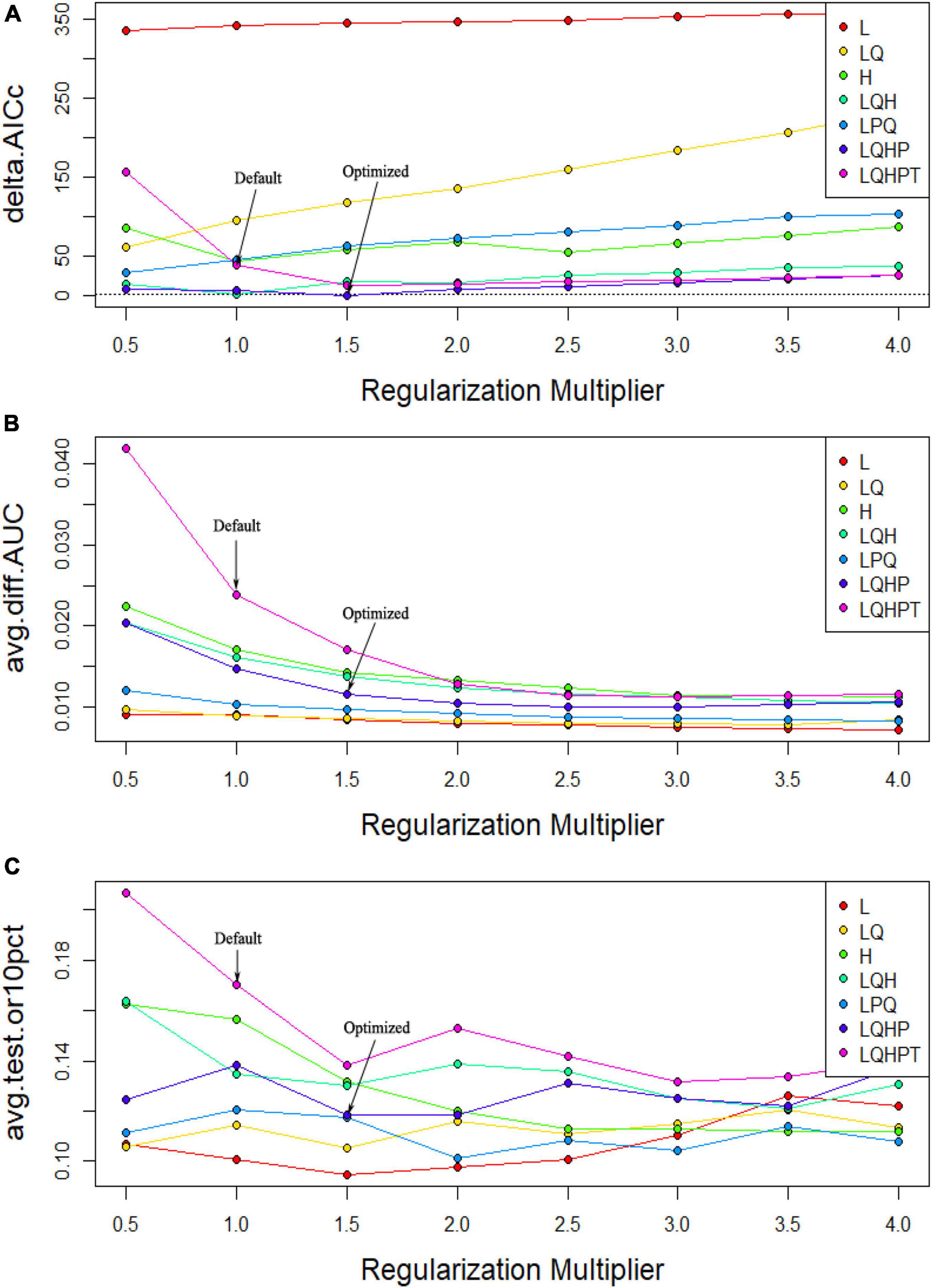
Figure 2. Evaluation results of the MaxEnt model under different parameters settings. (A) Delta AICc; (B) AUC_DIFF; (C) OR₁₀.

FIGURE 3

Figure 3. ROC curve of the reconstructed MaxEnt model. (A) Defaulted model; (B) optimized model.

The Main Environmental Variables Affecting This Species

The contribution rate and permutation importance of each environmental variable listed in Table 2 indicated that bio01 plays an important role in controlling the distribution of C. pilosula. Its contribution rate reaches 42.1%, and the permutation importance reaches 36.8%. In addition, the cumulative contribution rate of bio01, bio02, and bio03 reaches 83.8%, and the cumulative permutation importance reaches 70.8%.

TABLE 2

Table 2. Important environmental variables and corresponding metrics.

By analyzing the gain of each variable, it is found that the gain of using any environmental variable alone does not exceed the gain of using all the variables. Each environmental variable contributes to improving the prediction accuracy of the model, which is mutually verified with the calculation results of the contribution rate in Table 2. Among them, bio16, bio01, and bio17 are the top-three variables in terms of the normalized training gain, and bio16, bio17, and bio01 are the top-three variables in terms of the test gain and AUC value, so these variables have better matching and more effective information for the training data; when other variables are used, the three variables with the most decline in normalized training gain, test gain and AUC value are bio16, bio17, and bio15, indicating that the above variables contain valid information that other variables do not have. In conclusion, the main temperature factors affecting the distribution of C. pilosula are bio01, bio02, and bio03, and the main rainfall factors are bio15, bio16, and bio17.

The curves in Figure 4 show how each environmental variable affects the MaxEnt model prediction. The curves show how the predicted probability of presence changes as each environmental variable is varied, keeping all other environmental variables at their average sample value. The curves show the mean response of the 10 replicates. MaxEnt runs the mean (red) and +/− one standard deviation (blue). In a certain range, the distribution probability of C. pilosula increased with increasing bio01, bio02, bio03, bio15, bio16, and bio17. After reaching a certain peak, the distribution probability decreased with an increase in the values of the environmental factors. According to the response curve of the climate factors, we can judge the relationship between the existence of C. pilosula and the values of the ecological factors. When the distribution probability of this species is greater than 0.3324, its corresponding ecological factor value is suitable for the growth of C. pilosula. C. pilosula has certain adaptability to six major environmental factors, and the thresholds of each environmental factor are bio01 (4.02–23.17°C) (Figure 4A), bio02 (3.24–13.49°C) (Figure 4B), bio03 (23.69–40.46) (Figure 4C), bio15 (52.10–109.56) (Figure 4D), bio16 (242.83–861.02 mm) (Figure 4E), and bio17 (8.88–146.23 mm) (Figure 4F).

FIGURE 4

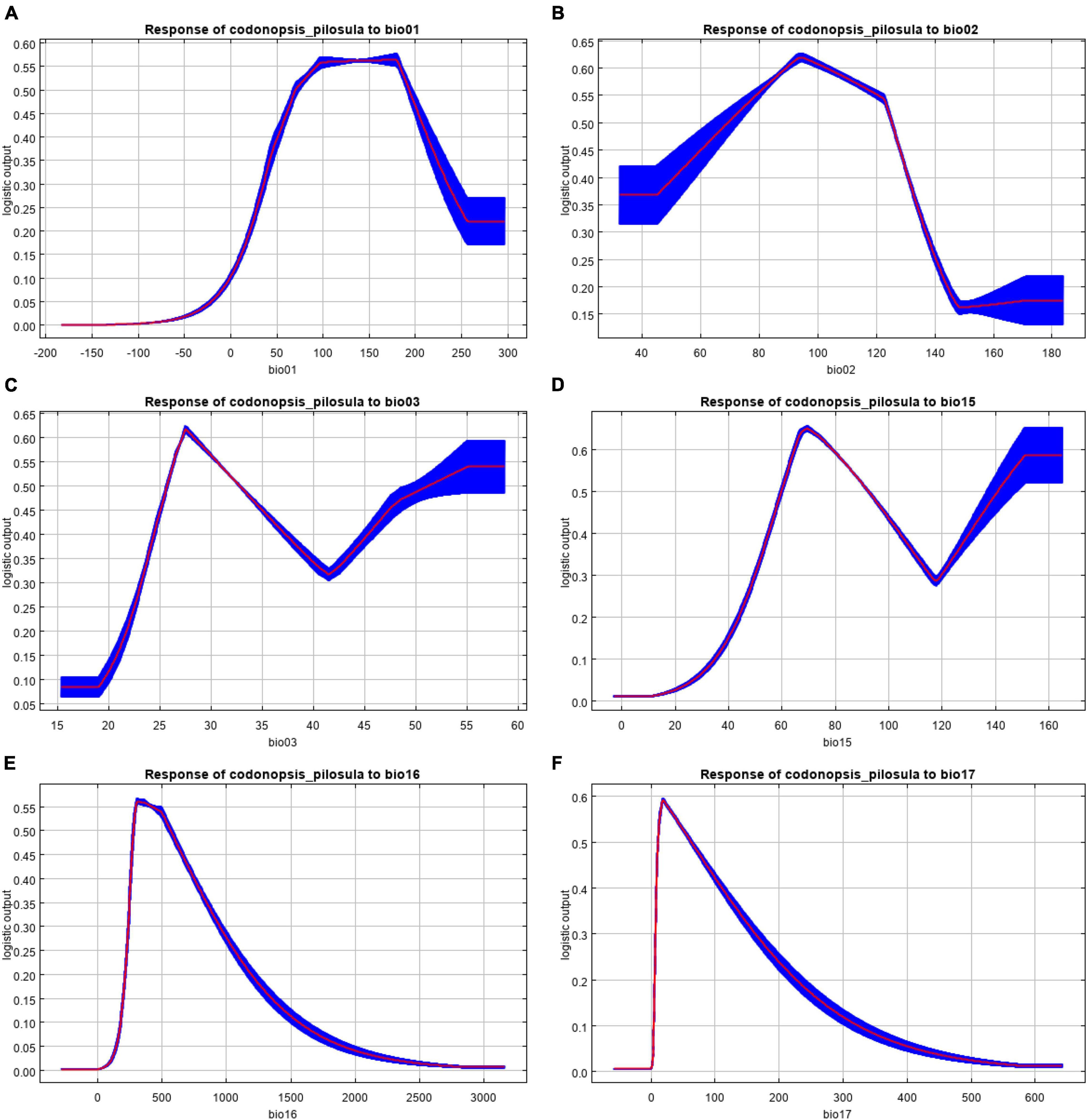
Figure 4. Response of Codonopsis pilosula to six major environmental factors. (A) bio01; (B) bio02; (C) bio03; (D) bio15; (E) bio16; (F) bio17 (A,B represent temperature in degrees Celsius, and its value is magnified by 10 times due to data synthesis).

The contribution rate of the annual mean temperature to the distribution area of C. pilosula is the largest. When the annual mean temperature is less than 0°C, the distribution probability of this species is almost 0. When the annual mean temperature is more than 0°C, the distribution probability of C. pilosula rises sharply, reaches its peak value and optimum growth condition at 17.91°C. Then, the distribution probability of C. pilosula decreases rapidly.

Forecast of the Distribution of Suitable Geographical Areas for Codonopsis pilosula

Characteristics of the Current Potential Geographical Distribution

Among the 264 records of the C. pilosula distribution, 70.08% are potential habitats, and 12.12% are high-potential habitats, which shows that the current potential habitats simulated by MaxEnt can basically cover the current distribution points. Current potential habitats are mainly distributed in most provinces and cities of China, and Xinjiang and Hainan are unsuitable habitats (Figure 5). Due to the sparse data of individual sampling points, although there are distribution records in Heilongjiang Province, they are not predicted as potential habitats. The high-potential habitats are located in the north of Henan Province, the junction of Sichuan and Gansu Provinces, the junction of Sichuan and Shaanxi Provinces, the junction of Sichuan and Chongqing Provinces, the junction of Shaanxi and Shanxi Provinces, and the central region of Shaanxi Province. The average suitability degree of the 264 distribution records is 0.536, and the three locations with the highest suitability degrees are Guangyuan City, Lizhou District, Sichuan Province (0.856); Xi’an city, Hu County, Shaanxi Province (0.839); and Daofu County, Ganzi Prefecture, Sichuan Province (0.823). The three locations with the lowest suitability degrees are Manzhouli city, Hulunbuir city, Inner Mongolia (0.014); Shaoyang City, Xinning County, Hunan Province (0.038); and Menyuan Hui Autonomous County, Haibei Tibetan Autonomous Prefecture, Qinghai Province (0.053).

FIGURE 5

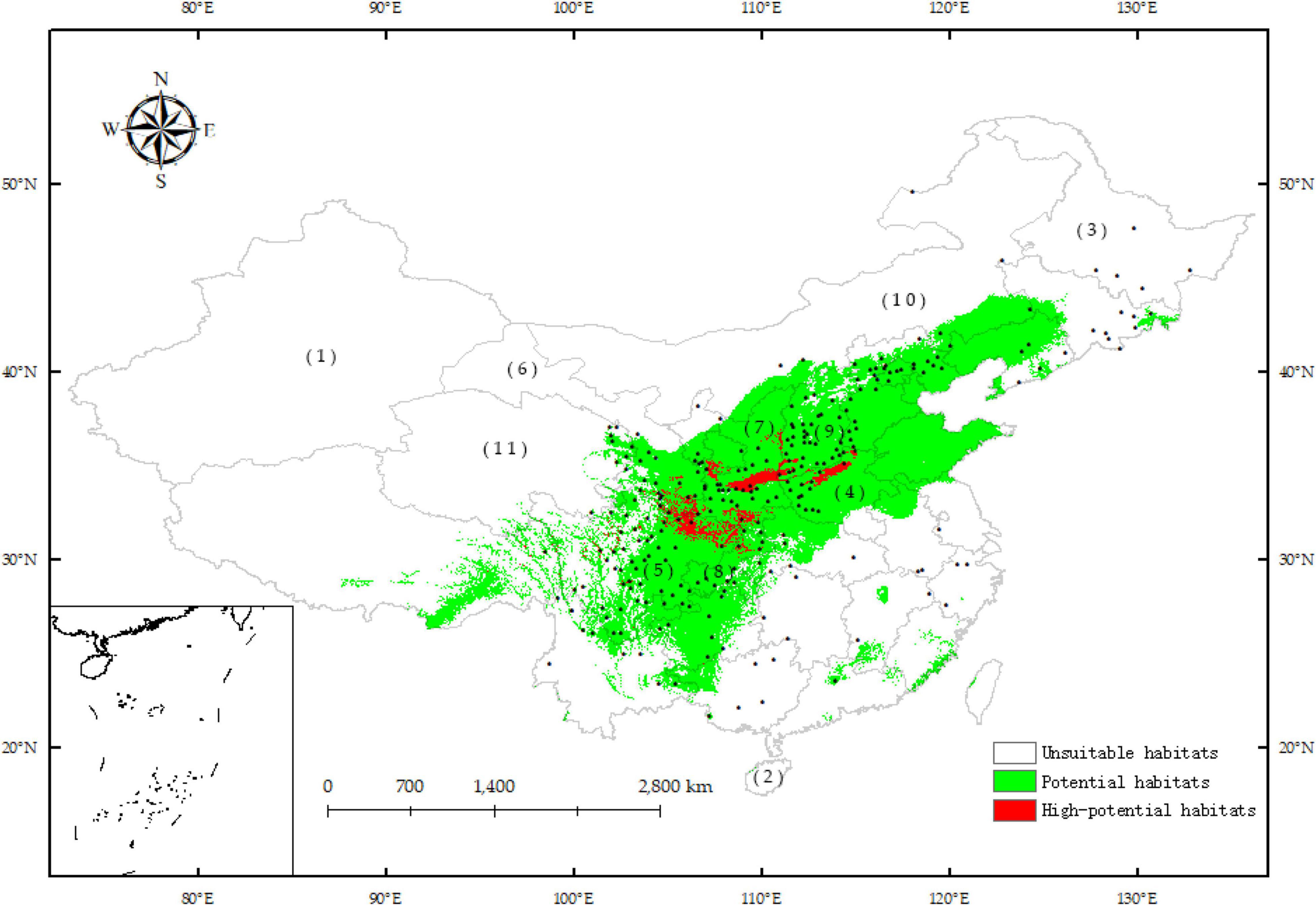
Figure 5. Potential distribution for C. pilosula under the current conditions predicted by the MaxEnt model based on the optimized parameters. (1) Xinjiang; (2) Hainan; (3) Heilongjiang; (4) Henan; (5) Sichuan; (6) Gansu; (7) Shaanxi; (8) Chongqing; (9) Shanxi; (10) Inner Mongolia; (11) Qinghai.

Potential Distribution Characteristics of the Past and the Future

Based on the MaxEnt model, the last two periods are predicted, which are the past interglacial period (Figure 6A) and the middle Holocene period (Figure 6B). Compared with the current distribution, the LIG period changed considerably. The area of potential suitable distribution habitats and high-potential suitable distribution habitats both decreased, the potential habitats decreased by 5.20% and the high-potential suitable habitats decreased the most, reaching 13.00% (Table 3). Only in the north of Sichuan Province, the middle and south of Shaanxi Province, and the sporadic areas in Shanxi and Henan Provinces are highly suitable. In the middle Holocene, the area of potential and high-potential areas increased compared with that of the last interglacial period, and the outline was similar to that of the current outline, but both areas were smaller than that of the current distribution.

FIGURE 6

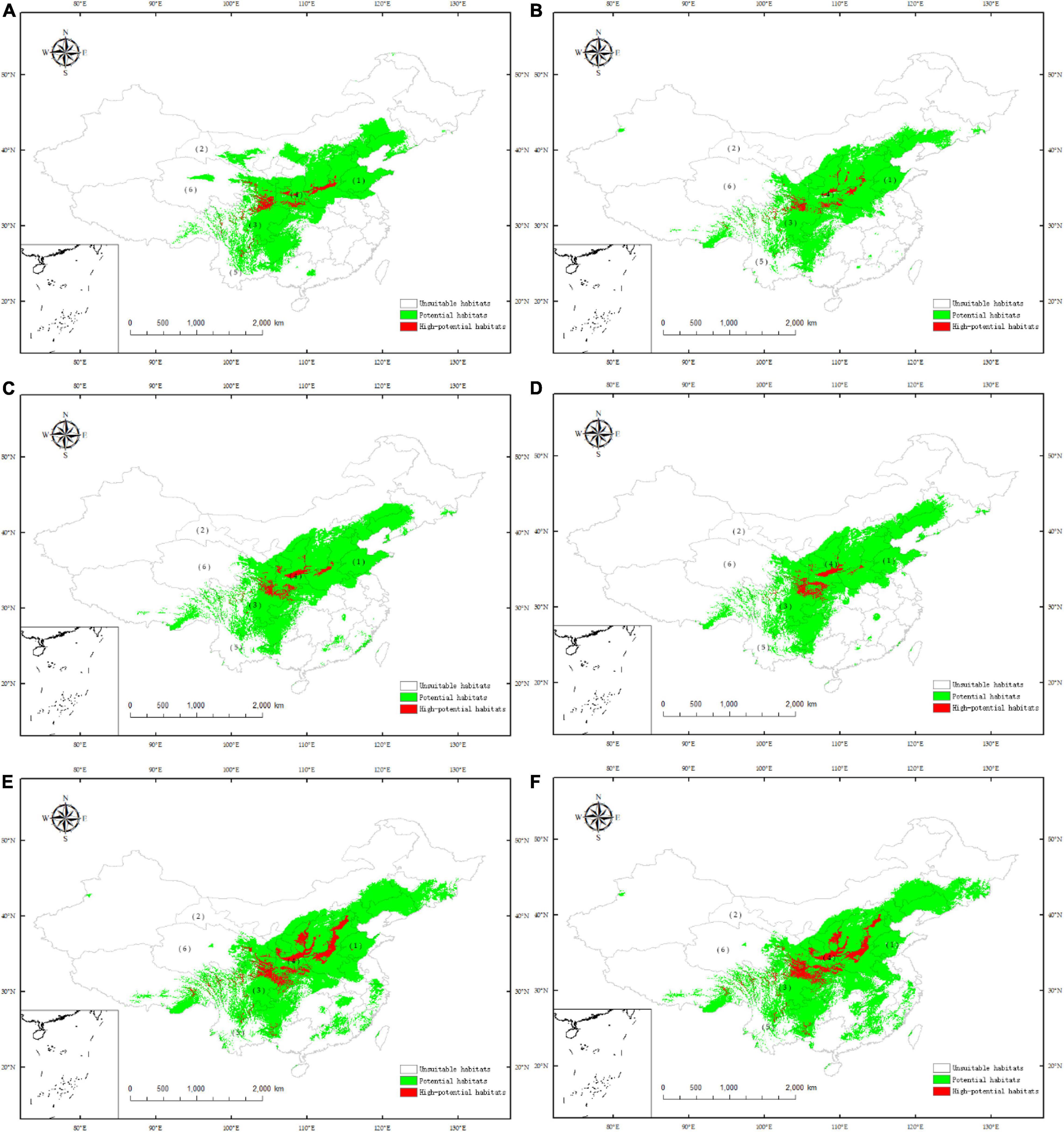
Figure 6. Potential distribution for C. pilosula during different periods predicted by the MaxEnt model based on the optimized parameters. (A) LIG; (B) MHC; (C) RCP 8.5-2050; (D) RCP 8.5-2070; (E) RCP 2.6-2050; (F) RCP 2.6-2070 (1) Shandong; (2) Gansu; (3) Sichuan; (4) Shannxi; (5) Yunnan; (6) Qinghai.

TABLE 3

Table 3. Characteristics of the potential distribution in different periods.

Based on the model of current distribution points, the future potential distribution areas of C. pilosula were predicted for 2050 and 2070 under two future climate scenarios (RCP 2.6 and RCP 8.5). Under the scenario with high levels of greenhouse gas emissions (RCP 8.5), it is estimated that by 2050, the range of potential habitats of this species will decrease by 2.03%, and the range of high-potential habitats will increase by 7.08%. The potential habitats will expand eastward, almost covering the whole province of Shandong, and the current high-potential habitats at the junction of Gansu and Sichuan Provinces will expand eastward to the junction of Gansu, Sichuan and Shaanxi Provinces (Figure 6C). Compared with the current distribution, in 2070, the potential habitats of this species will increase by 0.60%, and the range of high-potential habitats will increase by 11.41%. The potential habitats gradually appeared in the central and northern parts of Yunnan, central Qinghai and central Gansu Provinces, and the changes in other potential habitats were small. Most of the areas at the junction of Gansu, Sichuan and Shaanxi Provinces have high-potential habitat conditions (Figure 6D). Under RCP 8.5, it is estimated that by 2050, the range of potential habitats and high-potential habitats of this species will increase by 22.91 and 202.99%, respectively. Potential habitats tend to spread to the southeast provinces, and the size of high-potential habitats has also expanded correspondingly, reaching 250,500 square kilometers (Figure 6E). Compared with the current distribution, in 2070, the potential habitats of this species will increase by 28.38%, and the range of high-potential habitats will increase by 191.29%. At that time, the area of potential habitats will be as high as 2.5108 million square kilometers (Figure 6F).

According to the statistics of the geographical centers of the suitable distribution areas in different periods, it can be seen that the geographical centers of the two historical periods are south of 33.5°N, and the change in the current geographical centers is relatively small (only 28.50 km to the northeast), and then the geographical centers will continue to move to the northwest in the next two periods. By 2070, the geographical centers will move to the north to 33.55°N (Figure 7).

FIGURE 7

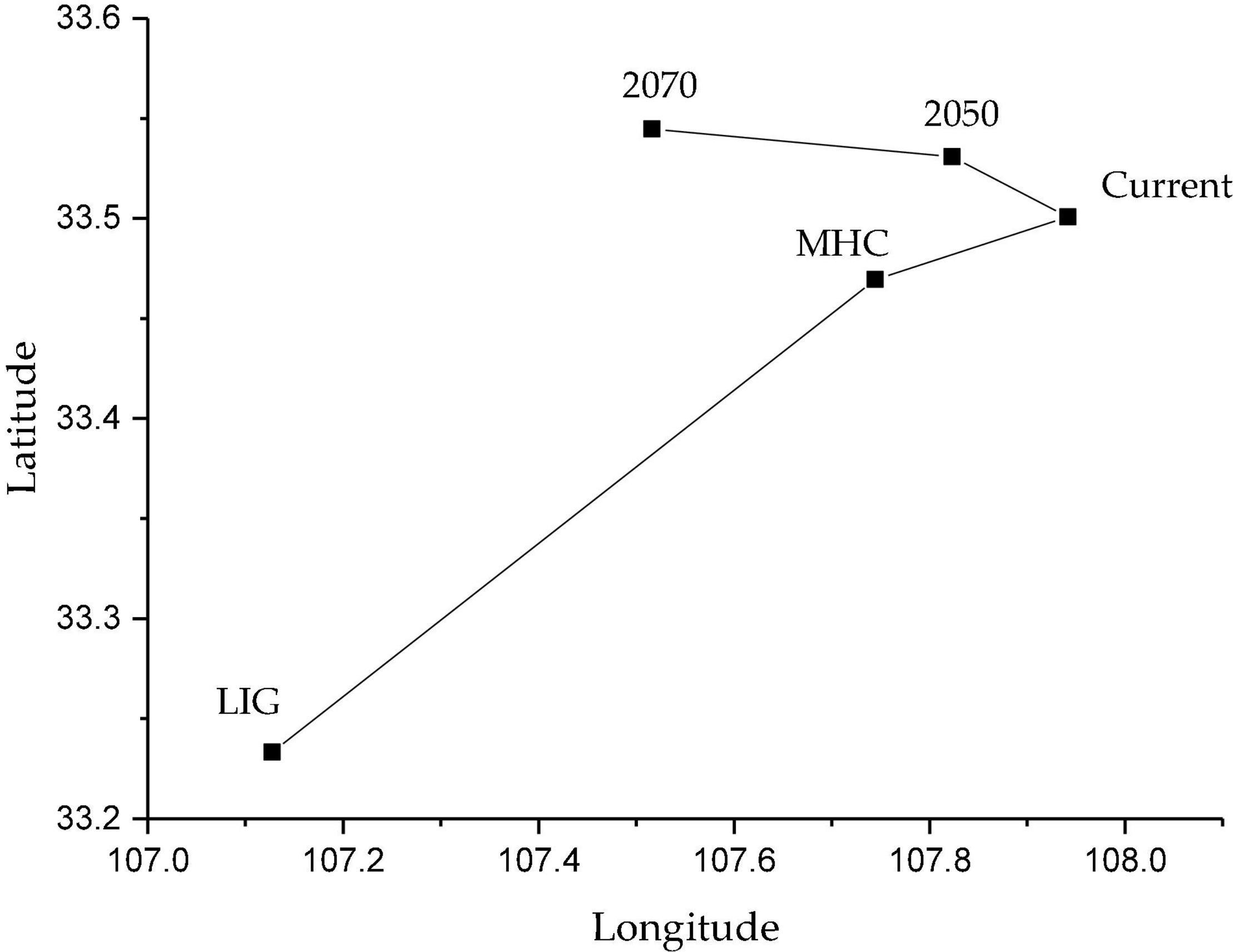
Figure 7. Changes in geographical centers of the potential distribution areas of C. pilosula in the different periods.

From the perspective of the change in the suitable area in different periods, from the last interglacial period to 2070, the distribution of C. pilosula experienced an overall gradual increase. The potential suitable area in the five periods was the smallest in the last interglacial period and the largest in 2070. The high-potential habitats changed greatly in five periods. In the last interglacial period, the high-potential habitat area is the smallest (only 72,000 square kilometers). In 2050, the area is the largest, reaching 250,500 square kilometers.

Under the trend of global warming, most of the multivariate environmental similarity surface (MESS) of climate scenarios in the future multi-period range is between 0 and 10 in the current suitable region, and some areas are 10–20. The areas with a MESS greater than 20 will only occupy a small area part. Under climate scenario RCP 2.6-2050 (Figure 8A), the mean value of the MESS under this climate scenario is 14.13, the first quartile is 1.96, and the third quartile is 24.68; Under RCP 8.5-2050 (Figure 8C), the mean value of the MESS is 9.94, the first quantile is 0.17, and the third quantile is 14.95; Under RCP 2.6-2070 (Figure 8B), the mean value of the MESS under this climate scenario is 13.13, the first quantile is 1.55, and the third quantile is 24.08; Under RCP 8. 5-2070 (Figure 8D), the mean value of the MESS under this climate scenario is 6.34, the first quantile is −2.15, and the third quantile is 10.20. Combining the values of MESS and change maps in different periods under future climate change, it can be seen that in different climate change scenarios in the same period, in 2050, the MESS values from large to small are RCP2.6 > RCP8.5; in 2070, the MESS values from large to small is RCP2.6 > RCP8.5. When the climate change scenarios in different periods are the same, under the climate scenario RCP2.6, the mean value of the MESS in the 2050 period is greater than 2070; under the climate scenario RCP8.5, the mean value of the MESS in the 2050 period is greater than 2070. That is, when the period is the same, and the climate change scenarios are different, the MESS value is positively correlated with the greenhouse gas emission concentration; when the period is different, the climate change scenario is the same, the MESS value decreases with the passage of time, and there is a negative correlation between the two relations.

FIGURE 8

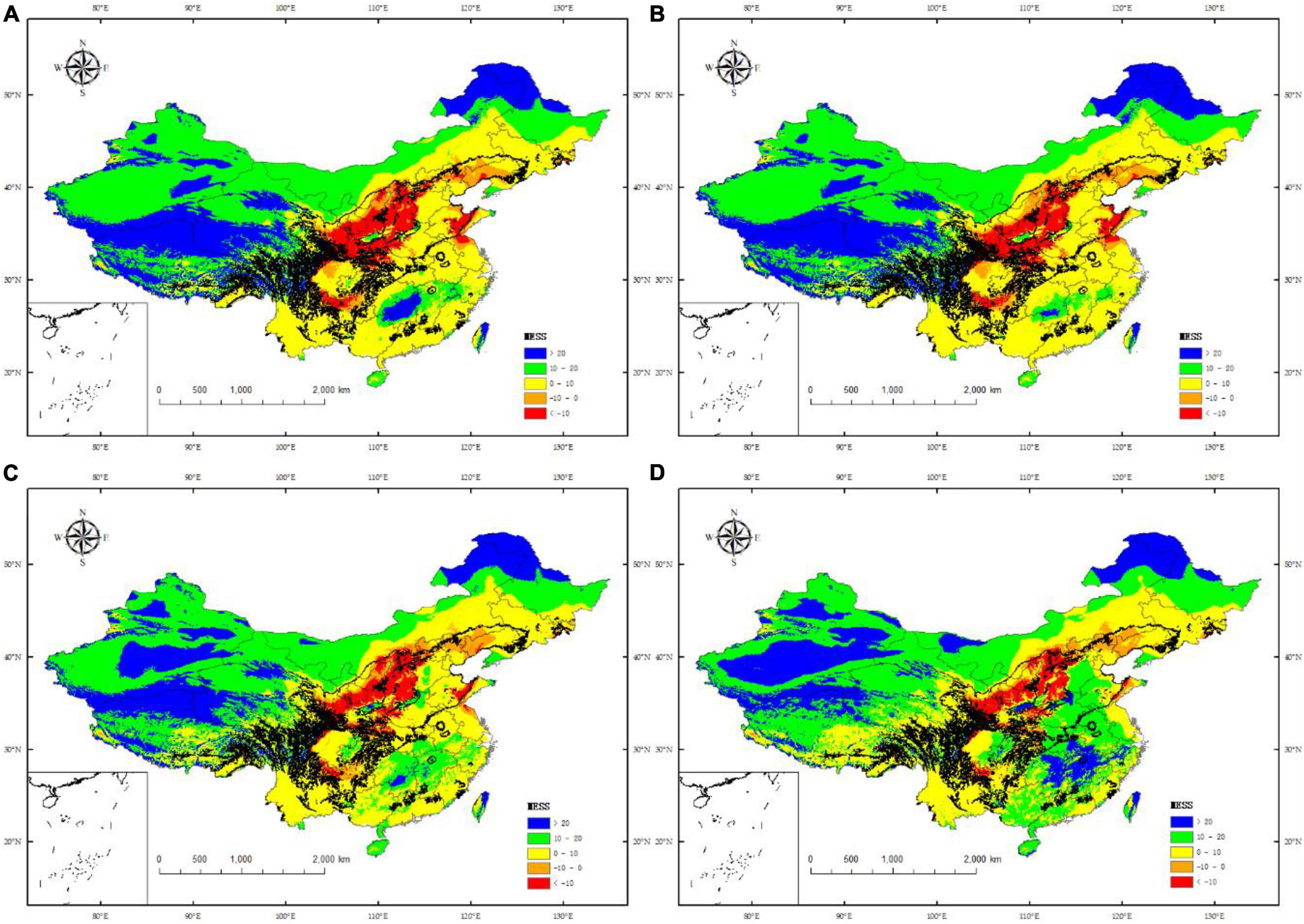
Figure 8. Multivariate environmental similarity surface (MESS) analysis for C. pilosula in China under different combinations of climate change scenarios. (A) RCP 2.6-2050; (B) RCP 2.6-2070; (C) RCP 8.5-2050; (D) RCP 8.5-2070.

The mean range of the MESS in different periods under future climate change scenarios ranges from 6.34 to 14.13. The degree of climate anomaly of each climate change scenario is similar, but there are some differences. In general, under future climate change scenarios, areas with high climate anomalies are mainly the two provinces, Shanxi and Shaanxi, located in the northwest of the current potential habitats; most of these regions have MESS values less than −10, while the areas with low climate anomalies are mainly located in Hebei, Shandong, and Henan in the east of the current potential habitats. The range of the MESS in these provinces is 0–20. The RCP 2.6-2050 climate scenario has the highest MESS value and the lowest climate anomaly degree; while the RCP 8.5-2070 climate scenario has the lowest MESS value and the highest climate anomaly degree.

Discussion

MaxEnt usually retains a random subset for data modeling and then uses the AUC to evaluate the model prediction ability, but the software has defects (Warren et al., 2014). First, when the training data and test data are affected by the sampling deviation, the AUC may overestimate the ability of the model (Veloz, 2009). Second, the MaxEnt model is a highly complex machine learning model. When simulating the potential distribution of species, it will lead to overfitting of the model, which will directly affect the transfer-ability of species (Zhu and Qiao, 2016). Although some domestic and foreign experts and scholars have carried out research on the prediction of the distribution area of the C. pilosula based on the MaxEnt model and achieved good prediction results, they did not consider the over-fitting phenomenon of maxent modeling, which caused the generalization ability of the model to be limited (Jie et al., 2017; Niu et al., 2021). The complexity of the model can be constrained by adjusting the regularization multiplier in the MaxEnt model and using AICc to select the appropriate feature combination (Warren and Seifert, 2011). In this study, AICc, AUC and OR₁₀ are used to select the best MaxEnt model with the smallest overfitting effect. The results show that RM = 1.5 and FC = LQHP have the lowest degree of overfitting. After using the optimized parameters to rebuild the model, the prediction of the C. pilosula habitats of the five periods is obtained, and the prediction accuracy is better than that of the default parameters.

The prediction results of the MaxEnt model show that the main ecological factor is temperature, followed by precipitation. The important factors affecting the geographical distribution of C. pilosula include the annual mean temperature (bio01), mean diurnal range (bio02), isothermality (bio03), precipitation seasonality (bio15), precipitation in the wettest quarter (bio16), and precipitation in the driest quarter (bio17). The suitable temperature range for growth in this species is 12.0–25.0°C, and its seed germination temperature is 18.0–20.0°C. When the temperature reaches 12.0–18.0°C, the underground stem sprouts. The temperature during which the fastest growing occurs is 15.0–25.0°C, and the most suitable temperature for flowering and seed setting is 15.0–22.0°C (Chang, 2013). The highest germination rates of C. pilosula seeds were 96.00 and 97.33%, respectively, at 20°C, and the germination duration was 9 days. At 30°C, the lowest germination rates were 17.00 and 28.00%, respectively, which indicated that the seeds of this species prefer cool but not hot temperatures (Su et al., 2012). C. pilosula is more cold resistant than other plants, and its growth above 30°C is limited (Zhao et al., 2006). The results show that the annual mean temperature range of C. pilosula is 4.02–23.17°C, and the best temperature is 17.91°C, which is in line with the suitable temperature for growth of this species and is very close to the temperature needed for seed germination. When C. pilosula is exposed to sustained hot temperatures in the main growth period, its aboveground parts will easily wither and suffer from diseases (Chang, 2013). Therefore, we should pay attention to the control of high temperatures in the cultivation of C. pilosula. The mean diurnal range plays an important role in the growth of C. pilosula. The suitable range of diurnal range is 3.24–13.49°C, the peak value is 9.26°C, and the higher diurnal range is conducive to the formation of tubers, promoting the growth of this species (Chang, 2013). In contrast, if the diurnal range is smaller than that above, the respiration function of C. pilosula will be strengthened. Under these conditions, the respiration loss is large, which is not conducive to the growth of tubers, and low drying rate of the tubers can easily occur. After processing, low-quality, inferior products are easily formed. The main precipitation factors affecting the growth of C. pilosula are the precipitation seasonality, the precipitation in the wettest quarter, and the precipitation in the driest quarter. The suitable range of the precipitation seasonality is 52.10–109.56, that of the precipitation in the driest season is 8.88–146.23 mm and that of the precipitation in the wettest season is 242.83–861.02 mm. The water demand of C. pilosula in different growth periods is different. In the sowing and transplanting periods, the water demand is higher, and the soil humidity needs to be approximately 70%. After planting, the water demand of C. pilosula is reduced, and if the soil is too wet, especially under high-temperature and high-humidity conditions, it is easy to have diseases and insect pests and rotten roots. In the mature period, the precipitation is too high, which is not conducive to the formation of the roots of this species (Wang et al., 2006). The seasonality of precipitation reflects the different demands of C. pilosula on precipitation in different growth periods. Precipitation has the greatest influence on C. pilosula in the sowing and transplanting periods than the other variables. During these periods, we should pay attention to providing sufficient water for C. pilosula.

The climate of the last interglacial period, which began 120,000 years ago, is the most similar to the current climate, but it is still very different. The global temperature is approximately 5°C lower than it is now. At that time, China’s climate was abnormal, cold and dry. China’s glacial area was 8.4 times larger than it is now. The cold and cold climate had a general impact on animals and plants (Chen et al., 2011), and most of the plants significantly reduced their distribution area after the temperature dropped in the ice age (Xu et al., 2017). The suitable area for warm and humid plants moved to the south as a whole, and most of the northern areas were occupied by plants that can tolerate a cold and dry climate (Shepherd et al., 2017). The results showed that out of the five periods, the geographical center of the suitable habitats of C. pilosula in the last interglacial period was the southernmost, and the distribution area was the smallest. The middle Holocene period, is the most recent warm period in history. In this period, the whole suitable area and the highly suitable area were increased compared with the current area. The prediction results of the MaxEnt model also show that the geographical distribution center has a trend of moving northward, and the outline is basically similar to that of now. The study of paleoclimate reconstruction shows that the average increases in the area, precipitation and precipitation intensity in China’s monsoon area during this period were 10.7, 18.7, and 7.3%, respectively, under different climatic patterns (Tian and Jiang, 2015). As a species that prefers a wet climate, the increase in rainfall in summer is beneficial to the growth of C. pilosula, and its suitable area and highly suitable area increased. Climate fluctuations caused the migration of the vegetation belt. Although most studies found that the vegetation belt moved northward in the peak of the warm period (Fang et al., 2011), the range of movement was not large (Xun, 2000). Therefore, compared with the current distribution, the potential suitable area of C. pilosula did not show a significant trend in movement, and the contour is close to the current contour. Compared with current times, when the greenhouse gas emission scenario is RCP 8.5, C. pilosula moved northward in 2050 and 2070, and its area expanded because, as a species that prefers a warm and humid climate, the increase in temperature and precipitation in the future may provide a more suitable growth environment for it. This finding is consistent with the conclusion that, on the premise that the temperature will continue to rise in the future, the suitable habitats of plants that prefer warm and humid climates will move to the north as a whole, and the zone of vegetation zone that adapts to cold and dry climates will gradually retreat (Zhang et al., 2017; Liu C. et al., 2018).

This study shows that since climate warming, the highly suitable habitats of C. pilosula are mainly in Sichuan, Gansu, Shaanxi, Shanxi, and Henan Provinces. The results are basically in line with the previous research results (Jie et al., 2017; Niu et al., 2021), which can provide a reference for the production layout of C. pilosula and the development of countermeasures against climate change. It should be pointed out that the potential suitable distribution of C. pilosula depends not only on the climatic conditions but also on the socio-economic structure, production technology level and other factors. At the same time, it is also affected by historical phenomena, human activities, geographical characteristics and genetic types. Therefore, there will be some deviation between the predicted results and the actual suitable distribution area of this species. Therefore, in actual production activities, the introduction, trial planting and planting of C. pilosula need to consider the role of various factors, especially the impact of economic factors and production factors.

A new method based on the MaxEnt model and ultra-high performance chromatographic fingerprint technique was developed to evaluate the effects of environmental factors on the quality of this species (Wan et al., 2021). Unlike this study, their research focuses on the distribution and quality of C. pilosula on a regional scale. In contrast, our research focuses on the distribution and influencing factors of this species on a national scale under climate change from the past to the future and considers modeling optimization. In addition, data sparsity is a problem in the MaxEnt modeling process (Haffner, 2006). Therefore, another future research direction is to combine this approach with other approaches, such as UPLC fingerprint technique, rough sets (Yan et al., 2016b,c, 2017a), Petri nets (Yan et al., 2016a), and a multidimensional cloud modeling (Yan et al., 2017b), which can effectively improve the space-time cost and processing speed in the age of big data (Wu et al., 2018a,b), and the results from these approaches can be compared with those provided by our model.

Conclusion

In this study, by setting two parameters of the MaxEnt model, namely, the regularization multiplier and the feature combination, we use the mean AUC_DIFF, OR₁₀, and delta AICc indicators to determine that the optimal regularization multiplier is 1.5, and the optimal parameter feature combination is LQHP. The main temperature factors affecting the distribution of C. pilosula are the annual mean temperature, mean diurnal range, and isothermality, and the main rainfall factors are the precipitation seasonality, precipitation in the wettest quarter, and precipitation in the driest quarter. Among these factors, the annual average temperature contributes the most to the distribution area of C. pilosula. When the annual average temperature is greater than 0°C, the distribution probability of C. pilosula rises sharply, reaches the peak value at 17.91°C, and reaches the optimum growth condition. Then, the distribution probability of C. pilosula decreases rapidly. The MaxEnt model predicts that the potential distribution habitats of C. pilosula early in the last interglacial period moved southward and that the suitable area was the smallest. With the warming of the climate, the high-potential habitats gradual expanded to the north to Sichuan, Gansu, Shaanxi, Shanxi, and Henan Provinces, and the area is the largest in 2070. The introduction and cultivation in these areas cannot only avoid economic loss and resource waste caused by blind introduction but also improve the yield of this species.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

HY: conceptualization. HY and JH: funding acquisition. JH: project administration. GW: supervision. LT and LF: resources. LZ and LQ: methodology. XG: validation. XX and XY: data curation. HY: editing. YQ: visualization. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the Youth Fund of Chongqing Technology and Business University (grant no. 1952033) and the Opening Research Platform of Chongqing Technology and Business University (grant no. KFJJ2018058).

Conflict of Interest

XX and XY were employed by State Grid Chongqing Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank to the reviewers for the constructive and valuable comments and the editors for their assistance in refining this article.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.773396/full#supplementary-material

Footnotes

1. ^ https://www.cvh.ac.cn
2. ^ http://www.gbif.org
3. ^ www.nsii.org.cn
4. ^ www.worldclimate.org
5. ^ http://www.cs.princeton.edu/~schapire/maxent
6. ^ http://cran.r-project.org/
7. ^ http://cran.r-project.org/web/packages/ENMeval/index.html

References

Abdelaal, M., Fois, M., Fenu, G., and Bacchetta, G. (2019). Using MaxEnt modeling to predict the potential distribution of the endemic plant Rosa arabica Crép. in Egypt. Ecol. Inform. 50, 68–75. doi: 10.1016/j.ecoinf.2019.01.003

CrossRef Full Text | Google Scholar

Akaike, H. (1998). “Information theory and an extension of the maximum likelihood principle,” in Selected Papers of Hirotugu Akaike, eds E. Parzen, K. Tanabe, and G. Kitagawa (New York, NY: Springer New York), 199–213. doi: 10.1007/978-1-4612-1694-0_15

CrossRef Full Text | Google Scholar

Anderson, R. P., and Gonzalez, I. (2011). Species-specific tuning increases robustness to sampling bias in models of species distributions: an implementation with Maxent. Ecol. Modell. 222, 2796–2811. doi: 10.1016/j.ecolmodel.2011.04.011

CrossRef Full Text | Google Scholar

Bi, H. Y., Zhang, L. P., Zhen, C., and Wu, B. (2008). An overview of research on germplasm resources of Radix Codonopsis and their utilization. China J. Chin. Mater. Med. 33, 590–594.

Google Scholar

Burnham, K. P., and Anderson, D. R. (2004). Multimodel inference: understanding AIC and BIC in model selection. Sociol. Methods Res. 33, 261–304. doi: 10.1177/0049124104268644

CrossRef Full Text | Google Scholar

Chang, L. (2013). The climatic condition suitable for Codonopsis pilosula in changzi county Shanxi Province. Chin. J. Agrometeorol. 9, 152–153.

Google Scholar

Chen, D. M., Kang, H. Z., and Liu, C. J. (2011). An overview on the potential quaternary glacial refugia of plants in China mainland. Bull. Bot. Res. 31, 623–632. doi: 10.7525/j.issn.1673-5102.2011.05.019

CrossRef Full Text | Google Scholar

Duan, Q. M., Liang, Z. S., Yang, D. F., Liu, Y., and Liu, F. H. (2012). Establisthment of quality evaluation system and difference analysis on roots of Codonopsis pilosula from different habitats. Chin. Tradit. Herb. Drugs 43, 995–999.

Google Scholar

Elith, J., Kearney, M., and Phillips, S. (2010). The art of modelling range-shifting species. Methods Ecol. Evol. 1, 330–342. doi: 10.1111/j.2041-210X.2010.00036.x

CrossRef Full Text | Google Scholar

Elith, J., Phillips, S. J., Hastie, T., Dudík, M., Chee, Y. E., and Yates, C. J. (2011). A statistical explanation of MaxEnt for ecologists. Divers. Distrib. 17, 43–57. doi: 10.1111/j.1472-4642.2010.00725.x

CrossRef Full Text | Google Scholar

Estes, L. D., Bradley, B. A., Beukes, H., Hole, D. G., Lau, M., Oppenheimer, M. G., et al. (2013). Comparing mechanistic and empirical model projections of crop suitability and productivity: implications for ecological forecasting. Glob. Ecol. Biogeogr. 22, 1007–1018. doi: 10.1111/geb.12034

CrossRef Full Text | Google Scholar

Fang, Y. M., Wang, T., and Zhang, J. C. (2011). Analysis of quaternary vegetation changes along the Beijing-Hangzhou Grand Canal. J. Nanjing For. Univ. Nat. Sci. Ed. 35, 113–119.

Google Scholar

Feng, P. P., Li, Z. X., and Yuan, Z. (2012). Review on the phytochemical and pharmacological study of Codonopsis Genus. J. Shenyang Pharm. Univ. 29, 61–65.

Google Scholar

Fielding, A. H., and Bell, J. F. (1997). A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 24, 38–49. doi: 10.1017/S0376892997000088

CrossRef Full Text | Google Scholar

Fortin, M. J. (1999). Effects of sampling unit resolution on the estimation of spatial autocorrelation. Ecoscience 6, 636–641. doi: 10.1080/11956860.1999.11682547

CrossRef Full Text | Google Scholar

Gong, J. W. (2011). Feasibility analysis of Codonpsis pliosula series developing to health care product. J. Shanxi Med. Coll. Contin. Educ. 21, 56–57.

Google Scholar

Guo, J., Liu, X. P., Zhang, Q., Zhang, D. F., Xie, C. X., and Liu, X. (2017). Prediction for the potential distribution area of Codonopsis pilosula at global scale based on Maxent model. Chin. J. Appl. Ecol. 28, 992–1000. doi: 10.13287/j.1001-9332.201703.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Haffner, P. (2006). “Fast transpose methods for kernel learning on sparse data,” in Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, 385–392.

Google Scholar

Huang, Y. Y., Zhang, Y., Kang, L. P., Yu, Y., and Guo, L. P. (2018). Research progress on chemical constituents and their pharmacological activities of plant from Codonopsis. Chin. Tradit. Herb. Drugs 49, 239–250.

Google Scholar

Jie, G., Xiao-ping, L., Qin, Z., Dong-fang, Z., Caixiang, X., and Xia, L. (2017). Prediction for the potential distribution area of Codonopsis pilosula at global scale based on Maxent model. Chin. J. Appl. Ecol. 28, 992–1000. doi: 10.13287/j.1001-9332.201703.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, S., and Stohlgren, T. J. (2009). Maxent modeling for predicting suitable habitat for threatened and endangered tree Canacomyrica monticola in New Caledonia. J. Ecol. Nat. Environ. 1, 094–098.

Google Scholar

Li, X., Li, Y., and Fang, Y. M. (2018). Prediction of potential suitable distribution areas of Quercus fabri in China based on an optimized Maxent model. Sci. Silvae Sin. 54, 153–164.

Google Scholar

Liu, M. X., Qi, J., and Yu, B. Y. (2018). Research progress on the pharmacological activity of Codonopsis pilosula. Strait Pharm. J. 30, 36–39.

Google Scholar

Liu, C., Huo, H. L., Tian, L. M., Dong, X. G., Qi, D., Zhang, Y., et al. (2018). Potential geographical distribution of Pyrus calleryana under different climate change scenarios based on the MaxEnt model. Chin. J. Appl. Ecol. 29, 3696–3704. doi: 10.13287/j.1001-9332.201811.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno-Amat, E., Mateo, R. G., Nieto-Lugilde, D., Morueta-Holme, N., Svenning, J.-C., and García-Amorena, I. (2015). Impact of model complexity on cross-temporal transferability in Maxent species distribution models: an assessment using paleobotanical data. Ecol. Modell. 312, 308–317. doi: 10.1016/j.ecolmodel.2015.05.035

CrossRef Full Text | Google Scholar

Muscarella, R., Galante, P. J., Soley-Guardia, M., Boria, R. A., Kass, J. M., Uriarte, M., et al. (2014). ENMeval: an R package for conducting spatially independent evaluations and estimating optimal model complexity for Maxent ecological niche models. Methods Ecol. Evol. 5, 1198–1205. doi: 10.1111/2041-210X.12261

CrossRef Full Text | Google Scholar

Niu, Y. T., Zhang, J., Wang, H. Z., Jin, L., Du, T., Song, P. S., et al. (2021). Study on planting suitability of Codonopsis radix. Chin. J. Inform. TCM 28, 13–16.

Google Scholar

Pearson, R. G., Raxworthy, C. J., Nakamura, M., and Townsend Peterson, A. (2007). Predicting species distributions from small numbers of occurrence records: a test case using cryptic geckos in Madagascar. J. Biogeogr. 34, 102–117. doi: 10.1111/j.1365-2699.2006.01594.x

CrossRef Full Text | Google Scholar

Peterson, A., Soberón, J., and Pearson, R. G. (2011). Ecological Niches and Geographic Distributions, Vol. 49. Princeton, NJ: Princeton University Press.

Google Scholar

Phillips, S. J. (2006). A brief tutorial on Maxent. AT T Res. 190, 231–259.

Google Scholar

Phillips, S. J., Anderson, R. P., and Schapire, R. E. (2006). Maximum entropy modeling of species geographic distributions. Ecol. Modell. 190, 231–259. doi: 10.1016/j.ecolmodel.2005.03.026

CrossRef Full Text | Google Scholar

Phillips, S. J., and Dudík, M. (2008). Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography 31, 161–175. doi: 10.1111/j.0906-7590.2008.5203.x

CrossRef Full Text | Google Scholar

Porfirio, L. L., Harris, R. M. B., Lefroy, E. C., Hugh, S., Gould, S. F., Lee, G., et al. (2014). Improving the use of species distribution models in conservation planning and management under climate change. PLoS One 9:e113749. doi: 10.1371/journal.pone.0113749

PubMed Abstract | CrossRef Full Text | Google Scholar

Shcheglovitova, M., and Anderson, R. P. (2013). Estimating optimal complexity for ecological niche models: a jackknife approach for species with small sample sizes. Ecol. Modell. 269, 9–17. doi: 10.1016/j.ecolmodel.2013.08.011

CrossRef Full Text | Google Scholar

Shepherd, L. D., de Lange, P. J., Perrie, L. R., and Heenan, P. B. (2017). Chloroplast phylogeography of New Zealand Sophora trees (Fabaceae): extensive hybridization and widespread last glacial maximum survival. J. Biogeogr. 44, 1640–1651. doi: 10.1111/jbi.12963

CrossRef Full Text | Google Scholar

Su, N. N., Zhang, L. P., Wang, Y. F., and Shi, J. Q. (2012). Study on the seed germination percentage of Codonopsis pilosula. Chin. Agric. Sci. Bull. 28, 294–298.

Google Scholar

Syfert, M. M., Smith, M. J., and Coomes, D. A. (2013). The effects of sampling bias and model complexity on the predictive performance of MaxEnt species distribution models. PLoS One 8:e55158. doi: 10.1371/journal.pone.0055158

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, Z. P., and Jiang, D. B. (2015). Mid-Holocene and last glacial maximum changes in monsoon area and precipitation over China. Chin. Sci. Bull. 60, 400–410. doi: 10.1360/n972014-00718

CrossRef Full Text | Google Scholar

Veloz, S. D. (2009). Spatially autocorrelated sampling falsely inflates measures of accuracy for presence-only niche models. J. Biogeogr. 36, 2290–2299. doi: 10.1111/j.1365-2699.2009.02174.x

CrossRef Full Text | Google Scholar

Wan, G.-Z., Wang, L., Jin, L., and Chen, J. (2021). Evaluation of environmental factors affecting the quality of Codonopsis pilosula based on chromatographic fingerprint and MaxEnt model. Ind. Crops Prod. 170:113783. doi: 10.1016/j.indcrop.2021.113783

CrossRef Full Text | Google Scholar

Wang, Z. L., Wu, Z. H., Wu, Q. J., and Sun, C. (2006). Regional planning of ecological climate conditions suitable for planting Dangshen in Longnan of Gansu Province. Chin. J. Agric. Resour. Reg. Plan. 27, 32–35.

Google Scholar

Warren, D. L., and Seifert, S. N. (2011). Ecological niche modeling in Maxent: the importance of model complexity and the performance of model selection criteria. Ecol. Appl. 21, 335–342. doi: 10.1890/10-1171.1

CrossRef Full Text | Google Scholar

Warren, D. L., Wright, A. N., Seifert, S. N., and Shaffer, H. B. (2014). Incorporating model complexity and spatial sampling bias into ecological niche models of climate change risks faced by 90 California vertebrate species of concern. Divers. Distrib. 20, 334–343. doi: 10.1111/ddi.12160

CrossRef Full Text | Google Scholar

Wei, B., Ma, S. M., Song, J., He, L. Y., and Li, X. C. (2019). Prediction of the potential distribution and ecological suitability of Fritillaria walujewii. Acta Ecol. Sin. 39, 228–234.

Google Scholar

Wu, D., Luo, X., Wang, G., Shang, M., Yuan, Y., and Yan, H. Y. (2018a). A highly accurate framework for self-labeled semisupervised classification in industrial applications. IEEE Trans. Ind. Inform. 14, 909–920. doi: 10.1109/TII.2017.2737827

CrossRef Full Text | Google Scholar

Wu, D., Shang, M. S., Luo, X., Xu, J., Yan, H. Y., Deng, W. H., et al. (2018b). Self-training semi-supervised classification based on density peaks of data. Neurocomputing 275, 180–191. doi: 10.1016/j.neucom.2017.05.072

CrossRef Full Text | Google Scholar

Wu, X. J., Zhang, X. B., Guo, L. P., Yu, Y., and Hunag, L. Q. (2017). Study on distribution division of Codonopsis Radix. China J. Chin. Mater. Med. 42, 126–130. doi: 10.19540/j.cnki.cjcmm.2017.0186

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z. P., Zhang, J. Q., Wan, T., Cai, P., and Yi, W. D. (2017). Study on the history distribution pattern of Gymnocarpos przewalskii and refuge area. Acta Bot. Boreali Occidentalia Sin. 37, 2074–2081.

Google Scholar

Xun, X. J. (2000). Pollen-based biome reconstruction at middle holocene (6ka BP) and last glacial maximum (18ka BP) in China. Acta Bot. Sin. 42, 1201–1209.

Google Scholar

Yan, H. Y., Feng, L., Zhao, Y. F., Feng, L., Zhu, C. P., Qu, Y. F., et al. (2020b). Predicting the potential distribution of an invasive species, Erigeron canadensis L., in China with a maximum entropy model. Glob. Ecol. Conserv. 21:e00822. doi: 10.1016/j.gecco.2019.e00822

CrossRef Full Text | Google Scholar

Yan, H. Y., Feng, L., Zhao, Y. F., Feng, L., Wu, D., and Zhu, C. P. (2020a). Prediction of the spatial distribution of Alternanthera philoxeroides in China based on ArcGIS and MaxEnt. Glob. Ecol. Conserv. 21:e00856. doi: 10.1016/j.gecco.2019.e00856

CrossRef Full Text | Google Scholar

Yan, H. Y., He, J., Zhao, Y. F., Zhang, L., Zhu, C. P., and Wu, D. (2020c). Gentiana macrophylla response to climate change and vulnerability evaluation in China. Glob. Ecol. Conserv. 22:e00948. doi: 10.1016/j.gecco.2020.e00948

CrossRef Full Text | Google Scholar

Yan, H. Y., Wang, G. Y., Zhang, X. R., Dong, J. H., Shan, K., Wu, D., et al. (2016b). A fast method to evaluate water eutrophication. J. Cent. South Univ. 23, 3204–3216. doi: 10.1007/s11771-016-3386-4

CrossRef Full Text | Google Scholar

Yan, H. Y., Zhang, X. R., Dong, J. H., Shang, M. S., Shan, K., Wu, D., et al. (2016c). Spatial and temporal relation rule acquisition of eutrophication in Da’ning River based on rough set theory. Ecol. Indic. 66, 180–189. doi: 10.1016/j.ecolind.2016.01.032

CrossRef Full Text | Google Scholar

Yan, H. Y., Huang, Y., Wang, G. Y., Zhang, X. R., Shang, M. S., Feng, L., et al. (2016a). Water eutrophication evaluation based on rough set and petri nets: a case study in Xiangxi-River, three gorges reservoir. Ecol. Indic. 69, 463–472. doi: 10.1016/j.ecolind.2016.05.010

CrossRef Full Text | Google Scholar

Yan, H. Y., Wang, G. Y., Wu, D., Huang, Y., Shang, M. S., Xu, J. J., et al. (2017a). Water bloom precursor analysis based on two direction S-rough set. Water Resour. Manag. 31, 1435–1456. doi: 10.1007/s11269-017-1579-8

CrossRef Full Text | Google Scholar

Yan, H. Y., Wu, D., Huang, Y., Wang, G. Y., Shang, M. S., Xu, J. J., et al. (2017b). Water eutrophication assessment based on rough set and multidimensional cloud model. Chemometr. Intell. Lab. Syst. 164, 103–112. doi: 10.1016/j.chemolab.2017.02.005

CrossRef Full Text | Google Scholar

Yang, X.-Q., Kushwaha, S. P. S., Saran, S., Xu, J., and Roy, P. S. (2013). Maxent modeling for predicting the potential distribution of medicinal plant, Justicia adhatoda L. in lesser Himalayan foothills. Ecol. Eng. 51, 83–87. doi: 10.1016/j.ecoleng.2012.12.004

CrossRef Full Text | Google Scholar

Zhang, D. F., Zhang, Q., Guo, J., Sun, C. Z., Wu, J., Nie, X., et al. (2017). Research on the global ecological suitability and characteristics of regions with Angelica sinensis based on the MaxEnt model. Acta Ecol. Sin. 37, 5111–5120. doi: 10.5846/stxb201605030837

CrossRef Full Text | Google Scholar

Zhang, Z. Q. (2006). A Study on Standardization Cultivating Technology for Codonopsis pilosula Nannf var. Xianyang: Northwest A&F University.

Google Scholar

Zhao, G. F., Zhang, L. P., and Wu, B. (2006). Study on GAP of Radix Codonopsis and Draw up of Its SOP. Res. Pract. Chin. Med. 20, 13–16.

Google Scholar

Zhu, G. P., Fan, J. Y., Wang, M. L., Chen, M., and Qiao, H. J. (2017). The importance of the shape of receiver operating characteristic(ROC) curve in ecological niche model evaluation - case study of Hlyphantria cunea. J. Biosaf. 26, 184–190.

Google Scholar

Zhu, G. P., Liu, G. Q., Bu, W. J., and Gao, Y. B. (2013). Ecological niche modeling and its applications in biodiversity conservation. Biodivers. Sci. 21, 90–98. doi: 10.3724/sp.j.1003.2013.09106

CrossRef Full Text | Google Scholar

Zhu, G. P., and Qiao, H. J. (2016). Maxent model’s complexity on the prediction of species potential distributions. Biodivers. Sci. 24, 1189–1196. doi: 10.17520/biods.2016265

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, G. P., Yuan, X. J., Fan, J. Y., and Wang, M. L. (2018). Effects of model parameters in MaxEnt modeling of ecological niche and geographic distribution: case study of the brown marmorated stink bug, Halyomorpha haly. J. Biosaf. 27, 118–123.

Google Scholar