The Combined Effects of Warming and Body Size on the Stability of Predator-Prey Interactions

Environmental temperature and body size are two prominent drivers of predation. Despite the ample evidence of their independent effects, the combined impact of temperature and predator-prey body size ratio on the strength and stability of trophic interactions is not fully understood. We experimentally tested how water temperature alters the functional response and population stability of dragonfly nymphs (Cordulegaster boltonii) feeding on freshwater amphipods (Gammarus pulex) across a gradient of their body size ratios. Attack coefficients were highest for small predators feeding on small prey at low temperatures, but shifted toward the largest predators feeding on larger prey in warmer environments. Handling time appeared to decrease with increasing predator and prey body size in the cold environment, but increase at higher temperatures. These findings indicate interactive effects of temperature and body size on functional responses. There was also a negative effect of warming on the stability of predator and prey populations, but this was counteracted by a larger predator-prey body size ratio at higher temperatures. Here, a greater Hill exponent reduced feeding at low prey densities when predators were much larger than their prey, enhancing the persistence of both predator and prey populations in the warmer environment. These experimental findings provide new mechanistic insights into the destabilizing effect of warming on trophic interactions and the key role of predator-prey body size ratios in mitigating these effects.

Introduction

The strength of trophic interactions is a key determinant of population, community, and ecosystem stability (McCann et al., 1998; McCann, 2000). Ongoing climate warming may reduce stability, not only by accelerating the risk of species extinctions (Urban, 2015), but also by modulating consumer-resource interactions (Post, 2013; Gilbert et al., 2014; Urban, 2015). Given that environmental warming exacerbates the need for energy uptake by consumers (Brown et al., 2004), warmer environments should be characterized by stronger feeding rates of predators up to their thermal tolerance limits. Studies across a large latitudinal gradient support this general prediction, and highlight that arthropods, as ectothermic organisms, are particularly susceptible to the effects of warming (Roslin et al., 2017; Romero et al., 2018). Stronger trophic linkages as a consequence of warming can negatively influence the stability of predator and prey populations (Vasseur and McCann, 2005; Rall et al., 2010; Vucic-Pestic et al., 2011). However, warming can also weaken trophic interactions and put predators at risk of extinction, particularly if their metabolic demands increase more than their predation rates (Rall et al., 2010; Vucic-Pestic et al., 2011; Fussmann et al., 2014). Coupled changes to interaction strength and energetic efficiency can ultimately destabilize ecological communities at lower temperatures, but have stabilizing effects in warmer environments (Synodinos et al., 2021).

Body size is among the most conspicuous characteristics of all organisms, and it can span up to 20 orders of magnitude from bacteria to whales (Andersen et al., 2016; Blanchard et al., 2017). Body size is often considered to be a “master trait” (Andersen et al., 2016) as it is closely linked to individual metabolism (Brown et al., 2004), growth (Gillooly et al., 2002), reproduction (Arendt, 2011), dispersal and locomotion (Jetz et al., 2004). At the community level, body size is a key predictor of population densities and food web structure (Damuth, 1981; Peters, 1983; Cohen et al., 2003; White et al., 2007; Perkins et al., 2019). The relative body size of predators and their prey (typically measured as their body mass) also underlies the strength of trophic interactions and food web stability. In general, experimental studies have indicated a positive association between predator-prey body size ratio and the strength of per capita predation (Emmerson and Raffaelli, 2004). On the other hand, large-bodied predators are disproportionately more prone to extinctions due to human-induced perturbations (Enquist et al., 2020), including overexploitation (Pauly et al., 1998) and climate warming (Petchey et al., 1999). Increasing predation rates in systems characterized by high predator-prey body size ratios and a greater sensitivity of large predators to climate warming can destabilize ecological communities and indicates that both these drivers should be investigated in concert.

Per capita predation rate as a function of prey density—the functional response of a predator (Holling, 1959, 1966)—is the main representation of trophic interactions and a central concept in food web ecology. Per capita predation rates commonly increase with prey density in a non-linear manner, with either hyperbolic (Type-II) or sigmoidal (Type-III) relationships (Holling, 1959, 1966). These functional response models are characterized by three key parameters. (i) The attack coefficient describes the rate of a successful search through an environmental area or volume. An increase in the attack coefficient translates to steeper ingestion rates at lower prey densities, which can reduce the stability of predator-prey interactions. (ii) Handling time describes the time a predator requires to subdue, ingest, and digest a single prey item. Handling time becomes relatively more important at higher prey densities and increases in this parameter translate to a decrease in maximum ingestion rate. (iii) The Hill exponent (from original work by Barcroft and Hill, 1909) describes how predators can switch between Type-II and Type-III functional responses. Smaller values of the Hill exponent tend toward Type-II, whereas higher values tend toward Type-III functional responses, due to increased and reduced feeding rates at low prey densities, respectively (Real, 1977).

Several studies have tested the independent impact of warming on functional response parameters. This work indicates that the attack coefficient generally increases, whereas handling time declines with rising temperatures (Rall et al., 2012; Uiterwaal and DeLong, 2018). Fewer experimental studies have investigated temperature effects on the Hill exponent, and those indicated an increase in the Hill exponent (Daugaard et al., 2019; Sohlström et al., 2021) or even a switch between Type-III and Type-II functional responses (Daugaard et al., 2019) after experimental warming. Across a large range of environmental temperatures, there is compelling evidence for a unimodal effect of warming on the functional response parameters, however, pointing to an optimal temperature that maximizes per capita predation rates (Englund et al., 2011; Uszko et al., 2017; Uiterwaal and DeLong, 2020).

The attack coefficient has been suggested to exhibit a hump-shaped relationship with predator-prey body mass ratio (Vucic-Pestic et al., 2010; McCoy et al., 2011; Rall et al., 2011), underpinned by increasing attack coefficients for larger predators and weaker or no effects of prey size (Rall et al., 2012; Uiterwaal and DeLong, 2020). In contrast, handling time has a U-shaped relationship with predator-prey body mass ratio (Rall et al., 2012), underpinned by decreasing handling time for larger predators and smaller prey (Vucic-Pestic et al., 2010; Kalinkat et al., 2011). Taken together, these findings suggest that there is an optimal predator-prey body size niche for foraging, whereby larger predators generally have a higher chance to encounter, successfully attack, and handle a single smaller prey (Gergs and Ratte, 2009), but the prey should become harder to perceive if they are too small, and harder to handle if they are too large. A recent meta-analysis has also suggested that separate body masses of predators and prey are better at explaining predation rates than the combined predator-prey mass ratio (Uiterwaal and DeLong, 2020). These findings have led to the development of a generalized allometric functional response framework, which allows a continuous transition between Type-II and Type-III functional responses depending on predator and prey body masses, and more accurate modeling of predator-prey dynamics (Kalinkat et al., 2013).

Although independent effects of warming and body size of predators and prey on the strength and stability of trophic interactions have received substantial research attention, much less is known about their combined impacts. This poses a critical gap in our knowledge as global climate change is not only increasing environmental temperatures (IPCC, 2018), but also altering the body size of predators and their prey (Gilbert and DeLong, 2014). The temperature-size rule and temperature-induced changes in community composition led to the suggestion that declining body mass may be a universal response to climate warming (Atkinson, 1994; Daufresne et al., 2009; Evans et al., 2020), although there are some emerging examples of the contrary (Gardner et al., 2011; Ruger and Sommer, 2012; O’Gorman et al., 2017). Smaller organisms can change their body size and shape in response to warming more rapidly than larger organisms due to their higher mass-specific metabolic rates and shorter generation times (Gillooly, 2000; Savage et al., 2004; Tan et al., 2021). This would result in differential temperature-size responses across trophic levels and an increase in predator-prey body mass ratios under the future warmer climate. A recent analysis of marine organisms also showed that warming increases the mean body size of prey consumed by smaller predators but reduces the size of prey consumed by larger predators (Gilbert and DeLong, 2014), with potentially strong and complex consequences for the strength and dynamics of trophic interactions. Thus, it is vital to mechanistically understand both the independent and combined impacts of temperature and body mass on functional responses, given the likelihood that these two factors will play an increasingly important role in altering trophic interactions in our changing world.

Here, we experimentally compared functional responses of a model predator-prey pair at three temperatures and across a gradient of predator-prey body mass ratios to determine the combined effects of warming and body size on the components of predation. Based on two recent syntheses of functional response experiments, we hypothesized (H1) that warming and increasing predator and prey body mass should increase the attack coefficient (Figures 1A,B; Rall et al., 2012; Uiterwaal and DeLong, 2020). We also expected (H2) that warming and increasing predator body mass and decreasing prey body mass should reduce the handling time (Figures 1C,D; Rall et al., 2012; Uiterwaal and DeLong, 2020). Finally, we predicted (H3) a decline in the Hill exponent, or an outright switch from a stabilizing Type-III to destabilizing Type-II functional response (Oaten and Murdoch, 1975), with increasing temperature and prey body mass and decreasing predator body mass (Figures 1E,F; Kalinkat et al., 2011; Daugaard et al., 2019). If the impacts of temperature and body mass are independent, we would only expect warming to alter the intercept or strength of the relationship (i.e., a change in the slope, but with the same sign) between body mass and functional response parameters (Figure 1). Alternatively, if there are interactive effects of temperature and body mass, warming should alter the directionality (i.e., a change in the slope and the sign) or shape of the relationship (i.e., a shift to a hump-shaped relationship). To test whether and how these responses to warming and body size influence persistence and stability of trophic interactions, we used the experimental data to parameterize a bioenergetic predator-prey model and simulated the population dynamics of both trophic levels.

FIGURE 1

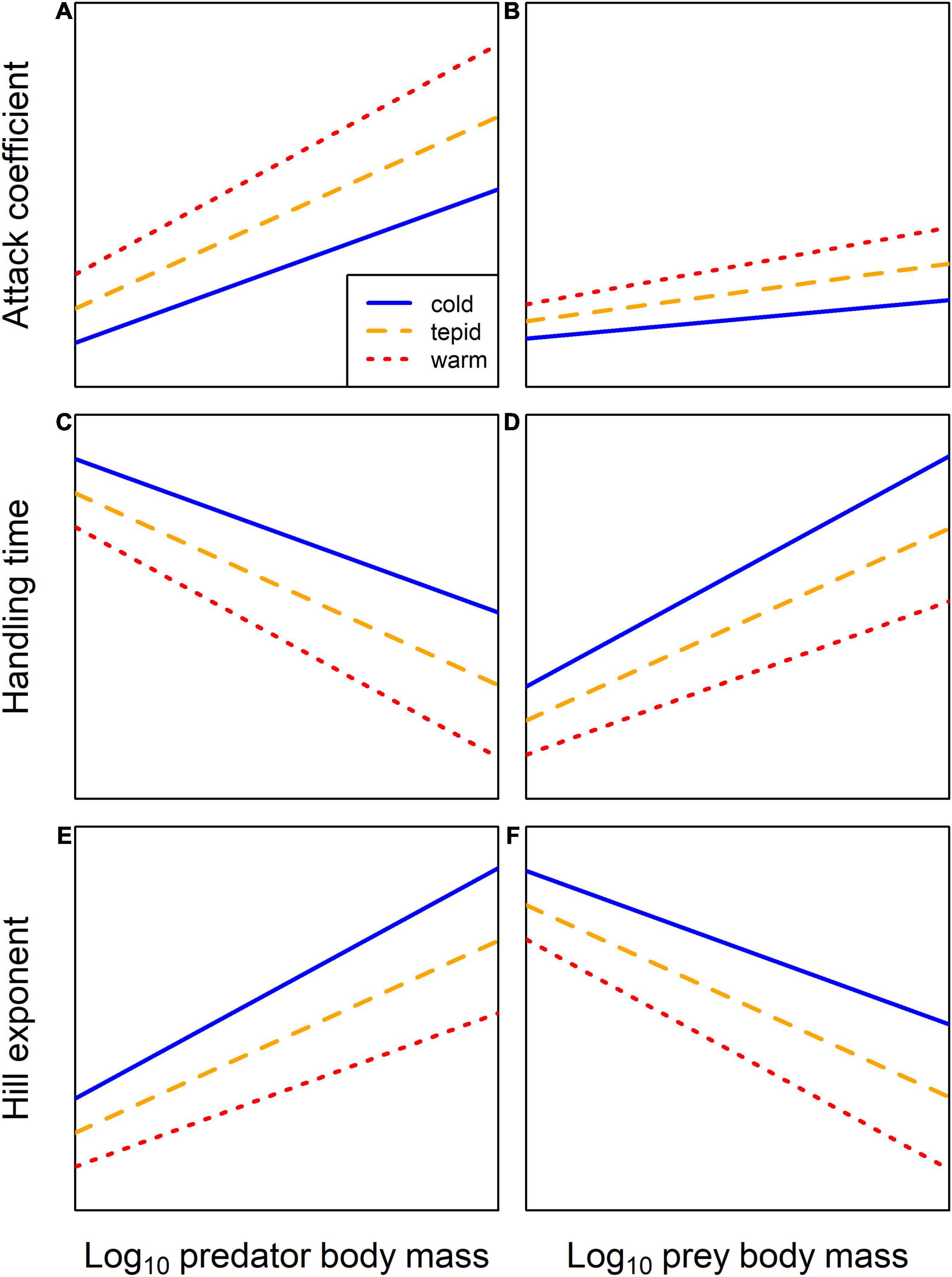
Figure 1. Conceptual illustration of the predicted independent effects of warming and predator or prey body mass on functional response parameters. (A,B) The attack coefficient is predicted to increase with predator body mass, with a much weaker increase for prey body mass, while the intercepts and slopes of these relationships are expected to increase with warming. (C,D) Handling time is predicted to decrease with predator body mass and increase with prey body mass, while the intercepts and slopes of these relationships are expected to decrease and increase with warming, respectively. (E,F) The Hill exponent is predicted to increase with predator body mass and decrease with prey body mass, while the intercepts and slopes of these relationships are expected to decrease with warming.

Materials and Methods

Experimental System: Predator and Prey

To test our hypotheses, we used model predator and prey species that are commonly found in streams throughout Europe. Cordulegastridae are freshwater dragonfly predators typically associated with lotic waters, streams, and brooks, where their nymphs often inhabit leaf packs and sediment. Cordulegaster boltonii (the golden-ringed dragonfly) is the most abundant Cordulegastridae species in Europe, ranging from southern Spain to southern Scandinavia (Askew, 1988). The species has 14 instars during larval development, which range from 0.4 mm up to more than 8.0 mm of head capsule width (HCW) (Woodward and Hildrew, 2002a). Cordulegaster boltonii is a sit-and-wait predator (Woodward and Hildrew, 2002b) with one of the fastest attack responses among all animals (Pritchard, 1965). It has a wide diet, ranging from small to very large prey which can be captured by the use of their labial mask and palps (Corbet, 1999). The model predators were hand-collected from Broadstone Stream, SE England, where there was an eruption of C. boltonii in the mid-1990s, with densities reaching 72 nymphs m^–2, increasing top-down control of the stream community (Woodward and Hildrew, 2001).

Gammarus pulex is an amphipod species which inhabits a wide variety of habitats due to its high adaptability to light availability, temperature fluctuations, and food sources. Gammarus pulex is an herbivorous shredder and detritivore (Friberg and Jacobsen, 1994; Rong et al., 1995; Gayte and Fontvieille, 1997), but there is also evidence that it feeds on fungi and algae which grow on detritus (Moenickes et al., 2011) and it can occasionally behave as a predator (MacNeil et al., 1997) and a cannibal (Summers et al., 1996; Kelly et al., 2002). The species plays a key role in many stream food webs by shredding leaf material, making it available for decomposers and filter feeders in the stream (Cummins and Klug, 1979), thus linking energetic transport from terrestrial to freshwater environments (Cummins and Klug, 1979; Graca et al., 2001; Felten et al., 2008). The life span of the amphipod varies between 1 and 2 years, with the highest growth rates recorded shortly after birth (Sutcliffe et al., 1981). Gammarus occur in Broadstone Stream in low densities, so the model prey for this study were hand-collected from the River Cray and several streams in the greater London area, where they reach high densities.

Experimental Design

We conducted functional response experiments, consisting of all possible combinations of small, medium, and large predators feeding on small, medium, and large prey at three experimental temperatures. The final three instars of the dragonfly nymph were attributed, respectively, to 4.0–5.4 mm head capsule width [HCW] (instar 12), 5.5–8.0 mm HCW (instar 13), and > 8.0 mm HCW (instar 14; after Ferreras-Romero and Corbet, 1999; Woodward and Hildrew, 2002a) to obtain three discrete size classes of the predator (small: 55.6 ± 14.1 mg; medium: 123.9 ± 27.2 mg; large 249.2 ± 66.8 mg; mean ± standard deviation). The amphipod prey were visually separated into three body size categories (small: 0.464 ± 0.309 mg; medium: 1.89 ± 0.11 mg; large: 5.86 ± 0.58 mg; mean ± standard deviation).

Functional response experiments were conducted in May–July of 2013 and 2016 in constant temperature rooms located at Queen Mary University of London, United Kingdom. The rooms were set to 5, 10, and 15 °C (which we will refer to henceforth as cold, tepid, and warm environments, respectively) and to a 12:12 h light:dark cycle. Wild populations of freshwater macroinvertebrates are known to be adapted to local environmental temperatures (Maazouzi et al., 2011) and the targeted range of experimental temperatures is within the range experienced by amphipods and odonates in United Kingdom rivers (Hannah and Garner, 2015). Identical 2-L plastic aquaria (18 cm long × 11.7 cm wide × 11 cm deep, SAVIC, Belgium), containing 2 cm of washed gravel substrate served as experimental arenas. Each experimental unit consisted of one predator individual and prey of different densities: 1, 2, 3, 4, 8, 16, 32, 48, or 64 individuals per experimental arena. We randomly assigned treatment combinations of predator body size, prey body size, and prey density in each constant temperature room. Predators were starved for at least 2 days prior to the beginning of each experiment. They were placed in the arenas for 1 h prior to the introduction of prey to allow them to acclimatize, which requires time to bury itself in the sediment for camouflage. After 24 h, predators were removed from each arena. The water and gravel were then sieved and sorted by hand to count the remaining prey individuals. Between three and five replicates were conducted for each treatment giving a total of 884 experiments.

Model Fitting and Parameter Estimates

We fitted three different functional response models (Type-II, strict Type-III, and generalized Type-III) to the experimental data. The Type-II functional response can be described as:

$F\left(N\right)=\frac{aN}{1+ahN},(1)$

where F is the feeding rate, N is the density of the prey, a is the attack rate, and h is the handling time. The Type-III functional responses can be described as:

$a=b{N}^q,(2)$

$F\left(N\right)=\frac{b{N}^{1+q}}{1+bh{N}^{1+q}},(3)$

where b is the attack coefficient and 1+q is the Hill exponent. Note that q = 1 for the strict Type-III functional response, whereas q is flexible (though always > 0) for the generalized Type-III functional response.

We incorporated body mass into the functional responses using established allometric scaling of the attack rate, attack coefficient, handling time, and Hill exponent as follows:

$a=a_{0}m_r{}^{{\beta }_r}R{e}^{\epsilon R},(4)$

$b=b_{0}m_r{}^{{\beta }_r}R{e}^{\epsilon R},(5)$

$h=h_{0}m_r{}^{{\alpha }_r}m_c{}^{{\alpha }_c},(6)$

$q=\frac{q_{\text{max}}{R}^2}{q_0^2+R^2},(7)$

where m_c is the consumer (i.e., predator) mass, m_r is the resource (i.e., prey) mass, and $R=\frac{m_c}{m_r}$ is the predator-prey body mass ratio. h₀, a₀ and b₀ are normalization constants, α_r and β_r are scaling exponents for resource mass, α_c is a scaling exponent for consumer mass, ε is a scaling exponent for predator-prey body mass ratio, and q_max denotes the maximum of the sigmoidal shaped curve for q, where the half-saturation density q₀ defines the predator-prey body mass ratio for which q = q_max × 0.5.

All model fitting and analyses were performed in R 4.0.2. All three functional response models (Type-II, strict Type-III, and generalized Type-III, with a or b, h and q predicted by the allometric model) were fitted to the three temperature treatments separately. We conducted numerical simulations of the following ordinary differential equation (ODE):

$\frac{dN}{dt}=-F(N),(8)$

These numerical simulations were combined with Bayesian parameter estimation by drawing samples from the posterior probability distribution P(θ| y) of the model parameters θ (scaling constants and exponents of Equations 4–7) given the data y, based on the likelihood function P(y| θ) and prior distributions P(θ). We coded the models using the “rstan” package (Stan Development Team, 2020). In each iteration of the Markov Chain Monte Carlo (MCMC) sampling (for a current sample θ), the numerical solution of Equation 8 was computed with the built-in Runge-Kutta ODE solver, to predict prey densities ${\widehat{N}}_{end}$ at the end of the experiment for each given initial prey density N_start. The likelihood was evaluated assuming binomial distributions of the observed numbers of eaten prey N_eaten with n = N_start trials and $p=\frac{N_{start}-{\widehat{N}}_{end}}{N_{start}}$ success probabilities. We used normal distributions with zero means, but different standard deviations (SD) for all priors. For the scaling exponents α_r, α_c, β_r, and ε we used weakly informative priors in the range of previous results (SD = 1, Kalinkat et al., 2013), but vague priors (a wider SD = 10) for the normalizing constants a₀, b₀, and h₀. For the generalized Type-III, we used weakly informative priors for the exponent maximum q_max (SD = 10) and the half-saturation density q₀ (SD = 1,000, corresponding to the range of experimental predator-prey body mass ratios).

We fitted all models by running four individual MCMC chains with an adaptation phase of 1,000 iterations and a sampling phase of 2,500 iterations each, summing up to 10,000 samples of the posterior distribution. Visual inspection of the trace plots and density plots showed a good mixture of the chains. Gelman-Rubin statistics of $\widehat{R}$ < 1.01 and an adequate effective sampling size (i.e., the estimated number of independent samples) verified convergence (Gelman and Hill, 2006). The Leave One Out Information Criterion (LOOIC) was used for model comparison, which was computed from the log-likelihood values of the posterior samples in the “loo” package (Vehtari et al., 2017, 2020).

Stability Analysis

The best performing functional response model was used to parameterize a Rosenzweig-MacArthur population dynamics model (Rosenzweig and MacArthur, 1963; Williams et al., 2007) for three temperatures and three predator × three prey body size combinations:

$\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right)-F\left(N\right)P,(9)$

$\frac{dP}{dt}=\frac{\mathrm{\omega }}{R}F\left(N\right)P-IP.(10)$

Here, the prey population N [individuals arena^–1 day^–1] undergoes logistic growth with population growth rate r and carrying capacity K, offset by a population-level predation rate, F(N)P, based on the best-fitting functional response model. The predator population P [individuals arena^–1 day^–1] increases based on the same functional response scaled by energetic efficiency ω and predator-prey body mass ratio R, offset by a loss term defined by metabolic rate I. We modeled the temperature dependence of population growth rate for G. pulex as per Sutcliffe et al. (1981):

$r=0.01\cdot 0.16\cdot T^{1.12},(11)$

where T is environmental temperature [°C]. We determined the temperature dependence of carrying capacity (see Supplementary Figure 1) using seasonal changes in abundance of G. pulex in an English stream from Welton (1979):

$K=e^{K_0+E_K\cdot T_{Arr}}\cdot A\cdot S,(12)$

$T_{Arr}=\frac{T-T_0}{kT{T}_0},(13)$

where K₀ [8.0374] is a normalization constant, E_K [1.8374 eV] is an activation energy, T₀ [283.15 K] is a normalization temperature, k is the Boltzmann constant [8.618 × 10^–5 eV K^–1], A is the area of the arena [m^–2], and S = 0.23 is an arbitrary constant that produced the most stable systems over all simulations. The temperature dependence of energetic efficiency was determined from Lang et al. (2017) as:

$\mathrm{\omega }=\frac{{\mathrm{\omega }}_0{e}^{E_{\mathrm{\omega }}{T}_{Arr}}}{1+{\mathrm{\omega }}_0{e}^{E_{\mathrm{\omega }}{T}_{Arr}}},(14)$

where ω₀ [e^2.266] is a normalization constant, E_ω [0.164 eV] is an activation energy, and T₀ [293.15 K] was the normalization temperature used in T_Arr. Finally, the temperature and body mass scaling of metabolic rate for the predator was determined from laboratory experiments on dragonfly nymphs (see Supplementary Figure 2):

$I=e^{I_0+E_I\cdot T_{Arr}+b_I\cdot \text{log}(m_c)}\cdot \frac{24}{m_c{C}_c},(15)$

where I₀ [–4.21198] is a normalization constant, E_I [0.93617 eV] is an activation energy, b_I [0.90356] is an allometric exponent, and C_c [21.40953 J mg^–1] is a calorific equivalent to convert metabolic rate from J h^–1 to day^–1 (Cummins and Wuycheck, 1971).

For each simulation, we defined stability as:

$stability=\frac{1}{1+lo{g}_{10}\left(maxP\right)-lo{g}_{10}\left(minP\right)},(16)$

where the range of predator densities was measured after the system reached a steady state or limit cycle. In this way, stability = 1 for steady states and declines toward 0 with an increasing amplitude of predator densities.

Results

The most parsimonious model was the generalized Type-III functional response (LOOIC = 3,658.8, r² = 0.63) across all treatment combinations, which had a considerably lower LOOIC value than both the Type-II model (ΔLOOIC ± SE = 69.6 ± 25.8, r² = 0.62) and the strict Type-III model (ΔLOOIC ± SE = 70.4 ± 37.2, r² = 0.62). Parameter value estimates for the best fitting model are shown in Table 1, with model fit to the data illustrated in Figure 2.

TABLE 1

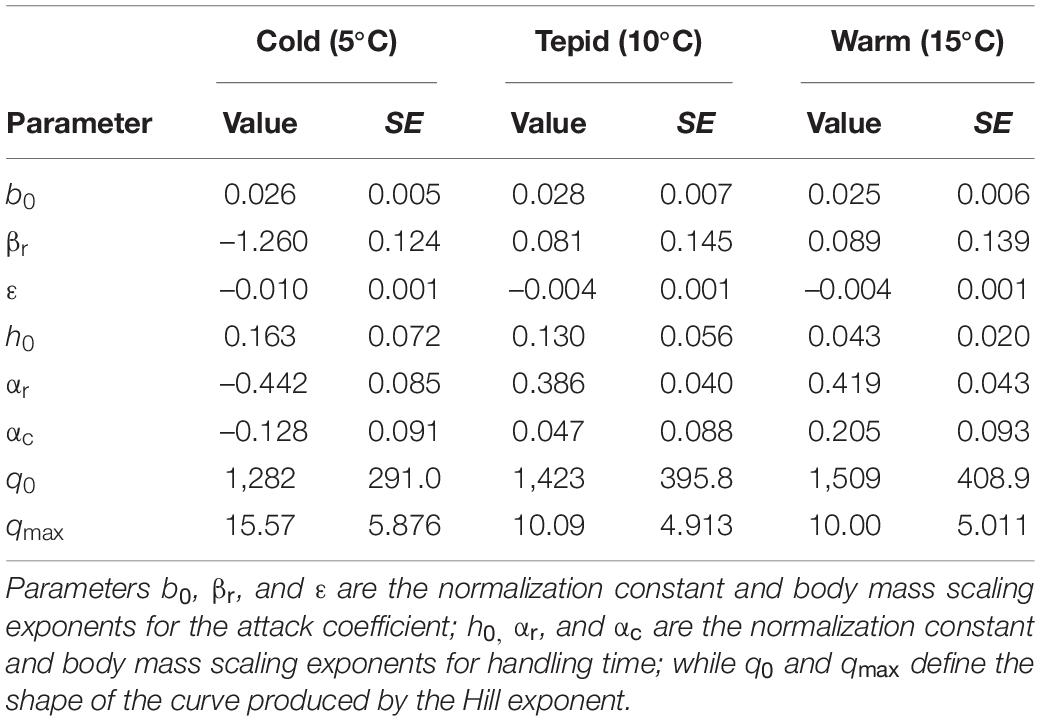
Table 1. Parameter value estimates with associated standard errors (SE) at each experimental temperature for the best-fitting generalized Type-III functional response model (see Equations 2–7 for the model derivation).

FIGURE 2

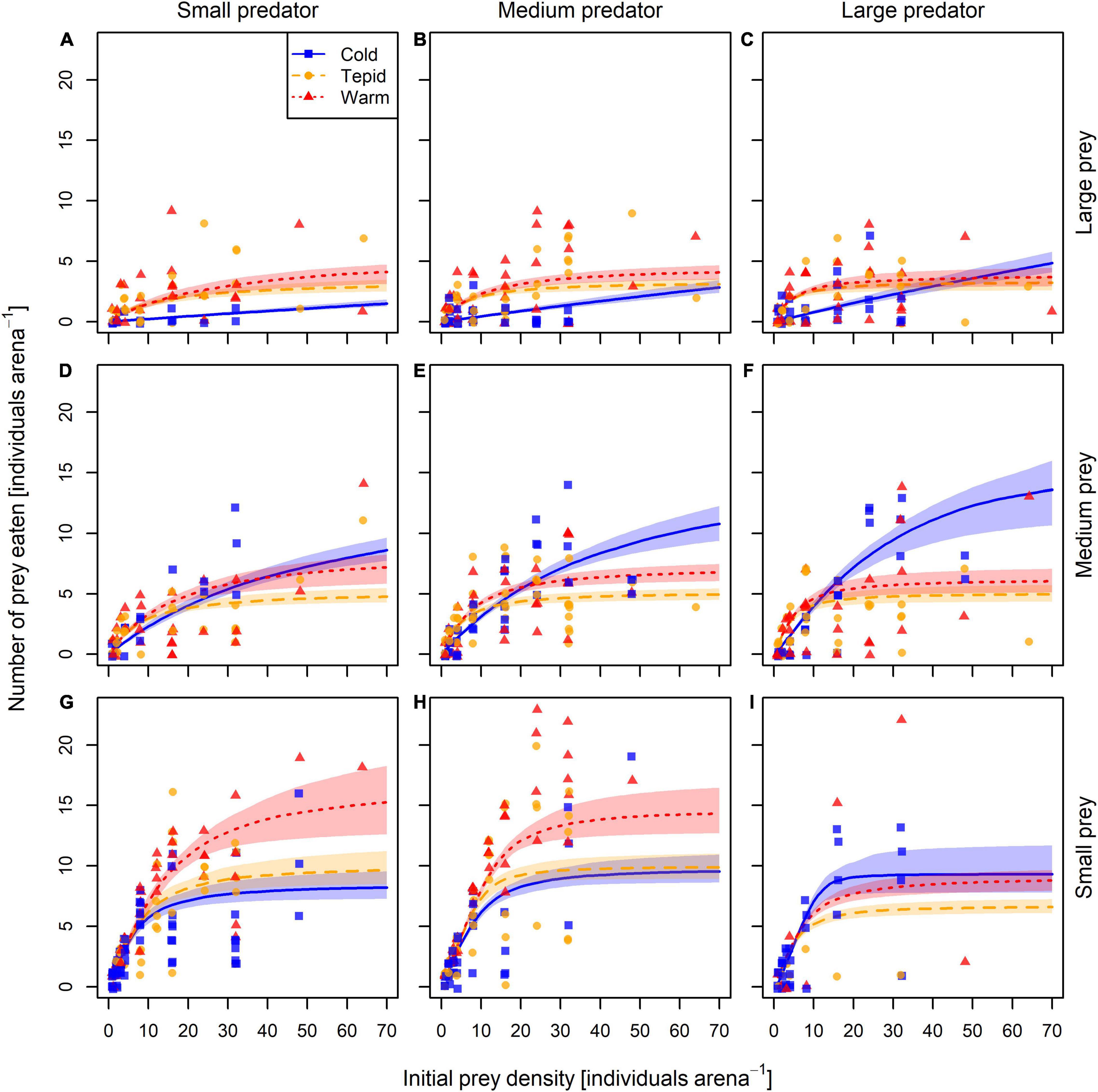
Figure 2. Generalized Type-III functional response curves fitted to the experimental data for each temperature × predator body mass × prey body mass combination. Panels are arranged from (A–I) in approximately increasing order of predator-prey mass ratio. Solid blue, dashed yellow, and dotted red curves (with transparent areas of the same color) represent the model fit ± 95% CI in the cold (5°C), tepid (10°C), and warm (15°C) temperature treatments, respectively. Solid symbols (blue squares, yellow circles, and red triangles) represent individual feeding experiments.

Attack Coefficient

The highest attack coefficients were found for the smallest predators feeding on the smallest prey in the cold environment (Figures 3A,D,G), but this shifted toward the largest predators consuming medium and large prey in the tepid (Figures 3B,E,H) and warm (Figures 3C,F,I) environments. This offers partial support for our first hypothesis, with attack coefficients generally increasing with predator body mass as temperature also increased, though with opposing effects for prey body mass. Importantly, this also shows an interactive effect of temperature and body size, with temperature altering the shape and directionality of the relationship between predator and prey body mass and the attack coefficient (compare with Figures 1A,B). Note that both the low m_c : low m_r and high m_c : high m_r combinations represent intermediate predator-prey body mass ratios. Thus, our results broadly indicate a hump-shaped response, with the smallest attack coefficients occurring for the largest predator-prey body mass ratio (i.e., the high m_c : low m_r combination) at all three temperatures, and the highest attack coefficients occurring at intermediate predator-prey body mass ratios (see Supplementary Figures 3A–C).

FIGURE 3

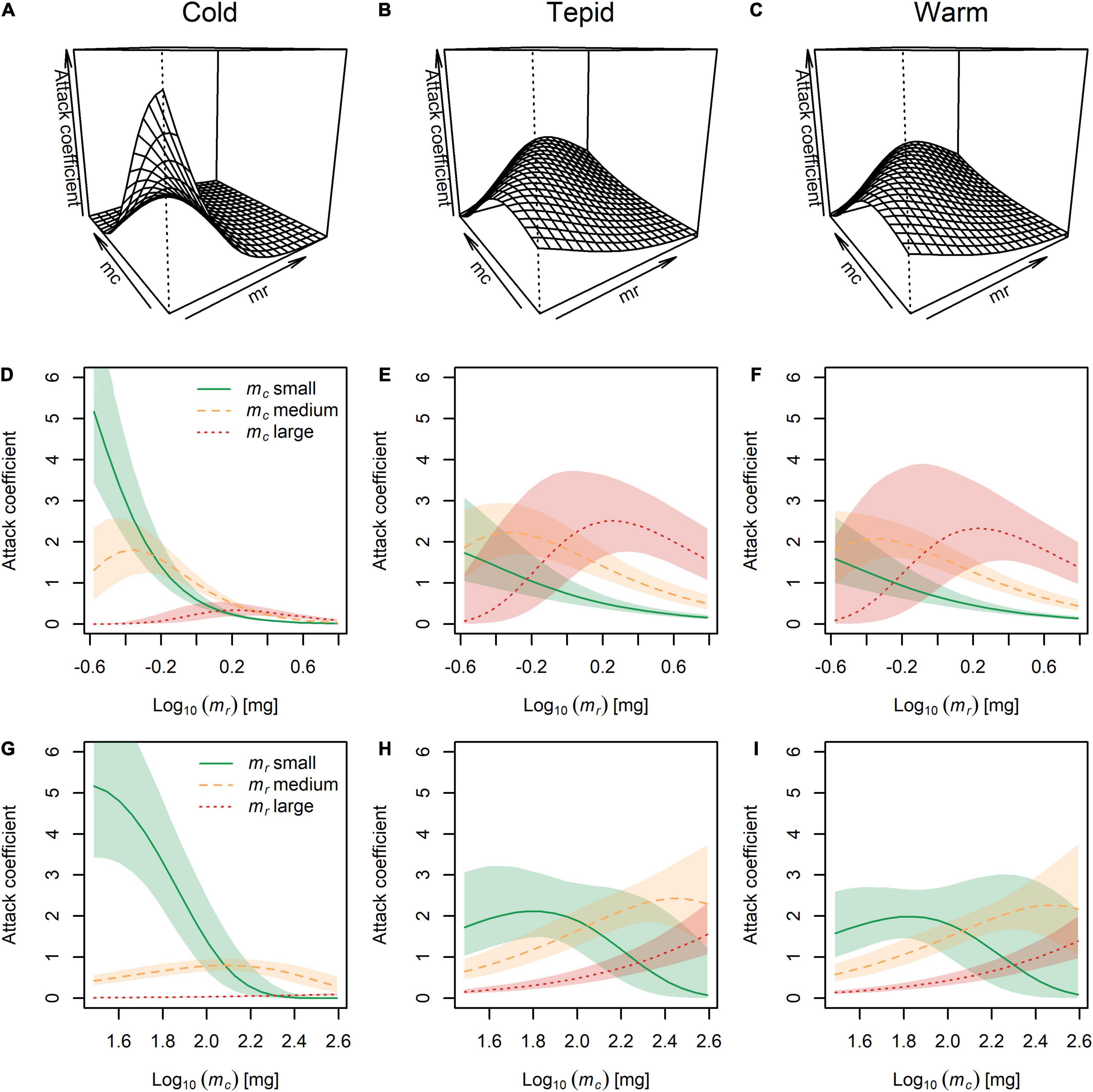
Figure 3. The combined effects of temperature and body mass of the predator (m_c) and prey (m_r) on the attack coefficient. (A–C) Three-dimensional visualization of attack coefficients across the full range of predator and prey body masses at each experimental temperature. (D–F) Attack coefficients for small, medium, and large predators across the full range of prey body masses at each temperature. (G–I) Attack coefficients for small, medium, and large prey across the full range of predator body masses at each temperature. Lines represent the model fit and shaded areas are the Bayesian 95% posterior probability intervals.

Handling Time

The lowest handling times occurred in the cold environment, where they also tended to decrease with increasing predator and prey body mass (Figures 4A,D,G). In contrast, handling times were generally greater and increased with both predator and prey body mass in the tepid (Figures 4B,E,H) and warm (Figures 4C,F,I) environments. This offers partial support for our second hypothesis, with handling times declining with decreasing prey mass as temperature also increased, though with opposing effects for predator body mass. It also indicates an interactive effect of temperature and body size, with temperature potentially altering the directionality of the relationship between predator-prey body mass and handling time (see Figures 1C,D).

FIGURE 4

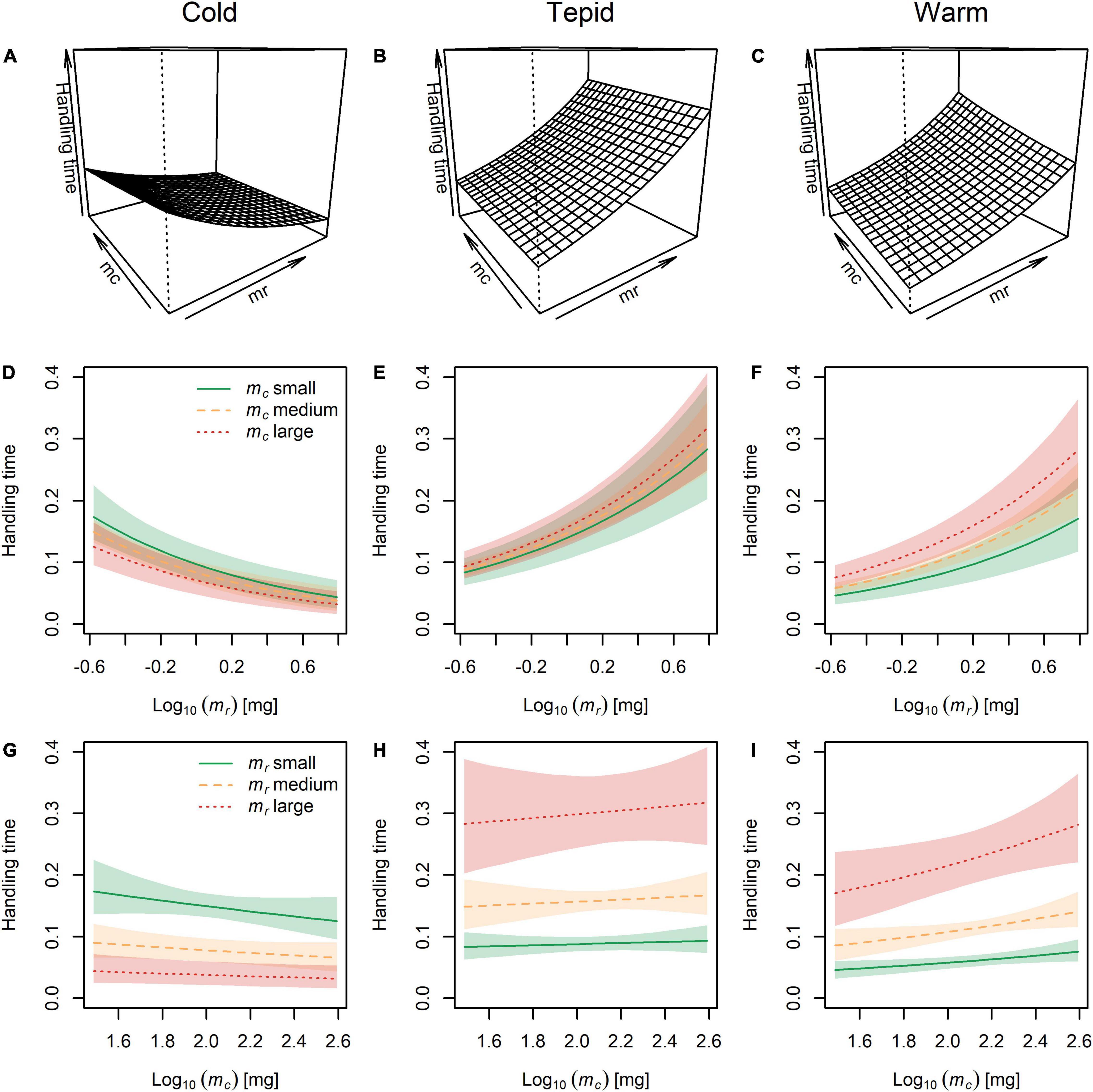
Figure 4. The combined effects of temperature and body mass of the predator (m_c) and prey (m_r) on handling time. (A–C) Three-dimensional visualization of handling times across the full range of predator and prey body masses at each experimental temperature. (D–F) Handling times for small, medium, and large predators across the full range of prey body masses at each temperature. (G–I) Handling times for small, medium, and large prey across the full range of predator body masses at each temperature. Lines represent the model fit and shaded areas are the Bayesian 95% posterior probability intervals.

Hill Exponent

The largest Hill exponents occurred in the cold environment and appeared to decrease with warming (Figures 5A–C), although the effect of temperature was associated with large 95% posterior probability intervals (Figure 5). The Hill exponent also decreased with increasing prey body mass (Figures 5D–F) and decreasing predator body mass (Figures 5G–I). These findings offer support for our third hypothesis, though note that there was no evidence for an outright switch from Type-III to Type-II functional response with warming or changing predator and prey body mass (Table 1). These results also indicate independent effects of temperature and body size on the Hill exponent, with temperature only altering the strength and not the directionality or shape of the relationships (see Figures 1E,F).

FIGURE 5

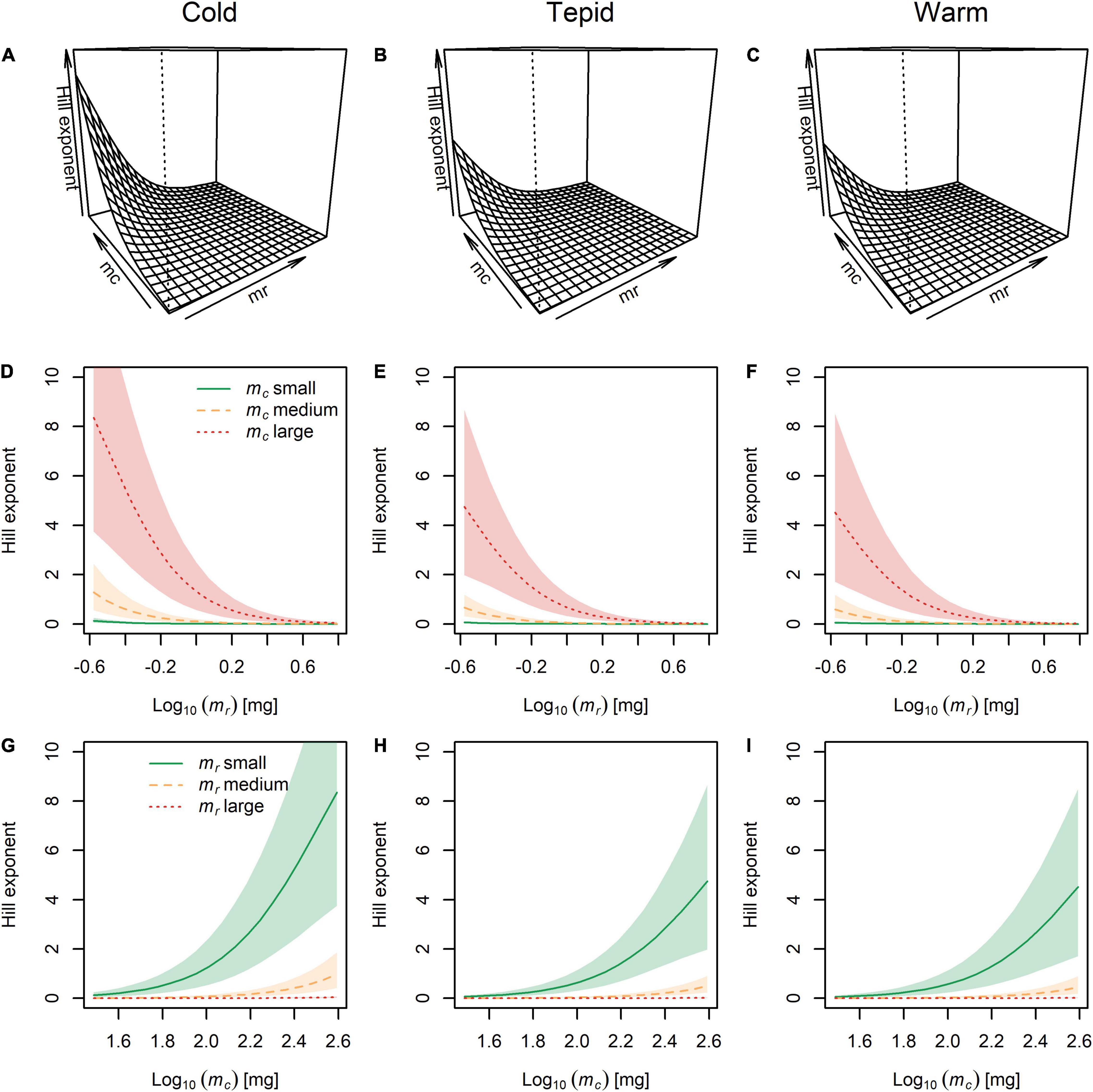
Figure 5. The combined effects of temperature and body mass of the predator (m_c) and prey (m_r) on the Hill exponent. (A–C) Three-dimensional visualization of Hill exponents across the full range of predator and prey body masses at each experimental temperature. (D–F) Hill exponents for small, medium, and large predators across the full range of prey body masses at each temperature. (G–I) Hill exponents for small, medium, and large prey across the full range of predator body masses at each temperature. Lines represent the model fit and shaded areas are the Bayesian 95% posterior probability intervals.

Population Stability

Predator-prey population dynamics were predicted to be stable for all body mass ratios in the cold environment (Supplementary Figure 4), but became much more variable in both the tepid (Supplementary Figure 5) and warm (Supplementary Figure 6) environments. An increase in predator-prey body mass ratio (i.e., when predators were much bigger than their prey) led to less variable population dynamics, however, and thus dampened the destabilizing effect of temperature (Figure 6). Furthermore, the most variable dynamics and thus lowest stability occurred at intermediate body mass ratios (Figure 6), indicating a non-linear effect of predator-prey body mass ratio on population stability in warmer environments.

FIGURE 6

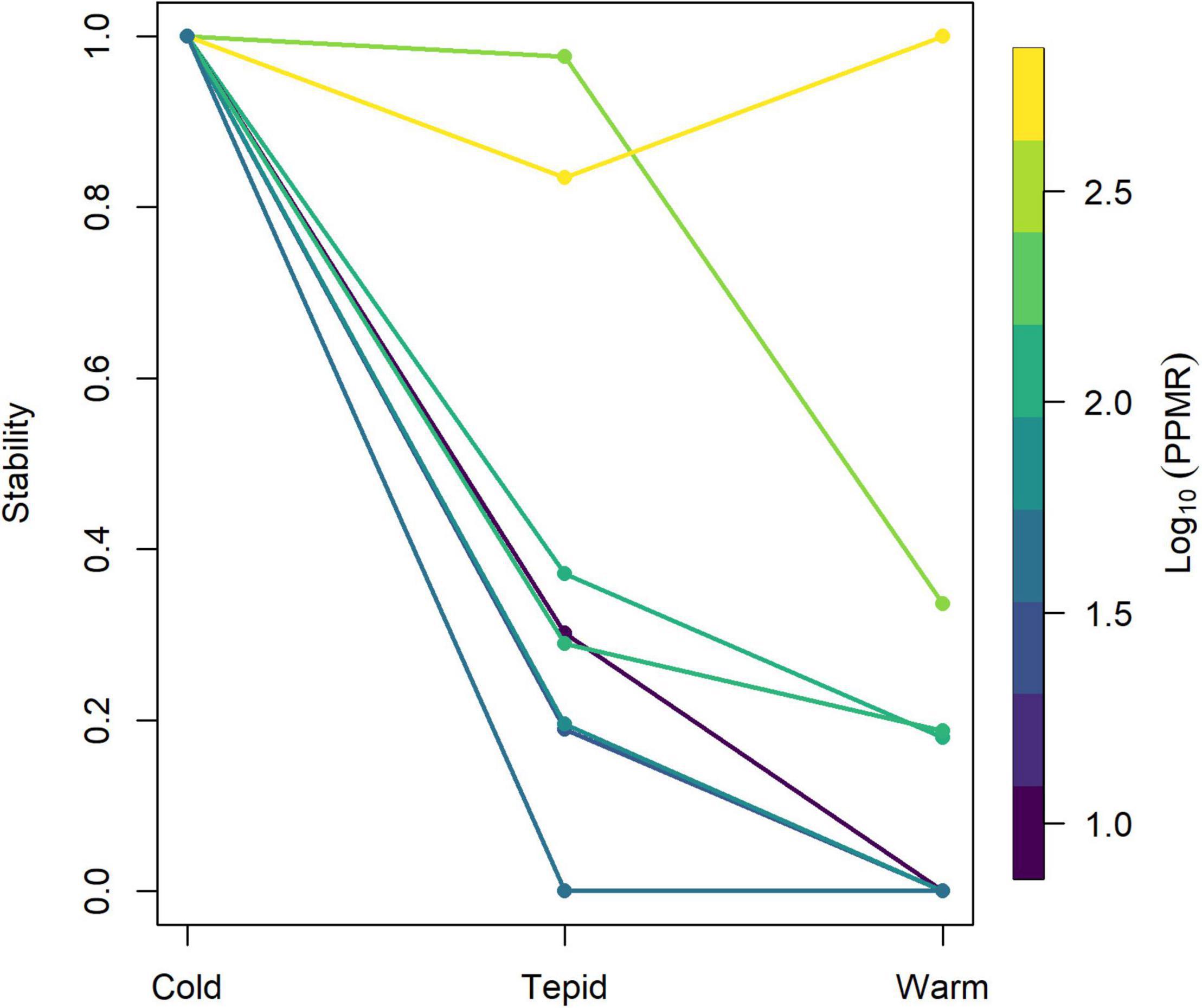
Figure 6. The combined effects of temperature and predator-prey mass ratio (PPMR) on the stability of predator-prey population dynamics. Note that stability is approximately the inverse of the amplitude of predator abundances through time from population dynamical modeling (see Equation 16). A stability value of 1 indicates that predator and prey populations reach a stable equilibrium point, while a value of 0 indicates that one or both populations are lost from the system.

Discussion

Our findings demonstrate interactive effects of warming and body mass on the mechanistic components of predation, particularly attack coefficients and handling times. Although previous studies have identified many similar independent effects of body size and temperature across the experimental gradients we used here (Englund et al., 2011; Rall et al., 2012; Uiterwaal and DeLong, 2020), we show that these factors need to be considered in tandem (i.e., interactively) when interpreting functional response data or modeling trophic relationships in the face of ongoing global warming. The Hill exponent also declined with prey body mass and increased with predator body mass, with no effect of warming on these relationships. Although not universal, larger Hill exponents are often associated with increased stability due to reduced predation at low prey densities (Uszko et al., 2015; Daugaard et al., 2019). This meant that the destabilizing impacts of warming on population biomasses were alleviated by an increase in the predator-prey body mass ratio and the associated larger Hill exponents.

In partial agreement with our first hypothesis, the attack coefficient tended to increase with predator body size, but only when they fed on medium and large prey in the warmer environments (Figures 3H,I). Large predators were less efficient at successfully attacking small prey individuals, which is in line with findings across a wide range of taxa showing that large and small consumers preferentially feed on large and small resources, respectively (Jonsson et al., 2005; Brose et al., 2006). This was particularly clear in the cold environment, where the largest attack coefficients occurred when small predators fed on small prey. Large predators exhibited a very low rate of successful attacks in the cold environment, indicating that they may have been largely inactive and require higher temperatures to start foraging. It also suggests that these predators are likely to have very low foraging rates during the colder winter months, with their strongest interactions occurring in summer, generating strong seasonal differences in energy flow through the food web. Our findings also provide strong support for a hump-shaped relationship between attack coefficient and predator-prey body mass ratio, which has been widely reported in the literature (Vucic-Pestic et al., 2010; McCoy et al., 2011; Rall et al., 2011). This indicates that C. boltonii has an optimum prey size that can be successfully attacked, and they may not perceive prey that are > 1,000 times smaller, or struggle to subdue prey that are < 10 times smaller than themselves (Supplementary Figures 3A–C).

Environmental temperature altered the directionality of the relationship between handling time and body size of predators and prey, which has not previously been demonstrated in functional response experiments. This interactive effect between temperature and body size should be treated with caution because highest prey density treatments were logistically difficult to establish, which resulted in either low or no replication (see Supplementary Table 1). However, all nine mass ratio treatment combinations were fitted together, with these handling times being informed by the data across all mass ratio combinations (Equation 6), increasing the robustness of these parameter estimates. Overall, the effects of prey body size were stronger (i.e., steeper slopes) than the effects of predator size. The predicted positive relationship between handling time and prey body mass (Rall et al., 2012; Uiterwaal and DeLong, 2020) was reversed in the cold environment, where predators were more efficient at handling large prey. These large and energetically important prey individuals are likely to evade the predators in tepid and warm environments, but their slower movements might make them easier to catch and subdue in cold environments. Interestingly, the predicted negative relationship between handling time and predator body mass (Rall et al., 2012; Uiterwaal and DeLong, 2020) was only observed in the cold environment. Although our experimental temperatures were well within the normal range over which such relationships are investigated (Englund et al., 2011; Uiterwaal and DeLong, 2020), longer handling times in warmer environments may indicate that predator foraging performance is impeded by warming, or that their prey are more actively trying to escape them (Domenici et al., 2019).

The Hill exponent appeared to decline with experimental warming, which adds to the broad range of contrasting responses that have been described recently (Uszko et al., 2017; Daugaard et al., 2019; Sohlström et al., 2021). However, this effect was associated with wide uncertainty and should be interpreted with caution. The associated high feeding rates at low prey densities most likely underpinned the negative effect of warming on the stability of predator and prey populations (Figure 6). Similar negative warming-stability relationships have recently been described at low and moderate environmental temperatures (Synodinos et al., 2021). Interestingly, our bioenergetic model simulations indicate that this destabilizing effect was buffered by larger predator-prey body mass ratios through the independent effects of predator and prey body mass on the Hill exponent. We found the greatest Hill exponents when the largest predators were feeding on the smallest prey individuals, which is similar to the stabilizing switch from Type-II to Type III functional response observed at the highest predator-prey body mass ratios in previous research (Vucic-Pestic et al., 2010). In combination with the high handling time for large prey in the warm environment, this may indicate a greater feeding efficiency for predators when consuming highly abundant small prey that are easier to catch and subdue. Thus, warming may alter the optimal size niche of predator-prey interactions by shifting the risk-reward trade-off between energy expenditure (i.e., foraging) and energy intake (i.e., successful predation). Future evidence for such a trade-off could come from an experimental characterization of the thermal performance curves for predator and prey species, coupled with mechanistic modeling of their population dynamics.

The lowest stability of predator and prey populations occurred at intermediate body mass ratios, suggesting a non-linear relationship between the two variables. While it may seem counterintuitive that the highest body mass ratios led to the greatest stability (e.g., in contrast to Jennings and Warr, 2003), our manipulated predator-prey size ratios only spanned the range of values where trophic interactions were still feasible (i.e., the largest and smallest predators could still consume the smallest and largest prey, respectively). Expanding this range to include much smaller or larger prey should eventually destabilize the trophic interactions through the inability of the predator to consume the prey. Overall, the application of a generalized allometric functional response (Kalinkat et al., 2013) allowed us to discover this novel stabilizing mechanism of larger body mass ratios under environmental warming, and it should be utilized more widely in predator-prey interaction research.

It is important to note that our experiments were conducted with just one model predator-prey pair. Further research is thus needed to determine the generality of the observed interactive effects of temperature and body size on functional response parameters and population stability. A growing number of studies also indicate that predator-prey interactions may exhibit different responses depending on the dimensionality of the interacting pair (Pawar et al., 2012; Uiterwaal and DeLong, 2020). Our study involved a sit-and-wait predator feeding on an active prey that can occupy three-dimensional space in the water column. The predator is thus likely to be less affected by warming than active hunters who rely on speed and agility for successful predation events, which are strongly influenced by environmental temperature (Öhlund et al., 2015; Cloyed et al., 2019). Similarly, interactions involving sessile prey may be more strongly determined by the response of the predator. Particular attention should be paid to investigating the combined effects of warming and body size on functional response parameters across a range of interaction types in future research.

Although previous studies have explored the independent effects of temperature or body size on trophic interactions and stability (Englund et al., 2011; Fussmann et al., 2014; Gilbert et al., 2014; Uiterwaal and DeLong, 2020; Synodinos et al., 2021), our understanding of the interactive effects between these two key variables remains incomplete. Here, we demonstrate how temperature alters the impact of body size on components of predation and how predator-prey body size ratio can buffer the destabilizing effect of warming. We also identify novel mechanisms by which these drivers can alter ecological communities, which should improve predictive models and thus our ability to manage natural systems in the face of climate change. The functional response, formalized by Holling (1959) and recently advanced by renewed interest (Kalinkat et al., 2013; Uszko et al., 2017; Rosenbaum and Rall, 2018), remains a central concept facilitating the mechanistic understanding of food web structure and stability. A growing number of studies now highlight the flexibility of the Hill exponent and its importance for the stability of populations exposed to warming (Daugaard et al., 2019; Sohlström et al., 2021). Further elucidation of how this component of predator-prey interactions responds to environmental stressors such as warming and biological traits such as body size is a promising avenue for future research.

Data Availability Statement

The data supporting this article and associated R code are deposited in the public archive figshare: https://doi.org/10.6084/m9.figshare.17081426.v1 (Rosenbaum et al., 2021).

Author Contributions

EO’G and PK designed the study. BG and ELH conducted the experiments. BR and EO’G analyzed the data and performed the model simulations. PK wrote the initial draft. All authors edited the manuscript.

Funding

This project was funded by internal support from the Queen Mary University of London to PK, BG, and ELH. PK was also supported by the Royal Society, Newton Advanced Fellowship (Grant No. NAF/R2/180791). EO’G was supported by NERC (NE/L011840/1 and NE/I009280/2). BR acknowledges the support of iDiv funded by the German Research Foundation (DFG-FZT 118, 202548816).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Paul Fletcher for his assistance with animal collection and experimental work. We also thank the editor and two reviewers for their insightful comments on an earlier version of this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.772078/full#supplementary-material

References

Andersen, K. H., Berge, T., Gonşalves, R. J., Hartvig, M., Heuschele, J., Hylander, S., et al. (2016). Characteristic sizes of life in the oceans, from bacteria to whales. Annu. Rev. Mar. 8, 217–241. doi: 10.1146/annurev-marine-122414-034144

PubMed Abstract | CrossRef Full Text | Google Scholar

Arendt, J. D. (2011). Size-fecundity relationships, growth trajectories, and the temperature-size rule for ectotherms. Evolution 65, 43–51. doi: 10.1111/j.1558-5646.2010.01112.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Askew, R. R. (1988). The Dragonflies of Europe. Colchester: Harley Books.

Google Scholar

Atkinson, D. (1994). Temperature and organism size—A biological law for ectotherms? Adv. Ecol. Res. 25, 1–58. doi: 10.1016/S0065-2504(08)60212-3

CrossRef Full Text | Google Scholar

Barcroft, J., and Hill, A. V. (1909). The nature of oxyhaemoglobin, with a note on its molecular weight. J. Physiol. 39, 411–428. doi: 10.1113/jphysiol.1910.sp001350

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanchard, J. L., Heneghan, R. F., Everett, J. D., Trebilco, R., and Richardson, A. J. (2017). From bacteria to whales: using functional size spectra to model marine ecosystems. Trends Ecol. Evol. 32, 174–186. doi: 10.1016/j.tree.2016.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Brose, U., Jonsson, T., Berlow, E. L., Warren, P., Banasek-Richter, C., Bersier, L. F., et al. (2006). Consumer – resource body-size relationships in natural food webs. Ecology 87, 2411–2417.

Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Cloyed, C. S., Dell, A. I., Hayes, T., Kordas, R. L., and O’Gorman, E. J. (2019). Long-term exposure to higher temperature increases the thermal sensitivity of grazer metabolism and movement. J. Anim. Ecol. 88, 833–844. doi: 10.1111/1365-2656.12976

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. E., Jonsson, T., and Carpenter, S. R. (2003). Ecological community description using the food web, species abundance, and body size. Proc. Natl Acad. Sci. U.S.A. 100, 1781–1786. doi: 10.1073/pnas.232715699

PubMed Abstract | CrossRef Full Text | Google Scholar

Corbet, P. S. (1999). Dragonflies: Behaviour and Ecology of Odonata. Colchester: Harley Books.

Google Scholar

Cummins, K. W., and Klug, M. J. (1979). Feeding ecology of stream invertebrates. Annu. Rev. Ecol. Evol. Syst. 10, 147–172.

Google Scholar

Cummins, K. W., and Wuycheck, J. C. (1971). Caloric equivalents for investigations in ecological energetics. Int. Vereinigung Theoretische Angewandte Limnol. 18, 1–158. doi: 10.1080/05384680.1971.11903918

CrossRef Full Text | Google Scholar

Damuth, J. (1981). Population density and body size in mammals. Nature 290, 699–700. doi: 10.1038/290699a0

CrossRef Full Text | Google Scholar

Daufresne, M., Lengfellner, K., and Sommer, U. (2009). Global warming benefits the small in aquatic ecosystems. Proc. Natl Acad. Sci. U.S.A. 106, 12788–12793. doi: 10.1073/pnas.0902080106

PubMed Abstract | CrossRef Full Text | Google Scholar

Daugaard, U., Petchey, O. L., and Pennekamp, F. (2019). Warming can destabilize predator–prey interactions by shifting the functional response from Type-III to Type-II. J. Anim. Ecol. 88, 1575–1586. doi: 10.1111/1365-2656.13053

PubMed Abstract | CrossRef Full Text | Google Scholar

Domenici, P., Allan, B. J., Lefrançois, C., and McCormick, M. I. (2019). The effect of climate change on the escape kinematics and performance of fishes: implications for future predator–prey interactions. Conserv. Physiol. 7:coz078. doi: 10.1093/conphys/coz078

PubMed Abstract | CrossRef Full Text | Google Scholar

Emmerson, M. C., and Raffaelli, D. (2004). Predator–prey body size, interaction strength and the stability of a real food web. J. Anim. Ecol. 73, 399–409. doi: 10.1111/j.0021-8790.2004.00818.x

CrossRef Full Text | Google Scholar

Englund, G., Öhlund, G., Hein, C. L., and Diehl, S. (2011). Temperature dependence of the functional response. Ecol. Lett. 14, 914–921. doi: 10.1111/j.1461-0248.2011.01661.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Enquist, B. J., Abraham, A. J., Harfoot, M. B. J., Malhi, Y., and Doughty, C. E. (2020). The megabiota are disproportionately important for biosphere functioning. Nat. Commun. 11:699. doi: 10.1038/s41467-020-14369-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, L. E., Hirst, A. G., Kratina, P., and Beaugrand, G. (2020). Temperature-mediated changes in zooplankton body size: large scale temporal and spatial analysis. Ecography 43, 581–590. doi: 10.1111/ecog.04631

CrossRef Full Text | Google Scholar

Felten, V., Tixier, G., Guérold, F., De Billy, V., and Dangles, O. (2008). Quantification of diet variability in a stream amphipod: implications for ecosystem functioning. Fundam. Appl. Limnol. 170, 303–313. doi: 10.1127/1863-9135/2008/0170-0303

CrossRef Full Text | Google Scholar

Ferreras-Romero, M., and Corbet, P. S. (1999). The life cycle of Cordulegaster boltonii (Donovan, 1807) (Odonata: Cordulegastridae) in the Sierra Morena Mountains (southern Spain). Hydrobiologia 405, 39–48. doi: 10.1023/A:1003763819991

CrossRef Full Text | Google Scholar

Friberg, N., and Jacobsen, D. (1994). Feeding plasticity of two detritivore-shredders. Fresh. Biol. 32, 133–142. doi: 10.1111/j.1365-2427.1994.tb00873.x

CrossRef Full Text | Google Scholar

Fussmann, K. E., Schwarzmüller, F., Brose, U., Jousset, A., and Rall, B. C. (2014). Ecological stability in response to warming. Nat. Clim. Chang. 4, 206–210. doi: 10.1038/nclimate2134

CrossRef Full Text | Google Scholar

Gardner, J. L., Peters, A., Kearney, M. R., Joseph, L., and Heinsohn, R. (2011). Declining body size: a third universal response to warming? Trends Ecol. Evol. 26, 285–291. doi: 10.1016/j.tree.2011.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Gayte, X., and Fontvieille, D. (1997). Autochthonous vs. allochthonous organic matter ingested by a macroinvertebrate in headwater streams: Gammarus as a biological probe. Arch. Hydrobiol. 140, 23–36. doi: 10.1127/archiv-hydrobiol/140/1997/23

CrossRef Full Text | Google Scholar

Gelman, A., and Hill, J. (2006). Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge: Cambridge University Press.

Google Scholar

Gergs, A., and Ratte, H. T. (2009). Predicting functional response and size selectivity of juvenile Notonecta maculata foraging on Daphnia magna. Ecol. Model. 220, 3331–3341. doi: 10.1016/j.ecolmodel.2009.08.012

CrossRef Full Text | Google Scholar

Gilbert, B., Tunney, T. D., McCann, K. S., DeLong, J. P., Vasseur, D. A., Savage, V., et al. (2014). A bioenergetic framework for the temperature dependence of trophic interactions. Ecol. Lett. 17, 902–914. doi: 10.1111/ele.12307

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilbert, J. P., and DeLong, J. P. (2014). Temperature alters food web body-size structure. Biol. Lett. 10:20140473. doi: 10.1098/rsbl.2014.0473

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillooly, J. F. (2000). Effect of body size and temperature on generation time in zooplankton. J. Plankton Res. 22, 241–251. doi: 10.1093/plankt/22.2.241

CrossRef Full Text | Google Scholar

Gillooly, J. F., Charnov, E. L., West, G. B., Savage, V. M., and Brown, J. H. (2002). Effects of size and temperature on developmental time. Nature 417, 70–73. doi: 10.1038/417070a

PubMed Abstract | CrossRef Full Text | Google Scholar

Graca, M. A. S., Cressa, C., Gessner, M. O., Feio, M. J., Callies, K. A., and Barrios, C. (2001). Food quality, feeding preferences, survival and growth of shredders from temperate and tropical streams. Fresh. Biol. 46, 947–957. doi: 10.1046/j.1365-2427.2001.00729.x

CrossRef Full Text | Google Scholar

Hannah, D. M., and Garner, G. (2015). River water temperature in the United Kingdom: changes over the 20th century and possible changes over the 21st century. Prog. Phys. Geogr. 39, 68–92. doi: 10.1177/0309133314550669

CrossRef Full Text | Google Scholar

Holling, C. S. (1959). The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320. doi: 10.4039/Ent91293-5

CrossRef Full Text | Google Scholar

Holling, C. S. (1966). The functional response of invertebrate predators to prey density. Mem. Ent. Soc. Can. 98, 5–86. doi: 10.4039/entm9848fv

CrossRef Full Text | Google Scholar

IPCC (2018). “Summary for policymakers,” in global warming of 1.5 ^°c. An IPCC Special Report on the Impacts of Global Warming of 1.5 ^°c Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty, eds V. Masson-Delmotte, P. Zhai, H.-O. Pörtner, D. Roberts, J. Skea, P. R. Shukla, et al. (Geneva: World Meteorological Organization), 32.

Google Scholar

Jennings, S., and Warr, K. J. (2003). Smaller predator-prey body size ratios in longer food chains. Proc. Royal Soc. B. 270, 1413–1417. doi: 10.1098/rspb.2003.2392

PubMed Abstract | CrossRef Full Text | Google Scholar

Jetz, W., Carbone, C., Fulford, J., and Brown, J. H. (2004). The scaling of animal space use. Science 306, 266–268. doi: 10.1126/science.1102138

PubMed Abstract | CrossRef Full Text | Google Scholar

Jonsson, T., Cohen, J. E., and Carpenter, S. R. (2005). Food webs, body size, and species abundance in ecological community description. Adv. Ecol. Res. 36, 1–84.

Google Scholar

Kalinkat, G., Rall, B. C., Vucic-Pestic, O., and Brose, U. (2011). The allometry of prey preferences. PLoS One 6:e25937. doi: 10.1371/journal.pone.0025937

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalinkat, G., Schneider, F. D., Digel, C., Guill, C., Rall, B. C., and Brose, U. (2013). Body masses, functional responses and predator–prey stability. Ecol. Lett. 16, 1126–1134. doi: 10.1111/ele.12147

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly, D. W., Dick, J. T. A., and Montgomery, W. I. (2002). The functional role of Gammarus (Crustacea, Amphipoda): shredders, predators, or both? Hydrobiologia 485, 199–203. doi: 10.1023/A:1021370405349

CrossRef Full Text | Google Scholar

Lang, B., Ehnes, R. B., Brose, U., and Rall, B. C. (2017). Temperature and consumer type dependencies of energy flows in natural communities. Oikos 126, 1717–1725. doi: 10.1111/oik.04419

CrossRef Full Text | Google Scholar

Maazouzi, C., Piscart, C., Legier, F., and Hervant, F. (2011). Ecophysiological responses to temperature of the “killer shrimp” Dikerogammarus villosus: is the invader really stronger than the native Gammarus pulex? Comp. Biochem. Physiol. A 159, 268–274. doi: 10.1016/j.cbpa.2011.03.019

PubMed Abstract | CrossRef Full Text | Google Scholar

MacNeil, C., Dick, J. T. A., and Elwood, R. W. (1997). The trophic ecology of freshwater Gammarus spp. (Crustacea: Amphipoda): problems and perspectives concerning the functional feeding group concept. Biol. Rev. 72, 349–364. doi: 10.1017/S0006323196005038

CrossRef Full Text | Google Scholar

McCann, K. (2000). The diversity-stability debate. Nature 405, 228–233. doi: 10.1038/35012234

PubMed Abstract | CrossRef Full Text | Google Scholar

McCann, K., Hastings, A., and Huxel, G. R. (1998). Weak trophic interactions and the balance of nature. Nature 395, 794–798. doi: 10.1038/27427

CrossRef Full Text | Google Scholar

McCoy, M. W., Bolker, B. M., Warkentin, K. M., and Vonesh, J. R. (2011). Predicting predation through prey ontogeny using size-dependent functional response models. Am. Nat. 177, 752–766. doi: 10.1086/659950

PubMed Abstract | CrossRef Full Text | Google Scholar

Moenickes, S., Schneider, A., Mühle, L., Rohe, L., Richter, O., and Suhling, F. (2011). From population-level effects to individual response: modelling temperature dependence in Gammarus pulex. J. Exp. Biol. 214, 3678–3687. doi: 10.1242/jeb.061945

PubMed Abstract | CrossRef Full Text | Google Scholar

Oaten, A., and Murdoch, W. W. (1975). Functional response and stability in predator–prey systems. Am. Nat. 109, 289–298. doi: 10.1086/282998

CrossRef Full Text | Google Scholar

O’Gorman, E. J., Zhao, L., Pichler, D. E., Adams, G., Friberg, N., Rall, B. C., et al. (2017). Unexpected changes in community size structure in a natural warming experiment. Nat. Clim. Chang. 7, 659–666. doi: 10.1038/nclimate3368

CrossRef Full Text | Google Scholar

Öhlund, G., Hedström, P., Norman, S., Hein, C. L., and Englund, G. (2015). Temperature dependence of predation depends on the relative performance of predators and prey. Proc. Royal Soc. B. 282:20142254. doi: 10.1098/rspb.2014.2254

PubMed Abstract | CrossRef Full Text | Google Scholar

Pauly, D., Christensen, V., Dalsgaard, J., Froese, R., and Torres, F. (1998). Fishing down marine food webs. Science 279, 860–863. doi: 10.1126/science.279.5352.860

PubMed Abstract | CrossRef Full Text | Google Scholar

Pawar, S., Dell, A. I., and Savage, V. M. (2012). Dimensionality of consumer search space drives trophic interaction strengths. Nature 486, 485–489. doi: 10.1038/nature11131

PubMed Abstract | CrossRef Full Text | Google Scholar

Perkins, D. M., Perna, A., Adrian, R., Cermenϸo, P., Gaedke, U., Huete-Ortega, M., et al. (2019). Energetic equivalence underpins the size structure of tree and phytoplankton communities. Nat. Commun. 10:255. doi: 10.1038/s41467-018-08039-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Petchey, O. L., McPhearson, P. T., Casey, T. M., and Morin, P. J. (1999). Environmental warming alters food-web structure and ecosystem function. Nature 402, 69–72. doi: 10.1038/47023

CrossRef Full Text | Google Scholar

Peters, R. H. (1983). The Ecological Implications of Body Size. New York, NY: Cambridge University Press.

Google Scholar

Post, E. (2013). Ecology of Climate Change: The Importance of Biotic Interactions. Princeton, NJ: Princeton University Press.

Google Scholar

Pritchard, G. (1965). Prey capture by dragonfly larvae (Odonata; Anisoptera). Can. J. Zool. 43, 271–289. doi: 10.1139/z65-026

CrossRef Full Text | Google Scholar

Rall, B. C., Brose, U., Hartvig, M., Kalinkat, G., Schwarzmüller, F., Vucic-Pestic, O., et al. (2012). Universal temperature and body-mass scaling of feeding rates. Phil. Trans. R. Soc. B. 367, 2923–2934. doi: 10.1098/rstb.2012.0242

PubMed Abstract | CrossRef Full Text | Google Scholar

Rall, B. C., Kalinkat, G., Ott, D., Vucic-Pestic, O., and Brose, U. (2011). Taxonomic versus allometric constraints on non-linear interaction strengths. Oikos 120, 483–492. doi: 10.1111/j.1600-0706.2010.18860.x

CrossRef Full Text | Google Scholar

Rall, B. C., Vucic-Pestic, O., Ehnes, R. B., Emmerson, M., and Brose, U. (2010). Temperature, predator–prey interaction strength and population stability. Glob. Change Biol. 16, 2145–2157. doi: 10.1111/j.1365-2486.2009.02124.x

CrossRef Full Text | Google Scholar

Real, L. A. (1977). The kinetics of functional response. Am. Nat. 111, 289–300. doi: 10.1086/283161

CrossRef Full Text | Google Scholar

Romero, G. Q., Gonçalves-Souza, T., Kratina, P., Marino, N. A. C., Petry, W. K., Sobral-Souza, T., et al. (2018). Global predation pressure redistribution under future climate change. Nat. Clim. Chang. 8, 1087–1091. doi: 10.1038/s41558-018-0347-y

CrossRef Full Text | Google Scholar

Rong, Q., Sridhar, K. R., and Barlocher, F. (1995). Food selection in three leaf-shredding stream invertebrates. Hydrobiologia 316, 173–181. doi: 10.1007/BF00017435

CrossRef Full Text | Google Scholar

Rosenbaum, B., Kratina, P., Gallo, B., Horas, E. L., and O’Gorman, E. J. (2021). Data and Code for: The Combined Effects of Warming and Body Size on the Stability of Predator-Prey Interactions. London: Figshare.

Google Scholar

Rosenbaum, B., and Rall, B. C. (2018). Fitting functional responses: direct parameter estimation by simulating differential equations. Methods Ecol. Evol. 9, 2076–2090. doi: 10.1111/2041-210X.13039

CrossRef Full Text | Google Scholar

Rosenzweig, M. L., and MacArthur, R. H. (1963). Graphical representation and stability conditions of predator–prey interactions. Am. Nat. 97, 209–223. doi: 10.1086/282272

CrossRef Full Text | Google Scholar

Roslin, T., Hardwick, B., Novotny, V., Petry, W., Andrew, N., Asmus, A., et al. (2017). Higher predation risk for insect prey at low latitudes and elevations. Science 356, 742–744. doi: 10.1126/science.aaj1631

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruger, T., and Sommer, U. (2012). Warming does not always benefit the small – Results from a plankton experiment. Aquat. Bot. 97, 64–68. doi: 10.1016/j.aquabot.2011.12.001

CrossRef Full Text | Google Scholar

Savage, V. M., Gillooly, J. F., Brown, J. H., West, G. B., and Charnov, E. L. (2004). Effects of body size and temperature on population growth. Am. Nat. 163, 429–441. doi: 10.1086/381872

PubMed Abstract | CrossRef Full Text | Google Scholar

Sohlström, E. H., Archer, L. C., Gallo, B., Jochum, M., Kordas, R. L., Rall, B. C., et al. (2021). Thermal acclimation increases the stability of a predator–prey interaction in warmer environments. Glob. Change Biol. 27, 3765–3778. doi: 10.1111/gcb.15715

PubMed Abstract | CrossRef Full Text | Google Scholar

Stan Development Team (2020). RStan: The R Interface to Stan. R Package Version 2.21.2. Sydney, NSW: Stan.

Google Scholar

Summers, R. B., Delong, M. D., and Thorp, J. H. (1996). Ontogenetic and temporal shifts in the diet of the amphipod Gammarus fasciatus in the Ohio River. Am. Midl. Nat. 137, 329–336. doi: 10.2307/2426852

CrossRef Full Text | Google Scholar

Sutcliffe, D. W., Carrick, T. R., and Willoughby, L. G. (1981). Effects of diet, body size, age and temperature on growth rates in the amphipod Gammarus pulex. Fresh. Biol. 11, 183–214. doi: 10.1111/j.1365-2427.1981.tb01252.x

CrossRef Full Text | Google Scholar

Synodinos, A. D., Haegeman, B., Sentis, A., and Montoya, J. M. (2021). Theory of temperature- dependent consumer-resource interactions. Ecol. Lett. 24, 1539–1555. doi: 10.1111/ele.13780

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, H., Hirst, A. G., Atkinson, D., and Kratina, P. (2021). Body size and shape responses to warming and resource competition. Funct. Ecol. 35, 1460–1469.

Google Scholar

Uiterwaal, S. F., and DeLong, J. P. (2018). Multiple factors, including arena size, shape the functional responses of ladybird beetles. J. Appl. Ecol. 55, 2429–2438. doi: 10.1111/1365-2664.13159

CrossRef Full Text | Google Scholar

Uiterwaal, S. F., and DeLong, J. P. (2020). Functional responses are maximized at intermediate temperatures. Ecology 101:e02975. doi: 10.1002/ecy.2975

PubMed Abstract | CrossRef Full Text | Google Scholar

Urban, M. C. (2015). Accelerating extinction risk from climate change. Science 348, 571–573. doi: 10.1126/science.aaa4984

PubMed Abstract | CrossRef Full Text | Google Scholar

Uszko, W., Diehl, S., Englund, G., and Amarasekare, P. (2017). Effects of warming on predator–prey interactions –A resource-based approach and a theoretical synthesis. Ecol. Lett. 20, 513–523. doi: 10.1890/15-0055.1

CrossRef Full Text | Google Scholar

Uszko, W., Diehl, S., Pitsch, N., Lengfellner, K., and Müller, T. (2015). When is a type III functional reponse stabilizing? Theory and practice of predicting plankton dynamics under enrichment. Ecology 96, 3243–3256.

Google Scholar

Vasseur, D. A., and McCann, K. S. (2005). A mechanistic approach for modeling temperature-dependent consumer-resource dynamics. Am. Nat. 166, 184–198. doi: 10.1086/431285

PubMed Abstract | CrossRef Full Text | Google Scholar

Vehtari, A., Gabry, J., Magnusson, M., Yao, Y., Bürkner, P., Paananen, T., et al. (2020). Loo: Efficient Leave-One-Out Cross-Validation and WAIC for Bayesian Models. R package version 2.4.1. Available online at: https://mc-stan.org/loo/ (accessed December 5, 2021).

Google Scholar

Vehtari, A., Gelman, A., and Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 27, 1413–1432. doi: 10.1007/s11222-016-9696-4

CrossRef Full Text | Google Scholar

Vucic-Pestic, O., Ehnes, R. B., Rall, B. C., and Brose, U. (2011). Warming up the system: higher predator feeding rates but lower energetic efficiencies. Glob. Change Biol. 17, 1301–1310. doi: 10.1111/j.1365-2486.2010.02329.x

CrossRef Full Text | Google Scholar

Vucic-Pestic, O., Rall, B. C., Kalinkat, G., and Brose, U. (2010). Allometric functional response model: body masses constrain interaction strengths. J. Anim. Ecol. 79, 249–256. doi: 10.1111/j.1365-2656.2009.01622.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Welton, J. S. (1979). Life-history and production of the amphipod Gammarus pulex in a Dorset chalk stream. Fresh. Biol. 9, 263–275. doi: 10.1111/j.1365-2427.1979.tb01508.x

CrossRef Full Text | Google Scholar

White, E. P., Ernest, S. K. M., Kerkhoff, A. J., and Enquist, B. J. (2007). Relationships between body size and abundance in ecology. Trends Ecol. Evol. 22, 323–330. doi: 10.1016/j.tree.2007.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J., Brose, U., and Martinez, N. D. (2007). “Homage to Yodzis and Innes 1992: scaling up feeding-based population dynamics to complex ecological networks,” in From Energetics to Ecosystems: The Dynamics and Structure of Ecological Systems, eds N. Rooney, K. S. McCann, and D. L. G. Noakes (Dordrecht: Springer), 37–51.

Google Scholar

Woodward, G., and Hildrew, A. G. (2001). Invasion of a stream food web by a new top predator. J. Anim. Ecol. 710, 273–288. doi: 10.1111/j.1365-2656.2001.00497.x

CrossRef Full Text | Google Scholar

Woodward, G., and Hildrew, A. G. (2002a). Body-size determinants of niche overlap and intraguild predation within a complex food web. J. Anim. Ecol. 71, 1063–1074. doi: 10.1046/j.1365-2656.2002.00669.x

CrossRef Full Text | Google Scholar

Woodward, G., and Hildrew, A. G. (2002b). The impact of a sit-and-wait predator: separating consumption and prey emigration. Oikos 99, 409–418. doi: 10.1034/j.1600-0706.2002.11210.x

PubMed Abstract | CrossRef Full Text | Google Scholar