Being the Winner Is Being the Loser When Playing a Parental Tug-of-War – A New Framework on Stability of Biparental Care

Because there are basic sexual differences in reproductive potential, and the cost of parental care is assumed to be high, biparental care is viewed as a constant tug-of-war between the partners. This raises the question of the system’s evolutionary stability. Several models have been proposed to resolve this problem but none has received unequivocal support. Here, I propose a framework that not only integrates the earlier theoretical ideas (sealed bids, negotiation) but also considers the importance of the environment (frequently neglected in previous models) and views the cost of parental care from a different perspective (costly in terms of parent’s survival only when performed close to the boundary of parental capacity). The framework suggests that sexual conflict may not be such a significant factor mediating parental care as commonly assumed, and that a parent trying to shift the parental burden onto the partner – assumed to be the winner in the tug-of-war interplay – is actually more likely to be a loser, as doing so may put the success of the current breeding attempt in jeopardy, thereby reducing overall fitness of the parent. Once it is realized that the importance of sexual conflict is actually much less than it seems, it becomes clear that the stability of the biparental care system no longer seems to be such a puzzling issue.

Introduction

Although biparental care is a rather rare form of rearing the offspring across animal kingdom (Lack, 1968; Clutton-Brock and Vincent, 1991; Bennett and Owens, 2002; Reynolds et al., 2002), it has repetitively evolved in birds, mammals, amphibians, fishes and insects (Balshine, 2012; Trumbo, 2012). This care system continues to be an intriguing topic of behavioral ecology, with as yet unanswered questions about its evolutionary stability. This is because males and females owing to differences in the number and the rate of gamete production, have different reproductive potentials, and this naturally imposes selection for different reproductive strategies, with females caring for their offspring if need be, and males chasing mating opportunities (Trivers, 1972; Clutton-Brock and Vincent, 1991). Biparental care, where both sexes care for progeny, is therefore viewed as a constant tug-of-war between the partners. In this context, the assumed high cost of parental care (Owens and Bennett, 1994; Ghalambor and Martin, 2001) merely adds fuel to the fire. Since each parent pays the cost of care on its own while benefitting not only from the own effort but also on that from the partner (Trivers, 1972), each could benefit even more if at least a part of these costs were shifted on the partner. In such a context the question arises as to how biparental care could be an evolutionarily stable strategy.

This problem, yet to be solved, has given rise to several theoretical models. A pioneering one assumed that parents operate independently, each investing a fixed level (“sealed bids”) of effort that maximizes its own fitness, given the effort invested by its partner (Chase, 1980; Houston and Davies, 1985). Later models have extended this framework, stressing the importance of behavioral negotiation between the parents (McNamara et al., 1999, 2000, 2003). The most recent model considers information about offspring need as an important regulator of parental care (Johnstone and Hinde, 2006). All the models predict that in the situation where one partner makes less effort, the other should not fully compensate for deficiency, as this will eventually lead to the uniparental care. To keep the biparental care strategy stable at an evolutionary scale, either partner’s reduced effort should be only temporarily and/or partially compensated for Chase (1980), Houston and Davies (1985), McNamara et al. (1999, 2000, 2003), and Johnstone and Hinde (2006).

All the aforementioned models have been experimentally tested. The most common approach is performing an experiment with one parent being handicapped in some way or removed, and then to examine the other’s response. The results of these studies are not consistent, however. There is indeed evidence on partial compensation as predicted by the theoretical models, but other types of compensation have also been found, such as mutual and sex-specific, and even none at all (Harrison et al., 2009; Santos and Nakagawa, 2012). Several studies have already drawn attention to this inconsistency: a few suggest environmental effect and/or limits of parental capacity (e.g., Smiseth et al., 2005; Nakagawa et al., 2007) – when already operating at their maximum level, parents may not respond to the experimental treatment as predicted by the models because of physiological constraints and/or challenging environmental conditions. However, none of the theoretical models and empirical studies carried out to date have explicitly considered the effect of the environment, while intuitively it is likely to be crucial for the evolution of biparental care (Owens and Bennett, 1997; Watson et al., 2015; Matysiokova and Remeš, 2018) and compensatory behavior (e.g., Smiseth et al., 2005; Nakagawa et al., 2007). Another issue is that all the models and the follow-up studies are based on the assumption that the costs of parental care are always high, i.e., there is a link between the parental care and parent survival. Indeed parental care is not free of costs (summarized by Alonso-Alvarez and Velando, 2012). However, there is an increasing amount of evidence showing that the trade-off between parental effort and parents survival is more complex that hitherto thought, and that the relationship between the two is not linear [as reviewed by Santos and Nakagawa (2012)]. This may have considerable consequences for understanding the question of the stability of biparental care. Here, I propose a new framework (a model) for considering the bi-parental care system that takes into account the environmental conditions in which the parents operate, and examines the costs of parental care from a slightly different perspective.

Description of the Framework

The framework (Figure 1) is quite straightforward, based on two lines, and four main assumptions. For even greater simplicity it assumes that the male and female contributions into parental care are equal, and that there is a straight-linear relationship between their contribution. Modifications of this simplistic approach (see below) are possible but should not affect the general predictions.

FIGURE 1

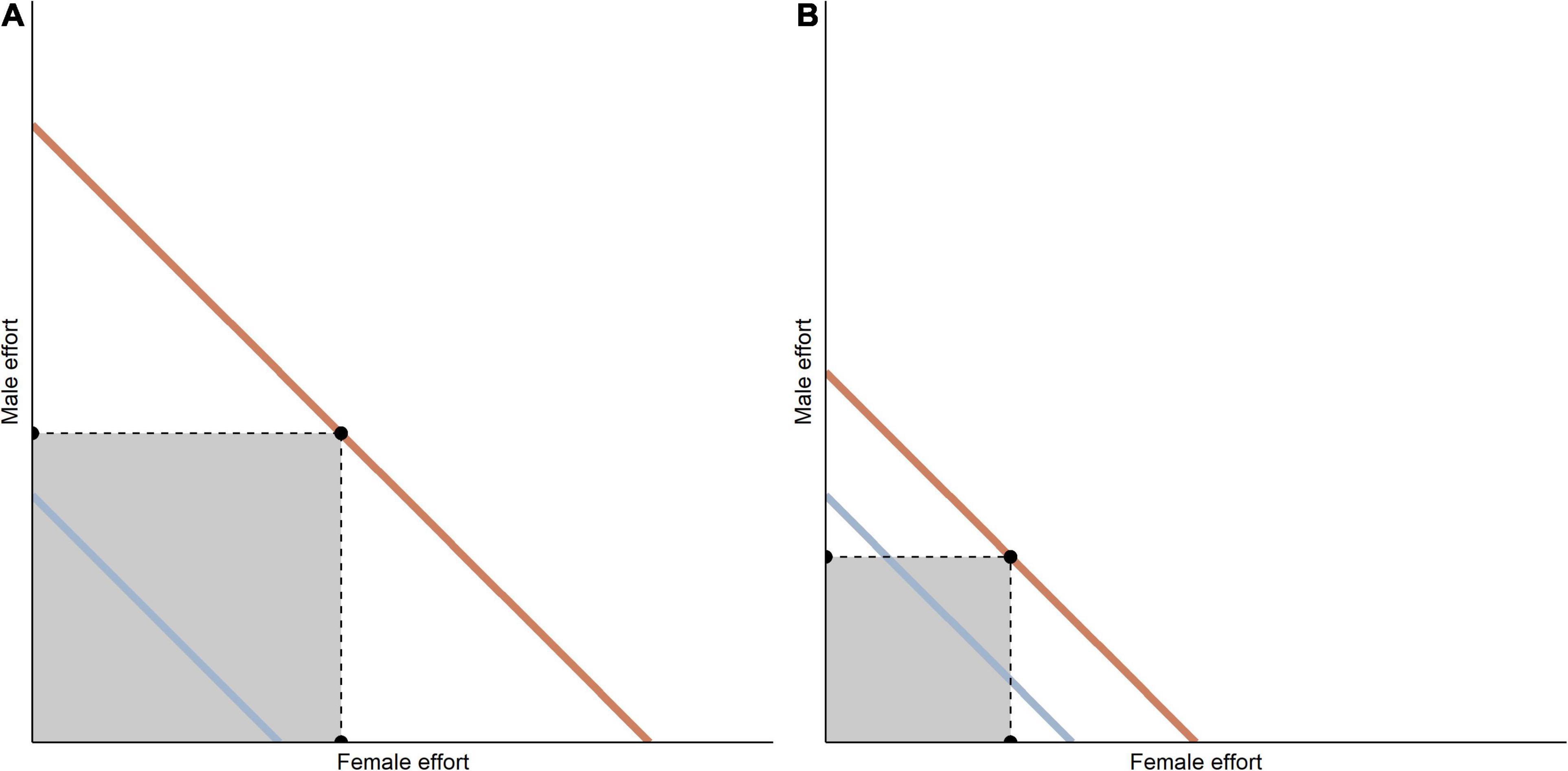
Figure 1. Total amount of parental care required by the offspring as a function of male and female parental effort. Multiple lines are possible within the ranges defined by the least (red solid) and the most favorable (blue solid) environmental conditions experienced by a species in an evolutionary scale. The two points on the axis for each parent and the grey area denote optimal range of parental capacity. (A) Species of wide parental capacity, adapted to highly variable environments. (B) Species of narrow parental capacity, adapted to harsh and/or predictable environment.

The most important component of this framework is the significance of the environment in mediating the amount of parental care required by the offspring, with environment being treated as the overall conditions experienced by parenting individuals (food availability, predation pressure, etc.; everything that parents can control, at least to a certain extent). There is ample evidence, both direct and indirect, to show that any parental care system is closely dependent on environmental conditions (Owens and Bennett, 1997; Watson et al., 2015; Matysiokova and Remeš, 2018). Birds provide many excellent examples of environmental influence on parental care, where harsh and/or unpredictable environmental conditions governing food availability impose obligatory male and female contributions to offspring raising, whereas habitats with temporarily abundant food resources makes biparental care facultative and condition-dependent (van Noordwijk and de Jong, 1986; Reznick et al., 2000; Cockburn, 2006; Vincze et al., 2013). Importantly, environmental conditions are rarely stable over a short time scale (like a life span of an individual) but at a long, evolutionary scale, there would be a fixed range of possible environmental scenarios regularly experienced by a species. Environmental scenarios being realized in the long time perspective thus shape firstly, parental reproductive system (biparental uniparental/etc) of a species, and secondly parental capacity (i.e., a function of cost of parental care in respect to the parental effort) of breeding individuals. Then, in all the species that evolved into biparental care system, each parent is evolutionarily prepared to provide parental care both in favorable and less favorable environmental scenarios.

Thus, the prime assumption of the present framework is that the total amount of parental care required by the offspring is a function of the environment, and that under certain conditions only the involvement of both parents can satisfy the needs of the offspring. This assumption can be considered from both the evolutionary and temporal perspective. From the evolutionary perspective, the mode of offspring development and the associated mode of parental care is the outcome of the interplay between natural selection and a range of environmental conditions in the species’ habitat. In harsh environmental conditions, for example, when food resources are frequently difficult to obtain and/or there is a constant, high predation risk, selection should favor biparental care (Balshine, 2012), as only the involvement of both parents will allow the offspring to be raised successfully [e.g., many seabird species (Schreiber and Burger, 2002)]. Where the environment is less challenging, biparental care may still be favored by selection, if only these environmental conditions are in some way unpredictable over the breeding season. From the temporal perspective, in species that exhibit biparental care, this system is also environment-dependent as some species may exhibit biparental care when conditions are challenging but may revert to a uniparental system when conditions become more favorable [e.g., some passerine species (Cockburn, 2006)]. More and more studies are demonstrating that the amount of parental care (both in uniparental and biparental systems) delivered to the offspring is adjusted to the brood’s needs and current environmental conditions (Royle et al., 2014; Matysiokova and Remeš, 2018).

Another important assumption of the framework is related to the cost of parental care. The framework assumes that caring for the offspring is costly for a parenting individual, in the sense that it may lower the parent’s own chances of survival (Clutton-Brock, 1991) and/or future fecundity (considered as a possibility to raise the offspring in regard to a body condition) only when it is operating beyond an optimal range of its parental capacity (i.e., above an evolutionarily optimized level). In other words, when a parent operates in favorable conditions in regard to both environment and social context (Royle et al., 2014), and so within an optimal range of its parental capacity (flat area of the function of costs of parental care on the Figure 2, Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/), it does have to pay some costs associated with parental care (see below), but these are not high enough to seriously jeopardize its survival and/or future reproductive output. Importantly, the optimal range of species’ parental capacity is the outcome of natural selection operating within the range of environmental conditions that the species has experienced over evolutionary time (Figures 1, 2; Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). Species evolving in predictable environment would have a narrow optimal range of parental capacity, with parental care quickly becoming considerably costly in terms of decrease in parent’s survival and future fecundity when parental effort increases beyond the optimal zone of parental capacity. In contrast, species in a constantly changing environment should have a greater optimal range of parental capacity, thus being able to exhibit a wide range of parental effort while apparently not sustaining cost in terms of lowered survival and/or future fecundity.

FIGURE 2

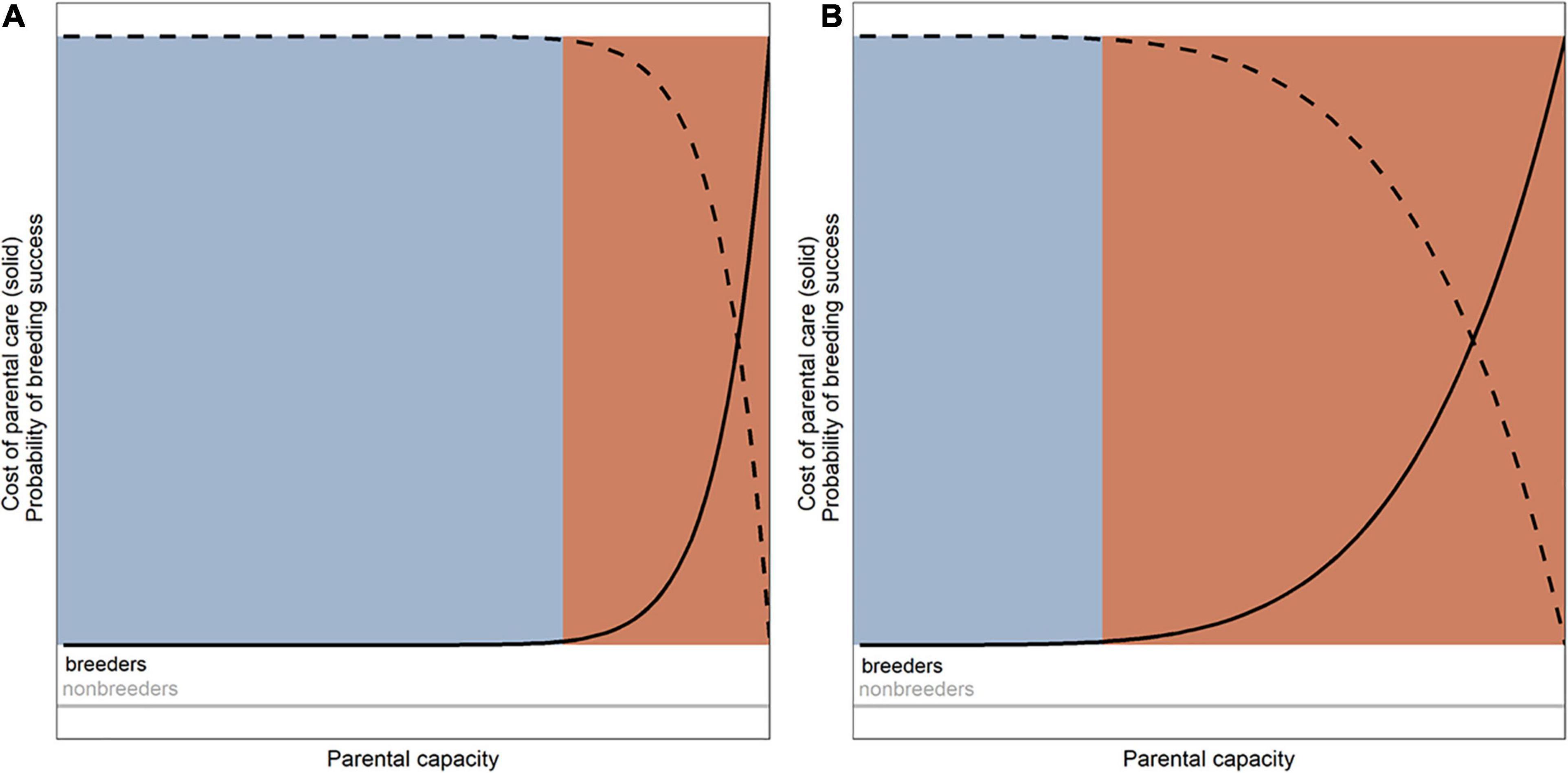
Figure 2. The cost of parental care of an individual (in terms of the parental survival and its future fecundity; solid line) and the related to that probability of the success in the current reproductive attempt (dashed lines) with regard to the concept of parental capacity. Blue and red areas denote optimal and suboptimal range of parental capacity, respectively. (A) Species of wide parental capacity, adapted to highly variable environments. (B) Species of narrow parental capacity, adapted to harsh and/or predictable environment.

Considering the costs of parental care in this way may seem to be controversial at first glance but I would argue this is not so. It is merely acknowledging the fact that the costs associated with parental care are not linearly dependent on parental effort (as already highlighted in the literature: e.g., van Noordwijk and de Jong, 1986; Reznick et al., 2000; Santos and Nakagawa, 2012; Williams, 2018). Undoubtedly, a parenting individual does experience many changes that are associated with certain costs, e.g., changes in time and energy allocation, physiological changes, immunosuppression and oxidative stress, as summarized by Alonso-Alvarez and Velando (2012). But how these costs affect the future survival and fecundity of the parent is a complex issue (van Noordwijk and de Jong, 1986; Reznick et al., 2000; Santos and Nakagawa, 2012; Williams, 2018). There are numerous studies that indeed demonstrate reduced parental survival and/or future fecundity, but there are other supporting the opposite case, as reviewed in Reznick et al. (2000) and Santos and Nakagawa (2012). Therefore, what I am suggesting here is that if parental effort is performed within the optimal range of parental capacity, there is no reason to assume that parental care is costly in the sense of decreased survival and/or future fecundity of the parent; only beyond this optimal range do the costs start to rise (i.e., jeopardizes the parent survival and/or future fecundity; Figure 2; Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/).

Another issue associated with the cost of parental care in the present framework is that a lost opportunity of mating with another partner (due to involvement into parental care) it is not considered as a component of the cost, as it is typically done in a payoff matrix for the evolution of parental care (Smith Maynard, 1977; Houston et al., 2013). This is because the current breeding attempt is a central focus here, and the cost of parental care is calculated and only for that attempt (i.e., not beyond). Although opportunities to remate after desertion has to be taken into account while considering stability of biparental care (Houston et al., 2013), in the present framework they are viewed as a separate variable/scenario (see below consideration of that in the context of game theory).

The third, important assumption of the framework is that if a parent operates beyond its optimal zone of parental capacity, the probability of the breeding success (e.g., number of offspring that would survive in given breeding attempt) decreases considerably (Figure 2). This is because the parenting performance of an individual operating at a suboptimal level of its parental capacity is likely to be deteriorated, and/or the individual is more likely to simply abandon the brood (e.g., Bókony et al., 2009). The relationship between this parental capacity and probability of the breeding success could be illustrated by a curve that starts with a plateau, and after reaching suboptimal zone it falls away (Figure 2 and Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). Similarly as for the cost of parental care (of which it is a reverse function), the range of the flat area of the curve depends on the environment in which a species has evolved (Supplementary Materials 1– https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). If we translate this into the costs of parental care (in the sense of the reduced survival and/or fecundity of the parent), the higher costs would incur the higher risk of brood failure when care is being performed beyond the optimal range of parental capacity (dark-gray area on Figure 2 and Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/).

Finally, it is worth considering the parents’ certainty of success in the current breeding attempt. It is not so important for the framework but may be useful for the interpretation and consideration of evolutionary stability of the biparental care. The caring parent always has a greater certainty of the reproductive success of the current breeding attempt than its deserting partner. This is obviously hard to prove, and may be why researchers have tended to avoid this issue, but it may be important for individuals making a decision about the amount of parental care, and I would argue that it has an evolutionary sense. A parent may reduce its effort (up to brood desertion), only if survival of the current offspring is not apparently jeopardized by this parental action. Parental behavior that violates this condition is unlikely to be promoted by selection. Thus, uncertainty about the environmental situation during current breeding attempt and/or about the partner’s parental capacity could be the driver behind remaining with the offspring, even if uniparental care would be sufficient in the current environment condition.

To illustrate the present framework for the stability of the biparental care, we can plot the total amount of parental care required by the offspring as a linear relationship (for simplicity), a function of the combined male and female effort. Multiple parallel lines (not necessarily straight) are possible for this relationship, with the intercept of the lines depending on environmental conditions. All these lines lie within evolutionary boundaries defined by the least (red line, Figure 1) and the most favorable (blue line, Figure 1) conditions regularly experienced by a species in an evolutionary time (hereafter, evolutionary tolerance of the environmental variability; see also dynamic plots on the application in Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). Importantly, half of the parental effort required by the offspring in the least favorable conditions sets the limit of the optimal range of parental capacity of a given parent. In the least favorable conditions, there must be an equal division of labor between the partners, otherwise they may both experience breeding failure. Consequently, in such a case there is a very little parental flexibility, no room for negotiations between the partners, no chance of any compensation of potential shortcomings/indisposition on the part of one, as under these conditions the parental care incurs extra costs because the parenting individual is operating at the edge of its optimal parental capacity (Figures 1, 2; Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_ gametheory/). Under more favorable conditions, equal contributions from both parents contribution may not be so crucial for the breeding success but any decrease in one partner’s contribution may shift the other partner into the suboptimal zone of parental capacity, and the probability of breeding success may decline (Figure 2; Supplementary Material 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). In other words, under favorable conditions with two parents caring, each pays relatively low costs of parental care, and so the chances of breeding success are then be the highest. In the situation when only one parent is caring for the offspring, the cost of this care is higher for the parenting individual, thus incurring the risk of breeding failure of both parents (Figures 1, 2; Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). In such a context, the cost of parental care (in the sense of reduced parental survival and/or fecundity) very much depends on the species’ environment and social situation (Figures 1, 2;Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/).

Discussion

Predictions

In the light of the presented framework, for species that have evolved in unpredictable and/or harsh environmental conditions, bi-parental care is a default and evolutionarily stable strategy. In environmentally challenging conditions, when both parents are crucial to raise the offspring successfully, none of the parent has an interest to abandon the brood. Besides two parents involvement in harsh conditions may keep individual cost of parental care at an optimal level, of which both parents obviously benefit. This may have particular significance for species that form long-term pair bonds, where breeding partners depend mutually on the their future survival and fecundity (Griffith, 2019). In more favorable conditions, when a single parent is potentially capable of successfully raising offspring, the unpredictability of the environment during the breeding attempt may still keep both parents engaged; even if conditions happen to be favorable at the onset of the breeding season, they may deteriorate over the time. Thus, leaving the partner at any point may jeopardize the current breeding attempt. This uncertainty may prevent a breeding individual from shifting the whole burden on to the partner. The only situation, when leaving the partner may be profitable in some way, is when two conditions are met simultaneously: 1) environmental conditions are sufficiently favorable/predictable that a single parent can successfully raise its offspring, and 2) the chance of the leaving individual for a successful breeding attempt with another partner are high. Then indeed, uniparental care is provided. This situation, however, happens irregularly over a long time perspective, thus bi-parental care remains a default breeding system in all these species. Obviously, in species that have evolved in an environment that regularly allows a single parent successfully raise the offspring, the uniparental care is the default system, and the condition of high chance of the leaving individual for a successful breeding attempt with another partner is then of strong selective power.

To illustrate this whole line of reasoning, let us consider the issue in the context of game theory, with a simple matrix of male and female fitness consequences of two parental behaviors (remaining with/deserting the offspring) in three different environmental conditions (unfavorable, moderately favorable, and favorable). The issue may be quite complex, as apart from the matrix components and various environmental scenarios, there is also a variety of evolutionary history of the species (i.e., narrow/wide environmental tolerance, and so narrow/wide optimal range of parental capacity). Thus for simplicity of the present text, I consider the issue for a species of wide environmental tolerance and so wide optimal range of parental capacity. To examine other possibilities and their effect on the cost of parental care and breeding success, I provide a simple shiny application that allows to vary both environmental scenario as well as the environmental tolerance of the species (Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/). For the example considered here, the values set in the application are: 15 for the evolutionary tolerance, and 90, 60, 20 for unfavorable, moderately favorable and favorable environmental conditions, respectively (Figure 3; Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/).

FIGURE 3

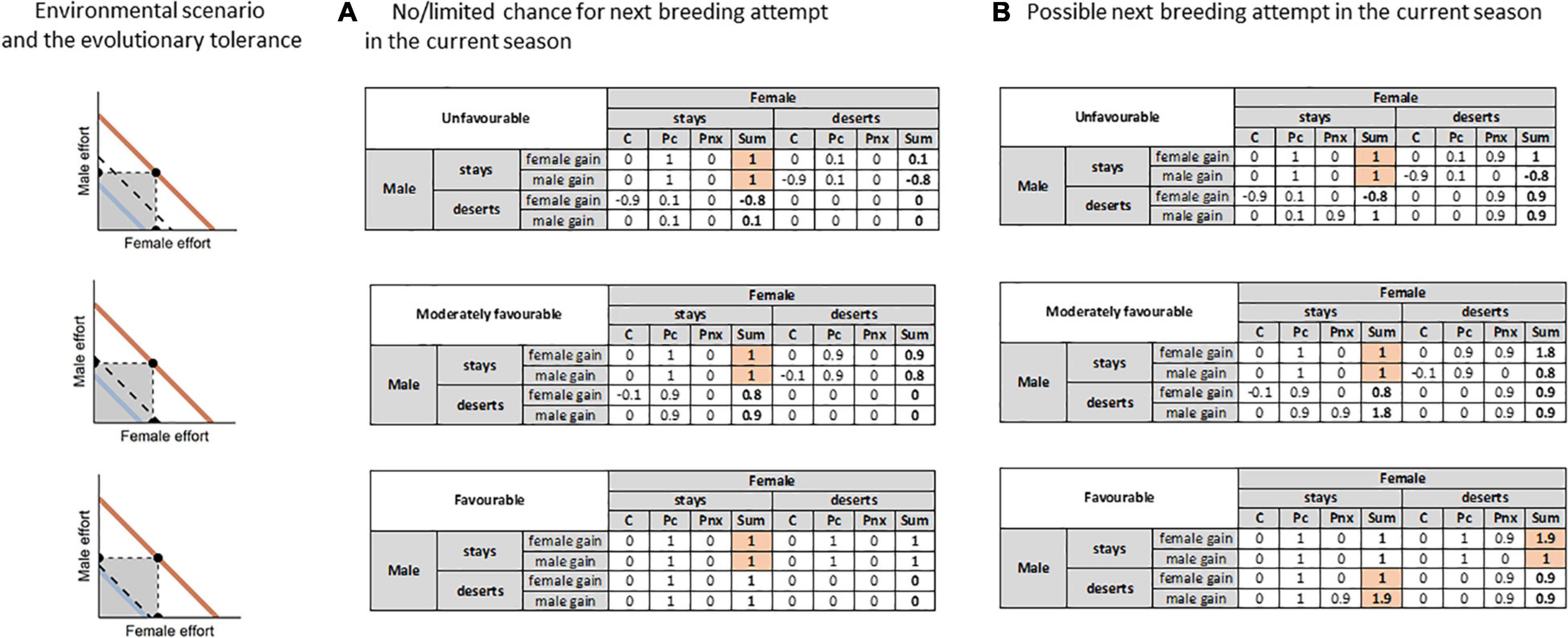
Figure 3. Matrices of males and females reproductive costs and benefits with respect to the mode of parental care and environment quality. The considered environmental quality and the evolutionary tolerance of the species for the environmental quality illustrated on the left panel. Two environmental scenarios are considered: (A) when there is no or only limited chance for successful re-mating in the current season, and (B) when another successful breeding attempt in the current season is possible. C – cost of parental care (see the main text for clarification of this issue) in the current breeding attempt, Pc – probability of the breeding success in the current breeding attempt, Pnx – probability of the breeding success in another breeding attempt in the same breeding season, Sum – outcome of cost and benefits; the sum of the three components: C, Pc, Pnx. The outcome likely to be promoted by selection marked in red. See the main text for a detailed description and interpretation.

There are three components of parental fitness in this matrix:

C – The cost of parental care with possible values within the range of <−1; 0>. In the line with the above assumptions, I assume here that in an evolutionarily established biparental care system, the cost of parental care in regards to the future survival and/or fecundity of the parent is relatively low when both parents undertake care. Again, for simplicity I assume 0 here for such a situation, although I would like to stress that this does not mean that parental care incurs no costs at all (see the reasoning above). When one parent deserts the brood, the cost of parental care may increase (the value becoming negative), so if all the components of the matrix will sum up, subtracting these costs will lower the final outcome. The exact value depends on and in proportion to environmental conditions (and evolutionary tolerance of the species), with the most extreme being −1 in unfavorable conditions, and everything in between −1 and 0 in more favorable conditions. Here, I assume −0.9 for unfavorable, −0.1 for moderately favorable and 0 for favorable conditions (based on the application, Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/).

Pc – The probability of breeding success in the current breeding attempt – possible values: <0; 1>. From the perspective of the present framework, I assume that the probability that the current breeding attempt will be successful is linked to the amount of parental care (one/two parents caring) and environmental conditions (Figure 2). When two parents care for their offspring the Pc takes the highest value. When one of the parents deserts, Pc may decrease, again depending on and in proportion to the environmental conditions (and evolutionary tolerance of the species), with the lowest value (0) in unfavorable conditions, and everything in between 0 and 1 in more favorable conditions. Here, I assume 0.1 for unfavorable, 0.9 for moderately favorable and 1 for favorable conditions (based on the application, Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/).

Pnx – The probability of breeding success in the next breeding attempt, possible values: <0; 1>. This is the probability of breeding success in the very next breeding attempt, within the same breeding season. In all the cases when potential breeding partners of the next breeding attempt are scarce, Pnx oscillates close to 0. With the increasing availability of potential breeding partners, Pnx also increases but can never achieve the maximum theoretical value of 1, given uncertainty associated with anything that might happen in the future. Thus here, for simplicity and acknowledging the strong selective power that is related to remating opportunities I assigned 0.9 to the deserting parent.

The three environmental scenarios are as follows:

Unfavorable – only when both parents are involved there is a chance of successful breeding attempt;

Moderately favorable – one parent is potentially capable of raising the offspring on its own, but this increases the cost of parental care and pushes the caring parent to sub-optimal range of its parental capacity;

Favorable – one parent is capable of raising the offspring on its own and the required parental effort is well within its optimal range of parental capacity.

Let us now consider the matrix, first when Pnx equals 0, e.g., colonially breeding species, with all breeders in the population starting the season roughly at the same time (Figure 3A).

With all the assumptions in mind, the outcome of the matrices reveals that for each parent and regardless of the environmental circumstances, remaining with the brood is the most profitable behavior (i.e., the highest possible outcome for each sex), and so can be an evolutionarily stable strategy (Figure 3A). In extraordinarily favorable conditions, the outcome of matrix with one leaving partner may be the same as for both parents caring, but with no apparent gain from anything else (Pnx = 0), there is no reason to leave the brood. Besides, there is always a risk that environmental conditions may change during the season and so deserted parent may shift into the sub-optimal range of its parental capacity, affecting the common breeding success. In other words, the biparental system is stable because, as the title of this paper perversely puts it, the parent that abandons the brood, leaving its partner in charge, might be considered a winner after having shifted the whole parental workload onto the partner. In fact, however, it will be a loser, because abandoning the brood will jeopardize the success of the current breeding attempt.

Now let us examine the same three matrices with just a single change of Pnx being higher than 0, e.g., a species with >1 breeding attempt in the breeding season, low partner fidelity, considerable asynchrony in the timing of breeding in the population, and hence the possibility of finding another partners after having deserted the first brood (Figure 3B).

Here, under unfavorable conditions, the biparental strategy remains the most profitable one (Figure 3B). When conditions are moderately favorable, one of the partners gain quite much and so might leave but as for the analogical environmental scenario presented above, leaving the partner imposes the risk of shifting it beyond its optimal range of parental capacity if the environmental condition deteriorated. Also, there is a bias in the value of the breeding outcome for the two sexes, with one sex gaining less than in biparental care system. Only in good and stable environmental conditions, and when there is a chance of a successful extra breeding attempt, the outcome of the payoff matrix is high enough for each of the partners, and so one of the them may leave without jeopardizing the current breeding attempt. Which of the partners leaves depends on the operational sex ratio and thus the chances of another breeding attempt (McNamara et al., 2000; Barta et al., 2002).

The concept of parental capacity potentially explains the great variation observed in a parent’s response to the experimental removal and/or handicapping of its partner. Species (also sexes, and individuals) with a narrow range of optimal parental capacity (Figure 1B) will rarely be observed to increase their effort in response to a partner shortage, as they usually operate close to the limit of their optimal parental capacity. In contrast, species with a wide optimal range of parental capacity will be more flexible (Figure 1A). Importantly, the parental response will very much depend on the current environmental conditions. Thus, sometimes even those with substantial range of optimal parental capacity may not be able to compensate for the partner’s loss/deficiency. Overall, however, each parent, so long as it is capable of doing so, should compensate for the partner’s absence as not doing so will decrease its own fitness by lowering reproductive success.

Modifications of the Framework

For reasons of simplicity, the present framework as illustrated in Figure 1 (and Supplementary Materials 1 – https://kasiawojczulanis-jakubas.shinyapps.io/biparental_care_gametheory/) is based on linear relationships and equal male and female contributions. The first thing that may be different in reality is the slope of the regression line describing the relationship between male and female parental effort, and the division of parental labor between the sexes. Different species may have different values of the slope, although it should always be negative, and male and female contributions may not be equal, although both parents will always be involved and their efforts always will add up to the total parental care required. In addition, parental body condition may further modify the shape of the relationship, transforming it from straight-linear to a logarithmic (also with a sex specific transformations). As a matter of fact, it does not have to be linear at all. Finally, the two regression lines forming the environmental buffer, i.e., the distance/space between the two boundaries, do not necessarily have to be parallel, and or have the slope of the same value. Nonetheless, even though all these modifications are possible, the overall predictions should hold true.

Concluding Remarks

The proposed framework integrates the extremes of the continuum of parental care scenarios proposed by the earlier sealed-bid and negotiation models (Chase, 1980; Houston and Davies, 1985; McNamara et al., 1999, 2000, 2003; Johnstone and Hinde, 2006), takes the environment into account as the most important factor shaping parental care at both the temporal and evolutionary scales, and considers parental care as being of relatively low cost in terms of parental survival/fecundity, if performed within the optimal range of parental capacity. The two aspects highlight fundamental differences between previous models and the present framework. Obviously, the present framework has not been either formally considered in a mathematical model or tested empirically, so I would encourage researchers to examine it thoroughly, as it has the potential to change the way we look at the parental care. If the model withstands testing, it may considerably contribute in a change to view biparental care from a tug-of-war interplay between the partners to cooperation between them; the idea that has recently become vivid in evolutionary ecology (Griffith, 2019).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KW-J conceived the idea and wrote the manuscript.

Funding

This study was supported by Polish National Science Centre (No: 2017/25/B/NZ8/01417).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author thank Dariusz Jakubas, Lech Stempniewicz, Marion Devogel, Martyna Cendrowska, and Nathan Sheeran for their inspirational discussions on the topic, Yuki Brooks for her overall support during the work on the manuscript, and also indebted to Peter Senn and Nathan Sheeran for improving the linguistic side of the text.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.763075/full#supplementary-material

References

Alonso-Alvarez, C., and Velando, A. (2012). “Benefits and costs of parental care,” in The Evolution of Parental Care, eds M. Kölliker, P. T. Smiseth, and N. J. Royle (Oxford: Oxford Univerity Press), 40–61. doi: 10.1093/acprof

CrossRef Full Text | Google Scholar

Balshine, S. (2012). “Patterns of parental care in vertebrates,” in The Evolution of Parental Care, eds N. Royle, P. Smiseth, and M. Kolliker (Oxford: Oxford Univerity Press), 62–80.

Google Scholar

Barta, Z., Houston, A. I., McNamara, J. M., and Székely, T. (2002). Sexual conflict about parental care: the role of reserves. Am. Nat. 159, 687–705. doi: 10.1086/339995

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, P., and Owens, I. (2002). in Evolutionary Ecology of Birds Life Histories, Mating Systems and Extinction, 1st Edn, eds P. M. Bennett and I. P. F. Owens (Oxford: Oxford University Press).

Google Scholar

Bókony, V., Lendvai, A. Z., Liker, A., Angelier, F., Wingfield, J. C., and Chastel, O. (2009). Stress response and the value of reproduction: are birds prudent parents? Am. Nat. 173, 589–598. doi: 10.1086/597610

PubMed Abstract | CrossRef Full Text | Google Scholar

Chase, I. D. (1980). Cooperative and noncooperative behavior in animals. Am. Nat. 115, 827–857. doi: 10.1086/283603

CrossRef Full Text | Google Scholar

Clutton-Brock, T. H. (1991). The Evolution of Parental Care. Princeton University Press.

Google Scholar

Clutton-Brock, T. H., and Vincent, A. C. J. (1991). Sexual selection and the potential reproductive rate of males and females. Nature 351, 58–60.

Google Scholar

Cockburn, A. (2006). Prevalence of different modes of parental care in birds. Proc. R. Soc. B Biol. Sci. 273, 1375–1383. doi: 10.1098/rspb.2005.3458

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghalambor, C. K., and Martin, T. E. (2001). Fecundity-survival trade-offs and parental parental risk-taking in birds. Science 292, 494–497.

Google Scholar

Griffith, S. C. (2019). Cooperation and coordination in socially monogamous birds: moving away from a focus on sexual conflict. Front. Ecol. Evol. 7:455. doi: 10.3389/fevo.2019.00455

CrossRef Full Text | Google Scholar

Harrison, F., Barta, Z., Cuthill, I., and Székely, T. (2009). How is sexual conflict over parental care resolved? A meta-analysis. J. Evol. Biol. 22, 1800–1812. doi: 10.1111/j.1420-9101.2009.01792.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Houston, A. I., and Davies, N. B. (1985). “The evolution of cooperation and life history in the dunnock, Prunella modularis,” in Behavioural Ecology: Ecological Consequences of Adaptive Behaviour, eds R. Sibly and R. Smith (Oxford: Blackwell), 471–487.

Google Scholar

Houston, A. I., Székely, T., and McNamara, J. M. (2013). The parental investment models of Maynard Smith: a retrospective and prospective view. Anim. Behav. 86, 667–674. doi: 10.1016/j.anbehav.2013.08.001

CrossRef Full Text | Google Scholar

Johnstone, R. A., and Hinde, C. A. (2006). Negotiation over offspring care — how should parents respond to each other’s efforts? Behav. Ecol. 17, 818–827. doi: 10.1093/beheco/arl009

CrossRef Full Text | Google Scholar

Lack, D. (1968). Ecological Adaptations for Breeding in Birds. London: Methuen & Co.

Google Scholar

Matysiokova, B., and Remeš, V. (2018). Evolution of parental activity at the nest is shaped by the risk of nest predation and ambient temperature across bird species. Evolution (N. Y) 72, 2214–2224. doi: 10.1111/evo.13580

PubMed Abstract | CrossRef Full Text | Google Scholar

McNamara, J. M., Gasson, C. E., and Houston, A. I. (1999). Incorporating rules for responding into evolutionary games. Nature 401, 368–371. doi: 10.1038/43872

CrossRef Full Text | Google Scholar

McNamara, J. M., Houston, A. I., Barta, Z., and Osorno, J. L. (2003). Should young ever be better off with one parent than with two? Behav. Ecol. 14, 301–310. doi: 10.1093/beheco/14.3.301

CrossRef Full Text | Google Scholar

McNamara, J. M., Székely, T., Webb, J. N., and Houston, A. I. (2000). A dynamic game-theoretic model of parental care. J. Theor. Biol. 205, 605–623. doi: 10.1006/jtbi.2000.2093

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakagawa, S., Gillespie, D. O. S., Hatchwell, B. J., and Burke, T. (2007). Predictable males and unpredictable females: sex difference in repeatability of parental care in a wild bird population. J. Evol. Biol. 20, 1674–1681. doi: 10.1111/j.1420-9101.2007.01403.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Owens, I. P. F., and Bennett, P. M. (1994). Mortality costs of parental care and sexual dimorphism in birds. Proc. R. Soc. B Biol. Sci. 257, 1–8.

Google Scholar

Owens, I. P. F., and Bennett, P. M. (1997). Variation in mating system among birds: ecological basis revealed by hierarchical comparative analysis of mate desertion. Proc. R. Soc. B Biol. Sci. 264, 1103–1110. doi: 10.1098/rspb.1997.0152

CrossRef Full Text | Google Scholar

Reynolds, J. D., Goodwin, N. B., and Freckleton, R. P. (2002). Evolutionary transitions in parental care and live bearing in vertebrates. Philos. Trans. R. Soc. B 357, 269–281. doi: 10.1098/rstb.2001.0930

PubMed Abstract | CrossRef Full Text | Google Scholar

Reznick, D., Nunney, L., and Tessier, A. (2000). Big houses, big cars, superfleas and the costs of reproduction. Trends Ecol. Evol. 15, 421–425. doi: 10.1016/S0169-5347(00)01941-8

CrossRef Full Text | Google Scholar

Royle, N. J., Russell, A. F., and Wilson, A. J. (2014). The evolution of flexible parenting. Science 345, 776–781. doi: 10.1126/science.1253294

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, E., and Nakagawa, S. (2012). The costs of parental care: a meta-analysis of the trade-off between parental effort and survival in birds. J. Evol. Biol. 25, 1911–1917. doi: 10.1111/j.1420-9101.2012.02569.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Schreiber, E., and Burger, J. (eds). (2002). Biology of Marine Birds. Boca Raton, FL: CRC Press.

Google Scholar

Smiseth, P. T., Dawson, C., Varley, E., and Moore, A. J. (2005). How do caring parents respond to mate loss? Differential response by males and females. Anim. Behav. 69, 551–559. doi: 10.1016/j.anbehav.2004.06.004

CrossRef Full Text | Google Scholar

Smith Maynard, J. (1977). Parental investment: a prospective analysis. Anim. Behav. 25, 1–9. doi: 10.1016/0003-3472(77)90062-8

CrossRef Full Text | Google Scholar

Trivers, R. (1972). “Parental investment and sexual selection,” in Sexual Selection and the Descent of Man, ed. B. Campbell (Chicago, IL: Aldine), 136–179.

Google Scholar

Trumbo, S. (2012). “Patterns of parental care in invertebrates,” in The Evolution of Parental Care, eds N. Royle, P. Smiseth, and M. Kolliker (Oxford: Oxford University Press), 81–100.

Google Scholar

van Noordwijk, A. J., and de Jong, G. (1986). Acquisition and allocation of resources: their influence on variation in life history tactics. Am. Nat. 128, 137–142. doi: 10.1086/284547

CrossRef Full Text | Google Scholar

Vincze, O., Székely, T., Küpper, C., AlRashidi, M., Amat, J. A., Ticó, A. A., et al. (2013). Local environment but not genetic differentiation influences biparental care in ten plover populations. PLoS One 8:e60998. doi: 10.1371/journal.pone.0060998

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, D. M., Anderson, S. E., and Olson, V. (2015). Reassessing breeding investment in birds: class-wide analysis of clutch volume reveals a single outlying family. PLoS One 10:e0117678. doi: 10.1371/journal.pone.0117678

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, T. D. (2018). Physiology, activity and costs of parental care in birds. J. Exp. Biol. 221:jeb169433. doi: 10.1242/jeb.169433

PubMed Abstract | CrossRef Full Text | Google Scholar