- 1Laboratory of Agricultural Zoology and Entomology, Department of Crop Science, Agricultural University of Athens, Athens, Greece
- 2Department of Plant Protection Products, Hellenic Ministry of Rural Development and Food, Athens, Greece
- 3School of Mathematical Sciences, University of Nottingham, Nottingham, United Kingdom
- 4School of Mathematical Sciences and Centre for Data Science, Queensland University of Technology, Brisbane, QLD, Australia
- 5Australian Research Council (ARC) Centre of Excellence for Mathematical and Statistical Frontiers, Queensland University of Technology, Brisbane, QLD, Australia
- 6Laboratory of Ecology and Environmental Science, Department of Crop Science, Agricultural University of Athens, Athens, Greece
Introduction
Functional responses describe the predator feeding rate with increasing prey density (Solomon, 1949) and are central to ecology, quantifying the energy transfer across trophic levels. Holling's approach (Holling, 1959a,b) has been the base upon which many of the critical aspects of predator-prey interactions can be detected (e.g., Abrams, 1980, 1989). The most frequently observed and widely used functional responses in describing predator-prey relationships are that of the type II and III (Jeschke et al., 2002, 2004), characterized by a curvilinear and a sigmoidal increase in feeding rate with prey abundance, respectively.
Accurate and robust approaches for quantifying functional responses are critical to the investigation of predator-prey coexistence (e.g., Aldebert and Stouffer, 2018; Uszko et al., 2020; Barraquand and Gimenez, 2021; Coblentz and DeLong, 2021). Therefore, the estimation, as well as a mechanistic understanding of the parameters that determine predator feeding behavior is of importance. In this paper, we summarize advances related to experimental design, statistical analysis, and the mechanistic interpretation of the predation process that are central to the robust quantification of functional responses and hence should be adopted broadly.
Statistical Inference
In many cases, several functional response models are fitted to experimental data using methods such as non-linear least squares optimization (e.g., Juliano and Williams, 1987; Pervez and Omkar, 2005). However, such an approach provides no information about the uncertainty around the estimates and it may well be the case that there are other plausible parameter values that offer an equally good fit. Furthermore, a frequentist approach to uncertainty quantification (most often using maximum likelihood estimation–MLE) assesses the performance of a statistical estimation procedure on the basis of the expected long-run performance given a hypothetical series of datasets collected under identical conditions. Furthermore, the methods by which the uncertainty is quantified are typically constructed under parametric assumptions of the MLEs and with increasing accuracy observed as the size of a dataset increases. However, in many cases an experimentalist will have a dataset of a fixed size and may not always be sufficiently large for these asymptotic results to hold. Novak and Stouffer (2021) have recently highlighted and demonstrated using a large compilation of public datasets that there is systematic bias in the statistical comparison of functional response models and the estimation of their parameters which are rooted in a lack of sufficient replication, or in other words, small sample sizes. Furthermore, although it is important to account and quantify the uncertainty around the model parameters, one should not ignore or forget that this is done under the assumption of a particular functional response model (e.g., Holling's Type II). However, there is also uncertainty around the structure of functional response model (e.g., Type II vs. Type III and beyond). We discuss below how one can jointly perform parameter inference and model selection within a coherent probabilistic framework.
We advocate the use of a Bayesian framework. Such an approach treats all the unknown model parameters as random variables and first assigns them a prior distribution that represents our beliefs about the unknown parameters before any experimental data are collected. This prior information is subsequently updated in light of experimental data using Bayes theorem, leading to the posterior distribution that contains all information regarding the model parameters given both the experimental data and prior knowledge.
Bayesian statistical inference is not limited to parameter estimation. We are often interested in assessing a particular scientific hypothesis related to the functional response. For example, discriminating between type II and III functional responses is a very common question, as type II functional responses are known to destabilize predator-prey dynamics, in contrast to type III (Oaten and Murdoch, 1975). A Bayesian approach to model selection treats the model itself (as well as its parameters) as unknown and hence in addition to quantifying uncertainty about the model parameters, uncertainty about the model too is also taken into account. Given a series of plausible models, representing for instance, different forms of functional response, we specify a prior distribution for each model and prior distributions for the model parameters for each model and in light of experimental data, we can then obtain posterior model probabilities which represent our beliefs. That is, having obtained experimental data, what is the chance that a particular model out of the pool of models we are considering is the true one. This can be formalized using the notion of Bayes Factors, which is a summary of the evidence provided by the data in favor of one hypothesis represented by a statistical model as opposed to another. When there are more than two different model/hypotheses considered, e.g., different types of functional response such as type I, type II or type III, then it is best to consider the posterior model probabilities to identify to what extent each model is supported by the data.
A detailed description of the proposed methodology above and its application to several functional response data can be found in Bolker (2008) and (Papanikolaou et al. 2016a,b, 2020, 2021).
Experimental Design
The previous section provides an overview of inferring model parameters and performing model selection after a dataset has been collected. However, it is often of interest to determine how best to conduct an experiment so that the resulting dataset that is collected will be most informative about the goals we are trying to achieve in an experiment, for example selecting the most appropriate model and estimating its parameters as precisely as possible. Such methods are referred to as optimal experimental design (OED, see for example Pukelsheim, 2006; Ryan et al., 2016). Formally, we define a utility function that encodes the goal of the study, and we plan an experiment that maximizes the expected utility function, i.e., the utility function averaged over all datasets that we might see for the planned experiment. By planning to collect the data in this statistically principled manner, we can reduce the amount of experimentation needed to achieve a particular statistical analysis goal, and hence reduce costs and required resources.
In OED there must be some variables that we can control in an experiment. In the context of functional response experiments, we are able to specify, for example, the initial prey density and time interval to use for an experiment. Therefore, OED tries to solve the problem of what initial prey densities and time intervals should be used such that the data collected will be as informative as possible. Once the initial prey densities and time intervals are determined, data can be collected, and the statistical inference methods in section 2 can be applied.
There are two main types of OED; static design and sequential design. In a static design, optimal input variables for all planned experiments are determined at the outset. In a sequential design, the optimal input variables for subsequent experiments are determined from the data obtained in previous experiments, by updating model structure and parameters. The sequential approach is generally more statistically efficient, since we use information from data collected sequentially to update our decisions, whereas the static design can only use information available prior to all experiments being conducted. One drawback of the sequential approach is that the overall data collection process may take longer since the experiments only take place one at a time or in small batches.
The first OED approach for functional response experiments is given in Zhang et al. (2018). The authors develop an approach to determine an optimal static design for estimating parameters of a functional response model. Here the utility function is based on the Fisher information matrix, which is one way to quantify how much information about model parameters we expect to gain from an experiment. This type of utility function assumes that maximum likelihood estimation will be performed on the data once the experiments at the optimal design are completed.
Moffat et al. (2020) develop a Bayesian sequential design method for functional response experiments. This approach allows for multiple competing functional response models, not just a single model as in Zhang et al. (2018). Here, the utility function is based on a quantity called the total entropy, which computes the expected change in posterior distributions for both model probabilities and parameters. We prefer initial prey densities that lead to larger changes in posterior distributions, as this allows us to learn more about the preferred model and its parameters with less experimentation. Through extensive simulation studies, Moffat et al. (2020) show that the Bayesian sequential design approach leads to substantially more informative data compared to a Bayesian static design and a random design where initial prey densities are generated randomly. The improvement of the sequential over the static design results from updating information about the predator-prey system to make better decisions about future experiments.
Biological Interpretation of the Handling Time
Holling defined the handling time as the time a predator spends in pursuing, subduing and eating a prey item. This definition has been extended in many studies to include digestion time. However, the time a predator spends on pursuing a prey is followed by the time of subduing and, subsequently, consuming it. Digestion is a process that is likely to occur in parallel with these activities, in the sense that a predator can digest its prey while handling it. While the processes of searching for and handling prey are mutually exclusive, digestion is not (Jeschke et al., 2002). It should be noted that some predators can search for prey while handling others. In addition, pursuing a prey often does not result in capture, as digestion prevents successful hunting in many species. This variation in components does not produce Holling's disk equation formula (Abrams, 1982; Anholt et al., 1987).
Literature suggests that the majority of functional response experiments are conducted using a time interval that digestion effects are likely to be included in the estimated handling times, i.e., the predator daily foraging cycle (e.g., Cabral et al., 2009; Jalali et al., 2010; Fathipour et al., 2018; Islam et al., 2021). Figure 1 depicts the functional response curve of a predatory ladybird beetle on its aphid prey over a 24-h time interval (data from Papanikolaou et al., 2014). We fitted the data to the disc equation, as well as the steady-state satiation (SSS) equation model presented by Jeschke et al. (2002) that incorporates Holling's original definition of handling time while explicitly accounting for satiation and digestion time through a separate parameter. Both models showed almost identical fit to the data, realistically explaining the functional response of the predator. We also fitted the two models assuming handling was known, i.e., the handling time obtained from short-term functional response experiments, so that digestion effects are largely excluded. In this case, the disc equation does not appear to explain the functional response of the predator well. Therefore, in experimental procedures where digestion acts in parallel with prey handling (long term experiments), the interpretation of the “handling time” (Th) estimated by the disc equation must be limited to the calculation of maximum attack rate (T/Th), i.e., the maximum number of prey that can be consumed by a predator during the time interval (T) considered.
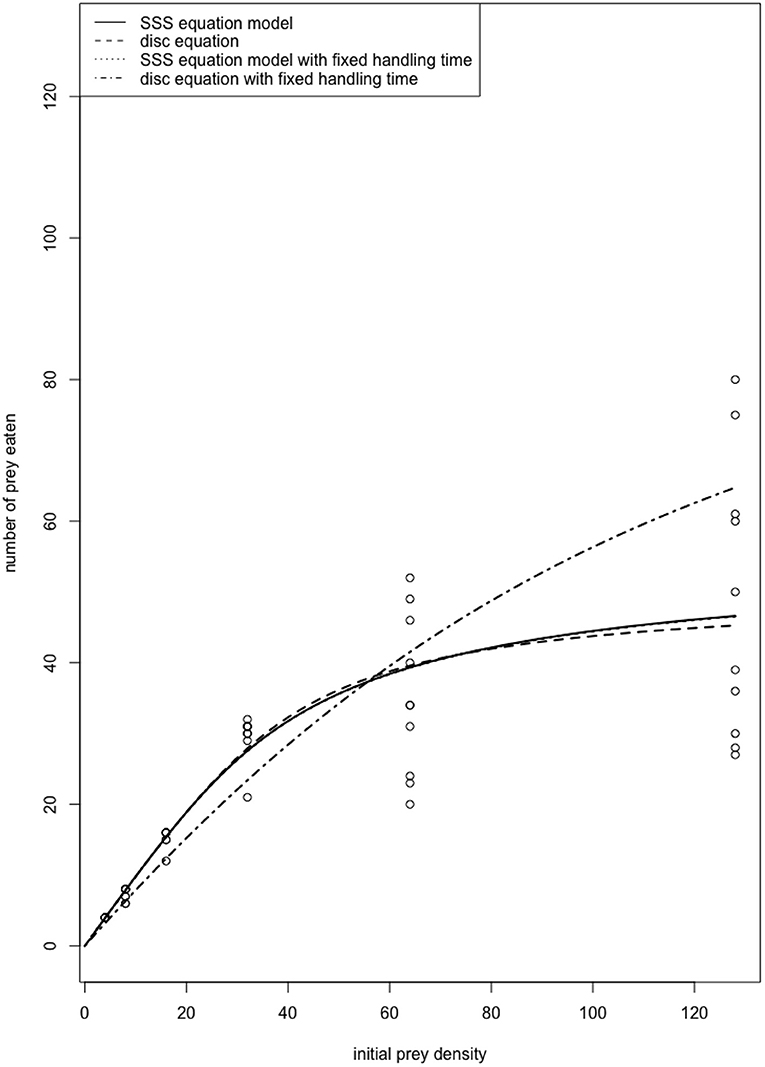
Figure 1. Functional response of the ladybird beetle Propylea quatuordecimpunctata (Coleoptera: Coccinellidae) male adults on Aphis fabae (Hemiptera: Aphididae). The fitted curves of the SSS equation with and without fixed handling time are indistinguishable. Also, the SSS equation reduces to the disc equation when there is no satiation (c = 0). Therefore, when a fixed handling time that is determined through separate short-term experiments thus excluding digestion effects is used, the disc equation no longer performs well for modeling consumption rates observed over a longer time period because the model does not take satiation into account.
Conclusions
Over half a century after its conceptualization, predator functional responses remain a core feature in ecology. Recently, Novak and Stouffer (2021) revealed that bias in model comparison, as well as in parameter estimation are common in functional response studies, mainly attributed to the relatively small sample sizes used. OED has great potential for conducting more efficient functional response experiments. In addition, Bayesian inference enables the quantification of model and parameter uncertainty in a coherent, probabilistic manner, through the use of probability distributions.
Our understanding of predation could be further improved by elucidating the components of handling time. For example, Sentis et al. (2013) revealed that the processes of handling and digesting prey have different thermal responses. However, most functional response models incorporate handling time in a way that does not permit a biological interpretation, combining handling and digestion time (Jeschke et al., 2002). Although several modeling approaches has been presented (e.g., Mills, 1982; Abrams, 1990), using the SSS equation model would permit a mechanistic interpretation of these components of the predation process (Papanikolaou et al., 2020).
In conclusion, we advocate for the adoption of OED, a Bayesian framework, and the use of the SSS equation to efficiently and robustly infer predator functional responses moving forward. We anticipate that OED in conjunction with Bayesian inference will improve the predictive power of functional response experiments and reduce the logistical burden. Furthermore, as the comprehension of predator feeding behavior can be improved discriminating different predation processes such as handling and digestive prey, we call for the application of the SSS equation in functional response studies, which can lead to a better understanding of predator-prey interactions.
Author Contributions
NP, AF, and DP provided ecological expertise. CD, TK, and HM provided statistical expertise. All authors contributed to the article and approved the submitted version.
Funding
CD was supported by an Australian Research Council Discovery Project (DP200102101).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abrams, P. A. (1980). Consumer functional response and competition in consumer-resource systems. Theor. Popul. Biol. 17, 80–102. doi: 10.1016/0040-5809(80)90016-7
Abrams, P. A. (1982). Functional responses of optimal foragers. Am. Nat. 120, 382–390. doi: 10.1086/283996
Abrams, P. A. (1989). Decreasing functional responses as a result of adaptive consumer behavior. Evol. Ecol. 3, 95–114. doi: 10.1007/BF02270915
Abrams, P. A. (1990). The effects of adaptive behavior on the type-2 functional response. Ecology 71, 877–885. doi: 10.2307/1937359
Aldebert, A., and Stouffer, D. B. (2018). Community dynamics and sensitivity to model structure: towards a probabilistic view of process-based model predictions. J. R. Soc. Interface 15:20180741. doi: 10.1098/rsif.2018.0741
Anholt, B. R., Ludwig, D., and Rasmussen, J. B. (1987). Optimal pursuit times: How long should predators pursue their prey? Theor. Popul. Biol. 31, 453–464. doi: 10.1016/0040-5809(87)90015-3
Barraquand, F., and Gimenez, O. (2021). Fitting stochastic predator–prey models using both population density and kill rate data. Theor. Popul. Biol. 138, 1–27. doi: 10.1016/j.tpb.2021.01.003
Cabral, S., Soares, A. O., and Garcia, P. (2009). Predation by Coccinella undecimpunctata L. (Coleoptera: Coccinellidae) on Myzus persicae Sulzer (Homoptera: Aphididae): effect of prey density. Biol. Contr. 50, 25–29. doi: 10.1016/j.biocontrol.2009.01.020
Coblentz, K. E., and DeLong, J. P. (2021). Estimating predator functional responses using the times between prey captures. Ecology 102:e03307. doi: 10.1002/ecy.3307
Fathipour, Y., Karimi, M., Farazmand, A., and Talebi, A. A. (2018). Age-specific functional response and predation capacity of Phytoseiulus persimilis (Phytoseiidae) on the two-spotted spider mite. Acarologia 58, 31–40. doi: 10.24349/acarologia/20184225
Holling, C. S. (1959a). The components of predation as revealed by a study of small mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320. doi: 10.4039/Ent91293-5
Holling, C. S. (1959b). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398. doi: 10.4039/Ent91385-7
Islam, Y., Shah, F. M., Rubing, X., Razaq, M., Yabo, M., Xihong, L., et al. (2021). Functional response of Harmonia axyridis preying on Acyrthosiphon pisum nymphs: the effect of temperature. Sci. Rep. 11:13565. doi: 10.1038/s41598-021-92954-x
Jalali, M. A., Tirry, L., and De Clercq, P. (2010). Effect of temperature on the functional response of Adalia bipunctata to Myzus persicae. BioControl 55, 261–269. doi: 10.1007/s10526-009-9237-6
Jeschke, J. M., Kopp, M., and Tollrian, R. (2002). Predator functional responses: discriminating between handling and digesting prey. Ecol. Monogr. 72, 95–112. doi: 10.1890/0012-9615(2002)072[0095:PFRDBH]2.0.CO;2
Jeschke, J. M., Kopp, M., and Tollrian, R. (2004). Consumer-food systems: why type I functional responses are exclusive to filter feeders. Biol. Rev. 79, 337–349. doi: 10.1017/S1464793103006286
Juliano, S. A., and Williams, F. M. (1987). A comparison of methods for estimating the functional response parameters of the random predator equation. J. Anim. Ecol. 56, 641–653. doi: 10.2307/5074
Mills, N. J. (1982). Satiation and the functional response: a test of a new model. Ecol. Entomol. 7, 305–315. doi: 10.1111/j.1365-2311.1982.tb00671.x
Moffat, H., Hainy, M., Papanikolaou, N. E., and Drovandi, C. (2020). Sequential experimental design for predator-prey functional response experiments. J. R. Soc. Interface 17:20200156. doi: 10.1098/rsif.2020.0156
Novak, M., and Stouffer, D. B. (2021). Systematic bias in studies of consumer functional responses. Ecol. Lett. 24, 580–593. doi: 10.1111/ele.13660
Oaten, A., and Murdoch, W. W. (1975). Functional response and stability in predator-prey systems. Am. Nat. 109, 289–298. doi: 10.1086/282998
Papanikolaou, N. E., Broufas, G. D., Papachristos, D. P., Pappas, M. L., Kyriakaki, C. h., Samaras, K., et al. (2020). On the mechanistic understanding of predator feeding behavior using the functional response concept. Ecosphere 11:e03147. doi: 10.1002/ecs2.3147
Papanikolaou, N. E., Demiris, N., Milonas, P. G., Prston, S., and Kypraios, T. (2016b). Does mutual interference affect the feeding rate of aphidophagous coccinellids? a modeling perspective. PLoS ONE 11:e0146168. doi: 10.1371/journal.pone.0146168
Papanikolaou, N. E., Dervisoglou, S., Fantinou, A., Kypraios, T., Giakoumaki, V., et al. (2021). Predator size affects the intensity of mutual interference in a predatory mirid. Ecol. Evol. 11, 1342–1351. doi: 10.1002/ece3.7137
Papanikolaou, N. E., Milonas, P. G., Demiris, N., Papachristos, D. P., and Matsinos, Y. G. (2014). Digestion limits the functional response of an aphidophagous coccinellid (Coleoptera: Coccinellidae). Ann. Entomol. Soc. Am. 107, 468–474. doi: 10.1603/AN13088
Papanikolaou, N. E., Williams, H., Demiris, N., Preston, S. P., Milonas, P. G., and Kypraios, T. (2016a). Bayesian inference and model choice for Holling's disc equation: a case study on an insect predator-prey system. Com. Ecol. 17, 71–78. doi: 10.1556/168.2016.17.1.9
Pervez, A., and Omkar (2005). Functional responses of coccinellid predators: an illustration of a logistic approach. J. Insect Sci. 5:5. doi: 10.1673/031.005.0501
Pukelsheim, F. (2006). Optimal Design of Experiments. Philadelphia, PA: Society for Industrial and Applied Mathematics.
Ryan, E. G., Drovandi, C. C., McGree, J., and Pettitt, A. N. (2016). A review of modern computational algorithms for bayesian optimal design. Int. Stat. Rev. 84, 128–154. doi: 10.1111/insr.12107
Sentis, A., Hemptinne, J.-L., and Brodeur, J. (2013). Parsing handling time into components: implications for responses to a temperature gradient. Ecology 94, 1675–1680. doi: 10.1890/12-2107.1
Solomon, M. E. (1949). The natural control of animal populations. J. Anim. Ecol. 18, 1–35. doi: 10.2307/1578
Uszko, W., Diehl, S., and Wickman, J. (2020). Fitting functional response surfaces to data: a best practice guide. Ecosphere 11:e03051. doi: 10.1002/ecs2.3051
Keywords: Bayesian inference, optimal experimental design, handling time, disc equation, mechanistic understanding
Citation: Papanikolaou NE, Kypraios T, Moffat H, Fantinou A, Perdikis DP and Drovandi C (2021) Predators' Functional Response: Statistical Inference, Experimental Design, and Biological Interpretation of the Handling Time. Front. Ecol. Evol. 9:740848. doi: 10.3389/fevo.2021.740848
Received: 13 July 2021; Accepted: 04 October 2021;
Published: 29 October 2021.
Edited by:
Dennis Murray, Trent University, CanadaCopyright © 2021 Papanikolaou, Kypraios, Moffat, Fantinou, Perdikis and Drovandi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nikos E. Papanikolaou, bmlrb3NwQGF1YS5ncg==
 Nikos E. Papanikolaou
Nikos E. Papanikolaou Theodore Kypraios
Theodore Kypraios Hayden Moffat4,5
Hayden Moffat4,5 Dionysios P. Perdikis
Dionysios P. Perdikis Christopher Drovandi
Christopher Drovandi