Modelling the Efficacy of Febrile Heating in Infected Endotherms

Fever is a response to infection characterised by an increase in body temperature. The adaptive value of this body temperature increase for endotherms is unclear, given the relatively small absolute temperature increases associated with endotherm fever, its substantial metabolic costs, and the plausibility for pathogens to adapt to higher temperatures. We consider three thermal mechanisms for fever's antimicrobial effect: (1) direct growth inhibition by elevating temperature above the pathogens optimal growth temperature; (2) further differentiating the host body from the wider environment; and (3) through increasing thermal instability of the pathogen environment. We assess these by modelling their effects pathogen on temperature dependent growth, finding thermal effects can vary from highly to minimally effective depending on pathogen species. We also find, depending on the specification of a simple physical model, intermittent heating can inhibit pathogen growth more effectively than continuous heating with an energy constraint.

1. Introduction

Fever is a response to infection characterised by an increase in temperature. Whether (and how) this response benefits the infected organism is unclear.

1.1. The Heating Hypothesis

One plausible mechanism of how fever is a beneficial host response to infection is that elevated body temperature has a direct antimicrobial effect (Casadevall, 2016). Pathogens are sensitive to the temperature of their environment. Fever, by heating the host body, alters the temperature of the pathogen environment, and inhibits pathogen growth.

There are three distinct mechanisms altering temperature can inhibit pathogen growth. One is a direct effect: If a pathogen grows optimally at a given absolute temperature, raising this temperature results in sub-optimal pathogen growth. The second is environmental filtering: Fever may also confer benefit by the difference in host body temperature from the wider environment. The elevated body temperature of the host body makes it a distinct ecological niche, which pathogens adapted to prevailing environmental temperatures are disadvantaged. The third is dynamic variation: Fever increases the thermal instability of the host body: no matter which temperature a pathogen grows optimally at, this variability means it endures periods of sub-optimal growth.

The heating hypothesis can draw on a large body of circumstantial evidence for ectotherms (Thomas and Blanford, 2003; Richards-Zawacki, 2010; Mohammed et al., 2016; Rakus et al., 2017). Fungal pathogens provide the clearest example. Almost all fungal pathogens share a similar pattern of temperature dependent growth: very few species grow effectively when temperatures rise above 30°C (Robert and Casadevall, 2009). Fungal pathogens inflict relatively little disease in non-hibernating endotherms (whose body temperatures are higher than 30°C), but much more in ectotherms or hibernating endotherms during their hibernation period. Increasing the body temperature of animals infected with prevalent fungal pathogens, either by placing them in a warm environment (Woodhams et al., 2003) or terminating hibernation (Meteyer et al., 2011) is sufficient to clear many fungal infections. These observations have also prompted the hypothesis that a major evolutionary driver for endothermy are these anti-fungal protective effects (Robert and Casadevall, 2009).

1.2. The Challenge of Fever in Endotherms

The heating hypothesis is less persuasive for fever in endothermic organisms. The principal challenge is the limited temperature increase of fever. In humans, a fever is classified as a temperature greater than 37.5–38°C (with ‘normal’ body temperature as 37.0°C), and temperatures increasing above 40°C are cause for increasing clinical concern. These small absolute increases make the mechanisms outlined above less plausible.

First, there is little reason to believe non-fungal pathogen species have similarly hard ceilings on their maximum (or optimum) growth temperature: many bacterial species out-range eukaryotes (leave alone animals) with respect to high-temperature extremophilia. For endotherms, their non-febrile temperatures tend to be already too hot for fungal pathogens to tolerate, yet they cannot themselves survive body temperatures which would prohibit non-fungal pathogen growth. Second, the small absolute difference in temperature an endotherm's fever can generate also challenges a significant environmental filtering effect. Intuitively, if a pathogen can adapt to grow optimally at 37°C, adapting to a temperature a couple of degrees higher seems unlikely to be a significant further obstacle. Third, an endotherm's body is typically a very temperature stable environment, especially when compared to ectotherm bodies and many environments free-living organisms inhabit. Fever in endotherms, with its small absolute changes, does not add enough variation to change this overall picture.

Across the scales from uncertainties as to how fever benefits an endotherm, there are clear costs. The most salient is energetic: fever is estimated to have an additional energetic cost of between 10 and 30% of basal metabolic rate in humans (Du Bois, 1921; Buskirk et al., 1964; Baracos et al., 1987; Benhariz et al., 1997).

Direct evidence on the benefit of fever in endotherms is also equivocal (Banet, 1986). In some animal studies, inducing fever in infected mammals can enhance survival, and inhibiting it can reduce survival (Small et al., 1986; Eyers et al., 2010); yet in others, the opposite effect is observed (Klastersky, 1972). Clinical observational studies in humans are also mixed, with varying direction of association between height of fever and anti-pyretic administration on survival (Hasday and Garrison, 2000).

A key challenge in interpretation is fever is not only an increase in body temperature, but elaborated with a panoply of immunological and behavioural changes (Hasday et al., 2011; Evans et al., 2015). Both observational and experimental approaches therefore struggle both to isolate and manipulate body temperature independently from the wider febrile response, and also to attribute any beneficial effects of fever to thermal effects in particular, vs. other effects for which the increase in temperature may be a mediator or confounder.

Thus, opinion is divided on whether fever is an effective host response for endotherms (Haahr and Mogensen, 1978; Kluger et al., 1998; Mackowiak, 2000; Blatteis, 2003). Clinically, fever—even in the context of infection—is typically treated by anti-pyretics by medical staff for their patients (Kiekkas et al., 2014), and parents for their children (Walsh et al., 2007), implying an overall judgement fever is not beneficial. It was not always so: inducing fever as a therapeutic intervention for particular infections was practised in the pre-antibiotic era (Simpson, 1936). ‘Abnormal’ body temperatures can be a therapeutic target in the management of some critical illnesses (e.g., therapeutic hypothermia in cardiac arrest), and there is a renewed interest in ‘thermal therapy’ (either localised or systemic) as a possible adjunct treatment for infectious diseases given the challenge of antimicrobial resistance (Gazel and Yılmaz, 2018; Skok et al., 2021).

1.3. Hypotheses for Endotherm Fever

We can distinguish a few alternative explanations for the evolution and adaptive value for fever in endotherms.

The heating hypothesis. Even if heating is a less effective means of host defence for endotherms than ectotherms, may still exert some antimicrobial effect. These benefits, even if smaller than in ectotherms, may still be worth their metabolic costs, and so remain adaptive.

Fever is adaptive, but heating plays an indirect role. Elevated body temperature may no longer provide an important direct antimicrobial action in endotherms, but retains adaptive value by inducing other responses which do. On this hypothesis, fever may be an exaptation: although directly antimicrobial for ectothermic ancestors, in endotherms it now serves an indirect role orchestrating an effective immune response.

Even if temperature elevation is a key stimulator of innate immune responses to infection, it may be an inefficient one. Raising temperature across the entire body seems a less energy-efficient signal than synthesising an interleukin: in principle, the energy of heating will be distributed across the entire body rather than targeted to the receptors; in practise, it is hard to imagine biosynthesis of a single protein could comprise 10–30% of basal metabolic rate. Yet even if so, the ancestral reliance on temperature to provide this signal during the evolutionary history of the organism makes it impossible to replace.

Fever is generally maladaptive A trait that was once adaptive but now maladaptive may be conserved if reversing it poses a fitness penalty. In host-pathogen co-evolution, immune adaptions could be beneficial for host individuals before they reach fixation in the host population, maladaptive after they reach fixation (and subsequent pathogen counter-adaptation), yet host individuals who reverse the adaptation are selected against, and thus the adaptation is stably maintained.

Temperature elevation as a credible signal in host-pathogen co-evolution. As fever is metabolically costly, an increased body temperature is an honest signal both of immune activation and risk of the host dying from infection. This signal is perceptible in the pathogen environment. Pathogens may face a trade-off between intensity and duration of infection (Alizon et al., 2009), some pathogen reproductive strategies could be enhanced by reduction in growth at febrile temperatures, as this may favour longer infections and greater fitness overall.

Thus, fever could benefit the host indirectly. By providing a honest signal to the pathogen, the host exerts selection pressure for pathogens pursuing prolonged infection strategies to respond to the signal of fever with reduced growth. As this response also enhances host fitness alongside pathogen fitness, responsive pathogens also exert selection pressure on the host species to preserve this honest signalling mechanism.

1.4. Motivation and Aims

Whether (and when) fever is beneficial is important in two respects. The first is clinical relevance. If fever is broadly beneficial for endotherms like humans, then the common practise of administering anti-pyretics could be unwise. For fevers which arise from infection and where the fever itself is not a threat to health, anti-pyrexials could worsen the course of the infection. Further, it suggests inducing fever, as was done in the pre-antibiotic era, may be a useful adjunct therapy for infectious disease worthy of renewed consideration.

The second is fever can be a useful test case for exploring host-pathogen co-evolutionary conflict. It is typically challenging to infer the original benefit or current value of a given adaptation when observing it after the fact of protracted host and pathogen adaptation and counter-adaptation.

This challenge is compounded by the 'ground truth' of fitness difference attributable to the adaption being near-impossible to observe directly, and challenging to isolate experimentally. Febrile heating is a promising target for theoretical approaches, as crisp (albeit imperfect) measures of fitness costs of changing temperature for both host and pathogen are accessible in terms of calorimetry and growth rates, respectively.

Here, we investigate temperature dependent growth to assess the utility of heating as mechanism of fever in endotherms using a set of mathematical models. First, we conduct a static analysis of how growth deteriorates for microbial pathogens as temperature is elevated above body temperature, comparing this to host metabolic investment in maintaining these temperature increases. Second, we assess how valuable additional thermal differentiation from the environment could be. Third, we investigate the idea that the variation in temperature that inducible fever provides poses an intrinsic cost on the pathogen no matter its coevolutionary response to this source of thermal instability, and evaluate the magnitude of this effect as a coevolutionary stable strategy. Finally, we construct a simple physical model of heating, to compare the energy efficiency of intermittent vs. continuous heating for inhibiting pathogen growth.

2. Modelling Temperature Dependent Growth

The archetype of a microbial temperature dependent growth curve is growth rising beyond a minimum growth temperature T_min, reaching an optimal growth temperature T_opt, and then a steep decline from this optimum to a maximum growth temperature T_max (Figure 1). This archetypal shape is widely observed across microbial organisms [e.g., phytoplankton (Grimaud et al., 2017), bacteriophages (Padfield et al., 2020), and fungi (Smits et al., 2003)]; we are unaware of any exceptions among pathogenic microbes.

FIGURE 1

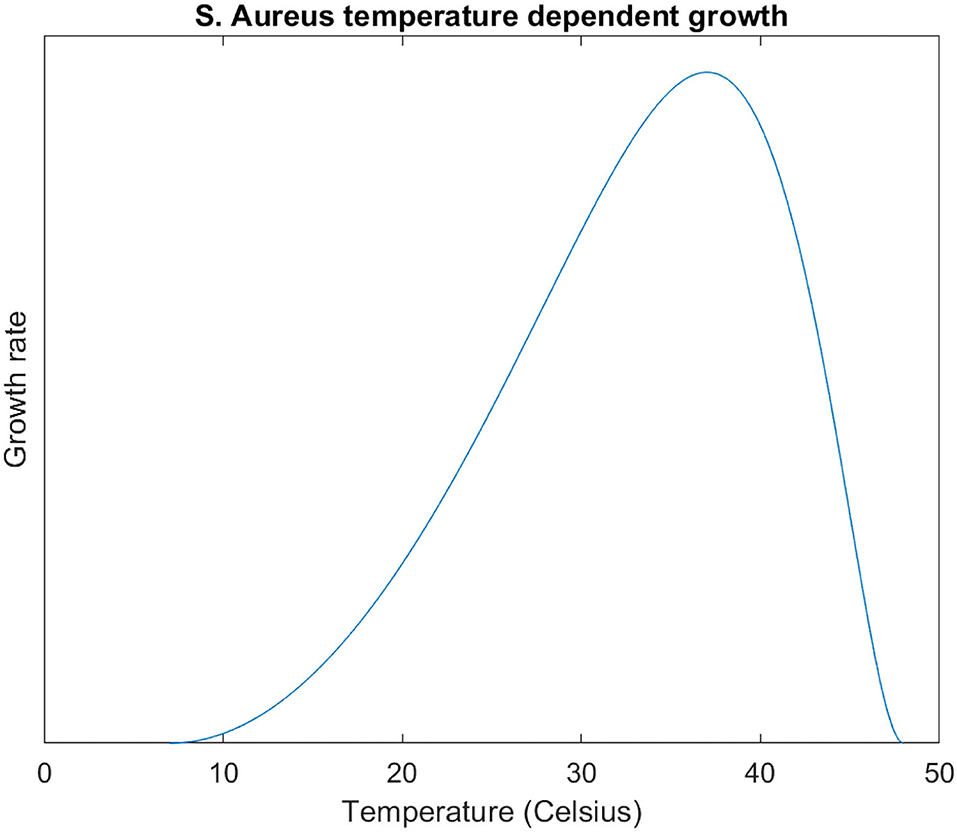
Figure 1. S. Aureus growth curve ($T_{min}=7^{°}C$, $T_{opt}=37^{°}C$, $T_{max}=48^{°}C$) modelled with the modified Ratkowsky equation ($\sqrt{r}=(T-T_{min})·(1-e^{0.16·(T-T_{max})})$. Equation plotted in the domain T_min ≤ T ≤ T_max.

By elevating body temperature, the host inflicts an energetic cost to the pathogen, by inhibiting its growth, and to itself, by increasing its metabolic rate. In this conflict, the strategy of elevating body temperature seems more effective the more disproportionate the costs are for the pathogen than for itself.

Energetic costs to the host of elevating temperature scale linearly with ΔT, given the heat transfer equation:

$\begin{array}{ll}Q=h·A·\Delta T& (1)\end{array}$

Where Q is the energy flux, h is the coefficient of heat transfer, A the surface area, and ΔT the difference in temperature.

There are a variety of mathematical models for temperature dependent growth inhibition and inactivation in microorganisms (Gil et al., 2017). Some are more empirically-driven, whilst others are theory-led. These models nonetheless share steep and non-linear (typically exponential) declines in growth as temperature exceeds T_opt. For example, the modified Ratkowsky equation (Ratkowsky et al., 1983):

$\begin{array}{ll}\sqrt{r}=b·(T-T_{min})·(1-e^{(c·(T-T_{max}))})& (2)\end{array}$

Where r is the growth rate, b a scaling parameter, and c a constant. For this equation, the growth rate penalty to the pathogen scales approximately ∝ e^ΔT as T increases above T_opt.

A strategy where costs scale linearly for the host but exponentially for the pathogen would be an effective host strategy if the host could increase its temperature without limit. Yet endotherms tend to be less thermally tolerant than their pathogens. For body temperature increases tolerable to the host, the impact on pathogen growth could be much more modest.

Although human pathogens have optimal temperatures around 37°C, they substantially vary in their T_max. We take two exemplars: S. dysenteriae has a T_max of 40°C, in the range human fever can reach; E. coli has a T_max of 45°C, much higher than safe limits on human body temperature (Altman and Dittmer, 1972). We would therefore expect S. dysenteriae to be more 'fever-sensitive' than E. coli, with its growth inhibited more at febrile temperatures.

To assess this quantitatively, we model the temperature-dependent growth of each pathogen by fitting the modified Ratkowsky equation to the observed values of T_min, T_max, and T_opt, for each pathogen finding the c coefficient numerically by computing T_opt for 0 ≤ c ≤ 2 in increments of 0.001, selecting the value of c for which T_opt is closest to 37°C. For S. dysenteriae, c is 1.247; for E. coli, c is 0.260. For S. dysenteriae, the modelled growth equation is:

$\begin{array}{ll}\sqrt{r}=(T-4)·(1-e^{1.247·(T-40)})& (3)\end{array}$

And for E. coli, it is:

$\begin{array}{ll}\sqrt{r}=(T-10)·(1-e^{0.260·(T-45)})& (4)\end{array}$

These curves are plotted in Figure 2. We calculate from these equations the relative growth (where 1 is the optimal growth rate) at febrile temperatures (Table 1). Febrile temperatures inhibit S. dysenteriae much more effectively than E. coli. Not only at 40°C (the T_max for S. dysenteriae, where E. coli still grows at 85% of its optimal growth, but also at milder fevers: a ‘high fever’ of 39°C almost halves S. dysenteriae growth, but reduces E. coli growth by 6%.

FIGURE 2

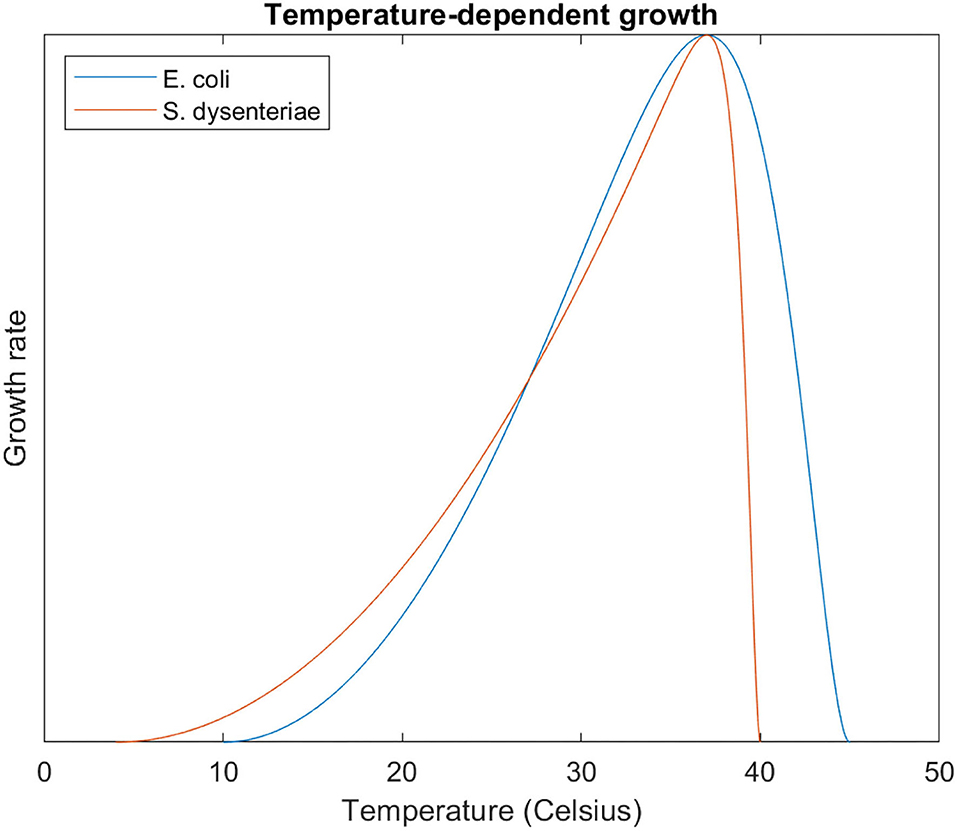
Figure 2. S. dysenteriae and E. coli temperature dependent growth curves, modelled with the modified Ratkowsky equation. Note the much steeper relative decline in growth for S. dysterentiae at temperatures > 37°C.

TABLE 1

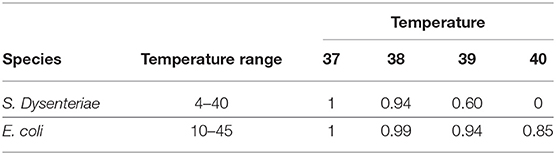
Table 1. Relative growth (T_opt = 1) at febrile temperatures for S. dysenteriae and E. coli, modelled with the Ratkowsky equation.

The plausibility of a direct thermal effect is much more credible for S. dysenteriae than E. coli. The substantial metabolic cost to the host of heating its body is much more easily justified when this inflicts substantial or complete growth inhibition (S. dysenteriae) compared to when this inhibition is very mild (E. coli), and could only become significant at body temperatures which are life-threatening to the host in their own right.

Many human pathogens, like S. dysenteriae, are sensitive to febrile temperatures (e.g., N. gonorrhoeae, S. typhi); and many human pathogens, like E. coli, are resistant to them (e.g., S. Aureus, V. comma). Thus the direct efficacy of febrile heating may depend on the pathogen causing the infection.

3. Marginal Environmental Filtering

As endotherms are commonly already warmer than their environment, a further elevation in body temperature through fever may have much greater effect restricting growth of pathogens adapted to environmental temperature than those adapted to body temperature. At the extreme, febrile temperatures above a pathogen's T_max thermally exclude it. The steep decline in growth above T_opt but below T_max means that small temperature increases in this range can have a out-sized effect in inhibiting pathogen growth.

To examine this, we construct a hypothetical scenario of a pathogen adapted to an environment of 37°C, with an identical temperature dependent growth curve to E. coli. We then consider endotherms with body temperatures higher than this environment, and then assess the relative impact on microbial growth of a fever which elevates body temperature further still. For example, the marginal effect of a 2°C fever for a host with a body temperature of 38°C is the value of the growth curve at T = 40°C divided by the value of the growth curve at T = 38°C: 0.87, corresponding to 13% growth inhibition (vs. 6% for a 2° temperature increase from 37 to 39°C.

For 37°C ≤ T ≤ 43°C, in the model, the equation for the relative growth of a 2°C further increment is given by:

$\begin{array}{ll}\frac{r(T+2)}{r(T)}=\frac{{((T-8)·(1-e^{(0.260·(T-43)}))}^2}{{((T-10)·(1-e^{(0.260·(T-45)}))}^2}& (5)\end{array}$

We plot this curve (alongside those for a 1 degree and 3 degree increase) in Figure 3. With increasing body temperature, the additional increment exerts a greater relative reduction in pathogen growth. At the extreme, this gives complete thermal restriction (relative growth = 0) when the sum of body temperature and increment equals T_max (44, 43, and 42°C for 1–3°C fevers, respectively).

FIGURE 3

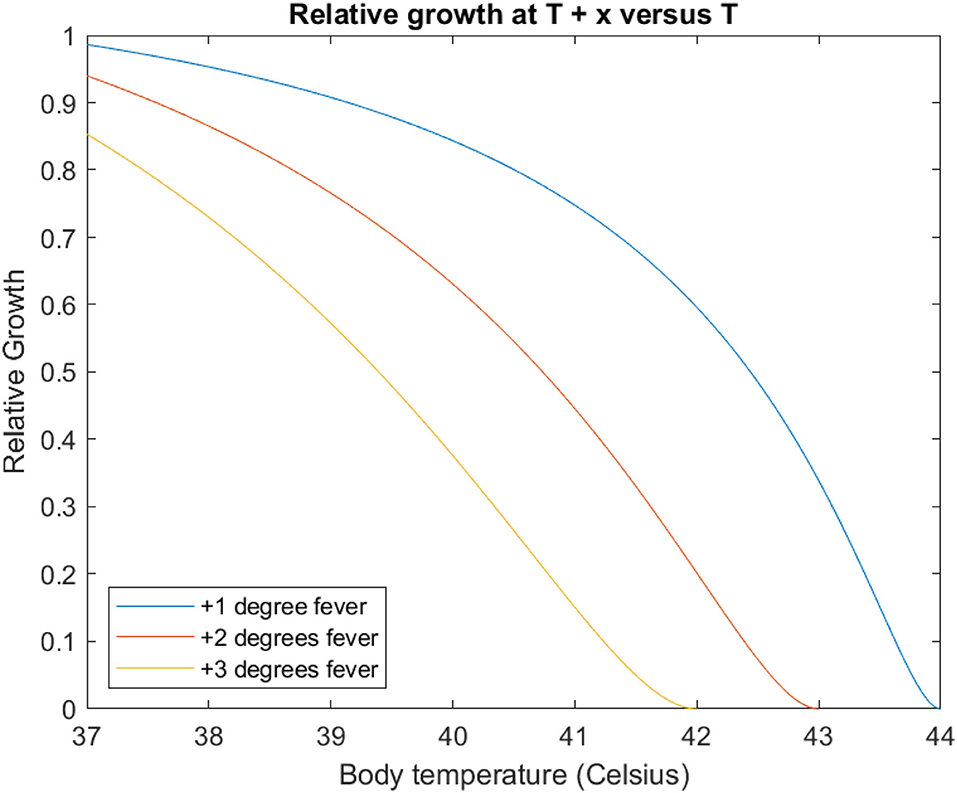
Figure 3. Each curve gives the relative ratio of growth rate at T+x°C (blue 1°C, red 2°C, yellow 3°C vs. a body temperature of T, modelled with the E. coli temperature-dependent growth curve. For example, the leftmost point of each curve corresponds to the impact of raising temperatures at 37°C of 0.99, 0.94, and 0.85, respectively, (cf. Table 1). Note each curve reaches zero when T + x = T_max.

However, as body temperature climbs further, the returns of incremental febrile heating diminish as it becomes increasingly redundant for environmental filtering. In our scenario a host with an (afebrile) body temperature greater than 45°C already thermally excludes the pathogen without any additional febrile heating.

In essence, these potential environmental filtering benefits of fever only apply to a narrow range of host body temperatures where the host body is somewhat (but not greatly) hotter than the environment: if Body Temperature >T_max, febrile heating is redundant. In the modelling scenario, this narrow range is for body temperatures < 8°C warmer than the 37°C environment. Endotherm body temperatures of 35–40°C are more than 20°C greater than mean global temperature, and few microbes have T_max > (T_opt + 10). This suggests ecological contexts where fever exerts a significant additional environmental filtering effect for endotherms are uncommon.

4. Dynamic Temperature Variation as a Robust Thermal Strategy

Even if a pathogen can adapt to grow optimally at any given temperature, optimal growth across a range of temperatures results in slower growth vs. a single temperature. Thus, fever may benefit the host through introducing thermal instability into the pathogen environment. Such a mechanism may only be incompletely mitigated by pathogen co-evolution, and so could prove a beneficial thermal strategy for the host robust to pathogen counter-adaptation.

To investigate, we consider the average growth ($\bar{r}$) over a range of temperatures: this would amount to the average of the growth at these temperatures, weighted by the proportion of time the pathogen spends at these temperatures. In the simplest case where this time is uniformly distributed over a continuous temperature interval, $\bar{r}$ is the average height of the function across this interval (analytically, the definite integral divided by the width of the interval).

To isolate dynamic variation effects from direct effects we consider the maximum $\bar{r}$ that can be achieved for a temperature range k: for an interval of width k, what value of T gives the greatest definite integral between T and T + k for the temperature dependent growth curve.

We then analyse the relationship between $\bar{r}$ and k: as the variation in temperature increases, how much does average growth fall.

To make this analysis more tractable, we replace the Ratkowsky equation with a gamma distribution function (Gamma(2, 1), $y=\frac{x·e^{-x}}{2}$), which is algebraically simpler and can approximate Ratkowsky growth curves when reflected, stretched and scaled (Figure 4). In terms of this new function $y=\frac{x·e^{-x}}{2}$, the point (0, 0) is the pathogen T_max, and positive values of x correspond to temperatures below T_max: the point (1, 2e), the maxima for the function, corresponds to T_opt, which is lower in temperature than T_max by one arbitrary unit.

FIGURE 4

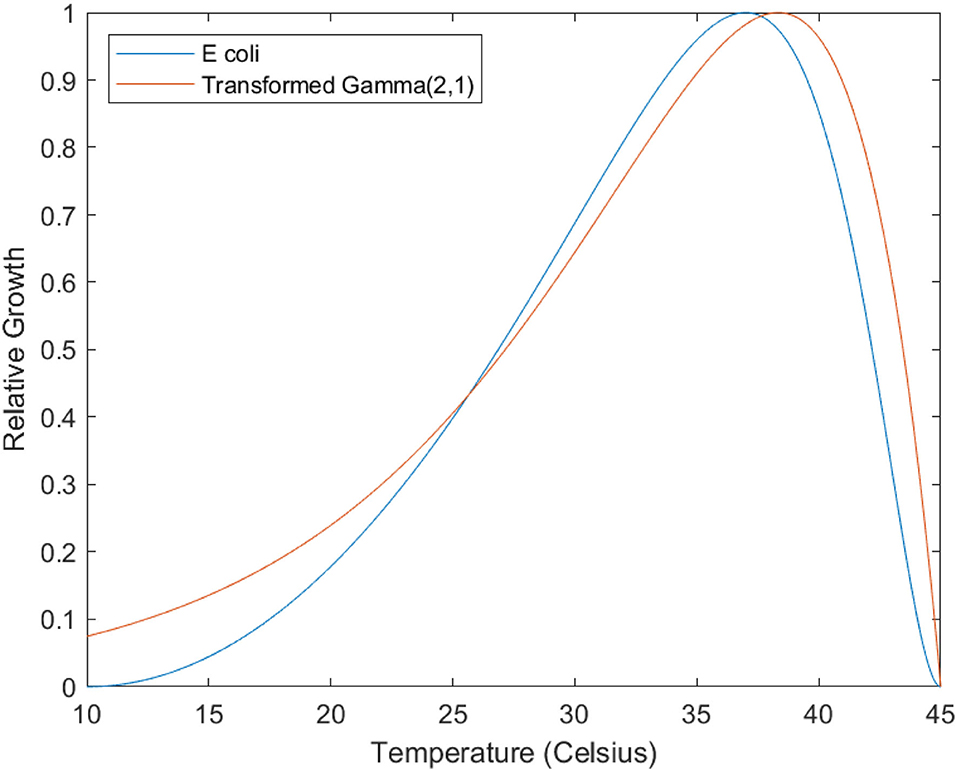
Figure 4. Illustrating similarity between Ratkowsky equation and Gamma distributions. The blue line is the modelled growth curve for E Coli (see Equation 4). The red line is a reflected, scaled, and stretched Gamma (2,1) distribution, the equation being r = 0.15(45 − t)·e ^{− 0.15(45−t)}·e. The fit is approximate, but serves to illustrate the fundamental similarity in shape between these two families of functions.

To find the maximum $\bar{r}$ that can be achieved for a temperature range k, we find the maxima of the definite integral of this function between T and T + k:

$\begin{array}{l}\frac{\text{d}}{\text{d}T}\left[{\displaystyle {\int }_T^{T+k}}\frac{T·e^{-T}}{2}\text{d}T\right]=\frac{(T+k)·e^{-(T+k)}}{2}-\frac{T·e^{-T}}{2}\\ =e^{-k-T}\left(\frac{k}{2}+T\left(\frac{1-e^k}{2}\right)\right)& (6)\end{array}$

This equation has a single root at $T=\frac{k}{e^k-1}$; k > 0. As the interval k increases, T decreases, and ${\lim }_{k\to 0^{+}}(T)=1$. In more concrete terms, for a uniform temperature distribution across an interval of k units, the highest $\bar{r}$ is observed when the upper limit of this range is $\frac{k}{e^k-1}$ units lower than T_max.

The value of this maximum $\bar{r}$ for an interval of k is given by taking the integral with these bounds, and dividing by the interval width k:

$\begin{array}{ll}\overline{r}=\left[{\displaystyle \underset{\frac{k}{e^k-1}}{\overset{\frac{k}{e^k-1}+k}{\int }}\frac{T·e^{-T}}{2}\text{d}T}\right]/k=\frac{(e^k-1)·e^{\frac{e^k·k}{1-e^k}}}{2k}& (7)\end{array}$

These values can be normalised by dividing by the maxima of this function ($\frac{1}{2e}$). Normalised $\bar{r}$ is plotted against k in Figure 5. This shows a sigmoidal response of $\bar{r}$ with increasing k: the reduction in average growth is initially small, accelerates, and tends to complete restriction at the extreme ranges of temperature variation (${\lim }_{k\to \infty }(\overline{r})=0$).

FIGURE 5

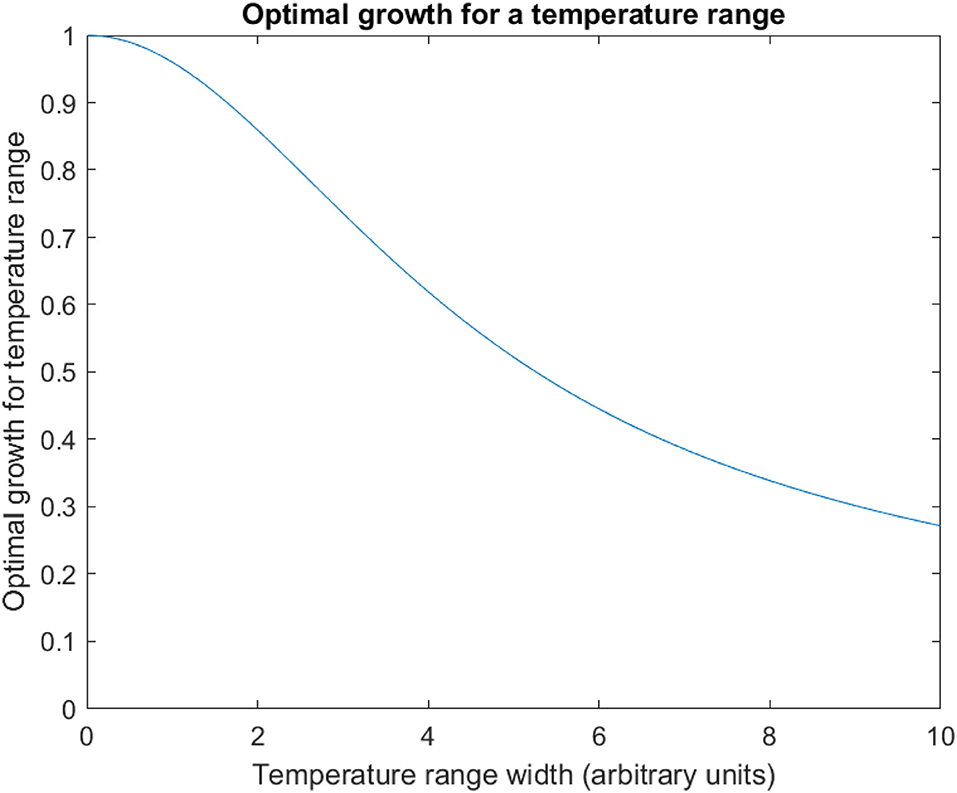
Figure 5. Optimal growth for a temperature range. The optimum solution for mean pathogen growth rate for uniform temperature variation is plotted against the width of this range (k in the text), for 0 ≤ k ≤ 10. This is normalised to optimal growth at a single temperature (thus is 1 when the temperature range is zero—i.e., a single point). As the temperature range increases, the optimal growth across this temperature range falls sigmoidally compared to growth at a single temperature.

This modelling suggests even in the best case, thermal variation inflicts a growth penalty on the pathogen vs. a single temperature. Further, increasing this variation inflicts a greater penalty to best case thermal performance of the pathogen.

How robust this thermal strategy is to pathogen co-evolution depends upon how it can adapt in response to thermal variation. Implicit in our analysis above is the pathogen growth curve is essentially fixed: a pathogen may be able to transpose its growth curve along the temperature axis to optimise thermal performance across an interval, but not alter its shape or width. Although the general observation of the archetypal growth curve (e.g., Figure 1) rules against dramatic shape changes, smaller changes in shape or width are credible (Sternberg and Thomas, 2014), although these may incur other trade-offs.

Also, the absolute effect size of thermal variation appears small when translated into concrete biological terms. The interval width k is currently in arbitrary units, with 1 unit corresponding to the temperature difference between T_opt and T_max. For E. coli, this corresponds to 8°C; for S. dysenteriae, 3°C (Altman and Dittmer, 1972). In our simplified model, thermal instability of 3° impedes pathogen growth by 1% in the first case, and 4% in the second.

5. Intermittent Fever and Optimal Thermal Restriction

Fever is not always a sustained elevation in temperature. Transient (“spiking”) or intermittent fevers are common clinical observations. We explore whether intermittent heating can be superior to constant heading for an infected host given a limited energy budget.

As a concrete model example, suppose a 1 kg mass of water (heat capacity 4,200 J/kg/°C) at an environmental temperature of 25°C is heated to maintain a temperature of 37°C, with a heat transfer coefficient of 10 J/s/°C/m² and a surface area of 1 m² (these latter two values are chosen for concreteness; as scaling constants, the comparative dynamic behaviour we investigate is insensitive to their particular value). Heat transfer from the water to the environment is, from Equation 1:

$\begin{array}{ll}10\text{J}/\text{s}{/}^{°}\text{C}/{\text{m}}^2·1{\text{m}}^2·({37}^{°}\text{C}-{25}^{°}\text{C})=120\text{W}& (8)\end{array}$

From the first law of thermodynamics, the water must be heated at 120 W to maintain a temperature of 37°C. We now compare two strategies of using additional energy to further increase this temperature. First, instantaneous heating to 40°C with subsequent cooling to return to 37°C. Second, using this energy of instantaneous heating to give sustained heating over the same period.

For the first strategy, the cooling equation is:

$\begin{array}{ll}\frac{\text{d}T}{\text{d}t}=\frac{[120\text{W}-10\text{J}/\text{s}{/}^{°}\text{C}/{\text{m}}^2·(T-{25}^{°}\text{C})]}{4200\text{J}/\text{kg}{/}^{°}\text{C}}& (9)\end{array}$

Solving for temperature as a function of time, with T(0) = 40:

$\begin{array}{ll}T=3·e^{\frac{-t}{420}}+37& (10)\end{array}$

The water has cooled to near its initial temperature (37.1°C) at t ≈ 1, 430 s. The time integral gives the overall temperature elevation:

$\begin{array}{ll}{\displaystyle {\int }_0^{1430}3}·e^{\frac{-t}{420}}\text{d}t\approx 1220{\text{s}}^{°}\text{C}& (11)\end{array}$

To compare to the second strategy of sustained heating, we take the energy required for instantaneous heating of this mass of water by 3°C (12600J), and instead use it to provide additional continuous heating over this period of 1,430 s (8.81 W). The temperature equilibrium that would result is given by:

$\begin{array}{l}20\text{W}+\frac{12600\text{J}}{1430\text{s}}=10\text{J}/\text{s}{/}^{°}\text{C}/{\text{m}}^2·1{\text{m}}^2·(T^{°}\text{C}-{25}^{°}\text{C})\\ T={37.88}^{°}\text{C}& (12)\end{array}$

The benefits of elevated temperature to inhibit pathogen growth are non-linear with temperature. We transform the temperature into “Utility” (U) with the temperature dependent growth curve of the pathogen, normalised to their maximum growth rates: For S. dysenteriae, this is (cf. Equation 3):

$\begin{array}{ll}U=1-\frac{\left[{\left((T-4)·(1-e^{(1.247·(T-40)})\right)}^2\right]}{1037.929}& (13)\end{array}$

U is zero at maximum pathogen growth (T_opt) and 1 at zero pathogen growth (T_max, T_min). The overall utility to the host gained with the 'burst heating' strategy is, by substitution:

$\begin{array}{l}{\displaystyle \underset{0}{\overset{1430}{\int }}1-\left[\frac{\left(\left[3·e^{\frac{-t}{420}}\right]-4\right)·{\left(1-e^{1.247·\left(\left[3·e^{\frac{-t}{420}}\right]-40\right)}\right)}^2}{1037.929}\right]}\text{d}t\\ \approx 183\text{Us}& (14)\end{array}$

‘Us’ is a unit of pathogen growth restriction: 1 Us is equivalent to completely halting pathogen growth for 1 s. The utility to the host with the sustained heating strategy is:

$\begin{array}{ll}{\displaystyle \underset{0}{\overset{1430}{\int }}1}-\left[\frac{(37.88-4)·{\left(1-e^{1.247·(37.99-40)}\right)}^2}{1037.929}\right]\text{d}t\approx 65\text{Us}& (15)\end{array}$

The same procedure for E. coli, gives (cf. equation 4):

$\begin{array}{l}{\displaystyle \underset{0}{\overset{1430}{\int }}1-\left[\frac{\left(\left[3·e^{\frac{-t}{420}}\right]-10\right)·{\left(1-e^{0.260·\left(\left[3·e^{\frac{-t}{420}}\right]-45\right)}\right)}^2}{558.23}\right]}\text{ d}t\\ \approx 28\text{Us}& (16)\end{array}$

Versus sustained heating:

$\begin{array}{ll}{\displaystyle \underset{0}{\overset{1430}{\int }}1}-\left[\frac{(37.88-10)·{\left(1-e^{0.260·(37.99-40)}\right)}^2}{558.23}\right]\text{d}t\approx 15\text{Us}& (17)\end{array}$

In these models 'burst heating' accrues more two to three times more utility in terms of pathogen growth inhibition than sustained heating with a fixed energy constraint. In absolute terms, the benefits still depend on the thermal sensitivity of the pathogen. For S. dysenteriae, burst heating is roughly equivalent to halting pathogen growth for 3 min out of every 22 (vs. 1 min with sustained heating); for E. coli, this is 30 s every 22 min vs. 15.

These results are sensitive to the ‘cut-off’ value for what counts as near the initial temperature of 37°C. Lower or higher values (e.g., 37.01 and 37.5°C) alter the total time period of analysis (≈ 2,400 and 750 s, respectively) and so alter the temperature generated by a continuous heating strategy. Repeating the analysis for these different values are given in Table 2. At the higher cut-off value (37.5°C), continuous heating slightly surpasses burst heating for both S. dysenteriae and E. coli.

TABLE 2

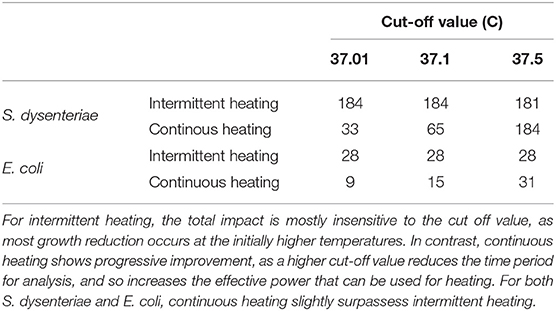
Table 2. Intermittent vs. continuous heating impact on pathogen growth reduction (in arbitrary units) with different temperature cut off values for the analysis.

This suggests the optimal strategy depends on the host's energy budget for febrile heating: although the energy used is identical across all scenarios in Table 2, the effective power for continuous heating approximately doubles between 37.01, 37.1, and 37.5°C, as the interval this energy is being deployed over approximately halves. Intermittent heating may be more effective than continuous heating with a stricter energy constraint, but continuous heating can be more effective with a more generous one.

6. Discussion

We have outlined three distinct mechanisms which could underlie the hypothesis that the temperature elevation of fever in endotherms directly inhibits pathogen growth. The first through simply elevating temperature to a point on the pathogen's temperature dependent growth curve in which it grows poorly (a direct effect). The second by further increasing the temperature difference between the host body and the environment, so pathogens adapted to environmental temperatures are poorly adapted to the host body environment (a environmental filtering effect). The third by increasing the temperature volatility of the host body environment, impeding pathogen growth no matter what temperature they are best adapated to (a dynamic variation effect).

Mathematical investigation of the relationship between the cost of temperature elevation to the host (in terms of energy) vs. the costs inflicted to the pathogen (in terms of growth restriction) share similar patterns. In theory, each mechanism can be a highly effective host strategy in the limit of unbounded febrile temperatures. The same applies for large temperature increases accessible to ectotherms.

In endotherms, where fever elevates body temperature by much smaller magnitudes, the picture is more equivocal. In terms of direct effects, febrile body temperatures still substantially inhibit growth for some species (like S. dysenteriae), and so plausibly justify the metabolic cost of fever alone. Other pathogens (like E. coli) are much more resilient to febrile temperatures: although there is still some growth inhibition, this benefit looks much smaller when balanced against the energetic costs to the host.

For both environmental filtering and dynamic variability, these mechanisms also have limited value whether or not the pathogen is fever-sensitive or not: in the first case, because it only applies in very limited temperature range where an environmental pathogen is not already thermally excluded by normal body temperature, but is by one a few degrees higher; in the second, although thermal variation imposes some residual inhibition of pathogen growth (even if the pathogen has adapted to grow optimally across this temperature range) this only amounts to a few percent worse than optimal growth for a single temperature.

We also assessed the potential value of intermittent or 'spiking' fever by comparing using the same energy budget to heat in bursts vs. a sustained temperature elevation over time in a simple physical model. Our findings are that heating in bursts is substantially more effective in terms of delaying pathogen growth when the energy constraint is stricter, owed to the non-linear effects of temperature on pathogen growth inhibition.

6.1. Limitations

All mathematical modelling strikes a balance between fidelity and simplicity. The modelling of marginal thermal restriction and intermittent fever are very simple. It is hoped this degree of abstraction is better than a more richly detailed model given the latter would likely become highly specific to the modelling scenario, and make general principles harder to infer from its behaviour.

Limitations to data also pose challenges: the pathogen growth curves are fitted on data-book values for species in laboratory conditions. The values of T_max etc. may vary from these due to factors like strain and local environment. Our analyses are also sensitive to how small changes in temperature between T_opt and T_max are modelled: whether, for example, a pathogen 0.2°C above its optimal growth temperature grows sub-optimally to the degree inferred from the Ratkowsky equation. The purpose of the examplar species is to demonstrate the range of possible behaviour, and the overall range is unlikely to be sensitive to this uncertainty.

We have deliberately isolated febrile heating from the wider fever response. Extrapolating our findings from the former to the latter requires caution. We have not assessed the impact of other mechanisms by which fever could protect an endotherm from infection, nor their relative importance vs. febrile heating.

Our scenarios for modelling were focused on two bacterial pathogens in humans at core body temperature. Extrapolating from this to other endotherms, other pathogens (such as non-bacterial microbes), and other host body environments (e.g., skin surfaces) should be done cautiously. We hope the broad principles used in constructing these models (e.g., basic thermodynamics, the Ratkowsky equation) make the broad trends in results have reasonable external validity.

6.2. Conclusions and Further Work

The heating hypothesis. Whether febrile heating is an effective mechanism for endotherms overall depends on the relative prevalence of fever-sensitive and fever-resistant pathogens. Even if febrile heating is sometimes ineffective, providing infections from pathogens which it is effective against are common enough, a host strategy which responds to infection with heating ‘by default’ can have positive expected value, and thus adaptive overall.

Quantitative assessment of when these mechanisms are effective vs. when they are not is very challenging: a given host typically susceptible to a wide number of pathogens, relative prevalence is often environmentally dependent, and the relative burden of disease attributable to different pathogen species is typically opaque. A lower-resolution qualitative assessment may still give good support for this hypothesis: for example, demonstrating fever sensitivity is sufficiently common among pathogens known to infect humans, or that a significant fraction of global human burden of disease can be attributed to pathogens which are sensitive to febrile temperatures.

The clinical value of fever. These results are not sufficient to resolve the clinical controversy around suppressing fever. Yet our results suggest febrile heating alone could have significant clinical utility for some infections.

Although this supplies cause for caution in suppressing fever, the overall clinical judgement in the context of a given infection needs to assess more than the plausibility of the heating hypothesis. For a given patient and a given infection, fever may be unwise to suppress even if febrile heating serves little purpose: its immunomodulatory effects may be crucial to combating the infection. The opposite could also be the case: for example, for an individual with limited physiological reserve the additional stress of fever may be harmful overall even if its thermal effect on the infection is significantly beneficial.

One approach to gain further insight would be to better understand what triggers different ‘types’ of fever: ‘spiking’, undulating, or continuous fever are all clinically observed (Cunha, 1996). One hypothesis could be fever is recruited for different purposes depending on the status of infection: a competing explanation for ‘spiking’ besides the energy efficiency we explored is that spiking principally serves as an immunological signal, whilst continuous fever is reserved for more severe infection where antimicrobial heating is resorted to. Understanding fever's correlates and mechanisms may inform which biological mechanisms are important in which circumstances, and thus give a principled rationale on when to intervene.

For the clinical question, inference from first principles is inferior to trial data. This data is scant: there are a small number of small trials which vary in their findings, and systematic reviews typically give inconclusive results (Jefferies et al., 2011; Niven et al., 2013; Drewry et al., 2017). Perhaps the best infection to investigate further would be Malaria, given parasite growth is significantly inhibited at febrile temperatures in vitro (Long et al., 2001), expert opinion varies, and the data is equivocal (Lell et al., 2001; Meremikwu et al., 2012). Given both the disease and anti-pyretic therapy are prevalent, resolving this uncertainty may bring significant humanitarian benefit.

Fever is indirectly adaptive. Our results also provide suggestive evidence for febrile heating being an exaptation. The mechanisms of thermal elevation are all in principle much more effective when temperature can vary in the range of ectothermic organisms. One hypothesis could be that raising body temperature in response to infection was highly adaptive in ectotherms, and ancestral immune systems co-adapted to be partly triggered by higher temperatures. After the development of endothermy (perhaps in part driven by the value of continuously, rather than intermittently, occupying a different thermal niche to avoid infection from environmental microbes) (Logan, 2019), the direct antimicrobial value of raising body temperature faded, but this mechanism was preserved due to ongoing reliance of the immune system on a temperature signal.

For this hypothesis, as well as fever being maladaptive, accessible evidence is unlikely to be better than suggestive. Even if one can rule out the thermal mechanisms of fever as an effective host response, isolating and assessing other mechanisms by which fever could combat infection is harder still. One may compare courses of fever between species: whether some endotherms can raise their body temperatures in fever much higher than others, and exploring what antimicrobial effects this has.

Fever as credible signal. Our exemplars, E. coli and S. dysenteriae are close phylogenetically, similar pathophysiologically, yet differ markedly in their sensitivity to febrile temperatures. What could explain the differences observed between endotherm pathogens in how they tolerate febrile temperatures?

One possibility is physiological differences: perhaps some aspect of S. dysenteriae's metabolism imposes a temperature restriction vs. E. coli. Another could be differences in lifecycle: perhaps S. dysenteriae spends more time in colder environments outside the host than E. coli, and so trades a lower T_min for a lower T_max.

One interesting hypothesis is sensitivity to febrile heating, and lower growth at febrile temperatures, could sometimes enhance pathogen fitness. If there are 'trade-offs' between length and intensity of infection, pathogen species adapted to longer milder infections may be advantaged if they respond to the host's credible signal of immune activation and threatened host death by reducing growth. Pathogens which lower the risk of earlier termination of their infection by host death or immune clearance may be at a selective advantage.

This hypothesis can be examined both theoretically and empirically. Theoretically, one can attempt to build upon prior theoretical work on the co-evolution of honest (and costly) signalling in predator-prey or aposematic contexts (Yachi, 1995; Lee et al., 2011): whether initially adaptive febrile heating can be maintained as a co-evolutionary stable ‘inducible aposematism’, whereby it is adaptive for hosts to thermally signal their physiological compromise, and for pathogens to respond to this with slower growth. Empirically, this hypothesis predicts pathogens which generate acute infections should tend to be less responsive to febrile temperatures than those which produce chronic infections.

Data Availability Statement

The analysis and figure generation code for this article is available at https://github.com/gjlewis37/fever.

Author Contributions

GL and MB conceived and designed the work in this manuscript. GL conducted the analysis and wrote the first draft, which was critically revised by MB. Both authors contributed to the article and approved the submitted version.

Funding

This work is supported by the Open Philanthropy Project.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Adrian Smith, Anders Sandberg, and members of the Mathematical Ecology Research Group journal club for helpful comments and review of this work.

References

Alizon, S., Hurford, A., Mideo, N., and Van Baalen, M. (2009). Virulence evolution and the trade-off hypothesis: history, current state of affairs and the future. J. Evol. Biol. 22, 245–259. doi: 10.1111/j.1420-9101.2008.01658.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Altman, P. L., and Dittmer, D. S. (1972). Biology Data Book. Bethesda, MD: Federation of American Societies for Experimental Biology.

Google Scholar

Banet, M. (1986). Fever in mammals: is it beneficial? Yale J. Biol. Med. 59, 117.

Google Scholar

Baracos, V. E., Whitmore, W., and Gale, R. (1987). The metabolic cost of fever. Can. J. Physiol. Pharmacol. 65, 1248–1254. doi: 10.1139/y87-199

PubMed Abstract | CrossRef Full Text | Google Scholar

Benhariz, M., Goulet, O., Salas, J., Colomb, V., and Ricour, C. (1997). Energy cost of fever in children on total parenteral nutrition. Clin. Nutr. 16, 251–255. doi: 10.1016/S0261-5614(97)80037-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Blatteis, C. M. (2003). Fever: pathological or physiological, injurious or beneficial? J. Therm. Biol. 28, 1–13. doi: 10.1016/S0306-4565(02)00034-7

CrossRef Full Text | Google Scholar

Buskirk, E., Thompson, R., Rubenstein, M., and Wolff, S. (1964). Heat exchange in men and women following intravenous injection of endotoxin. J. Appl. Physiol. 19, 907–913. doi: 10.1152/jappl.1964.19.5.907

PubMed Abstract | CrossRef Full Text | Google Scholar

Casadevall, A. (2016). Thermal restriction as an antimicrobial function of fever. PLoS Pathog. 12:e1005577. doi: 10.1371/journal.ppat.1005577

PubMed Abstract | CrossRef Full Text | Google Scholar

Cunha, B. A. (1996). The clinical significance of fever patterns. Infect. Dis. Clin. 10, 33–44. doi: 10.1016/S0891-5520(05)70284-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Drewry, A. M., Ablordeppey, E. A., Murray, E. T., Stoll, C. R., Izadi, S. R., Dalton, C. M., et al. (2017). Antipyretic therapy in critically ill septic patients: a systematic review and meta-analysis. Crit. Care Med. 45, 806. doi: 10.1097/CCM.0000000000002285

PubMed Abstract | CrossRef Full Text | Google Scholar

Du Bois, E. F. (1921). The basal metabolism in fever. Jama 77, 352–357. doi: 10.1001/jama.1921.02630310022006

CrossRef Full Text

Evans, S. S., Repasky, E. A., and Fisher, D. T. (2015). Fever and the thermal regulation of immunity: the immune system feels the heat. Nat. Rev. Immunol. 15, 335–349. doi: 10.1038/nri3843

PubMed Abstract | CrossRef Full Text | Google Scholar

Eyers, S., Weatherall, M., Shirtcliffe, P., Perrin, K., and Beasley, R. (2010). The effect on mortality of antipyretics in the treatment of influenza infection: systematic review and meta-analyis. J. R. Soc. Med. 103, 403–411. doi: 10.1258/jrsm.2010.090441

PubMed Abstract | CrossRef Full Text | Google Scholar

Gazel, D., and Yılmaz, M. (2018). Are infectious diseases and microbiology new fields for thermal therapy research? Int. J. Hyperther. 34, 918–924. doi: 10.1080/02656736.2018.1440015

PubMed Abstract | CrossRef Full Text | Google Scholar

Gil, M. M., Miller, F. A., Brand ao, T. R., and Silva, C. L. (2017). Mathematical models for prediction of temperature effects on kinetic parameters of microorganisms' inactivation: tools for model comparison and adequacy in data fitting. Food Bioprocess Technol. 10, 2208–2225. doi: 10.1007/s11947-017-1989-x

CrossRef Full Text | Google Scholar

Grimaud, G. M., Mairet, F., Sciandra, A., and Bernard, O. (2017). Modeling the temperature effect on the specific growth rate of phytoplankton: a review. Rev. Environ. Sci. Biotechnol. 16, 625–645. doi: 10.1007/s11157-017-9443-0

CrossRef Full Text | Google Scholar

Haahr, S., and Mogensen, S. (1978). Function of fever in infectious disease. Biomedicine 28, 305–307.

Google Scholar

Hasday, J. D., and Garrison, A. (2000). Antipyretic therapy in patients with sepsis. Clin. Infect. Dis. 31(Suppl. 5):S234–S241. doi: 10.1086/317514

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasday, J. D., Thompson, C., and Singh, I. S. (2011). Fever, immunity, and molecular adaptations. Compr Physiol. 4, 109–148. doi: 10.1002/cphy.c130019

PubMed Abstract | CrossRef Full Text | Google Scholar

Jefferies, S., Weatherall, M., Young, P., Eyers, S., Perrin, K. G., Beasley, C. W., et al. (2011). The effect of antipyretic medications on mortality in critically ill patients with infection: a systematic review and meta-analysis. Crit. Care Resusc. 13, 125.

PubMed Abstract | Google Scholar

Kiekkas, P., Konstantinou, E., Psychogiou, K.-S., Tsampoula, I., Stefanopoulos, N., and Bakalis, N. (2014). Nursing personnel's attitudes towards fever and antipyresis of adult patients: cross-sectional survey. J. Clin. Nurs. 23, 2949–2957. doi: 10.1111/jocn.12551

PubMed Abstract | CrossRef Full Text | Google Scholar

Klastersky, J. (1972). Etude experimentale et clinique des effets favorables et defavorables de la fievre et de l'administration de corticoides au cours d'infections bacteriennes. Acta Clin. Belg. 27(Suppl. 6):8–84. doi: 10.1080/17843286.1972.11716830

CrossRef Full Text | Google Scholar

Kluger, M. J., Kozak, W., Conn, C. A., Leon, L. R., and Soszynski, D. (1998). Role of fever in disease. Ann. N. Y. Acad. Sci. 856, 224–233. doi: 10.1111/j.1749-6632.1998.tb08329.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. J., Speed, M. P., Stephens, P. A., Andrade, A. E. M. C. B., and McPeek, E. M. A. (2011). Honest signaling and the uses of prey coloration. Am. Nat. 178, E1–E9. doi: 10.1086/660197

PubMed Abstract | CrossRef Full Text | Google Scholar

Lell, B., Sovric, M., Schmid, D., Luckner, D., Herbich, K., Long, H. Y., et al. (2001). Effect of antipyretic drugs in children with malaria. Clin. Infect. Dis. 32, 838–841. doi: 10.1086/319217

PubMed Abstract | CrossRef Full Text | Google Scholar

Logan, M. (2019). Did pathogens facilitate the rise of endothermy? Ideas Ecol. Evol. 12:1–8.

Google Scholar

Long, H., Lell, B., Dietz, K., and Kremsner, P. (2001). Plasmodium falciparum: in vitro growth inhibition by febrile temperatures. Parasitol. Res. 87, 553–555. doi: 10.1007/s004360100374

PubMed Abstract | CrossRef Full Text | Google Scholar

Mackowiak, P. A. (2000). Physiological rationale for suppression of fever. Clin. Infect. Dis. 31(Suppl. 5):S185–S189. doi: 10.1086/317511

PubMed Abstract | CrossRef Full Text | Google Scholar

Meremikwu, M. M., Odigwe, C. C., Nwagbara, B. A., and Udoh, E. E. (2012). Antipyretic measures for treating fever in malaria. Cochrane Database Syst. Rev. 2012:CD002151. doi: 10.1002/14651858.CD002151.pub2

PubMed Abstract | CrossRef Full Text | Google Scholar

Meteyer, C. U., Valent, M., Kashmer, J., Buckles, E. L., Lorch, J. M., Blehert, D. S., et al. (2011). Recovery of little brown bats (myotis lucifugus) from natural infection with geomyces destructans, white-nose syndrome. J. Wildl. Dis. 47, 618–626. doi: 10.7589/0090-3558-47.3.618

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammed, R. S., Reynolds, M., James, J., Williams, C., Mohammed, A., Ramsubhag, A., et al. (2016). Getting into hot water: sick guppies frequent warmer thermal conditions. Oecologia 181, 911–917. doi: 10.1007/s00442-016-3598-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Niven, D. J., Stelfox, H. T., and Laupland, K. B. (2013). Antipyretic therapy in febrile critically ill adults: a systematic review and meta-analysis. J. Crit. Care 28, 303–310. doi: 10.1016/j.jcrc.2012.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Padfield, D., Castledine, M., and Buckling, A. (2020). Temperature-dependent changes to host-parasite interactions alter the thermal performance of a bacterial host. ISME J. 14, 389–398. doi: 10.1038/s41396-019-0526-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Rakus, K., Ronsmans, M., and Vanderplasschen, A. (2017). Behavioral fever in ectothermic vertebrates. Dev. Compar. Immunol. 66, 84–91. doi: 10.1016/j.dci.2016.06.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Ratkowsky, D., Lowry, R., McMeekin, T., Stokes, A., and Chandler, R. (1983). Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 154, 1222–1226. doi: 10.1128/jb.154.3.1222-1226.1983

PubMed Abstract | CrossRef Full Text | Google Scholar

Richards-Zawacki, C. L. (2010). Thermoregulatory behaviour affects prevalence of chytrid fungal infection in a wild population of panamanian golden frogs. Proc. R. Soc. B Biol. Sci. 277, 519–528. doi: 10.1098/rspb.2009.1656

PubMed Abstract | CrossRef Full Text | Google Scholar

Robert, V. A., and Casadevall, A. (2009). Vertebrate endothermy restricts most fungi as potential pathogens. J. Infect. Dis. 200, 1623–1626. doi: 10.1086/644642

PubMed Abstract | CrossRef Full Text | Google Scholar

Simpson, W. M. (1936). Artificial fever therapy of syphilis and gonococcic infections. Br. J. Venereal Dis. 12, 133. doi: 10.1136/sti.12.3.133

PubMed Abstract | CrossRef Full Text | Google Scholar

Skok, K., Duh, M., Stožer, A., Markota, A., and Gosak, M. (2021). Thermoregulation: a journey from physiology to computational models and the intensive care unit. WIREs Mech. Dis. 13:e1513. doi: 10.1002/wsbm.1513

PubMed Abstract | CrossRef Full Text | Google Scholar

Small, P., Täuber, M. G., Hackbarth, C., and Sande, M. (1986). Influence of body temperature on bacterial growth rates in experimental pneumococcal meningitis in rabbits. Infect. Immun. 52, 484–487. doi: 10.1128/iai.52.2.484-487.1986

PubMed Abstract | CrossRef Full Text | Google Scholar

Smits, N., BriÈRe, J.-F., and Fargues, J. (2003). Comparison of non-linear temperature-dependent development rate models applied to in vitro growth of entomopathogenic fungi. Mycol. Res. 107, 1476–1484. doi: 10.1017/S095375620300844X

PubMed Abstract | CrossRef Full Text | Google Scholar

Sternberg, E. D., and Thomas, M. B. (2014). Local adaptation to temperature and the implications for vector-borne diseases. Trends Parasitol. 30, 115–122. doi: 10.1016/j.pt.2013.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, M. B., and Blanford, S. (2003). Thermal biology in insect-parasite interactions. Trends Ecol. Evol. 18, 344–350. doi: 10.1016/S0169-5347(03)00069-7

CrossRef Full Text | Google Scholar

Walsh, A., Edwards, H., and Fraser, J. (2007). Over-the-counter medication use for childhood fever: a cross-sectional study of australian parents. J. Paediatr. Child Health 43, 601–606. doi: 10.1111/j.1440-1754.2007.01161.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodhams, D. C., Alford, R. A., and Marantelli, G. (2003). Emerging disease of amphibians cured by elevated body temperature. Dis. Aquat. Organ. 55, 65–67. doi: 10.3354/dao055065

PubMed Abstract | CrossRef Full Text | Google Scholar

Yachi, S. (1995). How can honest signalling evolve? the role of handicap principle. Proc. R. Soc. Lond. Ser. B Biol. Sci. 262, 283–288.

Google Scholar