The Dynamic Hypercube as a Niche Community Model

Different models of community dynamics, such as the MacArthur–Wilson theory of island biogeography and Hubbell’s neutral theory, have given us useful insights into the workings of ecological communities. Here, we develop the niche-hypervolume concept of the community into a powerful model of community dynamics. We describe the community’s size through the volume of the hypercube and the dynamics of the populations in it through the fluctuations of the axes of the niche hypercube on different timescales. While the community’s size remains constant, the relative volumes of the niches within it change continuously, thus allowing the populations of different species to rise and fall in a zero-sum fashion. This dynamic hypercube model reproduces several key patterns in communities: lognormal species abundance distributions, 1/f-noise population abundance, multiscale patterns of extinction debt and logarithmic species-time curves. It also provides a powerful framework to explore significant ideas in ecology, such as the drift of ecological communities into evolutionary time.

Introduction

Empirical studies of ecological communities often call for a greater emphasis on time and on longer time intervals (Ripa and Lundberg, 2000; Hastings, 2004; Magurran, 2007). This call is urgent as we live in an age of major changes in biodiversity across the Earth via landscape transformation or migration (Dornelas et al., 2014). Additionally, in the last 50 years, there has been a reassessment of the dominant paradigm of community organization. The “balance of nature” paradigm has receded somewhat (Cuddington, 2001; Ergazaki and Ampatzidis, 2012; Simberloff, 2014) and we now have a more dynamic conception of persistence in natural ecosystems (Pimm, 1991). Variability exists on all timescales both within the ecological community itself (Pimm and Redfearn, 1988; Halley, 1996) and in the environment to which it responds (Wunsch, 2003; Franzke et al., 2020). Thus, we expect ecological equilibria to be more dynamic, more provisional and more diffuse (Halley and Inchausti, 2004). The simplifications of assuming an equilibrium will remain useful and compelling, such as for flux calculations and for the species-area relationship. That said, the greater attention to time calls for model development to help insights specifically into dynamic effects in communities.

The basis of most modeling in community ecology is the Lotka–Volterra model. This pair of equations with four interaction terms can describe relationships of competition, predation, herbivory and mutualism. While the Lotka–Volterra system is phenomenological, it can also be related to more mechanistic resource models (Schoener, 1973). A natural development for dynamic community modeling is to generalize this system to S species described by a set of first-order non-linear coupled differential equations. This generalized Lotka–Volterra system has had enormous impact on community ecology, including classical treatments such as that of May (May, 1973) and continues to be the subject of novel approaches (Forte and Vrscay, 1996; Bertuzzo et al., 2011; Fisher and Mehta, 2014; Kessler and Shnerb, 2015). The growth in computing power has circumvented many of the obvious technical difficulties of solving a system of this size. A more persistent challenge is how to populate the S² interaction terms with plausible parameter values. Assigning interaction strengths in an ecological community of hundreds of species remains a formidable problem and drives the development of various other community models, though these could arguably be seen as special cases of the generalized Lotka–Volterra system (Kessler and Shnerb, 2015).

One of the most widely applied community theories is that of island biogeography (MacArthur and Wilson, 1967). It ignores interactions entirely, so extinction and colonization processes drive the system’s biodiversity. The simplicity of this theory (MacArthur and Wilson, 1967) allowed many developments using metapopulation-type communities (Tilman, 1994; Matter et al., 2002). Another development for biodiversity ecology was Hubbell’s unified neutral theory of biodiversity (NTB). Hubbell’s model made the remarkable assumption of following Kimura’s model of genetic neutral evolution (Kimura, 1955), considering species to be ecologically indistinguishable from one another and then assuming that all stochasticity is demographic (Hubbell, 2001). This model violated obvious ecological realities. Nonetheless, it explained a wide variety of ecological patterns and processes such as near-lognormal species abundance distributions (McGill, 2003), Fisher’s α-parameter (Chave, 2004), and spatial clumping (Chave and Leigh, 2002). The application of neutral theory to extinction debt (Halley and Iwasa, 2011) that specifically used its dynamics was probably its first potential use in conservation. The NTB has since stimulated much theoretical work in community ecology — including this special issue. Nevertheless, limitations in the NTB (Clark and Mclachlan, 2003; Ricklefs, 2006; Leigh, 2007) show that it cannot be a useful tool for all phenomena. Its most obvious violation of ecological reality is it ignores niches. Various attempts have been made to merge these. Proposals combining niche and neutral models explore community dynamics (Adler et al., 2007; Zillio and Condit, 2007; Chisholm and Pacala, 2010). Since stochasticity is crucial to the operation of the NTB, the need to involve environmental stochasticity has been noted as particularly important (Kalyuzhny et al., 2015; Engen et al., 2017). Species-area relations have also been a problem. The neutral model found it difficult to reproduce observed spatial patterns such as the Arrhenius species-area relationship (Leigh, 2007; Halley et al., 2014).

Hutchinson’s niche-hypervolume concept (Hutchinson, 1957) has been an attractive and popular approach because of its intuitive simplicity and because it is readily visualized (e.g., Figures 1, 2 below). Interest in Hutchinson’s model is resurging recently (Barros et al., 2016; Díaz et al., 2016; Blonder, 2018). This growing popularity links to research contexts such as niche envelope models (Thomas et al., 2004; Soberón, 2010; Barros et al., 2016) and functional ecology (Lamanna et al., 2014; Díaz et al., 2016; Pigot et al., 2016). It drives considerable methodological research, mainly in the description and parameterisation of the hypervolumes (Blonder et al., 2018; Carvalho and Cardoso, 2021). There has also been progress in relating the niche to ideas of coexistence. Concepts of stable coexistence have evolved from strict associations with stable equilibria in the Lotka–Volterra system to concepts of invasibility (Chesson and Warner, 1981; Chesson, 2000). Theoretical developments have refined the relation between limiting similarity and competitive exclusion (Leibold, 1995; Chase and Leibold, 2003; Meszéna et al., 2006; Barabás et al., 2018).

FIGURE 1

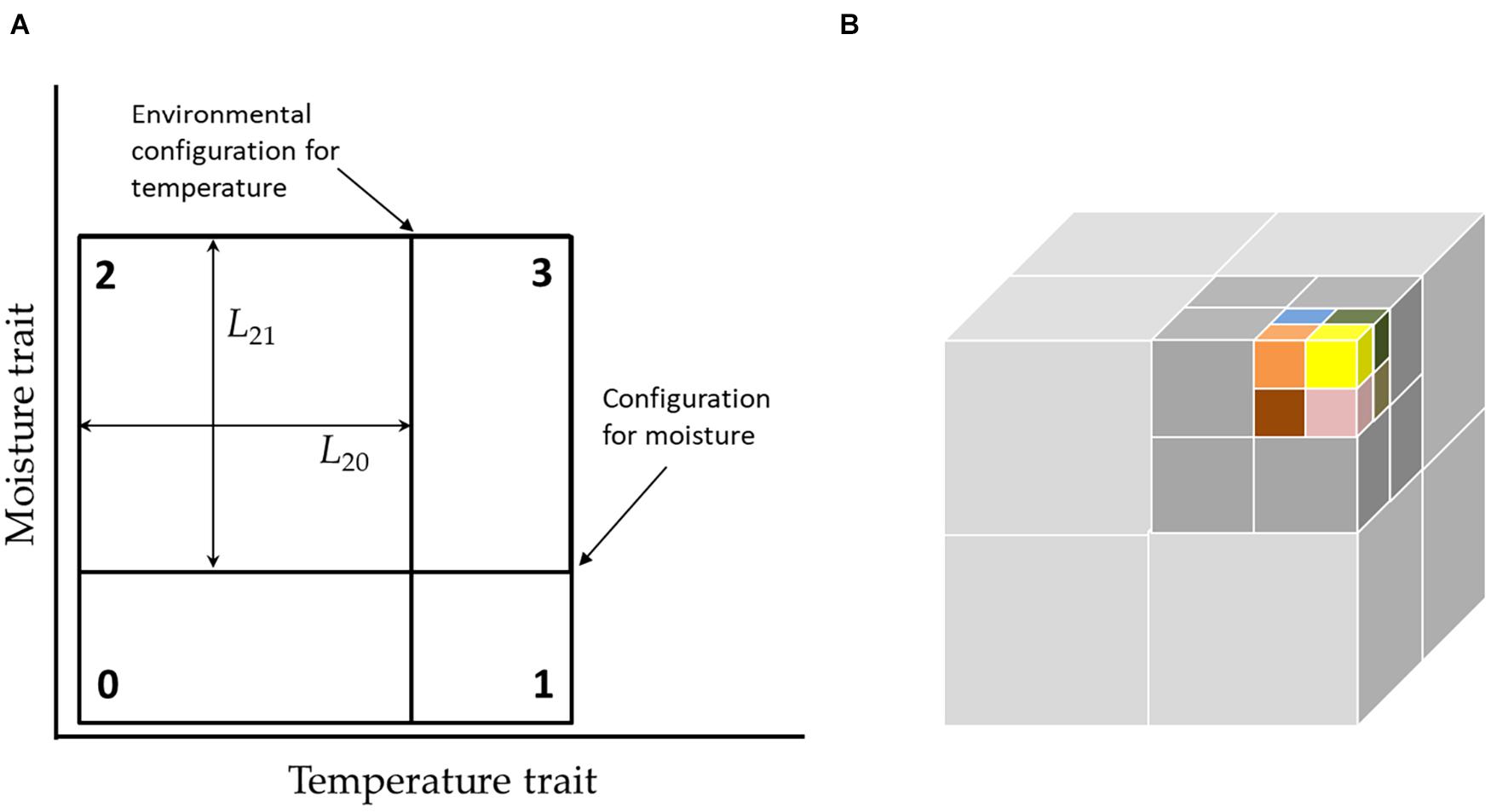
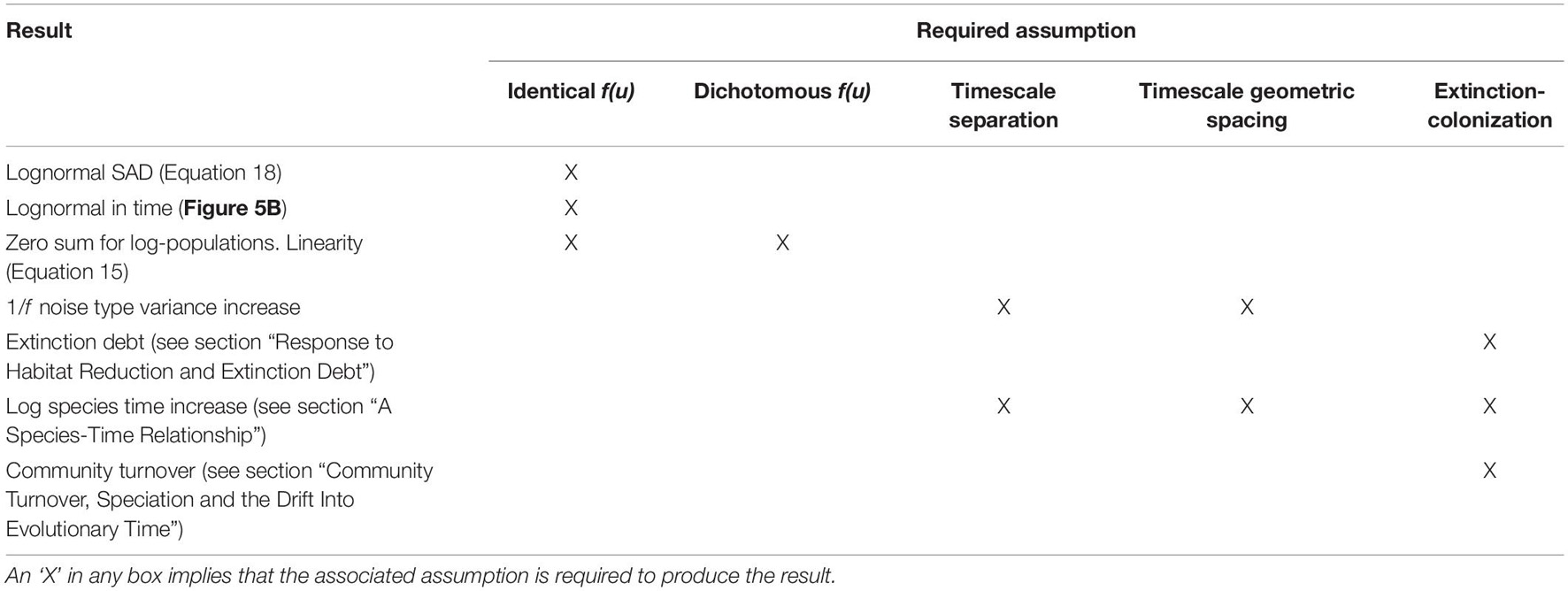
Figure 1. (A) Environmental configurations and niche widths in a two-axis hypercube. In this picture, the current configuration (position of partitions) favors species-2, which likes a cool but moist environment, since this has the largest area. In our graphic notation, note that the position of the environmental configuration, does not mean exactly temperature relative to the axis, but means that degree to which the environment favors hot or cold adapted species. (B) While the full niche hypercube cannot be depicted for more than 3 dimensions, the structure of the community can be depicted by “unfolding” the higher-dimensional hypercube into lower dimensions. Here, a six-dimensional community with 64 species is represented by 8 by 2 × 2 × 2 sub-cubes stacked to form a single “super-cube” of size 4 × 4 × 4. In turn this may be nested within another cube of size 8 × 8 × 8, and so on. This requires, that changes in the faster processes are mirrored in all super-cubes.

FIGURE 2

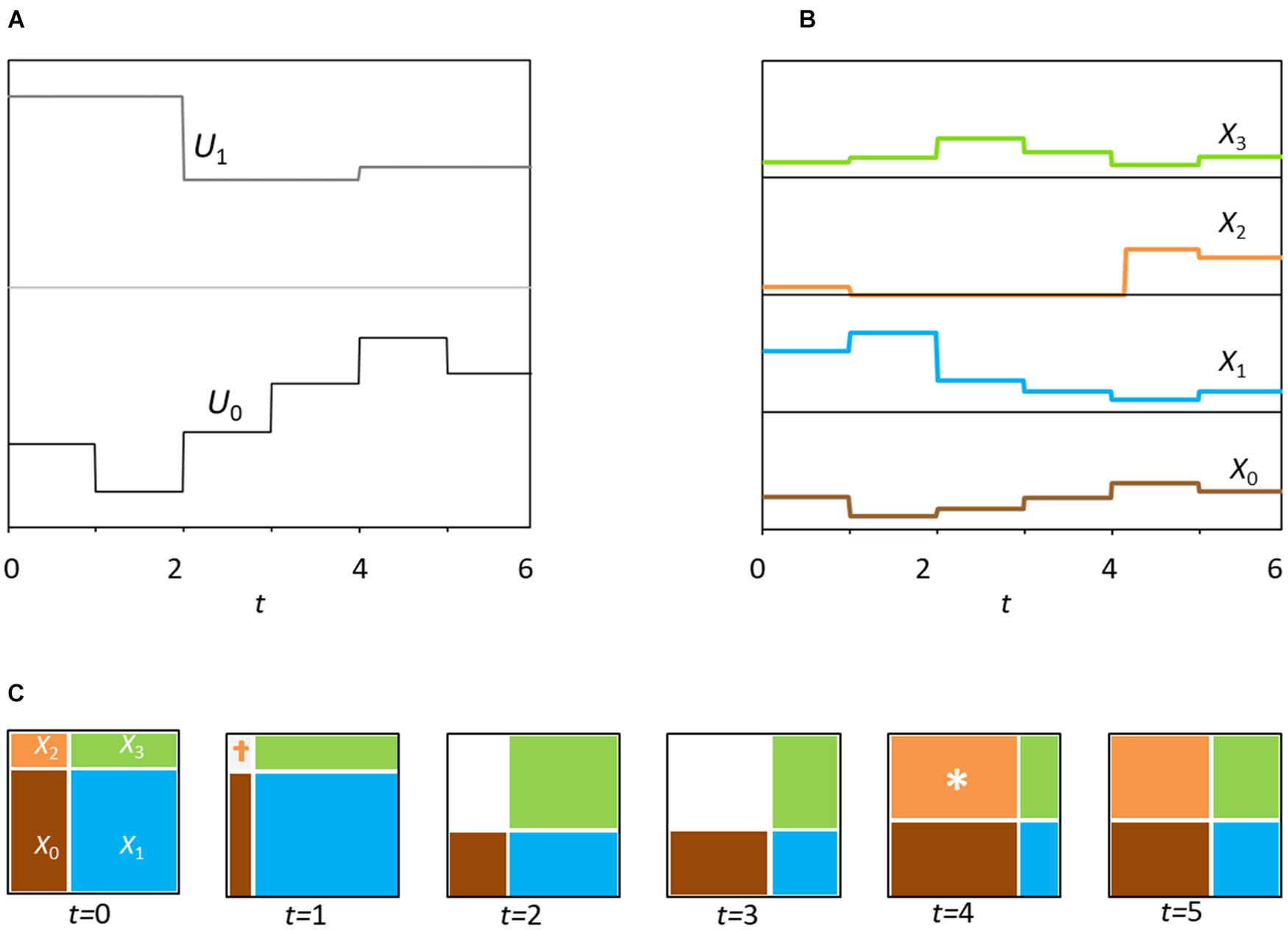
Figure 2. (A) Dynamics of the environmental variation in time for six steps (position of partitions, as in Figure 1A). Note that the partition for axis k assumes a new state at random every 2^k units of time, in this case one and two time steps, respectively. (B) Six time-steps of model dynamics for the four species. (C) Six panels showing the changes in niche-size (V_s) for consecutive time steps. Colors denote occupation by the corresponding population (X_s). Note the extinction of X₂ (species 2) at time t = 1 due to population falling below viability (‘†’), followed by two steps at zero and then at time t = 4, recolonization (‘^∗’).

In this paper, we develop a dynamic model, using Hutchinson’s hypervolume concept in a hypercube configuration. Much of the research on niche-related issues, as in community ecology generally, focuses on non-dynamic issues, seeking to explain patterns in space or in community organization. For example, in McGill’s (2010) survey of unified biodiversity models (McGill, 2010), only two of the six models feature dynamic descriptions of biodiversity. In seeking a model that is dynamic, we mean a model that can predict the time evolution of communities explicitly, something that has also been noted by others generally (Hastings, 2004; Magurran, 2007; Engen et al., 2017) and in hypervolume theory in particular (Holt, 2009). Many of the emerging problems in community ecology, such as extinction debt and colonization credit or the response of communities to climate change are dynamic in nature. They require the model to predict the state of the community at some specified time into the future. In addition, we sought a model that would generate several desirable features.

The Lognormal species-abundance distribution. Within a community, there are many rare species and a few common ones. The ensemble species abundance distribution at any time is often observed to be lognormal. Preston (1962) argued that a specific lognormal predominates — the “canonical” lognormal. It means, broadly, that most individuals in a community belong to the most abundant species, rather than, for example, to a large set of less abundant ones. Preston showed that this was consistent with the Arrhenius species-area curve having an exponent of 1/4, — a pattern frequently observed (Sugihara, 1980). McGill (2003) and others have shown that many theories generate such distributions, such as the zero-sum multinomial for the neutral model.

Lognormal distributions in time. Species abundance varies through time because of interactions with other species, demographic stochasticity, and in response to environmental stochastic factors (Halley and Iwasa, 1998; Engen et al., 2005). This variation can be considerable. Not surprisingly, species that vary most are at greater risk of extinction than those that are most constant. This is unless the variability is non-stationary (Halley and Kunin, 1999). Species abundances over time are typically distributed lognormally (Halley and Inchausti, 2002). Thus, as a species traces its trajectory of abundance X(t), its histogram tends to be lognormal.

More time, more variance. In this model, each species’ abundance responds entirely to the environmental pressures on that niche. According to Pimm (1991), the ecological community is fundamentally non-stationary. This is equivalent to saying that variability increases with time — the “more time means more variation” effect (Pimm and Redfearn, 1988; Inchausti and Halley, 2002). A series of studies using the Global Population Dynamics Database (GPDD) that examined the relation of variance to time systematically found that this increase of variance was universal (Inchausti and Halley, 2001, 2002). The spectral analysis showed that the model most consistent with this was a 1/f-noise model for which variance increases linearly with the logarithm of time (Halley, 1996; Halley and Inchausti, 2004).

Energy conservation: zero-sum properties. Since only a fixed amount of energy arrives in an ecosystem of fixed area, there is a limit on the number of organisms of a given size that can live there. This is an implied property of many models through the assumption of a constant number of individuals. This leads to a corresponding zero-sum principle, that populations add up to a constant community size in the absence of extinction-speciation and that all changes in populations sum to zero.

Below, we describe its outline and some properties. We then apply it to four different situations, showing how it can be useful in ecological research and applications.

Mathematical Description and Properties

We assume the simplified geometry of Hutchinson’s hypervolume to have the geometry of a hypercube, where there are many axes, each of which describes an environmental resource or limitation (We call these niche factors). The set of preferences for the various factors defines each niche. Only one species can occupy it, following Gause’s principle of competitive exclusion. After Hutchinson’s conception (Hutchinson, 1978), the niche is usually defined as the environmental conditions under which a given population has a positive growth rate. The volume of that niche is the probability that an individual can reproduce, if the state of the environment is picked randomly. However, if the area is large and it contains a large community, then we may interpret hypervolume as a number of individuals that can reproduce, and hence as a carrying capacity or ceiling for population. The intended target of our model is the community in a relatively large area. So, for both the niche and community hypervolumes (referred to J) the units of hypervolume (usually shortened hereafter to volume) are individual organisms. We interpret it as a ceiling on population for a species or for the community overall. This may be an issue when we have species of different sizes in the community (and hence different energy requirements) but refinements of this type are beyond the scope of this paper.

To simplify this model, our model has additional assumptions. (a) The world is binary. This includes binary niche factors: each factor can only be either “high” or “low.” Species responses are also binary: each species occupies only the position on the axis associated with its preferred level. Recognizing the existence of more developed concepts of limiting similarity (Leibold, 1995; Meszéna et al., 2006), we assume limited niche overlap is necessary and sufficient to avoid competitive exclusion. Thus, we do not consider hypervolume overlaps nor the possibility of morphological displacements as, for example, in Carvalho and Cardoso (2021). This also means that species do not evolve within our community, a statement of strong niche conservatism (Holt, 2009). (b) In addition, we assume that each factor fluctuates independently and on a different timescale. (c) The different timescales are spaced equally in log-time. (d) Population responds proportionally to changes in niche volume. These are the only drivers of population. Thus, we do not explicitly include population growth, species interactions or density dependence. The exception is that if the population goes extinct it remains extinct until recolonisation. (e) Species do not influence each other nor the niche structure.

The Niche as a Product of Traits

The axes of the niche hypercube are associated with niche factors. There are only two available positions on any axis, and these reflect corresponding traits to respond to this factor. The axis may be a niche factor such as moisture, in which case the organism is either moisture-loving or dry-loving, but it cannot be both. In Hutchinson’s perspective, each organism “chooses” an approach for each axis. We assume that each combination of all traits together generates one species associated with a single niche. Every such niche can be modeled by a corner on the hypercube. By Gause’s principle of competitive exclusion, two different species with the same traits cannot occupy the same niche. In our model, two species with the same traits are considered as the same species having the same traits.

Every niche, and so every species, is defined by K separate traits, one for each of the K dimensions. Thus, the species identity s can be associated with a binary number:

$$\mathbf{s}=(o_0,o_1,o_2,\mathrm{\dots }{o}_{K-1})$$

The index o_k is 0 or 1 depending on the trait, the position of the species relative to axis k, which can also be associated with a unique decimal number s, where 0 ≤ s ≤ 2^K − 1.

Thus, for any species, s, its functional relationships can be obtained by converting to binary. If the binary kth digit is ‘0’ then species-s likes a low value of niche factor k and if it is a ‘1’ then species-s likes a high value of niche factor k. When drawing diagrams, we follow matrix convention where the first index refers to the row number and the second to the column number. Thus, for K = 2, 01 is found on the lower row, rightmost column.

While the corners of the hypercube define the species traits, the dividing lines define the volumes of niches and reflect the environment (Figure 1A), which changes with time (see next section). The most obvious “visual” representation of the niche is as a hypercube in K-dimensional space. However, this excludes actual visual representation for K > 3. An alternative representation is through a series of nested cubes (Figure 1B).

The community hypercube is assumed to have a hypervolume of unity that is the sum of all the different niche hypercubes. For species-s the width on axis k is L_sk (see Appendix A for a list of symbols). The niche hypervolume of a species, is the product of its widths on all axes:

$$V_s=L_{s0}\cdot L_{s1}\cdot L_{s2}\cdot \mathrm{\dots }\cdot L_{s,K-1}=\prod _{k=0}^{K-1}{L}_{sk}(1)$$

Given this potential community of 2^K species, the environment will select the species that flourish. At any time, the environment has a configuration for each niche factor k. Axes may also represent stresses, such as radiation, or chemical pollution. A positive trait for a stress means the species is tolerant and has a potential advantage over other species. An example with two factors is given in Table 1.

TABLE 1

Table 1. Niche representations for two niche factor axes (K = 2) in the example of Figure 1 and the corresponding niche sizes when the environment is warm and moist.

The niche width, L_sk, is the outcome of the interaction of species orientation with the environmental configuration. We assume each niche’s width on axis k has two possibilities:

$$L_{sk}=\{\begin{array}{c}{U}_k\hfill \\ 1-U_k\hfill \end{array}(2)$$

Since we are working on the unit hypercube the total width of the two traits on any axis must add to unity. In general, U_k is different for each axis.

As an alternative way to quantify the two states on an axis, we introduce the constant B, such that U_k∝B and 1−U_k∝1/B. This, together with (2), and introducing a normalizing constant Γ_k, leads to the values for traits on each axis k:

$$L_{sk}=\{\begin{array}{c}\hfill {\mathrm{\Gamma }}_k\cdot B_k\hfill \\ \hfill {\mathrm{\Gamma }}_k/B_k\hfill \end{array},{\mathrm{\Gamma }}_k=1/(B_k+1/B_k)(3)$$

The reason for this alternative representation is that when dealing with populations it is often preferable to work with logarithms. When we take logarithm of Equation (3), it assumes a simple symmetric form:

$${\mathrm{\lambda }}_{sk}=\ln L_{sk}=\{\begin{array}{c}\hfill {\mathrm{\gamma }}_k+a_k\hfill \\ \hfill {\mathrm{\gamma }}_k-a_k\hfill \end{array}(4)$$

We calculate the factors a_k = lnB_k and γ_k = lnΓ_k through the formulas

$${\mathrm{\gamma }}_k=\ln \sqrt{U_k(1-U_k)},a_k=\ln \sqrt{\frac{U_k}{1-U_k}}(5)$$

Niche Factors and the Environmental Configuration

Clearly the configuration of the niche factors U₀, U₁, U₂, …, U_K−1 depends on the environment. In this paper, we will assume that U_k is an instance of a random variable taken from a distribution f(u). All the U_k’s are assumed independent and identically distributed. Note that even if the distribution is the same for all axes, any realization of the hypercube will in general have different configurations on each axis.

Special Case A: Broken stick model. If U is a realization of a uniform random variable:

$$\begin{array}{ccc}\hfill f(u)& \hfill =\hfill & \mathrm{\hspace{0.33em}1},\forall 0\le u\le 1\hfill \\ & \hfill =\hfill & \mathrm{\hspace{0.33em}0},\text{elsewhere}\hfill \end{array}$$

This has important similarities to the “broken stick” model used by MacArthur (1957) but differs in that we break each axis only once. Sugihara introduced a “sequential broken stick” model to model the community that would have a lognormal species abundance distribution (Sugihara, 1980). Our model also has important similarities to Sugihara’s model. The corresponding distribution for the niche factor is:

$$f_{\mathrm{\lambda }}(x)=e^x\mathit{\hspace{1em}}x\le 0$$

Note that here λ is the niche width in log space, so that this distribution comes simply from a change of variable.

Special Case B: Symmetric alternating states for all axes. An important special case, that will be explored in this paper, is when all traits have two possible values, so f(u) is a dichotomous distribution. This may be written as follows:

$$f(u)=\frac{\mathrm{\delta }(u-u_0)}{2}+\frac{\mathrm{\delta }(u-(1-u_0))}{2}$$

where the function δ(x) is the Dirac delta function. In this case, u₀ is the same for all axes, which means that also B is the same for all axes, so that u₀ = ΓB and 1–u₀ = Γ/B. Also, the distribution of log of niche factor, λ_sk, will be similarly dichotomous:

$$f_{\mathrm{\lambda }}(x)=\frac{\mathrm{\delta }(x-{\mathrm{\gamma }}_0+a_0)}{2}+\frac{\mathrm{\delta }(u-{\mathrm{\gamma }}_0-a_0)}{2}$$

Since B is the same for all axes, the unit volume of the community hypercube can be written as:

$$\begin{array}{c}\hfill 1={[\mathrm{\Gamma }B+\frac{\mathrm{\Gamma }}{B}]}^K={\mathrm{\Gamma }}^K[B^K+K{B}^{K-2}+K(K-1)B^{K-4}+\mathrm{\dots }+\hfill \\ \hfill C_k^K{B}^{K-2k}+\mathrm{\dots }+\frac{1}{B^K}]\hfill \end{array}$$

revealing the states of the community: the volume of any niche is Γ^KB^K–2k for any k ∈ {0, 1, 2, …, K}, while there are $C_k^K$ niches of that size in the community hypercube. There are thus maximum and minimum values for niche volume:

$${\left(\frac{\mathrm{\Gamma }}{B}\right)}^K\le V_S\le {\left(\mathrm{\Gamma }B\right)}^K$$

Special Case C: Asymmetric alternating states for all axes. This is the same as Special Case B, except that the two states between which a niche factor can alternate, are not equally probable. This may be written as follows:

$$f(u)=q\cdot \mathrm{\delta }(u-u_0)+(1-q)\cdot \mathrm{\delta }(u-(1-u_0))$$

In this case too, B will be the same for all axes, with u₀ = ΓB and 1-u₀ = Γ/B. For q = 0.5, special case C is the same as Special Case B.

In general, to relate the niche widths of Equation (4) in a more precise way to the environment, we introduce the matrix term c_sk and the vector element a_k:

$${\mathrm{\lambda }}_{sk}={\mathrm{\gamma }}_k+c_{sk}\cdot a_k(6)$$

Here, we have defined a_k as the environmental configuration of the kth niche factor, $a_k=\ln \sqrt{U_k/(1-U_k)}$, with U_k a realization of the random variable f(x). We define c_sk as the orientation of species-s to niche factor-k: if species-s responds positively to niche factor-k then c_sk = +1 and if it responds negatively to niche factor-k then c_sk = −1. Specifically, c_sk = +1 if the kth digit of s (in binary) is 1, otherwise it is −1.

In the logarithmic domain, the niche volume of Equation (1), becomes a sum and, for species-s, the overall niche volume can be written by substituting (6) as follows:

$$v_s=\ln V_s=\sum _{k=0}^{K-1}{\mathrm{\lambda }}_{sk}=\sum _{k=0}^{K-1}{\mathrm{\gamma }}_k+\sum _{k=0}^{K-1}{c}_{sk}{a}_k(7)$$

The community niche volume can be written in matrix form:

$$\mathbf{v}=K\overline{\mathrm{\gamma }}+\mathbf{C}\cdot \mathbf{a}(8)$$

Where $\overline{\mathrm{\gamma }}=1/K\sum {\mathrm{\gamma }}_k$. Thus, the log-hypervolume of the niche is a constant plus the product of a matrix representing species traits with a vector representing the environmental configuration.

Population Dynamics and Turnover

We associate the niche hypervolume with population size. So, if the entire community size is J, the number of individuals in species-s is the niche hypervolume times J, so X_s = JV_s and for the dynamics of the log-population vector x = lnJ+v we have:

$$\mathbf{x}(t)=\ln J+\mathbf{v}(t)=\ln J+K\overline{\mathrm{\gamma }}(t)+\mathbf{C}\cdot \mathbf{a}(t)(9)$$

The time-dependent environmental configuration vector, a(t) of size K, expresses the changing environment, while the orientation matrix C (of size S × K) describes the association between the species traits and this changing environment. This matrix is constant and is easy to construct. Its rows are simply all the numbers 0 to 2^K, written in binary form, with the ones remaining as +1 and the zeroes replaced by −1. The dimensions of this matrix are 2^K × K. Each species occupies one row and each column is a niche factor axis. Each column of C (or each row of C^T) has a sum of zero.

An important question is how we describe environmental changes that drive a(t), the niche factor axes. The elements of a are the configurations of the niche factors of each axis. At each time-step, each component of a_k(t) is based on U_k a realization of the random variable from the distribution f_U(x), specifically $a_k(t)=\ln \sqrt{U_k/(1-U_k)}$. We assume that axes have separate timescales, namely each axis has different timescale of change, τ_k, see Figure 2A. Moreover, we will assume that timescales are equally spaced logarithmically, such as τ_k∈{1, 2, 4, 8, …, 2^K–1} time units. We label the axes with indices 0, 1, 2, 3, …, K − 1 associated with the respective timescales 1, 2, 4, 8, …, 2^K–1 units. We will write the vector as follows:

$$\mathbf{a}(t)=[a_0(t),a_1(t),\mathrm{\dots },a_{K-2}(t),a_{K-1}(t)]$$

Thus, the element a_k(t) of a(t) assumes a new state every 2^k units of time.

In this theory, we suppose that species’ own population dynamics are not important — they respond to the changes in the environment and reach equilibrium rapidly. Certainly, within this framework, starting from Equation (8), more detailed population dynamics could be constructed at the price of greater complexity.

Figure 3 shows the typical pattern of fluctuations of the model. This is significantly different from the pattern where populations fluctuate within a basin of attraction around a fixed equilibrium. Here, the population remains within a “basin” only within a timescale. Long-term it departs from any basin of attraction. It is also different from populations in the neutral theory, where population trajectories that are essentially random walks (Brownian motion) that can drift anywhere within the bounds [0,J]. In the 1/f model (Halley and Inchausti, 2004), the populations can also drift but require a much longer time to depart far from the initial value.

FIGURE 3

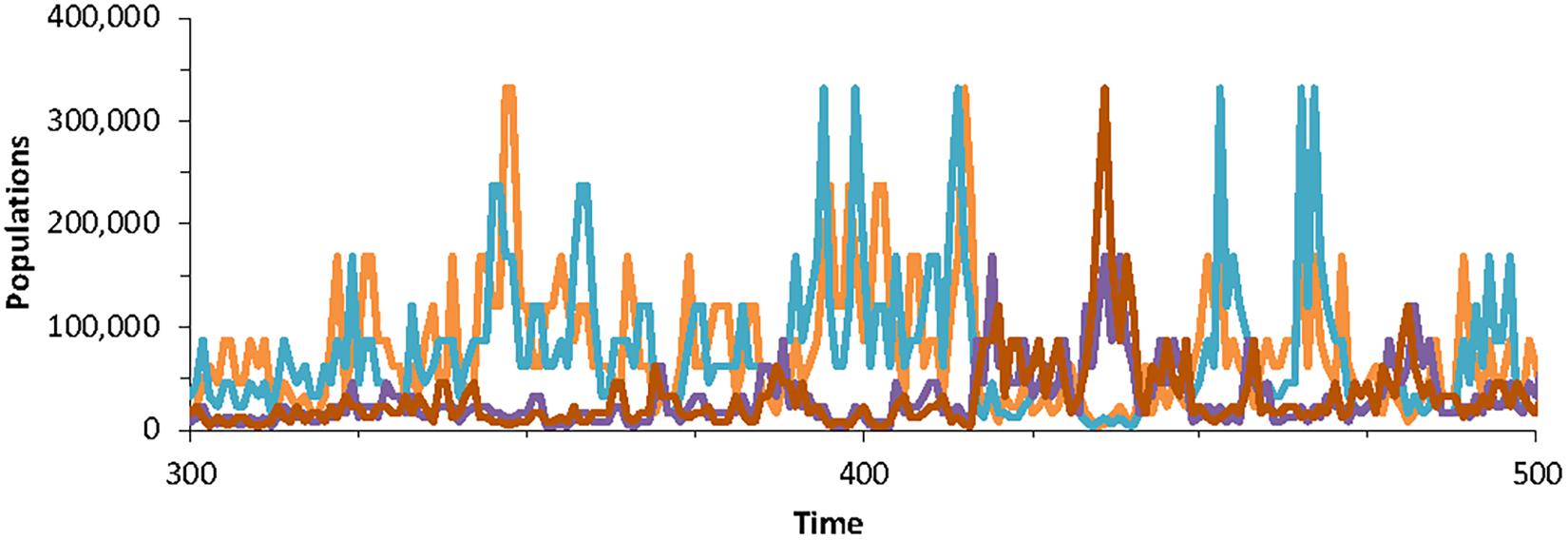
Figure 3. Population dynamics of four randomly chosen species in the community model generated using Special case B, with parameters K = 7, with J = 5 × 10⁶ for 200 time-steps. The dynamics are according to Equation (10) and thus do not include extinction-colonization.

The abundance for species-s is given by (8) as:

$$x_s(t)=K\overline{\mathrm{\gamma }}(t)+\ln J+\sum _{k=0}^{K-1}{c}_{sk}{a}_k(t)(10)$$

Equations (8) and (10) describes the dynamics of all the populations in the community in the absence of extinction and colonization or speciation. However, we can include local extinction or extirpation, which plays a major role in the ecological community, as a form of ecological turnover, offset by colonization. The population is extirpated if it falls below a minimum viable population, if x_s(t) < m, creating an empty niche. Recolonisation of an empty niche can be modeled by a constant probability. Thus, the overall population dynamics can be expressed in island-biogeographical terms. For any species s, the probability that the species is present at any time t changes as follows:

$$p(t+1)=c+\left[1-c-e_s(t)\right]p(t)(11)$$

Here c is the probability of colonization per unit time and p is the probability that the species is not extinct at time t. The probability of extirpation at time t is e_s(t) is the probability of the log-population being less than m, namely:

$$e_s(t)={\int }_{-\mathrm{\infty }}^m{f}_{xs}(z)\mathit{d}z(12)$$

This equation differs from the usual equation of island-biogeography because e_s is time dependent. If extinction occurs, then the niche becomes empty. Thus, in the presence of extinction, we rewrite Equation (10) as:

$$x_s(t)=\{\begin{array}{c}\hfill K\overline{\mathrm{\gamma }}(t)+\ln J+\sum _{k=0}^{K-1}{c}_{sk}{a}_k(t),\forall x_s(t-1)\ge m\hfill \\ \hfill <m,\forall x_s(t-1)<m\mathit{\hspace{1em}\hspace{1em}\hspace{0.5em}}\hfill \end{array}(13)$$

Example. Suppose K = 3, J = 1000, B₀ = B₁ = B₂ = 3 (Special Case B). Then there are 8 species, Γ = B/(1+B²) = 0.3, and the two values of niche width are L_s(t₀) = 0.9 or 0.1, from Equation (2A). The 8 niches have 4 possible sizes: 729, 81, 9 and 1 with one, three, three and one species, respectively. Thus, at any time there will be one niche with 729 individuals, three with 81, three with 9 and a single niche with one individual. The identities of the niches will move around according to the environmental signal, which we assume to be at t = t₀ and a(t₀) = lnB × (−1, −1, −1)^T. In the log domain, we have lnB = 1.10 and γ≈−1.20, while the orientation matrix C is:

$$\mathbf{C}={\left[\begin{array}{cccccccc}\hfill -1\hfill & \hfill +1\hfill & \hfill -1\hfill & \hfill +1\hfill & \hfill -1\hfill & \hfill +1\hfill & \hfill -1\hfill & \hfill +1\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill +1\hfill & \hfill +1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill +1\hfill & \hfill +1\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill +1\hfill & \hfill +1\hfill & \hfill +1\hfill & \hfill +1\hfill \end{array}\right]}^T$$

Thus, using Equation (8), the population vector x at time t, is given by:

$$\mathbf{x}(t)\cong \mathrm{\hspace{0.33em}3.30}+(1.10){[-3,-1,-1,+1,-1,+1,+1,+3]}^{\text{T}}$$

Note, that no reference is required to the previous states of the population here. Thus, in the absence of extinction, the states of the population are given entirely by the environmental process vector a(t).

The Zero-Sum Property and Linearity

One of the desirable properties for a model of the ecological community is the zero-sum property. This means that changes in populations add up to a constant community size. For example, this is also an implied property of neutral model that also has the attribute of a constant number of individuals. Here, as all niches are a partition of the unit hypercube then, by definition, the total hypervolume of all niches is unity. Thus, in Equation (8) even though the relative sizes of niches change, the overall community size always adds up to J individuals.

Surprisingly, the log-populations in this niche-space may also have the zero-sum property. Even if the abundances themselves are zero-sum, there is usually no reason for the log-populations to follow suit. To see how this second zero-sum property may emerge, we find the total community size by summing Equation (10) over all species:

$$\begin{array}{c}\begin{array}{ccc}\hfill \sum _{s=0}^{S-1}{x}_s(t)& \hfill =\hfill & \sum _{s=0}^{S-1}\left(K\overline{\mathrm{\gamma }}(t)+\ln J\right)+\sum _{s=0}^{S-1}\sum _{k=0}^{K-1}{c}_{sk}{a}_k(t)\hfill \end{array}\hfill \\ =\left(K\overline{\mathrm{\gamma }}(t)+\ln J\right)S+\sum _{s=0}^{K-1}{a}_k(t)\sum _{k=0}^{s-1}{c}_{sk}\hfill \\ =K\cdot S\cdot \overline{\mathrm{\gamma }}(t)+S\cdot InJ\hfill \end{array}(14)$$

The final term, in the second line of (14), disappears because we have a summation over a column of the orientation matrix, which sums to zero (see section “Population Dynamics and Turnover”), something that pertains irrespective of which distribution f(x) holds for niche factors. The second term on the last line of (14) is constant in time, but not the first term. This means that, in general, the total community size changes with time and therefore there is no zero-sum property. For Equation (14) not to change, γ_k should remain constant. The form of γ_k, given by Equation (5), shows that γ_k will remains constant in time provided U(t)[1−U(t)] does not change. This happens for a restricted class of distributions, including the dichotomous distributions of Special cases B and C. For such distributions, all population changes can be expressed relative to the mean log-population, $K\overline{\mathrm{\gamma }}+\ln J$, so that Equation (10) can be written as:

$$\mathbf{z}(t)=\mathbf{C}\cdot \mathbf{a}(t),\mathbf{z}(t)=\mathbf{x}(t)-\left(K\overline{\mathrm{\gamma }}+\ln J\right)(15)$$

This is important because it means that for this class of distributions of environmental change, population changes in the community can be related linearly to changes in the environment through Equation (15), which is a major mathematical simplification.

Variance in Time

According to Pimm (1991), the ecological community is fundamentally non-stationary. Subsequent studies of variance as a function of time in ecological populations found that this increase of variance was universal (Inchausti and Halley, 2001, 2002). The model of variability most consistent with ecological time-series was a 1/f-noise model for which variance increases linearly with the logarithm of time (Halley, 1996; Halley and Inchausti, 2004). It is thus important to see if such a pattern can arise in a community model (Figure 4).

FIGURE 4

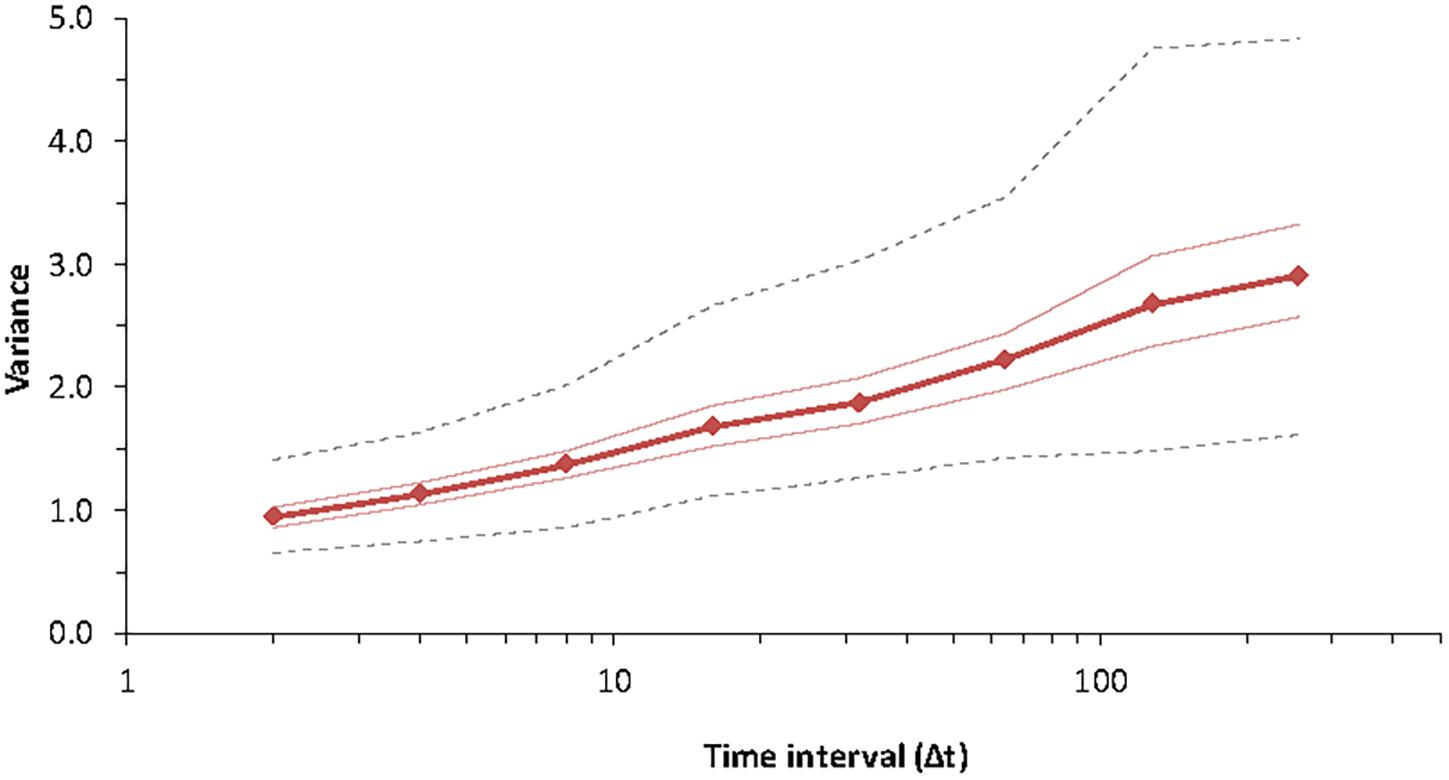
Figure 4. Pattern of variance growth in the model with observation time for Special Case B for species #3 (chosen at random) of the community, with parameters K = 7 and B = 1.9, J = 4 × 10⁴ for 256 time steps. The lines indicate the median, minimum, maximum and the two hinges (25th and 75th percentiles) for 1,000 replicates. The dynamics proceed as for Equation (10) and do not include extinction or colonization.

Here, the relevant question is how the population will fluctuate on short timescales (Δt << 2^K). Let us now consider the time series of length T << 2^K for species-s with log-population {x_s(1), x_s(2), …, x_s(t), …, x_s(T)}. Let us assume that each niche-factor has the same variance Var{U_k(t)} = V₀. The variance of this time series is the expected value of the variance of (10), which is:

$$\begin{array}{ccc}\hfill Var\left\{x_s(t)\right\}& \hfill =\hfill & Var\left\{\ln J+K\overline{\mathrm{\gamma }}(t)+\sum _{k=0}^{K-1}{c}_{sk}{a}_k(t)\right\}\hfill \\ & \hfill =\hfill & \sum _{k=0}^{K-1}Var\left\{{\mathrm{\gamma }}_k(t)+c_{sk}{a}_k(t)\right\}\hfill \end{array}(16)$$

Our problem reduces to finding the variance of one of the components γ_k(t) + c_ska_k(t). This is done rigourously for Special Case B in Appendix B but the following more general argument holds for all kinds of distributions.

If the cycle time is very long there is no variance because the series length is much shorter than the cycle time, that is T << τ_k, so the components associated with axis-k are unchanging and so the variance contribution is zero. At the other extreme, if the cycle time is very short, shorter than the distance between successive samples, then τ_k << T and we have:

$$\begin{array}{l}Var\left\{{\gamma }_k(t)+c_{sk}{a}_k(t)\right\}\hfill \\ =\frac{1}{2}Var\left\{\ln U_k+\ln (1-U_k)+c_{sk}\ln U_k-c_{sk}\ln (1-U_k)\right\}\hfill \\ =\frac{1}{2}Var\left\{(1+c_{sk})\ln U_k)+(1-c_{sk})\ln (1-U_k)\right\}\hfill \\ =Var\left\{\ln U_k\right\}=V_0\hfill \end{array}$$

The last line results because, since all the c’s are ±1, then either we have Var{lnU_k} or Var{ln(1−U_k)}, so provided the distribution of Var{lnU_k} and Var{ln(1−U_k)} are the same, we have the simple result for τ_k << T. Thus,

$$\begin{array}{ccc}\hfill Var\left\{{\mathrm{\gamma }}_k(t)+c_{sk}{a}_k(t)\right\}& \hfill =\hfill & 0,{\mathrm{\tau }}_k>>T\hfill \\ & \hfill =\hfill & V_0,{\mathrm{\tau }}_k\mathit{<<}T\hfill \end{array}$$

Thus, as a series gets longer, as it reaches each time-constant τ_k = 2^k, its variance increases by V₀. In the case where the time-constants are arranged uniformly on the log-axis, then the variance increases linearly in logarithmic time, as is the case for 1/f noise (Inchausti and Halley, 2001):

$$W_s\approx \sum _{2^k<T}{V}_0\approx V_0{\log }_{2}T(17)$$

This is equivalent to saying that variability increases with time — the “more time means more variation” effect (Pimm and Redfearn, 1988; Inchausti and Halley, 2002). This log-pattern is characteristic of 1/f-noise, which was the model most consistent with ecological time series, for which variance increases linearly with the logarithm of time (Halley, 1996; Halley and Inchausti, 2004). This result can be used, if we have an empirical time-series, to estimate V₀ from the rate of increase of variance. However, if the time constants are arranged otherwise, we could observe other patterns of variance increase (Halley and Inchausti, 2004).

The Species Abundance Distribution

Within real communities, there are many rare species and a few common ones. The ensemble species abundance distribution at any fixed time is often observed to be lognormal. Some have questioned the suitability of the lognormal (Williamson and Gaston, 2005). McGill (2003) argued that many theories generate such bell-shaped distributions and having a lognormal species abundance distribution is a weak test for a model. Nevertheless, the lognormal pattern is so frequently encountered in field data (Ulrich et al., 2010) that it constitutes an important model property. The niche-hypercube model leads naturally to a lognormal species abundance distribution.

In our model, the cube is divided into two pieces at a random point, 0 < U₁ < 1. Then the process is repeated independently along a second axis to get 0 < U₂ < 1 (Figure 1). At this point, the cube contains four sub-cubes. Repeating the process in higher dimensions creates new sub-cubes, 8, 16 and so on. For a process of k repetitions, we have 2^k segments in total. Without loss of generality, a sub-cube has a volume given by Equation (1). Since the U_k’s are random variables, it follows from Equation (2) that each L_sk is a random variable on [0,1]. If we take logarithms, we get Equation (7), where each λ_sk = ln(L_sk) is a random variable with a distribution g(x) on (−∞,0). Suppose this distribution has an expected mean of μ and an expected variance of σ². Then we can use the central limit theorem, provided all the moments of the distribution g(x) are finite, to show that the sum of k of these (for large k) will be approximately normal, with mean kμ and variance kσ², so that:

$$v_s\sim N(k\mathrm{\mu },k{\mathrm{\sigma }}^2)(18)$$

The fragments may be considered as species and their size the number of individuals of that species. If there are J individuals in the community any species has a population Je^z. This is a lognormal random variable.

In Special Case A, the distribution f(x) is uniform on [0,1], while the distribution of the logarithm of this is exponential with a mean of −1 and a variance of +1. Thus, the distribution of the niche hypervolume v_s is expected to be normal:

$$f_{vs}(x)=\sqrt{\frac{2}{\mathrm{\pi }K}}\exp \left[-\frac{{\left(x-K\right)}^2}{2K}\right](19)$$

This means, from Equation (9), that x_s is also distributed normally and hence that N_s has a lognormal distribution.

In Special Case B, the distribution f(x) has an expected mean of γ and an expected variance β ². Thus, the distribution of the niche hypervolume is expected to be:

$$f_{vs}(x)=\sqrt{\frac{2}{\mathrm{\pi }{\beta }^{2}K}}\exp \left[-\frac{{\left(x-K\mathrm{\gamma }\right)}^2}{2K{\beta }^2}\right](20)$$

Again, x_s will be distributed normally, so N_s has a lognormal distribution.

Both the species abundance distribution and the distribution of abundance in time are shown in Figure 5. The time series for a fixed species s at different times, namely of the set {x_s(1), x_s(2), x_s(3), …, x_s(T)} is found to be lognormal. This might be expected because each species in time traces out a sort of random course within the niche space defined by the species abundance distribution. However, in this case, the variables are not independent between different time-steps. Clearly, if T is very large, then the time-series will yield a distribution following (23), so we should expect this limit of the distribution in time to follow a lognormal.

FIGURE 5

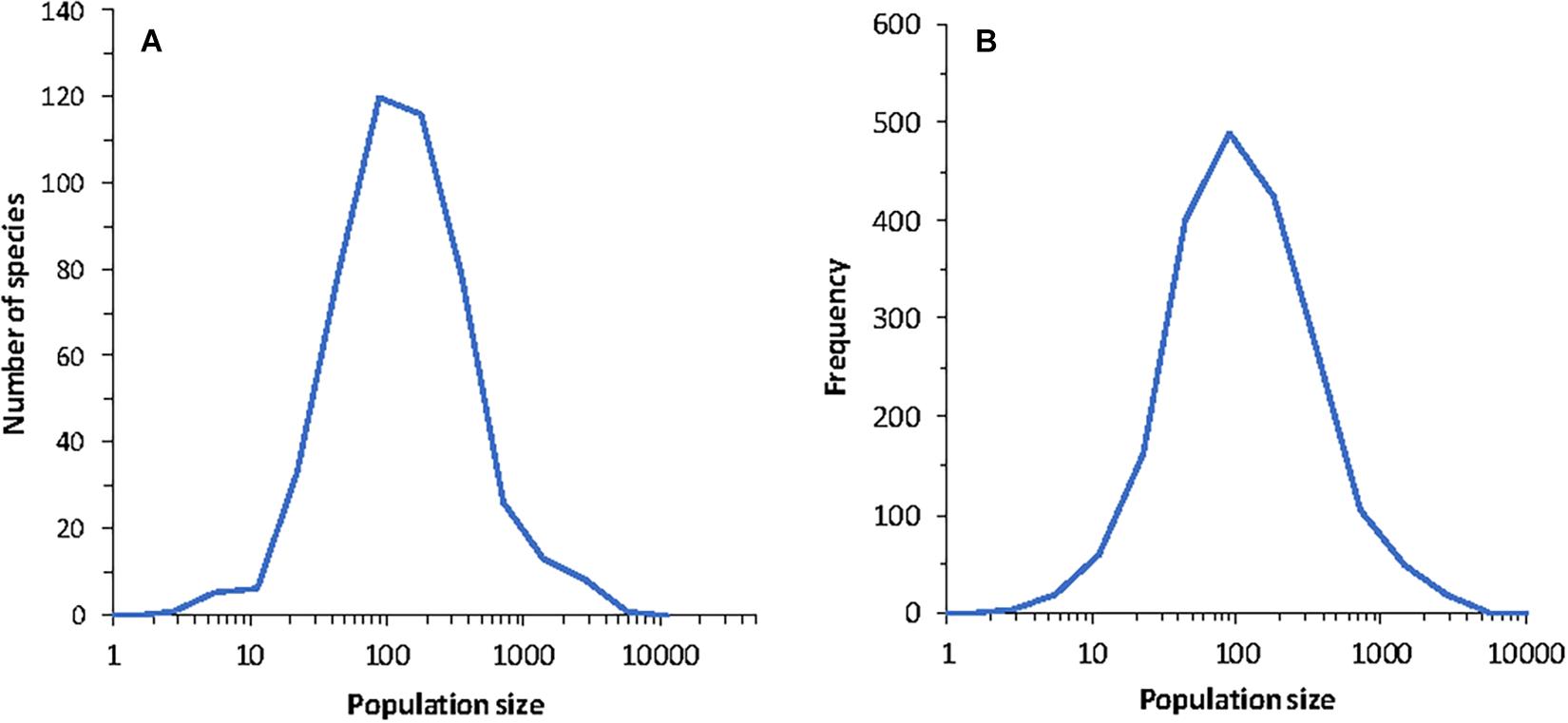
Figure 5. (A) Species abundance distribution for a single community in one run of the model. (B) Histogram of population size in time for a run covering 2,000 years for a randomly chosen species from the community. The parameters of the model were J = 10⁵, K = 9, B = 1.5 and MVP = 2. The dynamics are according to Equation (10) and do not include extinction or colonization.

Applications Using Simulation

The examples in this section all use Special Case B. The biodiversity of the community typically determines the number of dimensions K that must be used, since S = 2^K. The central parameter B is the measure of the fundamental variability of each niche factor and of the community. We can estimate this from the scaling behavior of population fluctuations. Together, these parameters describe the community and how it interacts with the environment.

In problems involving population dynamics, we can define the number of individuals in the community, J. We can calculate this for various types of organisms as a density of individuals per unit area. Thus J₀ = ρA₀. However, the magnitude of J becomes important mainly when relating problems such as extinction, for which we must also choose a value for the minimum viable population, m. Given the choices of the parameters above, this fixes the number of extinctions expected in each time-step of the model. It is also possible to choose the colonization probability.

Once the foregoing parameters have been chosen, the others follow and further changes in the model relate to the specific questions being asked. In problems involving community dynamics, one of the most difficult tasks is fitting the community observed to the niche hypercube. Although the explicit correspondence of the axes to specific species traits is not needed, it is seldom possible to find an integer K corresponding to the known species in the community. Provided that 2^K ≥ S₀, there are more niches in the hypercube than species, so some cells have zero population (empty niches).

For the applications which follow, we parameterised simulation models in C++ and an abridged version on an Excel spreadsheet.

Response to Habitat Reduction and Extinction Debt

When human actions reduce the size of a habitat, there follows a decrease in the overall population in the community. This leads to a decrease in the number of species, as reflected in the species-area relationship. This loss of species does not follow immediately. The community may appear to get along for a while without the loss of any species. Later, however, these extinctions will happen – this is the phenomenon of extinction debt. Extinction debts have been observed or inferred over a range of scales from months to thousands of years and depend on various covariates of which the strongest is the area of the habitat (Halley et al., 2016). One of the challenges of modeling extinction debt is this range of timescales, from a few weeks to thousands of years, virtually into evolutionary time.

From a theoretical perspective, two types of community mechanism explain extinction debt. One of these features in the original extinction debt study by Tilman et al. (1994) based on a Tilman’s spatial competition model (Tilman, 1994). In this model, the delay arises from the combined decline of various species found with metapopulations below the threshold when habitat is lost. An alternative approach was based on neutral drift (Halley and Iwasa, 2011). In a neutral model, all species perform random walks due to demographic stochasticity. When habitat is lost and the community shrinks, the locus of each species’ walk is forced closer to zero. As a result, species all have a higher probability of extinction, not matched by colonization. While this forces the community to lose species, it takes time. The dynamic hypercube model in this paper provides a third theoretical mechanism that leads to delayed extinctions. We can view the loss of area of a community as a general loss of hypercube volume. This reduces the populations of all species proportionally, including a loss of the lower limit. In our model, at any time, there is a species at the minimum population size, where it is vulnerable to extinction. As in the neutral-drift mechanism, this is a stochastic mechanism.

Delayed extinction has major implications for conservation. For example, how much time will pass before the extinctions start to happen? How long before the extinction debt is “paid”? Typically, we try to predict the rate of loss of species after a sudden loss of area, assuming we know the initial number of species. This problem has been addressed for the neutral model several times (Gilbert et al., 2006; Halley and Iwasa, 2011; Hugueny, 2017). The advantage of the model presented here for this kind of problem is that it is suitable for looking at a wide range of timescales.

We can model extinction debt by simulation. For this, the key question is the relationship between minimum viable population, m, and the minimum niche size, x_min. If m > x_min, then the characteristic timescale is a single time-step since every time-step a different species is potentially subject to the minimum niche size. On the other hand, if m < x_min then extinction never happens (without an extra noise term). It thus makes sense that m is related to x_min. We will assume that if m = x_min then there is a probability of extinction ε, the probability of extinction at the minimum viable population.

Figure 6 shows the results for a specific set of parameters, depicting the decay in species number over time. Compared to the simplest expectation — exponential decrease in the number of species — the trajectories we predict are substantially different. An exponential curve that had the same expected number of species losses at the mid-point of the time considered (i.e., 50 years) suggests more species would survive in the short-term, but few in the long-term. Put another way, our model suggests a transient rapid loss of species, followed by a deceleration with eventually few losses. The trajectory is also different from the neutral model because the dynamic hypercube model yields losses on a relatively short timescale. It is notable that, overall, the pattern of biodiversity decrease follows the logarithm of time.

FIGURE 6

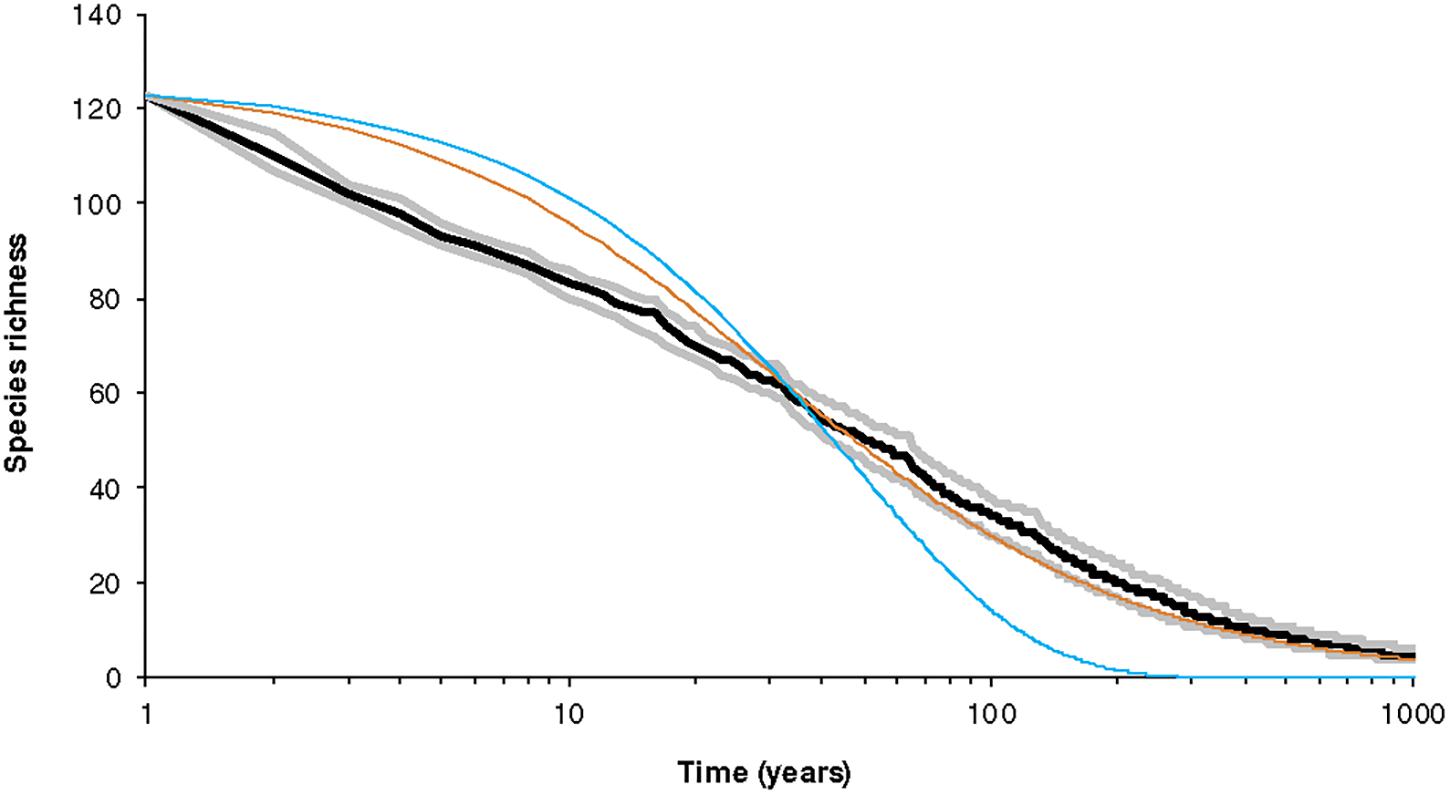
Figure 6. Pattern of survival as a function of time after habitat is reduced suddenly (at t = 0). The area initially has 123 species in broken-stick configuration with each species having a large population. The reduction in area is such that the reduced total number of individuals is 13,000 so the average population falls to just above 100. The model has K = 8 with B = 1.5 and the minimum viable population is set at M = 2. This figure summarizes 1,000 simulations. The curves correspond to the five quartiles of species richness at each year. Notice that decay occurs approximately linearly on a logarithmic scale. The black line is the median and the gray lines the hinges (25th and 75th percentiles). The other curves are the equivalent exponential decay (blue) and hyperbolic decay (brown, for neutral theory) with the same S₀ and the same t₅₀. The dynamics are according to Equations (11)–(13) and thus includes extinction. However, colonization is assumed to be zero.

It is worth noting that our model is like that Hubbell’s neutral theory, as model of unstable coexistence, where species eventually drift to zero unless there is a process of speciation or colonization (Huston, 1979; Chesson, 2000).

A Species-Time Relationship

The species-time relationship describes the increase in the number of species recorded at a site as that site is observed for increasingly long periods of time (Rosenzweig, 1995). In some ways the species-time relationship is the reverse of the species relaxation curve discussed above, though typically the emphasis is on the sampling aspects of the problem rather than recolonisation issues. This is because a process of Poisson sampling a fixed community at regular intervals will yield a steadily increasing cumulative number of observed species. For example, the corresponding author’s interest in Greek endemic orchids resulted in a collection of species on the University of Ioannina campus beginning with 5 in 2008. Thereafter sequence of annual new species was {0, 0, 4, 0, 1, 0, 4, 1, 1, 1} reaching a cumulative total of 17 in 2018. The randomness of a Poisson process does not convincingly explain this increase. The increase in species richness is clearly being driven by a combination of sampling processes and ecological processes on various scales (Preston, 1960; White et al., 2005). In contrast to the well-known species-area relationship, the species-time relationship has received relatively little attention. The evidence from wider studies of ecological communities suggests that species-time relationships are well fit either by power functions or by logarithmic functions. Large-scale analyses of species-time relationships have revealed both of these (White et al., 2005).

The species-time relationship is also very important in cases of real ecosystem restoration. For example, taking the case of the restoration of European forests after the ice age, Clark and Mclachlan (2003) showed that variance associated with population and species drift slows down or appears to reach an asymptote. In contrast the neutral model exhibits variance increasing almost linearly with time. A more niche-based model is thus needed to investigate problems like this. Clark and Mclachlan (2003) attributed the diminishing growth to a mechanism of density dependence and stabilization, other mechanisms may also contribute to this effect. Our model can explore this — it provides a powerful but simple niche-based dynamic framework to explore problems of this type. Figure 7 here shows a species-time curve for an environment that begins with no species but allows colonization to happen.

FIGURE 7

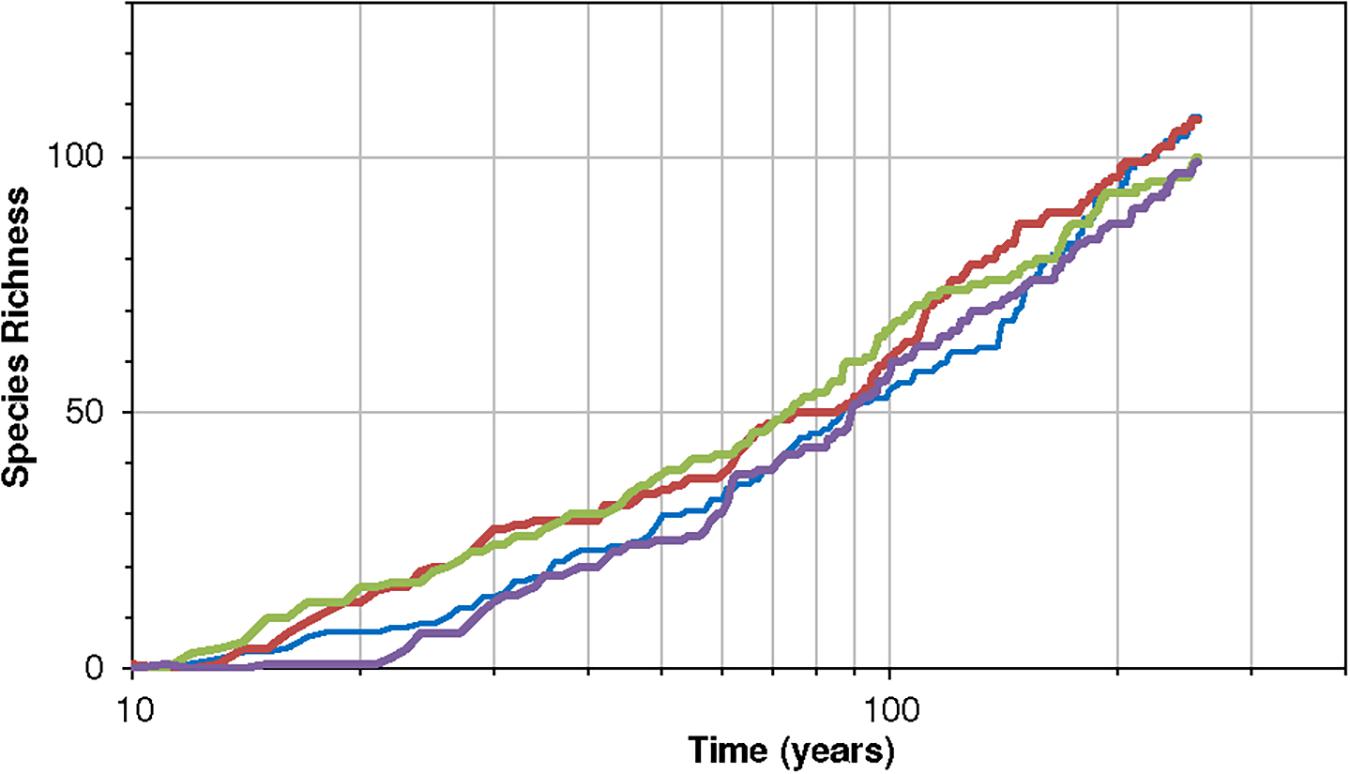
Figure 7. Four realizations of the species-time relationship for the community, with parameters K = 7 and B = 1.7, J = 4 × 10⁴ for 256 time-steps and the minimum viable population is M = 11. Notice the near linearity of the rise on a logarithmic scale of time (years). The probability of colonization is constant at 0.007 per species per year. The dynamics are according to Equations (11)–(13) and thus include extinction-colonization.

The above pattern exhibits a logarithmic type of increase in species richness with time. It demonstrates that a decelerating incidence of new species with time need not only imply a stabilization toward an asymptote or an equilibrium of the logistic variety. A slowing increase in species numbers also has a non-stationary interpretation because the 1/f community embodied in this model is non-stationary.

Community Turnover, Speciation and the Drift Into Evolutionary Time

One of the most interesting predictions of MacArthur and Wilson’s theory of island biogeography is that island communities, due to their rapid rates of extinction and recolonisation, are in a permanent state of flux regarding community composition. An observer returning to a small island, after a long absence, should find the new community virtually unrelated to the previous one. Similar community drift is also predicted in the neutral model because the species are constantly drifting in abundance relative to one another. Thus, in neutral theory, due to internal drift and lack of niche definition, any species can come to dominate the community. In fact, the drift associated with neutral dynamics has been used as a null model to calibrate the significance of changes attributed to global warming (Sgardeli et al., 2016). Both models feature community drift by virtue of their neutrality by virtue of not having niches. The absence of niches means that the community is not fixed and may drift between different structures.

The current model also generates community drift, but the drift means something different in this niche-based case. The model is neutral in a sense that no trait is associated with dominance, and so any of its species can dominate. It depends on which niche is pushed to the largest size by the environment. The drift of the community between different species compositions is also here. Figure 8 shows the average overlap as a function of time-separation.

FIGURE 8

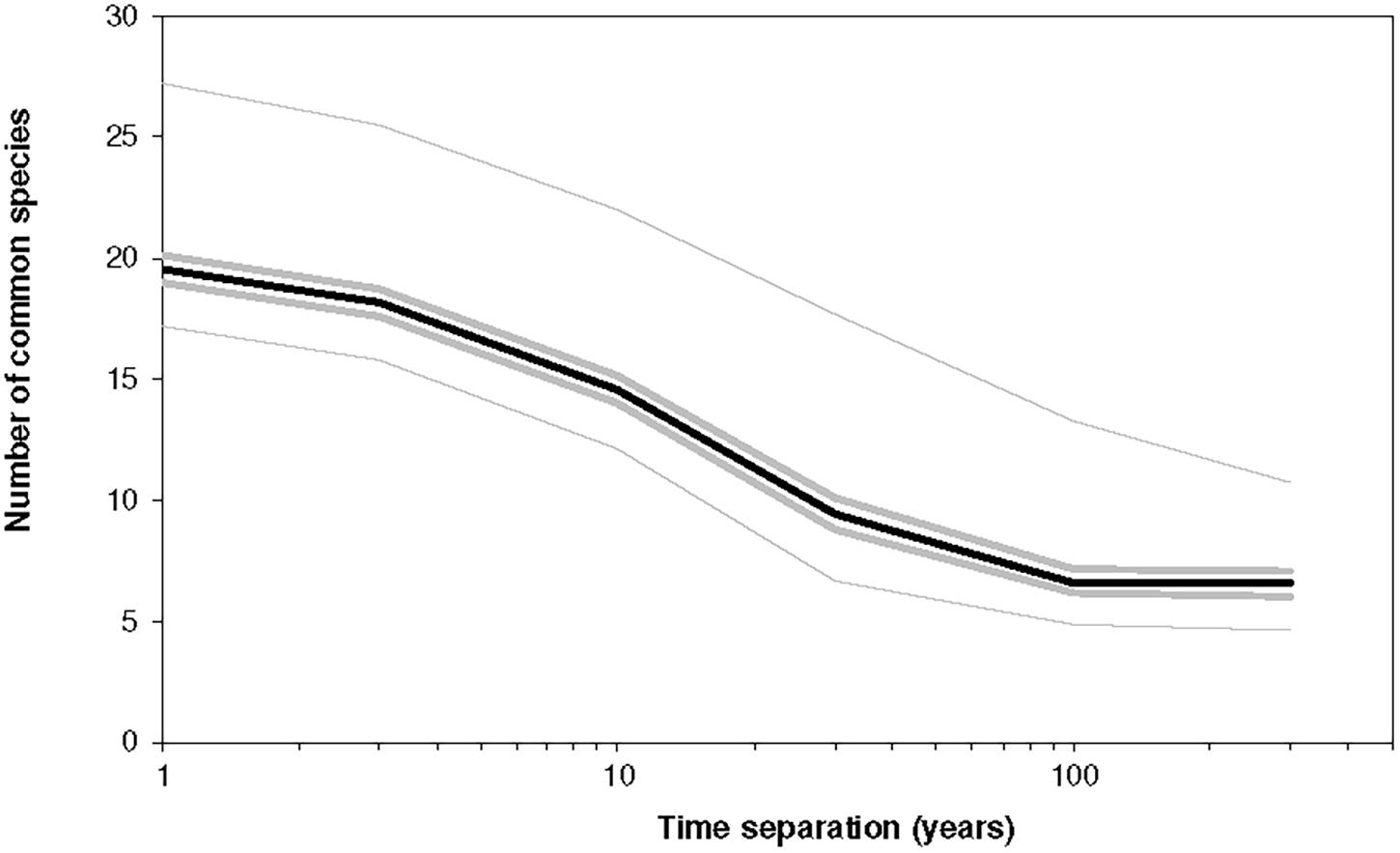
Figure 8. The number of common species between two instances of a community separated by Δt years for different values of Δt. The parameters were K = 6 and B = 1.5, J = 10⁴, and the simulation covered 750 time-steps. Initially, the community was unoccupied, but each niche was subject to a colonization probability of 0.02/year with an MVP of 22. The average diversity in any year (for the interval t = 50 to t = 750) was 21.3 ± 4.4 species, and the population was on average 4,000. The lines indicate the median, minimum, maximum and the two hinges (25th and 75th percentiles) for 1,000 replicates. The dynamics are according to Equations (11)–(13) and thus include extinction-colonization.

In this figure K = 6, so In this case the trait vector has the form (c₁,c₂,c₃,…,c₆) and the community has a potential size of 64 species and 10,000 individuals. Due to a high value of B, which leads to a high variability, coupled with a high value of minimum viable population (M = 22), the extinction rate was high. As a result, there were only ∼20 species present at any time, and so the average population was only ∼4,000, well below the carrying capacity of 10,000.

As the environment changes, different groups of species are favored. We can associate the twenty species in the community with a cluster of niches with larger volume. Each year the environment changes and causing some niches to shrink and others to grow. As this happens, those that shrink become more likely to lose their population while those that grow can be recolonised. The slowest of the processes changes on a scale of 64 years. Thus, on scales greater than 64 years, changes in the environment just retrace at random the previous configurations; there is no real evolution in the environment. So, for time separations above 64 the difference between the two communities does not decline further.

However, we can extend the current model to include variability on longer timescales. We can associate the still-longer timescales of environmental forcing in the evolution of other traits, ones that appear fixed on shorter timescales (Jackson and Overpeck, 2000). Thus, a system with a 25 traits and a vector (c₁,c₂,c₃,…,c₂₅) and a maximum timescale of 3.35 M years, reaches deep into evolutionary time. This includes a space of many millions of possible niches, which may be much larger than the community that interests us. The active community may be large enough to support only a thousand species. How can we visualize this? The initial community is inhabiting a hypercube in 10 dimensions, in which the traits are all changing, resulting in changing dominance hierarchies. However, on timescales above a thousand years, other traits will start to change too. What will happen, is that the initial community is no longer so competitive relative to some other species whose niche lies outside the initial hypercube. These species were not initially present in the community, but now there is an incentive for them to colonize or be created. Thus, the community will tend to drift according to the changing environment. Thus, if we fast-forward a few million years, the initial community moves within the larger hypercube to a different center (Figure 9). We still have a community whose short-term variability involves traits c1–c10 but other traits c10–c25 will also have changed so that very few species remain the same as for t = 0. This reflects the adaptive landscape of Wright as noted by Holt (2009) and Blonder (2018), but this is a dynamic adaptive landscape.

FIGURE 9

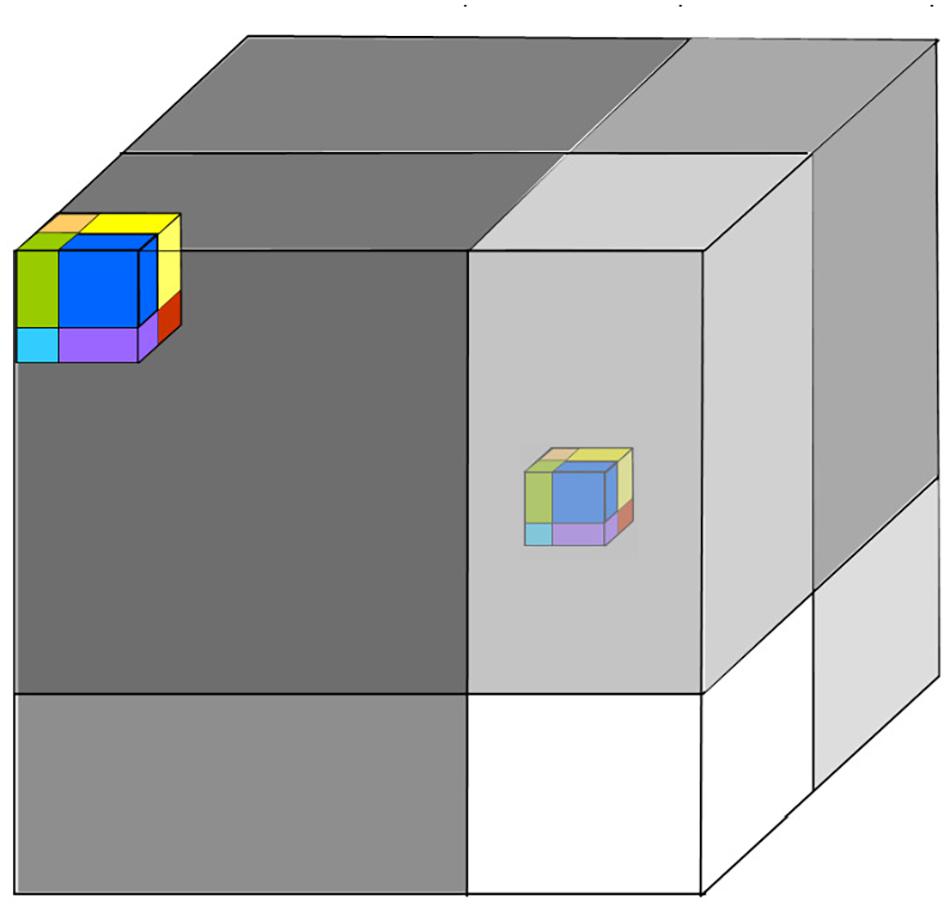
Figure 9. On a short timescale, the initial three axes are represented by a set of species in a compact niche, this changes and the cube moves around the hypercube on longer timescales.

Thus, we can see the ecological community slowly drifts away from its initial configuration. This shows that the current model can look at the ecological community in evolutionary time also. Hutchinson’s concept unifies ecological and evolutionary time. So, the community 1/f model described in this paper also predicts community drift on a longer evolutionary timescale. In contrast to the McArthur–Wilson and neutral model models, it is possible to identify traits. Part of this model is that there are processes in the environment that impact organisms that are stationary on a short timescale. They only change on longer timescales. But as they do, their influence is to change the balance toward organisms that were previously marginal. In contrast, organisms that were previously well-suited to the environment now find themselves “on the margins.”

Generality of Results

An important question that should be asked is how robust are the results we have obtained in the face of structural changes? The model we have developed rests on some fundamental assumptions that cannot be changed and other assumptions that are less critical which affect in different ways the results obtained for lognormality, variance growth and linearity.

The model is based on four fundamental structural assumptions. Foremost is the conception of Hutchinson’s niche itself, namely that the space in which a species operates can be defined by an area of hyperspace. A discussion by Leibold covers many of the difficulties this implies (Leibold, 1995). Most important among these is: since so many aspects of any species requirements are tied to interactions with other organisms, how can it be tied instead to a relatively fixed structure like a hypervolume? The main justification has always been that the simplification enabled by Hutchinson’s conception brings worthwhile results. Secondly, we have assumed a cuboidal geometry for niches. This contrasts with much of the work being carried out by researchers who are trying to build up a picture of the niche in more applied contexts such as discussed in the Section “Introduction.” Thirdly, we have assumed that organisms respond to each niche factor in a binary way: either a positive niche factor helps or hinders each species. This is obviously a simplification for the nuanced way that organisms respond to changing environment – real responses are rarely binary in this way. Finally, we assume that the states of the axes of the hypercube change independently. This too might seem restrictive for things like temperature and moisture that clearly influence one another. We argue that all these fundamental assumptions enable major simplifications in tractability, in parameterization and also enable intuitive understanding and visualization.

The most important additional assumption of the model is the choice of the distribution of niche factors, U_k on [0,1], for the different axes. The distributions have been assumed to be the same for all axes, though this could be relaxed at the expense of losing some results (e.g., for lognormality). The choice of distribution affects the dynamics considerably.

From Figure 10, It is notable that in the case of the models of Special Case B, the parameter B is an asymmetry parameter, increasing B increases the difference between species population sizes and the variability in time. In special cases A and B, there is no asymmetry between states of the niche factors. This means that every species, long-term, has the same average population; there are no privileged species. Introducing asymmetry between states (q≠0.5) means that the environment spends longer in some states than in others. Ecologically, this is clearly possible, as with moisture in an extreme desert, for example. Asymmetry, in this model, causes some states to have a greater average population size than others.

FIGURE 10

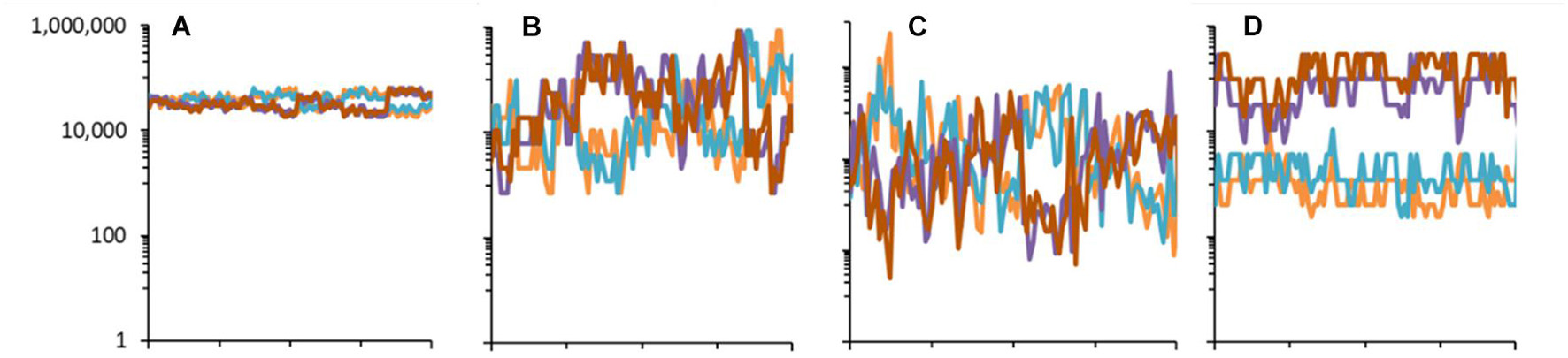
Figure 10. Population dynamics of four randomly chosen species in the community model generated using different distributions with parameters K = 7, with J = 5 × 10⁶ for 512 time-steps. (A) Special case B with B = 1.15. (B) Special case B with B = 1.73. (C) Special case A (uniform distribution for U). (D) Special case C with B = 1.73, with asymmetry q = 0.2. The dynamics are according to Equation (10) without extinction-colonization.

When deriving Equations (1–12), we made no special assumptions about the distribution of U_k, so these will hold in general. This is also true for Equation (18), the lognormality for species abundance distributions, which emerges from the central limit theorem. This only requires that there be a large number of axes and that the moments of ln(U_k) are finite. Thus, lognormality is a very general property of this model. Figure 11 shows this through the results of running different models.

FIGURE 11

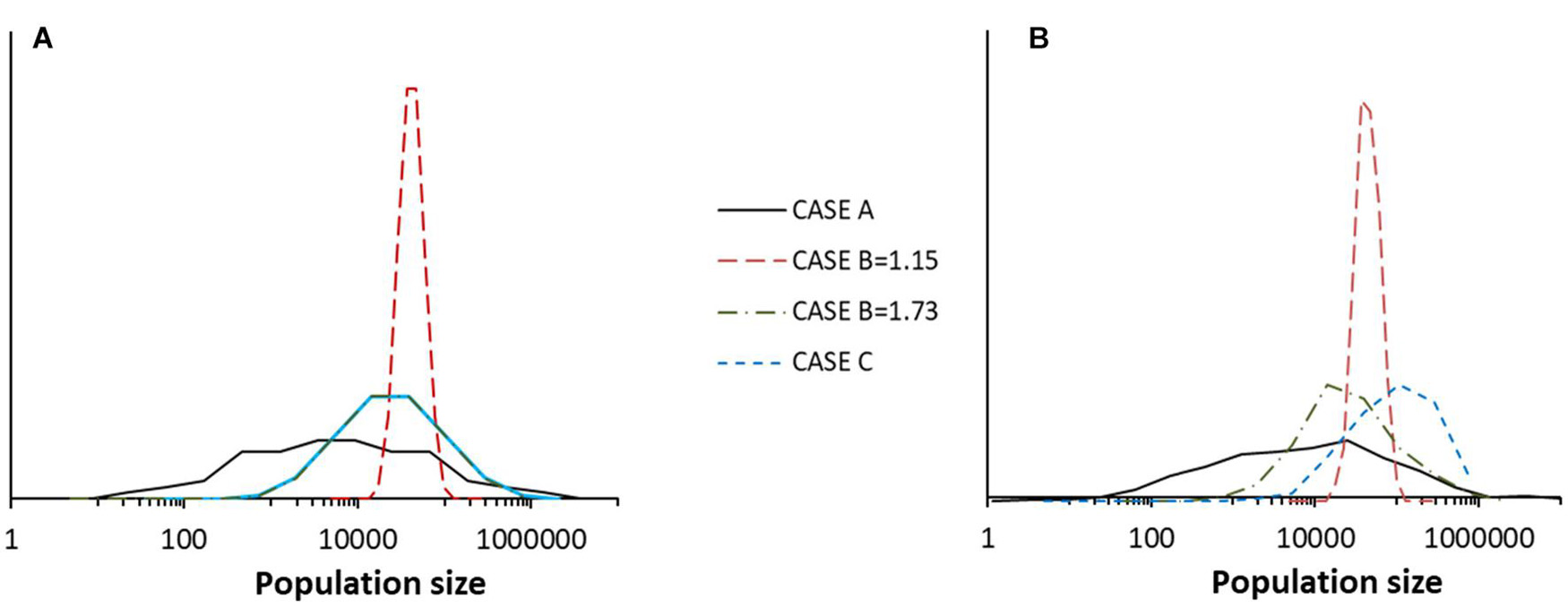
Figure 11. (A) Species abundance distribution for a single community in one run of four different models taken at time t = 511 in each case. The models were: Special case A, Special Case B with B = 1.15, Special Case B with B = 1.73 and Special Case C with q = 0.2 and B = 1.73. (B) For the same four models, the histogram of population size over time for a run covering 512 years for species number 126 in each case. The other parameters of the models were J = 10⁵, K = 7, and MVP = 2. The dynamics are according to Equation (10) without extinction-colonization.

In Figure 11, it is worth noting that the species abundance distribution (distribution of species population sizes in the community) conforms to a lognormal as shown by Equation (18). In simulations, this was also found for the distribution of species population sizes in time. It is also worth noting that in simulations, these two types of distribution were indistinguishable except in Special Case C, for which the distribution in time has a higher average value. This can be explained by the fact that in this asymmetric model, species have different distributions; some species have higher average populations than the overall community average.

The zero-sum property of log populations and the linear dependence of population on the environment, Equation (15), represent an important analytical simplification. This depends on the term $\overline{\mathrm{\gamma }}(t)$ being constant or not changing much. This only holds for a restricted set of models. For example, it does not hold for Special Case A but it does for Special cases B and C. In general, to secure constancy in time for $\overline{\mathrm{\gamma }}(t)$, we need U(t)[1 − U(t)] to remain constant in time, which is true for models where f(u) has a dichotomous distribution. From a biological perspective there is usually no reason to expect environmental variables to have a dichotomous distribution, although we often experience things this way (temperature is “cold” or “hot”, weather is “wet” or “dry”). The dichotomous distribution is thus a gross simplification for any environmental variable, but because of the Central Limit Theorem this may not matter too much. Even with such unrealistic distributions, model trajectories for populations are not so different from one using more biologically reasonable distributions.

The logarithmic increase of variance with time, as explained in Section “Variance in Time,” does not arise from intrinsic structure of the hypercube but is related to the arrangement of time-constants on the different axes, with each axis having a separate and unique timescale of switching and with timescales spaced geometrically. This assumption reflects that fact that often environmental changes themselves occur evenly across octaves. Other arrangements, with the time-constants spaced differently would produce patterns of variance increase more like fractional Brownian motion or fractional Gaussian noise (Halley and Inchausti, 2004). This is also the case for the manner of increase of the species-time curve.

A summary of the results in this paper, regarding the model, and the assumptions required to produce them, is given in Table 2 below.

TABLE 2

Table 2. The main additional assumptions required to produce the results in this paper.

While the simple switching between two states, producing “square” pulses (Figure 2B), may seem highly artificial, the resulting population changes, once all the niche factors are acting together, the artificial geometry of square pulses is no longer in evidence (Figure 3).

Equation (10) describes the population constraint caused by the environment but not the population response. The only part of this we have included is the extinction-colonization process modeled through Equations (11)–(13). Apart from these processes, this model does not include population dynamics, either interspecific or intraspecific. An easily envisaged extension of the model would be to include a demographic model in each niche, such as a simple discrete growth process with a carrying capacity, where the capacity value is equal to the niche hypervolume. The population dynamics within the niche would respond to changes in carrying capacity but there would be a delay due to the population dynamics. Interspecific interactions would be more challenging to incorporate but could be incorporated by including interactions between the species in different niches.

Discussion and Conclusion

We extend the niche-hypercube model of Hutchinson to form a niche-based dynamic hypercube (DH) model. This model is well-suited to exploring the dynamics of ecological communities from a niche-based perspective. The model has several features that make it desirable as a model of the community.

By dividing an ecosystem into a hypercube of finite size with a fixed number of organisms, the model reflects the fundamental limitation of energy input. Since only a fixed amount of energy arrives in an ecosystem, only a limited number of organisms of a given size can live there. Thus, when all niches are occupied, the populations add up to a constant community size. For a restricted class of niche fluctuations, this also holds for the logarithm of population; the fluctuations of the logarithm of population can then be expressed as a linear combination of the environmental fluctuations: z(t) = C.a(t), where z is a vector of all species’ populations and a represents environmental fluctuations and C is a constant orientation matrix.

The zero-sum principle is shared with the Hubbell’s neutral model among others. However, this model is not neutral in the same way as Hubbell’s, since each species occupies a fixed place in the community “hypercube.” Our model is still neutral with respect to biotic interactions. That is, competition is completely absent from this model and species do not interact in any other way. Their fitness is simply a by-product of their fundamental niche area, and there are no direct interactions between species.

For a very wide range of environmental fluctuations, this dynamic hypercube model generates a lognormal species-abundance distribution. Many theories generate similar distributions, bell-shaped on an octave scale, such as the zero-sum multinomial of the neutral model. Importantly, the dynamic hypercube reproduces the widespread observation that most individuals in the community belong to a small number of abundant species. This model also produces time-series for populations that are lognormally distributed in time, something observed as the most common distribution for a large number of ecological communities. Thus, as a species traces out its trajectory of abundance, the resulting histogram will tend to be lognormal.

As presented here, one of the most important features of the dynamic hypercube model is that it need not be stationary in time, depending on the environmental fluctuations on the niche factors. Studies of ecological time-series have shown that the “more time means more variation” effect is almost universal and is most consistent with a 1/f-noise model, where variance increases linearly with the logarithm of time. This type of environmental variability was used in the examples of this paper. The dynamic hypercube model provides a means to describe this variance growth in a community context. It shows that there is no balance of nature in one sense — as there is no permanent community. Nevertheless, neither is balance “discredited,” because communities remain similar for a long time and because certain quantities such as species richness and energy flow are conserved long-term.

This paper outlines three different applications in ecology, where the dynamic hypercube model provides results and new insights. One of the obvious applications of such as model, with conservation implications, is studying the dynamics of extinction. In recent years, because of the biodiversity crisis, there has been great interest in extinction risk. For example, species distribution models may be used to estimate extinction risk without a population-level model of the actual process of extinction. This has meant that things like extinction debt get overlooked. Certainly, the neutral model has been used to address the problem. Nevertheless, arguably the neutral model and its modifications cannot address issues on all timescales because they do not take environmental variability into account. The model described here spans both ecological and evolutionary time by taking into account the drift of the environment itself. Theoretical studies such as ours still have “barely scratched the surface of the universe of possible genetic architectures, landscape geometries, and demographic scenarios at play in niche evolution” (Holt, 2009). Nevertheless, by characterizing the drift of selective forces by an environment fluctuating on many scales as (Jackson and Overpeck, 2000) we are opening a bridge.

It is also worth noting that the dynamic hypercube model may be used to throw light on functional diversity. Since each axis of the model can be associated with a trait, it fits in with this perspective by dividing the ecosystem according to functional axes. The usefulness of a trait to any species changes in response to environmental changes. In this picture, the importance of different ecological traits rises and falls on different timescales. Some do so very rapidly but others change so slowly as the be imperceptible in most ecological studies. They correspond to the invisible long-term axes of our model, which only reveal themselves on longer scales, reaching into evolutionary time.

In constructing our model, we made several assumptions. The binary aspect, that each niche factor changes in a strictly binary fashion, is an obvious limitation relative to the real world. Another important limitation is the requirement that that each niche factor axis changes according to a specific and limited timescale. As we know that all niche factors tend to fluctuate over a range of timescales, a more realistic assumption would be for this to describe all axes, but that would severely limit the mathematical tractability of the system. Also, there are challenges with the interpretation of the size of the system we are describing. It is not obvious how the hypercube should interact with population size. Suppose we change the ecosystem’s size. Should this change the number of niches or just the size of number of individual organisms in the community? A change in the size of an ecosystem should immediately cause a loss of population, but should it lead to a contraction of the number of axes? Leaving aside the feedback element, we could associate a reduction of the axes with some physical reduction of the size of an ecosystem (e.g., a sea-level rise on an island), whereas the loss of the community within the hypercube reflects the killing of organisms without loss of habitat (e.g., a forest fire).

This model is a natural extension of the classical theory of the niche and of functional traits and brings many of the advantages of other dynamical theories such as the neutral model. It can be applied to numerous problems of community ecology to improve both explanatory and predictive power. It reveals how a community can have 1/f noise fluctuations and still be zero-sum. It is perhaps the first dynamic theory that links ecological time with evolutionary deep time.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

JH derived theoretical results and prepared figures. JH and SP wrote the manuscript. Both authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank reviewers DM and TK, also editor GB for helpful comments and insights.

References

Adler, P. B., HilleRislambers, J., and Levine, J. M. (2007). ‘A niche for neutrality’. Ecol. Lett. 10, 95–104. doi: 10.1111/j.1461-0248.2006.00996.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Barabás, G., D’Andrea, R., and Stump, S. M. (2018). ‘Chesson’s coexistence theory’. Ecol. Monogr. 88, 277–303. doi: 10.1002/ecm.1302

CrossRef Full Text | Google Scholar

Barros, C., Thuiller, W., Georges, D., Boulangeat, I., and Münkemüller, T. (2016). ‘N-dimensional hypervolumes to study stability of complex ecosystems’. Ecol. Lett. 19, 729–742. doi: 10.1111/ele.12617

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertuzzo, E., Suweis, S., Mari, L., Maritan, A., Rodríguez-Iturbe, I., and Rinaldo, A. (2011). ‘Spatial effects on species persistence and implications for biodiversity’. Proc. Natl. Acad. Sci. U.S.A. 108, 4346–4351. doi: 10.1073/pnas.1017274108

PubMed Abstract | CrossRef Full Text | Google Scholar

Blonder, B. (2018). ‘Hypervolume concepts in niche- and trait-based ecology’. Ecography 41, 1441–1455. doi: 10.1111/ecog.03187

CrossRef Full Text | Google Scholar

Blonder, B., Morrow, C. B., Maitner, B., Harris, D., Violle, C., Enquist, B. J., et al. (2018). ‘New approaches for delineating n-dimensional hypervolumes’. Methods Ecol. Evol. 9, 305–319. doi: 10.1111/2041-210X.12865

CrossRef Full Text | Google Scholar

Carvalho, J. C., and Cardoso, P. (2021). Decomposing the causes for niche differentiation between species using hypervolumes. Front. Ecol. Environ. doi: 10.3389/fevo.2020.00243

CrossRef Full Text | Google Scholar

Chase, J. M., and Leibold, M. A. (2003). Ecological Niches: Linking Classical and Contemporary Approaches. Chicago, IL: University of Chicago Press. doi: 10.7208/chicago/9780226101811.001.0001

CrossRef Full Text | Google Scholar

Chave, J. (2004). ‘Neutral theory and community ecology’. Ecol. Lett. 7, 241–253. doi: 10.1111/j.1461-0248.2003.00566.x

CrossRef Full Text | Google Scholar

Chave, J., and Leigh, E. G. (2002). ‘A spatially explicit neutral model of beta-diversity in tropical forests’. Theor. Popul. Biol. 62, 153–168. doi: 10.1006/tpbi.2002.1597

PubMed Abstract | CrossRef Full Text | Google Scholar

Chesson, P. (2000). ‘Mechanisms of maintenance of species diversity’. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343

CrossRef Full Text | Google Scholar

Chesson, P. L., and Warner, R. R. (1981). Environmental variability promotes coexistence in lottery competitive systems. Am. Nat. 117, 923–943. doi: 10.1086/283778

CrossRef Full Text | Google Scholar

Chisholm, R. A., and Pacala, S. W. (2010). ‘Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities.’. Proc. Natl. Acad. Sci. U.S.A. 107, 15821–15825. doi: 10.1073/pnas.1009387107

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, J. S., and Mclachlan, J. S. (2003). ‘Stability of forest biodiversity’. Nature 423, 635–638. doi: 10.1038/nature01632

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuddington, K. (2001). ‘The “balance of nature” metaphor and equilibrium in population ecology’. Biol. Philos. 16, 463–479. doi: 10.1023/A:1011910014900

CrossRef Full Text | Google Scholar

Díaz, S., Kattge, J., Cornelissen, J. H., Wright, I. J., Lavorel, S., Dray, S., et al. (2016). ‘The global spectrum of plant form and function’. Nature 529, 167–171. doi: 10.1038/nature16489

PubMed Abstract | CrossRef Full Text | Google Scholar

Dornelas, M., Gotelli, N. J., McGill, B., Shimadzu, H., Moyes, F., Sievers, C., et al. (2014). ‘Assemblage time series reveal biodiversity change but not systematic loss’. Science 344, 296–299. doi: 10.1126/science.1248484

PubMed Abstract | CrossRef Full Text | Google Scholar

Engen, S., Lande, R., Aether, B. E., and Weimerskirch, H. (2005). Extinction in relation to demographic and environmental stochasticity in age-structured models. Math. Biosci. 195, 210–227. doi: 10.1016/j.mbs.2005.02.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Engen, S., Solbu, E. B., and Sæther, B. E. (2017). ‘Neutral or non-neutral communities: temporal dynamics provide the answer’. Oikos 126, 318–331. doi: 10.1111/oik.03707

CrossRef Full Text | Google Scholar

Ergazaki, M., and Ampatzidis, G. (2012). ‘Students’ reasoning about the future of disturbed or protected ecosystems & the idea of the “balance of nature”’. Res. Sci. Educ. 42, 511–530. doi: 10.1007/s11165-011-9208-7

CrossRef Full Text | Google Scholar

Fisher, C. K., and Mehta, P. (2014). ‘The transition between the niche and neutral regimes in ecology’. Proc. Natl. Acad. Sci. U.S.A. 111, 13111–13116. doi: 10.1073/pnas.1405637111

PubMed Abstract | CrossRef Full Text | Google Scholar

Forte, B., and Vrscay, E. R. (1996). “No Title,” in Theory of Generalized Fractal Transforms, ed. Y. Fisher (New York, NY: Springer-Verlag), 36.

Google Scholar

Franzke, C., Barbosa, S., Blender, R., Fredriksen, H., Laepple, T., Lambert, F., et al. (2020). The structure of climate variability across scales. Rev. Geophys. 58:e2019RG000657. doi: 10.1029/2019RG000657

CrossRef Full Text | Google Scholar

Gilbert, B., Laurance, W. F., Leigh, E. G. Jr., and Nascimento, H. E. (2006). ‘Can neutral theory predict the responses of amazonian tree communities to forest fragmentation?’. Am. Nat. 168, 304–317. doi: 10.1086/506969

PubMed Abstract | CrossRef Full Text | Google Scholar

Halley, J., and Inchausti, P. (2002). Lognormality in ecological time series. Oikos 99, 518–530.

Google Scholar

Halley, J. M. (1996). ‘Ecology, evolution and 1/f-noise’. Trends Ecol. Evol. 11, 33–37. doi: 10.1016/0169-5347(96)81067-6

CrossRef Full Text | Google Scholar

Halley, J. M., and Inchausti, P. (2004). ‘The increasing importance of 1/f-noises as models of ecological variability’. Fluctuation Noise Lett. 4, R1–R26. doi: 10.1142/S0219477504001884

CrossRef Full Text | Google Scholar

Halley, J. M., and Iwasa, Y. (1998). ‘Extinction rate of a population under both demographic and environmental stochasticity’. Theor. Popul. Biol. 53, 1–15. doi: 10.1006/tpbi.1997.1336

PubMed Abstract | CrossRef Full Text | Google Scholar

Halley, J. M., and Iwasa, Y. (2011). ‘Neutral theory as a predictor of avifaunal extinctions after habitat loss’. Proc. Natl. Acad. Sci. U.S.A. 108, 2316–2321. doi: 10.1073/pnas.1011217108

PubMed Abstract | CrossRef Full Text | Google Scholar

Halley, J. M., and Kunin, W. E. (1999). Extinction risk and the 1/f family of noise models. Theor. Popul. Biol. 56, 215–230. doi: 10.1006/tpbi.1999.1424

PubMed Abstract | CrossRef Full Text | Google Scholar

Halley, J. M., Monokrousos, N., Mazaris, A. D., Newmark, W. D., and Vokou, D. (2016). ‘Dynamics of extinction debt across five taxonomic groups’. Nat. Commun. 7:12283. doi: 10.1038/ncomms12283

PubMed Abstract | CrossRef Full Text | Google Scholar

Halley, J. M., Sgardeli, V., and Triantis, K. A. (2014). ‘Extinction debt and the species-area relationship: a neutral perspective’. Glob. Ecol. Biogeogr. 23, 113–123. doi: 10.1111/geb.12098

CrossRef Full Text | Google Scholar

Hastings, A. (2004). ‘Transients: the key to long-term ecological understanding?’. Trends Ecol. Evol. 19, 39–45. doi: 10.1016/j.tree.2003.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Holt, R. D. (2009). ‘Bringing the Hutchinsonian niche into the 21st century: ecological and evolutionary perspectives’. Proc. Natl. Acad. Sci. U.S.A. 106(Suppl. 2), 19659–19665. doi: 10.1073/pnas.0905137106

PubMed Abstract | CrossRef Full Text | Google Scholar

Hubbell, S. P (ed.) (2001). The Unified Neutral Theory Of Biodiversity And Biogeography. Princeton, NJ: Princeton University Press.

Google Scholar

Hugueny, B. (2017). ‘Age-area scaling of extinction debt within isolated terrestrial vertebrate assemblages’. Ecol. Lett. 20, 591–598. doi: 10.1111/ele.12756

PubMed Abstract | CrossRef Full Text | Google Scholar

Huston, M. (1979). ‘A general hypothesis of species diversity’. Am. Nat. 113, 81–101. doi: 10.1086/283366

CrossRef Full Text | Google Scholar

Hutchinson, G. E. (1957). ‘Cold spring harbor symposium on quantitative biology’. Concluding Remarks 22, 415–427. doi: 10.1101/SQB.1957.022.01.039

CrossRef Full Text | Google Scholar

Hutchinson, G. E. (1978). An Introduction to Population Ecology. Yale University Press.

Google Scholar

Inchausti, P., and Halley, J. (2001). ‘Investigating long-term ecological variability using the global population dynamics database’. Science 293, 655–657. doi: 10.1126/science.293.5530.655

PubMed Abstract | CrossRef Full Text | Google Scholar

Inchausti, P., and Halley, J. (2002). ‘The long-term temporal variability and spectral colour of animal populations’. Evol. Ecol. Res. 4, 1033–1048.

Google Scholar

Jackson, S. T., and Overpeck, J. T. (2000). ‘Responses of plant populations and communities to environmental changes of the late Quaternary’. Paleobiology 26(4 Suppl.), 194–220. doi: 10.1666/0094-8373(2000)26[194:ROPPAC]2.0.CO;2

CrossRef Full Text | Google Scholar

Kalyuzhny, M., Kadmon, R., and Shnerb, N. M. (2015). ‘A neutral theory with environmental stochasticity explains static and dynamic properties of ecological communities’. Ecol. Lett. 18, 572–580. doi: 10.1111/ele.12439

PubMed Abstract | CrossRef Full Text | Google Scholar

Kessler, D. A., and Shnerb, N. M. (2015). ‘Generalized model of island biodiversity’. Phys. Rev. E Stat. Nonlinear Soft Matter. Phys. 91, 1–11. doi: 10.1103/PhysRevE.91.042705

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimura, M. (1955). ‘Random genetic drift in a multi-allelic locus’. Evolution 9, 419–435. doi: 10.1111/j.1558-5646.1955.tb01551.x

CrossRef Full Text | Google Scholar

Lamanna, C., Blonder, B., Violle, C., Kraft, N. J., Sandel, B., Šímová, I., et al. (2014). ‘Functional trait space and the latitudinal diversity gradient’. Proc. Natl. Acad. Sci. U.S.A. 111, 13745–13750. doi: 10.1073/pnas.1317722111

PubMed Abstract | CrossRef Full Text | Google Scholar

Leibold, M. A. (1995). ‘The niche concept revisited: mechanistic models and community context’. Ecology 76, 1371–1382. doi: 10.2307/1938141

CrossRef Full Text | Google Scholar

Leigh, E. G. (2007). ‘Neutral theory: a historical perspective’. J. Evol. Biol. 20, 2075–2091. doi: 10.1111/j.1420-9101.2007.01410.x

PubMed Abstract | CrossRef Full Text | Google Scholar

MacArthur, R. H. (1957). ‘On the relative abundance of bird species’. Proc. Natl. Acad. Sci. U.S.A. 43, 293–295. doi: 10.1073/pnas.43.3.293

PubMed Abstract | CrossRef Full Text | Google Scholar

MacArthur, R. H., and Wilson, E. O. (1967). The Theory of Island Biogeography. Princeton, NJ: Princeton University Press.

Google Scholar

Magurran, A. E. (2007). ‘Species abundance distributions over time’. Ecol. Lett. 10, 347–354. doi: 10.1111/j.1461-0248.2007.01024.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Matter, S. F., Hanski, I., and Gyllenberg, M. (2002). A test of the metapopulation model of the species-area relationship. J. Biogeogr. 29, 977–983. doi: 10.1046/j.1365-2699.2002.00748.x

CrossRef Full Text | Google Scholar

May, R. M. (1973). Stability And Complexity In Model Ecosystems. Princeton, NJ: Princeton University Press.

Google Scholar

McGill, B. J. (2003). ‘A test of the unified neutral theory of biodiversity’. Nature 422, 881–885. doi: 10.1038/nature01583

PubMed Abstract | CrossRef Full Text | Google Scholar

McGill, B. J. (2010). ‘Towards a unification of unified theories of biodiversity’. Ecol. Lett. 13, 627–642. doi: 10.1111/j.1461-0248.2010.01449.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Meszéna, G., Gyllenberg, M., Pásztor, L., and Metz, J. A. (2006). ‘Competitive exclusion and limiting similarity: a unified theory’. Theor. Popul. Biol. 69, 68–87. doi: 10.1016/j.tpb.2005.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Pigot, A. L., Trisos, C. H., and Tobias, J. A. (2016). ‘Functional traits reveal the expansion and packing of ecological niche space underlying an elevational diversity gradient in passerine birds’. Proc. R. Soc. B Biol. Sci. 283, 1–9. doi: 10.1098/rspb.2015.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Pimm, S. L. (1991). The Balance of Nature?: Ecological Issues in the Conservation of Species and Communities. Chicago, IL: University of Chicago Press.

Google Scholar

Pimm, S. L., and Redfearn, A. (1988). ‘The variability of population densities’. Nature 334, 613–614. doi: 10.1038/334613a0

CrossRef Full Text | Google Scholar

Preston, F. W. (1960). ‘Time and space and the variation of species’. Ecology 41, 611–627. doi: 10.2307/1931793

CrossRef Full Text | Google Scholar

Preston, F. W. (1962). ‘The canonical distribution of commonness and rarity: part 1’. Ecology 43, 185–215. doi: 10.2307/1931976

CrossRef Full Text | Google Scholar

Ricklefs, R. E. (2006). ‘The unified neutral theory of biodiversity: do the numbers add up?’. Ecology 87, 1424–1431. doi: 10.1890/0012-9658(2006)87[1424:TUNTOB]2.0.CO;2

CrossRef Full Text | Google Scholar

Ripa, J., and Lundberg, P. (2000). ‘The route to extinction in variable environments’. Oikos 90, 89–96. doi: 10.1034/j.1600-0706.2000.900109.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenzweig, M. L. (1995). Species Diversity In Space And Time. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511623387

CrossRef Full Text | Google Scholar

Schoener, T. W. (1973). ‘Effects of density- restricted food encounter on some single- level competition models’. Theor. Popul. Biol. 13, 365–381. doi: 10.1016/0040-5809(78)90052-7

CrossRef Full Text | Google Scholar

Sgardeli, V., Zografou, K., and Halley, J. M. (2016). ‘Climate change versus ecological drift: assessing 13 years of turnover in a butterfly community’. Basic Appl. Ecol. 17, 283–290. doi: 10.1016/j.baae.2015.12.008

CrossRef Full Text | Google Scholar

Simberloff, D. (2014). ‘The “balance of nature”—evolution of a panchreston’. PLoS Biol. 12:e1001963. doi: 10.1371/journal.pbio.1001963

PubMed Abstract | CrossRef Full Text | Google Scholar

Soberón, J. M. (2010). ‘Niche and area of distribution modeling: a population ecology perspective’. Ecography 33, 159–167. doi: 10.1111/j.1600-0587.2009.06074.x

CrossRef Full Text | Google Scholar

Sugihara, G. (1980). ‘Minimal community structure: an expanation of species abundance patterns’. Am. Nat. 116, 770–787. doi: 10.1086/283669

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, C. D., Cameron, A., Green, R. E., Bakkenes, M., Beaumont, L. J., Collingham, Y. C., et al. (2004). Extinction risk from climate change. Nature 427, 145–148. doi: 10.1038/nature02121

PubMed Abstract | CrossRef Full Text | Google Scholar

Tilman, D. (1994). ‘Competition and biodiversity in spatially structured habitats’. Ecology 75, 2–16. doi: 10.2307/1939377

CrossRef Full Text | Google Scholar

Tilman, D., May, R. M., Lehman, C. L., and Nowak, M. A. (1994). ‘Habitat destruction and the extinction debt’. Nature 371, 65–66. doi: 10.1038/371065a0

CrossRef Full Text | Google Scholar

Ulrich, W., Ollik, M., and Ugland, K. I. (2010). ‘A meta-analysis of species-abundance distributions’. Oikos 119, 1149–1155. doi: 10.1111/j.1600-0706.2009.18236.x

CrossRef Full Text | Google Scholar

White, E. P., Adler, P. B., Lauenroth, W. K., Gill, R. A., Greenberg, D., Kaufman, D. M., et al. (2005). ‘A comparison of the species-time relationship across ecosystmes and taxonomic groups’. Oikos 112, 185–195. doi: 10.1111/j.0030-1299.2006.14223.x

CrossRef Full Text | Google Scholar

Williamson, M., and Gaston, K. J. (2005). ‘The lognormal distribution is not an appropriate null hypothesis for the species-abundance distribution’. J. Anim. Ecol. 74, 409–422. doi: 10.1111/j.1365-2656.2005.00936.x

CrossRef Full Text | Google Scholar

Wunsch, C. (2003). ‘The spectral description of climate change including the 100 ky energy’. Clim. Dyn. 20, 353–363. doi: 10.1007/s00382-002-0279-z

CrossRef Full Text | Google Scholar

Zillio, T., and Condit, R. (2007). ‘The impact of neutrality, niche differentiation and species input on diversity and abundance distributions’. Oikos 116, 931–940. doi: 10.1111/j.2007.0030-1299.15662.x

CrossRef Full Text | Google Scholar

Appendix A. List of Symbols

a, Vector of environmental configurations of niche factors in logarithmic space.

a_k, Environmental configuration of the k^th niche factor in log-space (k∈0,1,2,…, K−1).

B_k, A constant related to U_k, such that U_k = Γ_k B_k and 1-U_k = Γ_k/B_k and with ${\mathrm{\Gamma }}_k=1/(B_k+1/B_k)=\sqrt{U_k(1-U_k)}$.

C, The orientation matrix (S × K).

c_sk, Element of the orientation matrix C for species (row) s and niche factor (column) k. All c_sk = ±1.

e_s(t), Probability of extirpation of the species s at time t.

f(u), Probability distribution function of the random variable U_k (assumed independent and identically-distributed on all axes).

f_xs(x), Probability distribution function of the log-population of species s.

f_vs(x), Probability distribution function of the log-hypervolume of species s.

g(x), Probability distribution function of the niche width λ_sk = ln(L_sk).

J, The size of the community (sum of all individuals from all species).

K, Number of niche factors (dimension of niche hypercube, number of axes)

k, Niche-factor index, k∈0,1,2,…, K−1.

L_sk, The niche width of species s for factor k.

M, Minimum viable population (assumed same for all species in the community).

m, Natural logarithm of M.

o_k, The k^th digit of the binary representation of species.

p, Probability that a given species is present in the community.

q, Probability that U_k takes value u₀ for the asymmetric dichotomous distribution of Special Case C, while 1−q is the probability that U_k takes the value 1−u₀.

S, The total number of possible species in the community (S = 2^K).

s, Species index (in decimal), s∈0,1,2,…, S−1.

s, Species index (in binary).

T, Length of time series T∈1,2,3…

t, Time: t∈0,1,2,3…

U_k, The random variable representing the division of axis for factor k.

u₀, The value defining the dichotomous distribution on Special Case B. In this case the random variable. U_k, can take only the values u₀ and 1−u₀.

V₀, Variance of random variable U_k.

V_s, Niche hypervolume of species s.

v, Vector of niche hypervolumes for all species in the community.

v_s, Natural logarithm of niche hypervolume of species s.

W_s, Total variance for time series of species s.

X_s, Population of species s.

x, Vector of log-populations of species in the community.

x_s, Logarithm of the population of species s.

z, Vector of deviations from the mean log-population, $K\overline{\mathrm{\gamma }}+\ln J$, for the case where the mean is constant in time.

β², Expected variance of f(x) for Special Case B.

Γ_k, A constant related to U_k and B_k. It is the geometric mean of the two partition sizes (U_k and 1−U_k) on axis-k:. i.e., ${\mathit{\Gamma }}_k=\sqrt{U_k(1-U_k)}$.

γ_k, A constant γ_k = ln(Γ_k). It is mean of the logarithms of the two partition sizes (U_k and 1−U_k) of the axis k.

${}_{\overline{\mathrm{\gamma }}}$, The average value of γ_k over all niche factors, namely $\overline{\mathrm{\gamma }}=1/K\sum \mathrm{\gamma }{}_k$.

λ_sk = lnL_sk.

μ, Expected mean of g(x).

ρ, Number of individuals per unit area.

τ_k, Timescale of changes happening for niche factor k.

σ², Expected variance of g(x).

Appendix B. Mathematical Proofs

Relation Between the Spectrum of Population and Environmental Forcing

We are interested in the relationship between the spectra of the environmental vector a_k(t) and that of the population response x_s(t). In the case of distributions for which $K\overline{\mathrm{\gamma }}(t)$ is constant (e.g., Special Cases B and C) we may express the dynamics in Equation (15) as:

$$z_s(t)=\sum _k{c}_{sk}{a}_k(t),z_k(t)=x_k(t)-\left(K\overline{\mathrm{\gamma }}+\ln J\right)(\mathrm{A1})$$

If we take the Fourier transform of both sides, we get the Fourier coefficient of z in the domain of frequency, ω, namely:

$${\tilde{z}}_s(\mathrm{\omega })=\sum _k{c}_{sk}{\tilde{a}}_k(\mathrm{\omega })(\mathrm{A2})$$

Since both a and z are random variables, it makes sense to find the power spectrum z. The power spectrum of the Fourier coefficient of z_s(t) is found by finding the norm of it. Thus:

$$S_{z_s}(\mathrm{\omega })={\tilde{z}}_s^{*}(\mathrm{\omega })\cdot {\tilde{z}}_s(\mathrm{\omega })={||{\tilde{z}}_s(\mathrm{\omega })||}^2(\mathrm{A3})$$

Where the z^∗ refers to the complex conjugate of z. If we substitute into this the Equation (A2) we get:

$$\begin{array}{ccc}\hfill S_z(\mathrm{\omega })& \hfill =\hfill & \sum _i\sum _k{c}_{si}\cdot c_{sk}\cdot {\tilde{a}}_i^{*}(\mathrm{\omega })\cdot {\tilde{a}}_k(\mathrm{\omega })\hfill \\ & \hfill =\hfill & \sum _k{c}_{sk}^2\cdot ||{\tilde{a}}_k^2(\mathrm{\omega })||\hfill \end{array}(\mathrm{A4})$$

In A4, the interaction terms are zero because the components are independent. Noting also that all components of the orientation matrix are ±1, we get:

$$S_z(\mathrm{\omega })=\sum _k{S}_{a_k}(\mathrm{\omega })(\mathrm{A5})$$

Thus, at least in cases where $K\overline{\mathrm{\gamma }}(t)$ is constant (e.g., Special Cases B and C), the spectrum of the species population is simply the sum of the spectra of its niche factors.

Variance of Sequence of Square Pulses

This shows, for Special Case B, that the variance goes to zero if the length of the series T is much less than the time-constant of the pulses and that it converges to a finite value as T heads to infinity.

We note that here Var{a_k(t)} is a sample variance in time rather than an ensemble variance, so the expected value of the variance estimator for the time series in question is:

$$E\left[\frac{1}{T-1}\sum _{t=1}^T{(a_t-\overline{a})}^2\right],\overline{a}=\frac{1}{T}\sum _{t=1}^T{a}_t$$

Here, we use the notation a_k(t) = a_t and τ_k = τ for simplicity. Following the approach of Halley and Kunin (1999), this can be expressed as:

$$Var\{a\}=\frac{1}{T^2(T-1)}\sum _{i,j,k}^{T}E\left[\mathrm{\Delta }{a}_{ji}\mathrm{\Delta }{a}_{jk}\right],\mathrm{\Delta }{a}_{ji}=a_j-a_i$$

Note that the random variable a_j = ±1 and that a_j changes state at random every τ time steps (at times j = τ, 2τ, 3τ,…). So, when they are well separated in time the expected correlation is zero. Conversely, if the time difference is small enough then a_j and a_i are the same then Δa_ji = 0 and similarly if a_j and a_k are the same. Thus:

$$Var\{a\}=\frac{1}{T^2(T-1)}\sum _{i,j,k}^T\left[E[a_j^2]-E[a_i{a}_j]-E[a_j{a}_k]+E[a_i{a}_k]\right]$$

We note that:

$$\begin{array}{l}{\displaystyle \sum _{i,j,k}^{T}E\left[\mathrm{\Delta }{a}_{ji}\mathrm{\Delta }{a}_{jk}\right]}={\displaystyle \sum _{i,j,k}^T\left[E[a_j^2]-E[a_i{a}_j]-E[a_j{a}_k]+E[a_i{a}_k]\right]}\hfill \\ ={\displaystyle \sum _{i,j,k}^{T}E[a_j^2]}-{\displaystyle \sum _{i,j,k}^{T}E[a_i{a}_j]}-{\displaystyle \sum _{i,j,k}^{T}E[a_j{a}_k]}+{\displaystyle \sum _{i,j,k}^{T}E[a_i{a}_k]}\hfill \\ =T^3-T{\displaystyle \sum _{i,j}^{T}E[a_i{a}_j]}-T{\displaystyle \sum _{j,k}^{T}E[a_j{a}_k]}+T{\displaystyle \sum _{i,k}^{T}E[a_i{a}_k]}\hfill \end{array}$$

Note that the last three terms on the r.h.s. are identical by symmetry among the indices. Thus, we can write:

$$\sum _{i,j,k}^{T}E\left[\mathrm{\Delta }{a}_{ji}\mathrm{\Delta }{a}_{jk}\right]=T^3-T\sum _{i,j}^{T}E[a_i{a}_j]$$

The value of E(a_i.a_j) depends on | i-j| because for a square-wave of the type of a_i, the following holds for a wave with period length τ:

$$\begin{array}{ccc}\hfill E[a_i{a}_j]& \hfill =\hfill & 1-\frac{|i-j|}{\mathrm{\tau }}\forall |i-j|<\mathrm{\tau }\hfill \\ & \hfill =\hfill & 0,\text{otherwise}\hfill \end{array}$$

Therefore, we arrange the summation by | i-j|. There are T diagonal elements so E(a_i.a_j) = 1 here. There are 2(T−1) off-diagonal by one step, for which E(a_i.a_j) = 1−1/τ, then 2(T−2) off-diagonal by two steps, for which E(a_i.a_j) = 1−2/τ and so on.

$$\begin{array}{ccc}\hfill \sum _{i,j,k}^{T}E\left[\mathrm{\Delta }{a}_{ji}\mathrm{\Delta }{a}_{jk}\right]& \hfill =\hfill & T^3-T[T+2(T-1)(1-1/\mathrm{\tau })+2(T-2)(1-2/\mathrm{\tau })++2(T-3)(1-3/\mathrm{\tau })+\mathrm{\dots }+]\hfill \\ & \hfill =\hfill & T^3-T\left[T\mathrm{\tau }+2(T-1)(\mathrm{\tau }-1)+2(T-2)(\mathrm{\tau }-2)+2(T-3)(\mathrm{\tau }-3)+\mathrm{\dots }+\right]/\mathrm{\tau }\hfill \\ & \hfill =\hfill & T^3-2\left(\frac{T}{\mathrm{\tau }}\right)\sum _{j=0}^{\min (T,\mathrm{\tau })}(T-j)(\mathrm{\tau }-j)-T^2\hfill \\ & \hfill =\hfill & T^2-(T-1)2\left(\frac{T}{\mathrm{\tau }}\right)\sum _{j=0}^{\min (T,\mathrm{\tau })}(T-j)(\mathrm{\tau }-j)\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill Var\{a\}& \hfill =\hfill & \frac{1}{T^2(T-1)}\left[T^2(T-1)-2\left(\frac{T}{\mathrm{\tau }}\right)\sum _{j=0}^{\min (T,\mathrm{\tau })}(T-j)(\mathrm{\tau }-j)\right]\hfill \\ & & \\ & \hfill =\hfill & 1-\left(\frac{2}{T(T-1)\mathrm{\tau }}\right)\sum _{j=0}^{\min (T,\mathrm{\tau })}(T-j)(\mathrm{\tau }-j)\hfill \end{array}$$

For short series, T << τ so then:

$$Var\{a\}\approx 1-\left(\frac{2}{T(T-1)\mathrm{\tau }}\right)\sum _{j=0}^T(T-j)\mathrm{\tau }=\mathrm{\hspace{0.33em}1}-\left(\frac{2}{T(T-1)}\right)\sum _{j=1}^{T-1}j=\mathrm{\hspace{0.33em}0}$$

On the other hand, if T >> τ then the summation

$$Var\{a\}\approx 1-\left(\frac{2}{T(T-1)\mathrm{\tau }}\right)T\sum _{j=0}^{\mathrm{\tau }}(\mathrm{\tau }-j)=1-\left(\frac{2}{(T-1)\mathrm{\tau }}\right)\frac{\mathrm{\tau }(\mathrm{\tau }-1)}{2}\approx 1-\frac{\mathrm{\tau }-1}{T}$$

When T = τ then,

$$Var\{a\}=1-\left(\frac{2}{T^2(T-1)}\right)\sum _{j=1}^{T-1}{j}^2=\mathrm{\hspace{0.33em}1}-\left(\frac{2}{T^2(T-1)}\right)\left(\frac{T(2T-1)(T-1)}{6}\right)=\mathrm{\hspace{0.33em}1}-\frac{2T-1}{3T}=\frac{T+1}{3T}$$