- 1Arthur R. Marshall Laboratory, Biology Department, University of Florida, Gainesville, FL, United States
- 2Chesapeake Biological Laboratory, University of Maryland Center for Environmental Science, Solomons, MD, United States
Contemporary systems ecology has long been occupied with mechanical explanations of behavior; however, the physical theory that undergirds such explanations has certain limits. It’s not that the physical force laws are ever violated, but with heterogeneous, irreversible relationships subject to aleatoric influences, physical laws can only constrain, but not determine, outcomes. Such complex systems are better treated in the framework of quantified networks of interrelations. The application of simple information theory to networks reveals that ecosystems cannot achieve maximal efficiency without growing vulnerable to novel disturbances. A degree of inefficient redundancies is always necessary to sustain ecological and social functioning; and, if they are to function reliably, such non-optimal features become requisite in the design of infrastructures like power grids, water distribution networks, traffic patterns, and supply chains. In particular, the postulate that economic market efficiency should never be compromised must be re-examined if society is to remain sustainable. Furthermore, the capability of networks to represent distributed causalities allows one to rationalize behaviors like endogenous selection, centripetal acquisition of resources, and the precedence of indirect mutualism over competition in living systems–all phenomena that challenge conventional evolutionary dogma.
Introduction
Over 55 years ago, the late media sage, Marshall McLuhan (1964), observed how, whenever a new tool emerged within an endeavor, practitioners tended to use it in the context of previous habits and remained blind for a while to its full potential. His example was IBM, which saw its purpose as the manufacture of business machines. It wasn’t until its leaders realized they were in the business of processing information that the enterprise began to take off.
McLuhan’s example bears analogy to what happened in the scientific literature at the turn of the century, when an interest in networks exploded upon the scene (Barabási, 2002). Everyone was enamored with the new tool, but the preponderance of research was devoted to interpreting networks in mechanical terms. “What are the mechanisms that give rise to small-world or scale-free networks?,” etc. Few bothered with any possibilities that networks might afford beyond the conventional confines of physics. But there is a multitude of new phenomena and system behaviors that can be illuminated using network analysis. This essay is an attempt to encourage network investigators to step out of the mechanical mindset and entertain an “out-of-the-box” perspective on ecological and social dynamics.
It is rarely pointed out, for example, that physics has shortcomings that render its laws inadequate to determine outcomes in complex and living systems. It is not that such limitations haven’t been known for a long while now. For example, it was demonstrated over a century ago that all the four laws1 of physics can operate on only homogeneous variables (Whitehead and Russell, 1913). That is, physical laws treat only collections of objects that are identical and interchangeable. In order to treat combinations of different objects, one must either ignore distinctions or link dissimilar collections of objects via boundary relationships. Physicist Walter Elsasser (1981) concluded, therefore, that any laws that might govern living systems would have to be qualitatively unlike the fundamental laws of physics.
In addition, physics focuses upon definable objects that are governed by the laws via the notion of fields. Thus, the crux of physics is “objects moving according to immutable laws.” Relationships are implicitly assigned a secondary status, so that connections among objects are assumed to be caused by the objects and not vice-versa.
Both assumptions limit the application of conventional physics toward understanding ecological or social ensembles. The most poignant features of these complex systems are their inherent (and sometimes overwhelming) heterogeneity and the relationships that coalesce the different entities into a functioning whole. To further complicate matters, the relationships among the categories often take the form of a process. A process is a temporal series of irreversible transformations leading from one state to another. The very temporality of processes is incongruent with the reversibility of the fundamental laws of physics. Furthermore, as the heterogeneity of a system increases, the number of possible combinations among the categories grows exponentially, eventually defeating any effort to formulate the closed set of boundary constraints necessary to apply the laws of physics (Kauffman, 2019). It’s not that the fundamental laws of physics are ever violated; it’s that under heterogeneity, irreversibility, and contingency, the laws can at most constrain, but not determine particular system outcomes (Ulanowicz, 2016).
A Fundamentally New Tool
Because physics is demonstrably insufficient to encompass the behaviors of complex living systems, a new metaphysics is required (Ulanowicz, 2009a). A promising tool with which to begin building this reformed worldview is the network. Heterogeneity is virtually definitional to what constitutes a network; and processes, while not the only type of relationship among categories, are nonetheless quite acceptable as connections.
There is yet a third attribute that networks portray that is virtually missing from most problems in physics–indeterminacy. True, stochasticity can be imposed upon a physical problem via a boundary condition or as an attribute of a parameter, but it is not inherent in the governing laws themselves. By contrast, almost all realistic networks exhibit an intrinsic degree of indeterminacy (Pahl-Wostl, 1995). The nodes in most networks of interest usually connect to more than one other node. For example, in Figure 1 there are five different compartments that receive output from the Zooplankton (compartment 4). Which node will receive a given organism is not determined beforehand. Therefore, there exists in most cases a proliferation of alternative pathways to get from one specific node to another, just as there is a combination of possible routes to get from one point of a city to another. While some routes may be more efficient than others, the network itself does not determine the one which a particular unit of exchange will transverse. Over time, observation can assign probabilities to each of the possible pathways.
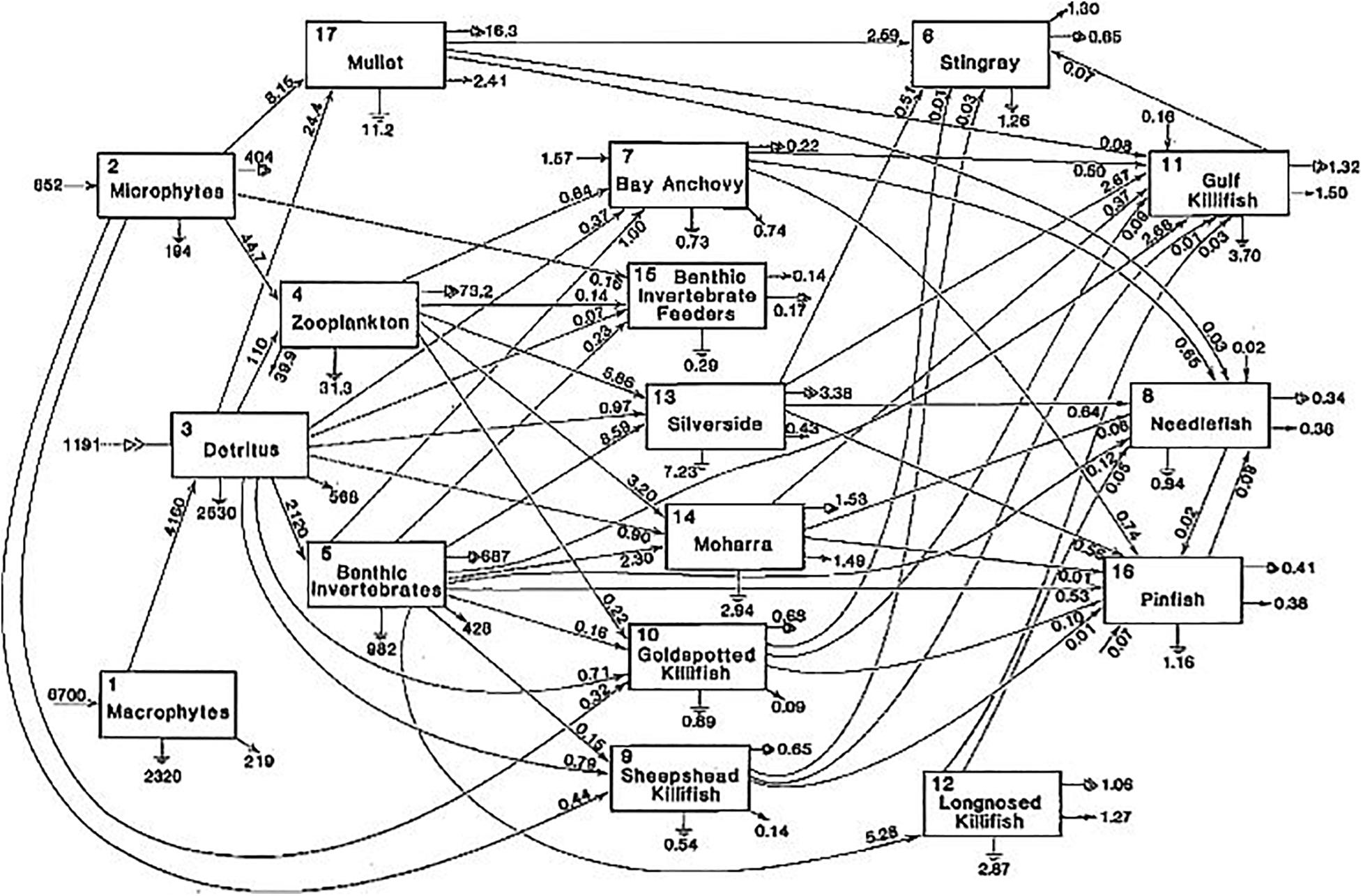
Figure 1. Arrows represent carbon transfers (mg m–2 d–1) among the taxa of a marsh gut ecosystem, Crystal River, Florida. The linked arrows signify returns to the detritus (Homer and Kemp, 1975).
Indeterminacy being acknowledged, the network still exerts constraints upon inter-nodal transfers. In directed networks it is often impossible to get from some points to all others. In Figure 1 there are no direct pathways from the Mullet (#17) to the Gold spotted Killifish (#10). As Pahl-Wostl (1995) noted, flow networks are an amalgam of constraint and freedom (indeterminacy). All of which makes it important to know the relative strength in any network of its constraint vs. freedom.
Quantifying Agonistic Dynamics
Fortunately, information theory provides a convenient method to quantify the degrees of order vs. disorganization in directed networks (Hirata and Ulanowicz, 1984). One begins by denoting the relationship between node i and any other node, j, as Tij, where T signifies some measure of the magnitude of the interaction2. The joint probability that a flow is occurring can be estimated by the ratio Tij/T.., where a dot in place of an index indicates summation over that index. i.e., T.. = Σi,j Ti,j. One can then employ a version of the familiar Shannon (1948) index to quantify the diversity of all activities in the web as:
where Tij/T.. is an estimate of the joint probability that a quantum of medium is currently flowing from i to j. Now, H is conventionally referred to as the “entropy” of the system, but this is usually a misnomer, because H represents entropy only when elements i and j are completely independent of each other, which is never the case in social or ecosystems.
Whenever i and j are related to (partially constrained by) one another, H can be decomposed into two non-negative components (Ulanowicz and Norden, 1990). Noting that the logarithm of the quotient of two variables is equal to the difference between their respective logarithms, Equation (1) can be rewritten as,
The magnitude of the terms in braces is not changed by adding and then subtracting the terms logTij and log(T.jTi.), or,
Grouping the first three terms and then the second three yields,
The reason for these particular algebraic manipulations is that the first summation is a non-negative variable in information theory called the “average mutual information,” I, (≥0) (Rothschild, 2015) and the second summation (in braces) is known as the “conditional entropy,” Φ, (also ≥0), so that
The average mutual information, I, quantifies the degree of constraint or coordination among all variables i and j. On the other hand, Φ is properly called the conditional entropy and quantifies the lack of constraint [or freedom (to assume different functionalities)] among the elements. Alternatively, it is said to represent the freedom among the i and j. In networks, it also quantifies the redundancy of pathways within the network. In simple terms, it measures the degree on average to which the i and j are independent of each other,
The key to understanding the nature of entropy is in the word “lack,” because entropy represents something that is rarely encountered in physics–an apophasis, or something that does not exist (Bateson, 1972). The reader may wonder how it is possible to quantify something that does not exist, but it is done all the time in reference to something that does exist. For example, “The glass is half empty.” quantifies how much fluid is missing in relation to the full capacity of the glass. There is a tendency for many to regard entropy as a positivist attribute, like the other variables of physics, and this misattribution is the source of much confusion about the actual nature of entropy (Ulanowicz, 2014).
Well before physicists discovered networks, there existed a tradition in ecology to represent trophic transfers in ecosystems as networks of flows among species (Lindeman, 1942; Mann et al., 1981). Figure 1, for example, depicts the transfers of carbon among the taxonomic components of a tidal embayment of Crystal River, Florida (Homer and Kemp, 1975). The numbers adjacent to each arrow are the Tij that appear in Eq. 2b.
In particular, it is informative to focus on the normalized mutual information, a = I/H, which can be referred to as the “degree of order” in the network, or the fraction of its activity that is constrained. This ratio can be considered a surrogate for system efficiency, or the ability of the system to process material. When a is close to one, the system is very streamlined, with most flow concentrated along the most efficient pathways. A high value of Φ/H, by contrast, reveals the presence of many small redundant pathways of lesser efficiency.
If one plots the magnitudes of a for different ecosystems in various habitats, it is somewhat surprising to find that their values cluster around the relatively low figure of 0.40 (Figure 2, Ulanowicz, 2009c). It is evident that ecosystems are performing nowhere near maximal efficiency. That so many less efficient processes should persist counters most thinking in evolutionary biology that only the fittest (most efficient) survive. One notices from Eq. 2b that efficiency and disorder (including redundancy) are mathematically complementary terms–more of one implies less of the other.
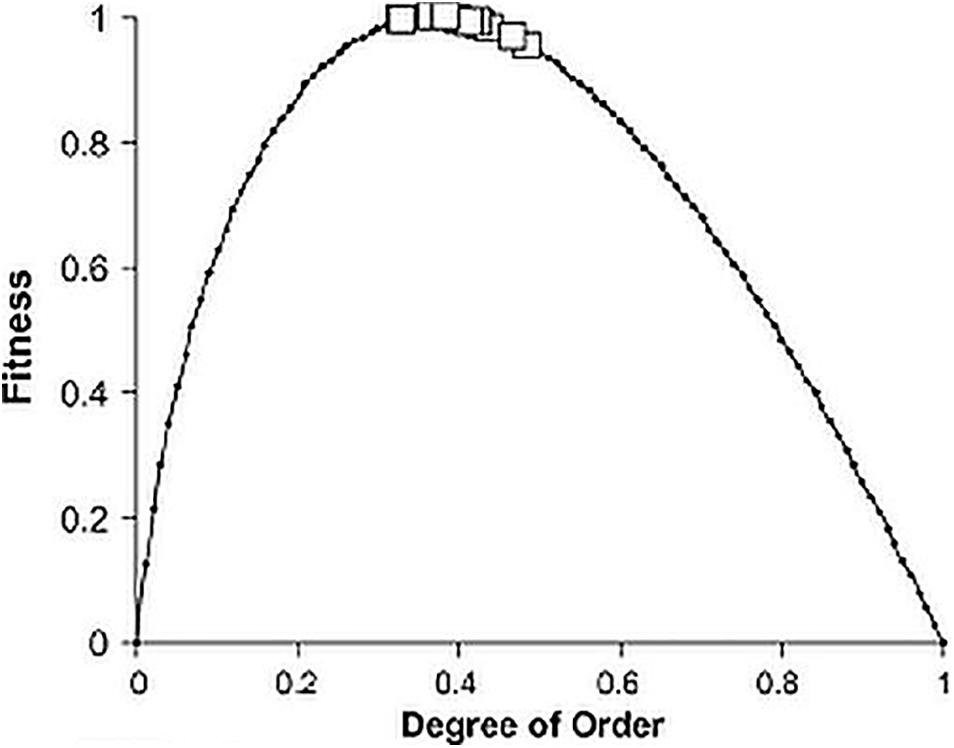
Figure 2. The degrees of order, a, plotted against corresponding magnitudes of fitness [–a log(a)] for a set of 17 ecosystem flow networks having a number of components, n > 12 (Ulanowicz, 2009c).
The Primacy of Efficiency?
Systems engineers have long recognized that redundancy is a key contributor to system reliability. Ecologists, in turn, have theorized that redundant pathways facilitate alternative supplies and functionalities when major routes have been impacted (Odum and Odum, 1953). So an important ecological inference can be drawn: Survival is not simply a matter of greatest efficiency; it is a balance between efficiency and reliability. It is important as well to recognize that the entropic side of this balance acts quite differently than those conventional dynamics that increase efficiency, i.e., entropy cannot cause events in the same way that positivist forms and forces do. Rather, absence affords opportunity for positivist tendencies to act. It functions as a secular form of kenosis.
The social ramifications of this alternative view of nature are revolutionary to a society that emphasizes efficiency. Most of what humanity designs is intended to be as efficient as possible, and in so many ways this goal is desirable. But in a complex world consisting of multitudinous processes, too much efficiency can be harmful, if not lead to catastrophe in the face of contingent events. This became abundantly clear during the recent COVID-19 pandemic, when global supply chains that had been honed to emphasize the most efficient and profitable pathways began to fail for lack of alternative connections (Taherian, 2020). Power grids, water supply systems and traffic routes designed for efficient distribution and flows have also been known to fail on a large scale when contingent perturbations intervene.
Perhaps the most overarching example of the devotion to efficiency is the field of economics, where the sine qua non of economics is that no activity or constraint should be allowed to hinder the efficient operation of markets. In the financial sector such laissez-faire attitude is considered to be the cause of boom-bust cycles in banking and national economies (Lietaer et al., 2009). The pursuit of maximal profits in franchised industries leads to much the same instabilities and inequities. A sustainable economy must allow for lesser efficient actors and sub-maximal profits (Kharrazi et al., 2013). Such has long been the justification for monopoly-busting legislation in many free economies.
Fortunately, the balance between efficiency and reliability observed in natural systems may provide ways of avoiding or mitigating crises due to overdevelopment. As mentioned above, information theory reveals that a natural balance between the organization (I) of a trophic network and its entropy (Φ) appears to exist in the ratio 40:60 (Ulanowicz, 2009c). If a system is far removed from this balance, simple calculus provides a way of reckoning how much and in which direction each Tij should be changed in order to move the whole system network toward the propitious balance (P1890, ibid.). Knowledge of such prescribed changes could be useful to managers engaged in ecosystem remediation.
This balancing protocol has been adopted by some engineers under the rubric of “biomimicry” whereby, if one has some knowledge of what an ideal balance should be, one can design a degree of redundancy and constraints that would allow the system to “fail-soft,” i.e., not collapse in the wake of major disturbance. Quantitative examples of implementing such reliability have been described in the literature for power grids (Panyam et al., 2019), water distribution networks (Bodini et al., 2012; Dave and Layton, 2020), traffic grids (Kiss and Kiss, 2018) and supply chains (Chatterjee and Layton, 2020). Lietaer (2019) suggested alternative currencies as a way to provide fail-soft economic performance.
Compound Causalities
Having considered the need for reliability in socio-ecological systems, one is now prompted to ask whether the network perspective might also cast light on the other side of the balance, i.e., on the causal roots of development in those ensembles? The chief advantage of considering patterns of relationships is that they can be examined for indirect propagation of simple binary interactions (Ulanowicz and Puccia, 1990). Fath and Patten (1999), for example, have suggested that indirect causalities usually dominate over direct bilateral interactions and that indirect relationships tend to have more positive consequences than direct ones.
Networks can be represented as matrices wherein each element represents the magnitude of the effect of row i upon column j. Multiplying such matrices together provides the magnitudes of all second–order (two-step) interactions, and further multiplications describe higher-order indirect influences. Leontief (1951) used such matrix products to quantify all indirect interactions over all pathways among the sectors of an economic community. His methodology has been carried over into ecosystems, where the goal has been modified somewhat to quantify the total effect that any one species has on any other element of the community (Hannon, 1973; Szyrmer and Ulanowicz, 1987). Ulanowicz and Puccia (1990) expanded this matrix toolbox to quantify both positive and negative influences.
An intriguing result of the last method was that direct interactions of a given sign (+ or −) can generate additive indirect effects of the opposite sign. Regarding second-order effects, this switch has been common knowledge for centuries (e.g., “The enemy of my enemy is my friend.”). The new method, however, allows one to ascertain the cumulative effect that any component has on any other over all possible pathways between them. Thus for example, when it was applied to a network of trophic interactions in the ecosystem of the Florida Everglades, the negative effect that predation by the American alligator has on several of its direct prey was more than compensated by the positive indirect effects it exerted on them along other pathways (Bondavalli and Ulanowicz, 1999). The alligator was found to provide cumulative benefits that more than compensate its negative impacts on eleven of its prey items–an example of Patten’s conjecture that indirect effects can dominate direct interactions. On the political scene it follows that, if affinities between global polities could be quantified, the overall effective relationships between all nations could be mapped for all to consider.
Some of the most important causal configurations in real systems appear as cycles among component elements. That is, the effect that a compartment has on another can be propagated further along various pathways, some of which might lead back to the original source (Ulanowicz, 1983). Such feedback is thought to play a crucial role in guiding system behavior. When the cyclical effect is uniformly positive, such indirect mutualism appears as generalized synergies. As with the alligator, such dynamics can engender surprising results. This is particularly true of a subclass of positive feedbacks known as autocatalysis.
An autocatalytic cycle is a circular configuration of causalities wherein the effects of any member upon the next in the cycle is always positive (Ulanowicz, 2016). For example, consider the simple three-member cycle in Figure 3. If process A facilitates process B, and B catalyzes C, which in turn benefits A, then the activity of A indirectly promotes itself. The same goes for B and C. In general, A, B, and C can be objects, processes or events. While the linkages can be deterministic (mechanical), the most interesting dynamics arise due to the intervention of some type of contingency (Ulanowicz, 1997).
A familiar ecological illustration of this simple triad is the community that establishes itself among the freshwater family of aquatic weeds known as Utricularia (Ulanowicz, 1995). The plant (A) does not obtain much sustenance from its roots, which only anchor the stems of feathery leaves. On the surface of its leaves always grows a film of nutrient-rich algae, known as periphyton (B). The periphyton provides food for very small heterotrophs (C, e.g., water fleas, copepods, etc.). Upon the stems of the Utricularia grow small capsules (utricles) with fine hairs on the end. When a heterotroph encounters the hairs, the utricle opens up and the tiny crustacean is sucked into it by a negative osmotic pressure maintained inside the utricle and ultimately serves as food for the plant (A).
Indirect causalities comprising autocatalysis, when they interact with contingent events, can give rise to phenomena that are uncharacteristic of mechanical scenarios. For example, they can exert selection pressure upon the participating elements and relationships. Should there happen to be an aleoteric change in the nature of B that happens either to make it more sensitive to A or impart more benefit to C, then that change would receive more benefit from A. Whenever there is some form of memory [either analog (Peng et al., 2020) or coded] in the system, that reward to B could be incorporated into system functioning. The same dynamic pertains to similar changes in C or A, so that contingencies that facilitate any component process will be favored and adopted.
The Driver of Evolution
Although they are not depicted in the Figure 3, the continuation of all component processes is dependent upon resources taken into the system (Ulanowicz, 2009a). Should a particular change happen to increase an input to a participant, that addendum would be favored under autocatalytic selection. Because autocatalytic selection acts upon all components, the net result over time is for the cycle as a whole to attract ever more resources into its orbit. Such progression could aptly be called “centripetality” as depicted in Figure 4. This endogenously generated drive is ubiquitous and fundamental to all living systems (although it rarely appears among published lists of the required attributes of life). So integral to the life process is centripetality that Bertrand Russell (1960) identified it as the primary drive behind all of evolution3.
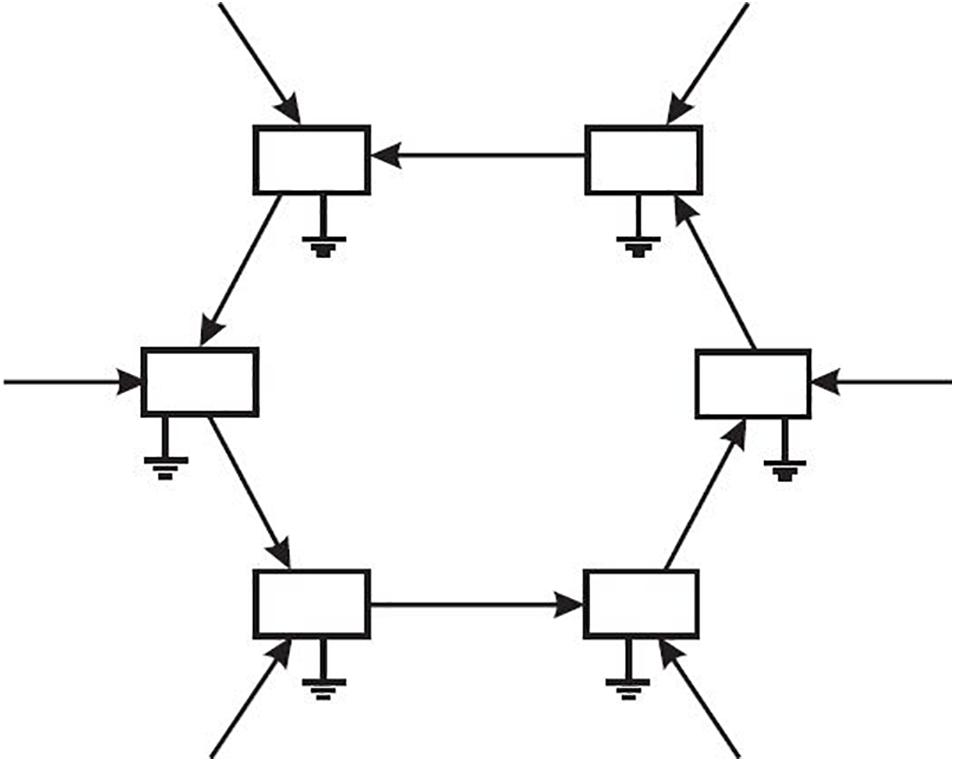
Figure 4. Schematic of a six-element autocatalytic cycle, where the enhancement of each element on the next results over time in centripetality, the tendency of the loop to draw ever more resources into its orbit.
The inclusion of indirect causality among heterogeneous networks that interact with contingent events has provided insight into a phenomenon that most investigators simply ignore, lest they be accused of trafficking in the transcendental. It is usually considered to be epi-phenomenal; but centripetality is real, palpable, and perhaps most importantly, primary. Consider, for example, a finite field of resources within which two autocatalytic cycles exist. Both will attract ever more of the resource into their respective orbits until the field starts to be depleted. That is, autocatalysis, comprised of forms of mutual benefaction, gives rise to competition at the next higher level. Effectively, no competition can exist unless it is driven by mutual beneficence at the next level down (Ulanowicz, 1997).
Recognizing that mutual beneficence is primary and competition is instead derivative, inverts the conventions of evolutionary theory. Evolution is not driven ultimately by competition, but rather has its origins in mutuality. Furthermore, the belief that the reversible laws of physics determine all events had led Hume to conclude that one cannot get an “ought” from an “is.” Autocatalysis, however, imparts an underlying directionality to ecological and social dynamics that could lead to an emergent ethos.
Not that all change is determined by positivist agency such as autocatalysis. It is necessary also to remember that the yan of centripetality must be balanced by the yin of dissipation and decay in order for a system to persist (Xu et al., 2018).
A New Metaphysics?
Conceiving of complex, heterogeneous systems in terms of networks broadens the scope of science to encompass more of what is familiar in human experience. Rather than picturing a world of only mechanical behaviors that are separated from the external forces that drive them, network systems can be motivated by endogenous agencies that struggle against, but sometimes can take advantage of, necessary dissipation, degradation, and apophasis. Investigators themselves are no longer required to separate themselves from the systems they are studying, but now become participants in a quasi-engineering endeavor to understand how the world around them develops.
On a more applied note, Gregory Bateson (1972) complained how many technocratic efforts to solve complex problems often fail or wind up making things worse. The almost universal obsession to make things more efficient often results in improvements. However, at the whole systems level, such intent can lead to dysfunction or even collapse. In order to survive and be sustainable, it is often necessary to foster reliability at the cost of some efficiency. Large, distributed systems many times do not fare well when designed to be maximally efficient, and some calculated degree of redundancy and freedom becomes necessary (Ulanowicz, 2020b). Nowhere is this consideration more important than in economics (Goerner et al., 2009). The fervid pursuits of unfettered markets and maximal profits inevitably encroach upon supporting resources to the detriment of all (Lietaer, 2001), and these attitudes must be tempered by greater concern for the commonweal.
Regarding whole-system ecology, indexes arising from networks are becoming useful tools for the comparison of the status of different ecosystems (Wulff and Ulanowicz, 1989; Baird et al., 1991; Monaco and Ulanowicz, 1997; Christian et al., 2005), the evaluation of system health (Mageau et al., 1995; Pinto et al., 2009; Fath et al., 2019) and the identification of roles in systems (Zorach and Ulanowicz, 2003).
Networks provide insights into how different categories interact and how causalities propagate beyond their origins and cooperate in ways that give rise to agency. No longer can concepts such as selfhood and intention (Juarrero, 1999) be dismissed as epi-phenomena. Relational dynamics even provide clues toward unraveling that most enigmatic of human phenomena–consciousness (Ulanowicz, 2020a). The realistic vision provided by networks of heterogeneous relationships is far richer than the conventional image of a mechanical universe subject to random noise. The goal of science is broader than just providing mechanisms to explain various classes of ensembles. The revelations that networks provide beg for an intellectual metanoia–a completely different metaphysics with which to portray the drama of life in a more meaningful way (Ulanowicz, 2009a). The survival of humanity demands as much.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
RU takes full responsibility for all elements of this article, unless otherwise attributed.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author is grateful to Antonio Bodini for wresting him out of retirement to undertake this plea for a change in scientific metaphysics. Publication Number 5965 of the University of Maryland Center for Environmental Science.
Footnotes
- ^ The four physical forces are strong and weak nuclear, columbic, and gravitation. The three laws of thermodynamics emerged out of engineering, not physics. In the late 19thCentury physicists attempted to “sanitize” thermodynamics by confining it to the realm of statistical mechanics (Boltzmann, 1872; Gibbs, 1902), but the core of their demonstrations hinged upon their creative use of boundary conditions, not inherent to the laws themselves (Ulanowicz, 2009b).
- ^ For binary, or unweighted networks, all Tij could be assumed to possess equal magnitudes.
- ^ Russell did not call the dynamic centripetality, preferring instead the negative connotation associated with “chemical imperialism.”
References
Baird, D., McGlade, J. M., and Ulanowicz, R. E. (1991). The comparative ecology of six marine ecosystems. Philos. Trans. R. Soc.Lond B 333, 15–29. doi: 10.1098/rstb.1991.0058
Bodini, A., Bondavalli, C., and Allesina, S. (2012). “Cities as ecosystems: functional similarities and the quest for sustainability,” in Developments in Environmental Modelling, Vol. 25, eds F. Jordán and S. E. Jørgensen (Oxford: Elsevier), 297–318. doi: 10.1016/B978-0-444-59396-2.00018-3
Boltzmann, L. M. (1872). Weitere studien über das wärmegleichgewicht unter gasmolekulen. Wien. Ber. 66, 275–370.
Bondavalli, C., and Ulanowicz, R. E. (1999). Unexpected effects of predators upon their prey: the case of the American alligator. Ecosystems 2, 49–63. doi: 10.1007/s100219900057
Chatterjee, A., and Layton, A. (2020). Bio-inspired design for sustainable and resilient supply chains. Procedia CIRP 90, 695–699. doi: 10.1016/j.procir.2020.01.127
Christian, R. R., Baird, D., Luczkovich, J., Johnson, J. C., Scharler, U. M., and Ulanowicz, R. E. (2005). “Role of network analysis in comparative ecosystem ecology of estuaries,” in Aquatic Food Webs, eds A. Belgrano, U. M. Scharler, J. Dunne, and R. E. Ulanowicz (Oxford: Oxford University Press), 25–40. doi: 10.1093/acprof:oso/9780198564836.003.0004
Dave, T., and Layton, A. (2020). Designing ecologically-inspired robustness into a water distribution network. J.Clean. Prod. 254:120057. doi: 10.1016/j.jclepro.2020.120057
Elsasser, W. M. (1981). “A form of logic suited for biology?,” in Progress in Theoretical Biology, Vol. 6, ed. R. Rosen (New York, NY: Academic Press), 23–62. doi: 10.1016/B978-0-12-543106-4.50009-X
Fath, B. D., Fiscus, D. A., Goerner, S. J., Berea, A., and Ulanowicz, R. E. (2019). Measuring regenerative economics: 10 principles and measures undergirding systemic economic health. Glob. Transit. 1, 15–27. doi: 10.1016/j.glt.2019.02.002
Fath, B. D., and Patten, B. C. (1999). Review of the foundations of network environ analysis. Ecosystems 2, 167–179. doi: 10.1007/s100219900067
Gibbs, J. W. (1902). Elementary Principles in Statistical Mechanics. New Haven, CT: Yale University Press.
Goerner, S. J., Lietaer, B., and Ulanowicz, R. E. (2009). Quantifying economic sustainability: implications for free-enterprise theory, policy and practice. Ecol. Econ. 69, 76–81. doi: 10.1016/j.ecolecon.2009.07.018
Hannon, B. (1973). The structure of ecosystems. J. Theor. Biol. 41, 535–546. doi: 10.1016/0022-5193(73)90060-X
Hirata, H., and Ulanowicz, R. E. (1984). Information theoretical analysis of ecological networks. Int. J.Syst. Sci. 15, 261–270. doi: 10.1080/00207728408926559
Homer, M., and Kemp, W. M. (1975). Trophic Exchanges in the Ecosystem of a Tidal Marsh Gut, Crystal River, Florida, unpl. report. Cambridge, MD: Univ. Md. Center for Env. Sci.
Juarrero, A. (1999). Dynamics in Action: Intentional Behavior as a Complex System. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/2528.001.0001
Kauffman, S. A. (2019). A World Beyond Physics: The Emergence and Evolution of Life. Oxford: Oxford University Press.
Kharrazi, A., Rovenskaya, E., Fath, B. D., Yarime, M., and Kraines, S. (2013). Quantifying the sustainability of economic resource networks: an ecological information-based approach. Ecol. Econ. 90, 177–186. doi: 10.1016/j.ecolecon.2013.03.018
Kiss, T., and Kiss, V. M. (2018). Ecology-related resilience in urban planning – a complex approach for Pécs (Hungary). Ecol. Econ. 144, 160–170. doi: 10.1016/j.ecolecon.2017.08.004
Leontief, W. (1951). The Structure of the American Economy, 1919–1939, 2nd Edn. New York, NY: Oxford University Press.
Lietaer, B. (2001). The Future of Money: Towards New Wealth, Work and a Wiser World. New York, NY: Random House Business. doi: 10.1108/ebr.2001.05413bab.008
Lietaer, B. (2019). Towards a Sustainable World: 3 Paradigm Shifts to Achieve. Vienna: Delta Institute.
Lietaer, B., Ulanowicz, R. E., and Goerner, S. J. (2009). Options for managing a systematic bank crisis. Sapiens 1, 1–15.
Lindeman, R. L. (1942). The trophic-dynamic aspect of ecology. Ecology 23, 399–418. doi: 10.2307/1930126
Mageau, M. T., Costanza, R., and Ulanowicz, R. E. (1995). The development and initial testing of a quantitative assessment of ecosystem health. Ecosyst. Health 1, 201–213.
Mann, K. H., Platt, T. C., and Ulanowicz, R. E. (eds) (1981). “Mathematical models in biological oceanography,” in UNESCO Monographs on Oceanographic Methodology, Vol. 7, eds K. H. Mann, T. C. Platt, and R. E. Ulanowicz (Paris: UNESCO Press).
Monaco, M. E., and Ulanowicz, R. E. (1997). Comparative ecosystem trophic structure of three U.S. Mid-Atlantic estuaries. Mar. Ecol. Prog. Ser. 161, 239–254. doi: 10.3354/meps161239
Pahl-Wostl, C. (1995). The Dynamic Nature of Ecosystems: Chaos and Order Entwined. New York, NY: Wiley.
Panyam, V., Huang, H., Davis, K., and Layton, A. (2019). Bio-inspired design for robust power grid networks. Appl. Energy 251:113349. doi: 10.1016/j.apenergy.2019.113349
Peng, Z., Plum, A. M., Gagrani, P., and Baum, D. A. (2020). An ecological framework for the analysis of prebiotic chemical reaction networks. J. Theor. Biol. 507:110451. doi: 10.1016/j.jtbi.2020.110451
Pinto, R., Patrício, J., Baeta, A., Fath, B. D., Neto, J. M., and Marques, J. C. (2009). Review and evaluation of estuarine biotic indices to assess benthic condition. Ecol. Indic. 9, 1–25. doi: 10.1016/j.ecolind.2008.01.005
Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Szyrmer, J., and Ulanowicz, R. E. (1987). Total flows in ecosystems. Ecol. Model. 35, 123–136. doi: 10.1016/0304-3800(87)90094-9
Ulanowicz, R. E. (1983). Identifying the structure of cycling in ecosystems. Math. Biosci. 65, 219–237. doi: 10.1016/0025-5564(83)90063-9
Ulanowicz, R. E. (1995). Utricularia’s secret: the advantage of positive feedback in oligotrophic environments. Ecol. Model. 79, 49–57. doi: 10.1016/0304-3800(94)00032-D
Ulanowicz, R. E. (1997). Ecology, the Ascendent Perspective. New York, NY: Columbia University Press.
Ulanowicz, R. E. (2009a). A Third Window: Natural Life beyond Newton and Darwin. West Conshohocken. Pennsylvania, PA: Templeton Foundation Press.
Ulanowicz, R. E. (2009b). Increasing entropy: heat death or perpetual harmonies?Des. Nat.Ecodyn. 4, 83–96. doi: 10.2495/DNE-V4-N2-83-96
Ulanowicz, R. E. (2009c). The dual nature of ecosystem dynamics. Ecol. Model. 220, 1886–1892. doi: 10.1016/j.ecolmodel.2009.04.015
Ulanowicz, R. E. (2014). Reckoning the nonexistent: putting the science right. Ecol. Model. 293, 22–30. doi: 10.1016/j.ecolmodel.2014.03.014
Ulanowicz, R. E. (2016). Process ecology: philosophy passes into Praxis. Process Stud. 45, 72–95. doi: 10.5840/process201645215
Ulanowicz, R. E. (2020a). Ecological clues to the nature of consciousness. Entropy 22, 611–621. doi: 10.3390/e22060611
Ulanowicz, R. E. (2020b). Quantifying sustainable balance in ecosystem configurations. Curr. Res.Environ. Sustain. 1, 1–6. doi: 10.1016/j.crsust.2019.09.001
Ulanowicz, R. E., and Norden, J. S. (1990). Symmetrical overhead in flow networks. Int. J. Syst. Sci. 1, 429–437. doi: 10.1080/00207729008910372
Whitehead, A. N., and Russell, B. (1913). Principia Mathematica. Cambridge: Cambridge University Press.
Wulff, F., and Ulanowicz, R. E. (1989). “A comparative anatomy of the Baltic Sea and Chesapeake Bay ecosystems,” in Network Analysis in Marine Ecology Coastal and Estuarine Studies Series, eds F. Wulff, J. G. Field, and K. H. Mann (Berlin: Springer-Verlag), 232–256. doi: 10.1007/978-3-642-75017-5_11
Xu, Z., Cheng, G., Ulanowicz, R. E., Song, X., Deng, X., and Zhong, F. (2018). The common developmental road: tensions among centripetal and centrifugal dynamics. Natl.Sci. Rev. 5, 417–426. doi: 10.1093/nsr/nwx033/3101042
Keywords: autocatalysis, centripetality, contingencies, ecosystems, indeterminacy, information theory, networks, sustainability
Citation: Ulanowicz RE (2021) Socio-Ecological Networks: A Lens That Focuses Beyond Physics. Front. Ecol. Evol. 9:643122. doi: 10.3389/fevo.2021.643122
Received: 17 December 2020; Accepted: 08 February 2021;
Published: 26 February 2021.
Edited by:
Ferenc Jordan, Centre for Ecological Research, Hungarian Academy of Science, HungaryReviewed by:
Marco Ortiz, University of Antofagasta, ChileStuart R. Borrett, University of North Carolina at Wilmington, United States
Copyright © 2021 Ulanowicz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Robert E. Ulanowicz, dWxhbkB1bWNlcy5lZHU=
 Robert E. Ulanowicz
Robert E. Ulanowicz