Modeling Recruitment of Birth Cohorts to the Breeding Population: A Hidden Markov Model Approach

Long-term capture-recapture studies provide an opportunity to investigate the population dynamics of long-lived species through individual maturation and adulthood and/or time. We consider capture-recapture data collected on cohorts of female gray seals (Halichoerus grypus) born during the 1990s and later observed breeding on the Isle of May, Firth of Forth, Scotland. Female gray seals can live for 30+ years but display individual variability in their maturation rates and so recruit into the breeding population across a range of ages. Understanding the partially hidden process by which individuals transition from immature to breeding members, and in particular the identification of any changes to this process through time, are important for understanding the factors affecting the population dynamics of this species. Age-structured capture-recapture models can explicitly relate recruitment, and other demographic parameters of interest, to the age of individuals and/or time. To account for the monitoring of the seals from several birth cohorts we consider an age-structured model that incorporates a specific cohort-structure. Within this model we focus on the estimation of the distribution of the age of recruitment to the breeding population at this colony. Understanding this recruitment process, and identifying any changes or trends in this process, will offer insight into individual year effects and give a more realistic recruitment profile for the current UK gray seal population model. The use of the hidden Markov model provides an intuitive framework following the evolution of the true underlying states of the individuals. The model breaks down the different processes of the system: recruitment into the breeding population; survival; and the associated observation process. This model specification results in an explicit and compact expression for the model with associated efficiency in model fitting. Further, this framework naturally leads to extensions to more complex models, for example the separation of first-time from return breeders, through relatively simple changes to the mathematical structure of the model.

1. Introduction

Understanding the recruitment process of new individuals to breeding populations is of fundamental importance to monitoring population dynamics. For those long-lived animals which typically breed annually, recruitment into the breeding population may require a maturation process of several years during which a range of biotic and abiotic factors may lead to cohort variability. Recruitment is often more temporally variable than other demographic processes (Nilsen et al., 2009) and its effect on the population dynamics is dependent on scale and the overall population structure. Temporal variability in recruitment in highly structured populations may be detectable over a long period. The link between environmental variability and offspring quality, as well as abundance, may also be important in some situations (Tuljapurkar et al., 2009; Sæther et al., 2013).

The UK gray seal (Halichoerus grypus) population has increased in recent decades (Thomas et al., 2019). Gray seals breed colonially at approximately 60 locations in Scotland but population trajectories differ by area: there are declines in pup production in some Outer Hebrides colonies but rapid growth of colonies in the North Sea (Smout et al., 2011b; Duck and Morris, 2016). Thomas et al. (2019) estimate gray seal abundance in UK waters through an age-structured population model within a Bayesian state-space modeling framework. This approach is sensitive to the accuracy, precision and how representative the estimates used to inform vital rate priors are, therefore it is important to improve these where possible (Øigård et al., 2012). The current model (Thomas et al., 2019) assumes female recruitment to have been completed by age 6. However, although female gray seals can start breeding at age 3, inter-individual and colony-specific variability exists so it is believed that recruitment into the breeding population occurs between the ages of 3 and 12 (Pomeroy et al., 2010). It is important to note that direct observation of recruitment is challenging. Although UK gray seals show fidelity to their previous breeding sites (Pomeroy et al., 1994; Twiss et al., 1994) and philopatry (returning to breed at their own birth colony) this may be true only for a proportion of the population or at low population densities (Pomeroy et al., 2000b). Pups born at one colony may breed elsewhere and not be detected and thus are either permanent or temporary emigrants.

Figure 1 shows the observed ages at first capture as a breeding adult for the 1991–1994 cohorts of female seal pups on the Isle of May, Firth of Forth, Scotland. Whilst the majority of seals are seen breeding by age 12, considering only the first observations does not allow for the imperfect detection of these seals which is known to occur; it is feasible that individuals may be breeding at the colony prior to their first observation.

FIGURE 1

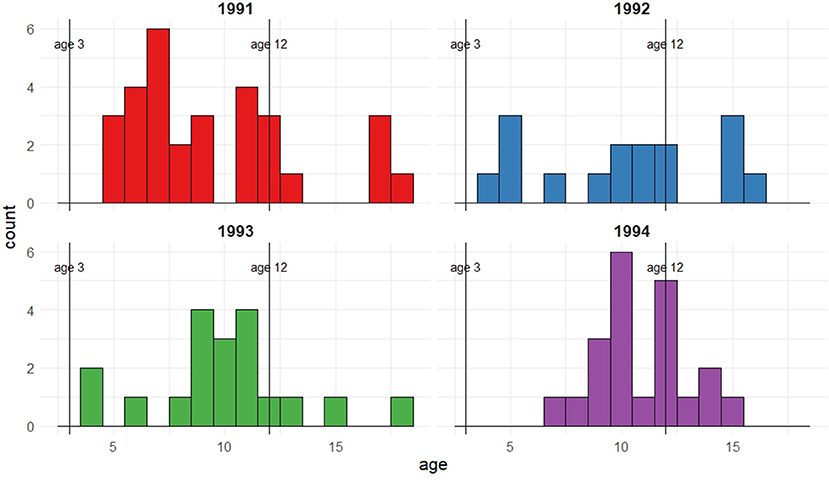
Figure 1. Female pups born and tagged in 1991, 1992, 1993, and 1994 that were recaptured as breeding mothers between 1992 and 2011. The figure shows frequencies corresponding to age of first recapture for the different cohorts.

From the first observation data, no seals from these cohorts are observed breeding as young as the earliest regarded age at which breeding may occur (i.e., 3 years old), but a few are seen breeding at 4 or 5 years old. This could be because they are present and breeding but not captured or, alternatively, they have not yet started to breed and therefore are not available for capture. The majority of the seals are seen breeding by age 12, which can be regarded as the upper age limit of initial breeding attempt, with a small proportion seen for the first time at an older age. Thus, for these individuals with an observed initial breeding age of greater than 12, it is implied that this is not their first breeding attempt but that their previous attempts were not observed or took place at a different colony. These observed ages also suggest potential bi- or multi-modality in age of first breeding; this feature will be explored through the use of mixtures on the recruitment distribution.

Data collection is performed via a capture-recapture protocol. Each year observers go to the Isle of May and record the tag numbers of observed individuals. Pups are tagged after birth and prior to the seals leaving the island. The tags are uniquely identifiable using a numerical identifier. Future observations of individual seals at subsequent capture occasions are obtained from the unique tag identifiers, in addition to any further covariate information; specifically in this case whether or not the individual is observed to be breeding. Whilst it is known that tags may be lost, from double-tagging some of the cohorts, this occurs relatively infrequently for the colony on the Isle of May (Smout et al., 2011a).

The observation data are collated from the capture occasions and typically presented in the form of individual capture histories indicating when each individual was observed at the Isle of May (0= unobserved; 1= observed). For example, an individual with capture history

$10011$

was initially captured and marked as a pup, missed on the following two occasions (indicated by the zeros) before being resighted on the final two occasions. Resighted seals were assumed to be breeding; resight probabilities for non-breeding seals are known to be very small (Smout et al., 2020). The observed data that we will analyse consist of the capture histories for female seals tagged as pups in 1991–1994 that have been recaptured as breeding adults on the Isle of May at least once during the 1992–2011 breeding seasons.

The progression of individuals from non-breeders to breeders can be modeled through age-structured capture-recapture models [see for example (McCrea and Morgan, 2015; Seber and Schofield, 2019) for an overview of capture-recapture models]. We consider here a single breeding site, a special case of age-structured multi-state capture-recapture models where individuals can disperse amongst several breeding sites (Clobert et al., 1994; Pradel, 1996; Pradel et al., 1997; Pradel and Lebreton, 1999; Lebreton and Cefe, 2002; Lebreton et al., 2003; Hénaux et al., 2007). These age-structured models are similar to stopover models (Pledger et al., 2009; Worthington et al., 2019a) where in addition to explicitly modeling the recruitment of individuals to the breeding population, demographic parameters can be further assigned a “time since recruitment” dependence (this is referred to as “age” within the stopover context and would correspond here to the number of years spent in the breeding population and need not necessarily correspond to the physical age of the individual). For this population we consider an age-dependence based on the known age of the individuals, i.e., time since tagging/birth; a stopover approach would additionally permit parameters to depend on the amount of time spent in the breeding population, the “time since recruitment.”

In this article we apply an age-structured model to investigate the recruitment of female seals to the breeding population on the Isle of May. Capture-recapture data with different marked cohorts (for example marking newborns each year) naturally have a cohort-structure. Cohort effects are known to occur in a range of different species, including seals (see for example, Beauplet et al., 2005; Payo-Payo et al., 2016; Sielezniew et al., 2020) and in this study such cohort effects are of particular interest in terms of the demographic parameters. Thus, we highlight this cohort-structure by grouping individuals by birth cohort since differences between the cohorts are of particular interest. This results in clear parameter interpretation and connections across the cohorts. The age- and cohort-structure leads to the likelihood being expressed as a product over cohorts and individuals within each cohort. This corresponds to an age- and time-dependence on the parameters in the general age-structured multi-state capture-recapture models where the likelihood is expressed simply over all individuals.

Cohort effects have been observed in studies of other seal species, for example sub-antarctic fur seals (Beauplet et al., 2005), but are not typically included in population dynamics models (Øigård and Skaug, 2014; Thomas et al., 2019). The amount of data available in this study is also very limited and there is particular interest in the ability to fit age-structured models in small data scenarios. The model we develop permits parameters to be cohort-dependent but also allows for the sharing of demographic parameters across the cohorts; particularly prudent when sample size is small whilst giving a flexible framework to investigate and identify differences between cohorts. The model is specified using the hidden Markov model (HMM) framework (King, 2014; Zucchini et al., 2017). An HMM expresses the likelihood function in a matrix format which leads to computational efficiency in the specification, and hence maximization, of the likelihood function. Further, this format can accommodate the extension to age-dependent survival such as the separation of first-time and return breeders, which we explore in section 3.1, through relatively small changes to the specification of the model.

In section 2, we define the age- and cohort-structured model and provide the associated likelihood function. In section 3, we apply the new model to the data on the Isle of May gray seals. Section 4 contains a simulation study that demonstrates the new model and investigates the effect of sample size on the identification of the recruitment process and the performance of the cohort-structured approach on the estimation of shared demographic parameters. The article concludes with a discussion in section 5.

2. Methods

Here we describe the age- and cohort-structured model. In deriving this model we keep the form of the parameter dependencies applicable to the particular data and gray seal population considered, but the model can be easily generalized. Alternative models can be achieved by changing the assumptions of the parameter dependencies (for example, constant or time-dependent capture probabilities). The model includes the following restrictions and assumptions: all seals within the study population enter the breeding population at some point within the study time frame; whilst a member of the breeding population individuals breed every year at the Isle of May (there is no temporary migration, see section 5 for more discussion of this issue); and individuals who leave the Isle of May breeding population can no longer be observed within the study (permanent migration is confounded with survival).

A hidden Markov model is described in two parts; an underlying hidden state process, and an observation process conditional on the former latent states. In the context of capture-recapture, the (partially) hidden states correspond to the availability of an individual for capture. These unknown states may be further augmented with additional individual covariates which may be discrete in nature (such as age, cohort, breeding status, etc., see for example Worthington et al., 2019a,b), or continuous (such as weight, length etc., see for example Langrock and King, 2013). The observation process part of the model describes the capture process of the animals corresponding to whether or not an individual is observed, given their availability for capture. An individual who is unavailable cannot be observed; however an individual who is available for capture may or may not be observed with some capture probability. For these models, the underlying state of availability is only partially observed due to imperfect detection. The capture of an individual naturally implies it was available for capture; the uncertainty in the state process arises in the case where an individual is not captured as (i) they may have been available for capture and simply not observed due to the imperfect capture detection; or (ii) they were not available for capture.

For capture-recapture data we consider a discrete-time approach where the capture occasions for this study correspond to the annual breeding season. There is one capture occasion per year of the study. We formulate the model primarily in a time-focused perspective, however, since it is natural to consider maturation in terms of the age of an individual, we consider the recruitment process from an age-perspective. Age and time are naturally related; combining the capture occasion with the known birth cohort determines the age of an individual. For a comparison of capture-recapture interpretation in a time or age perspective (see Sarzo et al., 2020). We consider a fully deterministic age increase (of 1 each year) but age classes or groups may be considered where parameters are in common within age classes.

To define the model we consider the two different processes (hidden-state and observation) separately before combining them to define the associated likelihood function.

2.1. Hidden-State Process

We begin by considering the hidden-state process and the latent states of the model. For ease of interpretation we label the hidden states as follows:

(1) Juvenile: the seal has not yet matured and returned to the island to breed. Seals in this state are not available for capture.

(2) Breeding: the seal is a member of the breeding population. Seals in this state are available for capture.

(3) Non-breeding: the seal has left the breeding population due to death, migration or age. Seals in this state are no longer available for capture.

We assume a stage-structured model where individuals can only remain in their current state or move to a “higher-order” state (i.e., from juvenile to breeding; and from breeding to non-breeding), where non-breeding is an absorbing state.

Notationally, we let t = 0, …, T denote the capture occasions of the study where t = 0 corresponds to the tagging of the first cohort and T is the total number of subsequent capture occasions. Let ${C}$ denote the set of cohorts where $c\in {C}$ indicates the occasions when cohorts are tagged; and n^c the number of tagged individuals in cohort c. For example, four cohorts in consecutive years would be denoted ${C}=\left\{0,1,2,3\right\}$. The age of a seal on any given capture occasion can be calculated as the difference between the occasion number and their cohort number, as all seals are tagged at age 0 and hence age is known with certainty.

To initialize the model we define the initial state distribution for each cohort which describes the state of individuals on the occasion in which they are tagged. All individuals are tagged as pups and so their initial state is that of a juvenile. We specify the initial state distribution for all individuals to be:

${\pi }^c=(100).$

We let $\beta =\left\{{\beta }_k^c:k=1,\dots ,K^c,c\in {C}\right\}$ denote the recruitment probabilities to be estimated such that ${\beta }_k^c$ is the probability an individual from cohort c joins the breeding population to breed for the first time on the Isle of May at age k; where K^c is the maximum recruitment age for the cohort. We consider the general case here where K^c may be different for each cohort, in particular permitting recruitment at any point up to the end of the study (K^c = T − c). Our data contain only known breeders therefore all individuals are known to have recruited at some point within the study necessitating that the sum of the recruitment probabilities must be equal to 1. Finally, we note that ${\beta }_k^c$ = 0 for all ages k outside the defined set of ages for which animals are assumed to breed for the first time. For our case this corresponds to k < 3. To estimate these recruitment probabilities we consider a parametric approach through a recruitment distribution. The parameters to be estimated are therefore the parameters of this chosen distribution and separate recruitment probabilities for each occasion can be obtained from this distribution (see sections 3, 4 for further details). In particular we consider the use of mixture distributions where there is interest in the mixture proportion itself and whether cohort effects are detectable and present for this parameter.

We let ϕ denote the apparent survival corresponding to the probability an individual survives to the following year and remains a member of the breeding population, given that they are alive and available for capture in the current year. Thus, we note that death, migration and “old-age” (in terms of stopping breeding) are confounded. For our data we assume that the apparent survival is constant over time and cohort for this colony (Smout et al., 2011a,b).

Transitions between the underlying states for occasions t = c, …, T − 1 and cohorts $c\in {C}$ are a function of the recruitment and survival probabilities,

${\Psi }_t^c=\left(\begin{array}{ccc}1-{\beta }_{t-c+1}^{*c}& {\beta }_{t-c+1}^{*c}& 0\\ 0& \varphi & 1-\varphi \\ 0& 0& 1\end{array}\right)$

where ${\Psi }_t^c\left[i,j\right]$ is the probability an individual is in state j on occasion t + 1 given they were in state i on occasion t. The term ${\beta }_k^{*c}=\frac{{\beta }_k^c}{\sum _{j=k}^{K^c}{\beta }_j^c}$ denotes the conditional recruitment probabilities, corresponding to the probability an individual is recruited at age k (where the age on occasion t can be calculated by k = t − c + 1) given they have not yet been recruited.

2.2. Observation Process

The observation process part of the model links the hidden states to the observed captures. The capture histories $x=\left\{x_{it}^c:i=1,\dots ,n^c,t=c+1,\dots ,T,c\in {C}\right\}$ store the recapture information for each individual (i = 1, …, n^c) in each cohort ($c\in {C}$) from the occasion following their tagging until the end of the study (i.e., for times t = c + 1, …, T). Let p denote the capture probability to be estimated which is shared across all cohorts. The observation process matrix at time t for individual i, denoted $Q_t(x_{it}^c)$, connects the probability of observing a capture ($x_{it}^c=1$) or not ($x_{it}^c=0$) given the underlying hidden state, for t = c + 1, …, T, and i = 1, …, n^c. The observation process matrix is a diagonal matrix with elements $Q_t(x_{it}^c)\left[j,j\right]$, corresponding to the probability of observation $x_{it}^c$ given the individual is in hidden state j. Thus, the matrix can be specified in the form:

$Q_t(x_{it}^c)=\{\begin{array}{c}\text{diag}(1,1-p,1)x_{it}^c=0\\ \text{diag}(0,p,0)x_{it}^c=1.\end{array}$

We consider here a constant capture probability across all occasions and all cohorts. Assuming an equal capture probability across these cohorts is reasonable for the environment and resighting procedure on the Isle of May (Pomeroy et al., 2010). There are no obvious biological reasons to suppose breeders of these different ages are less/more likely to be captured and identified than others. For this colony it is plausible that capture probabilities may vary through time. Models with time-dependent capture probabilities can be fitted within this framework (with elements of $Q_t(x_{it}^c)$ becoming a function of time-dependent p_t rather than a constant p). See section 5 for further discussion about the choice of a constant capture probability in this instance.

2.3. Likelihood Function

The likelihood can be specified as a product over each individual of their corresponding capture history probability using the HMM formulation given by:

$\begin{array}{ll}L(\beta ,\varphi ,p;x)={\displaystyle \prod _{c\in {C}}}{\displaystyle \prod _{i=1}^{n^c}}{\pi }^c\left({\displaystyle \prod _{t=c+1}^T}{\Psi }_{t-1}^c{Q}_t(x_{it}^c)\right)1_3& (1)\end{array}$

where 1₃ is an all-ones column vector of length 3 (as there are 3 underlying hidden states). Whilst the cohorts can be analyzed independently, structuring the likelihood in this way permits parameters to be shared across the cohorts (or a combination of cohort-dependent and shared parameters) and evaluated within a single expression. We note that efficiency may be gained in large populations by grouping individuals with the same capture history together and forming the product over unique histories rather than individuals.

3. Isle of May Gray Seals

The data (and code to reproduce the results presented here are available, Worthington, 2020) contain capture-recapture information on female Isle of May seals that were tagged as pups with flipper tags. We consider the 1991–1994 birth cohorts with recapture occasions corresponding to the 1992–2011 breeding seasons. Cohort sizes, corresponding to tagged female pups that are seen at least once as a breeding adult on the Isle of May, are 30, 16, 19, and 21, respectively.

To estimate separate recruitment probabilities for each cohort on each occasion requires 62 parameters (17, 16, 15, and 14 for each cohort, respectively). To reduce this number we assume a parametric form using normal or log-normal distributions. We discretise and truncate the recruitment distribution to permit recruitment from age 3 until the end of the study as described in the simulation study below. In the case of the normal distributions we specify that the mean must be positive. Capture probabilities are assumed to be constant and shared across all cohorts. Sharing the capture probabilities appears reasonable as sources of variability are likely to affect all cohorts in the same way. The restriction to constant rather than time-dependent capture probabilities is necessary due to the very small cohort sizes (see section 5). More generally, time-dependent capture probabilities can be estimated within the framework (Worthington et al., 2019a). The penalty for taking this approach appears to be slightly broader confidence intervals due to the unmodeled temporal variation. Confidence intervals are estimated through a nonparametric bootstrap with 999 bootstrap resamples (plus the original dataset), where resampling takes place within each cohort to retain constant cohort sizes.

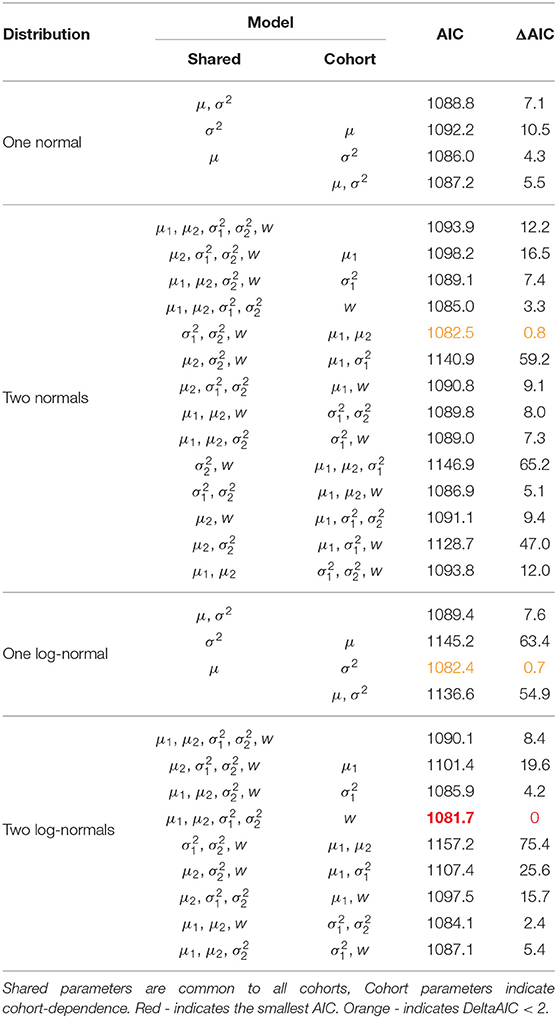
We consider a non-exhaustive range of models on the recruitment distribution using AIC values to distinguish. Cubaynes et al. (2012) explore model selection for capture-recapture analyses in the case of heterogeneous survival or capture probabilities using mixture models with up to three components. They found that AIC performs well when the aim is parameter estimation but caution that it can have a tendency to overestimate the number of mixture components. Within our study there is an ecological basis for considering a mixture model as individuals can display different recruitment behavior. The Isle of May has a finite area of suitable seal breeding habitat which is likely to limit the total number of seals using the island (Pomeroy et al., 2000a). Whilst individuals may recruit at a young age (from 3 onwards), there is competition for access to breeding spaces and inexperienced or first-time breeders (who typically breed later in the season) may simply experience difficulties getting ashore. In addition, female reproductive success is a function of mass (as capital breeders, small individuals cannot sustain successful reproduction) and as density increases individuals may take longer to reach the breeding state, delaying recruitment. For these reasons, and considering the small sample sizes, we restrict the search to include at most two mixture components to account for individuals being grouped by these behaviors.

Both the normal and log-normal distributions are specified through parameters μ and σ². Where there are two mixture components we subscript the parameters to indicate which component they belong to. We also estimate the mixture proportion w. We consider a bottom-up model search approach starting with all parameters shared across all cohorts. We relax this assumption to permit cohort-dependent parameters, stopping when further increasing the number of cohort-dependent parameters does not produce a reduction in AIC.

Table 1 presents all of the models considered and their respective AIC values. Table 2 presents the parameter estimates and 95% bootstrap confidence intervals for the parameters of the model deemed optimal via the AIC and Figure 2 visualizes the associated recruitment distributions, with associated 95% bootstrap confidence intervals for the four cohorts overlaid on top of the observed ages of first breeding (as seen in Figure 1).

TABLE 1

Table 1. Fitted models with AIC and ΔAIC scores for the Isle of May gray seal study.

TABLE 2

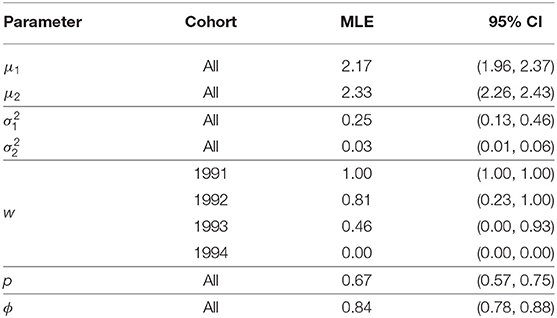
Table 2. Parameter estimates, and 95% bootstrap confidence intervals, for the Isle of May gray seal study model with constant capture and survival probability and cohort dependent mixture proportions (two log-normal mixture).

FIGURE 2

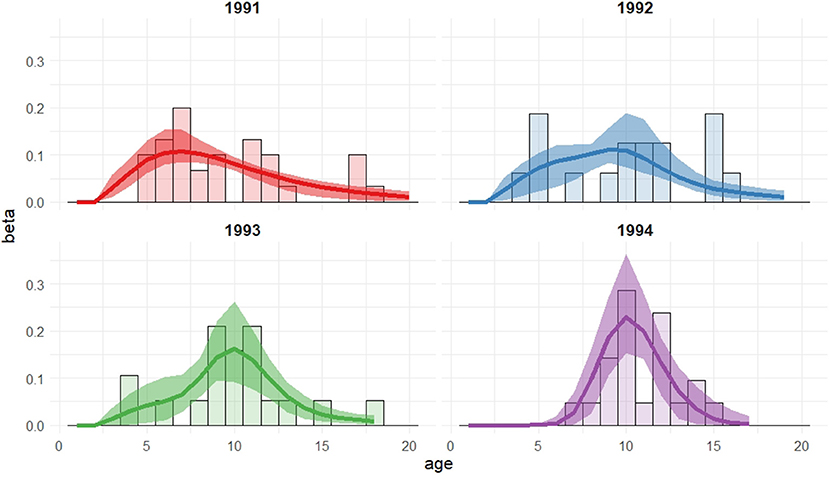
Figure 2. Recruitment distributions, with 95% bootstrap confidence intervals, for the Isle of May gray seal study model with cohort dependent mixture proportions (two log-normal mixture).

The model chosen through AIC includes a mixture of two log-normal distributions for the recruitment distribution where the mixture proportions are cohort-dependent but the mean and variance of both mixture components are common to all cohorts. Moving through the 1991 to 1994 cohorts there appears to have been a transition from one component of the mixture to the other, though there is considerable uncertainty for the 1992 and 1993 cohorts. The expected age at first breeding for mixture component 1 is approximately 9 years old (standard deviation 2.3 years) and for component 2 approximately 10.3 years old (standard deviation 0.3 years), indicating a slight shift in the average recruitment age by a little over a year to a distribution that is also more concentrated around the average.

3.1. First-Time Breeder Survival

We further extend the model described above to permit separate (apparent) survival probabilities for seals breeding for the first time on the Isle of May from returning breeders. This extension is relatively simple in the HMM format and requires augmenting the hidden states. Previously we had three hidden states corresponding to juvenile, breeding and non-breeding seals. To introduce the different survival probabilities we split the breeding state into two states; first-time breeders and return breeders. To accommodate this change the dimension of the HMM structures (initial state distribution, transition probability matrix and observation process matrix) must be increased to allow for four hidden states. The HMM structures are now:

initial state distribution

${\pi }^c=(1000);$

transition probability matrix

${\Psi }_t^c=\left(\begin{array}{cccc}1-{\beta }_{t-c+1}^{*c}& {\beta }_{t-c+1}^{*c}& 0& 0\\ 0& 0& {\varphi }_1& 1-{\varphi }_1\\ 0& 0& {\varphi }_b& 1-{\varphi }_b\\ 0& 0& 0& 1\end{array}\right);$

and observation process matrix

$Q_t(x_{it}^c)=\{\begin{array}{c}\text{diag}(1,1-p,1-p,1)x_{it}^c=0\hfill \\ \text{diag}(0,p,p,0)x_{it}^c=1;\hfill \end{array}$

where ϕ₁ and ϕ_b denote the first-time and return breeder survival probabilities, respectively and we continue to assume a constant capture probability, p. We note that the main changes are to the transition probability matrix where the new parameters have been introduced. In this formulation we again assume that the survival probabilities are constant and shared across all of the cohorts. The form of the likelihood is the same as in (1) with 1₃ replaced with 1₄ to match the number of hidden states.

As with the previous model we consider a non-exhaustive set of models for the recruitment distribution, distinguishing between models via the AIC statistic. We again take a bottom-up approach and stop when further inclusion of cohort-dependent parameters does not lead to a reduction in AIC. Table 3 displays the list of models considered with their AIC scores. Table 4 provides the parameter estimates from the model deemed optimal by the AIC with associated 95% bootstrap confidence intervals and Figure 3 displays the recruitment distributions and associated 95% bootstrap confidence intervals overlaid on the observed first recapture as a breeding adult (as in Figure 1).

TABLE 3

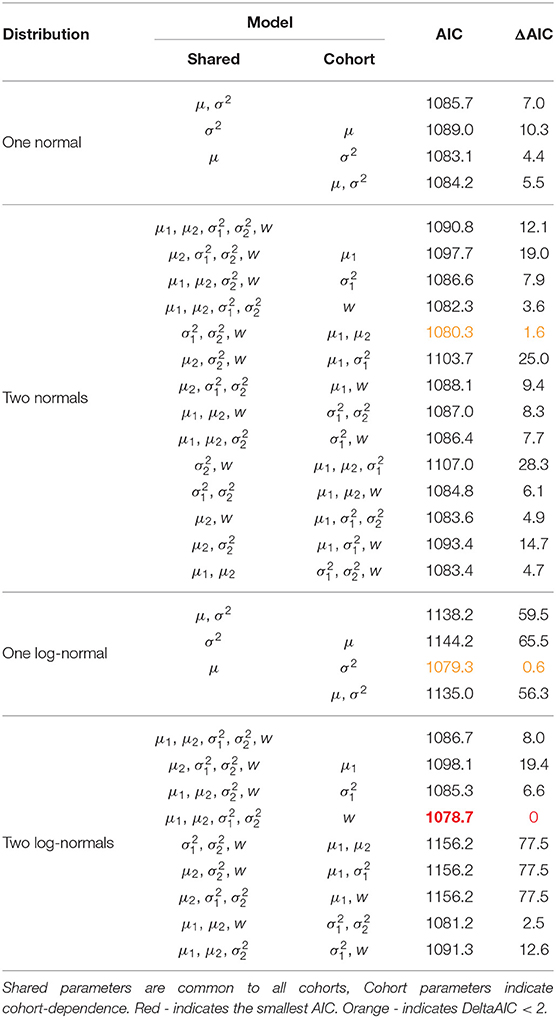
Table 3. Fitted models with AIC and ΔAIC scores for the Isle of May gray seal study first-time and return breeder model.

TABLE 4

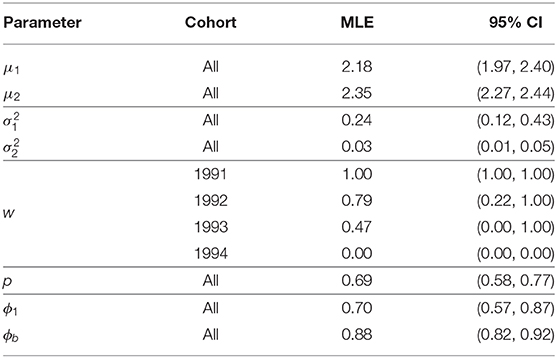
Table 4. Parameter estimates, and 95% bootstrap confidence intervals, for the Isle of May gray seal study first-time and return breeder model with constant capture and survival probabilities and cohort dependent mixture proportions (two log-normal mixture).

FIGURE 3

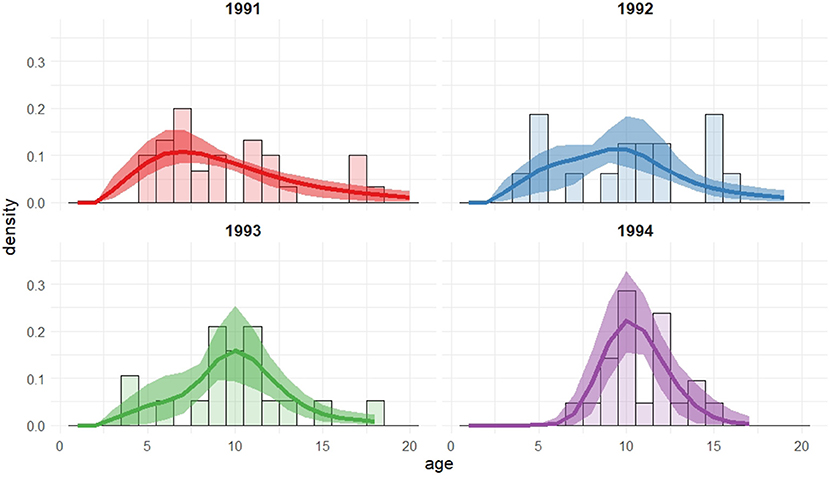
Figure 3. Recruitment distributions, with 95% bootstrap confidence intervals, for the Isle of May gray seal study first-time and return breeder model with cohort dependent mixture proportions (two log-normal mixture).

The model deemed optimal for the recruitment distribution when both first-time and return breeder survival probabilities are included is the same as when only a single survival parameter is used; cohort-dependence in the mixture proportions of a two log-normal mixture with all other parameters shared across all cohorts. The parameter estimates and their uncertainty are comparable between the two models. This second model identifies first-time breeders on the Isle of May having a lower survival probability than return breeders. We note that since we do not permit temporary migration in this model, the group of first-time breeders are likely to include some experienced breeders that have bred elsewhere prior to breeding on the Isle of May for the first time. See section 5 for further discussion.

4. Simulation Study

The Isle of May gray seal data of section 3 contains very small cohorts. Through simulation we will perform a power analysis to investigate the effect of cohort size on the estimation of the recruitment parameters. Additionally we explore the performance of the cohort-structured model, compared to a single-cohort approach, on the estimation of the demographic parameters. We base our choice of model (a two-component mixture on recruitment with cohort-dependent mixture proportions), the number of cohorts and the number of capture occasions on the gray seal data analyzed in section 3. Code to reproduce the simulation study is available (Worthington, 2020).

We will consider three different sample sizes; n = 20, 50, and 100 individuals in each cohort. We take four cohorts (C = 4) and assume pups are tagged on consecutive occasions, thus labeling them cohorts c = 0, 1, 2, 3. We set the number of capture occasions to be T = 20 (20 occasions after the tagging of the first cohort), and permit recruitment to the breeding population to occur between the ages of 3 and the end of the study (so that K^c = T − c).

To estimate separate recruitment probabilities for each occasion and cohort is extremely parameter intensive and not feasible for very small sample sizes. To reduce the number of parameters required for this part of the model we adopt a parametric approach; we model recruitment as a mixture of truncated log-normal distributions (based on the model from section 3). We then discretise this continuous distribution to obtain recruitment probabilities for each occasion. Specifically, let a random variable X follow a log-normal distribution with probability density function f (x; μ, σ²). The expectation and variance of X can be calculated by $𝔼(X)=exp\left(\mu +\frac{{\sigma }^2}{2}\right)$ and Var(X) = (exp(σ²) − 1)exp(2μ + σ²), respectively. We first discretise the distribution,

$g(x;\mu ,{\sigma }^2)={\displaystyle {\int }_{x-0.5}^{x+0.5}f}(x;\mu ,{\sigma }^2)dx,$

followed by truncation, and re-normalizing, to restrict recruitment to occur only between the age of 3 and the end of the study (therefore maximum age is cohort specific),

$g^{*}{(x;\mu ,{\sigma }^2)}^c=\frac{g(x;\mu ,{\sigma }^2)}{{\int }_{2.5}^{T-c+0.5}f(x;\mu ,{\sigma }^2)dx}.$

We form the recruitment distribution, β(x)^c for x = 3, …, T − c, c = 0, …, 3, as a mixture of two truncated and discretised log-normal distributions $g_1^{*}{(x;{\mu }_1,{\sigma }_1^2)}^c$ and $g_2^{*}{(x;{\mu }_2,{\sigma }_2^2)}^c$ such that

$\beta {(x)}^c=w^c{g}_1^{*}{(x;{\mu }_1,{\sigma }_1^2)}^c+(1-w^c)g_2^{*}{(x;{\mu }_2,{\sigma }_2^2)}^c,$

where the parameters to be estimated are μ₁, μ₂, ${\sigma }_1^2$, ${\sigma }_2^2$ (shared across all cohorts) and the mixture proportions w^c for c = 0, …, 3.

To simulate data we set μ₁ = 2, μ₂ = 2.5, ${\sigma }_1^2=0.25^2$, ${\sigma }_2^2=0.05^2$ (corresponding to 𝔼₁(X) = 7.6, sd₁(X) = 1.94 for mixture component 1 and 𝔼₂(X) = 12.2, sd₂(X) = 0.61 for mixture component 2). The mixture proportions are cohort-dependent and equal to w^c = 1, 0.7, 0.3, and 0 for cohorts c = 0, …, 3, respectively. We include a constant capture probability of 0.7 and a constant survival probability of 0.8. For each of the cohort sample sizes n = 20, 50, 100 we simulate 1,000 datasets. For each simulated dataset we fit both the age- and cohort-structured model for all of the cohort data combined and separate single-cohort models to each cohort independently in turn. We present plots of the estimated recruitment distributions along with estimates of the demographic parameters across the 1,000 simulations in Figures 4–6.

FIGURE 4

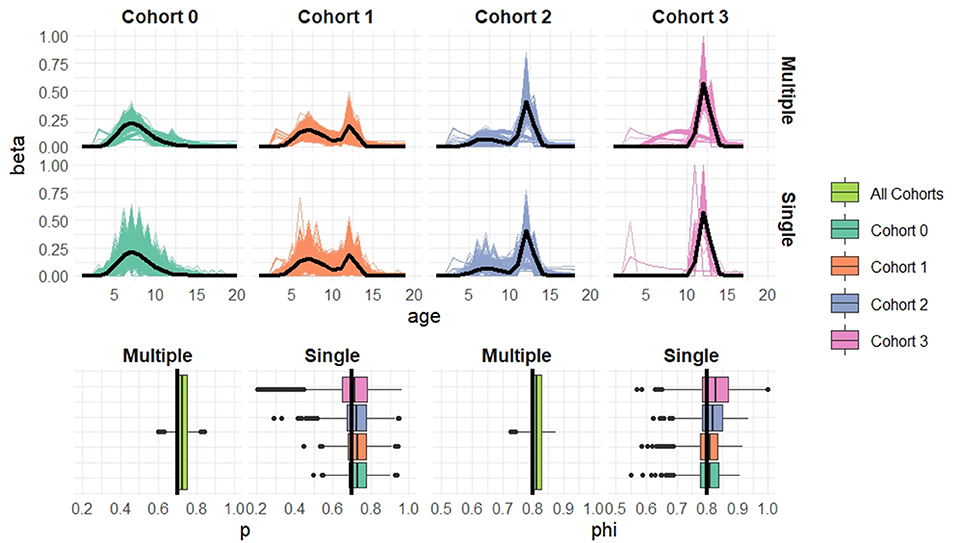
Figure 4. Simulation results when cohort sample size n = 20 based on 1,000 simulated datasets. Top: Estimated recruitment distributions from the cohort-structured model. Middle: Estimated recruitment distributions from the single-cohort models. Bottom: Estimated capture and survival probabilities for the cohort-structured model (multiple) and separate single-cohort models (single). The true values are indicated by black lines.

FIGURE 5

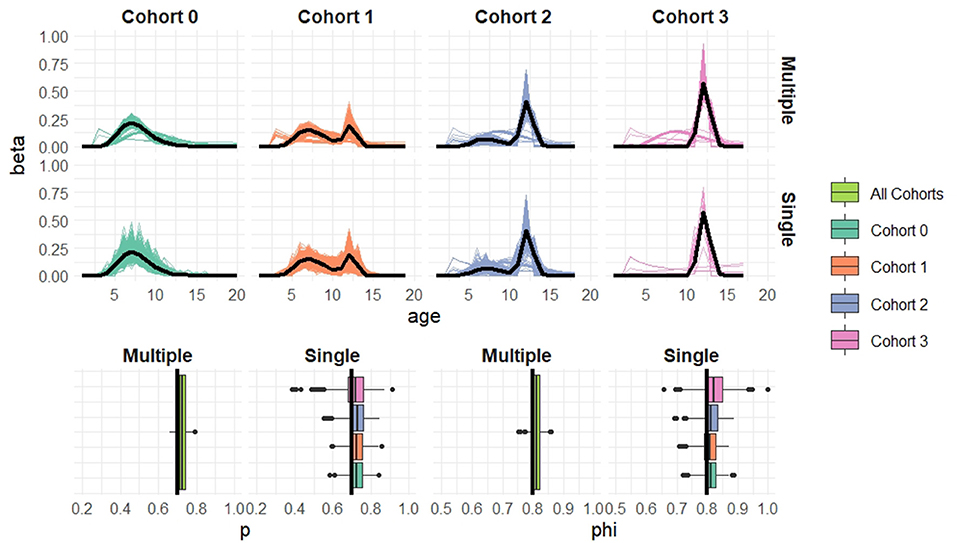
Figure 5. Simulation results when cohort sample size n = 50 based on 1,000 simulated datasets. Top: Estimated recruitment distributions from the cohort-structured model. Middle: Estimated recruitment distributions from the single-cohort models. Bottom: Estimated capture and survival probabilities for the cohort-structured model (multiple) and separate single-cohort models (single). The true values are indicated by black lines.

FIGURE 6

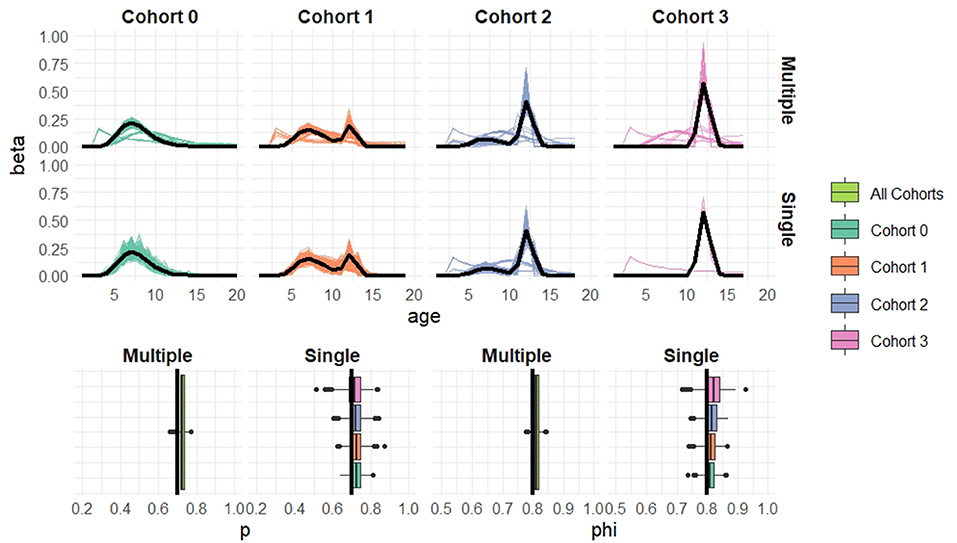
Figure 6. Simulation results when cohort sample size n = 100 based on 1,000 simulated datasets. Top: Estimated recruitment distributions from the cohort-structured model. Middle: Estimated recruitment distributions from the single-cohort models. Bottom: Estimated capture and survival probabilities for the cohort-structured model (multiple) and separate single-cohort models (single). The true values are indicated by black lines.

Overall the multiple-cohort model outperforms the single-cohort approach showing reduced variability in the parameter estimates across the 1000 simulations. Even for the smallest sample size, n = 20 individuals in each cohort, the multiple-cohort approach frequently captures the general shape of the recruitment distribution. As expected this improves with increased sample size. Similarly, the figures show that as the sample size increases, the precision of the parameter estimates also increases. The greatest improvement is seen in the variability of the demographic estimates.

5. Discussion

In this paper we explore an age- and cohort-structured stopover model to estimate the distribution of age at recruitment to the breeding population for female seals on the Isle of May alongside capture and survival probabilities. We demonstrate that it is possible to gain valuable ecological insights into a population from relatively small datasets through the use of shared parameters across cohorts. The cohort-structured model has improved performance in this regard over the more standard approach of analyzing each cohort independently of each other.

The model offers a powerful tool to be able to better understand recruitment patterns and changes in those patterns across multiple cohorts, as demonstrated through application to a field data set. This offers preliminary findings (from restricted sample sizes) to suggest there is cohort variability in recruitment: variability in vital rates tends to slow population growth (Lewontin and Cohen, 1969). In this particular study, there is a suggestion of directional change in the average age of recruitment as the mixture proportion for the mixture component with a higher mean recruitment age increases, recruitment on average becomes later by cohort. This would suggest pressure on this breeding population, with new recruits either maturing later perhaps due to food resource limitation, or new recruits finding it more difficult to establish a breeding site within the colony. Both such outcomes might relate to intensified intraspecific competition within a growing population of gray seals in the North Sea (Thomas et al., 2019). Food limitation might also relate to ecosystem change over this period with changing populations of sandeels and cod (ICES, 2017, 2020).

In the current UK gray seal population model (Thomas et al., 2019), a Bayesian approach is used to fit an age-structured model of British gray seal population dynamics to regular estimates of the number of pups born per year, synoptic estimates of total population size, and other data on demographic parameters, informing prior distributions. While the model is used mainly to derive an estimate of population size and trend, it is also used to assess region-level density dependence (Thomas et al., 2019). Harwood and Prime (1978) had considered pup survival the most likely parameter to be affected by density dependence and (Thomas et al., 2019) therefore modified the model to include a density dependent function. However, the age at which female gray seals recruit to the breeding population is likely to increase under density dependence as resources such as space and food become less abundant. Here we add to the evidence (Pomeroy et al., 2010) that recruitment at the Isle of May is incomplete by age 6 and has increased during the 1990s as pup production there increased, so that it may not be complete by age 10 (Figures 2, 3). Canadian gray seals showed an increase in average recruitment age of 1 year over a 15 year period (Bowen et al., 2006) so the effect seen at the Isle of May seems large and rapid in comparison and would have a greater influence on demographic models than the effect size seen in Canada.

The HMM framework facilitates efficient model fitting and allows model extensions and adaptations to be made with ease. We demonstrate one extension by allowing survival to differ between first-time and return breeders, better supporting the biological understanding of the species. Other extensions could be easily included in this framework, for example, accounting for state uncertainty (Pradel, 2005; King and McCrea, 2014) where states may be misidentified, augmenting the hidden states to account for further discrete state information (Worthington et al., 2019a), individual time-varying covariates and associated missing data issues (Langrock and King, 2013) or temporary migration (see below). In particular, it is known that initial postweaning survival of gray seal pups is linked to individual covariates such that larger pups survive better as do those with robust immune systems (Hall et al., 2001) therefore early condition is at least partially linked to probability of recruitment (Bowen et al., 2015). The model presented here offers the framework to include such covariate information.

For these data with limited sample size, care was needed in estimating large numbers of parameters. In particular, estimating large numbers of time-dependent capture probabilities led to boundary estimates and suspected near-redundancy in the model. Problems appear to arise when estimating the capture probabilities for the earlier occasions when very few individuals have been recruited. Nevertheless, the estimation of the recruitment distributions appear to be robust to such changes in the capture probability dependency. The issues in relation to (near) parameter redundancy are most likely related to the small cohort sizes available, and the further investigation of such redundancies is an ongoing area of research.

The estimation of separate survival rates for seals on their first breeding occasion is consistent with other studies in gray seals (Smout et al., 2011a). Two potential explanations are (1) primaparity may be associated with a higher risk of mortality than later pregnancies (2) first-time breeders may be more likely to be transient visitors that go on to breed more regularly elsewhere. The methodology used cannot distinguish mortality from permanent emigration.

It is therefore important to note that the model presented here is limited by the following assumptions: (1) all the seals observed on the Isle of May are breeding; (2) once a seal is recruited to the population they are assumed to breed every year on the Isle of May until they permanently leave the breeding population; and (3) that individuals in this population are only recruited to the Isle of May population, they do not breed elsewhere before joining and so all transition through being a first-time breeder. Assumption (1) can be accounted for through permitting state-uncertainty as described above, though this is likely to be a small effect since very few non-breeders are observed at colonies. The remaining two could be relaxed through the inclusion of temporary migration. Temporary migration would permit individuals to skip breeding seasons, which is known to happen (Smout et al., 2020), or to temporarily breed at a different colony. The consequence of not incorporating this into the model is that capture probabilities are likely to underestimate the true values and as a result there may be modest effects on the estimation of recruitment. Within a robust design framework (Kendall et al., 2019) it is often possible to incorporate temporary emigration into the model, see for example (Kendall et al., 1997; Zhou et al., 2019). It therefore seems prudent to develop temporary migration within the model to accommodate the idea that seals that are not seen until after the age of 12 are in fact breeding adults, but they are simply breeding at a site other than the Isle of May. Whilst the HMM framework can be adapted to include temporary migration (through the addition of further hidden states), it is likely to require significantly larger sample sizes than those available here. Supplementary data, such as estimated migration rates or individual covariates, that inform these behaviors would likely be advantageous and reduce reliance on only the capture-recapture data to estimate the form of these relationships.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/hannah-worthington/Seals_Frontiers.

Ethics Statement

Work involving animals in this study was licensed under UK Home Office project 60/4009 or preceding versions and conformed to the UK Animals (Scientific Procedures) Act, 1986. Research was approved by the University of St. Andrews Animal Welfare and Ethics Committee.

Author Contributions

All authors conceived the presented ideas and developed the modeling approach. HW developed the theory and performed the simulation study and data analysis. PP directed and carried out the long term fieldwork. PP and SS provided the data, data information, knowledge of the species, and insight into this population. All authors discussed the results and contributed to the final manuscript.

Funding

HW was supported by a Carnegie Scholarship from the Carnegie Trust for the Universities of Scotland; RK was supported by the Leverhulme research fellowship RF-2019-299; and RM was funded by NERC grant NE/J018473/1. Research at the Isle of May was supported by NERC core funding to SMRU.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank Scottish Natural Heritage for access to the Isle of May. Thanks to all who participated in fieldwork over the years particularly Sean Twiss and Simon Moss.

References

Beauplet, G., Barbraud, C., Chambellant, M., and Guinet, C. (2005). Interannual variation in the post-weaning and juvenile survival of subantarctic fur seals: influence of pup sex, growth rate and oceanographic conditions. J. Anim. Ecol. 74, 1160–1172. doi: 10.1111/j.1365-2656.2005.01016.x

CrossRef Full Text | Google Scholar

Bowen, W. D., den Heyer, C. E., McMillan, J. I., and Iverson, S. J. (2015). Offspring size at weaning affects survival to recruitment and reproductive performance of primiparous gray seals. Ecol. Evol. 5, 1412–1424. doi: 10.1002/ece3.1450

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowen, W. D., Iverson, S. J., McMillan, J. I., and Boness, D. J. (2006). Reproductive performance in grey seals: age-related improvement and senescence in a capital breeder. J. Anim. Ecol. 75, 1340–1351. doi: 10.1111/j.1365-2656.2006.01157.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Clobert, J., Lebreton, J.-D., Allaine, D., and Gaillard, J. M. (1994). The estimation of age-specific breeding probabilities from recaptures or resightings in vertebrate populations: II. Longitudinal models. Biometrics 50, 375–387. doi: 10.2307/2533381

PubMed Abstract | CrossRef Full Text | Google Scholar

Cubaynes, S., Lavergne, C., Marboutin, E., and Gimenez, O. (2012). Assessing individual heterogeneity using model selection criteria: how many mixture components in capture-recapture models? Methods Ecol. Evol. 3, 564–573. doi: 10.1111/j.2041-210X.2011.00175.x

CrossRef Full Text | Google Scholar

Duck, C., and Morris, C. (2016). Surveys of Harbour and Grey Seals on the South-East (Border to Aberlady Bay) and South-West (Sound of Jura to Solway Firth) Coasts of Scotland, in Shetland, in the Moray Firth and in the Firth of Tay in August 2015. Scottish Natural Heritage Commissioned Report.

Google Scholar

Hall, A. J., McConnell, B. J., and Barker, R. J. (2001). Factors affecting first-year survival in grey seals and their implications for life history strategy. J. Anim. Ecol. 70, 138–149. doi: 10.1111/j.1365-2656.2001.00468.x

CrossRef Full Text | Google Scholar

Harwood, J., and Prime, J. H. (1978). Some factors affecting the size of British grey seal populations. J. Appl. Ecol. 15, 401–411. doi: 10.2307/2402600

CrossRef Full Text | Google Scholar

Hénaux, V., Bregnballe, T., and Lebreton, J.-D. (2007). Dispersal and recruitment during population growth in a colonial bird, the great cormorant phalacrocorax carbo sinensis. J. Avian Biol. 38, 44–57. doi: 10.1111/j.2006.0908-8857.03712.x

CrossRef Full Text | Google Scholar

ICES (2017). Report of the Benchmark on Sandeel (WKSand 2016). Bergen.

Google Scholar

ICES (2020). Working Group on the Assessment of Demersal Stocks in the North Sea and Skagerrak (WGNSSK).ICES Scientific Reports.

Google Scholar

Kendall, W. L., Nichols, J. D., and Hines, J. E. (1997). Estimating temporary emigration using capture-recapture data with Pollock's robust design. Ecology 78, 563–578. doi: 10.1890/0012-9658(1997)078[0563:ETEUCR]2.0.CO;2

CrossRef Full Text | Google Scholar

Kendall, W. L., Stapleton, S., White, G. C., Richardson, J. I., Pearson, K. N., and Mason, P. (2019). A multistate open robust design: population dynamics, reproductive effort, and phenology of sea turtles from tagging data. Ecol. Monogr. 89:e01329. doi: 10.1002/ecm.1329

CrossRef Full Text | Google Scholar

King, R. (2014). Statistical ecology. Annu. Rev. Stat. Appl. 1, 401–426. doi: 10.1146/annurev-statistics-022513-115633

CrossRef Full Text | Google Scholar

King, R., and McCrea, R. (2014). A generalised likelihood framework for partially observed capture-recapture-recovery models. Stat. Methodol. 17, 30–45. doi: 10.1016/j.stamet.2013.07.004

CrossRef Full Text | Google Scholar

Langrock, R., and King, R. (2013). Maximum likelihood estimation of mark-recapture-recovery models in the presence of continuous covariates. Ann. Appl. Stat. 7, 1709–1732. doi: 10.1214/13-AOAS644

CrossRef Full Text | Google Scholar

Lebreton, J. D., and Cefe, R. P. (2002). Multistate recapture models: modelling incomplete individual histories. J. Appl. Stat. 29, 353–369. doi: 10.1080/02664760120108638

CrossRef Full Text | Google Scholar

Lebreton, J. D., Hines, J. E., Pradel, R., Nichols, J. D., and Spendelow, J. A. (2003). Estimation by capture-recapture of recruitment and dispersal over several sites. Oikos 101, 253–264. doi: 10.1034/j.1600-0706.2003.11848.x

CrossRef Full Text | Google Scholar

Lewontin, R. C., and Cohen, D. (1969). On population growth in a randomly varying environment. Proc. Natl. Acad. Sci. U.S.A. 62, 1056–1060. doi: 10.1073/pnas.62.4.1056

PubMed Abstract | CrossRef Full Text | Google Scholar

McCrea, R., and Morgan, B. (2015). Analysis of Capture-Recapture Data. New York, NY: Chapman and Hall/CRC. doi: 10.1201/b17222

CrossRef Full Text | Google Scholar

Nilsen, E. B., Gaillard, J.-M., Andersen, R., Odden, J., Delorme, D., Van Laere, G., et al. (2009). A slow life in hell or a fast life in heaven: demographic analyses of contrasting roe deer populations. J. Anim. Ecol. 78, 585–594. doi: 10.1111/j.1365-2656.2009.01523.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Øigård, T. A., Frie, A. K., Nilssen, K. T., and Hammill, M. O. (2012). Modelling the abundance of grey seals (Halichoerus grypus) along the Norwegian coast. ICES J. Mar. Sci. 69, 1436–1447. doi: 10.1093/icesjms/fss103

CrossRef Full Text | Google Scholar

Øigård, T. A., and Skaug, H. J. (2014). Fitting state-space models to seal populations with scarce data. ICES J. Mar. Sci. 72, 1462–1469. doi: 10.1093/icesjms/fsu195

CrossRef Full Text | Google Scholar

Payo-Payo, A., Genovart, M., Bertolero, A., Pradel, R., and Oro, D. (2016). Consecutive cohort effects driven by density-dependence and climate influence early-life survival in a long-lived bird. Proc. R. Soc. B 283:20153042. doi: 10.1098/rspb.2015.3042

PubMed Abstract | CrossRef Full Text | Google Scholar

Pledger, S., Efford, M., Pollock, K. H., Collazo, J. A., and Lyons, J. E. (2009). Stopover duration analysis with departure probability dependent on unknown time since arrival. Environ. Ecol. Stat. 3, 349–363. doi: 10.1007/978-0-387-78151-8_15

CrossRef Full Text | Google Scholar

Pomeroy, P., Smout, S. C., Twiss, S., Moss, S., and King, R. (2010). Low and delayed recruitment at grey seal breeding colonies in the UK. J. NorthWest Fisher. Assoc. 42, 125–133. doi: 10.2960/J.v42.m651

CrossRef Full Text | Google Scholar

Pomeroy, P. P., Anderson, S. S., Twiss, S. D., and McConnell, B. J. (1994). Dispersion and site fidelity of breeding female grey seals (Halichoerus grypus) on North Rona, Scotland. J. Zool. 233, 429–447. doi: 10.1111/j.1469-7998.1994.tb05275.x

CrossRef Full Text | Google Scholar

Pomeroy, P. P., Twiss, S. D., and Duck, C. D. (2000a). Expansion of a grey seal (Halichoerus grypus) breeding colony: changes in pupping site use at the Isle of May, Scotland. J. Zool. 250, 1–12. doi: 10.1111/j.1469-7998.2000.tb00573.x

CrossRef Full Text | Google Scholar

Pomeroy, P. P., Twiss, S. D., and Redman, P. (2000b). Philopatry, site fidelity and local kin associations within grey seal breeding colonies. Ethology 106, 899–919. doi: 10.1046/j.1439-0310.2000.00610.x

CrossRef Full Text | Google Scholar

Pradel, R. (1996). Utilization of capture-mark-recapture for the study of recruitment and population growth rate. Biometrics 52, 703–709. doi: 10.2307/2532908

CrossRef Full Text | Google Scholar

Pradel, R. (2005). Multievent: an extension of multistate capture-recapture models to uncertain states. Biometrics 61, 442–447. doi: 10.1111/j.1541-0420.2005.00318.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pradel, R., Johnson, A. R., Viallefont, A., Nager, R. G., and Cezilly, F. (1997). Local recruitment in the greater flamingo: a new approach using capture-mark-recapture data. Ecology 78, 1431–1445. doi: 10.1890/0012-9658(1997)078[1431:LRITGF]2.0.CO;2

CrossRef Full Text | Google Scholar

Pradel, R., and Lebreton, J.-D. (1999). Comparison of different approaches to the study of local recruitment of breeders. Bird Study 46(Suppl 1):S74–S81. doi: 10.1080/00063659909477234

CrossRef Full Text | Google Scholar

Sæther, B.-E., Coulson, T., Grøtan, V., Engen, S., Altwegg, R., Armitage, K. B., et al. (2013). How life history influences population dynamics in fluctuating environments. Am. Nat. 182, 743–759. doi: 10.1086/673497

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarzo, B., Conesa, D., and King, R. (2020). Cormack-Jolly-Seber models: time and age perspectives. Stochast. Environ. Res. Risk Assess. 34, 1683–1698. doi: 10.1007/s00477-020-01840-x

CrossRef Full Text | Google Scholar

Seber, G. A. F., and Schofield, M. R. (2019). Capture-Recapture: Parameter Estimation for Open Animal Populations. Cham: Springer International Publishing. doi: 10.1007/978-3-030-18187-1

CrossRef Full Text | Google Scholar

Sielezniew, M., Kostro-Ambroziak, A., and Korosi, A. (2020). Sexual differences in age-dependent survival and life span of adults in a natural butterfly population. Sci. Rep. 10:10394. doi: 10.1038/s41598-020-66922-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Smout, S., King, R., and Pomeroy, P. (2011a). Integrating heterogeneity of detection and mark loss to estimate survival and transience in UK grey seal colonies. J. Appl. Ecol. 48, 364–372. doi: 10.1111/j.1365-2664.2010.01913.x

CrossRef Full Text | Google Scholar

Smout, S., King, R., and Pomeroy, P. (2020). Environment-sensitive mass changes influence breeding frequency in a capital breeding marine top predator. J. Anim. Ecol. 89, 384–396. doi: 10.1111/1365-2656.13128

PubMed Abstract | CrossRef Full Text | Google Scholar

Smout, S. C., King, R., and Pomeroy, P. (2011b). Estimating demographic parameters for capture-recapture data in the presence of multiple mark types. Environ. Ecol. Stat. 18, 331–347. doi: 10.1007/s10651-010-0135-y

CrossRef Full Text | Google Scholar

Thomas, L., Russell, D. J., Duck, C. D., Morris, C. D., Lonergan, M., Empacher, F., et al. (2019). Modelling the population size and dynamics of the grey seal. Aquatic Conservation: Marine and Freshwater Ecosystems, 29(S1):6–23. doi: 10.1002/aqc.3134

CrossRef Full Text | Google Scholar

Tuljapurkar, S., Gaillard, J.-M., and Coulson, T. (2009). From stochastic environments to life histories and back. Philos. Trans. R. Soc. B. Biol. Sci. 364, 1499–1509. doi: 10.1098/rstb.2009.0021

PubMed Abstract | CrossRef Full Text | Google Scholar

Twiss, S. D., Pomeroy, P. P., and Anderson, S. S. (1994). Dispersion and site fidelity of breeding male grey seals (Halichoerus grypus) on North Rona, Scotland. J. Zool. 233, 683–693. doi: 10.1111/j.1469-7998.1994.tb05374.x

CrossRef Full Text | Google Scholar

Worthington, H. (2020). Seals_Frontiers. GitHub repository. Available online at: https://github.com/hannah-worthington/Seals_Frontiers

Google Scholar

Worthington, H., McCrea, R., King, R., and Griffiths, R. (2019a). Estimating abundance from multiple sampling capture-recapture data via a multi-state multi-period stopover model. Ann. Appl. Stat. 13, 2043–2064. doi: 10.1214/19-AOAS1264

CrossRef Full Text | Google Scholar

Worthington, H., McCrea, R. S., King, R., and Griffiths, R. A. (2019b). Estimation of population size when capture probability depends on individual states. J. Agric. Biol. Environ. Stat. 24, 154–172. doi: 10.1007/s13253-018-00347-x

CrossRef Full Text | Google Scholar

Zhou, M., McCrea, R. S., Matechou, E., Cole, D. J., and Griffiths, R. A. (2019). Removal models accounting for temporary emigration. Biometrics 75, 24–35. doi: 10.1111/biom.12961

PubMed Abstract | CrossRef Full Text | Google Scholar

Zucchini, W., MacDonald, I., and Langrock, R. (2017). Hidden Markov Models for Time Series: An Introduction Using R, 2nd Edn. Boca Raton, FL: Chapman and Hall/CRC.

Google Scholar