Simulating Growth and Competition on Wet and Waterlogged Soils in a Forest Landscape Model

Changes in CO₂ concentration and climate are likely to alter disturbance regimes and competitive outcomes among tree species, which ultimately can result in shifts of species and biome boundaries. Such changes are already evident in high latitude forests, where waterlogged soils produced by topography, surficial geology, and permafrost are an important driver of forest dynamics. Predicting such effects under the novel conditions of the future requires models with direct and mechanistic links of abiotic drivers to growth and competition. We enhanced such a forest landscape model (PnET-Succession in LANDIS-II) to allow simulation of waterlogged soils and their effects on tree growth and competition. We formally tested how these modifications alter water balance on wetland and permafrost sites, and their effect on tree growth and competition. We applied the model to evaluate its promise for mechanistically simulating species range expansion and contraction under climate change across a latitudinal gradient in Siberian Russia. We found that higher emissions scenarios permitted range expansions that were quicker and allowed a greater diversity of invading species, especially at the highest latitudes, and that disturbance hastened range shifts by overcoming the natural inertia of established ecological communities. The primary driver of range advances to the north was altered hydrology related to thawing permafrost, followed by temperature effects on growth. Range contractions from the south (extirpations) were slower and less tied to emissions or latitude, and were driven by inability to compete with invaders, or disturbance. An important non-intuitive result was that some extant species were killed off by extreme cold events projected under climate change as greater weather extremes occurred over the next 30 years, and this had important effects on subsequent successional trajectories. The mechanistic linkages between climate and soil water dynamics in this forest landscape model produced tight links between climate inputs, physiology of vegetation, and soils at a monthly time step. The updated modeling system can produce high quality projections of climate impacts on forest species range shifts by accounting for the interacting effects of CO₂ concentration, climate (including longer growing seasons), seed dispersal, disturbance, and soil hydrologic properties.

Introduction

Changes in abiotic conditions (CO₂ concentration and climate) have the potential to greatly modify forest dynamics by altering disturbance regimes and changing competitive outcomes among tree species. These modified competitive and disturbance dynamics can, over time, result in range shifts within biomes, and shifts in biome boundaries themselves (Liang et al., 2018). Competitive outcomes are determined by a host of interacting factors, including the biotic factors of intrinsic growth rates, drought tolerance, shade tolerance, heat and cold tolerance, and the abiotic factors of CO₂ concentration, temperature, precipitation, soil texture, soil depth, and nutrients. Furthermore, many relationships and interactions are non-linear. Disturbances interact with competitive relationships when they remove dominant cohorts or completely reset the successional sequence (Coop et al., 2020). Range expansions (or contractions) involve displacement of existing species or life forms through both dispersal and competitive superiority, although displacement may lag considerably behind a change in abiotic conditions in the absence of removal of extant cohorts by senescence or disturbance (Liang et al., 2018). Because of these many complex interactions, it is extremely difficult to predict future forest composition and individual tree species range shifts under the novel conditions expected in the future.

Waterlogged soils are common in many forested ecosystems, and can be produced either by topography, surficial geology, or permafrost at high latitudes. In glaciated landscapes without permafrost, the topography of glacial till and near-surface bedrock produces depressions that are perennially wet, and such conditions can occupy large portions of some landscapes. At high latitudes and elevations, permafrost can be the dominant driver of soil hydrology, limiting soil drainage to increase the occurrence of waterlogged conditions. A warming climate has the potential to alter permafrost hydrology such that the vegetation will change. Successional trajectories may move toward either a wetter or drier ecosystem in the near term (depending on specific conditions), but will ultimately become drier if the permafrost thaws completely where soils have good drainage (Jin et al., 2020). Predicting such successional trajectories is critical for forecasting shifts of species and biome boundaries and understanding impacts on carbon budgets.

Predicting the effects of global changes on forests requires models that formalize empirical knowledge acquired from field and laboratory experiments in terms of first principles to predict behavior under the novel conditions of the future (Gustafson, 2013). Assessments of the effects of global change on the dynamics of temperate and boreal forests have been conducted primarily using either eco-physiology models that simulate growth and materials fluxes within a forest plot or stand (e.g., Forest-GCB, Running and Gower, 1991; PnET-CN, Aber et al., 1997) or Dynamic Global Vegetation Models (DGVM, e.g., LPJ-DGVM, Quegan et al., 2011; CLM-FATES, Lawrence et al., 2018) that simulate competition among plant functional types (PFTs) at regional to global scales (Medlyn et al., 2011). Both of these classes of models tend to simulate the mechanisms of photosynthesis and competition for light and water, and are therefore relatively robust for making predictions for novel climatic conditions that are outside the conditions under which forests have been studied in the past (Gustafson, 2013).

Dynamic Global Vegetation Models play a key role for integrating climate-vegetation feedbacks within Global Circulation Models by projecting the spatial distribution of PFTs across the globe. However, it has been demonstrated that spatial processes not modeled by DGVMs (disturbances, seed dispersal and establishment, and the consequent sub-cell heterogeneity that results from those processes) degrade their ability to accurately scale up ecosystem processes to regional and global scales (Fisher et al., 2010), particularly in high-latitude biomes (Wullschleger et al., 2014), where disturbances (particularly fire) greatly alter living and dead carbon pools (Dolman et al., 2012). Also, because DGVMs model PFTs rather than individual species, the re-assortment of species into novel assemblages (and habitats) as climate and disturbance regimes change is poorly simulated. Alternatively, stand biophysical models (e.g., PnET, Aber et al., 1995; LINKAGES, Post and Pastor, 1996) also tend to have mechanistic formulations based on first principles, and can robustly account for competitive interactions, but they rarely include spatial interactions among stands, such as seed dispersal, contagious disturbances, and hydrologic links to the broader landscape. Such models are useful to predict stand-level responses to climate change and management interventions, but they omit many of the factors that operate at broader spatial scales and determine forest dynamics at landscape and regional scales.

Forest Landscape Models (FLMs) have proved useful for projecting future forest dynamics because they explicitly account for most of the factors that structure forested ecosystems at landscape spatial and temporal scales (He, 2008), and simulate seed dispersal and disturbances such that their interactions play out as an emergent property of the climate inputs, abiotic environment and vegetation state. Unlike DGVMs, FLMs are spatially explicit at a relatively fine resolution (10–500 m cells) and most simulate competition and succession at the species level. Unlike stand models, FLMs include spatial interactions among stands. However, FLMs tend to have weak or indirect links between climate and growth, often using slowly changing climate averages that fail to account for the importance of extreme events in structuring forests (Gustafson, 2013). Virtually all FLMs are unable to dynamically link climate to changes in hydrology, especially in hydrologic systems where soil waterlogging is possible, although a couple examples of loosely coupling a hydrology model with an FLM have recently been described (De Jager et al., 2019; Speich et al., 2019).

The LANDIS-II FLM (Scheller et al., 2007) simulates growth, death and succession of tree species cohorts (rather than individuals, PFTs or forest types) on grid cells (10–500 m) that interact spatially through seed dispersal and contagious disturbances. LANDIS-II requires one of several available succession extensions to simulate growth processes, and has many optional extensions to simulate disturbances relevant to the system under study. A relatively mechanistic succession extension was developed for LANDIS-II that relies on first principles related to growth via photosynthesis (De Bruijn et al., 2014). This extension (PnET-Succession) incorporates algorithms from the PnET-II eco-physiology model (Aber et al., 1995), and it represents a major advance in forest landscape modeling because it mechanistically simulates photosynthesis as in DGVMs and biophysical models, while LANDIS-II includes the spatial processes (e.g., seed dispersal and contagious disturbances) that are inadequately simulated in those models. This new modeling approach provides some key advances over other FLMs that operate at this intermediate scale. (1) Growth is tightly linked to climate and responds to climate dynamically at a monthly time step (vs. annual or decadal), better reflecting the major effect of weather extremes in structuring forests through growth and mortality. (2) Succession is an emergent property of species-level growth and competition under dynamic climate conditions rather than transition probabilities among forest types or assemblages (e.g., ALFRESCO, Rupp et al., 2000). (3) Mortality is mechanistic rather than probabilistic, occurring when carbon reserves drop below critical levels when photosynthetic output is insufficient to cover respiration costs. (4) Species cohorts compete for soil water, simulated using a relatively simple hydrologic bucket model. PnET-Succession also includes species-specific water stress parameters for both low (dry) and excessively high (waterlogged) water potentials. (5) The mechanistic approach integrates CO₂ effects on growth, conductance and water use efficiency; temperature effects on photosynthesis, respiration and evapotranspiration (including length of growing season); precipitation and consumption effects on water availability; incoming radiation and canopy layering effects on light extinction; and inter-cohort competition for light and water, all of which interact to determine species-cohort productivity and competitiveness under a given climate and hydrologic regime. It is virtually impossible to robustly simulate such interactions under novel climatic conditions using a phenomenological approach that uses the past to predict the future.

Despite the significant advantages of PnET-Succession for simulating the impacts of global abiotic change on future forest dynamics, its soil hydrology calculations assume that the water table is below the rooting zone and the simulation of hydrology has few links relevant to changes in climate other than precipitation inputs. Furthermore, the model assumes that water can drain through the soil profile into the water table sink, but it does not perform well when the water table normally fluctuates within the rooting zone (e.g., forested wetlands, flood plains) or when the size of the hydrologic “bucket” varies seasonally (e.g., permafrost). Therefore, to reliably simulate climate change effects on such forests, modifications are needed to more directly link PnET-Succession hydrology parameters to the monthly climate inputs of the model. Given that a large proportion of the world’s forests are located on wet or frozen soils (Brown et al., 1997; Lehner and Döll, 2004) where waterlogging is an important factor driving competitive outcomes, this limitation is not trivial.

Our primary objective was to strengthen links in PnET-Succession between climate and hydrology to specifically allow simulation of (1) fluctuating saturation of lowland soils in swamps and bogs, and (2) permafrost dynamics and their effect on soil water. We modified the model and tested its ability to project changes in competitive outcomes among species occurring on soils subject to waterlogging under changing climate using hypothetical ecosystem and climate scenarios. A secondary objective was to evaluate the feasibility of simulating range expansion and contraction induced by climate change at high latitudes by conducting simple experiments on a hypothetical landscape grid.

Materials and Methods

A major strength of PnET-Succession is its basis in well-established principles of tree physiology, so our first inclination was to take a first principles, mechanistic approach to improve the hydrologic component of the model. However, we quickly realized that doing so would add a prohibitive computation and parameterization burden to the model that would make it intractable at landscape scales. Mechanistically simulating water table dynamics is extremely complex and requires 3D terrain and soil data to compute vertical flow of water within the soil and bedrock profile as well as surface and subsurface horizontal flow of water between grid cells. Additionally, it is important to account for catchment-scale features such as natural and man-made impoundments, aquifer recharge and discharge areas, and broad-scale impervious soil layers (Carter, 1996). We therefore chose to implement relatively simple, intuitively understood hydrologic parameters that are linked to climate inputs to alter the hydrological behavior of individual cells in response to temperature and precipitation inputs at a monthly time scale. Our goal was to produce a generally realistic hydrologic response to climate that accounts for the soil type in each “ecoregion” in a map that represents the abiotic landscape within LANDIS-II. Ecoregions (i.e., biophysical land units) can be defined by a variety of characteristics, including soil characteristics, elevation, and disturbance regimes. In this paper, we use the ecoregion construct to define soil water saturation regimes reflective of lowland (i.e., saturated, excess water, etc.) versus upland (i.e., sufficient drainage to avoid saturation) biophysical land units. These capabilities are therefore necessarily phenomenological and somewhat simplistic, but they add a critical link to climate that is appropriately precise for the broad spatial and temporal scales at which landscape models operate.

Description of PnET-Succession

In PnET-Succession (De Bruijn et al., 2014), species-cohort (not individual tree) growth rates are calculated as a function of photosynthesis, which is fundamentally limited by water and light. Soil water availability is determined by precipitation inputs, loss to evaporation and runoff, leakage through the soil and consumption by species cohorts. Cohorts compete for water and light in each grid cell, and cohort biomass determines the priority of access to light, but not water. Growth is modeled as a competition of tree species cohorts at a monthly time step, and cohorts die when their respiration requirements chronically exceed their productivity (as determined by access to light and water). Maximum net photosynthetic capacity (Amax) is fundamentally determined by foliar nitrogen (FolN), and actual photosynthesis in a given month depends on the limiting (reduction) factors accounting for light, water, temperature, CO₂ concentration, age and optionally, ozone concentration. Each reduction factor is a multiplier (0.0–1.0) applied to species Amax to determine net photosynthesis (A) in each time step, such that a reduction factor of 1.0 is not limiting, and a value of 0.0 is limiting enough to completely shut off photosynthesis. Light availability varies vertically through the canopy, with canopy layering in the model represented by major canopy layers and subcanopy layers within each major canopy layer (Gustafson et al., 2020a). The light available in a given subcanopy layer is dependent on radiation at the top of the canopy, leaf area and extinction coefficients of cohorts in higher canopy layers. Temperature limits growth as it departs from the species-specific optimal temperature and as respiration costs increase with elevated temperatures. Length of growing season is annually dynamic and species-specific, beginning and ending when mean monthly daytime temperature is above user-defined thresholds. Mortality by extreme cold is simulated whenever minimum temperature drops below a species’ cold tolerance. We use the methods of Court (1951) to estimate minimum daily temperature in winter months from the standard deviation (WinterSTD) of empirical hourly temperatures, with WinterSTD being an ecoregion parameter. The coldest temperature extreme in a month is estimated as Tave-(3^∗WinterSTD), where Tave is the average of the monthly minimum and maximum temperature inputs for the month. Elevated CO₂ increases photosynthetic capacity (with acclimation) by increasing CO₂ concentrations within the leaf and increasing water use efficiency (Franks et al., 2013) as described in Gustafson et al. (2018). The age reduction factor gradually decreases photosynthesis as age approaches longevity to reflect senescence, ultimately causing respiration to exceed productivity. The age reduction factor interacts with the other reduction factors such that older cohorts are more likely to die when stressed.

Soil water can limit photosynthesis by either excess or scarcity, modeled as a reduction factor that reduces the maximum possible photosynthesis rate of the cohort in proportion to water stress. Soil water is tracked at the grid-cell level using a bulk-hydrology (“bucket”) model based on precipitation, loss to foliage interception, evaporation, runoff and percolation out of the rooting zone, and consumption by vegetation. A maximum rooting zone depth parameter (RootingDepth) defines the depth of the “bucket” and soil texture determines the maximum available water capacity of the “bucket,” calculated as the difference between field capacity and wilting point (Saxton and Rawls, 2004). Soil water potential is a function of soil texture, and the volumetric water content resulting from inputs and outputs (Supplementary Figure S1). The water stress reduction factor (fWater) is a multiplier that is calculated for each sub-layer within the canopy in each month as a function of the soil water potential of the grid cell after sub-layers having higher priority access to light have transpired the water required to support simulated photosynthesis. The order in which cohorts are processed for access to light and water is randomized within each layer, with the incoming monthly precipitation and/or snowmelt partitioned into a discrete number of precipitation events (defined by an ecoregion parameter) to increase chances for cohorts to get access to water. There are four species-specific soil water potential threshold parameters (H1–H4, Feddes et al., 1978) that determine water stress (fWater) at each month. H1 and H2 control species response to waterlogging and H3 and H4 control response to dry soil (drought tolerance). H1 specifies the water potential at which waterlogging completely shuts down photosynthesis (fWater = 0.0), and can be given a negative value to allow some photosynthesis on completely saturated soils (Figure 1). H2 specifies the water potential above which reductions in photosynthesis caused by waterlogging begin to occur. H3 specifies the soil water potential below which reductions in photosynthesis caused by dryness begin to occur and H4 specifies the potential at which photosynthesis completely shuts down. fWater is 1.0 (no reduction) at water potentials between H2 and H3. PnET-Succession uses water potential units of the absolute value of pressure head (m).

FIGURE 1

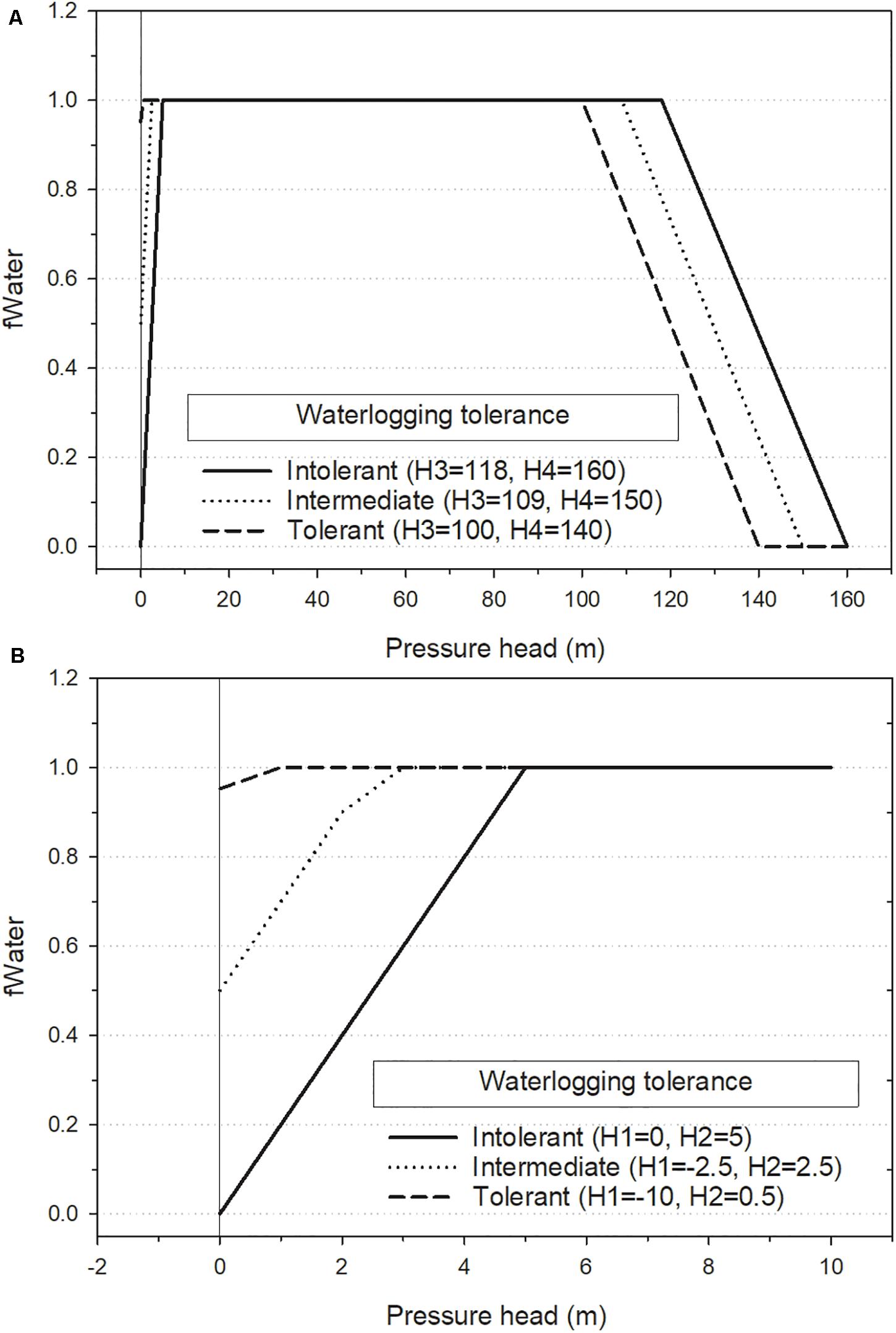
Figure 1. Effect of soil water potential threshold parameters (H1–H4) on water stress (fWater) for the hypothetical species used in the single-cell lowland and permafrost experiments. fWater is calculated by linear interpolation between parameters H1–H4, with values of 1.0 resulting in no water stress. (A) Shows H1–H4 parameters and (B) shows the detail around H1 and H2. Note that pressure head (Ψ) can never fall below zero (vertical reference line), so negative values of H1 are used to determine fWater when Ψ = 0.

In PnET-Succession, each grid cell has a hydrological budget that is independent of other cells of the landscape (i.e., there are no horizontal flows). The single water input is monthly precipitation in the form of rain or snow melt, with incoming water (but not snowmelt) reduced by foliage interception in proportion to the cohort foliage (PrecIntConst). Fixed fractional losses of this input are controlled by three user-specified parameters: loss to surface runoff due to slope or impermeability (PrecLossFrac), sublimation of snow (SnowSublimFrac) and percolation out of the rooting zone (LeakageFrac). Dynamic losses vary according to conditions on the site, and include evaporation (a function of vegetation on the site and temperature), runoff (inputs in excess of water holding capacity), and consumption by vegetation (transpiration). Water is unable to enter the soil when frozen, so any input that occurs with a frozen soil surface (including snow melt) is lost as runoff.

Simulation of Forested Lowland Dynamics

In PnET-Succession, soil texture and rooting depth parameters define the water capacity of the soil “bucket” on each cell (Figure 1), and the leakage parameter determines the ability of the soil to drain to field capacity. Water inputs that exceed saturation are assumed to run off and are not tracked. Depth to water table is also not tracked, but it is assumed to be below the rooting depth and to function as an infinite sink for water draining through the soil. In the real world, water table height is a function of topography, presence or absence of an impermeable subsurface layer, evaporation, interception, transpiration demand, and precipitation inputs (Richardson and Ritchie, 1973). Forested lowlands (also known as forested wetlands) have a water table near the surface primarily because they are surrounded by higher ground that greatly impedes runoff, and because their topographically low position produces soils that are high in silt, clay and organics (Falkner and Richardson, 1989), which can impede drainage (leakage). In a lowland forest system, water is lost by normal rates of evaporation, interception and transpiration, but with relatively low rates of runoff and/or leakage (Carter, 1996). Waterlogging effects vary with the height of the water table, such that the soil is saturated (water potential = 0) when the water table is at or above the surface, drains normally when the water table is below the rooting zone, and has mixed drainage properties when the top of the water table is within the rooting zone (Ernst, 1990).

In this context, we modified PnET-Succession to improve its ability to simulate growth and competition in response to dynamic lowland hydrologic conditions. First, we added an ecoregion-specific parameter [RunoffCapture-the maximum height above ground level that excess water (runoff) can accumulate] that can be used to reduce some or all of the runoff within lowland ecoregions so that soil water can remain above field capacity and reach (or exceed) saturation, and this excess water is retained as surface water that contributes to the soil “water bucket.” Thus, the soil remains excessively wet until runoff (beyond that allowed by RunoffCapture), evaporation, interception, transpiration and leakage (if any) collectively exceed cumulative precipitation inputs and any surface water (i.e., have consumed all excess water). In practice, the boundaries of the lowland ecoregions defined in model inputs would be derived from a DEM or by the location of existing lowland vegetation, and RunoffCapture would represent the average maximum depth of standing water, or could be calibrated to match the distribution of empirical water potentials given climate inputs or potentials consistent with the vegetation currently found in the ecoregion. For upland ecoregions (non-lowlands where runoff is generally unimpeded), RunoffCapture would typically be set to 0 (mm), and PnET-Succession would behave as in prior versions.

Second, the existing PnET-Succession ecoregion parameter LeakageFrac can be used to prevent some or all of the water from draining out of the rooting zone, to reflect the permeability of a non-porous layer and the basin configuration [i.e., ability of water to exit the lowland basin(s)]. This parameter could be estimated to reflect known sub-rooting-zone soil permeability, or to match empirically observed rates that water potential drops during drought and returns to a saturated condition after a drought is broken. These two simple modifications allow maximum flexibility for parameterization and calibration of lowland water dynamics with the addition of just one new parameter. The RunoffCapture parameter is conceptually linked to the mechanism of topographic position that impedes runoff, and the LeakageFrac parameter is linked to the mechanism of soil permeability at or near the bottom of the rooting zone.

With these modifications, water stress in lowland ecoregions can respond dynamically to monthly climate inputs and vegetation without the computational burden of mechanistically simulating hydrology across the entire landscape. Waterlogging stress can result whenever cumulative precipitation inputs chronically exceed the cumulative removal of water by runoff, evaporation, leakage and transpiration, and the growth of species with higher waterlogging tolerance would be favored. Lower water potentials can develop when vegetation growth increases transpiration rates sufficiently, or if precipitation declines for an extended period (e.g., drought, climate change). Climate change can also remove more water by increasing evaporation under higher temperatures. Most importantly, waterlogging stress responds dynamically at a monthly time step to variation in cumulative precipitation inputs and vegetation characteristics. Competitive interactions among species respond directly to available soil water through their drought and waterlogging tolerance parameters (H1–H4) and indirectly because establishment probability in PnET-Succession is dynamically proportional to the suitability of the light and water environment on each cell for growth of each species.

Cell-Scale Lowland Forest Experiment

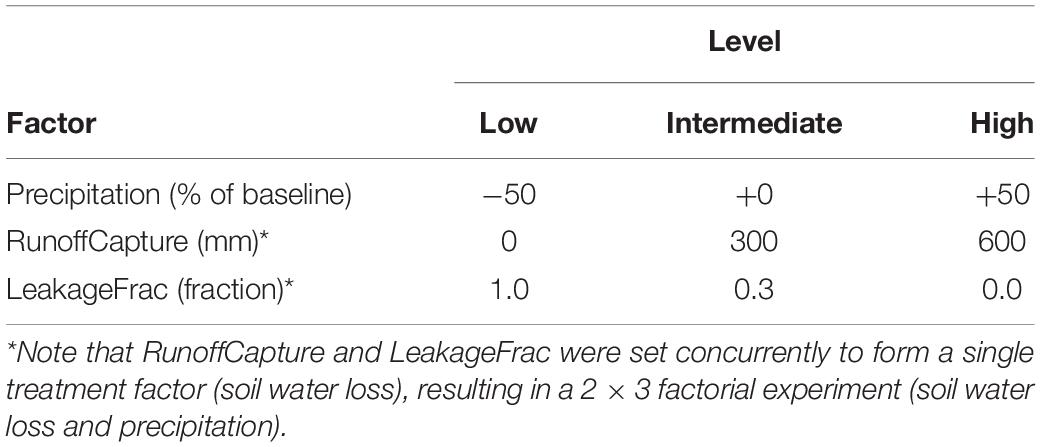
We tested the effects of these new capabilities for modeling forested wetland dynamics using a single-cell factorial experiment with two treatment factors: biophysical unit [encapsulating soil water loss (RunoffCapture/Leakage)] and precipitation (each with 3 levels). A hypothetical baseline climate mimicking monthly temperature and precipitation typical of high latitude forests was used, and the high and low precipitation levels were generated by adding or subtracting 50% from baseline precipitation. The RunoffCapture (mm) and Leakage (fraction) levels were concurrently set to represent upland (unimpeded runoff and drainage), intermediate and very wet biophysical units (ecoregions) (Table 1). Temperature and precipitation levels were held constant across years within each level, and all other abiotic inputs were held constant across treatments, including CO₂ (400 ppm) and latitude. We initialized each cell with an assemblage of 3 hypothetical species (age = 20), each having a different waterlogging tolerance (Supplementary Table S1). We set species optimal temperature for photosynthesis equal to the mean growing season temperature of the baseline climate input. All other parameters were constant across all treatments, and establishment of new cohorts was prevented to avoid confounding competitive interactions among the three initial cohorts. All input files are given as Supplementary Material. Three replicates of 50 years simulations were generated. We quantified the effect of the treatments using GLIMMIX (SAS v9.4) to compute 95% confidence intervals and investigate interactions among the treatment factors on mean net photosynthesis and water stress (fWater) of each cohort across the growing season months of the last decade of the simulations. GLIMMIX estimates marginal means over a balanced population and confidence intervals are adjusted for the covariance parameters in the model.

TABLE 1

Table 1. Factor levels used in the lowland forest experiment.

Our expectation was that upland sites should have higher photosynthesis because of less waterlogging stress, and that increased precipitation should increase photosynthesis by reducing drought stress. Greater waterlogging tolerance should allow cohorts on Intermediate and Very wet sites to maintain photosynthesis by reducing waterlogging stress.

Simulation of Soil Ice Dynamics

To optionally simulate seasonal soil ice dynamics (specifically, over permafrost), we modified PnET-Succession to make active rooting depth and leakage fraction dynamic at a monthly time step, driven by the temperature inputs to the model. Active rooting depth in this case is understood to represent the mean depth to the ice layer (0°C isotherm) in the month, although rooting depth is constrained in the model not to exceed the user-defined maximum depth that tree roots can typically extend (RootingDepth). When the ice layer retreats further below the rooting depth, we assume that the water column within the root zone is increasingly able to drain, and the effective leakage fraction is therefore increased linearly from 0.0 ^∗ LeakageFrac (when an ice layer is present within the rooting zone) to 1.0 ^∗ LeakageFrac when the ice layer is below the root zone by a user-specified depth (LeakageFrostDepth). Thus, the presence of an ice layer varies the available soil water within the rooting zone (active layer) according to temperature dynamics.

Soil temperature, T_soil at depth z (m) at month m is used to determine the depth to the ice layer as described for the LPJ DGVM in the appendix of Sitch et al. (2003):

$${\text{T}}_{\text{soil}}(z,m)=T_{\text{ave}}+A\times exp\left(\frac{-z}{d}\right)\times \text{sin}\left(\mathrm{\Omega }m-\frac{z}{d}\right)(1)$$

where T_ave is average air temperature for month m, A is the amplitude of air temperature over the previous 12 months, d is the damping depth (m), and Ω the angular frequency of oscillation (radians/month). The damping depth, d, and angular frequency of oscillation (Ω) are calculated as:

$$d=\sqrt{\frac{2k}{\mathrm{\Omega }}}(2)$$

$$\mathrm{\Omega }=\frac{2\mathrm{\pi }}{12}(3)$$

where k is the thermal diffusivity (mm² mo^–1) of the soil.

Thermal diffusivity (k) is estimated using the methods of Farouki (1986) and Jong van Lier and Durigon (2013), with inputs of total porosity (m³/m³), water content (m³/m³) and fraction clay (proportion), which make it dynamically dependent on the soil texture and its water content each month. These methods are generally consistent with those used in the LPJ DGVM (Beer et al., 2007), and produce dynamic soil temperature profiles (Supplementary Figure S2).

Equation [1] was additionally adapted to account for the insulating properties of snow and moss vegetation. As noted by Sitch et al. (2003), the $exp\left(\frac{-z}{d}\right)$ component of this equation effectively represents the reduction in temperature oscillation amplitude, which is due to the cumulative insulating properties of the soil at depth z. We used the same approach to apply snowpack and vegetation (i.e., moss, litter) impacts on the temperature oscillation by introducing two additional reduction factors.

$$\begin{array}{c}{T}_{\text{soil}}(z,m)=T_{\text{ave}}+A\times D_{\text{soil}}\times D{R}_{\text{snow}}\hfill \\ \times D{R}_{\text{moss}}\times \text{sin}\left(\mathrm{\Omega }m-{\displaystyle \frac{z}{d}}\right)\hfill \end{array}(4)$$

where D_soil = $exp\left(\frac{-z}{d}\right)$ as above, and DR_snow and DR_moss follow the damping ratio formulation from Liang et al. (2014):

$$D{R}_{\text{z}}=e^{-z{\left(\frac{\mathrm{\Omega }}{2k}\right)}^{1/2}}(5)$$

The calculations for snow include estimating thermal diffusivity (k_snow), thermal conductivity (λ_snow, W m-1 K-1 [Jordan, 1991]) and volumetric heat capacity (c_snow, kJ m^–3 K^–1) based on the established heat capacity of snow (2090 J kg^–1 K^–1):

$$D{R}_{\text{snow}}=e^{-snowdepth{\left({\frac{\mathrm{\Omega }}{2k}}_{\text{snow}}\right)}^{1/2}}(6)$$

$$k_{\text{snow}}=\frac{{\mathrm{\lambda }}_{\text{snow}}}{c_{\text{snow}}}(7)$$

$$\begin{array}{c}{\mathrm{\lambda }}_{\text{snow}}=({\mathrm{\lambda }}_{\text{air}}+((0.0000775\times p_{\text{sno}})+(0.000001105\times p_{{\mathrm{sno}}^2}))\hfill \\ \times ({\mathrm{\lambda }}_{\text{ice}}-{\mathrm{\lambda }}_{\text{air}}))\times 3.6\times 24\hfill \end{array}(8)$$

$$c_{\text{snow}}=\frac{2090\times p_{\text{sno}}}{1000}(9)$$

The values for thermal conductivity of air (λ_air) and ice (λ_ice) are 0.023 and 2.29 W m^–1 K^–1, respectively (Jordan, 1991). Snow density (p_sno, kg m^–3) is estimated using a relationship estimated from Figure 4a of Jonas et al. (2009), with density increasing over the length of winter:

$$p_{\text{sno}}=165+1.3\times WinterDays(10)$$

The calculations for moss use the same general damping ratio formula, with estimates of moss heat capacity (c_moss = 2500 kJ m^–3 K^–1) and thermal conductivity (λ_moss = 432 kJ m^–1 d^–1 K^–1) from Sazonova and Romanovsky (2003):

$$D{R}_{\text{moss}}=e^{-mossdepth{\left(\frac{\mathrm{\Omega }}{2k_{\text{moss}}}\right)}^{1/2}}(11)$$

$$k_{\text{moss}}=\frac{{\mathrm{\lambda }}_{\text{moss}}}{c_{\text{moss}}}(12)$$

Soil warming in this model is not dependent on the albedo and radiation associated with site vegetation other than as they may affect air temperature in the climate inputs. Incoming precipitation and melting snow cannot enter the frozen portion of the soil, ensuring that the depth of an ice layer will dynamically determine how much snow melt can enter the soil “bucket.” The water content of the soil when it thaws is the same as when it froze.

Cell-Scale Permafrost Experiment

We tested the effects of waterlogging induced by these permafrost dynamics using a simple single-cell factorial experiment with two factors: temperature and precipitation (3 levels each). The same baseline climate described above was used for the middle level of each factor, and the other factor levels were generated by adding or subtracting 3 degrees C from the baseline temperature and adding or subtracting 50% from baseline precipitation. Temperature and precipitation levels were held constant across years within each level, and all other abiotic inputs were held constant across all treatments, including CO₂ (400 ppm) and latitude. We used the same species parameters as for the forest lowlands test (Supplementary Table S1). All input files are given as Supplementary Material. To assess the consequences of omitting permafrost dynamics, we conducted the experiment with and without the simulation of soil freezing (ice), which served as a third experimental factor. We quantified the effect of the treatments using GLIMMIX (SAS v9.4) to compute 95% confidence intervals and investigate interactions among the treatment factors on mean net photosynthesis and water stress (fWater) of each cohort across the growing season months of the last decade of the simulations.

Our expectation was that increasing temperature in this high latitude experiment should increase photosynthesis by making more soil water available by increasing the depth of the active layer, that increased precipitation should increase photosynthesis by reducing water stress, and increased waterlogging tolerance should increase photosynthesis because permafrost reduces leakage and keeps soils wetter. We also expected an interaction between temperature and waterlogging tolerance, because increasing temperature should reduce soil wetness on permafrost sites.

Latitudinal Gradient Test Case

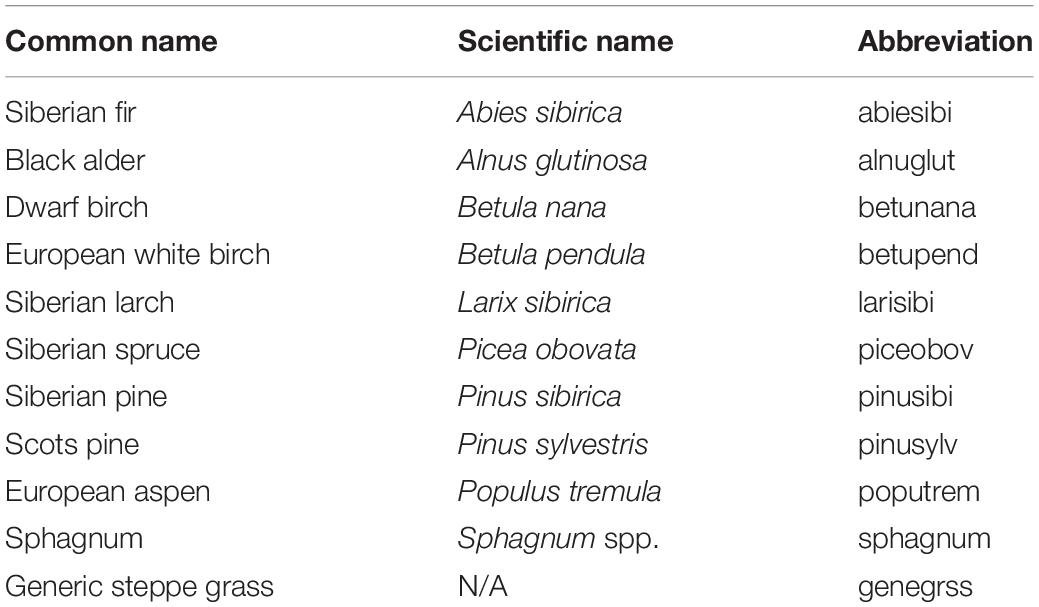
We then applied these new capabilities to a hypothetical “landscape” to evaluate the potential ability of PnET-Succession (v4.0) to model species colonization dynamics across a large latitudinal gradient in Siberian Russia in response to climate change. We constructed a simple 5 × 6 grid where each row represented a latitudinal zone located at approximately 100^oE longitude, and each cell represented a typical forest stand. The grid is an artificial construct created to efficiently implement what is essentially a collection of single-cell experiments that also allow colonization to occur between adjacent cells. The upper row represented the tundra biome with a latitude of 74^oN, initialized without woody vegetation. The second row was designated as latitude 70^oN, initialized with a cold-tolerant shrub species (Betula nana) and Siberian larch. Subsequent rows represented latitudes 66^oN (northern taiga), 62^oN (middle taiga) and 58^oN (southern taiga), initialized with Siberian species (Table 2) typically found at each latitude (Supplementary Table S2). The rows representing 66 and 58 ^oN also had additional cells parameterized as forested wetlands and initialized with more waterlogging tolerant species, including a sphagnum (66N) and grass (58N) pseudo-species (not trees). We conducted a factorial experiment with two factors: future climate (RCP 2.6, 6.0, 8.5) for each latitude and biophysical unit (upland, lowland). Individual cells in each row were assigned a unique climate/biophysical unit (ecoregion), with climate projections through the year 2099 for each location generated by the Hadley GEM2-ES earth system model (Collins et al., 2011) (Table 3). The last 10 years of each climate projection was repeated for the final 100 years of each simulation. All sites were simulated using a loamy sand soil; upland sites had rooting depth = 0.9 m (1.0 at 58^oN sites), LeakageFrac = 1.0 and RunoffCapture = 0 m, and lowland sites had a rooting depth = 0.7 m, LeakageFrac = 0.01 and RunoffCapture = 0.075 m. LeakageFracDepth was set at 3.0 m in all experiments. In this experiment, dispersal was simulated every 10 years, and was constrained to occur only between adjacent cells (including diagonal) to mimic colonization (range shifts) at ecotone boundaries, with establishment and growth being determined by the climate and extant competitors on each cell through time. Thus, the grid should not be interpreted as a spatially explicit landscape, but rather as a construct to conduct a highly controlled experiment, allowing colonization to occur between adjacent biomes. We evaluated simulations with and without a single stand-replacing disturbance (i.e., clear cut or wildfire, catalyzing species turnover) occurring independently on each cell at year 70. Four replicate simulations were run for 200 years to allow time for climate and disturbance effects to play out. All input files are given as Supplementary Material. For each treatment combination, we computed the change in species richness over 200 years, plotted the trajectory of biomass of each species on each cell, and quantified the number of invasions (species not initially present, but present after 200 years) and extirpations (initial species not present after 200 years) and maximum total biomass observed on each cell.

TABLE 2

Table 2. Siberian species used in the simulations.

TABLE 3

Table 3. Projected change in temperature and annual precipitation by 2099 made by the Hadley GEM2-ES earth system model under each CO₂ emissions scenario for each latitude of the latitudinal gradient test case.

Our expectation was that biomass should (1) increase as emissions increase because of CO₂ fertilization and longer growing seasons, (2) decrease with increasing latitude because the growing season is shorter, and (3) decrease with disturbance because cohorts are younger. Richness should (1) be unchanged even as assemblages change in response to changing climate (i.e., the number of niches is not changed), and (2) increase with disturbance (intermediate disturbance hypothesis). Invasions and extirpations should (1) increase with disturbance because niches are opened, (2) increase with climate change because ranges shift, and (3) decrease at lower latitudes because change in climate is less.

Results

Cell-Scale Lowland Forest Experiment

Model outputs confirmed that the model appropriately produces saturated or drained soils given the inputs for biophysical unit and precipitation, with corresponding water stress varying according to waterlogging tolerance (Figure 2). Surface flooding also responded appropriately to inputs (Table 4). Both biomass growth and water stress clearly responded to all three treatment factors in the forested lowlands test case (Figure 3). Species waterlogging tolerance was the strongest determinant of net photosynthesis (Figure 3A), followed by precipitation, with biophysical unit also having an effect such that the treatments producing the wettest conditions were the most productive. This result, along with the pressure head showing consistently high values expect for the wettest biophysical unit (Figure 2) suggests that the arbitrary drought tolerance parameters and relatively dry climate were perhaps too limiting on upland biophysical units. All interactions among treatment factors were highly significant (not shown), and biophysical unit appeared to have its greatest influence as it interacted with waterlogging tolerance. Water stress differed primarily based on species waterlogging tolerance and precipitation inputs, with biophysical unit having a less clear effect (Figure 3B). There was a highly significant interaction between biophysical unit and waterlogging tolerance (F = 32.45, p < 0.0001), reflecting the fact that the waterlogging tolerance parameters used were able to maintain productivity in very wet biophysical units, often allowing waterlogging tolerant species to overtop the others. Water stress can result from two factors: waterlogging and drought. Our treatments produced both conditions, varying by treatment combination. Waterlogging tolerant species were parameterized to also be drought intolerant. However, because the baseline climate was relatively dry, our arbitrary parameters caused species responses to be more sensitive to waterlogging than to drought.

FIGURE 2

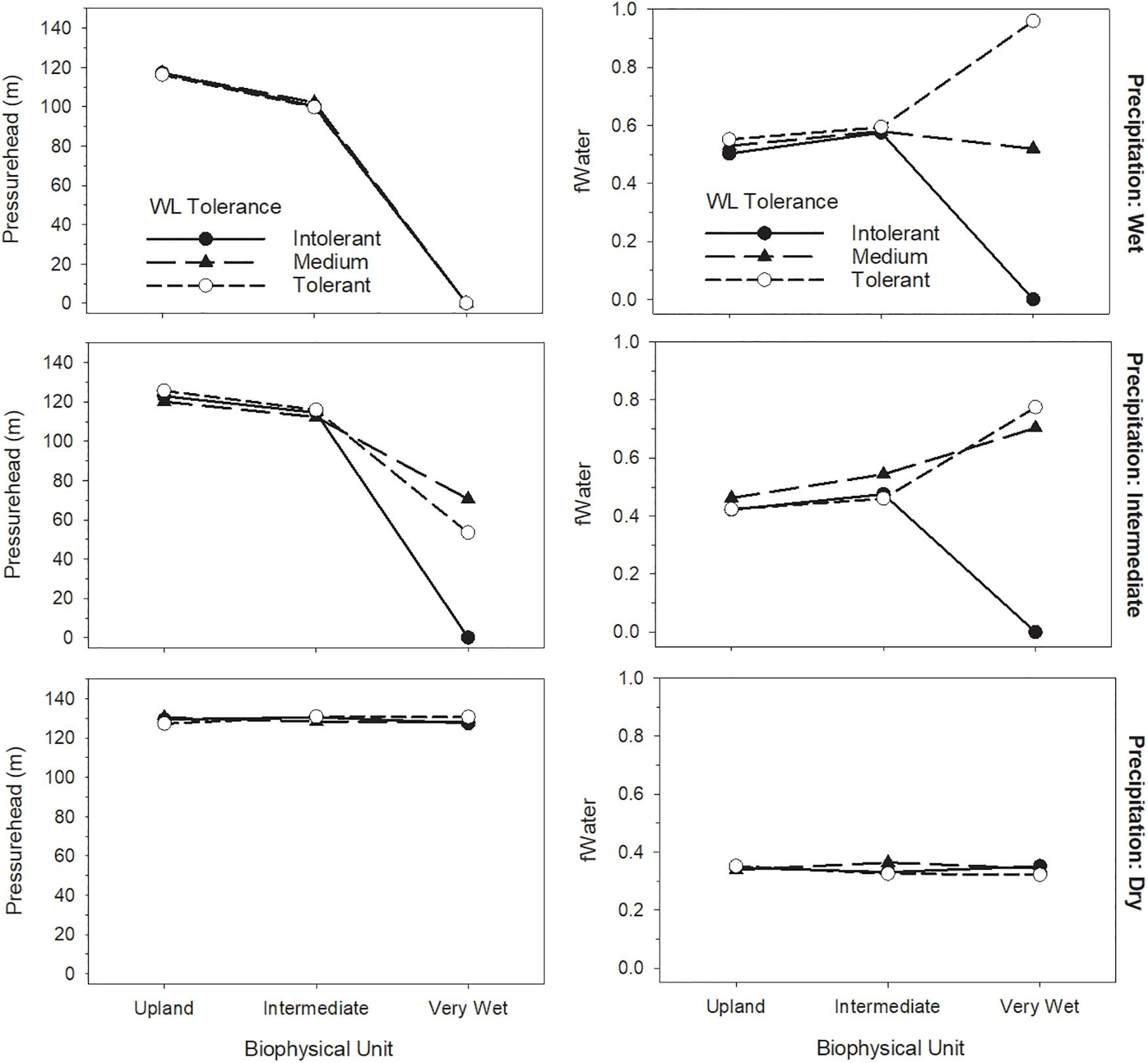
Figure 2. Response of water stress (fWater) during the growing season months of the last decade of the simulations to soil water potential (pressure head) as a function of biophysical unit, precipitation and species waterlogging tolerance.

TABLE 4

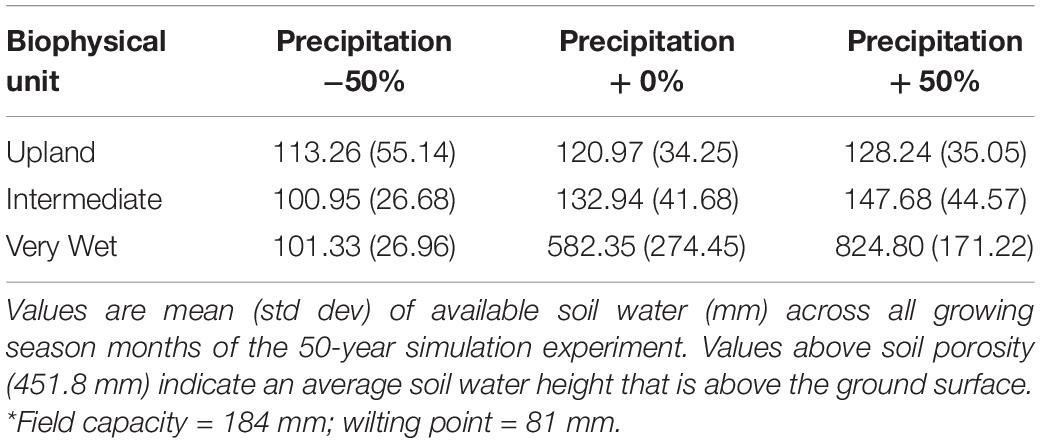
Table 4. Evaluation of surface flooding in response to treatments in the lowland forest experiment (on a SALO soil*).

FIGURE 3

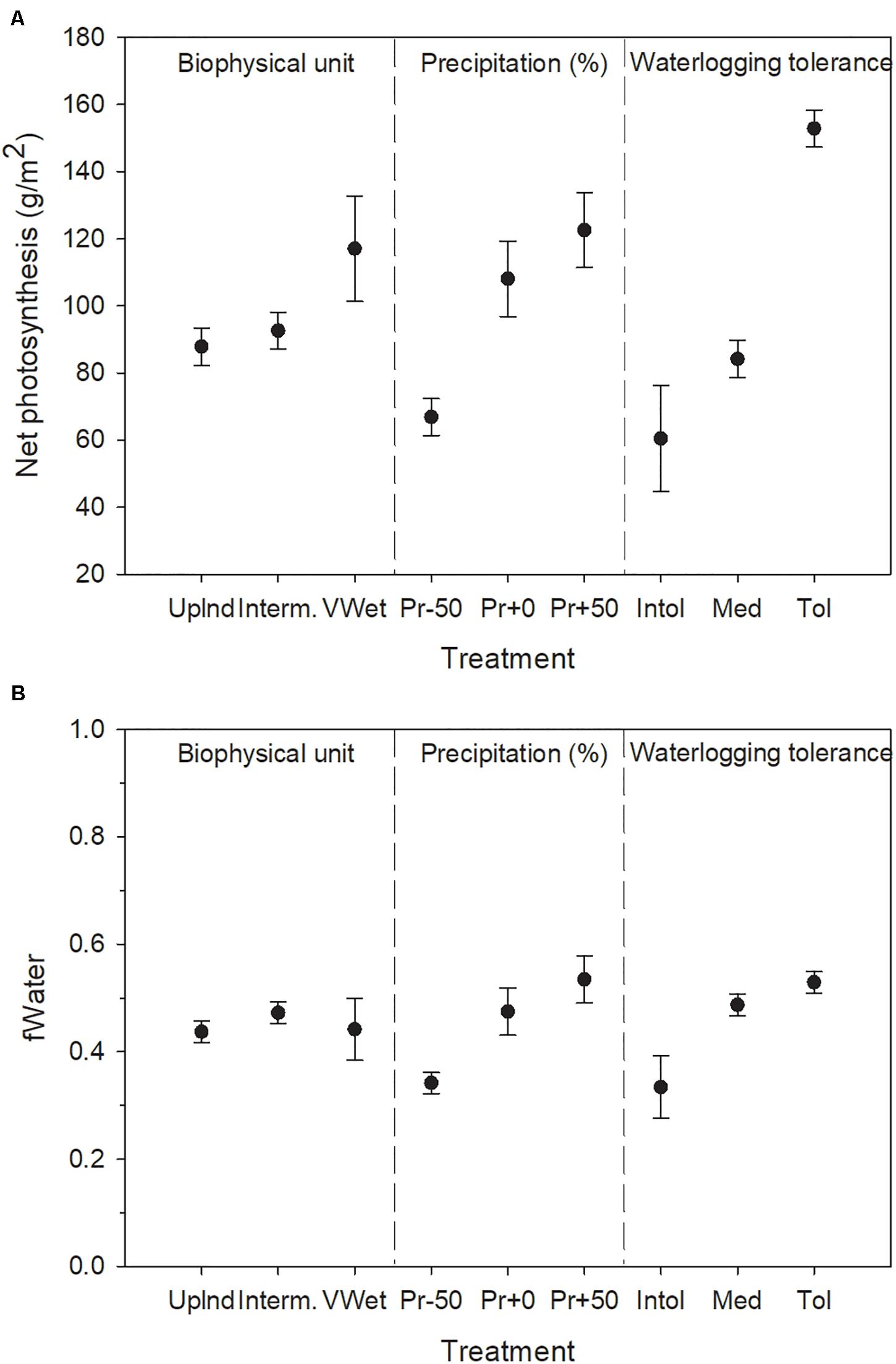
Figure 3. Response of (A) net photosynthesis and (B) water stress to the treatment factors in the single-cell lowland forest experiment (soil ice not simulated). Water stress is inversely proportional to fWater. Error bars indicate 95% confidence intervals computed across the growing season months of the last decade of the simulations using least squares means of three replicates.

Cell-Scale Permafrost Experiment

Mean growing season depth to ice varied between 0.8 and 1.4 m by growing season month across all treatments, and was linearly related to mean growing season temperature (R² = 0.96, not shown), with wetter soil tending to thaw somewhat deeper, as expected. Net photosynthesis and water stress clearly responded to all three treatment factors in the permafrost test case (Figure 4). When we omitted the simulation of soil ice, the effect of temperature and precipitation on the response variables was little changed from the permafrost scenario, but waterlogging tolerance had virtually no effect without soil ice to impede drainage.

FIGURE 4

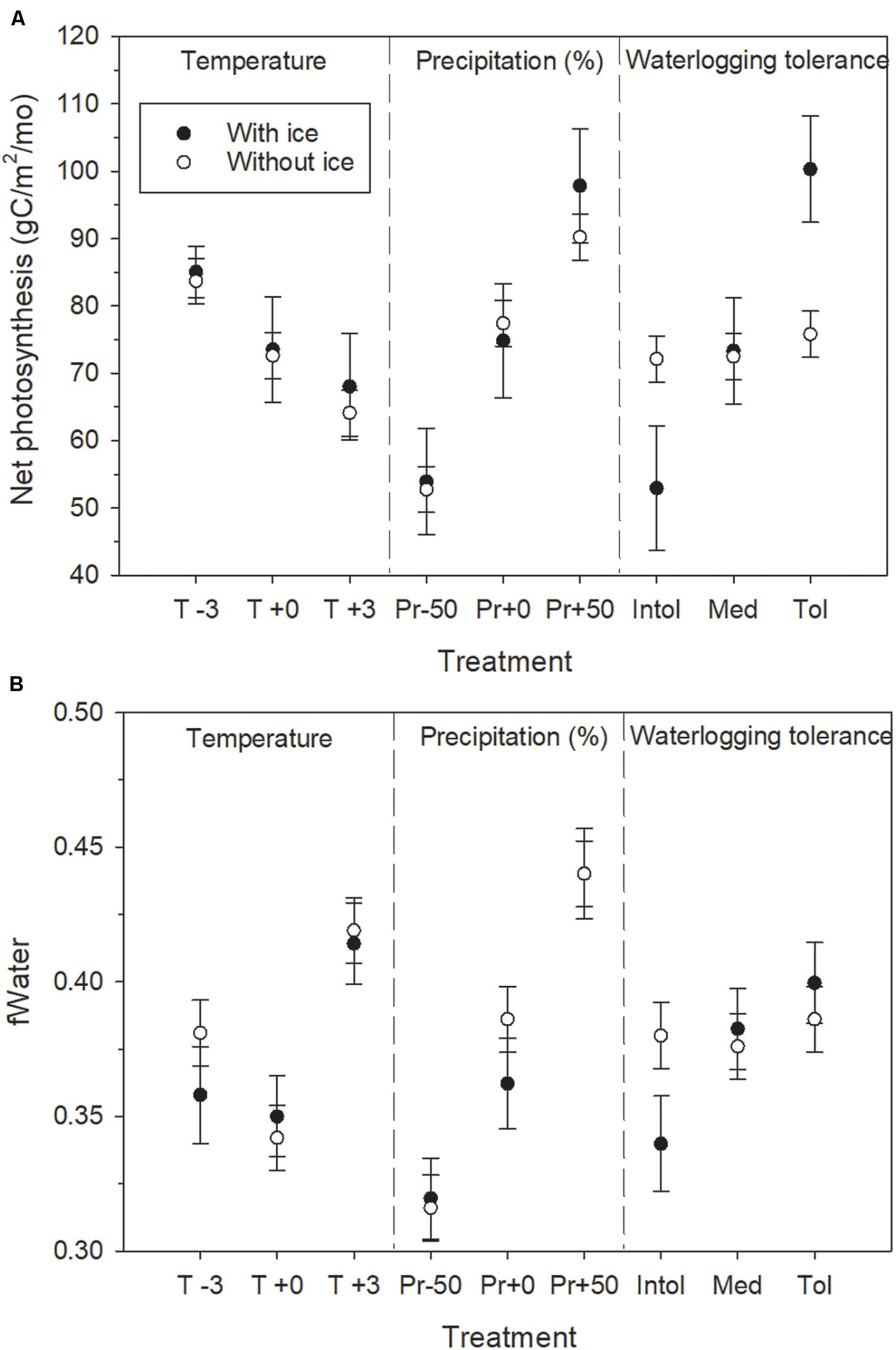
Figure 4. Response of (A) net photosynthesis, and (B) water stress, to growing season water availability as a function of the treatment factors with and without permafrost simulated in the single-cell permafrost experiment. Water stress is inversely proportional to fWater. Error bars indicate 95% confidence intervals computed across the growing season months of the last decade of the simulations using least squares means of three replicates.

Latitudinal Gradient Test Case

The growth (biomass) of individual species responded to both emissions scenario and latitude as a function of competition and establishment (Figures 5, 6). Trend lines with large uncertainty represent stochasticity, primarily of establishment and to a lesser extent, competition. We found that total biomass (all cohorts of all species) increased dramatically with increasing emissions scenario (Figure 7). This effect was more pronounced at higher latitudes, suggesting that temperature is an important driver. However the magnitude of the biomass increase seen under RCP 8.5 is likely related to longer growing seasons and the CO₂ fertilization effect. Biomass was generally higher without disturbance (Figures 5, 7), and disturbance often facilitated a change in species composition (Figure 6).

FIGURE 5

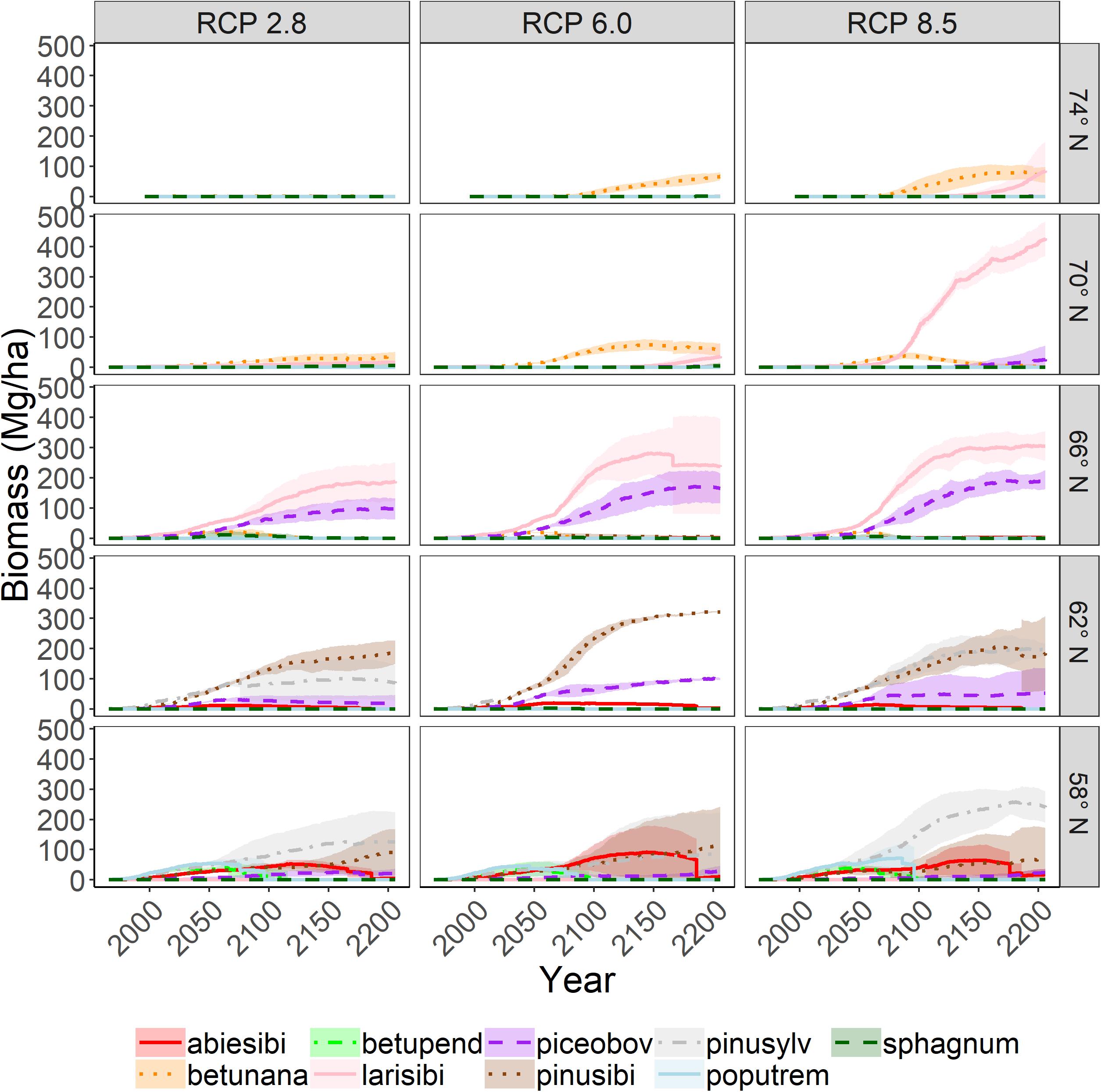
Figure 5. Aboveground woody biomass of tree species through time in the absence of disturbance on upland sites. Shading represents one standard deviation of four replicates.

FIGURE 6

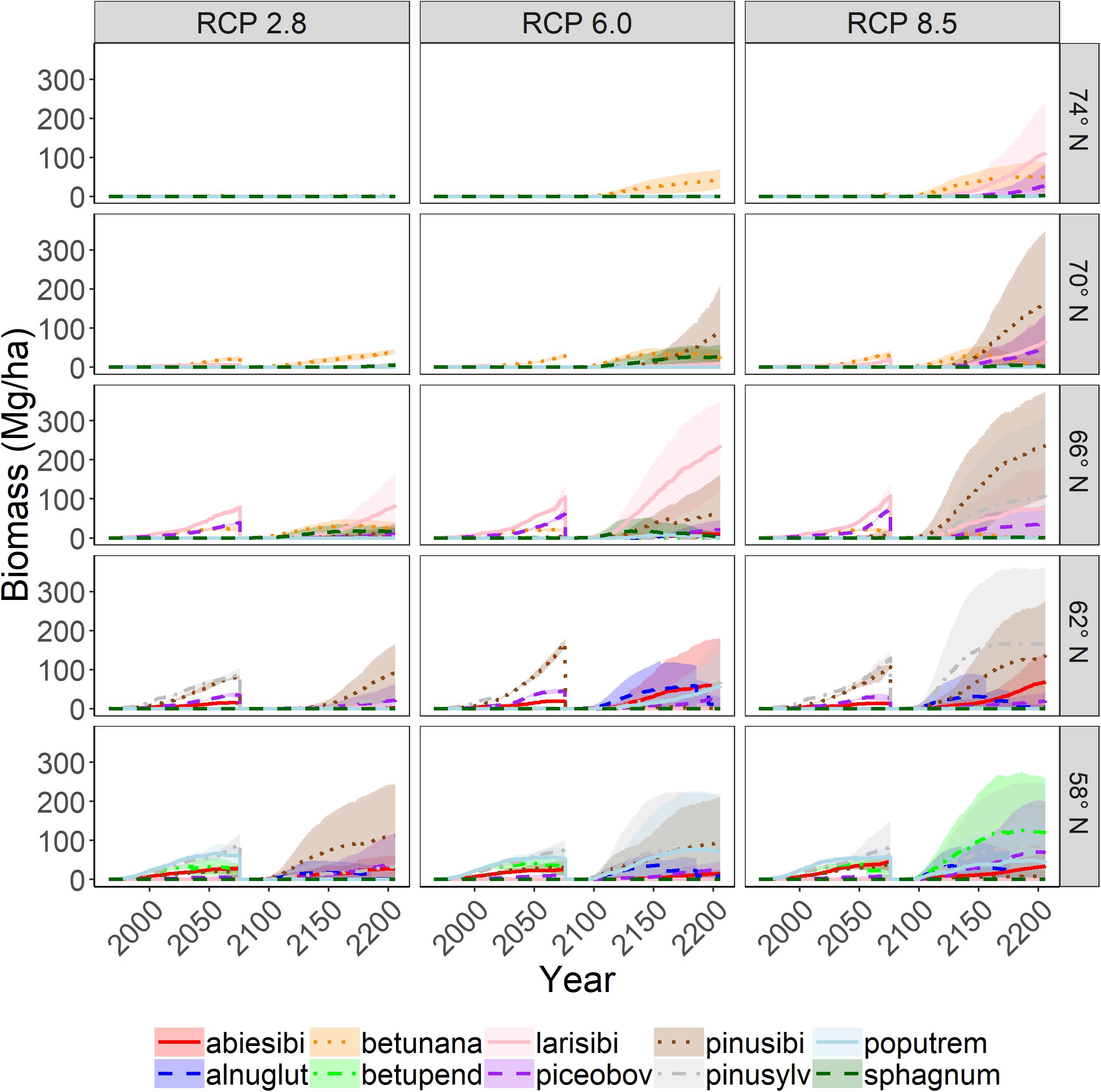
Figure 6. Aboveground woody biomass of tree species through time with a single stand-replacing disturbance on upland sites. Shading represents one standard deviation of four replicates.

FIGURE 7

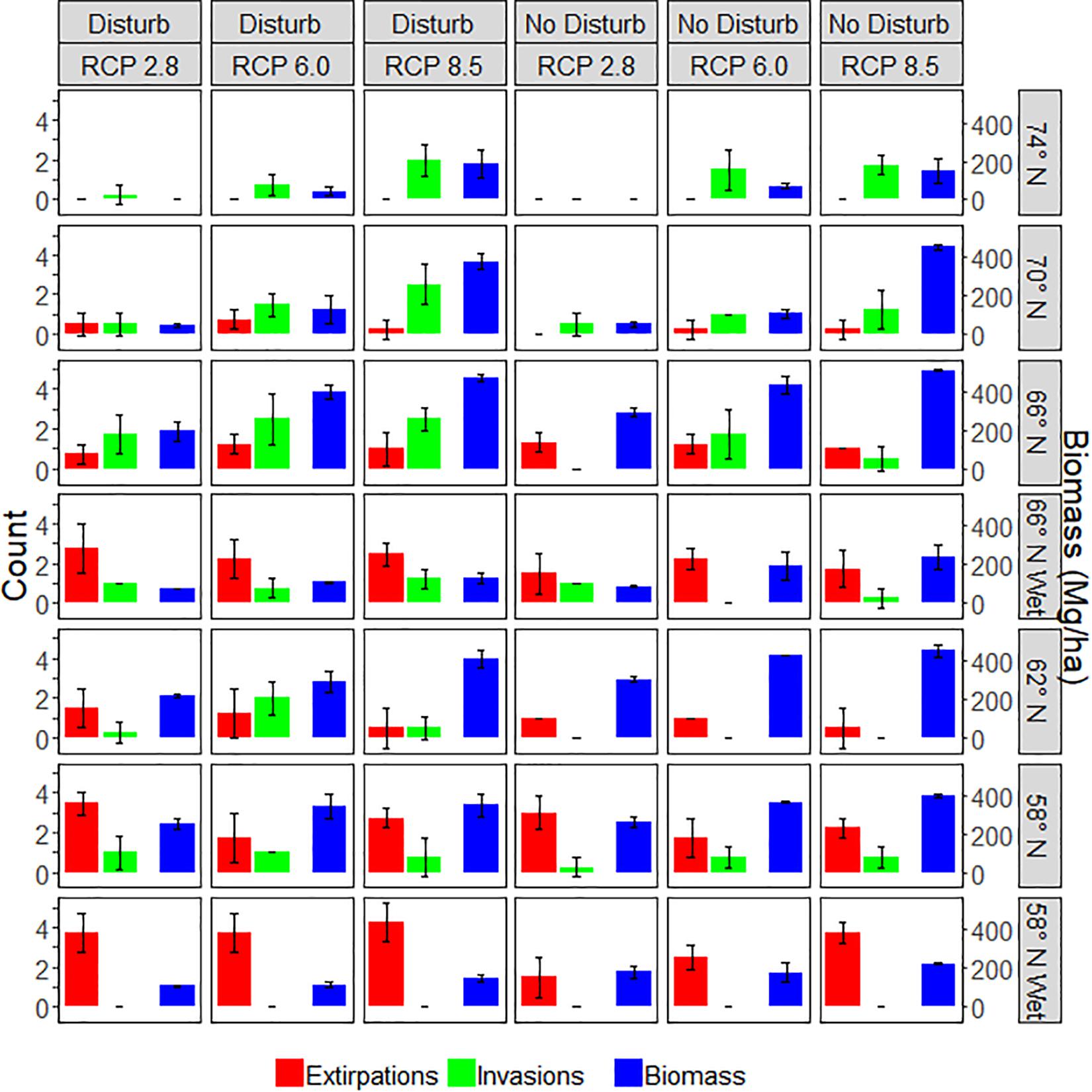
Figure 7. Productivity and range shift responses to treatments on upland and wetland sites. Invasions are species present after 200 years that were not present at the start, while extirpations are species not present after 200 years that were present at the start. Biomass is the maximum aboveground woody biomass observed on the site over 200 years. Error bars represent one standard deviation of four replicates.

Invasions were highest at latitude 66N and higher (Figure 7), partly because there were fewer extant species in the northern sites. Invasions tended to be higher with elevated emissions, although this did not hold true at all latitudes. Extirpations increased at lower latitudes, partly because there were more species initially at lower latitude sites. Extirpations did not consistently respond to emissions scenario. Disturbance appeared to have little effect on the number of extirpations, while disturbance generally increased invasions, presumably by opening up colonization opportunities.

On wetland sites, there was also a consistent trend of increasing biomass as emissions increased (Figure 8), but there was no clear trend for invasions and extirpations (Figure 7). Extirpations were primarily of tree species that were unable to survive for 200 years and unable to regenerate because of excessive wetness. Invasions were primarily by species highly tolerant of waterlogging, and sites tended to become dominated by one or two waterlogging tolerant species, mainly sphagnum and dwarf birch in the north, and grass and alder in the south. However, in the absence of disturbance, Siberian pine (P. sibiricus) cohorts were able to grow sufficiently large to reduce waterlogging by transpiration such that they were sometimes able to attain fairly high biomass. It appeared that temperatures became too warm for most species to thrive in southern sites during the last century of the RCP 8.5 scenario.

FIGURE 8

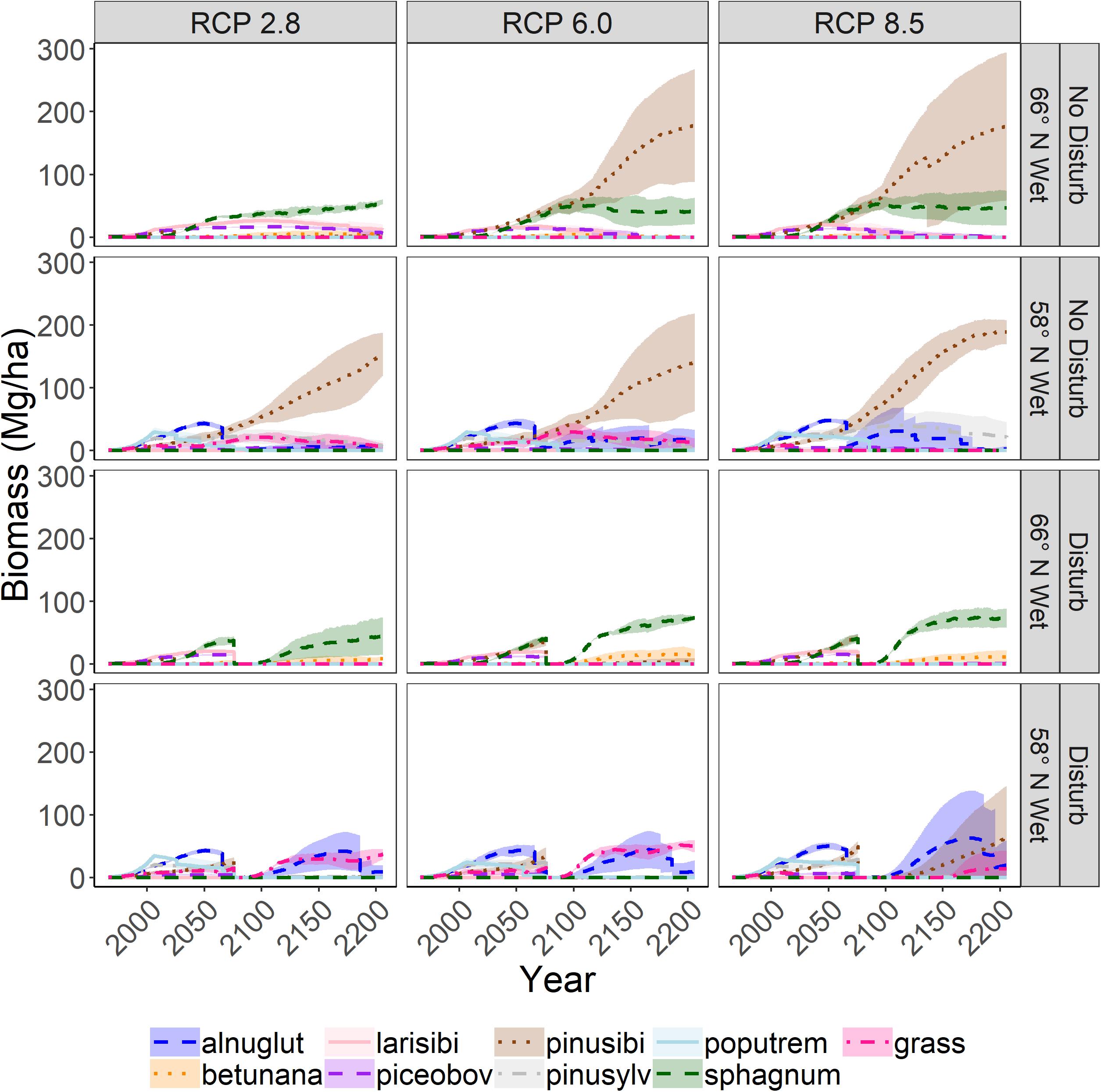
Figure 8. Aboveground woody biomass of tree species through time on wetland sites. Shading represents one standard deviation of four replicates.

On upland sites, species richness tended to increase at the higher latitudes and decrease at the lower latitudes, and was higher as emissions increased (Figure 9). Disturbance generally produced higher species richness, although perhaps not substantially so. On wetland sites, richness always declined because only the highly waterlogging tolerant species that were initialized were able to persist (Figure 9). Disturbance did not have a clear effect on species richness on wetland sites, likely because outcomes were determined primarily by waterlogging tolerance so that only quite tolerant species persisted.

FIGURE 9

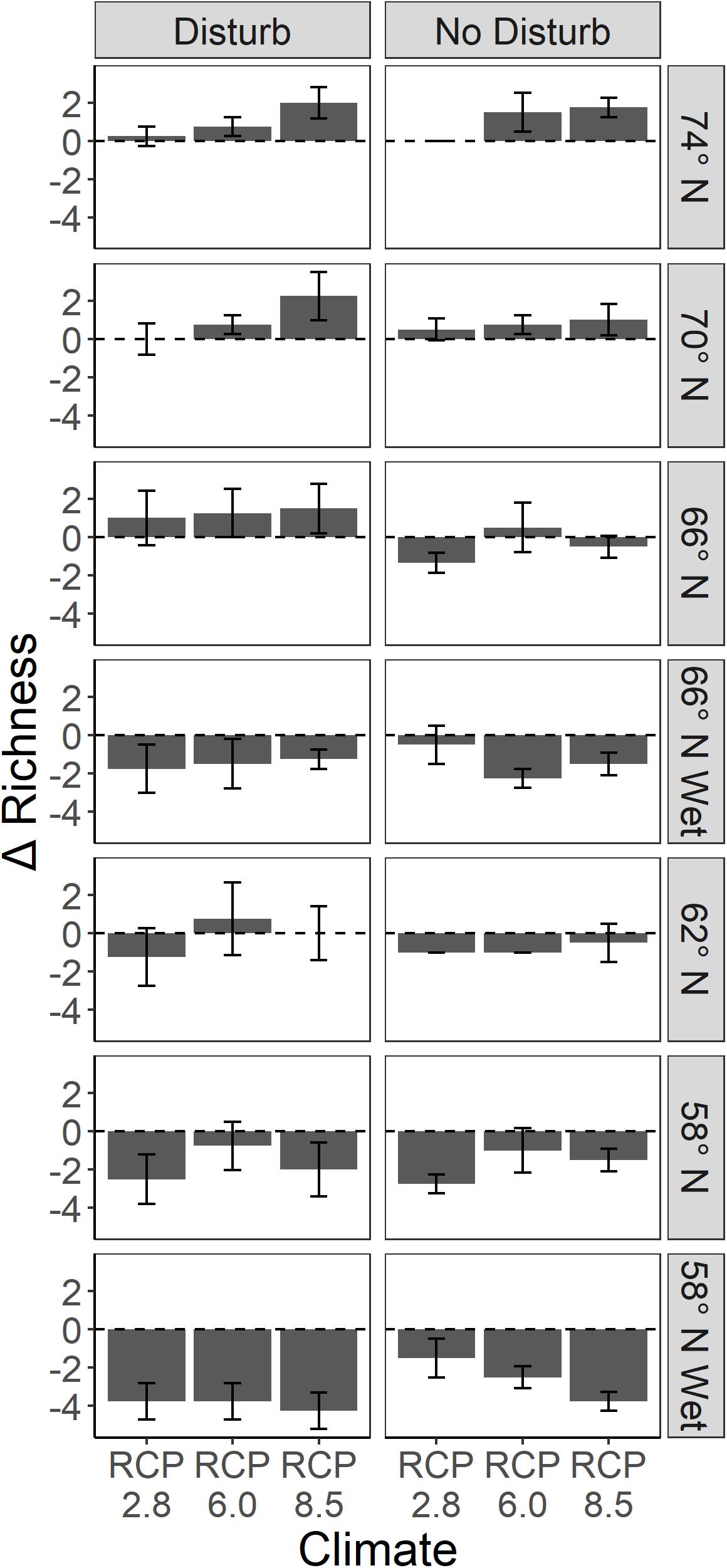
Figure 9. Change in mean species richness (number of species) over 200 years on upland and wetland sites in response to the treatments. Error bars represent one standard deviation of four replicates.

Discussion

Our primary objective was to strengthen links in PnET-Succession between climate and hydrology to explicitly simulate the effects of permafrost and lowlands on soil water potential and forest response to waterlogging. This was done with the addition of only two new input parameters (RunoffCapture, LeakageFrostDepth). Our tests of these capabilities demonstrated a strong relationship between climate inputs, hydrologic response, and competitive outcomes. This represents an important advance for projecting the consequences of landscape management and climate change on future compositional and pattern dynamics on forested landscapes that have a large forested lowland component, or where permafrost is currently found. FLMs (including LANDIS-II) have typically had to either ignore the effect of waterlogging on forest dynamics (e.g., Lucash et al., 2018), or make assumptions about when waterlogging has an effect, and what those effects might be. In another study, these new capabilities added to PnET-Succession produced more definitive results about the effectiveness of climate-adaptive silviculture in a sub-boreal ecosystem in northern Wisconsin (United States) because investigators were not forced to ignore the management of the abundant forested lowlands in the study area (Gustafson et al., 2020b).

Insights From Case Studies

For the lowland benchmark test, our expectation was that lowland sites should have lower photosynthesis because of waterlogging, and that greater waterlogging tolerance should allow cohorts on Intermediate and Very wet sites to maintain photosynthesis by reducing waterlogging. We found that in general, photosynthesis was greatest and water stress was least for scenarios with the most precipitation and for species with the greatest waterlogging tolerance (Figure 3). Upland sites had the lowest photosynthesis and the greatest water stress because our arbitrary water stress parameters produced more tolerance for wet soils than for dry soils and the climate produced relatively dry soils except when precipitation was high and/or leakage and runoff were constrained. It should be noted that dry conditions were possible on all biophysical units and precipitation treatments in some months in later years as cohorts grew large enough to become effective transpirers, perhaps explaining why fWater did not vary substantially by biophysical unit. Figure 2 shows that the lack of overall change in fWater is because the effects on the different species canceled each other out to have little average effect, but a strong individual species effect. Overall, this test confirmed that the model appropriately produces surface flooding given the ecoregion and precipitation inputs, with equally appropriate species responses given their waterlogging tolerance.

Our expectations for the permafrost benchmark test were that increasing temperature should increase photosynthesis by making more soil water available (deeper active layer), that increased precipitation should increase photosynthesis by reducing water stress, and increased waterlogging tolerance should increase photosynthesis. We found that water stress (fWater) and photosynthesis were not tightly coupled in response to temperature (Figure 4), suggesting that other stressors (e.g., direct temperature effects on photosynthesis) had conflicting influence on the response. However, the two response variables responded similarly to precipitation and waterlogging tolerance. When we compared the outcome with and without soil ice simulated (Figure 4), we found that waterlogging tolerance only provided an advantage when ice was simulated, and that collectively, the species (covering the full range of waterlogging tolerances) were able to maintain as much biomass as they did when ice was not simulated. One consequence of this outcome is that the relative biomass of each species is affected by the presence or absence of ice (depending on waterlogging tolerance), and eventually composition may be altered as the prevalence of ice changes. We also expected an interaction between temperature and waterlogging tolerance, because increasing temperature should reduce soil wetness on permafrost sites, but this expectation was not supported (F = 0.52, p < 0.0.7239), likely related to our arbitrary waterlogging stress parameters.

The latitudinal gradient test demonstrated the interaction of the many factors that determine forest successional dynamics and species range shifts. The modeled factors include temperature effects (heat and cold stress, cold killing, growing season length), precipitation, CO₂ fertilization effects (enhancement of photosynthesis and water use efficiency), permafrost effects on hydrology, and light (latitude effects on day length, cloudiness). Our expectation for the latitudinal gradient test was that biomass should (1) increase as emissions increase because of CO₂ fertilization and longer growing seasons, (2) decrease with increasing latitude because the growing season is shorter, and (3) decrease with disturbance because cohorts are younger. These expectations were generally met. CO₂ fertilization effects were constant across latitudes, but temperature (including growing season length) and precipitation varied considerably by latitude (Table 3). Thus, CO₂ fertilization effects can be seen across columns in the latitudinal gradient figures, and temperature and precipitation effects can be seen across rows. We note that scenarios with high CO₂ emissions greatly increased productivity at high latitudes, while productivity gains were limited at lower latitudes (similar to Shvidenko et al., 2008). We also expected that richness should (1) be unchanged, even as assemblages change (i.e., the number of niches is not changed), and (2) increase with disturbance (intermediate disturbance hypothesis). We found that on upland sites, richness was less changed in the absence of disturbance, and that richness tended to increase with disturbance, except at latitude 58N, where a large number of species were replaced with a small number of pioneers after disturbance. On wetland sites, richness always declined because only highly waterlogging tolerant species survived.

We expected that invasions and extirpations should (1) increase with disturbance because niches are opened, (2) increase with climate change because ranges shift, and (3) decrease at lower latitudes because change in climate is less. We found that disturbance sped up the process of climate-induced range shifts by reducing the dominance of established cohorts and giving pioneer species and new colonizers an opportunity to become a component of the new assemblage, consistent with Liang et al. (2018). Disturbance can also alter hydrology effects, primarily by reducing the transpiration rate on sites (increasing soil wetness), and also by potentially changing tree species composition to species with different drought and waterlogging tolerance. Disturbance (and warming climate) allowed larger-statured species to colonize and quickly become effective transpirers, altering hydrology and potentially displacing waterlogging-tolerant species, consistent with conclusions of Jin et al. (2020). In wetlands under climate change, disturbance was able to prevent development of effective transpirer cohorts (e.g., P. sibirica), maintaining the dominance of wetland species. Extirpations were higher and invasions were fewer on wetland sites compared to upland sites, reflecting the fact that most of the generalist tree species were not very competitive on saturated soil. However, wetland sites tended to have greater biomass than upland sites at the same latitude, presumably because large-statured species often became big enough to transpire the excess water, yet not be limited by low soil water availability.

The design of the latitudinal gradient test did not allow us to quantify the effect of permafrost thawing relative to direct temperature effects on productivity and composition changes caused by altered hydrology. In the model, the air temperature photosynthesis reduction factor would be less altered by the climate scenarios used than the water stress reduction factor would be altered by the changes in hydrology induced by thawing of permafrost (increased depth of the active layer) observed in the simulations. We observed that active layer depths increased nearly three meters under the RCP 8.5 scenario compared to the RCP 2.6 scenario at high latitude sites. When the active layer is shallow, there is not much available water and it is unable to drain, so the soil tends to be saturated with just a small amount of liquid water. As permafrost thaws, the active layer deepens, resulting in more available water, although if the active layer is deeper than the rooting zone, it also begins to drain, which would reduce water. Species adapted to permafrost are able to tolerate both waterlogging and limited total water availability, so as climate warms, their competitive advantage may be lost, resulting in altered species composition.

One of our objectives was to evaluate the feasibility of using our modified model to simulate range expansion and contraction induced by climate change at high latitudes. We believe that our latitudinal gradient test demonstrated a general feasibility based on our considerable knowledge of Siberian forests. Further work is needed to implement the model on real high-latitude landscapes, including important specific disturbances, and calibrating and validating system behavior using empirical observations. Our experience in this study was that we were able to control most aspects of simulated species growth and competition on our hypothetical high-latitude landscapes using the parameters now available in the model.

One consequence of climate change is greater temperature extremes, both hot and cold, and we observed that this can induce cold-killing of extant species, at least in the first 50 years. This result is perhaps not intuitively surprising, but it is a possible outcome of climate change that is not typically considered by forest managers and planners. If all cohorts of a species are catastrophically killed by a cold snap across entire landscapes, successional dynamics may not follow the path typically observed under past climate. This illumination of unexpected consequences of climate change illustrates another benefit of using a mechanistic FLM as part of any strategic forest management process that seeks to consider the effects of a changing climate.

In our attempts to find other landscape modeling results for comparison, we confirmed that there is indeed a need for these capabilities. We are aware of one other effort to simulate permafrost dynamics in a different LANDIS-II succession extension (DGS-Succession), but results have not yet been published (M. Lucash, personal communication). DGVMs use similar methods, having inspired our method, but their use of plant functional types instead of species cohorts makes direct comparison difficult. In a recent review of the impacts of climate-induced permafrost degradation on vegetation, Jin et al. (2020) call for improvement of process-based permafrost ecological models in order to predict and evaluate impacts of permafrost degradation on ecosystems and their adaptation.

Caveats

The interpretation of extirpations was confounded somewhat by the fact that many of the pioneer species at lower latitudes had relatively short longevity, meaning that some extirpations there were caused by senescence rather than competitive interactions. Similarly, invasions in the south may have been enhanced by a higher number of shade-intolerant pioneer species than found at more northerly latitudes. It should also be noted that there is a high degree of stochasticity associated with establishment, and therefore, invasion. For example, a species that establishes on a recently disturbed site decades before any other will likely dominate the site and exclude others more than in the case where several species establish simultaneously. The high variability seen in Figure 7 mostly reflects this stochasticity.

Our results suggest that productivity is highest on the wettest biophysical positions (Figure 3), which is demonstrably false empirically (e.g., Iwasaki et al., 2009). This result is partly an artifact of the values we arbitrarily assigned to the waterlogging and drought tolerance parameters (H1–H4) when designing the lowland test prior to conducting test runs, although nutrient limitations also reduce productivity on many lowland sites, and nutrient limitations are not currently modeled in PnET-Succession. The baseline climate inputs also contributed to this result by generating mostly dry conditions that resulted in drought stress except under the wet combinations of factors, which is realistic for high-latitude landscapes. We could have modified the values of the waterlogging parameters post hoc to achieve more realistic results, but we believed that would reduce the legitimacy of the test. The model produces outputs that reflect the inputs, and this test clearly demonstrates that the model responds appropriately to the water tolerance parameters used given the water inputs and the site parameters that control hydrology.

There are no feedbacks in PnET-Succession between simulated vegetation and climate. The presence of live vegetation has no effect on ice depth other than its effect on soil water (which has high thermal diffusivity) through transpiration. LANDIS-II also does not simulate herbaceous vegetation that could modify establishment rates. PnET-Succession does not currently account for the effect of soil nutrients on growth. It is possible that some of the increase in productivity seen under the RCP 6.0 and 8.5 emissions scenarios may not be realized because of nutrient limitations. Adding soil nutrient and carbon dynamics into PnET-Succession is under discussion, but is not yet available.

We did not include the uncertainty in the climate projections used as inputs, nor the uncertainty associated with input parameters, to avoid confounding the signal from our experimental treatments. Thus, the uncertainty shown in our figures does not reflect the uncertainty that would be expected when using the model to make realistic projections of future forest dynamics under climate change. However, increasing the number of simulation replicates could be used to reduce such uncertainty to some extent.

Sphagnum is a bryophyte, lacking stomata (Silvola and Aaltonen, 1984). The photosynthesis algorithms in PnET-Succession are stomatally constrained (as in Biome-BGC, Bond-Lamberty et al., 2007), and therefore cannot mechanistically simulate sphagnum growth, forcing us to constrain growth using an unrelated parameter (FracActWd) to reduce foliage. Consequently, the projections of sphagnum biomass are highly uncertain, while the establishment of sphagnum is as reliable as the other species.

Future Work

Our study verified the ability of the new capabilities added to PnET-Succession to reasonably simulate the response of forests to hydrological dynamics induced by wet biophysical units and permafrost thawing. However, these capabilities should be more thoroughly tested against empirical data in a diversity of ecosystems before they are used to make definitive projections of forest response to waterlogged conditions. We have such work underway at four sites across a latitudinal gradient in Siberia, but other tests are needed. The model currently is not able to simulate periodic flooding of trees growing in riparian flood plains. However, we believe that such a capability may be feasible within the conceptual framework of the model (e.g., Bond-Lamberty et al., 2007), but considerable development and testing would be required.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

EG designed the study and led the model development, and wrote 95% of the manuscript. BM implemented the model design and contributed significantly to algorithm development. AS provided knowledge of Siberian forest ecology, and helped with model calibration and validation. BS contributed to analysis and interpretation. All the authors contributed to the article and approved the submitted version.

Funding

Participation of AS was supported by Russian Science Foundation Project No. 19-77-30015. Funding provided by the Northern Research Station, USDA Forest Service.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank David Mladenoff for insights that helped us develop the algorithms implemented here. We also thank Thomas Brussel, Nathan DeJager, Melissa Lucash, and the two reviewers for their critique of earlier drafts of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.598775/full#supplementary-material

Supplementary Figure 1 | Soil water potential (m pressure head) as a function of soil water content and soil texture. Curves end at the soil saturation point, and their shape as soil water potential values approach zero is relevant to waterlogging tolerance. Wilting point and field capacity in terms of pressure are defined as 153 and 3.4 m of pressure head, respectively. Soil acronyms follow FAO conventions. Data from Saxton and Rawls (2004).

Supplementary Figure 2 | An example of monthly soil temperature (T_soil) profiles on a sandy, saturated soil for a single year under a hypothetical high-latitude climate.

Supplementary Table 1 | Water stress parameters for the hypothetical species used in both the lowland forest and permafrost test experiments. Values given in units of m of pressure head.

Supplementary Table 2 | Selected PnET-Succession parameter values for Siberian tree species.

References

Aber, J. D., Ollinger, S. V., and Driscoll, C. T. (1997). Modeling nitrogen saturation in forest ecosystems in response to land use and atmospheric deposition. Ecol. Model. 101, 61–78. doi: 10.1016/s0304-3800(97)01953-4

CrossRef Full Text | Google Scholar

Aber, J. D., Ollinger, S. V., Federer, C. A., Reich, P. B., Goulden, M. L., Kicklighter, D. W., et al. (1995). Predicting the effects of climate change on water yield and forest production in the northeastern United States. Clim. Res. 5, 207–222. doi: 10.3354/cr005207

CrossRef Full Text | Google Scholar

Beer, C., Lucht, W., Gerten, D., Thonicke, K., and Schmullius, C. (2007). Effects of soil freezing and thawing on vegetation carbon density in Siberia: a modeling analysis with the Lund-Potsdam-Jena Dynamic Global Vegetation Model (LPJ-DGVM). Glob. Biogeoch. Cycles 21:GB1012.

Google Scholar

Bond-Lamberty, B., Gower, S. T., and Ahl, D. E. (2007). Improved simulation of poorly drained forests using Biome-BGC. Tree Physiol. 27, 703–715. doi: 10.1093/TREEPHYS/27.5.703

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, J., Ferrians, O. J. Jr., Heginbottom, J. A., and Melnikov, E. S. (1997). Circum-Arctic Map of Permafrost and Ground-Ice Conditions. USGS Circum-Pacific Map Series CP-45 (Scale 1:10,000,000). Reston, VA: USGS.

Google Scholar

Carter, V. (1996). “Wetland hydrology, water quality, and associated functions,” in National Water Summary on Wetland Resources, United States Geological Survey, Water Supply Paper 2425, eds J. D. Fretwell, J. S. Williams, and P. J. Redman (Washington, DC: USDI, U.S. Geological Survey), 35–48.

Google Scholar

Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., et al. (2011). Development and evaluation of an earth-system model - HadGEM2. Geosci. Model. Dev. 4, 1051–1075. doi: 10.5194/gmd-4-1051-2011

CrossRef Full Text | Google Scholar

Coop, J. D., Parks, S. A., Stevens-Rumann, C. S., Crausbay, S. D., Higurea, P. E., Hurteau, M. D., et al. (2020). Wildfire-driven forest conversion in western North American landscapes. Bioscience 2020:biaa061. doi: 10.1093/biosci/biaa061

PubMed Abstract | CrossRef Full Text | Google Scholar

Court, A. (1951). Temperature frequencies in the United States. J. Meteorol. 8, 367–380. doi: 10.1175/1520-0469(1951)008<0367:tfitus>2.0.co;2

CrossRef Full Text | Google Scholar

De Bruijn, A., Gustafson, E. J., Sturtevant, B. R., Foster, J. R., Miranda, B. R., Lichti, N. I., et al. (2014). Toward more robust projections of forest landscape dynamics under novel environmental conditions: embedding PnET within LANDIS-II. Ecol. Model. 287, 44–57. doi: 10.1016/j.ecolmodel.2014.05.004

CrossRef Full Text | Google Scholar

De Jager, N. R., Van Appledorn, M., Fox, T. J., Rohweder, J. J., Guyon, L. J., Meier, A. R., et al. (2019). Spatially explicit modelling of floodplain forest succession: interactions among flood inundation, forest successional processes, and other disturbances in the Upper Mississippi River floodplain, USA. Ecol. Model. 405, 15–32. doi: 10.1016/j.ecolmodel.2019.05.002

CrossRef Full Text | Google Scholar

Dolman, A. J., Shvidenko, A., Schepaschenko, D., and Clais, P. (2012). An estimate of the terrestrial carbon budget of Russia using inventory-based, eddy covariance and inversion methods. Biogeosciences 9, 5323–5340. doi: 10.5194/bg-9-5323-2012

CrossRef Full Text | Google Scholar

Ernst, W. H. O. (1990). Ecophysiology of plants in waterlogged and flooded environments. Aqur. Bot. 38, 73–90. doi: 10.1016/0304-3770(90)90099-7

CrossRef Full Text | Google Scholar

Falkner, S. P., and Richardson, C. J. (1989). “Physical and chemical characteristics of freshwater wetland soils,” in Constructed Wetlands for Wastewater Treatment: Municipal, Industrial and Agricultural, ed. D. A. Hammer (Boca Raton, FL: Lewis Publishers), 41–72. doi: 10.1201/9781003069850-5

CrossRef Full Text | Google Scholar

Farouki, O. T. (1986). Thermal Properties of Soils, Vol. 11 of Series on Rock and Soil Mechanics. Warwick, NY: Trans Tech.

Google Scholar

Feddes, R. A., Kowalik, P. J., and Zaradny, H. (1978). Simulation of Field Water Use and Crop Yield. New York, NY: John Wiley & Sons.

Google Scholar

Fisher, R., McDowell, N., Purves, D., Moorcroft, P., Sitch, S., Cox, P., et al. (2010). Assessing uncertainties in a second-generation dynamic vegetation model caused by ecological scale limitations. New Phytol. 187, 666–681. doi: 10.1111/j.1469-8137.2010.03340.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Franks, P. J., Adams, M. A., Amthor, J. S., Barbour, M. M., Berry, J. A., and Ellsworth, D. S. (2013). Sensitivity of plants to changing atmospheric CO₂ concentration: from the geological past to the next century. New Phytol. 197, 1077–1094. doi: 10.1111/nph.12104

PubMed Abstract | CrossRef Full Text | Google Scholar

Gustafson, E. J. (2013). When relationships estimated in the past cannot be used to predict the future: using mechanistic models to predict landscape ecological dynamics in a changing world. Landsc. Ecol. 28, 1429–1437. doi: 10.1007/s10980-013-9927-4

CrossRef Full Text | Google Scholar

Gustafson, E. J., De Bruijn, A. M. G., and Miranda, B. R. (2020a). PnET-Succession v4.0 Extension User Guide. Published on the Internet by the LANDIS-II Foundation. Available online at: https://sites.google.com/site/landismodel/extensions/pnet-succession (accessed November 24, 2020).

Google Scholar

Gustafson, E. J., Kern, C. C., Miranda, B. R., Sturtevant, B. R., Bronson, D. R., and Kabrick, J. M. (2020b). Climate adaptive silviculture: how much will it take to produce resilient forest landscapes? For. Ecol. Manag. 470–471:118208. doi: 10.1016/j.foreco.2020.118208

CrossRef Full Text | Google Scholar

Gustafson, E. J., Kubiske, M. E., Miranda, B. R., Hoshika, Y., and Paoletti, E. (2018). Extrapolating plot-scale CO₂ and ozone enrichment experimental results to novel conditions and scales using mechanistic modeling. Ecol. Process. 7:31. doi: 10.1186/s13717-018-0142-148

CrossRef Full Text | Google Scholar

He, H. S. (2008). Forest landscape models: definitions, characterization, and classification. For. Ecol. Manag. 254, 484–498. doi: 10.1016/j.foreco.2007.08.022

CrossRef Full Text | Google Scholar

Iwasaki, H., Saito, H., Kuwao, K., Maximov, T. C., and Hasegawa, S. (2009). Forest decline caused by high soil water conditions in a permafrost region. Hydrol. Earth Syst. Sci. Discuss. 6, 6087–6610. doi: 10.5194/hessd-6-6087-2009

CrossRef Full Text | Google Scholar

Jin, X. Y., Jin, H.-U., Iwahana, G., Marchenko, S. S., Luo, D.-L., and Li, X.-U. (2020). Impacts of climate-induced permafrost degradation on vegetation: a review. Adv. Clim. Chang. Res. (in press). doi: 10.1016/j.accre.2020.07.002

CrossRef Full Text | Google Scholar

Jonas, T., Marty, C., and Magnusson, J. (2009). Estimating the snow water equivalent from snow depth measurements in the Swiss Alps. J. Hydrol. 378, 161–167. doi: 10.1016/j.jhydrol.2009.09.021

CrossRef Full Text | Google Scholar

Jong van Lier, Q., and Durigon, A. (2013). Soil thermal diffusivity estimated from data of soil temperature and single soil component properties. Rev. Brasil. Ciên. Solo 37, 106–112. doi: 10.1590/S0100-06832013000100011

CrossRef Full Text | Google Scholar

Jordan, R. (1991). A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM.89. Hanover: Cold Regions Research and Engineering Laboratory. Special Report 91-16.

Google Scholar

Lawrence, D., Fisher, R., Koven, C., Oleson, K., Swenson, S., and Vertenstein, M. (2018). CESM2 Community Land Model, CLM5 Technical Note. Boulder, CO: The National Center for Atmospheric Research.

Google Scholar

Lehner, B., and Döll, P. (2004). Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 296, 1–22. doi: 10.1016/j.jhydrol.2004.03.028

CrossRef Full Text | Google Scholar

Liang, L. L., Riveros-Iregui, D. A., Emanuel, R. E., and McGlynn, B. L. (2014). A simple framework to estimate distributed soil temperature from discrete air temperature measurements in datascarce regions. J. Geophys. Res. Atmos. 119, 407–417. doi: 10.1002/2013JD020597

CrossRef Full Text | Google Scholar

Liang, Y., Thompson, J. R., Duveneck, M. J., Gustafson, E. J., and Serra-Diaz, J. M. (2018). How disturbance, competition and dispersal interact to prevent tree range boundaries from keeping pace with climate change. Glob. Chang. Biol. 24, e335–e351. doi: 10.1111/gcb.13847

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucash, M. S., Scheller, R. M., Sturtevant, B. R., Gustafson, E. J., Kretchun, A. M., and Foster, J. R. (2018). More than the sum of its parts: how disturbance interactions shape forest dynamics under climate change. Ecosphere 9:e02293. doi: 10.1002/ecs2.2293

CrossRef Full Text | Google Scholar

Medlyn, B. E., Duursma, R. A., and Zeppel, M. J. B. (2011). Forest productivity under climate change: a checklist for evaluating model studies. Clim. Chang. 2, 332–355. doi: 10.1002/wcc.108

CrossRef Full Text | Google Scholar

Post, W. M., and Pastor, J. (1996). LINKAGES - An individual-based forest ecosystem model. Clim. Chang. 34, 253–261. doi: 10.1007/BF00224636

CrossRef Full Text | Google Scholar

Quegan, S., Beer, C., Shvidenko, A., McCallum, I., Handoh, I. C., Peylen, P., et al. (2011). Estimating the carbon balance of central siberia using a landscape-ecosystem approach, atmospheric inversion and dynamic global vegetation models. Glob. Chang. Biol. 17, 351–365. doi: 10.1111/j.1365-2486.2010.02275.x

CrossRef Full Text | Google Scholar

Richardson, C. W., and Ritchie, J. T. (1973). Soil water balance for small watersheds. Trans. Am. Soc. Agric. Eng. 16, 72–77.

Google Scholar

Running, S. W., and Gower, S. T. (1991). FOREST-BGC, a general model of forest ecosystem processes for regional applications, II. Dynamic carbon allocation and nitrogen budgets. Tree Phys. 9, 147–160. doi: 10.1093/treephys/9.1-2.147

PubMed Abstract | CrossRef Full Text | Google Scholar

Rupp, T. S., Starfield, A. M., and Chapin, F. S. III (2000). A frame-based spatially explicit model of subarctic vegetation response to climatic change: comparison with a point model. Landsc. Ecol. 15, 383–400.

Google Scholar

Saxton, K. E., and Rawls, W. J. (2004). Soil Water Characteristic Equations.xls. Available online at: http://hrsl.arsusda.gov/SPAW/SPAWDownload.html (accessed November 24, 2020).

Google Scholar

Sazonova, T. S., and Romanovsky, V. E. (2003). A model for regional-scale estimation of temporal and spatial variability of active layer thickness and mean annual ground temperatures. Permafrost. Periglac. Process. 14, 125–139. doi: 10.1002/ppp.449

CrossRef Full Text | Google Scholar

Scheller, R. M., Domingo, J. B., Sturtevant, B. R., Williams, J. S., Rudy, A., Gustafson, E. J., et al. (2007). Design, development, and application of LANDIS-II, a spatial landscape simulation model with flexible temporal and spatial resolution. Ecol. Model. 201, 409–419. doi: 10.1016/j.ecolmodel.2006.10.009

CrossRef Full Text | Google Scholar

Shvidenko, A., Schepashchenko, D., Nilsson, S., and Bouloui, Y. (2008). Tables and Models of Growth and Productivity of Forests of Major Forest Forming Species of Northern Eurasia (Standards and Reference Materials), 2nd Edn, Moscow: Federal Agency of Forest Management of the Russian Federation and IIASA.

Google Scholar

Silvola, J., and Aaltonen, H. (1984). Water content and photosynthesis in the peat mosses Sphagnum fuscum and S. angustifolium. Ann. Bot. Fenn. 21, 1–6. doi: 10.1007/978-3-319-23534-9_1

CrossRef Full Text | Google Scholar

Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., et al. (2003). Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 9, 161–185. doi: 10.1046/j.1365-2486.2003.00569.x

CrossRef Full Text | Google Scholar

Speich, M. J. R., Zappa, M., Scherstjanoi, M., and Lischke, H. (2019). FORHYCS v1.0: a spatially distributed model combining hydrology and forest dynamics. EGU Geosci. Model. Dev.-Discuss. doi: 10.5194/gmd-2019-117

CrossRef Full Text | Google Scholar

Wullschleger, S. D., Epstein, H. E., Box, E. O., Euskirchen, E. S., Goswami, S., Iversen, C. M., et al. (2014). Plant functional types in Earth system models: past experiences and future directions for application of dynamic vegetation models in high-latitude ecosystems. Ann. Bot. 114, 1–16. doi: 10.1093/aob/mcu077

PubMed Abstract | CrossRef Full Text | Google Scholar