- Institute of Ecology and Key Laboratory for Earth Surface Processes of the Ministry of Education, College of Urban and Envimental Sciences, Peking University, Beijing, China
When developing theories, designing studies, and interpreting the results, researchers are influenced by their perception of tree size. For example, we may compare two trees of the same size belonging to different species, and attribute any differences to dissimilarities between the species. However, the meaning of “same size” depends on the measures of size used. Wood density influences certain measures, such as biomass, but does not influence e.g., trunk diameter. Therefore, the choice of the measure of size can reverse any conclusions. Hence, it is import to consider which measure of size should be used. I argue that the most common measure of size, i.e., trunk diameter, is often a bad choice when wood density varies, as diameter is then not directly related to processes important in evolution. When trees with equal diameters but differing wood densities are compared, the tree with denser wood is larger if the measure of size is related to construction cost or trunk strength, a proxy of leaf area. From this perspective, the comparison is then conducted between a biologically larger heavy-wooded tree and a smaller light-wooded tree, and the differences between the trees may be caused by size instead of wood density. Therefore, trunk biomass and strength may often be more suitable measures of size, as they reflect the construction cost and biomechanical potency linked to leaf area crown height, often too challenging to estimate more directly. To assess how commonly inadequate measures of tree size have been used, I reviewed 10 highly cited journal articles. None of these 10 articles discussed the impact of wood density on biological size, and instead based the analyses on diameters or basal areas. This led to conclusions that could change or even reverse in an analysis based on biomass or strength. Overall, I do not suggest avoiding the use of diameter, but I recommend considering result sensitivity to the measure of size, particularly in studies ones with variable wood densities.
Tree Size
Many ecologically and evolutionarily important properties and processes are dependent on size. Therefore, “Size is one of the most important features of any organism,” as Niklas (2004) began review. Consequently, we take size into account when attempting to understand nature. We may compare two individuals of the same size, groups of individuals of the same total size, or individuals of different sizes but controlling for size either intuitively or rationally in our minds, or with statistical procedures. Our scientific ecological methods have developed significantly over the decades. However, we still choose our research topics instinctively and mainly use our intuition for setting up the studies. The understanding of common use of unconscious and biased thinking in decision-making have transformed economics in the past decades (Kahneman, 2011). Similarly, the combination of human perspective and intuitive thinking has led to a biased view of the evolutionary processes of animals that differ significantly from us (Kokko, 2017). In this essay, I explore how our human mind may influence how we perceive tree size and its potential dangers. I start in this section by discussing and comparing potential measure of tree size. I then examine whether inadequate perception on tree size may have influenced results in a sample of 10 articles. In section three I recap the ways in which things can go wrong, and in section four what to do in practice to avoid problems. I end this article with the fifth section answering playfully to the question of the title.
Humans are competent at noticing subtle differences in volume and even smaller differences in peoples' heights (Maskin et al., 2010). This has been valuable ability in our evolutionary history when identifying people and assessing their working, mobility, and fighting capabilities, and the rate at which they consume food. Because our fresh bulk density is nearly constant, and the same is true for most domestic and hunted animals, fresh mass and volume may, in practice, be used interchangeably. We can visually estimate volume but then, we talk about “weight” or more precisely fresh weight or fresh mass, which can be used nearly interchangeably, as gravity varies little. Human size, and perhaps the more commonly used closely related terms “large” and “small” are ambiguous. A taller but lighter person may be considered either larger or smaller than a shorter but heavier person, but this may be considered solely a semantic issue, as we have a clear vision of both in practice. The volume of a human individual rarely scales linearly to performance, but we intuitively good at relating it to the size of a person. We may, for example, estimate that four small men, each weighing 50 kg, would be able to carry a load that two large men, both weighing 120 kg, are merely able to carry, even though the total volume of the small men were smaller that of the large men.
Size is important for trees, as it is linked to construction and maintenance costs and to processes such as photosynthesis. Large fresh weight and volume cause transportation challenges for animals, and it is not difficult to imagine situations in which smaller individuals are fitter. Individuals of most mammal and bird species grow relative rapidly to their mature size, and remain then in this size that has presumably been optimal in their evolutionary history for the rest of their lives. However, trees may safely be assumed to grow as large as they are able during growth of individuals and have evolved as large as they are capable without an excessive risk of toppling over (Gardiner et al., 2016) or of having issues with xylem (Ryan and Yoder, 1997) or phloem transport (Woodruff, 2013). When expressed more scientifically, the “being capable” refers to construction and maintenance costs and it has been balanced with benefits originating from the large size, e.g., the ability to grow a large area of leaves and position them high up in the canopy and to transport water, nutrients, and carbohydrates up and down and to store them. These costs and benefits do not normally scale linearly with measures of tree size (Table 1) but can be understood based on them.
In contrast with the large number of potential measures of tree size (Table 1), laymen and forest ecologist like seem to focus on just a few measures. When we see a tree growing in the open from a distance, most of us probably consider it large if it is tall and the crown is wide. However, our perception of size changes for obvious reasons when we enter a forest. The distant view of a given tree is blocked by other trees and we are mainly only able to see the lower parts of the trunks of these closer trees. Therefore, a tree in a dense forest is typically considered larger than its neighbor when its diameter is larger. This focus on diameter is not just restricted to casual discussions regarding forests, but is also reflected in scientific publications, as diameter is also the size measure that is the easiest to measure with simple tools. The words “shrub” and “height” were used in many more articles (2,861) than “shrub” and “diameter” (1,537), while “tree” and “height” (26,207) were used only slightly more frequently than “tree” and “diameter” (24,438) (ISI Web of Science, Clarivate Analytics search on 28 May 2019). Shrub height may get more attention relative to diameter not only because their tops are visible, and their height can be defined and measured often more easily than diameters of multi-stemmed individuals, but also because we may intuitively consider differences close to our own height to be more important and interesting. Other measures (Table 1) are even more difficult to determine than height, and certain ones, such as biomass and strength, require species identification and prior information or a time-consuming protocol involving laboratory work.
Instead of measures of size that are easy to estimate with plain eye or seem intuitively significant, conclusions of scientific studies should be based on measures that scale with evolutionarily important processes. When the focus is on photosynthesis, leaf area and its height, indicating the light level to which a tree is exposed, would be a good option. Photosynthesis, as the source of energy, is specific for plants. However, respiration is similar in ectothermic animals and trees, but while only a minuscule portion of animal tissue is metabolically inactive, the biomass share of dead heartwood is often more than half. Autotrophic respiration of trees has been modeled based on dry mass, i.e., biomass (Mori et al., 2010), based on sapwood volume (Valentine and Mäkelä, 2012), and is also found to scale roughly linearly to surface area (Bosc et al., 2003). Construction costs are more straightforward to model and are often assumed to scale linearly with most of the biomass, i.e., woody parts. Of the size-related risks that trees face, the toppling over moment that the wind drag causes is related mainly to leaf area and tree height, as wind speeds increase upwards, and the longer a lever is the greater the moment or torque caused by a given force (Gardiner et al., 2016). Fresh weight, central in the notion of animal size, has little importance in trees. Fresh weight influences the maximum height that does not lead to elastic buckling. However, most trees are far below this height (McMahon, 1973). In addition, fresh weight contributes to the moment of toppling over once the wind bends a tree. In applied ecology, dry weight, dry mass, or biomass may be used to assess the role of trees in climate change mitigation, as the carbon content of biomass varies only little (Martin et al., 2018), while trunk volume has been traditionally an important measure in forestry.
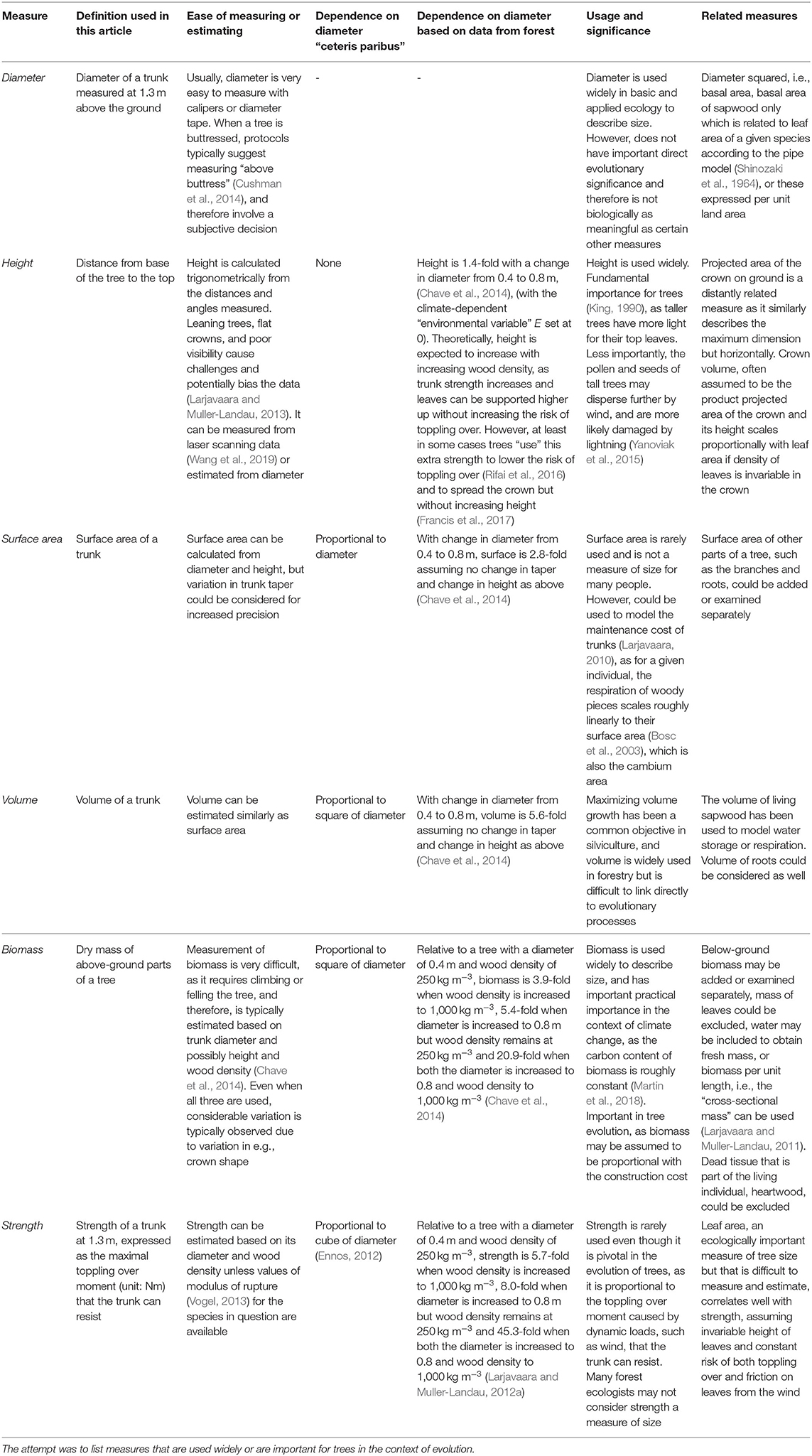
Dangerously, the choice for the measure of size may dramatically influence the conclusions made (Figure 1), and therefore it is important to carefully consider the choice. For example, when trunk dimensions of individuals of two species are the same but wood densities differ, the trees are equally large based on diameter but not based on biomass. Overall, despite the best-matching measures varying, both biomass and strength (Table 1) correspond well to several of the processes that have influenced growth, survival, and reproduction and have therefore probably had a strong linkage with tree evolution. Here, I call trees smaller based on biomass and strength “biologically smaller” and these measures of size more “biologically meaningful” than e.g., diameter. I admit that the relative importance of the linkages between these ecological measures and evolutionary processes depends on the research question but find this generalization useful in this article for simplicity.
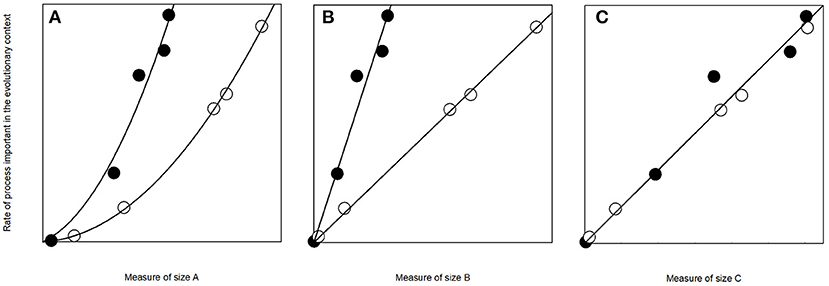
Figure 1. Hypothetical demonstration on how the measure of size may influence our perception of important processes. The tree species represented with open and closed circles appear different when compared relative to measures of size A and B but not based on C. The process on the Y-axis could for example be transpiration, and measure of size A diameter, B basal area, and C cross-section mass, i.e., biomass per unit length of the trunk, at breast height (instead of more common biomass as that would require assumptions on height, taper, and branches). I computed the data assuming a three-fold wood density for the species represented with closed circles and added some random variation so that the dataset appears more realistic. Scientists normally pay enough attention on differences between dimension-based measures such as A and B. However, this article focuses on impacts of wood density on size and how results may change when studying wood density related structures and processes when using measures based only on dimensions (A and B) or those influenced also by wood density (C). This is important as based on A and B a study could conclude that the species with higher wood density has higher transpiration. With more species with similar differences, a study based on measure A or B would conclude that increasing wood density increases transpiration, while a study based on C would claim that wood density does not influence transpiration.
Review of 10 Highly Cited Articles
The previous section remained somewhat theoretical or even philosophical and may not have revealed to most readers the importance of considering the measure of tree size. For this section, my objective was to review qualitatively a sample of articles and examine how tree size was perceived and how alternative perspectives may have influenced the results. I focused on recent and much-cited articles presenting data sets with variation in wood density so that biologically more meaningful measures of size, strength, and biomass vary for a given diameter. I performed a search on 22 May 2019 on the ISI Web of Science, Clarivate Analytics using “wood densit*” or “wood specific gravit*” as “topic.” I selected these strings of words as both wood density and wood specific gravity are commonly used and wanted to include the plurals and possibly other inflections. I obtained 2,250 articles published since 2010. I then selected the 10 most cited articles since 2018 that had at least one of the two searched strings of words in the title, abstract, or keywords (Supplementary Materials). Alas, as my approach was critical and I focused on steps of reasoning related to size that may have influenced conclusions, I do not describe the pivotal advancements that most of these articles made.
I begin with a comprehensively discussed case that possibly serves as a good starting point for other more general and complex circumstances. The only review article included in the sample (Adler et al., 2013) incidentally presented previously common thinking on the value of dense wood being of high strength but having a high construction cost and therefore slow growth. This logic has been explained to be a product of focusing misleadingly on a comparison of individuals of equal diameter and therefore differing biomass and strength (Anten and Schieving, 2010; Larjavaara and Muller-Landau, 2010, 2012a). The problem in the logic of comparing individuals of the same diameter but of differing wood densities (e.g., Lüttge, 2007) can be visualized with a seesaw (Figure 2). In this previously common erroneous thinking, A is wood density, B is strength, C is construction cheapness, and D is diameter that is assumed to not vary (Figure 2). Then, correctly, cheapness of construction trades off with strength, but this should not be applied to the ecological context or to understanding wood evolution, as D is not a biologically meaningful measure (Table 1). When D is changed to strength or biomass that remain constant, the plank of the seesaw breaks, as for a given biomass, the decreasing wood density increases strength without influencing construction cheapness assuming invariable height (Anten and Schieving, 2010; Larjavaara and Muller-Landau, 2010, 2012a), revealing how important it is that B, C, and D are all biologically meaningful when attempting to understand the ecological significance of A. The initial choice of comparing trees with identical diameters in the traditional thinking paradoxically leads to false conclusions despite a perfectly correct chain of reasoning.
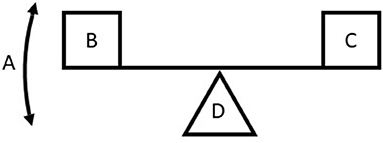
Figure 2. Seesaw representing a trade-off situation. When A changes, B improves, and C becomes worse for example from an evolutionary perspective, or vice versa. The fulcrum, D, is assumed to not change, normally gains less attention, as our mind easily focuses on only the moving parts. This is a problem, as D influences how B and C depend on A.
Based on the previous example, it is possible to see how comparisons over a narrow range of diameters, in which the biomass of the largest light-wooded species is lower than the biomass of the smallest heavy-wooded species, may lead to similar problems. However, the same problem persists when the diameter range is wide, when only one end is bound, or even without diameter limits if for example low wood density species have similar diameters and therefore average lower biomass. A minimum diameter is nearly always set for trees to be included in the sample to optimize the field efforts. Seven of the 10 included studies were based on data sets with such boundaries. This signifies that the smallest light-wooded trees included were lighter and biologically smaller than the smallest heavy-wooded trees. This is methodologically understandable and reasonable, and not a problem if the study is mensurational without ecological reasoning or if the significance of the trees close to the boundary on the discovered patterns is small. However, it is useful to consider the risks related to misleading conclusions relative to a biologically more meaningful way of setting the boundary. For example, with a size limit based on a biomass of 50 kg, the diameter limit for a light-wooded species with a very low wood density of 250 kg m3 would be at 15.3 cm, while the limit would be at 9.0 cm for a species with an exceptionally dense wood (1,000 kg m−3; Chave et al., 2014; computed with environmental variable set at zero). The two mensuration studies (Asner and Mascaro, 2014; Chave et al., 2014) did not aim to explain the life history of trees or formulate conclusions from an evolutionary or ecological perspective, and a boundary that was not biologically meaningful was not a problem. Three of the studies (Quesada et al., 2012; Kunstler et al., 2016; Peres et al., 2016) had lower diameter boundaries, but it seems unlikely that using, for example, a biomass-based boundary would have changed the results significantly. However, this could be verified.
Two of the seven studies, incorporating only trees with a diameter above a set minimum, focused on narrower diameter ranges in neotropical forests. Wright et al. (2010) found light-wooded trees, especially in the 1–5-cm diameter range to have higher mortality and relative diameter growth, and this finding was likely inflated by these saplings being biologically smaller than the heavy-wooded ones in the same diameter range, as mortality and relative diameter growth are likely to decrease with increasing biological size. Similarly, Phillips et al. (2010) found light-wooded and large trees to more likely die in a drought. They wished to confirm that low wood density directly increases the risk of mortality instead of larger diameters, by focusing on the 10–40-cm diameter range. However, as the light-wooded trees were biologically smaller, the effect of wood density on mortality for a given biological size was probably underestimated.
One of the studies with lower diameter boundaries (Kunstler et al., 2016) had another, and probably more significant issue, as the main variable of interest was absolute growth of basal area, which scales as diameter squared, inflating the biologically meaningful growth of light-wooded species. Furthermore, according to one of the main results light-wooded species influence their neighbors less, but again, the measure was that of basal area and the light-wooded species were therefore biologically smaller. This calls for reanalyzing the impressive data set based on biologically more meaningful measures of size rather than on basal area.
Gleason et al. (2016) used an exceptionally large dataset to study important patterns in efficiency and safety of upward water transport in the sapwood. Our intuition tells us that such examinations cannot be based on efficiency per plant or per branch as sizes vary. Gleason et al. (2016) based their analysis on “water transport through a given area and length of sapwood, across a given pressure gradient.” This unit can be visualized as the fulcrum (D) assumed not to change in Figure 2 on tradeoff of safety (B) and efficiency (C). Basing a comparison on transport per given cross-sectional area of sapwood would be a good starting point, if it linked either to the biologically meaningful size of the plants or to costs of constructing or maintaining the water conducting structures. Unfortunately, transport per given sapwood area falls in between these two. Assuming invariable conduit dimensions and density, and transport per given sapwood area, trunk or branch transport can increase “for free” without increasing trunk or branch cross-section mass, i.e., biomass per unit length, by both increasing sapwood-to-heartwood ratio or decreasing wood density. Likewise, transport per given area could increase simply by increasing conduit density in angiosperm trees and shrubs (lianas are different). Therefore, again the seesaw in Figure 2 breaks. An analysis based on construction or maintenance costs of the water conducting structures, or probably closely related maintenance cost of the trunk, could instead reveal a sharp safety-efficiency trends. Unfortunately, these measures would be very challenging to estimate.
Finally, Peres et al. (2016) simulated the effect of hunting on ecosystem carbon in the Amazon basin by assuming that the removal of animal dispersers of large-seeded and heavy-wooded species will lower the mean wood density and decrease the biomass per unit area assuming invariable basal area and number of individuals per unit land area. However, basal area per unit land area is not biologically meaningful and assuming it does not change should not be considered more natural or something to assume than for example basal area per unit land area increasing or decreasing a given percentage at the same time with changing wood density. This same assumption of constant basal area when wood density changes has been made in numerous influential papers. First, Bunker et al. (2005) simulated the carbon impacts of tree species extinctions and then the same logic was suggested for understanding the effects of hunting (Brodie and Gibbs, 2009). Even though this suggestion was initially criticized (Jansen et al., 2010), it has also been applied in other highly cited articles, although these are not included in my sample of the 10 most cited articles (Bello et al., 2015; Osuri et al., 2016), and seems to be widely accepted in conservation biology. If the assumption of constant basal area per unit land area is discarded, what can be said about potential changes in biomass owing to the hunting of dispersers of large-seeded heavy-wooded tree species? Assuming a constant number of trees per unit land area and a given gross primary productivity per unit land area, biomass may increase with increasing wood density if heavy-wooded species have lower maintenance costs per unit mass of their trunk. This could be further reinforced by the higher susceptibility of light-wooded species to disturbances and mortality and the forest being further away from the energy-balanced old-growth stage (Larjavaara and Muller-Landau, 2012b). However, all this is highly uncertain and the assumption of having an invariable number of trees per unit land area cannot be justified ecologically or physiologically. Moreover, any such changes may take centuries, and even then, may be minuscule compared to the much more rapid effect of animal- and hunting-triggered changes in semi-arid climates, where browsing may influence tipping the ecosystem into a forest or grassland (Staver et al., 2009).
Size-Myopia
I only reviewed 10 articles. However, as they were recent and highly cited, they probably give a much better outlook of ecological research on wood density than their small number suggests. In at least half of the articles, many of the key arguments seemed questionable because tree size was based on diameters or basal areas. Paradoxically, this is possible despite incorporating a perfect chain of reasoning if “size-myopia” has influenced the basis of the study (Figure 3). I wish to draw attention to this danger with this perhaps excessively provocative expression.
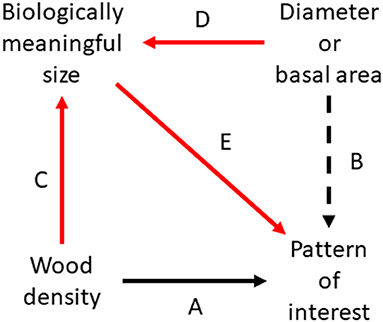
Figure 3. Flow chart showing size-myopic with black (A and B) and size-conscious inference with solid arrows (A, C, D, and E). The size-myopic logic focuses on arrow A but typically takes tree size into account based on diameter or basal area (arrow B). However, wood density not only influences the pattern or process of interest but also the biologically meaningful size (arrow C) together with dimension-based measures (arrow D). A size-conscious approach focuses on impact of wood density on the pattern of interest (arrow A) by taking the biological meaningful size into account (arrow E). Analogously, in studies e.g., focusing on crown shape instead of wood density, the impact of crown shape on size (arrow C) should be considered.
The comparison of apparently equally sized two trees with identical diameters but varying wood densities is perhaps the simplest case of size-myopia. This may be considered a special case of any comparison in which the focus is on wood density variation, but tree size expressed with biomass or strength covaries with wood density, and this is not discussed. This covariance is easy to see in the case of a fixed diameter or a narrow range of diameters, but is also a danger in (1) larger diameter ranges and (2) if diameters are bound only at one end, or (3) are even without any bounds if light-wooded trees in a given forest are biologically smaller even if they look at least as large when walking in the forest. Size-myopia is a danger also when whole or sapwood cross-sectional or basal area in the stand scale are used. It remains a problem over time if an increase in diameter or its derivatives is used in an attempt to understand biologically meaningful growth and wood density varies. Similarly, a temporally invariable basal area is a size-myopic assumption when wood density changes. In this case, assuming e.g., invariable biomass could be more natural.
I believe that our human mind is not tuned intuitively to consider the density of living creatures contributing to their size. This bias causes our size-myopia. We are not used to considering the variable bulk densities of living creatures, and we easily consider wood density solely a trait that we account for in complex analyses but do not consider it to contribute to the size of an individual when setting up a study. When thinking about size, and the adjectives “large” and “small” associated with it, we easily think of dimensions only and set aside wood density as a material property. Ecological questions are complicated and often best examined by fixing a part of the variables and then focusing on two variables, or occasionally more, that are varied to spatially or temporally understand the causes and consequences. Size is a typical variable to be fixed. For example, when studying differences in whole-plant-transpiration between species A and B with similar wood densities, we would intuitively reject a study design with measurements from a small individual of A and a mature tree of B with double diameter and roughly four-fold biomass compared to A. However, when comparing species B and C with four-fold wood density, unfortunately the norm would be to compare individuals with a roughly four-fold biomass difference and attribute the findings to differences in wood density and not in size, despite both being possible causes. Similarly, it is perhaps natural for our human mind to assume that basal area of a forest does not change temporally through certain environmental alterations, even though a temporally invariable biomass would probably be a better assumption from the perspective of a tree. However, both are likely to be rough, as a major shift in tree species composition is likely to involve major disturbances.
Size-Consciousness
When words are extensively discussed in research publications, the motivation is often to introduce terms that are new to most readers (e.g., Darwin, 1859) or to discuss alternative uses causing confusion (e.g., Hey, 2001). Sizes, i.e., “large” and "small' are extremely commonly used terms in forest ecology, and their meanings have been well established. One way to be size-conscious would be to continue using these terms as before simply based on dimensions and to consider wood density as a material property as before, but include it in analyses at an earlier time. However, I believe this to be difficult for our human mind, and it is intellectually easier to reconsider the meaning of size, i.e., “and” “small,” in tree studies of variable wood densities and to include wood density in their concepts and think in terms of e.g., biomass instead of dimensions.
How to avoid size-myopia and be size-conscious? I am not suggesting that fieldwork or remote measurements should be conducted differently, but that more attention should be paid to size-consciousness when analyzing data, communicating the results, and developing theories. We should also always consider how the measure of tree size influences the results when (1) wood density varies and we fix size for a comparison, (2) we set a size-based boundary or boundaries for the sample of trees, (3) we compare growth speeds, or (4) we make assumptions about temporal trends. This consideration does not need to be more complicated than when an economist converts gross domestic products from nominal to ones adjusted with purchasing power, or an atmospheric scientist converts relative humidity to absolute humidity and ponders for a while which to use when reporting their results to others.
The large number of alternatives for diameter presents a challenge for which measure to choose when reporting results (Table 1). Biomass or strength may be the natural alternatives for diameter in many cases. However, as they are typically estimated based on diameter, just using diameter to describe size is not normally a problem if wood density does not significantly vary in the dataset. When wood density varies, then biomass and strength are likely to vary for a given diameter but even this may not cause problems. Checking this can be done by observing the sensitivity of the results on converting diameter to other measures of size listed in Table 1. Obviously, estimating biomass or strength just based on diameter does not help in taking the wood density caused variation into account, but allometric models incorporating wood density or biomechanical equations including wood density, or even better, modulus of rupture, should be used. Sometimes intra-specific wood density variation should be included in estimation of biomass or strength. Use of diameter can sometimes be a better measure than e.g., biomass physiologically if the focus is on maintenance costs that are assumed to scale linearly with surface area (Table 1). However, this would be reasonable only occasionally. Biomass and strength are closely related measures. However, assuming invariable height, biomass scales to diameter squared, while strength scales to diameter cubed, therefore increasing the size difference between small- and large-diameter trees. Because shrubs and small trees can bend to the ground without breaking, their strength is not important for survival and fitness (Larjavaara, 2015), therefore backing usage of biomass when studying them. Crown-based measures of size are typically superior but crown area and volume are challenging to estimate and leaf area even more difficult. Fortunately, this could change with rapidly improving technology and knowledge to collect and analyze laser scanning data (Li et al., 2017).
How Large Are You?
How would a heavy-wooded emergent tree describe its own size (see Table 1 for biomass and strength for a diameter of 0.8 m and wood density of 1,000 kg m−3)? It would proudly explain that it is much older and heavier than its 21-neighbors combined and as strong as 45 of these much smaller neighbors (see Table 1 for biomass and strength for a diameter of 0.4 m and for wood density of 250 kg m−3). Size-myopic ecologists would then pull diameter tapes out of their pockets and observe that the diameters of just two neighbors need to be summed to equal the diameter of the heavy-wooded emergent tree, and they would wonder why it is bragging and exaggerating its own size. They would then begin flying a drone, bend their necks, first seeing how the long branches of the large one shade the tops of the smaller trees. Once the drone reaches the open sky, they would point the camera down and watch the canopy from the remote-control display. They would not see the dozens of smaller neighbors that have disappeared in the shady understory, but only the thousands of ripening fruits and nearly million leaves on the large tree basking in the sun and monopolizing all the direct light over a large area filling the screen. They would begin to wonder. The large one really looks grossly larger from above but not according to the diameter tapes. How come?
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was supported by Peking University.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank Mark Olson, Kasia Ziemińska, Jérôme Chave, Douglas Sheil, and Hanna Kokko for comments and Stella Thompson for English language editing.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.564302/full#supplementary-material
References
Adler, P. B., Fajardo, A., Kleinhesselink, A. R., and Kraft, N. J. B. (2013). Trait-based tests of coexistence mechanisms. Ecol. Lett. 16, 1294–1306. doi: 10.1111/ele.12157
Anten, N. P. R., and Schieving, F. (2010). The role of wood mass density and mechanical constraints in the economy of tree architecture. Am. Nat. 175, 250–260. doi: 10.1086/649581
Asner, G. P., and Mascaro, J. (2014). Mapping tropical forest carbon: calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 140, 614–624. doi: 10.1016/j.rse.2013.09.023
Bello, C., Galetti, M., Pizo, M. A., Magnago, L. F. S., Rocha, M. F., Lima, R. A. F., et al. (2015). Defaunation affects carbon storage in tropical forests. Sci. Adv. 1:10. doi: 10.1126/sciadv.1501105
Bosc, A., De Grandcourt, A., and Loustau, D. (2003). Variability of stem and branch maintenance respiration in a Pinus pinaster tree. Tree Physiol. 23, 227–236. doi: 10.1093/treephys/23.4.227
Brodie, J. F., and Gibbs, H. K. (2009). Bushmeat hunting as climate threat. Science 326, 364–365. doi: 10.1126/science.326_364b
Bunker, D. E., DeClerck, F., Bradford, J. C., Colwell, R. K., Perfecto, I., Phillips, O. L., et al. (2005). Species loss and aboveground carbon storage in a tropical forest. Science 310, 1029–1031. doi: 10.1126/science.1117682
Chave, J. M., Rejou-Mechain, A., Burquez, E., Chidumayo, M. S., Colgan, W. B. C., Delitti, A., et al. (2014). Improved allometric models to estimate the aboveground biomass of tropical trees. Global Change Biol. 20, 3177–3190. doi: 10.1111/gcb.12629
Cushman, K. C., Muller-Landau, H. C., Condit, R. S., and Hubbell, S. P. (2014). Improving estimates of biomass change in buttressed trees using tree taper models. Methods Ecol. Evolut. 5, 573–582. doi: 10.1111/2041-210X.12187
Ennos, A. R. (2012). Solid Biomechanics. Princeton, NJ: Princeton University Press. doi: 10.1515/9781400840649
Francis, E. J., Muller-Landau, H. C., Wright, S. J., Visser, M. D., Iida, Y., Fletcher, C., et al. (2017). Quantifying the role of wood density in explaining interspecific variation in growth of tropical trees. Global Ecol. Biogeogr. 26, 1078–1087. doi: 10.1111/geb.12604
Gardiner, B., Berry, P., and Moulia, B. (2016). Wind impacts on plant growth, mechanics and damage. Plant Sci. 245, 94–118. doi: 10.1016/j.plantsci.2016.01.006
Gleason, S. M., Westoby, M., Jansen, S., Choat, B., Hacke, U. G., Pratt, R. B., et al. (2016). Weak tradeoff between xylem safety and xylem-specific hydraulic efficiency across the world's woody plant species. New Phytol. 209, 123–136. doi: 10.1111/nph.13646
Hey, J. (2001). The mind of the species problem. Trends Ecol. Evolut. 16, 326–329. doi: 10.1016/S0169-5347(01)02145-0
Jansen, P. A., Muller-Landau, H. C., and Wright, S. J. (2010). Bushmeat hunting and climate: an indirect link. Science 327, 30–30. doi: 10.1126/science.327.5961.30-a
King, D. A. (1990). The adaptive significance of tree height. Am. Nat. 135, 809–828. doi: 10.1086/285075
Kokko, H. (2017). Give one species the task to come up with a theory that spans them all: what good can come out of that? Proc. R. Soc. B Biol. Sci. 284:8. doi: 10.1098/rspb.2017.1652
Kunstler, G., Falster, D., Coomes, D. A., Hui, F., Kooyman, R. M., Laughlin, D. C., et al. (2016). Plant functional traits have globally consistent effects on competition. Nature 529, 204–U174. doi: 10.1038/nature16476
Larjavaara, M. (2010). Maintenance cost, toppling risk and size of trees in a self-thinning stand. J. Theor. Biol. 265, 63–67. doi: 10.1016/j.jtbi.2010.04.021
Larjavaara, M. (2015). Trees and shrubs differ biomechanically. Trends Ecol. Evolut. 30, 499–500. doi: 10.1016/j.tree.2015.07.007
Larjavaara, M., and Muller-Landau, H. C. (2010). Rethinking the value of high wood density. Funct. Ecol. 24, 701–705. doi: 10.1111/j.1365-2435.2010.01698.x
Larjavaara, M., and Muller-Landau, H. C. (2011). Cross-section mass: an improved basis for woody debris necromass inventory. Silva Fenn. 45, 291–298. doi: 10.14214/sf.119
Larjavaara, M., and Muller-Landau, H. C. (2012a). Still rethinking the value of high wood density. Am. J. Bot. 99, 165–168. doi: 10.3732/ajb.1100324
Larjavaara, M., and Muller-Landau, H. C. (2012b). Temperature explains global variation in biomass among humid old-growth forests. Global Ecol. Biogeogr. 21, 998–1006. doi: 10.1111/j.1466-8238.2011.00740.x
Larjavaara, M., and Muller-Landau, H. C. (2013). Measuring tree height: a quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evolut. 4, 793–801. doi: 10.1111/2041-210X.12071
Li, Y., Guo, Q., Su, Y., Tao, S., Zhao, K., and Xu, G. (2017). Retrieving the gap fraction, element clumping index, and leaf area index of individual trees using single-scan data from a terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 130, 308–316. doi: 10.1016/j.isprsjprs.2017.06.006
Martin, A. R., Doraisami, M., and Thomas, S. C. (2018). Global patterns in wood carbon concentration across the world's trees and forests. Nat. Geosci. 11:915. doi: 10.1038/s41561-018-0246-x
Maskin, L. P., Attie, S., Setten, M., Rodriguez, P. O., Bonelli, I., Stryjewski, M. E., et al. (2010). Accuracy of weight and height estimation in an intensive care unit. Anaesth. Intensive Care 38, 930–934. doi: 10.1177/0310057X1003800519
McMahon, T. (1973). Size and shape in biology. Science 179, 1201–1204. doi: 10.1126/science.179.4079.1201
Mori, S., Yamaji, K., Ishida, A., Prokushkin, S. G., Masyagina, O. V., Hagihara, A., et al. (2010). Mixed-power scaling of whole-plant respiration from seedlings to giant trees. PNAS 107, 1447–1451. doi: 10.1073/pnas.0902554107
Niklas, K. J. (2004). Plant allometry: is there a grand unifying theory? Biol. Rev. 79, 871–889. doi: 10.1017/S1464793104006499
Osuri, A. M., Ratnam, J., Varma, V., Alvarez-Loayza, P., Astaiza, J. H., Bradford, M., et al. (2016). Contrasting effects of defaunation on aboveground carbon storage across the global tropics. Nat. Commun. 7:7. doi: 10.1038/ncomms11351
Peres, C. A., Emilio, T., Schietti, J., Desmouliere, S. J. M., and Levi, T. (2016). Dispersal limitation induces long-term biomass collapse in overhunted Amazonian forests. Proc. Natl. Acad. Sci. U.S.A. 113, 892–897. doi: 10.1073/pnas.1516525113
Phillips, O. L., van der Heijden, G., Lewis, S. L., Lopez-Gonzalez, G., Aragao, L., Lloyd, J., et al. (2010). Drought-mortality relationships for tropical forests. New Phytol. 187, 631–646. doi: 10.1111/j.1469-8137.2010.03359.x
Quesada, C. A., Phillips, O. L., Schwarz, M., Czimczik, C. I., Baker, T. R., Patino, S., et al. (2012). Basin-wide variations in Amazon forest structure and function are mediated by both soils and climate. Biogeosciences 9, 2203–2246. doi: 10.5194/bg-9-2203-2012
Rifai, S. W., Munoz, J. D. U., Negron-Juarez, R. I., Arevalo, F. R. R., Tello-Espinoza, R., et al. (2016). Landscape-scale consequences of differential tree mortality from catastrophic wind disturbance in the Amazon. Ecol. Appl. 26, 2225–2237. doi: 10.1002/eap.1368
Ryan, M. G., and Yoder, B. J. (1997). Hydraulic limits to tree height and tree growth. BioScience 47, 235–242. doi: 10.2307/1313077
Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T. (1964). A quantitative analysis on plant form—the pipe model theory. I—basic analyses. Jpn. J. Ecol. 14, 97–105.
Staver, A. C., Bond, W. J., Stock, W. D., van Rensburg, S. J., and Waldram, M. S. (2009). Browsing and fire interact to suppress tree density in an African savanna. Ecol. Appl. 19, 1909–1919. doi: 10.1890/08-1907.1
Valentine, H. T., and Mäkelä, A. (2012). Modeling forest stand dynamics from optimal balances of carbon and nitrogen. New Phytol. 194, 961–971. doi: 10.1111/j.1469-8137.2012.04123.x
Vogel, S. (2013). Comparative Biomechanics: Life's Physical World. Princeton, NJ: Princeton University Press.
Wang, Y., Lehtomäki, M., Liang, X., Pyörälä, J., Kukko, A., Jaakkola, A., et al. (2019). Is field-measured tree height as reliable as believed–A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. 147, 132–145. doi: 10.1016/j.isprsjprs.2018.11.008
Woodruff, D. R. (2013). The impacts of water stress on phloem transport in Douglas-fir trees. Tree Physiol. 34, 5–14. doi: 10.1093/treephys/tpt106
Wright, S. J., Kitajima, K., Kraft, N. J. B., Reich, P. B., Wright, I. J., Bunker, D. E., et al. (2010). Functional traits and the growth-mortality trade-off in tropical trees. Ecology 91, 3664–3674. doi: 10.1890/09-2335.1
Yanoviak, S. P., Gora, E. M., Fredley, J., Bitzer, P. M., Muzika, R. M., and Carson, W. P. (2015). Direct effects of lightning in temperate forests: a review and preliminary survey in a hemlock-hardwood forest of the northern United States. Can. J. For. Res. 45, 1258–1268. doi: 10.1139/cjfr-2015-0081
Keywords: biomass, DBH, diameter, ecophysiology, relativity, size, tree, wood specific gravity
Citation: Larjavaara M (2021) What Would a Tree Say About Its Size? Front. Ecol. Evol. 8:564302. doi: 10.3389/fevo.2020.564302
Received: 21 May 2020; Accepted: 15 December 2020;
Published: 13 January 2021.
Edited by:
George L. W. Perry, The University of Auckland, New ZealandReviewed by:
Stephen Charles Sillett, Humboldt State University, United StatesBradley S. Case, Auckland University of Technology, New Zealand
Copyright © 2021 Larjavaara. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Markku Larjavaara, bWFya2t1QHBrdS5lZHUuY24=
 Markku Larjavaara
Markku Larjavaara