- 1Department of Biology, University of Maryland, College Park, MD, United States
- 2Department of Applied Mathematics, University of California, Merced, Merced, CA, United States
- 3Department of Mathematics, University of California, Los Angeles, Los Angeles, CA, United States
- 4Department of Mathematics, Pomona College, Claremont, CA, United States
- 5Department of Mathematics & Statistics, Smith College, Northampton, MA, United States
- 6Department of Mathematics & Statistics, United States Merchant Marine Academy, Kings Point, NY, United States
- 7Department of Ecology and Evolutionary Biology, University of Tennessee, Knoxville, Knoxville, TN, United States
- 8Department of Mathematics, University of Tennessee, Knoxville, Knoxville, TN, United States
Members of social groups risk infection through contact with those in their social network. Evidence that social organization may protect populations from pathogens in certain circumstances prompts the question as to how social organization affects the spread of ectoparasites. The same grooming behaviors that establish social bonds also play a role in the progression of ectoparasitic outbreaks. In this paper, we model the interactions between social organization and allogrooming efficiency to consider how ectoparasitic threats may have shaped the evolution of social behaviors. To better understand the impacts of social grooming on organizational structure, we consider several dynamic models of social organization using network centrality measures as the basis of neighbor selection. Within this framework, we consider the impact of varying levels of social grooming on both the group structure and the overall ectoparasitic disease burden. Our results demonstrate that allogrooming, along with ongoing dynamic social organization, may be protective with respect to both the timing and the magnitude of ectoparasitic epidemics. These results support the idea that ectoparasitic threat should not be considered a single evolutionary factor in the evolution of host social systems, and may have operated in different ways depending on the broader ecology of the host-ectoparasite interaction.
1. Introduction
Among studies that consider how social species may have evolved, the risk of exposure to infectious pathogens is often mentioned as a potentially critical barrier against close or frequent contact among individuals (Hochberg, 1991; McCabe et al., 2015). Theories about how sociality may have evolved, despite these risks, range from reliance on physiological immunology to protective hygienic behaviors [both individual and social (Cremer et al., 2007; Schaller, 2011; Hock and Fefferman, 2012)]. Recent work has extended the role of individual behavioral choices to consider emergent social structure as itself being potentially protective against disease transmission (Rosengaus et al., 1998; Bonds et al., 2005; Hock and Fefferman, 2012). These insights build on the body of work that has demonstrated the critical impact that social structure can play in determining the course of an infectious disease epidemic in a population, but focus primarily on infectious pathogens, leaving the critical differences inherent in epidemiological dynamics of ectoparasitic infections unaddressed (Bansal et al., 2007, 2010; Craft, 2015; Sah et al., 2017).
Allogrooming, or social grooming, serves to signal and/or reinforce social bonds (Matheson and Bernstein, 2000; Kutsukake and Clutton-Brock, 2006), providing health benefits to both the groomer and groomee while developing and reinforcing relationships among group members. Immediate benefits to the groomer may include a decrease in tension (Shutt et al., 2007), access to nearby resources (Börger et al., 2008), and nutritional benefits from the consumption of groomed ectoparasites (Ramanantsalama et al., 2018). Over time, a groomer promotes social affiliations in the group, attains status, and forms alliances with others (Russell and Phelps, 2013). The groomee experiences a decrease in stress and tension via oxytocin and beta-endorphins, creates affiliative bonds, and contributes to the overall cohesion of the group (Schino et al., 1988). The act of allogrooming itself incurs opportunity costs in terms of loss of time and energy. For example, the focus required to be effective in allogrooming as a strictly hygienic act may distract groomers from noticing new opportunities, such as foraging for resources or detecting threats like predators (Maestripieri, 1993; Mooring and Hart, 1995). From an epidemiological perspective, allogrooming provides pathways for transmission of infection of ectoparasites that directly mirror those that would be relevant for pathogens, but also critically deviates from pathogen dynamics in that the groomer can decrease the ectoparasitic burden of the groomee. Hence, social contact is not solely a source of infection risk, but also a viable potential means for mitigation of risk.
There are many examples of social populations using allogrooming to reduce ectoparasite loads and mitigate the costs of congregating. In a study on various rodent populations, high levels of sociality and allogrooming correlated with a significant decrease in ectoparasites (Bordes et al., 2007). Female African ground squirrels were found to spend a greater amount of time allogrooming than their male counterparts and had significantly reduced ectoparasite loads (Hillegass et al., 2008). In the ant Formica selysi, social grooming decreases the number of fungal spores on contaminated workers and serves as a protective defense to the colony against the spread of fungal disease (Reber et al., 2011). Allogrooming provides benefits that self-grooming cannot; for example, impalas use allogrooming as an effective technique to reduce ticks on the head and neck, which could not be reached by self-grooming (Mooring and Hart, 1995).
The dynamics of allogrooming are themselves complicated and warrant careful consideration of their impact on disease transmission and the resulting selective pressures from ectoparasites that could act on the evolution of these behaviors. Species that live in social groups may be especially vulnerable to both infectious diseases and ectoparasite spread (Altizer et al., 2003a). As discussed above, the risk of ectoparasite spread is a cost of sociality (Bordes et al., 2007) and contact due to allogrooming provides a means for both pathogen and ectoparasite transmission.
However, ectoparasite transmission due to allogrooming differs from pathogen spread in some important ways. Perhaps most importantly, there exists the potential for re-exposure to critically alter disease burden. In other words, ectoparasites can be transmitted to already-infected hosts in ways that can meaningfully alter host health. This repeated transmission, resulting in an increased ectoparasite load, can have a deleterious effect on reproduction and survival (Cheney and Côtí, 2003; Brown and Brown, 2015). Previous modeling efforts by Nowak and May (1994) explore the effects of this so-called “super-infection” of ectoparasites, which allows for infection by a diverse number of ectoparasite species and leads to more complicated dynamics than classical susceptible-infected dynamics. From an evolutionary perspective, repeated super-infection by ectoparasites allows for co-evolution of host resistance and ectoparasite ability to infect the host (Gandon et al., 2002), which is not possible for single infection events. Additionally, as mentioned above, allogrooming may result in self-limiting ectoparasite transmission dynamics where an increase in contact reduces infection transmission. The nature of the infection dynamics and the selective pressures to adopt some social structures above others are likely to depend on the relative impact of grooming as an effective means of reducing ectoparasite load.
In this paper, we build on our previous work (Brooks et al., 2018; Williams et al., 2018) using an agent-based model of social structure emerging from ongoing grooming dynamics to consider the relative robustness of different strategies of social organizational structure with various efficiencies of allogrooming. While this model is hypothetical and abstract, it provides practical and predictive insight into the nature of evolutionary pressures from ectoparasite infections on the structure of allogrooming in social systems. Here, we specifically aim to characterize the effects of social organization on the progression of a ectoparasitic infection. We use a theoretical framework to determine whether or not social organization can provide protective qualities in the face of ectoparasitic outbreak. Finally, we compare the similarities and differences of our results to those found in the current literature relating to social organization and pathogenic infections.
2. Mathematical Formulation and Methods
We generalize a previous simulation framework depicting the dynamics of pathogens on static and dynamic networks (Fefferman and Ng, 2007). Our simulations track, in time, the evolution of social connections and ectoparasite load in a population of N hosts (in our results, N = 50). As indicated previously, allogrooming between neighbors acts to both decrease the ectoparasite load on the groomee and facilitate spread of the ectoparasites through the network. We compare these dynamics under four affiliation strategies for choosing neighbors, either randomly or preferentially according to the betweenness (B), closeness (C), or degree (D) of other hosts. For each simulation, all individuals in the network operate according to the same, pre-prescribed affiliation strategy. In each case, we model the progression of the social dynamics in the absence of ectoparasite infection for the first 150 discrete time steps. Then, ectoparasites are introduced to a single host in the population, and we monitor the spread of ectoparasites in the resulting dynamic network. Below we describe our implementation of both the social network and ectoparasite dynamics, in the order in which they occur in the simulations. For a schematic of our ectoparasite spreading algorithm, see Figure 1. Results presented in this work are derived from implementation of the pseudocode in Appendix A using release 2019a of MATLAB.
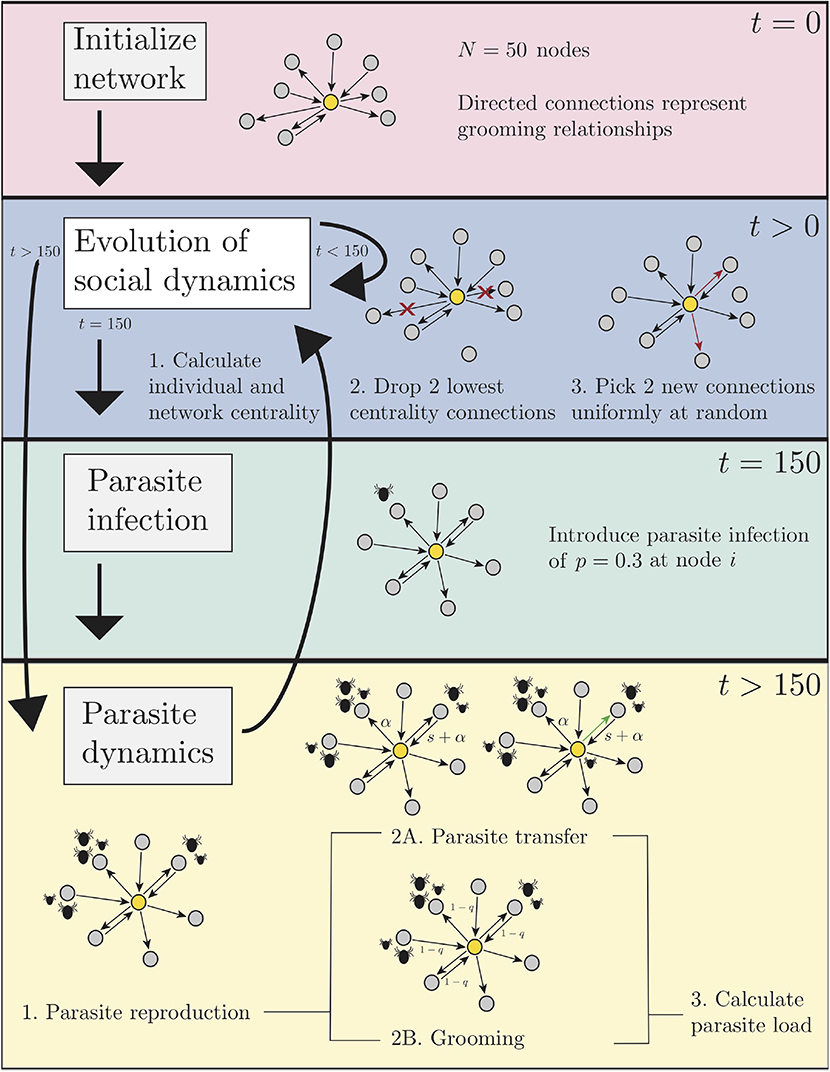
Figure 1. A schematic of our ectoparasite spreading algorithm as described in section 2. The four primary components of the algorithm are network initialization (pink section), network dynamics (blue section), ectoparasite infection (green section), and ectoparasite dynamics (yellow section). Ectoparasite dynamics include reproduction, grooming, and transmission. Pseudocode for the algorithm is available in Appendix A.
2.1. Social Dynamics
We consider populations of N individuals, each of which are connected to five neighbors. The graph G that represents this network consists of the N individuals (nodes) and the 5N edges between them. Edges between individuals are directed, where an edge from node i to node j indicates that individual i grooms individual j. At each step in the simulation, individuals assess the network centralities for each of its neighbors, drop the two neighbors with the lowest centralities, and select two new neighbors with uniform probability from the network (excluding the two neighbors they lost). As in Fefferman and Ng (2007), the choice of which neighbors to drop is random, or it is governed by a rule that depends on a network centrality measure. Each of these measures may be conceptualized at the level of the individual or the network. In accordance with the social evaluation measures first described in Freeman (1978), we describe the chosen centrality measures in more detail below.
1. Degree Centrality: The degree centrality of an individual i is proportional to its in-degree, din(i). The in-degree of node i is the number of individuals in the population grooming individual i. The degree centrality of node i is defined as:
The degree centrality of the graph G is given by:
where D* is the maximum degree of any individual in the network.
2. Closeness Centrality: The closeness of an individual i is a measure of how far node i is from every other node j according to its social connections. In calculating closeness, the distance d(i, j) between two nodes i and j is the shortest path in the undirected graph. We consider the undirected graph when calculating closeness because we want to measure paths that are representative of social connections in either direction (groomer or groomee). If there is no path between nodes i and j, we define the length of the path between them to be N. The closeness of individual i is defined as follows:
The closeness centrality of the graph G is the average individual closeness:
3. Betweenness Centrality: Betweenness measures how essential a node i is to connections between pairs of other nodes. There are several different definitions of betweenness in the literature; we choose the following. For each node i we associate a value, count(i), that counts the number of shortest paths between any two nodes in the network that contains node i. The betweenness centrality of an individual i is given by
and the corresponding betweenness centrality of the graph G is:
Finally, we also consider networks evolving under a random affiliation strategy. At each step in the random model, individuals drop two neighbors and select two new neighbors (excluding the two they just dropped) in a random and unbiased way, i.e., according to a uniform probability distribution on the available N−5 nodes.
We initialize the network at time t = 0 by having each individual select five neighbors at random. The social networks organize according to the assigned affiliation strategy (random, degree, closeness, or betweenness) from time 0 ≤ t ≤ 150. This agrees with previous work (Fefferman and Ng, 2007) and this time-span is chosen to allow the social dynamics to converge to a network with appropriate distributions of centrality measures. Figure 2 shows networks with 50 nodes at t = 150 corresponding to each of the four affiliation strategies. For time 150 < t ≤ 300, the social dynamics continue and ectoparasites are added to the network. We describe the ectoparasite dynamics below.
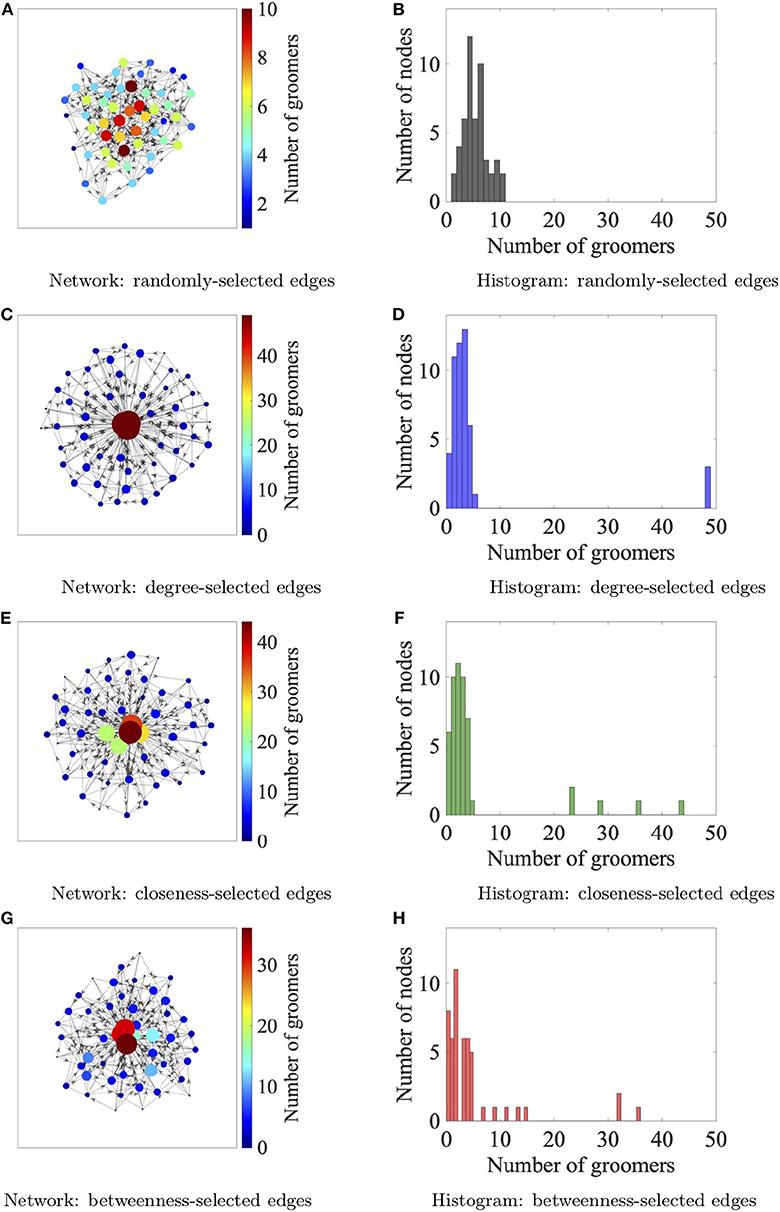
Figure 2. Network configurations after 150 iterations for the four neighbor affiliation strategies, from top to bottom: random (A,B), degree (C,D), closeness (E,F), and betweenness (G,H). One realization of each network are depicted in the left column, where the in-degree of each vertex is reflected in its size as well as color. The distribution of the in-degrees of the nodes in each network, which represents the number of groomers of each node, is shown in the right column. By looking down the right column, we see that the networks organized by the degree affiliation strategy are the most structured in the sense that there are three core nodes having exactly 49 groomers, and the rest (periphery nodes) have <5 groomers on average. The networks structured by closeness and betweenness affiliation strategies have a few nodes with many groomers, while the network structured by random affiliations has no nodes with more than 10 groomers.
2.2. Parasite Dynamics
In addition to the social connections, from step 150 onward, we track the ectoparasite load of each individual i. We denote this quantity by P(i). The ectoparasite load is represented by a real number between 0 and 1, where 0 corresponds to no ectoparasites and 1 corresponds to a maximum level of ectoparasites. At step t = 150, we select an individual uniformly at random from the network to be the host of an initial ectoparasite infection and grant them a ectoparasite load equal to 0.3. That is, the host has a ectoparasite infection of 30% of the maximal level. The ectoparasite populations in the network change according to three processes: reproduction, spread, and grooming.
1. Reproduction: At each time step, we allow a constant increase of ectoparasites by r = 1% (if the individual does not have the maximal ectoparasite load and increase is possible). That is, after reproduction (one time step), the ectoparasite load of individual i is given by
2. Spread by Grooming: Social interactions for grooming act as a way to spread ectoparasites throughout the network. During a grooming event, we consider the possibility of ectoparasites spreading bi-directionally, either from groomer to groomee or groomee to groomer. Again in keeping with Fefferman and Ng (2007), we assume that the probability of the spread of ectoparasites from individual i, while it either grooms or is groomed by its neighbors, is given by the ectoparasite load of i. That is, if there is an edge from i to j or an edge from j to i, then
If there is a bi-directional interaction, i.e., host i grooms host j and host j grooms host i, we increase the probability of transfer of ectoparasites by a fixed value α = 0.15. That is, in the case of bi-directional grooming both probabilities are updated to be the following
Similarly, through this same edge, the probability that host i gains ectoparasites from host j is
The probability that ectoparasites are transferred to i from any of its neighbors is considered to be independent. However, in keeping with Fefferman and Ng (2007), if ectoparasites are transferred to host i, the amount transferred to a host is taken to be a fraction of the average ectoparasite level of all the host's neighbors. In this case, we used 10% of the average ectoparasite load of all the neighbors. Hence, the potential increase in ectoparasite load due to transfer is
where ki is the number of groomers of node i and n is the number of groomees.
We also note this does not lower the ectoparasite load of any neighbor because transmitted ectoparasites are meant to capture the questing behavior of ectoparasitic offspring. We note that this assumption is easy to relax in future work.
3. Ectoparasite Reduction by Grooming: We assume that each groomer reduces the ectoparasite level of a groomee by a fixed fraction g that we refer to as the grooming efficiency. As such, after a single grooming, the ectoparasite level of host i becomes P(i)(1 − g). Since groomers act independently, if host i has ki groomers, the ectoparasite load of the host after grooming is
Finally, because we have a maximal ectoparasite load of m = 1, at the end of each step in the simulation if the ectoparasite load of an individual exceeds 1, we set it to 1.
2.3. Parameters
We construct (Figure 1) and parameterize (Table 1) our system to capture a dynamic in which adult ectoparasites are expected to remain resident on a host, but their offspring are expected to migrate to new hosts via the host-to-host contacts provided by the contact associated with allogrooming. We assume a net ectoparasite growth rate per time step (in the absence of grooming) of r = 0.01. At each time step, some fraction s of the juvenile ectoparasites on connected hosts can move from one to the other. In this study, we assume that any juvenile ectoparasite who does not successfully find a new host dies, and that 100% of the net juvenile ectoparasites are transmitted via contact, i.e., s = 1. To incorporate the increased probability of transmission associated with the increased closeness from mutual allogrooming (relative to unidirectional allogrooming), we define α = 0.15 as an increased factor for bidirectional spread of ectoparasitic infection.
3. Results
We begin by considering network evolution dynamics independent of ectoparasitic infection. We can gain some intuition about the results from Figure 2, which shows the degree distribution over one realization of a 50-node network for each of the different affiliation strategies. For this discussion, the critical degree is the in-degree, i.e., the number of individuals who are groomers of a specific node, which we denote by ki (sometimes dropping the i when it is unnecessary). For the random strategy, the expected value of ki is 5, while for the degree strategy, the expected value of ki is 2 for the periphery nodes, and ki = 49 for the three core nodes. The networks that organize with either betweenness or closeness affiliation strategies both exhibit a more widely-spread distribution of ki values with more nodes having 2 < ki < 49.
As a baseline for ectoparasite transmission dynamics, in the absence of allogrooming we find that the ectoparasite outbreak successfully saturates the host population, regardless of the considered social structures (Figure 5A). Early in the progression of the epidemic toward saturation (when total population-level ectoparasite burden is still small), the random affiliation strategy is actually protective, delaying the growth of the ectoparasite epidemic. When compared to the random affiliation strategy, the remaining strategies (degree, closeness, betweenness) lead to increased disease burden early on. However, later in the epidemic, the degree strategy leads to saturation of parasite burden along the same time-scale as the random affiliation strategy. Once ongoing ectoparasite transmission is widespread, the strategies switch efficacy: populations affiliating by betweenness and closeness delay saturation of ectoparasite burden relative to either random or degree (see Figures 3, 5).
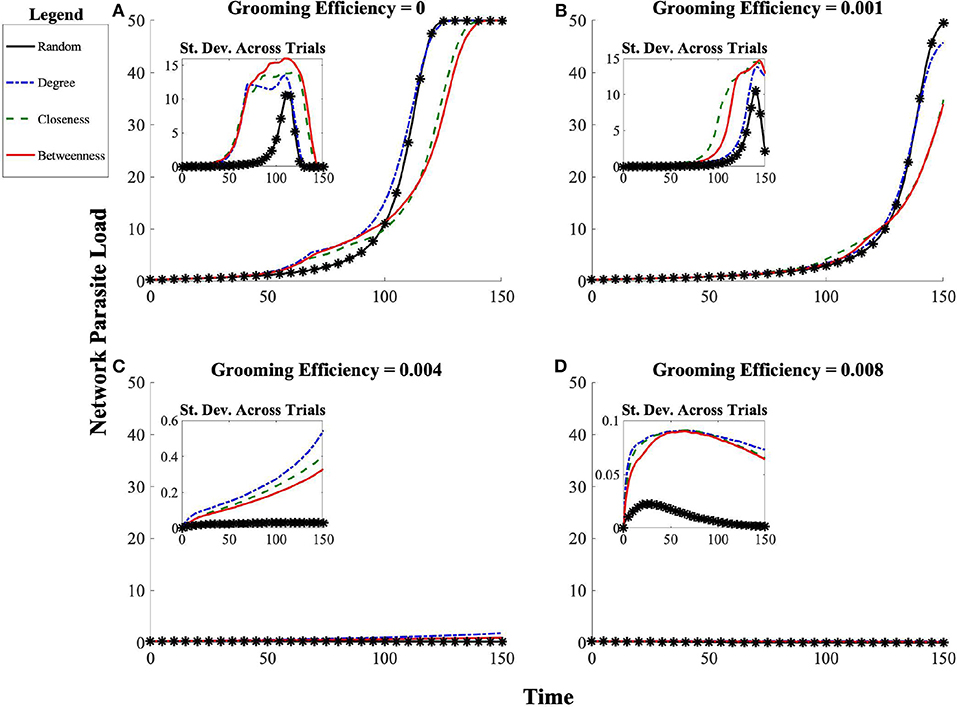
Figure 3. Progression of network ectoparasite load over time for each social affiliation strategy (random, betweenness, closeness, and degree) across grooming efficiencies (A) g = 0, (B) g = 0.001, (C) g = 0.004, (D) g = 0.008. The initial introduction of ectoparasites to the network occurs at t = 0. There is substantial fluctuation in ectoparasite burden early on in the time course of the epidemics. We expect and see greater consistency in the trajectory from the point at which most individuals have sustained a moderate ectoparasite load until total population saturation. The standard deviation across 100 simulated trials is shown in the inset. Note that even in cases of maximal outbreak (g = 0 and g = 0.001), social organization has an impact on the timing of the outbreak.
Of course, there are two potential pathways for a population to proceed to ectoparasite saturation following introduction into the community. Saturation can occur either by ongoing transmission, where each individual's ectoparasite load increases primarily due to repeated delivery of new ectoparasites from others, or by the ectoparasite population growing to saturation on each individual host following only few instances (or even just a single instance) of the introduction of (potentially few) ectoparasites to the host via delivery from others. Since grooming behavior both exposes individuals to each other (offering potential routes for transmission) and reduces individual ectoparasite burden for the individual being groomed (when grooming efficacy is not zero), another critical impact of social organization may be to shift the relative mode of population-level ectoparasitic burden between ongoing transmission and single-host ectoparasitic growth. An inherent property of the model dictates that there will be fewer opportunities for successful transmission as more and more individuals in the population hit an individual maximal sustainable ectoparasite load. Hence, we expect the number of transmissions to slow as population-level saturation is approached. Therefore, we focus on the number of instances of ectoparasite transmission between individuals before the population approaches ectoparasite saturation. In considering the results from this perspective, when grooming is completely ineffective at reducing individual ectoparasite burden, we find that populations employing the random and degree affiliation strategies have a larger number of transmissions before the population begins to saturate than do the populations employing either betweenness or closeness affiliation strategies (see Figure 4).
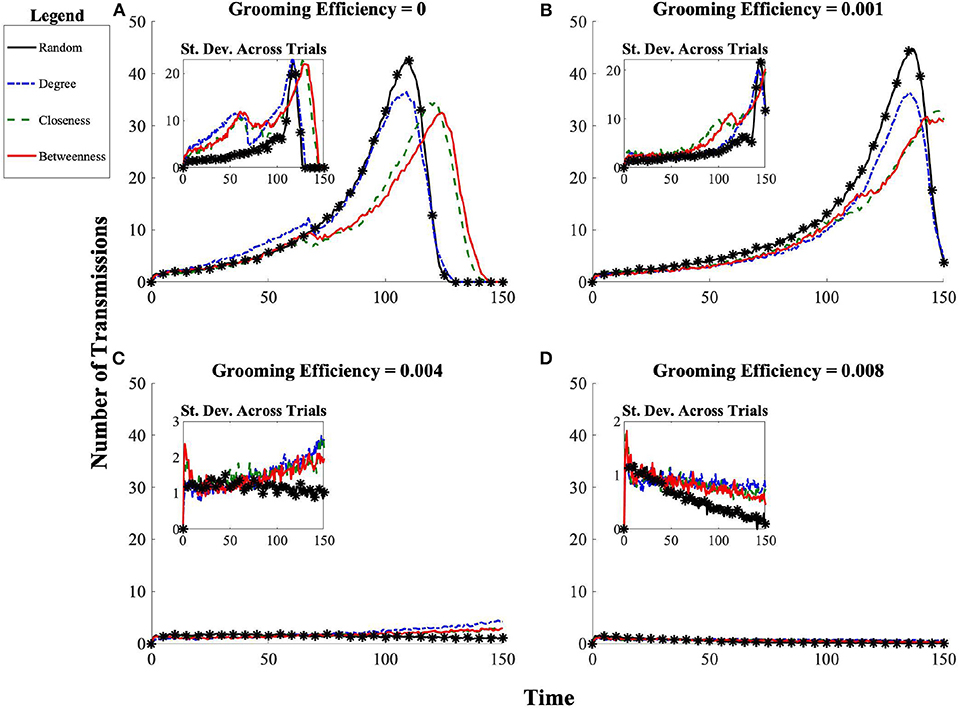
Figure 4. Progression of number of ectoparasite transmission events over time for each affiliation strategy (random, betweenness, closeness, and degree) across grooming efficiencies (A) g = 0, (B) g = 0.001, (C) g = 0.004, (D) g = 0.008. The initial introduction of ectoparasites to the network occurs at t = 0. The standard deviation across 100 simulated trials is shown in the inset. In the case of maximal outbreak (top panels), the number of transmissions per time unit increases until each individual has reached its maximal ectoparasite load and ectoparasites can no longer be transmitted, at which point the transmission rate drops to zero.
When instead we consider cases in which grooming has some benefit by reduction of ectoparasite load to those being groomed, we see that grooming benefits do have the potential to alter population-level outcomes of ectoparasite transmission and overall burden. At low grooming efficiency g = 0.001, we see that while populations employing either the closeness or betweenness affiliation strategies are still more protective, the magnitude of impact is less dependent on when in the progression of the epidemic dynamics we consider the state of the population (see Figure 4B). Populations employing the degree affiliation strategy are slightly more protected than those in populations using the random affiliation strategy. Across all social structures considered, all populations still reach ectoparasitic saturation, though more slowly than in the absence of effective allogrooming (see Figure 5B).
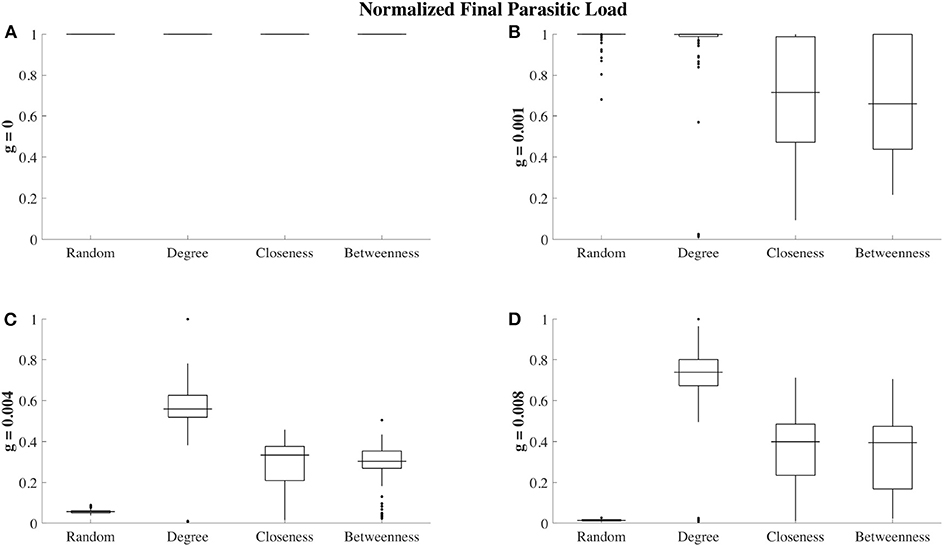
Figure 5. Ectoparasite loads at t = 300 (150 steps after ectoparasite introduction) for different grooming efficiencies and social affiliation strategies. Each box plot shows ectoparasite load over 100 trials, where ectoparasite load has been re-scaled between 0 (no ectoparasites on any node) and 1 (maximum infestation observed for a given grooming efficiency). In the absence of grooming (g = 0, A), all 4 of the social affiliation strategies result in maximal ectoparasite load in all trials. For low grooming efficiencies (g = 0.001, B), closeness and betweenness affiliation strategies are more effective at reducing ectoparasite load. When grooming efficiency is increased to g = 0.004 (C), the random affiliation strategy is most protective, followed by closeness and betweenness. The degree affiliation strategy is the least protective against ectoparasite infection load. We also observe this qualitative behavior when g = 0.008 (D).
At a grooming efficiency of g = 0.004, we discover a threshold behavior in the model. At this efficiency, grooming is capable of successfully controlling ectoparasite outbreaks, but it strongly depends on the affiliation strategy employed (Figures 4C, 5C). The population employing the random affiliation strategy is the only one capable of extinguishing the ectoparasitic outbreak, whereas in populations employing any non-random strategy, there is (very gradual) increase in ectoparasitic burden over time, which will still eventually lead to saturation of infection in the population. Exploring an even more efficient level of allogrooming (g = 0.008), all populations are capable of controlling ectoparasitic outbreaks (see Figures 4D, 5D). In each of these cases, we consider standard deviation (inset panels in Figure 4) to clarify whether outcomes at average success in ectoparasitic outbreak control rely more on the existence of a “typical” behavior that is representative of any expected ectoparasitic outbreak, or instead rely more on the arithmetic average of vastly different outcomes.
Finally, we consider the effects of social organization on the relationship between ectoparasite load and the total number of ectoparasite transmission events (total transmission events shown in Figure 6). Here, we aim to gain insight into whether the ectoparasitic load is primarily due to ectoparasite reproduction as opposed to new ectoparasite transmissions gained via social grooming. Here, we consider the network at t = 260 (110 time steps after parasite introduction). This time point was chosen specifically when considering the case with no grooming, g = 0 (Figure 3A). We chose a time point that was prior to network saturation but after the point at which betweenness and closeness strategies show themselves to be protective. For each grooming efficiency, we consider the correlation between these two quantities. High correlation between these quantities indicates that the increase in ectoparasite load is due to transmissions as opposed to ectoparasite reproduction. Figure 7 highlights the results of this analysis. For networks with random, betweenness, and closeness affiliation strategies, this correlation is high for g = 0 and g = 0.001 and low for mid-to-high grooming efficiencies. In the case of a social network organized using the degree affiliation strategy, we see that the correlation remains high across all grooming efficiencies. We interpret this to indicate that with little or no grooming, ectoparasite dynamics are dominated by transmission dynamics between individuals in the network. For networks with random, betweenness, and closeness affiliation strategies, this effect is not as strong with higher grooming efficiencies.
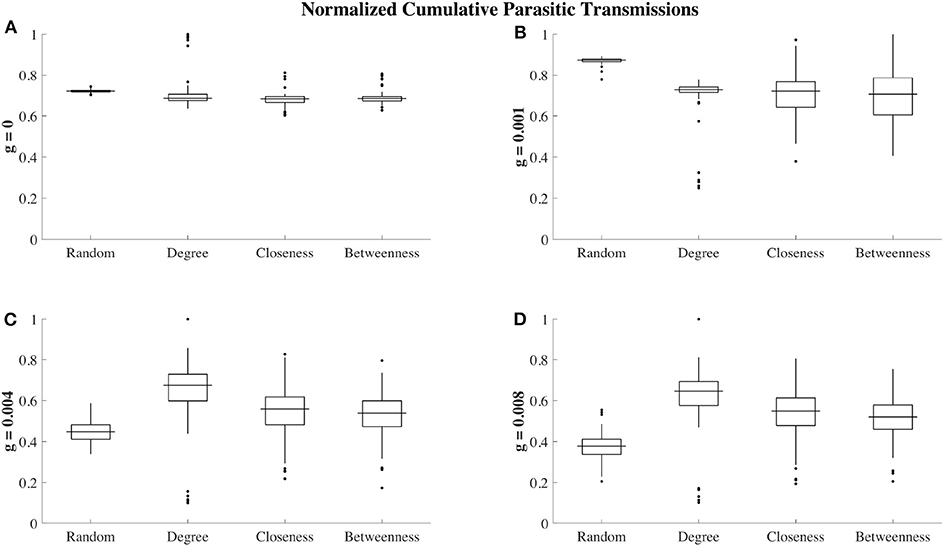
Figure 6. Cumulative number of ectoparasite transmissions over t = 300 steps (150 time-steps after ectoparasite introduction) for different grooming efficiencies and social affiliation strategies. Each box plot shows cumulative transmissions over 100 trials, where transmissions have been re-scaled between 0 (no transmissions occurred) and 1 (maximum number of transmissions observed for a given grooming efficiency). In the absence of grooming (g = 0, A), all 4 of the social affiliation strategies result in similar transmission levels in all trials, although there are outlier trials with large numbers of transmissions with the degree affiliation strategy. For low grooming efficiencies (g = 0.001, B), the most transmissions are instead observed for the random affiliation strategy. When grooming efficiency is increased to g = 0.004 (C), the random affiliation strategy then shows the fewest median number of transmissions, followed by closeness and betweenness. The degree affiliation strategy has the highest median number of transmissions, although there is a large spread and in some trials there are a very low number of transmissions. We also observe this qualitative behavior when g = 0.008 (D).
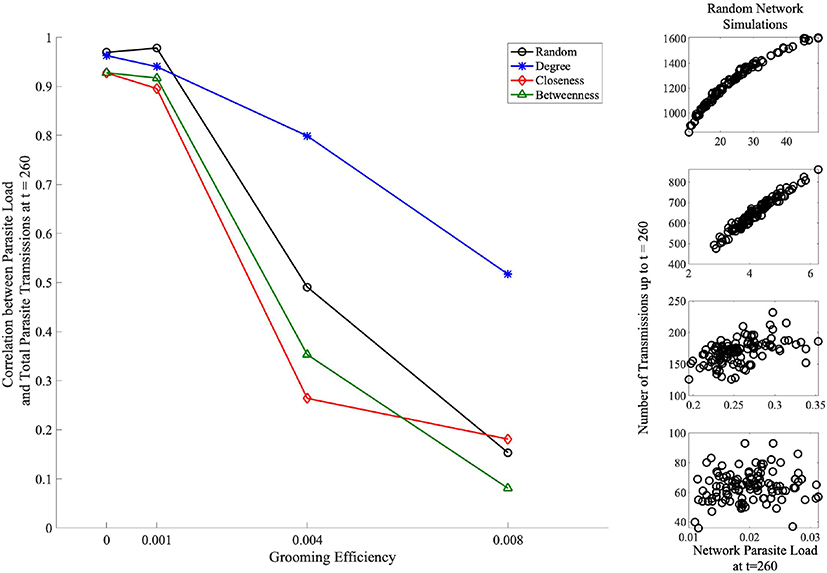
Figure 7. Correlation between network ectoparasite load at t = 260 (110 time steps after ectoparasite introduction) and total ectoparasite transmissions across affiliation strategies and grooming efficiencies. The right column shows the ectoparasite load vs. number of transmission data points for the random affiliation strategy for each of the grooming efficiencies, organized from top to bottom: g = 0, g = 0.001, g = 0.004, and g = 0.008. Here, we see the high correlation between these quantities when g = 0 and conversely almost zero correlation between these quantities for g = 0.008. For networks organized with random, betweenness, and closeness affiliation strategies, this correlation is high for g = 0 and g = 0.001 and low for mid-to-high grooming efficiencies (black, green, and red markers/lines). In the network organized using a degree affiliation strategy (blue markers/lines), we see that the correlation remains high across all grooming efficiencies.
4. Discussion
Our results demonstrate that emergent, self-organizing social behaviors can have a profound effect on both the transmission of ectoparasites and their overall burden to a population. This direct impact on an ecological relationship with clear fitness implications highlights the need to expand our discussion of the selective pressures that may have shaped the evolution of social complexity in ways that explicitly consider patterns and dynamics of ectoparasitism (Rigaud et al., 2010; Kappeler et al., 2015).
Intriguingly, our models demonstrate that patterns that emerge as a result of individual's adopting a degree-based affiliation strategy [a social phenotype seen in some allogrooming species where dominance and allogrooming are correlated (Kutsukake and Clutton-Brock, 2006)], is not an effective social organization for combating population-level ectoparasitic burden. This supports the idea that social grooming is likely to play a greater role in social bonding than it does at mitigating ectoparasitic infection risk. In fact, when grooming is highly efficient at removing ectoparasites from an individual, we see that the random affiliation strategy (when individuals provide indiscriminate allogrooming) confers a greater population-level protection against ectoparasitism. Even when grooming is inefficient at removing ectoparasites, the random affiliation strategy does not incur any substantial penalty in ultimate burden relative to degree affiliation. This clearly suggests that allogrooming, despite its seeming focus on removal of ectoparasites as a targeted action, may have to overcome a fitness penalty from ectoparasitic infection to confer ultimate fitness benefits from social bonding.
Of course, this argument focuses on the level of the population. It may equally be the case that the emergent protection of social structures associated with dominance hierarchies are concentrated in particular, dominant individuals (Duboscq et al., 2016), even at the expense of the broader population. In this case, allogrooming could actually constitute a “tragedy of the commons” (Hardin, 1968) in which all individuals vie to obtain the relative fitness benefits achieved only by a few at the top, and in doing so, decrease their fitness relative to choosing not to participate in structured algorithms to determine patterns in allogrooming. Further work to analyze these individual-level benefits is already underway (work in preparation). Alternatively, it may simply be that ectoparasitic infection has played so little role in the overall fitness of a population that the impact of even strongly-directed selective pressures have not been the driving factors in shaping the evolution of social behavior for allogrooming species. It is not unlikely that ectoparasites have exerted only one facet of the diversity of pressures faced by emerging sociality, thus it will also be important to consider under what types of selective pressures there might have been convergence in the direction of selection, and instead when there might have been conflicting pressures.
Of the potential selective pressures on social organization, the most natural comparator for ectoparasitic infection is, of course, pathogenic infection. Similar investigations exploring the differential fitness of self-organizing social strategies as a result of emergent robustness to pathogen transmission have been published (Altizer et al., 2003b; Fefferman and Ng, 2007; Williams et al., 2018). There are, however, some critical differences in the structure of these studies that makes their direct comparison challenging. Most basically, the pathogen studies followed standard epidemiological modeling practice of considering the disease state of an individual to be without magnitude (i.e., either infected or not, rather than considering “how” infected an individual might be, and therefore also having no impact on the probability of transmission of infection to others). As a result, there was also no potential for infected individuals to be the recipients of novel infection transmission (i.e., even considering the number of successful transmissions of infection reflected a subtly different phenomenon). Individuals were assumed to recover after a set period of time, reflecting immunological progression of a non-lethal infection (Fefferman and Ng, 2007), and only after that recovery were they able to be re-infected (Hethcote, 2000). Naturally, this dynamic also obviated the concept of saturation of infection in a population—while the disease could die out, any one instance of infection progressed over time to recovery without immune protection, rather than to an individual-level maximal disease burden. Lastly, of course, while social contact did still provide the mechanism by which exposure to infection occurred, no action (i.e., allogrooming) taken by either social partner was considered able to reduce the burden of infection in any way (Hethcote, 2000). Still, despite these fundamental differences, it is interesting to explore the qualitative comparison of protection afforded a population exhibiting the same self-organizing social strategies whether under threat of pathogens or ectoparasites. In comparing ectoparasitic to pathogenic infections, while the general conclusion of social organization providing protective qualities for the social unit, which social organizational strategy should be chosen differs depending on the type of threat. For pathogens, at low transmission rates, a closeness or degree affiliation strategy provides maximal protection (Fefferman and Ng, 2007). The natural comparison amongst ectoparasitic infections is at high grooming efficiencies. In this case, we observe that social organization by degree is the least protective, with closeness being a similarly poor strategy. This yields itself to further investigation related to evolutionary social organizational strategies related to the type of environmental pressures, rather than pathogenic versus ectoparasitic infestations.
While interesting as thought experiments, of course, the most important considerations of our study are not rooted in the specific performance of the self-organizing behaviors considered. Although a number of network measures have been investigated in biological systems (e.g., modularity, clustering, host density, and mating systems) (Altizer et al., 2003b; Nunn et al., 2015), the strategies proposed in the current work are not meant to capture meaningful, real-world behaviors. Instead, they allow us to consider how various self-organizing behaviors that lead to emergent social structures can have been shaped by the selective pressures from ectoparasitic threats. In this light, it becomes clear that our most important insight is that ectoparasitic infection can have acted on the fitness of social behaviors differently when selecting for protection from “growth” vs. protection from “transmission.” From this perspective, it becomes clear how the random affiliation strategy can exhibit the greatest number of transmissions of ectoparasitic infection when the efficacy of allogrooming is low: the ongoing re-wiring of the contact network allowed for the greatest number of opportunities to transmit additional ectoparasites to individuals who had not yet reached maximum ectoparasitic burden, while more organized re-wiring rapidly centralized the contacts such that the average contact was with an individual who had already hit saturation (by processes of both re-infection and ongoing growth of the ectoparasite population on the individual after introduction).
Another fundamental insight from these models is that demographic rates can play a critical, synergistic role in modulating how these self-organizing strategies perform under ectoparasite threat. If the epidemic spread of the ectoparasite is slow relative to the demographic turn-over of the population, this may shift the impact of selection toward limiting growth on individuals after exposure, rather than on limiting the possibility for novel exposure/transmission itself. Conversely, if an epidemic is likely to spread rapidly, within one generation, then social structures that serve to interrupt transmission to new individuals should be favored. This insight may have profound implications for the vulnerability of species to invasive ectoparasites, even in cases when there are already similar established ectoparasitic infections: combating established and endemic ectoparasitic risks requires a fundamentally different social structure than preventing the spread of a novel invasive threat (Rigaud et al., 2010; Kappeler et al., 2015). It may be that exactly those populations who have experienced intense selection to mitigate ectoparasitic growth on each host (e.g., in populations frequent environmental re-introduction for the average host), will be most susceptible to the rapid spread of a single point introduction of a novel invader.
5. Conclusion
We have here presented a model demonstrating the possible influence of parasite transmission dynamics on the evolution of social behavior and shown that these dynamics could have had an influence on the evolutionary success of social systems. While not likely to be the only (or even dominant) selective pressure on evolution of social behavior, explicit consideration of the factors involved reveals how nuanced social evolution must be to combat even single threats. Our studies demonstrate the interdependence of impacts from emergent, self-organizing social structure, spread of novel introduction of ectoparasites through a host population, and allogrooming-based control of endemic ectoparasitic growth.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
HB, MH, CP, NF, AR, SS, NW, and SW contributed to the editing, drafting, and the ideas contained within the manuscript. HB, NF, SS, and SW contributed to the model development, with NF, SS, and SW focused on the model parameterization. SS focused on the implementation of the model and SW analyzing the model output. Figures were generated by HB, AR, and SW.
Funding
This material was based upon work supported by the National Science Foundation under Grant No. DMS-1440140, and the National Security Agency under Grant No. H98230-18-1-0144 while several of the authors were in residence at the Mathematical Sciences Research Institute in Berkeley, California and later at the National Institute for Mathematical Biological Synthesis–a synthesis center sponsored by the National Science Foundation through award DBI-1300426 with additional support from The University of Tennessee, Knoxville.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
These authors would like to express their thanks to MSRI and NIMBioS for their kind hospitality.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.00054/full#supplementary-material
References
Altizer, S., Nunn, C. L., Thrall, P. H., Gittleman, J. L., Antonovics, J., Cunningham, A. A., et al. (2003a). Social organization and parasite risk in mammals: integrating theory and empirical studies. Annu. Rev. Ecol. Evol. Syst. 34, 517–547. doi: 10.1146/annurev.ecolsys.34.030102.151725
Altizer, S., Nunn, C. L., Thrall, P. H., Gittleman, J. L., Antonovics, J., Cunningham, A. A., et al. (2003b). Social organization and parasite risk in mammals: integrating theory and empirical studies. Annu. Rev. Ecol. Evol. Syst. 34, 517–547.
Bansal, S., Grenfell, B. T., and Meyers, L. A. (2007). When individual behaviour matters: homogeneous and network models in epidemiology. J. R. Soc. Interface 4, 879–891. doi: 10.1098/rsif.2007.1100
Bansal, S., Read, J., Pourbohloul, B., and Meyers, L. A. (2010). The dynamic nature of contact networks in infectious disease epidemiology. J. Biol. Dyn. 4, 478–489. doi: 10.1080/17513758.2010.503376
Bonds, M. H., Keenan, D. D., Leidner, A. J., and Rohani, P. (2005). Higher disease prevalence can induce greater sociality: a game theoretic coevolutionary model. Evolution 59, 1859–1866. doi: 10.1111/j.0014-3820.2005.tb01056.x
Bordes, F., Blumstein, D. T., and Morand, S. (2007). Rodent sociality and parasite diversity. Biol. Lett. 3, 692–694. doi: 10.1098/rsbl.2007.0393
Börger, L., Dalziel, B. D., and Fryxell, J. M. (2008). Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecol. Lett. 11, 637–650. doi: 10.1111/j.1461-0248.2008.01182.x
Brooks, H. Z., Hohn, M. E., Price, C. R., Radunskaya, A. E., Sindi, S. S., Williams, N. D., et al. (2018). “Mathematical analysis of the impact of social structure on ectoparasite load in allogrooming populations,” in Understanding Complex Biological Systems with Mathematics. Association for Women in Mathematics Series, Vol. 14, eds A. Radunskaya, R. Segal, and B. Shtylla (Cham: Springer), 47–61.
Brown, C. R., and Brown, M. B. (2015). Ectoparasitism shortens the breeding season in a colonial bird. R. Soc. Open Sci. 2:140508. doi: 10.1098/rsos.140508
Cheney, K. L., and Côté, I. M. (2003). The ultimate effect of being cleaned: does ectoparasite removal have reproductive consequences for damselfish clients? Behav. Ecol. 14, 892–896. doi: 10.1093/beheco/arg079
Craft, M. E. (2015). Infectious disease transmission and contact networks in wildlife and livestock. Philos. Trans. R. Soc. B Biol. Sci. 370:20140107. doi: 10.1098/rstb.2014.0107
Cremer, S., Armitage, S. A., and Schmid-Hempel, P. (2007). Social immunity. Curr. Biol. 17, R693–R702. doi: 10.1016/j.cub.2007.06.008
Duboscq, J., Romano, V., Sueur, C., and MacIntosh, A. J. (2016). Network centrality and seasonality interact to predict lice load in a social primate. Sci. Rep. 6:22095. doi: 10.1038/srep22095
Fefferman, N. H., and Ng, K. L. (2007). How disease models in static networks can fail to approximate disease in dynamic networks. Phys. Rev. E 76:031919. doi: 10.1103/PhysRevE.76.031919
Freeman, L. C. (1978). Centrality in social networks conceptual clarification. Soc. Netw. 1, 215–239. doi: 10.1016/0378-8733(78)90021-7
Gandon, S., van Baalen, M., and Jansen, V. A. (2002). The evolution of parasite virulence, superinfection, and host resistance. Am. Nat. 159, 658–669. doi: 10.1086/339993
Hardin, G. (1968). The tragedy of the commons. Science 162, 1243–1248. doi: 10.1126/science.162.3859.1243
Hethcote, H. W. (2000). The mathematics of infectious diseases. SIAM Rev. 42, 599–653. doi: 10.1137/S0036144500371907
Hillegass, M. A., Waterman, J. M., and Roth, J. D. (2008). The influence of sex and sociality on parasite loads in an African ground squirrel. Behav. Ecol. 19, 1006–1011. doi: 10.1093/beheco/arn070
Hochberg, M. E. (1991). Viruses as costs to gregarious feeding behaviour in the lepidoptera. Oikos 61, 291–296. doi: 10.2307/3545236
Hock, K., and Fefferman, N. H. (2012). Social organization patterns can lower disease risk without associated disease avoidance or immunity. Ecol. Complex. 12, 34–42. doi: 10.1016/j.ecocom.2012.09.003
Kappeler, P. M., Cremer, S., and Nunn, C. L. (2015). Sociality and health: impacts of sociality on disease susceptibility and transmission in animal and human societies. Philos. Trans. R. Soc. B Biol. Sci. 370:20140116. doi: 10.1098/rstb.2014.0116
Kutsukake, N., and Clutton-Brock, T. H. (2006). Social functions of allogrooming in cooperatively breeding meerkats. Anim. Behav. 72, 1059–1068. doi: 10.1016/j.anbehav.2006.02.016
Maestripieri, D. (1993). Vigilance costs of allogrooming in macaque mothers. Am. Nat. 141, 744–753. doi: 10.1086/285503
Matheson, M. D., and Bernstein, I. S. (2000). Grooming, social bonding, and agonistic aiding in rhesus monkeys. Am. J. Primatol. 51, 177–186. doi: 10.1002/1098-2345(200007)51:3<177::AID-AJP2>3.0.CO;2-K
McCabe, C. M., Reader, S. M., and Nunn, C. L. (2015). Infectious disease, behavioural flexibility and the evolution of culture in primates. Proc. R. Soc. B Biol. Sci. 282:20140862. doi: 10.1098/rspb.2014.0862
Mooring, M. S., and Hart, B. L. (1995). Costs of allogrooming in impala: distraction from vigilance. Anim. Behav. 49, 1414–1416. doi: 10.1006/anbe.1995.0175
Nowak, M. A., and May, R. M. (1994). Superinfection and the evolution of parasite virulence. Proc. R. Soc. Lond. B 255, 81–89. doi: 10.1098/rspb.1994.0012
Nunn, C. L., Jordán, F., McCabe, C. M., Verdolin, J. L., and Fewell, J. H. (2015). Infectious disease and group size: more than just a numbers game. Philos. Trans. R. Soc. B Biol. Sci. 370:20140111. doi: 10.1098/rstb.2014.0111
Ramanantsalama, R. V., Andrianarimisa, A., Raselimanana, A. P., and Goodman, S. M. (2018). Rates of hematophagous ectoparasite consumption during grooming by an endemic madagascar fruit bat. Parasit. Vectors 11:330. doi: 10.1186/s13071-018-2918-1
Reber, A., Purcell, J., Buechel, S., Buri, P., and Chapuisat, M. (2011). The expression and impact of antifungal grooming in ants. J. Evol. Biol. 24, 954–964. doi: 10.1111/j.1420-9101.2011.02230.x
Rigaud, T., Perrot-Minnot, M.-J., and Brown, M. J. F. (2010). Parasite and host assemblages: embracing the reality will improve our knowledge of parasite transmission and virulence. Proc. R. Soc. B Biol. Sci. 277, 3693–3702. doi: 10.1098/rspb.2010.1163
Rosengaus, R. B., Maxmen, A. B., Coates, L. E., and Traniello, J. F. (1998). Disease resistance: a benefit of sociality in the dampwood termite zootermopsis angusticollis (isoptera: Termopsidae). Behav. Ecol. Sociobiol. 44, 125–134. doi: 10.1007/s002650050523
Russell, Y., and Phelps, S. (2013). How do you measure pleasure? A discussion about intrinsic costs and benefits in primate allogrooming. Biol. Philos. 28, 1005–1020. doi: 10.1007/s10539-013-9372-4
Sah, P., Leu, S. T., Cross, P. C., Hudson, P. J., and Bansal, S. (2017). Unraveling the disease consequences and mechanisms of modular structure in animal social networks. Proc. Natl. Acad. Sci. U.S.A. 114, 4165–4170. doi: 10.1073/pnas.1613616114
Schaller, M. (2011). The behavioural immune system and the psychology of human sociality. Philos. Trans. R. Soc. B Biol. Sci. 366, 3418–3426. doi: 10.1098/rstb.2011.0029
Schino, G., Scucchi, S., Maestripieri, D., and Turillazzi, P. G. (1988). Allogrooming as a tension-reduction mechanism: a behavioral approach. Am. J. Primatol. 16, 43–50. doi: 10.1002/ajp.1350160106
Shutt, K., MacLarnon, A., Heistermann, M., and Semple, S. (2007). Grooming in barbary macaques: better to give than to receive? Biol. Lett. 3, 231–233. doi: 10.1098/rsbl.2007.0052
Williams, N. D., Brooks, H. Z., Hohn, M. E., Price, C. R., Radunskaya, A. E., Sindi, S. S., et al. (2018). “How disease risks can impact the evolution of social behaviors and emergent population organization,” in Understanding Complex Biological Systems with Mathematics. Association for Women in Mathematics Series, Vol. 14, eds A. Radunskaya, R. Segal, and B. Shtylla (Cham: Springer), 31–46.
Keywords: evolutionary sociobiology, hygienic behavior, social grooming, allogrooming network, dynamic social network
Citation: Wilson SN, Sindi SS, Brooks HZ, Hohn ME, Price CR, Radunskaya AE, Williams ND and Fefferman NH (2020) How Emergent Social Patterns in Allogrooming Combat Parasitic Infections. Front. Ecol. Evol. 8:54. doi: 10.3389/fevo.2020.00054
Received: 18 October 2019; Accepted: 19 February 2020;
Published: 31 March 2020.
Edited by:
Andrew James Jonathan MacIntosh, Kyoto University, JapanReviewed by:
Pratha Sah, Yale University, United StatesValeria Romano, University of Alicante, Spain
Copyright © 2020 Wilson, Sindi, Brooks, Hohn, Price, Radunskaya, Williams and Fefferman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shelby N. Wilson, c253aWxzb25AdW1kLmVkdQ==
 Shelby N. Wilson
Shelby N. Wilson Suzanne S. Sindi
Suzanne S. Sindi Heather Z. Brooks
Heather Z. Brooks Maryann E. Hohn
Maryann E. Hohn Candice R. Price
Candice R. Price Ami E. Radunskaya
Ami E. Radunskaya Nakeya D. Williams
Nakeya D. Williams Nina H. Fefferman
Nina H. Fefferman