
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Ecol. Evol., 30 January 2020
Sec. Behavioral and Evolutionary Ecology
Volume 8 - 2020 | https://doi.org/10.3389/fevo.2020.00007
Cooperation, ubiquitous in nature, is difficult to explain from an evolutionary perspective. Many modeling studies strive to resolve this challenge, but their simplifying assumptions on population and interaction structure are rarely met in ecological settings. Here we use a modeling approach that includes more ecological detail to investigate evolution of cooperation in spatially self-organized mussel beds. Mussels cooperate with each other through aggregative movement and attachment using byssal threads. These cooperative behaviors shape the spatial structure of the mussel bed, which can range from scattered distributions to labyrinth-like patterns and dense mussel clumps. The spatial pattern in turn impacts an individual’s fitness at two levels: (i) proper attachment to neighboring individuals decreases predation risk, and (ii) attachment to a sufficiently large group prevents dislodgement by wave stress. Without this second level of selection, our simulations do typically not result in evolutionary attractors that lead to the labyrinth-like spatial patterns that are characteristic for natural mussel beds. Yet, when group-level selection is included, labyrinth-like patterns emerge under a wide range of conditions. Our model demonstrates that multiple selection factors working at different spatial scales – predation of individuals and dislodgement of entire mussel clumps – combinedly determine evolution of cooperative traits in mussels and thereby result in emergence of the labyrinth-like spatial patterns that we observe in natural mussel beds.
Fighting the elements is a challenging task that is frequently best achieved by cooperation. Under harsh environmental conditions, many organisms join forces to reduce predation risk, locate resources, or build shelters. Although cooperative behavior is widespread throughout nature, cooperation can potentially be exploited by free-riders that benefit but do not contribute (e.g., West et al., 2007; Van Dyken and Wade, 2012). This “paradox of cooperation” has fascinated theoreticians and empirical biologists alike, making the evolutionary emergence and stability of cooperation one of the most intensely studied questions in biology (Lehmann and Keller, 2006; West et al., 2007, 2008).
Theoretical and empirical studies demonstrate that the evolution of cooperation has many interesting facets, and that a multitude of factors (such as spatial structure, relatedness, reciprocity, and punishment) are of potential relevance for resolving the paradox of cooperation (Dugatkin, 1997; Nowak and Sigmund, 2005; Foster and Wenseleers, 2006; Lion and van Baalen, 2008; Clutton-Brock, 2009; Archetti et al., 2011; Bourke, 2011; Raihani et al., 2012). Adding to the list, we demonstrate that multi-scale selection – selection occurring at different spatial scales – can lead to cooperative efforts in self-organized mussel beds, which results in the emergence of labyrinth-like patterns.
We developed and analyzed a mechanistic model for investigating cooperation between mussels in self-organized mussel beds. Mussels partake in a social dilemma similar to a Snowdrift game (Doebeli and Hauert, 2005); they benefit from their own as well as other’s aggregative movements and byssal attachments (De Jager et al., 2017). Mussels live in a harsh environment where they compete for food while risking dislodgement by wave stress and predation by birds and other animals (Bertness and Grosholz, 1985; Hunt and Scheibling, 2001, 2002; Van de Koppel et al., 2005). In order to survive, mussels move into aggregations and affix themselves to neighboring conspecifics using byssus threads (a glue-like substance; Maas Geesteranus, 1942). Mussels that are well secured to neighbors are less likely to be predated than conspecifics with fewer attached neighbors. Furthermore, large clumps of attached mussels have a smaller chance to become dislodged by wave stress than smaller clumps. While the individual-level struggle against predation may be considered as by-product mutualism, cooperation between multiple individuals is required to actively decrease the risk of wave stress dislodging entire mussel clumps (Dugatkin et al., 1992).
To understand the evolution of cooperation in mussel beds, we developed an individual-based model (IBM) that considers the joint evolution of several traits, the emergence of spatial structure, and the resulting multi-scale selection in a population with dynamic group structure. In a first step, we simulated within-generation ecological processes using an IBM. In a second step, we determined the two-dimensional selection gradients for the joint evolution of attachment and movement across generations. Based on these selection gradients, we then studied how the evolutionary dynamics of attachment and movement were affected by environmental factors, such as food availability, predation risk, and wave action. We compared simulations with and without predation to those including and excluding the effects of wave action to examine the importance of these different selection factors.
Our model implicitly includes two time scales: a short time scale (within generations) at which behavioral and ecological processes take place; and a longer time scale (across generations) at which the heritable characteristics of a population change due to evolution by natural selection. Within a generation, individuals move and attach to each other, leading to pattern formation, which in turn affects dislodgement risk by predation and wave stress. These short-term processes are explicitly represented in individual-based simulations. The long-term simulations subsequently allow us to estimate the fitness consequences for a spectrum of heritable strategies. These fitness estimates will subsequently be used to predict the outcome of adaptive evolution.
In natural mussel beds, young mussels move around until they have aggregated into a labyrinth-like pattern. Such a pattern may be viewed as an optimal compromise between minimizing predation pressure and wave stress (requiring dense local aggregation) on the one hand and avoidance of dense aggregations to minimize competition (requiring low competitor density at a larger scale) on the other hand (Van de Koppel et al., 2005, 2008). As shown in Van de Koppel et al. (2008), a self-organized labyrinth-like pattern can emerge from the movements of individual mussels that follow the rule to leave their spot if (a) the mussel density in their local “attachment range” (the range where mussels can affix themselves to conspecifics and thereby find protection from predation and wave stress) is too low, or if (b) the mussel density in the larger “competition range” (the range where mussels experience competition for food from others) is too high.
Here, we adopt this model of aggregative movement. Three parameters of this model are kept fixed at values that were estimated from experimental data (Van de Koppel et al., 2008; De Jager et al., 2011): the size of the attachment range (1.1 cm ø), the size of the competition range (3.3 cm ø), and the competition threshold density (0.7 cm–2; determining whether a mussel will stay or leave in order to avoid competition). In contrast, the attachment threshold density τ (determining whether a mussel will stay or leave in order to find a denser cluster of conspecifics) is an evolving parameter in our model. As illustrated in Figure 1, the value of τ strongly affects the spatial distribution of mussels in the mussel bed.
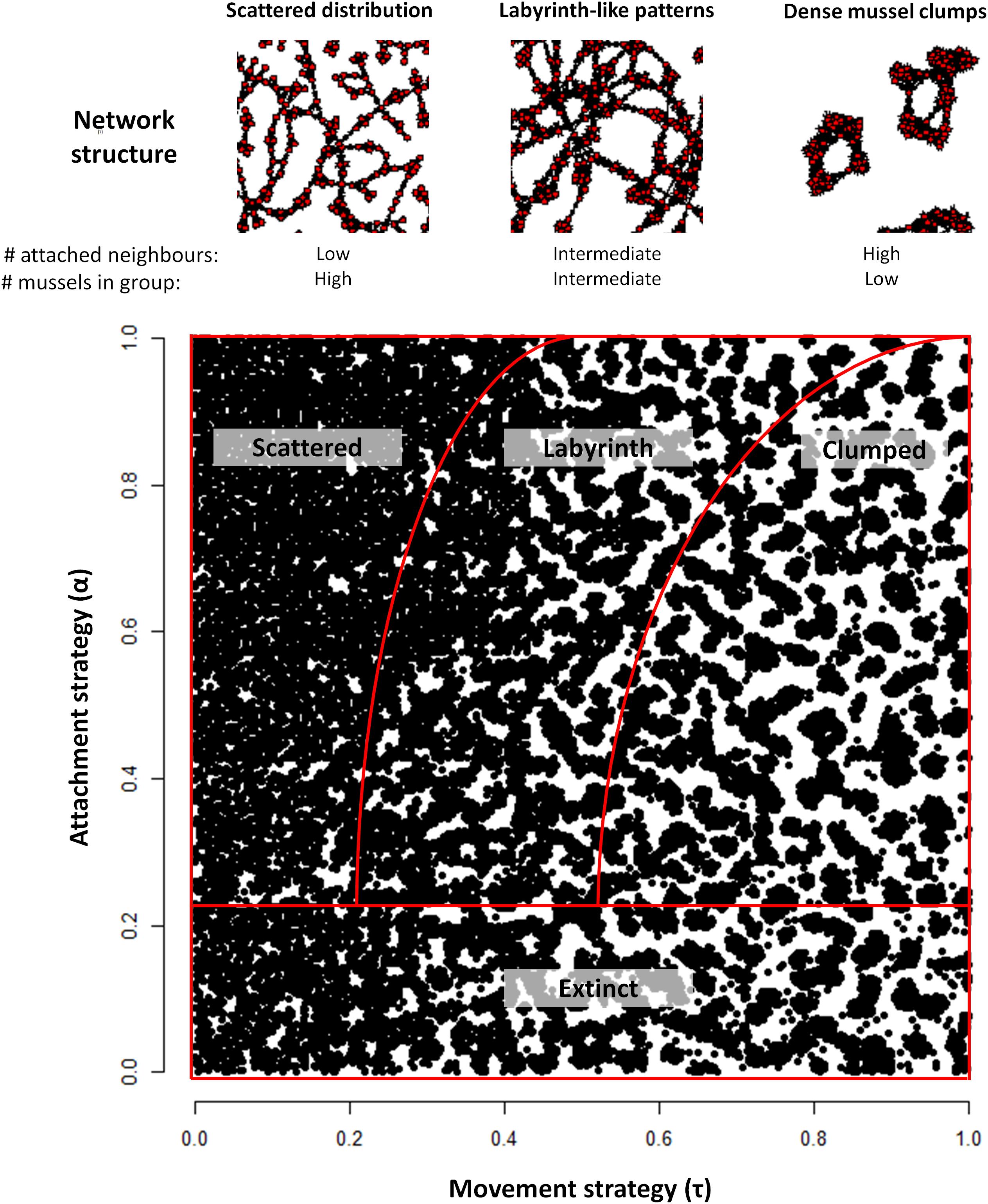
Figure 1. Illustration of the cooperative network (Top) and patterns (Bottom) generated by mussel populations with different combinations of the movement threshold τ and the attachment rate α. In the cooperative networks shown in the top panels, red dots correspond to individual mussels and black arrows indicate byssal attachments. Here, α = 1. In scattered distributions, a low number of direct neighbors is attached to a mussel, while it is part of a large group. In contrast, mussels in dense clumps are attached to many direct neighbors, yet their group size is limited. In labyrinth-like patterns, both group size and number of direct attachments are intermediate, thereby compromising safety against individual-level predation and group-level dislodgement by wave stress. Different spatial patterns emerge, ranging from random distributions, to labyrinths and dense clumps, for different combinations of α and τ. When α < 0.2, the population does not survive under most levels of environmental stress. The bottom panel was created by joining the final mussel distributions of 5⋅5 simulations. As such, it holds a too large number of mussels to clearly show that scattered distributions are indeed scattered. Each black dot represents a single mussel; individual byssal attachments are not illustrated here.
More specifically, our IBM considers 1600 individuals with a cross-section of 1 cm that are initially spread evenly on a 50 × 50 cm surface. Within a generation, there are 500 decision moments, where each individual has to make a movement or an attachment decision. At a decision moment, the “local density” (i.e., the density of mussels within the attachment range of 1.1 cm ø) and the “long-range density” (i.e., the density of mussels within the competition range of 3.3 cm ø) are calculated for each individual. These densities are compared with the competition threshold density (0.7 individuals/cm2) and the attachment threshold density (the heritable parameter τ). If the local density is lower than the attachment threshold density, or if the long-range density is higher than the competition threshold density, the individual moves away in search for a better location. Those individuals that move away make a step in a random direction, where the step length is drawn from a truncated power law distribution, as the movement of solitary mussels can be approximated by a Lévy walk (De Jager et al., 2011). Whenever a moving individual encounters a conspecific, the move ends prematurely (De Jager et al., 2014). With 1600 individuals in our model environment, we simulate a natural mussel density. At higher mussel densities in such a torus-shaped space, modeled mussels cannot generate patterns; the density would remain higher than the competition threshold density and individuals would continuously move to find a less dense location. At lower mussel densities, only small, scattered clumps are generated, as the space between aggregated mussel clusters would be too large to bridge using byssal threads (De Jager et al., 2017).
Mussel beds are regularly threatened by wave stress, currents, and predation. Because dislodged mussels are less efficient filter feeders and are more prone to predation (Hunt and Scheibling, 2001), we assume that they have a lower survival chance than properly affixed individuals. In order to reduce the risk of dislodgement, mussels produce byssus threads to attach themselves to conspecifics. In the model, individuals can attach byssus threads to neighbors in their attachment range (1.1 cm ø). If an individual does not move during a simulation step and if suitable neighbors are present, it attaches itself to a random neighbor with probability α (0 ≤ α ≤ 1). This parameter is a heritable strategy that can be interpreted as the attachment tendency of a mussel (De Jager et al., 2017).
A trade-off exists between movement and attachment: while moving, an individual cannot attach, and attached individuals cannot move away because of their binds. As real mussels are able to remove some of the byssus threads attached to them, the individuals in our model can destroy the attachment in a decision moment and move away in a subsequent one if they are attached with a single byssus thread only. To put some boundaries to our model, each individual can attach a maximum of 50 byssus threads to its neighbors within the 500 time steps of each simulation run. No additional byssus threads are produced once this maximum is reached.
Due to this trade-off, spatial genetic structure might occur in mussel beds consisting of individuals with different attachment or movement strategies (see Supplementary Tables S1, S2). For example, low byssus producing mussels cluster more together than high byssus producing individuals when the value of the movement strategy is low (τ < 0.5), because these low byssus producing mussels are less restricted by potential byssal attachments and can therefore move further into aggregations.
All these actions have their costs and benefits in terms of Darwinian fitness. Moving into a patterned distribution takes energy, but also helps an individual in finding conspecifics to attach to. Consequently, attaching to a neighbor requires the production of a byssus thread, but can improve a mussel’s survival. We assume that fitness corresponds to expected lifetime reproductive success of a semelparous organism, that is, to the product of the probability to survive until reproduction (S) and expected fecundity (F) once reproductive age has been reached. As the number of individuals per generation is fixed at 1600, reproduction is modeled as a weighed stochastic process based on relative fitness. Although mussels are not truly semelparous, mussel seeds are dispersed by the water flow over long distances and are unlikely to settle down in the parental mussel bed, but will establish a new bed elsewhere. Assuming semelparity substantially simplifies the model, while it does not affect the outcomes qualitatively. We further assume that fecundity is reduced by the total costs of movement and the total costs of attachment (see Supplementary Appendix S1 for details), that the probability to survive predation (SP(N)) is positively related to the number N of neighbors an individual is connected with via byssus threads, and that the probability to survive dislodgement risk by wave stress (SW(G)) is positively related to the clump size (G). To be more specific, we assume that SP(N) is a logistic function of N, which is characterized by a single parameter n50 that corresponds to the number of attached neighbors required for a 50% survival probability (see Supplementary Appendix S1 for details). This parameter can be viewed as a measure of predation risk: the higher the risk, the more attachments are necessary to achieve 50% survival. Close attachment to immediate neighbors can protect against predation, if predators have a preference for loosely attached food that can be picked up and eaten at a faster rate.
Attachment to neighbors can, however, have an additional effect. The totality of individuals that are connected by byssus threads forms a network, which – depending on the spatial configuration of the mussels – can be quite large. All the mussels sticking together form a clump, and it is plausible that larger clumps can be less easily dislodged and washed away by the action of waves than smaller clumps. To investigate this hypothesis, we performed a simple field experiment on an intertidal flat near the island of Schiermonnikoog, Netherlands (53°47′ N 6°21′ E). We collected mussels from an existing mussel bed and relocated them to create 80 groups of 1, 3, 10, and 30 mussels. Groups were placed parallel to the shoreline with a minimum distance of 10 cm between groups. Two days after the start of the experiment, we recorded the presence and absence of groups. As shown in Figure 2, there was a clear positive relationship between the size of a group and the probability of finding the group back after 48 h (Chi-square test of independence: χ2 = 14.4, df = 3, p = 0.002). Due to wave stress and strong currents, small groups of mussels are apparently more easily dislodged from the sediment and removed from their original location than larger clumps.
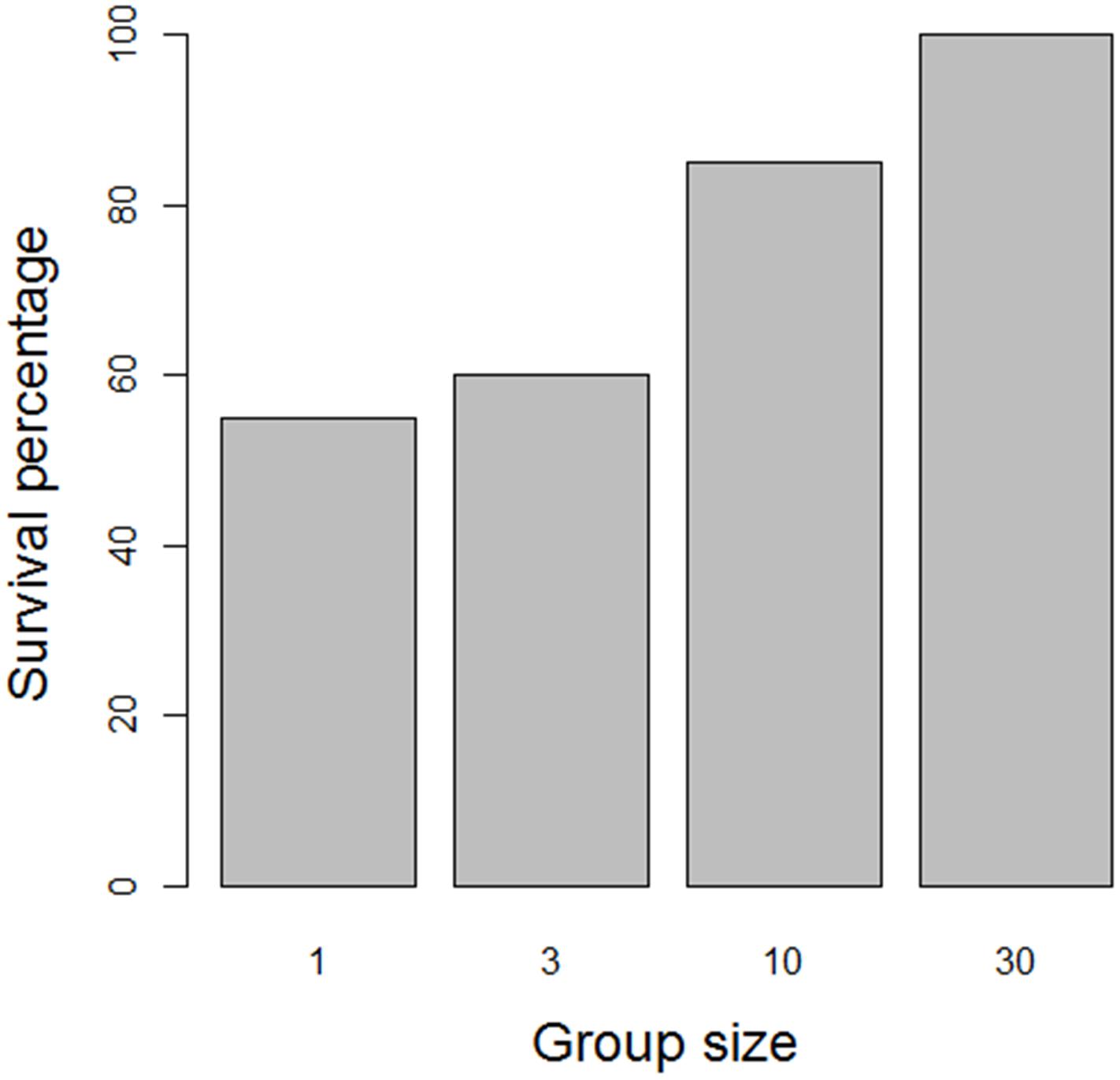
Figure 2. Effect of clump size on the dislodgement of mussel clumps in a field experiment. Small clumps were dislodged significantly more often than large clumps.
Dislodgement of mussel clusters is likely to decrease the survival chance of all mussels within the detached clump. We incorporated this effect by assuming that overall survival has two components: survival of predation SP(N) that depends on the number N of attached neighbors as described above; and survival of dislodgement by wave action SW(G) that is positively related to the size G of the group (clump) to which an individual is attached. A group is specified as the number of mussels that is directly and indirectly linked to the focal individual (including itself). We assume that SW(G) is a logistic function of G. We examine three different scenarios: (i) survival is just given by surviving predation events (S = SP(N)), (ii) survival is affected only by wave action (S = SW(G)), and (iii) survival is given by the geometric mean of surviving predation and wave action (S = SP(N)0.5⋅SW(G)0.5; see Supplementary Appendix S1). The above considerations allow us to calculate in each within-generation simulation a fitness value for each genotype, where genotypes are characterized by the combination of a movement strategy τ and an attachment strategy α. Subsequently, these fitness values can be used for making evolutionary predictions.
To get a picture of the selective forces acting on the two strategies, we need to determine the local vector field of selection gradients in the fitness landscape. To this end, we performed 100 replicate within-generation simulations for all combinations of 21 equidistant values of τ (0 ≤ τ ≤ 1) and 21 equidistant values of α (0 ≤ α ≤ 1) as follows. We simulated mussel bed formation with a population consisting of 1592 residents and 8 mutants. The residents were characterized by a resident movement threshold density τ and resident attachment strategy α, whereas the mutants differed in their strategy from the residents with respect to the movement strategy (τ+ or τ–), the attachment strategy (α+ or α–), or both, resulting in eight possible mutant strategies (i.e., τ–α–, τ–α, τ–α+, τα–, τα+, τ+α–, τ+α, τ+α+). After 500 simulation steps, the moved distance, number of byssal attachments, number of attached neighbors, and group size were recorded for each mutant and a random resident. We determined the relative fitness of the eight mutant strategies. As we assume no genetic covariance between mutations in τ and α, we could obtain the local selection gradient by a linear regression of these fitness values for each resident trait combination (see Supplementary Appendix S2).
Following the selection gradients of the 21⋅21 = 441 different combinations of resident movement strategy and attachment strategy, we explored the locations of joint evolutionary attractors. These joint attractors are points within the two-dimensional trait-space where both τ and α are evolutionary attractors which cannot be destabilized by any upcoming small mutation in the movement strategy and/or the attachment strategy (Leimar, 2009; Brown and Taylor, 2010). We localized these attractors by iterating evolution of the two traits, starting from all simulated trait combinations. As (i) each initial resident trait combination evolves toward one of the joint attractors, (ii) each attracting strategy produces a characteristic self-organized spatial pattern (Figure 1), and (iii) assuming that an original resident population could have had any of the 441 different strategies, we are able to record the probability of evolving strategies that produce labyrinth-like patterns similar to what we observe in nature.
To determine the type of pattern produced by the attracting strategy (i.e., “scattered,” “labyrinth,” or “dense clumps”), we calculated the average ratio between local and long-range density (μd) as well as its variance (σd). We consider a mussel bed “scattered” when the average ratio between local and long-range density is low (μd < 1.3), “labyrinth-like” when this average is high (μd ≥ 1.3) and the average minus the variance is high (μd –σd ≥ 1.05), and “clumped” when μd ≥ 1.3 and μd –σd < 1.05. In comparison to natural mussel beds, we recorded the positions of real mussels in a natural, labyrinth-like mussel bed in the Wadden Sea and found similar results (μd = 1.33 and μd – σd = 1.06). We assumed that the population goes extinct when α ≤ 0.2, as too little attachments are made in these situations for sufficient survival at most environmental stress levels. We have no direct information on where the actual threshold value should lie in natural populations, as it will vary for each bed and even location within a bed depending on environmental settings.
Below, we outline the general outcome of analyses predicting what evolutionary attractor would evolve as a function of the costs associated with movement and attachment. First, we describe the general trends in the relation between evolutionary dynamics predicted by the model and the spatial patterns that are associated with these evolutionary attractors. Second, we focus on the differences in the predictions when predation of individuals or dislodgement of entire clumps by wave action would dominate, and when both risks are present.
Analysis of the model revealed that a variety of qualitatively different evolutionary outcomes are possible under a wide range of conditions. As we discussed earlier, the pattern that is generated in a self-organized mussel bed strongly depends on the movement threshold density and the level of attachment (Figure 1). For low values of the movement threshold density, the population is homogeneously distributed, even more so at high levels of attachment (as attachment prevents movement). At intermediate levels of aggregative movement, labyrinth-like patterns are produced, and high movement threshold densities give rise to dense mussel clumps. Within the range of parameter combinations that we examined, we found four qualitatively different evolutionary outcomes (Table 1 and Figure 3): extinction of the population (when the average fitness is extremely low, Figure 3A), emergence of scattered distributions (Figure 3B), evolution of labyrinth-producing traits (Figure 3C), and formation of dense clumps (Figure 3D).
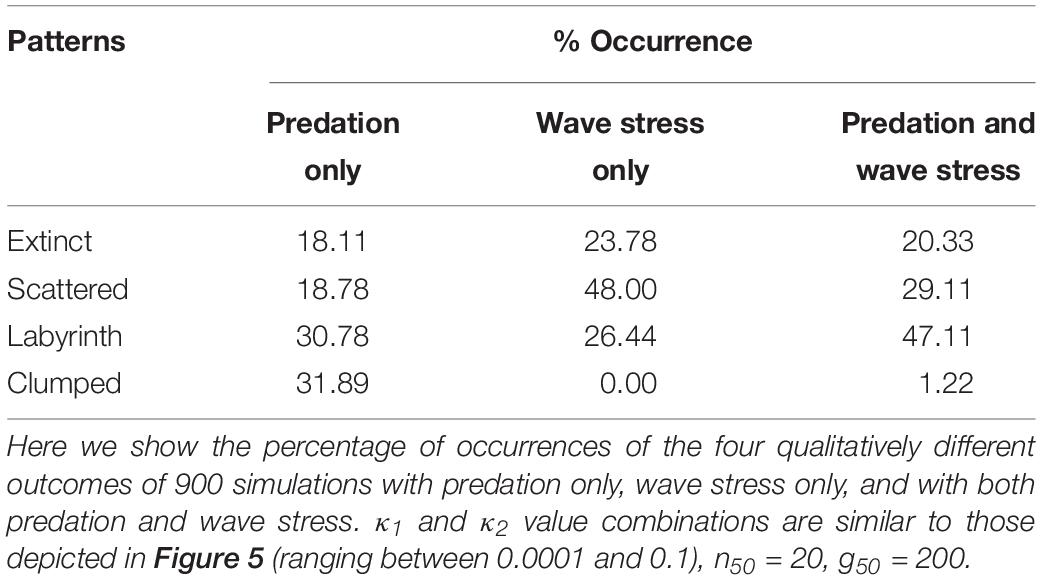
Table 1. Each set of parameters brings about different selection gradients, resulting in different evolutionary attractors and corresponding emergent spatial patterns.
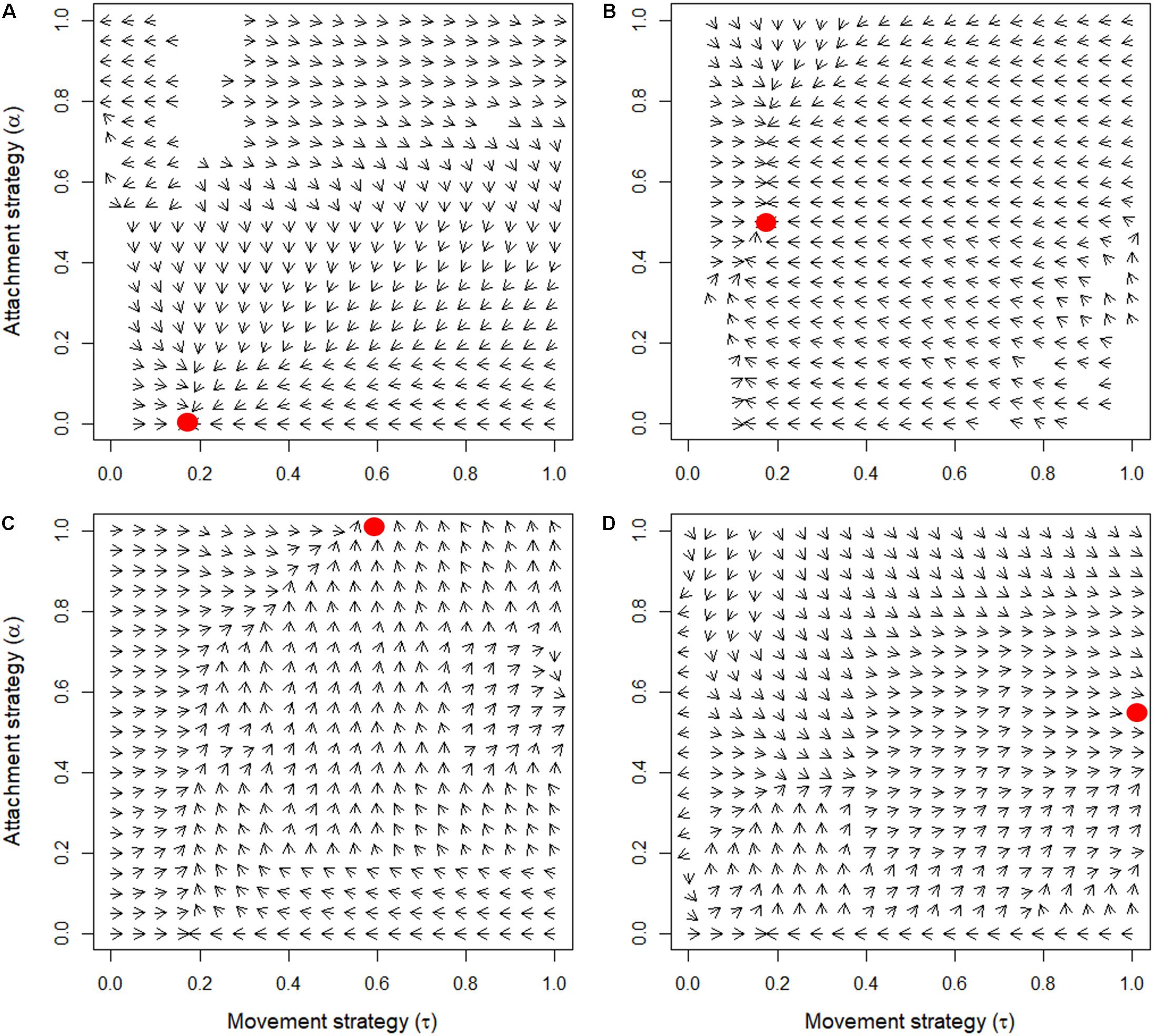
Figure 3. Effect of cost of movement (κ1) and cost of attachment (κ2) on the joint evolution of mussel movement and attachment strategies. The red dots correspond to the joint evolutionary attractors and the arrows indicate the direction of evolution. No arrows are shown when the mutants and residents have zero fitness difference. In panel (A), the population goes extinct, as the attachment strategy evolves to full defection (κ1 = 0.01 and κ2 = 0.1). In panel (B), scattered distributions emerge after joint evolution of mussel movement and attachment (κ1 = 0.1 and κ2 = 0.01). In panel (C), labyrinth-producing trait combinations evolve (κ1 = 0.0015, κ2 = 0.0015). In panel (D) dense clumps emerge after evolution toward the evolutionary attractor (κ1 = 0.0001 and κ2 = 0.01).
When we only allow predation to shape mussel evolution, the model predicts that quite different movement and attachment strategies will evolve, depending on attachment and movement costs, which produce a variety of spatial patterns (Figure 4 top panels, Table 1). When the costs of attachment (κ2) are low, strategies will evolve that result in spatial patterns ranging from isolated clumps via labyrinth-like patterns to scattered distributions with increasing costs of movement (κ1). When attachment costs are high, mussels will inevitably develop an attachment strategy of full defection that – in the end – will not allow them to survive.
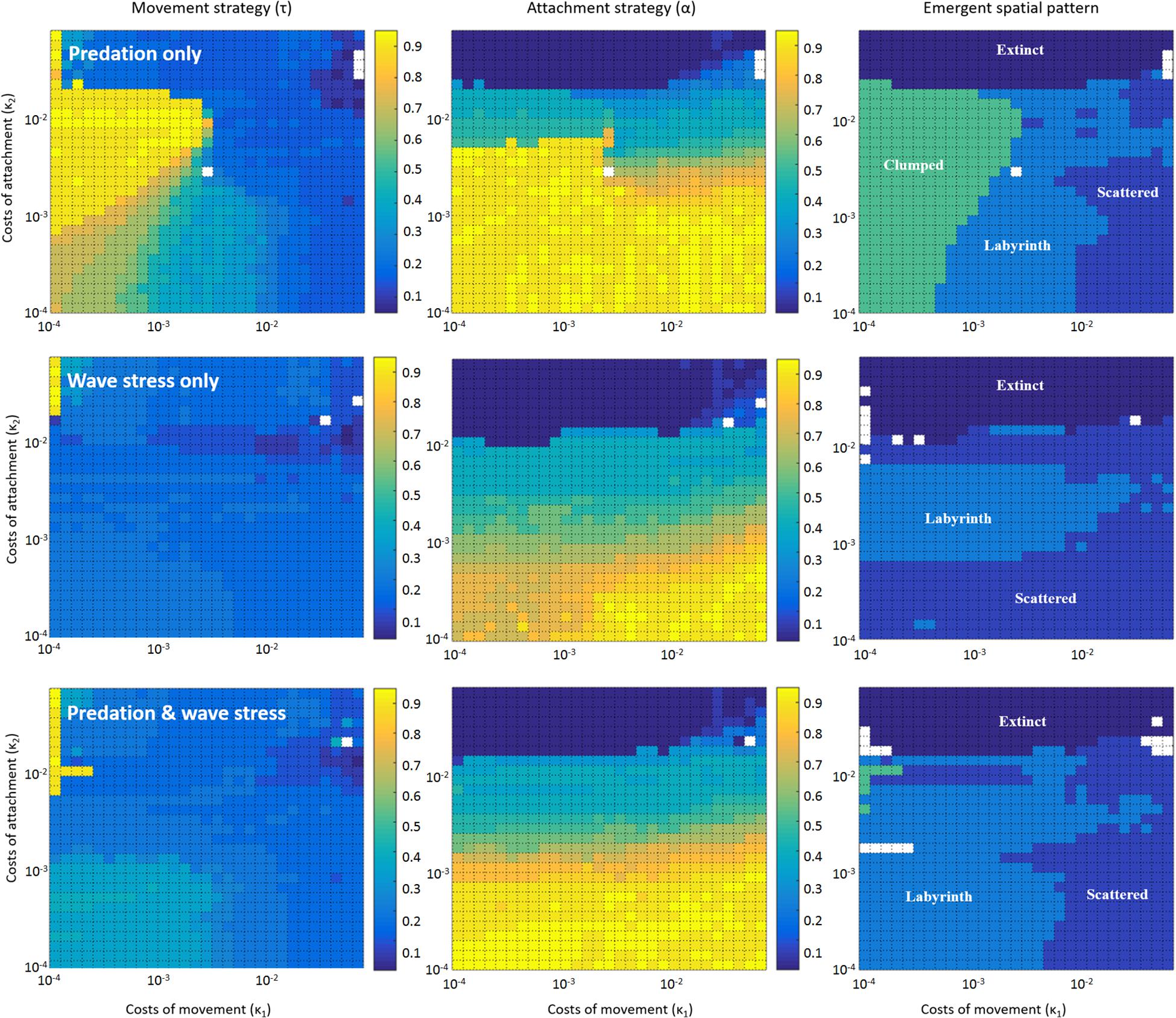
Figure 4. Dependence of evolved spatial patterns on the cost parameters in case of predation only (Top; n50 = 20); wave stress only (Middle; g50 = 200); and the joint action of predation and wave stress (Bottom; n50 = 20 and g50 = 200). Left, Middle, and Right panels show the evolved movement strategy (τ), the evolved attachment strategy (α), and the emergent spatial pattern, respectively, for different combinations of movement cost (κ1) and attachment cost (κ2).
When only dislodgement of entire mussel clumps by wave action would determine the co-evolution of attachment and movement strategies, the results change radically (Figure 4 middle panels, Table 1). Particularly, the parameter space in which clumped patterns emerge is drastically reduced (from 31.89% to 0%); instead, these combinations of movement and attachment costs now give rise to scattered distributions and labyrinth-like patterns. Low attachment costs produce evolutionary attractors that cause the emergence of scattered distributions. Intermediate attachment costs produce attractors that give rise to scattered distributions at high movement costs, and labyrinth-like patterns at lower movement costs. Similar to the model with selection by individual predation only, extremely high movement costs result in extinction of the population.
After considering selection by predation and wave action separately, we now examine results of model simulations where we assume both the local-scale predation effect and the large-scale impact of wave action to be equally important (Figure 4 bottom panels, Table 1). Again, the most substantial difference with the two earlier models can be found in the parameter space where both costs of movement and attachment are relatively low. Whereas dense clumps emerge here in models with selection by predation only, and scattered distributions or labyrinth-like patterns arise in models with selection by wave action only, labyrinth-like patterns dominate this part of the parameter space when both stressors are included. Overall, dense mussel clumps become a highly unlikely evolutionary outcome when wave stress is included in the model (Table 1: from 31.89% in simulations with predation only, to 0.00 and 1.22% in simulations with wave stress only or that include both predation and wave stress). Scattered distributions, which form the largest groups but with the lowest numbers of direct neighbors, are most common in simulations with wave stress only (48.00%); they are a far less common outcome of simulations with predation only (18.78%) or with both stressors included (29.11%). A striking result is that the parameter space in which labyrinth-producing traits evolve has increased from 26.44 and 30.78% in simulations with wave stress or predation only, to 47.11% in simulations that include both predation and wave stress. Hence, assuming multiple stressors working at different spatial scales rather than selection at only one spatial scale considerably increases the parameter space in which labyrinth-like patterns can emerge, similar to those found in real-world mussel beds.
First, we systematically varied the cost parameters of the model, keeping the parameters quantifying the harshness of the environment constant (n50 = 20 and g50 = 200). Conversely, we now vary the environmental parameters, keeping the cost parameters constant (κ1 = 0.001 and κ2 = 0.01; Figure 5). When wave stress is low to intermediate (g50 ≲ 100), evolutionary attractors result in labyrinth-like patterns for low (n50 ≲ 5) and high (n50 ≳ 15) levels of predation risk, and in dense clumps at intermediate levels of predation. When wave stress is high (g50 ≳ 100), scattered distributions and labyrinth-like patterns are produced at low levels of predation, dense clumps emerge at intermediate levels of predation, and high levels of predation risk result in scattered distributions. Overall, evolution of labyrinth-producing traits appears to be well represented within the parameter space (Figure 5), indicating that multiple selection mechanisms working at different spatial scales – predation of individuals and dislodgement of entire mussel clumps by wave action – may explain the prevalence of labyrinth-like patterns in mussel beds.
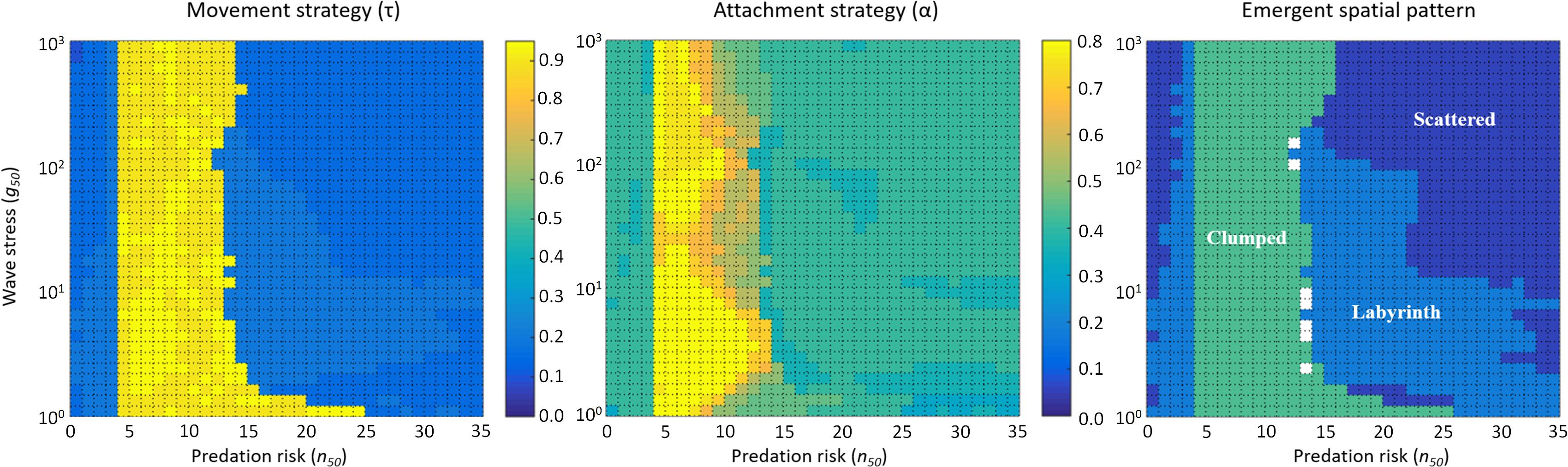
Figure 5. Simulations with various combinations of predation risk (n50) and wave stress (g50) produce qualitatively different evolutionary outcomes. Left, Middle, and Right panels show the evolved movement strategy (τ), the evolved attachment strategy (α), and the emergent spatial pattern, respectively, for different combinations of predation risk (n50) and wave stress (g50). Here, κ1 = 0.001 and κ2 = 0.01.
We present an eco-evolutionary analysis that demonstrates that selection processes at multiple spatial scales can considerably affect the evolution of self-organizing behaviors in animals. Using the joint evolution of mussel movement and attachment strategies as a model system, we show that the interplay of ecological (spatial pattern formation determining selection gradients) and evolutionary processes (adaptive changes in the parameters determining the process of pattern formation) are critical in explaining both specific adaptations of the mussels and the spatial structure of the mussel bed. The comparison of selection by predation of individuals, dislodgement of mussel clumps by wave action, and selection by both predation and wave stress revealed the importance of including all levels of selection in the model, in order to explain eco-evolutionary feedback processes and their consequences.
Our simulations demonstrate that labyrinth-producing traits evolve for many parameter combinations, when both local and large-scale selection processes are considered. These results can easily be explained by the structure of labyrinth-like mussel beds, which provide the optimal compromise between local attachment to neighboring conspecifics and a sufficiently large clump size. Our results provide a potential explanation for the prevalence of the labyrinth-like patterns that are characteristic for natural mussel beds, emphasizing the power of real-world-based models rather than more simplified, general models in providing insight in evolutionary processes in nature.
For our model, we made use of many previous studies that provided a rather detailed picture of mussel movement and spatial self-organization of mussel beds (e.g., Van de Koppel et al., 2008; De Jager et al., 2011, 2014). This allowed us to take over parameters of the movement model that are well supported by experimental and field data [i.e., the size of the attachment range (1.1 cm ø), the size of the competition range (3.3 cm ø), and the competition threshold density (0.7 cm–2)]. Other aspects of our model are less well supported. In particular, our assumptions on the costs and benefits of movement and attachment are more based on plausibility arguments than on empirical evidence. For this reason, our model cannot yield specific, quantitative predictions. Yet, we hope that it provides interesting qualitative insights into how eco-evolutionary feedbacks shape the spatial structure of mussel beds.
Our modeling approach contrasts with previous evolutionary models of cooperation in various respects, such as emergent versus given spatial structuring, multivariate versus univariate evolution, and emergent versus imposed levels of selection. First, we model spatial population structure as resulting from the mussels’ self-organized aggregative movements and attachments rather than as an imposed structure. The spatial structure in which mussels interact with their neighbors is not a given a priori pattern but an emergent property of the interplay of movement and attachment (Van de Koppel et al., 2008). The characteristic labyrinth-like pattern frequently observed in mussel beds can only persist due to between-mussel attachments; without such byssal attachments (and, hence, cooperation), there would be no spatial structure. As a consequence, there is a reciprocal causality (Laland et al., 2011) between movement and attachment strategies (which are shaped by selective forces and strongly depend on the spatial configuration) and spatial structure (which is an emergent property reflecting the underlying movement and attachment patterns). Although it is widely acknowledged that spatial structure plays a crucial role in the evolution of cooperation (Nowak and May, 1992; Ohtsuki et al., 2006; Allen et al., 2013; De Jager et al., 2017), many model studies consider spatial structure as externally given and fixed rather than an emergent property (e.g., Nowak and May, 1992; Vainstein and Arenzon, 2001; Zhang et al., 2005; Ohtsuki et al., 2006; Hui and McGeoch, 2007; Allen et al., 2013). In contrast, our model takes account of the fact that, in many organisms, spatial population structure is actively modified by the activities of the organisms themselves and therefore emerges through spatial self-organization (e.g., Bonabeau et al., 1997; Gautrais et al., 2004; Jeanson et al., 2005; Moussaid et al., 2009; De Jager et al., 2011, 2017).
Second, we investigate joint evolution of two traits, aggregation and attachment, rather than univariate evolution. Movement affects attachment: since byssus threads have a limited length, attachment requires the presence of conspecifics in the vicinity, and the clustering of individuals is to a large extent caused by their movement strategy (De Jager et al., 2011; Liu et al., 2013). Conversely, attachment directly affects movement, because mussels attached to many neighbors are strongly restricted in their movement. Accordingly, models for the evolution of mussel cooperation should consider the joint evolution of movement and attachment strategies. Although some studies exist that examine the connection between movement and cooperation (El Mouden and Gardner, 2008; Hochberg et al., 2008) and/or the joint evolution of several traits in models for the evolution of cooperation (e.g., Gardner and West, 2004; Le Galliard et al., 2005; Brown and Taylor, 2010; Mullon et al., 2016), most consider cooperation as a univariate strategy (e.g., Dugatkin, 1997; Nowak and Sigmund, 2005; Foster and Wenseleers, 2006; Lion and van Baalen, 2008; Clutton-Brock, 2009; Archetti et al., 2011; Bourke, 2011; Raihani et al., 2012; De Jager et al., 2017). Our study highlights that investigating the evolution of just a single trait without considering mutually dependent companion traits can be misleading. Studying the interplay of multiple traits that – through the interactions of their ecological functions – define the fitness of individual organisms may prove crucial for a thorough understanding of eco-evolutionary dynamics.
Third, we demonstrate that selection at larger spatial scales can be an emergent property of individual behavior. Mussel attachment leads to the formation of clumps, and the survival of a mussel in times of intense wave action is positively related to the size of its clump. While predation targets individuals, entire mussel clumps can get dislodged by means of wave action. Hence, predation and wave action are selection factors that act on different spatial scales, where fitness of a mussel is determined by both its attachment to direct neighbors and by the size of the clump (Wilson and Wilson, 2007; Krupp, 2016). However, selection in mussel beds is more complicated than described in standard models of group structured populations (Van Boven and Weissing, 1999; Thompson, 2000; Traulsen and Nowak, 2006; Kohn, 2008; Burton et al., 2012; Molleman et al., 2013). In mussel beds, both the number of direct neighbors and clump size are emergent properties of mussel movement and attachment and accordingly highly dynamic and variable in size.
By aggregating into tight clumps, mussels improve their own survival, but also that of the others in the group, as the persistence of clusters of mussels is determined by group-level properties such as clump size. As persistence on a mussel bed strongly affects survival, there is a considerable effect of the properties of the clump on individual fitness (Krupp, 2016). Strikingly, this clump effect emerges from the evolution of traits that determine aggregative movement and attachment, through the processes of ecological self-organization (De Jager et al., 2011). Considering a large range of environmental and cost parameter combinations, mussels seem to thrive best in labyrinth-like patterns, where the balance between local clustering and large group formation reduces losses by both predation and wave stress. Although our model is restricted to selection at two spatial scales – i.e., local, nearest-neighbor protection against predation, and clump-scale protection against wave stress – selection at intermediate spatial scales may be explored in future studies. Overall, our study highlights the importance of ecological self-organization on the effect of selection pressures in real-world populations. To understand evolutionary processes in the context of real-world ecosystems, it is crucial to realize that the interplay of ecological and evolutionary processes can be an important determinant of the adaptations of individual species.
The datasets generated for this study are available on request to the corresponding author.
MJ designed the study, created the model, analyzed the data, and wrote the first draft of the manuscript. FW verified the analytical methods. EW helped setting up the field experiment. FW and JK provided critical feedback on the study, analysis, and manuscript.
MJ was supported by a grant from the Netherlands Organization for Scientific Research – Earth and Life Sciences (NWO-ALW) and Project Group Movement Ecology by the KNAW Strategic Fund. FW was supported by a grant 823.01.006 from the Netherlands Organization for Scientific Research.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The content of this manuscript first appeared in the thesis “Eco-evolutionary feedbacks in self-organized ecosystems” (De Jager, 2015).
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.00007/full#supplementary-material
Allen, B., Nowak, M. A., and Dieckmann, U. (2013). Adaptive dynamics with interaction structure. Am. Nat. 181, E139–E163. doi: 10.1086/670192
Archetti, M., Scheuring, I., Hoffman, M., Frederickson, M. E., Pierce, N. E., and Yu, D. W. (2011). Economic game theory for mutualism and cooperation. Ecol. Lett. 14, 1300–1312. doi: 10.1111/j.1461-0248.2011.01697.x
Bertness, M. D., and Grosholz, E. (1985). Population dynamics of the ribbed mussel, Geukensia demissa: the costs and benefits of an aggregated distribution. Oecologia 67, 192–204. doi: 10.1007/bf00384283
Bonabeau, E., Theraulaz, G., Deneubourg, J.-L., Aron, S., and Camazine, S. (1997). Self-organization in social insects. Trends Ecol. Evol. 12, 188–193. doi: 10.1016/s0169-5347(97)01048-3
Bourke, A. F. G. (2011). The validity and value of inclusive fitness theory. Proc. R. Soc. Lond. B Biol. Sci. 278, 3313–3320. doi: 10.1098/rspb.2011.1465
Brown, S. P., and Taylor, P. D. (2010). Joint evolution of multiple social traits: a kin selection analysis. Proc. R. Soc. Lond. B Biol. Sci. 277, 415–422. doi: 10.1098/rspb.2009.1480
Burton, S., Fletcher, J. A., and Doebeli, M. (2012). Towards a general theory of group selection. Evolution 76, 1561–1572. doi: 10.1111/j.1558-5646.2012.01835.x
Clutton-Brock, T. (2009). Cooperation between non-kin in animal societies. Nature 462, 51–57. doi: 10.1038/nature08366
De Jager, M. (2015). Eco-Evolutionary Feedbacks in Self-Organized Ecosystems. Ph.D. thesis, University of Groningen, Groningen.
De Jager, M., Bartumeus, F., Kölzsch, A., Weissing, F. J., Hengeveld, G. M., Nolet, B. A., et al. (2014). How superdiffusion gets arrested: ecological encounters explain shift from Lévy to Brownian movement. Proc. R. Soc. Lond. B Biol. Sci. 281:20132605. doi: 10.1098/rspb.2013.2605
De Jager, M., Weissing, F. J., Herman, P. M. J., Nolet, B. A., and van de Koppel, J. (2011). Lévy walks evolve through interaction between movement and environmental complexity. Science 332, 1551–1554.
De Jager, M., Weissing, F. J., and van de Koppel, J. (2017). Why mussels stick together: spatial self-organization affects the evolution of cooperation. Evol. Ecol. 31, 547–558. doi: 10.1007/s10682-017-9888-1
Doebeli, M., and Hauert, C. (2005). Models of cooperation based on the Prisoner’s Dilemma and the Snowdrift game. Ecol. Lett. 8, 748–766. doi: 10.1111/j.1461-0248.2005.00773.x
Dugatkin, L. A. (1997). Cooperation Among Animals: An Evolutionary Perspective. Oxford: Oxford University Press.
Dugatkin, L. A., Mesterton-Gibbons, M., and Houston, A. I. (1992). Beyond the Prisoner’s Dilemma: toward models to discriminate among mechanisms of cooperation in nature. Trends Ecol. Evol. 7, 202–205. doi: 10.1016/0169-5347(92)90074-l
El Mouden, C., and Gardner, A. (2008). Nice natives and mean migrants: the evolution of dispersal-dependent social behaviour in viscous populations. J. Evol. Biol. 21, 1480–1491. doi: 10.1111/j.1420-9101.2008.01614.x
Foster, K. R., and Wenseleers, T. (2006). A general model for the evolution of mutualisms. J. Evol. Biol. 19, 1283–1293. doi: 10.1111/j.1420-9101.2005.01073.x
Gardner, A., and West, S. A. (2004). Cooperation and punishment, especially in humans. Am. Nat. 164, 753–764. doi: 10.1086/425623
Gautrais, J., Jost, C., Jeanson, R., and Theraulaz, G. (2004). How individual interactions control aggregation patterns in gregarious arthropods. Interact. Stud. 5, 245–269. doi: 10.1075/is.5.2.05gau
Hochberg, M. E., Rankin, D. J., and Taborsky, M. (2008). The coevolution of cooperation and dispersal in social groups and its implications for the emergence of multicellularity. BMC Evol. Biol. 8:238. doi: 10.1186/1471-2148-8-238
Hui, C., and McGeoch, M. A. (2007). Spatial patterns of Prisoner’s Dilemma game in metapopulations. Bull. Math. Biol. 69, 659–676. doi: 10.1007/s11538-006-9145-1
Hunt, H. L., and Scheibling, R. E. (2001). Patch dynamics of mussels on rocky shores: integrating process to understand pattern. Ecology 82, 3213–3231. doi: 10.1890/0012-9658(2001)082[3213:pdomor]2.0.co;2
Hunt, H. L., and Scheibling, R. E. (2002). Movement and wave dislodgment of mussels on a wave-exposed rocky shore. Veliger 45, 273–277.
Jeanson, R., Rivault, C., Deneubourg, J., Blanco, S., Fournier, R., Jost, C., et al. (2005). Self-organized aggregation in cockroaches. Anim. Behav. 69, 169–180. doi: 10.1162/artl.2008.14.4.14400
Krupp, D. B. (2016). Causality and the levels of selection. Trends Ecol. Evol. 31, 255–257. doi: 10.1016/j.tree.2016.01.008
Laland, K. N., Sterelny, K., Odling-Smee, J., Hoppitt, W., and Uller, T. (2011). Cause and effect in biology revisited: is Mayr’s proximate-ultimate dichotomy still useful? Science 334, 1512–1516. doi: 10.1126/science.1210879
Le Galliard, J. F., Ferriere, R., and Dieckmann, U. (2005). Adaptive evolution of social traits: origin, trajectories, and correlations of altruism and mobility. Am. Nat. 165, 206–224. doi: 10.1086/427090
Lehmann, L., and Keller, L. (2006). The evolution of cooperation and altruism – a general framework and a classification of models. J. Evol. Biol. 19, 1365–1376. doi: 10.1111/j.1420-9101.2006.01119.x
Lion, S., and van Baalen, M. (2008). Self-structuring in spatial evolutionary ecology. Ecol. Lett. 11, 277–295. doi: 10.1111/j.1461-0248.2007.01132.x
Liu, Q.-X., Doelman, A., Rottshäfer, V., de Jager, M., Herman, P. M. J., Rietkerk, M., et al. (2013). Phase separation explains a new class of self-organized spatial patterns in ecological systems. Proc. Natl. Acad. Sci. U.S.A. 110, 11905–11910. doi: 10.1073/pnas.1222339110
Maas Geesteranus, R. A. (1942). On the formation of banks by Mytilus edulis L. Arch. Neerl. Zool. 6, 283–326. doi: 10.1163/036551642x00080
Molleman, L., Quinones, A. E., and Weissing, F. J. (2013). Cultural evolution of cooperation: the interplay between forms of social learning and group selection. Evol. Hum. Behav. 34, 342–349. doi: 10.1371/journal.pone.0068153
Moussaid, M., Helbing, D., Garnier, S., Johansson, A., Combe, M., and Theraulaz, G. (2009). Experimental study of the behavioral mechanisms underlying self-organization in human crowds. Proc. R. Soc. Lond. B Biol. Sci. 276, 2755–2762. doi: 10.1098/rspb.2009.0405
Mullon, C., Keller, L., and Lehmann, L. (2016). Evolutionary stability of jointly evolving traits in subdivided populations. Am. Nat. 188, 175–195. doi: 10.1086/686900
Nowak, M. A., and May, R. M. (1992). Evolutionary games and spatial chaos. Nature 359, 826–829. doi: 10.1038/359826a0
Ohtsuki, H., Hauert, C., Lieberman, E., and Nowak, M. A. (2006). A simple rule for the evolution of cooperation in graphs and social networks. Nature 441, 502–505. doi: 10.1038/nature04605
Raihani, N. J., Thornton, A., and Bshary, R. (2012). Punishment and cooperation in nature. Trends Ecol. Evol. 27, 288–295. doi: 10.1016/j.tree.2011.12.004
Thompson, N. S. (2000). Shifting the natural selection metaphor to the group level. Behav. Philos. 28, 83–101.
Traulsen, A., and Nowak, M. A. (2006). Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. U.S.A. 103, 10952–10955.
Vainstein, M. H., and Arenzon, J. J. (2001). Disordered environments in spatial games. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 64(Pt 1):051905.
Van Boven, M., and Weissing, F. J. (1999). Segregation distortion in a deme-structured population: opposing demands of gene-individual, and group selection. J. Evol. Biol. 12, 80–93. doi: 10.1046/j.1420-9101.1999.00011.x
Van de Koppel, J., Gascoigne, J. C., Theraulaz, G., Rietkerk, M., Mooij, W. M., and Herman, P. M. J. (2008). Experimental evidence for spatial self-organization and its emergent effects in mussel bed ecosystems. Science 322, 739–742. doi: 10.1126/science.1163952
Van de Koppel, J., Rietkerk, M., Dankers, N., and Herman, P. M. J. (2005). Scale-dependent feedback and regular spatial patterns in young mussel beds. Am. Nat. 165, E66–E77.
Van Dyken, J. D., and Wade, M. J. (2012). Detecting the molecular signature of social conflict: theory and a test with bacterial quorum sensing genes. Am. Nat. 179, 436–450. doi: 10.1086/664609
West, S. A., Griffin, A. S., and Gardner, A. (2007). Social semantics: altruism, cooperation, mutualism, strong reciprocity and group selection. J. Evol. Biol. 20, 415–432. doi: 10.1111/j.1420-9101.2006.01258.x
West, S. A., Griffin, A. S., and Gardner, A. (2008). Social semantics: how useful has group selection been? J. Evol. Biol. 21, 374–385. doi: 10.1111/j.1420-9101.2007.01458.x
Wilson, D. S., and Wilson, E. O. (2007). Rethinking the theoretical foundation of sociobiology. Q. Rev. Biol. 82, 327–348. doi: 10.1086/522809
Keywords: cooperation, group-level selection, eco-evolutionary dynamics, joint evolution, aggregative movement, individual-based model
Citation: de Jager M, van de Koppel J, Weerman EJ and Weissing FJ (2020) Patterning in Mussel Beds Explained by the Interplay of Multi-Level Selection and Spatial Self-Organization. Front. Ecol. Evol. 8:7. doi: 10.3389/fevo.2020.00007
Received: 03 July 2019; Accepted: 15 January 2020;
Published: 30 January 2020.
Edited by:
Mauro Santos, Autonomous University of Barcelona, SpainReviewed by:
José F. Fontanari, University of São Paulo, BrazilCopyright © 2020 de Jager, van de Koppel, Weerman and Weissing. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Monique de Jager, bS5kZWphZ2VyQG5pb28ua25hdy5ubA==; TS5kZUphZ2VyQHV1Lm5s
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.