Conditional Cooperation and Turn-Taking in Parental Care

Introduction

Parents that raise dependent young together face a much-studied conflict of interest, because both stand to gain from successful reproduction, but (as with any common good) each does better if the other bears a greater share of the costs this entails (Hardin, 1968; Trivers, 1972). This conflict is typically thought to result in under-investment by parents, with negative consequences for their offspring (Houston and Davies, 1985; Royle et al., 2002; McNamara et al., 2003; Lessells and McNamara, 2012). More recently, Johnstone et al. (2014) suggested that if parental care is delivered over a series of discrete “visits,” the conflict between parents provisioning young might be more efficiently resolved through a simple form of conditional cooperation: turn-taking. Using a game-theoretical model, they showed that if parents can monitor one another's visits to the nest, then selection might favor a strategy in which a parent who has once visited the young refrains from doing so again until its partner has visited in turn. Such a strategy, which gives rise to strict turn-taking when adopted by both parents, leads to an efficient resolution of the conflict between them (i.e., both invest at a level that maximizes their total fitness payoff).

Johnstone et al. (2014) also presented data on timing of nest visits by great tit (Parus major) parents raising chicks together that suggested a tendency toward turn taking, with parents apparently reducing their own rate of visiting the nest while waiting for their partner to visit. While the statistical methods used to infer a process of active turn-taking have attracted some discussion and controversy (Johnstone et al., 2016; Schlicht et al., 2016; Santema et al., 2019), a number of other studies have since found similar evidence of alternation in avian bi-parental (Iserbyt et al., 2017, 2019; Leniowski and Wegrzyn, 2018) and cooperatively breeding systems (Bebbington and Hatchwell, 2016; Koenig and Walters, 2016; Savage et al., 2017), though it is also clear that such tendencies are not universal (see for example Khwaja et al., 2017).

The model of Johnstone et al. (2014), however, relies on the unrealistic assumption that parents can monitor one another's visits to the nest with perfect accuracy, which leads to the equally unrealistic prediction that parents should exhibit “strict” or “perfect” turn-taking, with each individual “refusing” to visit twice in a row. By contrast, even those empirical studies which have found strong tendencies toward alternation of visits do not report strict turn-taking (Bebbington and Hatchwell, 2016; Koenig and Walters, 2016; Iserbyt et al., 2017; Savage et al., 2017; Wojczulanis-Jakubas et al., 2018). Indeed, Johnstone et al. (2014) themselves found that great tit parents reduced their own visit rate only by about 25% while waiting for their partner to feed the young, leading to a frequency of alternation of 72%. Thus, even if one accepts that parental coordination may indeed help to resolve conflict over care, there is a clear discrepancy between observed behavior and that predicted by the model.

At least two other potential influences on turn-taking are also overlooked by the Johnstone et al. model. Firstly, when turn-taking is strict, parental visit rates are constrained to be identical for the members of a pair, yet there is abundant evidence of differences in investment between mates, driven by variation in extra-pair paternity and adult sex ratio (Kokko and Jennions, 2012; Liker et al., 2015), sex-biased dispersal (Kuijper and Johnstone, 2017), or task specialization (Iserbyt et al., 2017). Does the notion of turn-taking still make sense when investment is asymmetric, and can models help to predict how patterns of parental coordination vary when the sexes differ in their division of care roles or in the costs and benefits of care? Secondly, the assumption that parents incur only personal costs during care is violated whenever individuals stand to gain if their partner survives to the next breeding attempt (Mariette and Griffith, 2015). If finding a new partner is costly (Johnstone and Bshary, 2008; Song and Feldman, 2013), or if familiar partners are more effective or efficient at rearing offspring (Black, 2001; Sánchez-Macouzet et al., 2014; Wiley and Ridley, 2018), individuals are also impacted by costs incurred by their partner, and hence might be expected to adopt a more forgiving turn-taking strategy. Under the extreme case of “true” monogamy, in which the death of either individual ends reproduction for the survivor, costs of care are entirely shared and there is no sexual conflict.

Here, we explore whether turn-taking strategies are robust when parents monitor one another's behavior with less than perfect accuracy, and whether a more realistic model can account for the kind of “imperfect” alternation observed in empirical studies. We extend the simple model of Johnstone et al. (2014) to incorporate, successively, (i) imperfect monitoring of partner visits, (ii) time-dependent costs and benefits of care, (iii) differences between partners in payoffs (and consequently in behavior), (iv) differences between partners in the accuracy with which they can monitor one another's behavior, and (v) shared costs of care.

Modeling Parental Turn-Taking

In the model of Johnstone et al. (2014), two parents stay together for the time required to raise their offspring, during which they make repeated visits to provision their brood of young. Each parent can monitor the other's behavior with perfect accuracy, and visits randomly at rate λ_f or λ_m (for the female or male parent, respectively) when its partner was the last to visit the young, and at rate μ_f or μ_m when it was itself the last to visit the young. The system thus switches back and forth between two states, defined by the identity of the last parent to visit (see Figure 1, upper panel), with the visit rates of each parent changing accordingly. Each parent's payoff is equal to the sum of (i) fitness gained from the current brood, which is given by a smoothly increasing, concave function of the total mean visit rate of both parents together, f(x_f + x_m), where x_f and x_m denote mean visit rate of the female and male parent, respectively, and (ii) fitness gained from future broods, which is given by a smoothly decreasing, concave function of the focal parent's own individual mean visit rate, g(x_f) or g(x_m). The benefits and costs of care are assumed to be identical for both parents. Assuming that the benefits of care are not too small compared to the costs, this model yields a convergently unstable equilibrium, at which λ_f = λ_m = μ_f = μ_m > 0, and two convergently stable equilibria (see Figure 1, lower panel, and Supplementary Information for further details). At one of these two equilbria, λ_f = λ_m = 0 and μ_f = μ_m > 0, implying that biparental care breaks down (i.e., one parent gives up on care entirely; Beissinger and Snyder, 1987); at the other equilibrium, μ_f = μ_m = 0 and λ_f = λ_m > 0, implying that after feeding the young once, a parent will not feed again until its partner has visited in turn, which leads to strictly alternating visits. The latter, “turn taking” equilibrium, features an “efficient” level of investment at which the parents both visit at a rate that maximizes their total joint payoff.

FIGURE 1

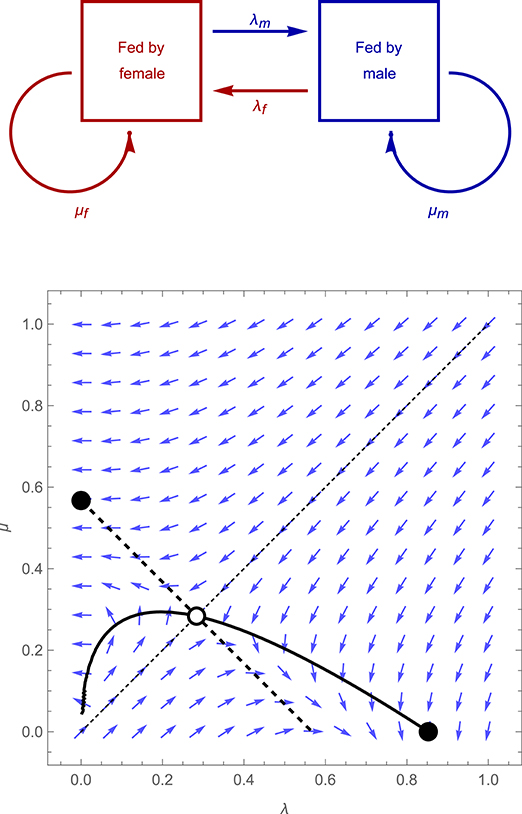
Figure 1. Structure of the model of Johnstone et al. (2014) (upper panel), and the direction of selection for an illustrative case (lower panel) in which λ_f = λ_m = λ and μ_f = μ_m = μ, the fitness gained from the current brood is given by f(x_f + x_m) = 1− Exp(−x_f − x_m), where x_f and x_m denote mean female and male visit rates, respectively, and the expected fitness a parents gains from future broods is given by g(x_f) = K x_f² or g(x_f) = K – x_m². Blue arrows show the direction of selection for a population characterized by particular values of λ and μ, thick curves represent the null-clines for λ (solid curve) and μ (dashed curves), along which the selection gradient for the trait in question is zero, while empty and filled circles denote convergently unstable and stable equilibria, respectively.

Imperfect Monitoring

Here, we extend the above model to allow for imperfect monitoring of partner behavior (and, subsequently, for time-dependent costs and benefits, asymmetries between parents in the benefits and costs of care, and cost-sharing). We suppose a focal parent detects each visit by its partner with probability d_f or d_m (for the female or male parent, respectively); with probability (1 − d_f) or (1 − d_m) the visit goes undetected. As a result, the pair at any given moment may be in one of three informational states (see Figure 2, upper panel): (i) both parents may be aware that the female was last to visit the young, (ii) both parents may be aware that the male was last to visit the young, or (iii) each parent may believe it was itself the last to visit the young (a situation we refer to as one of “conflicting information”). The last of these states can only arise when a parent visits unobserved. In the Supplementary Information we derive the expected proportions of time that a pair spends in each of these three states, and from these the mean visit rates and fitness payoffs to each parent.

FIGURE 2

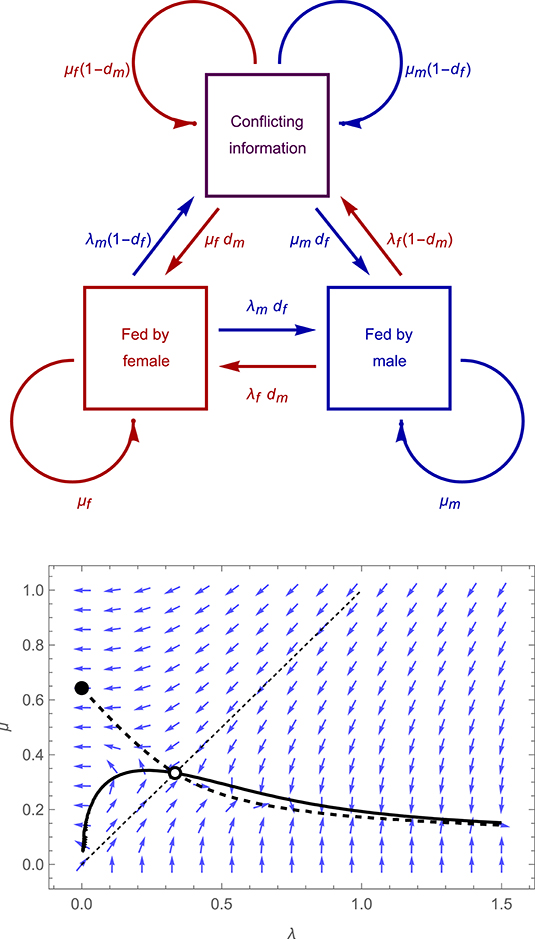
Figure 2. Structure of the “imperfect monitoring” model described in the main text, which incorporates the possibility that either parent may fail to detect visits by the other (upper panel), and adaptive dynamics for an illustrative case (lower panel) in which λ_f = λ_m = λ, μ_f = μ_m = μ, d_f = d_m = 0.8 (with payoffs as specified in the legend to Figure 1). Blue arrows show the direction of the selection gradient for a population characterized by particular values of λ and μ, thick curves represent the null-clines for λ (solid curve) and μ (dashed curves), while empty and filled circles denote convergently unstable and stable equilibria, respectively.

To explore the implications of imperfect monitoring for the evolution of visit rates, we begin by treating the model as a symmetric game, in which parents of both sexes experience precisely equivalent costs and benefits of feeding, and are assumed to adopt the same strategy (λ_f = λ_m = λ, μ_f = μ_m = μ); below, we also explore asymmetries in costs, benefits and behavior. As illustrated in Figure 2, lower panel, imperfect monitoring results in dramatic consequences for the outcome of the symmetric game. As in the original perfect assessment model, the new model incorporating missed detections features a convergently unstable equilibrium at which λ = μ > 0, and a convergently stable equilibrium at which λ = 0 and μ > 0, implying that biparental care breaks down. However, there is no longer a stable equilibrium featuring alternating visits (as can be seen in the figure, there is no intersection between the λ and μ null-clines within the region for which λ > μ). Rather, when there is a tendency for parents to alternate, selection favors indefinitely increasing values of λ, and decreasing values of μ, leading to increasingly rapid “flurries” of alternating visits separated by ever longer gaps during which neither parent feeds. This outcome arises because a parent's mean visit rate depends upon both λ and μ_. It is thus always possible for an individual to maintain the same overall mean visit rate while simultaneously increasing its own value of λ and decreasing its own value of μ (such that the two effects cancel out). This leaves the focal individual's own investment unchanged, but (assuming λ > μ) encourages the focal's partner to feed the young more frequently, by reducing the proportion of time during which the partner is waiting for the focal to visit.

Time-Dependent Costs and Benefits

The above analysis suggests that imperfect monitoring of partner behavior leads to the breakdown of alternation. However, this outcome relies on the simplistic assumption of the original model that payoffs depend only on mean parental visit rates, and are unaffected by the temporal distribution of visits. In reality, an outcome such as the one described (in which visits become increasingly clumped in time) will entail fitness costs, since offspring are likely to become satiated during bursts of frequent feeding, and risk starving during periods in which neither parent visits. In addition, phases of frequent feeding are likely to increase costs to parents who may be unable to feed themselves while repeatedly feeding the young at a high rate.

To better capture the fitness costs of clumped feeding visits, we can therefore introduce time-dependent costs and benefits of feeding. We suppose that the cost to a parent of feeding the young decreases exponentially with time since its last feeding visit, with the rate of exponential decay denoted r_f or r_m for the female or male parent. Conversely, the benefit to the young increases with time since they were last fed, approaching an asymptotic value exponentially, with rate coefficient h (see Figure 3).

FIGURE 3

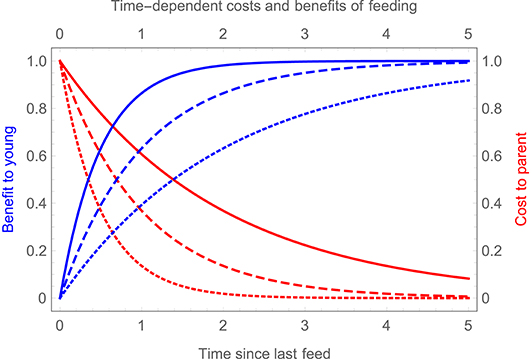
Figure 3. Time dependent costs and benefits of feeding. Blue curves show the benefit to the young of receiving a feed (relative to the maximum possible benefit), as a function of the time since they were last fed, for three different values of h (solid blue curve, h = 2; dashed blue curve, h = 1; dotted blue curve, h = 0.5). Red curves show the cost to a parent of delivering a feed (relative to the maximum possible cost) as a function of the time since it last fed, assuming that r_f = r_m = r, for three different values of r (solid red curve, r = 0.5; dashed red curve, r = 1; dotted red curve, r = 2).

To implement these time-dependent costs and benefits, we introduce two new state variables. We will suppose that immediately after feeding, a parent enters a “refractory” state in which further feeding visits incur a cost. The parent, however, spontaneously reverts at rate r_f or r_m to a “ready” state in which feeding visits are cost-free. The probability of incurring a cost when feeding thus declines exponentially with time since the parent's last visit (giving an expected cost function similar to that illustrated in Figure 3) and overall, the loss of fitness from future broods that a parent suffers is proportional to its long-term average rate of visiting while in a refractory state. Similarly, we will suppose that after being fed, the young enter a “satiated” state in which further feeding provides no benefit. The offspring, however, spontaneously revert at rate h to a “hungry” state in which feeding is once again beneficial. The probability of gaining from a feeding visit thus increases with time since the last feed, approaching an asymptote of 1 exponentially (giving an expected benefit function similar to that illustrated in Figure 3), and overall, fitness gained through the current brood is proportional to the long-term average rate of visits made (by either parent) while the young are in a “hungry” state.

Note that in this version of the model, a parent's fitness payoff is simply equal to a weighted sum of benefits (B), given by the mean rate of visits (by either parent) while the young are hungry and costs (C_f or C_m), given by the rate of visits by the focal parent while it is in a refractory state. We do not need to invoke concave payoff functions f(x_f + x_m) and g(x_f) or g(x_m) because the time-dependent costs and benefits of individual visits themselves ensure that increases in feeding rate yield diminishing returns – as parents feed more often, visits follow more rapidly one after another, thus occurring more often when the young are satiated or the parents in a refractory state. In addition, payoffs are also sensitive to the temporal distribution of visits as well as simple mean visit rates. A more evenly spaced visit pattern yields a higher payoff than one in which visits are temporally clumped, again because the latter increases the chance that parents visit when in a refractory state or when the young are satiated.

In the Supplementary Information we derive the expected costs and benefits of feeding given the above assumptions, which allow one to determine equilibrium visit rates and resulting levels of alternation, which we illustrate and discuss below. As before, we first treat the model as a symmetrical game in which both sexes experience precisely equivalent costs and benefits of feeding (so that r_f = r_m = r), and are assumed to adopt the same strategy (λ_f = λ_m = λ, μ_f = μ_m = μ), before going on to explore asymmetries in costs, benefits and behavior.

Figure 4 shows the adaptive dynamics of the symmetrical game. The graph reveals that incorporating time-dependent costs and benefits of feeding restores the “turn-taking” equilibrium that was eliminated by the introduction of imperfect monitoring. As in the original model of Johnstone et al. (2014), we see a convergently unstable equilibrium lying between two convergently stable equilibria, at one of which λ = 0 and μ > 0, implying that biparental care breaks down, while at the other, λ > μ > 0, implying that after feeding the young, a parent slows down its rate of return until it perceives its partner to have visited in turn. Unlike in the original model, however, this latter equilibrium does not feature perfect turn-taking. Since μ > 0, while a parent speeds up after it perceives its partner to have visited the young, and slows down after visiting itself, it does not “refuse” entirely to make repeated visits (a resolution that makes adaptive sense, as such a refusal would lead to cessation of all care whenever one parent failed to observe the other's visit).

FIGURE 4

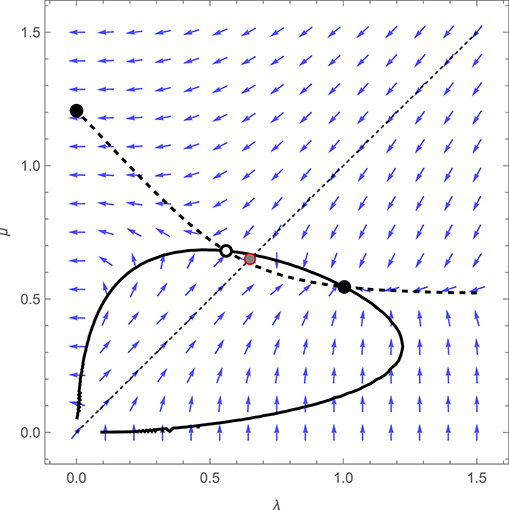
Figure 4. Adaptive dynamics of the extended model described in the main text, when the costs and benefits of feeding are time-dependent, for an illustrative symmetrical case in which λ_f = λ_m = λ, μ_f = μ_m = μ, with d_f = d_m = 0.8, h = 1 and r_f = r_m = 0.2. The fitness payoff to a parent is equal to bB − cC_f or bB − cC_m, where B denotes the mean rate at which offspring receive feeds while hungry and C_f or C_m the mean rate at which the female or male parent visits the young while in a refractory state, with b = 1 and c = 0.2. Blue arrows show the direction of the selection gradient for a population characterized by particular values of λ and μ, thick curves represent the null-clines for λ (solid curve) and μ (dashed curves), while empty and filled circles denote convergently unstable and stable equilibria, respectively. The gray-filled red circle represents the equilibrium outcome of the model when parents cannot respond to one another's visits (i.e., under the constraint that λ = μ).

Also shown in Figure 4 (as a red, shaded circle) is the equilibrium of the model when parents are constrained to ignore one another's visits (i.e. when λ and μ are constrained to be equal). In the original analysis of Johnstone et al. (shown in Figure 1), and in the extension featuring imperfect monitoring described above (shown in Figure 2), this constrained equilibrium coincided precisely with the unstable equilibrium of the unconstrained model (which is why it was not visible in Figures 1 or 2). The implication is that in those models, the initial evolution of responsiveness in a population of unresponsive parents could equally well lead toward turn-taking or toward a breakdown of parental care (because the constrained equilibrium fell on the boundary between two basins of attraction). However, as Figure 4 reveals, the introduction of time-dependent costs and benefits shifts the position of the unstable equilibrium such that the constrained equilibrium now falls into the basin of attraction of the turn-taking equilibrium. When the benefits of feeding the young increase with the time since they were last visited, while the costs of feeding decrease with the time since a parent last fed, selection favors an initial tendency to slow down after visiting the young and speed up after the partner visits in turn, even if the partner does not itself respond in the same way, because this serves to ensure a more even distribution of visits by the focal parent. It is thus easier to explain the initial evolution of turn-taking in a model with time-dependent costs and benefits.

Figure 5 shows how the equilibrium values of λ and μ at the turn-taking equilibrium change with the probability of detecting a partner's visit, and the consequences for overall mean visit rate (which is identical for both parents in this symmetrical case) and for the proportion of alternated vs. repeat visits. The graph reveals that as the probability of detection drops, the sensitivity of feeding rates to partner behavior, and the consequent proportion of alternated visits, also decline rapidly. However, the equilibrium remains stable even in the face of frequent missed detections, with parents slowing down and speeding up to some degree in response to own and partner visits, yielding a frequency of alternation that is less than 100% but nevertheless greater than would otherwise be expected by chance. The greater the accuracy of detection, and the more precisely the parents are able to alternate visits, the greater the overall mean visit rate at equilibrium, highlighting the benefits of turn-taking in resolving the conflict between parents over investment in care.

FIGURE 5

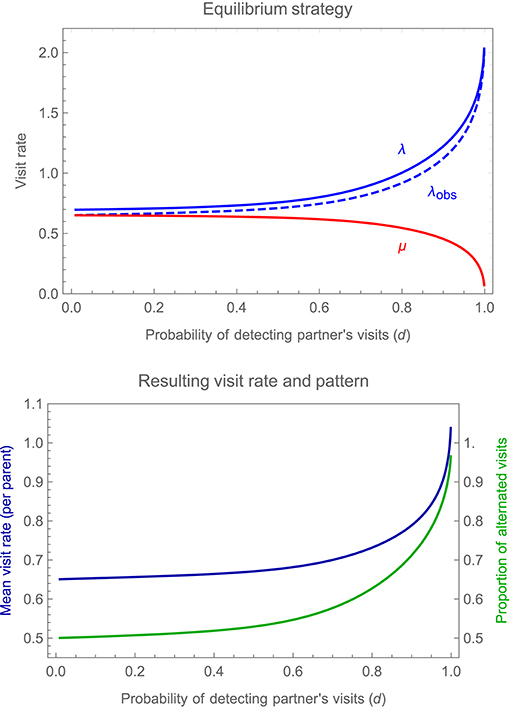
Figure 5. Changes in the equilibrium alternating strategy, for the illustrative symmetrical case considered in Figure 4, as one varies the probability d of detecting a partner's visits (assuming that this is the same for both parents, i.e., that d_f = d_m = d); other parameter values and payoffs are as specified in the legend to Figure 4. The upper panel shows the equilibrium values of λ (a focal individual's visit rate immediately after it detects a visit by its partner), plotted in blue, and μ (a focal individual's visit rate immediately after visiting the young itself), plotted in red, as a function of the probability of detecting a partner's visits (d); also shown is λ_obs, a focal individual's visit rate immediately after a fully-informed human observer records a visit by its partner (allowing for the possibility that the focal individual itself may fail to detect the partner's visit). The lower panel shows the resulting overall mean visit rate by a parent, plotted in blue, and the proportion of alternated visits, plotted in green, again as a function of the probability of detecting a partner's visits (d).

One complication to bear in mind for testing these predictions empirically is that λ denotes feeding rate when the partner is perceived to have visited last. A well-informed, human observer attempting to measure these visit rates, however, is more likely to calculate them based on the identity of the last parent actually to visit, as it may prove difficult to infer whether or not a focal parent perceived its partner's last feed. As shown in Figure 5, the mean feeding rate after a partner visits (whether the focal parent detected this visit or not), denoted λ_obs, is lower than the rate after a partner is perceived to visit, precisely because the visit may have been overlooked, so that the focal parent continues to feed at the lower rate μ. However, the difference is slight and the qualitative pattern of results unchanged, regardless of whether one focuses on λ or λ_obs.

Asymmetries in Costs and Benefits

Next, we explore the consequences of introducing asymmetries between males and females in the fitness consequences of care, and allowing for differences in feeding behavior between parents. Because it is difficult to illustrate adaptive dynamics in the asymmetric case (with four evolving visit rates, λ_f, λ_m, μ_f and μ_m), we simply focus on how the strategies at the “turn-taking” equilibrium vary with the relevant model parameters.

Figure 6 illustrates how changes in the recovery rate parameter of a focal parent, r₁ (which determines how rapidly the cost of feeding decays after a visit) affect the strategy of the focal parent and that of its partner, while holding the latter's recovery rate r₂ constant (note that asymmetries in the relative weighting of benefits and costs when calculating the overall payoff to either parent have qualitatively similar effects to asymmetries in recovery rate, and so are not illustrated in the main text; see Supplementary Information for additional results). The figure shows that as the focal parent's recovery rate increases, it visits at a higher rate, while the partner compensates for this change by reducing its own visit rate. Both individuals, however, continue to respond to one another's behavior, speeding up after the partner visits and slowing down after they visit themselves, thus maintaining alternation.

FIGURE 6

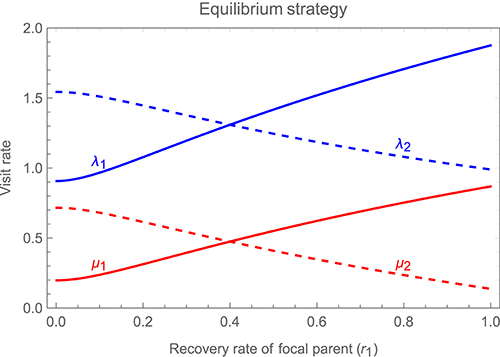
Figure 6. Changes in the stable alternating strategy, as one varies a focal parent's recovery rate independently of its partner's recovery rate (i.e., allowing for asymmetries between the parents). Solid curves show the visit rates of the focal parent, λ₁ (immediately after it detects a visit by its partner) in blue and μ₁ (immediately after visiting the young itself) in red, while dashed curves show the corresponding visit rates of the partner, λ₂ in blue and μ₂ in red, all as a function of the focal parent's recovery rate r₁ (while holding the partner's recovery rate r₂ constant at a value of 0.4). As in Figures 4, 5, the fitness payoff to a parent is equal to bB − cC_f or bB − cC_m, where B denotes the mean rate at which offspring receive feeds while hungry and C_f or C_m the mean rate at which the female or male parent visits the young while in a refractory state, with b = 1 and c = 0.2. Other parameter values are d_f = d_m = 0.9 and h = 1.

Figure 7 shows the consequences of these strategic changes for mean visit rates (upper panel), and for the proportion of alternated visits (lower panel). As the upper panel makes clear, compensation for changes in a partner's visit rate is incomplete. An increase in the focal parent's recovery rate, for instance, is associated with a decrease in the partner's visit rate, but the latter effect is smaller in magnitude than the former, so that overall mean visit rate (by both parents combined) increases with either parent's recovery rate. When parents differ in visit rate (due to differences in their recovery rate) the parent that visits more frequently makes more repeat visits, while the parent that visits less frequently makes more alternated visits. The overall proportion of alternated visits, however, is much less sensitive to differences between parents. Alternation is most pronounced when parents work equally hard, but decreases only slowly as asymmetries are introduced.

FIGURE 7

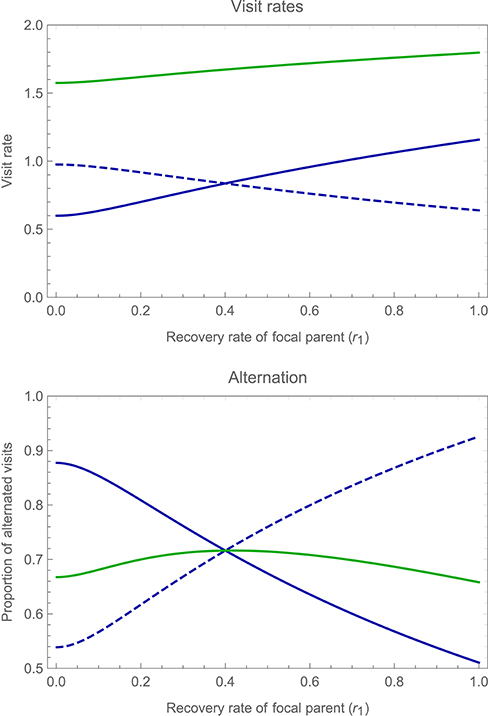
Figure 7. Changes in the overall mean visit rates and proportion of alternated visits by both parents, as one varies a focal parent's recovery rate independently of its partner's recovery rate (i.e., allowing for asymmetries between the parents). The upper panel shows the overall mean visit rate of the focal parent (solid blue curve) and of its partner (dashed blue curve), as well as the total mean visit rate (green curve), as a function of the focal parent's recovery rate r₁ (while holding the partner's recovery rate r₂ constant at a value of 0.4). The lower panel shows the proportion of alternated visits by the focal parent (solid blue curve) and by its partner (dashed blue curve), as well as the total proportion of alternated visits by both parents (green curve), again as a function of the focal parent's recovery rate r₁. Other parameter values and payoffs are as specified in the legend to Figure 6.

Asymmetries in Accuracy of Monitoring

As well as asymmetries in the costs and benefits of care, we can also allow for asymmetries in the accuracy with which partners can monitor one another's behavior. Figure 8 (upper panel) shows how changes in the accuracy of monitoring by a focal parent, d₁, affects the strategy of the focal parent and that of its partner, while holding the latter's accuracy d₂ constant at a value of 0.5; the lower panel of the figure shows the impact on overall mean visit rates by the focal parent, its partner, and by both parents together. The figure reveals that as the focal parent's accuracy improves, its visit rates decrease relative to those of its partner. As result, the parent who can monitor its partner more accurately works less hard (while total visit rates increase, albeit slightly, with the accuracy of either parent).

FIGURE 8

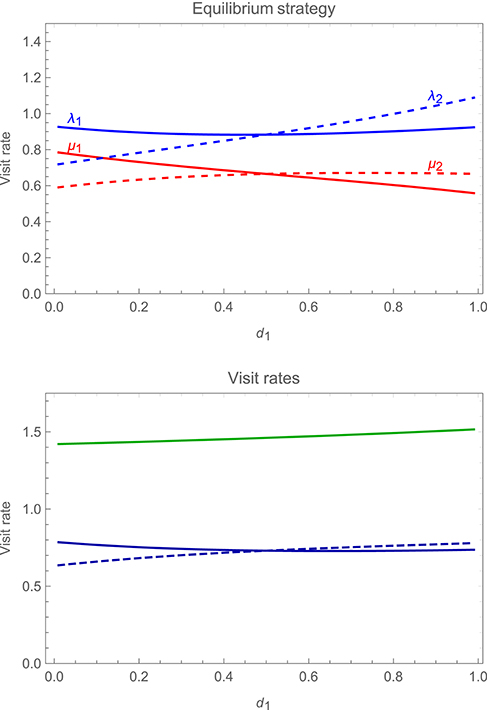
Figure 8. Changes in the stable alternating strategy (upper panel), and in overall mean visit rates (lower panel), as one varies a focal parent's probability of detecting its partner's visits (d₁), while holding the latter's probability of detection d₂ constant at a value of 0.5. In the upper panel, solid curves show the visit rates of the focal parent, λ₁ (immediately after it detects a visit by its partner) in blue and μ₁ (immediately after visiting the young itself) in red, while dashed curves show the corresponding visit rates of the partner, λ₂ in blue and μ₂ in red. In the lower panel, the solid blue curve shows the mean visit rate of the focal parent and the dashed blue curve the mean visit rate of its partner, while the green curve shows the total mean visit rate by the pair. Payoffs are as specified in the legend to Figure 6, with other parameter values r₁ = r₂ = 0.4 and h = 1.

Cost-Sharing Between Parents

Finally, we briefly investigate how turn-taking strategies change when individual costs of care incurred by either parent also reduce the fitness of the other. This kind of “cost-sharing” will apply whenever individuals benefit from their partner surviving to the following breeding season. We introduce a parameter z that specifies the degree of cost-sharing, such that the female parent incurs fitness costs of care equal to zC_f + (1 − z)C_m, and the male zC_m + (1 − z)C_f. A value of z = 0 recovers the results above, with costs borne by a parent reflecting only its own efforts, while the opposite extreme of z = 0.5 implies that costs are shared equally by both parents, as in a system with “true” monogamy in which there is no sexual conflict because the death of either individual ends reproduction for the survivor (Lessells, 2006).

Figure 9 shows how parental visit rates and the proportion of alternated visits vary with cost-sharing under symmetric parental care (upper panel), and also how the inequality in parental contributions changes with cost-sharing when parents differ in their recovery rate (lower panel). The figure reveals that turn-taking becomes less strict as cost-sharing becomes more pronounced, with individuals becoming less responsive to their partner and the proportion of alternated visits decreasing. The overall visit rate increases as costs are shared to a greater extent, reflecting the decrease in conflict between carers, and the inequality in parental contributions becomes more pronounced when parents differ in their ability to provide care, with the parent that accrues lower costs taking on an increasing fraction of the effort of care, and investing more overall.

FIGURE 9

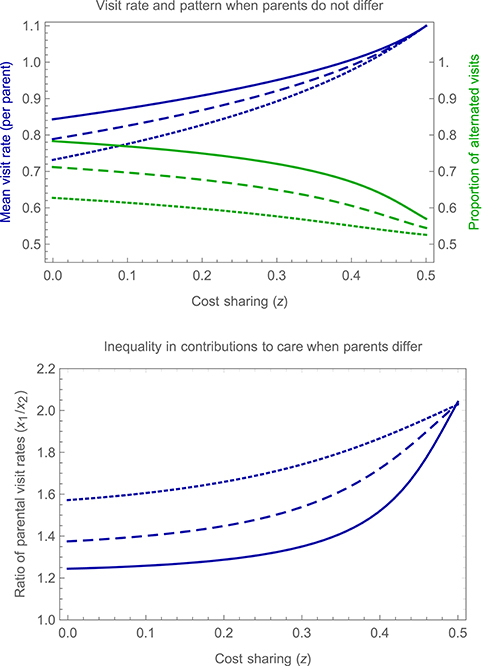
Figure 9. Impact of cost sharing on turn-taking. The upper panel shows, for an illustrative symmetrical case in which parents do not differ from one another, the mean visit rate per parent (in blue) and proportion of alternated visits (in green) as a function of the extent of cost sharing (z), for three different values of d, the probability of detecting a partner's visists (d = 0.95, solid curves; d = 0.85, dashed curves; d = 0.7, dotted curves). Other parameter values are b = 1, c = 0.2, h = 1, and r = 0.2. The lower panel shows, for an illustrative asymmetrical case in which parent 1 enjoys a recovery rate r₁ = 0.4 that is higher than that of the second parent r₂ = 0.2, the ratio of mean parental visit rates (x₁/x₂), again as a function of the extent of cost sharing (z), for the same three values of d. Other parameter values are as specified for the upper panel.

Discussion

Our model suggests that turn-taking is a robust form of conditional cooperation that can help to resolve conflicts over parental care, even in cases where parents cannot monitor one another's contributions with perfect accuracy, and/or where parents differ in their individual ability to provide care. However, this finding is contingent on the assumption that the costs and benefits of care events are time-dependent, with a given care event being more valuable to offspring and less costly to parents when further separated in time from the previous event. We also find that turn-taking strategies become less strict when the costs of care are shared between parents, suggesting—perhaps counter-intuitively—that when sexual conflict is weaker care may appear less coordinated.

Under imperfect monitoring, the strict turn-taking rule predicted by Johnstone et al. (2014) is replaced by a more forgiving rule in which a parent decreases its visit rate after visiting the young itself (but does not cease to visit entirely), and increases its visit rate after the partner is observed to visit again. This prediction aligns with results from empirical studies showing elevated but imperfect alternation of carer visits (Bebbington and Hatchwell, 2016; Koenig and Walters, 2016; Savage et al., 2017), assuming such patterns are driven by responsiveness rather than environmental effects that affect both parents (Ihle et al., 2019; Santema et al., 2019). In natural systems the difficulty of accurately monitoring one's partner varies with aspects of ecology and behavior, and is (for example) likely to be lower in more open habitats, when food items are less variable, and when individuals cannot false-feed (Boland et al., 1997). Consequently, we should anticipate more strict turn-taking rules under these conditions, and weaker rules when monitoring is difficult. In extreme cases, individuals might have little or no ability to monitor their partner's contributions, except indirectly via offspring condition, and under these circumstances individuals should contribute care at a rate that does not change with partner visits. Conversely, we should expect stricter turn-taking when environmental factors incentivise partners to associate with each other in space, allowing them to monitor each other more easily at no cost; for example if pairs forage more efficiently due to increased vigilance, or if visiting offspring together lowers predation risk on the young (Raihani et al., 2010).

Our results also help to reconcile turn-taking models with classical models of parental care. There appears to be a tension between the two, because turn-taking involves positive (matching) responses to partner effort: a parent reduces its own visit rate after it has visited the nest, but speeds up again once the partner has visited in turn, so that greater visit rates by the latter encourage greater visit rates by the former. In contrast, classical models generally predict negative (compensatory) responses to changes in partner effort (Houston and Davies, 1985; McNamara et al., 1999; Johnstone, 2011; Lessells and McNamara, 2012) at least when parents are similarly informed about offspring need (Johnstone and Hinde, 2006). In our turn-taking model, while individuals respond to each visit by their partner with a matching response, when costs are asymmetric an individual's total visit rate is lower when its partner visits more, and higher when its partner visits less (see Figures 6, 7), recovering the classical prediction of incomplete compensation to changes in partner effort that is broadly supported by the empirical literature on biparental care (Harrison et al., 2009). Our analysis thus suggests that one might expect to observe different patterns of response at different time-scales, with “visit-by-visit” matching shifting to compensation over longer periods of time.

As well as asymmetries in the cost of care, our model allows us to explore the impact of asymmetries between parents in their ability to monitor partner behavior. As shown in Figure 8, we find that the parent that can monitor its partner's behavior with greater accuracy provides the smaller share of total care, while its partner ends up shouldering a greater burden. There is thus a benefit to be gained from better information about partner behavior, which might favor monitoring even where this entails costs. The more reliably a focal parent can detect visits by its partner, and adjust its own visit rate in response, the more effective is this strategy of conditional cooperation in eliciting greater effort by the partner (and the more the focal parent can afford to reduce its own efforts in compensation).

Our finding that time-dependency of the costs and benefits of care is required for stability of turn-taking under imperfect monitoring implies that parental investment rules are likely to be sensitive to the details of offspring demand and resource allocation. It is reasonable to assume that parental visits will often increase in value with time since a previous visit, as repeated visits might satiate offspring, and long periods without feeding could lead to starvation or affect development. However, this assumption is most plausible for parents rearing a single offspring; by contrast, when parents rear multiple offspring, sibling rivalry and dominance hierarchies will influence the optimal patterns of care by parents (Mock and Parker, 1997), and our assumptions may no longer hold. In particular, the form of time-dependency implemented in our model is less well suited to cases in which (a) there are many offspring with a strong dominance hierarchy, (b) parents visit at a low rate, (c) parents deliver single food items that can be monopolized by offspring, and (d) offspring control food allocation (Mock and Parker, 1997; Krebs, 2002). In such circumstances, rapid bouts of investment by parents are likely to result in a greater payoff through a reduction in sibling competition (Shen et al., 2010), and we would expect less strict turn-taking. Similarly, our assumption that visiting in rapid succession is more costly to a parent is most plausible in species where parents must regularly feed themselves, and in environments where food items are indivisible and distributed homogeneously.

Our prediction that alternation should decrease when parents' costs are shared makes sense when one views turn-taking as a way of policing a partner with conflicting interests. As parents increasingly benefit from the survival of their partner (and the bond between them) beyond the present breeding attempt, they should increasingly optimize costs and benefits for the pair rather than the individual (Mariette and Griffith, 2015). When parental interests are fully aligned, there is no risk of exploitation and hence parents can “trust” that their partner is investing appropriately based on their individual costs. In other words, a strategy of conditional cooperation is pointless when partners unconditionally cooperate. Under asymmetric costs, any degree of cost-sharing results in the partner that can provide care at lower cost taking on a greater share of investment, and although we do not explicitly model multiple dimensions of care this would logically lead to greater task specialization if the asymmetry is reversed for other care modes. Although we have framed this discussion in terms of a bi-parental pair bond, this cost-sharing argument applies equally to cooperative systems in which carers are influenced by costs incurred by other carers. For example, when individuals do better in larger groups (Kokko et al., 2001), philopatric group members will benefit from every other group member surviving, unless they stand to inherit that member's breeding position.

The stability of the “turn-taking” equilibrium, even under imperfect detection and asymmetries between carers, can be viewed as another example of the effectiveness of retaliatory strategies in reaching an efficient outcome between individuals that repeatedly interact under a conflict of interest. Similarly to the successful tit-for-tat (TFT) strategy in the iterated Prisoners' dilemma (Axelrod, 1984), adopting a turn-taking strategy during care allows individuals to punish a defecting partner and effectively work with a cooperative partner. As with TFT, the strict turn-taking strategy of Johnstone et al. (2014) is not stable when individuals cannot perfectly monitor their partner, as a mistake or misperception leads to a failure to revisit, analogous in result to the joint retaliatory defection in TFT. However, our model illustrates that just as under noisy conditions forgiving strategies such as generous TFT, or one-step memory strategies such as tit-for-two-tats and contrite TFT can outperform strict TFT (Boerlijst et al., 1997), when parents imperfectly detect each other's contributions to care, an imperfect turn-taking strategy is likewise the best response.

While our model is more flexible than previous theory on turn-taking, it is still limited to circumstances under which both parents are free to modify their visit rates, and care is delivered in discrete units. In some cases, care is delivered over a period of time and parents are constrained to strictly alternate contributions to care, for example when one parent must remain at a nest to incubate or defend offspring. In these cases, rather than altering visit rates, individuals may mediate the duration of bouts by signaling to one another (Boucaud et al., 2017; Takahashi et al., 2017). In addition, our model only considers a single dimension of parental investment delivered during a single stage, while previous work has suggested that sex-based asymmetries across modes of care (Barta et al., 2014) or across care stages (Savage et al., 2013; Iserbyt et al., 2017) can strongly influence the resulting behavioral rules and outcomes for offspring. We also ignore the possibility of death or desertion of one partner part-way through the period of care, as well as changes in parental behavior with chick age.

Our model makes a number of predictions about conditions under which one might expect stricter or less strict turn-taking during parental care, and we encourage comparative and experimental tests of these predictions. Even the existence of active turn-taking during parental care remains contentious, as the analysis methods and null models used by prior empirical studies leave open the possibility that the observed turn-taking is a result of environmental influences that drive correlated changes in parental visit rate on the scale of individual care events (Ihle et al., 2019; Santema et al., 2019). Future studies should carefully manipulate short-term parental investment (Santema et al., 2017), the ability to monitor partner investment (Iserbyt et al., 2015), or cost asymmetries within pairs (Firth et al., 2015) to create a more complete picture of the degree to which parents respond to each other, under what contexts, and at what temporal scale.

Author Contributions

RJ developed the model. RJ and JS interpreted the model and wrote the manuscript.

Funding

This work was supported by NERC grant NE/N011171/1.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Camilla Hinde and Fumiaki Nomano for helpful discussion.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00335/full#supplementary-material

References

Axelrod, R. (1984). The Evolution of Cooperation. New York, NY: Basic Books.

Google Scholar

Barta, Z., Székely, T., Liker, A., and Harrison, F. (2014). Social role specialization promotes cooperation between parents. Am. Nat. 183, 747–761. doi: 10.1086/676014

PubMed Abstract | CrossRef Full Text | Google Scholar

Bebbington, K., and Hatchwell, B. J. (2016). Coordinated parental provisioning is related to feeding rate and reproductive success in a songbird. Behav. Ecol. 27, 652–659. doi: 10.1093/beheco/arv198

CrossRef Full Text | Google Scholar

Beissinger, S. R., and Snyder, N. (1987). Mate desertion in the snail kite. Anim. Behav. 35, 477–487.

Google Scholar

Black, J. M. (2001). Fitness consequences of long-term pair bonds in barnacle geese: monogamy in the extreme. Behav. Ecol. 12, 640–645. doi: 10.1093/beheco/12.5.640

CrossRef Full Text | Google Scholar

Boerlijst, M. C., Nowak, M. A., and Sigmund, K. (1997). The logic of contrition. J. Theor. Biol. 185, 281–293.

PubMed Abstract | Google Scholar

Boland, C. R. J., Heinsohn, R., and Cockburn, A. (1997). Deception by helpers in cooperatively breeding white-winged chougts and its experimental manipulation. Behav. Ecol. Sociobiol. 41, 251–256.

Google Scholar

Boucaud, I. C. A., Perez, E. C., Ramos, L. S., Griffith, S. C., and Vignal, C. (2017). Acoustic communication in zebra finches signals when mates will take turns with parental duties. Behav. Ecol. 28, 645–656. doi: 10.1093/beheco/arw189

CrossRef Full Text | Google Scholar

Firth, J. A., Voelkl, B., Farine, D. R., and Sheldon, B. C. (2015). Experimental evidence that social relationships determine individual foraging behavior. Curr. Biol. 25, 3138–3143. doi: 10.1016/j.cub.2015.09.075

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1968). The tragedy of the commons. Science 162, 1243–1248.

PubMed Abstract | Google Scholar

Harrison, F., Barta, Z., Cuthill, I., and Székely, T. (2009). How is sexual conflict over parental care resolved? A meta-analysis. J. Evol. Biol. 22, 1800–1812. doi: 10.1111/j.1420-9101.2009.01792.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Houston, A. I., and Davies, N. B. (1985). “The evolution of cooperation and life history in the dunnock, Prunella modularis,” in Behavioural Ecology: Ecological Consequences of Adaptive Behaviour, eds R. M. Sibly and R. H. Smith (Oxford: Blackwell Scientific Publications), 471–487.

Google Scholar

Ihle, M., Pick, J. L., Winney, I. S., Nakagawa, S., and Burke, T. (2019). Measuring up to reality: null models and analysis simulations to study parental coordination over provisioning offspring. Front. Ecol. Evol. 7:142. doi: 10.3389/fevo.2019.00142

CrossRef Full Text | Google Scholar

Iserbyt, A., Farrell, S., Eens, M., and Müller, W. (2015). Sex-specific negotiation rules in a costly conflict over parental care. Anim. Behav. 100, 52–58. doi: 10.1016/j.anbehav.2014.11.014

CrossRef Full Text | Google Scholar

Iserbyt, A., Fresneau, N., Kortenhoff, T., Eens, M., and Müller, W. (2017). Decreasing parental task specialization promotes conditional cooperation. Sci. Rep. 7:6565. doi: 10.1038/s41598-017-06667-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Iserbyt, A., Griffioen, M., Eens, M., and Müller, W. (2019). Enduring rules of care within pairs - how blue tit parents resume provisioning behaviour after experimental disturbance. Sci. Rep. 9, 1–9. doi: 10.1038/s41598-019-39139-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnstone, R. A. (2011). Load lightening and negotiation over offspring care in cooperative breeders. Behav. Ecol. 22, 436–444. doi: 10.1093/beheco/arq190

CrossRef Full Text | Google Scholar

Johnstone, R. A., and Bshary, R. (2008). Mutualism, market effects and partner control. J. Evol. Biol. 21, 879–888. doi: 10.1111/j.1420-9101.2008.01505.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnstone, R. A., and Hinde, C. A. (2006). Negotiation over offspring care—how should parents respond to each other's efforts? Behav. Ecol. 17, 818–827. doi: 10.1093/beheco/arl009

CrossRef Full Text | Google Scholar

Johnstone, R. A., Manica, A., Fayet, A. L., Stoddard, M. C., Rodriguez-Gironés, M. A., and Hinde, C. A. (2014). Reciprocity and conditional cooperation between great tit parents. Behav. Ecol. 25, 216–222. doi: 10.1093/beheco/art109

CrossRef Full Text | Google Scholar

Johnstone, R. A., Manica, A., Fayet, A. L., Stoddard, M. C., Rodriguez-Gironés, M. A., and Hinde, C. A. (2016). Evidence for conditional cooperation: a response to Schlicht et al. Behav. Ecol. 27, e6–e7. doi: 10.1093/beheco/arw051

CrossRef Full Text | Google Scholar

Khwaja, N., Preston, S. A. J., Hatchwell, B. J., Briskie, J. V., Winney, I. S., and Savage, J. L. (2017). Flexibility but no turn-taking in provisioning riflemen (Acanthisitta chloris). Anim. Behav. 125, 25–31. doi: 10.1016/j.anbehav.2016.12.021

CrossRef Full Text | Google Scholar

Koenig, W. D., and Walters, E. L. (2016). Provisioning patterns in the cooperatively breeding acorn woodpecker: does feeding behaviour serve as a signal? Anim. Behav. 119, 125–134. doi: 10.1016/j.anbehav.2016.06.002

CrossRef Full Text | Google Scholar

Kokko, H., and Jennions, M. D. (2012). “Sex differences in parental care,” in The Evolution of Parental Care, eds N. J. Royle, P. T. Smiseth, and M. Kölliker (Oxford: Oxford University Press), 101−116.

Google Scholar

Kokko, H., Johnstone, R. A., and Clutton-Brock, T. H. (2001). The evolution of cooperative breeding through group augmentation. Proc. R. Soc. B Biol. Sci. 268, 187–196. doi: 10.1098/rspb.2000.1349

PubMed Abstract | CrossRef Full Text | Google Scholar

Krebs, E. A. (2002). “Sibling competition and parental control: patterns of begging in parrots,” in The Evolution of Begging, eds J. Wright and M. L. Leonard (Dordrecht: Springer, 319–336.

Google Scholar

Kuijper, B., and Johnstone, R. A. (2017). How sex-biased dispersal affects sexual conflict over care. Am. Nat. 189, 501–514. doi: 10.1086/691330

PubMed Abstract | CrossRef Full Text | Google Scholar

Leniowski, K., and Wegrzyn, E. (2018). Synchronisation of parental behaviours reduces the risk of nest predation in a socially monogamous passerine bird. Sci. Rep. 8, 1–9. doi: 10.1038/s41598-018-25746-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lessells, C. M. (2006). The evolutionary outcome of sexual conflict. Philos. Trans. R. Soc. B Biol. Sci. 361, 301–317. doi: 10.1098/rstb.2005.1795

PubMed Abstract | CrossRef Full Text | Google Scholar

Lessells, C. M., and McNamara, J. M. (2012). Sexual conflict over parental investment in repeated bouts: negotiation reduces overall care. Proc. R. Soc. B Biol. Sci. 279, 1506–1514. doi: 10.1098/rspb.2011.1690

PubMed Abstract | CrossRef Full Text | Google Scholar

Liker, A., Freckleton, R. P., Remeš, V., and Székely, T. (2015). Sex differences in parental care: gametic investment, sexual selection, and social environment. Evolution 69, 2862–2875. doi: 10.1111/evo.12786

PubMed Abstract | CrossRef Full Text | Google Scholar

Mariette, M. M., and Griffith, S. C. (2015). The adaptive significance of provisioning and foraging coordination between breeding partners. Am. Nat. 185, 270–280. doi: 10.1086/679441

PubMed Abstract | CrossRef Full Text | Google Scholar

McNamara, J. M., Gasson, C. E., and Houston, A. I. (1999). Incorporating rules for responding into evolutionary games. Nature 401, 368–371. doi: 10.1038/43869

PubMed Abstract | CrossRef Full Text | Google Scholar

McNamara, J. M., Houston, A. I., Barta, Z., and Osorno, J. L. (2003). Should young ever be better off with one parent than with two? Behav. Ecol. 14, 301–310. doi: 10.1093/beheco/14.3.301

CrossRef Full Text | Google Scholar

Mock, D. W., and Parker, G. A. (1997). The Evolution of Sibling Rivalry. Oxford: Oxford University Press.

Google Scholar

Raihani, N. J., Nelson-Flower, M. J., Moyes, K., Browning, L. E., and Ridley, A. R. (2010). Synchronous provisioning increases brood survival in cooperatively breeding pied babblers. J. Anim. Ecol. 79, 44–52. doi: 10.1111/j.1365-2656.2009.01606.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Royle, N. J., Hartley, I. R., and Parker, G. A. (2002). Sexual conflict reduces offspring fitness in zebra finches. Nature 416, 733–736. doi: 10.1038/416733a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sánchez-Macouzet, O., Rodríguez, C., and Drummond, H. (2014). Better stay together: pair bond duration increases individual fitness independent of age-related variation. Proc. R. Soc. B Biol. Sci. 281:20132843. doi: 10.1098/rspb.2013.2843

PubMed Abstract | CrossRef Full Text | Google Scholar

Santema, P., Schlicht, E., and Kempenaers, B. (2019). Testing the conditional cooperation model: what can we learn from parents taking turns when feeding offspring? Front. Ecol. Evol. 7:94. doi: 10.3389/FEVO.2019.00094

CrossRef Full Text | Google Scholar

Santema, P., Schlicht, E., Schlicht, L., and Kempenaers, B. (2017). Blue tits do not return faster to the nest in response to either short- or long-term begging playbacks. Anim. Behav. 123, 117–127. doi: 10.1016/j.anbehav.2016.10.016

CrossRef Full Text | Google Scholar

Savage, J. L., Browning, L. E., Manica, A., Russell, A. F., and Johnstone, R. A. (2017). Turn-taking in cooperative offspring provisioning: by-product of individual provisioning behaviour or active response rule? Behav. Ecol. Sociobiol. 71:162. doi: 10.1007/s00265-017-2391-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, J. L., Russell, A. F., and Johnstone, R. A. (2013). Maternal costs in offspring production affect investment rules in joint rearing. Behav. Ecol. 24, 750–758. doi: 10.1093/beheco/ars203

CrossRef Full Text | Google Scholar

Schlicht, E., Santema, P., Schlicht, R., and Kempenaers, B. (2016). Evidence for conditional cooperation in biparental care systems? A comment on Johnstone et al. Behav. Ecol. 27, e2–e5. doi: 10.1093/beheco/arw036

CrossRef Full Text | Google Scholar

Shen, S.-F., Chen, H.-C., Vehrencamp, S. L., and Yuan, H.-W. (2010). Group provisioning limits sharing conflict among nestlings in joint-nesting Taiwan yuhinas. Biol. Lett. 6, 318–321. doi: 10.1098/rsbl.2009.0909

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Z., and Feldman, M. W. (2013). The coevolution of long-term pair bonds and cooperation. J. Evol. Biol. 26, 963–970. doi: 10.1111/jeb.12111

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, L. S., Storey, A. E., Wilhelm, S. I., and Walsh, C. J. (2017). Turn-taking ceremonies in a colonial seabird: does behavioral variation signal individual condition? Auk 134, 530–541. doi: 10.1642/AUK-17-26.1

CrossRef Full Text | Google Scholar

Trivers, R. L. (1972). “Parental investment and sexual selection,” in Sexual Selection and the Descent of Man 1871-1971, ed B. Campbell (Chicago, IL: Aldine-Atherton), 136–207.

Google Scholar

Wiley, E. M., and Ridley, A. R. (2018). The benefits of pair bond tenure in the cooperatively breeding pied babbler (Turdoides bicolor). Ecol. Evol. 8, 1–8. doi: 10.1002/ece3.4243

PubMed Abstract | CrossRef Full Text | Google Scholar

Wojczulanis-Jakubas, K., Araya-Salas, M., and Jakubas, D. (2018). Seabird parents provision their chick in a coordinated manner. PLoS ONE 13:0189969. doi: 10.1371/journal.pone.0189969

PubMed Abstract | CrossRef Full Text | Google Scholar