The role of root dynamics on the climate sensitivity of ecohydrological processes of over- and understory in a semi-arid groundwater-dependent ecosystem

Plant roots connect belowground moisture with aboveground vegetation functionalities, making root plasticity critical for drought resilience. This study employs an enhanced land surface ecohydrological model, Duke Coupled Hydrology Model with Vegetation and Dynamic Roots (DCHM-VDR), to investigate how root dynamics affect vegetation adaptation under a range of climate conditions. DCHM-VDR features a moisture-driven root parameterization that simulates dynamic root profiles and hydraulic redistribution (HR). Applied to a semiarid woodland with groundwater-dependent mesquites and shallow-rooted shrubs, model results compare well against AmeriFlux tower data and capture observed soil moisture patterns tied to root water uptake, including mesquite’s dimorphic root profile and shifts in water source and the direction of HR. Accounting for HR lowers overall water use efficiency (WUE) by more than 50% in the dry season due to release of deep root water uptake to moisten dry soil layers. Dynamic root profiles reduce water demand by avoiding dry soil patches and utilizing moist layers with increased WUE, especially for shrubs. Mesquites with a dimorphic root profile show a 3-fold annual transpiration (Tr) increase from 183 mm to 629 mm/year and reduced HR/Tr from 34% to 6%, along with a small reduction of around 10% for shrubs, reflecting the importance of groundwater sourcing and the codependence of shrubs on mesquite for water stress resilience. Future climate scenarios were examined using the Thermodynamic Global Warming downscaled data. Mesquites and shrubs respond positively to wetter winters, albeit with opposite water use strategies in the drier growing seasons due to different rooting depths and HR modulation of soil moisture. Mesquites increase transpiration by adjusting root fraction, water uptake, and HR closer to the saturated zone, while shrubs reduce transpiration and increase WUE by 17% compared to a decrease of 13% in mesquite WUE under the driest scenario. The intertwined water use strategies of mesquites and shrubs expressed by the root water uptake dynamics determine ecosystem response aboveground under more extreme climate conditions, highlighting the importance of modeling root architecture dynamics and co-adaptive ecohydrological processes in predicting ecosystem responses to climate change.

1 Introduction

The relationship between vegetation dynamics and water availability plays a key role in water and carbon exchange between the land and the atmosphere in water-limited regions. Under high water stress during seasonal or prolonged droughts, plant communities develop a range of adaptations, including the downregulation of stomatal conductance, redistribution of moisture in the soils by plant roots, and deep root systems (Oren et al., 1999; Amenu and Kumar, 2008; Wang et al., 2018). As leaves control the rate of transpiration and carbon assimilation based on atmospheric conditions, roots respond to soil moisture heterogeneity and alter their source of water uptake based on precipitation patterns and water table depth (WTD) (Drewniak, 2019; Arora and Boer, 2003). However, the belowground root dynamics and interactions of coexisting species, especially in deep soil near the saturated zone, are often challenging to measure and thus are poorly represented in most land surface models, limiting our ability to provide robust predictions of ecosystem responses to water stress (Wang et al., 2022; Wang et al., 2018). Since atmospheric drying is projected to intensify in the future (Lian et al., 2021; Jones et al., 2023), how vegetation with different rooting depths facilitates or competes for soil moisture has great implications for overall ecosystem functioning and resilience.

In regions where groundwater is shallow and upper soil is dry, extensive studies report tree roots extending to the saturated zone and the ability of roots to wet shallow soil layers during dry periods (Hultine et al., 2004; Fan et al., 2017; Wang et al., 2018). Although observations of groundwater use by deep roots are uncommon, groundwater withdrawal by plants is suggested by diurnal fluctuations and the gradual decline of water table levels following the onset of the growth period, as well as from growth periods that are out of phase with precipitation patterns (e.g., Scott et al., (2004)). Consequently, annual evapotranspiration (ET) of ecosystems with groundwater-dependent species often exceeds yearly precipitation (Scott et al., 2006). As roots penetrate through the soil, they also serve as a conduit that guides the passive transport of water from humid soil layers to drier soil layers, a process often termed hydraulic redistribution (HR) (Amenu and Kumar, 2008). Although HR can occur in any ecosystem that experiences temporary drought regardless of annual rainfall, higher HR is usually found in water-limited regions with shallow groundwater where the vertical water potential gradients are large driving water flow from deep moist soils to shallow dry soils (Neumann and Cardon, 2012). The redistributed water by deep-rooted trees provides additional moisture for the coexisting shrubs, which have relatively shallow rooting depths and are more dependent on precipitation. Besides upward redistribution of soil moisture (i.e., from deep to shallow soil), seasonally wet periods with ample precipitation can stimulate root water uptake in shallow soil layers and the redistribution of surface moisture downward (Hultine et al., 2004; Scott et al., 2004). Therefore, while deep-rooted plants maintain groundwater access throughout the year, the distinct wet-dry periods drive seasonal shifts in the vertical distribution of roots, giving roots plasticity to switch water sources between soil moisture and groundwater (Fan et al., 2017; Scott et al., 2008).

Due to the lack of observational data to develop benchmarking root models and the scale gap between model resolution (hundreds to thousands of meters) and the heterogeneity of microenvironments roots experience (typically at millimeter scale), many land-atmospheric models typically represent root profiles by a static, exponentially decaying distribution of root fractions (Wang et al., 2016; Drewniak, 2019). Some models define root fraction as the fraction of total root biomass or root area index from a root physiology perspective, while others define root fraction as the fraction of total root water uptake from a plant hydraulics perspective (Arora and Boer, 2003; Wang et al., 2018). Although root biomass or density usually decreases with depth, the amount of water uptake may not decrease monotonically with depth, especially in groundwater-dependent ecosystems (Zeng, 2001; Wang et al., 2018). In water-limited regions, where the water table is reachable by tree roots, an exponential distribution of root fraction in models can overestimate soil water stress by limiting most root activities in the upper 2 m soil. In addition, a static root profile does not capture the seasonal variability of soil depths where roots get their water depending on WTD and precipitation patterns (Wang et al., 2016).

A self-optimizing root fraction profile that responds to resource availability can greatly enhance vegetation functionality in dry climates and overcome the complex parameterization needed to simulate detailed carbon allocation of root biomass and hydraulics between soil and different compartments of roots. Various approaches have been pursued to implement self-optimizing root fraction profiles, including maximizing carbon gain while minimizing water cost under different environmental conditions (Arora and Boer, 2003; Schymanski et al., 2008; Wang et al., 2018) and adjusting rooting depths based on changes in local resources, such as moisture and nutrient availability (Wang et al., 2016; Drewniak, 2019; Wang et al., 2022). Given the importance of groundwater in arid climates, Wang et al. (2016) and Wang et al. (2022) further implemented a fluctuating water table along with dynamic root profiles and found improved simulation results when deep-rooted plants grow more roots into the saturated zone and adapt to water stress.

Qualitatively, trees with stable groundwater access enhance ecosystem resilience by shifting water uptake from shallow soil during wet seasons to deep groundwater during dry seasons and providing additional moisture to shallow soil by HR. However, studies focused on root profile in ecohydrological processes associated with more than one vegetation type and maximum rooting depth, including the interactions between deep- and shallow-rooted species and their mutual responses to water stress, are rare in the literature. In this study, we incorporate a time-varying, moisture-driven root fraction profile and water uptake parameterization into an existing ecohydrological model (DCHM-V) to investigate how root dynamics of vegetations with different water sources influence soil moisture and aboveground vegetation activity at a semi-arid woodland site. At this study site, overstory trees (i.e., mesquites) have constant access to groundwater and share shallow soil moisture with shorter and shallow-rooted shrubs (Scott et al., 2004). The dynamic root profile characterizes the vertical distribution of effective root water uptake based on soil moisture, while an updated root water uptake scheme governs water transport through the groundwater-soil-plant continuum, allowing for HR. The model is first evaluated against observations. We then drive the model with atmospheric forcing projected by Thermodynamic Global Warming (TGW) simulations to project how the interactions between the overstory and understory may change under more extreme climates (Jones et al., 2023). The main goal of this study is to address the following questions:

1) How do coexisting trees and shrubs optimize their root fraction profiles based on local soil moisture and precipitation patterns at seasonal and interannual scales?

2) How do the time-varying root profiles facilitate or moderate the competition for soil moisture between different vegetation species?

3) How will the below- and above-ground vegetation activities adapted to the current climate respond to a warmer, more extreme climate?

The manuscript is organized as follows. Section 2 describes the study site. Section 3 provides a brief overview of the existing DCHM-V model followed by detailed formulations of newly added belowground. Section 4 describes the experimental design and data sets used in this study, including the forcing and parameters used in each experimental simulation. Analysis and discussion of results are provided in Section 5. In particular, the model is first evaluated using atmospheric forcing and vegetation parameters from different sources and compared against observations and related previous studies in the literature. The sensitivity of ecohydrological simulations to water table depth, dynamic root parameterization, and root structures and flexibility under current climates are discussed in Section 5.2, and Section 5.3 presents how vegetation with dynamic roots adapted to current climate responds to more extreme climates. Section 6 provides a summary and concludes the manuscript.

2 Study site

Our study is conducted in a mesquite woodland site on an floodplain terrace adjacent to the main channel of the San Pedro River in southeastern Arizona (Figure 1). The climate of the river valley is semiarid, with summer average maximum temperatures around 34°C and an annual precipitation of 288 mm (Scott et al., 2004). Winter frontal storms, usually occurring between November and March, provide 30% of the mean annual precipitation, and convective storms during the North American Monsoon, usually from July to September, provide about 60% of the annual precipitation (Scott et al., 2006). The soil texture is reportedly composed mainly of sandy loam interspersed with layers of clay and gravel (Scott et al., 2004).

Figure 1

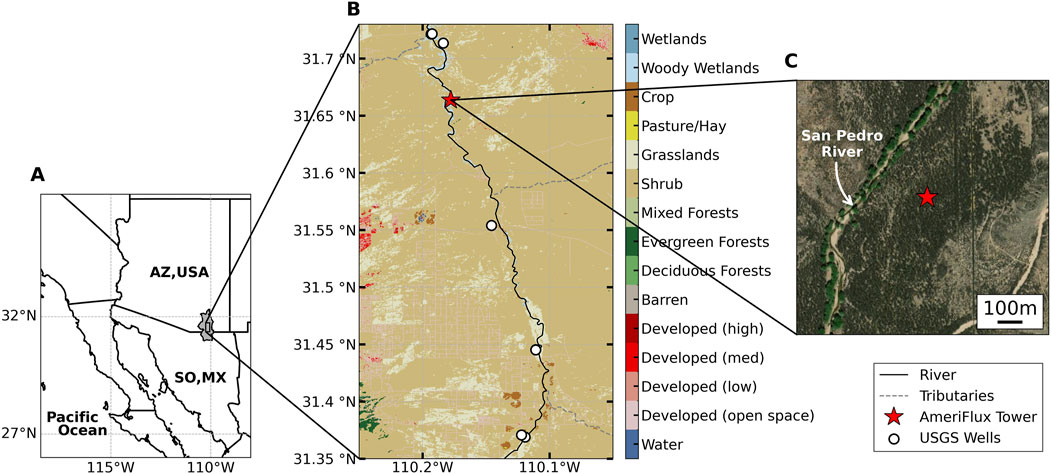
Figure 1. Maps showing the location and land cover of the study site in the Upper San Pedro River Basin. The basin (shaded in grey) extends into both Arizona, USA (AZ, USA) and Sonora, Mexico (Sonora, MX); (A) [U.S. Geological Survey (USGS), 2023b]. In (B), the locations of the AmeriFlux tower site (red star), the San Pedro River (black solid line) and its tributaries (grey dashed lines), and the USGS wells (white circles) used to train the Water Table Depth prediction model are plotted on top of a land cover map of the zoomed portion of the basin. The land cover map is from the National Land Cover Database 2004; [Wickham et al., 2014]. In (C), an enlarged satellite imagery highlights the range of the riparian mesquite woodland (dark green colors) around the tower (red star) and the location of the San Pedro River. Source for river location and satellite imagery: Esri; National Atlas of the United States; USGS; available at https://www.arcgis.com/home/item.html?id=8206e517c2264bb39b4a0780462d5be1.

Velvet mesquite trees dominate the woodland ecosystem with an understory layer primarily composed of shrub species (Scott et al., 2004). Velvet mesquite trees have deep-rooted systems that depend on groundwater sources (Scott et al., 2003). The root system of mesquite trees often consists of a deep taproot to access groundwater sources and a large number of lateral roots to harness soil moisture (Hultine et al., 2004; Scott et al., 2004). In contrast, understory roots have not been observed beyond 2–3 m soil depths, suggesting that they cannot reach groundwater typically at around 10 m at this site (Scott et al., 2004).

3 Methods

This study expands the coupling of ecohydrological processes to the Duke Couple Hydrology Model with Vegetation (DCHM-V) to study the role of vegetation adaptations in land-atmosphere interactions under a changing climate by improving the vertical soil profile of the rootzone, incorporating parameters and processes for desert climates, and developing a parsimonious parameterization of root dynamics. DCHM-V is a land surface model that solves for water mass and energy balance, coupled with a biochemical representation of both C3 and C4 photosynthesis pathways and a substrate-structure dark respiration parameterization (Barros, 1995; Devonec and Barros, 2002; Garcia-Quijano and Barros, 2005; Lowman and Barros, 2016; Lowman et al., 2018). Gebremichael and Barros (2006) and Lowman et al. (2018) have applied DCHM-V in the Sonoran Desert and South Africa, respectively, and successfully captured the observed magnitude and variations of the coupled water-carbon cycles in ecosystems spanning from semi-arid savanna to humid forests. The model is also part of a 3-D distributed land hydrology model that captures surface-subsurface interactions and channel routing at a sub-kilometer scale without calibration and is used for flood prediction (Yildiz and Barros, 2005, Yildiz and Barros, 2007, Yildiz and Barros, 2009; Tao and Barros, 2013, 2014; Liao and Barros, 2023). However, previous applications do not make distinction between species within a model column and did not account for HR, and thus, were not capable of examining the belowground dynamics and interactions between vegetation and soil moisture or between coexisting species.

Here, the 1-D (column) version of DCHM-V is used to simulate vertical land-vegetation-atmosphere interactions. Heat and water fluxes are evaluated at individual pixels and at each timestep between each soil layer and exchange with the atmospheric boundary layer at the surface. Given our study site’s coexisting tree and shrub vegetation composition, shading provided by the overstory trees divides the lower vegetation layer (i.e., shrubs) and the land surface into shaded and unshaded areas. While all shrubs in the lower vegetation layer share the same vegetation parameters, the shaded portion is termed “understory shrubs,” and the rest that is exposed to direct sunlight is termed “open shrubs.” A generic term “shrubs” is used to indicate the entire lower vegetation layer, adding together the understory and open shrubs. Below ground, the overstory rootzone extends to the capillary fringe above the water table, so a groundwater layer is introduced in the model to capture the interactions between mesquite roots and groundwater. The roots of the shrubs only occupy the top 3-m soil column, where they share the available water with the overstory. Due to a deeper soil column that extends to the water table reaching 11 m in depth (Scott et al., 2008), the original 3-layer soil column with 1 m depth in DCHM-V is expanded to 16 layers with 12 m depth. While soil depths and vegetation parameters used here represent soil and vegetation characteristics for this study site, the model formulation can be applied to any ecosystem. Next, we introduce the essential modification and formulation for dryland vegetation processes added to DCHM-V and refer to the enhanced model as DCHM-VDR hereafter.

Figure 2 shows a conceptual depiction of the model. A flowchart of the model and a conceptual diagram to illustrate the fractional representation of land cover classes at sub-grid scale are presented in Supplementary Figure S1. A glossary of the variables and acronyms used in this manuscript is presented in the Supplementary Material.

Figure 2

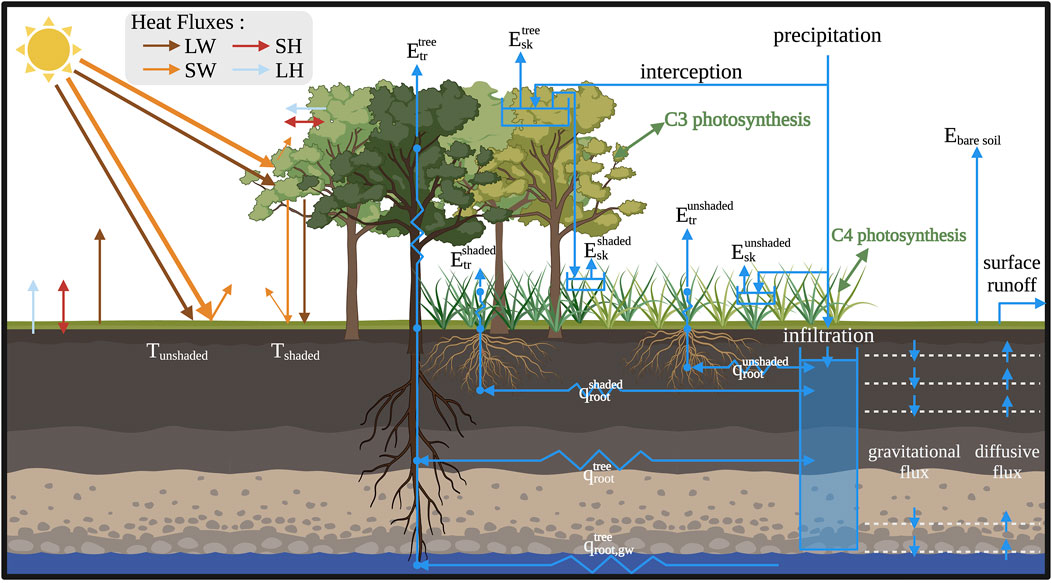
Figure 2. Conceptual depiction of surface energy balance and water fluxes and reservoirs in DCHM-VDR (created in Biorender.com). LW: incoming longwave radiation. SW: incoming shortwave radiation. SH: sensible heat. LH: latent heat. T_unshaded: bare soil temperature; T_shaded: soil temperature of the shaded portion of the model grid. E_tr: transpiration, E_sk: skin evaporation, E_{bare soil}: bare soil evaporation; q_root: root water fluxes. The superscripts of the evapotranspiration and root water fluxes represent the vegetation type. Tree: overstory layer; shaded: the portion of the lower vegetation layer shaded by overstory; unshaded: the unshaded portion of the lower vegetation layer.

3.1 Stomatal conductance

The model relies on an empirical stomatal conductance model following Stewart, (1998), which is described in detail in Devonec and Barros (2002) and Garcia-Quijano and Barros (2005). Mesquites are phreatophytic and highly efficient in extracting water from deep saturated zones (Hultine et al., 2004; Scott et al., 2004). To simulate the high transpiration and carbon assimilation rates measured in the field during prolonged drought periods, simulations of the stomatal opening of mesquites need to capture their high tolerance in vapor pressure deficit (VPD) and soil water stress. A glossary of model parameters is provided in Supplementary Material.

The VPD control in the stomatal conductance model follows Oren et al. (1999), where stomatal conductance ($g_s$) is linearly related to the natural log of vapor pressure deficit (VPD; Equation 1). The intercept ($g_{sref}$) and the slope ($m$) characterize the maximum $g_s$ when VPD is at 1 kPa and the sensitivity of $g_s$ to VPD, respectively. Based on a linear regression of available data from field measurements for mesquites (Lin et al., 2015), $g_{sref}=0.3043mol/m^2/s$ and $m=0.3609g_{sref}$. No specific data were found for the major shrub species at the study site. Hence, the median values of $g_{sref}=0.228mol/m^2/s$ and $m=0.317g_{sref}$ for the shrubs in the Sonoran Desert were adopted here (Ogle et al., 2012).

$g_s=g_{sref}-m\cdot \mathit{ln}\left(VPD\right)(1)$

To reduce stomatal opening when soil moisture is low, a linear response of $g_s$ to soil moisture stress based on the soil’s wilting point (${\theta }_{wp}$) and field capacity (${\theta }_{fc}$) is implemented as follows:

$f_2\left(\overline{\theta }\right)=\left\{\begin{array}{l}0,\overline{\theta }<{\theta }_{wp}\\ \frac{\overline{\theta }-{\theta }_{wp}}{{\theta }_{fc}-{\theta }_{wp}},{\theta }_{wp}\le \overline{\theta }\le {\theta }_{fc}\\ 1,\overline{\theta }\ge {\theta }_{fc}\end{array}\right.(2)$

The average soil moisture ($\overline{\theta }$) sensed by the canopy is estimated by averaging the soil moisture in soil layer $j$ where water extraction occurs and scaled by the root fraction ($f_{root,j}$; Equation 3).

$\overline{\theta }=\frac{{\displaystyle \sum _j}\left(f_{root,j}\cdot {\theta }_j\right)}{{\displaystyle \sum _j}{f}_{root,j}}(3)$

This parameterization ensures that soil moisture availability is only critical to plants in layers where roots extract water. For instance, the middle soil layers not reached by either precipitation infiltration or capillary rise contribute little to the soil moisture stress sensed by the mesquite.

3.2 Hydraulic redistribution (HR)

The plant hydraulics approximation in DCHM-VDR was updated to enable HR based on the “plant hydraulic stress” configuration in Community Land Model version 5.0 (Kennedy et al., 2019). The original formulation in DCHM-V uses Darcy’s law to approximate one-way water flow from soil to vegetation, which is more appropriate for shallow soils and humid regions (Devonec and Barros, 2002; Garcia-Quijano and Barros, 2005). The new formulation simultaneously solves root potential (${\psi }_{root}$) and leaf water potentials (${\psi }_{leaf}$), assuming no change in plant water storage (Equation 4).

$\left\{\begin{array}{c}{C}_v\cdot \sum q_{root,i}=q_{leaf}\\ q_{leaf}=C_v\cdot E_v\end{array}\right.(4)$

where $C_v$ is the vegetation cover fraction, $\sum q_{root,i}$ is the total root water fluxes between plant roots and all soil layers (Equation 5), $q_{leaf}$ is the root-to-leaf water flux (Equation 6), and $E_v$ is vegetation transpiration. Root water uptake from each soil layer $i$ and the evaporative demand at the plant leaves are tied to the soil water potentials (${\psi }_{soil,i}$), plant water potentials (${\psi }_{root}$ and ${\psi }_{leaf}$), and gravitational potentials ($g{z}_i$ and $gh$, where $z_i$ and $h$ are soil layer depth and vegetation height, respectively) and scaled by root fraction ($f_{root}$) and leaf area index (LAI).

$q_{root,i}=f_{root,i}\cdot \frac{{\psi }_{soil,i}-{\psi }_{root}-g{z}_i}{{\mathrm{\Gamma }}_{s-r,i}}(5)$

$q_{leaf}=LAI\cdot \frac{{\psi }_{root}-{\psi }_{leaf}-gh}{{\mathrm{\Gamma }}_{r-l}}(6)$

The resistances between soil and roots and between roots and leaves are estimated by ${\mathrm{\Gamma }}_{s-r,i}$ and ${\mathrm{\Gamma }}_{r-l}$, respectively, following Garcia-Quijano and Barros (2005). Since root water uptake is a function of the potential gradient between the soil and plant roots, roots extract water from the wet soil layers (i.e., ${\psi }_{soil,i}-{\psi }_{root}-g{z}_i<0$ and $q_{root,i}<0$). Conversely, roots release water, directly contributing to the soil moisture storage, when soil is dry due to low soil water potential (i.e., ${\psi }_{soil,i}-{\psi }_{root}-g{z}_i>0$ and $q_{root,i}>0$).

As shrubs and mesquites share soil moisture storage in the shallow root zone (upper 3 m), they both have access to the released water by HR. While the two species withdraw water from each shallow soil layer’s soil water resource pool, assuming their roots are equally effective, the total released water by HR is partitioned among the species based on LAI fraction ($f_{LAI}$) and root fraction ($f_{root}$). We estimate the released water available to each vegetation ($p$) in each soil layer ($i$) as follows:

${f\left(HR\right)}_{i,p}=\frac{f_{root,i,p}\cdot f_{LAI,p}}{{\displaystyle \sum _p}\left(f_{root,i,p}\cdot f_{LAI,p}\right)}(7)$

where $f_{root,i,p}=\frac{f_{root,i,p}}{{\displaystyle {\sum }_p}{f}_{root,i,p}}$ and $f_{LAI,p}=\frac{{LAI}_p}{{\displaystyle {\sum }_p}{LAI}_p}$. Vegetation with higher LAI and root fraction in a soil layer occupies a higher fraction of total HR.

3.3 Root dynamics

A new moisture-driven dynamic root system was also introduced in the DCHM-VDR. The model uses root fractions to quantify how much water is extracted from each soil layer as a fraction of total root water uptake controlled by soil moisture availability and evaporative demand. Rather than defining each layer’s root density or biomass, a root fraction profile directly estimates root activity (e.g., which layers are actively exchanging water with the roots). This parameterization does not distinguish between tap roots, fine roots, or lateral roots, but rather, the goal is to estimate the overall effective root water transport. For instance, tap roots near the saturated zone are very efficient in transporting water upwards and thus may have a high root fraction, even if the actual root biomass may be small. It is further assumed that the root systems are mature, which is true to reality at the study site (Scott et al., 2003).

The architecture of a mature root system remains relatively stable under typical climatic fluctuations but can adaptively adjust its water extraction depth in response to changes in precipitation patterns and fluctuations in WTD. Thus, the dynamic rooting profile in the model updates root fractions in each soil layer $i$ based on the daily average soil moisture ($\overline{{\theta }_i}$) at the end of each day ($t$) for the next day ($t+1$; Equation 8).

$f_{root,i}^{t+1}=\frac{f_{root,i}^t+∆f_{root,i}^t}{{\displaystyle \sum _{i=2}^N}\left(f_{root,i}^t+∆f_{root,i}^t\right)}(8)$

The daily change in root fraction in each layer ($∆f_{root,i}^t$; Equation 9) is controlled by a daily change coefficient (${∆k}_i^t$), layer thickness ($∆z_i$), and layer bottom depth ($z_{i,b}$). A maximum rate of change ($G_{rmax}$) further caps the daily changes in root fraction in each layer, such that $∆f_{root,i}^t$ cannot exceed the value of $G_{rmax}$.

$∆f_{root,i}^t=G_{rmax}·{∆k}_i^t·\frac{∆z_i}{z_{i,b}}(9)$

A critical soil moisture threshold (${\theta }_{cr}$) controls whether root fraction changes in each layer, and the amplitude of the change coefficient depends on $\overline{{\theta }_i}$ compared against field capacity and wilting point. Waterlogging is set to limit root growth when soil moisture reaches 95% of saturation (θ_sat), as most roots cannot survive under anaerobic conditions (Equation 10).

$∆k_i=\left\{\begin{array}{l}\frac{\overline{{\theta }_i}-{\theta }_{cr}}{{\theta }_{fc}-{\theta }_{wp}}if{{\theta }_{cr}\le \theta }_i<0.95{\theta }_{sat}\\ 0else\end{array}\right.(10)$

As a result, roots are more active in moister and shallower layers. Specifically for this study site, where shrubs and mesquites share soil moisture in the upper 3 m soil, $\overline{{\theta }_i}$ is the same for both vegetation species in the shallow soil layers. However, mesquite roots have access to deeper, moister soil layers, especially during dry periods, leading to higher root fractions distributed to deeper layers. The sensitivity of root profiles and vegetation dynamics to the two most important parameters in the model, $G_{rmax}$ and ${\theta }_{cr}$, is examined in Section 5.2.1. The new self-optimizing rooting profile directly impacts the soil moisture profile by shifting the water extraction depths along the root column. Changes to the soil moisture profile, in turn, influence soil water stress and aboveground vegetation processes.

The architecture and flexibility of root profiles control roots’ sensitivity to changes in the vertical soil moisture profile and where roots extract water. Plant hydraulics control vegetation’s ability to extract water, with more effort needed to draw water from deep and dryer soil layers. In combination, they influence the water use strategy of plants in response to different levels of water stress, that is, the water use efficiency (WUE) of the entire plant in its ecohydrologic context. In this study, we define hydrological WUE (${WUE}_h$) as the ratio of gross primary productivity (GPP) over total gross root water uptake (i.e., ${WUE}_h=GPP/\sum q_{root,i},where{q}_{root,i}<0$), which includes the water released to the soil by roots through HR. We further define plant WUE (${WUE}_p$) as the ratio of GPP over transpiration, which is the net water uptake reaching the canopy after subtracting the water released to the soil by HR.

4 Experimental design and data

DCHM-VDR was first forced by historical climate and evaluated against AmeriFlux tower observations to establish confidence in the model’s ability to capture the processes that govern the water and energy budgets. To explore sensitivity and adaptation to climate change in the region, two sets of ten-year-long simulations were conducted for the mesquite woodland site to explore the interaction of above- and belowground vegetation compartments under varying climate conditions driven by the Thermodynamic Global Warming (TGW) simulation dataset (described in Section 4.1): (1) historical climate (2000–2009) and (2) future climate (2090–2099) (Jones et al., 2023). Under the historical climate, we further examine the sensitivity of the ecosystem to WTD, root fraction parameterization, and different root structures. Table 1 provides a summary description of the simulations conducted.

Table 1

Table 1. A description of the experiments conducted in this study, along with the source of atmospheric forcing and vegetation parameters used in each run.

Model evaluation simulations use atmospheric forcing primarily from the AmeriFlux tower observations or the historical scenario of the TGW simulation dataset from 2003 to 2004. Vegetation dynamics are derived from Moderate Resolution Imaging Spectroradiometer (MODIS) products and Landsat imagery. Climate change experiments are forced by the future climate scenarios that follow the shared socioeconomic pathway with the highest emission (SSP585) in the TGW simulation dataset. The future LAI trend is derived from comparing the Sixth Coupled Model Intercomparison Project Phase (CMIP6) historical model outputs and SSP585 future global climate projections. In this study, we focus on the response of vegetation to climate variations and assume vegetation structures, including vegetation cover, fraction of photosynthetically active radiation (FPAR) absorbed by vegetation, and surface albedo, will remain the same in the future. Soil parameters are also assumed to be static and derived from the Soil Web Survey (USDA-NRCS, 2023).

A complete list of the data used in the model is provided in Supplementary Table S1. Dynamic WTD is predicted by a Multilayer Perceptron (MLP) model trained using nearby well observations, described in Section 4.3.

4.1 Atmospheric forcing data

For model evaluation, atmospheric forcing from the local AmeriFlux Tower observations is used first (Scott, 2002), except for downward longwave surface radiation and surface pressure due to limited tower observations. These two missing variables are obtained from the North America Land Data Assimilation System Phase 2 (NLDAS-2) atmospheric forcing data, which integrates multiple sources of observation-based and model reanalysis data and is primarily used to drive offline land-surface models (Mitchell et al., 2004; Xia et al., 2012). For the short period that longwave surface radiation observations are available from the tower, the variations and amplitude of NLDAS-2 match well with the observations (not shown here).

The TGW dataset used to force the climate change experiments is available over the U.S. at a spatial resolution of 12 km and hourly and 3-hourly temporal resolution. The dataset first uses the Weather Research Forecasting Model to dynamically downscale past weather data from the European Centre for Medium-Range Weather Forecasts version 5 re-analysis as a historical reference. Thermodynamic warming signals are derived from 8 global circulation models (GCMs) following SSP585 available via CMIP6 and used to forecast future warming trajectories. The GCMs are grouped into two categories based on their relative climate sensitivity. The trajectories predicted by signals derived from GCMs with a higher sensitivity are referred to as the hotter scenario, and the trajectories predicted by models with lower sensitivity are referred to as the cooler scenario. More details on the dataset are provided in Jones et al. (2023).

Incoming shortwave and longwave radiation at the land surface are corrected for the shading effects of the overstory canopy cover since subcanopy measurements are unavailable. A simple Beer-Lamber Law approach is adopted to estimate the transmissivity of shortwave radiation in vegetation canopy based on LAI and solar zenith angle ($\xi$) as follows:

${\tau }_{veg}^{SW}=e^{-\frac{LAI}{2\mathit{cos}\xi }}(11)$

One limitation of this approach is the inability to capture artifacts tied to the canopy structure (e.g., heterogeneity in the porosity space between leaves within the canopy). We further assume that canopy-emitted longwave radiation is the only source of downward longwave radiation under the tree canopies. Tower observed canopy temperature is gap-filled using a half-hourly lapse rate for each day of the year between canopy temperature measured at 10 m and air temperature measured at 3 m when observations are available. To estimate future canopy-emitted longwave radiation, future canopy temperatures are interpolated from the 2 m air temperature using lapse rates derived from air temperatures at 2-m and the lowest model level from the TGW simulation dataset. Due to the lack of temperature profile data, this approach cannot capture the daytime temperature inversion at the canopy layer, and therefore, it only provides a lower bound estimate of canopy temperatures during the daytime.

Land surface albedo was acquired from the NLDAS-2 Mosaic Land Surface Model L4 dataset at hourly temporal resolution and 12.5 km spatial resolution (Xia et al., 2012). For simplicity, we assume land surface heterogeneity will not change in the future, and thus, land surface albedo remains the same for all model runs.

4.2 Vegetation parameters

One of the sources for observed LAI and FPAR is MODIS Terra (MOD15A2H) and combined Terra and Aqua (MCD15A2H) products, available at 500-m spatial resolution and 8-day temporal resolution (Myneni et al., 2021a; Myneni et al., 2021b). Since overstory canopies usually hinder remote sensing observations of understory, we use the average values of the gap-filled and smoothed MODIS results for all the 500-m pixels that have a land cover type of shrubland according to the combined Terra and Aqua product (MCD12Q1) in an area of 6 km × 6 km centered over the tower location to represent the dynamics of shrub near/under trees (Friedl and Sulla-Menashe, 2022). Specifically for mesquite, another source of observed LAI and FPAR with finer spatial resolution is the Enhanced Vegetation Index (EVI) derived from Landsat-7 imagery data [Landsat-7 image courtesy of the U.S. Geological Survey]. The estimates assume a linear relationship between FPAR and EVI and an exponential, non-linear relationship between LAI and EVI (Myneni et al., 1997). The adaptive Savitzky-Golay filter in TIMESAT was used to fill gaps and reduce noise in vegetation time series of both data products (Jönsson and Eklundh, 2004). For both products, spring and autumn air temperatures control the mesquite growing season (i.e., LAI >0) between the last freeze in spring and the first freeze in autumn, while open shrubs and understories are perennial (Scott et al., 2004).

A total of 13 models in CMIP6 provide daily LAI outputs for historical and SSP585 scenarios (Supplementary Table S2). However, a comparison of historical CMIP6 LAI outputs with the satellite-observed LAI data demonstrates that CMIP6 models fail to capture the phase and amplitude of LAI seasonality at the study site. Furthermore, CMIP6 models do not differentiate between understory and overstory vegetation. Instead of directly assimilating CMIP6 LAI outputs into DCHM-VDR, we calculate how much LAI increases for each day of the year (DOY) in the future scenarios based on CMIP6 multi-model ensembled (MME) LAI outputs. Then, we use the CMIP6 MME mean increase ratio ($r_{\mu ,DOY}$) in LAI to scale observed mesquite and shrub LAI to represent future vegetation dynamics (Equation 12).

$r_{\mu ,DOY}=\frac{{LAI}_{\mu ,DOY,SSP585}}{{LAI}_{\mu ,DOY,historical}}(12)$

Satellite-observed vegetation cover fraction (${CV}_{satellite}$) is estimated using the Normalized Difference Vegetation Index (NDVI) from Landsat 7 Band 3 (the red band) and Band 4 (the near-infrared band), where bare soil NDVI (${NDVI}_0$) is 0.05 and full vegetation NDVI (${NDVI}_s$) is 0.8 (Equations 13, 14).

$NDVI=\left(\frac{Band4-Band3}{Band4+Band3}\right)(13)$

${CV}_{satellite}=\left(\frac{NDVI-{NDVI}_0}{{NDVI}_s-{NDVI}_0}\right)(14)$

Based on the literature, ${CV}_{satellite}$ is partitioned into mesquite, understory shrub, and open shrub cover fractions such that mesquites dominate around 70% of the canopy cover during peak growth periods (Scott et al., 2014), and shrubs (the combination of understory and open shrub) cover ranges from around 10% in pre-monsoon periods to 50% in monsoon periods (Scott et al., 2003; Yepez et al., 2007). Since we assume land cover and vegetation composition and structures will remain the same in the future, we use the observed vegetation cover fraction and FPAR data for future climate scenarios.

4.3 Regional water table depth (WTD) prediction

Groundwater is a crucial water source for mesquite trees, especially during the dry periods. However, WTD observations are not publicly available at the study site, and predictions need to be made for the future climate. In this study, we train an MLP model to predict WTD using climate and vegetation data, field-based groundwater observations, and geographical variables (Supplementary Figure S2). Eight groundwater wells with more than 5 years of publicly available daily observations near the San Pedro River in the Upper San Pedro River Basin, where our study site is, are selected [U.S. Geological Survey, 2023c; Figure 1]. At each site, daily minimum and maximum temperatures are obtained from Daymet (Thornton et al., 2022), daily total precipitation is obtained from Stage IV (Du, 2011), and LAI is obtained by averaging the quality-filtered MOD15A2H and MCD15A2H products (Myneni et al., 2021a; Myneni et al., 2021b). The minimum horizontal and vertical distances between each well and the San Pedro River are derived from 1-m Digital Elevation Models (U.S. Geological Survey, 2023a) and National Hydrography Dataset flowline data (U.S. Geological Survey, 2023b).

MLP is selected because of its nonlinear modeling ability, flexibility in input data formats, and effectiveness in generalizing data (Sahu et al., 2020). After testing 20 different sets of MLP hyperparameters to tune the number of layers and number of nodes per layer, a two-layer MLP with a hidden size of 64 and 128 in each layer, respectively, is chosen and trained using a learning rate of 0.0001 for 10 epochs. Cross-validation is used to check the ability of MLP to capture seasonal and spatial variations in WTD. The last 2 years of data at each site are grouped into a test set, withheld from training and validation. After leaving out the test set, each fold of the cross-validation uses data from one of the wells as the validation set and data from the other sites as the training set. After each site is used as a validation set at least once, the average root-mean-square error (RMSE) is 0.3 m. The average RMSE and coefficient of determination (R²) on the test set are 0.4 m and 0.96, respectively. The model performance on the test set shows good agreement in the seasonal variations and the amplitude of WTD between prediction and observations. However, the model cannot capture non-stationarity, such as strong WTD uprising in extremely wet years and the potential influence of anthropogenic groundwater withdrawal (Supplementary Figure S3).

After validating and testing the model, WTD is predicted by forcing the MLP model with the climate conditions of each period. Due to the limited land cover types characterized by the training data, the trained MLP can only capture the seasonal trend of WTD at the riparian woodland site in this study but underestimates the absolute depth or the range of fluctuation. Instead, the range of seasonal variations of the predicted WTD aligns better with the observation at the shrubland and grassland sites upstream (Scott et al., 2006). In Section 5.2.2, we scale and shift the predicted WTD under historical climate, such that the average depth extends to 10 m and the decline of the water table after mesquite leaf-out reaches 1 m according to the literature (Scott et al., 2008), and discuss in detail how the bias in the predicted dynamic WTD do not affect the overall root water uptake patterns and future trends. Another limitation in using the trained MLP to predict future WTD at the study site is that this approach assumes the current relationship between atmospheric forcing and WTD still holds in the future, yet such a relationship is likely going to change due to complex interactions among hydrological processes, especially at a riparian site. However, accounting for the non-stationarity in WTD is beyond the scope of this study and will be addressed in more detail when integrating DCHM-VDR into the 3-D distributed land hydrology model.

5 Results and discussion

5.1 Model evaluation for historical climate

To evaluate DCHM-VDR’s performance on riparian woodland in a semi-arid climate, simulation results are compared with field measurements. The model is uncalibrated, and model results are grid-based and spatially averaged. Thus, we do not expect a perfect agreement between model simulations and the point-scale measurements made at the AmeriFlux tower. Rather, the goal is to establish the model’s ability to simulate the water processes and photosynthesis rates consistent with observed seasonal and inter-annual variability.

5.1.1 Comparisons of model simulations against observation

5.1.1.1 Evaluation of simulated soil moisture

Simulated shallow soil moisture responds to rainfall pulses similar to tower observations (Supplementary Figure S4). The model is generally more sensitive to intense and consecutive precipitation events while less sensitive to small and isolated precipitation events, partly due to a lack of representation for preferential infiltration pathways tied to roots and soil in the model. Also, our column model cannot capture lateral subsurface flow at times of increased precipitation and when water levels are on the rise, which lowers the sensitivity of modeled soil moisture at mid-depths (Supplementary Figures S4D, E). Although no observations are available near the water table, DCHM-VDR captures the seasonal drawdown of deep soil moisture during the mesquite peak growing season (May–October) and the replenishment during the dormancy (October–May; Supplementary Figure S4F).

5.1.1.2 The seasonality of aboveground vegetation activities

The seasonality of modeled latent heat, GPP, and Bowen ratio (i.e., the ratio of sensible heat to latent heat) matches well with tower observations (Figure 3). Both latent heat fluxes and GPP remain low between the first nighttime freeze event in late fall and the last freeze event in mid-spring, which signal the senescence and leaf-out of mesquites, respectively. As mesquites begin transpiring water and assimilating carbon actively after leaf-out, latent heat and GPP rise simultaneously. After entering the monsoon season, frequent and large precipitation events replenish shallow soil moisture (Supplementary Figures S4A–D) and facilitate the growth of shrubs, further increasing the latent heat and GPP (Figures 3A, C). Towards the end of the growing season, decreasing temperatures lowers mesquite and shrub activities and reduces latent heat and GPP.

Figure 3

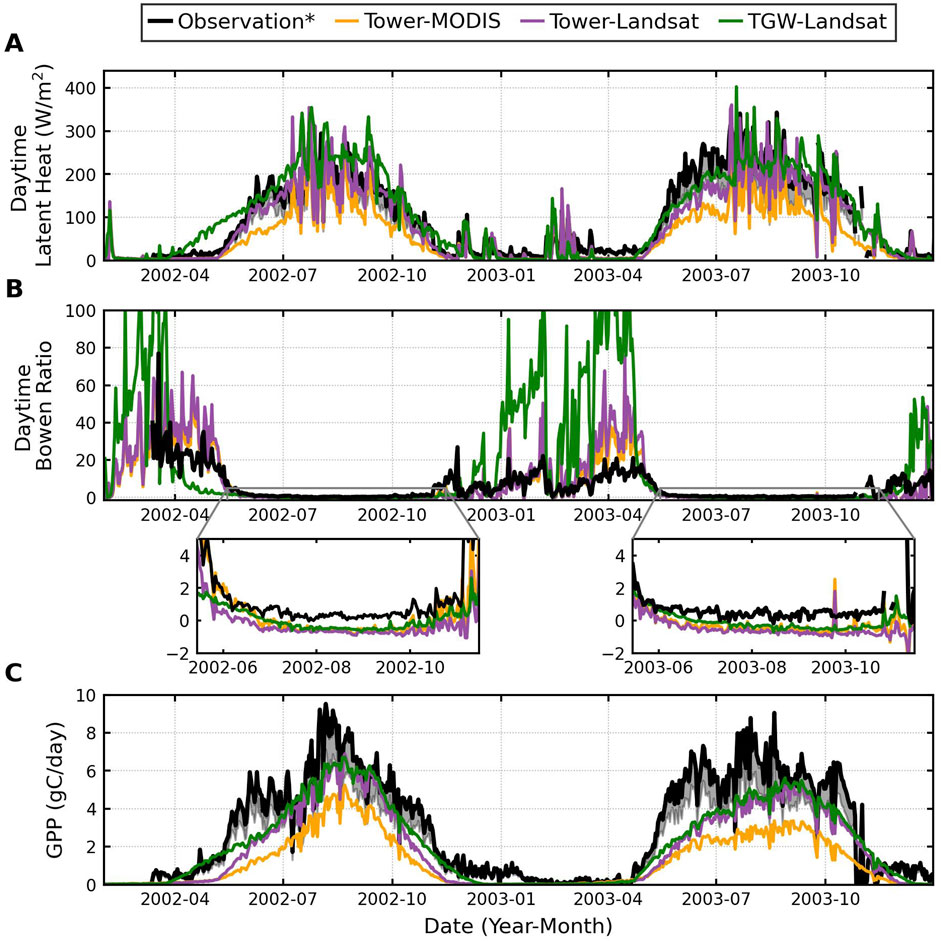
Figure 3. A comparison of tower observed and modeled daytime average latent heat (A), daytime average Bowen ratio (B), and daily total GPP (C). Simulations using atmospheric forcing from tower observations and vegetation parameters from MODIS and Landsat are shown in orange and purple, respectively. Simulations using atmospheric forcing from the historical scenario of the TGW dataset and vegetation parameters from Landsat are shown in green. An asterisk is put next to “Observation” in the legend to highlight that tower estimates of latent heat and sensible heat were modified to impose daily energy balance closure while preserving the daily Bowen ratio; CO₂ fluxes were modified in the same way as sensible and latent heat (typically a positive correction of ∼25%) (Scott et al., 2004). The grey shaded lines in (A, C) aim to represent the uncorrected tower data and were derived by reducing the latent heat and GPP by 25%.

The Bowen ratio follows the opposite trend of latent heat (Figure 3B). In winter, the Bowen ratio is highly sensitive and can reach above ten because vegetation is mostly dormant under low temperatures, leading to low latent heat. During mesquite’s growth period, high latent heat due to active transpiration and monsoon activities reduce Bowen ratio to below one, as shown in the insets that enlarge Bowen ratio from May 15 to November 15 in Figure 3B. The underestimation of the modeled Bowen ratio during mesquite’s growth period is due to a difference in reference height used by the model (2 m) and the measurement height of the tower (14 m). The overstory has a maximum canopy height of approximately 12 m, so the tower measures energy balance above the canopy. However, our model simulates energy balance below the canopy, near the surface, and thus, cannot be compared to tower observations directly. The shading of the canopy reduces the heat exchange between surface soil and sub-canopy air and, subsequently, the Bowen ratio. Model simulations without shading effects match tower observations more closely, demonstrating the cooling effects of shading on reducing sub-canopy sensible heat and Bowen ratio (Supplementary Figure S5).

5.1.1.3 The effects of different forcing

Simulations forced by TGW atmospheric data have an earlier onset of the mesquite growth period due to the temperature difference between measurements made at a point scale and reanalysis forcing data at a grid scale. The study site is in a riparian corridor, where in situ nighttime temperatures are generally 5°C–10°C lower than outside of the corridor (Scott et al., 2004). Because subgrid-scale heterogeneity cannot be captured, temperatures from the TGW dataset are generally higher than tower measurements, triggering earlier onsets of the mesquite growth period. Higher temperatures before mesquite’s growth period also result in higher sensible heat and Bowen ratios. In addition, the differences in precipitation between Tower (black) and TGW (grey) during the monsoon (Supplementary Figure S6B) explain the lower modeled soil moisture using TGW forcing, especially in 2002 (Supplementary Figures S4B–D).

Simulation results using vegetation parameters derived from satellite products at different spatial resolutions illustrate the impacts of uncertainties in vegetation parameters on modeled vegetation activity. As shown by a series of sensitivity tests performed by Yildiz and Barros (2007), vegetation properties of vegetation cover fraction and LAI are the key model parameters governing ET, especially in a dry climatic regime. First, land cover changes from dense mesquite forest to desert shrubland at a distance greater than 150 m southeast of the tower (Figure 1) (Scott et al., 2004). Landsat has a spatial resolution of 30 m, while MODIS LAI/FPAR products have a spatial resolution of 500 m. Hence, MODIS averages across a mixture of mesquite woodland and desert shrubland, whereas Landsat primarily senses the mesquite forest within the tower pixel. Previous studies have measured an average LAI of around 1.0 m/m and 1.6 m/m before and after the leaf-out of mesquites at this site (Scott et al., 2004), which can be successfully captured by Landsat EVI-derived LAI but not by MODIS (Supplementary Figure S7). Consequently, simulations using Landsat-derived LAI and FPAR (purple) produce latent heat and GPP more comparable with tower observations than MODIS (yellow, Figures 3A, C).

However, the seasonality and amplitude of understory LAI are difficult to describe because the obstruction by the forest canopy makes it difficult for remote sensing observations to capture understory vegetation dynamics. In this study, we average the values of the surrounding shrubland pixels identified by MODIS to obtain understory LAI, where overstory shading is substantially lower. Hence the values we use are likely an underestimate of the understory LAI in the mesquite woodland.

Moreover, the underestimation of simulated GPP and overestimation of Bowen ratio during pre-monsoon and post-monsoon periods can be associated with uncertainties in the partitioning of overstory and understory vegetation cover fractions. Specifically, fixing the mesquite vegetation cover at 70% according to ground measurements (Scott et al., 2004), which is consistent with the value derived from LAI at the monsoon peak, significantly increases latent heat flux and GPP during the mesquite green-up phase (Supplementary Figure S8) to better agree with the tower observations corrected for energy budget closure. However, using globally available data, such as MODIS and Landsat, enhances the model’s applicability across various ecosystem types and different hydroclimatic regimes, providing greater transferability and reproducibility.

5.1.2 Temporal variations in root dynamics

5.1.2.1 Root fraction profile and groundwater use

Figure 4 depicts the seasonally averaged root water fluxes and root fraction profiles as a function of depths in 2002 and 2003 simulated using atmospheric forcing from tower observations and vegetation parameters derived from Landsat. Since the evolution of the dynamic root profile is primarily driven by soil moisture gradients, the optimized root fraction profiles closely follow the precipitation patterns. Particularly, mesquite roots transition from mainly extracting near the water table during pre-monsoon periods (orange solid lines) to near the surface and near the water table during the monsoon periods (green solid lines, Figure 4). Recorded field data shows minimal fluctuations in soil water content to rain pulses at 1-m depth (Scott et al., 2004), which is also illustrated by the insensitivity of simulated soil moisture in Supplementary Figure S4E. Constrained by the depth of precipitation infiltration and capillary rise, most root activities are concentrated in the top 1 m and near the water table of the soil column. This dimorphic root profile matches well with field observations in regions with dry seasons and relatively shallow water tables (Bleby et al., 2010; Fan et al., 2017).

Figure 4

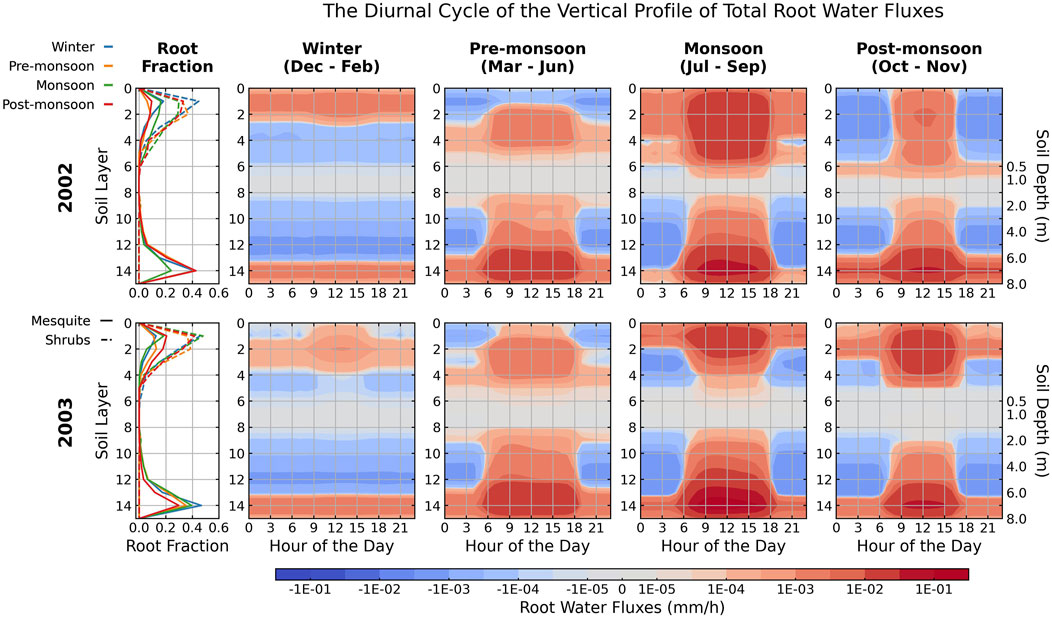
Figure 4. Diurnal cycle of seasonally averaged root water fluxes as a function of soil layer depth by both vegetation types in 2002 (top row) and 2003 (bottom row). Plant roots extract water from the red-shaded soil layers and release water in the blue-shaded layers. Seasonally averaged mesquite and shrubs (both understory and open shrubs) root fraction profiles are plotted in the first column for 2002 (top row) and 2003 (bottom row). The colors of the root fraction plots represent different seasons. Solid lines represent mesquites, and dashed lines represent shrubs. All results are from model simulations using atmospheric forcing from tower observations and vegetation parameters from Landsat and plotted on a log scale. Each day starts at midnight, 0:00 local time.

Although trees may supplement groundwater sources with shallow soil moisture sources during the monsoon period, their root distribution is unlikely to undergo significant changes as the changes require an alteration of mesquites’ hydraulic architecture and investment of additional resources (Scott et al., 2003). Scott et al. (2006) analyzed field measurements in the 2003 growing season (May–November) and reported a groundwater use estimate of 473 mm, contributing to 74% of total ET. Similarly, in our simulations, most mesquite roots remain in the deep soil layers (layers 8–14) regardless of precipitation patterns (Figure 4). Consequently, root water uptake from deep soil, where the only water source is the capillary rise from groundwater and HR by mesquite, constitutes 72% (374 mm) of total ET (522 mm) over the growing season in 2003 (Supplementary Table S3). The groundwater access allows mesquite to tolerate high water stress during the dry periods and grow out of phase with precipitation, explaining the observed and simulated high latent heat and GPP and low Bowen ratio during the pre-monsoon period (March–June) despite minimal precipitation (Figure 3). On the other hand, shrubs have a shallower rooting depth and thus have relatively fewer variations in the depths of root water uptake though the trend of a higher fraction of shallow roots during wet periods resembles that of mesquites.

5.1.2.2 HR in dry and wet seasons

Guided by the dynamic root fraction profiles, root water uptake and redistribution demonstrate distinctive daily and seasonal patterns (Figure 4). During daytime (6:00–18:00), active transpiration prompts net root water uptake, and little water is released to the soil by roots. At night (18:00–6:00), root water potential rises due to low transpiration demand, and HR occurs frequently. The water potential differences between roots and soil lead to root water extraction in moist soil layers and root water release in the dry soil layers.

During the monsoon season, direct precipitation infiltration due to frequent rain events increases soil moisture in the top 0.5 m soil (Supplementary Figures S4B–D). Higher soil moisture prompts higher root fractions (green lines) and water uptake in shallow rootzone (soil layers 0–7, Figure 4). As transpiration ceases at night, the shallow rootzone moisture is redistributed downward to the deeper soil layers. Our model estimates an average root water release rate of 0.24 ± 0.15 mm/day by mesquites during the monsoon season (July–September, Supplementary Table S4). Previous studies in the San Pedro River Basins estimate an average downward HR of 0.16 ± 0.13 and 0.46 ± 0.37 mm/day from mesquites without groundwater access and 1.48 ± 1.23 from mesquites with groundwater access during the monsoon season (Neumann and Cardon, 2012). Our model results fall within the range of field measurements.

Besides the monsoon season, winters at the study site are also relatively wet. Despite mesquite dormancy in winter, belowground vegetation processes are still active because nighttime soil temperatures are above zero all year round, and the transport by root is hydraulically done and detached from metabolic energy. As intermittent rain events wet the shallow soil layers, shrubs and mesquites extract water from the wet shallow rootzone (top three soil layers) and release the water to deeper soil layers (Supplementary Figure S9). Total HR in winter on average release 0.12 mm/day, which is 38% of the average release rate (0.32 mm/day) during the monsoon season (Supplementary Table S4). The redistributed moisture stored in deeper soil columns during the dormant season could provide crucial additional water supply for mesquite and shrubs at the beginning of the growing season before the monsoon season arrives (Hultine et al., 2004). On the contrary, pre-monsoon and post-monsoon seasons are usually dry with little precipitation. Large potential gradients drive mesquite and shrubs to lift water from deeper, moister soil layers to surface soil layers.

The simulated patterns of hydraulic descent during wet periods and hydraulic lift during dry periods align with previous studies at this study site (Hultine et al., 2004; Scott et al., 2008; Lee et al., 2021). The redistributed water lowers the soil water stress and supports mesquite and shrub transpiration during the day. As mesquite roots extend through the middle dry soil columns and reach the saturated zone, mesquites on average uptake (1.22 mm/day) and release (0.15 mm/day) a greater amount of water than shrubs, which uptake and release 0.15 mm/day and 0.05 mm/day, respectively (Supplementary Table S4). However, the release rate of mesquites is much lower than their uptake rate compared to shrubs since mesquites can utilize groundwater to meet transpiration demand, implying that mesquites are less dependent on HR.

5.1.2.3 Interannual variations in root dynamics

When comparing the precipitation patterns in the two consecutive years (2002 and 2003), 2002 had an extended drought period before the monsoon season but experienced relatively more concentrated and intense precipitation during the monsoon season (Supplementary Figure S6). The prolonged dry period in the 2002 pre-monsoons season negatively affected mesquite and shrub at the beginning of the growth period and resulted in lower total transpiration (393 mm) in 2002 compared to 2003 (462 mm; Supplementary Table S3). Although precipitation intensity during the 2003 monsoon season is weaker than in 2002, vegetation activities are unaffected as latent heat and GPP are comparable with those in 2002 (Figures 3A, C). The wetter post-monsoon period in 2003 further extended the high transpiration rates towards the end of the growing season and changed the direction of HR from upward in 2002 to downward in 2003 (post-monsoon column in Figure 4). The reduced transpiration rates caused by the prolonged dry period in 2002 highlight the importance of moisture conditions before the onset of the mesquite growth period.

5.2 Root plasticity under historical climate

5.2.1 Sensitivity of roots under historical climate

The two critical parameters in the dynamic root parameterization, maximum rate of change ($G_{rmax}$, fraction of total roots per day) and soil moisture threshold (${\theta }_{cr}$, m/m), regulate the rate of change in roots and the sensitivity of root fractions to soil moisture conditions. The difference in aboveground vegetation activity is trivial as long as $G_{rmax}$ is above zero (Supplementary Figure S10A). The significant difference between a changing and non-changing root profile will be discussed in Section 5.2.3 when comparing static and dynamic root profiles. Shrub roots are generally insensitive to $G_{rmax}$, but more shallow mesquite roots are allocated to deeper soil layers as $G_{rmax}$ increases, especially in the shoulder seasons when mesquite roots retract more quickly to groundwater source (Supplementary Figure S11E). The higher deep root fraction associated with faster changing rates, especially in the shoulder seasons, promotes the hydraulic lift of groundwater, which increases the deep soil moisture (Supplementary Figure S11D).

The soil moisture threshold (${\theta }_{cr}$), on the contrary, has a larger influence on vegetation activities, root fraction, and soil moisture profile. Roots are less sensitive to soil dryness at a lower soil moisture threshold, and the distribution is more uniform throughout the soil column (Supplementary Figure S12E). A more uniform root profile signifies a more uniform root water extraction profile from all soil layers, lowering the overall soil moisture (Supplementary Figures S12B–D). The higher presence of roots in drier layers also increases the plants’ soil moisture stress and reduces transpiration and GPP at the canopy level (Supplementary Figure S10B). During mesquite’s growth period, mesquites maintain their connectivity to groundwater, so the Bowen ratio, GPP, and WUE are less sensitive to the fraction of roots in shallow soil layers. Overall, the lower sensitivity of ecosystem functions to the rate of change in roots and the higher sensitivity to soil moisture threshold suggest that the dynamic root profile optimizes based on antecedent soil moisture conditions and precipitation durations with less dependence on the speed of reaching optimization.

5.2.2 The influence of varying water table depth

While precipitation drives shallow root profiles, groundwater level inhibits deep roots due to the anoxic environment associated with waterlogging. Although the column version of DCHM-VDR cannot capture the groundwater flow and the two-way coupling between root water extraction and variations in the water table, we use an MLP-predicted, time-varying water table to capture the control of WTD on rooting depths. As discussed in Section 4.3., the trained MLP underestimates WTD and seasonal groundwater drawdown at the mesquite woodland site due to data availability limitation in the training set. Here, we scale and shift the predicted WTD under historical climate to match literature-reported values (Supplementary Figure S13) to test whether a slightly deeper WTD significantly changes the interactions between vegetation and water sources.

The overall root architecture and water uptake patterns remain unchanged after using a deeper water table (Supplementary Figure S14). However, the higher potential difference between surface and deep soil as roots extend deeper to meet the bias-corrected WTD requires more effort for mesquites to lift deep groundwater, so mesquite increases its root fraction and water uptake in the shallow rootzone using the bias-corrected WTD (Supplementary Figure S15). Deeper WTD does not affect mesquite transpiration and ${WUE}_p$, but increases gross root water uptake and decreases ${WUE}_h$ in the shoulder seasons when the surface soil is dry as mesquites compete with shrubs for moisture and need to lift more groundwater to shallow rootzone (Supplementary Figure S16B). Increased competition also reduces shrub root water uptake and increases both shrub ${WUE}_p$ and ${WUE}_h$ (Supplementary Figure S16C). Regardless of the changes in belowground dynamics, using bias-corrected WTD does not influence the Bowen ratio or GPP (Supplementary Figure S16A). In general, deeper WTD leads to higher shrub WUE and lower mesquite WUE, but a 2-m shift does not result in significant changes in aboveground vegetation.

5.2.3 The importance of both the structure and flexibility of root profiles

5.2.3.1 Differences in root water uptake patterns when using different root profiles

To better understand the influence of root fraction profile on belowground and aboveground moisture availability, we compare model simulations using three root fraction parameterizations: (1) static exponential: static, exponentially decaying root fraction profiles for both shrubs and mesquites, (2) static dimorphic: static root fraction profiles obtained from averaging the root profiles optimized by the dynamic root fraction parameterization, such that mesquite root profile is dimorphic, and (3) dynamic: dynamic root fraction profiles calculated using Equations 8–10. Each type of root fraction profile and its associated seasonally averaged total root water fluxes are shown in Figure 5, with root dynamics for mesquites and shrubs separately shown in Supplementary Figure S17. The static exponential profile allocates more roots between 1–6 m depths, while the static dimorphic and dynamic profiles invest more roots in the top 0.5 m and 2 m above the water table. Accordingly, roots work at different depths using different root profiles.

Figure 5

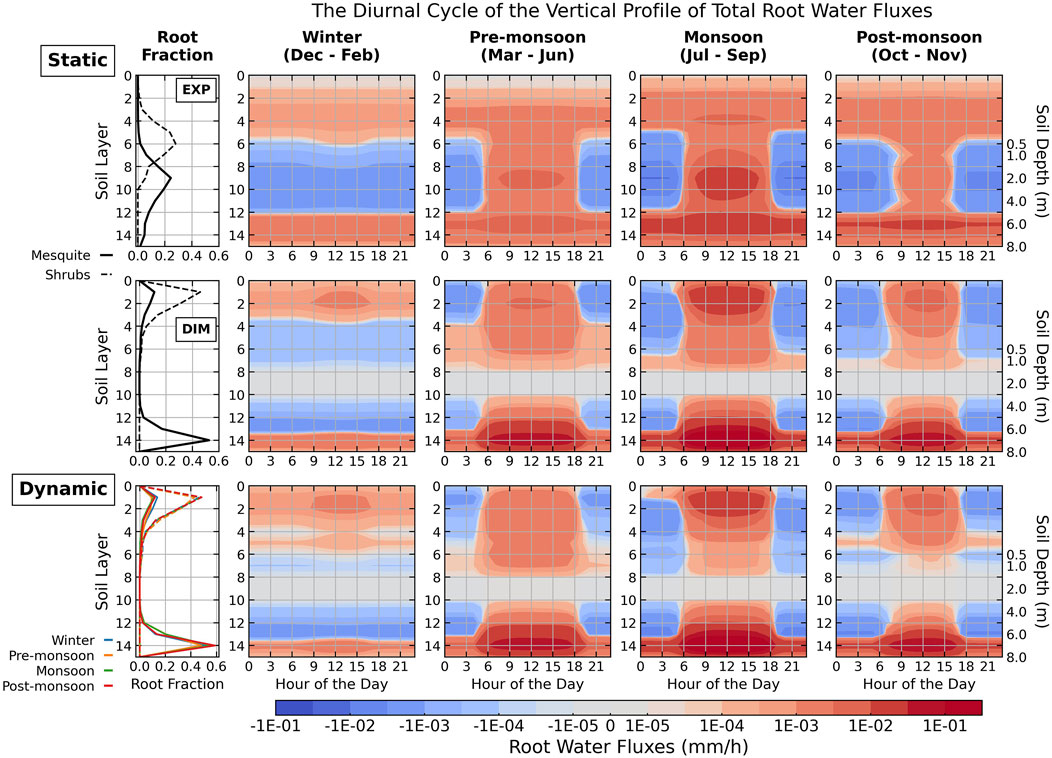
Figure 5. The diurnal cycles of seasonally average root water uptake (red) or release (blue) as a function of soil layers and depths by both vegetation types for different root fraction parameterizations: top row–static, exponentially decaying root fraction profiles (EXP); middle row–static, dimorphic root fraction profiles averaged from the dynamic root simulation (DIM); and bottom row - dynamic root fraction profiles. Results are plotted on a log scale. Seasonally averaged mesquite and shrubs (both understory and open shrubs) root fraction profiles are plotted in the first column for different root profiles in each row. Solid lines represent mesquites, and dashed lines represent shrubs. Static root profiles are shown in black in the top two rows. The colors of the dynamic root fraction plots represent different seasons. Each day starts at midnight, 0:00 local time.

When using a static exponential root profile, roots uptake and release significant amounts of water in the middle soil layers (1–6 m depth) regardless of the dry and wet seasons (Figure 5). Dry middle soil prompts high HR at night, causing shrubs to constantly redistribute moisture downward and mesquites to lift groundwater upward to wet the middle layers (layers 6–12, Supplementary Figure S17).

In contrast, the dimorphic or dynamic profiles focus root activity in the top 2 m and bottom 4 m of soil, changing water extraction depths and HR directions seasonally (Figure 5). During wet seasons, uptake increases near the surface in response to precipitation replenishment, while HR redistributes shallow soil moisture to mid-depths and near the saturated zone at night (Supplementary Figure S17). During dry seasons, uptake primarily occurs near the water table, and HR lifts water to drier shallow layers. Although roots overlap more in the shallow soil layers, unlike the static exponential root profiles, precipitation recharge during the monsoon period and shifts in water source during the dry periods can still sustain transpiration demand during the day.

The differences in root water uptake patterns between static dimorphic and dynamic root profiles are less pronounced when averaged annually, which is expected since the static dimorphic root profiles are the decadal average of the dynamic root profiles. However, at a seasonal scale, the dynamic root profile operates better in responding to changing precipitation by shifting uptake depths (Supplementary Figure S18). Water uptake concentrates more in mid-depths (layers 6–8) or near the water table (layers 10–14) during pre-monsoon seasons, then shifts from mid-depth (light green) to the surface (dark green) during the wet seasons, and stays near the surface during post-monsoon season as the preceding monsoons replenish shallow soil moisture (Supplementary Figure S18). Increased competition also occurs as roots shift to shallow wet layers and avoid the dry soil layers, lowering shrub uptake and transpiration during the monsoon season while showing minimal impact in other seasons or on mesquites.

Figure 6 summarizes the annual water budget and the fraction of HR over transpiration when different root profiles are used. Due to a higher fraction of roots allocated to the dry middle soil layers, mesquite with a static exponential root profile withdraws only 256 mm/year on average and releases 73 mm/year, leading to a transpiration rate of 183 mm/year (Figure 6A; Supplementary Tables S5, S6). With a dimorphic root profile, root water uptake and release by mesquite reaches 692 mm/year and 63 mm/year, respectively, resulting in an annual transpiration of 629 mm, 3-fold of that with exponential profiles. More importantly, the higher dependence of mesquites with dimorphic roots on groundwater reduces the fraction of HR over transpiration for mesquites from 34% to 6% (calculated using Equation 6), indicating a much less reliance on HR (Figure 6B). Shrubs have higher uptake using exponential than dimorphic profiles due to less competition but release more water to the middle dry soil layers, reducing overall transpiration from 40 to 31 mm/year and increasing the fraction of HR over transpiration from 73% to 79%. Using dynamic root profiles results in the least fraction of HR over transpiration (69% for shrubs and 6% for mesquites), demonstrating the effectiveness of dynamic roots in utilizing soil moisture and modulating HR and the influence of roots on the interactions between shrubs and mesquites.

Figure 6

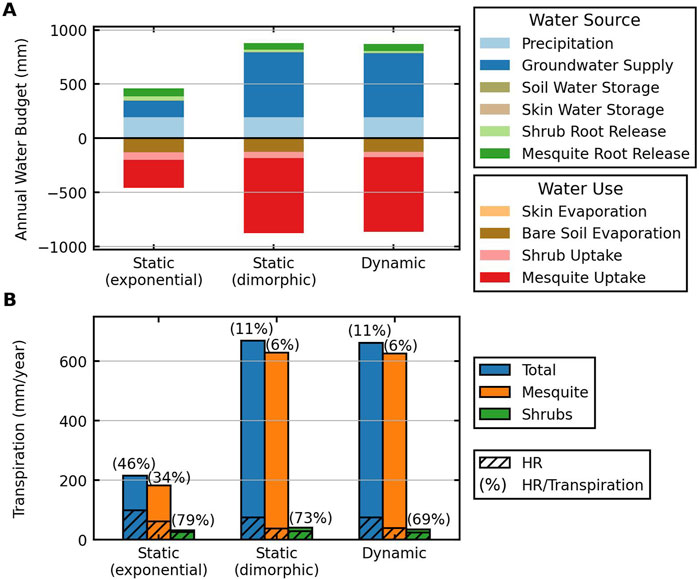
Figure 6. Annual water budget (A) and annual transpiration and release (B) in DCHM-VDR simulations under the historical scenario based on values in Supplementary Tables S5, S6. In (A), water sources are plotted positively, and water uses are plotted negatively. Skin water storage and evaporation are less than 1% of total water supplied and used, thus not visible. In (B), the percentage of root water released by HR over transpiration (i.e., the contribution of released water to transpiration), calculated using Equation 6, is indicated on top of the bars that show total transpiration and transpiration by each vegetation.

5.2.3.2 Correlations between root profile and soil moisture

Figure 7 illustrates the decadal average difference in soil moisture between dynamic and static root profiles. With a static exponential root profile, high root fraction and strong water potential gradients result in more water released in the middle, dry soil layers in all seasons since neither infiltration nor capillary rise can reach these depths. However, a comparison of the soil moisture profiles using different root profiles demonstrates that HR, the primary water input in these soil depths, cannot fully compensate for the transpiration loss as soil moisture is consistently higher if roots are relatively less active in the middle layers (Figure 7A). In contrast, dimorphic and dynamic profiles preserve soil moisture in mid-depths while exploiting shallow infiltration and groundwater. The lower shallow soil moisture when using dimorphic and dynamic root profiles reflects the effective utilization of precipitation during the wet season.

Figure 7

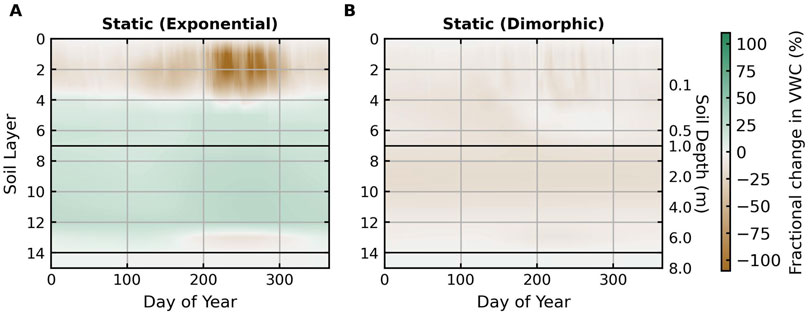
Figure 7. Differences in daily mean soil moisture profiles between dynamic and static root profiles averaged across 2000–2010. (A) shows the difference between dynamic and static, exponentially decaying root fraction profiles. (B) shows the difference between dynamic and static, dimorphic root fraction profiles obtained from averaging the root fraction profile simulated using the dynamic root fraction scheme under historical climate. Green colors represent a higher soil moisture using dynamic root profiles. Brown colors represent lower soil moisture using a dynamic root profile. Day of the year refers to Julien’s day of the year. The two black horizontal lines mark the bottom of the infiltration zone (top 1 m) and the top of the capillary fringe (0.5 m above the water table) in the soil column.

Although differences in soil moisture between the dynamic and static dimorphic root profiles are more trivial, dynamic roots generally lead to slightly lower soil moisture at all depths (Figure 7B). Frequent rain events during the monsoon periods prompt higher root water uptake near the surface with dynamic root profiles, lowering shallow soil moisture. This reduction is most significant in years with strong monsoons (e.g., layers 2 – 8 between DOY 200–300 in 2001, 2006, 2007, and 2008), while surface soil moisture is preserved as dynamic roots work in deeper, moister layers (layers 6–8) in years with drier pre-monsoon and monsoon periods (e.g., 2002–2004; Supplementary Figure S19). The slightly lower soil moisture in deeper soil columns with dynamic roots could be caused by increased water uptake when mesquite roots shift between shallow and deep rootzone in different seasons. In general, dynamic roots better respond to intra-annual variations in moisture availability. The opposite signs of the difference in soil moisture profile when comparing an exponential and a dimorphic static root profile against dynamic root profiles highlight the importance of the architecture of root systems in shaping soil moisture.

5.2.3.3 The impact of root profiles on aboveground vegetation activities

Figure 8 compares the monthly trajectories of the Bowen ratio, WUE, and GPP when using different root profiles. Overall, the Bowen ratio decreases as GPP increases during the pre-monsoon period, signaled by mesquite growth onset (Figure 8A). For both vegetation types, WUE is low in winter due to inactive canopies and high in growing seasons as all vegetation begins transpiring (Figures 8B, C). ${WUE}_h$, the ratio of GPP over gross root water uptake, is generally lower than ${WUE}_p$, the ratio of GPP over transpiration, since part of the root water uptake is released to dry soil layers rather than transpired. With stable groundwater access, mesquite has a lower and more stable WUE than shrubs, implying that shrubs are more sensitive to seasonal variations of moisture availability and more conservative in water use.

Figure 8

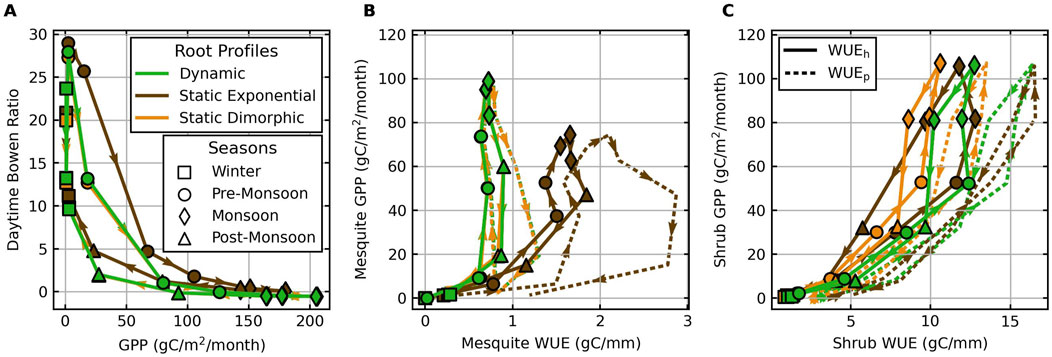
Figure 8. Monthly mean daytime Bowen ratio vs. total GPP (A) and monthly total GPP vs. mean WUE for mesquites (B) and shrubs (C) averaged across the 10-year period of the historical climate scenario. Arrows indicate the direction of the trajectories, starting in January and ending in December. Colors represent different root fraction profiles. Marker symbols represent different seasons. Solid lines represent ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{h}}$ - the fraction of GPP over gross root water uptake (including the released water, i.e., ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{h}}=\mathit{G}\mathit{P}\mathit{P}/\sum {\mathit{q}}_{\mathit{r}\mathit{o}\mathit{o}\mathit{t},\mathit{i}},\mathit{w}\mathit{h}\mathit{e}\mathit{r}\mathit{e}{\mathit{q}}_{\mathit{r}\mathit{o}\mathit{o}\mathit{t},\mathit{i}}<\mathbf{0}$), and dashed lines represent ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{p}}$ - the fraction of GPP over net root water uptake (subtracting released water from gross uptake, i.e., ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{p}}=\mathit{G}\mathit{P}\mathit{P}/\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}\mathit{p}\mathit{i}\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}$).

Using a static exponential root profile increases overall WUE during the growth period but at the cost of a lower GPP and higher Bowen ratio, especially in the pre-monsoon season (Figure 8A). Differences in GPP and WUE between exponential and dimorphic root profiles are mainly due to mesquites experiencing higher soil water stress with exponential profiles. The significantly higher ${WUE}_p$ (dashed dark brown line) compared to ${WUE}_h$ (solid dark brown line) further shows that a large amount of water is released such that gross root water uptake is much higher than transpiration (Figure 8B). Shrub roots are more concentrated near the surface and separated from mesquite roots, allowing shrubs to take full advantage of precipitation infiltration after monsoons arrive. Hence, shrubs with static exponential root profiles are less conservative in water use and have a low WUE after entering the monsoon season (dark brown triangles) and vice versa in pre-monsoon seasons (dark brown circles, Figure 8C).

The differences in WUE between static dimorphic (orange) and dynamic roots (green) are contributed mainly by shrubs. Dynamic profiles prompt higher uptake competition near the surface, particularly during wet seasons, leading shrubs to optimize water use and increase WUE (Figure 8C). Mesquite WUE shows minimal changes, as they primarily rely on groundwater rather than seasonally varying precipitation infiltration. Yet, dynamic roots have a more significant impact on shrub WUE, particularly during dry years, underscoring their role in optimizing water use under stress. Yet, monthly trajectories of WUE vs. GPP in the driest and the wettest year of the simulation period demonstrate more significant impacts of dynamic roots on WUE (Supplementary Figure S20). During the wettest year (2001), dynamic roots increase uptake and competition near the surface instead of keeping mesquite roots deeper near the water table since the post-monsoon season is exceptionally wet, which increases mesquite WUE. During the driest year (2009), dynamic roots increase shrub WUE the most since shrubs are more sensitive to precipitation, highlighting the significance of dynamic roots in optimizing water use under water stress.

5.3 Ecohydrological responses to future warming

5.3.1 Future climate conditions

By the end of the century, TGW simulations forecast a substantial decrease in rainfall intensity during the monsoon seasons by 70% under the hotter scenario and 33% under the cooler scenario, such that the drought in pre-monsoon seasons effectively increases in intensity and duration (Supplementary Figure S21A; Supplementary Table S7). Air temperature is projected to increase in all seasons at a similar rate at the study site, as indicated by the parallel but shifted linear regression curves in Supplementary Figure S21B. The cooler scenario, projected by less sensitive CMIP6 models (i.e., cooler scenarios), shows a smaller temperature increase, as expected, leading to a less extreme atmospheric dryness condition. Under the most extreme case, the temperature will be 7.6 °C higher by the end of the century. Reduced precipitation and higher temperatures induce high VPD during the growth period (Supplementary Figure S21C). Despite the drying trend in the growth periods, winter precipitation will continue to increase, potentially due to higher temperatures and moisture-holding capacities. Hence, VPD in winter does not change significantly in the future.

The increase in temperature also leads to an earlier leaf-out and later senescence of mesquite as the first and last freeze events are further apart due to warmer temperatures (Supplementary Figure S22A). CMIP6 MME outputs project higher LAI in all seasons. In response to the more extended growth period of mesquite and reduced precipitation in the monsoon period in the future, WTD declines earlier and more rapidly at the beginning of the growth period and reaches a deeper depth but still does not exceed the maximum rooting depth of mesquites (Supplementary Figure S22B). However, as described in Section 4.3, the predicted future WTD does not consider any potential influence of land cover and land use change on the precipitation-recharge relationship and recharge processes of the existing aquitards. The model also assumes that root penetration through soil is not impeded by any clay aquitards. Therefore, mesquite maintain their stable access to groundwater in all future climate scenarios.

5.3.2 Root dynamics and soil moisture in the future

5.3.2.1 Future changes in soil moisture

Figure 9 illustrates the differences in modeled soil moisture profiles between the hotter future and the historical climate scenarios. Differences for the cooler future scenario have a similar pattern shown in Supplementary Figure S23. Increased projected winter precipitation results in higher shallow rootzone moisture, providing additional early growth period moisture. Whereas reduced precipitation in both intensity and variability throughout the growth period (DOY 100–330) lowers shallow soil moisture (Figure 9). Regardless of the variations in the changes in future shallow soil moisture, deep soil moisture (below 1 m) shows a consistent reduction, implying that the changes are more likely associated with vegetation dynamics rather than precipitation patterns. The different responses of shallow and deep soil moisture to climate change demonstrate that different processes control surface and deep soil moisture (Lian et al., 2021).

Figure 9

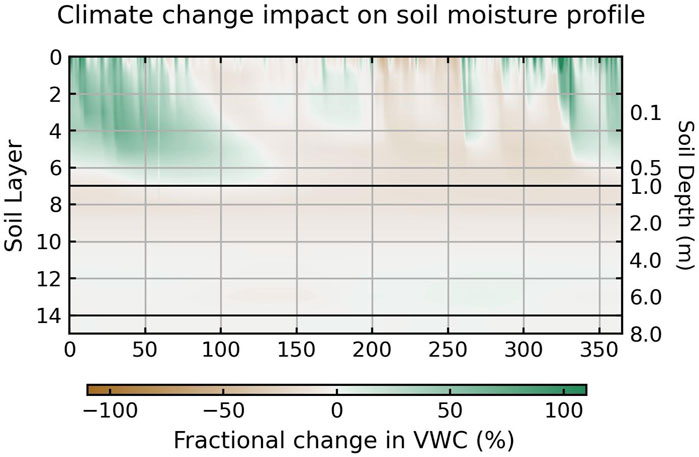
Figure 9. Differences in daily mean soil moisture in each soil layer between the hotter future scenario and historical scenario averaged across the 10-year simulation period. Brown shades mean the soil will be drier in the future. Green shades indicate moister soil in the future. The two black horizontal lines mark the bottom of the infiltration zone (top 1 m) and the top of the capillary fringe (0.5 m above the water table) in the soil column. The differences for the cooler future scenario are shown in Supplementary Figure S23.

5.3.2.2 Seasonal changes in root water uptake patterns

Seasonal differences in root profiles and diurnal cycles of root water flux between future and historical scenarios are shown in Figure 10. The differences contributed by mesquites and shrubs separately are shown in Figures 11, 12, respectively. A negative root fraction difference indicates a future reduction and vice versa for a positive difference. HR shifts from light to dark purple layers, and root water uptake shifts from light to dark green in the future. Shrub roots shift to deeper soil layers under all future scenarios, while changes in mesquite roots are more variable.

Figure 10

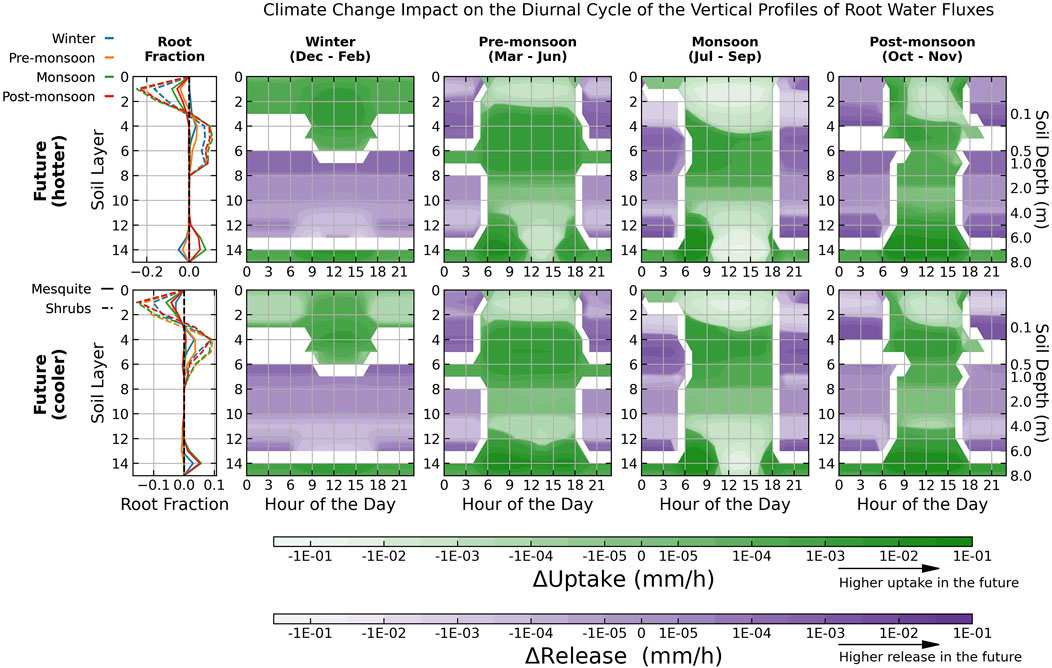
Figure 10. Differences in future and historical seasonally average root profiles and water fluxes as a function of soil layer depth by mesquite and shrubs (both understory and open shrubs). Results are plotted on a log scale. Darker (lighter) green shades indicate higher (lower) uptake in the future. Darker (lighter) purple shades indicate higher (lower) releases (i.e., HR) in the future. Root activities shift from light-colored soil layers in the historical climate to dark-colored soil layers in the future. Values are not shown for layers that switch between release and uptake between future and historical climate scenarios. Solid (dashed) lines represent changes in mesquite (shrub) root profiles. Note that the range of the x-axis for the root fraction profile is different. Each day starts at midnight, 0:00 local time.

Figure 11

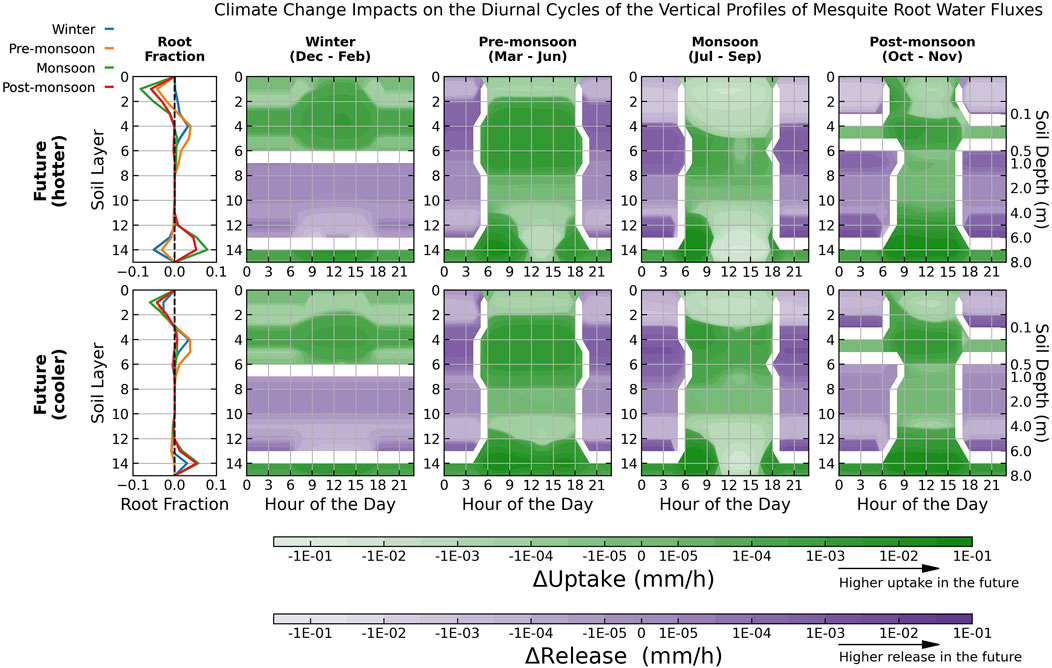
Figure 11. Differences in future and historical seasonally average root profiles and water fluxes as a function of soil layer depth by mesquite only. Results are plotted on a log scale. Darker (lighter) green shades indicate higher (lower) uptake in the future. Darker (lighter) purple shades indicate higher (lower) releases (i.e., HR) in the future. Root activities shift from light-colored soil layers in the historical climate to dark-colored soil layers in the future. Values are not shown for layers that switch between release and uptake between future and historical climate scenarios. Each day starts at midnight, 0:00 local time.

Figure 12

Figure 12. Same as Figure 11, but for shrubs (both understory and open shrubs) in the upper 2 m soil.

In winter, a uniform increase in total water uptake and a shift of mesquite and shrub root fraction towards the shallow rootzone (layers 0–8) reflect a positive vegetation response to more frequent rain events and higher temperatures. Warming causes earlier onset of mesquite growing seasons, increasing transpiration demand and reducing deeper soil HR as mesquite root fraction increases in shallow rootzone (Figure 11). Shrubs also more actively redistribute moisture from near-surface to mid-depth soil (Figure 12), providing additional water storage for daytime transpiration.

Greater precipitation infiltration and HR in winter leads to higher soil moisture stored in the shallow rootzone (layers 4–6, Figure 9), beneficial for subsequent pre-monsoon water uptake. Consequently, although the subsequent pre-monsoon seasons are projected to become even drier, water uptake increases in middle rootzone (layers 4–8) as root activities shift away from the arid surface soil and utilize the moisture stored in winter (Figure 10), leading to an increase in total root water uptake by 14%–22% for mesquite and 10%–11% for shrubs (Supplementary Table S8). Furthermore, although both mesquites and shrubs still redistribute moisture upward from near the water table and from mid-depth soil (Figures 11, 12), a higher fraction of mesquite roots occupies the upper soil column following the rainy winters, reducing mesquite HR by 9%–10% and boosting transpiration.

Since future monsoon seasons will receive much less precipitation, root water uptake patterns align more towards the pre-monsoon seasons, extracting less near the surface and more active at mid-depths (Figure 10). As the prolonged drought period depletes the soil moisture stored in the upper rootzone, shrubs are more negatively impacted due to their shallow root systems, decreasing uptake by up to 37% under the hotter scenario (Supplementary Table S8). Mesquite roots are less impacted by severe droughts, with no significant change in water uptake under the cooler scenario and a decrease of 11% under the hotter future scenario (Supplementary Table S8), because they shift deeper towards the saturated zone instead of staying in the mid-depths like during the wetter winter and pre-monsoon seasons (Figure 11). There is also a slight reduction in uptake (-2 – 4%) co-occurring with a higher release (7%–14%) by mesquite, which could be the reason for the increase in shrub uptake in the sub-surface soil (layers 4–8; Figure 12).

The trend of decreasing competition as precipitation decreases (e.g., during the monsoon period under the hotter future scenario) aligns well with the stress-gradient hypothesis in ecology, which predicts that ecological interactions shift positively with decreasing stress (Dohn et al., 2013). In particular, Dohn et al. (2013) found a shift from competitive to facilitative interactions between trees and understory grass productivity as precipitation decreases in semi-arid regions. Similarly, mesquites compete with shrubs for shallow soil moisture in winter as more rainfall events take place but facilitate the redistribution of water during prolonged droughts as surface moisture becomes more limited in the future.

5.3.3 Aboveground vegetation activity in the future

The decadal average fractional changes in annual total transpiration and GPP, along with the direction of WUE change in the future, are plotted in Figure 13. At the ecosystem level, transpiration increases under both future scenarios, while GPP increases under the cooler scenario but decreases under the hotter scenario. The decrease in total GPP under the hotter future scenario is primarily due to mesquite GPP reduction, indicating mesquite vulnerability to heat stress compared to C4 shrubs. The increase in total transpiration is also mostly contributed by mesquite, showing the advantage of deep rooting systems with groundwater access. Shrub transpiration has a large interannual variability and, on average, decreases in the future. The large uncertainty associated with shrub transpiration is in part due to low transpiration under the current climate, so small fluctuations lead to large fractional changes, but also implies a high sensitivity of shrubs to water stress.

Figure 13

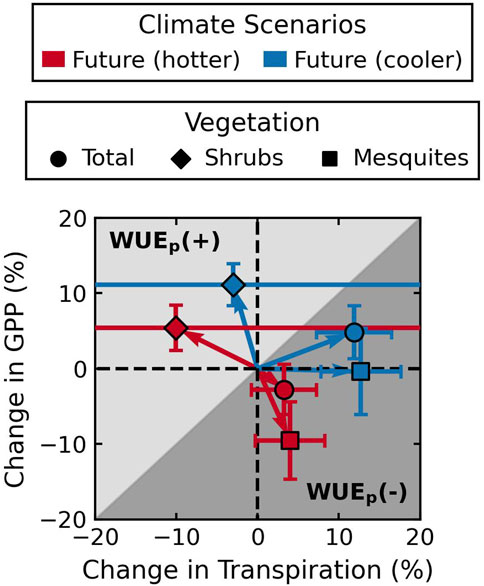
Figure 13. The decadal average fractional change in annual total GPP and transpiration in the future compared to historical climate based on values in Supplementary Table S7. Markers represent fluxes for total or individual vegetation. Colors represent different future climate scenarios compared against the historical climate. Horizontal (vertical) error bars show the standard deviation of annual fractional change in transpiration (GPP) across the 10-year period. Points that fall in the dark grey area indicate an increase in ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{p}}$, and a decrease for those that fall in the light grey area. The horizontal error bars for shrubs are shown in full in Supplementary Figure S26.

The higher tolerance of mesquites to rising water stress has already been observed under historical climate in the past years, demonstrated by woody plants encroaching large areas of riparian habitats and exploiting groundwater resources (Scott et al., 2006). Furthermore, the positive response of mesquite transpiration to warming-induced reduction in water availability may impact future rainfall recycling as more moisture is delivered to the atmosphere (Lowman et al., 2018), especially in semi-arid to arid climates, where ET largely exceeds precipitation. However, it is important to note that the increase in mesquite transpiration due to warming largely depends on the access of mesquite roots to groundwater. Rapid and significant decline in future water table due to changes in the recharge processes and land use, such as increased anthropogenic freshwater withdrawal, may disconnect mesquite roots from the saturated zone and reduce mesquite transpiration. Hence, all analyses presented here depend on the assumption that the rate and range of WTD decline do not exceed the growth rate and maximum rooting depth of mesquites.

A comparison of future and historical monthly trajectories of Bowen ratio and GPP highlights significant changes during winter and pre-monsoon seasons as warming increases winter precipitation and extends the mesquite growing season (circled in Figure 14A). Higher soil water availability during the early stage of growth periods reduces Bowen ratio and increases total latent heat and GPP as vegetation more actively transpires and assimilates carbon. However, responses to warming are not uniform between vegetation types.

Figure 14

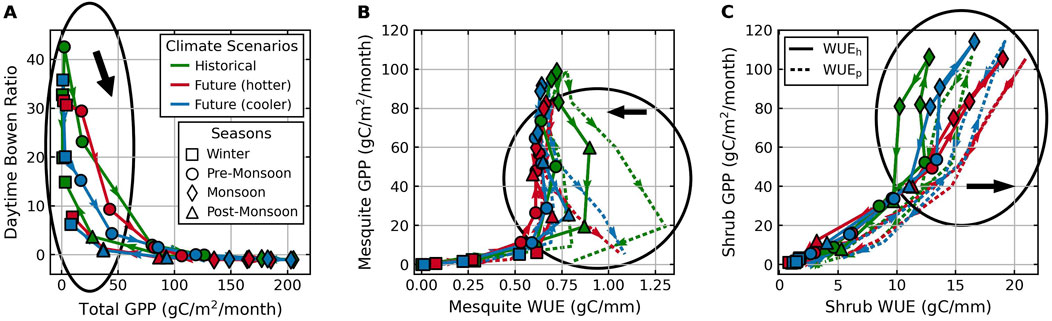
Figure 14. Monthly mean daytime Bowen ratio vs. total GPP (A) and monthly total GPP vs. mean WUE for mesquites (B) and shrubs (C) averaged across all simulation years. Circled areas mark the most significant climate change impacts with thick black arrows to point the direction of the impact. Colors of the lines and markers represent each of the TGW climate scenarios listed in Table 1. Colored arrows indicate the direction of the monthly trajectories, starting in January and ending in December. Symbols of the markers represent different seasons. Solid lines represent ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{h}}$ - the fraction of GPP over gross root water uptake (including the released water, i.e., ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{h}}=\mathit{G}\mathit{P}\mathit{P}/\sum {\mathit{q}}_{\mathit{r}\mathit{o}\mathit{o}\mathit{t},\mathit{i}},\mathit{w}\mathit{h}\mathit{e}\mathit{r}\mathit{e}{\mathit{q}}_{\mathit{r}\mathit{o}\mathit{o}\mathit{t},\mathit{i}}<\mathbf{0}$), and dashed lines represent ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{p}}$ - the fraction of GPP over net root water uptake (subtracting released water from gross uptake, i.e., ${\mathit{W}\mathit{U}\mathit{E}}_{\mathit{p}}=\mathit{G}\mathit{P}\mathit{P}/\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}\mathit{p}\mathit{i}\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}$).

During the growth period, a positive response of mesquite water uptake and transpiration to warming lowers mesquite WUE (Figure 14B). The larger decrease in mesquite ${WUE}_p$ than ${WUE}_h$ during the shoulder seasons implies that transpiration increases more than the gross root water uptake, which is expected since atmospheric dryness lowers leaf water potential and draws more water toward the canopy instead of releasing it to the soil. On the other hand, shrub WUE increases in the future with a similar change in ${WUE}_h$ and ${WUE}_p$, implying that shrubs become more conservative in water use in response to the increasing soil water stress while keeping their dependence on HR (Figure 14C). However, it is important to note that the interannual variations in shrub root water uptake are relatively large such that the monthly trajectory of shrub GPP vs. WUE under the most extreme future scenario still falls between the historically wettest and driest year (Supplementary Figure S25A). In contrast, mesquite WUE will decrease below the historical range during the shoulder seasons but change little during the peak growing season (Supplementary Figure S25B).

Overall, the different responses between mesquite and shrubs to future warming can be attributed to their different sensitivity to precipitation. Shrubs depend on precipitation to reduce soil moisture stress, so their future water-use strategy is similar to the historically driest year since the average precipitation during the growth period in the future is comparable with the lower end of precipitation under historical climate. Mesquite transpiration is more proportional to the evaporative demand and less limited by soil water stress as mesquites primarily rely on groundwater. Hence, atmospheric drying and longer growing seasons in the future will increase mesquite root water uptake, such that mesquites will become water spenders while shrubs will become more conservative in water use.

6 Conclusion

The role of root profiles in modulating belowground moisture conditions and aboveground vegetation activity was characterized using a coupled land surface hydrology model equipped with a potential-driven plant hydraulics representation and dynamic root parameterization. The revised model can capture well the belowground interactions and dynamics of mesquites and shrubs compared to AmeriFlux tower observations, along with the seasonality and amplitude of the water and energy fluxes (i.e., latent heat, GPP, and Bowen ratio).

Driven by moisture gradients, the self-optimizing root parameterization produces a dimorphic mesquite root profile and an exponentially decaying shrub root profile that are sensitive to antecedent soil moisture and precipitation regime. Mesquites with dimorphic root profiles increase transpiration by 3-fold, from 182 to 628 mm/year, and reduce the fraction of HR over transpiration from 34% to 6%. Following the seasonal march of wet-dry periods at the study site, plants with dynamic roots increase their root fraction and water uptake in shallow rootzones during wet periods and shift to deeper soil layers during dry periods. By leveraging soil moistening during events and avoiding the dry patches in soil, plants with dynamic roots, especially shrubs, reduce water loss and optimize water use strategy, leading to a 10% decrease in the HR over transpiration ratio and a higher WUE.

In the future, increased winter precipitation and higher temperatures stimulate root activity and competition for moisture in the shallow rootzone, while the opposite occurs during the drier growth periods. With access to a stable groundwater source, mesquite transpiration increases by 4%–13% in the future and has relatively small uncertainties as mesquites primarily rely on groundwater rather than precipitation. However, mesquite GPP has a clear decrease (−10%) under the more extreme warming scenario, suggesting an amplified negative response to high temperatures. On the contrary, shrubs decrease transpiration by 3%–10% with significant interannual variations but increase GPP by 5%–13%. As a result, drier growing seasons in the future lead to a reduction in mesquite WUE by 12%–13% and an increase of shrub WUE by 14%–17%, so shrubs adopt a more conservative water use strategy while mesquites are relatively insensitive to warming-induced atmospheric drying.

The results presented here are limited by the uncertainty in vegetation parameters regarding the partition of overstory and understory, and future phenology and vegetation cover. In particular, the model does not have an acclimation mechanism to simulate plants’ adaptation to higher temperatures and CO₂ concentrations. However, we determine that the ensembled mean of CMIP6 model outputs is the best currently available for future vegetation dynamics and can represent some of the stimulating effects of CO₂ fertilization on vegetation density. The TGW simulation data also cannot account for multi-decadal climate variabilities in future climate projections. Hence, this study is more focused on investigating the influence of warming and changing precipitation patterns on the ecohydrological processes.

While model parameterization used in this study is specific to a semi-arid, groundwater-dependent ecosystem with coexisting mesquite and shrubs, the improved model formulation permits more detailed analysis on the coupled above -and below-ground vegetation response to climate change. The introduction of a dynamic root parameterization has significant practical implications in inferring root architecture when observations are scarce, particularly for deep-rooted species. Moreover, adaptive roots optimize water use strategy based on heterogeneous moisture profiles, leading to significantly different aboveground vegetation responses to drought under a warmer climate. Belowground root dynamics and capturing root water uptake profiles are essential in understanding the eco-hydrological process of coexisting species with different root structures and estimating the water budget in water-limited regions, thus playing a key role in ecosystem adaptation and resilience.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

QL: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. AB: Conceptualization, Formal Analysis, Methodology, Supervision, Writing–review and editing, Resources, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The first author declares support for research from the Croucher Foundation through the Croucher Scholarship for Doctoral Study.

Acknowledgments

The authors would like to thank the editor and reviewers for their valuable time reviewing the manuscript. Special acknowledgment goes to reviewers for their constructive comments and support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2024.1477059/full#supplementary-material

References

Amenu, G. G., and Kumar, P. (2008). A model for hydraulic redistribution incorporating coupled soil-root moisture transport. Hydrol. Earth Syst. Sci. 12, 55–74. doi:10.5194/hess-12-55-2008

CrossRef Full Text | Google Scholar

Arora, V. K., and Boer, G. J. (2003). A representation of variable root distribution in dynamic vegetation models. Earth Interact. 7 (6), 1–19. doi:10.1175/1087-3562(2003)007<0001:AROVRD>2.0.CO;2

CrossRef Full Text | Google Scholar

Barros, A. P. (1995). Adaptive multilevel modeling of land-atmosphere interactions. J. Clim. 8, 2144–2160. doi:10.1175/1520-0442(1995)008<2144:ammola>2.0.co;2

CrossRef Full Text | Google Scholar

Bleby, T. M., Mcelrone, A. J., and Jackson, R. B. (2010). Water uptake and hydraulic redistribution across large woody root systems to 20 m depth. Plant, Cell & Environ. 33 (12), 2132–2148. doi:10.1111/j.1365-3040.2010.02212.x

CrossRef Full Text | Google Scholar

Devonec, E., and Barros, A. P. (2002). Exploring the transferability of a land-surface hydrology model. J. Hydrology 265 (1–4), 258–282. doi:10.1016/S0022-1694(02)00111-7

CrossRef Full Text | Google Scholar

Dohn, J., Dembélé, F., Karembé, M., Moustakas, A., Amévor, K. A., and Hanan, N. P. (2013). Tree effects on grass growth in savannas: competition, facilitation and the stress-gradient hypothesis. J. Ecol. 101 (1), 202–209. doi:10.1111/1365-2745.12010

CrossRef Full Text | Google Scholar

Drewniak, B. A. (2019). Simulating dynamic roots in the energy exascale earth system land model. J. Adv. Model. Earth Syst. 11 (1), 338–359. doi:10.1029/2018MS001334

CrossRef Full Text | Google Scholar

Du, J. (2011). NCEP/EMC 4KM gridded data (GRIB) stage IV data. UCAR/NCAR - Earth Obs. Lab. doi:10.5065/D6PG1QDD

CrossRef Full Text | Google Scholar

Fan, Y., Miguez-Macho, G., Jobbágy, E. G., Jackson, R. B., and Otero-Casal, C. (2017). Hydrologic regulation of plant rooting depth. Proc. Natl. Acad. Sci. 114 (40), 10572–10577. doi:10.1073/pnas.1712381114

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedl, M., and Sulla-Menashe, D. (2022). “MODIS/Terra+Aqua land cover type yearly L3 global 500m SIN grid V061,” in NASA EOSDIS land processes distributed active archive center. doi:10.5067/MODIS/MCD12Q1.061

CrossRef Full Text | Google Scholar

Garcia-Quijano, J. F., and Barros, A. P. (2005). Incorporating canopy physiology into a hydrological model: photosynthesis, dynamic respiration, and stomatal sensitivity. Ecol. Model. 185 (1), 29–49. doi:10.1016/j.ecolmodel.2004.08.024

CrossRef Full Text | Google Scholar

Gebremichael, M., and Barros, A. (2006). Evaluation of MODIS gross primary productivity (GPP) in tropical monsoon regions. Remote Sens. Environ. 100 (2), 150–166. doi:10.1016/j.rse.2005.10.009

CrossRef Full Text | Google Scholar

Hultine, K. R., Scott, R. L., Cable, W. L., Goodrich, D. C., and Williams, D. G. (2004). Hydraulic redistribution by a dominant, warm-desert phreatophyte: seasonal patterns and response to precipitation pulses. Funct. Ecol. 18 (4), 530–538. doi:10.1111/j.0269-8463.2004.00867.x

CrossRef Full Text | Google Scholar

Jones, A. D., Rastogi, D., Vahmani, P., Stansfield, A. M., Reed, K. A., Thurber, T., et al. (2023). Continental United States climate projections based on thermodynamic modification of historical weather. Sci. Data 10 (1), 664. doi:10.1038/s41597-023-02485-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Jönsson, P., and Eklundh, L. (2004). TIMESAT—a program for analyzing time-series of satellite sensor data. Comput. & Geosciences 30 (8), 833–845. doi:10.1016/j.cageo.2004.05.006

CrossRef Full Text | Google Scholar

Kennedy, D., Swenson, S., Oleson, K. W., Lawrence, D. M., Fisher, R., Lola Da Costa, A. C., et al. (2019). Implementing plant hydraulics in the community land model, version 5. J. Adv. Model. Earth Syst. 11 (2), 485–513. doi:10.1029/2018MS001500

CrossRef Full Text | Google Scholar

Kropp, H., and Ogle, K. (2015). Seasonal stomatal behavior of a common desert shrub and the influence of plant neighbors. Oecologia 177 (2), 345–355. doi:10.1007/s00442-014-3187-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, E., Kumar, P., Knowles, J. F., Minor, R. L., Tran, N., Barron-Gafford, G. A., et al. (2021). Convergent hydraulic redistribution and groundwater access supported facilitative dependency between trees and grasses in a semi-arid environment. Water Resour. Res. 57 (6), e2020WR028103. doi:10.1029/2020WR028103

CrossRef Full Text | Google Scholar

Lian, X., Piao, S., Chen, A., Huntingford, C., Fu, B., Li, L. Z. X., et al. (2021). Multifaceted characteristics of dryland aridity changes in a warming world. Nat. Rev. Earth & Environ. 2 (4), 232–250. doi:10.1038/s43017-021-00144-0

CrossRef Full Text | Google Scholar

Liao, M., and Barros, A. P. (2023). Toward optimal rainfall for flood prediction in headwater basins—orographic QPE error modeling using machine learning. Water Resour. Res. 59 (11), e2023WR034456. doi:10.1029/2023WR034456

CrossRef Full Text | Google Scholar

Lin, Y.-S., Medlyn, B. E., Duursma, R. A., Prentice, I. C., Wang, H., Baig, S., et al. (2015). Optimal stomatal behaviour around the world. Nat. Clim. Change 5 (5), 459–464. doi:10.1038/nclimate2550

CrossRef Full Text | Google Scholar

Lowman, L., Wei, T., and Barros, A. (2018). Rainfall variability, wetland persistence, and water–carbon cycle coupling in the upper zambezi River Basin in southern Africa. Remote Sens. 10 (5), 692. doi:10.3390/rs10050692

CrossRef Full Text | Google Scholar

Lowman, L. E. L., and Barros, A. P. (2016). Interplay of drought and tropical cyclone activity in SE U.S. gross primary productivity. J. Geophys. Res. Biogeosciences 121 (6), 1540–1567. doi:10.1002/2015JG003279

CrossRef Full Text | Google Scholar

Mitchell, K. E., Lohmann, D., Houser, P. R., Wood, E. F., Schaake, J. C., Robock, A., et al. (2004). The multi-institution North American Land Data Assimilation System (NLDAS): utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. Atmos. 109 (D7). doi:10.1029/2003JD003823

CrossRef Full Text | Google Scholar

Myneni, R., Knyazikhin, Y., and Park, T. (2021a). MODIS/Terra+Aqua leaf area index/FPAR 8-day L4 global 500m SIN grid V061. NASA EOSDIS Land Process. Distrib. Act. Arch. Cent. doi:10.5067/MODIS/MCD15A2H.061

CrossRef Full Text | Google Scholar

Myneni, R., Knyazikhin, Y., and Park, T. (2021b). MODIS/Terra leaf area index/FPAR 8-day L4 global 500m SIN grid V061. NASA EOSDIS Land Process. Distrib. Act. Arch. Cent. doi:10.5067/MODIS/MOD15A2H.061

CrossRef Full Text | Google Scholar

Myneni, R. B., Ramakrishna, R., Nemani, R., and Running, S. W. (1997). Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geoscience Remote Sens. 35 (6), 1380–1393. doi:10.1109/36.649788

CrossRef Full Text | Google Scholar

Neumann, R. B., and Cardon, Z. G. (2012). The magnitude of hydraulic redistribution by plant roots: a review and synthesis of empirical and modeling studies. New Phytol. 194 (2), 337–352. doi:10.1111/j.1469-8137.2012.04088.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogle, K., Lucas, R. W., Bentley, L. P., Cable, J. M., Barron-Gafford, G. A., Griffith, A., et al. (2012). Differential daytime and night-time stomatal behavior in plants from North American deserts. New Phytol. 194 (2), 464–476. doi:10.1111/j.1469-8137.2012.04068.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Oren, R., Sperry, J. S., Katul, G. G., Pataki, D. E., Ewers, B. E., Phillips, N., et al. (1999). Survey and synthesis of intra- and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant, Cell & Environ. 22 (12), 1515–1526. doi:10.1046/j.1365-3040.1999.00513.x

CrossRef Full Text | Google Scholar

Sahu, R. K., Müller, J., Park, J., Varadharajan, C., Arora, B., Faybishenko, B., et al. (2020). Impact of input feature selection on groundwater level prediction from a multi-layer Perceptron neural network. Front. Water 2. doi:10.3389/frwa.2020.573034

CrossRef Full Text | Google Scholar

Schymanski, S. J., Sivapalan, M., Roderick, M. L., Beringer, J., and Hutley, L. B. (2008). An optimality-based model of the coupled soil moisture and root dynamics. Hydrology Earth Syst. Sci. 12 (3), 913–932. doi:10.5194/hess-12-913-2008

CrossRef Full Text | Google Scholar

Scott, R. (2022). AmeriFlux BASE US-CMW charleston mesquite woodland. Ver 2-5. AmeriFlux AMP (Dataset). doi:10.17190/AMF/1660339

CrossRef Full Text | Google Scholar

Scott, R. L., Cable, W. L., Huxman, T. E., Nagler, P. L., Hernandez, M., and Goodrich, D. C. (2008). Multiyear riparian evapotranspiration and groundwater use for a semiarid watershed. J. Arid Environ. 72 (7), 1232–1246. doi:10.1016/j.jaridenv.2008.01.001

CrossRef Full Text | Google Scholar

Scott, R. L., Edwards, E. A., Shuttleworth, W. J., Huxman, T. E., Watts, C., and Goodrich, D. C. (2004). Interannual and seasonal variation in fluxes of water and carbon dioxide from a riparian woodland ecosystem. Agric. For. Meteorology 122 (1–2), 65–84. doi:10.1016/j.agrformet.2003.09.001

CrossRef Full Text | Google Scholar

Scott, R. L., Huxman, T. E., Barron-Gafford, G. A., Darrel Jenerette, G., Young, J. M., and Hamerlynck, E. P. (2014). When vegetation change alters ecosystem water availability. Glob. Change Biol. 20 (7), 2198–2210. doi:10.1111/gcb.12511

CrossRef Full Text | Google Scholar

Scott, R. L., Huxman, T. E., Williams, D. G., and Goodrich, D. C. (2006). Ecohydrological impacts of woody-plant encroachment: seasonal patterns of water and carbon dioxide exchange within a semiarid riparian environment. Glob. Change Biol. 12 (2), 311–324. doi:10.1111/j.1365-2486.2005.01093.x

CrossRef Full Text | Google Scholar

Scott, R. L., Watts, C., Payan, J. G., Edwards, E., Goodrich, D. C., Williams, D., et al. (2003). The understory and overstory partitioning of energy and water fluxes in an open canopy, semiarid woodland. Agric. For. Meteorology 114 (3), 127–139. doi:10.1016/S0168-1923(02)00197-1

CrossRef Full Text | Google Scholar

Stewart, J. B. (1988). Modelling surface conductance of pine forest. Agric. For. Meteorology 43 (1), 19–35. doi:10.1016/0168-1923(88)90003-2

CrossRef Full Text | Google Scholar

Tao, J., and Barros, A. P. (2013). Prospects for flash flood forecasting in mountainous regions – an investigation of Tropical Storm Fay in the Southern Appalachians. J. Hydrology 506, 69–89. doi:10.1016/j.jhydrol.2013.02.052

CrossRef Full Text | Google Scholar

Tao, J., and Barros, A. P. (2014). Coupled prediction of flood response and debris flow initiation during warm- and cold-season events in the Southern Appalachians, USA. Hydrology Earth Syst. Sci. 18 (1), 367–388. doi:10.5194/hess-18-367-2014

CrossRef Full Text | Google Scholar

Thornton, M. M., Shrestha, R., Wei, Y., Thornton, P. E., and Kao, S.-C. (2022). Daymet: daily surface weather data on a 1-km grid for North America, version 4 R1. Tennessee, United States: Oak Ridge National laboratory, Oak Ridge. doi:10.3334/ORNLDAAC/2129

CrossRef Full Text | Google Scholar

USDA-NRCS (2023). United States Department of Agriculture (USDA), Natural Resources Conservation Service (NRCS). Web Soil Surv. Available at: http://websoilsurvey.nrcs.usda.gov/. Accessed November 11, 2023].

Google Scholar

U.S. Geological Survey (2023a). 3D elevation program 1-meter resolution digital elevation model (published 20200606). Available at: https://www.usgs.gov/the-national-map-data-delivery (Accessed November 1, 2023).

Google Scholar

U.S. Geological Survey (2023b). National Hydrography dataset ver. USGS national Hydrography dataset best resolution (NHD) for hydrologic unit (HU) 4 - 2001. Available at: https://www.usgs.gov/national-hydrography/access-national-hydrography-products.

Google Scholar

U.S. Geological Survey (2023c). National water information system data available on the world wide Web (water data for the nation), accessed [November 10, 2023], Available at: http://waterdata.usgs.gov/nwis/.

Google Scholar

Wang, P., Niu, G., Fang, Y., Wu, R., Yu, J., Yuan, G., et al. (2018). Implementing dynamic root optimization in noah-MP for simulating phreatophytic root water uptake. Water Resour. Res. 54 (3), 1560–1575. doi:10.1002/2017WR021061

CrossRef Full Text | Google Scholar

Wang, T., Wang, P., Wu, Z., Yu, J., Pozdniakov, S. P., Guan, X., et al. (2022). Modeling revealed the effect of root dynamics on the water adaptability of phreatophytes. Agric. For. Meteorology 320, 108959. doi:10.1016/j.agrformet.2022.108959

CrossRef Full Text | Google Scholar

Wang, Y., Xie, Z., and Jia, B. (2016). Incorporation of a dynamic root distribution into CLM4.5: evaluation of carbon and water fluxes over the Amazon. Adv. Atmos. Sci. 33 (9), 1047–1060. doi:10.1007/s00376-016-5226-8

CrossRef Full Text | Google Scholar

Wickham, J., Homer, C., Vogelmann, J., McKerrow, A., Mueller, R., Herold, N., et al. (2014). The multi-resolution land characteristics (MRLC) consortium—20 Years of development and integration of USA national land cover data. Remote Sens. 6 (8), 7424–7441. doi:10.3390/rs6087424

CrossRef Full Text | Google Scholar

Xia, Y., Mitchell, K., Ek, M., Sheffield, J., Cosgrove, B., Wood, E., et al. (2012). Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 117 (D3). doi:10.1029/2011JD016048

CrossRef Full Text | Google Scholar

Yepez, E. A., Scott, R. L., Cable, W. L., and Williams, D. G. (2007). Intraseasonal variation in water and carbon dioxide flux components in a semiarid riparian woodland. Ecosystems 10 (7), 1100–1115. doi:10.1007/s10021-007-9079-y

CrossRef Full Text | Google Scholar

Yepez, E. A., Williams, D. G., Scott, R. L., and Lin, G. (2003). Partitioning overstory and understory evapotranspiration in a semiarid savanna woodland from the isotopic composition of water vapor. Agric. For. Meteorology 119 (1–2), 53–68. doi:10.1016/S0168-1923(03)00116-3

CrossRef Full Text | Google Scholar

Yildiz, O., and Barros, A. P. (2005). “Climate variability, water resources, and hydrologic extremes – modeling the water and energy budgets,” in Climate and hydrology in mountain areas. Editors C. De Jong, D. Collins, and R. Ranzi 1st ed. (Wiley), 291–306. doi:10.1002/0470858249.ch20

CrossRef Full Text | Google Scholar

Yildiz, O., and Barros, A. P. (2007). Elucidating vegetation controls on the hydroclimatology of a mid-latitude basin. J. Hydrology 333 (2–4), 431–448. doi:10.1016/j.jhydrol.2006.09.010

CrossRef Full Text | Google Scholar

Yıldız, O., and Barros, A. P. (2009). Evaluating spatial variability and scale effects on hydrologic processes in a midsize river basin. Sci. Res. Essays 4 (4), 217–225. doi:10.5897/SRE.9000465

CrossRef Full Text | Google Scholar

Zeng, X. (2001). Global vegetation root distribution for land modeling. J. Hydrometeorol. 2 (5), 525–530. doi:10.1175/1525-7541(2001)002<0525:gvrdfl>2.0.co;2

CrossRef Full Text | Google Scholar