Optimization of the rural domestic waste recycling network based on the path planning site selection model

Introduction: In the context of rural revitalization strategies, effectively managing rural waste is a critical task for achieving ecological environmental sustainability. The current state of garbage collection and transportation is examined in this paper, focusing on the rural waste management practices in Dongfeng County, Liaoyuan City, Jilin Province, through mathematical modeling.

Methods: By analyzing the rural domestic waste collection network, the volume of waste generated at various points is fuzzified using the fuzzy mathematical theory.

Results: The results of path optimization for waste collection and transportation were derived from a case study, demonstrating the feasibility and practicality of the rural domestic waste recycling network model.

Dicussion: Additionally, sensitivity analysis was conducted to assess the impact of changes on the total cost. Potential solutions for rural waste recycling and treatment are offered in this paper, providing valuable insights for the development of a rural domestic waste recycling network in Jilin Province.

1 Introduction

Currently, China’s economy is experiencing rapid development, leading to an increase in the wealth of its population and a diversification of lifestyles. However, this swift economic growth has also resulted in significant environmental pollution, with environmental issues becoming increasingly prominent. Whereas urban waste management has shown marked improvement, the garbage problem in rural areas has not received adequate attention or resolution. Consequently, a substantial amount of waste is improperly disposed of, adversely affecting both the living conditions and health of rural residents. Figure 1 (Taghipour et al., 2016) illustrates the volume of rural waste generated in China from 2013 to 2019. The data presented in Figure 1 indicate a consistent increase in waste generation in rural areas during this period, despite a concurrent decline in the rural population. Additionally, it is evident that per capita waste generation in these areas has risen significantly.

Figure 1

Figure 1. Waste generation in China, 2013–2019.

Through research in Dongfeng County, Liaoyuan City, Jilin Province, and a review of government policies, it has been found that rural waste treatment now mainly adopts the program of village collection–town transfer–county treatment. The entire rural living waste is handled by the county level, and the main treatment methods are incineration and landfill. Compared to the city, there is still a gap in waste classification and recycling treatment work in rural areas. There are still many villagers who dump waste in the ditches, roadside, and other places, which not only pollutes the environment but also the water sources, causing great pollution. The reasons for this are as follows: first, most of the people left behind in the countryside are old people and children, the average cultural level is low, and the awareness of environmental protection is weak. Second, the recycling of rural rubbish has not received enough attention from the government and the residents, and the role of education of the public is limited. Third, due to the economic development of the countryside, the investment in environmental protection is relatively small, the construction of infrastructure is insufficient, and the rubbish recycling facilities and equipment are limited. Limited investment is another factor. Some governments have handed over rubbish removal to a third party, and the removal of rubbish is only a simple treatment. The report of the 19th National Congress clearly puts forward the implementation of the strategy of rural revitalization, the main contents of which include adhering to the harmonious coexistence of man and nature, and building an ecologically livable environment, in which the treatment of rural rubbish is an important part of improving the living environment of the residents. Therefore, it is of great significance to carry out research on rural household waste. The collection and classification of rubbish is for the secondary use of resources and environmental protection, recyclable resources reuse, and protection of the ecological environment; however, at present, there is no complete rubbish recycling system, facilities, and equipment. Poor collection and low transportation efficiency easily cause secondary pollution of the environment, which will also be caused to a certain extent by the facilities, equipment, and other resources. In addition, rubbish collection should also be classified for different purposes. Therefore, from the perspective of logistics, it is of great practical significance to carry out site selection and path planning for rural domestic waste. The challenges in rural domestic waste recycling logistics related to sorting station siting, vehicle scheduling, route planning, and final disposal points are explored in this paper. From a macro perspective, the selection of waste sorting and transfer stations, final processing points, vehicle configuration, and recycling routes can enhance the comprehensive effectiveness of waste recycling, ensure the use value of waste, effectively shorten the waiting time required for recycling processing and transfer, effectively reduce the impact of the recycling process on the quality of life of the residents, and alleviate the pressure of recycling work. From a micro point of view, the establishment of reasonable facility locations helps to reduce the cost of recycling waste, boosts the employment rate of rural residents, effectively reduces the operating costs of environmental protection units, maximizes the benefits for vehicles and personnel, improves the overall management of villages, and prevents environmental pollution and irrational recycling routes due to inappropriate siting.

Domestic waste management in rural areas faces numerous challenges, with many types of domestic waste being inadequately treated due to issues such as insufficient infrastructure and ineffective recycling systems, resulting in exacerbated pollution problems (Zeng et al., 2015; Han et al., 2019). Optimizing the rural waste recycling network can enhance resource recovery efficiency and mitigate environmental pollution while promoting ecological sustainability. Within this network, facility location plays a crucial role in optimization; a well-considered facility location can significantly reduce transportation costs and time, thereby improving recycling efficiency (El-Hallaq and Mosabeh, 2019). This assertion is supported by a study that analyzed domestic waste disposal patterns and methods in the Yaoundé region of Africa, which found that the distance between the facility site and residents significantly influences waste placement behavior (Teixeira et al., 2004). Facility siting methods primarily rely on quantitative approaches, including multi-objective planning (Yang et al., 2007; Moreno et al., 2016), stochastic planning (Mete and Zabinsky, 2010), and the Euclidean distance method (Yadav et al., 2017; Chen et al., 2021). However, in recent years, qualitative analysis methods have also been increasingly applied in site selection. By summarizing and analyzing the theories and modeling techniques related to site selection, some scholars have employed simulation methods to operate and assess actual models, ultimately determining the optimal location for transit stations (Du and Guo, 2015). Subsequently, academics have verified the feasibility of qualitative analysis for research in the field of siting. For instance, Yang et al. examined the fundamental principles and concepts underlying the siting of secondary waste transfer stations in the urban area of Changsha. They established a waste transfer station siting assessment system that prioritizes the minimum economic cost and maximum ecological quality, visualizing their findings through GIS technology and providing an associated optimization scheme (Yang and Tao, 2020). In contrast, Liu analyzed the current state of rural domestic waste recycling in County L and employed cluster analysis for transfer station siting based on the region’s existing development characteristics (Liu M. H., 2021). However, relying on a single facility location is insufficient to effectively address the rural garbage recycling challenge; the study of the transportation network layout is equally crucial. An efficient transportation network ensures that waste is transported effectively from each collection point to the recycling facility, enhancing transportation efficiency while simultaneously reducing carbon dioxide emissions, thereby positively impacting the environment (Chen et al., 2021; Wang et al., 2022). The layout of the waste recycling network is essentially a vehicle scheduling problem in waste collection and transportation. This issue is critical, as changes in it can significantly affect recycling efficiency, thereby influencing vehicle usage and transportation costs. Research on transportation network optimization primarily aims to minimize costs or time, with proposed optimization methods including integer programming (Nema and Gupta, 1999; Mourao and Almeida, 2000), GIS networks (Karadimas and Loumos, 2008), recursive neural networks (Xie and Li, 2022), time windows (Liang, 2015), and multi-objective optimization (Shang et al., 2021). With the gradual deepening of research into rural recycling network optimization, traditional approaches focusing solely on single site selection or path studies are increasingly inadequate to address the complexities of reality. Consequently, more scholars are conceptualizing site selection, transfer station paths, and final transportation routes as an integrated system to better study the multifaceted recycling environment. For instance, Bhat highlighted that significant time is wasted during the collection and transportation of waste, leading to increased variable costs. To address this issue, he developed a heuristic-based optimization model aimed at minimizing both delivery and waiting times for waste disposal, thereby further reducing disposal costs (Bhat, 1996). Building on this, Andrzej introduced an optimization method based on genetic local search for determining the collection frequency of waste collection points, which demonstrated the shortest running time compared to other search methods (Lubotzky et al., 2015). Additionally, some research workers have explored system simulation using hybrid evolutionary algorithms (Caroline, 2011), ant colony algorithms (Zhang et al., 2012; Mou et al., 2021), and genetic algorithms (Deng et al., 2018; Chen et al., 2007). Other scholars have examined the system from a macro perspective. For example, He et al. proposed a comprehensive network recycling system for waste management; however, its implementation requires a solid economic foundation (He, 2012). These findings were corroborated in a study, revealing that sanitation funding, environmental awareness, and management systems are key challenges facing rural waste recycling and treatment, as evidenced by research conducted on domestic waste in a specific area of Tianjin (Zheng, 2018).

2 Modeling of a rural domestic waste recycling network

2.1 Problem formulation and description

Currently, in most rural areas of China, the volume of domestic garbage is increasing annually and has not been managed effectively. Garbage management is no longer solely a concern for individual villages or towns; it has evolved into a widespread issue affecting the majority of the rural regions in China. With the diversification of rural development, the characteristics of domestic waste in these areas are both numerous and varied. In comparison to urban regions, rural garbage management faces numerous challenges, including inadequate facilities, low levels of environmental awareness among villagers, and poorly structured management organizations. In November 2015, ten departments, led by the Ministry of Housing and Urban-Rural Development, jointly issued the document “Comprehensively Promoting the Guiding Opinions on Rural Garbage Management” (Ministry of Housing and Urban-Rural Development, 2015). This document proposes a rural garbage collection and transportation model characterized by “village collection, town transfer, and county treatment.” The operational process of this model involves initially concentrating rural waste in villages, after which the town government dispatches collection and transportation vehicles to gather all waste from the villages within its jurisdiction. This waste is then transported to a transfer station or a designated treatment facility. Ultimately, the garbage from a county is processed at several different final treatment points.

Effective garbage recycling in rural areas requires not only government management but also an enhancement of environmental protection awareness among villagers. Villagers must dispose off their waste in designated locations within the village, where it can be collected centrally and prepared for transfer to a sorting facility (Jia et al., 2021; Xp et al., 2020). A three-layer network for rural domestic waste recycling is examined in this study, consisting of three types of nodes: the waste generation point, the sorting and transfer station, and the final processing point, along with the connections between these nodes. The process operates as follows: within a county area, multiple garbage trucks depart from the waste sorting transfer station to collect waste from each village, ensuring that every rural area is serviced at least once (assuming the total waste generated in a rural area does not exceed the maximum capacity of the garbage trucks) (Chen and Hu, 2018). Once a truck reaches or approaches its maximum capacity, it must return to the waste sorting transfer station to unload the collected garbage. At the sorting and transfer station, the waste is sorted based on various characteristics and subsequently transported to different treatment facilities. This process is illustrated in Figure 2.

Figure 2

Figure 2. Rural three-tier recycling network design.

In the rural domestic waste recycling network, waste generation points are dispersed across various locations in the countryside, and as such, they are not considered the focus of the network planning study. Instead, the siting of final waste treatment points including recycling and treatment plants, incineration facilities, and landfill sites is of particular importance and is therefore included in the analysis. The number of waste transfer points is substantial, and the selection of their number and locations significantly influences the cost and efficiency of the entire rural domestic waste recycling system; hence, these factors are also addressed in the study. The optimization of collection and transportation functions emphasizes the location of waste collection transfer points and the compatibility between various waste generation points and these transfer points, which can be viewed as both the site selection for waste collection transfer points and the optimization of collection and transportation routes. In summary, taking into account the uncertainty surrounding waste recycling quantities, the optimization of the rural domestic waste recycling network can be examined from two primary aspects: first, the research on the placement of waste recycling transfer points and final treatment points, and second, the optimization of waste recycling routes from the transfer points to each village. The specific performance includes the following:

(1) Considering the negative effects of sorting transfer stations on the surrounding residents and the transportation costs between the upper and lower levels of the network, and considering the location of sorting transfer stations.

(2) Minimizing the system cost and considering the matching relationship between the sorting station and the waste generation point and the costs, and selecting the location of the sorting station and the final waste disposal point.

(3) Optimizing the vehicle transportation path of the distribution network from the waste generation point to the sorting and transfer station with the goal of minimizing the system path.

In this study, waste is categorized into three distinct types for the sake of clarity: the first category, referred to as type I waste, includes materials that can be repurposed through secondary processing, such as glass, waste paper, and metals. These materials can be sorted and subsequently recycled by a recycling and treatment facility. The second category, known as type II waste, consists of non-directly recyclable materials that require incineration, including non-recyclable fabrics. These materials are processed at an incineration plant. The third category, termed type III waste, encompasses non-recyclable garbage that is suitable for direct landfilling. This waste is transported directly to landfills for disposal, as illustrated in Table 1.

Table 1

Table 1. Classification of rural domestic waste.

2.2 Model assumptions

The problem of recycling of rural household waste was a relatively complex problem, and to build this mathematical model and be closer to the actual problem, many practical constraints and factors needed to be taken into account. Therefore, in order to simplify the problem and establish a reasonable mathematical model, the following rationalization assumptions about the problem under study are made in this paper:

(1) Each village must be served every day, the garbage must be removed that day, and each garbage generation point can only be served by one garbage collection vehicle. The amount of waste generated at each waste generation point was not determined.

(2) Waste from the waste generation point cannot be transported directly to the final disposal point (including recycling treatment plants, incineration plants, and landfills), but it must be processed through a waste sorting transfer station before being transported to the final disposal point.

(3) The waste generation points were interconnected with each other by road.

(4) There were only two types of vehicles, waste collection vehicles and sorting and transportation vehicles, and the waste collection vehicles are different from the vehicles that are used for sorting and sending waste to the treatment points.

(5) The vehicles travel at a fixed average speed without consideration of uncertainties during the journey.

(6) The construction area of various infrastructures (space for placement of rural garbage bins, construction area of transfer stations, and end disposal facilities) was adequate.

(7) The fixed costs of garbage generation points are known (including the costs of garbage bins, garbage cleaning personnel, and electric tricycles).

(8) The construction cost of each infrastructure and the capacity and capability of garbage disposal were known and sufficient.

(9) According to the recyclable characteristics of the waste, the waste collected at the waste generation point was divided into three categories at the sorting transfer point: type I (recyclable waste), type II (incinerable waste), and type III (landfillable waste), and the proportion of the total waste volume in the three categories was known.

(10) Type I waste from each sorting station was transported to recycling treatment plants for secondary processing, and landfills and incineration plants are each fixed, but the final treatment center and the sorting station had a “one-to-many” or “many-to-many” relationship.

(11) The alternative locations of waste sorting and transfer stations were known, and the parking lot was located at the waste sorting and transfer station. Vehicles were returned to the parking lot after service was completed.

(12) The alternative locations of the final disposal points (including incineration plants, landfills, and recycling treatment plants) were known

(13) In this paper, it was assumed that when waste collection and transportation was performed, straight-line distances were considered when calculating the transportation distance between facilities, and there was no traffic congestion or traffic restrictions.

2.3 Parameter description

2.3.1 Collection

$I-$ collection of waste generation points, $i=1,2,3,\cdots ,i\in I$.

$J-$ sorting staging area collection, $j=1,2,3,\cdots ,j\in J$.

$K-$ collection of all transport vehicles; $K_1-$ collection of garbage collection vehicles; $K_2-$ collection of vehicles that are sorted and transported to the final disposal point.

$A-$ collection of recycling treatment plants to be selected.

$B-$ collection of incineration plants to be selected.

$C-$ collection of landfill sites to be selected. $\mathrm{w}-\mathrm{a}\text{nnual\hspace{0.17em}working\hspace{0.17em}days}.$

2.3.2 Model parameters

$u_1-k_1$ vehicle capacity.

$u_2-k_2$ vehicle capacity.

$Q_a-$ capacity of the recycling treatment plant.

$Q_b-$ incineration plant capacity.

$Q_c-$ landfill capacity.

$V_n-$ the average travel speed of garbage collection vehicle $n$ ($km/h$).

$d_{ij}-$ the distance from the waste generation point to the sorting and transfer station ($km$),

where the distance considering straight line distance $:d_{ij}=\sqrt{{\left(x_j-x_i\right)}^2+{\left(y_j-y_i\right)}^2}$.

$d_{ja}-$ the distance from the sorting transfer station to the recycling processing plant ($km$).

$d_{jb}-$ the distance from the sorting transfer station to the incineration plant ($km$).

$d_{jc}-$ the distance from the sorting transfer station to the landfill ($km$).

$d_{ia}-$ the distance from the waste generation point to the recycling treatment plant ($km$).

$d_{ib}-$ the distance from the waste generation point to the incineration plant ($km$).

$d_{ic}-$ the distance from the point of waste generation to the landfill ($km$).

$q_i-$ the daily waste generation at waste generation point $i$.

${\stackrel{\sim }{q}}_i-$ the fuzzy amount of daily waste generation for waste generation point $i$.

$\alpha -$ the proportion of type I waste.

$\beta -$ the proportion of type II waste.

$\gamma -$ the proportion of type III waste.

(Note: $\alpha +\beta +\gamma =1$, where the equation indicates that all waste has been processed in the model).

$D-$ the service radius of recycling waste vehicle $k_1$.

2.3.3 Description of related costs

$F_i-$ the fixed cost of waste generation point construction.

$F_j-$ the fixed costs for sorting staging areas.

$\left(F_j=FixedCosts+Sizeofsortingtransitstation\ast UnitvariableCost\right).$

$F_{k_1}-$ the fixed cost of recycling waste vehicles.

$F_{k_2}-$ the fixed cost of transport vehicles used after classification.

$F_a-$ the fixed costs for recycling treatment plants.

$F_b-$ the fixed costs of incineration plants.

$F_c-$ the fixed costs of landfills.

Annual compensation cost per capita available to residents whose straight-line distance from $D_j$ to the sorting staging area is $d_{ij}$ kilometers.

$c_1-$ the cost per unit distance of waste collection and transportation.

$c_2-$ the storage cost of storable waste per unit of waste in a $T_j$.

$c_3-$ the transportation cost per unit distance of waste.

2.3.4 Decision variables

$T_j-$ the average number of days in stock at sorting staging area $j$.

$X_{ja}-$ the volume of waste shipped from sorting transfer station $j$ to recycling treatment plant $a$.

$X_{jb}-$ the volume of waste shipped from sorting transfer station $j$ to incineration plant $b$.

$X_{jc}-$ the volume of waste shipped from sorting transfer station $j$ to landfill $c$.

$X_{ja{k}_2}\left\{\begin{array}{c}1,\text{If\hspace{0.17em}}\mathrm{a}\text{\hspace{0.17em}connection\hspace{0.17em}exists\hspace{0.17em}from\hspace{0.17em}}j\text{\hspace{0.17em}to\hspace{0.17em}}a\text{\hspace{0.17em}and\hspace{0.17em}is\hspace{0.17em}serviced\hspace{0.17em}by\hspace{0.17em}vehicle\hspace{0.17em}}{k}_2\left(a,j\in A\cup J\right)\\ 0,\text{Other}\end{array}\right..$

$X_{jb{k}_2}\left\{\begin{array}{c}1,\text{If\hspace{0.17em}}\mathrm{a}\text{\hspace{0.17em}connection\hspace{0.17em}exists\hspace{0.17em}from\hspace{0.17em}}j\text{\hspace{0.17em}to\hspace{0.17em}}b\text{\hspace{0.17em}and\hspace{0.17em}is\hspace{0.17em}serviced\hspace{0.17em}by\hspace{0.17em}vehicle\hspace{0.17em}}{k}_2\left(b,j\in B\cup J\right)\\ 0,\text{Other}\end{array}\right..$

$X_{jc{k}_2}\left\{\begin{array}{c}1,\text{If\hspace{0.17em}}\mathrm{a}\text{\hspace{0.17em}connection\hspace{0.17em}exists\hspace{0.17em}from\hspace{0.17em}}j\text{\hspace{0.17em}to\hspace{0.17em}}c\text{\hspace{0.17em}and\hspace{0.17em}is\hspace{0.17em}serviced\hspace{0.17em}by\hspace{0.17em}vehicle\hspace{0.17em}}{k}_2\left(c,j\in B\cup J\right)\\ 0,\text{Other}\end{array}\right..$

$Y_j\left\{\begin{array}{c}1,\text{If\hspace{0.17em}}\mathrm{a}\text{\hspace{0.17em}sorting\hspace{0.17em}center\hspace{0.17em}is\hspace{0.17em}established\hspace{0.17em}}\left(j\in J\right)\\ 0,\text{Other}\end{array}\right..$

$Y_a\left\{\begin{array}{c}1,\text{If\hspace{0.17em}}\mathrm{a}\text{\hspace{0.17em}recycling\hspace{0.17em}treatment\hspace{0.17em}plant\hspace{0.17em}is\hspace{0.17em}established\hspace{0.17em}}\left(a\in A\right)\\ 0,\text{Other}\end{array}\right..$

$Y_b\left\{\begin{array}{c}1,\text{If\hspace{0.17em}an\hspace{0.17em}incineration\hspace{0.17em}plant\hspace{0.17em}is\hspace{0.17em}established\hspace{0.17em}}\left(b\in B\right)\\ 0,\text{Other}\end{array}\right..$

$Y_c\left\{\begin{array}{c}1,\text{If\hspace{0.17em}}\mathrm{a}\text{\hspace{0.17em}landfill\hspace{0.17em}plant\hspace{0.17em}is\hspace{0.17em}established\hspace{0.17em}}\left(c\in C\right)\\ 0,\text{Other}\end{array}\right..$

$Z_{ij}\left\{\begin{array}{c}1,\text{If\hspace{0.17em}waste\hspace{0.17em}generation\hspace{0.17em}point\hspace{0.17em}}\mathrm{i}\text{\hspace{0.17em}is\hspace{0.17em}assigned\hspace{0.17em}to\hspace{0.17em}sorting\hspace{0.17em}center\hspace{0.17em}}j\left(i\in I,j\in J\right)\\ 0,\text{Other}\end{array}\right..$

2.4 Site selection model construction: objective function and constraints

The traditional recycling network vehicle path planning problem has primarily been approached by scholars as a single-objective function problem, focusing on either minimizing total cost or maximizing satisfaction (Mao et al., 2021; Mao et al., 2019). However, in the context of rural waste recycling networks, solely considering cost in model development does not adequately address the evolving needs of rural infrastructure. In light of the 19th National Congress advocating for rural green development, it is essential to consider the impact of management practices on the living environment of households (Tian et al., 2022; Jiang et al., 2020). Consequently, two objective functions aimed at minimizing both cost and negative environmental effects to effectively address the siting problem of waste recycling networks are established in this paper.

2.4.1 Minimum total cost objective function

Rural domestic waste recycling involves various costs, necessitating a detailed analysis to identify the minimum cost model for the recycling process. Given the characteristics of rural domestic waste recycling, the associated costs can be categorized into several types: recycling costs, treatment costs, transportation costs, and indirectly generated costs.

2.4.1.1 Costs generated from the waste generation point to the sorting and transfer center

In the rural domestic waste recycling network, the associated costs encompass several components: the construction costs of facilities at the waste generation point, the transportation costs incurred when moving waste from the generation point to the sorting and transfer center, the construction costs of the sorting and transfer center itself, the costs associated with sorting the waste, and the storage costs for recyclable materials at the sorting and transfer station.

2.4.1.2 Costs incurred from the sorting and transfer center to final disposal

In addition to the costs incurred at the sorting and transfer stations, transportation costs arise from the sorting and transfer centers to various final treatment locations, along with the construction costs of facilities at these final treatment points. Analyzing the rural domestic waste recycling network reveals that the costs associated with it can be categorized into three primary types: fixed facility construction costs, transportation costs, and recycling network operation costs. Specifically, the fixed construction costs encompass the initial investment required for constructing facilities at the waste generation points, sorting and transfer stations, and final treatment points. The operation costs pertain to the operational expenses of the sorting and transfer centers as well as the final treatment points. Transportation costs are divided into two stages: costs associated with transporting waste from the generation points to the sorting and transfer centers, and costs for transporting waste from the sorting and transfer centers to the final treatment points. Following this analysis, a minimum cost objective function was established (see Equation 1).

$\mathit{min}\left\{\begin{array}{l}{\displaystyle \sum _{j\in J}}\left(a+b{\displaystyle \sum _{i\in I}}{\stackrel{\sim }{q}}_i\right)Y_j\\ +{\displaystyle \sum _{a\in A}}{F}_a{Y}_a+{\displaystyle \sum _{b\in B}}{F}_b{Y}_b+{\displaystyle \sum _{c\in C}}{F}_c{Y}_c\\ +{\displaystyle \sum _{k_1\in K_1}}{F}_{k_1}{\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{X}_{ij{k}_1}+{\displaystyle \sum _{k_2\in K_2}}{F}_{k_2}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{a\in A}}{X}_{ja{k}_2}+{\displaystyle \sum _{k_2\in K_2}}{F}_{k_2}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{b\in B}}{X}_{jb{k}_2}+{\displaystyle \sum _{k_2\in K_2}}{F}_{k_2}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{c\in C}}{X}_{jc{k}_2}\\ +w{c}_1{\displaystyle \sum _{i\in I\cup J}}{\displaystyle \sum _{j\in I\cup J}}{\displaystyle \sum _{k_1\in K_1}}{\stackrel{\sim }{q}}_j{d}_{ij}{X}_{ijk}\\ +\frac{w}{T_j}{c}_2\alpha {\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_j\\ +w{c}_3\left(\alpha {\displaystyle \sum _{a\in A}}{Y}_a\left({\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_i{d}_{ja}\right)\frac{1}{T_j}+\beta {\displaystyle \sum _{b\in B}}{Y}_b{\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_j{d}_{jb}+\gamma {\displaystyle \sum _{c\in C}}{Y}_c{\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_j{d}_{jc}\right)\end{array}\right\}.(1)$

2.4.2 Negative effect objective function

As the decision was made by the government, it is essential to consider the impact of the waste sorting and transfer center, as well as the various treatment points, on the surrounding residents when building the rural household waste recycling network. This includes addressing potential negative effects of site selection, such as noise pollution and odors from the sorting and transfer center’s processing of household waste, along with the broader environmental implications for the area. The negative effects on the surrounding community, including noise pollution and odors, must be thoroughly evaluated. In the literature, He, B. proposed a model to address these negative effects as a function of the distance and proximity to residential areas, establishing a positive and negative proportion (He et al., 2007). Liu, M. H. approached the issue by translating the negative effects into compensation costs for residents through government policies (Liu M. H., 2021). A brief discussion of these two methods follows. In He, B.'s analysis, the challenge of selecting a location for the waste sorting and transfer center is highlighted. As the facility is intended to sort waste at the point of generation, residents generally prefer it to be located as far away from residential areas as possible. Thus, in addition to cost considerations, the location must account for the negative impacts on nearby residents. He constructed a mathematical expression for the negative effect function, indicating that the negative impact of the sorting and transfer station is inversely proportional to the distance from households. This relationship is articulated in the following objective function (see Equation 2):

$\mathit{min}{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{k_1}}{\displaystyle \sum _j}{X}_{ij{k}_1}{d}_{ij}^r.(2)$

(Here, $\theta ,r$ are parameters that indicate the degree of influence of different coefficients on the resulting negative utility.)

In Liu’s treatment of the negative effect, the negative effect generated by the sorting transfer station was converted into the compensation cost of environmental pollution to the surrounding residents. According to the technical specification for domestic waste transfer station, there are standard restriction requirements for the distance between the waste transfer station and adjacent living buildings for regulation, as shown in Table 2 (The Ministry of Construction on, 2006). Determining the compensation mechanism generated by the establishment of the waste sorting transfer point to the nearby villagers requires a comprehensive consideration based on the environmental impact caused to the villagers and the actual income of the local villagers.

Table 2

Table 2. Spacing requirements for transfer stations and adjacent buildings.

He assumed that the transfer station established is medium-sized III, so it can be assumed that the amount of compensation from residents within 15 m of the waste sorting transfer station is infinite. On the basis of the above regulations, the following functional relationship is established between the straight-line distance from the residential area to the waste sorting transfer station and the per capita compensation rate (see Equation 3):

$D_{ij}=\left\{\begin{array}{l}\infty d_{ij}<0.015km\\ e\left(30-d_{ij}\right)+f0.015km\le d_{ij}<0.03km\\ f0.03km\le d_{ij}<0.045km\\ 0d_{ij}\ge 0.045km\end{array}\right..(3)$

Therefore, based on the above analysis, the negative effects generated by the waste sorting transfer station were translated into compensating costs for the environment of the population, as follows (see Equation 4):

$\mathit{min}={\displaystyle \sum _{j\in J}}{D}_j.(4)$

Parameter description

$e$: when the straight-line distance from the waste sorting station was in the range of 0.015–0.03 km, for every 0.001 km increase in distance, then the corresponding reduction in annual compensation cost per capita.

$f$: annual compensation cost per capita within a 0.03–0.045 km straight line distance from the sorting and staging station.

The values of $e,f$ were related to the per capita income of local residents and the scale of the sorting and transfer station, and the higher the per capita income, the higher the compensation standard.

Considering the situation discussed in this paper, the distances considered are closer to the reality as alternative sites to be selected have been given.

Through the analysis, the sorting and transfer stations and the final treatment points (including recycling plants, incineration plants, and landfills) are to be sited in this paper. Considering that all these facilities have negative effects on the nearby residents, they need to be located as far as possible from the villages, that is, the waste generation points, to minimize the negative effects; thus, the distance from the waste generation points is inversely proportional to the negative effects generated (see Equation 5).

$\mathit{min}{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{a\in A}}\frac{{\displaystyle \sum _{a\in A}}{\left(Q_a{Y}_a\right)}^p}{{\left(d_{ia}\right)}^r}+{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{b\in B}}\frac{{\displaystyle \sum _{b\in B}}{\left(Q_b{Y}_b\right)}^p}{{\left(d_{ib}\right)}^r}+{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{c\in C}}\frac{{\displaystyle \sum _{c\in C}}{\left(Q_c{Y}_c\right)}^p}{{\left(d_{ic}\right)}^r}+{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{k_1}}{\displaystyle \sum _j}{X}_{ij{k}_1}\frac{1}{{\left(d_{ij}\right)}^r}.(5)$

(Here, $\theta ,p,r$ were parameters that indicated the extent to which different coefficients affect the resulting negative utility.)

2.4.3 Site selection objective function

2.4.3.1 Objective function

Therefore, the final objective function can be obtained as the following two equations (see Equations 6, 7):

$\mathit{min}\left\{\begin{array}{c}{\displaystyle \sum _{j\in J}}\left(a+b{\displaystyle \sum _{i\in I}}{\stackrel{\sim }{q}}_i\right)Y_j\\ +{\displaystyle \sum _{a\in A}}{F}_a{Y}_a+{\displaystyle \sum _{b\in B}}{F}_b{Y}_b+{\displaystyle \sum _{c\in C}}{F}_c{Y}_c\\ +{\displaystyle \sum _{k_1\in K_1}}{F}_{k_1}{\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{x}_{ij{k}_1}+{\displaystyle \sum _{k_2\in K_2}}{F}_{k_2}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{a\in A}}{x}_{ja{k}_2}+{\displaystyle \sum _{k_2\in K_2}}{F}_{k_2}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{b\in B}}{x}_{jb{k}_2}+{\displaystyle \sum _{k_2\in K_2}}{F}_{k_2}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{c\in C}}{x}_{jc{k}_2}\\ +w{c}_1{\displaystyle \sum _{i\in I\cup J}}{\displaystyle \sum _{j\in I\cup J}}{\displaystyle \sum _{k_1\in K_1}}{\stackrel{\sim }{q}}_j{d}_{ij}{x}_{ijk}\\ +\frac{w}{T_j}{c}_2\alpha {\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_j\\ +w{c}_3\left(\alpha {\displaystyle \sum _{a\in A}}{Y}_a\left({\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_i{d}_{ja}\right)\frac{1}{T_j}+\beta {\displaystyle \sum _{b\in B}}{Y}_b{\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_j{d}_{jb}+\gamma {\displaystyle \sum _{c\in C}}{Y}_c{\displaystyle \sum _{i\in I}}{\displaystyle \sum _{j\in J}}{Z}_{ij}{\stackrel{\sim }{q}}_j{d}_{jc}\right)\end{array}\right\}.(6)$

$\mathit{min}{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{a\in A}}\frac{{\displaystyle \sum _{a\in A}}{\left(Q_a{Y}_a\right)}^p}{{\left(d_{ia}\right)}^r}+{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{b\in B}}\frac{{\displaystyle \sum _{b\in B}}{\left(Q_b{Y}_b\right)}^p}{{\left(d_{ib}\right)}^r}+{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{c\in C}}\frac{{\displaystyle \sum _{c\in C}}{\left(Q_c{Y}_c\right)}^p}{{\left(d_{ic}\right)}^r}+{\displaystyle \sum _{i\in I}}{\left({\stackrel{\sim }{q}}_i\right)}^{\theta }{\displaystyle \sum _{k_1}}{\displaystyle \sum _j}{X}_{ij{k}_1}\frac{1}{{\left(d_{ij}\right)}^r}.(7)$

2.4.3.2 Constraints

Constraint that indicates that all type I waste, recyclable waste, was transported to the recycling treatment plant is as follows (see Equation 8):

$\alpha {\displaystyle \sum _{i\in I}}{\stackrel{\sim }{q}}_i={\displaystyle \sum _{a\in A}}{X}_{ja},j\in J.(8)$

Constraint that indicates that all type II waste, incinerable waste, was transported to the incineration plant is as follows (see Equation 9):

$\beta {\displaystyle \sum _{i\in I}}{\stackrel{\sim }{q}}_i={\displaystyle \sum _{a\in A}}{X}_{jb},j\in J.(9)$

Constraint that indicates that type III waste, direct landfill waste, can be transported to landfill in its entirety is as follows (see Equation 10):

$\gamma {\displaystyle \sum _{i\in I}}{\stackrel{\sim }{q}}_i={\displaystyle \sum _{a\in A}}{X}_{jc},j\in J.(10)$

Capacity constraints for final disposal sites at recycling treatment plants, incineration plants, and landfills are included with the amount of waste transported to each final disposal site not exceeding the capacity of each final disposal site (see Equation 11).

$\begin{array}{c}{\displaystyle \sum _{j\in J}}{X}_{ja}\le Q_a{Y}_a,a\in A\\ {\displaystyle \sum _{j\in J}}{X}_{jb}\le Q_b{Y}_b,b\in B\\ {\displaystyle \sum _{j\in J}}{X}_{jc}\le Q_c{Y}_c,c\in C\end{array}.(11)$

The range of values of each variable is described as follows (see Equation 12):

$\begin{array}{c}{X}_{ij{k}_1}\in \left\{0,1\right\},i\in I,j\in J,k_1\in K_1\\ Y_j,Y_a,Y_b,Y_c\in \left\{0,1\right\},j\in J,a\in A,b\in B,c\in C\\ T_j\in \left[0,1,2,3,4,5,6,7\right],\forall j\in J\end{array}.(12)$

2.5 Route planning model

From the content of the waste recycling network, the waste recycling path optimization solved the route problem between the multi-waste generation point and the waste sorting transfer station. The model was based on the waste sorting transfer station siting model, and then the optimization of the shortest path between the waste generation point and the waste sorting transfer station was carried out with the vehicle capacity as the constraint, as well as the adaptation relationship among the vehicle, the waste generation point, and the sorting transfer station.

The commonly used objective parameters for solving path optimization problems are: cost (minimum total cost) distance (shortest total path) and time (shortest time spent)." In this paper, the shortest path is selected as the research target when building the garbage collection path optimization model (see Equation 13).

$\mathit{min}{\displaystyle \sum _{k_1\in K_1}}{\displaystyle \sum _{i,j=1}}{d}_{ij}{x}_{ij{k}_1}.(13)$

2.5.1 Constraints

The service radius of the sorting transfer station, indicating that the service radius was not less than the distance to each subordinate waste generation point (see Equation 14) was obtained as follows:

$d_{ij}\cdot X_{ij{k}_1}\le D\left(i,j,k_1\in I\cup J\cup K\right).(14)$

There was one and only one service vehicle that limits individual waste generation (see Equation 15).

${\displaystyle \sum _{k_1\in K_1}}{\displaystyle \sum _{i\in I\cup J}}{X}_{ij{k}_1}=1,i\in I.(15)$

Vehicle capacity constraint, where the amount of waste transported did not exceed the vehicle capacity constraint (see Equation 16), is obtained as follows:

${\displaystyle \sum _{i\in I}}{\stackrel{\sim }{q}}_i{\displaystyle \sum _{j\in I\cup J}}{X}_{ij{k}_1}\le u_1,k_1\in K_1.(16)$

It was ensured that the collection vehicle arrived at a waste generation point and then left that point (see Equation 17).

${\displaystyle \sum _{i\in I\cup J}}{X}_{ij{k}_1}-{\displaystyle \sum _{i\in I\cup J}}{X}_{ij{k}_1}=0,k_1\in K_1,i\in I\cup J.(17)$

3 Algorithm selection for the rural domestic waste recycling network

The transfer station siting model in the optimization framework for rural domestic waste recycling, established in the previous section, identifies key variables for investigation. These include the number of sorting transfer stations, their locations, the transportation schemes connecting these stations to waste generation points, and the matching relationships between sorting transfer stations and waste generation points. Analyzing the data reveals that on average, each county in China comprises approximately 12 townships and 200 villages, indicating a substantial data scale. Existing exact algorithms, which are effective for small-scale, high-demand problems, are not suitable for this context. However, heuristic algorithms demonstrate effectiveness across a broader range of problems, accommodating the model’s multiple constraints to achieve satisfactory solutions. The solution method for the recycling network model will be selected from among these heuristic algorithms. Whereas various meta-heuristic algorithms possess distinct characteristics that may be more suited to this problem, the particle swarm optimization algorithm, although influenced by the randomness of iteration speed, shows promise for continuous variable optimization. Nevertheless, it has limitations in optimizing discrete facility siting. Both the ant colony algorithm and the particle swarm optimization algorithm fall under the category of swarm intelligence algorithms, and leveraging group feedback can significantly enhance the optimization speed of these algorithms while ensuring strong stability.

3.1 Site selection issues

3.1.1 Solving multi-objective optimization problems using PSO algorithm

As the problem of selecting the location of the waste sorting transfer station is a mixed integer programming problem based on continuity solution, the PSO algorithm is chosen to deal with this multi-objective optimization problem. The advantage of the PSO algorithm is that it has the memory function and is simple and easy to be implemented.

In the 1990s, Shi and Eberhart proposed the concept of inertia weight $w$, which aimed to improve the performance of the PSO algorithm (Shirazi et al., 2017). After that, other scholars have continuously studied and analyzed the inertia weight, and concluded that inertia weight w greatly affects the optimization results. For any particle $i$ in the particle swarm, when the position and velocity of the $kth$ update are $x_{id}^k$ and $v_{id}^k$, respectively, the velocity and position of particle $i$ in the $\left(k+1\right)$th iteration can be expressed as follows Equations 18 and 19:

$v_i{d}^{\left(k+1\right)}=w{v}_i{d}^k+c_1{r}_1\left(p_i{d}^k-x_i{d}^k\right)+c_2{r}_2\left(p_g{d}^k-x_i{d}^k\right),(18)$

$x_i{d}^{\left(k+1\right)}=x_i{d}^k+v_i{d}^{\left(k+1\right)}.(19)$

$w-$ the inertia weight, which is how much the velocity in front of the particle affects the current velocity.

$c_1、c_2-$ the learning factor, usually taken as $c_1=c_2=2$, in order to facilitate the convergence of the solution; generally, the larger the learning factor, the better the convergence $c_1,c_2\in \left(0,4\right)$.

$r-$ the constraint coefficients, and $r_1、r_2$ are random numbers between $\left[0,1\right]$.

$p_d^k-$ the best position of a particle after updating itself $k$ times is called $Pbest$.

$p_g^k-$ the position of the best particle that occurs in the $kth$ update in the particle swarm is called $Gbest.$

Shi and Eberhart pointed out through analysis that if weight w is varied linearly between [0.4, 1.4], then the optimization effect of the algorithms are slightly better than other values of the weight factor; they also illustrate that when the inertia weights are small, it is suitable for local search, and when it is large, it is suitable for global search.

Currently, most of the research studies are using the strategy of linearly decreasing weights for dynamic changes, and its expression can be described as follows Equation 20:

$w=w_{\mathit{max}}-\frac{w_{\mathit{max}}-w_{\mathit{min}}}{k_{\mathit{max}}}\times k.(20)$

${wmin}_{\mathit{max}}-$ the maximum and minimum values of inertia coefficients.

$k_{\mathit{max}}-$ the maximum number of iterations.

$k-$ the current number of iterations.

In order to avoid falling into local optimization during the particle swarm solving process, an adaptive mutation method is generally used to adjust the position of the particles, and the expression can be described as follows Equations 21 and 22:

$x_{id}=x_{0\mathit{max}},(21)$

$i=m\times r_0.(22)$

$m-$ the population size.

3.1.2 Multi-objective PSO flow

The specific optimization algorithm flow is illustrated through an example of objective function minimization.

Step 1 involves initialization, where a population size of $N$ is defined, and the positions of random particles are generated as $X$ and $V$. The fitness value is calculated for each objective function, leading to the determination of both the individual extreme value and the global extreme value.

Step 2 focuses on updating the particle population, where velocity $X_i$ and position $V_i$ are adjusted based on the global vector mean $G_{best}$ and the individual extreme value $P_{best}$ of the computed functions.

Step 3 entails updating the set of non-inferior solutions.

Step 4 involves updating the optimal solution identified by each particle.

Step 5 assesses the termination condition; if the condition is satisfied, then the program terminates; otherwise, it returns to step 2 to continue the optimization process.

3.2 Path optimization issues

The path planning problem can be described in terms of a traveler’s problem. According to the characteristics of the problem that needs to be solved in this paper, only the sorting transfer station has multiple vehicle departures to collect and transport all the waste from all the waste generation points. Therefore, the mathematical model of the multi-traveler problem is used for modeling and solving in this study.

3.2.1 Solving the path planning problem using the ant colony algorithm

The number of ants located in city $i$ at moment $t$ is denoted by $b_i\left(t\right)$, the pheromone value on edge $\left(i,j\right)$ at moment t is denoted by ${\tau }_{ij}\left(t\right),th$ the total number of cities in the traveler problem is denoted by $n$, and the total number of ants in the colony is denoted by $m$, i.e., $m={\displaystyle {\sum }_{i=1}^n}{b}_i\left(t\right)$. When $t=0$, i.e., at the initial moment, the same pheromone is set for each path, and m ants are arbitrarily put into one of the $m$ cities among the $n$ cities and set as ${\tau }_{ij}\left(0\right)={\tau }_0$.

Any ant $k$ in the course of action decides the direction of movement based on the start information of the path and the size of the pheromone. Then, path selection probability $p_{ij}^k\left(t\right)$ of ant $k$ moving from city $i$ to city $j$ at moment $t$ can be expressed as the following equation:

$p_{ij}^k\left(t\right)=\left\{\begin{array}{l}\frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{\alpha }{\left[{\eta }_{ij}\left(t\right)\right]}^{\beta }}{{\displaystyle \sum _{s\in allowe{d}_k}}{\left[{\tau }_{is}\left(t\right)\right]}^{\alpha }{\left[{\eta }_{is}\left(t\right)\right]}^{\beta }}\text{\hspace{0.17em}if\hspace{0.17em}}j\in allowe{d}_k\\ 0else\end{array}\right..(23)$

In the above equation, the place where the ant is currently located is denoted as $i$ and the place that the ant has not yet been to is denoted as $j$. In this cycle, the set of places that ant $k$ has not yet been to is denoted by $allowe{d}_k$; the information heuristic factor is $\alpha$, which reflects the relative importance of the size of the pheromone in the ants’ choice of paths; the smaller the value of $\alpha$ is, it indicates that the ants’ choice of the next path seldom relies on the pheromone, and the bigger the value of $\alpha$ is, it indicates that the path choice mainly relies on pheromone for path selection; the expectation heuristic factor is $\beta$, which reflects the relative importance of path length for path selection; the larger the value of $\beta$, it indicates that ants choose the next path with a shorter path as a measure. ${\eta }_{ij}\left(t\right)$ is used to denote the heuristic function, which is generally taken as the inverse of the distance $d_{ij}$ between the two cities $i,j$, i.e., Equation 24

${\eta }_{ij}\left(t\right)=\frac{1}{d_{ij}}.(24)$

In order to prevent ants from making repetitive choices of the places they have already visited, the taboo table $tab{u}_k$ will be used to save the places that ant $k$ has already visited. If all the places have been recorded by $tab{u}_k$, it indicates that ant $k$ has already traveled to all the places, forming a loop once, which means that a feasible solution to the traveler’s problem has been obtained.

After the above steps are completed, the pheromones on the path are updated according to the following principles. Updating the size of the pheromone on edge $\left(i,j\right)$ at moment $t+n$ is done according to the following rule:

${\tau }_{is}\left(t+n\right)=\left(1-\rho \right){\tau }_{is}\left(t\right)+\Delta {\tau }_{ij},(25)$

$\Delta {\tau }_{ij}={\displaystyle \sum _{k=1}^m}{\Delta }_{ij}^k\left(t\right).(26)$

In the above equation, the volatilization factor of the pheromone is represented by $\rho$, and this factor always satisfies $\rho <1$; in contrast, the corresponding $1-\rho$ is the residual factor of the pheromone. The amount of change on the edge of the $kth$ ant during that cycle is represented by ${\Delta }_{ij}^k\left(t\right)$.

${\Delta }_{ij}^k\left(t\right)=\left\{\begin{array}{l}\frac{Q}{L_k}Ifantkpassesthroughedgeijinthisloop\\ 0else\end{array}\right..(27)$

3.2.2 Steps for solving the path planning problem using the ACO algorithm

Step 1: Initialization of parameters. The maximum number of cycles $N_{c-\mathit{max}}$ is set; first, the number of cycles $N_c=0$ is set, and the taboo table $tab{u}_k$ is cleared so that the initialized pheromone of each edge $\left(i,j\right)$ satisfies ${\tau }_{ij}\left(0\right)={\tau }_0$, where ${\tau }_0$ is a constant, and the incremental amount of pheromone at the initial moment $\Delta {\tau }_{ij}\left(0\right)=0$.

Step 2:    The number of cycles $N_c=N_c+1$.

Step 3:    Place $m$ ants on $n$ cities, and then add the city where ant $k$ is located to the taboo table $tab{u}_k$ of ant $k$.

Step 4:    The number of ants $k=1$.

Step 5:    The probability $p_{ij}^k\left(t\right)$ that ant $k$ chooses a path to move to the next city $j$ according to Equation 23, and then $j$ is added to the taboo table $tab{u}_k$ of ant $k$.

Step 6:    The number of ants $K=K+1$.

Step 7:    If $K\ge m$ is satisfied, perform step 5; otherwise, perform step 8.

Step 8:    Update the path pheromone according to Equation 25 and Equation 26.

Step 9:    If the verification of $N_c\ge N_{\mathit{max}}$ is satisfied, then continue to the next step; if not, then the taboo table $tab{u}_k$ has to be emptied, and go back to step 2 for solving.

Step 10: Output the shortest path and end.

4 Case studies and model solving

Dongfeng County, which is part of Liaoyuan City in Jilin Province, is situated in the south-central region of Jilin Province. It comprises 12 towns, including Dongfeng Town, Lalahe Town, and Nadanbo Town, among others, with a combined population of approximately 400,000 residents. In Dongfeng County, rural waste management is implemented through a third-party service model, wherein the government contracts third-party service companies to collect, transfer, and treat household waste. However, the current model lacks a systematic approach for the planning and management of waste collection and transportation. The dispersed nature of villages, particularly in mountainous areas, exacerbates this issue, as inadequate planning results in elevated costs for waste collection and transportation. Consequently, the entire recycling process is characterized by high operating costs and low efficiency. Furthermore, villages lack waste bins for garbage separation and do not have centralized recycling sites. The prevailing waste disposal method relies on direct dumping and landfilling of unsegregated waste, which constitutes a relatively uniform approach.

4.1 Data preparation

Through research and information gathering, the essential data required have been collected. To enhance the numerical simulation experiment’s relevance to real-world conditions, Dongfeng County in Liaoyuan City, Jilin Province, is selected in this paper as the scope of experimental analysis. Fifty-two villages are identified as garbage generation points, with their specific coordinates and the volume of waste produced at each location presented in the table below. Based on the current waste disposal situation in Dongfeng County, which operates under a three-level network of village, town, and county, and considering the distribution of the selected village samples, ten sorting and transfer stations are proposed as experimental alternatives, distributed across each town. Additionally, three incineration plants, three landfills, and two recycling plants are selected as alternatives. The coordinates of these alternative locations are detailed in Table 3. The fundamental principles guiding the layout of each implementation are as follows:

Table 3

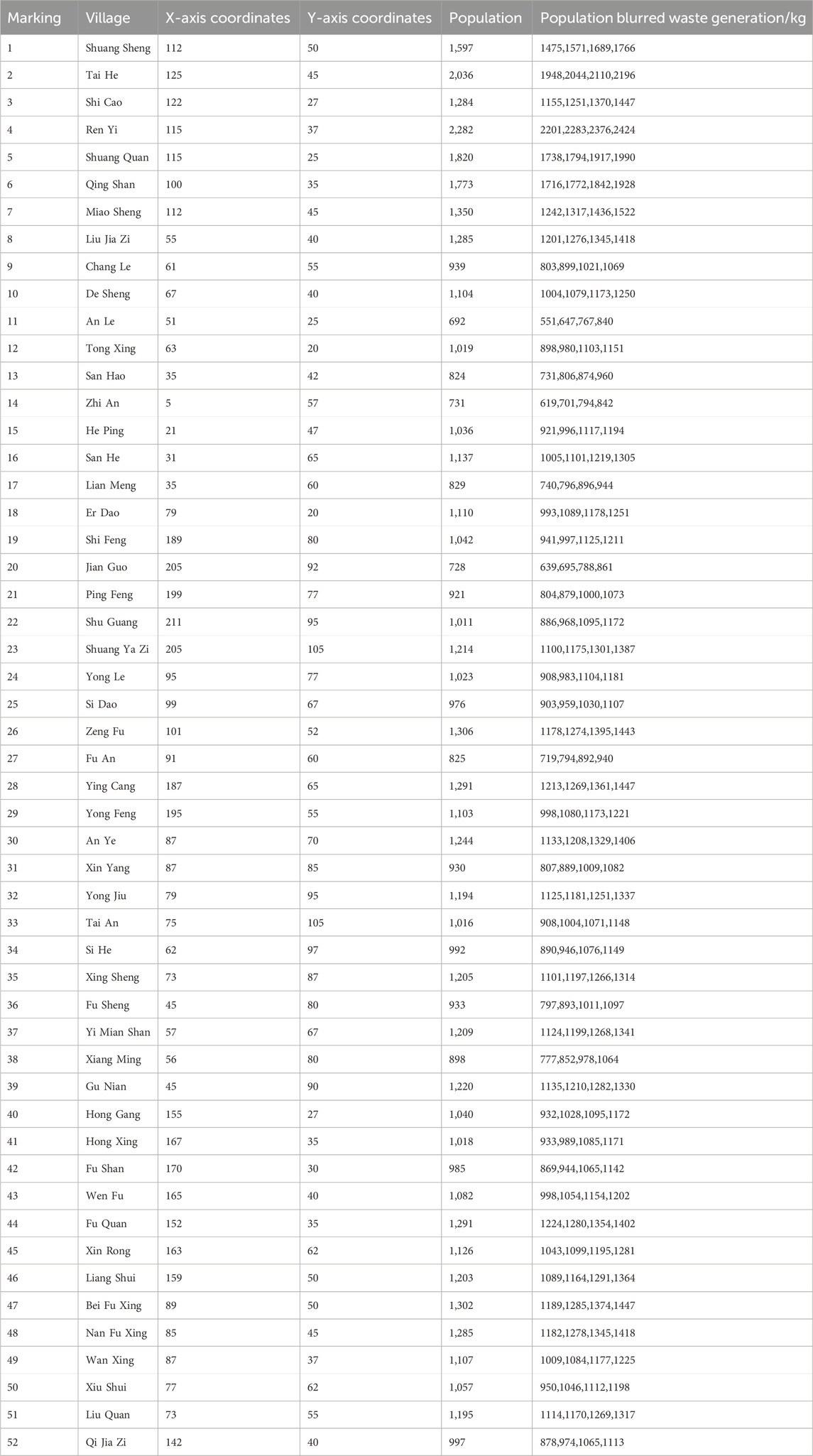
Table 3. Coordinate information of the location of each village (waste generation point) and fuzzy waste yield.

(1) The final treatment facilities, including incineration plants, recycling treatment plants, and landfills, must be situated away from the waste generation points, specifically distanced from residential areas. (2) The distribution of sorting and transfer stations should be closer to the waste generation points than the incineration plants and landfills, while still being relatively distant from residential areas.

Note: in the actual site selection process, the operation of waste recycling treatment facilities may significantly impact the lives of villagers. Therefore, the location of these facilities should consider various factors, including rural planning, water resources, geographic conditions, and transportation infrastructure.

The fuzzy waste generation was specified to obtain data, as in Table 4.

Table 4

Table 4. Waste production of each waste generation point.

Based on the actual construction needed of each site and the population distribution and geographical characteristics of Dongfeng County, alternative sites for sorting and transfer stations, incineration plants, landfill plants, and waste recycling plants were drawn up, as shown in Table 5.

Table 5

Table 5. Alternative coordinates for each site.

Based on the above data, the following coordinates including the location of waste generation points, sorting transfer stations, and incineration plants, landfills, and waste treatment plants in the Cartesian coordinate system are plotted. This is shown in Figure 3.

Figure 3

Figure 3. Location distribution of all sites.

Through the results of the research and the search for information, the parameters required for the construction of the rural household waste recycling network were estimated and determined. The specific data are shown in Table 6.

Table 6

Table 6. Parameters required for network construction.

According to the above parameters, the particle swarm optimization algorithm was used for optimal site selection using the established objective function.

4.2 Experimental platform

The arithmetic experiments in this paper were conducted with MATLAB 2019a software application as the platform. MATLAB, launched by MathWorks, is a set of high-performance numerical calculation and operation software applications that can be visualized, which is powerful for scientific calculation, flexible in programming process, and has a high quality in graphic display and clear results when solving with the design of visual interface, so the software application is globally used.

4.3 Facility siting solution

4.3.1 Facility siting model solving

In this paper, the analytically selected algorithm and the designed algorithm flow were applied and programmed on the MATLAB platform. The algorithm flow used the particle swarm optimization algorithm flow. The previous model value settings and the analysis of the particle swarm optimization algorithm solution process were combined, and the assignment of the relevant parameters in the model for this solution is shown in Table 7.

Table 7

Table 7. Partial parameter settings of the particle swarm optimization algorithm.

According to the above parameter settings, the particle swarm optimization algorithm was used to find the minimum cost according to the requirements of the objective function and constraints, and the number and location coordinates of each sorting transfer station, recycling plant, incineration plant, and landfill plant were output on the basis of the minimum cost obtained. After the optimization algorithm, the results are shown in Figure 4.

Figure 4

Figure 4. Distribution of site coordinates after site selection.

From the distribution diagram, we can see the number of each target site required by the particle swarm optimization algorithm to find the optimal number of sites, of which the optimal number of sorting transfer stations required is five, which are evenly distributed near each waste generation point. The optimal number of incineration plants required is one, located on the left side of the more concentrated waste generation point, in line with the actual needs of reality. The optimal number of landfill plants required is one, located in the middle. The optimal number of recycling plants required is two. The specific coordinate locations of each site are shown in Table 8.

Table 8

Table 8. Specific coordinate locations of each site.

The algorithm iteration diagram is shown in Figure 5.

Figure 5

Figure 5. Algorithm iteration diagram. (A) Minimum cost. (B) Negative effect.

From Figure 5A, it can be seen that the algorithm found the optimal solution at 3,133 iterations and got the minimum cost of 347,321,480,000 and the negative effect of 863.0287. From Figure 5B, the optimal number of sorting transfer stations needed to be five, which are uniformly distributed in the vicinity of all waste generation points, and the coordinates of the waste generation points belonging to the vicinity of each sorting transfer station attributed by the particle swarm optimization algorithm can be determined and marked using different colors, as shown in Figure 6.

Figure 6

Figure 6. Distribution of garbage generation points.

The number of coordinated and coordinate points of waste generation points attributed in the vicinity of each sorting and transfer station is shown in Table 9.

Table 9

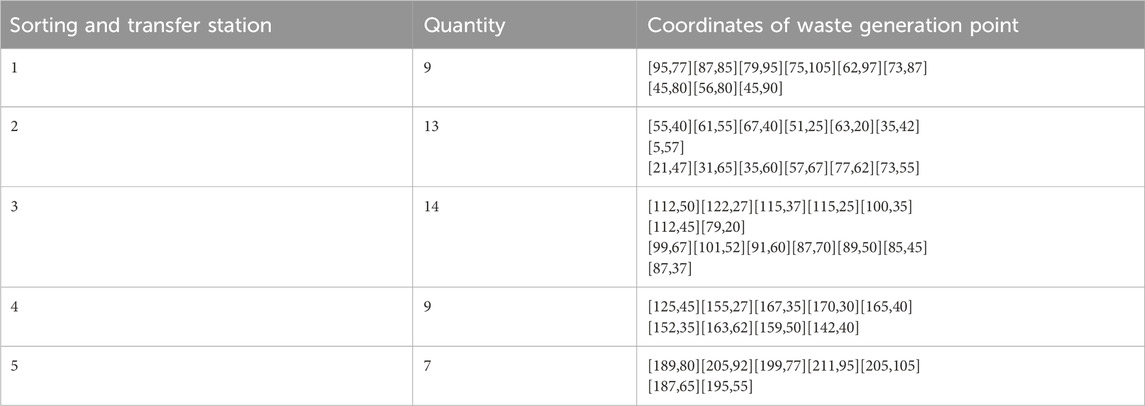
Table 9. Number and coordinated of waste generation points attributed to the vicinity of the sorting and transfer station.

4.3.2 Sensitivity analysis

In the domestic waste recycling network, the change of transportation cost will also have some effect on the total cost. Therefore, the unit transportation cost of waste at [100,180] was divided into five groups, and the final experimental calculation results are shown in Table 10.

Table 10

Table 10. Results of transportation cost sensitivity analysis.

From Figure 7, it can be seen that there was a linear positive relationship between unit transportation cost and total cost. In addition, it can be seen from the data of cost change that the total cost of transportation increases by approximately 3% for every 20 CNY increase in the transportation cost.

Figure 7

Figure 7. Transportation cost sensitivity analysis chart.

4.3.2.1 Sensitivity analysis of collection cost

In the rural household waste recycling network, waste collection cost occupies an important position, and its change has a huge impact on the cost. Therefore, in order to study the law of its influence on cost, it was analyzed. The garbage unit collection cost [460,580] was divided into five groups and run several times for each collection cost, and the optimal results were recorded, as shown in Table 11.

Table 11

Table 11. Collection cost sensitivity analysis results.

From Figure 8, it can be concluded that the total cost and the cost per unit of garbage collection are linearly and positively related to each other. From the data of cost changes, it can be seen that when the cost of garbage collection increased by 40 CNY, the total cost increased by approximately 2.8%. The number of sorting stations fluctuates as the unit collection cost increases, and when the unit collection cost reaches 540 CNY, the number of sorting stations increases from five to eight, indicating that the increase in the total cost due to the high collection cost can be avoided by increasing the number of sorting stations. It shows that there was a dynamic balance between the number of sorting stations and the unit collection cost. When the unit collection cost is too high, the total cost can be reduced by increasing the number of sorting stations and indirectly reducing the distance from the waste generation point to the sorting station.

Figure 8

Figure 8. Collection cost sensitivity analysis chart.

4.4 Route planning solution

Based on the results of the facility siting problem, the waste collection routes for the different sorting transfer stations are solved. The coordinates of the waste generation points to be collected by each sorting transfer station are shown in Table 12, as shown in the previous section for the siting of sorting transfer stations, incineration plants, landfill plants, and recycling plants.

Table 12

Table 12. Coordinates of waste generation points near sorting and transfer stations.

According to the objective function obtained from the path planning model, path planning is carried out for the waste generation points of each sorting and transfer station in turn. The serial numbers on the path planning are the default coordinate point ordering of the algorithm, and they do not represent the actual waste generation point location serial numbers. The planning results are shown in Figures 9–13.

Figure 9

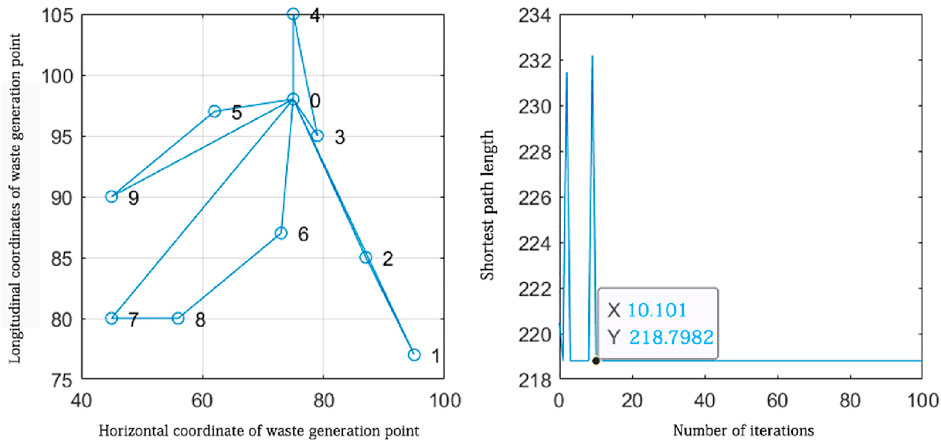
Figure 9. Path planning of waste generation points attributed to the vicinity of sorting transfer station 1.

Figure 10

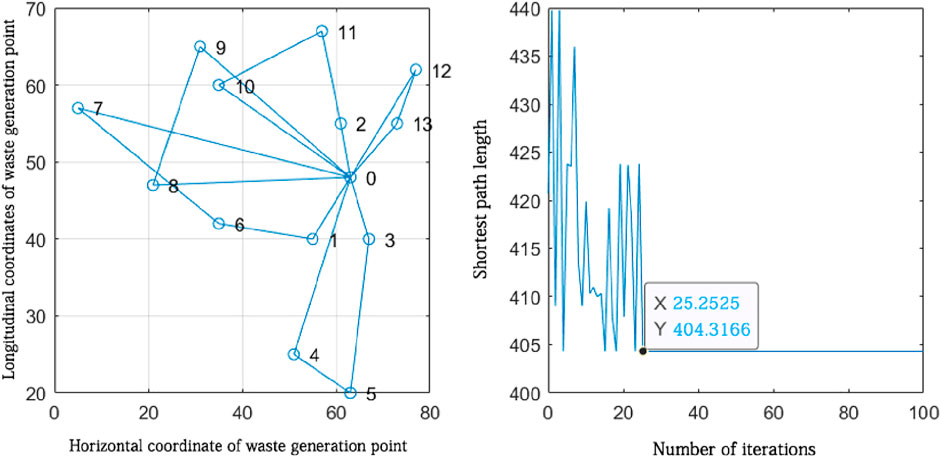
Figure 10. Path planning of waste generation points attributed to the vicinity of sorting transfer station 2.

Figure 11

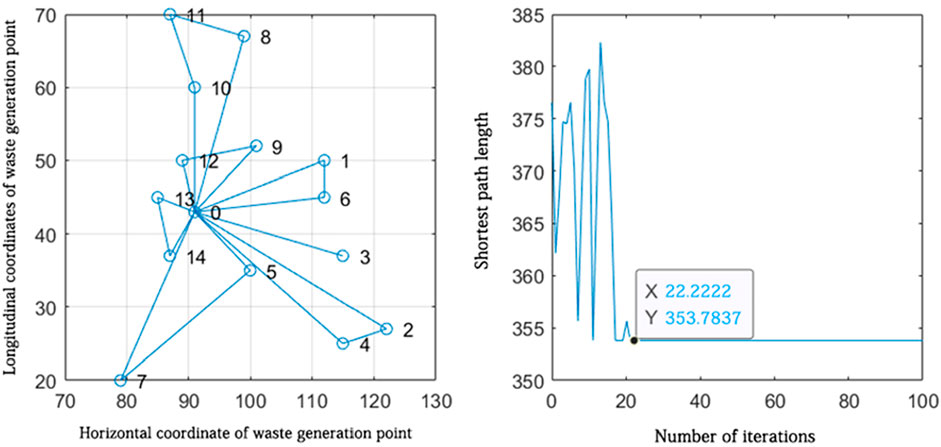
Figure 11. Route planning for waste generation points attributed to the vicinity of sorting transfer station 3.

Figure 12

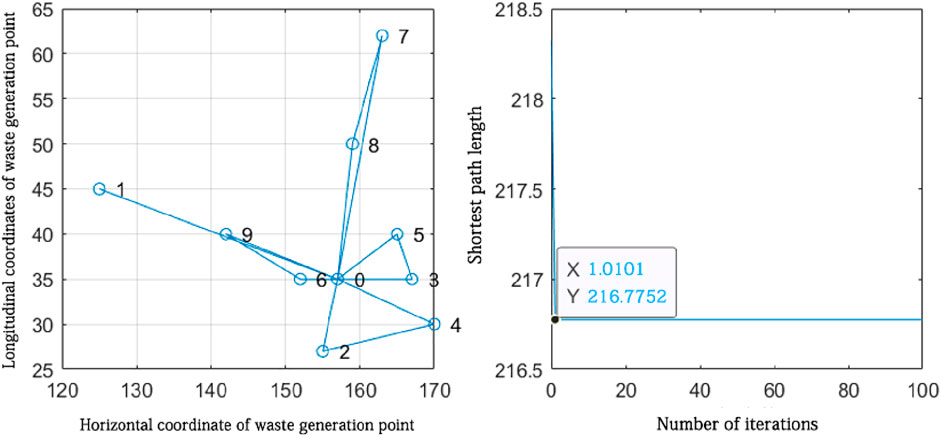
Figure 12. Route planning for waste generation points attributed to the vicinity of sorting transfer station 4.

Figure 13

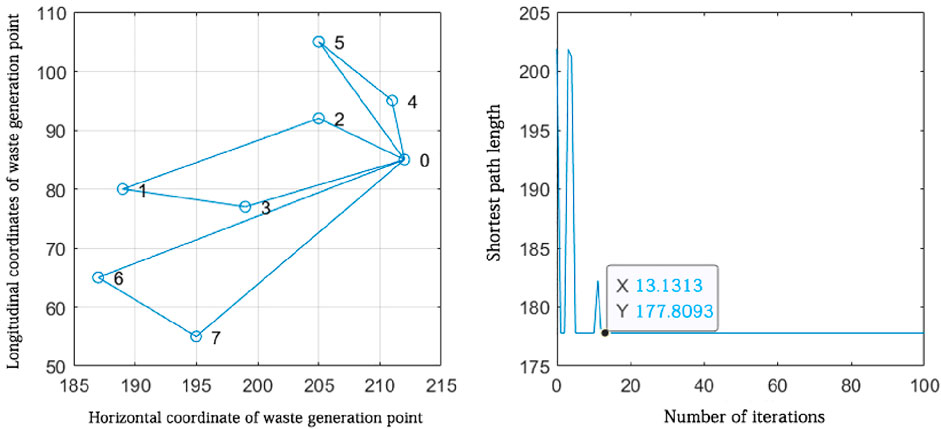
Figure 13. Route planning for waste generation points attributed to the vicinity of sorting transfer station 5.

The path planning of the waste generation points attributed to the vicinity of sorting transfer station 1.

According to the route planning results in Figure 10, it can be seen that four closed routes were formed from sorting transfer station 1, which were 0-5-9-0, 0-7-8-6-0, 0-1-2-0, and 0-3-4-0. The four routes were the optimal routes obtained from the solution, and the algorithm finds the shortest distance of 218.7982 km after approximately 10 iterations. According to the route planning results, four vehicles were needed to collect waste from the waste generation points distributed near sorting transfer station 1.

The route planning for waste generation points attributed near sorting transfer station 2.

According to the path planning results in Figure 11, it can be seen that five closed routes were formed from sorting staging area 2, which are 0-13-12-0, 0-2-11-10-0, 0-9-8-0, 0-7-6-1-0, and 0-4-5-3-0. The five routes were the optimal routes obtained from the solution, and the algorithm found the shortest distance after approximately 25 iterations as 404.3166 km. According to the route planning results, five vehicles are needed to collect waste from the waste generation points distributed around sorting transfer station 2.

The route planning for waste generation points attributed near sorting transfer station 3.

According to the path planning results in Figure 12, it can be seen that seven closed routes were formed from sorting staging area 3, which are 0-13-14-0, 0-7-5-0, 0-4-2-0, 0-3-0, 0-6-1-0, 0-9-12-0, and 0-8-11-10-0. Seven routes were the optimal routes obtained by solving the algorithm after approximately 22 iterations to find the shortest distance. The shortest distance is 535.7837 km. According to the route planning results, seven vehicles were needed to collect waste from the waste generation points distributed around sorting transfer station 3.

The route planning for waste generation points attributed to the vicinity of sorting transfer station 4.

According to the route planning results in Figure 13, it can be seen that five closed routes are formed from sorting transfer station 4, which are 0-1-0, 0-9-6-0, 0-2-4-0, 0-3-5-0, and 0-7-8-0. The five routes are the optimal routes obtained from the solution, and the algorithm found the shortest distance of 216.7752 km. According to the route planning results, five vehicles were needed to collect waste from the waste generation points distributed near sorting transfer station 4.

The route planning for waste generation points attributed near sorting transfer station 5.

According to the route planning results in Figure 14, it can be seen that three closed routes are formed from sorting transfer station 5, which are 0-4-5-0, 0-2-1-3-0, and 0-6-7-0. The three routes are the optimal routes obtained from the solution, and the algorithm finds the shortest distance of 177.8093 km in approximately 13 iterations. According to the route planning results, three vehicles were needed to collect waste from the waste generation points distributed near sorting and transfer station 5.

Figure 14

Figure 14. Summary results of route planning.

Through the above route planning, we got the route planning results for the vicinity of five sorting and transfer stations. From the results, we find that a total of 24 vehicles are needed to collect the garbage from all the garbage generation points, and the shortest route distance for collecting the garbage is approximately 1,553.4776 km in total. The summary results of the route planning are shown in Figure 14.

After the route planning, all the waste generation points were divided into five areas, and the number of waste generation points and the location of sorting and transfer stations in each area are relatively reasonable. Therefore, the effectiveness of rural domestic waste recycling network planning was verified by bringing in simulated data using randomly generated random points within the area. The optimal incineration plant, recycling treatment plant, landfill, and sorting transfer station sites and the corresponding path optimization are finally obtained. Model sensitivity is also analyzed in this study in terms of transportation cost and waste share, and the degree of influence of the corresponding parameters on the model is obtained. The effectiveness of the model and algorithm is finally verified.

5 Conclusion

In the context of the strategy of rural revitalization put forward in the report of the 19th Party Congress, adherence to ecological environment is the key to rural construction work. As the economy continues to develop, the amount of rubbish in rural areas is increasing yearly, and the rural rubbish recycling infrastructure is underdeveloped, with limited treatment methods. Villagers have low awareness of rubbish classification, and rubbish generation points are scattered. A village–town–county collection and transport model that integrates waste transfer stations with classification functions is proposed in this paper. Waste is sorted and transferred through these sorting transfer stations, with site selection and route optimization based on a three-tier waste recycling network. Trapezoidal fuzzy numbers were introduced to address the uncertainty of waste generation at the point of generation. Subsequently, the optimization problem of the rural domestic waste recycling network was investigated, including two sub-problems of facility siting and route optimization. The problems of the current waste recycling network were analyzed, and a siting model considering negative utility and minimum cost was developed. This model facilitates siting studies for waste sorting and transfer stations, as well as final disposal sites, including recycling and treatment plants, incineration plants, and landfills. In order to improve the efficiency of vehicle pooling at sorting and transfer stations, a path optimization model centered on the shortest path was developed. By analyzing the advantages and disadvantages of various algorithms and considering the characteristics of the model, the particle swarm algorithm is selected to solve the dual-objective site selection model and the ant colony algorithm is used for path optimization. Taking Dongfeng County, Liaoyuan City, Jilin Province, as an example, the actual data of Dongfeng County is collated, and MATLAB 2019a is used to verify the validity and feasibility of the model, providing valuable insights into rural waste resource treatment. The challenges faced by rural waste recycling networks are explored in this paper. Although some results have been achieved, there are still some shortcomings that require further research and analysis in the following three areas:

1. In the waste collection and transport process, the calculation of transport distances between facilities is based on straight-line distances. Future research should take into account actual road conditions. The application of GIS technology can also improve the accuracy of the study by reflecting real-world scenarios.

2. Due to data collection limitations and specific circumstances, only one collection vehicle and a limited collection timeframe were considered in the solution process. This aspect can be further refined in subsequent studies. Meanwhile, classical algorithms have limitations in improving performance, and quantum computing methods, convolutional neural methods, etc., can be discussed for performance studies in future research.

3. In solving the site selection problem, the calculations were based only on the local area and villages in Dongfeng County, without considering the local geography and neighboring developments. These factors should be integrated into future optimization efforts. Future research will focus on addressing these identified shortcomings.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JC: conceptualization, methodology, software, and writing–original draft. YW: conceptualization, methodology, writing–original draft, formal analysis, and data curation. XL: data curation, writing–original draft, investigation, project administration, resources, and validation. XiW: conceptualization, formal analysis, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The study was funded by the National Open University Youth Research Program “Investment in Education and Personal Income Distribution” (Q22A0021) and Jilin Provincial Science and Technology Department Project(20250402068GH).

Conflict of interest

Author XL was employed by Jilin Province Yuanjing Information Consulting Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

ACO, ant colony optimization; PSO, particle swarm optimization; GIS, geographic information system.

References

Bhat, V. N. (1996). A model for the optimal allocation of trucks for solid waste management. Waste Manag. and Res. 14 (1), 87–96. doi:10.1006/wmre.1996.0008

CrossRef Full Text | Google Scholar

Caroline, P. (2011). A hybrid evolutionary algorithm for the periodic location-routing problem. Eur. J. Operational Res. 209 (2), 195–202. doi:10.1016/j.ejor.2010.09.021

CrossRef Full Text | Google Scholar

Chen, K., and Hu, J. (2018). A study on the classification behavior of urban household waste: a case study of Beijing. Urban Insight.

Google Scholar

Chen, Y., Lai, Z., Wang, Z., Yang, D., and Wu, L. (2021). Optimizing locations of waste transfer stations in rural areas. PLOS ONE 16, e0250962. doi:10.1371/journal.pone.0250962

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y. D., Liu, G. F., Song, S. X., and Liu, H. (2007). Research on reverse logistics network modeling based on home appliance recycling. Value Eng. 26 (3), 72–75. doi:10.3969/j.issn.1006-4311.2007.03.025

CrossRef Full Text | Google Scholar

Deng, H., Wang, W., and Zhao, Y. (2018). Optimization design of end-of-life vehicle recycling system based on extendsim. Univ. Politehnica Buchar. Sci. Bull. Ser. C-Eleectrical Eng. Comput. Sci. 80 (3), 95–108.

Google Scholar

Du, Y. J., and Guo, Q. (2015). Research on optimal site selection of waste transfer station and optimal waste transfer scheme. Comput. Eng. Appl. 51 (10), 252–256.

Google Scholar

El-Hallaq, M. A., and Mosabeh, R. (2019). Optimization of municipal solid waste management of bins using GIS. A case study: nuseirat city. A Case Study Nuseirat Geogr. Inf. Syst. (GIS) 11, 32–43. doi:10.4236/jgis.2019.111003

CrossRef Full Text | Google Scholar

Han, Z. Y., Ye, C. W., Zhang, Y., Dan, Z., Zou, Z., Liu, D., et al. (2019). Characteristics and management modes of domestic waste in rural areas of developing countries: a case study of China. Environ. Sci. Pollut. Res. Int. 26 (9), 8485–8501. doi:10.1007/s11356-019-04289-w

PubMed Abstract | CrossRef Full Text | Google Scholar

He, B., Yang, C., and Zhang, H. (2007). Study on the optimization design of multi-layer reverse logistics network for waste recycling. China Manag. Sci. 15 (3), 7. doi:10.3321/j.issn:1003-207X.2007.03.010

CrossRef Full Text | Google Scholar

He, P. J. (2012). Municipal solid waste in rural areas of developing country: do we need special treatment mode? Waste Manag. 32 (7), 1289–1290. doi:10.1016/j.wasman.2012.03.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Jia, Y., Cheng, S., and Shi, R. (2021). Decision-making behavior of rural residents' domestic waste classification in northwestern of China —analysis based on environmental responsibility and pollution perception. J. Clean. Prod. 326, 129374. doi:10.1016/j.jclepro.2021.129374

CrossRef Full Text | Google Scholar

Jiang, X., Li, J., Lu, Y., and Tian, G. (2020). Design of reverse logistics network for remanufacturing waste machine tools based on multi-objective gray wolf optimization algorithm. IEEE Access 99, 141046–141056. doi:10.1109/.ACCESS.2020.3011509

CrossRef Full Text | Google Scholar

Karadimas, N. V., and Loumos, V. G. (2008). Gis-based modelling for the estimation of municipal solid waste generation and collection. Waste Manag. and Res. J. Int. Solid Wastes and Public Clean. Assoc. Iswa 26 (4), 337–346. doi:10.1177/0734242X07081484

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, X. Y. (2015). Research on intelligent management of urban domestic waste collection and transportation--Taking Dalian City as an example. Dalian: Dalian University of Technology.

Google Scholar

Liu, M. H. (2021a). Research on site selection of rural waste recycling transfer station in County. China Logist. Purch. (07), 75–76. doi:10.16079/j.cnki.issn1671-6663.2021.07.041

CrossRef Full Text | Google Scholar

Liu, M. H. (2021b). Research on route optimization of rurai waste sorting and recycling and location of transfer station in L country town. Doctoral dissertation. Beijing: Beijing Jiaotong University.

Google Scholar

Lubotzky, A., Luria, Z., and Rosenthal, R. (2015). Random steiner systems and bounded degree coboundary expanders of every, dimension. Discrete and Comput. Geometry 62 (1), 813–831. doi:10.1007/s00454-018-9991-2

CrossRef Full Text | Google Scholar

Mao, J., Liu, R. P., and Zhang, X. Z. (2019). Research on smart surveillance system of internet of things of straw recycling process based on optimizing genetic algorithm. J. Intelligent and Fuzzy Syst. 37, 4717–4723. doi:10.3233/JIFS-179306

CrossRef Full Text | Google Scholar

Mao, J., Sun, Q., Ma, C., and Tang, M. (2021). Site selection of straw collection and storage facilities considering carbon emission reduction. Environ. Sci. Pollut. Res. (3). doi:10.1007/s11356-021-15581-z

CrossRef Full Text | Google Scholar

Mete, H. O., and Zabinsky, Z. B. (2010). Stochastic optimization of medical supply location and distribution in disaster management. Int. J. Prod. Econ. 126 (1), 76–84. doi:10.1016/j.ijpe.2009.10.004

CrossRef Full Text | Google Scholar

The Ministry of Construction on the release of industry standards “domestic waste transfer station operation and maintenance technical regulations” Notice No. 421 (2006). Eng. Constr. Stand., (03).

Google Scholar

Ministry of Housing and Urban-Rural Development (2015). Guid. Opin. ministry Hous. urban-rural Dev. other Dep. comprehensively Promot. rural waste Manag. [EB/OL]. Available at: https://www.gov.cn/zhengce/2016-05/22/content_5075653.htm.

Moreno, A., Alem, D., and Ferreira, D. (2016). Heuristic approaches for the multiperiod location-transportation problem with reuse of vehicles in emergency logistics. Comput. and Operations Res. 69, 79–96. doi:10.1016/j.cor.2015.12.002

CrossRef Full Text | Google Scholar

Mou, N. Y., Jia, C. F., Kang, Q. P., and Gong, D. (2021). Optimization of shared express box distribution and recycling network based on ant colony algorithm. J. Transp. Eng. Inf. 19 (01), 33–42. doi:10.3969/j.issn.1672-4747.2021.01.004

CrossRef Full Text | Google Scholar

Mourao, M. C., and Almeida, M. T. (2000). Lower-bounding and heuristic methods for a refuse collection vehicle routing problem. Eur. J. Operational Res. 121 (2), 420–434. doi:10.1016/S0377-2217(99)00045-4

CrossRef Full Text | Google Scholar

Nema, A. K., and Gupta, S. K. (1999). Optimization of regional hazardous waste management systems:an improved formulation. Waste Manag. 19 (7), 441–451. doi:10.1016/S0956-053X(99)00241-X

CrossRef Full Text | Google Scholar

Shang, C. J., Ma, L., and Liu, Y. (2021). Model and algorithm for heterogeneous periodic hybrid vehicle path problem with time window under garbage classification. Syst. Eng. 39 (06), 131–145.

Google Scholar

Shirazi, M. Z., Pamulapati, T., Mallipeddi, R., and Veluvolu, K. C. (2017) “Particle swarm optimization with ensemble of inertia weight strategies,” in International conference on swarm intelligence (ICSI). Fukuoka.

CrossRef Full Text | Google Scholar

Taghipour, H., Amjad, Z., Aslani, H., Armanfar, F., and Dehghanzadeh, R. (2016). Characterizing and quantifying solid waste of rural communities. J. Material Cycles Waste Manag. 18 (2), 790–797. doi:10.1007/s10163-015-0365-z

CrossRef Full Text | Google Scholar

Teixeira, J., Antunes, A. P., and Sousa, J. (2004). Recyclable waste collection planning - a case study. Eur. J. Operational Res. 158 (3), 543–554. doi:10.1016/S0377-2217(03)00379-5

CrossRef Full Text | Google Scholar

Tian, G., Yuan, G., Aleksandrov, A., Zhang, T., Li, Z., Fathollahi-Fard, A. M., et al. (2022). Recycling of spent Lithium-ion Batteries: a comprehensive review for identification of main challenges and future research trends. Sustain. Energy Technol. Assessments 53, 102447. doi:10.1016/j.seta.2022.102447

CrossRef Full Text | Google Scholar

Wang, X., Ning, W., Wang, K., and Yu, D. (2022). Study on the optimization of agricultural production waste recycling network under the concept of green cycle development. Sustainability 15 (1), 165. doi:10.3390/su15010165

CrossRef Full Text | Google Scholar

Xie, X. B., and Li, C. P. (2022). Research on e-commerce logistics transportation route planning method based on recurrent neural network. Cham: Springer. doi:10.1007/978-3-030-94551-0_27

CrossRef Full Text | Google Scholar

Xp, B., Qiu, X., and Yf, D. (2020). Designing recycling networks for construction and demolition waste based on reserve logistics research field - sciencedirect. J. Clean. Prod. 260. doi:10.1016/j.jclepro.2020.120841

CrossRef Full Text | Google Scholar

Yadav, V., Karmakar, S., Dikshit, A. K., and Bhurjee, A. K. (2017). Interval-valued facility location model: an appraisal of municipal solid waste management system. J. Clean. Prod. 171 (pt.1), 250–263. doi:10.1016/j.jclepro.2017.09.233

CrossRef Full Text | Google Scholar

Yang, F., and Tao, Y. Z. (2020). Economic and ecological two-dimensional assessment of urban waste transfer station site selection under the “double M” orientation--Take Changsha City as an example. Ecol. Econ. 36 (05), 80–84.

Google Scholar

Yang, L., Jones, B. F., and Yang, S. H. (2007). A fuzzy multi-objective programming for optimization of fire station locations through genetic algorithms. Eur. J. Operational Res. 181 (2), 903–915. doi:10.1016/j.ejor.2006.07.003

CrossRef Full Text | Google Scholar

Zeng, C., Niu, D., and Zhao, Y. (2015). A comprehensive overview of rural solid waste management in China. Front. Environ. Sci. and Eng. 9 (6), 949–961. doi:10.1007/s11783-015-0816-8

CrossRef Full Text | Google Scholar

Zhang, X. N., Fan, H. M., and Li, J. S. (2012). The study on recovery vehicle scheduling problem of industrial Waste Recycling. Appl. Mech. and Mater. 120, 148–153. doi:10.4028/www.scientific.net/AMM.120.148

CrossRef Full Text | Google Scholar

Zheng, D. F. (2018). Research on rural household waste management in the context of ecological civilization construction. Beijing: Beijing University of Posts and Telecommunications.

Google Scholar