
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci. , 10 September 2024
Sec. Environmental Informatics and Remote Sensing
Volume 12 - 2024 | https://doi.org/10.3389/fenvs.2024.1442644
Particulate matter with a diameter of 2.5 microns or less (
Maintaining a healthy atmosphere is vital for both humans and other living creatures. Air quality refers to the absence of harmful pollutants in the air. However, there are several deadly and fatal contaminants in the air nowadays, including
In the past, many researchers have developed solutions to this problematic air pollution issue. In this context, many researchers have applied classical regression, time series, machine learning, and hybrid models to find the optimum solution according to the nature of the data (Zhan et al., 2017; Xu et al., 2018; Abdullah et al., 2019; Dutta and Jinsart, 2021). For instance, the work (Geetha and Prasika, 2019) provides an LSTM in addition to two conventional forecasting models for estimating the levels of air pollutants (NO2, NOx, CO, SO2, O3, PM2.5, and PM10) in metropolises. The outcomes demonstrated that LSTM outperformed LR and ARIMA. Zaman et al. (2024) attempt intends to create machine learning models that are computationally efficient and simpler than those found in earlier studies. Findings indicated that the RF methodology performed marginally better than the XG-Boost and SVR techniques. In another research work, Zaman et al. (2021) predict
This work (Freeman et al., 2018), a forecast model for ozone levels averaged over 8 hours, was trained using novel deep learning techniques. A new technique for imputation was used to replace missing data and outliers in the collected data set. This method produced computed values based on the time and season closer to the predicted value. (Carbo-Bustinza et al., 2023). Using a comparison of numerous hybrid varieties of time series models, this work extensively studies projecting ozone concentrations. According to the study, the suggested models perform noticeably superior to the standard models that were considered. However, this research (Xie et al., 2021) aims to apply the Hausdorff distance method to huge data to improve future cyclone effect predictions (Rakholia et al., 2023). Analyzed to develop a multi-step-ahead with multi-output type multivariate statistical model (NBEATS) to estimate the air quality with the auxiliary information. The data set was collected from six healthcare air quality centers in Vietnam. To compare the results and efficiency with the existing model, accuracy indices such as MAPE and RMSE were used. The result indicated that the developed (d-BEATS) multi-dimensional co-variate model outperforms the existing models. In the work Bhatti et al. (2021), the researcher conducted a comparative study to estimate the air quality index for Pakistan. They used the SARIMA and factor analysis approaches to achieve this end. The study found that the SARIMA model outperforms others in attaining better estimation accuracy for Pakistan’s air quality index. In another work, Ashraf et al. (2022) conducted an analysis based on the comparative study of machine learning and classical forecasting models to forecast air pollution data. This article uses the metrics, i.e., RMSE, MAE, and MAPE, to compare the classical and traditional models. The study suggested that the machine learning model performed more efficiently than the existing time series methods.
In the same way, Lin et al. (2019) performed an analysis based on machine learning and integrated assimilation data techniques to expand the air quality prediction for the Netherlands. The findings disclosed that the developed approach, which incorporates data-driven machine learning and a physics-based model, significantly improved the air quality forecast statistically. However, Kleine Deters et al. (2017) modeled
On the other hand, Wang et al. (2019) proposed a hybrid model for air quality variables forecasting. This proposed method is a hybridization of the Long Short-Term Memory Neural Network and Gated Recurrent Unit (LSTM and GRU), an enhancement of ordinary LSTM. This work uses the data set of 74 cities in China for a comparative study. The outcomes disclosed that the proposed hybrid model outperformed the existing approaches. In the same way, Ejohwomu et al. (2022) conducted a comprehensive study to model the
In contrast to the research mentioned earlier, this study introduces a comparatively simple and easily implemented new time series ensemble technique based on various linear (autoregressive, simple exponential smoothing, autoregressive moving average, and theta) and nonlinear (nonparametric autoregressive and neural network autoregressive) models to accurately and efficiently forecast short-term
This section elucidates the proposed time series ensemble technique for short-term (one-day-ahead)
This work uses daily
That is, the log
Thus, once the air pollutant (
This section briefly overviews the forecasting models and their proposed ensemble models: the autoregressive, the simple exponential smoothing, the autoregressive moving average, the Theta, the nonparametric autoregressive, and the neural network autoregressive models.
A linear autoregressive (AR) model is used to understand the short-term dynamics of
In Equation 3,
The Exponential Smoothing Model (ESM) is a group of forecasting models that apply exponentially decreasing weights to previous observations. It is a time-series forecasting model that uses a weighted average of past observations to predict the future value of a variable. The ES model assumes that a variable’s future value depends on its past values, with greater emphasis placed on recent values than on older ones. The ESM model can be expressed as follows:
In the given Equation 4,
The autoregressive moving average (ARMA) models incorporate lagged values from a time series and factor in error terms passed into the model. This study utilized a model representing the residual series
In Equation 5, where
The Neural Network Autoregressive (NNA) model is a machine learning approach that uses historical observations to predict future values in a time series. It does this by analyzing a mathematical function that considers the previous values, denoted by
The nonparametric autoregressive model (NPAR) presents an alternative to the conventional parametric AR model, departing from the latter’s reliance on specific mathematical equations to elucidate the relationship between past and future values. In contrast, NPAR models employ flexible and adaptive techniques, such as kernel regression or spline functions, to capture dynamic patterns in the data without explicit parameter estimation. These models are distinguished by their flexibility, absence of predefined parameters, emphasis on local relationships, and reliance on data-driven structures to address intricate and nonlinear dependencies within time series data. This model’s association between
here in Equation 6,
The Theta Model is a forecasting method that predicts future values based on the average change in the time series data. It involves calculating the average change between consecutive time points and extrapolating it into the future. The equation for the Theta Model is given by in Equation 7:
At its core, an ensemble technique integrates outcomes from various models, each meticulously calibrated before unity. This approach capitalizes on the inherent strengths of individual models while compensating for their inherent limitations. Within the scope of this study, ensemble techniques are initially employed to compute weights for the results derived from individual models (Iftikhar et al., 2024a; Gonzales et al., 2024). Consequently, the proposed ensemble encompasses three distinct weighting strategies: a) equitable distribution of weight among all single models, denoted as ESME; b) weight assignment based on training average accuracy errors (1), designated as ESMT; and c) weight assignment based on validation mean accuracy measures, denoted as ESMV. The model allocates greater weight to the ensemble model for training and validation datasets with lower mean accuracy errors, while models exhibiting higher mean accuracy errors contribute comparatively less weight to the ensemble. Notably, the model weights assume small positive values, and their accumulation equates to one, signifying the percentage of reliance or anticipated performance from each model.
Thus, after estimating the linear trend component and annual periodicity using the multiple regression model discussed above, the next step is forecasting the remaining part
This study examines two evaluation criteria for the proposed time series ensemble forecasting technique: accuracy average errors and an equal forecast accuracy test.
Primarily, Table 1 presents the accuracy average errors, outlining the formulas for computing each metric. The metrics encompass the mean absolute error (MAE), an indicator of errors within pair samples reflecting the same phenomena. The mean absolute percent error (MAPE) is a metric used to assess how accurate a forecasting system is in making predictions. The mean scaled absolute error (MASE), it is calculated by dividing the mean absolute error of the prediction values by the mean absolute error of the one-step naive forecast made in the sample. The root mean squared error (RMSE) calculates the average disparity between the values a statistical model predicts and the observed values. The root relative squared error (RRSE) root of the squared prediction error in comparison to a simple model that predicts the mean. After applying the log to both, the root mean log squared error (RMSLE) is computed by considering the differences between the actual and anticipated values, Iftikhar et al. (2024b).
The table presents the actual
Second, a statistically equal forecast test, the Diebold–Marino (DM) test (Diebold, 2015), is performed to evaluate the forecasting ensemble time series proposed approach. In the literature, It is used to evaluate time series forecasting models, determining whether the forecast errors from one model are statistically different from another model’s forecast errors (Iftikhar et al., 2023a; Shah et al., 2019; Iftikhar et al., 2023b). To perform the DM test, the forecast errors of each model are calculated using a loss function. Then, a statistical value is computed by comparing the errors of each model. The test statistic is based on the difference between the mean squared errors of the two models. Suppose the test statistic is above a certain threshold and the p-value is below a significance level
To complete this section, the main steps, including the introduced time series ensemble forecasting approach in bullet form, are listed below, and the flowchart is presented in Figure 1.
Where
In order to obtain short-term

Table 2. Details about the considered original, missing, and imputed datasets are provided in this work.
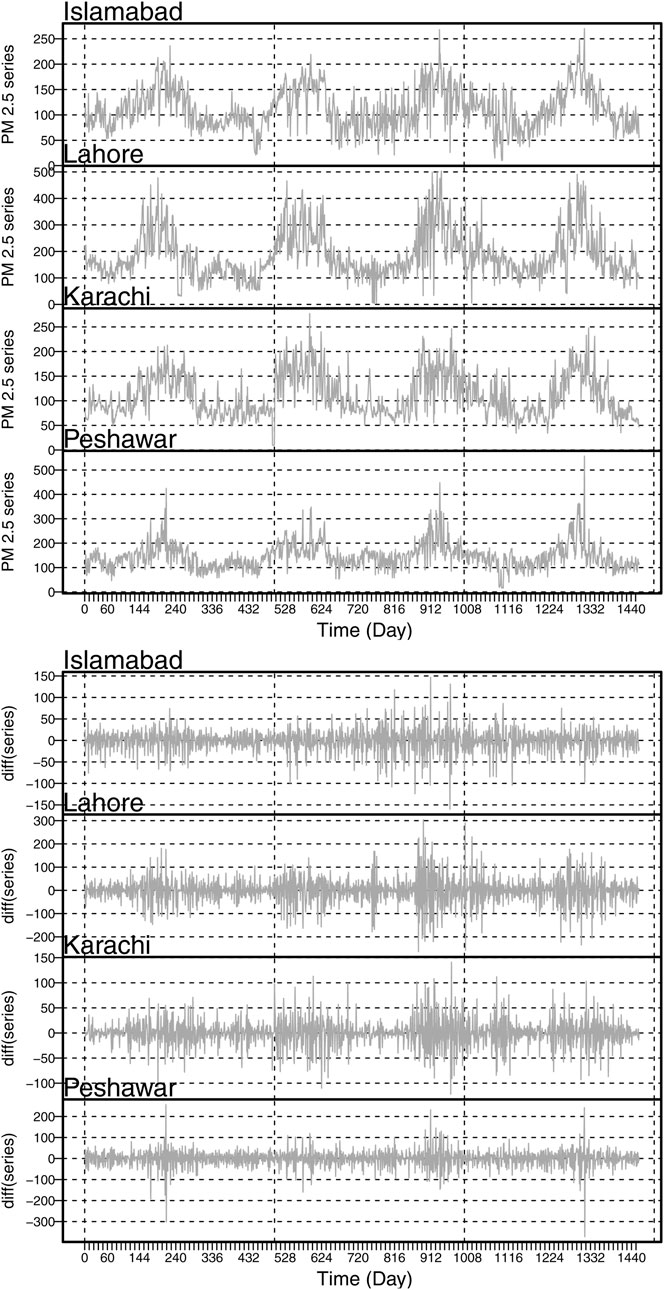
Figure 3. Time Series Plot: Original time series (top) and the first ordered difference time series for all four megacities (bottom).
On the other hand, Table 3 represents a comprehensive overview of the statistical properties (with and without log descriptive statistics) for
The given steps must be followed to obtain the forecast for
Hence, for all nine models for the four monitoring megacities, including Lahore, Islamabad, Karachi, and Peshawar, one-day-ahead out-of-sample forecast outcomes (MAE, MASE, MAPE, RMSE, RRSE, and RMSLE) are listed in Table 4. Table 4 shows that the ESMV produced the best forecasting results compared to all nine forecasting models within the proposed time series ensemble forecasting approach in all four monitoring megacities. For instance, the average accuracy errors for these magacities are the following: Islamabad (MAPE = 0.1739, MAE = 15.2718, MASE = 0.9237, RMSE = 20.3203, RRSE = 0.4830, and RMLSE = 0.2354); Lahore (MAPE = 0.2167, MAE = 34.1786, MASE = 0.9207, RMSE = 48.3090, RRSE = 0.5837, and RMLSE = 0.2701); Karachi (MAPE = 0.1679, MAE = 16.0982, MASE = 0.9122, RMSE = 22.9913, RRSE = 0.5464, and RMLSE = 0.2215); and Peshawar (MAPE = 0.1973, MAE = 24.1188, MASE = 0.8858, RMSE = 35.0552, RRSE = 0.5998, and RMLSE = 0.2594). However, the ESMT model shows the second-best forecasting results among all nine forecasting models in all four monitoring megacities, while the third-best forecasting accuracy average error results are given in the following manner: Islamabad (the Theta model; MAPE = 0.1835, MAE = 16.3457, MASE = 0.9887, RMSE = 21.2335, RRSE = 0.5047, and RMLSE = 0.2370); Lahore (the Theta model; MAPE = 0.2179, MAE = 35.0539, MASE = 0.9442, RMSE = 49.9617, RRSE = 0.6037, and RMLSE = 0.2723); Karachi (the ARMA model; MAPE = 0.1702, MAE = 16.3909, MASE = 0.9287, RMSE = 23.3728, RRSE = 0.5555, RMSLE = 0.2226); and Peshawar (the NPAR model; MAPE = 0.2010, MAE = 25.0597, MASE = 0.9204, RMSE = 36.1912, RRSE = 0.6037, and RMLSE = 0.2723); Karachi (the ARMA model; MAPE = 0.1702, MAE = 16.3909, MASE = 0.9287, RMSE = 23.3728, RRSE = 0.5555, RMSLE = 0.2226); and Peshawar (the NPAR model; MAPE = 0.2010, MAE = 25.0597, MASE = 0.9204, RMSE = 36.1912, RRSE = 0.6192, RMSLE = 0.2610). Therefore, it is seen that within all nine forecasting models, the proposed ensemble models (the ESMV and the ESMT models) generally perform better than single models; however, within the single models, different cities have different single best models, as mentioned previously. Note that the best model is an ESMV or equivalent for all four mountaineering megacities. Also, using the proposed ensemble learning leads to marked error reduction (see Table 4). The proposed ensemble learning approach, thus, proves to be particularly effective in forecasting short-term
On the other hand, after the evaluation of the proposed time series ensemble modeling and forecasting technique by the average mean errors and the DM test, another check can be made to evaluate the accuracy of the selected best ensemble models by the graphical representation of the observed data and the predicted data. To do this, each city’s scatter plot (correlation) is drawn, and the correlation coefficient is calculated. Figures 4A–D shows the graph for each megacity. In Figure 5A for Islamabad city, it is noticed that the correlation coefficient value between the forecasted and actual data set is 0.97, indicating a strong and positive correlation. Moreover, from Figure 4B for Lahore city, the coefficient value between forecasted and actual data is 0.86, which shows a strong positive correlation between forecasted and actual data. Figure 4C for Karachi city and Figure 4D for Peshawar city, the coefficient values are 0.85 and 0.94, which shows a strong positive correlation between forecasted and actual data. In addition, the diagnostic checking (final residuals) plays an essential role in model selection, and this is tracked by the auto-correlation (ACF) plot and the partial auto-correlation plot (PACF), also known as the correlogram plot. As stated earlier, the proposed ensemble model is significant and efficient in forecasting the
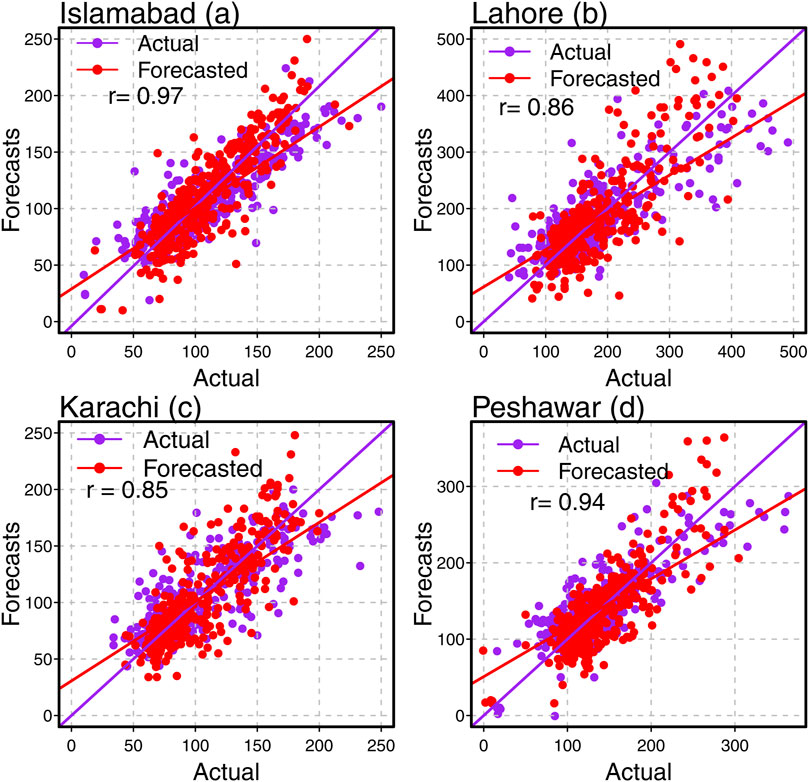
Figure 4. The correlation plots for the best models among all nine considered models in each city: Islamabad (a), Lahore (b), Karachi (c), and Peshawar (d).

Figure 5. The autocorrelation function and partial autocorrelation plots for the best models among all nine considered models in each megacity case: (A, B) Islamabad, (C, D) Lahore, (E, F) Karachi, (G, H) Peshawar.
This section elaborates an overview of comparing the proposed best model of this work versus the literature that found the best forecasting models. On the other hand, it also explains the future
In this subsection, we compared the results of our best ensemble model with those reported in the literature models. Our model showed high comparability with the other methods. Our best (ESMV) model produced the most negligible mean errors and the highest correlation coefficient (MAPE = 0.1679, MAE = 16.0982, MASE = 0.9122, RMSE = 22.9913, RRSE = 0.5464, and RMLSE = 0.2215) compared to the best models reported in the literature. For example, the best autoregressive distributed lag model (the ARDL model) proposed in Qayyum et al. (2021) was applied to the dataset used in our study and showed accuracy measures (MAPE = 0.1835, MAE = 21.3457, MASE = 0.9887, RMSE = 21.2335, RRSE = 0.5047, and RMLSE = 0.2370) that were significantly greater than those of our best (ESMV) model. The best model proposed in another study (see Bhatti et al., 2021) - the seasonal autoregressive moving average factor analysis approach - was also applied to our dataset and obtained average mean errors (MAPE = 0.1823, MAE = 20.1038, MASE = 0.9483, RMSE = 36.1853, RRSE = 0.7214, and RMLSE = 0.2901) that were higher than those of our best (ESMV) model. Similarly, in reference Waseem et al. (2022), the best proposed LSTM encoder-decoder applied to our dataset obtained performance metrics (MAPE = 0.2010, MAE = 25.0597, MASE = 0.9204, RMSE = 36.1912, RRSE = 0.6192, RMSLE = 0.2610) worse than those obtained with our best combination model (ESMV). In conclusion, our study’s best final model (ESMV) showed high efficacy and accuracy compared to the best models reported in the literature.
On the other hand, once the best models were assessed through average accuracy errors (MAPE, MAE, MASE, RMSLE, RRSE, and RMSE), an equal forecast statistical test (the DM test), graphical evaluation (the ACF, PCAF, and correlogram plots), and comparing with the literature best models this work proceeded to future short-term forecasting with the superior model (the ESMV). In this regard, the current work used the ESMV for the

Table 6. Forecasted values exercise for all megacities for the next 15 days using the best model in each case.
As per the Air Quality Index by the Environment Protection Agency, US, the following ranges and their health level concerns: 0–12
This work proposes a novel time series ensemble approach using the daily
In addition, using the best ensemble model in this work, a forecast was made for the next 15 days (1 June to 15 June 2023); the forecast exercise shows that the elevated levels of
However, the study’s main limitation is that it only incorporates
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
HI: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. MQ: Data curation, Formal Analysis, Investigation, Writing–review and editing. JZ: Funding acquisition, Project administration, Supervision, Writing–review and editing. JL-G: Investigation, Project administration, Resources, Supervision, Writing–review and editing. OA: Investigation, Resources, Supervision, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abdullah, S., Ismail, M., Ahmed, A. N., and Abdullah, A. M. (2019). Forecasting particulate matter concentration using linear and non-linear approaches for air quality decision support. Atmosphere 10, 667. doi:10.3390/atmos10110667
Alshanbari, H. M., Iftikhar, H., Khan, F., Rind, M., Ahmad, Z., and El-Bagoury, A. A.-A. H. (2023). On the implementation of the artificial neural network approach for forecasting different healthcare events. Diagnostics 13, 1310. doi:10.3390/diagnostics13071310
Álvarez-Díaz, M. (2020). Is it possible to accurately forecast the evolution of brent crude oil prices? an answer based on parametric and nonparametric forecasting methods. Empir. Econ. 59, 1285–1305. doi:10.1007/s00181-019-01665-w
Ameer, S., Shah, M. A., Khan, A., Song, H., Maple, C., Islam, S. U., et al. (2019). Comparative analysis of machine learning techniques for predicting air quality in smart cities. IEEE Access 7, 128325–128338. doi:10.1109/access.2019.2925082
Ashraf, M. U., Akram, F., and Usman, S. (2022). Comparative analysis of machine learning techniques for predicting air pollution. Lahore Garrison Univ. Res. J. Comput. Sci. Inf. Technol. 6, 40–54. doi:10.54692/lgurjcsit.2022.0602270
Bai, Y., Zeng, B., Li, C., and Zhang, J. (2019). An ensemble long short-term memory neural network for hourly pm2. 5 concentration forecasting. Chemosphere 222, 286–294. doi:10.1016/j.chemosphere.2019.01.121
Bhatti, U. A., Yan, Y., Zhou, M., Ali, S., Hussain, A., Qingsong, H., et al. (2021). Time series analysis and forecasting of air pollution particulate matter (pm 2.5): an sarima and factor analysis approach. Ieee Access 9, 41019–41031. doi:10.1109/access.2021.3060744
Borse, S. K. (2020). A review: predicting air quality using different technique. Acta Tech. Corviniensis-Bulletin Eng. 13, 153–157.
Box, G. E. P., Jenkins, G. M., Reinsel, G. C., and Ljung, G. M. (2015). Time series analysis: forecasting and control. John Wiley and Sons.
Brown, R. G. (1956). Exponential smoothing for predicting demand. cambridge, mass. NBER Cambridge, MA, United States: arthur d. little. Book exponential smoothing for predicting demand.
Carbo-Bustinza, N., Iftikhar, H., Belmonte, M., Cabello-Torres, R. J., De La Cruz, A. R. H., and López-Gonzales, J. L. (2023). Short-term forecasting of ozone concentration in metropolitan lima using hybrid combinations of time series models. Appl. Sci. 13, 10514. doi:10.3390/app131810514
Chen, G., Kuang, R., Li, W., Cui, K., Fu, D., Yang, Z., et al. (2024). Numerical study on efficiency and robustness of wave energy converter-power take-off system for compressed air energy storage. Renew. Energy 121080.
Chen, J., Chen, H., Wu, Z., Hu, D., and Pan, J. Z. (2017). Forecasting smog-related health hazard based on social media and physical sensor. Inf. Syst. 64, 281–291. doi:10.1016/j.is.2016.03.011
Diebold, F. X. (2015). Comparing predictive accuracy, twenty years later: a personal perspective on the use and abuse of diebold–mariano tests. J. Bus. and Econ. Statistics 33, 1. doi:10.1080/07350015.2014.983236
Du, W., and Wang, G. (2013). Intra-event spatial correlations for cumulative absolute velocity, arias intensity, and spectral accelerations based on regional site conditions. Bull. Seismol. Soc. Am. 103, 1117–1129. doi:10.1785/0120120185
Dutta, A., and Jinsart, W. (2021). Air pollution in indian cities and comparison of mlr, ann and cart models for predicting pm10 concentrations in guwahati, India. Asian J. Atmos. Environ. 15, 2020131. doi:10.5572/ajae.2020.131
Ejohwomu, O. A., Shamsideen Oshodi, O., Oladokun, M., Bukoye, O. T., Emekwuru, N., Sotunbo, A., et al. (2022). Modelling and forecasting temporal pm2. 5 concentration using ensemble machine learning methods. Buildings 12, 46. doi:10.3390/buildings12010046
Freeman, B. S., Taylor, G., Gharabaghi, B., and Thé, J. (2018). Forecasting air quality time series using deep learning. J. Air and Waste Manag. Assoc. 68, 866–886. doi:10.1080/10962247.2018.1459956
Garg, S., and Jindal, H. (2021). “Evaluation of time series forecasting models for estimation of pm2. 5 levels in air,” in 2021 6th international conference for convergence in technology I2CT (IEEE), 1–8.
Geetha, S., and Prasika, L. (2019). Smog prediction model using time series with long-short term memory. Int. J. Mech. Eng. Technol. 10, 1026–1032.
Gonzales, S. M., Iftikhar, H., and López-Gonzales, J. L. (2024). Analysis and forecasting of electricity prices using an improved time series ensemble approach: an application to the peruvian electricity market. AIMS Math. 9, 21952–21971. doi:10.3934/math.20241067
Holt, C. C. (2004). Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 20, 5–10. doi:10.1016/j.ijforecast.2003.09.015
Iftikhar, H., Bibi, N., Canas Rodrigues, P., and López-Gonzales, J. L. (2023a). Multiple novel decomposition techniques for time series forecasting: application to monthly forecasting of electricity consumption in Pakistan. Energies 16, 2579. doi:10.3390/en16062579
Iftikhar, H., Gonzales, S. M., Zywiołek, J., and López-Gonzales, J. L. (2024a). Electricity demand forecasting using a novel time series ensemble technique. IEEE Access 12, 88963–88975. doi:10.1109/access.2024.3419551
Iftikhar, H., Khan, M., Turpo-Chaparro, J. E., Rodrigues, P. C., and López-Gonzales, J. L. (2024b). Forecasting stock prices using a novel filtering-combination technique: application to the Pakistan stock exchange. AIMS Math. 9, 3264–3288. doi:10.3934/math.2024159
Iftikhar, H., Khan, M., Żywiołek, J., Khan, M., and López-Gonzales, J. L. (2024c). Modeling and forecasting carbon dioxide emission in Pakistan using a hybrid combination of regression and time series models. Heliyon 10, e33148. doi:10.1016/j.heliyon.2024.e33148
Iftikhar, H., Turpo-Chaparro, J. E., Canas Rodrigues, P., and López-Gonzales, J. L. (2023b). Day-ahead electricity demand forecasting using a novel decomposition combination method. Energies 16, 6675. doi:10.3390/en16186675
Iftikhar, H., Turpo-Chaparro, J. E., Canas Rodrigues, P., and López-Gonzales, J. L. (2023c). Forecasting day-ahead electricity prices for the Italian electricity market using a new decomposition—combination technique. Energies 16, 6669. doi:10.3390/en16186669
Iftikhar, H., Zafar, A., Turpo-Chaparro, J. E., Canas Rodrigues, P., and López-Gonzales, J. L. (2023d). Forecasting day-ahead brent crude oil prices using hybrid combinations of time series models. Mathematics 11, 3548. doi:10.3390/math11163548
Jenkins, G. M., and Box, G. E. P. (1976). Time series analysis: forecasting and control. Hoboken, New Jersey, United States: Prentice Hall.
Kleine Deters, J., Zalakeviciute, R., Gonzalez, M., and Rybarczyk, Y. (2017). Modeling pm 2.5 urban pollution using machine learning and selected meteorological parameters. J. Electr. Comput. Eng. 2017, 1–14. doi:10.1155/2017/5106045
Lin, H.-X., Jin, J., and van den Herik, H. J. (2019). Air quality forecast through integrated data assimilation and machine learning. ICAART 2, 787–793.
Liu, D.-R., Lee, S.-J., Huang, Y., and Chiu, C.-J. (2020). Air pollution forecasting based on attention-based lsm neural network and ensemble learning. Expert Syst. 37, e12511. doi:10.1111/exsy.12511
Luo, J., Zhuo, W., Liu, S., and Xu, B. (2024). The optimization of carbon emission prediction in low carbon energy economy under big data. IEEE Access 12, 14690–14702. doi:10.1109/access.2024.3351468
Manisalidis, I., Stavropoulou, E., Stavropoulos, A., and Bezirtzoglou, E. (2020). Environmental and health impacts of air pollution: a review. Front. public health 8, 14. doi:10.3389/fpubh.2020.00014
Pakistan, U. C. (2021). Air quality data. The U.S. Environmental Protection Agency, Washington, D.C.: US Consulate Pakistan.
Qayyum, F., Mehmood, U., Tariq, S., Haq, Z. u., and Nawaz, H. (2021). Particulate matter (pm2. 5) and diseases: an autoregressive distributed lag (ardl) technique. Environ. Sci. Pollut. Res. 28, 67511–67518. doi:10.1007/s11356-021-15178-6
Qiu, L., Xia, W., Wei, S., Hu, H., Yang, L., Chen, Y., et al. (2024). Collaborative management of environmental pollution and carbon emissions drives local green growth: an analysis based on spatial effects. Environ. Res. 259, 119546. doi:10.1016/j.envres.2024.119546
Quispe, F., Salcedo, E., Iftikhar, H., Zafar, A., Khan, M., Turpo-Chaparro, J. E., et al. (2024). Multi-step ahead ozone level forecasting using a component-based technique: a case study in lima, Peru. AIMS Environ. Sci. 11, 401–425. doi:10.3934/environsci.2024020
Rakholia, R., Le, Q., Ho, B. Q., Vu, K., and Carbajo, R. S. (2023). Multi-output machine learning model for regional air pollution forecasting in ho chi min city, vietnam. Environ. Int. 173, 107848. doi:10.1016/j.envint.2023.107848
Shah, I., Iftikhar, H., and Ali, S. (2020). Modeling and forecasting medium-term electricity consumption using component estimation technique. Forecasting 2, 163–179. doi:10.3390/forecast2020009
Shah, I., Iftikhar, H., and Ali, S. (2022). Modeling and forecasting electricity demand and prices: a comparison of alternative approaches. J. Math. 2022, 3581037. doi:10.1155/2022/3581037
Shah, I., Iftikhar, H., Ali, S., and Wang, D. (2019). Short-term electricity demand forecasting using components estimation technique. Energies 12, 2532. doi:10.3390/en12132532
Shang, K., Xu, L., Liu, X., Yin, Z., Liu, Z., Li, X., et al. (2023). Study of urban heat island effect in Hangzhou metropolitan area based on sw-tes algorithm and image dichotomous model. Sage Open 13, 21582440231208851. doi:10.1177/21582440231208851
Shang, M., and Luo, J. (2021). The tapio decoupling principle and key strategies for changing factors of Chinese urban carbon footprint based on cloud computing. Int. J. Environ. Res. Public Health 18, 2101. doi:10.3390/ijerph18042101
Taskaya-Temizel, T., and Casey, M. C. (2005). A comparative study of autoregressive neural network hybrids. Neural Netw. 18, 781–789. doi:10.1016/j.neunet.2005.06.003
Ullah, S., Ullah, N., Rajper, S. A., Ahmad, I., and Li, Z. (2021). Air pollution and associated self-reported effects on the exposed students at malakand division, Pakistan. Environ. Monit. Assess. 193, 708–717. doi:10.1007/s10661-021-09484-2
Van Buuren, S., and Oudshoorn, C. G. M. (2011). Mice: multivariate imputation by chained equations inR. J. Stat. Softw. 45, 1–67. doi:10.18637/jss.v045.i03
Wang, B., Kong, W., Guan, H., and Xiong, N. N. (2019). Air quality forecasting based on gated recurrent long short term memory model in internet of things. IEEE Access 7, 69524–69534. doi:10.1109/access.2019.2917277
Waseem, K. H., Mushtaq, H., Abid, F., Abu-Mahfouz, A. M., Shaikh, A., Turan, M., et al. (2022). Forecasting of air quality using an optimized recurrent neural network. Processes 10, 2117. doi:10.3390/pr10102117
Xie, X., Xie, B., Cheng, J., Chu, Q., and Dooling, T. (2021). A simple Monte Carlo method for estimating the chance of a cyclone impact. Nat. Hazards 107, 2573–2582. doi:10.1007/s11069-021-04505-2
Xu, J., Zhou, G., Su, S., Cao, Q., and Tian, Z. (2022). The development of a rigorous model for bathymetric mapping from multispectral satellite-images. Remote Sens. 14, 2495. doi:10.3390/rs14102495
Xu, Y., Ho, H. C., Wong, M. S., Deng, C., Shi, Y., Chan, T.-C., et al. (2018). Evaluation of machine learning techniques with multiple remote sensing datasets in estimating monthly concentrations of ground-level pm2. 5. Environ. Pollut. 242, 1417–1426. doi:10.1016/j.envpol.2018.08.029
Yin, Z., Liu, Z., Liu, X., Zheng, W., and Yin, L. (2023). Urban heat islands and their effects on thermal comfort in the us: New york and New Jersey. Ecol. Indic. 154, 110765. doi:10.1016/j.ecolind.2023.110765
Zaman, N. A. F. K., Kanniah, K. D., Kaskaoutis, D. G., and Latif, M. T. (2021). Evaluation of machine learning models for estimating pm2. 5 concentrations across Malaysia. Appl. Sci. 11, 7326. doi:10.3390/app11167326
Zaman, N. A. F. K., Kanniah, K. D., Kaskaoutis, D. G., and Latif, M. T. (2024). Improving the quantification of fine particulates (pm2. 5) concentrations in Malaysia using simplified and computationally efficient models. J. Clean. Prod. 448, 141559. doi:10.1016/j.jclepro.2024.141559
Zhan, Y., Luo, Y., Deng, X., Chen, H., Grieneisen, M. L., Shen, X., et al. (2017). Spatiotemporal prediction of continuous daily pm2. 5 concentrations across China using a spatially explicit machine learning algorithm. Atmos. Environ. 155, 129–139. doi:10.1016/j.atmosenv.2017.02.023
Zhou, G., Lin, G., Liu, Z., Zhou, X., Li, W., Li, X., et al. (2023). An optical system for suppression of laser echo energy from the water surface on single-band bathymetric lidar. Opt. Lasers Eng. 163, 107468. doi:10.1016/j.optlaseng.2022.107468
Keywords: air pollution, concentration, short-term PM 2.5 forecasting, single time series models, ensemble time series models, sustainable development, early warning system, decision making
Citation: Iftikhar H, Qureshi M, Zywiołek J, López-Gonzales JL and Albalawi O (2024) Short-term
Received: 02 June 2024; Accepted: 23 August 2024;
Published: 10 September 2024.
Edited by:
Dimitris G. Kaskaoutis, National Observatory of Athens, GreeceReviewed by:
Nurul Amalin Fatihah Kamarul Zaman, University of Science Malaysia (USM), MalaysiaCopyright © 2024 Iftikhar, Qureshi, Zywiołek, López-Gonzales and Albalawi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hasnain Iftikhar, aGFzbmFpbkBzdGF0LnFhdS5lZHUucGs=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.