- School of Petroleum Engineering, Yangtze University, Wuhan, China
Introduction: Simulating oil and water flow in shale reservoirs is challenging due to heterogeneity caused by fractures. Conventional grid-based methods often have convergence issues. We propose a new approach using fractal theory and meshless methods to accurately model flow.
Methods: A mathematical model describing oil-water flow in fractured horizontal shale wells was developed. The meshless weighted least squares (MWLS) method was used to numerically solve the model. Modeling points were placed flexibly, informed by fractal theory.
Results: The MWLS solution aligned well with reference solutions but had enhanced flexibility. Comprehensive analysis showed the effects of modeling parameters like fracture properties on production.
Discussion: The proposed methodology enabled accurate prediction of shale oil production. Convergence was improved compared to grid-based methods. The flexible modeling approach can be tailored to specific reservoir conditions. Further work could expand the model complexity and types of reservoirs.
1 Introduction
Shale oil is an unconventional type of oil found in organic-rich black shale or nanoscale pores in shale. With vast reserves distributed worldwide, shale oil has become the most promising unconventional oil resource for development. However, shale oil reservoirs exhibit low matrix pore permeability and significant heterogeneity (Jia et al., 2019). Consequently, low fracture flowback rates often occur during the flowback process (Zhang et al., 2019), making accurate prediction of the oil and water flow in shale reservoirs crucial (Daneshy, 2004; Bertoncello et al., 2014; Su et al., 2016).
Due to the multi-scale nature and complex fluid distribution in shale oil reservoirs, traditional Darcy flow equations are insufficient for accurately depicting their flow characteristics. Researchers have adopted apparent porosity and permeability models to characterize the unique migration mechanisms in shales. These models can be grouped into three primary categories: Javadour models (based on fracture aperture) (Javadpour, 2009; Akkutlu et al., 2015; Singh and Javadpour, 2016), Civan models (based on the Knudsen number) (Civan, 2010; Wu et al., 2015; Song et al., 2016), Civan models (based on the Knudsen number) (Mason et al., 1983; Li et al., 2017; Zeng et al., 2017). In the study of oil behavior within nanopores, researchers have explored the use of organic/inorganic apparent porosity models. These models offer a valuable approach to characterize the oil state within nanopores, considering the influence of both organic and inorganic components. By incorporating the concept of apparent porosity, researchers aim to gain a deeper understanding of the distribution and behavior of oil within these nanoscale spaces (Sheng et al., 2019; Sheng et al., 2020). Furthermore, integrating the conventional dual-medium model with apparent permeability/porosity models has been found to provide a more accurate depiction of shale oil flow behavior (Sheng et al., 2018).
The heterogeneity of porosity and permeability in shale oil reservoirs poses challenges for numerical simulation, such as high computational costs and poor convergence (Li et al., 2023). Conventional grid-based finite difference methods are complex and not suitable for complex boundary conditions. Wei (Wei et al., 2021a) proposed a discontinuous discrete fracture model for coupled flow and geomechanics and used the finite element method to optimize the reservoir stress evolution (Shiming et al., 2022) and fracturing schemes for encrypted wells throughout the drilling-fracturing-producing wells (Wei et al., 2021b). Finite element meshes may experience severe distortion, requiring remeshing, which increases computational time and significantly affects accuracy. Describing complex geometric computational domains becomes cumbersome as further mesh refinement complicates preprocessing. Finite difference/volume methods are known for their accuracy; however, they have limitations when it comes to grid uniformity. High-precision difference schemes are often designed for regular Cartesian grids, which poses challenges when dealing with complex boundaries or reservoirs with intricate geological conditions. As a result, handling such situations becomes difficult using traditional finite difference/volume methods (Rao et al., 2020; Rao et al., 2022). Given the limitations of conventional numerical methods in simulating shale oil reservoirs, the meshless method emerges as a promising and efficient alternative. This method entails positioning points throughout the reservoir area to precisely delineate the intricate boundary of the shale oil reservoir. In this manner, the meshless technique develops a potent numerical model to emulate the movement of oil and water inside the shale oil deposit.
Introduced by Lucy in 1977, the Smoothed Particle Hydrodynamics (SPH) method is a mesh-free approach that has found success in addressing astrophysical problems. This method has been widely utilized in the simulation of various astrophysical phenomena, showcasing its effectiveness in capturing complex dynamics and fluid behavior without relying on traditional meshes (Lucy, 1977). Radial Basis Function (RBF) interpolation is an effective approach for generating smooth, continuous approximations of scattered data. In this technique, a collection of radial basis functions, such as Gaussian or multiquadric functions, are employed to estimate the solution at any point within the domain (Wright, 2003). The Element-free Galerkin (EFG) method is a meshless alternative to the Galerkin method, which is widely used in finite element analysis. Utilizing moving least squares (MLS) approximation, EFG constructs shape functions and integrates the PDE’s weak form throughout the domain. This method is applicable to both linear and nonlinear problems. (Belytschko et al., 1995). Li (Yu-kun, 2007) proposed the Mesh-Free Weighted Least Squares (MWLS) method, which has been recognized for its high accuracy and excellent stability, particularly in generating a symmetric coefficient matrix. Unlike the Galerkin method, the MWLS method does not require Gaussian integration, making it more efficient. Xu and Rao (Rao et al., 2021; Xu et al., 2021) applied the MWLS method to study shale gas water seepage problems, analyzing the influence of weight functions and nodes in the MWLS method. However, they did not specifically analyze the characteristics of shale oil.
In this paper, the concept of fractal permeability is introduced, and a numerical model is developed to simulate oil and water flow in a fractured horizontal well situated in a fractal shale oil reservoir. The Mesh-Free Weighted Least Squares (MWLS) method is employed to solve the problem. Additionally, a comparative analysis is conducted to evaluate the impacts of fracture distribution patterns, initial water saturation, and reservoir reconstruction degree on reservoir utilization scope and production performance. Through this analysis, insights are gained into the effective utilization and production performance of reservoirs under different conditions.
2 Equations for the meshless method in modeling oil-water flow in shale oil reservoirs
The meshless technique employs a collection of field nodes distributed across the computational domain’s boundary and body to delineate the boundary and the domain itself. Because these field nodes do not form any mesh, this technique can overcome the constraints of the finite difference approach, which necessitates a Cartesian mesh, as well as the finite element approach, which demands high-quality mesh production and remodeling.
The meshless method unfolds in three primary stages:
Step 1. Field Nodes in Meshless Techniques for Conveying Field Variable Values
Within the meshless approach, field variable values, encompassing unknown functions, are expressed by the nodal values assigned to field points. The precision of the computation is directly impacted by the concentration of these field points, which are typically spread evenly across the domain.
Step 2. Localized Approximation of Field Variables in Meshless Techniques
In meshless techniques, where a grid is not utilized, the field variables at a specific point x=(x1,x2) within the computational domain are approximated through interpolation using the field node values within the localized superconductive area centered around that point. This approach enables accurate estimation of field variable values at arbitrary locations, ensuring precise representation of the underlying physical phenomena.
Where, n denotes quantity of field nodes within a specific point’s local support domain x, ui signifies the nodes’s value of the ith field node; Us is The vector composed of the values at each field node; and φi(x) represents the shape function associated with the ith node in the support region of a given point x.
Step 3. Deriving Nodal Values of the Unknown Function in Meshless Techniques
Through the application of localized field variable approximations, the derivation of the shape function is done for the field points. The MLS approach is proficient in providing a shape function of high continuity across the overall problem sphere. Generally, when considering a global optimization problem, MLS simplifies the attainment of a globally optimal solution. Consequently, this paper leverages the MLS approach for the local approximation of field variables. In the scope of MLS, the approximation of the unknown function u(x) within x’s influence domain is performed.
Here, x represents the position in space of every node within the support region
Where n represents the quantity of nodes held in the support domain of the weight function
That is,
In which,
Then a(x) is:
On substituting Eq. 6 into Eq. 2, it leads us to the conclusion that
In this context, Φ(x) represents a vector built from shape functions, determined by
So φ i(x) is defined as
It is important to note that while the shape function constructed on the basis of the point interpolation local approximation method possesses the Kronecker property, its usage of the local support domain fails to ensure compatibility throughout the entire domain.
2.1 Oil-water flow model of shale oil reservoir
In the geologic model for fractured horizontal wells within shale oil reservoirs, a binary porosity medium is proposed, comprised of two parts: the matrix substance and the fracture web. The matrix substance functions as the primary storage space, while the fracture network operates as the main channel for shale oil. Both oil and water have the capacity to move within the fractures, however, only oil has the ability to flow within the matrix. The dual-porosity model encompasses both the matrix and fracture systems: the former is the chief repository for shale oil, and the latter is the primary passage for it. Three basic assumptions are taken into account:
(1) The flow of oil-water takes place in the fracture system, while solely single-phase shale oil migrates towards fractures in the matrix, disregarding the flow within the matrix system;
(2) The influence of gravity and capillary forces is disregarded;
(3) Fluids exhibit minor compressibility, while rock material remains incompressible.
2.1.1 Flow model for the matrix system
Adhering to the principles of mass conservation and the Darcy flow equation, the oil flow equation within the matrix can be articulated as follows:
where μo denotes the oil viscosity, in mPa·s; ρo denotes the oil density, in kg/m³; kapp represents the matrix apparent permeability, in mD; pm refers to the matrix pressure, in MPa; pf signifies the fracture network pressure, in MPa; φapp stands for the matrix apparent porosity and t denotes time;
The fracture system under scrutiny in this study is planar, possessing a uniform fracture spacing equal to 12/Lm, where Lm corresponds to the length of the matrix rock block’s side.
2.1.2 Flow model for the fracture system
Considering the principle of mass conservation along with Darcy’s law of flow, the equation for the water phase within a fracture system can be expressed as follows:
The oil flow within the fracture is described as follows:
where ρw signifies the water’s density, kg/m3; krw, kro denote the relative permeability of water and oil, respectively, mD; kf represents the fracture’s permeability, mD;μw is the water’s viscosity, mPa•s; pwf is the pressure within the water phase of the fracture, in MPa; φf is the fracture’s porosity; Sw and So indicate the water and oil saturations within the fracture, respectively; Qmo is the mass flow rate, as shown in Eq. 14,
Characteristics of the fracture system, like porosity and permeability, can be articulated as follows:
in this context, x denotes the distance from the origin, measured in meters (m), and xw refers to the hydraulic fracture’s width, also measured in meters (m). The parameters
2.1.3 Supporting equations
For the purpose of this analysis, capillary forces are not considered. Therefore, the pressure of the oil within the fracture system equilibrates with the pressure of the water phase, resulting in the flow of only oil within the matrix system. Consequently, the pressures within the fracture and the matrix are denoted by Pf and Pm, respectively.
Initial:
2.2 Model solution
The meshless method, which is based on the weighted residual technique, utilizes the moving least squares (MLS) strategy to construct the approximation function. The governing equation is discretized using the least square method, resulting in the development of MWLS, a meshless technique. For a comprehensive understanding of the MWLS, please refer to the cited literature. (Yu-kun, 2007).
By reorganizing Eqs 11–13, we can derive the subsequent Eq. 18.
In the process of executing MWLS for inferential purposes, the problem domain, represented by Ω, and its boundary, denoted by Г, undergo discretization through the use of n points. The fracture system’s pressure and water saturation are then modeled by meshless approximate functions, established courtesy of MLS, which can be expressed following the template of Eq. 19.
where
By replacing Eq. 18-①) with Eq. 19 from above, the residual can be derived, as depicted in Eq. 20.
Thus, the computational scheme of MWLS for determining the pressure in the fracture system unfolds as follows:
In Eq. 21,
By transforming Eq. 22 into matrix system and taking into account the freedom of
Among them:
Eq. 24 provides the fracture’s pressure at the t+1 time step. This value is then utilized in Eq. (18-②) for substitution. Subsequently, the MLS method is employed to construct an approximate equation for the Sw in the fracture. Ultimately, Eq. 24 is derived:
Eq. 24 provides the fracture’s Sw at the next time step.
The variables and parameters involved are as follows:
The matrix system’s pressure can be determined using a similar approach. By inserting the fracture system’s pressure at the next time step into formula (18-③), the final MWLS equation can be derived:
Eq. 25 provides the matrix’s pressure at the next time step.
The variables and parameters involved are as follows:
Where s represents the number of points used for calculations; Let n represent t the total number of points used for calculations within the neighborhood Ω, and let ni (i = 1,2) represent the total number of points used for calculations on boundary Γi.
3 Examining and confirming the accuracy of computational examples
3.1 Model validation
A field case was constructed to validate the model’s accuracy, considering the fractal features in a shale oil reservoir where the horizontal well is fractured. The reservoir area are 500 m × 400 m × 10m, with the model and layout depicted in Figure 1. The corresponding physical properties of the reservoir can be found in Table 1. Due to its superior continuity and higher computational accuracy, we used the Gaussian formulation as the weighting function in the grid-independent approach. The layout scheme used is 50 × 40, and a node spacing of 3 times (30 m) is used for the node influence domain.
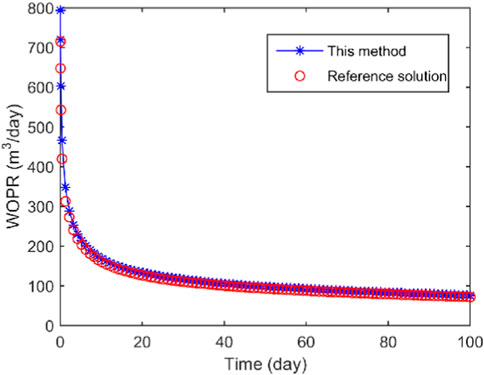
This study incorporated Table 1 data into the oil-water flow fractal shale reservoir model to obtain daily oil production variations. This paper set a result calculated using EDFM as the reference solution. The results were then compared to those of a reference solution, as shown in Figure 2. The proposed method closely matched the reference solution, demonstrating its reliability, accuracy, and high computational efficiency. Furthermore, Figure 3 presents the pressure distribution at different times, showing that the matrix pressure gradually decreases during production. Although there were some discrepancies between the reference solution and the MWLS results, these errors fall within acceptable bounds and can be attributed to inherent differences between the approaches.

FIGURE 3. The Distribution of fracture pressure. (A) MWLS, 1 day; (B) Refence solution, 1 day; (C) MWLS, 50 day; (D) Refence solution, 50 day; (E) MWLS, 100 day; (F) Refence solution, 100 day.
3.2 Sensitivity analysis of nodal influence domain
After applying the theories and solutions mentioned earlier, a sensitivity analysis of the nodal influence domain is conducted to evaluate its impact on the accuracy of meshless method computations. The solution of the flow of oil and water in horizontally fractured wells. is used to verify the validity of the method. While the MWLS method is inherently precise, the accuracy of its results is also dependent on the process of choosing the nodal influence domain. The optimal parameter values vary depending on the specific problem at hand.
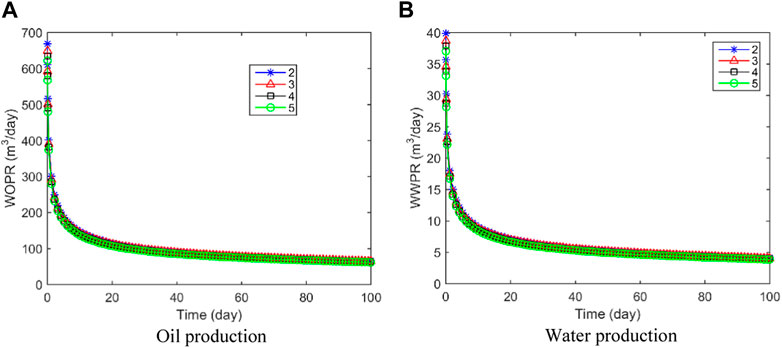
Consequently, the nodal influence domain was chosen to be 2, 3, 4, and 5 times the nodal spacing (10 m), with the initial water saturation is 0.25 while keeping other parameters constant. By doing so, the established mathematical model is further validated and analyzed to ensure its reliability and applicability in solving real-world problems associated with the flow of oil and water in horizontally fractured wells.
Figure 4 demonstrates the variation curves of daily oil and water production for different nodal influence domains. The calculated results demonstrate varying levels of consistency when the nodal influence domain is set at 2, 3, 4, and 5 times the nodal spacing. This suggests that the method is characterized by good stability and convergence in its calculations. This validates its effectiveness and robustness for simulating the flow of oil and water in horizontally fractured wells. Figure 5 shows the crack pressure distribution at 100 days for different nodal influence domains. The calculated crack pressure distributions do not differ significantly under different conditions. When the influence domain size is 5 times the nodal spacing, the pressure drop area is marginally larger than that for the influence domain size of 2, 3, and 4 times the nodal spacing. However, the overall difference is less than 2% because the area of pressure drop increases slightly with the size of the influence domain.
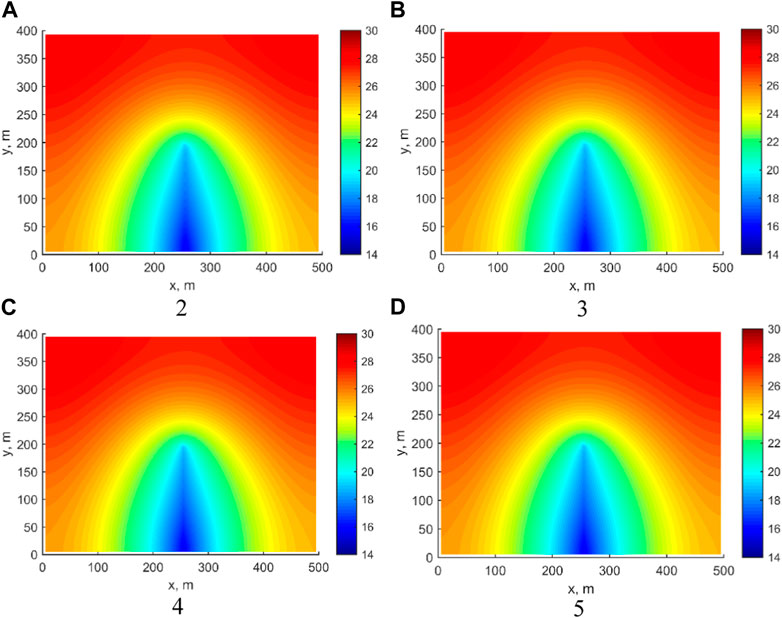
FIGURE 5. The distribution of frature pressure under different node influence domains. (A) 2; (B) 3; (C) 4; (D) 5.
3.3 Sensitivity analysis of initial Sw
The initial Sw level is a crucial factor affecting shale oil production. To investigate the impact of different initial Sw levels on reservoir recovery and fractured well production while keeping other parameters constant, data from Table 1 were utilized. The initial Sw values were set at 0.35, 0.45, 0.55, and 0.65. Figure 6 illustrates the pressure in the reservoir for different initial levels of Sw after 100 days of production. It is evident that an increase in the initial Sw level leads to a reduction in the pressure difference between the matrix and fracture in the reservoir. This underscores the importance of accurately modeling and understanding initial Sw when simulating and predicting shale oil production. At an initial Sw of 0.35, the matrix pressure in the upper part of the model is about 30 MPa at 100 days, while at this value of 0.65, the matrix pressure in the upper part of the model is only about 26 MPa.
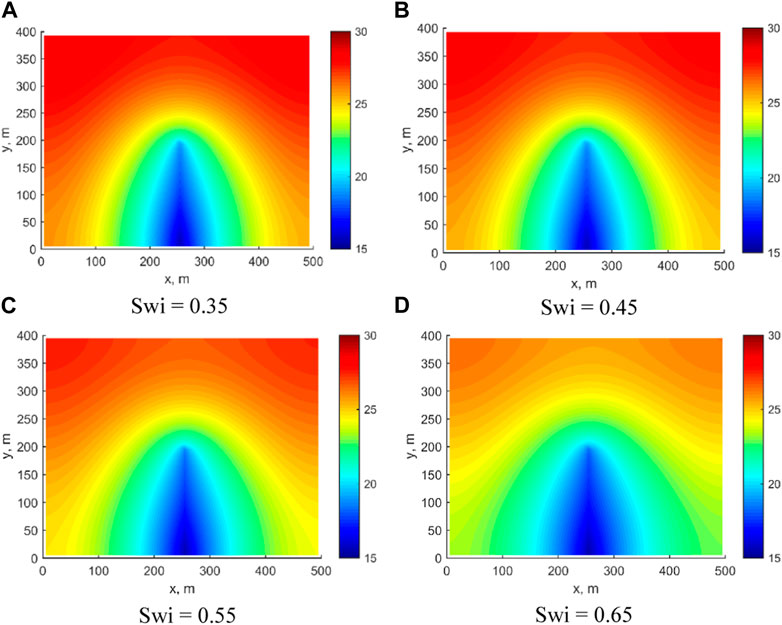
FIGURE 6. Pressure distribution under different initial Sw. (A) Swi = 0.35; (B) Swi = 0.45; (C) Swi = 0.55; (D) Swi = 0.65.
In Figure 7, the Sw distribution in the reservoir at 100 days are shown for different initial Sw levels. When the initial Sw is set at 0.35, the Sw at the fracture increases slightly to 0.3506 after 100 days. However, as the initial Sw level increases, the Sw at the fracture decreases after 100 days. This phenomenon is mainly due to the increase in Sw, which results in a significant rise in water flow capacity. Accurately modeling and predicting the behavior of oil-water flow in shale reservoirs requires an understanding of the relationship between initial Sw and its impact on fracture Sw over time.
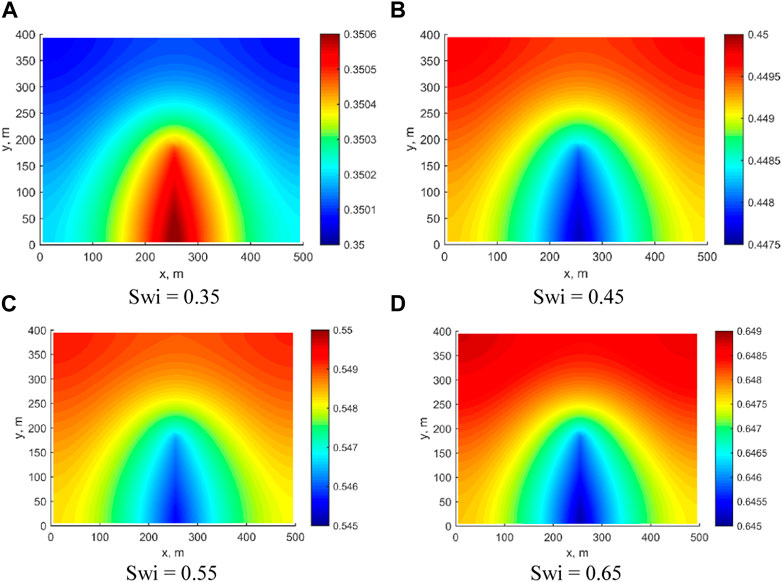
FIGURE 7. Fracture Sw distribution under different initial Sw. (A) Swi = 0.35; (B) Swi = 0.45; (C) Swi = 0.55; (D) Swi = 0.65.
In Figure 8, the fluid production under different initial Sw conditions is displayed. As the initial Sw increases, there is less free oil stored in the fractures and reservoirs. Consequently, the initial oil production is significantly reduced when the initial Sw is higher. Moreover, higher Sw reduces the relative permeability of the oil phase, hindering oil flow within the reservoir. Thus, larger initial Sw levels result in lower daily oil production and higher daily water production. For instance, when the initial Sw is set at 0.65, the initial daily well water production rate can reach 1024 m³/day. Understanding these relationships is crucial for optimizing reservoir management and production strategies.
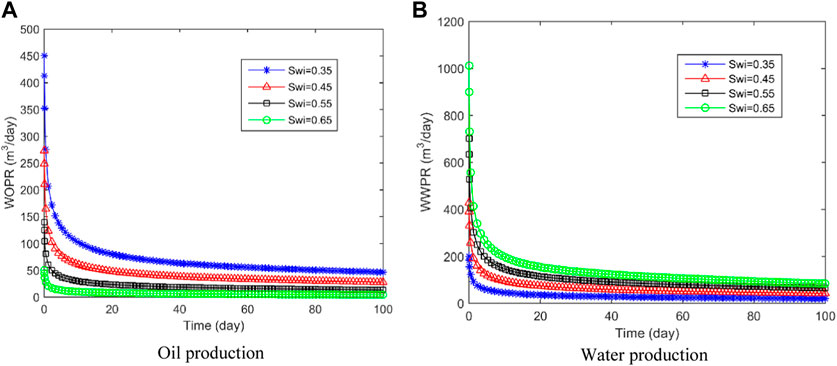
FIGURE 8. Production of different initial water saturation conditions. (A) Oil production; (B) Water production.
3.4 Sensitivity analysis of fracture half-lengths
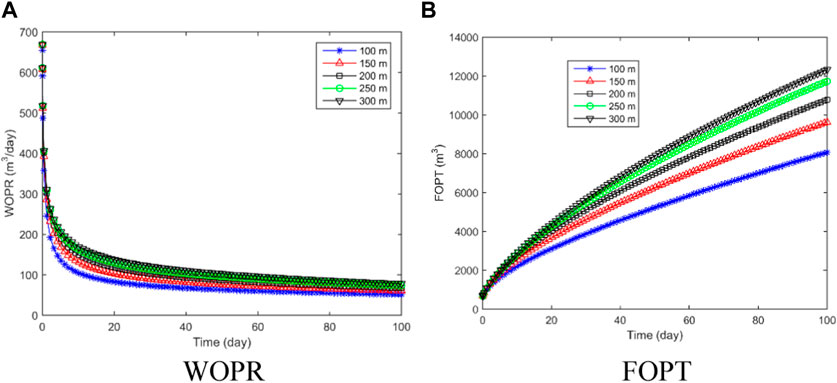
We investigate the effects of different fracture half-lengths on the proposed model by setting the values to 100 m, 150 m, 200 m, 250 m, and 300 m, while keeping other parameters unchanged. This analysis helps to understand how variations in fracture half-length and SRV influence the production performance and recovery efficiency in shale oil reservoirs.
Figure 9 displays the pressure distribution field for different fracture half-lengths at 100 days. Increasing the fracture half-length results in a more rapid and extensive drop in matrix pressure. For instance, with a fracture half-length of 100 m, the matrix pressure in the upper part of the reservoir was maintained at 30 MPa, while at a fracture half-length of 300 m, it decreased to 27 MPa.
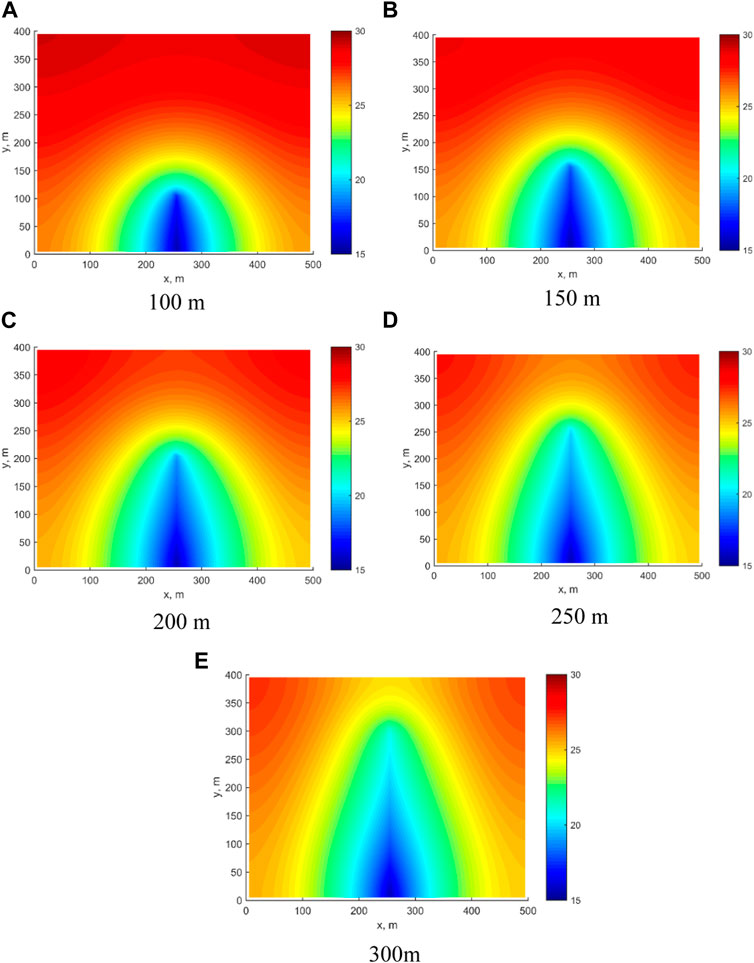
FIGURE 9. Pressure distribution of different fracture half-lengths. (A) 100 m; (B) 150 m; (C) 200 m; (D) 250 m; (E) 300 m.
Figure 10 depicts the comparison curves of daily and cumulative oil production for various fracture half-lengths. Daily oil production rises with an increase in the fracture half-length, as shown in Figure 10A. Figure 10B indicates a positive correlation between cumulative oil production and fracture half-length, mainly due to the larger stimulated reservoir volume and pressure ripple area as the fracture half-length increases. Despite this, the incremental gain in cumulative oil production diminishes as the fracture half-length increases. For example, when the fracture half-length is 100 m, the cumulative oil production for 100 days is 8075 m3. When the fracture half-length is extended to 150 m, the cumulative oil production increases by 1556 m3 to reach 9631 m3. However, when the fracture half-length is increased from 250 m to 300 m, the increase in cumulative oil production is only 602 m3.
3.5 Effects of fracture numbers
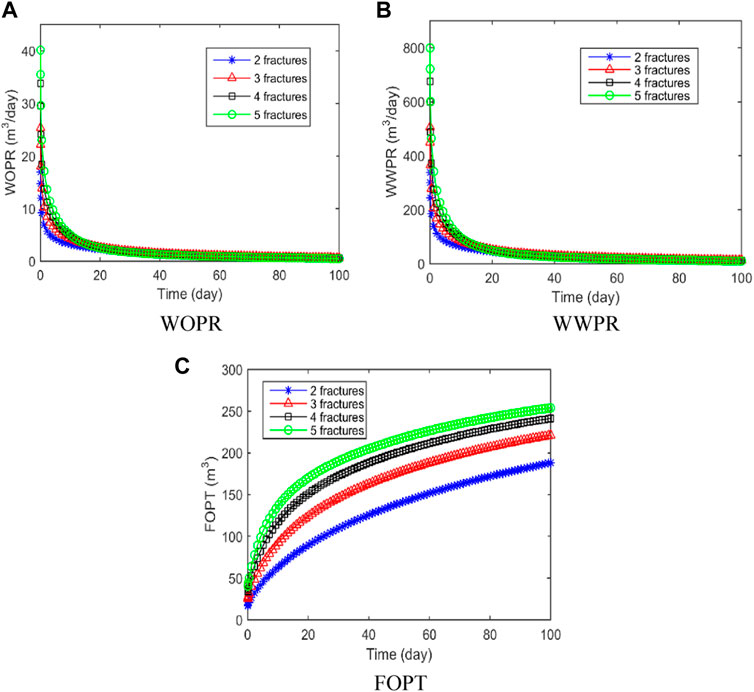
There are multiple factors affecting oil well productivity, among which the number of fractures is one of the key factors. The optimization of fracture numbers is also an important aspect of design of hydraulic fractures for horizontal wells. By fixing fracture half-length at 200 m, setting the initial Sw at 0.65, we change the number of fractures to 2, 3, 4, and 5, keeping other parameters consistent with the previous example.
The pressure distribution at 100 days for different fracture numbers is displayed in Figure 11. The relationship between the number of fractures and the pressure in the reservoir is evident, with an increase in fractures leading to a more rapid decline in pressure and a larger affected area. For example, when there are 2 fractures, the matrix pressure at the upper end of the reservoir can still be maintained at 25 MPa. However, when there are 5 fractures, the matrix pressure at the upper end of the reservoir is only 20 MPa. Figure 12 presents the changes in production capacity under different fracture numbers. Figures 12A, B display the wopr and wwpr curves, respectively, indicating that as the number of fractures increases, the corresponding WOPR and WWPR also increase. Figure 12C shows the FOPT curve, which is also shows a positive correlation with the number of fractures, but the rate of increase is diminishing. Increasing the number of fractures from 2 to 4 results in a 1.28-fold increase in cumulative oil production. However, increasing the number of fractures from 4 to 5 only leads to a 1.05-fold increase in cumulative oil production.
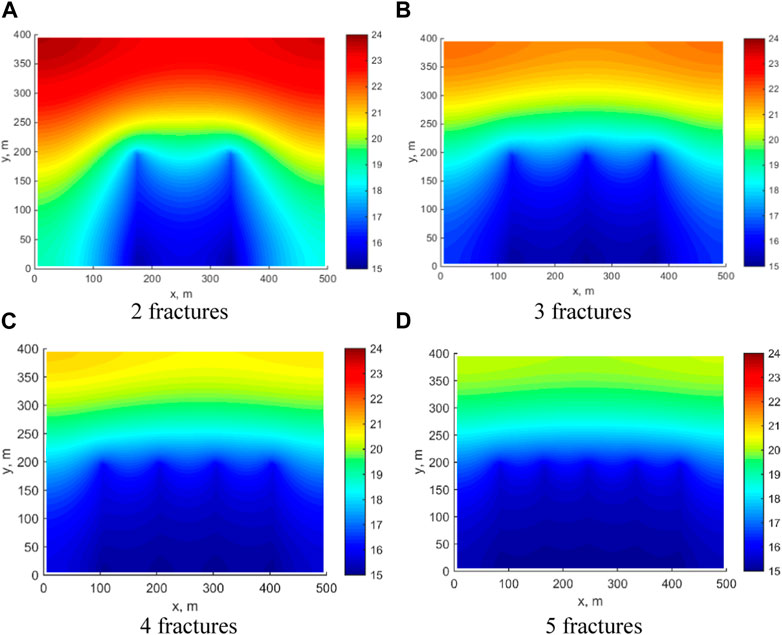
FIGURE 11. Pressure distribution at 100 days. (A) 2 fractures; (B) 23 fractures; (C) 4 fractures; (D) 5 fractures.
4 Conclusion
1) A mathematical model for oil-water fractal diffusion in fractured horizontal wells considering fracture network heterogeneity was developed and numerically solved using the MWLS method. Field example validation confirmed the model’s accuracy.
2) The impact of nodal domains in MWLS method was explored. The method shows robust stability. With an expanding nodal influence domain, the calculated results converge towards true values.
3) Employing the model, we examined the effects of initial Sw and reservoir modification on reservoir utilization and production. Increasing initial Sw increases oil flow resistance, hence reducing oil production. During reservoir modification, expanding fracture half-length and count enhances oil production, but with diminishing growth rate.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
WL conceptualization, methodology, software, writing—original draft, formal analysis GZ supervision, Project administration. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akkutlu, I. Y., Efendiev, Y., and Savatorova, V. J. T. i. P. M. (2015). Multi-scale asymptotic analysis of gas transport in shale matrix. Transp. Porous Media 107, 235–260. doi:10.1007/s11242-014-0435-z
Belytschko, T., Lu, Y. Y., Gu, L., and Tabbara, M. (1995). Element-free Galerkin methods for static and dynamic fracture. Int. J. Solids Struct. 32, 2547–2570. doi:10.1016/0020-7683(94)00282-2
Bertoncello, A., Wallace, J., Blyton, C., Honarpour, M., and Kabir, C. (2014). Imbibition and water blockage in unconventional reservoirs: well-management implications during flowback and early production. SPE Res. Eval. & Eng. 17, 497–506. doi:10.2118/167698-PA
Civan, F. (2010). Effective correlation of apparent gas permeability in tight porous media. Transp. Porous Media 82, 375–384. doi:10.1007/s11242-009-9432-z
Daneshy, A. (2004). “Analysis of off-balance fracture extension and fall-off pressures,” in SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, Louisiana, February 2004. doi:10.2118/86471-MS
Javadpour, F. J. J. o. C. P. T. (2009). Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). J. Can. Pet. Technol. 48, 16–21. doi:10.2118/09-08-16-da
Jia, B., Tsau, J. S., and Barati, R. (2019). A review of the current progress of CO2 injection EOR and carbon storage in shale oil reservoirs. Fuel 236, 404–427. doi:10.1016/j.fuel.2018.08.103
Li, Z., Lei, Z., Shen, W., Martyushev, D. A., and Hu, X. (2023). A comprehensive review of the oil flow mechanism and numerical simulations in shale oil reservoirs. Energies 16, 3516. doi:10.3390/en16083516
Li, Z., Zhang, X., and Liu, Y. J. G. (2017). Pore-scale simulation of gas diffusion in unsaturated soil aggregates: Accuracy of the dusty-gas model and the impact of saturation. Geoderma 303, 196–203. doi:10.1016/j.geoderma.2017.05.008
Lucy, L. B. (1977). A numerical approach to the testing of the fission hypothesis. Astronomical J. 82, 1013–1024. doi:10.1086/112164
Rao, X., Cheng, L., Cao, R., Jia, P., Liu, H., and Du, X. (2020). A modified projection-based embedded discrete fracture model (pEDFM) for practical and accurate numerical simulation of fractured reservoir. J. Petroleum Sci. Eng. 187, 106852. doi:10.1016/j.petrol.2019.106852
Rao, X., Xin, L., He, Y., Fang, X., Gong, R., Wang, F., et al. (2022). Numerical simulation of two-phase heat and mass transfer in fractured reservoirs based on projection-based embedded discrete fracture model (pEDFM). J. Petroleum Sci. Eng. 208, 109323. doi:10.1016/j.petrol.2021.109323
Rao, X., Zhan, W., Zhao, H., Xu, Y., Liu, D., Dai, W., et al. (2021). Application of the least-square meshless method to gas-water flow simulation of complex-shape shale gas reservoirs. Eng. Analysis Bound. Elem. 129, 39–54. doi:10.1016/j.enganabound.2021.04.018
Sheng, G., Javadpour, F., and Su, Y. (2018). Effect of microscale compressibility on apparent porosity and permeability in shale gas reservoirs. Int. J. Heat Mass Transf. 120, 56–65. doi:10.1016/j.ijheatmasstransfer.2017.12.014
Sheng, G., Javadpour, F., and Su, Y. J. F. (2019). Dynamic porosity and apparent permeability in porous organic matter of shale gas reservoirs. Fuel 251, 341–351. doi:10.1016/j.fuel.2019.04.044
Sheng, G., Zhao, H., Su, Y., Javadpour, F., Wang, C., Zhou, Y., et al. (2020). An analytical model to couple gas storage and transport capacity in organic matter with noncircular pores. Fuel 268, 117288. doi:10.1016/j.fuel.2020.117288
Shiming, W., Yan, J., Jiawei, K., Yang, X., and Botao, L. (2022). Reservoir stress evolution and fracture optimization of infill wells during the drilling-fracturing-production process. Acta Pet. Sin. 43, 1305. doi:10.7623/syxb202209009
Singh, H., and Javadpour, F. J. F. (2016). Langmuir slip-Langmuir sorption permeability model of shale. Fuel 164, 28–37. doi:10.1016/j.fuel.2015.09.073
Song, W., Yao, J., Li, Y., Sun, H., Zhang, L., Yang, Y., et al. (2016). Apparent gas permeability in an organic-rich shale reservoir. Fuel 181, 973–984. doi:10.1016/j.fuel.2016.05.011
Su, Y., Sheng, G., Wang, W., Zhang, Q., Lu, M., and Ren, L. J. F. (2016). A mixed-fractal flow model for stimulated fractured vertical wells in tight oil reservoirs. Fractals 24, 1650006. doi:10.1142/s0218348x16500067
Wei, S., Jin, Y., Liu, X., and Xia, Y. (2021b). “The optimization of infill well fracturing using an integrated numerical simulation method of fracturing and production processes,” in Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, November 2021. doi:10.2118/207978-MS
Wei, S., Kao, J., Jin, Y., Shi, C., and Liu, S. (2021a). A discontinuous discrete fracture model for coupled flow and geomechanics based on FEM. J. Petroleum Sci. Eng. 204, 108677. doi:10.1016/j.petrol.2021.108677
Wright, G. B. (2003). Radial basis function interpolation: Numerical and analytical developments. Colorado: University of Colorado at Boulder.
Wu, K., Li, X., Wang, C., Chen, Z., and Yu, W. J. A. J. (2015). A model for gas transport in microfractures of shale and tight gas reservoirs. AIChE J. 61, 2079–2088. doi:10.1002/aic.14791
Xu, Y., Sheng, G., Zhao, H., Hui, Y., Zhou, Y., Ma, J., et al. (2021). A new approach for gas-water flow simulation in multi-fractured horizontal wells of shale gas reservoirs. J. Petroleum Sci. Eng. 199, 108292. doi:10.1016/j.petrol.2020.108292
Zeng, Y., Ning, Z., Lei, Y., Huang, L., Lv, C., and Hou, Y. (2017). “Analytical model for shale gas transportation from matrix to fracture network,” in SPE Europec featured at 79th EAGE Conference and Exhibition, Paris, France, June 2017. doi:10.2118/185794-MS
Keywords: shale reservoir, oil-water flow, MWLS method, multi-fractured horizontal well, reservoir simulation
Citation: Liu W and Zhang G (2023) Enhancing oil-water flow simulation in shale reservoirs with fractal theory and meshless method. Front. Environ. Sci. 11:1244543. doi: 10.3389/fenvs.2023.1244543
Received: 22 June 2023; Accepted: 17 July 2023;
Published: 27 July 2023.
Edited by:
Shiming Wei, China University of Petroleum, ChinaReviewed by:
Can Shi, Chengdu University of Technology, ChinaZhi Chang, CNPC Engineering Technology R & D Company Limited, China
Copyright © 2023 Liu and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guangming Zhang, MTg0OTc5ODcxNEBxcS5jb20=
 Wenbo Liu
Wenbo Liu Guangming Zhang*
Guangming Zhang*