Assessing the environmental impact of industrial pollution using the complex intuitionistic fuzzy ELECTREE method: a case study of pollution control measures

Ashraf, Shahzaib; Ali, Mubashar; Sohail, Muhammad; Eldin, Sayed M.

doi:10.3389/fenvs.2023.1171701

ORIGINAL RESEARCH article

Front. Environ. Sci., 18 May 2023

Sec. Environmental Economics and Management

Volume 11 - 2023 | https://doi.org/10.3389/fenvs.2023.1171701

This article is part of the Research Topic Fuzzy Mathematical Model and Optimization in Digital Green Innovation for Industry 5.0 View all 14 articles

Assessing the environmental impact of industrial pollution using the complex intuitionistic fuzzy ELECTREE method: a case study of pollution control measures

¹Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, Pakistan
²Center of Research, Faculty of Engineering, Future University in Egypt New Cairo, New Cairo, Egypt

Environmental pollution has become a major issue in today’s world, and controlling it is crucial for the sustainable development of our planet. Industries play a significant role in environmental pollution, and their impact must be controlled and minimized. In this paper, we present a novel approach, the complex intuitionistic fuzzy ELECTREE method (CIF–ELECTREE), for environmental impact assessment of industries. The method combines the principles of CIF sets and the ELECTREE method to provide a comprehensive and reliable assessment of the environmental impact of industries. The proposed method has been applied to real-world data, and the results obtained demonstrate the effectiveness of the CIF–ELECTREE method in controlling and reducing the environmental impact of industries. The results show that the CIF–ELECTREE method can provide a more accurate assessment of the environmental impact of industries compared to traditional methods. This study contributes to the existing literature by introducing a novel approach for environmental impact assessment and highlights the importance of considering both the uncertainty and vagueness in real-world data for reliable decision making.

1 Introduction

Multi-attribute and multi-criteria decision making plays a crucial role in everyday life as well as in many complex decision-making scenarios. These techniques are used to make informed decisions based on multiple objectives, criteria, and attributes, which helps in taking into account the trade-off between conflicting goals. For example, in personal life, multi-attribute decision making is often used when making choices such as buying a car, choosing a school, or purchasing a home. These decisions require weighing multiple factors such as cost, location, quality, and personal preferences, and therefore, multi-attribute decision making provides a useful framework for making such choices. In business and other organizations, multi-criteria decision making is frequently used in decision-making scenarios such as selecting suppliers, choosing a marketing strategy, or making investment decisions. These decisions often involve multiple objectives that must be considered, such as financial performance, customer satisfaction, and environmental impact. Despite the importance of multi-attribute and multi-criteria decision making, the process of making decisions based on multiple factors is often difficult due to the complexity of the data and the uncertainty surrounding the information. In many cases, the information used in decision making is incomplete, uncertain, and ambiguous, making it difficult to reach a reliable conclusion. Additionally, conflicting criteria and objectives can lead to trade-offs that are difficult to reconcile. To overcome these difficulties, the use of multi-attribute and multi-criteria decision making in the context of fuzzy set theory provides a useful framework for representing and handling uncertainty and ambiguity in decision-making problems. This allows for a more robust and informed decision-making process, taking into account the trade-off between conflicting objectives and criteria.

The process of making decisions is becoming more difficult as a consequence of the ambiguity that exists in the information, particularly when the data are accessible in a crisp form. In order to accomplish this goal, Zadeh invented the fuzzy set (Zadeh et al., 1996), and the philosophy behind fuzzy sets is an important consideration when it comes to making decisions in the face of ambiguity. He devised the membership grade as a defense mechanism against uncertainty. The development of mathematics has reached an all-time high thanks to fuzzy theory, since it is so useful in decision making. Many researchers work on fuzzy theory. For example, fuzzy theory has been used to improve digital mammography (Hassanien and Badr, 2003), play a big role in pharmacology (Sproule et al., 2002), create a system to help make decisions about nitrogen fertilizer (Yu et al., 2018), develop a system for risk assessment (Ebadi and Shahraki, 2010) and audit detection (Chang et al., 2008), and look at the social factors of migrant workers with HIV/AIDS (Kandasamy and Smarandache, 2004). The FSDEs (Jafari et al., 2021) are used in real-world systems such as those found in economics and finance, where the phenomena are tied to randomness and fuzziness as two separate forms of uncertainty. However, there are certain limitations to Zadeh’s fuzzy sets. For example, when there are more than two alternative values to address uncertainty, the method does not function well.

It has been found that intuitionistic fuzzy sets (IFSs), which were first introduced by Atanassov (1986), Atanassov (1989), and Atanassov (1999), are among the best higher-order fuzzy sets for dealing with ambiguity. In situations in which the information at hand is insufficient for the precise definition of an imprecise concept using a traditional fuzzy set, the idea of an IFS can be viewed as an alternative method for defining a fuzzy set. This can be performed by considering the concept of an IFS as an alternative approach to defining a fuzzy set. IFS theory may be thought of as a broader version of the original fuzzy set theory. Consequently, it is anticipated that IFSs might be used to imitate human decision-making processes and other tasks involving human experience and knowledge (Li, 1999; Li, 2003) which are inherently imprecise or unreliable. The idea of ambiguous sets was first described in the work of Gau and Buehrer (1993). Burillo and Bustince (Dengfeng and Chuntian, 2002; Xiao and Pedrycz, 2022) showed that the concepts of IFSs and ambiguous sets are synonymous with one another. Some operations on IFSs were defined by De et al. (2000). Szmidt and Kacprzyk (2000) studied the distances between IFSs. Szmidt and Kacprzyk (1996) and Szmidt and Kacprzyk (1997) considered the use of IFSs for building soft decision-making models with imprecise information. They proposed two solution concepts: the intuitionistic fuzzy core and the consensus winner for group decision making utilizing IFSs.

In terms of membership functions, making crisp sets into fuzzy sets is the same as making a set of integers into a set of real numbers. Changing the range of the membership function from {0, 1} to [0,1] is the same as changing I to R. Obviously, the development of numbers did not stop with the introduction of the real number system. In the past, we started with real numbers and then added complex numbers to their range. As a result, this modification might be the starting point for future work in fuzzy set theory. In the context of fuzzy set theory, a complex fuzzy set is the result of this kind of extension; it is a fuzzy set that differs from other fuzzy sets by having a membership function that accepts values in the complex number range. The theories that have been proposed by Ramot et al. have examined the decision-making problems that arise when using the fuzzy set and its generalizations, which can only deal with the ambiguity and uncertainty present in the data. These cannot account for the differences in data at a given moment. For this reason, Ramot et al. (2002) looked into the CFS, whereby the degree of membership is a complex integer that belongs to a unit disc on a complex plane. A complex fuzzy set (CFS) processes the data in a single set, which is just two dimensions deep. Despite the fact that Nguyen et al. (2000) were the ones to first propose a CFS, Ramot et al.’s conceptual space is more accommodating to decision makers. Over the last several years, the CFS has received a lot of research and media coverage. CFS operations (Zhang et al., 2009), power aggregation operators (Hu et al., 2019), and continuity of complex fuzzy operations (Hu et al., 2018) all had different operation features and distance measures. (Li and Chiang (2012) proposed a method through the use of CFSs for conducting the dual-output forecasting experiments (Xiao et al., 2022) with real-world financial time series, such as the Dow Jones Industrial Average, the Taiwan Stock Exchange Capitalization Weighted Stock Index, and the National Association of Securities Dealers Automated Quotation System.

In light of the significance of similarity measures (SMs), many researchers have recently opted for SMs based on the fuzzy set (FS) (Beg and Ashraf, 2009), CFS (Bi et al., 2019; Xiao, 2020a), and hesitant fuzzy set (HFS) (Xu and Xia, 2011). However, when a decision maker assigns membership grades in the form of groups, the complex values render the existing measures inadequate. In this work, the authors establish a complex intuitionistic fuzzy set (CIFS), a hybrid of the IFS and CFS , to deal with such problems while retaining the benefits of the SMs. Complex-valued membership degrees are presented in a polar form in CIFS theory. When a decision maker is presented with a set of data that only has two dimensions, all of the available theories, including the fuzzy set and CFS, perform admirably.

Benayoun et al. (1966) were the pioneers of the ELECTREE technique. The original inspiration for its core notions of concordance, discordance, and outranking was drawn from practical use cases. In addition, it uses concordance and discordance indices to examine the ordering of options. Energy (Beccali et al., 1998; Xiao, 2022), environment or water management (Ahrens and Kantelhardt, 2009), finance (Doumpos and Zopounidis, 2001), and decision analysis (Almeida, 2005; Xiao, 2020b) are just some of the domains where ELECTREE methodologies have been put to use. We have already shown that the ELECTREE technique, one of the most well-known outranking models, may be used to address the multi-criteria decision making (MCDM) issue. This approach is excellent because of its obvious logic, but it has been used in very little CIFS research. The ELECTREE technique involves contrasting potential solutions head-to-head in light of the decision maker’s own evaluations of the available options. Relationships of concordance, discordance, and superiority are of interest to this methodology. In this study, we provide a novel approach to using the ELECTREE technique in CIF systems, making it possible to solve MCDM issues there. People may use the CIFS to express uncertain scenarios in a decision-making dilemma, and its features are concerned with the degree of membership, the degree of complex membership, the degree of non-membership, the degree of complex non-membership grades, and the intuitionistic index all at once. In the ELECTREE assessment process, decision makers use CFS data with several values rather than a single value, and they are provided CFS data with multiple criteria to choose from.

The rest of the paper is organized as follows: In Section 2 we define some fundamental preliminaries, basic operations, and properties, and the construction of the CIF decision matrix is described. In Section 3, the proposed complex intuitionistic fuzzy ELECTREE method is described briefly along with the algorithm. In Section 4, the case study of the paper is discussed. Last, in Section 6, we discuss the paper’s final findings and conclusions.

2 Preliminaries

Definition 2.1. Suppose we have a finite universal set M such that M = {m₁, m₂, m₃, …m_n}; then, an IFS B in M is defined in the following form:

B = \{⟨ m_{k}, {\hat{μ}}_{B} (m_{k}), {\hat{ν}}_{B} (m_{k}) ⟩ | m_{k} \in M\}, (1)

where the functions $m_{k} \in M \to {\hat{ν}}_{B} (m_{k}) \in [0,1]$ and $m_{k} \in M \to {\hat{μ}}_{B} (m_{k}) \in [0,1]$ describe the degree of non-membership and degree of membership, respectively, of the given element m_k ∈ M to the set B ⊆ M, and for each m_k ∈ M,

0 \leq {\hat{ν}}_{B} + {\hat{μ}}_{B} \leq 1 .

Definition 2.2. A set C of the form given below defined upon M universal set is called as the CFS.

C = \{(h, {\hat{μ}}_{C} (h)) | h \in H\},

where

{\hat{μ}}_{C} (h) = \{ψ C (h) \cdot {\hat{e}}^{2 π ι (ω_{ψ C} (h))}\}

are the representation of the complex-valued certainty grade generally, which is subset of the unit disc in a complex plane having condition $ψ C (h), ω_{ψ C} (h) \in [0,1]$ .

Definition 2.3. A CIFS W defined on the universal set M is given as follows:

W = \{(z, {\hat{μ}}_{W} (z), {\hat{ν}}_{W} (z)) : z \in M\}, (2)

where ${\hat{ν}}_{w}$ and ${\hat{μ}}_{w}$ are complex-valued non-membership and membership functions, respectively, and ${\hat{μ}}_{W} (z) = {\hat{Y}}_{W} (z) {\hat{e}}^{2 π ι {\hat{W}}_{\hat{Y} W} (z)}$ , and ${\hat{ν}}_{W} (z) = {\hat{S}}_{W} (z) {\hat{e}}^{2 π ι {\hat{W}}_{\hat{S} W} (z)}$ such that ${\hat{Y}}_{W} (z) \geq 0$ , and ${\hat{S}}_{W} (z) \leq 1; 0 \leq {\hat{Y}}_{W} (z) + {\hat{S}}_{W} (z) \leq 1$ and $0 \leq {\hat{W}}_{\hat{Y} W} (z), {\hat{W}}_{\hat{S} W} (z) \leq 2 \hat{π}; 0 \leq {\hat{W}}_{\hat{Y} W} (z) + {\hat{W}}_{\hat{S} W} (z) \leq 2 \hat{π} \forall z \in M$ . We can also denote the CIFS W as

\{(z, ({\hat{Y}}_{W} (z), {\hat{W}}_{\hat{Y} W} (z)), ({\hat{S}}_{W} (z), {\hat{W}}_{\hat{S} W} (z))) : z \in M\} .

2.1 Some basic operations upon the intuitionistic fuzzy set and complex intuitionistic fuzzy set We considered

{\hat{π}}_{B} (m_{k}) = 1 - {\hat{ν}}_{B} - {\hat{μ}}_{B} (3)

as the intuitionistic index of the member m_k in the set M. This is the degree of indeterminacy membership of the element m_k to the set M. It is sure that for each $m_{k} \in M, 0 \leq {\hat{π}}_{B} (m_{k}) \leq 1$ .

The operations of the IFS (Atanassov, 1986; Atanassov, 1989; Atanassov, 1999) are given as follows. For every B, C ∈ A-IFS (M),

(1) B ⊂ C if $\forall m \in M, ({\hat{μ}}_{B} (m) \leq {\hat{μ}}_{C} (m)$ and ${\hat{ν}}_{B} (m) \geq {\hat{ν}}_{C} (m))$ .

(2) B = C if B ⊂ C and C ⊂ B.

(3) $\bar{B} = {(m, {\hat{ν}}_{B} (m), {\hat{μ}}_{B} (m))}$ .

(4) $\hat{d} (B, C) =$

\sqrt{\frac{1}{2 n} \sum_{k = 1}^{n} {({\hat{μ}}_{B} (m_{k}) - {\hat{μ}}_{C} (m_{k}))}^{2} + {({\hat{ν}}_{B} (m_{k}) - {\hat{ν}}_{C} (m_{k}))}^{2} + {({\hat{π}}_{B} (m_{k}) - {\hat{π}}_{C} (m_{k}))}^{2}}, (4)

where $\hat{d} (B, C)$ is the normalized Euclidian distance between A and B.

Definition 2.4. Let $W = {(z, ({\hat{Y}}_{W} (z), {\hat{W}}_{\hat{Y} W} (z)), ({\hat{S}}_{W} (z), {\hat{W}}_{\hat{S} W} (z))) : z \in M}$ and $H = {(z, ({\hat{Y}}_{H} (z), {\hat{W}}_{\hat{Y} H} (z)), ({\hat{S}}_{H} (z), {\hat{W}}_{\hat{S} H} (z))) : z \in M}$ be the two CIFSs defined upon H. Then, we can say that

(1) $W^{c} = {(z, ({\hat{S}}_{W} (z), {\hat{W}}_{\hat{S} W} (z)), ({\hat{Y}}_{W} (z), {\hat{W}}_{\hat{Y} W} (z))) : z \in M}$ .

(2) H ⊆ W if ${\hat{Y}}_{H} (z) \leq {\hat{Y}}_{W} (z), {\hat{S}}_{H} (z) \geq {\hat{S}}_{W} (z)$ and ${\hat{W}}_{\hat{Y} H} (z) \leq {\hat{W}}_{\hat{Y} W} (z), {\hat{W}}_{\hat{S} H} (z) \geq {\hat{W}}_{\hat{S} W} (z)$ .

(3) H = W if H ⊆ W and W ⊆ H.

(4) $H \cup W = \{\begin{matrix} (z, (\max {{\hat{Y}}_{H} (z), {\hat{Y}}_{W} (z)}, \max {{\hat{W}}_{\hat{Y} H} (z), {\hat{W}}_{\hat{Y} W} (z)}), \\ (\min {{\hat{S}}_{H} (z), {\hat{S}}_{W} (z)}, \min {{\hat{W}}_{\hat{S} H} (z), {\hat{W}}_{\hat{S} W} (z)})) : z \in M \end{matrix}\}$ .

(5) d(H, W) =

\sqrt{\frac{1}{2 n} \sum_{k = 1}^{n} ({({\hat{Y}}_{H} (z) - {\hat{Y}}_{W} (z))}^{2} + {({\hat{W}}_{\hat{Y} H} (z) - {\hat{W}}_{\hat{Y} W} (z))}^{2} + {({\hat{S}}_{H} (z) - {\hat{S}}_{W} (z))}^{2} + {({\hat{W}}_{\hat{S} H} (z) - {\hat{W}}_{\hat{S} W} (z))}^{2})} . (5)

2.2 Construction of the complex intuitionistic fuzzy decision matrix

A decision matrix may be used to represent an MCDM problem in which each element represents the evaluation or value of the kth alternative ${\hat{A}}_{k}$ in relation to the nth criteria ${\hat{Z}}_{l}$ . We extend the canonical matrix format to a CIF decision matrix P in this study. In other words, decision makers are expected to assign the non-membership and membership degree based on their perspectives and encapsulate the extent to which the alternative ${\hat{A}}_{k}$ fulfils the criterion ${\hat{Z}}_{l}$ . They can offer evaluation data for each criterion’s options. Let M be the MCDM issue setting’s discussion universe, including the decision criteria. The set of all criteria is shown as C = {c₁, c₂, c₃, …, c_n}. A CIFS G_k of the kth alternative on M is given as G_k = {⟨m_l, M_kl⟩|m_l ∈ M}, where $M_{k l} = ({\hat{μ}}_{k l}, {\hat{ν}}_{k l})$ , where ${\hat{ν}}_{k l}$ and ${\hat{μ}}_{k l}$ are complex-valued non-membership and membership functions, respectively, and ${\hat{μ}}_{k l} = {\hat{Y}}_{k} (l) {\hat{e}}^{2 π ι {\hat{W}}_{\hat{Y} k} (l)}$ , and ${\hat{ν}}_{k l} = {\hat{S}}_{k} (l) {\hat{e}}^{2 π ι {\hat{W}}_{\hat{S} k} (l)}$ such that ${\hat{Y}}_{k} (l) \geq 0$ , and ${\hat{S}}_{k} (l) \leq 1; 0 \leq {\hat{Y}}_{k} (l) + {\hat{S}}_{k} (l) \leq 1$ and $0 \leq {\hat{W}}_{\hat{Y} k} (l), {\hat{W}}_{\hat{S} k} (l) \leq 2 \hat{π}; 0 \leq {\hat{W}}_{\hat{Y} k} (l) + {\hat{W}}_{\hat{S} k} (l) \leq 2 \hat{π} \forall l \in M$ , and also denotes the degree of membership and non-membership of the kth alternative ${\hat{A}}_{k}$ in relation to the nth criteria ${\hat{Z}}_{l}$ such that ${\hat{π}}_{k l} = 1 - {\hat{μ}}_{k l} - {\hat{ν}}_{k l}$ and k = 1, 2, 3, …m and l = 1, 2, 3, …, n. The CIF decision matrix, $\bar{Z}$ , is described as follows:

\bar{Z} = [\begin{matrix} ({\hat{μ}}_{11}, {\hat{ν}}_{11}) & . & . & . & ({\hat{μ}}_{1 n}, {\hat{ν}}_{1 n}) \\ . & . & . \\ . & . & . \\ . & . & . \\ ({\hat{μ}}_{m 1}, {\hat{ν}}_{m 1}) & . & . & . & ({\hat{μ}}_{m n}, {\hat{ν}}_{m n}) \end{matrix}] . (6)

The decision makers assign a set of grades of importance, $\hat{W}$ , because it is impossible to assume that all factors are equally important. An IFS $\hat{W}$ in M is defined as follows:

\hat{W} = \{⟨ m_{l}, {\hat{w}}_{l} ⟩ | m_{l} \in M\} (7)

such that $0 \leq {\hat{w}}_{l} \leq 1$ and ${\sum^{̂}}_{l = 1}^{n} {\hat{w}}_{l} = 1$ , and ${\hat{w}}_{l}$ is the grade of reliability that is given to each criteria, which we can also be said as the weight of each criteria. In order to build the CIF decision matrix, the decision maker must pay four times to acquire the assessed data: twice for the degrees of membership and twice for the non-membership data. In terms of mathematics, the interval-valued fuzzy set (IVFS) theory and the IFS theory are interchangeable (Deschrijver and Kerre, 2003; Dubois et al., 2005; Montero et al., 2007). Due to the restriction of the total of membership and non-membership degrees, the decision maker’s assessment using IVFS data is simpler than that with CIF data. The collection of all closed subintervals of $[0,1]$ is represented by interval $([0,1])$ . A complex interval value intuitionistic fuzzy set (CIVFS) G_m of the kth alternative on M is given as G_k = {⟨m_l, M_kl⟩|m_l ∈ M}, where M_kl: M → Int $([0,1])$ such that $m_{l} \to M_{k l} = [M_{k l}^{-}, M_{k l}^{+}]$ . The probable level at which the alternative G_k meets the requirement m_l is indicated by M_kl. $M_{k l}^{+}$ and $M_{k l}^{-}$ are the upper and the lower bounds, sequentially, of the aforementioned interval M_kl.

Starting at the beginning of the closed interval $[M_{k l}^{-}, M_{k l}^{+}]$ , the decision maker considers each option. Suppose $M_{k l}^{-} = {\hat{μ}}_{k l}$ , and $M_{k l}^{+} = 1 - {\hat{ν}}_{k l}$ such that $[M_{k l}^{-}, M_{k l}^{+}] = ({\hat{μ}}_{k l}, 1 - {\hat{ν}}_{k l})$ . A complex interval can be mapped into the CIFS, i.e., $({\hat{μ}}_{k l}, 1 - {\hat{ν}}_{k l})$ . The idea that the CIFS and CIVFS are mathematical equivalents may be used to convert CIVF data into CIFS data. Additionally, a decision maker must assess a lot of information using CIVFS data, making it difficult to compile all available options based on their expertise and experience. Decision makers may provide ranking and incomplete or missing data and convert it into CIF data. The approach determines the number of alternatives that are categorically better and worse than a given option. Given that not all options may be rated in accordance with a criteria, it permits partial ordinal data. We create two functions, ${\hat{A}}_{k l}$ and ${\hat{E}}_{k l}$ , for each G_m with regard to m_l in order to account for missing data or non-comparable results. Let ${\hat{A}}_{k l}$ represent the number of alternatives that are unquestionably worse than G_m, such as G₁, G₂, …, G_m−1, G_m+1, G_m+2, …, and G_m, while ${\hat{E}}_{k l}$ indicates the number of alternatives that are unquestionably superior than G_m, such as G₁, G₂, …, G_m−1, G_m+1, G_m+2, …, and G_m. The following are the levels of non-membership and membership, respectively:

{\hat{ν}}_{k l} = \frac{{\hat{E}}_{k l}}{m - 1}, (8)

{\hat{μ}}_{k l} = \frac{{\hat{A}}_{k l}}{m - 1} . (9)

3 ELECTREE methods based on complex intuitionistic fuzzy data

The CIF–ELECTREE technique (with the algorithm) and concordance and discordance sets are introduced in this section. For numerical examples, we will utilize the CIF–ELECTREE method algorithm. Binary outranking relations are used to simulate ELECTREE procedures; the connection is constructed by the decision maker and need not be transitive. Non-dominant alternative partial ordering is enabled by the connection. For each pair of alternatives x and $y (x, y = 1,2, \dots, m$ , and $x \neq y)$ , each criterion can be divided into two separate subsets. The concordance set A_xy of G_x and G_y includes all of the criteria for which G_x is preferable to G_y. We can also say that A_xy = {l|m_xl ≥ m_yl}, where L = {l|l = 1, 2, 3, …, n}. The discordance set, which is a complementary subset, is B_xy = {l|m_xl < m_xy}. The concepts of scoring function, accuracy function, and complex intuitionistic index are used in the proposed CIF-ELECTREE technique to categorize various concordance and discordance sets, and concordance and discordance sets are used to generate concordance and discordance matrices, respectively. Using the ideas of optimum and non-optimum points, decision makers may select the optimum option.

3.1 Discordance and concordance sets

The ideas of scoring function, accuracy function, and hesitant degree of the CIF value allow us to evaluate many alternatives to their CIF values. When two alternatives have the same score degree, the better option has a higher score degree or a higher accuracy degree. A greater accuracy degree denotes a lower hesitation degree, and a higher score degree denotes a bigger membership degree or a smaller non-membership degree. With the principles of the score function and accuracy function, we categorize various concordance sets as “concordance sets,” medium concordance sets,” and “weak concordance sets.” The discordance set, intermediate discordance set, and weak discordance set are further terms for the many sorts of discordance sets. The score function was developed by Chen and Tan (1994) to measure how well an option meets a decision maker’s needs. Suppose $M_{k l} = ({\hat{μ}}_{k l}, {\hat{ν}}_{k l})$ is an CIF value such that ${\hat{μ}}_{k l} = {\hat{Y}}_{k} (l) {\hat{e}}^{2 π ι {\hat{W}}_{\hat{Y} k} (l)}$ and ${\hat{ν}}_{k l} = {\hat{S}}_{k} (l) {\hat{e}}^{2 π ι {\hat{W}}_{\hat{S} k} (l)}$ such that ${\hat{Y}}_{k} (l) \geq 0$ , and ${\hat{S}}_{k} (l) \leq 1; 0 \leq {\hat{Y}}_{k} (l) + {\hat{S}}_{k} (l) \leq 1$ and $0 \leq {\hat{W}}_{\hat{Y} k} (l), {\hat{W}}_{\hat{S} k} (l) \leq 2 \hat{π}; 0 \leq {\hat{W}}_{\hat{Y} k} (l) + {\hat{W}}_{\hat{S} k} (l) \leq 2 \hat{π}$ . We can evaluate the score function $\overset{̌}{S}$ as $\overset{̌}{S} (M_{k l}) = {\hat{μ}}_{k l} - {\hat{ν}}_{k l}$ . Although a higher $\overset{̌}{S} (M_{k l})$ score correlates with a higher CIF value M_kl, we are unable to compare alternatives with equal scores. In order to assess the level of accuracy of ambiguous values, Hong and Choi (2000) introduced the accuracy function. The accuracy function $\overset{̌}{D}$ can be used to assess how accurate M_kl is. The degree function $\overset{̌}{D} (M_{k l})$ is evaluated as $\overset{̌}{D} (M_{k l}) = {\hat{μ}}_{k l} + {\hat{ν}}_{k l}$ . The correctness of the CIF value membership grade increases with an increase in the value of $\overset{̌}{D} (M_{k l})$ . We may infer from (2) and the accuracy function that a lower hesitation degree ${\hat{π}}_{k l}$ correlates with a greater accuracy degree $\overset{̌}{D} (M_{k l})$ . As said previously, the concordance set A_xy of G_x and G_y includes all of the criteria for which G_x is preferable to G_y. We calculate it with the principles of the score function and accuracy function and a hesitant degree for the classification of the concordance sets of CIF. It is possible to formulate the concordance set A_xy as follows:

A_{x y} = \{l | {\hat{μ}}_{x l} \geq {\hat{μ}}_{y l}, {\hat{ν}}_{x l} < {\hat{ν}}_{y l} and {\hat{π}}_{x l} < {\hat{π}}_{y l}\}, (10)

where L = {l|l = 1, 2, 3, …, n}, a higher degree of accuracy translates to a lower degree of hesitation, a higher score translates to a higher CIF value, and Eq. 10 is more concordant than Eq. 11 or Eq. 12.The midrange concordance set $A_{x y}^{◦}$ is defined as follows:

A_{x y}^{◦} = \{l | {\hat{μ}}_{x l} \geq {\hat{μ}}_{y l}, {\hat{ν}}_{x l} < {\hat{ν}}_{y l} and {\hat{π}}_{x l} \geq {\hat{π}}_{y l}\} . (11)

The hesitancy degree is the main distinction between Eq. 10 and Eq. 11; in the midrange concordance set, the hesitancy degree at the xth alternative with regard to the lth criterion is higher than at the yth alternative with respect to the lth criterion. Thus, Eq. 10 is more quadrant than Eq. 11.The least concordant set is given as follows:

A_{x y}^{◦ ◦} = \{l | {\hat{μ}}_{x l} \geq {\hat{μ}}_{y l}, {\hat{ν}}_{x l} \geq {\hat{ν}}_{y l}\} . (12)

Eq. 11 is more concordant than Eq. 12 because the degree of non-membership at the xth alternative with respect to the lth criteria in the weak concordance set Eq. 12 is greater than the degree of non-membership at the yth alternative with respect to the lth criteria.

The discordance set consists of all criteria where G_x is inferior to G_y. Using the aforementioned principles, the discordance set B_xy can be expressed as follows:

B_{x y} = \{l | {\hat{μ}}_{x l} < {\hat{μ}}_{y l}, {\hat{ν}}_{x l} \geq {\hat{ν}}_{y l} and {\hat{π}}_{x l} \geq {\hat{π}}_{y l}\} . (13)

The middle discordant set is defined as follows:

B_{x y}^{◦} = \{l | {\hat{μ}}_{x l} < {\hat{μ}}_{y l}, {\hat{ν}}_{x l} \geq {\hat{ν}}_{y l} and {\hat{π}}_{x l} < {\hat{π}}_{y l}\} . (14)

Eq. 13 is more discordant than Eq. 14. The least discordant set is given as follows:

B_{x y}^{◦ ◦} = \{l | {\hat{μ}}_{x l} < {\hat{μ}}_{y l}, {\hat{ν}}_{x l} < {\hat{ν}}_{y l}\} . (15)

Eq. 14 is more discordant than Eq. 15.

We use the idea of discordant and concordant sets to compute matrices of concordant and discordant and the CIF–ELECTREE technique to calculate the aggregate dominance matrix. We then select the optimal option.

3.2 The complex intuitionistic fuzzy ELECTREE method

The CIF–ELECTREE technique is a combination of the CIFS and ELECTREE methods using evaluation data. The concordant index is a way to figure out the worth of the concordance set of the CIF–ELECTREE method. The concordance index is equal to the sum of the weights for the criteria and relationships in the concordance sets. So, for this paper, the concordance index ${\hat{A}}_{x y}$ between G_x and G_y is as follows:

{\hat{g}}_{x y} = {\hat{w}}_{A} \times \sum_{l \in A_{x y}} {\hat{w}}_{l} + {\hat{w}}_{A^{◦}} \times \sum_{l \in A_{x y}^{◦}} {\hat{w}}_{l} + {\hat{w}}_{A^{◦ ◦}} \times \sum_{l \in A_{x y}^{◦ ◦}} {\hat{w}}_{l}, (16)

where ${\hat{w}}_{A^{◦ ◦}}$ , ${\hat{w}}_{A^{◦}}$ , and ${\hat{w}}_{A}$ are the weights of the least, middle, and the concordance sets, respectively. The ${\hat{w}}_{l}$ is the weight of the defined criteria already defined in (7). Based on how much weight is given to each successive decision criterion, the concordance index shows how much more important one alternative choice is than another. Here is how we characterize the $\hat{G}$ concordance matrix:

\hat{G} = [\begin{matrix} _ & {\hat{g}}_{12} & \dots & \dots & \dots & {\hat{g}}_{1 m} \\ {\hat{g}}_{21} & _ & {\hat{g}}_{23} & \dots & \dots & {\hat{g}}_{2 m} \\ \dots & \dots & _ & \dots & \dots & \dots \\ \dots & \dots & \dots & _ & \dots & \dots \\ {\hat{g}}_{(m - 1) 1} & \dots & \dots & \dots & _ & {\hat{g}}_{(m - 1) 1} \\ {\hat{g}}_{m 1} & {\hat{g}}_{m 2} & \dots & \dots & {\hat{g}}_{m (m - 1)} & _ \end{matrix}], (17)

where the highest possible value of ${\hat{g}}_{x y}$ is represented by the symbol ${\hat{g}}^{*}$ , which stands for the positive ideal point, and a larger value of ${\hat{g}}_{x y}$ implies that G_x is preferred over G_y.

A certain G_x has lower ratings than an alternative G_y. Here, we provide a formal definition of the discordance index:

{\hat{h}}_{x y} = \frac{\max_{l \in B_{x y} {\hat{W}}_{B}^{* *} \times \hat{d} (M_{x l}, M_{y l})}}{\max_{l \in L} \hat{d} (M_{x l}, M_{y l})}, (18)

where $\hat{d} (M_{x l}, M_{y l})$ is defined in Eq. 5 and ${\hat{W}}_{B}^{* *}$ is equal to ${\hat{W}}_{B}$ , ${\hat{W}}_{B}^{'}$ , or ${\hat{W}}_{B}^{''}$ depending on different classification of discordance sets. These sets have the settings for light discordance, medium discordance, and heavy discordance, in that order.

Here is how we characterize $\hat{H}$ , the matrix of discordance:

\hat{H} = [\begin{matrix} _ & {\hat{h}}_{12} & \dots & \dots & \dots & {\hat{h}}_{1 m} \\ {\hat{h}}_{21} & _ & {\hat{h}}_{23} & \dots & \dots & {\hat{h}}_{2 m} \\ \dots & \dots & _ & \dots & \dots & \dots \\ \dots & \dots & \dots & _ & \dots & \dots \\ {\hat{h}}_{(m - 1) 1} & \dots & \dots & \dots & _ & {\hat{h}}_{(m - 1) 1} \\ {\hat{h}}_{m 1} & {\hat{h}}_{m 2} & \dots & \dots & {\hat{h}}_{m (m - 1)} & _ \end{matrix}], (19)

where ${\hat{h}}^{*}$ , the negative ideal point, is the highest value of ${\hat{h}}_{x y}$ , and a bigger ${\hat{h}}_{x y}$ value means that G_x is less desirable than G_y.

The way to figure out the concordance dominance matrix is based on the idea that the best choice is the one that is closest to the positive ideal solution. This is how the concordance dominance matrix $\hat{K}$ is defined:

\hat{K} = [\begin{matrix} _ & {\hat{k}}_{12} & \dots & \dots & \dots & {\hat{k}}_{1 m} \\ {\hat{k}}_{21} & _ & {\hat{k}}_{23} & \dots & \dots & {\hat{k}}_{2 m} \\ \dots & \dots & _ & \dots & \dots & \dots \\ \dots & \dots & \dots & _ & \dots & \dots \\ {\hat{k}}_{(m - 1) 1} & \dots & \dots & \dots & _ & {\hat{k}}_{(m - 1) 1} \\ {\hat{k}}_{m 1} & {\hat{k}}_{m 2} & \dots & \dots & {\hat{k}}_{m (m - 1)} & _ \end{matrix}], (20)

where

{\hat{k}}_{x y} = {\hat{g}}^{*} - {\hat{g}}_{x y} . (21)

It means how far away each potential option is from the optimum answer. If ${\hat{k}}_{x y}$ is larger than zero, then G_x is less preferable than G_y. The discordance dominance matrix $\hat{L}$ is used to find the best option based on the idea that it should be the most different from the negative ideal solution. For anyone interested, this is how we characterize $\hat{L}$ in the discordance dominance matrix:

\hat{L} = [\begin{matrix} _ & {\hat{l}}_{12} & \dots & \dots & \dots & {\hat{l}}_{1 m} \\ {\hat{l}}_{21} & _ & {\hat{l}}_{23} & \dots & \dots & {\hat{l}}_{2 m} \\ \dots & \dots & _ & \dots & \dots & \dots \\ \dots & \dots & \dots & _ & \dots & \dots \\ {\hat{l}}_{(m - 1) 1} & \dots & \dots & \dots & _ & {\hat{l}}_{(m - 1) 1} \\ {\hat{l}}_{m 1} & {\hat{l}}_{m 2} & \dots & \dots & {\hat{l}}_{m (m - 1)} & _ \end{matrix}], (22)

where

{\hat{l}}_{x y} = {\hat{h}}^{*} - {\hat{h}}_{x y} . (23)

This describes how to distinguish each alternative from the negative optimum point. For G_x to be preferred over G_y, ${\hat{l}}_{x y}$ must increase.

The distance from both negative and positive optimal points can be used in the aggregate dominance matrix decision procedure to rank the many possibilities. The definition of the total dominance matrix $\hat{R}$ is as follows:

\hat{R} = [\begin{matrix} _ & {\hat{r}}_{12} & \dots & \dots & \dots & {\hat{r}}_{1 m} \\ {\hat{r}}_{21} & _ & {\hat{r}}_{23} & \dots & \dots & {\hat{r}}_{2 m} \\ \dots & \dots & _ & \dots & \dots & \dots \\ \dots & \dots & \dots & _ & \dots & \dots \\ {\hat{r}}_{(m - 1) 1} & \dots & \dots & \dots & _ & {\hat{r}}_{(m - 1) 1} \\ {\hat{r}}_{m 1} & {\hat{r}}_{m 2} & \dots & \dots & {\hat{r}}_{m (m - 1)} & _ \end{matrix}], (24)

where

{\hat{r}}_{x y} = \frac{{\hat{l}}_{x y}}{{\hat{l}}_{x y} + {\hat{k}}_{x y}} (25)

such that ${\hat{l}}_{x y}$ and ${\hat{k}}_{x y}$ are as defined in Eq. 23 and Eq. 21, respectively, and the degree to which a solution is near is optimal, denoted by the symbol ${\hat{r}}_{x y}$ . When comparing two options, if ${\hat{r}}_{x y}$ for option G_x is larger than that for option G_y, it means G_x is more optimal since it is closer to the positive ideal point and further from the negative ideal point. Choosing the most appropriate alternative procedure is defined as follows:

{\hat{T}}_{x} = \frac{1}{m - 1} \sum_{x = 1, x \neq y}^{m} {\hat{r}}_{x y}, y = 1,2,3, \dots, m, (26)

and ${\hat{T}}_{x}$ is the final evaluation. ${\hat{T}}_{x}$ allows for the ranking of all alternatives under consideration. The optimal solution ${\hat{A}}^{* *}$ may be constructed and defined as follows: ${\hat{A}}^{* *}$ is the distance from the positive ideal point and the maximum distance from the negative ideal point, which is defined as follows:

{\hat{A}}^{* *} = \max [{\hat{T}}_{x}], (27)

where the best alternative is ${\hat{A}}^{* *}$ .

The CIF–ELECTREE method is described here as a new MCDM method for making decisions. It combines the CIFS and ELECTREE techniques with assessment data. The algorithm for the suggested method will be built in three separate steps: evaluation, aggregation, and selection. In the assessment phase, decision makers use the CIFS to choose relevant criteria, recognize alternatives (with varying weights assigned to various criteria), and establish a decision matrix based on the assessed data. During the aggregation phase, we use the suggested method to build concordance and discordance dominance matrices by comparing each option to the others to confirm the dominance connection. After that, we calculate a matrix that represents the overall dominant structure. The CIF–ELECTREE technique is used during the selection phase to determine which option is the best and to rank the options in the order of preference.

Algorithm: The CIF–ELECTREE method’s algorithm and decision-making process may be summed up in the following eight phases:

Step (1). We can use evaluation data to build the choice matrix and include input from decision makers in the form of CIF values or comparisons between options. There are three substeps inside this larger phase.

(1) We can select the problem-specific criteria and non-inferior alternatives; various MCDM issues need different criteria. Most criteria may be classified as either subjective or objective. The decision makers find and take into account potential options.

(2) We can obtain a scorecard with relative weights for various factors to consider. With the help of Eq. 7, ${\sum^{̂}}_{l = 1}^{n} {\hat{w}}_{l} = 1$ , we can figure out how important each criterion is.

(3) Decision makers gather cardinal information and use it to build an CIF decision matrix $\bar{Z}$ , Eq. 6. If the people making decisions give us some baseline information, we can use transformations Eq. 8 and Eq. 9 to come to some good conclusions.

Step (2). We can use the scoring function, the accuracy function, and the degree of hesitation of the CIF value to tell the difference between the different concordance and discordance sets. Using Eqs 10–15, we can obtain the chi-squared values A_xy, $A_{x y}^{◦}$ , $A_{x y}^{◦ ◦}$ , B_xy, $B_{x y}^{◦}$ , and $B_{x y}^{◦ ◦}$ for paired comparisons of alternatives to be chosen.

Step (3). We can determine the matrix $\hat{G}$ of concordance by combining the definitions of the various types of concordance sets and their weights given in Eq. 16 and Eq. 17.

Step (4). Here is how to figure out matrix $\hat{H}$ of discordance: the matrix of discordance index is the result of the different types of discordance sets and their weights, as shown in Eq. 18 and Eq. 19.

Step (5). We can assemble the dominance matrix $\hat{K}$ of concordance, whereby its index is calculated as the difference between the concordance matrix’s maximum index and its own index, as described by Eqs 20, 21.

Step (6). We can construct the dominant matrix $\hat{L}$ discordance, whose index is the difference between the discordance matrix’s maximum index and its own index, as stated by Eqs 22, 23.

Step (7). The indices of the dominant matrices of concordance and discordance, defined in Eq. 24 and Eq. 25, respectively, are used to form the aggregate dominant matrix $\hat{R}$ .

Step (8). We can pick the optimal solution: the sum of the evaluation’s final values using Eq. 26 and Eq. 27. All possible options are ranked, and the one with the highest score is deemed the best.

4 Case study: the environmental impact of three industries

Introduction: This case study aims to compare the environmental impact of three industries: oil and gas, coal mining, and paper manufacturing. These industries have been selected as they are known to have a significant impact on the environment, and the study will focus on four common criteria: air pollution, water pollution, land degradation, and waste generation.

Oil and gas industry: The oil and gas industry is known to have a significant impact on air pollution, primarily due to the emissions from drilling and transportation. The burning of fossil fuels also contributes to the release of greenhouse gases, which contribute to climate change. In addition, oil spills and leaks can cause water pollution and damage to marine life. The industry also requires large amounts of water for extraction, which can put a strain on local water resources. However, the industry also creates jobs, income, and energy resources that are important for the human economy.

Coal mining industry: The coal mining industry is known to cause land degradation, as the process of extracting coal requires the removal of large areas of land, including forests and wildlife habitats. This can also lead to soil erosion and landslides. The burning of coal also contributes to air pollution and the release of greenhouse gases. The industry also generates large amounts of waste, including coal ash and slurry, which can contaminate water resources.

Paper manufacturing industry: The paper manufacturing industry generates large amounts of waste, including wood waste and chemical by-products. The industry also requires large amounts of water for production, which can put a strain on local water resources. The production of paper also contributes to air pollution, primarily due to the emissions from the burning of fossil fuels used in the production process. The industry also causes deforestation which is one of the major causes of land degradation and loss of biodiversity.

Conclusion: All three industries have a significant impact on the environment, with the oil and gas industry primarily affecting air pollution, the coal mining industry primarily affecting land degradation, and the paper manufacturing industry primarily affecting waste generation. It is important to note that the study is based on the common criteria only, and there are many other factors that should be considered when evaluating the environmental impact of an industry. It is important to find a balance between economic development and environmental protection and to implement sustainable practices in these industries to minimize their impact on the environment.

4.1 Numerical example

Phase (1):

(1) Taking expert advice into account, we consider the four criteria listed as follows: c₁(air pollution), c₂(water pollution), c₃(land degradation), and c₄(waste generation) in the problem. As an alternative, we consider the following industries: I₁, I₂, and I₃.

(2) In the end, it is up to the specialists making the decisions to give each factor a subjective value $(\hat{W})$ as $\hat{W} = [{\hat{w}}_{1}, {\hat{w}}_{2}, {\hat{w}}_{3}, {\hat{w}}_{4}] = [0.3, 0.35, 0.25, 0.1]$ .

(3) The specialists making the decisions to give each factor a relative value $({\hat{W}}^{◦})$ as; ${\hat{W}}^{◦} = [{\hat{w}}_{A}, {\hat{w}}_{A^{◦}}, {\hat{w}}_{A^{◦ ◦}}, {\hat{w}}_{B}, {\hat{w}}_{B^{◦}}, {\hat{w}}_{B^{◦ ◦}}] = [1, \frac{2}{3}, \frac{1}{3}, 1, \frac{2}{3}, \frac{1}{3}]$ .

Given the CIVF decision-making matrix $\bar{Z}$ , the CIF matrix decision with cardinal information is changed.

\bar{Z} = [\begin{matrix} c_{1} & c_{2} \\ I_{1} & [0.12 e^{2 π ι (0.3)}, 0.29 e^{2 π ι (0.4)}] & [0.14 e^{2 π ι (0.2)}, 0.81 e^{2 π ι (0.4)}] \\ I_{2} & [0.33 e^{2 π ι (0.5)}, 0.42 e^{2 π ι (0.9)}] & [0.33 e^{2 π ι (0.3)}, 0.52 e^{2 π ι (0.6)}] \\ I_{3} & [0.12 e^{2 π ι (0.7)}, 0.84 e^{2 π ι (0.8)}] & [0.62 e^{2 π ι (0.1)}, 0.33 e^{2 π ι (0.3)}] \\ c_{3} & c_{4} \\ I_{1} & [0.42 e^{2 π ι (0.2)}, 0.54 e^{2 π ι (0.5)}] & [0.13 e^{2 π ι (0.1)}, 0.31 e^{2 π ι (0.3)}] \\ I_{2} & [0.32 e^{2 π ι (0.1)}, 0.64 e^{2 π ι (0.7)}] & [0.42 e^{2 π ι (0.3)}, 0.53 e^{2 π ι (0.6)}] \\ I_{3} & [0.81 e^{2 π ι (0.5)}, 0.11 e^{2 π ι (0.7)}] & [0.51 e^{2 π ι (0.7)}, 0.39 e^{2 π ι (0.9)}] \end{matrix}],

[\begin{matrix} c_{1} & c_{2} \\ I_{1} & [0.12 e^{2 π ι (0.3)}, 0.71 e^{2 π ι (0.6)}, 0.17 e^{2 π ι (0.1)}] & [0.14 e^{2 π ι (0.2)}, 0.19 e^{2 π ι (0.6)}, 0.67 e^{2 π ι (0.2)}] \\ I_{2} & [0.33 e^{2 π ι (0.5)}, 0.58 e^{2 π ι (0.1)}, 0.09 e^{2 π ι (0.4)}] & [0.33 e^{2 π ι (0.3)}, 0.48 e^{2 π ι (0.4)}, 0.19 e^{2 π ι (0.3)}] \\ I_{3} & [0.12 e^{2 π ι (0.7)}, 0.16 e^{2 π ι (0.2)}, 0.72 e^{2 π ι (0.1)}] & [0.62 e^{2 π ι (0.1)}, 0.27 e^{2 π ι (0.7)}, 0.11 e^{2 π ι (0.2)}] \\ c_{3} & c_{4} \\ I_{1} & [0.42 e^{2 π ι (0.2)}, 0.46 e^{2 π ι (0.5)}, 0.12 e^{2 π ι (0.3)}] & [0.13 e^{2 π ι (0.1)}, 0.69 e^{2 π ι (0.7)}, 0.18 e^{2 π ι (0.2)}] \\ I_{2} & [0.32 e^{2 π ι (0.1)}, 0.36 e^{2 π ι (0.3)}, 0.32 e^{2 π ι (0.6)}] & [0.42 e^{2 π ι (0.3)}, 0.37 e^{2 π ι (0.4)}, 0.21 e^{2 π ι (0.3)}] \\ I_{3} & [0.81 e^{2 π ι (0.5)}, 0.09 e^{2 π ι (0.3)}, 0.1 e^{2 π ι (0.2)}] & [0.51 e^{2 π ι (0.7)}, 0.26 e^{2 π ι (0.1)}, 0.23 e^{2 π ι (0.2)}] \end{matrix}] .

Phase (2). Using the outcomes of Steps 1–3, we determine which sets exhibit concordance and which exhibit discordance.

The concordance set compiled using Eq. 10 is given as follows:

A_{x y} = [\begin{matrix} \{-, -\} & \{-, -\} & \{-, -\} \\ \{1, -\} & \{-, -\} & \{-, -\} \\ \{3,3\} & \{-, 1\} & \{-, -\} \end{matrix}],

where in matrix A_xy, the first element of A₃₁ = (3, 3) present in the third (horizontal) row and first (vertical) column represents the simple membership concordant, and the second element represents the complex membership concordant. A₁₁ = (−, −) is empty.

The midrange concordance set compiled using Eq. 11 is given as follows:

A_{x y}^{◦} = [\begin{matrix} \{-, -\} & \{-, -\} & \{-, 2\} \\ \{4, (1,2,4)\} & \{-, -\} & \{4,2\} \\ \{(1,4), (1,4)\} & \{-, -\} & \{-, -\} \end{matrix}] .

The weak concordance set compiled using Eq. 12 is given as follows:

A_{x y}^{◦ ◦} = [\begin{matrix} \{-, -\} & \{3,3\} & \{1, -\} \\ \{2, -\} & \{-, -\} & \{-, -\} \\ \{2, -\} & \{1, (1,3)\} & \{-, -\} \end{matrix}] .

The discordance set compiled using Eq. 13 is given as follows:

B_{x y} = [\begin{matrix} \{-, -\} & \{1, -\} & \{3, (3,4)\} \\ \{-, -\} & \{-, -\} & \{-, (3,4)\} \\ \{-, 2\} & \{(2,3), -\} & \{-, -\} \end{matrix}] .

The midrange discordance set compiled using Eq. 14 is given as follows:

B_{x y}^{◦} = [\begin{matrix} \{-, -\} & \{4, (1,2,4)\} & \{4, -\} \\ \{-, -\} & \{-, -\} & \{-, -\} \\ \{-, -\} & \{4,2\} & \{-, -\} \end{matrix}] .

The least discordance set compiled using Eq. 15 is given as follows:

B_{x y}^{◦ ◦} = [\begin{matrix} \{-, -\} & \{2, -\} & \{2,1\} \\ \{3,3\} & \{-, -\} & \{1,1\} \\ \{-, -\} & \{-, -\} & \{-, -\} \end{matrix}] .

Phase (3). The concordance matrix $\hat{G}$ compiled using Step (3) is given as follows:

\hat{G} = [\begin{matrix} - & 0.083 e^{2 π ι (0.083)} & 0.3 e^{2 π ι (0.23)} \\ 0.476 e^{2 π ι (0.5)} & - & 0.067 e^{2 π ι (0.234)} \\ 0.633 e^{2 π ι (0.516)} & 0.1 e^{2 π ι (0.85)} & - \end{matrix}] .

For example, ${\hat{g}}_{31} = {\hat{w}}_{A} \times {\hat{w}}_{3} + {\hat{w}}_{A^{◦}} \times ({\hat{w}}_{1} + {\hat{w}}_{4}) + {\hat{w}}_{A^{◦ ◦}} \times {\hat{w}}_{2}$ $= [1 \times 0.25 e^{2 π ι (0.25)}] + [\frac{2}{3} \times 0.4 e^{2 π ι (0.4)}] + [\frac{1}{3} \times 0.35 e^{2 π ι (-)}] = 0.633 e^{2 π ι (0.516) .}$ .

Phase (4). The disconcordance matrix $\hat{H}$ compiled using Step (4) is given as follows:

\hat{H} = [\begin{matrix} - & 0.4874 e^{2 π ι (0.6667)} & 0.6916 e^{2 π ι (1.0)} \\ 0.1379 e^{2 π ι (0.2023)} & - & 0.333 e^{2 π ι (1.0)} \\ 0.0 e^{2 π ι (0.25)} & 0.7651 e^{2 π ι (0.4410)} & - \end{matrix}] .

For example, ${\hat{h}}_{13} = \frac{\max_{l \in B_{13} {\hat{W}}_{B}^{* *} \times \hat{d} (M_{1 l}, M_{3 l})}}{\max_{l \in L} \hat{d} (M_{1 l}, M_{3 l})} = \frac{0.3804 e^{2 π ι (0.6)}}{0.5500 e^{2 π ι (0.6)}} = 0.6916 e^{2 π ι (1.0)}$ , where $\hat{d} (M_{11}, M_{31}) = {[\frac{1}{2} {{(0.12 e^{2 π ι (0.3)} - 0.12 e^{2 π ι (0.7)})}^{2} + {(0.71 e^{2 π ι (0.6)} - 0.16 e^{2 π ι (0.2)})}^{2} + {(0.17 e^{2 π ι (0.1)} - 0.72 e^{2 π ι (0.1)})}^{2}}]}^{\frac{1}{2}} = 0.55 e^{2 π ι (0.4)}$ , $\hat{d} (M_{12}, M_{32}) = {[\frac{1}{2} {{(0.14 e^{2 π ι (0.2)} - 0.62 e^{2 π ι (0.1)})}^{2} + {(0.19 e^{2 π ι (0.6)} - 0.27 e^{2 π ι (0.7)})}^{2} + {(0.67 e^{2 π ι (0.2)} - 0.11 e^{2 π ι (0.2)})}^{2}}]}^{\frac{1}{2}} = 0.525 e^{2 π ι (0.1)}$ , $\hat{d} (M_{13}, M_{33}) = {[\frac{1}{2} {{(0.42 e^{2 π ι (0.2)} - 0.81 e^{2 π ι (0.5)})}^{2} + {(0.46 e^{2 π ι (0.5)} - 0.09 e^{2 π ι (0.3)})}^{2} + {(0.12 e^{2 π ι (0.3)} - 0.1 e^{2 π ι (0.2)})}^{2}}]}^{\frac{1}{2}} = 0.380 e^{2 π ι (0.264)}$ , and $\hat{d} (M_{14}, M_{34}) = {[\frac{1}{2} {{(0.13 e^{2 π ι (0.1)} - 0.51 e^{2 π ι (0.7)})}^{2} + {(0.69 e^{2 π ι (0.7)} - 0.26 e^{2 π ι (0.1)})}^{2} + {(0.18 e^{2 π ι (0.2)} - 0.23 e^{2 π ι (0.2)})}^{2}}]}^{\frac{1}{2}} = 0.407 e^{2 π ι (0.6)}$ and ${\hat{W}}_{B} \times \hat{d} (M_{13}, M_{33}) = (1 \times 0.380) e^{2 π ι (1 \times 0.264)} = (0.380) e^{2 π ι (0.264)}$ , ${\hat{W}}_{B}^{'} \times \hat{d} (M_{14}, M_{34}) = (\frac{2}{3} \times 0.407) e^{2 π ι (1 \times 0.6)} = (0.271) e^{2 π ι (0.6)}$ , ${\hat{W}}_{B}^{''} \times \hat{d} (M_{12}, M_{32}) = (\frac{1}{3} \times 0.525) e^{2 π ι (1 \times 0.1)} = (0.175) e^{2 π ι (0.1)}$ , and ${\hat{W}}_{B}^{''} \times \hat{d} (M_{11}, M_{31}) = (0.0 \times 0.55) e^{2 π ι (\frac{1}{3} \times 0.4)} = (0.0) e^{2 π ι (0.133)}$ .

Phase (5). The dominant concordance matrix $\hat{K}$ compiled using Step (5) is given as follows:

\hat{K} = [\begin{matrix} - & 0.55 e^{2 π ι (0.767)} & 0.333 e^{2 π ι (0.62)} \\ 0.157 e^{2 π ι (0.35)} & - & 0.566 e^{2 π ι (0.616)} \\ 0.0 e^{2 π ι (0.334)} & 0.533 e^{2 π ι (0.0)} & - \end{matrix}] .

Phase (6). The dominant discordance matrix $\hat{L}$ compiled using Step (6) is given as follows:

\hat{L} = [\begin{matrix} - & 0.2777 e^{2 π ι (0.0)} & 0.0735 e^{2 π ι (- 0.333)} \\ 0.6272 e^{2 π ι (0.464)} & - & 0.4321 e^{2 π ι (- 0.333)} \\ 0.7651 e^{2 π ι (0.416)} & 0.0 e^{2 π ι (0.225)} & - \end{matrix}] .

Phase (7). The aggregate dominant matrix $\hat{R}$ compiled using Step (7) is given as follows:

\hat{R} = [\begin{matrix} - & 0.336 e^{2 π ι (0.0)} & 0.181 e^{2 π ι (- 1.163)} \\ 0.8 e^{2 π ι (0.570)} & - & 0.433 e^{2 π ι (- 1.179)} \\ 1.0 e^{2 π ι (0.555)} & 0.0 e^{2 π ι (1.0)} & - \end{matrix}] .

Phase (8). The best alternative using Step (8) is chosen as follows:

\begin{matrix} {\hat{T}}_{1} = 0.2582 e^{2 π ι (- 0.5813)} \\ {\hat{T}}_{2} = 0.6164 e^{2 π ι (- 0.3044)} \\ {\hat{T}}_{3} = 0.5 e^{2 π ι (0.7775)} \end{matrix} .

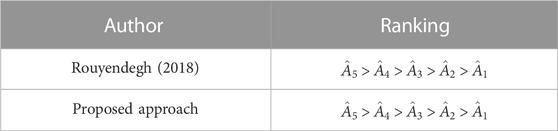
The optimized order of alternatives is given as ${\hat{A}}_{2}^{* *} > {\hat{A}}_{3}^{* *} > {\hat{A}}_{1}^{* *}$ .

5 Comparison analysis

So far, we have compared the suggested technique to the intuitionistic ELECTREE method (Benayoun et al., 1966). We look at the five options ${{\hat{A}}_{1}, {\hat{A}}_{2}, {\hat{A}}_{3}, {\hat{A}}_{4}, {\hat{A}}_{5}}$ and decide which one is best by giving each one a weight $\hat{w_{i}} = [0.449, 0.293, 0.177, 0.081]$ based on four standard criteria ${{\hat{c}}_{1}, {\hat{c}}_{2}, {\hat{c}}_{3}, {\hat{c}}_{4}}$ .

The relative weights of the criteria are given as ${\hat{W}}^{◦} = [{\hat{w}}_{A}, {\hat{w}}_{A^{◦}}, {\hat{w}}_{A^{◦ ◦}}, {\hat{w}}_{B}, {\hat{w}}_{B^{◦}}, {\hat{w}}_{B^{◦ ◦}}] = [1, \frac{2}{3}, \frac{1}{3}, 1, \frac{2}{3}, \frac{1}{3}]$ .

The intuitionistic fuzzy decision matrix $\hat{M}$ is given as follows:

\hat{M} = [\begin{matrix} {\hat{c}}_{1} & {\hat{c}}_{1} & {\hat{c}}_{1} & {\hat{c}}_{1} \\ (0.805, 0.084, 0.111) & (0.713, 0.176, 0.111) & (0.759, 0.100, 0.141) & (0.805, 0.084, 0.111) \\ (0.699, 0.194, 0.107) & (0.727, 0.162, 0.111) & (0.699, 0.194, 0.107) & (0.727, 1.162, 0.111) \\ (0.784, 0.129, 0.087) & (0.784, 0.129, 0.087) & (0.794, 0.094, 0.112) & (0.851, 0.05, 0.099) \\ (0.762, 0.085, 0.153) & (0.698, 0.194, 0.108) & (1.000, 0.000, 0.000) & (1.000, 0.000, 0.000) \\ (1.000, 0.000, 0.000) & (0.804, 0.085, 0.111) & (0.828, 0.065, 0.107) & (1.000, 0.000, 0.000) \end{matrix}] .

The concordance set compiled using Eq. 10 is given as follows:

A_{x y} = [\begin{matrix} - & - & - & [1] & - \\ - & - & - & [1] & - \\ [2,3,4] & [1,2,4] & - & [2] & - \\ [3,4] & [3,4] & [3,4] & - & [3] \\ [1,3,4] & [1,4] & [1,3,4] & [1] & - \end{matrix}] .

The midrange concordance set compiled using Eq. 11 is given as follows:

A_{x y}^{◦} = [\begin{matrix} - & [1,3,4] & [1] & [2] & - \\ [2] & - & [1] & [2] & - \\ - & [3] & - & - & - \\ - & [1] & - & - & - \\ [2] & [2,3] & [2] & [2] & - \end{matrix}] .

The weak concordance set compiled using Eq. 12 is given as follows:

A_{x y}^{◦ ◦} = [\begin{matrix} - & - & - & - & - \\ - & - & - & - & - \\ - & - & - & [1] & - \\ - & - & - & - & [4] \\ - & - & - & [4] & - \end{matrix}] .

The discordance set compiled using Eq. 13 is given as follows:

B_{x y} = [\begin{matrix} - & [2] & [2,3,4] & [3,4] & [1,2,3,4] \\ [4] & - & [1,2,4] & [3,4] & [1,2,3,4] \\ - & - & - & [3,4] & [1,3,4] \\ [1] & - & [2] & - & [1] \\ - & - & - & [3] & - \end{matrix}] .

The midrange discordance set compiled using Eq. 14 is given as follows:

B_{x y}^{◦} = [\begin{matrix} - & - & - & - & - \\ [1,3] & - & [3] & [1] & - \\ [1] & - & - & - & [2] \\ [2] & [2] & - & - & [2] \\ - & - & - & - & - \end{matrix}] .

The least discordance set compiled using Eq. 15 is given as follows:

B_{x y}^{◦ ◦} = [\begin{matrix} - & - & - & - & - \\ - & - & [1,2,3,4] & - & - \\ - & - & - & - & - \\ - & - & [1] & - & - \\ - & - & - & - & - \end{matrix}] .

The concordance matrix $\hat{G}$ compiled using Step (3) is given as follows:

\hat{G} = [\begin{matrix} - & 0.471 & 0.299 & 0.644 & 0.0 \\ 0.195 & - & 0.299 & 0.644 & 0.0 \\ 0.551 & 0.941 & - & 0.443 & 0.0 \\ 0.258 & 0.557 & 0.258 & - & 0.204 \\ 0.902 & 0.843 & 0.902 & 0.671 & - \end{matrix}] .

The disconcordance matrix $\hat{H}$ compiled using Step (4) is given as follows:

\hat{H} = [\begin{matrix} - & 0.132 & 1.0 & 1.0 & 1.0 \\ 0.722 & - & 0.55 & 1.0 & 1.0 \\ 0.414 & 0.0 & - & 1.0 & 1.0 \\ 0.205 & 0.078 & 0.436 & - & 1.0 \\ 0.0 & 0.0 & 0.0 & 0.718 & - \end{matrix}] .

The dominant concordance matrix $\hat{K}$ compiled using Step (5) is given as follows:

\hat{K} = [\begin{matrix} - & 0.470 & 0.642 & 0.297 & 0.0 \\ 0.746 & - & 0.642 & 0.297 & 0.0 \\ 0.390 & 0.0 & - & 0.498 & 0.0 \\ 0.683 & 0.384 & 0.683 & - & 0.737 \\ 0.039 & 0.098 & 0.039 & 0.270 & - \end{matrix}] .

The dominant discordance matrix $\hat{L}$ compiled using Step (6) is given as follows:

\hat{L} = [\begin{matrix} - & 0.868 & 0.0 & 0.0 & 0.0 \\ 0.278 & - & 0.450 & 0.0 & 0.0 \\ 0.586 & 1.0 & - & 0.0 & 0.0 \\ 0.795 & 0.922 & 0.564 & - & 0.0 \\ 1.0 & 1.0 & 1.0 & 0.282 & - \end{matrix}] .

The aggregate dominant matrix $\hat{R}$ compiled using Step (7) is given as follows:

\hat{R} = [\begin{matrix} - & 0.649 & 0.0 & 0.0 & 0.0 \\ 0.271 & - & 0.412 & 0.0 & 0.0 \\ 0.6 & 1.0 & - & 0.0 & 0.0 \\ 0.538 & 0.706 & 0.452 & - & 0.0 \\ 0.962 & 0.911 & 0.962 & 0.511 & - \end{matrix}] .

The best alternative using Step (8) is chosen as follows:

F X 1 .

The optimized order of alternatives is given as ${\hat{A}}_{5} > {\hat{A}}_{4} > {\hat{A}}_{3} > {\hat{A}}_{2} > {\hat{A}}_{1}$ .

Table 1 provides a comparison of the final assessments of the suggested approach to those of another technique.

TABLE 1

TABLE 1. Comparison table.

6 Conclusion

In this study, we proposed a CIF–ELECTREE and TODIM method to evaluate the ranking of different alternatives discussed under the available criteria. In the proposed ELECTREE method, for the selection criteria of the optimum alternative, we use the relative weights of the criteria given by the decision makers to construct the discordant and discordant matrices. The complex intuitionistic concept of “fuzzy distance” is used to determine the distance of each point from the positive and negative optimum points. While the CIFS, which is made up of membership and non-membership functions represented by a set of possible values, is a new way to express human uncertainty in everyday life, in this paper, we also propose a new method, called the CIF–TODIM method, for solving MCDM problems with uncertain fuzzy information. The best thing about the CIF–TODIM method is that it can deal with decision-making problems in which CIFEs show how alternatives rank on each criterion while also taking into account how the decision makers (DMs) act psychologically. The proposed complex intuitionistic fuzzy ELECTREE and TODIM methods are effective in dealing with the issues of decision making in ambiguous and complex situations. The proposed approaches are effective as they allow for multi-attribute decision making with multiple criteria and also allow us to visualize the membership grades in dual dimensions (2D). In this study, CIF–ELECTREE and TODIM methods are used along with four criteria to figure out how different sectors affect the environment. In conclusion, the CIF–ELECTREE and TODIM methods have different strengths and can be used in different decision-making situations depending on the issue and the preferences of the person making the decision. However, in the future, researchers may use complex IFSs in fields as different as weather forecasting, fuzzy time series forecasting, and data analysis, in addition to studying how they might be used in MADM.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahrens, H., and Kantelhardt, J. (2009). Accounting for farmers’ production responses to environmental restrictions within landscape planning. Land Use Policy 26 (4), 925–934. doi:10.1016/j.landusepol.2008.11.003

CrossRef Full Text | Google Scholar

Almeida, A. T. (2005). Multicriteria modelling of repair contract based on utility and ELECTRE I method with dependability and service quality criteria. Ann. Operations Res. 138, 113–126. doi:10.1007/s10479-005-2448-z

CrossRef Full Text | Google Scholar

Atanassov, K. (1986). Intuitionistic fuzzy sets. fuzzy sets Syst. 20 (1), 87–96. doi:10.1016/s0165-0114(86)80034-3

CrossRef Full Text | Google Scholar

Atanassov, K. T. (1999). Fuzzy sets and systems, intuitionistic fuzzy sets: Theory and applications. New York: Physica-Verlag, Heidel.

Google Scholar

Atanassov, K. T. (1989). More on intuitionistic fuzzy sets. Fuzzy sets Syst. 33 (1), 37–45. doi:10.1016/0165-0114(89)90215-7

CrossRef Full Text | Google Scholar

Beccali, M., Cellura, M., and Ardente, D. (1998). Decision making in planning: The ELECTRE multicriteria analysis approach compared to a FUZZY-SETS methodology. Energy Convers. Manag. 39 (16-18), 1869–1881. doi:10.1016/s0196-8904(98)00053-3

CrossRef Full Text | Google Scholar

Beg, I., and Ashraf, S. (2009). Similarity measures for fuzzy sets. Appl. Comput. Math. 8 (2), 192–202.

Google Scholar

Benayoun, R., Roy, B., and Sussman, B. (1966). Electre: Une m éthode pour guider le choix en présence de points de vue multiples. Note trav. 49, 2–120.

Google Scholar

Bi, L., Zeng, Z., Hu, B., and Dai, S. (2019). Two classes of entropy measures for complex fuzzy sets. Mathematics 7 (1), 96. doi:10.3390/math7010096

CrossRef Full Text | Google Scholar

Chang, S. I., Tsai, C.172.16.32.141F., Shih, D. H., and Hwang, C. L. (2008). The development of audit detection risk assessment system: Using the fuzzy theory and audit risk model. Expert Syst. Appl. 35 (3), 1053–1067. doi:10.1016/j.eswa.2007.08.057

CrossRef Full Text | Google Scholar

Chen, S. M., and Tan, J. M. (1994). Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy sets Syst. 67 (2), 163–172. doi:10.1016/0165-0114(94)90084-1

CrossRef Full Text | Google Scholar

De, S. K., Biswas, R., and Roy, A. R. (2000). Some operations on intuitionistic fuzzy sets. Fuzzy sets Syst. 114 (3), 477–484. doi:10.1016/s0165-0114(98)00191-2

CrossRef Full Text | Google Scholar

Dengfeng, L., and Chuntian, C. (2002). New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit. Lett. 23 (1-3), 221–225. doi:10.1016/s0167-8655(01)00110-6

CrossRef Full Text | Google Scholar

Deschrijver, G., and Kerre, E. E. (2003). On the relationship between some extensions of fuzzy set theory. Fuzzy sets Syst. 133 (2), 227–235. doi:10.1016/s0165-0114(02)00127-6

CrossRef Full Text | Google Scholar

Doumpos, M., and Zopounidis, C. (2001). Assessing financial risks using a multicriteria sorting procedure: The case of country risk assessment. Omega 29 (1), 97–109. doi:10.1016/s0305-0483(00)00028-1

CrossRef Full Text | Google Scholar

Dubois, D., Gottwald, S., Hajek, P., Kacprzyk, J., and Prade, H. (2005). Terminological difficulties in fuzzy set theory—the case of “intuitionistic fuzzy sets”. Fuzzy sets Syst. 156 (3), 485–491. doi:10.1016/j.fss.2005.06.001

CrossRef Full Text | Google Scholar

Ebadi, M. J., and Shahraki, M. S. (2010). Determination of scale elasticity in the existence of non-discretionary factors in performance analysis. Knowledge-Based Syst. 23 (5), 434–439. doi:10.1016/j.knosys.2010.02.005

CrossRef Full Text | Google Scholar

Gau, W. L., and Buehrer, D. J. (1993). Vague sets. IEEE Trans. Syst. man, Cybern. 23 (2), 610–614. doi:10.1109/21.229476

CrossRef Full Text | Google Scholar

Hassanien, A. E., and Badr, A. (2003). A comparative study on digital mamography enhancement algorithms based on fuzzy theory. Stud. Inf. control 12 (1), 21–32.

Google Scholar

Hong, D. H., and Choi, C. H. (2000). Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy sets Syst. 114 (1), 103–113. doi:10.1016/s0165-0114(98)00271-1

CrossRef Full Text | Google Scholar

Hu, B., Bi, L., and Dai, S. (2019). Complex fuzzy power aggregation operators. Math. problems Eng. 2019, 1–7. doi:10.1155/2019/9064385

CrossRef Full Text | Google Scholar

Hu, B., Bi, L., Dai, S., and Li, S. (2018). Distances of complex fuzzy sets and continuity of complex fuzzy operations. J. Intelligent Fuzzy Syst. 35 (2), 2247–2255. doi:10.3233/jifs-172264

CrossRef Full Text | Google Scholar

Jafari, H., Malinowski, M. T., and Ebadi, M. J. (2021). Fuzzy stochastic differential equations driven by fractional Brownian motion. Adv. Differ. Equations 2021 (1), 16–17. doi:10.1186/s13662-020-03181-z

CrossRef Full Text | Google Scholar

Kandasamy, W. V., and Smarandache, F. (2004). Analysis of social aspects of migrant labourers living with HIV/AIDS using Fuzzy Theory and Neutrosophic Cognitive Maps. Hyderabad, Telangana: Infinite Study.

Google Scholar

Li, C., and Chiang, T. W. (2012). Complex neurofuzzy ARIMA forecasting—A new approach using complex fuzzy sets. IEEE Trans. Fuzzy Syst. 21 (3), 567–584. doi:10.1109/tfuzz.2012.2226890

CrossRef Full Text | Google Scholar

Li, D. F. (2003). Fuzzy multiobjective many-person decision makings and games. Beijing: National Defense Industry Press, 138–158.

Google Scholar

Li, D. (1999). Fuzzy multiattribute decision-making models and methods with incomplete preference information. Fuzzy Sets Syst. 106 (2), 113–119. doi:10.1016/s0165-0114(97)00272-8

CrossRef Full Text | Google Scholar

Montero, J., Gómez, D., and Bustince, H. (2007). On the relevance of some families of fuzzy sets. Fuzzy sets Syst. 158 (22), 2429–2442. doi:10.1016/j.fss.2007.04.021

CrossRef Full Text | Google Scholar

Nguyen, H. T., Kandel, A., and Kreinovich, V. (2000). “Complex fuzzy sets: Towards new foundations,” in Ninth IEEE international conference on fuzzy systems. FUZZ-IEEE 2000 (cat. No. 00CH37063) (New Jersey, United States: IEEE), 2, 1045–1048.

Google Scholar

Ramot, D., Milo, R., Friedman, M., and Kandel, A. (2002). Complex fuzzy sets. IEEE Trans. fuzzy Syst. 10 (2), 171–186. doi:10.1109/91.995119

CrossRef Full Text | Google Scholar

Rouyendegh, B. D. (2018). The intuitionistic fuzzy ELECTRE model. Int. J. Manag. Sci. Eng. Manag. 13 (2), 139–145. doi:10.1080/17509653.2017.1349625

CrossRef Full Text | Google Scholar

Sproule, B. A., Naranjo, C. A., and Türksen, I. B. (2002). Fuzzy pharmacology: Theory and applications. Trends Pharmacol. Sci. 23 (9), 412–417. doi:10.1016/s0165-6147(02)02055-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Szmidt, E., and Kacprzyk, J. (2000). Distances between intuitionistic fuzzy sets. Fuzzy sets Syst. 114 (3), 505–518. doi:10.1016/s0165-0114(98)00244-9

CrossRef Full Text | Google Scholar

Szmidt, E., and Kacprzyk, J. (1997). “Intuitionistic fuzzy sets for more realistic group decision making,” in International conference on transition to advanced market institutions and economies, Warsaw, 430–433.

Google Scholar

Szmidt, E., and Kacprzyk, J. (1996). Some remarks on assigning weights to experts in multi-attribute group decision making using intuitionistic fuzzy sets. Notes IFS 2 (1), 43–51. doi:10.7546/nifs.2020.26.3.43-51

CrossRef Full Text | Google Scholar

Xiao, F., Cao, Z., and Lin, C. T. (2022). “A complex weighted discounting multisource information fusion with its application in pattern classification IEEE Transactions on Knowledge and Data Engineering,” in IEEE transactions on knowledge and data engineering (New York: IEEE).

Google Scholar

Xiao, F. (2022). Generalized quantum evidence theory. Appl. Intell., 1–16. doi:10.1007/s10489-022-04181-0

CrossRef Full Text | Google Scholar

Xiao, F. (2020). Giq: A generalized intelligent quality-based approach for fusing multisource information. IEEE Trans. Fuzzy Syst. 29 (7), 2018–2031. doi:10.1109/tfuzz.2020.2991296

CrossRef Full Text | Google Scholar

Xiao, F. (2020). On the maximum entropy negation of a complex-valued distribution. IEEE Trans. Fuzzy Syst. 29 (11), 3259–3269. doi:10.1109/tfuzz.2020.3016723

CrossRef Full Text | Google Scholar

Xiao, F., and Pedrycz, W. (2022). Negation of the quantum mass function for multisource quantum information fusion with its application to pattern classification. IEEE Trans. Pattern Analysis Mach. Intell. 45 (2), 2054–2070. doi:10.1109/tpami.2022.3167045

CrossRef Full Text | Google Scholar

Xu, Z., and Xia, M. (2011). Distance and similarity measures for hesitant fuzzy sets. Inf. Sci. 181 (11), 2128–2138. doi:10.1016/j.ins.2011.01.028

CrossRef Full Text | Google Scholar

Yu, D., Xu, Z., and Wang, W. (2018). Bibliometric analysis of fuzzy theory research in China: A 30-year perspective. Knowledge-Based Syst. 141, 188–199. doi:10.1016/j.knosys.2017.11.018

CrossRef Full Text | Google Scholar

Zadeh, L. A., Klir, G. J., and Yuan, B. (1996). Fuzzy sets, fuzzy logic, and fuzzy systems: Selected papers, 6. Singapore: World Scientific.

Google Scholar

Zhang, G., Dillon, T. S., Cai, K. Y., Ma, J., and Lu, J. (2009). Operation properties and b-equalities of complex fuzzy sets. Int. J. Approx. Reason. 50 (8), 1227–1249. doi:10.1016/j.ijar.2009.05.010

CrossRef Full Text | Google Scholar

Keywords: complex intuitionistic fuzzy set, ELECTREE method, multi-attribute decision making, decision making, CIF–ELECTREE method

Citation: Ashraf S, Ali M, Sohail M and Eldin SM (2023) Assessing the environmental impact of industrial pollution using the complex intuitionistic fuzzy ELECTREE method: a case study of pollution control measures. Front. Environ. Sci. 11:1171701. doi: 10.3389/fenvs.2023.1171701

Received: 22 February 2023; Accepted: 03 May 2023;
Published: 18 May 2023.

Edited by:

Dragan Pamucar, University of Belgrade, Serbia

Reviewed by:

Zhenkun Liu, Dongbei University of Finance and Economics, China
Fuyuan Xiao, Chongqing University, China

Copyright © 2023 Ashraf, Ali, Sohail and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Shahzaib Ashraf, c2hhaHphaWIuYXNocmFmQGtmdWVpdC5lZHUucGs=; Sayed M. Eldin, c2F5ZWQuZWxkaW4yMkBmdWUuZWR1LmVn

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.