Identification and classification of digital green innovation based on interaction Maclaurin symmetric mean operators by using T-spherical fuzzy information

The digital green concept refers to the devotion to digital technology, i.e., techniques of procedures in the area of ecological or sustainable conservation. It contains leveraging digital techniques, procedures, and new tools to evaluate environmental problems and promote sustainable development. The major influence of this article is to evaluate the selection of the best digital green technology. For this, we aim to propose the idea of Maclaurin symmetric mean (MSM) operators based on interaction operational laws for T-spherical fuzzy (TSF) information, such as TSF interaction weighted averaging (TSFIWA), generalized TSF interaction weighted averaging (GTSFIWA), TSF interaction weighted geometric averaging (TSFIWGA), TSF interaction MSM (TSFIMSM), TSF interaction Bonferroni mean (TSFIBM), and TSF interaction weighted Maclaurin symmetric mean (TSFIWMSM) operators. Some dominant and reliable properties are also invented for evaluation. Moreover, to address the best digital green innovation (DGI) among the top five DGIs, we illustrate the procedure of the multi-attribute decision-making (MADM) technique under the presence of the derived operators. Finally, we demonstrate a numerical example for evaluating the comparative study between the proposed and existing or prevailing operators to enhance the worth of the derived theory.

1 Introduction

The term “digital green sustainable” describes how digital technology and procedures are used to support environmental sustainability and lower carbon emissions. It includes many facets of technology with an emphasis on reducing their environmental effect, including data centers, cloud computing, software applications, and gadgets. The goal of digital green sustainable practices is to maximize technology’s benefits while reducing its environmental harm. Organizations and people may help create a digital ecosystem that is more environmentally friendly and sustainable by using these practices. Moreover, to discover the best or finest decision from the collection of preferences, the theory of the multi-attribute decision-making (MADM) technique is very famous and reliable for evaluating the best pick from the array of choices, where the idea of the MADM approach is the sub-division of the decision-making procedure. However, in the presence of classical information, we faced a lot of complications because we have only two possibilities, such as 0 or 1, but not between unit intervals. Therefore, the theory of fuzzy set (FS) was proposed by Zadeh (1965), which described the membership whose values are contained in the unit interval. Furthermore, many scholars have raised the question of what would happen if we involved the falsity grade in the FS because the negative or falsity information is an initial and central part of every real-life problem. Therefore, Atanassov (1986) discovered the idea of intuitionistic FS (IFS). The IFS deals with yes or no types of theory, with the role that the sum of both degrees in the duplet should be contained in the unit interval. Furthermore, Yager (2013) improved or modified the theory of Pythagorean FS (PyFS). Moreover, Yager (2016) initiated the idea of q-rung orthopair FS (qROFS) with a valuable and robust condition such as $0\le {\nu }^{է}+d^{է}\le 1,է{\in \mathbb{Z}}^{+}$. When there are more than three possibilities, such as when there is voting between two parties, some individuals choose party A, some choose party B, some damage their vote by stamping both, and others choose not to vote, structures like IFS, PyFS, and qROPFS fail. Cuong and Kreinovich (2014) proposed the picture fuzzy set (PFS) to handle this information. The PFS requires that the sum of the MD, abstinence degree (AD), and NMD must lie within $\left[\mathrm{0,1}\right]$. Decision-makers feel hesitant to resolve their issues because the sum of MD, AD, and NMD does not contain $\left[\mathrm{0,1}\right]$, and PFS fails. Mahmood et al. (2019) proposed a generalization of PFSs termed spherical fuzzy sets (SFSs) which cover those types of information that the picture fuzzy set fails to explain. For example, we consider the information $\left(0.6,0.5,0.4\right)$ where $0\le 0.6+0.5+0.4=1.5\ge 1$. However, $0\le {0.6}^2+{0.5}^2+{0.4}^2=0.67\le 1$, which shows that the SFS is more easily applicable than the PFS. However, at some point, even the SFS is not enough to deal with uncertain information and ${\nu }^2+u^2+d^2$ exceeds to 1, e.g., we consider $\left(0.8,0.6,0.4\right)$, for which ${0.8}^2+{0.6}^2+{0.4}^2=1.16\ge 1$, so to overcome this flaw without any restriction, Mahmood et al. (2019) introduced T-spherical fuzzy sets (TSFS) allowing $0\le {\nu }^{է}+u^{է}+d^{է}\le 1$, where $է{\in \mathbb{Z}}^{+}$ and because of such a framework, any information of the type $\left(0.8,0.6,0.4\right)$ can be of use as for $է=3$ we have ${0.8}^3+{0.6}^3+{0.4}^3=0.792\le 1$. The impressive literature is discovered in Mahmood (2020); Mahmood and Ali (2020); Akram et al. (2022); Hussain et al. (2022); Khan et al. (2022).

The most accurate way for an information alliance is an aggregate operator. Numerous writers have presented multiple aggregation operators over the past 10 years. The average mean (AM) operator is the most commonly used AO since it makes it simple to aggregate all the different data into a comprehensive form. Several practical AOs have also been developed that are useful for collecting data in ambiguous and complex fuzzy decision-making contexts, such as geometric mean (GM), Bonferroni mean (BM), and Heronian mean (HM). Other AM AOs for MADM have been created in past years. Any of the operators mentioned previously do not consider the relationships between the values being used. To resolve this issue, Yager developed the concept of power AO (Yager, 2001). Power AOs significantly impact the relationship of the data being aggregated. Maclaurin symmetric mean (MSM) operators in the aggregation theory are one of the research topics that have gained the most significant interest. The MSM was first proposed by Maclaurin (Jstor, 2022) and later made famous by Detemple and Robertson (Jstor, 2022). The relationship of numerous input arguments can be overcome by MSM, which defines its characteristics. The significant difference between MSM and BM is that MSM may represent interactions among more than input data arguments, but BM cannot. For the given statements, MSM monotonically decreases concerning the parameter value. MSM accepts the fact that opinions are transformed into crisp numbers.

However, Liu et al. (2020) investigated partitioned MSM operators for MADM applications within IFSs. Qin and Liu. (2014) introduced IF MSM (IFMSM) operators. In the technology domain, Wei and Lu. (2018) investigated the Pythagorean fuzzy MSM (PyFMSM) operators. By creating transactional PyFMSM operators for the applications of MADM, Yang and Pang. (2018) also enhanced the efficiency of PyFMSM operators. For the MADM, Wei et al. (2019) proposed the q-Rung orthopair fuzzy MSM (qROFMSM) operators. At the same time, Wang et al. (2019) enhanced the concept of the qROFMSM operator. MSM operations for linguistic variables were examined by Liu and Qin. (2017) using an IF layout, while Qin et al. (2015) introduced the MSM operators in hesitant fuzzy contexts. Further information and applications of MSM operators are shown in Wang et al. (2018); Yu et al. (2018); Ju et al. (2016); Ullah (2021); Ashraf et al. (2022).

In particular circumstances, the aggregating outcomes from IFS’s traditional operations are illogical, especially when there is zero NMD of the TSFS. Because operations of IFSs cannot consider interactions between truth and non-membership, He et al. (2014b) suggested the operational interaction laws of IFNs to solve this issue. When the NMD of IFNs is 0, the issues may be resolved, and these rules appropriately consider interactions between the membership and non-membership functions. Our proposed work is more appropriate than the that of existing operators because if any of the NMDs is 0, utilizing the existing operators affects all the other NMD values and gives zero aggregated value, whereas utilizing the proposed work zero does not affect the other ones. In our proposed work, we are using the TSFS as it is more useful than the other extensions of the FS because it gives independency to choose NMD by our own choice between $\left[\mathrm{0,1}\right]$ and also to take $է$ of our choice. There are many extensions of the TSFS to get some more information regarding TSFS from more literature that can be seen here. Karaaslan and Al-Husseinawi. (2022) presented the concept of hesitant T-spherical fuzzy (HT-SF) set (HT-SFS) by combining concepts of the HF set and T-SFS, and present some set theoretical operations of HT-SFSs. Özlü and Karaaslan. (2022) introduced the concept of type-2 hesitant fuzzy set (HFS), which is a generalization of the HFS. The concept of complex T-spherical fuzzy Dombi aggregation operators was developed by Karaaslan and Dawood (2021).

Green innovation” is the technological innovation that involves energy conservation, pollution prevention, waste recycling, green product design, or corporate environmental management. Digital technology is crucial for green innovation, and FS theory is typically the best option when it comes to assessing and modeling human knowledge during the process of digital green innovation (DGI). The purpose of this article is to discuss new developments in FS models and their use in DGI in engineering processes and practical accomplishments. Green innovation indicates all forms of invention that minimize green destruction and guarantee that biological supplies are utilized most effectively and efficiently as possible. A study on DGI can be seen in Yin et al. (2022); Yin and Yu (2022); Dong et al. (2023). Furthermore, fuzzy set theory is a valuable and dominant technique for modeling and evaluating human knowledge regarding DGI. Inspired by the aforementioned information, the major influence of this analysis is stated as follows:

1. To derive the theory of GTSFIWA, GTSFIA, TSFIWA, TSFIA, and TSFIWGA operators.

2. To discover the idea of TSFIMSM, TSFIBM, and TSFIWMSM operators.

3. To expose some valuable properties for the evaluated work.

4. To discuss the MADM technique under the presence of the derived operators.

5. To illustrate, a numerical example for evaluating the comparative study between proposed and existing or prevailing operators is applied to enhance the worth of the derived theory.

The rest of our work is divided into different sections. We primarily introduce the basic ideas of T-SFSs and interaction MSM operators in Section 2. We introduce the GTSFIWA, GTSFIA, TSFIWA, TSFIA, TSFIWGA, TSFIGA, and GTSFIWGA operators in Section 3. We defined the TSFIMSM and TSFIWMSM operators in Section 4 and described their properties. Using the proposed operators, we provide a new MADM technique in Section 5 and step-by-step instructions. In Section 6, we illustrate the effectiveness of the proposed MADM method and compare it with that of the recent techniques using a real-world application. The conclusions of this paper are presented in Section 7.

2 Preliminaries

Here, we aim to revise the theory of TSF information and its operational laws, such as algebraic and interaction laws, for TSF information. Throughout the paper, $ἶ$ will denote the indexing term, and $\mathcal{R}$ will represent a non-empty set. Furthermore, we have used the $\nu \left(r\right),u\left(r\right),d\left(r\right)$ and $\mathcal{R}$ for truth, abstinence, falsity, and universal set, respectively, where $\oplus$ and $\otimes$ are used for addition and multiplications, respectively.

Definition 1. (Ullah et al., 2018) A TSFS $\breve{t}$ is expressed by

$\breve{t}=\left\{〈r,\nu \left(r\right),u\left(r\right),d\left(r\right)〉|r\in \mathcal{R}\right\}.(1)$

With a valuable characteristic:

$0\le {\nu }^{է}+u^{է}+d^{է}\le 1,է{\in \mathbb{Z}}^{+}.$

Under the presence of the aforementioned information, we derive the theory of neutral information $\mathfrak{R}$, such as

$\mathfrak{R}=\sqrt[է]{1-\left({\nu }^{է}+u^{է}+d^{է}\right).}(2)$

From now onward, the information in triplet $\breve{t}=\left(\nu ,u,d\right)$ is used as the TSF value (TSFV). Various exceptional cases are stated and derived; for instance, to put the value of $է=2$ in the TSFS, we obtain the theory of the SFS to set the value of $է=1$ in the TSFS. We obtain the theory of the PFS to set the value of $u=0$ in the TSFS, then we obtain the view of q-ROFS, and finally, to set the value of $u=0$ and $է=2$ in the TSFS. Then we get the idea of PyFS.

Definition 2. (Garg et al., 2018) Assume any two TSFVs be ${\breve{t}}_i=\left({\nu }_{ἶ},u_{ἶ},d_{ἶ}\right)$. Then, some operational laws of TSFVs are as follows:

${\breve{t}}_1⨁{\breve{t}}_2=\left(\sqrt[է]{{\left({\nu }_1\right)}^{է}+{\left({\nu }_2\right)}^{է}-{\left({\nu }_1\right)}^{է}{\left({\nu }_2\right)}^{է}},u_1{u}_2,d_1{d}_2\right),(3)$

${\breve{t}}_1⨂{\breve{t}}_2=\left({\nu }_1{\nu }_2,\sqrt[է]{{\left(u_1\right)}^{է}+{\left(u_2\right)}^{է}-{\left(u_1\right)}^{է}{\left(u_2\right)}^{է}},\sqrt[է]{{\left(d_1\right)}^{է}+{\left(d_2\right)}^{է}-{\left(d_1\right)}^{է}{\left(d_2\right)}^{է}}\right),(4)$

$\zeta \breve{t}=\left(\sqrt[է]{1-{\left(1-{\nu }^{է}\right)}^{\zeta }},u^{է},d^{է}\right),(5)$

${\left(\breve{t}\right)}^{\zeta }=\left({\nu }^{է},\sqrt[է]{1-{\left(1-u^{է}\right)}^{\zeta }},\sqrt[է]{1-{\left(1-d^{է}\right)}^{\zeta }}\right),(6)$

$\left({\breve{t}}^c\right)=\left(d,u,\nu \right).(7)$

Definition 3. (Naseem et al., 2022) Assume any two TSFVs be ${\breve{t}}_i=\left({\nu }_{ἶ},u_{ἶ},d_{ἶ}\right)$. The score and accuracy values are stated by

$\mathfrak{𝔰}\left(\breve{t}\right)={\nu }^{է}-u^{է}.{\mathfrak{R}}^{է}\in \left[-\mathrm{1,1}\right],(8)$

$\mathrm{\AA }\left(\breve{t}\right)=\left({\nu }^{է}+u^{է}+d^{է}\right)\in \left[\mathrm{0,1}\right].(9)$

Example 1. Let three TSFVs be ${\breve{t}}_1=\left(\mathrm{0.6,0.5,0.4}\right)$, ${\breve{t}}_2=\left(\mathrm{0.5,0.7,0.6}\right)$, and ${\breve{t}}_3=\left(\mathrm{0.7,0.4,0.0}\right)$, and $\omega =\left({\omega }_1,{\omega }_2,{\omega }_3\right)=\left(\mathrm{0.25,0.4,0.35}\right)$ be the weight vector where $է=3$.Solution: As we know $\breve{t}={\omega }_1{\breve{t}}_1⨁{\omega }_2{\breve{t}}_2⨁{\omega }_3{\breve{t}}_3=\left(0.61263,0.52906,0\right)$. Thus, $d_{ἶ}$ of ${\breve{t}}_3$ is $″0″$, that affects all the other $d_{ἶ}$ by using the previously required operations, and $d$ of $\breve{t}$ becomes $0$, which is illogical. To overcome the drawback of these operational laws, several updated operational laws for the TSFS are given as follows:

Definition 4. Let ${\breve{t}}_1=\left({\nu }_1,u_1,d_1\right)$ and ${\breve{t}}_2=\left({\nu }_2,u_2,d_2\right)$ be two TSFVs, $\lambda >0$. Then, the operational laws can be expressed as follows:

${\breve{t}}_1⨁{\breve{t}}_2=\left(\begin{array}{c}\sqrt[է]{{\nu }_1^{է}+{\nu }_2^{է}-{\nu }_1^{է}{\nu }_2^{է}},\sqrt[է]{u_1^{է}+u_2^{է}-u_1^{է}{u}_2^{է}-{\nu }_1^{է}{u}_2^{է}-u_1^{է}{\nu }_2^{է}},\\ \sqrt[է]{d_1^{է}+d_2^{է}-d_1^{է}{d}_2^{է}-{\nu }_1^{է}{d}_2^{է}-d_1^{է}{\nu }_2^{է}}\end{array}\right),(10)$

${\breve{t}}_1⨂{\breve{t}}_2=\left(\sqrt[է]{{\nu }_1^{է}+{\nu }_2^{է}-{\nu }_1^{է}{\nu }_2^{է}-u_1^{է}{\nu }_2^{է}-{\nu }_1^{է}{u}_2^{է}},\sqrt[է]{u_1^{է}+u_2^{է}-u_1^{է}{u}_2^{է}},\sqrt[է]{d_1^{է}+d_2^{է}-d_1^{է}{d}_2^{է}}\right),(11)$

$\lambda \breve{t}=\left(\sqrt[է]{1-{\left(1-{\nu }^{է}\right)}^{\lambda }},\sqrt[է]{{\left(1-{\nu }^{է}\right)}^{\lambda }-{\left(1-\left({\nu }^{է}+u^{է}\right)\right)}^{\lambda }},\sqrt[է]{{\left(1-{\nu }^{է}\right)}^{\lambda }-{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\lambda }}\right),(12)$

${\left(\breve{t}\right)}^{\lambda }=\left(\sqrt[է]{{\left(1-d^{է}\right)}^{\lambda }-{\left(1-\left(d^{է}+{\nu }^{է}\right)\right)}^{\lambda }},\sqrt[է]{1-{\left(1-u^{է}\right)}^{\lambda }},\sqrt[է]{1-{\left(1-d^{է}\right)}^{\lambda }}\right).(13)$

The first two equations can be written in the respective ways shown in the following equations:

${\breve{t}}_1⨁{\breve{t}}_2=\left(\begin{array}{c}\sqrt[է]{1-\left(1-{\nu }_1^{է}\right)\left(1-{\nu }_2^{է}\right)},\sqrt[է]{\left(1-{\nu }_1^{է}\right)\left(1-{\nu }_2^{է}\right)-\left(1-\left({\nu }_1^{է}+u_1^{է}\right)\right)\left(1-\left({\nu }_2^{է}+u_2^{է}\right)\right)},\\ \sqrt[է]{\left(1-{\nu }_1^{է}\right)\left(1-{\nu }_2^{է}\right)-\left(1-\left({\nu }_1^{է}{+d}_1^{է}\right)\right)\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}\end{array}\right)=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-{\nu }_{յ}^{է}\right)},\sqrt[է]{{\displaystyle \prod _{յ=1}^2}\left(1-{\nu }_{յ}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{յ}^{է}+u_{յ}^{է}\right)\right)},\\ \sqrt[է]{{\displaystyle \prod _{յ=1}^2}\left(1-{\nu }_{յ}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{յ}^{է}+d_{յ}^{է}\right)\right)}\end{array}\right),(14)$

${\breve{t}}_1⨂{\breve{t}}_2=\left(\begin{array}{c}\sqrt[է]{\left(1-d_1^{է}\right)\left(1-d_2^{է}\right)-\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)},\\ \sqrt[է]{1-\left(1-u_1^{է}\right)\left(1-u_2^{է}\right)},\sqrt[է]{1-\left(1-d_1^{է}\right)\left(1-d_2^{է}\right)}\end{array}\right)=\left(\sqrt[է]{{\displaystyle \prod _{յ=1}^2}\left(1-d_{յ}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{յ}^{է}+u_{յ}^{է}+d_{յ}^{է}\right)\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-u_{յ}^{է}\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-d_{յ}^{է}\right)}\right).(15)$

Example 2. Let three TSFVs be ${\breve{t}}_1=\left(\mathrm{0.6,0.5,0.4}\right)$, ${\breve{t}}_2=\left(\mathrm{0.5,0.7,0.6}\right)$, and ${\breve{t}}_3=\left(\mathrm{0.7,0.4,0.0}\right)$, and $\omega =\left({\omega }_1,{\omega }_2,{\omega }_3\right)=\left(\mathrm{0.25,0.4,0.35}\right)$ be the weight vector where $է=3$.Solution: Solving Example 1 by using Definition 3, we overcome the drawbacks and obtain that $\breve{t}={\omega }_1{\breve{t}}_1⨁{\omega }_2{\breve{t}}_2⨁{\omega }_3{\breve{t}}_3=\left(0.61263,0.58198,0.46232\right)$. As $\mathit{min}\left(d_1,d_2,d_3\right)=0\le 0.46232\le 0.6=\mathit{max}\left(d_1,d_2,d_3\right)$. From the perspective of averages, the outcomes obtained by Definition 3 are more authentic than those of Definition 2.

3 Generalized TSF interaction aggregation operators

In the section on the development of green manufacturing engineering, we concentrate on utilizing the theory IMSM in the environment of TSF set theory, such as GTSFIWA, GTSFIA, TSFIWA, TSFIA, and TSFIWGA operators. Some dominant and reliable properties are also invented for evaluated work.

Definition 5. The GTSFIWA operator is particularized by

${GTSFIWA}_{\lambda }\left({\breve{t}}_1,{\breve{t}}_2{,\dots ,\breve{t}}_{\mathfrak{q}}\right)={\left({\oplus }_{ἶ=1}^{\mathfrak{q}}{\omega }_{ἶ}{\breve{t}}_{ἶ}^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}={\left({\omega }_1{\breve{t}}_1^{\lambda }⨁{\omega }_2{\breve{t}}_2^{\lambda }\oplus \dots \oplus {\omega }_{\mathfrak{q}}{\breve{t}}_{\mathfrak{q}}^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}.(16)$

Theorem 1. Using the information in Eq. 16, we derive the following theory, such as

${GTSFIWA}_{\lambda }\left({\breve{t}}_1,{\breve{t}}_2{,\dots ,\breve{t}}_{\mathfrak{q}}\right)=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-{\left(1-d_{յ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{յ}^{է}+d_{յ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{յ}}+{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{յ}^{է}+d_{յ}^{է}\right)\right)}^{\lambda {\omega }_{յ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{յ}^{է}+d_{յ}^{է}\right)\right)}^{{\omega }_{յ}}\end{array}\right)},\\ \sqrt[է]{1-{\left(1-{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-{\left(1-u_{յ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{յ}^{է}+u_{յ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{յ}}+{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{յ}^{է}+u_{յ}^{է}\right)\right)}^{\lambda {\omega }_{յ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}},\\ \sqrt[է]{1-{\left(1-{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-{\left(1-d_{յ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{յ}^{է}+d_{յ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{յ}}+{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{յ}^{է}+d_{յ}^{է}\right)\right)}^{\lambda {\omega }_{յ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}\end{array}\right).(17)$

Proof: By using mathematical induction, we concentrate to derive the theory in Eq. 17. For this, we have the following procedure. When $\mathfrak{q}=2$, then

${{\omega }_1\breve{t}}_1^{\lambda }=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(1-\left({\left(1-d_1^{է}\right)}^{\lambda }-{\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_1}\right)},\\ \sqrt[է]{{\left(1-\left({\left(1-u_1^{է}\right)}^{\lambda }-{\left(1-\left({\nu }_1^{է}+u_1^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_1}-{\left(1-\left({\nu }_1^{է}+u_1^{է}\right)\right)}^{{\omega }_1\lambda }},\\ \sqrt[է]{{\left(1-\left({\left(1-d_1^{է}\right)}^{\lambda }-{\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_1}-{\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)}^{{\omega }_1\lambda }}\end{array}\right),$

${{\omega }_2\breve{t}}_2^{\lambda }=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(1-\left({\left(1-{\nu }_2^{է}\right)}^{\lambda }-{\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_2}\right)},\\ \sqrt[է]{{\left(1-\left({\left(1-u_2^{է}\right)}^{\lambda }-{\left(1-\left({\nu }_2^{է}+u_2^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_2}-{\left(1-\left({\nu }_2^{է}+u_2^{է}\right)\right)}^{{\omega }_2\lambda }},\\ \sqrt[է]{{\left(1-\left({\left(1-d_2^{է}\right)}^{\lambda }-{\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_2}-{\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}^{{\omega }_2\lambda }}\end{array}\right).$

Thus,

${{\omega }_1\breve{t}}_1^{\lambda }⨁{{\omega }_2\breve{t}}_2^{\lambda }=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(1-{\left(1-d_1^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_1}*{\left(1-{\left(1-d_2^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_2}\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\left(1-{\left(1-u_1^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_1^{է}+u_1^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_1}*{\left(1-{\left(1-u_2^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_2^{է}+u_2^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_2}\\ -{\left(1-\left({\nu }_1^{է}+u_1^{է}\right)\right)}^{{\omega }_1\lambda }{\left(1-\left({\nu }_2^{է}+u_2^{է}\right)\right)}^{{\omega }_2\lambda }\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\left(1-{\left(1-d_1^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_1}*{\left(1-{\left(1-d_2^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_2}\\ -{\left(1-\left({\nu }_1^{է}+d_1^{է}\right)\right)}^{{\omega }_2\lambda }{\left(1-\left({\nu }_2^{է}+d_2^{է}\right)\right)}^{{\omega }_2\lambda }\end{array}\right)}\end{array}\right),$

$=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod _{ἶ=1}^2}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}},\\ \sqrt[է]{{\displaystyle \prod _{ἶ=1}^2}{\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^2}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}},\\ \sqrt[է]{{\displaystyle \prod _{ἶ=1}^2}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^2}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}}\end{array}\right),$

${\left({{\omega }_1\breve{t}}_1^{\lambda }⨁{{\omega }_2\breve{t}}_2^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{ἶ=1}^2}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^2}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{ἶ=1}^2}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\end{array}\right)},\\ \sqrt[է]{1-{\left(1-\left({\displaystyle \prod _{ἶ=1}^2}{\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^2}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}},\\ \sqrt[է]{1-{\left(1-\left({\displaystyle \prod _{ἶ=1}^2}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^2}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}\end{array}\right).$

For $\mathfrak{q}=2,$ the information in Eq. 17 is valid. Therefore, we assume that the information in Eq. 17 is also accurate for $\mathfrak{q}=\rho$, such as

${\left({⨁}_{ἶ=1}^{\rho }{{\omega }_{ἶ}\breve{t}}_{ἶ}^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\end{array}\right)},\\ \sqrt[է]{1-{\left(1-\left({\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}},\\ \sqrt[է]{1-{\left(1-\left({\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\lambda \omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}\end{array}\right).$

Then, we aim to derive it for $\mathfrak{q}=\rho +1$, such as

${\left({⨁}_{ἶ=1}^{\rho +1}{{\omega }_{ἶ}\breve{t}}_{ἶ}^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}={\left(\left({⨁}_{ἶ=1}^{\rho }{{\omega }_{ἶ}\breve{t}}_{ἶ}^{\lambda }\right)⨁\left({{\omega }_{\rho +1}\breve{t}}_{\rho +1}^{\lambda }\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.},$

$={\left(\begin{array}{c}\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}},\\ \sqrt[է]{{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}},\\ \sqrt[է]{{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho }}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}}\end{array}\right)\oplus \\ \left(\begin{array}{c}\sqrt[է]{1-{\left(1-{\left(1-d_{\rho +1}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{\rho +1}^{է}+d_{\rho +1}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{\rho +1}}},\\ \sqrt[է]{{\left(1-{\left(1-u_{\rho +1}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{\rho +1}^{է}+u_{\rho +1}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{\rho +1}}-{\left(1-\left({\nu }_{\rho +1}^{է}+u_{\rho +1}^{է}\right)\right)}^{\lambda {\omega }_{\rho +1}}},\\ \sqrt[է]{{\left(1-{\left(1-d_{\rho +1}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{\rho +1}^{է}+d_{\rho +1}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{\rho +1}}-{\left(1-\left({\nu }_{\rho +1}^{է}+d_{\rho +1}^{է}\right)\right)}^{\lambda {\omega }_{\rho +1}}}\end{array}\right)\end{array}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.},$

$=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(1-{\left({\displaystyle \prod _{ἶ=1}^{\rho +1}}\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho +1}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{ἶ=1}^{\rho +1}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\end{array}\right)},\\ \sqrt[է]{{\left(1-\left(1-{\displaystyle \prod _{ἶ=1}^{\rho +1}}{\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho +1}}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}},\\ \sqrt[է]{{\left(1-\left(1-{\displaystyle \prod _{ἶ=1}^{\rho +1}}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\rho +1}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}\end{array}\right).$

Hence, the theory in Eq. 17 is also valid for $\mathfrak{q}=\rho +1$.Furthermore, by setting the value of the weight vector $\left(\frac{1}{\mathfrak{q}},\frac{1}{\mathfrak{q}},\dots ,\frac{1}{\mathfrak{q}}\right)$ in the information in Eq. 17, then we obtain the GTSFIA operator, such as

$GTSFIA\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left({⨁}_{ἶ=1}^{\mathfrak{q}}\frac{1}{\mathfrak{q}}{\breve{t}}_{ἶ}^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{\frac{1}{\mathfrak{q}}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\frac{\lambda }{\mathfrak{q}}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\frac{1}{\mathfrak{q}}}\end{array}\right)},\\ \sqrt[է]{1-{\left(1-\left({\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\left(1-u_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{\frac{1}{\mathfrak{q}}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\frac{\lambda }{\mathfrak{q}}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}},\\ \sqrt[է]{1-{\left(1-\left({\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\left(1-d_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{\frac{1}{\mathfrak{q}}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\frac{\lambda }{\mathfrak{q}}}\right)\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}}\end{array}\right).(18)$

Property 1. (Idempotency) Let ${\breve{t}}_{ἶ}=\left({\nu }_{ἶ},u_{ἶ},d_{ἶ}\right)$ and ${\breve{t}}_{ἶ}=\breve{t}$, then idempotency for GTSFIWA is defined as follows:

${GTSFIWA}_{\lambda }\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\breve{t}.(19)$

Furthermore, by setting the value of $\lambda =1$ in Eq. 17, then we obtain the TSFIWA operator, such as

$TSFIWA\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\nu }_{ἶ}^{է}\right)}^{{\omega }_{ἶ}}},\sqrt[է]{{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\nu }_{ἶ}^{է}\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{{\omega }_{ἶ}}},\\ \sqrt[է]{{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\nu }_{ἶ}^{է}\right)}^{{\omega }_{ἶ}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\omega }_{ἶ}}}\end{array}\right).(20)$

Finally, for $\lambda =1$, we use the value of the weight vector $\left(\frac{1}{\mathfrak{q}},\frac{1}{\mathfrak{q}},\dots ,\frac{1}{\mathfrak{q}}\right)$ in Eq. 17, and then we obtain the TSFIA operator, such as

$TSFIA\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\frac{1}{\mathfrak{q}}{⨁}_{յ=1}^{\mathfrak{q}}{\breve{t}}_{յ}=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\nu }_{ἶ}^{է}\right)}^{\frac{1}{\mathfrak{q}}}},\sqrt[է]{{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\nu }_{ἶ}^{է}\right)}^{\frac{1}{\mathfrak{q}}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\frac{1}{\mathfrak{q}}}},\\ \sqrt[է]{{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\nu }_{ἶ}^{է}\right)}^{\frac{1}{\mathfrak{q}}}-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\frac{1}{\mathfrak{q}}}}\end{array}\right).(21)$

Definition 6. A GTSFIWGA operator is particularized by

${GTSFIWGA}_{\lambda }\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\frac{1}{\lambda }\left({\otimes }_{ἶ=1}^{\mathfrak{q}}{\left(\lambda {\breve{t}}_{ἶ}\right)}^{{\omega }_{ἶ}}\right)=\frac{1}{\lambda }\left({\left(\lambda {\breve{t}}_1\right)}^{{\omega }_1}⨂{\left(\lambda {\breve{t}}_2\right)}^{{\omega }_2}⨂\dots ⨂{\left(\lambda {\breve{t}}_{\mathfrak{q}}\right)}^{{\omega }_{\mathfrak{q}}}\right).(22)$

Theorem 2. Using the information in Eq. 22, we derive the following theory, such as

${GTSFIWGA}_{\lambda }\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\left(\begin{array}{c}\sqrt[է]{1-{\left(1-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\left(1-{\nu }_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}+{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}},\\ \sqrt[է]{\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\left(1-{\nu }_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}+{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+u_{ἶ}^{է}\right)\right)}^{{\omega }_{ἶ}}\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-{\left(1-{\nu }_{ἶ}^{է}\right)}^{\lambda }+{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda }\right)}^{{\omega }_{ἶ}}+{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{\lambda {\omega }_{ἶ}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\\ -{\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\left(1-\left({\nu }_{ἶ}^{է}+d_{ἶ}^{է}\right)\right)}^{{\omega }_{ἶ}}\end{array}\right)}\end{array}\right).(23)$

Proof: Omitted.

Example 3. Suppose five TSFVs be, ${\breve{t}}_1=\left(\mathrm{0.80,0.50,0.30}\right),{\breve{t}}_2=\left(\mathrm{0.40,0.60,0.70}\right),{\breve{t}}_3=\left(\mathrm{0.85,0.45,0.25}\right),{\breve{t}}_4=\left(\mathrm{0.50,0.30,0.00}\right)$, and ${\breve{t}}_5=\left(\mathrm{0.55,0.55,0.55}\right)$ and $\omega =\left(\mathrm{0.25,0.20,0.15,0.10,0.30}\right)$, by using the suggested operators GTSFIWGA and GTSFIWA and the existing operator TSF Frank weighted averaging (TSFFWA) to assemble these TSFVs for various $\lambda$. There are some current approaches to determine the entire values. Table 1 illustrates the results.Table 1 is the aggregated matrix of the given TSFVs, which shows that if the NMD of any one of the TSFVs is 0, then by using the TSFFWA operator, the aggregated value of NMD becomes 0 through all the various values of $\lambda$ as one NMD affect all the other values of NMD. While utilizing GTSFIWGA and GTSFIWA operators, the aggregated values of NMD through various $\lambda$ are different as it does not affect any other value of NMD. Table 2 shows the score value by utilizing Table 1.

TABLE 1

TABLE 1. Aggregated matrix of TSFVs.

TABLE 2

TABLE 2. Matrix of score value $\mathfrak{s}\left(\breve{\mathit{t}}\right)$.

4 Interaction MSM operators for TSF information

In the section on the development of green manufacturing engineering, we concentrate on utilizing the IMSM theory in the environment of TSF set theory, such as TSFIMSM, TSFIBM, and TSFIWMSM operators. Some dominant and reliable properties are also invented for evaluated work.

Definition 7. (Maclaurin, 1729) Suppose ${\breve{t}}_{ἶ}\left(ἶ=\mathrm{1,2},\dots ,\mathfrak{q}\right)$ and $\zeta =\mathrm{1,2},\dots ,\mathrm{Иͷ}$ be the collection of positive real numbers. The MSM operator is stated by

${MSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{\displaystyle \sum }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{\zeta }}.(24)$

With various valuable properties, such as

${MSM}^{\left(\zeta \right)}\left(\mathrm{0,0},\dots ,0\right)=0,(25)$

${MSM}^{\left(\zeta \right)}\left(\mathrm{1,1},\dots ,1\right)=1,(26)$

${MSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)\le {MSM}^{\left(\zeta \right)}\left({\widehat{t}}_1,{\widehat{t}}_2,\dots ,{\widehat{t}}_{\mathfrak{q}}\right),\mathrm{i}\mathrm{f}{\breve{t}}_{ἶ}\le {\widehat{t}}_{ἶ}\forall ἶ,(27)$

${\mathit{min}}_{ἶ}\left\{{\breve{t}}_{ἶ}\right\}\le {MSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)\le {\mathit{max}}_{ἶ}\left\{{\breve{t}}_{ἶ}\right\}.(28)$

Furthermore, we expose some special cases of the evaluated theory, such asWhile adding $\zeta =1$ in Eq. 24, we obtain the AM operator, such as:

${MSM}^{\left(1\right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{{\displaystyle \sum }}_{1\le ἶ\le \mathfrak{q}}{\breve{t}}_{ἶ}}{C_{\mathfrak{q}}^1}\right)}^1=\frac{1}{\mathfrak{q}}{\displaystyle \sum _{ἶ=1}^{\mathfrak{q}}}{\breve{t}}_{ἶ}.(29)$

While adding $\zeta =2$ in Eq. 24, then we obtain the BM operator for $p=է=1$, such as

${MSM}^{\left(2\right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{{\displaystyle \sum }}_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^2}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^2}\right)}^{\frac{1}{2}}={\left(\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}{\displaystyle \sum _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\breve{t}}_{{ἶ}_1}{\breve{t}}_{{ἶ}_2}\right)}^{\frac{1}{2}}.(30)$

While adding $\zeta =2$ in Eq. 24, then we obtain the GBM operator for $p=է=r=1$, such as

${MSM}^{\left(3\right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{{\displaystyle \sum }}_{1\le {ἶ}_1<{ἶ}_2<{ἶ}_3\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^3}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^3}\right)}^{\frac{1}{3}}={\left(\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)\left(\mathfrak{q}-2\right)}{\displaystyle \sum _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2{\ne ἶ}_3}^{\mathfrak{q}}}{\breve{t}}_{{ἶ}_1}{\breve{t}}_{{ἶ}_2}{\breve{t}}_{{ἶ}_3}\right)}^{\frac{1}{3}}.(31)$

While adding $\zeta =\mathfrak{q}$ in Eq. 24, then we obtain the GM operator, such as

${MSM}^{\left(\mathfrak{q}\right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{{\displaystyle \sum }}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\mathfrak{q}}\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\mathfrak{q}}}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^{\mathfrak{q}}}\right)}^{\frac{1}{\mathfrak{q}}}={\left({\displaystyle \prod _{ἶ=1}^{\mathfrak{q}}}{\breve{t}}_{ἶ}\right)}^{\frac{1}{\mathfrak{q}}}.(32)$

Definition 8. A TSFIMSM operator is stated by

$TSFI{MSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{{\displaystyle \sum }}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{\zeta }}.(33)$

Furthermore, we derive that the following theory is valid, such as

${\displaystyle \prod _{յ=1}^{\zeta }}{\breve{t}}_{{ἶ}_{յ}}=\left(\begin{array}{c}\sqrt[է]{{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)},\\ \sqrt[է]{1-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)}\end{array}\right).(34)$

Then, we obtain

${⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left({\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left({\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)}\end{array}\right).(35)$

According to the presence of the theory of the TSFIWA operator, we have

${⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}=\left(\begin{array}{c}\sqrt[է]{{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)},\\ \sqrt[է]{1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)}\end{array}\right).$

For $\zeta =2$, we have

${⨁}_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}={⨁}_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}\left(\begin{array}{c}\sqrt[\mathit{q}]{{\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)},\\ \sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)}\end{array}\right),=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)},\\ \sqrt[է]{{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)},\\ \sqrt[է]{{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)}\end{array}\right).$

For $\zeta =2$, we obtain the correct result. Furthermore, for we assume that the theory in Eq. 35 also holds for $\zeta =\kappa$, we have

${⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{⨂}_{յ=1}^{\kappa }{\breve{t}}_{{ἶ}_{յ}}=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)}\end{array}\right),$

${=\nu }_{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{⨂}_{յ=1}^{\kappa }{\breve{t}}_{{ἶ}_{յ}}}^{է}+u_{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{⨂}_{յ=1}^{\kappa }{\breve{t}}_{{ἶ}_{յ}}}^{է}+d_{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{⨂}_{յ=1}^{\kappa }{\breve{t}}_{{ἶ}_{յ}}}^{է},$

$=\left(\begin{array}{c}1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right),$

$=\left(1+{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa }}\left(u_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa }\le \mathfrak{q}}\left(1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right).$

Then, we prove that the information in Eq. 35 is also valid for $\zeta =\kappa +1$; we have

${⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}{⨂}_{յ=1}^{\kappa +1}{\breve{t}}_{{ἶ}_{յ}}={⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left({⨂}_{յ=1}^{\kappa }{\breve{t}}_{{ἶ}_{յ}}⨂{\breve{t}}_{{ἶ}_{\kappa +1}}\right),$

$={⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left(\begin{array}{c}\sqrt[\mathit{q}]{{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)},\\ \sqrt[\mathit{q}]{1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)},\sqrt[\mathit{q}]{1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)}\end{array}\right)⨂{\breve{t}}_{{ἶ}_{\kappa +1}},$

$={⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left(\begin{array}{c}\sqrt[\mathit{q}]{{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)\left(1-d_{{ἶ}_{\kappa +1}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\left(1-\left({\nu }_{{ἶ}_{\kappa +1}}^{է}+d_{{ἶ}_{\kappa +1}}^{է}\right)\right)},\\ \sqrt[է]{1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-u_{{ἶ}_{յ}}^{է}\right)\left(1-u_{{ἶ}_{\kappa +1}}^{է}\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^{\kappa }}\left(1-d_{{ἶ}_{յ}}^{է}\right)\left(1-d_{{ἶ}_{\kappa +1}}^{է}\right)}\end{array}\right),$

$={⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left(\begin{array}{c}\sqrt[է]{{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)},\\ \sqrt[\mathit{q}]{1-{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-u_{{ἶ}_{յ}}^{է}\right)},\sqrt[\mathit{q}]{1-{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-d_{{ἶ}_{յ}}^{է}\right)}\end{array}\right),$

$=\left(\begin{array}{c}\sqrt[\mathit{q}]{1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\kappa +1}\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\kappa +1}}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)}\end{array}\right).$

Hence, we obtain our required result.

Theorem 3. Here, we derive the theory of the TSFIMSM operator in the presence of TSF information, such as

$TSFI{MSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{\displaystyle \sum }_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{\zeta }},$

$=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\begin{array}{c}{\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\\ -\left({\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\end{array}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)}\end{array}\right).(36)$

Proof: Consider

${⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)}\end{array}\right).$

Then, we have

${\nu }_{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}}^{է}+u_{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}}^{է}+d_{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}}^{է}=\left(\begin{array}{c}1+{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\\ -{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(\left(u_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right),$

$\frac{1}{C_{\mathfrak{q}}^{\zeta }}\left({⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}\right)=\left(\begin{array}{c}\sqrt[է]{1-{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\\ -{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\\ -{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}\end{array}\right).$

Therefore,

$={\nu }_{\frac{1}{C_{\mathfrak{q}}^{\zeta }}\left({⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}\right)}^{է}+u_{\frac{1}{C_{\mathfrak{q}}^{\zeta }}\left({⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}\right)}^{է}+d_{\frac{1}{C_{\mathfrak{q}}^{\zeta }}\left({⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }{\breve{t}}_{{ἶ}_{յ}}\right),}^{է}$

$=\left(\begin{array}{c}1+{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\\ -{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(u_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right),$

${\left(\frac{{{\displaystyle \sum }}_{1\le {ἶ}_1<{ἶ}_2<\dots \le {ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}{\breve{t}}_{{ἶ}_{յ}}}{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{\zeta }}=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\\ -\left({\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\end{array}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)}\end{array}\right).$

Property 4. When ${\breve{t}}_{ἶ}=\breve{t}=\left(\nu ,u,d\right)$, then we have

$TSFI{MSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\breve{t}.(37)$

Proof: Assume that ${\breve{t}}_{ἶ}=\breve{t}=\left(\nu ,u,d\right)$, then we have

${TSFIMSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(\begin{array}{c}{\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+d^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-\\ {\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+d^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\\ -\left({\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+d^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\end{array}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left({\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-u^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+u^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)-\\ \left({\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+u^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\end{array}\right)\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left({\left(1-\left({\displaystyle \prod _{յ=1}^{\zeta }}\left(1-d^{է}\right)-{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+d^{է}\right)\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)-\\ \left({\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{յ=1}^{\zeta }}\left(1-\left({\nu }^{է}+d^{է}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\end{array}\right)\right)}^{\frac{1}{\zeta }}\right)}\end{array}\right),$

$=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(\begin{array}{c}{\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(\left(\begin{array}{c}\left({\left(1-{\left(1-d^{է}\right)}^{\zeta }-{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)-\\ \left({\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\end{array}\right)\right)}^{\frac{1}{\zeta }}\\ -{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(\begin{array}{c}\left({\left(1-\left({\left(1-u^{է}\right)}^{\zeta }-{\left(1-\left({\nu }^{է}+u^{է}\right)\right)}^{\zeta }\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)-\\ \left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\nu }^{է}+u^{է}\right)\right)}^{\zeta }\right)\end{array}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}\left(\begin{array}{c}\left({\left(1-\left({\left(1-d^{է}\right)}^{\zeta }-{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)-\\ \left({\displaystyle \prod }_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)\end{array}\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)}\end{array}\right),$

$=\left(\begin{array}{c}\sqrt[է]{\left(1-\left({\left(\begin{array}{c}{\left(\left({\left(1-{\left({\left(1-d^{է}\right)}^{\zeta }-{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)-{\left({\left({\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\\ -{\left({\left({\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\right)\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\left({\left(1-\left({\left(1-u^{է}\right)}^{\zeta }-{\left(1-\left({\nu }^{է}+u^{է}\right)\right)}^{\zeta }\right)\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-{\left({\left(1-\left({\nu }^{է}+u^{է}\right)\right)}^{\zeta }\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(1-{\left({\left({\left(1-\left({\left(1-d^{է}\right)}^{\zeta }-{\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}-{\left({\left(1-\left({\nu }^{է}+d^{է}\right)\right)}^{\zeta }\right)}^{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)}^{\frac{1}{\zeta }}\right)}\end{array}\right),$

$=\sqrt[է]{\left(1-d^{է}\right)-\left(1-\left({\nu }^{է}+d^{է}\right)\right)},\sqrt[է]{\left(1-\left(1-\left(1-\left(1-u^{է}\right)\right)\right)\right)},\sqrt[է]{\left(1-\left(1-\left(1-\left(1-d^{է}\right)\right)\right)\right)},$

$=\left(\nu ,u,d\right)=\breve{t}.$

Property 5. Suppose $\breve{t}=\left(\mathrm{1,0}\right)$ and $\breve{t}=\left(\mathrm{0,1}\right)$ then

$\breve{t}\le {TSFIMSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)\le \breve{t}.$

Proof: Using Theorem 6, the property of boundedness can be proven.Few specific cases of the ${TSFIMSM}^{\left(\zeta \right)}$ operator are discussed as follows:When $\zeta =1$, then ${TSFIMSM}^{\left(\zeta \right)}$ the operator becomes the TSF interaction averaging (TSFIA) operator in Eq.36. When $\zeta =2$, then ${TSFIMSM}^{\left(\zeta \right)}$ the operator becomes the special TSF interaction BM (TSFIBM) operator $\left(p=է=1\right)$ as follows:

$TSFIBM\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)=\sqrt[է]{\left(\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}{\oplus }_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}\left({\stackrel{\mathrm{ˇ}}{t}}_{{ἶ}_1}⨂{\stackrel{\mathrm{ˇ}}{t}}_{{ἶ}_2}\right)\right)},(\mathrm{37a})$

$=\left(\begin{array}{c}\sqrt[է]{\left({\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\right)\\ -\left({\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\right)-\\ \left({\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{2\mathfrak{q}\left(\mathfrak{q}-1\right)}}\right)\end{array}\right)}^{\frac{1}{2}}\right)},\\ \sqrt[է]{\left(1-{\left(1-\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\end{array}\right)\right)}^{\frac{1}{2}}\right)},\\ \sqrt[է]{\left(1-{\left(1-\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\end{array}\right)\right)}^{\frac{1}{2}}\right)}\end{array}\right),$

where ${\breve{t}}_{{ἶ}_1}=\left({\nu }_{{ἶ}_1},u_{{ἶ}_1},d_{{ἶ}_1}\right),{\breve{t}}_{{ἶ}_2}=\left({\nu }_{{ἶ}_2},u_{{ἶ}_2},d_{{ἶ}_2}\right)$,Proof:

${\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}=\left(\begin{array}{c}\sqrt[է]{\left(\left(\left(1-d_{{ἶ}_1}^{է}\right)*\left(1-d_{{ἶ}_2}^{է}\right)\right)-\left(\left(1-\left({\nu }_{{ἶ}_1}^{է}+d_{{ἶ}_1}^{է}\right)\right)*\left(1-\left({\nu }_{{ἶ}_2}^{է}+d_{{ἶ}_2}^{է}\right)\right)\right)\right)},\\ \sqrt[է]{\left(1-\left(\left(1-u_{{ἶ}_1}^{է}\right)*\left(1-u_{{ἶ}_2}^{է}\right)\right)\right)},\sqrt[է]{\left(1-\left(\left(1-d_{{ἶ}_1}^{է}\right)*\left(1-d_{{ἶ}_2}^{է}\right)\right)\right)}\end{array}\right),$

$=\sqrt[է]{{\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)},\sqrt[է]{1-{\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)},$

${\nu }_{{\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}}^{է}+u_{{\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}}^{է}+d_{{\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}}^{է}=2-{\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right),$

${⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)=\left(\begin{array}{c}\sqrt[է]{\left(1-\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\right)\right)},\\ \sqrt[է]{\left(\begin{array}{c}1-\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)-\\ \left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}1-\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)-\\ \left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\end{array}\right)}\end{array}\right),$

${\nu }_{{⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)}^{է}+u_{{⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)}^{է}+d_{{⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right),}^{է}=\left(\begin{array}{c}2-\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)\\ -\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)-\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)\end{array}\right),$

$=2-\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)+\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(u_{{ἶ}_{յ}}^{է}-d_{{ἶ}_{յ}}^{է}\right)\right),$

$\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}\left({⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)\right)=\left(\begin{array}{c}\sqrt[է]{\left(1-{\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\end{array}\right)},\\ \sqrt[է]{\left(\begin{array}{c}{\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^{\mathfrak{q}}}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{\mathfrak{q}\left(\mathfrak{q}-1\right)}}\end{array}\right)}\end{array}\right),$

${\nu }_{\frac{1}{\mathfrak{q}\left(q-1\right)}\left({⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)\right)}^{է}+u_{\frac{1}{q\left(q-1\right)}\left({⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)\right)}^{է}+d_{\frac{1}{q\left(q-1\right)}\left({⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)\right),}^{է}$

$=\left(\begin{array}{c}1-{\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\end{array}\right),$

$=\left(1-{\left(\begin{array}{c}1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-\\ {\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\end{array}\right)}^{\frac{1}{q\left(q-1\right)}}+{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(u_{{ἶ}_{յ}}^{է}-d_{{ἶ}_{յ}}^{է}\right)\right)}^{\frac{1}{q\left(q-1\right)}}\right),$

${\left(\frac{1}{q\left(q-1\right)}\left({⨁}_{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q\left({\breve{t}}_{{ἶ}_1}⨂{\breve{t}}_{{ἶ}_2}\right)\right)\right)}^{\frac{1}{2}}=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\right)\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\end{array}\right)}^{\frac{1}{2}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{2q\left(q-1\right)}}\end{array}\right)},\\ \sqrt[է]{\left(1-{\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}\left({\displaystyle \prod _{յ=1}^2}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\right)\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\end{array}\right)}^{\frac{1}{2}}\right)},\\ \sqrt[է]{\left(1-{\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}\left({\displaystyle \prod _{յ=1}^2}\left(1-d_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\right)\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2=1,{ἶ}_1\ne {ἶ}_2}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)}}\end{array}\right)}^{\frac{1}{2}}\right)}\end{array}\right),$

When $\zeta =3,$ then the ${TSFIMSM}^{\left(\zeta \right)}$ operator becomes the special generalized TSFIBM operator $\left(p=1,է=1,r=1\right)$ ἶs:

$TSFIBM\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_q\right)={\left(\frac{1}{q\left(q-1\right)\left(q-2\right)}{\oplus }_{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q\left({\stackrel{\mathrm{ˇ}}{t}}_{{ἶ}_1}⨂{\stackrel{\mathrm{ˇ}}{t}}_{{ἶ}_2}⨂{\stackrel{\mathrm{ˇ}}{t}}_{{ἶ}_3}\right)\right)}^{\frac{1}{3}},$

$=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}{\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}\left({\displaystyle \prod _{յ=1}^3}\left(1-d_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^3}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)\left(q-2\right)}}\right)\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)\left(q-2\right)}}\end{array}\right)}^{\frac{1}{3}}\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{3q\left(q-1\right)\left(q-2\right)}}\end{array}\right)},\\ \sqrt[է]{\left(1-{\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}\left({\displaystyle \prod _{յ=1}^3}\left(1-u_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^3}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)\left(q-2\right)}}\right)\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+u_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)\left(q-2\right)}}\end{array}\right)}^{\frac{1}{3}}\right)},\\ \sqrt[է]{\left(1-{\left(\begin{array}{c}1-\left({\left(1-{\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}\left({\displaystyle \prod _{յ=1}^3}\left(1-d_{{ἶ}_{յ}}^{է}\right)\right)-{\displaystyle \prod _{յ=1}^3}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)\left(q-2\right)}}\right)\\ -{\left({\displaystyle \prod _{{ἶ}_1,{ἶ}_2,{ἶ}_3=1,{ἶ}_1\ne {ἶ}_2\ne {ἶ}_3}^q}{\displaystyle \prod _{յ=1}^2}\left(1-\left({\nu }_{{ἶ}_{յ}}^{է}+d_{{ἶ}_{յ}}^{է}\right)\right)\right)}^{\frac{1}{q\left(q-1\right)\left(q-2\right)}}\end{array}\right)}^{\frac{1}{3}}\right)}\end{array}\right),$

where ${\breve{t}}_{{ἶ}_1}=\left({\nu }_{{ἶ}_1},u_{{ἶ}_1},d_{{ἶ}_1}\right),{\breve{t}}_{{ἶ}_2}=\left({\nu }_{{ἶ}_2},u_{{ἶ}_2},d_{{ἶ}_2}\right)$ and ${\breve{t}}_{{ἶ}_3}=\left({\nu }_{{ἶ}_3},u_{{ἶ}_3},d_{{ἶ}_3}\right)$.When $\zeta =q,$ then the ${TSFIMSM}^{\left(\zeta \right)}$ operator becomes the T-spherical fuzzy interaction geometric averaging (TSFIGA) operator in Eq. 11.When every ${\breve{t}}_{ἶ}=\left({\nu }_{ἶ},u_{ἶ},d_{ἶ}\right)\left(ἶ=\mathrm{1,2},\dots ,q\right)$ becomes ${\breve{t}}_{ἶ}=\left(1,0\right)\left(ἶ=\mathrm{1,2},\dots ,q\right)$ then

${TSFIMSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_q\right)=\left(1,0\right).$

When every ${\breve{t}}_{ἶ}=\left({\nu }_{ἶ},u_{ἶ},d_{ἶ}\right)\left(ἶ=\mathrm{1,2},\dots ,q\right)$ becomes ${\breve{t}}_{ἶ}=\left(0,1\right)\left(ἶ=\mathrm{1,2},\dots ,q\right)$, then

${TSFIMSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_q\right)=\left(\mathrm{0,1}\right).$

Definition 9. A TSFIWMSM operator is particularized by

${TSFIWMSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }\left({\omega }_{{ἶ}_{յ}}{\breve{t}}_{{ἶ}_{յ}}\right)}{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{\zeta }}.(38)$

Theorem 5. Using the theory in Eq. 38, we derive the following information, such as

${TSFIWMSM}^{\left(\zeta \right)}\left({\breve{t}}_1,{\breve{t}}_2,\dots ,{\breve{t}}_{\mathfrak{q}}\right)={\left(\frac{{⨁}_{1\le {ἶ}_1<{ἶ}_2<\dots <{ἶ}_{\zeta }\le \mathfrak{q}}{⨂}_{յ=1}^{\zeta }\left({\omega }_{{ἶ}_{յ}}{\breve{t}}_{{ἶ}_{յ}}\right)}{C_{\mathfrak{q}}^{\zeta }}\right)}^{\frac{1}{\zeta }}.$

$=\left(\begin{array}{c}\sqrt[է]{\left(\begin{array}{c}1-{\left(\begin{array}{c}\left({\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}\left(1-\left(\begin{array}{c}{\displaystyle \prod _{j=1}^{\zeta }}\left(1-\left({\left(1-{\nu }_{i_j}^{է}\right)}^{{\omega }_{i_j}}-{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)\right)\\ -{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\end{array}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\\ -{\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\\ -{\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)}^{\frac{1}{\zeta C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)},\\ \sqrt[է]{\left(1-{\left(\begin{array}{c}1-\left({\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}\left(1-\left(\begin{array}{c}{\displaystyle \prod _{j=1}^{\zeta }}\left(1-\left({\left(1-{\nu }_{i_j}^{է}\right)}^{{\omega }_{i_j}}-{\left(1-\left({\nu }_{i_j}^{է}+u_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)\right)\\ -{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+u_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\end{array}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\\ -{\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+u_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\right)},\\ \sqrt[է]{\left(1-{\left(\begin{array}{c}1-\left({\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}\left(1-\left(\begin{array}{c}{\displaystyle \prod _{j=1}^{\zeta }}\left(1-\left({\left(1-{\nu }_{i_j}^{է}\right)}^{{\omega }_{i_j}}-{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)\right)\\ -{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\end{array}\right)\right)\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\right)\\ -{\left({\displaystyle \prod }_{1\le i_1<i_2<\dots <i_{\zeta }\le \mathfrak{q}}{\displaystyle \prod _{j=1}^{\zeta }}{\left(1-\left({\nu }_{i_j}^{է}+d_{i_j}^{է}\right)\right)}^{{\omega }_{i_j}}\right)}^{\frac{1}{C_{\mathfrak{q}}^{\zeta }}}\end{array}\right)}^{\frac{1}{\zeta }}\right)}\end{array}\right).(39)$

Example 4. Suppose ${\breve{t}}_1=\left(\mathrm{0.8,0.5,0.3}\right),{\breve{t}}_2=\left(0.9,0.7,0.0\right),{\breve{t}}_3=\left(\mathrm{0.5,0.2,0.1}\right),{\breve{t}}_4=\left(\mathrm{0.4,0.3,0.2}\right)$ be four TSFVs and $\omega =\left(\mathrm{0.15,0.40,0.25,0.20}\right)$. Some methods are utilized to calculate the aggregated values. Table 3 and Table 4 show the results.From the aforementioned information, we noticed that the derived theory has a lot of benefits because the proposed theory is the modified theory of a bundle of existing knowledge. Furthermore, we aim to prove the supremacy and effectiveness of the derived idea with the help of comparative analysis.

TABLE 3

TABLE 3. Aggregated results by using different methods.

TABLE 4

TABLE 4. Aggregated matrix of score values $\mathfrak{s}\left(\breve{t}\right)$ by using the information in Table 3.

5 Application in MADM technique

In this part, we describe the exact procedures for a novel MADM method using the suggested operators in a TSF environment. Suppose $\left\{F_1,F_2,\dots ,F_m\right\}$ be a collection of alternatives, the collection of attributes be $\left\{C_1,C_2,\dots ,C_{\mathfrak{q}}\right\}$ associated with the weight vector $\left({\omega }_1,{\omega }_2,\dots ,{\omega }_{\mathfrak{q}}\right)$, satisfying ${\omega }_{ἶ}\ge 0$ and ${\displaystyle \sum _{ἶ=1}^{\mathfrak{q}}}{\omega }_{ἶ}=1$. Utilizing TSFV ${\breve{t}}_{{ἶ}_j}=\left({\nu }_{{ἶ}_j},u_{{ἶ}_j},d_{{ἶ}_j}\right)$, the decision maker calculates alternatives concerning attribute to form $D={\left({\breve{t}}_{{ἶ}_j}\right)}_{m\times n}$. The proposed multiple attribute decision-making method’s particular steps are listed as follows, along with the given aggregation operators.

Step 1: While calculating alternatives $F_{ἶ}$ concerning attributes $C_j$, the decision makers give TSFV ${\breve{t}}_{{ἶ}_j}=\left({\nu }_{{ἶ}_j},u_{{ἶ}_j},d_{{ἶ}_j}\right)$ and formed a decision matrix as $D={\left({\breve{t}}_{{ἶ}_j}\right)}_{m\times n}$.The normalized decision matrix is created by transforming the TSF matrix. The higher attribute values are better if the attributes are beneficial whereas lower attribute values are better if the attributes are cost attributes. The normalized TSF decision matrix is obtained by converting the cost-type attribute value into benefit-type value, which results in $D^{\prime }={\left({\breve{t}}_{{ἶ}_j}^{\prime }\right)}_{m\times n}$.

${\breve{t}}_{{ἶ}_j}^{\prime }=\left\{\begin{array}{c}{\breve{t}}_{{ἶ}_j}forbenifitattribute{C}_j\\ {\breve{t}}_{{ἶ}_j}^{c}forcostattribute{C}_j\end{array}\right\},$

where $,{\breve{t}}_{{ἶ}_j}^c=\left(d_{{ἶ}_j},u_{{ἶ}_j},{\nu }_{{ἶ}_j}\right)$.

Step 2: Add alternative ranking values ${\breve{t}}_{{ἶ}_j}=\left({\nu }_{{ἶ}_j},u_{{ἶ}_j},d_{{ἶ}_j}\right)\left(ἶ=\mathrm{1,2},\dots ,\mathfrak{q},j=\mathrm{1,2},\dots ,m\right)$ that have been normalized into collaborative units ${\breve{t}}_{ἶ}=\left({\nu }_{ἶ},u_{ἶ},d_{ἶ}\right)$. If the attribute weights are known, ${\breve{t}}_{ἶ}$ are used to aggregate by using Eqs 21, 26.

Step 3: Evaluate the score value of ${\breve{t}}_{ἶ}$.

Step 4: Utilizing the score function according to the technique in definition (3), rank ${\breve{t}}_{ἶ}$.

Step 5: The optimal alternative should be chosen after ranking the other options using ${\breve{t}}_{ἶ}$.

5.1 Application in digital green innovation

Green innovation is a process that involves developing green technologies, products, and processes as well as the accompanying companies, management, and systems. Digital innovation creates new possibilities for climate change mitigation and adaptation. Based on the Paris Agreement and the United Nations Framework Convention on Climate Change, a fundamental framework for the world’s response to climate change has been formed. Green innovation” is technological innovation that involves energy conservation, pollution prevention, waste recycling, green product design, or corporate environmental management. These innovations can significantly lessen the negative effects on the environment while also generating value for the company and its stakeholders. How to improve the green competitiveness and profit of enterprises in the environment of climate change is an important issue. In this case, we need to choose the most talented entrepreneurs from a large number of alternative projects to invest in. The criteria and methods presented in this paper are applicable to the selection of DGI investment projects.

Example 1: Pakistan has been listed as one of the top 10 nations in the world most impacted by climate change. The country’s environmental sustainability strategy is managed by the government. All people concerned must take responsibility for maintaining the ecosystem and its resources, both the governmental and private organizations and particular people. To encourage the development of ideas and solutions for some of the most serious issues we face, the National Incubation Center regularly hosts tech conferences and innovation challenges. It is an honor to have teamed up with Pak Mission Society to find solutions to issues related to climate change, given the situation of the environment at the moment. We will be asking Pakistan’s most talented entrepreneurs $F_m=\left\{F_1,F_2,F_3,F_{4,}{F}_5\right\}$ for business ideas based on these attributes:

Based on the theory, this study constructs a framework system for enterprises to choose DGI investment projects.

${\mathit{C}}_{\mathbf{1}};$ Green entrepreneurs should also have perceived credibility, bravery, and intellectual abilities.

${\mathit{C}}_{\mathbf{2}}$: They also possess planning and time management abilities, which are essential for the profession because they must remember particular rules and knowledge.

${\mathit{C}}_{\mathbf{3}}$: They should have effective interpersonal and communication skills and good management and entrepreneurial abilities.

${\mathit{C}}_{\mathbf{4}}$: They must be able to think strategically and work for sustainability and the planet’s future alongside our future generations.

Solving the numerical example using decision-making steps is the best way to get the optimal solution.

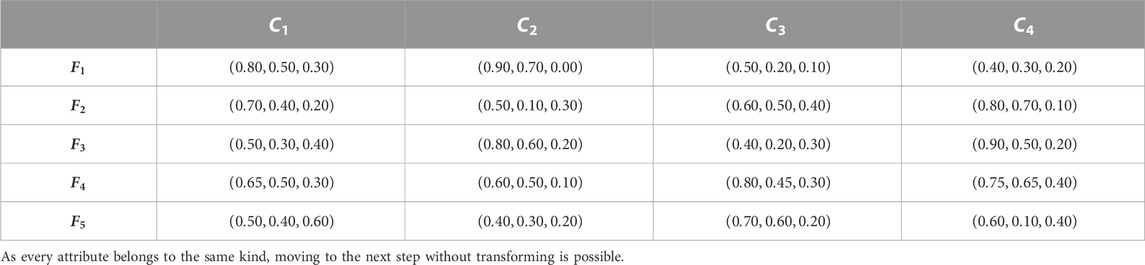
Step 1: The TSFV is used to calculate the alternatives concerning the attributes, and the decision matrix $D={\left({\breve{t}}_{{ἶ}_j}\right)}_{5\times 4}$ is created and shown in Table 5.

Step 2: The attribute weight vector is assumed to be. We utilize Eq. 26 to calculate each alternate collective evaluation value. In this case, we use ${TSFIWMSM}^{\left(\zeta \right)}$ operator with $\zeta =3$.

TABLE 5

TABLE 5. T-spherical fuzzy decision matrix.

Figure 1 is the graphical representation of the TSFIWMSM operator using Table 6, which shows that when $\zeta =1,$ the optimal alternative is $F_1$ and for all $\zeta =2$, $3$, and $4,$ the optimal alternative is $F_3$.

FIGURE 1

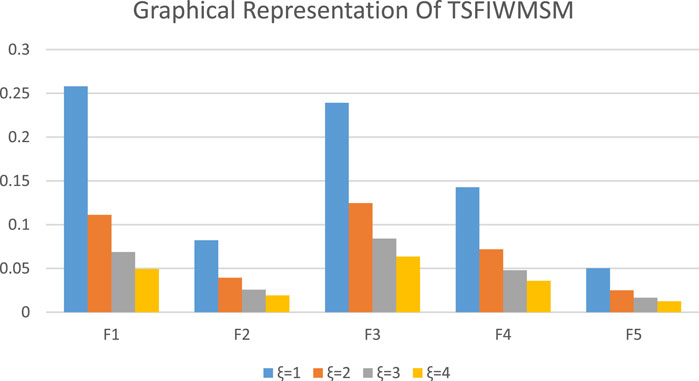
FIGURE 1. Demonstration of various $\zeta$ using TSFIWMSM in Table 6.

TABLE 6

TABLE 6. Results of various $\zeta$ in the ${TSFIWMSM}^{\left(\zeta \right)}$ operator.

Figure 2 is the graphical representation of the TSFIMSM operator using Table 7, which shows that when $\zeta =1$, $2$, and $3,$ the optimal alternative is $F_1$, and when $\zeta =4$, the optimal alternative is $F_3$.

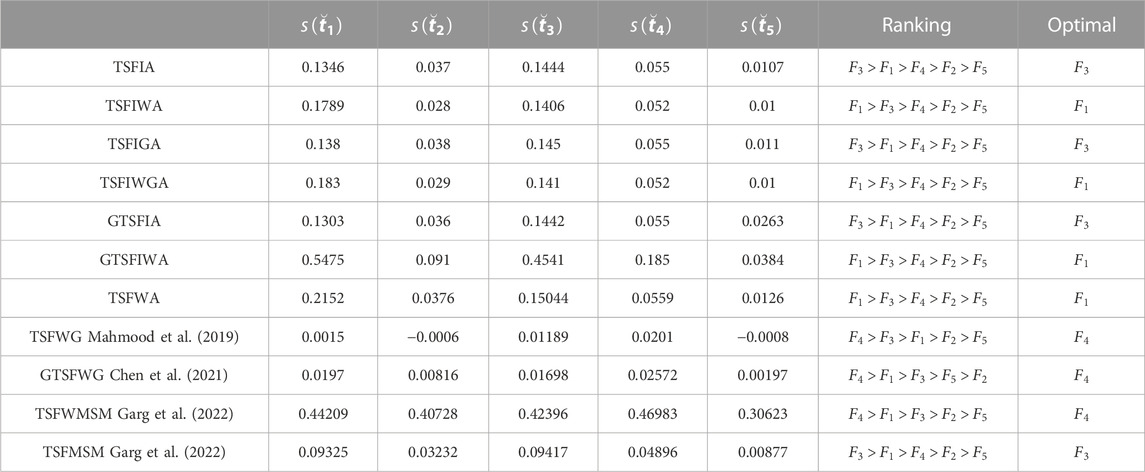
Step 3: Eq. 2 can be used to determine the scores $\mathfrak{s}\left({\breve{t}}_{ἶ}\right)\left(ἶ=\mathrm{1,2},\dots ,5\right)$ of the TSFIWMSM and TSFIMSM operator to obtain Table 8.

Step 4: According to the ranking of scores, ${\breve{t}}_{ἶ}\left(ἶ=\mathrm{1,2},\dots ,5\right)$ can be ranked as Table 9.

Step 5: Ranking of the alternatives would be

FIGURE 2

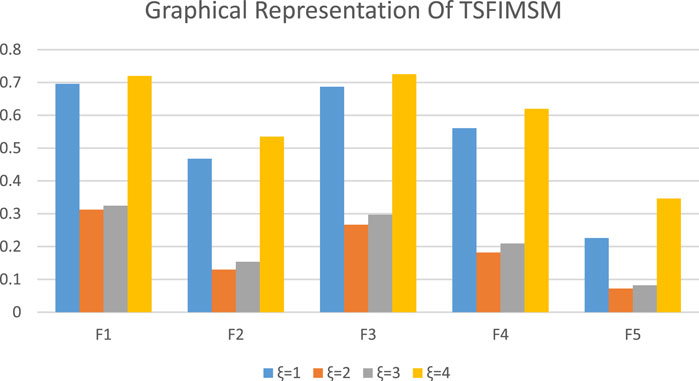
FIGURE 2. Graphical demonstration of various $\zeta$ by using the data in Table 7.

TABLE 7

TABLE 7. Results of various $\mathit{\zeta }$ in the ${\mathit{T}\mathit{S}\mathit{F}\mathit{I}\mathit{M}\mathit{S}\mathit{M}}^{\left(\mathit{\zeta }\right)}$ operator.

TABLE 8

TABLE 8. Aggregated matrix of the score value using Tables 6, 7.

TABLE 9

TABLE 9. Ranking of scores utilizing the aforementioned operators.

5.2 Parameter sensitivity and comparative analysis

This section discusses the impact factor of various $\mathit{\zeta }$ using TSFIWMSM and TSFIMSM operators. Here, we also discuss the comparison of proposed operators with existing operators.

5.3 Impact of the parameter $\mathit{\zeta }$

In the ${TSFIWMSM}^{\left(\zeta \right)}$ operator, other $\mathit{\zeta }$ can also be taken into consideration. Table 6 shows the outcomes if other ζ is taken into consideration. The ranking for $\zeta =\mathrm{2,3,4}$ is similar and $F_3$ is the optimal choice. If $\zeta =1$, then $F_1$ reduces to the optimal choice and $F_3$ reduces to the suboptimal alternative. In actuality, the ${TSFIWMSM}^{\left(\zeta \right)}$ The operator becomes the TSFIGA operator when $\zeta =1$, and the interrelation among arguments has not been considered. Outcomes of different rankings are, therefore, valid.

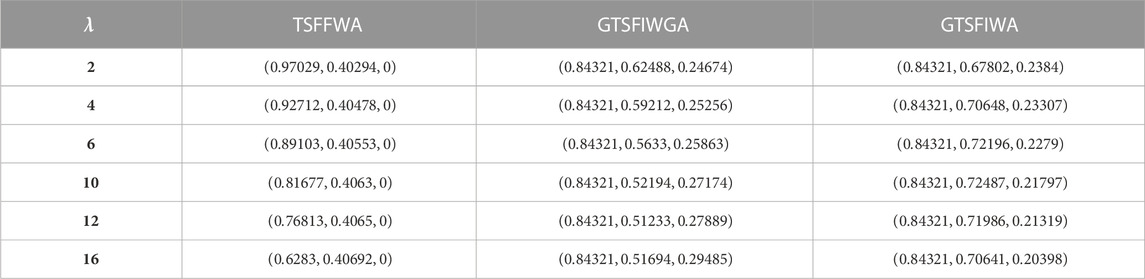
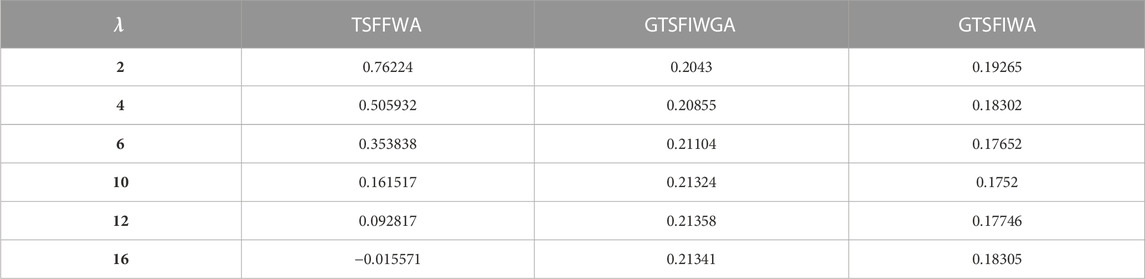
Table 7 shows the outcomes of utilizing the ${TSFIMSM}^{\left(\zeta \right)}$ operator in the aggregation technique in Step 2. Utilizing the ${TSFIWMSM}^{\left(\zeta \right)}$ operator, except $\zeta =1,$ the optimal alternative is $F_1$, whereas by using the ${TSFIMSM}^{\left(\zeta \right)}$ operator, when $\zeta =4,$ the optimal alternative is $F_3$. As different attribute weights might reflect the significance of various attributes, the outcomes are valid. Following the actual requirements and the features of the decision problems, decision makers can choose the attribute weights.

5.4 Sensitivity of the parameter $\mathit{է}$

This section examines the sensitivity of the relevant parameter and how it affects the aggregation outcomes. To see the effects, we change the variable parameter and present the ranking outcomes in Table 11.

The TSFIMSM and TSFIWMSM operators also allow for the consideration of other $է$. Table 11 shows the outcomes when $է$ is taken into account. For $\zeta =3$, if we take $է=4$, the optimal alternative of TSFIWMSM is $F_3$ and if we take $է=6$ and so on, the ranking value is the same and the optimal alternative is $F_1$. For the TSFIMSM operator when $\zeta =3$ we take $է=4$ and so on, the ranking value is the same and the optimal solution is $F_1$.

6 Comparison

The interrelation among membership, abstinence, and non-membership is not considered if operations of TSFVs in Definition 2 are utilized in the aggregation procedure. In Step 2, the aggregation operations mentioned previously are utilized, and the outcomes are shown in Table 12. It is clear from the outcomes that these differ from those of the TSFI operators, including the TSFIA, TSFIWA, TSFIGA, TSFIWGA, GTSFIA, and GTSFIWA operators, which are displayed in Table 12. With regards to the attribute $C_2$, the evaluation value of alternative $F_1$ is $\left(\mathrm{0.90,0.70,0.0}\right)$, satisfying $\zeta =2$ and $է=9$. If the operational laws in Definition 2 are utilized, all of the non-memberships in $F_1$ have no impact on the outcomes in the aggregated operators including the TSF weighted averaging (TSFWA) operator, TSF weighted geometric (TSFWG) operator (Mahmood et al., 2019), generalized TSFWA (GTSFWA) operator (Chen et al., 2021), generalized TSFWG (GTSFWG) operator, TSFMSM operator (Garg et al., 2022), and TSFWMSM operator (Garg et al., 2022), which are not reasonable. TSFI operators have been created to overcome the limitations. As a result, the outcomes obtained by utilizing TSFI operators are more logical. TSFVs are used to represent the evaluation values, which are more flexible than existing operators to describe uncertain and fuzzy information. Using the MSM, the relationship between more than two input arguments has been considered. The relationship between MD and NMD has been viewed by utilizing the new operation laws. Thus, the proposed method can produce more logical and scientific decision-making outcomes.

It is worth noticing that the results obtained using different operators are different. This is because of the nature of the operators and the parameters involved. For instance, the TSFIA operator has no associated weight vector, while the TSFIWA operator has a weight factor. Similar is the case with TSFIG and TSFWIG operators. However, the results of Tables 10–12 clearly show that the operators proposed in the paper have better results because of their advanced nature as the MSM operators proposed in Garg et al. (2022) have certain limitations which were discussed at the beginning of the paper. Furthermore, we have also compared the proposed work with Spearman’s rank correlation coefficient measures, which was proposed by Sedgwick [Sedgwick, P. (2014) Spearman’s rank correlation coefficient. Bmj, 349.] in 2014, which is very valuable and dominant measures based on classical set theory. For these measures, it is not possible to evaluate the proposed types of data because the arranged information is given in the shape of T-spherical fuzzy numbers, and the existing measure was computed based on the crisp set which is the special case of the proposed theory, but in the future, we aim to derive it for T-spherical fuzzy sets to improve the worth of the proposed theory.

TABLE 10

TABLE 10. Ranking of alternatives utilizing the aforementioned operators.

TABLE 11

TABLE 11. Influence of the parameter.

TABLE 12

TABLE 12. Comparison of various proposed and existing aggregation operators.

Figure 3 is the graphical representation of the proposed and existing operators utilizing Table 12, making it easy to understand the optimal alternative. Figure 3 graphically shows that $F_3$ is the optimal alternative to TSFIA, TSFIGA, GTSFIA, and TTSFMSM. $F_1$ is the optimal alternative of TSFIWA, TSFIWGA, GTSFIWA, and TSFWA, and $F_4$ is the optimal alternative to TSFWG, GTSFWG, and TSFWMSM.

FIGURE 3

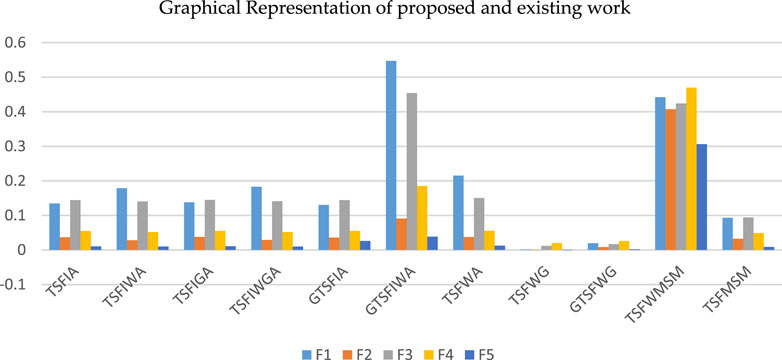
FIGURE 3. Graph illustrating the comparison between the proposed and existing operator utilizing the information in Table 12.

6.1 Advantages of the proposed operator

The following section will elaborate on the method’s superiority in dealing with situations of uncertainty by examining its properties in the context of some previous studies. As we all know, the traditional operator does not consider the interaction between MD, NMD, and AD with $է{\in \mathbb{Z}}^{+}$ of different TSFVs, so they can get unreasonable results in some special cases, especially when abstinence and non-memberships are 0. On the contrary, the interaction operational rules can consider the interactions between MD, NMD, and AD sufficiently, so the method proposed in this paper is more reasonable to produce the ranking result because it can overcome the weakness when abstinence and non-memberships are 0. Hence, in today’s complicated policymaking and risk management-related issues, data aggregation will be managed and useful for dealing with decision-making issues. The proposed operators reduce to earlier versions if we employ certain cases and are given in Remark 1:

Remark 1. The results obtained in Theorem 3 and Theorem 5 reduce to the framework of

1) SFSs if we place $է=2$.

2) PFSs if we place $է=1$.

3) qROFSs if we place $u\left(r\right)=0$.

4) PyFSs if we place $u\left(r\right)=0$ and $է=2$.

5) IFSs if we place $u\left(r\right)=0$ and $է=1$.

Because of Remark 1, we claim that the proposed work is more generalized than the previous one and the other fuzzy frameworks cannot be applied to the current example because of the diverse nature of the information.

7 Conclusion

In this section, we will learn about the following operators and techniques, such as

1. Based on the interaction operations for TSFVs, this research suggested several interaction MSM operators for TSFVs and generalized the MSM operator to TSFVs. After that, we talked about several of their desirable traits, like idempotency and commutativity.

2. An approach for the MADM problems was also proposed under the consideration of derived operators.

3. We further examined some particular examples of these operators and compared the presented results with those of many existing operators to justify the validity and supremacy of the stated approaches.

4. While comparing the current operators, we know that the proposed method is more extensive than several other existent methods.

The primary benefit is that they can capture the relationships between several flexible input arguments due to the parameter $է$. Moreover, they can consider how the MD, AD, and NMD of TSFVs interact to help solve various issues when one of the NMDs is 0. Using these operators’ applications in recent studies is necessary to address decision-making issues. In future, we aim to target the derived theory and try to utilize them in the field of modern information fusion theory, artificial intelligence, machine learning, evaluations about resources and the environment, and decision-making analysis.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4310396DSR66.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akram, M., Ullah, K., and Pamucar, D. (2022). Performance evaluation of solar energy cells using the interval-valued T-spherical fuzzy Bonferroni mean operators. Energies 15, 292. doi:10.3390/en15010292

CrossRef Full Text | Google Scholar

Ashraf, A., Ullah, K., Hussain, A., and Bari, M. (2022). Interval-valued picture fuzzy Maclaurin symmetric mean operator with application in multiple attribute decision-making. Rep. Mech. Eng. 3, 301–317. doi:10.31181/rme20020042022a

CrossRef Full Text | Google Scholar

Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20, 87–96. doi:10.1016/s0165-0114(86)80034-3

CrossRef Full Text | Google Scholar

Chen, Y., Munir, M., Mahmood, T., Hussain, A., and Zeng, S. (2021). Some generalized T-spherical and group-generalized fuzzy geometric aggregation operators with application in MADM problems. J. Math. 2021, 1–17. doi:10.1155/2021/5578797

CrossRef Full Text | Google Scholar

Cuong, B. C., and Kreinovich, V. (2014). Picture fuzzy sets. J. Comput. Sci. Cybern. 30, 409–420. doi:10.15625/1813-9663/30/4/5032

CrossRef Full Text | Google Scholar

Dong, T., Yin, S., and Zhang, N. (2023). New energy-driven construction industry: Digital green innovation investment project selection of photovoltaic building materials enterprises using an integrated fuzzy decision approach. Systems 11, 11. doi:10.3390/systems11010011

CrossRef Full Text | Google Scholar

Garg, H., Ahmad, A., Ullah, K., Mahmood, T., and Ali, Z. (2022). Algorithm for multiple attribute decision-making using T-spherical fuzzy Maclaurin symmetric mean operator. Iran. J. Fuzzy Syst. 19, 111–124. doi:10.22111/ijfs.2022.7215

CrossRef Full Text | Google Scholar

Garg, H., Munir, M., Ullah, K., Mahmood, T., and Jan, N. (2018). Algorithm for T-spherical fuzzy multi-attribute decision making based on improved interactive aggregation operators. Symmetry 10, 670. doi:10.3390/sym10120670

CrossRef Full Text | Google Scholar

Hussain, A., Ullah, K., Yang, M.-S., and Pamucar, D. (2022). Aczel-alsina aggregation operators on T-spherical fuzzy (TSF) information with application to TSF multi-attribute decision making. IEEE Access 10, 26011–26023. doi:10.1109/access.2022.3156764

CrossRef Full Text | Google Scholar

Jstor 2022 ON generalized symmetric means of two variables on jstor. Available at:https://www.jstor.org/stable/43668126 (Accessed July 26, 2022).

Google Scholar

Ju, Y., Liu, X., and Ju, D. (2016). Some new intuitionistic linguistic aggregation operators based on Maclaurin symmetric mean and their applications to multiple attribute group decision making. Soft Comput. 20, 4521–4548. doi:10.1007/s00500-015-1761-y

CrossRef Full Text | Google Scholar

Karaaslan, F., and Al-Husseinawi, A. H. S. (2022). Hesitant T-spherical Dombi fuzzy aggregation operators and their applications in multiple criteria group decision-making. Complex & Intelligent Syst. 8, 3279–3297. doi:10.1007/s40747-022-00669-x

CrossRef Full Text | Google Scholar

Karaaslan, F., and Dawood, M. A. D. (2021). Complex T-spherical fuzzy Dombi aggregation operators and their applications in multiple-criteria decision-making. Complex Intell. Syst. 7, 2711–2734. doi:10.1007/s40747-021-00446-2

CrossRef Full Text | Google Scholar

Khan, M. R., Ullah, K., Pamucar, D., and Bari, M. (2022). Performance measure using a multi-attribute decision-making approach based on complex T-spherical fuzzy power aggregation operators. J. Comput. Cognitive Eng. 1 (3), 138–146. doi:10.47852/bonviewJCCE696205514

CrossRef Full Text | Google Scholar

Liu, P., Chen, S.-M., and Wang, Y. (2020). Multiattribute group decision making based on intuitionistic fuzzy partitioned Maclaurin symmetric mean operators. Inf. Sci. 512, 830–854. doi:10.1016/j.ins.2019.10.013

CrossRef Full Text | Google Scholar

Liu, P., and Qin, X. (2017). Maclaurin symmetric mean operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision-making. J. Exp. Theor. Artif. Intell. 29, 1173–1202. doi:10.1080/0952813x.2017.1310309

CrossRef Full Text | Google Scholar

Maclaurin, C. A. (1729). Second letter to martin folkes, esq.; concerning the roots of equations, with demonstration of other rules of algebra. Philos. Trans. R. Soc. Lond. Ser. A 1729, 59–96. doi:10.1098/rstl.1729.0011

CrossRef Full Text | Google Scholar

Mahmood, T., and Ali, Z. (2020). Aggregation operators and VIKOR method based on complex Q-rung orthopair uncertain linguistic informations and their applications in multi-attribute decision making. Comp. Appl. Math. 39, 306. doi:10.1007/s40314-020-01332-2

CrossRef Full Text | Google Scholar

Mahmood, T. A. (2020). Novel approach towards bipolar soft sets and their applications. J. Math. 2020, 4690808. doi:10.1155/2020/4690808

CrossRef Full Text | Google Scholar

Mahmood, T., Ullah, K., Khan, Q., and Jan, N. (2019). An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 31, 7041–7053. doi:10.1007/s00521-018-3521-2

CrossRef Full Text | Google Scholar

Naseem, A., Ullah, K., Akram, M., Božanić, D., and Ćirović, G. (2022). Assessment of smart grid systems for electricity using power Maclaurin symmetric mean operators based on T-spherical fuzzy information. Energies 15, 7826. doi:10.3390/en15217826

CrossRef Full Text | Google Scholar

Özlü, Ş., and Karaaslan, F. (2022). Correlation coefficient of T-spherical type-2 hesitant fuzzy sets and their applications in clustering analysis. J. Ambient Intell. Humaniz. Comput. 13, 329–357. doi:10.1007/s12652-021-02904-8

CrossRef Full Text | Google Scholar

Qin, J., and Liu, X. (2014). An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J. Intelligent Fuzzy Syst. 27, 2177–2190. doi:10.3233/IFS-141182

CrossRef Full Text | Google Scholar

Qin, J., Liu, X., and Pedrycz, W. (2015). Hesitant fuzzy Maclaurin symmetric mean operators and its application to multiple-attribute decision making. Int. J. Fuzzy Syst. 17, 509–520. doi:10.1007/s40815-015-0049-9

CrossRef Full Text | Google Scholar

Ullah, K., Mahmood, T., and Jan, N. (2018). Similarity measures for T-spherical fuzzy sets with applications in pattern recognition. Symmetry 10, 193. doi:10.3390/sym10060193

CrossRef Full Text | Google Scholar

Ullah, K. (2021). Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math. Problems Eng. 2021, 1–13. doi:10.1155/2021/1098631

CrossRef Full Text | Google Scholar

Wang, J., Wei, G., Wang, R., Alsaadi, F. E., Hayat, T., Wei, C., et al. (2019). Some Q-rung interval-valued orthopair fuzzy Maclaurin symmetric mean operators and their applications to multiple attribute group decision making. Int. J. Intelligent Syst. 34, 2769–2806. doi:10.1002/int.22156

CrossRef Full Text | Google Scholar

Wang, J., Yang, Y., and Li, L. (2018). Multi-criteria decision-making method based on single-valued neutrosophic linguistic Maclaurin symmetric mean operators. Neural Comput. Appl. 30, 1529–1547. doi:10.1007/s00521-016-2747-0

CrossRef Full Text | Google Scholar

Wei, G., and Lu, M. (2018). Pythagorean fuzzy Maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intelligent Syst. 33, 1043–1070. doi:10.1002/int.21911

CrossRef Full Text | Google Scholar

Wei, G., Wei, C., Wang, J., Gao, H., and Wei, Y. (2019). Some Q-rung orthopair fuzzy Maclaurin symmetric mean operators and their applications to potential evaluation of emerging technology commercialization. Int. J. Intelligent Syst. 34, 50–81. doi:10.1002/int.22042

CrossRef Full Text | Google Scholar

Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 25, 1222–1230. doi:10.1109/tfuzz.2016.2604005

CrossRef Full Text | Google Scholar

Yager, R. R. (2013). “Pythagorean fuzzy subsets,” in Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, June 24-28, 2013, 57–61.

CrossRef Full Text | Google Scholar

Yager, R. R. (2001). The power average operator. IEEE Trans. Syst. Man, Cybern. - Part A Syst. Humans 31, 724–731. doi:10.1109/3468.983429

CrossRef Full Text | Google Scholar

Yang, W., and Pang, Y. (2018). New pythagorean fuzzy interaction Maclaurin symmetric mean operators and their application in multiple attribute decision making. IEEE Access 6, 39241–39260. doi:10.1109/ACCESS.2018.2856270

CrossRef Full Text | Google Scholar

Yin, S., and Yu, Y. (2022). An adoption-implementation framework of digital green knowledge to improve the performance of digital green innovation practices for industry 5.0. J. Clean. Prod. 363, 132608. doi:10.1016/j.jclepro.2022.132608

CrossRef Full Text | Google Scholar

Yin, S., Zhang, N., Ullah, K., and Gao, S. (2022). Enhancing digital innovation for the sustainable transformation of manufacturing industry: A pressure-state-response system framework to perceptions of digital green innovation and its performance for green and intelligent manufacturing. Systems 10, 72. doi:10.3390/systems10030072

CrossRef Full Text | Google Scholar

Yu, S.-M., Zhang, H., and Wang, J. (2018). Hesitant fuzzy linguistic Maclaurin symmetric mean operators and their applications to multi-criteria decision-making problem. Int. J. Intelligent Syst. 33, 953–982. doi:10.1002/int.21907

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8, 338–353. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar