Time-varying risk aversion and dynamic dependence between crude oil futures and European Union allowance futures markets

1 Introduction

With the rapid development of the global economy, the burning of fossil energy has produced a large amount of greenhouse gases, which has exacerbated global warming and brought irreversible catastrophic consequences to the earth on which human beings depend for survival and development. As a consequence, the global climate change that hinders economic development, threatens human health and affects environmental improvement has attracted more and more concerns of people (Han et al., 2019; Tol, 2020; Zhao et al., 2020; Ahonen et al., 2022). In order to control greenhouse gas emissions, the United Nations Framework Convention on Climate Change and the Kyoto Protocol have been proposed. The Kyoto Protocol shows that on the basis of limiting the total amount of carbon emissions, enterprises can purchase a certain amount of carbon allowances from enterprises with excess carbon allowances to achieve their emission reduction targets. In this context, the European Union established the earliest, largest and most active carbon emission trading market to reduce the emission of greenhouse gas.(Bruninx et al., 2020). Furthermore, as a typical fossil energy, crude oil combustion is one of the main sources of carbon emission. Therefore, studying the dynamic conditional dependence between crude oil futures market and EUA futures market is of great importance for designing effective strategies to reduce greenhouse gas emissions and to achieve the goal of carbon neutralization.

However, in recent years, the EUA futures prices have exprienced great fluctuations, which may be closely related to crude oil prices (Liu et al., 2017; Dutta, 2018; Xia et al., 2019; Krokida et al., 2020). Some scholar have further studied the dependence between crude oil futures and EUA futures markets. For instance, Yu et al. (2015) decompose the returns of the EUA futures market and crude oil futures market in different time-scales, and study the causal relationship between EUA futures market and crude oil futures market by using a multi-scale analysis and causality testing approach. They show that in a long time-scale, the long-term trend of the two futures markets exhibits an obvious linear relationship. Wang and Guo (2018) quantitatively study the time-varying spillover effect between EUA futures market and crude oil futures market by using the spillover index introduced by Diebold and Yilmaz (2012) through the variance decomposition of the prediction error, and reveal the asymmetric spillover effects between two types of futures markets in return and volatility series. Ma et al. (2021) propose a smooth transformation regression (STR) model to study the correlation between crude oil futures market and EUA futures market using the WTI futures and EUA futures prices, and show that crude oil futures prices and EUA futures prices have a mutual effect on each other, and there is a significant linear correlation between the two markets. Zheng et al. (2021) investigate the asymmetric relationship between oil prices shocks and the carbon emission trading market in China by using the nonlinear autoregressive distributed lag (NARDL) model, and show that oil prices shocks have a long-term asymmetric effect on carbon emission allowance prices, and the oil supply shocks are the main factor causing carbon allowance prices changes. Ren et al. (2022a) study the asymmetric relationship between different oil prices shocks and EUA futures market from the perspective of supply, demand and risk shocks. They show that the role of oil prices shocks in affecting the inefficiency degree of the EUA futures market varies depending on the source of the oil prices shocks. Ahonen et al. (2022) use the dynamic correlation model combined with the generalized spillover index proposed by Diebold and Yilmaz (2012) to study the volatility spillover effect of the crude oil futures market on the EUA futures market when the futures price of West Texas Intermediate Crude Oil (WTI) was in a negative period in 2020. Their empirical results show that when the futures price of WTI was in a negative period, the spillover effect of the crude oil futures market on the EUA futures market increased significantly. Ren et al. (2022b) study the short-term, medium-term and long-term effects of the crude oil futures prices on the EUA futures prices by using the quantile Granger causality test and the quantile-on-quantile regression methods, and show that the effects of the crude oil futures prices on the EUA futures prices are different in different time dimensions. In the short term, the crude oil futures prices have a significantly negative impact on the EUA futures prices, and have a significantly positive impact in the medium-term and long-term. Although a large number of scholars have studied the dependence between crude oil futures and EUA futures markets, there is no consistent views.

Dispite the fact that EUA futures market is found to be closely related to crude oil futures market at the theoretical and empirical level, most of existing literature that focues on the dependence between crude oil futures and EUA futures markets ignores the influence of exogenous variables, such as economic, political and investor sentiment (Qadan and Nama, 2018; Zhang and Li, 2019; Wang et al., 2021). Qadan and Nama (2018) study the influence of investor sentiment on the crude oil futures market and find that volatility shocks spill over from investor sentiment to the crude oil futures market, leading to fluctuation in crude oil futures prices. Zhang and Li (2019) study the influence of investor sentiment on the risk of crude oil futures market by using wavelet analysis, and find that investor sentiment leads to downside risk in the crude oil futures market. Wang et al. (2021) find that investor sentiment is closely related to crude oil futures market under extreme shocks. Recently, Bams et al. (2017) document that investor sentiment is highly correlated with the risk aversion. Guiso et al. (2018) find that after the 2008–2009 global financial crisis, both the qualitative and quantitative indicators of risk aversion increased significantly. Demirer et al. (2022) explore the predictive ability of RA on the crude oil futures volatility. However, to the best of our knowledge, few authors have studied the influence of RA on the conditional dependence between crude oil and EUA futures markets. Thus, this paper main objective is to investigate the impact of RA on the dynamic conditional dependence between crude oil futures and EUA futures markets.

In order to empirically investigate the impact of RA on the dynamic conditional dependence between crude oil futures and EUA futures markets, we use the RA index recently developed by Bekaert et al. (2021). The RA index is constructed based on a dynamic arbitrage-free asset pricing model using six financial instruments, including the term spread, credit spread, detrended dividend yield, realized and risk-neutral equity return variance and realized corporate bond yield variance, which takes into account the impact of different economic environments on investor risk aversion. Note that the RA index is low frequency monthly variables with different frequencied from daily crude oil futures and EUA futures data. In order to deal with the problem of mixed frequency data, the copula-MIDAS framework proposed by Gong et al. (2018) is employed in this papaer. The copula-MIDAS model provides a convenient framework for describing the dependence between financial assets that exhibits obvious time-varying characteristics, which allows explanatory variables to be directly included in the dependence structure (Jiang et al., 2020; Nguyen and Javed, 2021; Gong et al., 2022; Shi et al., 2022; Wu et al., 2022). However, the copula-MIDAS model fails to investigate the influence of RA on the dependence between crude oil futures and EUA futurres merkats. Furthermore, a large number of literature show that it is useful for time-varying copula model to investigate the dynamic dependence (Patton, 2006; Hussain and Li, 2018; Oh and Patton, 2018; Yao and Sun, 2018).

Inspired by the above insights, in this paper we propose the copula-MIDAS-RA model to study the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets. For implementation, we first use the AR-GARCH model to fit the marginal distributions of crude oil futures returns and EUA futures returns, and then use the copula-MIDAS-RA model to estimate the joint distributions of crude oil futures returns and EUA futures returns and to explore the impact of RA on the dynamic conditional dependence between crude oil futures market and EUA futures market. The empirical results show that the RA have a significant positive impact on the dynamic dependence between crude oil futures market and EUA futures market.

The main contributions of this paper are as follows. Firstly, the dynamic dependence between crude oil futures market and EUA futures market is studied from the perspective of RA. Secondly, the time-varying copula-MIDAS-RA model is proposed to measure the dynamic dependence between crude oil futures and EUA futures markets. Thirdly, an empirical analysis based on the daily data on the Brent crude oil futures and EUA futures returns and the monthly data on the RA index confirms that the RA does have a significant impact on the dynamic dependence between crude oil futures market and EUA futures market. Finally, we provide evidence that accounting for the impact of RA on the dependence between crude oil futures and EUA futures can improve the accuracy in risk management.

The remainder of the paper is organized as follows. In Section 2, we introduce our methodology, including the marginal distribution model, the copula-MIDAS-RA model and the estimation method. In Section 3, we describes the data. Section 4 presents the empirical results, and Section 5 concludes.

2 Methodology

We use the copula-MIDAS approach to investigate the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets. For implementation, we first model the margin of the return series using the AR-GARCH model, and obtain the standardized residuals. We then apply the (re-scaled) empirical cumulative distribution function to the standardized residuals and estimate the copula-MIDAS-RA model via the two-step maximum likelihood estimation procedure.

2.1 Models for marginal distributions

It has been well documented in the literature that financial returns show some important stylized facts such as the autocorrelation, conditional heteroscedasticity (time-varying volatility) and volatility clustering. It is paramount to model such features of the financial returns. A natural and simple model for the financial returns is the AR-GARCH model. In this paper we adopt the AR-GARCH model to model the margin of the crude oil futures and EUA futures return series. The AR-GARCH models for describing the return dynamics of the crude oil futures and EUA futures can be written as.

$r_{i,t}=c_0+c_1{r}_{i,t-1}+{\epsilon }_{i,t},i=\mathrm{o}\mathrm{i}\mathrm{l},\mathrm{e}\mathrm{u}\mathrm{a}(1)$

${\epsilon }_{i,t}={\sigma }_{i,t}{z}_{i,t}(2)$

${\sigma }_{i,t}^2=\omega +\alpha {\epsilon }_{i,t-1}^2+\beta {\sigma }_{i,t-1}^2(3)$

Where r_i,t is the return series for the crude oil futures or EUA futures, z_i,t is the independently and identically distributed (i.i.d.) random variable with zero mean and unit variance (standardized residuals), and ${\sigma }_{i,t}^2$ is the conditional variance of return series. We impose the restrictions: ω > 0, α > 0, β > 0 and α + β < 1, which ensure the non-negativity and stationarity of the conditional variance process.

It has been documented in the literature that the empirical results from the copula models are not sensitive to the choice of GARCH specifications when the copula parameters are estimated through the maximum likelihood, which is also adopted in this paper (Aloui et al., 2013).

2.2 Copula functions

Copula introduced by Sklar (1959) has gained increasing popularity in finance over the past decade. It provides a flexible and efficient way to model correlated multivariate data. In fact, copula is a multivariate distribution function with uniform margins, which fully captures the dependence structure between the variables. To investigate the interdependence between financial data, one can simply construct a multivariate joint distribution by first specifying marginal univariate distributions, and then choosing an appropriate copula to examine the dependence structure between the variables.

Let F_oil and F_eua be the marginal distribution functions of z_oil,t and z_eua,t, and F(z_oil,t, z_eua,t) the joint distribution function of z_oil,t and z_eua,t. According to Sklar’s theorem, there exists a copula function C: [0,1]² → [0, 1] such that

$F\left(z_{\text{oil},t},z_{\text{eua},t}\right)=C\left(u_{\text{oil},t},u_{\text{eua},t}|\mathrm{\Theta }\right)(4)$

where u_oil,t ≡ F_oil(z_oil,t), u_eua,t ≡ F_eua(z_eua,t), and Θ is the parameter vector of the copula function. It is clear that by the probability integral transform a copula is a multivariate distribution function that can be characterized by the uniform (0,1) margins and a dependence (copula) function.

Compared to the traditional approaches that can only capture the linear dependence between the variables, copula is able to characterize more flexible dependence structure, such as the non-linear and tail dependence. In particular, the lower tail dependence coefficient λ^L and the upper tail dependence coefficient λ^U are defined respectively as.

${\lambda }^L=\underset{u\to 0^{+}}{\lim }\mathrm{Pr}\left[u_{\text{eua},t}\le u|u_{\text{oil},t}\le u\right]=\underset{u\to 0^{+}}{\lim }\frac{C\left(u,u|\mathrm{\Theta }\right)}{u}(5)$

${\lambda }^U=\underset{u\to 1^{-}}{\lim }\mathrm{Pr}\left[u_{\text{eua},t}>u|u_{\text{oil},t}>u\right]=\underset{u\to 1^{-}}{\lim }\frac{1-2u+C\left(u,u|\mathrm{\Theta }\right)}{1-u}(6)$

Where λ^L(λ^U) ∈ [0, 1]. If λ^L(λ^U) is positive, there exists lower (upper) tail dependence. If λ^L = λ^U, there exists a symmetric tail dependence between crude oil futures and EUA futures markets.

In the paper, we consider six popular copula functions: Gaussian copula, Student-t copula, Gumbel copula, Clayton copula, Survival Gumbel copula and Survival Clayton copula. They can be written as follows.

Gaussian copula:

$C^{\mathit{Gaussian}}\left(u,v|\theta \right)={\int }_{-\infty }^{{\mathrm{\Phi }}^{-1}\left(u\right)}{\int }_{-\infty }^{{\mathrm{\Phi }}^{-1}\left(v\right)}\frac{1}{2\pi \sqrt{1-{\theta }^2}}\exp \left\{-\frac{s^2-2\theta st+t^2}{2\left(1-{\theta }^2\right)}\right\}dsdt(7)$

where θ ∈ (−1, 1) and Φ⁻¹(⋅) is the inverse of the standard normal cumulative distribution function. The Gaussian copula does not have tail dependence (zero tail dependence).

Student-t copula:

$C^{\mathit{Student-t}}\left(u,v|\theta ,\nu \right)={\int }_{-\infty }^{t_{\nu }^{-1}\left(u\right)}{{\int }_{-\infty }^{t_{\nu }^{-1}\left(v\right)}\frac{1}{2\pi \sqrt{1-{\theta }^2}}\left(1+\frac{s^2-2\theta st+t^2}{\nu \left(1-{\theta }^2\right)}\right)}^{-\frac{\nu +2}{2}}dsdt(8)$

where θ ∈ (−1, 1), ν is the degree of freedom, and $t_{\nu }^{-1}(\cdot )$ denotes the inverse of the standard Student-t distribution function. The Student-t copula has symmetric tail dependence.

Gumbel copula:

$C^{\mathit{Gumbel}}\left(u,v|\theta \right)=\exp \left\{-{\left[{\left(-\ln u\right)}^{\theta }+{\left(-\ln v\right)}^{\theta }\right]}^{1/\theta }\right\}(9)$

where θ ∈ (1, + ∞). The Gumbel copula has upper tail dependence.

Clayton copula:

$C^{\mathit{Clayton}}\left(u,v|\theta \right)={\left(u^{-\theta }+v^{-\theta }-1\right)}^{-1/\theta }(10)$

where θ ∈ (0, + ∞). The Clayton copula has lower tail dependence.

Survival Gumbel copula:

$C^{\mathit{SurvivalGumbel}}\left(u,v|\theta \right)=u+v-1+C^{\mathit{Gumbel}}\left(1-u,1-v|\theta \right)(11)$

where θ ∈ (1, + ∞). The Survival Gumbel copula has lower tail dependence.

Survival Clayton copula:

$C^{\mathit{SurvivalClayton}}\left(u,v|\theta \right)=u+v-1+C^{\mathit{Clayton}}\left(1-u,1-v|\theta \right)(12)$

where θ ∈ (0, + ∞). The Survival Clayton copula has upper tail dependence.

The above copulas capture different patterns of tail dependence. Table 1 summarizes the tail dependence of the above copulas.

TABLE 1

TABLE 1. Tail dependence of the copulas.

2.3 Copula-MIDAS-RA model

This paper aims to study the impact of RA on the dependence between crude oil futures and EUA futures markets. Nevertheless, the traditional copula models do not allow us to link the dynamics dependence to exogenous explanatory variables such as the RA. To overcome this problem, we employ the copula-MIDAS approach, which allows to directly incorporate RA into the dynamic dependence structure. The copula-MIDAS model with RA (copula-MIDAS-RA) can be written as.

$\left(u_{\text{oil},t},u_{\text{eua},t}\right)\sim C\left(u_{\text{oil},t},u_{\text{eua},t}|{\theta }_t,\nu \right),{\theta }_t=\mathrm{\Psi }\left({\lambda }_t\right)(13)$

${\lambda }_t=c_{\tau }+{\beta }_c{\lambda }_{t-1}+{\alpha }_c\frac{1}{S}\sum _{s=1}^S\left[{\mathrm{\Phi }}^{-1}\left(u_{t-s}\right){\mathrm{\Phi }}^{-1}\left(v_{t-s}\right)\right](14)$

$c_{\tau }=\bar{c}+\gamma \sum _{k=1}^{K_c}{\varphi }_k\left({\omega }_c\right)R{A}_{\tau -k}(15)$

Where θ_t is the time-varying parameter, which is assumed to be driven by the latent dynamic process λ_t satisfying θ_t = Ψ(λ_t), ν is the time-invariant parameter (for the Student-t copula), Ψ(⋅) is a appropriate transformation to ensure that θ_t remains in its domain, and Φ(⋅) is the standard normal cumulative distribution function. We assume that $\left|{\beta }_c\right|<1$, which ensures that λ_t is a stationary process. S is the lag order, which is determined by the Akaike information criterion (AIC) and Schwarz information criterion (SC) criteria.

In the copula-MIDAS-RA model, c_τ is referred to as the long-run dependence, which is assumed to be time-varying, and is specified by smoothing (monthly) RA in the spirit of MIDAS approach. It is clear that γ captures the impact of the RA on the long-run dependence. ϕ_k(⋅) is the Beta weighting function, which can be written as

${\varphi }_k\left({\omega }_c\right)=\frac{{\left(1-i/K_c\right)}^{{\omega }_c-1}}{{\sum }_{i=1}^{K_c}{\left(1-i/K_c\right)}^{{\omega }_c-1}}(16)$

where ω_c is the weight coefficient, K_c is the number of MIDAS lags, and ${\sum }_{k=1}^{K_c}{\varphi }_k({\omega }_c)=1$.

The copula-MIDAS-RA model is flexible to capture the dynamic dependence, and allows us to examine the impact of the RA on the long-run dependence. Moreover, it includes the time-varying copula model without incorporating explanatory variable as a special case when γ = 0 $(c_{\tau }=\bar{c})$.

2.4 Estimation

We denote the marginal density of r_i,t as f_i(r_i,t, Θ_i) with Θ_i = (c₀, c₁, ω, α, β)′ for i = oil, eua and ${\mathrm{\Theta }}_C={({\alpha }_c,{\beta }_c,\bar{c},\gamma ,{\omega }_c,v)}^{\prime }$ is the parameter of the copula dependence structure. Thus, we can obtain the parameter $\mathrm{\Theta }={({\mathrm{\Theta }}_{\text{oil}}^{\prime },{\mathrm{\Theta }}_{\text{eua}}^{\prime };{\mathrm{\Theta }}_C^{\prime })}^{\prime }$. According to Sklar’s theorem, the loglikelihood function can be decomposed into the marginal distribution and the copula structure. The log-likelihood function can be writen as

$\begin{array}{ccc}\hfill \mathcal{L}\left(r_{\text{oil},t},r_{\text{eua},t};\mathrm{\Theta }\right)& =\hfill & \sum _{t=1}^T\log \left(r_{\text{oil},1},r_{\text{eua},1},\dots ,r_{\text{oil},t},r_{\text{eua},t};\mathrm{\Theta }\right)\hfill \\ \hfill & =\hfill & \sum _{t=1}^T\log \left\{f_{\text{oil}}\left(r_{\text{oil},t};{\mathrm{\Theta }}_{\text{oil}}\right)f_{\text{eua}}\left(r_{\text{eua},t};{\mathrm{\Theta }}_{\text{eua}}\right)c\left(u_{\text{oil},t},u_{\text{eua},t};{\mathrm{\Theta }}_C\right)\right\}\hfill \\ \hfill & =\hfill & {\mathcal{L}}_{r_{\text{oil}}}\left({\mathrm{\Theta }}_{\text{oil}}\right)+{\mathcal{L}}_{r_{\text{eua}}}\left({\mathrm{\Theta }}_{\text{eua}}\right)+{\mathcal{L}}_C\left({\mathrm{\Theta }}_C\right)\hfill \end{array}(17)$

where u_oil,t and u_oil,t are marginal distribution.

According to Eq. 17, we can estimate the copula-MIDAS-RA model using the two-step maximum likelihood estimation procedure, which is also known as the inference functions for margins (IFM). Notably, the IFM approach is computationally less intensive relative to the one-step full maximum likelihood. Moreover, Joe and Xu (1996) and Chen and Fan (2006) show that the IFM method is highly efficient compared to the maximum likelihood method.

In the first step, we estimate the parameters of the marginal distribution models (AR-GARCH) through maximizing the marginal likelihood:

${\widehat{\mathrm{\Theta }}}_{\text{oil}}=\underset{{\mathrm{\Theta }}_{\text{oil}}}{\text{a}\text{r}\text{g}\text{m}\text{a}\text{x}}{\mathcal{L}}_{r_{\text{oil}}}\left({\mathrm{\Theta }}_{\text{oil}}\right)(18)$

${\widehat{\mathrm{\Theta }}}_{\text{eua}}=\underset{{\mathrm{\Theta }}_{\text{eua}}}{\text{a}\text{r}\text{g}\text{m}\text{a}\text{x}}{\mathcal{L}}_{r_{\text{eua}}}\left({\mathrm{\Theta }}_{\text{eua}}\right)(19)$

Where ${\mathcal{L}}_{r_{\text{oil}}}({\mathrm{\Theta }}_{\text{oil}})$ and ${\mathcal{L}}_{r_{\text{eua}}}({\mathrm{\Theta }}_{\text{eua}})$ are the likelihood of the margins, which are given by.

${\mathcal{L}}_{r_{\text{oil}}}\left({\mathrm{\Theta }}_{\text{oil}}\right)=-\frac{1}{2}\sum _{t=1}^T\left[\ln 2\pi +\ln {\sigma }_{\text{oil},t}^2+z_{\text{oil},t}^2\right](20)$

${\mathcal{L}}_{r_{\text{eua}}}\left({\mathrm{\Theta }}_{\text{eua}}\right)=-\frac{1}{2}\sum _{t=1}^T\left[\ln 2\pi +\ln {\sigma }_{\text{eua},t}^2+z_{\text{eua},t}^2\right](21)$

Once the marginal models (AR-GARCH) are estimated for the crude oil and EUA futures returns, we extract the filtered residuals z_oil,t and z_eua,t and construct their marginal distributions F_oil and F_eua nonparametrically via the following (re-scaled) empirical cumulative distribution functions.

${\widehat{u}}_{\text{oil}}\equiv {\widehat{F}}_{\text{oil}}\left(z\right)=\frac{1}{T+1}\sum _{t=1}^{T}1\left\{z_{\text{oil},t}<z\right\}(22)$

${\widehat{u}}_{\text{eua}}\equiv {\widehat{F}}_{\text{eua}}\left(z\right)=\frac{1}{T+1}\sum _{t=1}^{T}1\left\{z_{\text{eua},t}<z\right\}(23)$

Where 1{⋅} denotes the indicative function.

In the second step, we estimate the unknown parameter vector Θ_C of the copula as

${\widehat{\mathrm{\Theta }}}_C=\underset{{\mathrm{\Theta }}_C}{\text{a}\text{r}\text{g}\text{m}\text{a}\text{x}}{\mathcal{L}}_C\left({\mathrm{\Theta }}_C\right)(24)$

where ${\mathcal{L}}_C\left({\mathrm{\Theta }}_C\right)={\sum }_{t=1}^T\ln c({\widehat{u}}_{\text{oil},t},{\widehat{u}}_{\text{eua},t}|\mathrm{\Theta })$ is the copula likelihood.

It is clear that the IFM method separately estimates the parameters of the marginal distributions and the copula functions, which is flexible and can reduce the computational burden.

3 Data

For our empirical analysis, we use the daily (log) return data on the Brent crude oil futures and EUA futures and the monthly data on the RA index. The Brent crude oil is chosen as it dominates the oil market, and most oil is priced using Brent crude oil as the benchmark. The daily (log) returns are calculated as r_i,t = log(p_i,t) − log(p_i,t−1), where p_i,t is the closing price on day t and i = oil, eua. The daily return data for the Brent crude oil futures and EUA futures are obtained from the Wind Database of China for the period from 2 January 2008 to 31 December 2021, resulting in a total of 3,606 daily observations. The monthly RA data are obtained from the website https://www.nancyxu.net/risk-aversion-index, for the period from January 2008 to December 2021, resulting in a total of 168 monthly observations. Figure 1 presents the time-series plots of daily Brent crude oil futures returns and EUA futures returns. It can be seen from the figure that both the returns series exhibit well-known behaviors of time-varying volatility and volatility clustering. Figure 2 presents the time-series plot of the monthly RA index. As can be seen from the figure, during the periods of 2008–2009 global financial crisis and COVID-19 outbreak, RA reaches very high levels.

FIGURE 1

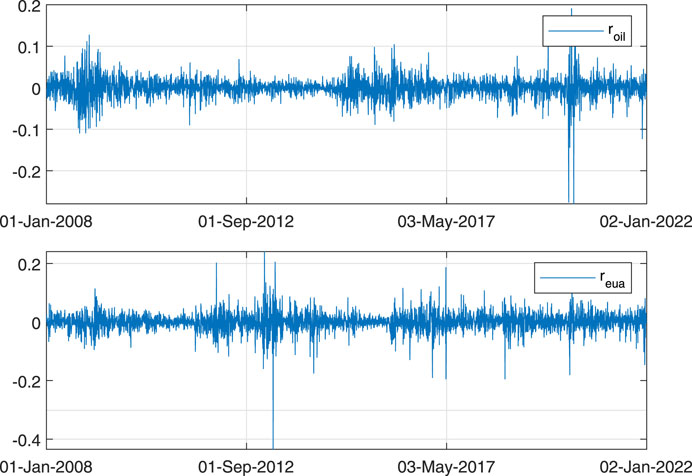
FIGURE 1. Time-series plots of daily Brent crude oil futures returns (r_oil) and EUA futures returns (r_eua). Source: Authors.

FIGURE 2

FIGURE 2. Time-series plot of monthly RA index. Source: Authors.

Table 2 reports the summary statistics of the daily Brent crude oil futures returns (r_oil) and EUA futures returns (r_eua) as well as the monthly RA index. We can observe that the EUA futures returns is more volatile than the Brent crude oil futures returns, since it has higher standard deviation. In addition, we find that both the Brent crude oil futures and EUA futures returns exhibit negative skewness and excess kurtosis, which deviate significantly from the normal distribution in terms of the Jarque-Bera statistics. Furthermore, the Ljung-Box statistics of Q(20) reveals the existence of autocorrelation and heteroscedasticity of the return series. Therefore, it is reasonable to apply AR-GARCH model to fit the returns series.

TABLE 2

TABLE 2. Summary statistics.

4 Empirical results

In this section, we first present the estimation results for the marginal AR-GARCH models for the Brent crude oil futures and EUA futures returns. Then, we report the estimation results for the static copula models and time-varying copula models. Finally, we assess the economic significance of accounting for the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets from a risk management point of view.

4.1 Marginal model estimation

To use the copula approach to explore the dependence between crude oil futures and EUA futures markets, we need first to estimate the marginal models for the Brent crude oil futures and EUA futures returns, and then construct the marginal distributions. Table 3 reports the estimation results for the marginal AR-GARCH models for the Brent crude oil futures and EUA futures returns. As can be seen from the table, the volatility persistence coefficient α + β is estimated to be close to one, suggesting that the volatility process of the Brent crude oil futures and EUA futures returns is highly persistent. Once the AR-GARCH models are estimated, we can obtain the standardized residuals (z_oil, z_eua), which are presented in Figure 3. The QQ plots of the standardized residuals presented in Figure 4 show that the standardized residuals obviously deviate from the standard normal distribution. Using Eqs 22, 23, we can construct the (re-scaled) empirical cumulative distribution functions $({\widehat{u}}_{\text{oil}},{\widehat{u}}_{\text{eua}})$. The copula model requires the marginal distributions $({\widehat{u}}_{\text{oil}},{\widehat{u}}_{\text{eua}})$ have a uniform distribution on (0,1). The Kolmogorov-Smirnow test results reported in Table 3 suggest the null hypothesis that the marginal model is correctly specified (marginal distributions have a uniform distribution on (0,1)) can not be rejected. Thus, the marginal AR-GARCH models we employ in this paper can fit the non-normal and heteroscedastic crude oil futures and EUA futures returns data well.

TABLE 3

TABLE 3. Estimation results of marginal AR-GARCH models.

FIGURE 3

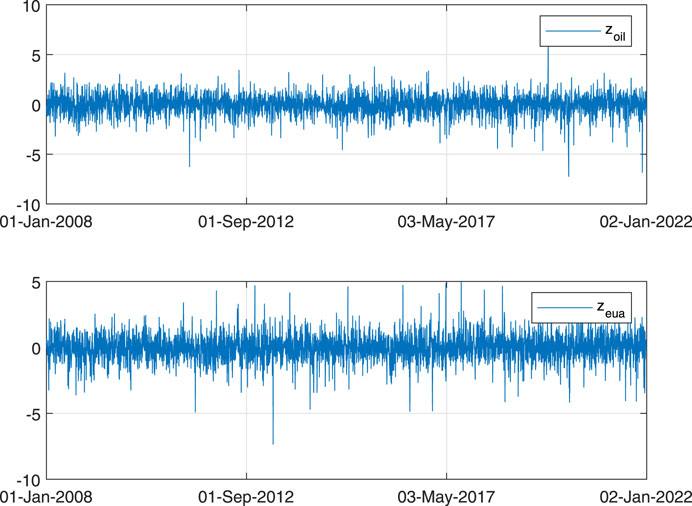
FIGURE 3. Standardized residuals for Brent crude oil futures and EUA futures returns. Source: Authors.

FIGURE 4

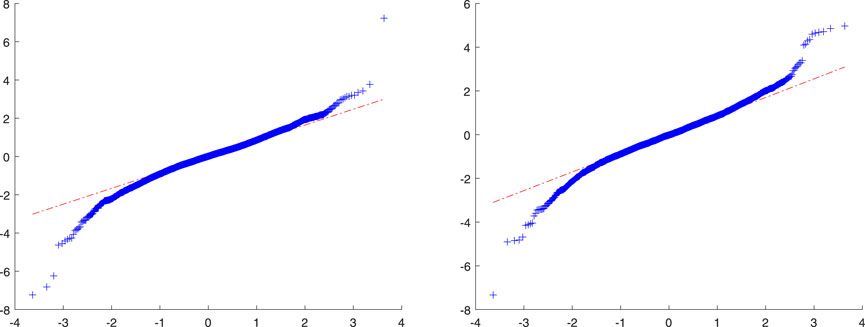
FIGURE 4. QQ plots of standardized residuals for Brent crude oil futures and EUA futures returns. Source: Authors.

4.2 Static copula estimation

After appropriately constructing the marginal distributions, we need to select an appropriate copula function to describe the dependence between crude oil futures and EUA futures markets. We consider six static copulas described in Section 2.2, including the Gaussian, Student-t, Gumbel, Survival Gumbel, Clayton and Survival Clayton. The estimation results for the six static copulas are presented in Table 4. As can be seen from the table, the dependence parameter θ for all copulas is estimated to be positive and highly significant, which indicates the existence of the dependence between crude oil futures and EUA futures markets. The reason for the result is because the rapid development of the economy will lead to an increase in the use of crude oil, thereby increasing the demand for crude oil, increasing the price of crude oil, and crude oil combustion will also increase greenhouse gas emissions, thus increasing the demand for carbon allowances, thereby increasing EUA prices. In particular, we observe that the Student-t copula achieves the highest log-likelihood values and the lowest AIC values, followed by the Gaussian copula, which suggests that the Student-t copula has better goodness-of-fit than other copulas. This finding implies that the tail dependence between crude oil futures and EUA futures markets is symmetric.

TABLE 4

TABLE 4. Estimation results of static copulas.

4.3 Time-varying copulas estimation

This paper aims to study the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets. To do so, we use the two best-performing static copulas to construct the corresponding time-varying copula models, namely the time-varying Gaussian copula-MIDAS-RA model and the time-varying Student-t copula-MIDAS-RA model. The time-varying Gaussian copula-MIDAS-RA model focuses on the linear correlation between crude oil futures and EUA futures without tail dependence, while the time-varying Student-t copula-MIDAS-RA model focuses on the symmetric tail dependence between crude oil futures and EUA futures. In contrast to the traditional copulas, the time-varying Gaussian copula-MIDAS-RA and time-varying Student-t copula-MIDAS-RA models are able to capture the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets.

The estimation results for the time-varying Gaussian copula-MIDAS-RA and time-varying Student-t copula-MIDAS-RA models are presented in Table 5. For the purpose of comparison, we also report the estimation results for the time-varying Gaussian copula and time-varying Student-t copula models without incorporating RA in Table 5. It can be seen from the table that the estimated values of α_c are positive and significant in all cases, suggesting that the dependence between crude oil futures and EUA futures is time-varying and the static copula models may not be adequate for describing the dynamic dependence between crude oil futures and EUA futures markets. Furthermore, the estimates of β_c are statistically significantly negative in all cases, implying that the dependence between crude oil futures and EUA futures exhibits negative autocorrelation. The reason for this result is because, in the short-term, rising crude oil prices will reduce the use of fossil energy, thereby reducing greenhouse gas emissions, thereby reducing the demand for carbon emission allowances, thereby reducing the price of the EUA. It is interesting to note that the estimated γ is positive and significant, which indicates that the RA has a significantly positive impact on the dependence between crude oil futures and EUA futures markets. Crude oil futures and EUA futures have investment value and crude oil futures can be used as hedging products for EUA futures, so RA can affect correlation by affecting investor sentiment.

TABLE 5

TABLE 5. Estimation results of time-varying copula models.

In terms of the log-likelihood and AIC values, the time-varying Student-t copula-MIDAS-RA model has the best goodness-of-fit performance. This result demonstrates that the tail dependence between crude oil futures and EUA futures returns is not only symmetric, but also displays short-run fluctuations and a long-run trend. The outperformance of the time-varying Student-t copula-MIDAS-RA model relative to the time-varying Student-t copula model highlights the importance of accounting for the RA in explaining the dynamic dependence between crude oil futures and EUA futures markets.

Figure 5 plots the estimated dynamic dependence between crude oil futures and EUA futures based on the time-varying Gaussian copula model and time-varying Gaussian copula-MIDAS-RA model. Figure 6 plots the dynamic dependence between crude oil futures and EUA futures based on the Student-t copula and Student-t copula-MIDAS-RA models. We can find from Figures 5, 6 that the dynamic dependence between crude oil futures and EUA futures increases obviously when RA reaches high levels during the periods of 2008–2009 global financial crisis and 2020 COVID-19 outbreak, suggesting that the time-varying copula-MIDAS-RA models help us to understanding the dependence structure between crude oil futures and EUA futures markets and to explore more useful information than other copulas without RA on the dependence between crude oil futures and EUA futures markets.

FIGURE 5

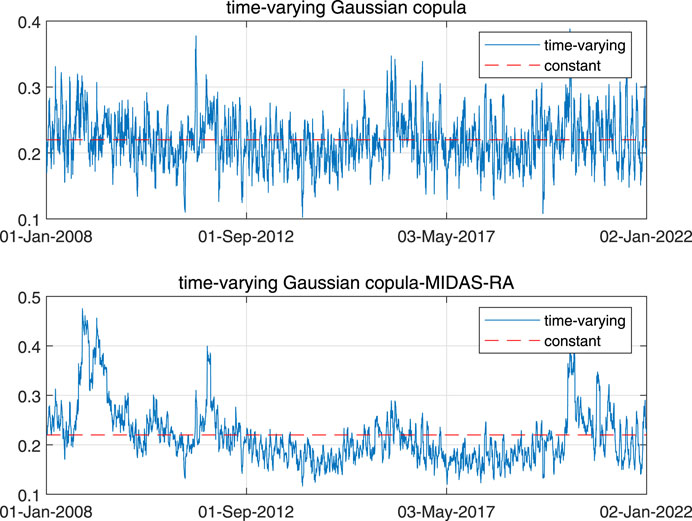
FIGURE 5. Dynamic dependence between crude oil futures and EUA futures markets from the time-varying Gaussian copula-MIDAS-RA model. Source: Authors.

FIGURE 6

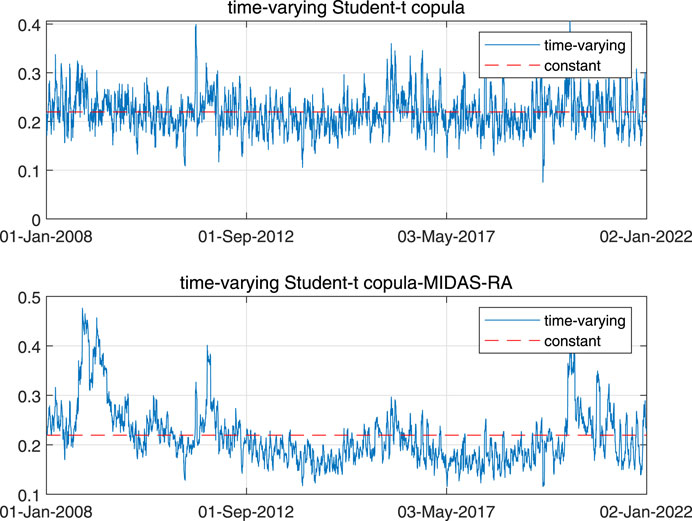
FIGURE 6. Dynamic dependence between crude oil futures and EUA futures markets from the time-varying Student-t copula-MIDAS-RA model. Source: Authors.

4.4 Risk analysis

In this section, we assess the economic significance of accounting for the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets from a risk management point of view. In a world characterized by fast changes, uncertainties and large fluctuations, risk measurement and management have become an imperative task as well as an integral part of the operations of banking and financial institutions. The recent financial crisis has also definitively emphasized the need for a better understanding of risk and its quantification. To measure the portfolio risk, we use the popular Value-at-Risk (VaR).

4.4.1 VaR model

VaR measures the maximum possible loss of financial assets held by investors within a given period under a given confidence level, such as 99% and 95%. VaR was first proposed by J.P Morgan, which has become a standard tool for measuring and managing market risk. Different from traditional risk measurement methods such as the standard deviation, VaR is a useful risk measurement tool that focuses on more sensitive downside risk of assets.

Let X be a loss variable and F_X the distribution function of X. For a given confidence level, p, the VaR_p is defined as the p − quantile of the distribution, F_X:

$Va{R}_p\left(X\right)=F_X^{-1}\left(p\right)(25)$

In this section, we use Monte Carlo simulation method to calculate the VaR of portfolio. To be specific, we follow Jiang et al., 2020 and rely on the following four-step procedure to measure the portfolio risk.

Step 1: Based on the cumulative distribution function obtained by the optimal time-varying copula models, we can generate random numbers u_i (i = oil, eua).

Step 2: We transform the random numbers obtained from Step 1 into residual series via the inverse of probability integral transformation and apply AR-GARCH model to obtain simulated daily returns of financial assets r_i (i = oil, eua).

Step 3: We calculate the resulting portfolio returns R = w_oilr_oil + w_euar_eua, where 0≤ w_oil, w_eua ≤ 1, and w_oil + w_eua = 1. In order to simplify the analysis, we assume equal-weight portfolio, that is, we consider w_oil = w_eua = 0.5.

Step 4: We repeat the above steps 5,000 times, and calculate the VaR.

4.4.2 Backtesting

To evaluate the accuracy of VaR estimates, we employ the backtesting approach. To be specific, we adopt the failure ratio (FR) test proposed by Kupiec (1995) to examines whether the number of exceptions is consistent with the given confidence level. Further, considering the null hypothesis which is expressed as $H_0:FR=\widehat{FR}=N/T$, where $\widehat{FR}$ is the observed (empirical) FR, N is the number of exceptions and T is the number of total observations. To formally test the null hypothesis, the likelihood rate (LR) statistic is given by

$LR=-2\ln \left[{\left(1-p\right)}^{T-N}{p}^N\right]+2\ln \left[{\left(1-N/T\right)}^{T-N}{\left(N/T\right)}^N\right](26)$

where LR follows χ² distribution with degree of freedom one. For the LR test, the null hypothesis is that the risk model can produce accurate risk measurement.

4.4.3 VaR results

For comparison purpose, we calculate the VaR for time-varying Student-t copula, time-varying Gaussian copula, time-varying Student-t copula-MIDAS-RA and time-varying Gaussian copula-MIDAS-RA models for three different significance levels: 0.01, 0.05, and 0.10, corresponding to 99%, 95% and 90% confidence levels. Figures 7–10 present the VaR estimates for the time-varying Student-t copula, time-varying Student-t copula-MIDAS-RA, time-varying Gaussian copula and time-varying Gaussian copula-MIDAS-RA models, respectively. To evaluate the effectiveness of different models, we conduct the backtesting of VaR-based portfolio. The results are reported in Table 6. We observe that the copulas incorporating RA generally perform better than those without RA in terms of FR and LR tests. In particular, we find that the time-varying Student-t Copula-MIDAS-RA model consistently exhibits optimal VaR results as the FR of the time-varying Student-t copula-MIDAS-RA model is closer to the corresponding VaR significance level (10%, 5% or 1%) than that of other models (time-varying Gaussian copula, time-varying Student-t copula, time-varying Gaussian copula-MIDAS-RA). Moreover, we find that the time-varying Student-t copula-MIDAS-RA model passes the LR test in all cases, while the time-varying Gaussian copula-MIDAS-RA and time-varying Gaussian copula models do not pass the LR test for 1% VaR. Overall, the time-varying Student-t copula-MIDAS-RA model can better measure the extreme risk than other copula models, and incorporating RA can significantly improve the accuracy of VaR estimates.

FIGURE 7

FIGURE 7. VaR results of the time-varying Student-t copula model. Source: Authors.

FIGURE 8

FIGURE 8. VaR results of the time-varying Student-t copula-MIDAS-RA model. Source: Authors.

FIGURE 9

FIGURE 9. VaR results of the time-varying Gaussian copula model. Source: Authors.

FIGURE 10

FIGURE 10. VaR results of the time-varying Gaussian copula-MIDAS-RA model. Source: Authors.

TABLE 6

TABLE 6. Back-testing results of VaR-based portfolio.

5 Conclusion and discussion

In this paper, we propose the time-varying copula-MIDAS-RA model to investigate the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets. Our empirical results show that the tail dependence between the crude oil futures and EUA futures markets is symmetric and time-varying, and the Student-t copula-MIDAS-RA model has better goodness-of-fit than other copulas. Moreover, we observe that the RA has a significantly positive impact on the dynamic dependence between crude oil futures and EUA futures markets. That is, with the increase of the level of RA, the dynamic dependence between crude oil futures and EUA futures markets is expected to increase. Furthermore, we assess the economic significance of accounting for the impact of RA on the dynamic dependence between crude oil futures and EUA futures markets from a risk management point of view. Our empirical results show that the time-varying Student-t copula-MIDAS-RA model can improve the accuracy in risk management relative to other copulas which has important theoretical and practical significance for financial market risk management and control.

According to the research results, we put forward the following suggestions: First, for investors, crude oil futures and EUA futures can be attractive investment asset in the financial market as well. Constructing a portfolio including EUA futures and crude oil futures can effectively reduce the investment risk of investors. Second, the government should formulate the trade mechanism of the EUA futures market and enhance EUA futures stability to increase investors confidence. Third, the government should make relevant policies to assist relevant enterprises to reduce greenhouse gas emission. This paper proposed the copula-MIDAS-RA model to investigate the impact of RA on the dynamic dependence between crude oil futures and EUA futures, which is of great importance for policymakers and investors.

It is worth noting that this paper can be further studied. Firstly, we can further investigate the influence of multiple variables on dynamic dependence between crude oil futures and EUA futures, Secondly, we can investigate the spillover effect. Finally, it is also meaningful to study the dynamic dependence by using the stochastic copula model.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XW: Conceptualization, Methodology, Formal analysis, Supervision, Funding acquisition. ZZ: Data curation, Software, Validation, Writing–review and editing.

Funding

This work was supported by the National Natural Science Foundation of China under Grant No. 71971001; Natural Science Foundation of Anhui Province Excellent Youth Scientists Fund Project under Grant No. 2208085Y21; Academic Funding Project for Top Academic Talents in Universities in Anhui Province under Grant No. gxbjZD2022019; Innovative Research Project for Graduates of Anhui University of Finance and Economics under Grant No. ACYC2021294. That is Outstanding Youth Research Project for Anhui Universities under Grant No. 2022AH020047.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aloui, R., Hammoudeh, S., and Nguyen, D. K. (2013). A time-varying copula approach to oil and stock market dependence: The case of transition economies. Energy Econ. 39, 208–221. doi:10.1016/j.eneco.2013.04.012

CrossRef Full Text | Google Scholar

Ahonen, E., Corbet, S., Goodell, J. W., Gnay, S., and Larkin, C. (2022). Are carbon futures prices stable? New evidence during negative oil. Finance Res. Lett. 47 (B), 102723. doi:10.1016/j.frl.2022.102723

CrossRef Full Text | Google Scholar

Bams, D., Honarvar, I., and Lehnert, T. (2017). Risk aversion, sentiment and the cross-section of stock returns. Limburg Institute of Financial Economics (LIFE. Working Paper.

Google Scholar

Bekaert, G., Engstrom, E. C., and Xu, N. R. (2021). The time variation in risk appetite and uncertainty. Manag. Sci. 68 (6), 3975–4004. doi:10.1287/mnsc.2021.4068

CrossRef Full Text | Google Scholar

Bruninx, K., Ovaere, M., and Delarue, E. (2020). The long-term impact of the market stability reserve on the EU emission trading system. Energy Econ. 89, 104746. doi:10.1016/j.eneco.2020.104746

CrossRef Full Text | Google Scholar

Chen, X., and Fan, Y. (2006). Estimation and model selection of semiparametric copula-based multivariate dynamic models under copula misspecification. Journal of econometrics 135(1-2), 125–154. doi:10.1016/j.jeconom.2005.07.027

CrossRef Full Text | Google Scholar

Demirer, R., Gkillas, K., Gupta, R., and Pierdzioch, C. (2022). Risk aversion and the predictability of crude oil market volatility: A forecasting experiment with random forests. J. Operational Res. Soc. 73 (8), 1755–1767. doi:10.1080/01605682.2021.1936668

CrossRef Full Text | Google Scholar

Diebold, F. X., and Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 28 (1), 57–66. doi:10.1016/j.ijforecast.2011.02.006

CrossRef Full Text | Google Scholar

Dutta, A. (2018). Modeling and forecasting the volatility of carbon emission market: The role of outliers, time-varying jumps and oil price risk. J. Clean. Prod. 172 (20), 2773–2781. doi:10.1016/j.jclepro.2017.11.135

CrossRef Full Text | Google Scholar

Gong, Y., Bu, R., and Chen, Q. (2022). What affects the relationship between oil prices and the U.S. Stock market? A mixed-date sampling copula approach. J. Financial Econ. 20 (2), 253–277. doi:10.1093/jjfinec/nbz043

CrossRef Full Text | Google Scholar

Gong, Y., Chen, Q., and Liang, J. (2018). A mixed data sampling copula model for the return-liquidity dependence in stock index futures markets. Econ. Model. 68, 586–598. doi:10.1016/j.econmod.2017.03.023

CrossRef Full Text | Google Scholar

Guiso, L., Sapienza, P., and Zingales, L. (2018). Time varying risk aversion. J. Financial Econ. 128 (3), 403–421. doi:10.1016/j.jfineco.2018.02.007

CrossRef Full Text | Google Scholar

Han, M., Ding, L., Zhao, X., and Kang, W. (2019). Forecasting carbon prices in the shenzhen market, China: The role of mixed-frequency factors. Energy 171 (15), 69–76. doi:10.1016/j.energy.2019.01.009

CrossRef Full Text | Google Scholar

Hussain, S. I., and Li, S. (2018). The dynamic dependence between stock markets in the greater China economic area: A study based on extreme values and copulas. Financial Mark. Portfolio Manag. 32, 207–233. doi:10.1007/s11408-018-0308-5

CrossRef Full Text | Google Scholar

Jiang, C., Ding, X., Xu, Q., and Tong, Y. (2020). A TVM-copula-MIDAS-GARCH model with applications to VaR-based portfolio selection. North Am. J. Econ. Finance 51, 101074. doi:10.1016/j.najef.2019.101074

CrossRef Full Text | Google Scholar

Joe, H., and Xu, J. (1996). The estimation method of inference functions for margins for multivariate models. University of British Columbia. Working Paper.

Google Scholar

Krokida, S. I., Lambertides, N., Savva, C. S., and Tsouknidis, D. A. (2020). The effects of oil price shocks on the prices of EU emission trading system and European stock returns. Eur. J. Finance 26 (1), 1–13. doi:10.1080/1351847x.2019.1637358

CrossRef Full Text | Google Scholar

Kupiec, P. H. (1995). Techniques for verifying the accuracy of risk measurement models. J. Deriv. 3, 73–84. doi:10.3905/jod.1995.407942

CrossRef Full Text | Google Scholar

Liu, X., Zhang, S., and Bae, J. (2017). The nexus of renewable energy-agriculture-environment in BRICS. Appl. Energy 204 (15), 489–496. doi:10.1016/j.apenergy.2017.07.077

CrossRef Full Text | Google Scholar

Ma, Z., Yan, Y., Wu, R., and Li, F. (2021). Research on the correlation between WTI crude oil futures price and European carbon futures price. Front. Energy Res. 9, 735665. doi:10.3389/fenrg.2021.735665

CrossRef Full Text | Google Scholar

Nguyen, H., and Javed, F. (2021). Dynamic relationship between stock and bond returns: A gas MIDAS copula approach. Örebro University. Working Paper.

Google Scholar

Oh, D. H., and Patton, A. J. (2018). Time-varying systemic risk: Evidence from a dynamic copula model of cds spreads. J. Bus. Econ. Statistics 36, 181–195. doi:10.1080/07350015.2016.1177535

CrossRef Full Text | Google Scholar

Patton, A. J. (2006). Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 47, 527–556. doi:10.1111/j.1468-2354.2006.00387.x

CrossRef Full Text | Google Scholar

Qadan, M., and Nama, H. (2018). Investor sentiment and the price of oil. Energy Econ. 69, 42–58. doi:10.1016/j.eneco.2017.10.035

CrossRef Full Text | Google Scholar

Ren, X., Dou, Y., Dong, K., and Li, Y. (2022a). Information spillover and market connectedness: Multi-scale quantile-on-quantile analysis of the crude oil and carbon markets. Appl. Econ. 54 (38), 4465–4485. doi:10.1080/00036846.2022.2030855

CrossRef Full Text | Google Scholar

Ren, X., Li, Y., Qi, Y., and Duan, K. (2022b). Asymmetric effects of decomposed oil-price shocks on the EU carbon market dynamics. Energy 254 (B), 124172. doi:10.1016/j.energy.2022.124172

CrossRef Full Text | Google Scholar

Shi, W., Gong, Y., Yin, J., Nguyen, S., and Liu, Q. (2022). Determinants of dynamic dependence between the crude oil and tanker freight markets: A mixed-frequency data sampling copula model. Energy 254 (B), 124354. doi:10.1016/j.energy.2022.124354

CrossRef Full Text | Google Scholar

Sklar, M. (1959). Fonctions de repartition an dimensions et leurs marges. Publ. inst. statist. univ. Paris 8, 229–231.

Google Scholar

Tol, R. S. J. (2020). The economic impacts of climate change. Rev. Environ. Econ. Policy 12 (1), 4–25. doi:10.1093/reep/rex027

CrossRef Full Text | Google Scholar

Wang, L., Ma, F., Niu, T., and Liang, C. (2021). The importance of extreme shock: Examining the effect of investor sentiment on the crude oil futures market. Energy Econ. 99, 105319. doi:10.1016/j.eneco.2021.105319

CrossRef Full Text | Google Scholar

Wang, Y., and Guo, Z. (2018). The dynamic spillover between carbon and energy markets: New evidence. Energy 149 (15), 24–33. doi:10.1016/j.energy.2018.01.145

CrossRef Full Text | Google Scholar

Wu, X., Zhang, M., Wu, M., and Cui, H. (2022). Economic policy uncertainty and conditional dependence between China and US stock markets. Complexity 2022, 1–9. doi:10.1155/2022/8137932

CrossRef Full Text | Google Scholar

Xia, T., Ji, Q., Zhang, D., and Han, J. (2019). Asymmetric and extreme influence of energy price changes on renewable energy stock performance. J. Clean. Prod. 241 (20), 118338. doi:10.1016/j.jclepro.2019.118338

CrossRef Full Text | Google Scholar

Yao, C.-Z., and Sun, B.-Y. (2018). The study on the tail dependence structure between the economic policy uncertainty and several financial markets. North Am. J. Econ. Finance 45, 245–265. doi:10.1016/j.najef.2018.03.005

CrossRef Full Text | Google Scholar

Yu, L., Li, J., Tang, L., and Wang, S. (2015). Linear and nonlinear granger causality investigation between carbon market and crude oil market: A multi-scale approach. Energy Econ. 51, 300–311. doi:10.1016/j.eneco.2015.07.005

CrossRef Full Text | Google Scholar

Zhang, Y. J., and Li, S. H. (2019). The impact of investor sentiment on crude oil market risks: Evidence from the wavelet approach. Quant. Finance 19 (8), 1357–1371. doi:10.1080/14697688.2019.1581368

CrossRef Full Text | Google Scholar

Zhao, L., Wen, F., and Wang, X. (2020). Interaction among China carbon emission trading markets: Nonlinear granger causality and time-varying effect. Energy Econ. 91, 104901. doi:10.1016/j.eneco.2020.104901

CrossRef Full Text | Google Scholar

Zheng, Y., Zhou, M., and Wen, F. (2021). Asymmetric effects of oil shocks on carbon allowance price: Evidence from China. Energy Econ. 97, 105183. doi:10.1016/j.eneco.2021.105183

CrossRef Full Text | Google Scholar