- 1Khwaja Fareed University of Engineering and Information Technology, Rahim Yar Khan, Pakistan
- 2Department of Mathematics, Deanship of Applied Sciences, Umm Al-Qura University, Mecca, Saudi Arabia
- 3Center of Research, Faculty of Engineering, Future University in Egypt, New Cairo, Egypt
The main objective of this study is to identify the green suppliers that would most effectively assist manufacturing producers in implementing green manufacturing production while including uncertainty and reliability in their decision-making. For this firstly, we justify and manifest the idea of Pythagorean Fuzzy Z-numbers (PyFZNs). It has significant implications for improving the effectiveness of decision-making processes in several theories of uncertainty. It can more flexibly explain real-world data and human cognition due to its capacity to express imprecise and reliable information. Thus it is a more accurate mathematical tool for addressing accuracy and uncertainty. Secondly, we defined the Pythagorean fuzzy Z-number arithmetic aggregation operators and geometric aggregation operators. Thirdly, based on the proposed operators and EDAS (Evaluation based on distance from average solution) approach, a fast decision model is designed to deal with the issue of multi-criteria decision-making. Finally, using PyFZN data we also provide a numerical example to demonstrate the usability of the created multicriteria decision-making (MDM) approach. Moreover, a case study also proves its efficacy.
1 Introduction
Multi attribute group decision making is a problem in several disciplines, such as management, engineering, and economics. For a very long time, it has been considered that such data which accesses the options in terms of requirement and weight is expressed in actual numbers. The majority of the desired values however are contaminated by uncertainty, which making a decision difficult for the decision-makers to correct judgment as the system becomes more complex every day. To deal with the uncertainties, Zadeh (Zadeh, 1965) introduced the fuzzy set theory notion in 1965, which described the degree of membership. It performed a very significant role in decision making (Ashraf et al., 2022a; Ashraf et al., 2022b; Zhang et al., 2022). In 2011, Zadeh (Zadeh, 2011) further proposed the idea of Z-numbers to better highlight the limitations and reliability of the evaluation by an ordered pair of fuzzy numbers in unpredictable conditions. Compared to the traditional fuzzy number, it is a more extensive concept that is intimately linked to reliability. Given this, the Z-number suggests that a pair of fuzzy numbers in the order of restriction and reliability could be better equipped to explain human knowledge and judgments. Theoretically, the Z-numbers reflect the numeric values of internal machine-mind processes that facilitate adapted real-world understanding (Banerjee and Pal, 2015). The four basic mathematical operations in linear programming addition, subtraction, multiplication, and division as well as algebraic operations like maximum, minimum, square, and square root of continuous Z-numbers were established in 2016 (Aliev et al., 2016). On the basis of the extension principle applied to Z-numbers, a technique for the creation of functions was proposed. This methodology is very helpful in the reduction of uncertainty, while computing the values of Z-valued functions. Z-numbers can be arranged using the proposed total utility of Z-number, which can also be used to make multi criteria judgments under uncertain conditions (Kang et al., 2018b). Ronald proposes a Dempster-Shafer such as belief structure representation of Z-values that incorporates type-2 fuzzy logic (Yager, 2012). Ronald R discusses mixing Z-number and the Dempster-Shafer (D-S) evidence theory, where the Z-number is used to simulate the fuzziness and dependability of sensor data and the D-S evidence theory is used to combine the complex information from Z-numbers (Jiang et al., 2016). Numerous scholars created the TODIM technique based on the Choquet integral for circumstances involving multi-criteria decision-making using linguistic Z-numbers (Wang et al., 2017). Using the Z-number application, the supplier selection problem’s idea was illustrated (Jabbarova, 2017). The BWM technique and the Z-number extension were studied in order to handle the informational uncertainty in a multi-criteria decision system (Aboutorab et al., 2018). He created the QUALIFLEX method’s linguistic Z-QUALIFLEX extension, which uses linguistic Z-numbers to solve the LGEDM problem (Ding et al., 2020). In (Kang et al., 2018a), reliable methods that can more accurately and flexibly simulate the process of human competition and cooperation are presented for study analysis based on the usefulness of the Z-number in evolutionary games. They present a generalized Z-number that is more in line with human expression tendencies and a multi-criteria decision-making approach based on the Dempster-Shafer (DS) theory and generalized Z-numbers (Ren et al., 2020). To demonstrate the suggested framework and demonstrate its effectiveness in environmental evaluations, the provides an environmental evaluation framework based on the Dempster-Shafer theory and Z-numbers (Kang et al., 2020).
A class of non-standard Pythagorean fuzzy subsets with pairs of membership grades (a, b) meeting the requirement 0 ≤ a2 + b2 ≤ 1 was introduced using the Pythagorean complement and alternative definitions of complement operations. They provided a number of aggregation techniques and investigated multicriteria decision making in the scenario for these Pythagorean fuzzy set (Yager, 2013). According to (Garg, 2016), some of the aggregator operators discussed include generalized Pythagorean fuzzy Einstein weighted averaging, generalized Pythagorean fuzzy Einstein ordered weighted averaging, and Pythagorean fuzzy Einstein weighted averaging. The Einstein sum, product, and exponentiation as well as geometric aggregation operators and the intuitionistic fuzzy Einstein weighted and ordered weighted geometric operators were only a few of the operations on intuitionistic fuzzy sets that were discussed (Wang and Liu, 2011). The geometric aggregation operators, the intuitionistic fuzzy Einstein weighted and ordered weighted geometric operators, as well as the Einstein sum, product, and exponentiation, were all discussed (Rahman et al., 2017). The Pythagorean Dombi fuzzy aggregation operators introduced by (Akram et al., 2019), ELECTRI-I approach for it by (Akram et al., 2020) and TOPSIS approach by (Akram et al., 2021b). Garg and Sharaf (Garg et al., 2022) presented the spherical fuzzy EDAS approach. Generalized aggregation operators are proposed in (Ashraf and Abdullah, 2019; Chinram et al., 2020; Ashraf et al., 2023). Many scholars worked on its hybrid structures such as cubic Pythagorean linguistic fuzzy numbers (Naeem et al., 2021), rough Pythagorean fuzzy bipolar soft information (Akram and Ali, 2020) and sine trigonometric Pythagorean fuzzy information (Ashraf et al., 2021). It performs better role than fuzzy sets in decision making (Khan et al., 2019; Akram et al., 2021a; Zeng et al., 2023). Saeed et al. (Saeed et al. (2023) presented the refined Pythagorean fuzzy sets and interval-valued complex Pythagorean fuzzy set based methodology is developed in (Yazbek et al., 2023). We refer some decision making techniques (Ashraf et al., 2022c; Garg and Sharaf, 2022) for more details.
We looked at the connection between Z-numbers and linguistic summaries, For instance Dempster-Shafer belief systems and type-2 fuzzy logic were used to describe Z values (Kang et al., 2020). Theoretical components of mathematical operations including addition, subtraction, multiplication, division, and computing the square root of a Z-number over discrete Z-numbers have been proposed (Aliev et al., 2015b). They suggested a Z-number-based computing with words (CWW) algorithm, defined a Z-number-based operator for assessing the degree of requirement satisfaction, described CWW simulation experiments using Z-numbers, examined the benefits and drawbacks of Z-numbers, and offered potential resolution approaches (Pal et al., 2013). The authors developed Z-TOPSIS, a novel variant of the TOPSIS approach that streamlines multi-criteria decision-making problems based on the idea of Z-numbers, in order to support the concept of ranking alternatives using Z-numbers. Additionally, the authors offered a link to some existing information in fuzzy sets (Yaakob and Gegov, 2016). The researchers advise researching the fully Z-number based LP (Z-LP) model and utilizing a method to address Z-LP problems that combines differential evolution optimization and Z-number arithmetic created by the authors in order to better fit real-world problems within the LP framework. Using a benchmark LP problem, the suggested model and solution approach for Z-LP are then shown (Aliev et al., 2015a). For replicating the effects of Pilates exercises on students’ motivation, concentration, anxiety, and academic success, they have presented an innovative way. Due to the ambiguity of data relating to cognitive assessment of psychological features and their partial reliability, the use of “Z-if … then rules” for modelling the considered relationship has been pushed for the first time (Aliev and Memmedova, 2015). The topic (Kang et al., 2016) is split into two parts: the first explains how to use the fuzzy expectation to convert a Z-number into a concept of fuzzy number, and the second explains how to use the genetic algorithm to determine the best priority weight for supplier selection. This method of calculating the priority weight of the judgment matrix is quick and flexible. The first recommendation in this study is an enhanced ranking approach for generalized fuzzy numbers that take into account the weight of centroid points, fuzziness levels, and fuzzy number spreads. This approach is particularly effective for evaluating symmetric fuzzy numbers and crisp numbers, among other things, and can alleviate some of the drawbacks of existing approaches (Jiang et al., 2017). For the first time, a multi-layer method of grading Z-numbers is proposed in this work. This method has two layers: fuzzy number ranking and Z number conversion (Bakar and Gegov, 2015).
Few articles, to our knowledge, seek to explore the rationality and certainty of information in efficient and effective decision-making in a systematic and comprehensive manner. For handling uncertainty effectively in real-world applications, fuzzy sets, intuitionistic fuzzy sets, Pythagorean fuzzy sets, picture fuzzy sets, hesitant fuzzy sets, etc. all are unable to deal with the reliability of their membership levels. While reliability or certainty is the core component to deal with making decisions efficiently and trustworthy. In order to eliminate this constraint, this research uses the strategic illustration, conceptual evolution map, and major route analysis to explain the development of the novel Pythagorean fuzzy Z-number (PyFZN) field comprehensively. We suggest a PyFZN by considering Pythagorean fuzziness in terms of both membership and non-membership degrees with reliability. We defined some fundamental properties and aggregation operators, which perform a very significant role in making decisions. Furthermore, we suggested a multicriteria decision-making (MDM) approach, which aims to reduce the overall uncertainty of the decision matrix to increase the credibility of the conclusions. To demonstrate the effectiveness of this novel concept we illustrated a real-life example based on it. Moreover, we also presented a comparative analysis with the existing studies to show its supremacy. The primary goals of this study are: 1. To investigate a number of distinct interactive averaging and geometric AOs concerning PyFZNs to circumvent the constraints. 2. Getting some key characteristics and unique cases of the newly defined AOs. 3. To create a novel MDM strategy using the interactive AOs in a fuzzy Pythagorean context that has been suggested. 4. To present the benefits and viability of the developed MDM strategy.
The main goals of this study are to address the aforementioned research topics and close a knowledge gap.
The rest of this article is organized as follows. Preliminary definitions and concepts are presented in Section 2 and are required to support our primary findings. The concept of Pythagorean fuzzy Z-number, their properties, and score function is explained in Section 3. A thorough investigation of this idea is done in Section 4 where we defined a Pythagorean fuzzy Z-number with arithmetic and geometric aggregation operators and also demonstrate some theorems related to these ideas. In Section 5 we defined a Pythagorean fuzzy Z-number ordered weighted arithmetic and geometric aggregation operators and also demonstrate some theorems related to these ideas. The MDM technique based on intended operators clarified in Section 6, which also provided a numerical example for selecting the riskiest companies to invest money as business partners. We provide an EDAS approach for PyFZNs in Section 7 and also illustrate it with the aid of an example. Finally, in Section 8, we presented a comparative analysis and in Section 9, the conclusion and future research directions for this paper are depicted.
2 Preliminaries
Definition 1. (Zadeh, 1965) Let X be a nonempty set, a fuzzy set A in X is characterized by a membership function
where μA: X → [0, 1], the function defines the degree of membership of the element, x ∈ X.
That is: A fuzzy set A in X is an object having the form:
Definition 2. (Yager, 2013) Assume that B is the Pythagorean fuzzy set and here M is a universal set described as
where the function
Definition 3. The concept of Z-number first introduced by zadeh in 2011 (Zadeh, 2011). The Z-number is discussed as, taking order pair of fuzzy numbers
3 Pythagorean fuzzy Z-number
Now we define Pythagorean fuzzy Z-number (PyFZN) as given below.
Definition 4. Assume that Gz is a Pythagorean fuzzy Z-number
where the funtion
It meets the following requirements:
Now we will discussing the properties of Pythagorean fuzzy Z-numbers which already discuss in Definition 4.
Definition 5. Let
Definition 6. Let Gz1 =
where
Example 1. Consider two pythagorean fuzzy z-number as Gz1 =
Hence, the score of J (Gz1) ≥ J (Gz2), then Gz1 ≥ Gz2.
4 Pythagorean fuzzy Z-numbers weighted aggregation operators
We may propose the weighted aggregation operators for PyFZNs in this part based on actions (6) to (9) in Definition 2.
4.1 PyFZNW operator
We can talk about the PyFZNW operator of PyFZNs in relation to the basis operations (6) and (8) in Definition 2.
Definition 7. Let Gzd =
where
Theorem 1. Let Gzd =
where
Proof. Using mathematical induction to prove the above Theorem 1. In Definition 4 using operation (6) and (8), if
(2). If
(3). If
It is true for all
Theorem 2. The PyFZNW operator implies the following properties:(1) Idempotency: Let
Then,
can keep(3) Monotonoicity: set
Proof. (1) If
(2) Since Gzmin and Gzmax are given by the minimum PyFZN and the maximum PyFZN, then the inequality Gzmin ≤ Gz ≤ Gzmax exists. Thus, there is
4.2 PyFZNWG operator
Using the operation (7) and (9) in Definition 4, we give the PyFZNWG operator of PyFZNs.
Definition 8. Let Gzd =
where
Theorem 3. Let Gzd =
where
Theorem 4. The PyFZNWG operator of also implies the following properties(1) Idempotency:Set: Let
Then,
5 Pythagorean fuzzy Z-numbers ordered weighted aggregation operators
On the basis of the operations (6)–(9) in Definition 4, we may suggest the weighted aggregation operators of PyFZNs in this section.
5.1 PyFZNOW operator
We are able to provide PyFZNW operators for PyFZNs.
Definition 9. Let
where
Theorem 5. Let
where
Proof. Using mathematical induction to to prove the above Theorem 1. In Definition 4 using operation (6) and (8), if
(2). If
(3). If
It is true for all
Theorem 6. The PyFZNOW operator implies the following properties:(1) Idempotency: Let
Then,
can keep. (3) Monotonoicity: set αd =
Proof. (1) If
(2) Since αmin and αmax are given by the minimum PyFZN and the maximum PyFV, then the inequality αmin ≤ α ≤ αmax exists. Thus, there is
5.2 PyFZNOWG operator
Using the operation (7) and (9) in Definition 4, we give the PyFZNOWG operator of PyFZNs.
Definition 10. Let
where
Theorem 7. Let
where
Theorem 8. The PyFZNOWoperator implies the following properties:
(1) Idempotency: Let
(2) Boundedness: Let
Then,
can keep
(3) Monotonoicity: set αd =
Can also be confirmed Theorem 2 using the aforementioned properties corresponding to the PyFZNWG operator, which is not repeated here.
6 MDM approach using the PyFZNW and PyFZNWG operator and the score funtion
In order to handle MDM difficulties, this part develops an MDM methodology using assessment data for both Pythagorean values and Pythagorean reliability measures. This approach relates to PyFZNW and PyFZNW Goperators and the score function. Since a set of n criteria
and
Step 2: Using Eq. 3.1, the score values of J (GZj)(j = 1, 2, … m) are calculated.
Step 3: The best option among the rated options is chosen based on the score values.
Step 4: End.
6.1 An illustrative example and relative comparative analysis
To illustrate the relevance and efficacy of the developed MDM technique with PyFZN information, this section gives an example concerning the challenge of choosing business partners or suppliers. An example of a complex piece of machinery is an aircraft, which has intricate manufacturing processes and strict supplier criteria. Due to the complexity of airplanes, it is challenging for the major manufacturers to complete production on their own time. Therefore, other suppliers work with the primary manufacturers to finish the production of airplanes with a high degree of personalization in the aircraft’s features. For instance, the structure, a component of an aircraft, is crucial to the manufacturing process. An essential component of the skeleton and aerodynamic form of the aircraft body, an aircraft structural part is available in a wide range of complex designs and a number of materials. The weight and strength requirements must be fully taken into account throughout the design and production of aircraft structural elements. The fabrication of structural components for airplanes is a challenging process with stringent standards (Tong and Zhu, 2020a).
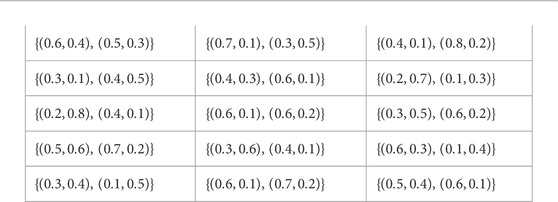
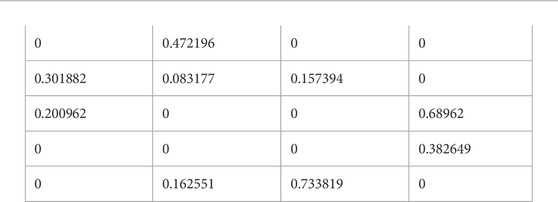
Suppose a manufacturer needs to select a reliable supplier from among potential suppliers. Expert panel presents a set of five suppliers or alternatives Q = {Q1,Q2, … Q5}, which must meet the assessment standards of the criteria: l1 is the product cost; l2 is the product quality and l3 is the delivery lead time.The three criteria’s weight vector is written as (0.2, 0.5, 0.3) to denote their relative importance. Then, the PyZNs that are made up of their membership and non-membership fuzzy values and the measurements of associated reliabilities encourage the experts/decision-makers to evaluate the four suppliers/alternatives over the three criteria. As a result, the following PyZN decision matrix can be used to create all PyZNs:
On the other hand we can apply PyFZNW Step 1: To find PyZNs GZj (j = 1, 2, 3, 4, 5) using (7.1) equation is defined as:
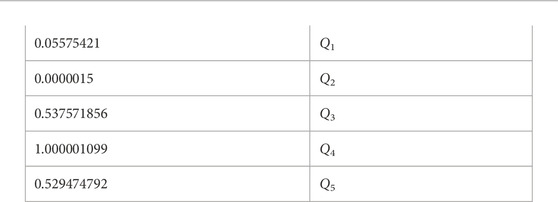
Step 2: The score values J (Gzj) of PyFZNW for the alternatives Qj = {1, 2, 3, 4, 5} are given below:
Step 3: According to the score values J (Gz4) ≥ J (Gz2) ≥ J (Gz5) ≥ J (Gz3) ≥ J (Gz1), the five alternatives are ranked as Q4 ≥ Q2 ≥ Q5 ≥ Q3 ≥ Q1.Hence the best supplier is Q4
Now we can apply PyFZNWGA, in MDM problem can be solved using the invented MDM approach using the PyFZNWG operator, which is illustrated by the following decision-making process:
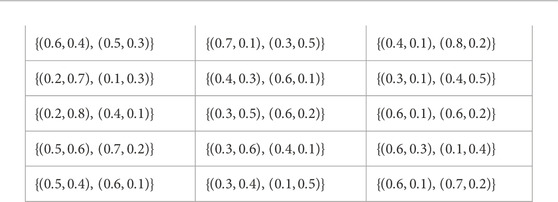
Step 1: The overall collected PyFZN Gzj (j = 1, 2, 3, 4, 5) are obtained as follow:
Step 2: The score values J (Gzj) of PyFZNWG for the alternatives Qj = {1, 2, 3, 4, 5} are given below:
Step 3: According to the score values J (Gz4) ≥ J (Gz5) ≥ J (Gz3) ≥ J (Gz2) ≥ J (Gz1), the five alternatives are ranked as Q4 ≥ Q5 ≥ Q3 ≥ Q2 ≥ Q1.Hence the best supplier is Q4. Here we first order the given matrix with the help of score funtion then the origional matrix becomes:
On the other hand we can apply PyFZNOW
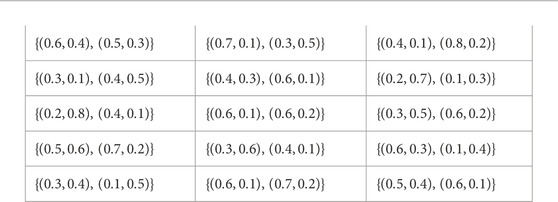
Step 1: To find PyZNs GZj (j = 1, 2, 3, 4, 5) using Eq. 7.1 equation is defined as:
Step 2: The score values J (Gzj) of PyFZNOW for the alternatives Qj = {1, 2, 3, 4, 5} are given below:
Step 3: According to the score values J (Gz4) ≥ J (Gz5) ≥ J (Gz2) ≥ J (Gz3) ≥ J (Gz1), the five alternatives are ranked as Q4 ≥ Q5 ≥ Q2 ≥ Q3 ≥ Q1.Hence the best supplier is Q4
Now we can apply PyFZNOWG, in MDM problem can be solved using the invented MDM approach using the PyFZNOWG operator, which is illustrated by the following decision-making process:
Step 1: The overall collected PyFZN Gzj (j = 1, 2, 3, 4, 5) are obtained as follow:
Step 2: The score values J (Gzj) of PyFZNOWG for the alternatives Qj = {1, 2, 3, 4, 5}are given below:
Step 3: According to the score values J (Gz4) ≥ J (Gz3) ≥ J (Gz5) ≥ J (Gz2) ≥ J (Gz1), the five alternatives are ranked as Q4 ≥ Q3 ≥ Q5 ≥ Q2 ≥ Q1. Hence the best supplier is Q4
According to the created MDM approach that makes use of the PyFZNW, PyFZNOW, PyFZNWG and PyFZNOWG operators as well as the score function, we can observe that the four types of ranking orders mentioned above for the five options and the best option are the same. As a result, the developed MDM strategy works.
7 The extended EDAS method based on novel pythagorean fuzzy Z-number
Evaluation Based on Distance from Average Solution (EDAS), a brand-new and powerful MCDM technique, was created. This method estimates the desirableness of an option based on how far from the average answer they are. In order to verify the efficacy of the Pythagorean fuzzy z-number weighted geometric AOs, a novel extended EDAS approach is developed here to manage the complex uncertain data in real-life DS situations. Assume there are a number of “alternatives” {∅1, ∅2, … , ∅l‘}, and a satisfactory rating {R1, R2, … , Rm} for each. Then,
Step 1: Choose a series of attributes that can be applied to assess the issue: Through a review of the literature, prospective assessment characteristics are gathered, and an expert DM committee is formed to screen the characteristics in order to create a respectable set of evaluation Rd (d = 1, 2, … , m).
Step 2: The normalized decision matrix is created using normalization as follows:
if Rd (d = 1, 2, … , m) is a benefit criterion, the statement use CI, if Rd (d = 1, 2, … , m) is a cost criterion, the statement CII use.
Step 3: Aggregated Data: The skilled uncertain data of required situations are aggregated using established PyFZNWG operators.
Step 4: Verify the average solution (AVS), which is based on all the criteria given.
Step 5: Using the AVS values, the positive distance from average (PDAv) and the negative distance from average (NDAv) can be be calculated:
To compute the PDA and NDA, we can use the score function of PyFZNs mentioned in Definition 3 as follows:
where W shows the score value.
Step 6: Calculate SPDA and SNDA, which represent for PDA and NDA′s weighted average, respectively:
Step 7: Normalize weighted sum of PDA and NDA is defined as repectively:

Step 8: Compute the values of appraisal score (ASC) depends on each alternative’s as
Step 9: Depending on the ASC calculations, alternatives are sorted in decreasing order, and the higher the ASC number, the better options will be chosen.
7.1 An illustrative example
Step 1: Consider the decision matrix as discussed in previous example.
Step 2: The normalized decision matrix is created using normalization as follows:
if Rd (d = 1, 2, … , m) is a benefit criterion, the statement use CI, if Rd (d = 1, 2, … , m) is a cost criterion, the statement CII use.Here the given system is already normalized
Step 3: Now we can apply PyFZNWGA, in MDM problem can be solved using the invented MDM approach using the PyFZNWG operator, which is illustrated by the following decision-making process.The overall collected PyFZN Gzj (j = 1, 2, 3, 4, 5) are obtained as follow:
Step 4: The score values J (Gzj) of PyFZNWG for the corresponding Qj = {1, 2, 3, 4, 5} are given below:
And verify the average solution (AVS) as:
Score funtion of average solution (AVS) we have:
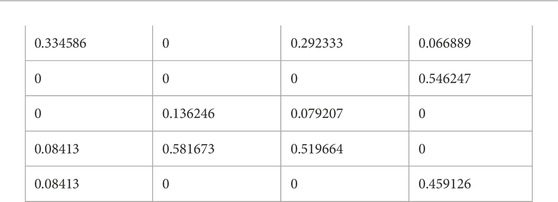
Step 5: Using the AVS values, the positive distance from average (PDAv) and the negative distance from average (NDAv) can be be calculated:
Positive distance from average
Negative distance from average
To compute the PDA and NDA, we can use the score function of PyFZNs mentioned in Definition 3 as follows:
Find PDA using average of PyFZNWG
Find NDA using average of PyFZNWG
Step 6: Calculate SPDA and SNDA, which represent for PDA and NDA′s weighted average, and attributes weighting vector L = = (0.333, 0.333, 0.333, 0.333, 0.333), we can obtain the results as:respectively:
Find SPDA using weight vector
Find NPDA using weight vector
Step 7: Normalize weighted sum of PDA and NDA is defined as repectively:
NSPDA
NSNDA
Step 8: Compute the values of appraisal score (ASC) depends on each alternative’s as:
appraisal score (ASC)
Step 9: Ranking of EDAS method based on Pythagorean fuzzy Z-number weighted geometric aggregation operator
Ranking of EDAS method based on PyFZNWG
Q4 ≥ Q3 ≥ Q5 ≥ Q1 ≥ Q2.Hence the best supplier is Q4.
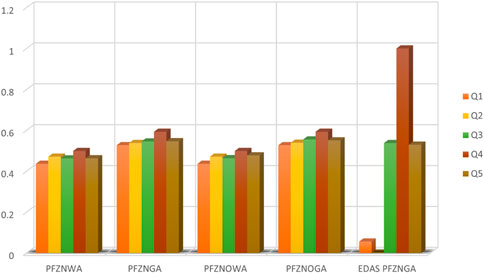
An analysis has been performed using the suggested operators, and the results are summarised in the table below in order to study the trend of variation in score and ranking of all options with the change in the aggregation procedure. From this tabular number, we see that the best choice stays the same, indicating that the outcomes are unbiased and cannot be affected by decision-makers preferences on aggregating processes. So the ranking results are trustworthy. While the comparison graph of all methods which are used in this article is represented in Figure 1. Therefore, our suggested technique is more flexible since the decision-maker(s) may pick operators based on their preferences and actual scenarios.
Comparison of all method
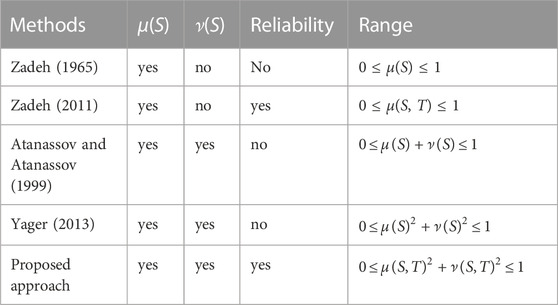
8 Comparasion analysis
Using the idea of constraints in combination with multiattribute and multiobjective decision making approaches, we devised a way to address challenging real-world problems. To demonstrate the usefulness of the proposed approach in contrast to the existing ones for multi-criteria decision-making, a comparative study was conducted using various structures developed by different researchers. Table 1 provides an analytical comparison of the CPHFNS technique to the existing approaches. When such data as CPHFNSS is supplied to a decision maker, none of the existing works can appropriately address it. While the suggested technique is capable of handling existing approaches data. Thus, our proposed methods are superior and more reliable than those now used.
9 Conclusion
In this study, we analyzed the limitation of the current Pythagorean sets and presented a new set, PyFZN, that may handle the issue of hybrid information representation that occurs when Pythagorean values and their related reliability measures are stated simultaneously. The novel score function, basic operations, and the PyFZNW and PyFZNWG operators of PyFZNs also introduced to aggregate information and MDM modeling in the PyFZN context. We also defined their properties and theorems with proofs. To deal with multicriteria decision making issues we offered an algorithm. We view the decision matrix Gz assessment measures of corresponding reliabilities as a special case of the definite. In this paper an example of supplier selection problem at large scale showed how well the created MDM technique worked in the PyFZN environment more effectively than the existing approaches. However, the created MDM strategy offers a fresh approach to resolving MDM issues with PyFZNs. We also presented the EDAS technique on the perposed concept and a comparative analysis with the existing studies to check the efficacy and supermecy of this study.
In the future to enhance the quality of the information provided we plan to apply various aggregation operators such as Einstein, Dombi, average hybrid, etc., with TOPSIS and VIKOR technique and justify their application with the help of medical diagnostics, network signaling, and artificial intelligence.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
Muhammad Naeem would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4310396DSR56.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aboutorab, H., Saberi, M., Asadabadi, M. R., Hussain, O., and Chang, E. (2018). Zbwm: The Z-number extension of Best Worst Method and its application for supplier development. Expert Syst. Appl. 107, 115–125. doi:10.1016/j.eswa.2018.04.015
Akram, M., and Ali, G. (2020). Hybrid models for decision-making based on rough Pythagorean fuzzy bipolar soft information. Granul. Comput. 5, 1–15. doi:10.1007/s41066-018-0132-3
Akram, M., Dudek, W. A., and Dar, J. M. (2019). Pythagorean Dombi fuzzy aggregation operators with application in multicriteria decision-making. Int. J. Intelligent Syst. 34 (11), 3000–3019. doi:10.1002/int.22183
Akram, M., Ilyas, F., and Garg, H. (2020). Multi-criteria group decision making based on ELECTRE I method in Pythagorean fuzzy information. Soft Comput. 24, 3425–3453. doi:10.1007/s00500-019-04105-0
Akram, M., Luqman, A., and Alcantud, J. C. R. (2021). Risk evaluation in failure modes and effects analysis: Hybrid TOPSIS and ELECTRE I solutions with pythagorean fuzzy information. Neural Comput. Appl. 33, 5675–5703. doi:10.1007/s00521-020-05350-3
Akram, M., Luqman, A., and Kahraman, C. (2021). Hesitant Pythagorean fuzzy ELECTRE-II method for multi-criteria decision-making problems. Appl. Soft Comput. 108, 107479. doi:10.1016/j.asoc.2021.107479
Aliev, R. A., Alizadeh, A. V., Huseynov, O. H., and Jabbarova, K. I. (2015). Z-number-based linear programming. Int. J. Intelligent Syst. 30 (5), 563–589. doi:10.1002/int.21709
Aliev, R. A., Alizadeh, A. V., and Huseynov, O. H. (2015). The arithmetic of discrete Z-numbers. Inf. Sci. 290, 134–155. doi:10.1016/j.ins.2014.08.024
Aliev, R. A., Huseynov, O. H., and Zeinalova, L. M. (2016). The arithmetic of continuous Z-numbers. Inf. Sci. 373, 441–460. doi:10.1016/j.ins.2016.08.078
Aliev, R., and Memmedova, K. (2015). Application of Z-number based modeling in psychological research. Comput. Intell. Neurosci. 2015, 760403–760411. doi:10.1155/2015/760403
Ashraf, S., Abdullah, S., and Chinram, R. (2022). Emergency decision support modeling under generalized spherical fuzzy Einstein aggregation information. J. Ambient Intell. Humaniz. Comput. 13, 2091–2117. doi:10.1007/s12652-021-03493-2
Ashraf, S., Abdullah, S., and Khan, S. (2021). Fuzzy decision support modeling for internet finance soft power evaluation based on sine trigonometric Pythagorean fuzzy information. J. Ambient Intell. Humaniz. Comput. 12, 3101–3119. doi:10.1007/s12652-020-02471-4
Ashraf, S., and Abdullah, S. (2019). Spherical aggregation operators and their application in multiattribute group decision-making. Int. J. Intelligent Syst. 34 (3), 493–523. doi:10.1002/int.22062
Ashraf, S., Razzaque, H., Naeem, M., and Botmart, T. (2023). Spherical q-linear Diophantine fuzzy aggregation information: Application in decision support systems. AIMS Math. 8 (3), 6651–6681. doi:10.3934/math.2023337
Ashraf, S., Rehman, N., Al Salman, H., and Gumaei, A. H., (2022). A decision-making framework using q-rung orthopair probabilistic hesitant fuzzy rough aggregation information for the drug selection to treat COVID-19. Complexity.
Ashraf, S., Rehman, N., and Khan, A. (2022). Q-rung orthopair probabilistic hesitant fuzzy rough aggregation information and their application in decision making. Int. J. Fuzzy Syst., 1–14. doi:10.1007/s40815-022-01322-y
Bakar, A. S. A., and Gegov, A. (2015). Multi-layer decision methodology for ranking Z-numbers. Int. J. Comput. Intell. Syst. 8 (2), 395–406. doi:10.1080/18756891.2015.1017371
Banerjee, R., and Pal, S. K. (2015). Z*-numbers: Augmented Z-numbers for machine-subjectivity representation. Inf. Sci. 323, 143–178. doi:10.1016/j.ins.2015.06.026
Chinram, R., Ashraf, S., Abdullah, S., and Petchkaew, P. (2020). Decision support technique based on spherical fuzzy yager aggregation operators and their application in wind power plant locations: A case study of jhimpir, Pakistan. J. Math. 2020, 1–21. doi:10.1155/2020/8824032
Ding, X. F., Zhu, L. X., Lu, M. S., Wang, Q., and Feng, Y. Q. (2020). A novel linguistic Z-number QUALIFLEX method and its application to large group emergency decision making. Sci. Program. 2020, 1–12. doi:10.1155/2020/1631869
Garg, H. (2016). A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int. J. Intelligent Syst. 31 (9), 886–920. doi:10.1002/int.21809
Garg, H., Krishankumar, R., and Ravichandran, K. S. (2022). Decision framework with integrated methods for group decision-making under probabilistic hesitant fuzzy context and unknown weights. Expert Syst. Appl. 200, 117082. doi:10.1016/j.eswa.2022.117082
Garg, H., and Sharaf, I. M. (2022). A new spherical aggregation function with the concept of spherical fuzzy difference for spherical fuzzy EDAS and its application to industrial robot selection. Comput. Appl. Math. 41 (5), 212. doi:10.1007/s40314-022-01903-5
Jabbarova, A. I. (2017). Application of Z-number concept to supplier selection problem. Procedia Comput. Sci. 120, 473–477. doi:10.1016/j.procs.2017.11.266
Jiang, W., Xie, C., Luo, Y., and Tang, Y. (2017). Ranking Z-numbers with an improved ranking method for generalized fuzzy numbers. J. intelligent fuzzy Syst. 32 (3), 1931–1943. doi:10.3233/jifs-16139
Jiang, W., Xie, C., Zhuang, M., Shou, Y., and Tang, Y. (2016). Sensor data fusion with z-numbers and its application in fault diagnosis. Sensors 16 (9), 1509. doi:10.3390/s16091509
Kang, B., Chhipi-Shrestha, G., Deng, Y., Hewage, K., and Sadiq, R. (2018). Stable strategies analysis based on the utility of Z-number in the evolutionary games. Appl. Math. Comput. 324, 202–217. doi:10.1016/j.amc.2017.12.006
Kang, B., Deng, Y., and Sadiq, R. (2018). Total utility of Z-number. Appl. Intell. 48, 703–729. doi:10.1007/s10489-017-1001-5
Kang, B., Hu, Y., Deng, Y., and Zhou, D. (2016). A new methodology of multicriteria decision-making in supplier selection based onZ-numbers. Math. problems Eng. 2016, 1–17. doi:10.1155/2016/8475987
Kang, B., Zhang, P., Gao, Z., Chhipi-Shrestha, G., Hewage, K., and Sadiq, R. (2020). Environmental assessment under uncertainty using Dempster–Shafer theory and Z-numbers. J. Ambient Intell. Humaniz. Comput. 11, 2041–2060. doi:10.1007/s12652-019-01228-y
Khan, A. A., Ashraf, S., Abdullah, S., Qiyas, M., Luo, J., and Khan, S. U. (2019). Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry 11 (3), 383. doi:10.3390/sym11030383
Naeem, M., Ashraf, S., Abdullah, S., and Al-Harbi, F. M. (2021). Redefined “maclaurin symmetric mean aggregation operators based on cubic pythagorean linguistic fuzzy numbers”. Math. Problems Eng. 2021, 1–19. doi:10.1155/2021/5518353
Pal, S. K., Banerjee, R., Dutta, S., and Sarma, S. S. (2013). An insight into the Z-number approach to CWW. Fundam. Inf. 124 (1-2), 197–229. doi:10.3233/fi-2013-831
Rahman, K., Abdullah, S., Khan, M. A., Ibrar, M., and Husain, F. (2017). Some basic operations on Pythagorean fuzzy sets. J. Appl. Environ. Biol. Sci. 7 (1), 111–119.
Ren, Z., Liao, H., and Liu, Y. (2020). Generalized Z-numbers with hesitant fuzzy linguistic information and its application to medicine selection for the patients with mild symptoms of the COVID-19. Comput. Industrial Eng. 145, 106517. doi:10.1016/j.cie.2020.106517
Saeed, M., Ahmad, M. R., and Rahman, A. U. (2023). Refined pythagorean fuzzy sets: Properties, set-theoretic operations and axiomatic results. J. Comput. Cognitive Eng. 2 (1), 10–16.
Wang, J. Q., Cao, Y. X., and Zhang, H. Y. (2017). Multi-criteria decision-making method based on distance measure and Choquet integral for linguistic Z-numbers. Cogn. Comput. 9, 827–842. doi:10.1007/s12559-017-9493-1
Wang, W., and Liu, X. (2011). Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int. J. intelligent Syst. 26 (11), 1049–1075. doi:10.1002/int.20498
Yaakob, A. M., and Gegov, A. (2016). Interactive TOPSIS based group decision making methodology using Z-numbers. Int. J. Comput. Intell. Syst. 9 (2), 311–324. doi:10.1080/18756891.2016.1150003
Yager, R. R. (2012). On Z-valuations using Zadeh’s Z-numbers. Int. J. Intelligent Syst. 27 (3), 259–278. doi:10.1002/int.21521
Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Trans. fuzzy Syst. 22 (4), 958–965. doi:10.1109/tfuzz.2013.2278989
Yazbek, H. A., Surriya, F., Khan, S. U., Jan, N., and Marinkovic, D. (2023). A novel approach to model the economic characteristics of an organization by interval-valued complex pythagorean fuzzy information. J. Comput. Cognitive Eng. 2 (1), 75–87.
Zadeh, L. A. (2011). A note on Z-numbers. Inf. Sci. 181 (14), 2923–2932. doi:10.1016/j.ins.2011.02.022
Zeng, S., Hu, Y., and Llopis-Albert, C. (2023). Stakeholder-inclusive multi-criteria development of smart cities. J. Bus. Res. 154, 113281. doi:10.1016/j.jbusres.2022.08.045
Keywords: pythagorean fuzzy z-number, pythagorean fuzzy z-number weighted arithmetic operator, pythagorean fuzzy z-number weighted geometric operator, decision making, EDAS method
Citation: Ashraf S, Abbasi SN, Naeem M and Eldin SM (2023) Novel decision aid model for green supplier selection based on extended EDAS approach under pythagorean fuzzy Z-numbers. Front. Environ. Sci. 11:1137689. doi: 10.3389/fenvs.2023.1137689
Received: 04 January 2023; Accepted: 01 March 2023;
Published: 30 March 2023.
Edited by:
Harish Garg, Thapar Institute of Engineering and Technology, IndiaReviewed by:
Shouzhen Zeng, Ningbo University, ChinaMuhammad Akram, University of the Punjab, Pakistan
Copyright © 2023 Ashraf, Abbasi, Naeem and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shahzaib Ashraf, c2hhaHphaWIuYXNocmFmQGtmdWVpdC5lZHUucGs=; Sayed M. Eldin, c2F5ZWQuZWxkaW4yMkBmdWUuZWR1LmVn
 Shahzaib Ashraf
Shahzaib Ashraf Shahzad Noor Abbasi
Shahzad Noor Abbasi Muhammad Naeem
Muhammad Naeem Sayed M. Eldin
Sayed M. Eldin