The manufacturers’ strategy selection of carbon emission reduction and pricing under carbon trading policy and consumer environmental awareness

Carbon trading policy and consumer environmental awareness are increasingly important to manufacturers’ carbon emission reduction and pricing. To analyze their strategy selection of carbon emission reduction and pricing, this paper develops three game models, where two manufacturers could choose no cooperation (NC), only cooperation in carbon emission reduction (SC), or simultaneous cooperation in carbon emission reduction and pricing (CC). By solving these models and comparing their environmental R&D levels, net carbon emissions, and profits, the paper finds strategy selection for manufacturers and its conditions. Results show that from the view of the environmental R&D level and supply chain’s profit, NC and SC may be the optimal strategy and the second-best strategy, respectively. From the net carbon emission point of view, CC and SC should be the optimal strategy and the second-best strategy, respectively. As to manufacturers’ profits, CC should be the optimal strategy, and NC or SC should be the second-best strategy. From comprehensive views, none of these strategies could be the optimal strategy, but SC may be the second-best strategy. This paper contributes in three aspects. First, this paper designs three strategies of carbon emission reduction and pricing for two manufacturers. Second, this paper takes the initial carbon emission allowances of the government as one of decision variables. Finally, this paper investigates the effects of different strategies and finds strategy selections for manufacturers from a single view and comprehensive views.

1 Introduction

Environmental damage caused by carbon emission has been one of the most important issues globally, and how to reduce carbon emission has drawn much attention. In recent years, the digital economy has shown a significant spatial effect on carbon emission reduction (Yi et al., 2022; Li and Wang, 2022). However, carbon tax policy (CT) and carbon trading policy (CET) have been more widely put into practice to curb carbon emissions. However, with advantages in the effect and cost of carbon emission reduction, CET is more attractive to many countries (Wang and Wang, 2015) and can increase the potential of firms to reduce carbon emissions (Chu et al., 2021). In practice, the EU, the United States, Australia, and some other developed economies have implemented carbon trading policy. As a developing country, China has been putting great emphasis on the environment issue in recent years and has made a promise to peak its carbon dioxide emissions by 2030 and achieve carbon neutrality by 2060. In practice, China is already taking strong nationwide actions toward the carbon peak and carbon neutrality targets. China’ national carbon emission trading market is a good example. As of the start of 2022, there are 25 operational emission trading systems around the world, in jurisdictions representing 55% of global GDP and covering 17% of global emissions¹. In addition, many countries continue to strengthen the concept of environmental conservation and gradually integrate the requirements of low carbon into consumers’ daily life, and some consumers with strong environmental awareness may pay higher prices for low-carbon products (Chitra, 2007; Yalabik and Fairchild, 2011) and induce firms to design corporate resource allocation (Su et al., 2023) and produce low-carbon products (Basiri and Heydari, 2017). Under these backgrounds, firms should invest more in environmental R&D, and some strong firms produced many lower-emission products. For example, companies in the fashion apparel industry such as H&M and Levi’s have adopted cleaner technologies to generate less carbon emissions during their production (Li and Li, 2014), and consumers with strong environmental awareness were willing to pay an average premium of 33% for green goods². However, since firms non-cooperatively investing in environmental R&D will bring additional cost pressure on themselves, some of them choose to cooperate with their rivals. For example, the truck units of Toyota Motor and Volkswagen AG are forming an alliance to develop lower-emission vehicles and can spend R&D money only once instead of twice or thrice than they would when alone³.

To summarize, it is profound for manufacturers to rethink the strategy of carbon emission reduction and pricing when they are faced with CET and consumer environmental awareness (CEA). Though previous researchers studied carbon emission reduction under CET, carbon emission reduction under CEA, and carbon emission reduction under CET and CEA, most of them considered the cooperation between the manufacturer and the retailer in the same supply chain. Taking these backgrounds into account, we consider two two-echelon supply chains consisting of two manufacturers and a common retailer, where manufacturers make decisions on environmental R&D levels and wholesale prices of products and the retailer makes a decision on retail prices of products. Then, we provide three strategies of carbon emission reduction and pricing for manufacturers including no cooperation (NC), only cooperation in carbon emission reduction (SC), and simultaneous cooperation in carbon emission reduction and pricing (CC), meaning that manufacturers make all their decisions non-cooperatively, make their decisions on environmental R&D levels cooperatively and on wholesale prices non-cooperatively, and make all their decisions cooperatively, respectively. Questions of interest in this paper are as follows: 1) what effects do the three strategies of carbon emission reduction and pricing have on the carbon emission level, net carbon emission, and profit? 2) from a single view, which strategy should be chosen by manufacturers? 3) from comprehensive views, which strategy should be chosen by manufacturers?

To answer these questions, we develop three four-staged game models of the two supply chains faced with the CET and CEA from the perspective of game theory. Then, based on the equilibriums of these models, we compare the carbon emission level, net carbon emission, and profits of manufacturers and the supply chain and find the optimal strategy and the second-best strategy for manufacturers from a single view. Finally, we make a comprehensive comparison and find the second-best strategy for manufacturers and its condition from comprehensive views. Through this research, we can analyze effects of different strategies and find strategy selection from different views for manufacturers and provide a scientific basis for supply chain management and related policy improvement.

The remainder of this paper is organized as follows. Section 2 presents the literature review. Section 3 describes model formulation and notation. Section 4 presents the three game models. Section 5 provides the results and discussion. Section 6 concludes this paper.

2 Literature review

2.1 Carbon emission reduction under CET

Some researchers only took manufacturers as an objective. Wang et al. (2018) divided manufacturers into under-emitter manufacturers and over-emitter manufacturers and found conditions under which the over-emitter manufacturers’ decisions were identified. Given carbon emission reduction, Xia et al. (2020) divided manufacturers into low-carbon manufacturers and ordinary product manufacturers and analyzed impacts of the CET on retail prices, sales, and profits. Other researchers took the supply chain consisting of a manufacturer and a retailer as the objective. Wang et al. (2016) designed a wholesale price premium contract and a cost-sharing contract and found that these two contracts could increase the manufacturer’s carbon emission reduction rate and the supply chain’s profit; the cost-sharing contract could increase profits of both the manufacturer and the retailer, and the wholesale price premium contract could increase the profit of the supply chain. Yang et al. (2018) analyzed the effects of the manufacturer’s promotion and the retailer’s promotion through the manufacturer’s channel and a retail channel. However, all these researchers only took CET into account and neglected CEA.

2.2 Carbon emission reduction under CEA

CEA could prompt the supply chain to provide green products (Zhang et al., 2020) and always benefit the manufacturer (Li et al., 2021). Under the three structures, Liu et al. (2012) constructed three models where the manufacturer (manufacturers) decided carbon emission reduction and wholesale prices and the retailer (retailers) decided the retail prices of products separately and analyzed the impacts of CEA on the supply chain players. In a supply chain compromised of a manufacturer and a retailer, Du et al. (2015) found that compared to the wholesale-price contract, both the revenue-sharing contract and the quantity-discount contract could increase the supply chain’s profit, and the carbon emission reductions in the decentralized supply chain could be the same as those in the centralized supply chain. Zhang et al. (2019) found that retailer’s fairness concerns would not change the carbon emission reduction but could influence the wholesale price and retail price. Liu and Li (2020) found that the introduction of CEA could increase the carbon emission reduction of the supply chain, both the carbon emission reduction and profit of the supply chain in the centralized scenario are higher than those in the decentralized scenario, and the bilateral cost-sharing contract could effectively encourage the manufacturer and the retailer to engage in carbon emission reduction. Wang et al. (2021) found that both carbon emission reduction and production in the centralized model are much higher than those in the decentralized model. However, all these researchers only took CEA into account and neglected CET. Xia et al. (2022) found that either with or without a cost-sharing contract, the carbon emission reduction in the decentralized scenario was no more than that in the centralized scenario.

2.3 Carbon emission reduction under CET and CEA

Luo et al. (2016) considered two manufacturers with different carbon reduction efficiencies and constructed two models where manufacturers made decisions cooperatively or non-cooperatively. They found that manufacturers who made decisions cooperatively could increase profit and decrease total carbon emissions. However, they neglected the cooperation in pricing. Cao et al. (2017) analyzed the impacts of CET on the production and carbon emission reduction level of the manufacturer.

In the supply chain consisting of a manufacturer and a retailer, Xia et al. (2018) considered that the manufacturer decided the emission reduction rate and the retailer decided the promotion level and investigated their optimal decisions and profits. Wang et al. (2020) designed several contracts and found that the one-way cost-sharing contract was beneficial for the supply chain, the two-way cost-sharing contract could also achieve this effect if the sharing rate is small, and the joint carbon-emission reduction could be an optimal choice for the supply chain. Liu et al. (2021) provided three carbon emission reduction modes and found that the carbon emission reduction level was the highest in the joint carbon emission reduction, and firms would prefer the single carbon emission reduction or the joint carbon emission reduction under different conditions. However, these studies analyzed the interaction between the manufacturer and the retailer and were not able to investigate the cooperation between manufacturers.

In the two two-echelon supply chains, each of which consists of a manufacturer and a retailer, Yang et al. (2017) found that compared to the structure in which both chains were decentralized, vertical cooperation could increase carbon emission reduction but decrease retail prices and horizontal cooperation could damage retailers’ profit. In the supply chain consisting of a supplier and a manufacturer, Bai et al. (2018) found that compared to the decentralized scenario, the centralized decision scenario could increase the supply chain’s profit and decrease its carbon emission. However, these studies neglected the cooperation in pricing and took initial carbon emission allowances of the government and the price of carbon emission trading as given.

Our key contributions lie in the following aspects. First, this paper designs three strategies of carbon emission reduction and pricing for two manufacturers, which can be better to describe the operation practice. Second, this paper takes the initial carbon emission allowances of the government as one of decision variables, which can extend the existing game models to four-staged ones. Finally, this paper investigates the effects of different strategies and finds strategy selections for manufacturers from a single view and comprehensive views, which contributes to explaining various strategies between manufacturers.

3 Model formulation and notation

This paper considers two two-echelon supply chains consisting of two manufacturers producing a homogeneous product and a common retailer. The production of the manufacturer $m\left(m=\mathrm{1,2}\right)$ is $q_m$ and is sold to the retailer $R$ with a wholesale price ${\omega }_m$; then, the retailer $R$ sells the product to consumers with a retail price $p_m$. During the production, the production of a one-unit product produces one-unit carbon emission. Under CET and CEA, the manufacturer invests in environmental R&D to reduce carbon emission. For carbon emission reduction and pricing, the manufacturer $m$ can choose NC, SC, or CC. In each carbon emission reduction and pricing strategy, the government and members in the two supply chains play a four-staged game, which is shown in Figure 1. At the first stage, the government decides the amount of free allocation of carbon allowance for each manufacturer. At the second stage, each manufacturer decides the environmental R&D level. At the third stage, each manufacturer decides the wholesale price. At the last stage, the retailer decides the retailer price. The meaning of parameters, variables, and functions in this paper is given in Table 1.

FIGURE 1

FIGURE 1. Game rules for each carbon emission reduction and pricing strategy.

TABLE 1

TABLE 1. Meaning of parameters, variables, and functions.

3.1 The cost structure

For simplicity, the marginal production cost of each manufacturer is neglected. To reduce carbon emission, the manufacturer $m$ can invest in environmental R&D. The cost of environmental R&D for manufacturer $m$ is $C_m=x_m^2/2$ (Bai et al., 2018), where $x_m$ is the environmental R&D level of manufacturer $m$. Then, net carbon emission of manufacturer $m$ is $e_m=q_m-x_m-\beta x_n,m,n=\mathrm{1,2},$ $m\ne n$, where $\beta \left(0<\beta <1\right)$ is the environmental R&D spillover rate.

3.2 The demand function

Based on Katsoulacos et al. (2001), consumer surplus is $CS={\left(q_m+q_n\right)}^2/2$, and we introduce a sensitive parameter $\theta \left(0<\theta <1\right)$ to measure consumers’ environmental awareness, and the product is sold to consumers at a retail price $p_m=1-q_m-q_n-\theta e_m$. Then, consumers’ demand function can be obtained as follows:

$q_m=\left[\theta -\left(1+\theta \right)p_m+p_n+\theta \left(1+\theta \right)\left(x_m+\beta x_n\right)-\theta \left(\beta x_m+x_n\right)\right]/\left[\theta \left(2+\theta \right)\right].(1)$

3.3 The CET

Carbon emission damages the environment, and environmental damage caused by carbon emission is $D={\left(e_m+e_n\right)}^2/2$ (Poyago-Theotoky, 2007). The government’s free allocation of carbon allowance for the manufacturer $m$ is ${\overline{e}}_m$. The manufacturer $m$ needs to buy additional allowance from the carbon trading market if $e_m>{\overline{e}}_m$; otherwise, the manufacturer $m$ can sell additional allowance on the carbon trading market, and the clear price of carbon allowance in the carbon trading market is $p_e$.

Therefore, profit functions of the retailer and the manufacturer $m$ are shown as follows:

${\pi }_r=\left(p_m-{\omega }_m\right)q_m+\left(p_n-{\omega }_n\right)q_n,(2)$

${\pi }_m={\omega }_m{q}_m-x_m^2/2-p_e\left(e_m-{\overline{e}}_m\right).(3)$

The welfare function of the government is $W={\pi }_m+{\pi }_n+{\pi }_r+CS-D$, which is as follows after arranging:

$W=p_m{q}_m+p_n{q}_n+{\left(q_m+q_n\right)}^2/2-\left(x_m^2+x_n^2\right)/2-{\left(e_m+e_n\right)}^2/2.(4)$

4 Model solutions

With backward induction, we obtain solutions for the aforementioned models.

4.1 Model solutions for NC

In the last stage, the retailer determines retail prices to maximize its profit. Substituting (1) in (2), the problem of optimal retail prices can be described as follows:

$\begin{array}{l}\underset{p_m,p_n}{\mathit{max}}{\pi }_r=\left\{\left(p_m-{\omega }_m\right)\left[\theta -\left(1+\theta \right)p_m+p_n+\theta \left(1+\theta \right)\left(x_m+\beta x_n\right)-\theta \left(\beta x_m+x_n\right)\right]\right.\\ +\left(p_n-{\omega }_n\right)\left[\theta +p_m-\left(1+\theta \right)p_n+\theta \left(1+\theta \right)\left(\beta x_m+x_n\right)-\theta \left(x_m+\beta x_n\right)\right]\}/\left[\theta \left(2+\theta \right)\right].\end{array}(5)$

Combining $\partial {\pi }_r/\partial p_1=0$ and $\partial {\pi }_r/\partial p_2=0$, the optimal retail price for the product of the manufacturer $m$ can be solved as follows:

$p_m^{*}=\left[1+{\omega }_m+\theta \left(x_m+\beta x_n\right)\right]/2.(6)$

Substituting (6) in (2), consumers’ demand function for the product of the manufacturer $m$ can be rewritten as follows:

$q_m^{*}=\left\{\theta -\left(1+\theta \right){\omega }_m+{\omega }_n+\theta \left[\left(1+\theta \right)\left(x_m+\beta x_n\right)-\left(\beta x_m+x_n\right)\right]\right\}/\left[2\theta \left(2+\theta \right)\right].(7)$

In the third stage, the problem of the optimal wholesale price of the product of the manufacturer $m$ under the NC model can be described as follows:

$\underset{{\omega }_m}{\mathit{max}}{\pi }_m={\omega }_m{q}_m^{*}-x_m^2/2-p_e\left(q_m^{*}-x_m-\beta x_n-{\overline{e}}_m\right).(8)$

Combining $\partial {\pi }_m/\partial {\omega }_m=0$ with $\partial {\pi }_n/\partial {\omega }_n=0$, the optimal wholesale price for the product of the manufacturer $m$ can be solved as follows:

$\begin{array}{ll}{\omega }_m^{*}=& \left[\theta \left(3+2\theta \right)+\left(1+\theta \right)\left(3+2\theta \right)p_e+\theta \left(2{\theta }^2+4\theta +1\right)\left(x_m+\beta x_n\right)-\theta \left(1+\theta \right)\left(\beta x_m+x_n\right)\right]/\left[\left(1+2\theta \right)\left(3+2\theta \right)\right].\end{array}(9)$

In the second stage, the problem of the optimal environmental R&D level of the manufacturer $m$ under the NC model can be described as follows:

$\underset{x_m}{\mathit{max}}{\pi }_m={\omega }_m^{*}{q}_m^{*}-x_m^2/2-p_e\left(q_m^{*}-x_m-\beta x_n-{\overline{e}}_m\right).(10)$

Combining $\partial {\pi }_m/\partial x_m=0$ with $\partial {\pi }_n/\partial x_n=0$, the optimal environmental R&D level of the manufacturer $m$ can be solved as follows:

$x_m^{*}=-\left[\theta {\alpha }_1\left({\alpha }_2-\beta {\alpha }_1\right)+\left({\alpha }_3{\alpha }_4+\beta \theta {\alpha }_1^2\right)p_e\right]/\left({\alpha }_5+\beta {\theta }^2{\alpha }_1{\alpha }_6\right),(11)$

where ${\alpha }_1=1+\theta ,{\alpha }_2=2{\theta }^2+4\theta +1,{\alpha }_3=2{\theta }^2+6\theta +3,{\alpha }_4=3{\theta }^2+6\theta +2,{\alpha }_5=2{\theta }^5-2{\theta }^4-31{\theta }^3-53{\theta }^2$ $-31\theta -6,{\alpha }_6=2{\theta }^2+3\theta -{\alpha }_1\beta \theta$. Taking into account the clear condition of the carbon trading market ($e_m-{\overline{e}}_m+e_n-{\overline{e}}_n=0$), its clear price is solved as follows:

$\begin{array}{ll}{p}_e^{*}=& \{{\alpha }_1\left[2\theta {\alpha }_1{\beta }^2-2{\theta }^2\left(2{\alpha }_1+1\right)\beta -4{\theta }^2{\alpha }_1+3\left(2{\alpha }_1-1\right)\right]+\left({\alpha }_5+\beta {\theta }^2{\alpha }_1{\alpha }_6\right)\left({\overline{e}}_m+{\overline{e}}_n\right)\}/\left[2\theta {\alpha }_1^2{\beta }^2+\left(2{\alpha }_1+1\right){\alpha }_7\beta +{\alpha }_8\right],\end{array}(12)$

where ${\alpha }_7=4{\theta }^3+19{\theta }^2+17\theta +4,{\alpha }_8=8{\theta }^4+52{\theta }^3+99{\theta }^2+68\theta +15$.

In the first stage, the problem of optimal allocation of carbon allowance under the NC model can be described as follows:

$\underset{{\overline{e}}_1,{\overline{e}}_2}{\mathit{max}}W={\displaystyle \sum }_{m=1}^2{p}_m^{*}{q}_m^{*}+{\left({\displaystyle \sum }_{m=1}^2{q}_m^{*}\right)}^2/2-{\displaystyle \sum }_{m=1}^2{\left(x_m^{*}\right)}^2/2-{\left({\displaystyle \sum }_{m=1}^2{e}_m^{*}\right)}^2/2.(13)$

Combining $\partial W/\partial {\overline{e}}_1=0$ and $\partial W/\partial {\overline{e}}_2=0$, the optimal allocation of carbon allowance under the NC model can be solved as follows:

${\overline{e}}_m^{nc}=-{\alpha }_1\left(2{\alpha }_1-1\right)\left(2{\alpha }_1+1\right)\left[4{\theta }^2{\alpha }_1^2{\beta }^3+4\theta {\alpha }_9{\beta }^2+{\alpha }_{10}\beta -\left({\alpha }_1-2\right){\alpha }_{11}\right]/\left(2{\Delta }_1\right),(14)$

where ${\Delta }_1=4{\beta }^4{\theta }^2{\alpha }_1^4-2{\beta }^3\theta {\alpha }_1^2\left(2{\alpha }_1+1\right){\alpha }_{12}-{\beta }^2{\alpha }_{13}-2\beta {\alpha }_{14}-{\alpha }_{15},{\alpha }_9=4{\theta }^4+24{\theta }^3+41{\theta }^2+24\theta +4,{\alpha }_{10}$ $=32{\theta }^5+180{\theta }^4+288{\theta }^3+139{\theta }^2+3\theta -6,{\alpha }_{11}=16{\theta }^4+92{\theta }^3+162{\theta }^2+103\theta +21,{\alpha }_{12}=2{\theta }^4-5{\theta }^3-37{\theta }^2$ $-34\theta -8,{\alpha }_{13}=32{\theta }^9+224{\theta }^8+156{\theta }^7-2522{\theta }^6-9281{\theta }^5-14824{\theta }^4-12731{\theta }^3-6038{\theta }^2-1476\theta -144,$ ${\alpha }_{14}=32{\theta }^9+204{\theta }^8+24{\theta }^7-2887{\theta }^6-9921{\theta }^5-15722{\theta }^4-13700{\theta }^3-6706{\theta }^2-1722\theta -180,{\alpha }_{15}=32{\theta }^9$ $+120{\theta }^8-812{\theta }^7-6372{\theta }^6-17839{\theta }^5-26404{\theta }^4-22448{\theta }^3-10964{\theta }^2-2853\theta -306$. Substituting 14 in 12, 11, 9, 7, and 6, the equilibrium clear price of carbon allowance ($p_e^{nc}$), environmental R&D level ($x_m^{nc}$), wholesale price (${\omega }_m^{nc}$), production ($q_m^{nc}$), and retail price ($p_m^{nc}$) under the NC model can be solved. It is easy to find that when $\beta ,\theta \in \left(\mathrm{0,1}\right)$, $x_m^{nc}>0,{\omega }_m^{nc}>0,q_m^{nc}>0,p_m^{nc}>0$ will always hold, and $\text{sign}\left({\overline{e}}_m^{nc}\right)=\text{sign}\left(-\left(4{\theta }^2{\alpha }_1^2{\beta }^3+4\theta {\alpha }_9{\beta }^2+{\alpha }_{10}\beta -\left({\alpha }_1-2\right){\alpha }_{11}\right)\right)$. Figure 2 shows conditions where ${\overline{e}}_m^{nc}=0$, ${\overline{e}}_m^{nc}>0$, and ${\overline{e}}_m^{nc}<0$ can satisfy. Let $4{\theta }^2{\alpha }_1^2{\beta }^3+4\theta {\alpha }_9{\beta }^2+{\alpha }_{10}\beta -\left({\alpha }_1-2\right){\alpha }_{11}$ $=0$, we can get the solution $\theta =g_1\left(\beta \right)$; then, we have ${\overline{e}}_m^{nc}=0$. If $\theta <g_1\left(\beta \right)$, $4{\theta }^2{\alpha }_1^2{\beta }^3+4\theta {\alpha }_9{\beta }^2+{\alpha }_{10}\beta -\left({\alpha }_1-2\right){\alpha }_{11}<0$ will hold; then, ${\overline{e}}_m^{nc}>0$ will hold; otherwise, ${\overline{e}}_m^{nc}<0$ will hold.

FIGURE 2

FIGURE 2. Condition for a positive solution of free allocation of carbon allowance under NC.

4.2 Model solutions for SC

Solutions for the optimal retail price and wholesale price under the SC model are the same as those under the NC model shown in 6 and 9; then, we solve the second stage and the first stage under the SC model.

In the second stage under the SC model, manufacturers determine environmental R&D levels to maximize their joint profit ${\pi }_{mn}={\pi }_m+{\pi }_n$. The problem of the optimal environmental R&D level of the manufacturer $m$ under the SC model can be described as follows:

$\underset{x_m,x_n}{\mathit{max}}{\pi }_{mn}={\omega }_m^{*}{q}_m^{*}+{\omega }_n^{*}{q}_n^{*}-\left(x_m^2+x_n^2\right)/2.(15)$

Combining $\partial {\pi }_{mn}/\partial x_m=0$ and $\partial {\pi }_{mn}/\partial x_n=0$, the optimal environmental R&D level of the manufacturer $m$ can be solved as follows:

${\stackrel{\sim }{x}}_m^{*}=-\left(1+\beta \right)\left[{\theta }^2{\alpha }_1+\left(3{\alpha }_1-1\right){\delta }_1{p}_e\right]/\left[\beta \left(2+\beta \right){\theta }^3{\alpha }_1+{\delta }_2\right],(16)$

where ${\delta }_1={\theta }^2+3\theta +1,{\delta }_2={\theta }^4-3{\theta }^3-12{\theta }^2-9\theta -2$. The clear price of carbon allowance is solved as follows:

${\stackrel{\sim }{p}}_e^{*}=-\left\{{\alpha }_1\left(2{\theta }^2{\beta }^2+4{\theta }^2\beta +{\delta }_3\right)-\left[\beta \left(2+\beta \right){\theta }^3{\alpha }_1+{\delta }_2\right]\left({\overline{e}}_m+{\overline{e}}_n\right)\right\}/\left({\beta }^2{\delta }_4+2\beta {\delta }_4+{\delta }_5\right),(17)$

where ${\delta }_3=2{\theta }^2-2\theta -1,{\delta }_4=4{\theta }^3+19{\theta }^2+17\theta +4,{\delta }_5=4{\theta }^3+21{\theta }^2+20\theta +5$.

In the first stage, the problem of optimal allocation of carbon allowance under the SC model can be described as follows:

$\underset{{\overline{e}}_1,{\overline{e}}_2}{\mathit{max}}W={\displaystyle \sum }_{m=1}^2{p}_m^{*}{q}_m^{*}+{\left({\displaystyle \sum }_{m=1}^2{q}_m^{*}\right)}^2/2-{\displaystyle \sum }_{m=1}^2{\left(x_m^{*}\right)}^2/2-{\left({\displaystyle \sum }_{m=1}^2{e}_m^{*}\right)}^2/2.(18)$

Combining $\partial {\stackrel{\sim }{W}}^{*}/\partial {\overline{e}}_1=0$ and $\partial {\stackrel{\sim }{W}}^{*}/\partial {\overline{e}}_2=0$, the optimal allocation of carbon allowance under the SC model can be solved as follows:

${\overline{e}}_m^{sc}={\alpha }_1\left(2{\alpha }_1-1\right)\left[{\left(1+\beta \right)}^2\theta -1\right]\left(2{\beta }^2{\delta }_6+4\beta {\delta }_6+{\delta }_7\right)/\left(2{\Delta }_2\right),(19)$

where ${\Delta }_2={\beta }^4{\delta }_8+4{\beta }^3{\delta }_8+2{\beta }^2{\delta }_9+4\beta {\delta }_{10}+{\delta }_{11},{\delta }_6=4{\theta }^3+17{\theta }^2+14\theta +3,{\delta }_7=8{\theta }^3+36{\theta }^2+31\theta +7,{\delta }_8=8{\theta }^7+30{\theta }^6-69{\theta }^5-432{\theta }^4-655{\theta }^3-438{\theta }^2-136\theta -16,{\delta }_9=24{\theta }^7+79{\theta }^6-296{\theta }^5-1550{\theta }^4-2293{\theta }^3-1525{\theta }^2-474\theta -56,{\delta }_{10}=8{\theta }^7+19{\theta }^6-158{\theta }^5-686{\theta }^4-983{\theta }^3-649{\theta }^2-202\theta -24,{\delta }_{11}=8{\theta }^7+8{\theta }^6-$ $251{\theta }^5-960{\theta }^4-1348{\theta }^3-892{\theta }^2-281\theta -34$. Substituting 19 in 17, 16, 9, 7, and 6, the equilibrium clear price of carbon allowance ($p_e^{sc}$), environmental R&D level ($x_m^{sc}$), wholesale price (${\omega }_m^{sc}$), production ($q_m^{sc}$), and retail price ($p_m^{sc}$) under the SC model can be solved. It is easy to find that when $\beta ,\theta \in \left(\mathrm{0,1}\right)$, $x_m^{sc}>0,{\omega }_m^{sc}>0,q_m^{sc}>0,p_m^{sc}>0$ will always hold, and $\text{sign}\left({\overline{e}}_m^{sc}\right)=\text{sign}\left(-\left({\left(1+\beta \right)}^2\theta -1\right)\right)$. Figure 3 shows conditions where ${\overline{e}}_m^{sc}=0$, ${\overline{e}}_m^{sc}>0$, and ${\overline{e}}_m^{sc}<0$ can satisfy. Let ${\left(1+\beta \right)}^2\theta -1=0$, we can get the solution $\theta =1/{\left(1+\beta \right)}^2=g_2\left(\beta \right)$; then, we have ${\overline{e}}_m^{sc}=0$. If $\theta <g_2\left(\beta \right)$, ${\left(1+\beta \right)}^2\theta -1<0$ will hold; then, ${\overline{e}}_m^{sc}>0$ will hold; otherwise, ${\overline{e}}_m^{sc}<0$ will hold.

FIGURE 3

FIGURE 3. Condition for a positive solution of free allocation of carbon allowance under SC.

4.3 Model solutions for CC

Solutions for the optimal retail price under the CC model are the same as those under the NC model, which is shown in (6); then, we solve the third stage, the second stage, and the first stage under the CC model.

In the third stage under the CC model, manufacturers determine their wholesale prices to maximize their joint profit. This problem under the CC model can be described as follows:

$\underset{{\omega }_m,{\omega }_n}{\mathit{max}}{\pi }_{mn}={\omega }_m{q}_m^{\ast }+{\omega }_n{q}_n^{\ast }-\left(x_m^2+x_n^2\right)/2.(20)$

Combining $\partial {\pi }_{mn}/\partial {\omega }_m=0$ and $\partial {\pi }_{mn}/\partial {\omega }_n=0$, the optimal wholesale price of the manufacturer $m$ can be solved as follows:

${\stackrel{\sim }{\omega }}_m^{\ast \ast }=\left[1+\theta \left(x_m+\beta x_n\right)+p_e\right]/2.(21)$

In the second stage under the CC model, manufacturers also determine their environmental R&D levels to maximize their joint profit. The problem of the optimal environmental R&D level of the manufacturer $m$ under the CC model can be described as follows:

$\underset{x_m,x_n}{\mathit{max}}{\pi }_{mn}={\stackrel{\sim }{\omega }}_m^{\ast \ast }{q}_m^{\ast }+{\stackrel{\sim }{\omega }}_n^{\ast \ast }{q}_n^{\ast }-\left(x_m^2+x_n^2\right)/2.(22)$

Combining $\partial {\pi }_{mn}/\partial x_m=0$ and $\partial {\pi }_{mn}/\partial x_n=0$, the optimal environmental R&D level of the manufacturer $m$ can be solved as follows:

${\stackrel{\sim }{x}}_m^{\ast \ast }=-\left(1+\beta \right)\left[\theta +\left(8+3\theta \right)p_e\right]/\left[{\theta }^2{\left(1+\beta \right)}^2-4\left({\alpha }_1+1\right)\right].(23)$

The clear price of carbon allowance is solved as follows:

${\stackrel{\sim }{p}}_e^{\ast \ast }=-\left\{2\left[\theta {\left(1+\beta \right)}^2-1\right]-\left[{\theta }^2{\left(1+\beta \right)}^2-4\left({\alpha }_1+1\right)\right]\left({\overline{e}}_m+{\overline{e}}_n\right)\right\}/\left\{2\left[2{\left(1+\beta \right)}^2\left({\alpha }_1+3\right)+1\right]\right\}.(24)$

In the first stage, the problem of optimal allocation of carbon allowance under the CC model can be described as follows:

$\underset{{\overline{e}}_1,{\overline{e}}_2}{\mathit{max}}{\stackrel{\sim }{W}}^{\ast \ast }={\displaystyle \sum }_{m=1}^2{p}_m^{\ast }{q}_m^{\ast \ast }+{\left({\displaystyle \sum }_{m=1}^2{q}_m^{\ast \ast }\right)}^2/2-{\displaystyle \sum }_{m=1}^2{\left({\stackrel{\sim }{x}}_m^{\ast \ast }\right)}^2/2-{\left({\displaystyle \sum }_{m=1}^2{\stackrel{\sim }{e}}_m^{\ast \ast }\right)}^2/2.(25)$

Combining $\partial {\stackrel{\sim }{W}}^{\ast \ast }/\partial {\overline{e}}_1=0$ and $\partial {\stackrel{\sim }{W}}^{\ast \ast }/\partial {\overline{e}}_2=0$, the optimal allocation of carbon allowance under the CC model can be solved as follows:

${\overline{e}}_m^{cc}=\left[\theta {\left(1+\beta \right)}^2-1\right]\left[2\left(2{\alpha }_1+5\right){\left(1+\beta \right)}^2+1\right]/{\Delta }_3,(26)$

where ${\Delta }_3=2\left(4+\beta \right){\beta }^3{\delta }_{12}+{\beta }^2{\delta }_{13}+2\beta {\delta }_{14}+{\delta }_{15},{\delta }_{12}=2{\theta }^3+3{\theta }^2-32\theta -64,{\delta }_{13}=24{\theta }^3+25{\theta }^2-452\theta -864,$ ${\delta }_{14}=8{\theta }^3+{\theta }^2-196\theta -352,{\delta }_{15}=4{\theta }^3-5{\theta }^2-134\theta -228$. Substituting 26 in 24, 23, 21, 7, and 6, the equilibrium clear price of carbon allowance ($p_e^{cc}$), environmental R&D level ($x_m^{cc}$), wholesale price (${\omega }_m^{cc}$), production ($q_m^{cc}$), and retail price ($p_m^{cc}$) under the CC model can be solved. It is easy to find that when $\beta ,\theta \in \left(\mathrm{0,1}\right)$, $x_m^{cc}>0,{\omega }_m^{cc}>0,q_m^{cc}>0,p_m^{cc}>0$ will always hold, and $\text{sign}\left({\overline{e}}_m^{cc}\right)=\text{sign}\left(-\left({\left(1+\beta \right)}^2\theta -1\right)\right)$. As under SC, if $\theta <g_2\left(\beta \right)$, ${\overline{e}}_m^{cc}>0$ will hold; otherwise, ${\overline{e}}_m^{cc}<0$ will hold.

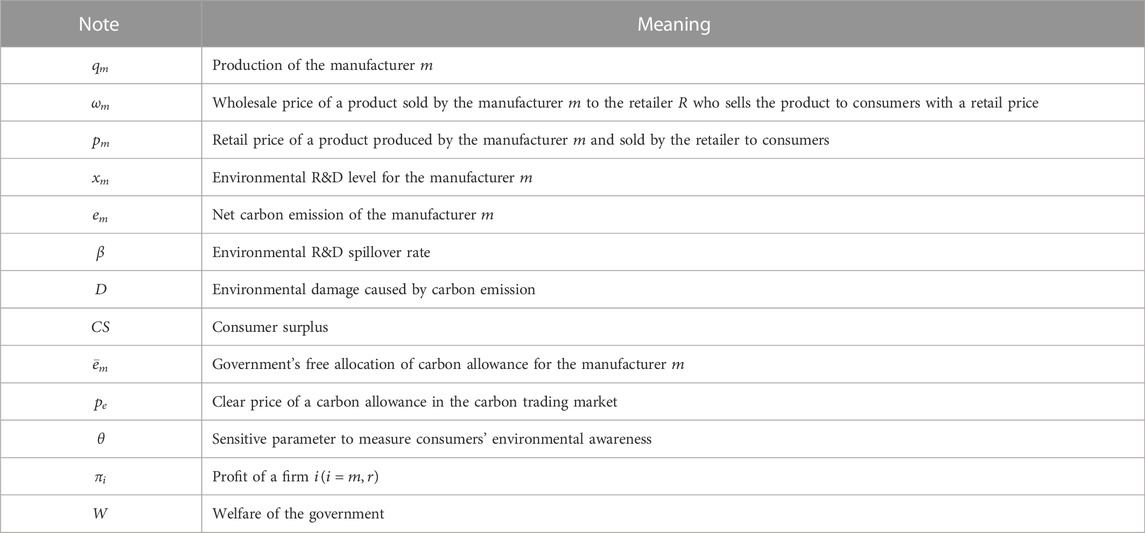
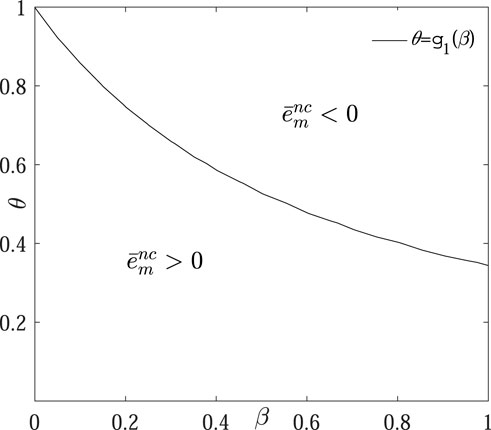
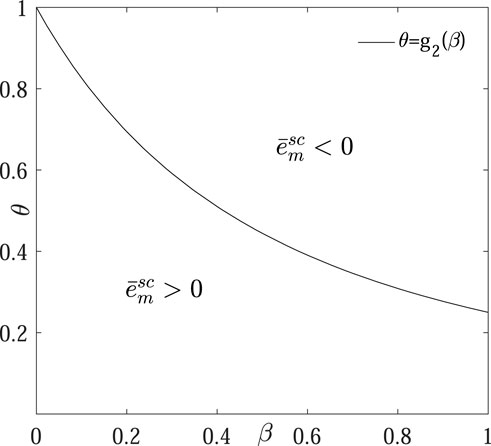
Putting Figures 2, 3 together, we can get Figure 4 to get the condition for a positive solution of free allocation of carbon allowance under each model. Then, we can find $g_2\left(\beta \right)<g_1\left(\beta \right)$ when $0<\beta ,\theta <1$. Therefore, if $\theta <g_2\left(\beta \right)$, all the equilibrium allocations of carbon allowance under the NC model, SC model, and CC model are positive, meaning that ${\overline{e}}_m^{nc}>0,{\overline{e}}_m^{sc}>0,{\overline{e}}_m^{cc}>0$ will hold.

FIGURE 4

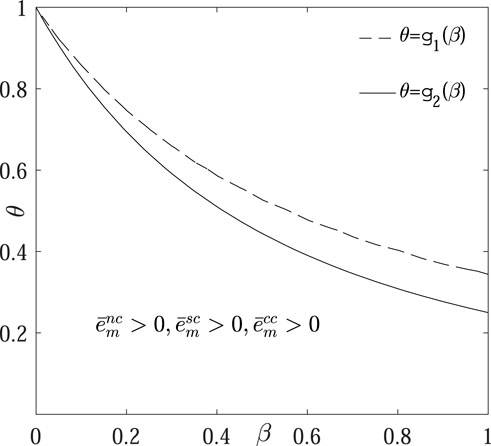
FIGURE 4. Condition for a positive solution of free allocation of carbon allowance under each model.

5 Results and discussions

5.1 Environmental R&D level

This paper first compares the environmental R&D level under the three models, and their results are summarized in Proposition 1.

Proposition 1. When $\theta <g_2\left(\beta \right)$, $x_m^{cc}<x_m^{sc}<x_m^{nc}$ will hold if $f\left(\beta \right)<\theta <g_2\left(\beta \right)$, but $x_m^{cc}<x_m^{nc}<x_m^{sc}$ will hold if $0<\theta <\min \left(f\left(\beta \right),g_2\left(\beta \right)\right)$.

Proposition 1 indicates that from the view of the environmental R&D level, CC is a dominated strategy and NC and SC may be the optimal strategy or second-best strategy, respectively. The environmental R&D level under CC is always much lower than that under NC and SC, but the environmental R&D level under NC may be much lower or higher than that under SC. Especially, the environmental R&D level under NC is much higher than that under SC if the spillover rate and consumers’ environmental awareness can satisfy $f\left(\beta \right)<\theta <g_2\left(\beta \right)$. Therefore, the environmental R&D level under NC is the highest, that under SC is much higher, and that under CC is the lowest if $f\left(\beta \right)<\theta <g_2\left(\beta \right)$, meaning that NC is the optimal strategy, SC is the second-best strategy, and CC is the dominated strategy at this time. However, the environmental R&D level under SC is much higher than that under NC if the spillover rate and consumers’ environmental awareness can satisfy $0<\theta <\min \left(f\left(\beta \right),g_2\left(\beta \right)\right)$. Therefore, the environmental R&D level under SC is the highest, that under NC is much higher, and that under CC is the lowest if $0<\theta <\min \left(f\left(\beta \right),g_2\left(\beta \right)\right)$, meaning that SC is the optimal strategy and NC is the second-best strategy, and CC is also the dominated strategy at this time.

5.2 Net carbon emission

This paper then compares the net carbon emission under the three models. Let net carbon emissions under NC, SC, and CC be $e_m^{nc}=q_m^{nc}-x_m^{nc}-\beta x_n^{nc}$, $e_m^{sc}=q_m^{sc}-x_m^{sc}-\beta x_n^{sc}$, and $e_m^{cc}=q_m^{cc}-x_m^{cc}-\beta x_n^{cc}$, respectively, and their comparisons are summarized in Proposition 2.

Proposition 2. When $\theta <g_2\left(\beta \right)$, $e_m^{cc}<e_m^{sc}<e_m^{nc}$ will always hold.

Proposition 2 reveals that from the view of net carbon emission, CC is the optimal strategy, SC is the second-best strategy, and NC is the dominated strategy. Compared to NC, the manufacturer $m$ chooses SC or CC that can decrease net carbon emission and chooses CC that can decrease more net carbon emission than NC can. Therefore, the net carbon emission under NC is the highest, that under SC is much higher, and that under CC is the lowest, meaning that NC is the dominated strategy, SC is the second-best strategy, and CC is the optimal strategy.

5.3 Profit

This paper next compares profits of each manufacturer and the supply chain under the three models.

5.3.1 Manufacturer’s profit

Profit comparison results of the manufacturer $m$ under the three models are summarized in Proposition 3.

Proposition 3. When $\theta <g_2\left(\beta \right)$, ${\pi }_m^{nc}<{\pi }_m^{sc}<{\pi }_m^{cc}$ will hold if ${\rho }_1\left(\beta \right)<\theta <g_2\left(\beta \right)$, but ${\pi }_m^{sc}<{\pi }_m^{nc}<{\pi }_m^{cc}$ will hold if $0<\theta <\min \left({\rho }_1\left(\beta \right),g_2\left(\beta \right)\right)$.

Proposition 3 indicates that from the view of profit of the manufacturer $m$, CC is the optimal strategy and both NC and SC may be the second-best strategy or dominated strategy under certain conditions, respectively. Compared to NC and SC, the manufacturer $m$ chooses CC that will always increase profit. Especially, profit of the manufacturer $m$ under SC is much higher than that under NC if the spillover rate and consumers’ environmental awareness can satisfy ${\rho }_1\left(\beta \right)<\theta <g_2\left(\beta \right)$, meaning that profit of the manufacturer $m$ under CC is the highest, that under SC is much higher, and that under NC is the lowest. Therefore, CC is the optimal strategy, SC is the second-best strategy, and NC is the dominated strategy under ${\rho }_1\left(\beta \right)<\theta <g_2\left(\beta \right)$. However, profit of the manufacturer $m$ under SC is much lower than that under NC if the spillover rate and consumers’ environmental awareness can satisfy $0<\theta <\min \left({\rho }_1\left(\beta \right),g_2\left(\beta \right)\right)$, meaning that profit of the manufacturer $m$ under CC is the highest, that under NC is much higher, and that under SC is the lowest. Therefore, CC is the optimal strategy, NC is the second-best strategy, and SC is the dominated strategy under ${\rho }_1\left(\beta \right)<\theta <g_2\left(\beta \right)$.

5.3.2 Supply chain’s profit

Let supply chain’s profits under NC, SC, and CC be ${\pi }^{nc}={\pi }_m^{nc}+{\pi }_n^{nc}+{\pi }_r^{nc}$, ${\pi }^{sc}={\pi }_m^{sc}+{\pi }_n^{sc}+{\pi }_r^{sc}$, and ${\pi }^{cc}={\pi }_m^{cc}+{\pi }_n^{cc}+{\pi }_r^{cc}$, respectively, and their comparisons are summarized in Proposition 4.

Proposition 4. When $\theta <g_2\left(\beta \right)$, ${\pi }^{cc}<{\pi }^{sc}<{\pi }^{nc}$ will hold if $0<\theta <\min \left({\rho }_2\left(\beta \right),g_2\left(\beta \right)\right)$, but ${\pi }^{cc}<{\pi }^{nc}<{\pi }^{sc}$ will hold if ${\rho }_2\left(\beta \right)<\theta <g_2\left(\beta \right)$.

Proposition 4 reveals that from the view of the supply chain’s profit, CC is a dominated strategy and both NC and SC may be the optimal strategy or second-best strategy, respectively. Especially, the supply chain’s profit under CC is always much lower than that under NC and that under SC. If the spillover rate and consumers’ environmental awareness can satisfy $0<\theta <\min \left({\rho }_2\left(\beta \right),g_2\left(\beta \right)\right)$, the supply chain’s profit under NC is much higher than that under SC, meaning that the supply chain’s profit under NC is the highest, that under SC is much higher, and that under CC is the lowest. Therefore, NC is the optimal strategy, SC is the second-best strategy, and CC is the dominated strategy under $0<\theta <\min \left({\rho }_2\left(\beta \right),g_2\left(\beta \right)\right)$. However, if the spillover rate and consumers’ environmental awareness can satisfy ${\rho }_2\left(\beta \right)<\theta <g_2\left(\beta \right)$, the supply chain’s profit under SC is much higher than that under NC, meaning that the supply chain’s profit under SC is the highest, that under NC is much higher, and that under CC is the lowest. Therefore, SC is the optimal strategy, NC is the second-best strategy, and CC is the dominated strategy under ${\rho }_2\left(\beta \right)<\theta <g_2\left(\beta \right)$.

5.4 Environmental R&D level, net carbon emission, and profit

Finally, this paper makes a comprehensive comparison of the environmental R&D level, net carbon emission, and profit under the three models, and results are summarized in Proposition 5.

Proposition 5. When $\theta <g_2\left(\beta \right)$, $e_m^{nc}>e_m^{sc}>e_m^{cc}$ will always hold; $x_m^{cc}<x_m^{sc}<x_m^{nc},{\pi }_m^{nc}<{\pi }_m^{sc}<{\pi }_m^{cc}$ and ${\pi }^{cc}<{\pi }^{sc}<{\pi }^{nc}$ will hold if $f\left(\beta \right)<\theta <g_2\left(\beta \right)$, $x_m^{cc}<x_m^{nc}<x_m^{sc},{\pi }_m^{nc}<{\pi }_m^{sc}<{\pi }_m^{cc},{\pi }^{cc}<{\pi }^{sc}<{\pi }^{nc}$ will hold if ${\rho }_1\left(\beta \right)<\theta <\min \left(f\left(\beta \right),g_2\left(\beta \right)\right)$, $x_m^{cc}<x_m^{nc}<x_m^{sc},{\pi }_m^{sc}<{\pi }_m^{nc}<{\pi }_m^{cc},{\pi }^{cc}<{\pi }^{sc}<{\pi }^{nc}$ will hold if $0<\theta <\min \left({\rho }_1\left(\beta \right),{\rho }_2\left(\beta \right)\right)$, and $x_m^{cc}<x_m^{nc}<x_m^{sc},{\pi }_m^{sc}<{\pi }_m^{nc}<{\pi }_m^{cc},{\pi }^{cc}<{\pi }^{nc}<{\pi }^{sc}$ will hold if ${\rho }_2\left(\beta \right)<\theta <g_2\left(\beta \right)$.

Proposition 5 indicates that from the comprehensive comparison of the environmental R&D level, net carbon emission, and profit under the three models, none of the three strategies could be the optimal strategy or dominated strategy, but SC may be the second-best strategy. If $f\left(\beta \right)<\theta <g_2\left(\beta \right)$, compared to NC, the environmental R&D level, net carbon emission of the manufacturer $m$, and supply chain’s profit are much lower, but profit of the manufacturer $m$ is much higher under SC and CC. Compared to SC, net carbon emission of the manufacturer $m$ and the supply chain’s profit are much lower, but profit of the manufacturer $m$ is much higher under CC. These mean that the environmental R&D level, net carbon emission of the manufacturer $m$, and supply chain’s profit under NC are the highest, those under SC are much higher, and those under CC are the lowest, but profit of the manufacturer $m$ under NC is the lowest, that under SC is much higher, and that under CC is the highest. Therefore, as a whole, there is no optimal strategy or dominated strategy, but SC can be the second-best strategy if $f\left(\beta \right)<\theta <g_2\left(\beta \right)$. If ${\rho }_1\left(\beta \right)<\theta <\min \left(f\left(\beta \right),g_2\left(\beta \right)\right)$, compared to NC, the environmental R&D level and profit of the manufacturer $m$ are much higher, but net carbon emission of the manufacturer $m$ and the supply chain’s profit are much lower under SC; the environmental R&D level and net carbon emission of the manufacturer $m$ and the supply chain’s profit are much lower, but profit of the manufacturer $m$ is much higher under CC. Compared to SC, the environmental R&D level, net carbon emission of the manufacturer $m$, and supply chain’s profit are much lower, but profit of the manufacturer $m$ is much higher. These mean that the environmental R&D level of the manufacturer $m$ under SC is the highest, that under NC is much higher, and that under CC is the lowest; net carbon emission of the manufacturer $m$ and the supply chain’s profit under NC are the highest, those under SC are much higher, and those under CC are the lowest; profit of manufacturer $m$ under NC is the lowest, that under SC is much higher, and that under CC is the highest. Therefore, as a whole, there is also no optimal strategy or dominated strategy, but SC can be the second-best strategy if ${\rho }_1\left(\beta \right)<\theta <\min \left(f\left(\beta \right),g_2\left(\beta \right)\right)$. If $0<\theta <\min \left({\rho }_1\left(\beta \right),{\rho }_2\left(\beta \right)\right)$, compared to NC, the environmental R&D level of the manufacturer $m$ is much higher, but net carbon emission and profit of the manufacturer $m$ are much lower under SC. Compared to NC and SC, the environmental R&D level, net carbon emission of the manufacturer $m$, and supply chain’s profit are much lower, but profit of the manufacturer $m$ is much higher under CC. Therefore, as a whole, there is no optimal strategy, second-best strategy, or dominated strategy if $0<\theta <\min \left({\rho }_1\left(\beta \right),{\rho }_2\left(\beta \right)\right)$. If ${\rho }_2\left(\beta \right)<\theta <g_2\left(\beta \right)$, compared to NC, the environmental R&D level of the manufacturer $m$ and supply chain’s profit are much higher, but net carbon emission and profit of the manufacturer $m$ are much lower. Compared to NC and SC, environmental R&D level and net carbon emission of the manufacturer $m$ and supply chain’s profit are much lower, but profit of manufacturer $m$ is much higher. Therefore, as a whole, there is also no optimal strategy, second-best strategy, or dominated strategy if ${\rho }_2\left(\beta \right)<\theta <g_2\left(\beta \right)$.

6 Conclusion

Three carbon emission reduction and pricing strategies of manufacturers are NC, SC, and CC. This paper develops three game models where two manufacturers could choose NC, SC, or CC to analyze manufacturers’ strategies of carbon emission reduction and pricing under the CET and CEA. This paper solves these models and compares their environmental R&D levels, net carbon emissions, and profits. Results show that from the view of the environmental R&D level or supply chain’s profit, manufacturers may choose NC or SC as their strategy. From the net carbon emission point of view, CC and SC should be their optimal strategy and second-best strategy, respectively. As to manufacturers’ profits, CC should be their optimal innovation strategy, and NC or SC should be their second-best strategy. As a whole, manufacturers would choose none of these strategies as their optimal strategy but may choose SC as their second-best strategy.

From the aforementioned information, we propose the following management insights. First, manufacturers should select their strategy of carbon emission reduction and pricing according to their own situations. Participation in further cooperation in carbon emission reduction and pricing may damage manufacturers’ benefits, even their development. As to manufacturers with weak strength, NC may be their choice. When they enhance their strength in future, SC and CC may be their choices. As to manufacturers with strong strength and social responsibility, CC may be their choice. Second, the government should a design dynamic support system based on the extent of cooperation manufacturers engaged. The government can provide more environmental R&D fund, tax reduction and exemption, financing, and other supports to manufacturers when they engage in further cooperation in environmental R&D and pricing, to lead manufacturers form and deepen their cooperation, undermine their carbon emission reduction potential, and make a greater contribution to ecological civilization construction. Finally, members in the supply chain should properly share their profits. Different cooperation strategies in carbon emission reduction and pricing cause different, even opposite, influence on members in the supply chain. Manufacturers’ participation in deeper cooperation is good for the retailer to make a higher retail price on a low-carbon product, which may increase the retailer’s profit but may decrease manufacturers’ profits. Therefore, members in the same supply chain should design a proper profit-sharing contract and properly share their profits.

This study also exhibits several limitations. First, we focus on the carbon emission reduction and pricing strategy of manufacturers. In fact, manufacturers and retailers also cooperate in carbon emission reduction, such as retailers share carbon emission reduction costs of manufacturers, and manufacturers share low-carbon promotion costs of retailers. This leads to an extension to analyze a full cooperation between members in the same supply chain or even between different supply chains. Second, we assume that the two manufacturers have the same environmental R&D efficiency. In fact, manufacturers are different in finance, technology, and other aspects. Future research could examine the effect of different environmental R&D on strategy selection. Finally, this paper applies the backward induction to solve the game models. However, there have been many different domains where advanced optimization algorithms have been applied as solution approaches, such as carbon emission reduction (Dulebenets et al., 2017), online learning (Zhao and Zhang, 2020), scheduling (Kavoosi et al., 2019; Dulebenets, 2021), multi-objective optimization (Zhao and Zhang, 2020), and medicine (Rabbani et al., 2017). These approaches could be more effective in solving decision problems. Future research should explore more advanced optimization algorithms for this decision problem.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YD: conceptualization and project administration; HW: investigation, resources, and data curation; HP: methodology, software, validation, formal analysis, writing—original draft preparation, writing—review and editing, and funding acquisition; and LL: visualization and supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Key Science and Technology Projects of China Southern Power Grid Co., Ltd. (Grant No. ZBKJXM20210229).

Conflict of interest

Authors YD and LL are employed by Carbon Asset Management (Guangzhou) Co., Ltd., CSG, Guangzhou, Guangdong Province, China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from China Southern Power Grid Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at the following links: https://www.frontiersin.org/articles/10.3389/fenvs.2023.1120165/full#supplementary-material

Footnotes

¹https://icapcarbonaction.com/en/publications/emissions-trading-worldwide-2022-icap-status-report.

²http://i.aliresearch.com/file/20160803/20160803103534.pdf

³https://www.reuters.com/article/hino-motors-volkswagen-idINL3N1RP32F

References

Bai, Q., Xu, J., and Zhang, Y. (2018). Emission reduction decision and coordination of a make-to-order supply chain with two products under cap-and-trade regulation. Comput. Industrial Eng. 119, 131–145. doi:10.1016/j.cie.2018.03.032

CrossRef Full Text | Google Scholar

Basiri, Z., and Heydari, J. (2017). A mathematical model for green supply chain coordination with substitutable products. J. Clean. Prod. 145, 232–249. doi:10.1016/j.jclepro.2017.01.060

CrossRef Full Text | Google Scholar

Cao, K., Xu, X., Wu, Q., and Zhang, Q. (2017). Optimal production and carbon emission reduction level under cap-and-trade and low carbon subsidy policies. J. Clean. Prod. 167, 505–513. doi:10.1016/j.jclepro.2017.07.251

CrossRef Full Text | Google Scholar

Chitra, K. (2007). In search of the green consumers: A perceptual study. J. Serv. Res. 7. papers://248E978A-D3F2-453E-A670-D29D7166B452/Paper/p2578.

Google Scholar

Chu, J., Shao, C., Emrouznejad, A., Wu, J., and Yuan, Z. (2021). Performance evaluation of organizations considering economic incentives for emission reduction: A carbon emission permit trading approach. Energy Econ. 101, 105398. doi:10.1016/j.eneco.2021.105398

CrossRef Full Text | Google Scholar

Du, S., Zhu, J., Jiao, H., and Ye, W. (2015). Game-theoretical analysis for supply chain with consumer preference to low carbon. Int. J. Prod. Res. 53, 3753–3768. doi:10.1080/00207543.2014.988888

CrossRef Full Text | Google Scholar

Dulebenets, M. A. (2021). An adaptive polyploid memetic algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 565, 390–421. doi:10.1016/j.ins.2021.02.039

CrossRef Full Text | Google Scholar

Dulebenets, M. A., Moses, R., Ozguven, E., and Vanli, A. (2017). Minimizing carbon dioxide emissions due to container handling at marine container terminals via hybrid evolutionary algorithms. IEEE Access 5, 8131–8147. doi:10.1109/ACCESS.2017.2693030

CrossRef Full Text | Google Scholar

Katsoulacos, Y., Ulph, A., and Ulph, D. (2001). The effects of environmental policy on the performance of environmental research joint ventures. NBER Chapters 35. doi:10.5840/enviroethics19879426

CrossRef Full Text | Google Scholar

Kavoosi, M., Dulebenets, M. A., Abioye, O. F., Pasha, J., Wang, H., and Chi, H. (2019). An augmented self-adaptive parameter control in evolutionary computation: A case study for the berth scheduling problem. Adv. Eng. Inf. 42, 100972. doi:10.1016/j.aei.2019.100972

CrossRef Full Text | Google Scholar

Li, J., Liang, J., Shi, V., and Zhu, J. (2021). The benefit of manufacturer encroachment considering consumer’s environmental awareness and product competition. Ann. Operations Res. doi:10.1007/s10479-021-04185-y

CrossRef Full Text | Google Scholar

Li, X., and Li, Y. (2014). Chain-to-chain competition on product sustainability. J. Clean. Prod. 112, 2058–2065. doi:10.1016/j.jclepro.2014.09.027

CrossRef Full Text | Google Scholar

Li, Z., and Wang, J. (2022). The dynamic impact of digital economy on carbon emission reduction: Evidence city-level empirical data in China. J. Clean. Prod. 351, 131570. doi:10.1016/j.jclepro.2022.131570

CrossRef Full Text | Google Scholar

Liu, Hao, Kou, X., Xu, G., Qiu, X., and Liu, Haibin (2021). Which emission reduction mode is the best under the carbon cap-and-trade mechanism? J. Clean. Prod. 314, 128053. doi:10.1016/j.jclepro.2021.128053

CrossRef Full Text | Google Scholar

Liu, L., and Li, F. (2020). Differential game modelling of joint carbon reduction strategy and contract coordination based on low-carbon reference of consumers. J. Clean. Prod. 277, 123798. doi:10.1016/j.jclepro.2020.123798

CrossRef Full Text | Google Scholar

Liu, Z., Anderson, T. D., and Cruz, J. M. (2012). Consumer environmental awareness and competition in two-stage supply chains. Eur. J. Operational Res. 218, 602–613. doi:10.1016/j.ejor.2011.11.027

CrossRef Full Text | Google Scholar

Luo, Z., Chen, X., and Wang, X. (2016). The role of co-opetition in low carbon manufacturing. Eur. J. Operational Res. 253, 392–403. doi:10.1016/j.ejor.2016.02.030

CrossRef Full Text | Google Scholar

Poyago-Theotoky, J. A. (2007). The organization of R&D and environmental policy. J. Econ. Behav. Organ. 62, 63–75. doi:10.1016/j.jebo.2004.09.015

CrossRef Full Text | Google Scholar

Rabbani, M., Oladzad-Abbasabady, N., and Akbarian-Saravi, N. (2017). Ambulance routing in disaster response considering variable patient condition: NSGA-II and MOPSO algorithms. J. Industrial Manag. Optim. 13, 1035. doi:10.3934/jimo.2021007

CrossRef Full Text | Google Scholar

Su, M., Pang, Q., Kim, W., Yao, J., and Fang, M. (2023). Consumer participation in reusable resource allocation schemes: A theoretical conceptualization and empirical examination of Korean consumers. Resour. Conservation Recycl. 189, 106747. doi:10.1016/j.resconrec.2022.106747

CrossRef Full Text | Google Scholar

Wang, Q., Zhao, D., and He, L. (2016). Contracting emission reduction for supply chains considering market low-carbon preference. J. Clean. Prod. 120, 72–84. doi:10.1016/j.jclepro.2015.11.049

CrossRef Full Text | Google Scholar

Wang, S., Wan, L., Li, T., Luo, B., and Wang, C. (2018). Exploring the effect of cap-and-trade mechanism on firm’s production planning and emission reduction strategy. J. Clean. Prod. 172, 591–601. doi:10.1016/j.jclepro.2017.10.217

CrossRef Full Text | Google Scholar

Wang, Y., Yu, Z., Jin, M., and Mao, J. (2021). Decisions and coordination of retailer-led low-carbon supply chain under altruistic preference. Eur. J. Operational Res. 293, 910–925. doi:10.1016/j.ejor.2020.12.060

CrossRef Full Text | Google Scholar

Wang, Z., Brownlee, A. E. I., and Wu, Q. (2020). Production and joint emission reduction decisions based on two-way cost-sharing contract under cap-and-trade regulation. Comput. Industrial Eng. 146, 106549. doi:10.1016/j.cie.2020.106549

CrossRef Full Text | Google Scholar

Wang, Z., and Wang, C. (2015). How carbon offsetting scheme impacts the duopoly output in production and abatement: Analysis in the context of carbon cap-and-trade. J. Clean. Prod. 103, 715–723. doi:10.1016/j.jclepro.2014.04.069

CrossRef Full Text | Google Scholar

Xia, L., Bai, Y., Ghose, S., and Qin, J. (2022). Differential game analysis of carbon emissions reduction and promotion in a sustainable supply chain considering social preferences. Ann. Operations Res. 310, 257–292. doi:10.1007/s10479-020-03838-8

CrossRef Full Text | Google Scholar

Xia, L., Hao, W., Qin, J., Ji, F., and Yue, X. (2018). Carbon emission reduction and promotion policies considering social preferences and consumers’ low-carbon awareness in the cap-and-trade system. J. Clean. Prod. 195, 1105–1124. doi:10.1016/j.jclepro.2018.05.255

CrossRef Full Text | Google Scholar

Xia, X., Li, C., and Zhu, Q. (2020). Game analysis for the impact of carbon trading on low-carbon supply chain. J. Clean. Prod. 276, 123220. doi:10.1016/j.jclepro.2020.123220

CrossRef Full Text | Google Scholar

Yalabik, B., and Fairchild, R. J. (2011). Customer, regulatory, and competitive pressure as drivers of environmental innovation. Int. J. Prod. Econ. 131, 519–527. doi:10.1016/j.ijpe.2011.01.020

CrossRef Full Text | Google Scholar

Yang, L., Wang, G., and Ke, C. (2018). Remanufacturing and promotion in dual-channel supply chains under cap-and-trade regulation. J. Clean. Prod. 204, 939–957. doi:10.1016/j.jclepro.2018.08.297

CrossRef Full Text | Google Scholar

Yang, L., Zhang, Q., and Ji, J. (2017). Pricing and carbon emission reduction decisions in supply chains with vertical and horizontal cooperation. Int. J. Prod. Econ. 191, 286–297. doi:10.1016/j.ijpe.2017.06.021

CrossRef Full Text | Google Scholar

Yi, M., Liu, Y., Sheng, M. S., and Wen, L. (2022). Effects of digital economy on carbon emission reduction: New evidence from China. Energy Policy 171, 113271. doi:10.1016/j.enpol.2022.113271

CrossRef Full Text | Google Scholar

Zhang, L., Zhou, H., Liu, Y., and Lu, R. (2019). Optimal environmental quality and price with consumer environmental awareness and retailer’s fairness concerns in supply chain. J. Clean. Prod. 213, 1063–1079. doi:10.1016/j.jclepro.2018.12.187

CrossRef Full Text | Google Scholar

Zhang, Q., Zhao, Q., Zhao, X., and Tang, L. (2020). On the introduction of green product to a market with environmentally conscious consumers. Comput. Industrial Eng. 139, 106190. doi:10.1016/j.cie.2019.106190

CrossRef Full Text | Google Scholar

Zhao, H., and Zhang, C. (2020). An online-learning-based evolutionary many-objective algorithm. Inf. Sci. 509, 1–21. doi:10.1016/j.ins.2019.08.069

CrossRef Full Text | Google Scholar