Simple model of morphometric constraint on carbon burial in boreal lakes

Cael, B. B.; Seekell, David A.

doi:10.3389/fenvs.2023.1101332

PERSPECTIVE article

Front. Environ. Sci., 20 February 2023

Sec. Freshwater Science

Volume 11 - 2023 | https://doi.org/10.3389/fenvs.2023.1101332

Simple model of morphometric constraint on carbon burial in boreal lakes

B. B. Cael¹*

David A. Seekell^2,3

¹National Oceanography Centre, Southampton, United Kingdom
²Department of Ecology and Environmental Science, Umea University, Umea, Sweden
³Climate Impacts Research Centre, Umea University, Abisko, Sweden

A geometric theory was developed to explain the empirical relationship between carbon burial and lake shape in boreal lakes. The key feature of this model is an attenuation length scale, analogous to models of marine organic carbon fluxes. This length scale is the ratio of how fast carbon is displaced vertically versus how fast it is respired and engenders a simple model with a single easily constrained free parameter. Lake depths are modeled based on fractal area–volume relationships that reflect the approximate scale invariance of Earth’s topography on idealized lake geometries. Carbon burial is estimated by applying the attenuation length scale to these depths. Using this model, we demonstrate the relationship between the dynamic ratio—a metric of lake morphometry calculated by dividing the square root of surface area by the mean depth—and carbon burial. We use scaling relationships to predict how dynamic ratio, and by extension carbon burial, varies across the lake size spectrum. Our model also provides a basis for generalizing empirical studies to the biome scale. By applying our model to a boreal lake census, we estimate boreal lake carbon burial to be 1.8 $\pm$ 0.5 g C/m2/yr or 1.1 $\pm$ 0.3 Tg C/yr among all boreal lakes.

Introduction

Despite covering <1% of Earth’s surface, lakes are believed to bury globally significant amounts of organic carbon. (Mendonça et al., 2017). Carbon burial rates vary by almost six orders of magnitude among lakes, and explaining this variation is an important priority for understanding the contributions of lakes to the global carbon cycle (Clow et al., 2015; Tranvik et al., 2018). Most lakes are in the high northern latitudes, especially in the boreal biome, the largest terrestrial biome occurring approximately between 50 and 60°N (Verpoorter et al., 2014). A specific understanding of patterns of carbon burial in these lakes is important both because of their abundance and large cumulative areal extent and because patterns of carbon cycling from other biomes often do not extrapolate to boreal lakes (e.g., Karlsson et al., 2009; Seekell et al., 2018a).

Process-based models contribute to understanding lake carbon burial because they are general in the sense that their parameters can be adjusted to reflect diverse lake and landscape characteristics and, therefore, can generate predictions for many scenarios (Evans et al., 2013). However, these models typically contain dozens of free parameters, which are rarely measured in even the most comprehensively studied lakes; hence, data limitation precludes such models from quantifying and explaining patterns of carbon cycling beyond small numbers of lakes (e.g. <5 in Hanson et al., 2004; Lonergan, 2014; Carey et al., 2018; McCullough et al., 2018). Descriptive studies based on burial measurements from sediment cores also contribute to understanding carbon burial by quantifying broader-scale patterns of carbon burial, which is typically higher at lower latitudes and in warmer climates than at higher latitudes and in cooler climates (Heathcote et al., 2015; Mendonça et al., 2017). Several studies have included measurements from hundreds of lakes, allowing for the development of statistical models to explain the variability observed among these systems (Kortelainen et al., 2004; Clow et al., 2015). However, such models are uncertain, in part because the numbers of lakes studied are still a tiny fraction of the total number of lakes (Heathcote et al., 2015; Tranvik et al., 2018). Additionally, the model fits are typically non-linear, invalidated by independent data and selected through step-wise procedures that often produce unreliable models for prediction (Flack and Chang, 1987; Whittingham et al., 2006). This creates the potential for overfitting and that different variables have been identified as describing significant variation by different studies suggests that none of these models should be used for extrapolation beyond the calibration dataset. There is a clear need for an approach between process-based modeling and empirical statistical fits.

We present a simple model to explain the empirical relationship between carbon burial and boreal lake shape, where carbon burial is controlled by lake morphometry and the ratio of how fast carbon is displaced vertically versus how fast it is mineralized. The former of these is well-constrained by morphological theories for lakes both on the individual and collective global scale, while the latter is a free parameter that can be constrained by observations. Hence, our approach is informed by process but retains the simplicity of statistical models. Our model captures the general observed trend well and can be utilized alongside other morphological scaling relationships to estimate total boreal lake carbon burial.

Burial model

Carbon fixation and mineralization are balanced for the benthic habitats of boreal lakes (Ask et al., 2012; see Discussion). Therefore, we assume the organic carbon relevant for patterns of burial enters the lake at or near the surface, primarily in the form of allochthonous dissolved organic carbon (DOC) and phytoplankton but also other particulates (von Wachenfeldt and Tranvik, 2008). We also assume the carbon input $C$ is mineralized in the water column at a characteristic rate $k$ . DOC flocculates, phytoplankton, and the other particulates are reported to have similar sinking rates in lakes (Carpenter et al., 2016), and all particles will be equally affected by turbulence, particularly within the epilimnion (MacIntyre et al., 2021). We describe the vertical displacement of $C$ with the characteristic speed $w$ , which subsumes the vertical displacement due to both turbulent processes and particles sinking. It should be noted that k and w are bulk parameters that represent the collective effect of many processes (e.g. Carpenter et al., 1985; Cael et al., 2018). If we then define $b$ as the fraction of vertically fluxed carbon that reaches the bottom of the lake, the lakes’ burial/evasion ratio $B E$ is then

B E = \frac{b C}{(1 - b) C} = \frac{b}{(1 - b)} .

We frame burial efficiency in terms of the burial/evasion ratio $B E$ to aide comparison with observations (see as follows) which do not measure the carbon input $C$ directly but later recast this in terms of burial efficiency $b$ to calculate total boreal lake carbon burial (see as follows). The ratio $L = w / k$ is an attenuation length scale, which describes the mineralization of carbon as it is fluxed downward. Specifically, L is the depth interval over which the downward flux of C decreases by a factor of 1/e. A low attenuation length scale reflects the presence of labile carbon that is rapidly mineralized, while a high attenuation length scale reflects the dominance of recalcitrant carbon. From these assumptions, the fraction $f = e^{- z / L}$ is the proportion of input carbon that reaches the depth $z$ . This approach is borrowed from oceanography, where it has been used to describe organic carbon fluxes for >30 years (Banse, 1990). Therefore, for a whole lake, the fraction of input carbon that reaches the sediment and is buried (b) is this fraction averaged over the entire lake:

b = \frac{1}{A} \int \int e^{- z (x, y) / L} d x d y,

where $A$ is the total surface area of the lake, $z (x, y)$ is the lake depth as a function of where on the lake’s surface (x,y) one is, and the integrals represent integration over the lake’s surface. In other words, b is the average of $e^{- Z / L}$ over the lake. For conic lakes, $z (x, y) \propto z_{\max} - \sqrt{x^{2} + y^{2}}$ , and for parabolic lakes, $z (x, y) \propto z_{\max} - {(x}^{2} + y^{2})$ , with the proportionality coefficient determined according to the lake area–volume scaling relationship, as described in the following section. Because measurements of lake carbon burial are adjusted to represent a basin-wide average (e.g; Ferland et al., 2014), we formulate our model accordingly so it can be calibrated with such data. Lake morphometry is, thereby, a constraint on carbon burial because the burial efficiency of the vertical flux decreases exponentially with lake depth. On the other hand, the characteristic mineralization and vertical displacement rates $k$ and $w$ drop out of the final relationship of interest; only their ratio is relevant.

Relationship to lake area

Earth’s topography is approximately scale-invariant (Turcotte and Huang, 1995) for many landforms including lakes. In particular, Earth’s topography is self-affine, meaning it behaves like a self-similar fractal but with a different scaling in the vertical and horizontal directions (Turcotte and Huang, 1995). These characteristics engender power–law relationships between the lake area and mean depth and volume that extend over about eight orders of magnitude of the surface area (Cael et al., 2017). These scaling relationships can be used to calculate $b$ by assuming a particular lake shape (i.e., a specific depth ratio of mean to maximum depth).

The boreal biome is dominated by lakes with glacial origins that typically have a depth ratio (of mean to maximum depth) of about DR = 1/3 (Meybeck, 1995; Seekell et al., 2021), with relatively large littoral zones and relatively small open-water zones. It should be noted that DR = 1/3 corresponds to an approximately conic lake shape (Carpenter, 1983). Based on this depth ratio, an idealized lake’s full geometry is determined by its area and mean depth, which we relate using the scaling $z_{m e a n} = 5.7 {(A)}^{0.16}$ for boreal lakes (Cael et al., 2017). From this, an average $E [e^{- z / L}] = b$ is then obtained by integrating over the areas of boreal lakes once the free parameter L is constrained.

To summarize, we assume the carbon input at the surface of the lake has a characteristic ratio of vertical displacement rate to respiration rate. We then assume that mean depth and area are related in a fashion consistent with lake observations and Earth’s topography and an idealized lake shape consistent with mean-to-max depth ratios for boreal lakes. We then integrate over the lake’s surface to calculate $b = E [e^{- Z / L}]$ . For a given simulated lake, we can then calculate the dynamic ratio $D = \sqrt{A} / z_{m e a n}$ and burial/evasion ratio $B E = b / (1 - b)$ for a given value of the free parameter $L$ .

Model fitting and application

We fit L in our burial model to previously published burial/evasion ratios for 17 boreal lakes approximately representative of boreal lakes’ morphological and chemical characteristics (Einola et al., 2011; Ferland et al., 2014; Chmiel et al., 2016) by varying L to find the minimum sum of squared residuals between predicted and observed values (Table 1). We compared our model fit to empirical regressions of burial/evasion ratios against the dynamic ratio using the Bayesian information criterion (BIC), which accounts for the different number of free parameters in each model (one in our model versus two in empirical regressions). Altogether for each observed value of dynamic ratio, we generate a conic (or parabolic) virtual lake that has the same dynamic ratio and also has an area and mean depth that conform with the boreal area–volume scaling relationship described previously; calculate b (and thereby BE) for that lake according to the aforementioned equation for a given L, compute the residual between this predicted value and the corresponding observed value for BE, compute the sum of squared residuals across all observations, and use these to calculate the BIC.

TABLE 1

TABLE 1. Data used to calibrate the burial model.

We then applied the model to a boreal lake database in order to estimate the biome-scale carbon burial rate. Specifically, we extracted 600,917 lake areas (total 584,028 km²) and geographic positions from the publicly available and widely used HydroLAKES database (https://hydrosheds.org) based on the boreal zone boundaries designated by the World Wildlife Fund (Olson et al., 2001; Messager et al., 2016). We excluded known reservoirs because their rates of carbon burial are significantly different than natural lakes (Clow et al., 2015; Mendonça et al., 2017). We then estimated the volume (V) of each lake by $V = 5.7 \times l o g n o r m a l (0,0.29) \times A^{1.16}$ , according to Cael et al. (2017). We calculated mean depth ( $z_{m e a n} = V / A$ ) based on these estimated volumes and maximum depth based on the depth ratio DR = 1/3 (e.g., Seekell et al., 2018b).

Empirical patterns of carbon burial exhibit strong latitudinal patterns related to greater ecosystem production in warmer regions than colder regions (Clow et al., 2015; Heathcote et al., 2015). To estimate burial B with our model of the burial:evasion ratio also requires an estimate for the productivity (P) occurring within lakes, according to

B = \frac{B E}{B E + 1} P .

To estimate burial, we combine our model of the burial:evasion ratio with the estimate of P based on the surface area and latitude in Cael and Seekell. (2022), wherein $P = f (y) \times A$ and $f (y)$ is a function of latitude that accounts for the latitudinal dependence of solar insolation, ice-free days per year, and the metabolic effects of temperature (Cael and Seekell, 2022). We applied these equations to each lake in the boreal biome, yielding a distribution of simulated burial rates for boreal lakes, from which the areal burial rate can be calculated by summing total burial and dividing by the total area. Standard errors were computed by bootstrapping and propagating uncertainties in parameter values into total estimates.

Results

The optimal value for the free-parameter was L = 1.2 m. Typical sinking rates for organic carbon in lakes are between 0.1 m/d and 1 m/d (Carpenter et al., 2016), and vertical turbulent diffusivities range from 10 to 3 m 2 s-1 at lake surfaces on very windy days to 10–7 m 2 s-1 below the epilimnion (MacIntyre et al., 2021), corresponding to daily vertical displacements of 0.1–10 m/d. Observed mineralization rates for boreal lakes are typically around 0.4/d, indicating the plausibility of this fit (e.g., Jonsson et al., 2001; Hall et al., 2019). With this value, our model accurately reflects the first-order patterns of carbon burial/evasion ratios relative to the dynamic ratio (Figure 1). This result is robust to variation in lake shape. For example, assuming that lakes are paraboloids ( $D_{R}$ = 1/2), the free parameter is optimized at L = 1.2 m, and the overall patterns are indistinguishable.

FIGURE 1

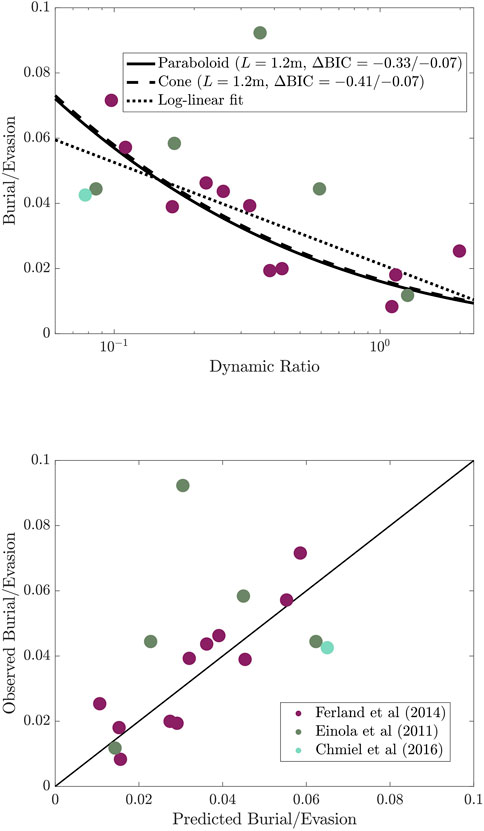
FIGURE 1. Top: Dynamic ratio versus the lake carbon burial/evasion ratio for the theory, an empirical fit, and observations. The black lines give the theoretical burial/evasion ratio as a function of the dynamic ratio for parabolic (solid) and conic (dashed) lake shapes and for a log-linear empirical fit to the data. Colored points give empirical results for comparison. L is the free parameter for our theoretical model, which is estimated as L = 1.2 m for both idealized lake shapes. ∆BIC is the difference in the Bayesian information criterion for each theoretical model versus the empirical model (with/without the outlier point above the legend); a negative value indicates that the theoretical model is a better fit to the data. Bottom: Predicted vs. observed burial/evasion ratios for the conic model with L = 1.2 m. The legend shows the study corresponding to each data point.

A linear empirical relationship between burial:evasion and log(D) was previously reported as best-fitting (Ferland et al., 2014). Our model outperforms this log-linear model for both conic and parabolic lake shapes, including/excluding the outlier lake. Although the difference in goodness of fit is slight, the more important advantage of our model is that its functional form is based on a mechanism, rather than chosen ad hoc. Our model does not have an exact closed-form expression but is extremely well-approximated by the function $y = - 0.303 x^{- . 243} + 0.320 x^{- 0.264}$ (r2 = 0.9999).

Using our model to estimate global boreal carbon burial, we find 1.1 $\pm$ 0.3 TgC/yr burial or an areal burial rate of 1.8 $\pm$ 0.5 g C/m2/yr. This is consistent with previous estimates (Table 2), although produced differently and entirely mechanistically, from geometric first principles. The mean of lake-specific burial rates is 2.5 g C/m2/yr. This is lower than the mean burial rate of the lakes shown in Figure 1 (3.7 g C/m2/yr), underscoring that taking the approach we do makes a difference relative to a simple upscaling using this average rate, which would produce a total burial rate of 2.2 TgC/yr. It should be noted that larger lakes have more overall productivity and lower burial/evasion ratios; hence, the overall areal burial rate is lower than the average of lake-specific rates.

TABLE 2

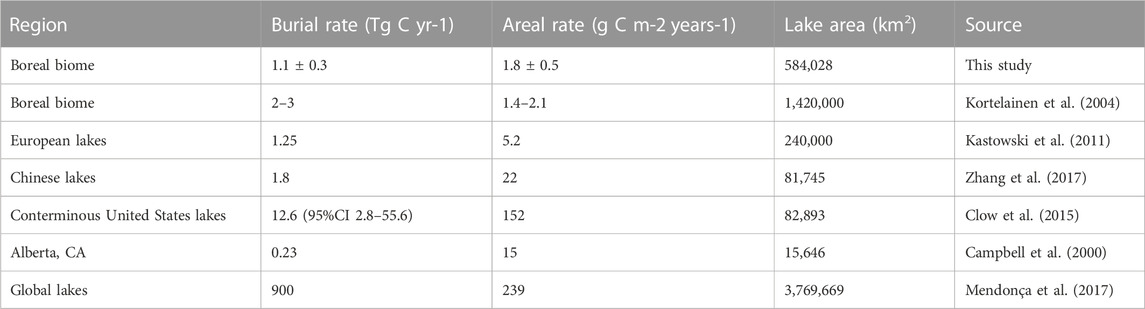
TABLE 2. Comparison of large-scale estimates of carbon burial rates. It should be noted that such estimates come from descriptive studies which inevitably have biases in data collection and uncertainty in measurements and calculations due to the logistical constraints of bottom-up scaling.

A corollary to our main result is that boreal lakes have an overall burial to evasion ratio of 0.05 ± 0.01. This implies that boreal lakes evade 32 TgC/yr as CO₂, about 55 g C/m2/yr, less than estimates of 140 g C/m2/yr by Hastie et al. (2017) and 85 g C/m2/yr by Raymond et al. (2013). These and other previous estimates are based on descriptive upscaling approaches with significant limitations, including aggregation biases during upscaling, geographic biases in sampling, uncertainties related to the methods used to measure CO₂ in lake water, massive uncertainties related to the estimation and scaling of gas transfer coefficients, and the use of single CO₂ measurements to extrapolate annual fluxes (Seekell et al., 2014; Klaus et al., 2019; Klaus et al., 2020). Estimates may also vary for other definitional regions, such as whether, e.g., outflows or the emergence of insects, is included in evasion alongside the standard definition of the outgassing of CO₂ through the lake surface. Because most global limnological studies take only minor variations of the same approach, they integrate many of the same limitations and errors. This discrepancy between estimates based on different approaches suggests more research is needed to improve understanding of evasion rates in boreal lakes.

Discussion

Variations in lake area estimates remain despite significant efforts to develop methods—statistical, remote sensing, and new map compilations—for quantifying lake abundance and area (Cael et al., 2017; Seekell, 2018). Such variations affect total burial estimates appreciably (Table 2). Measuring the abundance and area of small lakes particularly remains a major priority for understanding the contribution of lakes to the global carbon budget both through models like ours and through more traditional and descriptive upscaling analyses (Downing, 2009; Seekell et al., 2013).

It is sensible that lakes with high dynamic ratios (i.e., shallow for their size) have low carbon burial rates because these systems are subjected to resuspension activity across much of their area (Håkanson, 1982). Based on the mean depth scales with surface area, larger lakes will, on average, have higher dynamic ratios than smaller lakes (Cael et al., 2017). Boreal lakes are predominantly small; hence, relatively high burial:evasion ratios are common, and these systems contribute disproportionately to overall annual burial (Verpoorter et al., 2014; Cael and Seekell, 2016). Fundamentally, these patterns relate to the approximate self-affinity of Earth’s topography, emphasizing the far-reaching implications of this characteristic for global limnology.

Our model is highly idealized and mechanistic; although such models have been the driver of ecological theory for many decades and are an important complement to data-driven empirical approaches, they also have distinct limitations. Additional factors affect carbon burial among lakes at smaller scales that are not represented in our model, including the sources of carbon, oxygen penetration depth in the sediments, and temperature (Sobek et al., 2009; Gudasz et al., 2010; Guillemette et al., 2017). Such factors could contribute to the lake-to-lake variation seen around the overall pattern in Figure 1; additional sources of error between the theoretical curves and the empirical observations could be caused by variability in the lake volume–area scaling relationship, variability in L, measurement error, or inadequacy of the theory (e.g., a particular lake’s bathymetry is significantly different from the shape assumed in our model). Sources of error in the underlying data are also rarely quantified (Klaus and Vachon, 2020). A merit of our model is that the parameter L can be independently verified in the future based on measurements of particle-sinking speeds (using various techniques, (Cael et al., 2021)), vertical turbulent diffusivities (using microstructure profilers), and the respiration rate (using oxygen sondes).

Our model excludes sedimentary processes. Previous research not only often emphasized mineralization in sediments in controlling long-term carbon burial (e.g., Gudasz et al., 2010; Ferland et al., 2014) but also often neglected benthic primary production which is similarly intense (e.g. Ask et al., 2012; Seekell et al., 2015a; Seekell et al., 2015b). Most lakes are small and shallow, with sufficient light penetration to support photosynthesis across most or all of the sediments (Cael et al., 2017; Seekell et al., 2021). Concurrent measurements reveal primary production and respiration are roughly balanced in boreal lakes, including those with wide variation in the concentration of colored dissolved organic carbon (Vesterinen et al., 2016; FIGURE). This observation is the basis for assuming that the relevant carbon in our model enters at the surface. This assumption may not hold outside of the boreal biome. For example, benthic primary production often exceeds sediment respiration in oligotrophic arctic and alpine lakes, evidenced by accumulations of oxygen in the hypolimnion when these lakes stratify (e.g., Klaus et al., 2020). These lakes typically have higher rates of carbon burial and lower rates of carbon evasion than boreal lakes (Lundin et al., 2015). In its current form, our model will not accurately predict burial lakes for these lakes. However, the basic theory can be modified for such regions, for example, by assuming that carbon input is equal across depths.

Our estimates for carbon burial are based on a productivity estimate which depends only on the lake area and a correction for latitudinal differences in insolation and temperature. Other factors, such as nutrient inputs, allochthonous carbon fluxes, and trophic status, are also expected to play a role. The influences of total nitrogen and dissolved organic carbon concentrations and the vertical light attenuation coefficient were tested for and not found in Cael and Seekell. (2022), but these and other variables are likely to affect the burial rates of individual lakes. The basic theory developed here could easily be modified to account for such factors, e.g., by changing the attenuation length scale as a function of nutrient status.

In general, the development of alternate approaches that integrate different advantages and limitations, like the model described in our study, stands to strengthen and advance collective understanding of the contribution of lakes to the global carbon cycle.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

BC and DS contributed equally to this work, conceived the study, and wrote the paper; DS compiled the data; BC developed the model.

Funding

This paper is based on research supported by the National Environmental Research Council (grants NE/N018087/1, NE/T010622/1, and NE/R015953/1), the Knut and Alice Wallenberg Foundation, and Umeå University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2023.1101332/full#supplementary-material

References

Ask, J., Jansson, J., and Karlsson, J. (2012). Net ecosystem production in clear-water and brown-water lakes. Glob. Biogeochem. Cy. 26, GB1017. doi:10.1029/2010GB003951