SPH modeling of substance transport in flows with large deformation

The velocity field in coastal and oceanic currents is mostly non-uniform, which will result in irregular particle distribution when the fluid is represented by an amount of moving discrete particles as in smoothed particle hydrodynamics (SPH). When the non-uniformity of the flow is big, i.e., with large deformation, the conventional SPH method can hardly solve the associated advection-diffusion process (e.g., substance transport). To accurately simulate the substance transport in flows with large deformation, two types of particle shifting techniques (PSTs) are incorporated into the conventional SPH in this paper. One is based on current particle distance, and the other is based on Fick’s law. In the second type, the repulsive force (RF) term for suppressing the paring instability that occurs in particle shifting technique (PST) is studied and the effect of the kernel function is examined. By introducing a particle disorder measurement, the simulated results of SPH with the two types of PSTs and their modifications are evaluated and the influence of the shifting magnitude is analyzed. The suggestions for how to set reasonable parameters in PSTs are provided by a systematic parametric study. For further illustration, the simulation of the anisotropic diffusion is also examined. To give reliable reference solutions, the high-resolution modified total variation diminishing Lax Friedrichs scheme with Superbee limiter (MTVDLF-Superbee) with fine mesh is also implemented. The validated Lagrangian particle model with optimized PST is applied to a practical application.

1 Introduction

Substances (including sediment, salt and soluble pollutants, etc.) transport in surface and subsurface water is modeled by the advection-diffusion equation, for which various numerical methods have been developed (Finlayson, 1992; Ewing and Wang, 2001; Wang and Hutter, 2001; Alhumaizi, 2004). The difficulties to obtain good solutions for advection-diffusion equation mainly exist in two aspects. One is the treatment of the advection term, especially when the problem is advection dominated, and the other is that there exist steep fronts in the solution. Compared with Eulerian methods, the major advantage of the Lagrangian methods is that the advective term is not involved in the Lagrangian form of the advection-diffusion equation, so that the numerical problems of both spurious oscillations and diffusion error caused by spatial discretization of the advection can be easily eliminated, leading to accurate solutions (Zimmermann et al., 2001; Liu and Liu, 2006; Devkota and Imberger, 2009). Compared with mesh-based Eulerian methods, the smoothed particle hydrodynamics (SPH) is more competitive and attractive due to its good properties of Lagrange and meshfree. It is considered to have the competence to tackle intractable problems in the CFD field, such as big deformation, free-surface and multi-phase flows (Monaghan and Kocharyan, 1995; Kum et al., 2003; Larbe and Price, 2012; Monaghan, 2012; Ye et al., 2019; Gu et al., 2022).

However, SPH has two inherent drawbacks, i.e., boundary deficiency and particle inconsistency, which are still the key issues for research and application in the SPH society (Monaghan, 2000; Kum et al., 2003; Ye et al., 2019; Gu et al., 2022). To solve the governing partial differential equations (PDEs) using SPH, there are two main procedures. One is the kernel approximation in continuous form, and the other is the particle approximation in discretization form. To obtain reasonable solutions, the kernel needs to satisfy some requirements, such as normalization of kernel integration, symmetry of the kernel and anti-symmetry of kernel gradients (Violeau, 2012). These properties can be well preserved in the procedure of particle approximation when the particles maintain regularly spaced, otherwise numerical instability and accuracy degradation cannot be fully avoided. The conventional SPH has second-order accuracy for organized particles, while it cannot even achieve first order as the particles become disorganized (Ye et al., 2019). This is known as particle inconsistency, which mainly results from the discrepancy between kernel approximation and particle approximation when the particles are irregularly spaced.

SPH is applicable in solving the advection-diffusion and heat conduction equations, to which some studies have devoted (Cleary and Monaghan, 1999; Monaghan, 2005; Aristodemo et al., 2010; Bai et al., 2018; Wang et al., 2019). Noticing that both of them have identical form in Lagrangian frame, the discrepancy between them is the zero advection in heat conduction problems, while attention also needs to be paid to particle inconsistency when heat conduction couples with the large deformation flows (Cleary and Monaghan, 1999). Arising from advection, particle disorder affects the simulation of the diffusion process. Chaniotis et al. (2002) approximated the diffusion terms by directly discretizing the second-order derivatives, but this approach is sensitive to particle disorder, then particle remeshing schemes have to be added. Most of the studies (Cleary and Monaghan, 1999; Shao and Lo, 2003; Aristodemo et al., 2010; Ryan et al., 2010; Chang and Chang, 2017; Zheng et al., 2018) adopted a scheme that can be regarded as the hybrid of SPH and difference method. In this scheme, the simulation of diffusion terms merely includes the first-order derivative approximation of SPH. Via this hybrid scheme, Cleary and Monaghan (1999), Aristodemo et al. (2010), Chang and Chang (2017) expressed the diffusion coefficient in a symmetric form to ensure continuity of the flux when the diffusion coefficient is discontinuous and to reduce the influence of particle disorder. Ryan et al. (2010) also used the hybrid scheme to handle the diffusion terms in flows with small deformation, and the focus was on the treatment of the complicated boundary conditions. Recently, Alvarado-Rodríguez et al. (2019) improved the consistency of SPH via setting smoothing length and the number of neighboring particles relevant to the total number of particles, aiming to simulate the anisotropic diffusion with irregular particle distribution. In this paper, the SPH format for diffusion terms differs from the two methods mentioned above. It is a complete SPH form and does not directly approximate the second-order derivatives.

To restore particle consistency, many high-order SPH methods have been proposed, which are known as corrective SPH schemes. To enhance the approximation accuracy, the reproducing kernel particle method (RKPM) modifies the kernel function by a correction function (Liu et al., 1995; Liu and Jun, 1998). The corrective smoothed particle method (CSPM) (Chen et al., 1999; Chen and Beraun, 2000) improves the conventional SPH on the basis of Taylor series expansion, whose discretization form is equivalent to the normalization for the function and its first derivatives. Based on CSPM, the finite particle method (FPM) was put forward by Liu and Liu (2006), which approximates the function and its first derivatives simultaneously and has higher order accuracy than CSPM. The kernel gradient correction (KGC) (Bonet and Lok, 1999; Shao et al., 2012) method corrects the kernel gradient by multiplying the original kernel gradient with an invertible matrix. This method is easy to code on account of retaining the structure of conventional SPH. For the ease of choosing kernel function, the kernel gradient free (KGF) SPH method was proposed (Huang et al., 2015), whose corrective matrix is invertible even if the particles are highly disordered, because the corrective matrix is symmetric. Recently, the decoupled finite particle method (DFPM) (Zhang and Liu, 2018) was developed, in which the corrective matrix is diagonally dominant and it is not necessary to calculate the inverse matrix particle by particle, so it becomes less sensitive to the particle disorder. In fact, the high-order SPH methods mentioned above correct the conventional SPH by some kernel properties which are satisfied only when the particle distribution is regular. On that account, the accuracy of these algorithms will degrade to some extent when particles are disordered.

Apart from the corrective SPH methods, some other ones, namely particle regularization techniques, are also capable of restoring particle consistency. The XSPH scheme (Monaghan, 1988; Shahriari et al., 2013; Ye et al., 2019) uses the adjacent particles to calculate the local velocity, by which the movement of particles tends to mitigate. However, this method may result in non-physical solutions especially when large velocity gradient exists. To improve particle consistency, Monaghan (2000) adopted a repulsive force (RF) term in the equation of motion to avoid the clumping of particles. Similar to RF, Tsuruta et al. (2013) employed a stabilizing force to prevent interparticle penetration. In this work, the same RF term as that of Monaghan (2000) is brought into particle shifting techniques (PST) to redistribute particles. The state of the art PSTs gained much attention in recent years (Nestor et al., 2009; Xu et al., 2009; Lind et al., 2012; Skillen et al., 2013; Antuono et al., 2014; Khorasanizade and Sousa, 2016; Huang et al., 2018). They try to make the particles distribute as uniformly as possible according to certain rules. Xu et al. (2009) brought the PST proposed originally in the finite volume particle method (Nestor et al., 2008; Nestor et al., 2009) into SPH. They applied this technique to simulate incompressible flows by coupling with incompressible SPH (ISPH) method. This PST depends on the calculation of particle distance to decide the shifting of particles. Lind et al. (2012) proposed another type of method on the basis of Fick’s law aiming at the incompressible flows too. Several improvements (Skillen et al., 2013; Khorasanizade and Sousa, 2016; Huang et al., 2018) for Xu et al. (Xu et al., 2009) and Lind et al. (Lind et al., 2012) methods are suggested in succession to stabilize the PSTs. In this paper, we contribute to the parameter optimization and stabilities improvement for the PSTs. The purpose of studying PSTs in this paper is to solve the particle cavity problem which leads to the failure of the simulation of advection-diffusion process.

The rest of the paper is organized as follows. Section 2 presents the governing equation and the SPH-based Lagrangian particle transport model. In Section 3, to deal with substance transport in large deformation flows, several typical PSTs are presented. An evaluation method for the degree of particle disorder is also described. In Section 4, the Lagrangian particle transport model based on SPH combined with PSTs is applied to the isotropic and anisotropic diffusion problems in flows with large deformation, and the results are compared with the exact and reference solutions. The performance of different PSTs and the effect of involved parameters are also evaluated. In Section 5, the SPH method with optimized PST is applied to a case study to show its applicability to practical problems. Section 6 summarizes the concluding remarks.

2 Lagrangian particle transport model

2.1 Governing equations

The governing equation for substance transport adopted in this paper is the two-dimensional (2D) advection-diffusion equation

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=k\left(\frac{{\partial }^{2}C}{{\partial x}^2}+\frac{{\partial }^{2}C}{{\partial y}^2}\right)(1)$

where $C\left(x,y\right)$ is the concentration of the substance; $u$ and $v$ are the velocity of the flow field; $k$ is the coefficient for isotropic diffusion; $x$ and $y$ are the spatial coordinates and $t$ is time. In coastal flow, the physical process of diffusion should consider the longitudinal dispersion and turbulent diffusion at least, i.e., behaves as anisotropic diffusion. To denote the anisotropic diffusion, the mixed second-order derivatives should be included in Eq. 1 as

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=\frac{\partial }{\partial x}\left(k_{11}\frac{\partial C}{\partial x}\right)+\frac{\partial }{\partial x}\left(k_{12}\frac{\partial C}{\partial y}\right)+\frac{\partial }{\partial y}\left(k_{21}\frac{\partial C}{\partial x}\right)+\frac{\partial }{\partial y}\left(k_{22}\frac{\partial C}{\partial y}\right)(2)$

where the diffusion coefficients can be symbolized by a tensor $\mathit{K}$ ($\mathit{K}=k_{ij}\left(i,j=\mathrm{1,2}\right)$).

Note that Eqs 1, 2 are derived for incompressible fluid and hence the divergence of the velocity is zero. The given velocity field in Section 4 is consistent with this assumption. The velocities of the flow field can either be given analytically or numerically calculated by any suitable methods, which are supposed to be known here.

With the definition of the material derivative $\frac{\mathrm{d}}{\mathrm{d}t}=\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}$, the Lagrangian form of Eq. 1 is expressed as

$\frac{\mathrm{d}C}{\mathrm{d}t}=k\left(\frac{{\partial }^{2}C}{{\partial x}^2}+\frac{{\partial }^{2}C}{{\partial y}^2}\right)(3)$

on the moving coordinate system

$\frac{\mathrm{d}x}{\mathrm{d}t}=u\mathrm{a}\mathrm{n}\mathrm{d}\frac{\mathrm{d}y}{\mathrm{d}t}=v(4)$

The Lagrangian form of Eq. 2 can be constructed following the same way.

2.2 SPH-based Lagrangian particle model

The SPH method is introduced briefly in this section, the foundation of which is the interpolation theory (Violeau, 2012). The kernel approximation in continuous form and the particle approximation in discretization form are its two main ingredients.

There are three typical approximation forms for second derivatives in SPH. They can be directly approximated via the second derivatives of the kernel (Monaghan, 2005) as

${\langle \frac{{\partial }^{2}C}{{\partial x}^2}\rangle }_a={\displaystyle \sum }_b{C}_b\frac{{\partial }^2{W}_{ab}}{{\partial x}^2}\frac{m_b}{{\rho }_b}(5)$

where $m_b$ and ${\rho }_b$ are the mass and density of particle $b$; $C_b$ is the concentration at position ${\mathit{x}}_b$; $W_{ab}=W\left(\left|{\mathit{x}}_a-{\mathit{x}}_b\right|,h\right)$ is the kernel function and $h$ stands for the smoothing length. The formulation (5) is sensitive to irregular particle distribution and may lead to numerical results inconsistent with physics due to instability of the second derivative of the kernel (Monaghan, 2005).

To circumvent the weakness of Eq. 5, other forms approximating the second derivatives are developed, among which the hybrid scheme and the approach presented in this work have been widely used. By the hybrid scheme (Cleary and Monaghan, 1999; Monaghan, 2005), the diffusion term can be discretized as

${⟨\frac{{\partial }^{2}C}{{\partial x}^2}⟩}_a={\displaystyle \sum }_b(k_a+k_b)(C_a-C_b)\frac{x_a-x_b}{{\left|x_a-x_b\right|}^2}\frac{\partial W_{ab}}{\partial x}\frac{m_b}{{\rho }_b}(6)$

in which only the first derivative of kernel is contained. The formulation (6) can be considered as the hybrid of SPH and finite difference (Cleary and Monaghan, 1999), hence its stability and accuracy is vulnerable to be effected by the finite difference part.

In this paper, another scheme for approximating diffusion terms is applied, in which only first-order derivatives need to be treated (Jeong et al., 2003; Liu et al., 2020). By this scheme, Eq. 1 can be rewritten by the diffusive flux $\mathit{q}$ (Liu et al., 2020)

$\{\begin{array}{c}\mathit{q}=-k\nabla C\\ \frac{\mathrm{d}C}{\mathrm{d}t}=-\nabla \bullet \mathit{q}\end{array}(7)$

Again $k$ needs to be changed into $\mathit{K}$ for anisotropic diffusion. With this form, the diffusion terms can be solved by approximating the first-order derivative twice. It is easy to code and converted flexibly between isotropic and anisotropic diffusion codes. Better yet, it is a totally SPH based model. The kernel approximation of the concentration gradient in SPH is (Liu et al., 2020)

$\langle \nabla C_a\rangle =\underset{\Omega }{{\displaystyle \int }}C\left(\mathit{x}\right){\nabla }_{a}Wd\mathit{x}(8)$

where ${\nabla }_{a}W$ is the kernel gradient with respect to the position of particle $a$. To make the discretization form of (8) less sensitive to particle distribution, the anti-symmetry property of the kernel gradient (Violeau, 2012)

$\underset{\Omega }{{\displaystyle \int }}{\nabla }_{a}Wd\mathit{x}=0(9)$

can be used to extend Eq. 8 as

$\langle \nabla C_a\rangle =\underset{\Omega }{{\displaystyle \int }}C\left(\mathit{x}\right){\nabla }_{a}Wd\mathit{x}-C_a\underset{\Omega }{{\displaystyle \int }}{\nabla }_{a}Wd\mathit{x}(10)$

The particle discretization form of Eq. 10 is

$⟨\nabla C_a⟩={\displaystyle \sum }_b\left(C_b-C_a\right){\nabla }_a{W}_{ab}\frac{m_b}{{\rho }_b}(11)$

Note that Eq. 11 can mitigate the particle inconsistency problem to some degree, although the discretization of Eq. 9 is only true for regularly distributed particles.

Applying Eq. 11 to the first-order derivatives in Eq. 7, the semi-discretization form of the substance transport equation is derived as (Liu et al., 2020)

$\{\begin{array}{c}\frac{\mathrm{d}{C}_a}{\mathrm{d}t}={\displaystyle \sum }_b\frac{m_b}{{\rho }_b}\left({\mathit{q}}_b-{\mathit{q}}_a\right){\bullet \nabla }_a{W}_{ab}\\ {\mathit{q}}_a=k{\displaystyle \sum }_b\frac{m_b}{{\rho }_b}\left(C_b-C_a\right){\nabla }_a{W}_{ab}\end{array}(12)$

Note that a similar formulation can be obtained for anisotropic diffusion, which eases the coding of anisotropic diffusion process (Liu et al., 2020). Since the diffusive flux is included, it is also easy to handle Neumann type boundary. The accuracy of Eq. 12 is the same order as that of Eq. 6 when particles are regularly spaced (Fatehi and Manzari, 2011). Together with a time integration algorithm, the above semi-discretization form and the change of the coordinate can be integrated. For simplicity, the first-order one-step Euler method is used here, which gives accurate results if the used time step is sufficiently small.

Equation 12 has been derived in Liu et al. (2020) with more details. In that work, the capability of the Lagrangian particle transport model to handle the grid anisotropic problem, dominated advection, pure advection and discontinuity have been validated in the flows with small deformation. Its accuracy, efficiency and stability were compared with the mesh-based Eulerian method, and the particle cavity problem was also recognized. In this work, the SPH-based model is further applied to substance transport problem in flows with large deformation. Since the model given by Eq. 12 cannot simulate the diffusion process when particles are in cavity state, the PSTs for eliminating particle cavities need to be incorporated, which is presented below.

3 Particle shifting techniques

When the particles become disordered due to non-uniform velocity field, SPH cannot accurately approximate the first- and second-order derivatives (Monaghan, 2000; Xu et al., 2009; Lind et al., 2012), and PSTs are good remedies. PSTs can be categorized into two classes. One is based on the distance between particles (Xu’s approach and its modified ones), and the other is based on the Fick’s law of diffusion (Lind’s approach and its modified ones). The latter ones are more feasible for free surface flow. In this section, the representative PSTs and their modified ones are presented. Moreover, a measurement to evaluate the degree of particle disorder is introduced.

3.1 PST of Xu (Xu et al., 2009)

In Xu’s approach, the particles are shifted in terms of the distance between the center particle and its neighbors (those in the support domain of the kernel). On the basis of Tailor series expansion, the concentration in the new position is interpolated by

$C_{a^{\prime }}=C_a+\delta {\mathit{r}}_{a{a}^{\prime }}\bullet {\left(\nabla C\right)}_a+O\left({\delta r}_{a{a}^{\prime }}^2\right)(13)$

where $C_{a^{\prime }}$ denote the concentration of particle $a$ at the new position ${\mathit{x}}_{a^{\prime }}$, $\delta {\mathit{r}}_{a{a}^{\prime }}$ is the distance vector between ${\mathit{x}}_{a^{\prime }}$ and ${\mathit{x}}_a$, and $\delta r_{a{a}^{\prime }}$ is the distance between the two positions. Note that Eq. 13 will be adopted to interpolate the concentration in all the PSTs demonstrated in this paper.

In Xu’s approach, the regulation directing particle redistribution is given by

$\delta {\mathit{r}}_{\mathit{a}}=-A\alpha {\mathit{R}}_a(14)$

${\mathit{R}}_a={\displaystyle \sum }_{b=1}^{N_a}\frac{{\mathit{r}}_{ab}}{r_{ab}^3}{\overline{r}}_a^2(15)$

${\overline{r}}_a=\frac{1}{N_a}{\displaystyle \sum }_{b=1}^{N_a}{r}_{ab}(16)$

where $A$ is a constant ranging from 0.01 to 0.1, and $\alpha =U_{\mathit{max}}\mathrm{d}t$ is the shifting magnitude which is assigned to be the maximum advection distance. $N_a$ is the number of neighbors of particle $a$ , ${\mathit{r}}_{ab}={\mathit{x}}_a-{\mathit{x}}_b$, $r_{ab}=\left|{\mathit{r}}_{ab}\right|$, and ${\overline{r}}_a$ is the averaged distance between particle $a$ and its neighbors. The anisotropic features of particles are achieved by the summation of unit distance vector ${\mathit{r}}_{ab}/r_{ab}$ in Eq. 15 and the term ${\overline{r}}_a^2/r_{ab}^2$ decreases the influence of particles in far distance. The parameter $A$ should be properly chosen to restrict the shifting magnitude to a reasonable range, because it affects both the interpolation accuracy of the concentration and the degree of particle disorder.

3.2 Modified Xu’s algorithm

In Xu’s approach, $U_{\mathit{max}}$ in the shifting magnitude is the global maximum velocity, which increases the shifting distance of particles with lower velocities. To solve this problem, Khorasanizade and Sousa (2016) introduced the local maximum velocity. For the purpose of obtaining appropriate shifting magnitude, i.e., the product of $A$ and $\alpha$ in Eq. 14, they proposed a set of algebraic equations, by which the shifting magnitude was determined ultimately. Replacing $A\alpha$ with $A^{\prime }$, the whole set algebraic equations is given by

$\{\begin{array}{c}{a}_1=U_{\mathit{max}}dtA\\ a_2=U_{\mathit{max},a}^{local}dtA\\ b=C_F{\overline{r}}_a\\ d=\mathit{max}\left(a_2,b\right)\\ A^{\prime }=\mathit{min}\left(a_1,d\right)\end{array}(17)$

where $U_{\mathit{max},a}^{local}$ stands for the local maximum velocity related to particle $a$; $C_F$ is a constant with the best choice of 0.001. The anisotropic degree of particles is determined by the parameter $d$, and the maximum advection distance is still a limitation for particle shifting in this modified approach. Its main contribution is the introduction of the local maximum velocity, which regulates the shifting distance of slower particles to be moderate. Due to the ambiguous description of $U_{\mathit{max},a}^{local}$ (Khorasanizade and Sousa, 2016), it is assigned to be the same as $U_a$ in Eq. 24 in this work.

3.3 Lind’s approach

In Lind’s approach, the movement of particles is determined by the gradient of particle concentration. To distinguish the diffusion process of pollutant concentration in Lagrangian Particle Transport Model Section from that of particle number concentration in this section, we use $D$ to represent the particle number concentration and $K$ for its diffusion coefficient. The diffusion flux can be presumed to be the number of particles crossing the unit area in unit time, which means that the flux is directly proportional to the particle shifting velocity. Define $P_s$ as the proportional scale between the flux and the shifting velocity ${\mathit{v}}_a$, then the relation is given by

$-K\nabla D_a=P_s{\mathit{v}}_a(18)$

Colagrossi et al. (2012) showed that $-\nabla D$ can direct particles to move along the maximum anisotropic direction.

Substituting Eq. 18 into the shifting displacement of particle $a$, i.e., $\delta {\mathit{r}}_a={\mathit{v}}_{a}dt$, yields

$\delta {\mathit{r}}_a=-K/P_s\mathrm{d}\mathrm{t}{\nabla D}_a(19)$

The gradient of particle concentration can be discretized by SPH as (Lind et al., 2012)

$\nabla D_a={\displaystyle \sum }_b{{\mathrm{V}}_b{\nabla }_{a}W}_{ab}(20)$

where ${\mathrm{V}}_b=m_b/{\rho }_b$ is the volume of the neighboring particle b.

Monaghan (2000) showed that when Eq. 20 is applied, the kernel gradient deviates from its physical meaning and will result in unphysical solution. For instance, the gradient of the cubic spline is zero in the origin, which will impose unphysical influence on the results when particle $b$ is close enough to particle $a$. Physically speaking, the kernel gradient is supposed to increase with the decrease of particle distance. To make up for this kernel deficiency, Monaghan (2000) employed the term of RF (in fluid dynamics, it is regarded as artificial pressure) to eliminate the tensile instability. The expression for the RF is

$f_{ab}=\frac{W\left(r_{ab}\right)}{W\left({\mathrm{d}x}_0\right)}(21)$

where ${\mathrm{d}x}_0$ is the initial particle spacing. In Lind’s approach, Eq. 21 is employed to calculate the gradient of particle concentration and Eq. 20 is then modified as

$\nabla D_a={\displaystyle \sum }_b{{\mathrm{V}}_b{\left(1+R{f}_{ab}^n\right)\nabla }_{a}W}_{ab}(22)$

The parameters $R$ and $n$ are suggested to be 0.2 and 4, respectively (Monaghan, 2000). Via the modification, the kernel gradient is in better agreement with its physical meaning. For details, Figure 1 can be referred.

FIGURE 1

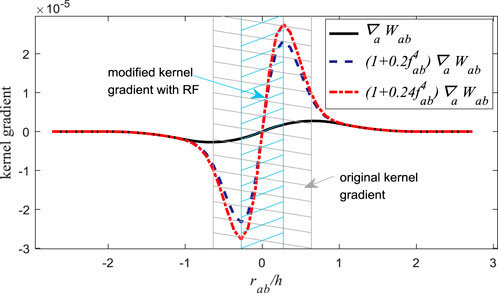
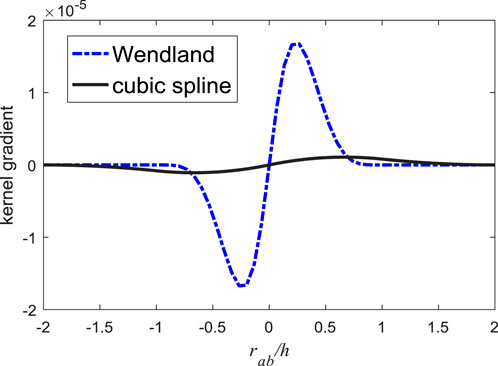
FIGURE 1. Comparison of the original kernel gradient (cubic spline kernel, solid line) with the modified ones by adding RF.

Using the symbol $K^{\prime }=K/P_s$ to stand for integration of the scaling constants, the coefficient $K^{\prime }$ has similar meaning as parameter $A^{\prime }$ in Eq. 17 and is of great importance to decide the shifting magnitude. Its value is determined on the basis of von Neumann stability theory with the expression (Lind et al., 2012)

$K^{\prime }\le L_p{h}^2/dt(23)$

where $L_p$ is taken as a constant of 0.5 by Lind et al. (2012), but it can be different values as tested in Section 4. Note that as the shifting distance has the possibility to exceed the smoothing length, Lind et al. (2012) gave an upper limit for it with the value of $0.2h$.

3.4 Modified Lind’s algorithms

Skillen et al. (2013) improved Lind’s approach via the CFL condition for the purpose of bringing in the local velocity which makes a similar sense as $U_{\mathit{max},a}^{local}$ in Eq. 17. According to the CFL condition, the time step should satisfy

$\mathrm{d}t\le \frac{h}{U_a}(24)$

in which $U_a$ is the velocity magnitude of particle $a$. Taking $\mathrm{d}t=0.5h/U_a$ and $L_p=0.5$, and substituting them into Eq. 23 yields

$K^{\prime }\le h{U}_a(25)$

Then the local velocity can be used to control the shifting magnitude. In fact, there should be a dimensionless parameter as $L_p$ to adjust the shifting magnitude. For the sake of distinction, this parameter is symbolized by $S_p$. As the upper limit is not necessary to be set, the shifting of all the particles satisfies the Fick’s law, while the shifting distance of some particles is clipped by $0.2h$ in Lind’s approach.

Recently, by using the maximum advection distance to replace one $h$ in Eq. 23 and slightly changing the constant $R$, Huang et al. (2018) derived a new formula as

$\delta {\mathit{r}}_a=U_{\mathit{max}}\mathrm{d}t\frac{h}{2}{\displaystyle \sum }_b{{\mathrm{V}}_b{\left(1+0.24f_{ab}^4\right)\nabla }_{a}W}_{ab}(26)$

Note that although these PSTs do not strictly preserve momentum, they are still valuable in solving the particle inconsistency problem because they have good features in convergence, accuracy and stability (Lind et al., 2012).

In Figure 1, the original kernel gradient (derivative with respect to $x_a$) is compared with those with added RF. As demonstrated above, the portion between the two inflexions (see Figure 1) does not conform to its physical meaning. If possible, the smoothing length $h$ should be chosen properly to make the nearest neighboring particle outside the misleading portion, otherwise particle clustering will be resulted (Lind et al., 2012). Physically speaking, the repulsive force between two particles should become larger when they get closer, while the kernel gradient indicating that the repulsive force shows the opposite effect. After the RF term is added, the improper zone gets narrower and the curve becomes much steeper (see Figure 1), which implies a larger shifting distance and a more flexible selection of $h$. In theory, a larger shifting distance can lead to more regular particle distribution.

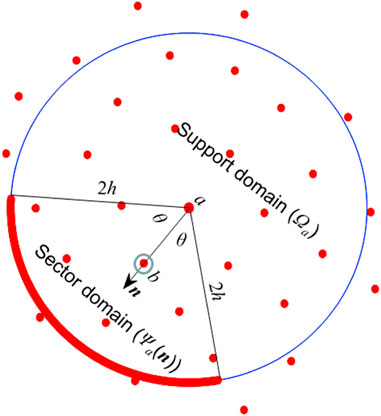
3.5 Particle disorder measurement

For judging the performance of different PSTs and the effect of related parameters, a measurement to evaluate the degree of particle disorder is presented in this section. The algorithm proposed by Antuono et al. (2014) is adopted here to figure out the best choice of parameters in different schemes and to appraise which scheme can lead to the best consequence in the simulation of the advection-diffusion process.

In the evaluation of particle consistency, there are two main steps. The first step is to search the neighbors of particle $a$ in its support domain ${\Omega }_a$ (see Figure 2), and the second is to find the maximum nearest distance among all the sectors which partition the support domain by specific rules (see Figure 2). In the first step, the minimum distance $r_{\mathit{min}}$ between particles $a$ and $b$ is calculated by

$r_{\mathit{min}}=\underset{b\in {\Omega }_a}{\min }\Vert {\mathit{x}}_a-{\mathit{x}}_b\Vert (27)$

FIGURE 2

FIGURE 2. The schematic of particle disorder measurement.

In the second step, the sector domain ${\Psi }_a\left(\mathit{n}\right)$ is defined firstly, where $\mathit{n}$ is the unit vector to denote its direction. In terms of proper angle $\theta$ (see Figure 2) and sector numbers suggested by Antuono et al. (2014), $\theta =7\pi /18$ and eight sectors are used to divide the support domain. For the ease of segmentation, the first sector direction is determined by the vector ${\mathit{r}}_{\mathit{min}}={\mathit{x}}_a-{\mathit{x}}_b^{\mathit{min}}$, where ${\mathit{x}}_b^{\mathit{min}}$ symbolizes the nearest neighboring particle in ${\Omega }_a$. The next sector direction needs to plus $\pi /4$ since eight sectors are used. It means that there are certain areas are overlapped between two adjacent sectors. In every sector region, the nearest neighboring particle to the center particle $a$ is searched by

$r_{\mathit{min}}\left(\mathit{n}\right)=\underset{b\in {\Psi }_a\left(\mathit{n}\right)}{\min }\Vert {\mathit{x}}_a-{\mathit{x}}_b\Vert (28)$

Accordingly, the maximum value $R_{\mathit{min}}$ among the eight minimum distances $r_{\mathit{min}}\left(\mathit{n}\right)$ is obtained, which is compared with $r_{\mathit{min}}$ to judge the anisotropic degree of particles.

The function for quantitating particle disorder is given by

${\lambda }_a=\frac{R_{\mathit{min}}^a-r_{\mathit{min}}^a}{R_{\mathit{min}}^a+r_{\mathit{min}}^a}(29)$

Then the effect of particle inconsistency can be evaluated by averaging all of ${\lambda }_a$ as

$\Lambda =\frac{{\displaystyle \sum }_{a=1}^N{\lambda }_a}{N}(30)$

where $N$ is the total number of particles in the computational domain. If the distribution of particles is regular, the index $\Lambda$ is equal to zero, which means that the closer $\Lambda$ is to zero, the more regular the particles are. For more details, one is referred to Antuono et al. (2014).

4 Numerical results and discussion

In this section, we aim to confirm the feasibility of SPH coupled with PST in solving the advection-diffusion process when particle cavity problem occurs. An anisotropic rotation flow field with strong deformation (Pudykiewicz and Staniforth, 1984) is used for validation. The pure advection simulation is carried out firstly to illustrate the cavity phenomenon, which still exists even a large number of particles are used. Under this circumstance, the diffusion terms cannot be accurately approximated. For eliminating the cavity problem and regulating the particle distribution, PSTs are added to the Lagrangian particle transport model (Liu et al., 2020) and a series of tests are then conducted. Through the numerical experiments, the efficiency of different PSTs is compared, the factors affecting the stability of PSTs are optimized, and the accuracy is examined by comparing with the reference solution of MTVDLF-Superbee. The performances of PSTs are discussed in detail to guide their possible application to real engineering problems. The anisotropic diffusion simulations are also performed to further state the feasibility of the particle model.

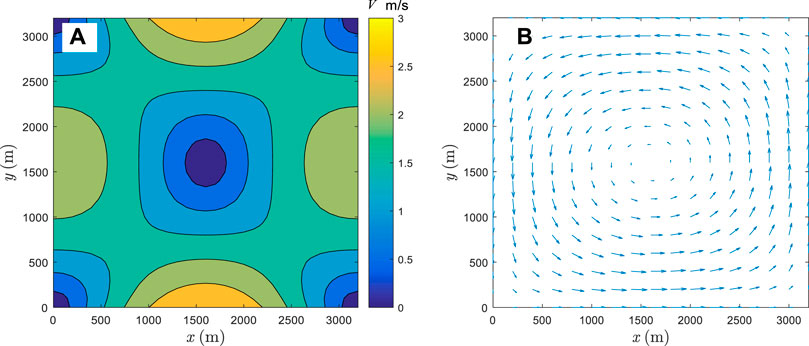
In this test, the flow field is given by the streamline function

$\psi =-\frac{L{V}_{\mathit{max}}}{4}\left(1-\frac{4x^2}{L^2}\right)\cos \left(\frac{\pi y}{L}\right)(31)$

Then the velocities in $x$ and $y$ directions are

$u=\frac{\mathrm{d}x}{\mathrm{d}t}=-{\psi }_y=-\frac{\pi V_{\mathit{max}}}{4}\left(1-\frac{4x^2}{L^2}\right)\sin \left(\frac{\pi y}{L}\right)(32)$

$v=\frac{\mathrm{d}y}{\mathrm{d}t}={\psi }_x=2V_{\mathit{max}}\frac{x}{L}\cos \left(\frac{\pi y}{L}\right)(33)$

where $V_{\mathit{max}}=3$ m/s is used herein. The absolute velocity and the velocity vector are shown in Figure 3. It is a circulating non-uniform flow. The computational domain is $0\le x,y\le 3200\mathrm{m}$.

FIGURE 3

FIGURE 3. The absolute velocity (A) and velocity vector (B) for the large deformation flow.

The initial distribution of pollutant is given by the Gaussian as

$C\left(x,y,0\right)=\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}-\frac{{\left(y-y_0\right)}^2}{2{\sigma }_y^2}\right)(34)$

where $\left(x_0,y_0\right)$ is the center of the pollutant, and $\left(x_0,y_0\right)=\left(1000\mathrm{m},1700\mathrm{m}\right)$ is set in this test; ${\sigma }_x$ and ${\sigma }_y$ are the variance in the $x$ and $y$ direction, respectively, and ${\sigma }_x={\sigma }_y=100$ are assigned here. The initial value of the concentration is from $0$ mg/L to 1 mg/L, which is assigned for all the numerical experiments in Section 4 except for the anisotropic case.

4.1 Advection-diffusion simulation without PSTs

The pure advection case is simulated to verify the existence of cavity problem even a large number of particles are used. First, particles with a uniform spacing of 50 m (4096 particles) are distributed in the domain (see Figure 4A). The time step is 2.5 s and the simulation time is 3400 s, which approximately equals to the time needed for one rotation. As shown in Figure 4B, after one rotation, the particle distribution becomes highly irregular and some cavities appear, which is also shown in (Liu et al., 2020). Note that in the following figures, the color bar means pollutant concentration unless otherwise mentioned.

FIGURE 4

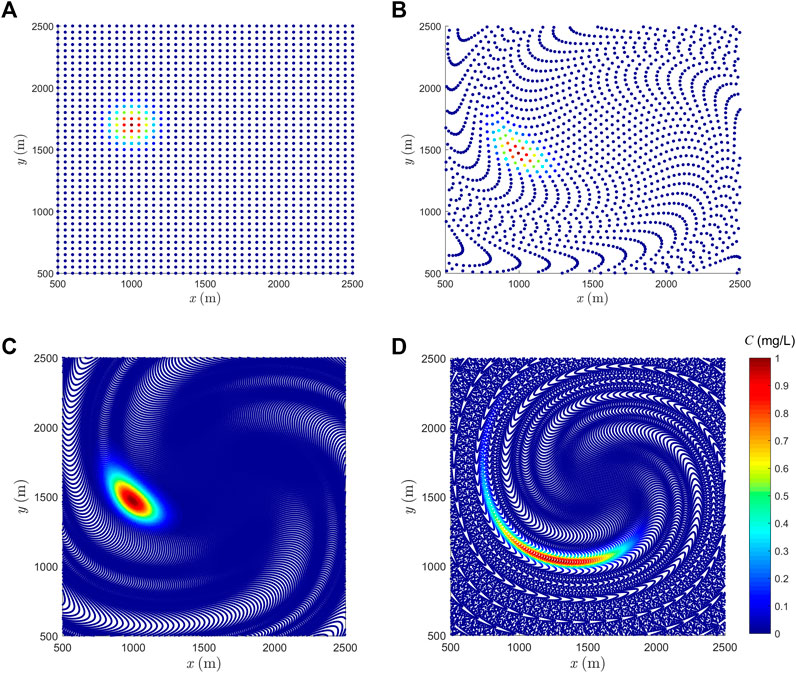
FIGURE 4. Pure advection simulation by SPH: concentration and particle distribution. (A) t = 0 s and 4096 particles, (B) t = 3400 s (roughly one rotation) and 4096 particles, (C) t = 3400 s and 102400 particles and (D) t = 6800 s and 102400 particles.

A uniform spacing of 10 m (102,400 particles) is then applied. The results after one rotation are presented in Figure 4C, where the cavity problem is still evident. After two rotations, the particle cavity phenomenon gets worse (see Figure 4D). They indicate that increasing particle number does not help to remove the cavity problem and higher computational cost will be caused.

For the advection-diffusion process in the given flow field, there is no exact solution available. To provide a good reference solution for comparison and evaluation, MTVDLF-Superbee method is implemented. In this case, the initial concentration distribution is smooth and no steep front forms within the simulation time, for which MTVDLF-Superbee can achieve second-order accuracy (Wang and Hutter, 2001). As the diffusion coefficient is assigned to be 20 m²/s, this is a diffusion dominated case, for which MTVDLF-Superbee gives good reference solutions (Liu et al., 2020). The grid number is 400 by 400 and the time step is 0.005 s. The reference solution after one rotation is shown in Figure 5. On a laptop machine (Core i7-5600U, 2.6 GHz), the CPU time for MTVDLF-Superbee is roughly 6 h.

FIGURE 5

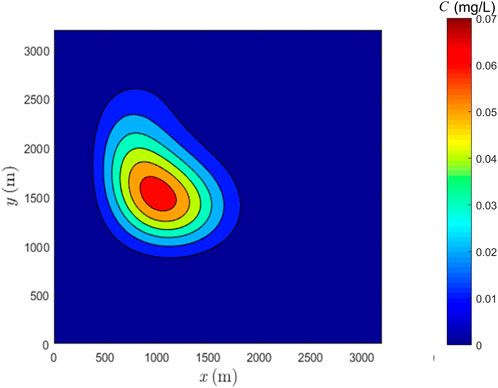
FIGURE 5. Reference solution obtained by MTVDLF-Superbee with grid number 400 by 400 and dt = 0.005 s.

In the SPH-based model, 160 by 160 particles are used to test its performance without PSTs. The smoothing length of $h=1.5\mathrm{d}x$ is set for the purpose of sufficient neighboring particles and the time step is 1 s. As the cubic spline kernel is used, the searching radius is $2h$. The simulated result after 1000 s is shown in Figure 6, where incorrect concentrations have appeared at the boundary region. The solution at one rotation cannot be obtained due to the breakdown of the calculation caused by particle cavities. Therefore, to obtain correct results for substance transport in natural flows where both longitudinal dispersion and turbulent diffusion play a vital role, PST-like measures have to be taken.

FIGURE 6

FIGURE 6. Simulation result of advection-diffusion by SPH without PSTs.

4.2 Advection-diffusion simulation with PSTs

As it is not necessary to arrange a large number of particles in view of applying PSTs, the particle number is set to be 64 by 64 for all the tests in this section. For SPH combined with PSTs, the CPU time is about half an hour. In general, Lind’s PST needs one-third more time than Xu’s PST because it is based on SPH approximations, whereas Xu’s PST is just based on a set of algebraic expressions.

To quantitatively evaluate the SPH results, the L₂ norm error is taken here to measure the discrepancy between the solution of SPH with PST and the one of MTVDLF-Superbee with finer grids.

$L_2=\frac{{\left[{\displaystyle \sum }_{a=1}^N{\left(C_a^e-C_a^n\right)}^2\right]}^{1/2}}{{\left[{\displaystyle \sum }_{a=1}^N{\left(C_a^e\right)}^2\right]}^{1/2}}(35)$

where $c_a^e$ is the exact solution and $c_a^n$ is the numerical solution; N is the total number of particles.

Moreover, the irregularity index $\Lambda$ presented in Section 3.5 is used to judge which method can achieve more regular particle distribution. For a numerical solution, if both the value of the L₂ norm error and the index $\Lambda$ are the minimum among those for comparison, it can be judged as the best one. However, they are used herein mainly to evaluate the performance of PSTs and to optimize the involved parameters.

4.2.1 Factors affecting the stability of PSTs

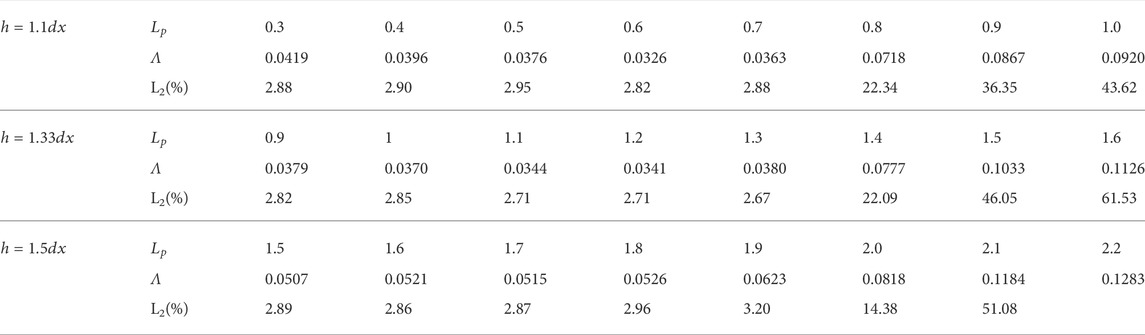
1) Paring instability affected by kernel types in Lind’s PST

In Lind’s PST, the paring instability often occurs. To avoid it, the smoothing length $h$ should be chosen carefully, unless the RF term is added. Without adding RF, the SPH results with Lind’s PST are compared in Figure 7 for cases with different smoothing lengths. Note that the different smoothing length set here is used only in PSTs, while $h=1.33dx$ is adopted for the discretization of the diffusion terms. The pairing instability phenomenon gets more evident with the increase of $h$. On the other hand, when the RF is added, no matter what $h$ is chosen, no pairing instability appears;see Figure 8. It means that adding RF can avoid pairing instability.

FIGURE 7

FIGURE 7. Simulation results for one rotation by Lind’s PST with cubic spline kernel without RF in different smoothing length. (A) h = 1.1dx, (B) h = 1.2dx, (C) h = 1.33dx, (D) h = 1.4dx and (E) h = 1.5dx.

FIGURE 8

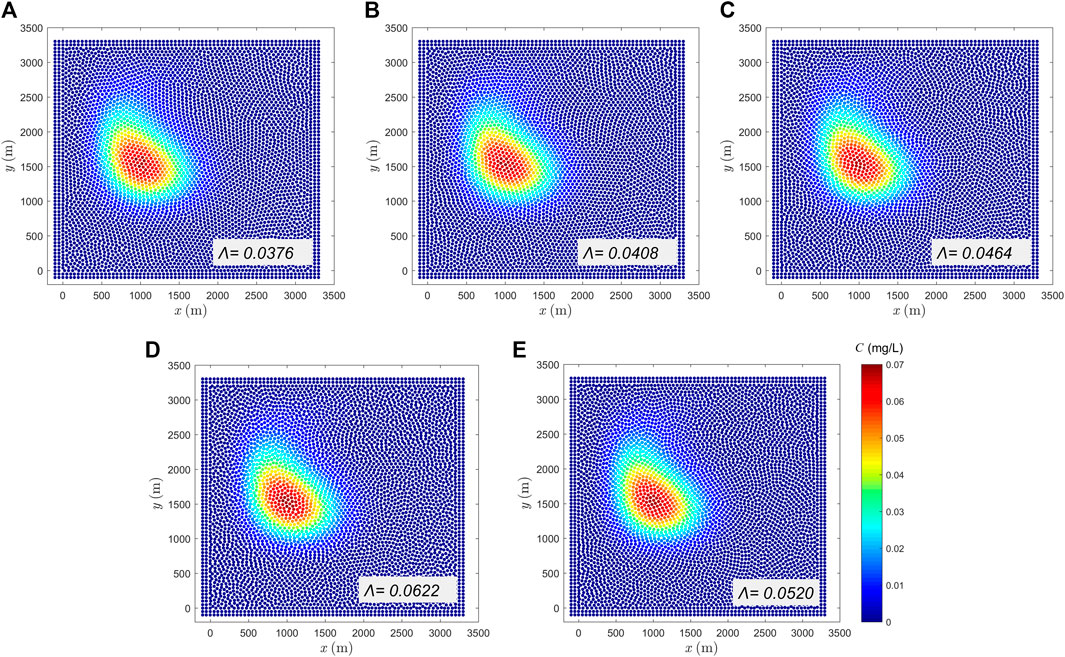
FIGURE 8. Simulation results for one rotation by Lind’s PST with cubic spline kernel with RF in different smoothing length. (A) h = 1.1dx, (B) h = 1.2dx, (C) h = 1.33dx, (D) h = 1.4dx and (E) h = 1.5dx.

As mentioned in Section 3.4, the misleading portion of the kernel gradient should be narrow to alleviate the paring instability, from which aspect the Wendland type kernel (see Figure 9) is termed to be a better option (Dehnen and Aly, 2012; Alvarado-Rodríguez et al., 2019). Since the paring instability only occurs in PST and the simulation of diffusion is free of it, only the cubic spline kernel is replaced by Wendland. For ease of comparison, the same smoothing length with that in Figure 8E is used. In the solution obtained with the Wendland kernel without RF, paring instability has been completely resolved; see Figure 10. The value of $\Lambda$ is 0.0622 for Figure 8E and it is 0.0702 for Figure 9, which means that the performance of the Wendland kernel without RF is more or less the same as that of the cubic spline kernel with RF. Furthermore, when the Wendland kernel is used, $R$ and $n$ in Eq. 22 and in the modified methods can be removed, which simplifies the algorithm to some extent.

FIGURE 9

FIGURE 9. Gradient comparison between Wendland kernel and cubic spline kernel.

FIGURE 10

FIGURE 10. Simulation results for one rotation by Lind’s PST with Wendland kernel without RF.

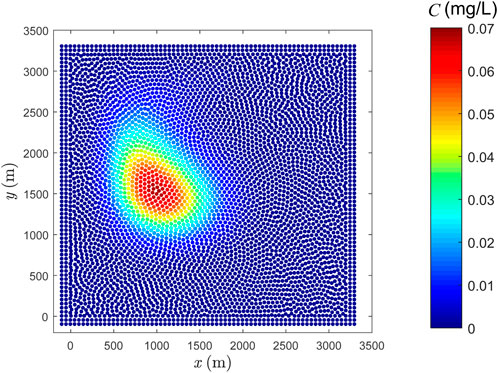
In Figure 11, the contours of simulated result by Lind’s PST with Wendland kernel are compared with the reference solution. For clearness, the concentration profiles along $y=1500$ m are also compared in Figure 11C. The good agreement demonstrates that the SPH combined with Lind’s PST can perfectly simulate the advection-diffusion process in flows with large deformation.

FIGURE 11

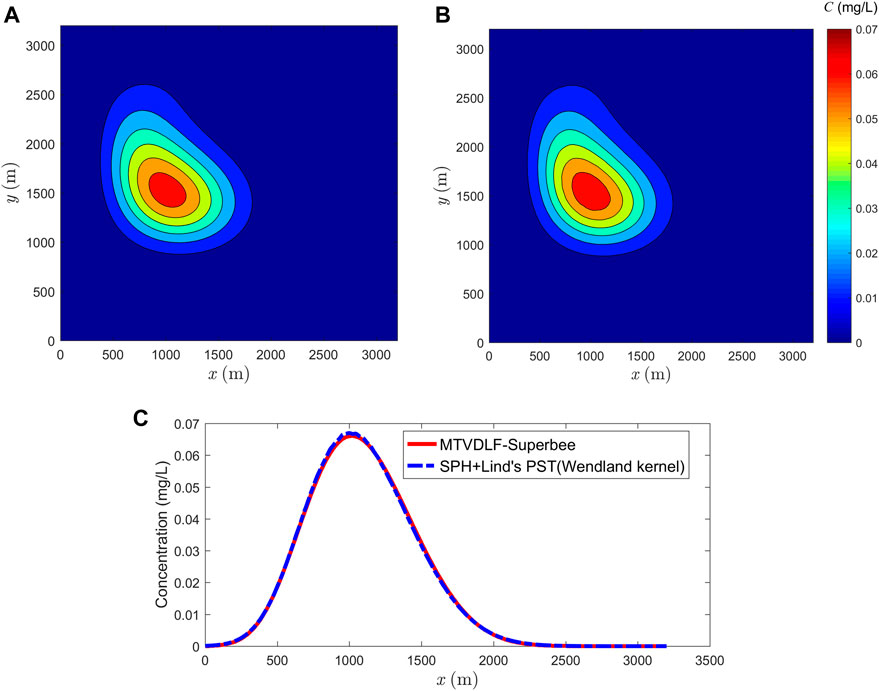
FIGURE 11. Comparison between reference solution and the result obtained by SPH combined with Lind’s PST. (A) Reference solution yielded by MTVDLF-Superbee, (B) solution of particle scheme (Lind’s PST with Wendland kernel) and (C) concentrations along $y=1500$ m.

In summary, when the cubic spline kernel is adopted, paring instability appears, unless small smoothing length is applied or the RF term is added. While when the Wendland kernel is employed, there is no need to add RF to avoid paring instability, even a large smoothing length is used.

2) Parameters controlling the shifting amplitude

In Lind’s approach, the shifting magnitude depends on the value of $L_p$ whose range can be determined by the von Neumann stability analysis as presented in Section 3.3, and the recommended value is 0.5 (Lind et al., 2012). In Table 1, with changing $L_p$, the variation of the indicator $\Lambda$ for particle inconsistency and the L₂ norm error are listed. The smoothing length for PST is taken as $h=1.1dx$, 1.33dx and 1.5dx, respectively. In this section, $h$ is also $1.33dx$ for the discretization of diffusion terms. When $h=1.1dx$ and $L_p\le 0.7$, its effect on particle disorder and numerical accuracy is not significant, while when $L_p>0.7$, the numerical accuracy decreases rapidly and the degree of particle disorder largely increases. Whereas, the limit becomes $L_p=1.3$ when $h=1.33dx$ and $L_p=1.8$ when $h=1.5dx$. Based on the results shown in Table 1, it can be concluded that the reasonable range of $L_p$ is related to the smoothing length $h$, and it expands as $h$ becomes larger.

TABLE 1

TABLE 1. Influence of $L_p$ on particle inconsistency and numerical error in Lind’s PST.

To visually show whether the results are stable or not, several simulations with different $L_p$ and $h$ are exhibited in Figure 12. When $L_p=1$, the concentration distribution has become distorted for $h=1.1dx$, but it is still satisfactory for $h=1.33dx$.

FIGURE 12

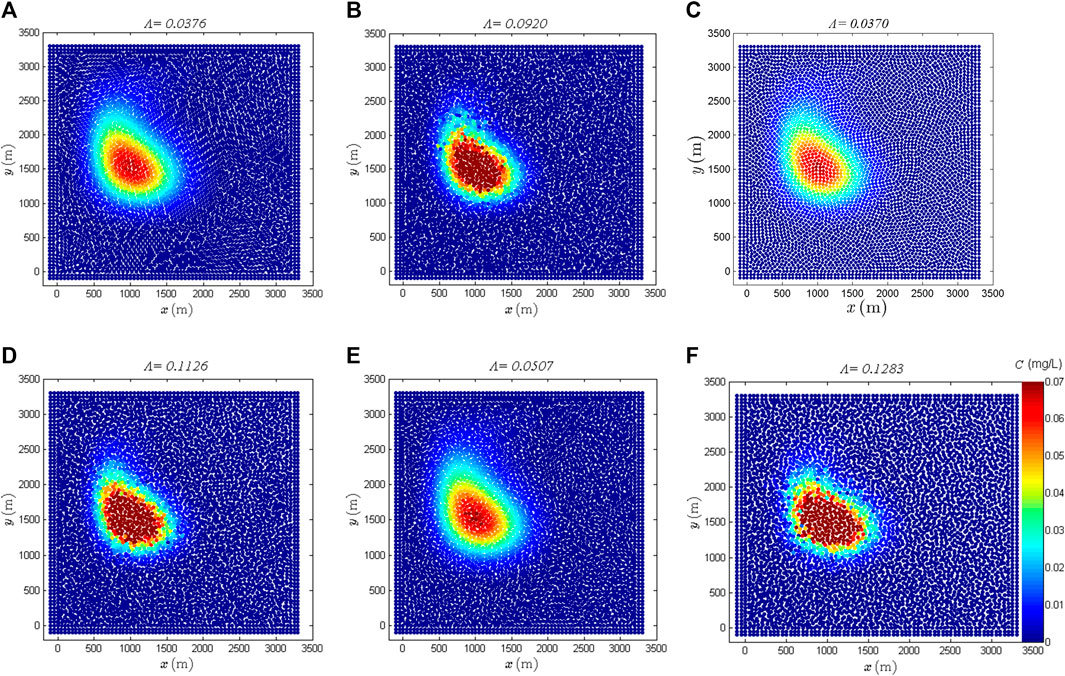
FIGURE 12. Simulation results of SPH combined with Lind’s PST with RF in different smoothing length and different L_p. (A) h = 1.1dx and L_p = 0.5, (B) h = 1.1dx and L_p = 1, (C) h = 1.33dx and L_p = 1, (D) h = 1.33dx and L_p = 1.6, (E) h = 1.5dx and L_p = 1.6 and (F) h = 1.5dx and L_p = 2.2.

In Xu’s approach, the shifting magnitude relies on parameter $A$, the range of which is suggested to be 0.01∼0.1 and 0.04 is considered to be the best choice (Xu et al., 2009). This is tested for the concerned case. The variation of the indicator $\Lambda$ for particle inconsistency and the L₂ norm error are listed in Table 2, which shows that no matter $h=1.1dx$ or $h=1.33dx$ is taken, the results are nearly equivalent. That is to say, $A$ is independent of the smoothing length $h$. The indicator $\Lambda$ tends to be smaller when $A$ gets bigger and the L₂ norm error in all the cases shows subtle distinction. It demonstrates that the influence of $A$ is not so significant as that of $L_p$ in Lind’ PST.

TABLE 2

TABLE 2. Influence of $A$ on particle distribution and numerical error in Xu’s PST.

The concentration for three typical values of $A$ are shown in Figure 13. For all the cases, the particle distribution is reasonable. In Figure 13D, the concentration profiles for different $A$ along $y=1500$ m are compared with that of MTVDLF-Superbee. The three curves with $A=0.01$, $A=0.05$ and $A=0.1$ show almost the same difference from the solution of MTVDLF-Superbee, which is consistent with the error analysis shown in Table 3.

FIGURE 13

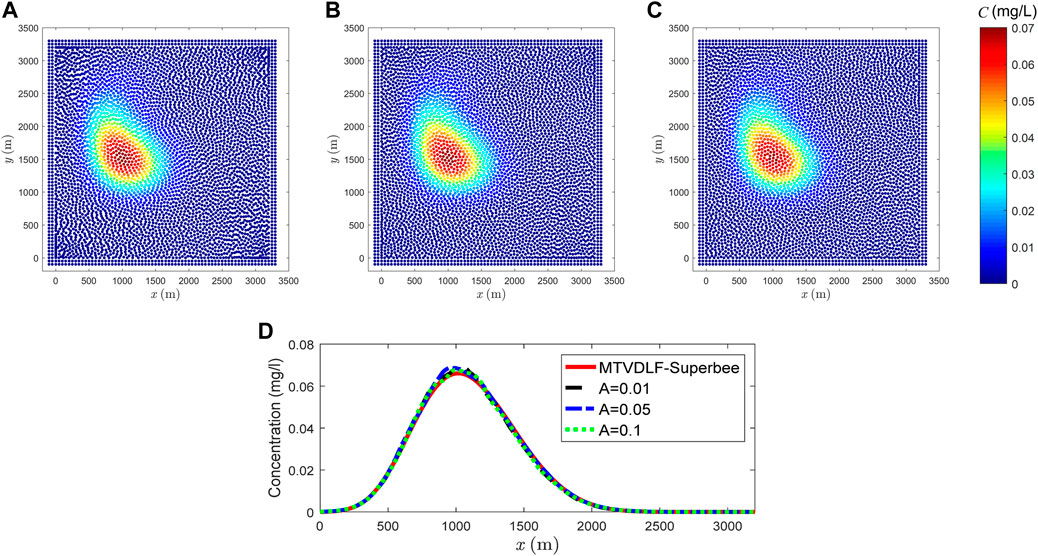
FIGURE 13. Simulation results by Xu’s PST with different A. (A) A = 0.01, (B) A = 0.05, (C) A = 0.1 and (D) concentration profiles along y = 1500 m.

TABLE 3

TABLE 3. Comparison of numerical results of different PSTs.

According to the numerical results, it is seen that the solution of Lind’s PST within stable range is more accurate and has more regular particle distribution, while Xu’s PST is more stable. For the key parameter $L_p$ in Lind’s PST with RF, its stable range is related to the smoothing length $h$, and it should be set according to the value of $h$, otherwise distorted results might be generated.

3) Encoding details for mixed particle position

The test in this section is only for Lind’s PST. In the above simulations, the PST is executed after the advection process, which means that the particle position needs to be updated twice in each time step. For illustration, two symbols are used to distinct the particle positions in the current time step $n$. The one is $n_a$ denoting the position after advection, and the other is $n_p$ standing for the position after PST. If a particle has been shifted in the PST, its position $n_p$ will be updated. When it is searched as a neighbor, its position $n_p$ should be used to shift the position of the center one, while for a particle (belong to the neighboring particles) whose position has not been shifted, $n_a$ will be used. All the results shown above are obtained by using the mixed particle positions of both $n_p$ and $n_a$.

Note that the PST can be done by solely using $n_a$, but it is not as stable as that using the mixed $n_p$ and $n_a$. This is illustrated below. In Figure 14, the results are obtained by using Lind’s approach (with RF) with $h=1.1dx$. In Figure 14A, $n_p$ and $n_a$ are mixed to carry out the PST with $L_p=0.4$, while only $n_a$ is used to shift particles in Figure 14B with $L_p=0.4$. The latter result is seriously distorted and is not correct. Meanwhile, if $L_p$ is set to be smaller than 0.4, acceptable results can still be obtained by using $n_a$ only (see Figure 14C). As shown in Table 1, when mixed particle positions are used, good results are still obtained for $L_p$ up to 0.$7$. This implies that by using mixed particle position in the PST, the stable range of $L_p$ can be enlarged. In addition, when mixed particle positions are used, in theory, computation sequence of the particles decided by the identity number might affect the final solution, i.e., different ways of ordering particles could lead to different results in PST. It is because the particles are shifted one by one in a certain time step according to the identity number and the shifting distance depends on the position of their neighboring particles. However, numerical experiments showed that this effect can be neglected.

FIGURE 14

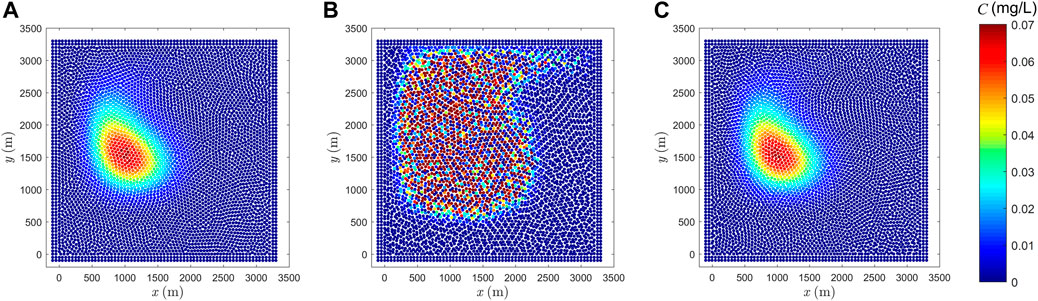
FIGURE 14. Simulation results by SPH with PST using (A) mixed particle position $n_p$ and $n_a$ and $L_p=0.4$, (B) advected particle position $n_a$ and $L_p=0.4$, and (C) advected particle position $n_a$ and $L_p=0.3$.

In terms of the results presented in this section, mixed particle positions after both advection and PST should be used, otherwise the solution will become less stable, if only particle positions after advection are used.

4.2.2 Results of modified PSTs

To better control the shifting distance, the local velocity of particles or the maximum advection distance is introduced in the modified PSTs, which stabilizes the original algorithms and deletes the upper limit for the shifting magnitude. In this section, the results of the modified PSTs presented in Section 3 are compared with those of the original ones. The smoothing length $h$ for all the PSTs is still taken as $1.33dx$.

In the PST of Skillen et al. (2013) (modified Lind), numerical results with three different $S_p$ are computed. In the PST of Huang et al. (2018), the computation directly follows Eq. 23. In the PST of Khorasanizade and Sousa (2016) (modified Xu), the same $A$ is assigned as that in Xu’s PST. Together with the solutions of the original PSTs of Xu and Lind, results of the modified ones are listed in Table 3. Although all the results are not better than those of the original ones, they are all acceptable and the merits of the modified PSTs stated in Section 3 are still reasonable from the aspect of theoretical basis.

4.3 Simulation of anisotropic diffusion

Different from the isotropic diffusion cases studied above, the anisotropic diffusion process brings two mixed derivatives. In this section, the capability of the developed particle scheme to simulate the anisotropic diffusion process with different $\mathit{K}$ is tested.

4.3.1 Transport in uniform flow

The ability of the SPH-based transport model (Eq. 12) to solve the anisotropic diffusion process is firstly verified by simulating an example with analytical solution.

The initial distribution of the concentration is also the Gaussian type and the exact solution is

$C\left(x,y,t\right)=\frac{∆M}{2\pi \sqrt{4t^2\left(k_{11}{k}_{22}-k_{12}^2\right)+{\epsilon }^4+2{\epsilon }^{2}t\left(k_{11}+k_{22}\right)}}\exp \left[\frac{-x^2\left(2t{k}_{22}+{\epsilon }^2\right)-y^2\left(2t{k}_{11}+{\epsilon }^2\right)+xy4t{k}_{12}}{8t^2\left(k_{11}{k}_{22}-k_{12}^2\right)+2{\epsilon }^4+4{\epsilon }^{2}t\left(k_{11}{+k}_{22}\right)}\right](36)$

where $∆M$ is the total mass of the substance; $\epsilon$ is related to the distribution range of the concentration. The coefficient $k_{21}$ disappears as it equals to $k_{12}$.

In this case, $∆M$ is set to be 125,000 g and $\epsilon$ is $400\mathrm{m}$; the computational domain is $0\le x,y\le 6400\mathrm{m}$; the central point of concentration is initially located at $\left(x_0,y_0\right)=\left(3200\mathrm{m},3200\mathrm{m}\right)$; the flow velocity is $u=v=1$m/s; and the simulation time is 1500 s. In MTVDLF, the grids are set to be 256 by 256 and dt is 0.025 , while in the particle method, the number of particles is 128 by 128 and dt is 25 s. Two groups of $\mathit{K}$ are assigned to test the discrepancy between the particle model and the grid method. One is that the diffusivity of the mixed derivative terms is less than that of the remaining two terms, i.e., $k_{11}{k}_{22}-k_{12}^2>0$, and the other is $k_{11}{k}_{22}-k_{12}^2<0$. For the first group, $k_{11}=k_{22}=12$${\mathrm{m}}^2/\mathrm{s}$, $k_{12}=k_{21}=8{\mathrm{m}}^2/\mathrm{s}$, and for the second one, $k_{11}=k_{22}=8{\mathrm{m}}^2/\mathrm{s}$, $k_{12}=k_{21}=12{\mathrm{m}}^2/\mathrm{s}$. The two occasions denoted the different degree of anisotropic. Since the mesh method is prone to produce unstable results, such as negative concentration and artificial mixing (Nordbotten and Aavatsmark, 2005; Mlacnik and Durlofsky, 2006; Yuan and Sheng, 2008; Dehnen and Aly, 2012), especially when the degree of anisotropic diffusion is large, we want to verify whether the SPH-based model is susceptible to tensor $\mathit{K}$.

The numerical results of the first group are shown in Figure 15, where the results of both the particle and grid methods agree well with the analytical solution. For more clearness, all of them are compared through the concentration profiles along $y$ = 4700 m; see Figure 15D. With regard to the second group (see Figure 16), the result of the particle method still agrees well with the analytical solution (Figure 16B), while that of the grid method loses stability (Figure 16C).

FIGURE 15

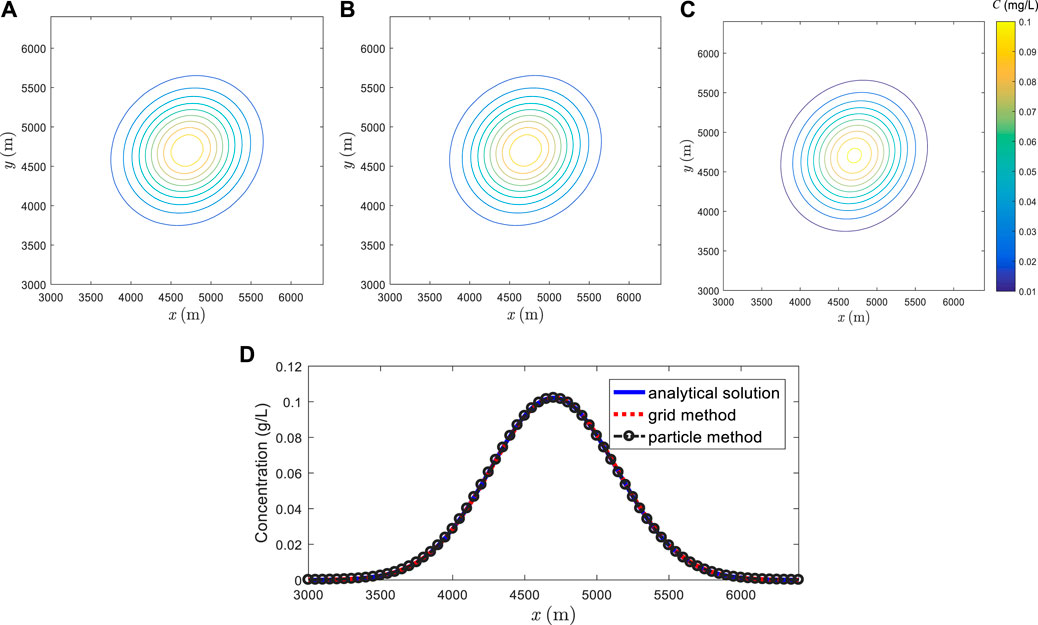
FIGURE 15. Results of the anisotropic diffusion under condition of $k_{11}{k}_{22}-k_{12}^2<0$. (A) Analytical solution, (B) particle solution, (C) grid solution and (D) comparison of concentration profiles along $y=\mathit{4700}$ m.

FIGURE 16

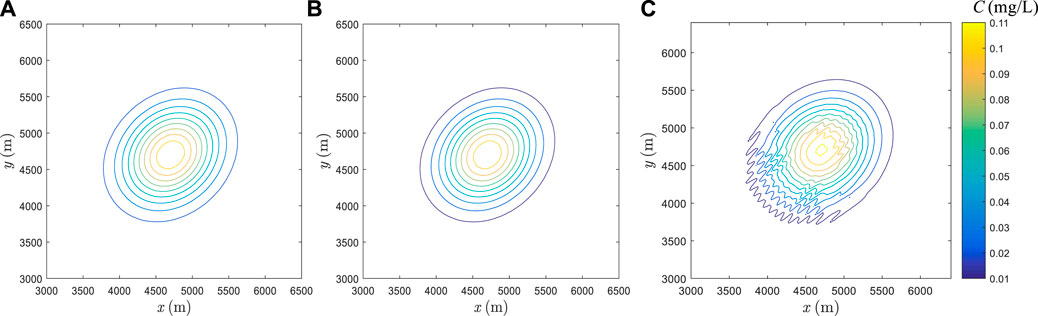
FIGURE 16. Results of the anisotropic diffusion under condition of $k_{11}{k}_{22}-k_{12}^2>0$. (A) Analytical solution, (B) particle solution, and (C) grid solution.

4.3.2 Transport in cavity problem

The flow field is still that with large deformation given by Eq. 31 and the initial concentration distribution is identical with that shown in Figure 4A. For the reference solution obtained by the grid method, the parameters are consistent with those used in the isotropic case in Section 4.1. In SPH the particles are 64 by 64 and the time step is 2.5 s. The simulation time is 3400 s. The diffusion coefficients $k_{11}=20{\mathrm{m}}^2/\mathrm{s},k_{22}=8{\mathrm{m}}^2/\mathrm{s}$, and $k_{12}=k_{21}=10{\mathrm{m}}^2/\mathrm{s}$ are set, giving the condition of $k_{11}{k}_{22}-k_{12}^2>0$, under which the grid method gives accurate and stable solutions as shown in Section 4.3.1.

As shown in Figure 17, although a slight discrepancy still exists, good agreements between particle solution and reference solution are observed. That is, the developed particle model can also give reliable solutions for the anisotropic diffusion in the cavity problem.

FIGURE 17

FIGURE 17. Simulations of anisotropic diffusion in flow with cavities by (A) grid method and (B) particle method and comparison of concentration profiles along (C) $y=\mathit{1500}$ m and (D) $x=\mathit{1000}$ m.

5 Case study

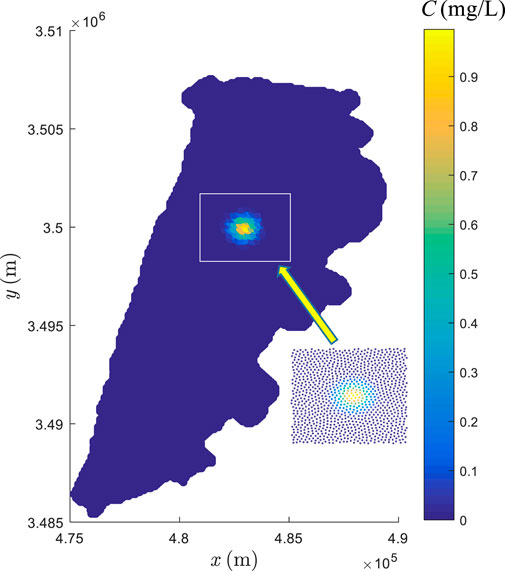
To show the capacity of the developed model for real problems, an engineering case study is presented in this section. The Gehu Lake is an artificial lake located in Jiangsu Province, China, the area of which is about 164 square kilometers. Its geometry is shown in Figure 18. To meet the ecological and landscape needs, the renewal time of the water body has to be determined. As the maximum water depth is only 4 m, the horizontal scale is much larger than the vertical scale. Meanwhile, the calculation of water renewal time involves the convection and diffusion of substances in the water. Therefore, this case study can be simplified into a problem of substance transport in 2D space. With the given shoreline, topography, outlet water level and inlet flow velocity, the flow field is firstly calculated by solving the shallow water equation on triangular meshes (see Figure 18A). As seen from the calculated velocity shown in Figure 18B, the flow is governed by the inlet and the two outlets.

FIGURE 18

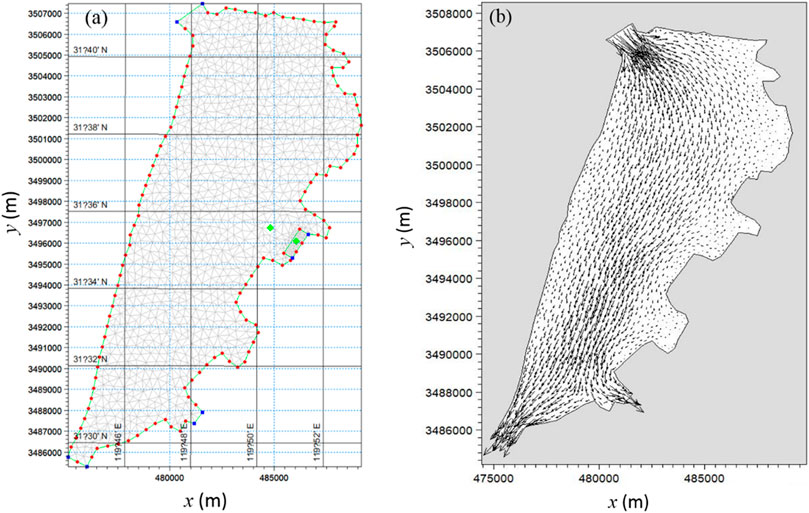
FIGURE 18. The geometry of Gehu Lake discretized with triangular meshes (A) and calculated flow velocity (B).

Different from the idealized case with given analytical velocity field (e.g., Figure 3), the velocity distribution in this real case is known only on the nodes of the triangular meshes (see Figure 18A). To interpolate the velocity of particles moving through the grids, the symmetric smoothed particle hydrodynamics (SSPH) method (Batra and Zhang, 2008) is used, which is third order accurate when up to third-order derivatives are remained in the Taylor’s expansion. Since the computational domain is irregular, the triangular mesh is adopted for initial particle distribution. In this case, as the transportation of pollutants along the central axis of this lake is the main concern, the zero concentration for the dummy particles is applied. For the PST, sufficient dummy particles are needed to prevent fluid particles clustering near the boundary or escaping from the computational domain.

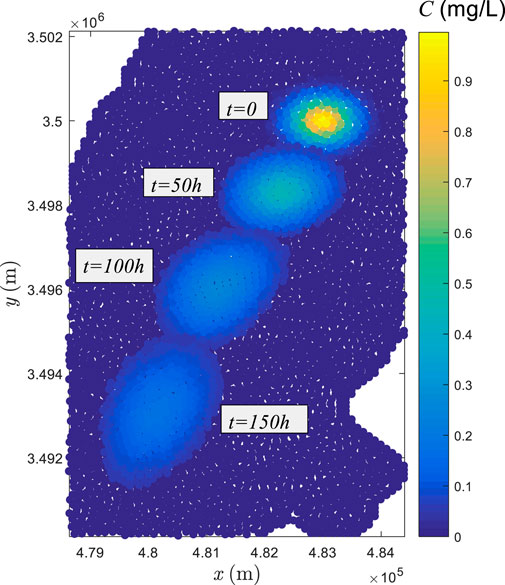
To determine how substances transport in this lake and how long they cross the lake, the Gaussian type pollutant given by Eq. 34 is supposed to be released into the water instantaneously at the upstream (See Figure 19), for which the maximum concentration value is 1 mg/L. Initially 9000 fluid particles are set at the triangular mesh point with a spacing of 100 m. An enlarged view of the area around the pollutants shows that initially the particles are more or less uniformly distributed. The time step can be assigned with a large value, up to 3000 s, which still satisfies the stability condition due to the slow velocity. A constant diffusion coefficient of $k=10{\mathrm{m}}^2/\mathrm{s}$ is applied. As shown in Figure 20, when the simulation starts, the pollutant moves downstream gradually and is still along the central axis. As a result of diffusion, the area of the pollutant goes broader and the concentration is diluted. Since Lind’ PST is added, the particles remain uniform all the time. When the pollutant is close to the first outlet, it takes roughly 150 h, and it takes roughly 10 days for all the pollutants flowing out of the lake. In this work, we only discussed the transportation along the central axis, for which the pollutant can be expelled from the lake and its impact on the water body is diminished because of diffusion. If they were released near the boundary, how long it would take to get out of the lake would be a challenging problem.

FIGURE 19

FIGURE 19. The initial distribution of particles and pollutant.

FIGURE 20

FIGURE 20. The concentration distribution at different time.

6 Conclusion

The SPH method under Lagrangian frame has advantages in solving the advection-diffusion problems. It can well handle the advection-dominated transport problems with discontinuity which are tough for mesh-based Eulerian methods, and has characters of high efficiency and precision (Liu et al., 2020). However, when complicated velocity field is encountered, the particle distribution will become disordered and even forms particle cavities. On this condition, the simulation of the diffusion process easily fails because the insufficient or asymmetry of neighboring particles leads to inaccuracy of kernel approximation. To settle this problem, the particle shifting techniques (PSTs) are introduced to eliminate the particle cavities and make the Lagrangian particle transport model run accurately and smoothly. It can well resolve both the isotropic and anisotropic diffusion process in large deformation flow. Reasonable results are obtained when it is applied in practical flow. The stability, efficiency and accuracy of different PSTs are compared. Lind’s approach gives more regular particle distribution and hence higher accuracy, while Xu’s PST is more stable and its efficiency is higher. When Lind’s approach is adopted, to prevent paring instability, the Wendland kernel is a better choice than the cubic spline, since the RF term is not needed. In addition, to carry out the PST for a given particle, the updated positions of its neighbors after both advection and PST should be applied, otherwise instability might be induced if only the advected positions are used. Comparing with the original PSTs of Xu and Lind, the modified ones do not show noticeable improvements, at least for the cases studied in this work.

The flow field in the present work, either steady in the real case or straightly given by the streamline function, is relatively simple. How the developed scheme performs in the more practical problems, e.g., in the complicated and time-variant ocean flow field (Luo et al., 2021), should be further explored. The involvement of irregular boundaries could be more intractable, which has not been fully discussed in this work. The PST introduced intents to make the particle method available in the transportation simulation of real flows. We will focus on promoting the capability of the proposed numerical model in solving the practical problems in future.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WL: methodology, investigation, simulation, visualization, validation, analysis, and writing original draft. QH: supervision, conceptualization, methodology, analysis, investigation and writing, review and editing. XL: conceptualization, supervision, review and editing. JL: supervision, review and editing. JD: supervision, review and editing.

Funding

This study was supported by the National Key Research and Development Program of China (No. 2020YFC1807905), National Natural Science Foundation of China (No. 52079090) and Basic Research Program of Qinghai Province (No. 2022-ZJ-704).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alhumaizi, K. (2004). Comparison of finite difference methods for the numerical simulation of reacting flow. Comput. Chem. Eng. 28, 1759–1769. doi:10.1016/j.compchemeng.2004.02.032

CrossRef Full Text | Google Scholar

Alvarado-Rodríguez, C. E., Sigalotti, L. D. G., and Klapp, J. (2019). Anisotropic dispersion with a consistent smoothed particle hydrodynamics scheme. Adv. Water Resour. 131, 103374. doi:10.1016/j.advwatres.2019.07.004

CrossRef Full Text | Google Scholar

Antuono, M., Bouscasse, B., Colagrossi, A., and Marrone, S. (2014). A measure of spatial disorder in particle methods. Comput. Phys. Commun. 185, 2609–2621. doi:10.1016/j.cpc.2014.06.008

CrossRef Full Text | Google Scholar

Aristodemo, F., Federico, I., Veltri, P., and Panizzo, A. (2010). Two-phase SPH modelling of advective diffusion processes. Environ. Fluid Mech. 10, 451–470. doi:10.1007/s10652-010-9166-z

CrossRef Full Text | Google Scholar

Bai, B., Rao, D. Y., Xu, T., and Chen, P. P. (2018). SPH-FDM boundary for the analysis of thermal process in homogeneous media with a discontinuous interface. Int. J. Heat. Mass Transf. 117, 517–526. doi:10.1016/j.ijheatmasstransfer.2017.10.004

CrossRef Full Text | Google Scholar

Batra, R. C., and Zhang, G. M. (2008). SSPH basis functions for meshless methods, and comparison of solutions with strong and weak formulations. Comput. Mech. 41, 527–545. doi:10.1007/s00466-007-0209-3

CrossRef Full Text | Google Scholar

Bonet, J., and Lok, T. S. L. (1999). Variational and momentum preservation aspects of smooth particle hydrodynamic formulations. Comput. Methods Appl. Mech. Eng. 180, 97–115. doi:10.1016/s0045-7825(99)00051-1

CrossRef Full Text | Google Scholar

Chang, Y. S., and Chang, T. J. (2017). SPH simulations of solute transport in flows with steep velocity and concentration gradients. Water 9, 132. doi:10.3390/w9020132

CrossRef Full Text | Google Scholar

Chaniotis, A. K., Poulikakos, D., and Koumoutsakos, P. (2002). Remeshed smoothed particle hydrodynamics for the simulation of viscous and heat conducting flows. J. Comput. Phys. 182, 67–90. doi:10.1006/jcph.2002.7152

CrossRef Full Text | Google Scholar

Chen, J. K., and Beraun, J. E. (2000). A generalized smoothed particle hydrodynamics method for nonlinear dynamic problems. Comput. Methods Appl. Mech. Eng. 190, 225–239. doi:10.1016/s0045-7825(99)00422-3

CrossRef Full Text | Google Scholar

Chen, J. K., Beraun, J. E., and Carney, T. C. (1999). A corrective smoothed particle method for boundary value problems in heat conduction. Int. J. Numer. Methods Eng. 46, 231–252. doi:10.1002/(sici)1097-0207(19990920)46:2<231::aid-nme672>3.0.co;2-k

CrossRef Full Text | Google Scholar

Cleary, P. W., and Monaghan, J. J. (1999). Conduction modelling using smoothed particle hydrodynamics. J. Comput. Phys. 148, 227–264. doi:10.1006/jcph.1998.6118

CrossRef Full Text | Google Scholar

Colagrossi, A., Bouscasse, B., Antuono, M., and Marrone, S. (2012). Particle packing algorithm for SPH schemes. Comput. Phys. Commun. 183, 1641–1653. doi:10.1016/j.cpc.2012.02.032

CrossRef Full Text | Google Scholar

Dehnen, W., and Aly, H. (2012). Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 425, 1068–1082. doi:10.1111/j.1365-2966.2012.21439.x

CrossRef Full Text | Google Scholar

Devkota, B. H., and Imberger, J. (2009). Lagrangian modeling of advection-diffusion transport in open channel flow. Water Resour. Res. 45 (12406), 1–14. doi:10.1029/2009wr008364

CrossRef Full Text | Google Scholar

Ewing, R. E., and Wang, H. (2001). A summary of numerical methods for time-dependent convection-dominated partial differential equations. J. Comput. Appl. Math. 128 (1-2), 423–445. doi:10.1016/S0377-0427(00)00522-7

CrossRef Full Text | Google Scholar

Fatehi, R., and Manzari, M. T. (2011). Error estimation in smoothed particle hydrodynamics and a new scheme for second derivatives. Comput. Math. Appl. 61, 482–498. doi:10.1016/j.camwa.2010.11.028

CrossRef Full Text | Google Scholar

Finlayson, B. A. (1992). Numerical methods for problems with moving fronts. Seattle: Ravenna Park Publishing.

Google Scholar

Gu, S., Zheng, W., Wu, H., Chen, C., and Shao, S. (2022). DualSPHysics simulations of spillway hydraulics: A comparison between single- and two-phase modelling approaches. J. Hydraulic Res. 60, 835–852. doi:10.1080/00221686.2022.2064343

CrossRef Full Text | Google Scholar

Huang, C., Lei, J. M., Liu, M. B., and Peng, X. Y. (2015). A kernel gradient free (KGF) SPH method. Int. J. Numer. Meth. Fluids 78, 691–707. doi:10.1002/fld.4037

CrossRef Full Text | Google Scholar

Huang, C., Zhang, D. H., Shi, Y. X., Si, Y. L., and Huang, B. (2018). Coupled finite particle method with a modified particle shifting technology. Int. J. Numer. Methods Eng. 113, 179–207. doi:10.1002/nme.5608

CrossRef Full Text | Google Scholar

Jeong, J. H., Jhon, M. S., Halow, J. S., and van Osdol, J. (2003). Smoothed particle hydrodynamics: Applications to heat conduction. Comput. Phys. Commun. 153, 71–84. doi:10.1016/s0010-4655(03)00155-3

CrossRef Full Text | Google Scholar

Khorasanizade, S., and Sousa, J. M. M. (2016). An innovative open boundary treatment for incompressible SPH. Int. J. Numer. Meth. Fluids 80, 161–180. doi:10.1002/fld.4074

CrossRef Full Text | Google Scholar

Kum, O., Hoover, W. G., and Hoover, C. G. (2003). Smooth-particle boundary conditions. Phys. Rev. E 68, 017701. doi:10.1103/physreve.68.017701

PubMed Abstract | CrossRef Full Text | Google Scholar

Larbe, G., and Price, D. J. (2012). Dusty gas with smoothed particle hydrodynamics–II. Implicit time stepping and astrophysical drag regimes. Mon. Not. R. Astron. Soc. 420 (3), 2365–2376. doi:10.1111/j.1365-2966.2011.20201.x

CrossRef Full Text | Google Scholar

Lind, S. J., Xu, R., Stansby, P. K., and Rogers, B. D. (2012). Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 231, 1499–1523. doi:10.1016/j.jcp.2011.10.027

CrossRef Full Text | Google Scholar

Liu, M. B., and Liu, G. R. (2006). Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 56, 19–36. doi:10.1016/j.apnum.2005.02.012

CrossRef Full Text | Google Scholar

Liu, W., Hou, Q., Lian, J. J., Zhang, A. M., and Dang, J. W. (2020). Coastal pollutant transport modeling using smoothed particle hydrodynamics with diffusive flux. Adv. Water Resour. 146, 103764. doi:10.1016/j.advwatres.2020.103764

CrossRef Full Text | Google Scholar

Liu, W. K., and Jun, S. (1998). Multiple-scale reproducing kernel particle methods for large deformation problems. Int. J. Numer. Methods Eng. 41, 1339–1362. doi:10.1002/(sici)1097-0207(19980415)41:7<1339::aid-nme343>3.0.co;2-9

CrossRef Full Text | Google Scholar

Liu, W. K., Jun, S., and Zhang, Y. (1995). Reproducing kernel particle methods. Int. J. Numer. Meth. Fluids 20, 1081–1106. doi:10.1002/fld.1650200824

CrossRef Full Text | Google Scholar

Luo, M., Khayyer, A., and Lin, P. (2021). Particle methods in ocean and coastal engineering. Appl. Ocean Res. 114, 102734. doi:10.1016/j.apor.2021.102734

CrossRef Full Text | Google Scholar

Mlacnik, M. J., and Durlofsky, L. J. (2006). Unstructured grid optimization for improved monotonicity of discrete solutions of elliptic equations with highly anisotropic coefficients. J. Comput. Phys. 216, 337–361. doi:10.1016/j.jcp.2005.12.007

CrossRef Full Text | Google Scholar

Monaghan, J. J. (1988). An introduction to SPH. Comput. Phys. Commun. 48 (1), 89–96. doi:10.1016/0010-4655(88)90026-4

CrossRef Full Text | Google Scholar

Monaghan, J. J., and Kocharyan, A. (1995). SPH simulation of multi-phase flow. Comput. Phys. Commun. 87 (1-2), 225–235. doi:10.1016/0010-4655(94)00174-z

CrossRef Full Text | Google Scholar

Monaghan, J. J. (2005). Smoothed particle hydrodynamics. Rep. Prog. Phys. 68, 1703–1759. doi:10.1088/0034-4885/68/8/r01

CrossRef Full Text | Google Scholar

Monaghan, J. J. (2012). Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 44, 323–346. doi:10.1146/annurev-fluid-120710-101220

CrossRef Full Text | Google Scholar

Monaghan, J. J. (2000). SPH without a tensile instability. J. Comput. Phys. 159, 290–311. doi:10.1006/jcph.2000.6439

CrossRef Full Text | Google Scholar

Nestor, R., Basa, M., Lastiwka, M., and Quinlan, N. (2009). Extension of the finite volume particle method to viscous flow. J. Comput. Phys. 228, 1733–1749. doi:10.1016/j.jcp.2008.11.003

CrossRef Full Text | Google Scholar

Nestor, R., Basa, M., and Quinlan, N. (2008). Moving boundary problems in the finite volume particle method. in Proceedings of 3rd International SPHERIC Workshop, Lausanne, Switzerland, 4-6 June 2008. 109–114.

Google Scholar

Nordbotten, J. M., and Aavatsmark, I. (2005). Monotonicity conditions for control volume methods on uniform parallelogram grids in homogeneous media. Comput. Geosci. 9 (1), 61–72. doi:10.1007/s10596-005-5665-2

CrossRef Full Text | Google Scholar

Pudykiewicz, J., and Staniforth, A. (1984). Some properties and comparative performance of the semi-Lagrangian method of Robert in the solution of the advection-diffusion equation. Atmosphere-Ocean 22 (3), 283–308. doi:10.1080/07055900.1984.9649200

CrossRef Full Text | Google Scholar

Ryan, E. M., Tartakovsky, A. M., and Amon, C. (2010). A novel method for modeling Neumann and Robin boundary conditions in smoothed particle hydrodynamics. Comput. Phys. Commun. 181, 2008–2023. doi:10.1016/j.cpc.2010.08.022

CrossRef Full Text | Google Scholar

Shahriari, S., Hassan, I. G., and Kadem, L. (2013). Modeling unsteady flow characteristics using smoothed particle hydrodynamics. Appl. Math. Model. 37 (3), 1431–1450. doi:10.1016/j.apm.2012.04.017

CrossRef Full Text | Google Scholar

Shao, J. R., Li, H. Q., Liu, G. R., and Liu, M. B. (2012). An improved SPH method for modeling liquid sloshing dynamics. Comput. Struct. 100-101, 18–26. doi:10.1016/j.compstruc.2012.02.005

CrossRef Full Text | Google Scholar

Shao, S. D., and Lo, E. Y. M. (2003). Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 26, 787–800. doi:10.1016/s0309-1708(03)00030-7

CrossRef Full Text | Google Scholar

Skillen, A., Lind, S., Stansby, P. K., and Rogers, B. D. (2013). Incompressible smoothed particle hydrodynamics (SPH) with reduced temporal noise and generalised Fickian smoothing applied to body–water slam and efficient wave–body interaction. Comput. Methods Appl. Mech. Eng. 265, 163–173. doi:10.1016/j.cma.2013.05.017

CrossRef Full Text | Google Scholar

Tsuruta, N., Khayyer, A., and Gotoh, H. (2013). A short note on dynamic stabilization of moving particle semi-implicit Method. Comput. Fluids 82, 158–164. doi:10.1016/j.compfluid.2013.05.001

CrossRef Full Text | Google Scholar

Violeau, D. (2012). Fluid mechanics and the SPH method: The theory and applications. Oxford: Oxford University Press.

Google Scholar

Wang, J. Q., Hu, W., Zhang, X. B., and Pan, W. X. (2019). Modeling heat transfer subject to inhomogeneous Neumann boundary conditions by smoothed particle hydrodynamics and peridynamics. Int. J. Heat. Mass Transf. 139, 948–962. doi:10.1016/j.ijheatmasstransfer.2019.05.054

CrossRef Full Text | Google Scholar

Wang, Y. Q., and Hutter, K. (2001). Comparisons of numerical methods with respect to convectively dominated problems. Int. J. Numer. Meth. Fluids 37, 721–745. doi:10.1002/fld.197

CrossRef Full Text | Google Scholar

Xu, R., Stansby, P., and Laurence, D. (2009). Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 228, 6703–6725. doi:10.1016/j.jcp.2009.05.032

CrossRef Full Text | Google Scholar

Ye, T., Pan, D. Y., Huang, C., and Liu, M. B. (2019). Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 31, 1–41. doi:10.1063/1.5068697

CrossRef Full Text | Google Scholar

Yuan, G., and Sheng, Z. (2008). Monotone finite volume schemes for diffusion equations on polygonal meshes. J. Comput. Phys. 227, 6288–6312. doi:10.1016/j.jcp.2008.03.007

CrossRef Full Text | Google Scholar

Zhang, Z. L., and Liu, M. B. (2018). A decoupled finite particle method for modeling incompressible flows with free surfaces. Appl. Math. Model. 60, 606–633. doi:10.1016/j.apm.2018.03.043

CrossRef Full Text | Google Scholar

Zheng, X., Ma, Q. W., and Shao, S. D. (2018). Study on SPH viscosity term formulations. Appl. Sci. 8, 249. doi:10.3390/app8020249

CrossRef Full Text | Google Scholar

Zimmermann, S., Koumoutsakos, P., and Kinzelbach, W. (2001). Simulation of pollutant transport using a particle method. J. Comput. Phys. 173 (1), 322–347. doi:10.1006/jcph.2001.6879

CrossRef Full Text | Google Scholar