Agricultural resource and risk management with multiperiod stochastics: A case of the mixed crop-livestock production system in the drylands of Jordan

Generally, agricultural production involves several challenges. In the drylands, it is further complicated by weather-related risks and resource degradation. In this paper, we present a case study of the mixed crop-livestock production system in Jordan. To better capture the nature of response farming in the drylands, we develop a methodology for using crop simulation models to directly generate data for optimizing production practices of an integrated crop-livestock producing household in a dynamic stochastic context. The approach optimizes producer’s adaptations to random events, such as weather, which are realized throughout the planning horizon. To ensure the sustainability of the optimized production decisions, long-term valuations of end of horizon soil attributes are included in the objective function. This approach endogenizes the tradeoff between short-and long-run productivity. Model results show that due to the limited natural resource endowments and financial liquidity constraints of the typical farm households in the study area, we find these households have limited options. To optimally respond to weather conditions during the production season, better manage risk, and achieve improvements in soil attributes, a typical household would need larger farm size, larger flock, and better financial liquidity than it currently commands. Like all such models, the farm household model used in this paper is not suitable for drawing policy implications. Therefore, targeted analysis using appropriate sectoral or economy-wide models will be needed in the future to identify and test the efficacy of different policy and institutional interventions including land consolidation, establishment of producer and marketing cooperatives, access to financial services including agricultural credit, and crop insurance in expanding the resource base of farmers—thereby positioning them for higher earnings, ensuring soil conservation, and enhancing the sustainability of the production system.

1 Introduction

Smallholder farmers in dry areas manage risk and liquidity in part through diversification of enterprises and dynamic responses to weather and other random events. By raising cereal crops with livestock, farmers reduce inefficiencies in the system by lowering transaction costs that are prevalent in many developing nations (Goetz, 1992; Key et al., 2000). To help us understand how integrated crop-livestock production systems respond to change, models of those systems should reflect the biophysical impacts of producer choices and the effects of random variables such as weather, as well as the economic incentives that motivate decisions. Integrating biophysical relationships typically developed by agricultural scientists with economic models of decision making with recourse presents modeling challenges.

In this paper, we analyze the challenges of smallholder mixed crop-livestock producers in the drylands of Jordan and attempt to identify optimal courses of actions. Response farming is a characteristic feature of agriculture in such environments because of weather risk and natural resource degradation. To better capture the Jordanian farmers’ desire to optimize in the face of risk and for ensuring the sustainability of the system, we developed a stochastic dynamic programming model that combines biophysical simulations into which economic decision analysis is superimposed.

Understanding integrated smallholder agricultural production systems is beneficial because they represent some of the most vulnerable households globally. An increasing number of models have analyzed farming households using an agricultural systems approach. Janssen and van Ittersum (2007) provide a review of much of this work. As is pointed out in that review, effectively incorporating the dynamics of farmer decisions with biophysical processes has been a significant modeling challenge. At any point in time, farmers make decisions based on previous choices, realizations of weather, and beliefs regarding the joint distribution of future random outcomes. This means a farmer might choose to delay planting or select an alternative crop variety depending on how weather unfolds, as well as adjusting management practices (such as intra-seasonal fertilizer applications or harvesting technique) later in the season. These dynamic conditional responses to random events have been shown important for farmers in developing nations (Fafchamps 1993; Rosenzweig and Udry 2014). Ignoring potential conditional responses understates farmers’ ability to adapt to weather as it is realized during the year (Boussios et al., 2019). These adaptive responses are missed when the analysis is based on unconditional static production strategies that do not allow for recourse (Gibbons et al., 2005).

One challenge with including these short-run, within-year conditional responses is that the outcomes of the decisions can have long-run, multi-year impacts on soil properties. This requires a modeling system that realistically links short-run responses with long-run outcomes. Stochastic dynamic programming (SDP) has been extensively applied to analyzing crop rotation decisions because it can be used to determine optimal farming strategies over long-time horizons, including the infinite horizon case (Burt and Allison 1963; El- Nazer and McCarl 1986; Livingston et al., 2015; Boussios et al., 2019). However, the challenge in using SDP for modeling whole-farm decisions beyond crop rotations is that decisions often involve inequality constraints or objectives that are not additively separable across time—making optimization of the agricultural system intractable for SDP.

By incorporating crop farmer’s intra-seasonal responses to stochastic events in an SDP over an infinite horizon, Boussios et al. (2019) presented a partial solution to this problem. However, to make the choice set of tractable size for the optimization, they were forced to limit decisions to discrete choices, omitting the possibility of crop diversification or selecting input levels heterogeneously to manage risk. SDP is also limited in its ability to account for various inter-temporal budget constraints and strategies, such as borrowing, that may be used in only some situations.

Agriculture in the drylands including the Middle East and North Africa (MENA) region is generally constrained by low and erratic rainfall, land degradation, and economic risk which is aggravated by climate change (Dregne, 2002; Sterk et al., 2021; Ahmed et al., 2022; Devkota et al., 2022). Despite these challenges, 84 million people (28% of the region’s total population including 20%–25% of Lebanon and Jordan’s active populations) are entirely dependent on agriculture (MEI@75. 2021). Even though agriculture has such a high importance, to the best of our knowledge, no models have been developed to study the production decisions of mixed crop-livestock farms in the drylands of Jordan.

This research, which we believe is the first of its kind in the West Asian region including Jordan, tries to answer three main questions: 1) what are the courses of actions, at different stages during a typical production year cycle, that will maximize the expected net incomes of farmers in Karak region Jordan, who have different levels of resource endowments? And 2) If the optimal courses of actions are different from the current practice, how much net income and soil attribute gains can these farm households expect from following the optical courses of actions? To answer these questions, we propose a dynamic modeling approach that optimizes the decisions of an integrated crop-livestock producer in the arid climate of Jordan. Farming in dryland Jordan presents a meaningful case study for demonstrating our modeling approach because farmers are observed to adapt to uncertain weather throughout the year. In addition, soil resources are fragile, underscoring the importance of ensuring that current choices do not result in excessive reductions in future productivity. The modeling approach here optimizes the decisions of a representative integrated crop-livestock farmer under risk, taking into account, the trade-offs between current and future returns. Our approach demonstrates how to integrate results from biophysical simulation models, such as APSIM (Keating et al., 2003), with an optimizing framework that includes decision making with recourse in response to outcomes of random variables. To reflect the fact that current choices impact future earnings potential through their impacts on soil properties, an approach to valuing end of planning horizon soil properties, such as available nitrogen, is introduced. This helps to ensure that cropping decisions are sustainable and is an alternative to approaches that may over-exploit soil resources by ignoring their impact on future productivity, or arbitrarily restrict soil property levels without accounting for the tradeoff between current and future returns.

The approach we proposed here uses a combination of weather and crop growth simulation models to reflect the impacts of multiple dynamic and conditional farmer decisions on biophysical outcomes. The crop growth simulation models are used to generate data for a discrete stochastic programming formulations (Cocks, 1968; Rae, 1971a; Kaiser et al., 1993; Maatman et al., 2002; Emirhüseyinoğlu and Ryan, 2020). We use results from related research (Boussios et al., 2019) to value soil attributes at the end of the planning horizon to ensure the sustainability of the production system. The inclusion of biophysical soil attributes and management choices in a system that effectively values the dynamic tradeoffs of short-and long-run returns under risk allows us to assess the ability of smallholder farms to manage soil health and meet the needs of their household. Such formulations enable modeling of risk by constructing probabilities of different regimes using simulated multi-year weather data which improves on past studies involving risk (e.g., Engel et al., 2015; Djanibekov and Villamor. 2017).

We illustrate our approach with an analysis of production strategies in rain-fed agricultural production in Jordan. The location serves as a case study due to the high variability of weather and production outcomes that necessitate dynamic production management. The following section presents the integrated crop-livestock production system in Jordan which is followed by the presentation of the empirical approach and modeling where we illustrate how the model was applied to rain-fed agricultural production in Jordan. In a subsequent section, we present the results of the analysis. We draw conclusions in the final section.

2 Background on integrated crop-livestock production in Jordan

We examine the integrated crop-livestock production decisions of smallholder farms in the Karak Governorate of Jordan, which is in Central-Western Jordan, southeast of the Dead Sea. These agricultural households typically produce both small ruminants (sheep and goats) and cereal grains (barley and wheat). Farmers’ choices for both livestock and crops are often influenced by the harsh arid climate of the region and the absence of sufficient water for irrigation. Rainfall is highly variable, averaging 330 mm annually, though high and low quantities calculated from 1980 to 2010 were 640 and 120 mm, respectively.

In addition to the limited annual rainfall, the seasonal distribution of rain is also unpredictable, posing further challenges for crop production decisions. Since planting usually follows the onset of the winter rains, the beginning of the rainy season effectively defines the growing season. Some farmers may choose to plant prior to the coming of the rains to extend the season. This, however, runs the risk of seeds failing to germinate due to the lack of soil moisture.

While livestock performance is usually less affected by weather outcomes than crops, in an integrated production system, livestock production choices are indirectly influenced by the availability of feed throughout the year. Because crop production is one source of livestock feed, the timing and quantity of harvest directly affects livestock related decisions (i.e., breeding herd expansion or contraction, as well as the timing of sales for the lambs not needed to maintain the herd).

Farmers in the region are smallholder agricultural households that are often financially constrained, and some of their decisions are either determined by limiting their financial exposure to losses during dry years or responding to liquidity constraints to meet household expenses. By evaluating decisions in an integrated, financially constrained agricultural system that allows for responses to random events as they unfold, this research aims to analyze the influence of these factors on household decision making and how they differ across alternative endowments of resources in the form of land and initial livestock inventory.

3 Empirical approach and modeling

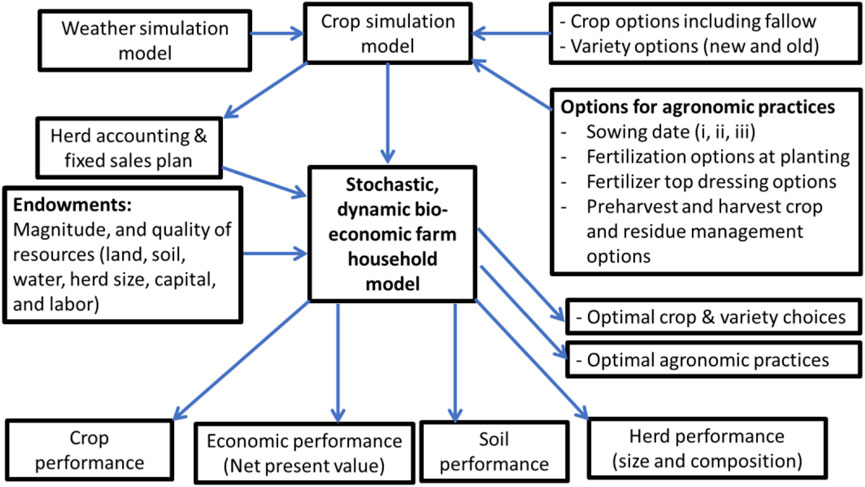
The modelling framework used in this study involved the use of a simulation-based weather model which, along with the crop and variety choices, and alternative options of various agronomic practices, was used as an input for a crop simulation model. Then, the crop simulation model, a livestock (herd size and composition) accounting scheme, and household endowments of different productive assets were used to generate data for an integrated crop-livestock production bio-economic model that includes inter-temporal constraints on liquidity, choices, and resources (Figure 1). Building on the discrete stochastic programing (DSP) method as espoused by Cocks (1968) and Rae (1971b), allows the incorporation of random variables in both the objective function and constraints of the multi-period planning problem. Because size is often a limiting factor for DSP models, a 1-year dynamic model with intra-seasonal decision is developed to optimize choices. However, to reflect the importance of maintaining soil resources to ensure the sustainability of the choices for the long term, non-linear valuations of terminal soil resource levels based on previous work (Boussios et al., 2019) are included in the objective function.

FIGURE 1

FIGURE 1. The modelling framework used in this study.

3.1 Data and simulations

Model parameters were obtained from four sources. The Agricultural Production Systems Simulator (APSIM) by Keating et al. (2003) was used to link crop production decisions to biophysical and soil resources outcomes. APSIM takes management choices as inputs to simulate crop yields and soil outcomes for alternative crops and farming practices for each simulation year characterized by weather. As an input to APSIM, daily weather was simulated for 500 crop years using the LARS-WG 5.5 model (Semenov 2010), which was calibrated based on daily data from 1980 to 2010 from Karak. We chose simulated weather data over historical data to increase the number of weather years to provide a richer distribution of weather.

Livestock is treated via a deterministic livestock-unit (LU) formulation due to the limited data for reflecting the impact of weather on animal performance. Though deterministic, livestock production is responsive to stochastic events due to the availability of feedstuffs for the animals. As opposed to overlapping livestock generation (OLG) models, which track individual animals or age cohorts over time (Upton 1993; Guimarães, Tedeschi, and Rodrigues 2009), LUs were chosen because OLG models are difficult to manage as they grow very large in a dynamic, stochastic framework.

One shortcoming of the typical LU approach is the rigidity of how sales and purchases of animals occur, as individual animals are sold on pre-specified schedules. In a financially constrained environment, this ignores some of the options available to farmers to meet liquidity needs, such as varying the timing of sales of animals not required for sustaining the herd. For a more realistic treatment of farmer’s adaptive strategies, we treat the breeding herd (and their replacement lambs) and the extra lambs not required for maintaining the herd as separate units.

Because households have unavoidable expenses throughout the year, we impose additional budget constraints and expenditures by time period that are unrelated to farming but important in household decision making. Data on these expenses were obtained from the Economic Research Forum (ERF, 2014) and further corroborated by Jordanian extension staff and through project CRP-DS led by the International Center for Agricultural Research in the Dry Areas (ICARDA).

Equations for the valuations of terminal soil attributes were formulated based on a previous study in the region (Boussios et al., 2019). The prior study optimized discrete farming decisions over an infinite time horizon. Soil attributes were valued by regressing the optimized value function of the prior study’s SDP on quadratic functional forms of the initial soil states. These functions translate the marginal values of soil attributes when the farmer optimizes decisions over an infinite time planning horizon, thus providing an approximation to the “true value” of soil attributes in a sustainable production system. This approach is discussed in more detail in Supplementary Appendix SA.

3.2 Optimization approach

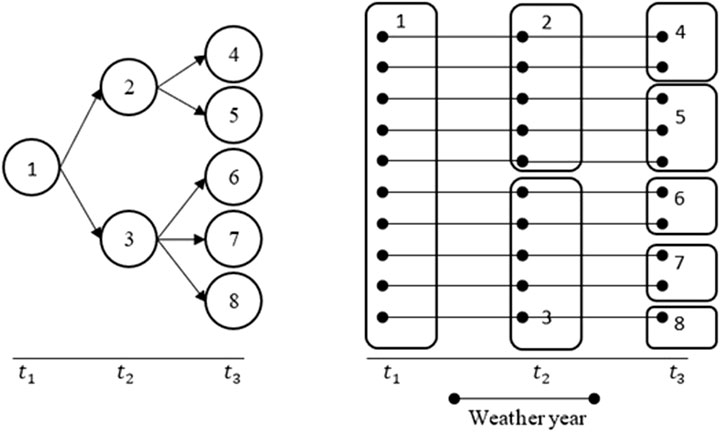
DSP optimizes decisions from a dynamic and stochastic perspective. The challenge in applying this approach to crop simulation models is that it requires approximating conditional production functions and their associated probabilities for each choice, period, and outcome of the dynamic tree. To mitigate this problem and avoid additional data processing steps, we propose the use of a “threshold method” of partitioning weather years over time based on realized stochastic outcomes. The thresholds define relationships between random variables and states. E.g., two states might be represented in terms of accumulated rainfall level at a point in time, and choices can differ depending on whether rainfall is above or below the threshold level. Any number of states could be defined for each period based on ranges for the random variable(s) and the threshold cut-offs.

Figure 2 visually contrasts two DSP approaches. The left-hand figure presents the typical stochastic process in a DSP tree (e.g., Rae, 1971a) with outcomes descending from the original decision point (1), and expanding to the second stage nodes (either 2 or 3), and finally the last stage nodes (4 through 8). Decisions are made at each point with uncertainty regarding future outcomes, but conditional on prior outcomes. Activities at each stage are conditioned on past events by indexing the states for realized random variables. “Inventory-like” constraints create linkages between previous decision variables and current period decision variables.

FIGURE 2

FIGURE 2. Decisions Tree and Threshold Partitioning Approach.

The right-hand figure shows the weather years sorted into threshold categories corresponding to the terminal nodes of the left-hand tree. Each simulated weather year is represented by a horizontal line in the figure. The stochastic variable in our application is weather because it is economically and biophysically important and exogenous to the farmers. The optimization approach indexes weather years based on meeting threshold criteria for each period. This creates indexing for each weather year in each period. For example, the highest represented weather year depicted vertically in Figure 1 is indexed by 1 in period $t_{\mathit{1}}$, 2 in $t_{\mathit{2}}$, and 4 in $t_{\mathit{3}}$; while the lowest weather year is vertically indexed 1, 3, and 8, for $t_{\mathit{1}}$, $t_{\mathit{2}}$, and $t_{\mathit{3}}$ respectively.

Identical to the DSP approach, the decisions in each period are linked to the prior choices through inventory-like constraints. The decision in any given weather year is constrained by the choices made earlier in the year and connected through the indexing of choices and states. The choices in period $t_{\mathit{2}}$ are constrained by those selected for state 1 in $t_{\mathit{1}}$. For example, if planting occurs in the first period, the second period choice for a given weather year is constrained by the decision on crop type and acreage planted from the prior period. The farmer can only choose to top-dress the crop planted in the prior period up to the area planted. Choices for all weather years within the same index are constrained to be identical. By using inequality constraints for the choices in each period, decisions for each weather year are grouped by the threshold criteria. This approach ensures the rigidity of prior choices and a dynamic process of updating information for optimizing in each period without perfect foresight.

The DSP and threshold approach are mathematically equivalent though differ in terms of how the stochastic states are defined. Instead of requiring estimation of conditional probabilities and production functions for each time period and state (e.g., Jones, Cacho, and Sinden, 2006), the threshold approach links similar weather years for optimizing production decisions in a stochastic environment. The approach can be thought of as a dynamic information system, with decisions allowed to differ across threshold categories but not within them. The advantages of this approach over the standard DSP using crop simulation models are that it does not require estimation of conditional production functions (which adds another layer of processing to the data) and provides a better representation of biophysical relationships (i.e., the data from the validated crop simulation models is used directly).

3.3 Crop production

For crop production, the household chooses when and what to plant, how much fertilizer to apply at planting, whether to top-dress additional fertilizer after planting, and whether to let livestock graze the field early or harvest the crop at maturity. Planting can occur at any of three points in time: at the beginning of December, January, and February. The farmer selects the optimal planting period conditional on realized weather to date. The farmer can plant barley (mid-maturing Rum or late-maturing Steptoe), wheat (early-mid maturing composite variety), or fallow in each period. Three levels (0, 50, or 100 kg/ha) of diammonium phosphate (DAP) may be applied at planting.

Following planting, 40 kg/ha of Urea fertilizer may optionally be applied as top-dressing 2 months after planting. The decision to top-dress is made conditional on prior outcomes and decisions. Farmers often avoid this second application of fertilizer when the crop is not developing well due to inadequate rainfall to limit losses in poor weather years.

In other similar areas with relatively higher rainfall, green stage grazing is practiced with anticipation of normal harvest at the end of the season. Owing to the low rainfall in the study area, farmers may let livestock graze the crop prior to maturity but do not harvest afterward. This option can still be optimal if the prospect of good grain harvest is low and liquidity constraints prevent purchasing feed for the livestock herd.

At crop maturity, yields and end-of-year soil attributes are known, and the farmer harvests the grain mechanically, separating the grain from the straw and allowing the farmer to market the grain or feed it on farm. Additionally, the residual straw can be “stored” in the field for later feeding to livestock. While manual harvesting is also observed in Karak, the mechanical method was chosen for this model, because it is the preferred method due to substantial savings in labor and threshing equipment rental costs. When farmers sell their crops, they incur transaction costs which reduce the value of their production. To reflect these market inefficiencies the price for barley (wheat) grain is 65% (80%), and straw is 80% (67%) of the market purchase price.

While planting choices in each period are driven primarily by the distributions of financial returns of the enterprises, the model also optimizes for the values of terminal soil properties. The soil attributes valued are Extractable Soil Water (ESW; mm), Nitrates (NO₃; kg/ha), and Soil Organic Matter (SOM; kg/ha). The terminal values for soil attributes are functions of the levels of the attributes. We estimate the value functions as quadratic relationships that are increasing at a decreasing rate (Supplementary Appendix SA). Including a terminal valuation is in contrast to the typical approaches of: fixed terminal constraint levels (Tessema et al., 2015), which imposes the ending levels of soil attributes regardless of marginal cost/benefits; omitting it (Maatman, et al., 2002) leading to potentially extractive solutions; or the use of theoretically unjustified tradeoff functions that require strong assumptions about multi-attribute utility functions (Van Kooten, Weisensel, and Chinthammit 1990).

3.4 Livestock production

Livestock production is categorized into two sections, the LUs and culling lamb units. While livestock production is not treated directly as stochastic, animal populations can vary by state of nature due to the availability of feed produced. The composition of a LU in this model is a single breeding ram, 25 milking ewes, and replacement lambs (both male and female) required to have a steady-state self-replacing herd, accounting for deaths, reproductive fertility, and animal growth (see, e.g., Upton, 1993). There are three alternative feeding rate choices for the ewes within the LUs that target milk production levels (1, 1.5, 2 L per ewe per day). Feed levels required for these production rates are included in the Supplementary Appendix SB. The optimal feeding rate for the LUs is chosen for the entire year due to a lack of data regarding the impact of fluctuating feeding rates on productivity.

For a given feeding regime, inputs and outputs of the LUs are defined in aggregate. Maintenance costs of a LU are calculated by summing the feed requirements across all animals within the unit.¹ In addition to the grain they produce for feeding livestock, farmers have the option of purchasing wheat and barley at the market rate. They also have an opportunity to purchase a fixed amount of barley per sheep owned at a subsidized government rate. Subsidized prices are 30% and 90% of the market prices for barley grain and straw, respectively. Monthly revenues associated with the LUs are from milk and the culling of mature animals. Following the breeding season, rams over 8 years are sold, as are ewes that did not achieve pregnancy. Likewise, ewes that exceed the milking age are sold. Values of the LUs change each period reflecting the changing composition of the herd within the year due to births and growth of replacement animals, as well as mortality and sales of animals. To account for the transaction costs of changing the herd size, the price to purchase additional LUs is 10% higher than the sales price in all periods. Markets for animals are generally small and informal, and transaction costs are expected to be accordingly substantial.

From the breeding unit, a fixed proportion of “cull lambs” are born from October to February conditional on the number of LUs owned. Cull lambs are tracked separately from the other lambs in the herd because they are not required for maintaining the herd size. This allows the farmer flexibility in the timing of lamb sales, not possible with modeling livestock through only LUs. Flexibility is crucial under scenarios with binding liquidity constraints. Cull lambs are tracked by birth month to enable accurate modeling of their weight gain and feed consumption as a function of their age. Five different target growth feeding rates are available for each group of cull lambs (0, 25, 50, 100, and 150 g of weight gain per day).

The livestock units serve the household primarily as a means of production, but they also serve as a form of savings (Rosen et al., 1993), especially in developing economies (Fafchamps et al., 1998). Farmers incur maintenance costs for the livestock units in anticipation of income from the sales of milk, culled lambs, and old animals. They also serve as a means for storing wealth that increases in value from the growth of juvenile units. The advantage of storing value in the herd rather than holding cash is that the herd increases in value due to animal growth, whereas cash does not grow. To the extent that the farmer prefers at least some minimum amount of liquidity (for goods purchases or investments outside the model scope), the results may overstate the optimal herd size. We reduce the impact of this limited view of the investment opportunities by expressing wealth at the end of the year in cash terms.

3.5 Household decisions and temporal model structure

Household budget and expenditure constraints are included to reflect a typical household in the region. These include monthly expenditures and seasonal costs, such as schooling. Borrowing or cash loans are also available to manage liquidity. A fee is associated with borrowing.² Data used for calculating the steady-state LU, including nutrient contents of feedstuffs, mortality rates, feeding requirements, animal prices, and the resulting herd distribution are displayed in Supplementary Appendix SB.

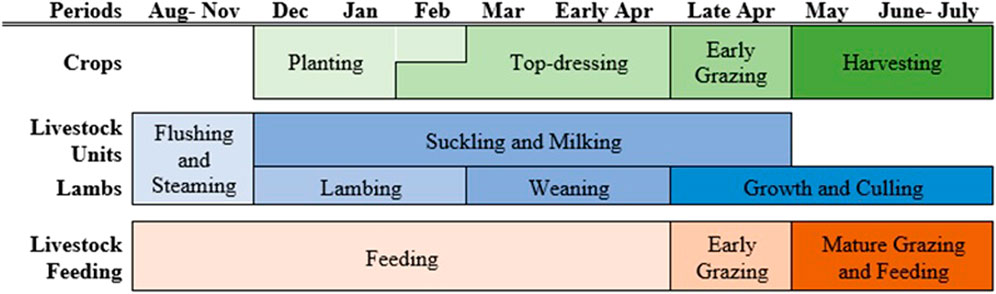
Figure 3 visually depicts the timeline, overlap, and simultaneity of crop and livestock management decisions in the model. These activities are modeled across nine time periods corresponding to important production decisions. December through May correspond to realizations of stochastic weather outcomes affecting crop production decisions. Livestock feeding decisions are made in the first period, for the LUs and each period new lambs are born. The farmer is faced with meeting the nutrient requirements of the animals given the growth and milk production targets selected in the first period. The only adaptive response in terms of livestock feeding is to increase or decrease the size of the herd. The timing of planting and top-dressing varies by the weather realizations and the optimal crop choices of the farmer. The livestock management decisions respond to the weather realizations through changes in the herd, the timing of lamb culling, and the choice of whether to graze early.

FIGURE 3

FIGURE 3. The timimg of decisions of the integrated household.

3.6 Stochastic processes based on simulation modeling

Rather than using the simulation models to generate datasets to enable estimation of many conditional production functions, we use the weather years and weather threshold events to define the stochastic process for crop outcomes for alternative management choices. As depicted in Figure 1, indices are used to partition the weather years into groups over time with the number of states/weather-year-groups in each period expanding. Based on discussions with farmers and extension agents in Jordan, we selected accumulated rainfall at each decision point as the partitioning variable for defining the stochastic process. The use of the timing and accumulation of rainfall as a trigger for most farming decisions in the model is based on the production system being rain fed, thus dictating most of the farmer’s decisions.

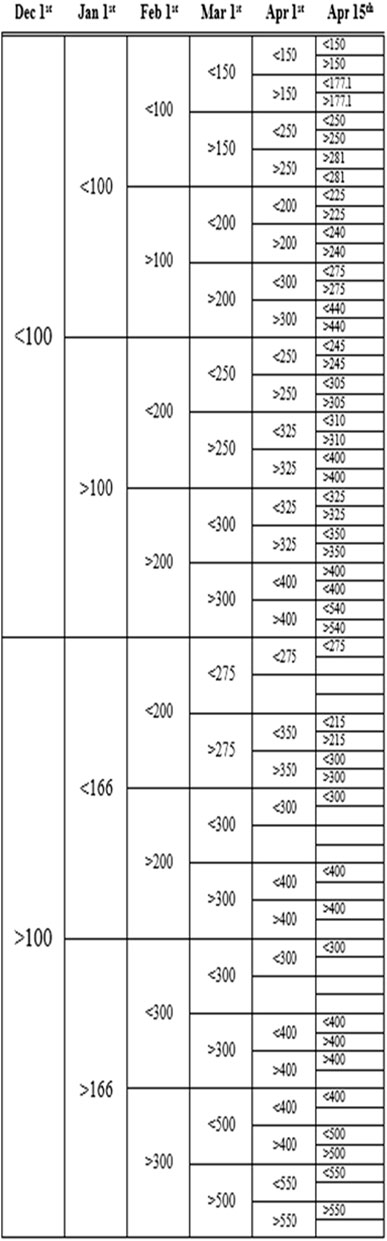
Figure 4 presents the threshold levels used for partitioning the weather years in each period. Stochastic outcomes are realized in periods 2 (Dec.) through 8 (May). The final stochastic states are not depicted in the figure because they are represented by each of the 500 crop years. Once yields are realized, all other outcomes are also known. The threshold levels for each period were selected based on a combination of extension advice and a desire to balance the number of weather years in each state.

FIGURE 4

FIGURE 4. Accumulated rainfall threshold levels for partitioning weather years.

While the threshold DSP models the stochastic process differently from a traditional DSP formulation, the advantage is that it allows direct use of the results from the weather/crop simulations. Operationally, the database of weather, simulated yield, and soil attribute realizations is used to construct the outcomes for each conditional management choice for each weather year, allowing the optimal management strategy to be identified.

3.7 Model formulation

For ease of exposition, we start with a deterministic, multi-period formulation in the first subsection. In the second subsection, the simulation data is introduced along with the framework and notation for “grouping” realizations based on similarities between random outcomes up to some point in the model time horizon. In a third subsection, the deterministic formulation is generalized to the stochastic case.

3.7.1 Deterministic multi-period model

We consider a general, finite horizon, multi-period planning problem in the non-stochastic case. The formulation is:

$\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}u\left[{\sum }_{t=1}^T{f}_t\left(x_t\right)\right](1)$

Subject to:

$A_t{x}_t\le b_{t}t=1,...,T(2)$

$B_{t+1}{x}_t+D_{t+1}{x}_{t+1}\le d_{t}t=1,...,T-1(3)$

$x_t\ge 0t=1,...,T(4)$

where the notation is defined as follows:

∑ – summation operator

$t$ – index of time periods ($t=1,...,T$);

$x_t$ – vector of decision variables at time $t$;

$f_t\left(x_t\right)$ – current period benefit of decision $x_t$

$u\left[\right]$ – function of the sum of current benefits yielding the overall objective;

$A_t$ – matrix of constraint coefficients representing resource utilization per unit of activity $x_t$ in period $t$;

$b_t$ – vector of constraint right-hand sides representing resource availability in period $t$;

$B_{t+1}$ – matrix of constraint coefficients defining the linking relationships between activity $x_t$ in period $t$ and activity $x_{t+1}$ in period $t+1$;

$D_{t+1}$ – matrix of constraint coefficients defining the linking relationships between activity $x_{t+1}$ in period $t+1$ and activity $x_t$ in period $t$, where x_t+1 is conditional on actual realization of x_t, while x_t is conditional on E (x_t+1) where E is the expectation operator; and

$d_t$ – vector of constraint right-hand sides defining the linking relationships between activity $x_t$ in period $t$ and activity $x_{t+1}$ in period $t+1$.

The objective defined in (1) is sufficiently general to accommodate discounting for the time value of money through $f_t\left(x_t\right)$ and terminal values of resources through $f_T\left(x_T\right)$, as well as a utility function, $u\left[\right]$, to reflect goals more general than profit maximization. The latter will be more important when the formulation becomes stochastic.

The restrictions in (2) allow for constraints on resource use as well as other limitations needed to reflect the producer’s choices. The restrictions in (3) enforce relationships between choices from the current period and the next period, allowing for management of inventories of resources as well as work in process (i.e., growing crops or livestock) and products. The relationships in (2) and (3) are expressed in linear form, but in general nonlinear relationships could be accommodated, although computation would become more challenging. Finally, the non-negativity conditions in (4) are typically needed for proper interpretation of the variable values (i.e., negative values might not make physical or economic sense).

3.7.2 Simulation-based random outcomes

A wide variety of flexible models for simulation of weather (Maher and Earnshaw, 2022), crop growth (e.g., Berre et al., 2015), and livestock growth (Teleken et al., 2017; Niloofar et al., 2020) have been developed and validation procedures have been established. In general, these growth models can determine the inputs and yields per unit (typically of land area) for a given biological organism and set of production practices. Often these models take the weather as inputs, and by feeding the outputs of a weather simulator directly to the growth model(s), outcomes in terms of inputs and outputs can be established.

Each simulation run will be called a “draw” in the Monte Carlo simulation sense. The following notation is used to refer to the random variables and groupings of simulation draws. Let $i$ denote the index for draws and let ${\beta }_i$ denote the vector of all random variables involved in the $i-\mathrm{t}\mathrm{h}$ draw. Let $I=\left\{\mathit{1},...,N\right\}$denote the set of all draws and I_j(t) is a subset of I(t) where I_j(t) = $\left\{\mathit{1},...,n\right\}$ and I(t) = {1, … ,R}, where n<R<N and the union of I_j over all the j groupings in period t is I(t) and the union of I(t) over all time periods t is the whole set I. This means that, for each time period $t$, every draw $i$ in $I$belongs to exactly one grouping I_j(t). The grouping I_j(t) is defined by common features of the random variables that have been realized before time period $t$. Which grouping draw $i$ belongs to in period $t$ is indicated by the operator I_j(t). In addition to partitioning the draws within each period, these subsets also satisfy a relationship across periods. Specifically, each grouping in time period $t$ is sub-partitioned into groupings in period $t+1$. To make this concept precise, it is helpful to define an operator $c\left(i,t\right)$ that indicates the child grouping, or subset of draws, in period $t+1$ of which draw $i$ is a member. This means that $i$ is in I_j(c(i,t), t+1). Then the sub-partition satisfies the following property – the union across $i$ in I_j(t) of I_j(c(I,t), t+1) is equal to I_j(t).

For example, if achieving 100 mm of rainfall from time period 1 to time period 2 is deemed to be a critical event, then there might be two groupings of the draws in period 2 with I₁(2) containing all of the draws that achieve 100 mm rainfall by time period 2 and I₂(2) containing all of the draws that do not achieve 100 mm rainfall by time period 2. To extend our example, consider the case where the period by which 100 mm rainfall has accumulated is important for decision making. The groupings I₁(2) and I₂(2) are as before. For period 3, regardless of additional accumulation the draws in I₁(2) have achieved the rainfall threshold, and so, the same grouping is maintained for period 3—I₁(3) contains the same subset of draws as I₁(2). However, I₂(2), with members that did not achieve 100 mm rainfall by period 2, is further partitioned into the draws that achieve 100 mm rainfall by period 3, I₂(3), and those that do not achieve the threshold, I₃(3).

Note that the components of vector${\beta }_i$ are realized over time, e.g., rainfall occurring up to each time period $t$. For the formulation in the next section, it is useful to be able to denote the subsets of random variables that have been realized up to period $t$, which we write as ${\beta }_i^t$. In our example, the components of ${\beta }_i$ would include rainfall accumulation by period 2, rainfall accumulation by period 3, etc. The sub-vector ${\beta }_i^2$ would contain rainfall accumulation through period 2, but not through period 3, while the sub-vector ${\beta }_i^3$ would contain all accumulated rainfall quantities from period1 through period 3.

3.7.3 Stochastic multi-period model

Given the notation described in the previous section, it is now straightforward to formulate the stochastic model:

$\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}{\displaystyle \sum }_{i=1}^n{p}_{i}u\left[{\sum }_{t=1}^T{f}_{ti}\left(x_{ti}\right)\right](5)$

Subject to:

$A_{ti}{x}_{ti}\le b_{ti}t=1,...,T;i=1,...,n(6)$

$B_{t+1,i}{x}_{ti}+D_{t+1,i}{x}_{t+1,i}\le d_{ti}t=1,...,T-1;i=1,...,n(7)$

$x_{ti}={\sum }_{i\in s\left(m\left(i,t\right),t\right)}{x}_{ti}t=1,...,T;i=1,...,n(8)$

$x_{t,i}\ge 0t=1,...,T;i=1,...,n(9)$

where the notation is defined as follows:

$x_{ti}$ – vector of decision variables at time $t$ for draw $i$;

$f_{ti}\left(x_{ti}\right)$ – current period benefit of decision $x_{ti}$ where this benefit may depend on draw $i$;

$u\left[\right]$ – function of the sum of current benefits yielding the overall objective;

$p_i$ – is the probability of draw $i$ (typically $\mathit{1}/\left(n-t\right)$) indicating that the uncertainty about rainfall accumulation reduces as time passes by as we will be drawing from fewer possibilities;

$A_{ti}$ – matrix of constraint coefficients representing resource utilization per unit of activity $x_t$ in period $t$, where the draw subscript $i$ indicates dependence of the coefficients on the random outcomes that have been realized up to period $t$, ${\beta }_i^t$;

$b_{ti}$ – vector of constraint right-hand sides representing resource availability in period $t$, where the draw subscript $i$ indicates dependence of the coefficients on ${\beta }_i^t$;

$B_{t+1,i}$ – matrix of constraint coefficients defining the linking relationships between activity $x_t$ in period $t$ and activity $x_{t+1}$ in period $t+1$, where the draw subscript $i$ indicates dependence of the coefficients on ${\beta }_i^t$;

$D_{t+1,i}$ – matrix of constraint coefficients defining the linking relationships between activity $x_{t+1}$ in period $t+1$ and activity $x_t$ in period $t$, where the draw subscript $i$ indicates dependence of the coefficients on ${\beta }_i^t$; and

$d_{ti}$ – vector of constraint right-hand sides defining the linking relationships between activity $x_t$ in period $t$ and activity $x_{t+1}$ in period $t+1$, where the draw subscript $i$ indicates dependence of the coefficients on ${\beta }_i^t$.

The objective defined in (5) is now an expected value of the function of the sum of current benefits, that is, the sum of the probabilities of the outcomes specified by draw $i$times the function of the sum of the current benefits that are conditional on the outcomes specified by draw $i$. The constraints in (6)–(7) and (9) are interpreted as they were in (2)–(4) in the deterministic formulation, except that they are now treated as the constraints, conditional on the outcomes specified by draw $i$. The constraints in (8) specify that while the variables $x_{ti}$ are indexed by draw $i$, they are constrained to have identical values across each sub-partition in time period $t$. This effectively prevents the optimization solution from exploiting knowledge of the outcome of draw $i$ beyond knowledge of which sub-partition $i$ belongs to in choosing the level of $x_{ti}$.

While this formulation will generally be quite large when the number of simulation draws, $n$, is large, it avoids the steps of approximating conditional distributions and estimating relationships between random variables and outcomes of interest. Thus, the process of incorporating simulation data into the DSP framework is simplified in a way that should be relatively straightforward to automate. In the next section, we apply this framework to model rain fed agricultural management for smallholder farmers in Jordan.

3.7.4 Inputs for the base model

The model is applied to a representative agricultural farming household in Karak, Jordan. In the base model, the household owns 2 ha of land and 2 livestock units. The household is endowed with 2,000 Jordanian Dinars (JD) of initial financial capital to be used for agricultural production and household expenditures and has obligations for 4,784 JD in household expenditures spread across the year.³ The exogenous household expenditure figure is based on the average annual expenditures for a farming household in Karak, calculated from a survey by Economic Research Forum and the Department of Statistics of The Hashemite Kingdom of Jordan in 2013 (ERF, 2014). This expenditure was seasonally adjusted through consultation with farmers and extension agents to account for differences in spending throughout the year and to line up with the model time periods. The household can borrow up to 3,000 JD, which must be paid back by the end of the year including fees.

4 Results

We begin by presenting the results for a base scenario where understanding the results of a risk-neutral agent is a logical first step, and that the model could easily be modified to reflect a risk-averse agent a la von Neumann and Morgenstern (Featherstone et al., 1993). To this effect, all scenario simulations are carried under the assumption of risk neutrality. Sensitivity analysis is used to assess the impact of alternative endowments of cropland area and size of the initial sheep herd (measured in LUs). The base model includes the valuation of the end of year stocks of soil attributes. To assess the implications of this modeling addition, results are also determined without inclusion of these terminal values. Scenarios that varied risk aversion and initial soil conditions were also tested but not presented here. While these scenarios provide greater information, the differences in results across scenarios were limited and did not change the results in a significant way.

For the base model, the representative farmer begins the production year in period 1 (Aug. To Nov.). They use their initial cash holdings and 2,426JD of their 3,000JD borrowing limit to purchase feed for current consumption and storage. In addition, they sell 0.007 LUs in period 1. The farmer chooses target milk production (i.e., the feeding program) for the milking ewes and growth targets for the lambs, selecting both to be at the highest production level. These levels are 2 L of milk per head per day for the milking ewes and daily growth rates of 150 g per day for the cull lambs. The farmer is locked into this feeding regime for the entire year and can only change herd size thereafter. In December (the second decision period), the farm household chooses to plant all owned land to Rum barley with 100 kg/ha of diammonium phosphate (DAP), regardless of the level of rainfall. While this planting strategy is uniform across realized weather, it is selected because it produces the highest expected biomass, which can be used for feeding livestock. This strategy is optimal even though planting in December bears some risk related to poor germination.⁴ Since fertilizer is also a significant contributor to the growth of biomass, the highest application rate is selected by the farmer. The decision to use the highest feeding rate for December born cull lambs (150 g of weight gain per day) is also selected. As all the available land is planted in December, results show the remaining choices in the third period (January) are limited to feeding the livestock owned and selecting a feeding rate for the January born lambs (also 150 g per day). While the option exists, no lambs are sold in any stochastic state during this period.

In the fourth period (February), the barley that germinated is top-dressed with 40 kg/ha of Urea regardless of the January or February weather realization. While weather information has been revealed and tightens the conditional distribution of yields, it remains optimal to top-dress the crop because yields are substantially higher with the additional nitrogen application (97% higher levels on average). After the births of all lambs, in periods 5 (March) and 6 (April 1st to 14th), the household uses the earnings from milk production to increase the livestock units from 2.0 to 2.17 through purchases in all states/weather years.

The decisions begin to vary across the stochastic states in period 7 (April 15th to 30th) due to the tighter conditional distributions of outcomes where the farmer expects only a limited number of possible outcomes from a given state once period 7 is reached. The farmer can choose to graze the barley prior to maturity to reduce short-term liquidity constraints caused by the feeding of livestock, though this comes at the expense of future crop growth and potential to harvest the grain. In years with good weather and hence higher biomass production levels, farmers respond by purchasing additional LUs, with purchases of up to 0.07 LUs. The farmer also early grazes up to 23% of total area planted to barley. There is a high negative correlation between the amount of early grazing and purchases of additional LUs. The farmer can graze less land to meet the livestock needs when production is high, allowing the farmer to also purchase more LUs.

In the eighth period (May), yield levels are realized for all crop years, and decisions/outcomes vary substantially by state. Harvesting is undertaken, then grain is sold or stored on farm. Crop residues remaining after harvest are “stored” in the field for current and future grazing. Cull lambs born in November and December are sold in period eight at various rates across the stochastic states. All the November-born lambs that are culled are sold across all states (except for one bad production year where only 40% are sold). December lambs are sold slightly less frequently with sales of all lambs in 484 out of 500 states. In three low rainfall states, only some December lambs are sold, and in the other 13 states, none are sold. The choice to sell lambs is a reaction to feed shortages. In years of low production, it is more cost effective to hold lambs longer to gain weight than to purchase more LUs. Differences in feed efficiency make the sales of larger November-born lambs more profitable than sales of December-born lambs. Sales of excess grain and culled lambs allow the farmer to repay loans and fees and/or purchase more LUs. Purchases of additional LUs in May reach up to 0.306, conditional on the amount of grain and biomass produced, with higher production levels allowing the purchase of more LUs.

The quantities of grain and straw produced are key for determining whether it is better to hold lambs versus purchase additional LUs. Those states that keep December-born lambs are characterized by either a crop that failed to germinate or low biomass production. This is because the trade-off for the farmer is either to keep lambs and allow them to grow (which is cost effective in the short-run) or sell the lambs and use the revenue generated to proportionally increase the number of LUs (which is beneficial for the long-run). When grain yields are high, the farmer can better afford to feed the LUs, which consume more feed. However, when the yields are low, they only have enough money or grain to feed lambs.

In the final period (June through July), all cull lambs are sold, and the proceeds net of loan repayments are treated as net returns to farming. Since yields are realized in the prior period, there are no stochastic variables remaining, making the final period deterministic. In years when the crop fails to germinate, farmers must sell part of their herd to repay loans and meet household living expenses. In the final period, no livestock are purchased since LU values are made equivalent to cash, though still incur feeding costs. Thus, if purchase of LUs was profitable following the realization of yield, then it is done in the preceding period to obtain the benefit from lamb growth. Net farm returns above the starting endowments and net of household expenditures show monetary valued net returns ranging from negative 1,890 JD to positive 1,795 JD, with an average of 1,144 JD. Negative net returns are infrequent, occurring only 2.8% of the time, and are mostly due to the failure of the crop to germinate after planting.

4.1 Sensitivity of results to resource endowments

Within Karak, household livestock ownership as well as cropland area vary significantly, and hence understanding the impact of these endowments on management choices is necessary for understanding the

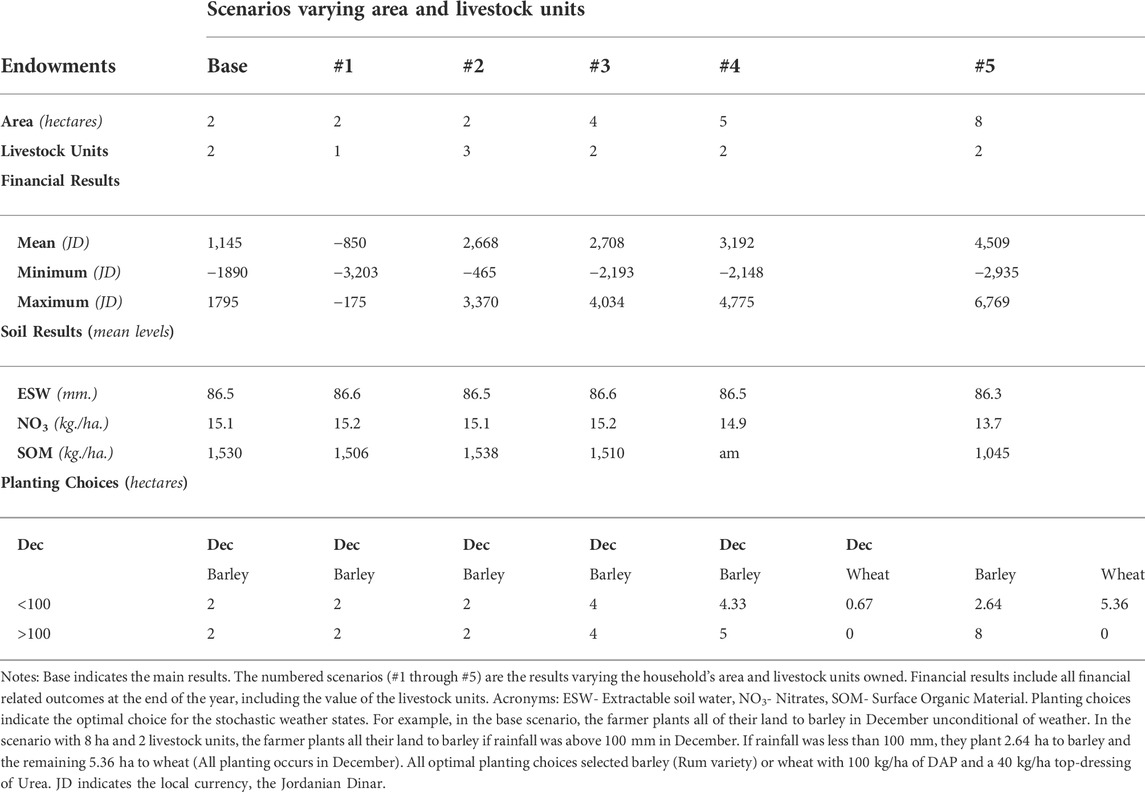
Heterogeneity of responses across farms. The results for heterogeneous farm endowments are examined by considering five scenarios relative to the base scenario: (#1) reduce the initial number of LUs to one, (#2) increase the initial LUs to three (#3) double the land holdings, (#4) increase land to 5 ha, and (#5) increase land to 8 ha.

The results of these five scenarios are summarized in Table 1, focusing on three main outcomes: the distribution of financial net returns (which includes the valuation of the livestock at the end of the model horizon), ending soil attributes, and the allocation of land across planting dates. Not surprisingly, the financial returns vary significantly by farm size, as both crops and livestock are profitable on average. Planting choices are similar across scenarios, where it is always optimal to plant the Rum barley variety with maximum fertilizer levels. Only when total land owned reaches 5 ha or more does the planting date change to a conditional strategy. In this scenario, using heterogeneous conditional planting dates results in higher average incomes and higher soil quality. The average terminal value of soil resources is 6.2% higher in scenario #5 than in the base.

TABLE 1

TABLE 1. Results from base soil, varying land and livestock unites.

Planting choices across all endowment levels are similar - highlighting noteworthy features of the system and the household’s optimal choices. Recall, the model requires a fixed level of exogenous non-farm expenditure per period for such needs as food and goods/services. Negative values would require the household to cut back on their non-farm expenditures or reduce the end-period number of LUs. Livestock production is the main contributor to farm profits even in low production years because of the availability of subsidized feed for portions of the livestock’s rations. Due to the low input costs of producing cereal grains and straw, as well as the substantial difference in buying and selling prices, the typical farmer’s strategy is initially to provide feed for livestock and then sell any excess grain for profit.

The scenarios with the highest ratio of land to LUs, and thus the least pressure to produce feed per hectare of land, have the highest variability in planting date. Planting late removes the risk of crops failing to germinate while increasing the expected production of grain relative to straw. Once the feed needs of livestock have been met, the farmer chooses to focus on producing grain to be sold in the market, as well as conserving soil resources. Delaying planting allows greater retention of valuable NO₃ as it is not lost to straw production. While ESW is lower with more flexible planting, SOM is even lower. This result is optimal due to the relatively small valuations of ESW, and SOM compared to NO₃.

4.2 Sensitivity to terminal soil valuations

Past research often either omits the valuation of terminal soil attributes or places arbitrary bounds on the final levels. By including terminal value functions for soil attribute levels in the objective function, the approach here allows the optimization to capture the trade-offs between current income and the future productive potential of the soil. Results without terminal soil valuations are presented in Table 2.

TABLE 2

TABLE 2. Model results with zero terminal soil valuations.

Cropping and livestock strategies are similar with and without the terminal soil valuations, although they differ when land area increases. The optimal choices remain to plant the Rum barley variety with the highest fertilizer levels across the first three scenarios. As area increases above 5 ha, wheat is also introduced and planted in December. When the household has the greatest flexibility in choice provided by larger endowments of land, the results show optimal planting remains in December but partially switches land from barley to wheat. Without considering final soil resource levels, the optimizing farmer can extract nearly 10% more short-run income in scenario #5 relative to the case with terminal valuations. This difference in income comes at the cost of lower ending NO₃ levels in the soil (13.7 versus 17.4 kg/ha). While the results with and without terminal soil valuations indicate limited flexibility with production choices when the household is endowed with fewer resources, they signal the importance of not setting arbitrary constraints on the farm’s production decisions.

4 Discussions

Planting time is one of the major decisions in drylands. In this study, we conditioned planting decisions on the accumulation of 100 mm rainfall, which may happen late depending on the timing of onset and distribution of rainfall. Our results show that planting all available farmland in December (the second decision period) to Rum barley variety with 100 kg/ha of diammonium phosphate (DAP), regardless of the level of rainfall, is optimal for the farmer. While planting late reduces the probability of crop loss and fertilizer (at least that which is used for top dressing), it also carries the risk of lower yields as seeds may fail to germinate, and even if they germinate, crops are left with shorter growing periods. Studies carried in neighboring Syria showed that the introduction of zero-tillage (ZT) can help farmers to plant early into residual moisture and to conserve soil moisture during the growing season (Piggin et al., 2015), which also helps in boosting productivity, reducing cost, and hence generating higher income in the dryland conditions (El-shater et al., 2016). In a study carried in Karak region of Jordan, Akroush et al. (2015), also demonstrated that ZT carries economic benefits for the Jordanian farmers. Yigezu et al. (2021) also documented that ZT leads to higher yield and gross margins in the drylands of Morocco which are also characterized with mixed crop-livestock production systems—indicating that introduction of ZT may go a long way in improving the condition of the farmers in Karak by providing a possible solution to the problem of late planting which is necessitated by the delay of early rains.

Our study considered several weather scenarios along with variations of farmers’ financial and soil endowments that result in different herd sizes, financial returns, soil values, and cash holdings. While it is possible to look at the results from each combination of scenario simulations and draw important lessons as presented in the results section, what is true across all endowment levels and prior conditions is that drought makes farmers worse off. Sensitivity analysis showed that farmers with better endowments of land, financial capital, and starting herd size are in a better position to make optimal decisions that lead to higher returns and better soil attributes. In their study carried in a similar agro-ecology in Tunisia, Jendoubi et al. (2020) concluded that farmers in the low-livelihoods and high-livelihoods categories make production choices which degrade the land. They argue that the decisions of the farmers in the high-livelihoods category are driven mainly by financial gains while that of those in the low-livelihoods are driven by immediate constraints of their livelihoods and subsistence than the medium and long-term sustainable land management. Compared to the other two groups, their study found that farmers in the medium-livelihoods assets category have the best perceptions and flexibility for sustainable land management compared to the other two categories. It is however not clear which livelihood category in Tunisia would the Jordanian “higher resource base” group be comparable with.

Assessment of the Jordanian government’s policy objectives, i.e., whether they want to reduce financial risk, increase financial well-being, lower soil degradation, maintain/improve soil qualities, some combination of all of these, or others, and analysis of their policy response options along with their outcomes is beyond the scope of this study. The analysis of producers’ ensuing responses to policy presents an array of challenges and complexity that require targeted modelling that involves including the policy makers’ objectives and constraints into the model which is not done in this study. However, we examined some of these tradeoffs implicitly with the endowments but only to provide conditional policy responses to producer outcomes. With this caveat, our results show that increasing farmers’ liquidity increases farmers expected income and improves soil attributes. We would not, however, know which policy and institutional options for expanding farmers’ resource base will be effective in brining about improved socio-economic and ecological outcomes. Identifying such options, determining their impacts, and if they are worth the investment, however, will require targeted policy analysis in the future.

5 Conclusion

Microeconomic theory suggests that farmers have the incentives to extract and build wealth from a finite resource base in a dynamic stochastic environment. This is a long-term view implying that decisions are not strictly based on short-run financial outcomes but also on the effect of choices on resource levels, and hence future earning capacity. The interactions of the biological processes of agriculture and the stochastics of weather require modeling approaches that include the long term perspectives, as well as the conditional responses of farming choices to the realization of stochastic events. Economic models which do not account for the interactions of choices and biological outcomes misrepresent the system.

By creating a model with biophysical simulations and dynamic stochastic optimization that values future soil conditions, this research was able to better understand the challenges of the integrated cereal-livestock producing household in Karak, Jordan. By modeling the integrated household and resulting soil conditions of choices, the results highlight key features of the system. The results of the base case showed farmers choices are constrained in their decisions by the needs to feed livestock and provide income to their household. Especially the financial needs during the cropping season limit farmers’ ability to wait until the crop is fully matured before they harvest and/or graze their livestock. As livestock provide a large source of income to households, much of the efforts of the farmer are intended to reduce the costs of maintaining sheep through producing their own feed due to high transaction costs of purchases. Farmers select the planting choices that provide the highest biomass yields in order to feed their livestock. Additionally, due to the constraints on their finances, farmers choose to graze the crop prior to maturity to reduce this burden, however detrimental effect this decision may have on future yields. The impacts of transaction costs on feed purchases and the need to feed livestock from a limited amount of land define much of this system where these impacts reduce many of the options available to the farmer.

For sensitivity analysis, we varied the dimensions of household endowments of land and livestock. The results of these tests further highlight the importance of the amount of land owned relative to the number of sheep reared. Many decisions of the household are similar across endowment levels, especially planting date. However, when area is increased relative to the number of livestock, the constraints on ensuring cheap feed for livestock are relaxed, and farmers shift planting strategies toward producing crops for sales, as well as maintaining the soil resource base.

The results of the model without terminal conditions on soil, show while much of the planting decisions are influenced by the need to cheaply feed livestock, when area is increased, the timing of planting decisions and resulting soil conditions are also influenced. The limited difference of planting choices when the household endowments are constrained toward ensuring feed availability shows that the system is potentially extractive of soil resources if farmers are constrained by land area. Farmers must endure that family needs are met each year, therefore can adjust adopting less extractive production methods only when land size is not limiting.

A key limitation of this study is that the bio-economic farm household model developed here for decision analysis does not include the objectives and constraints of the policy makers—there by making it difficult to draw policy implications. For this reason, targeted policy analysis will be needed in the future to test the efficacy of one or a combination of different interventions including land consolidation, establishment of producer and marketing cooperatives, access to financial services including agricultural credit to meet urgent financial needs of the households during the cropping season and insurance to buffer the risk in case of crop failure in expanding the resource base of farmers, inducing optimal farm decisions, increasing farmers’ income, improving soil properties, and ultimately enhancing the sustainability of the system.

Data availability statement

The data used in the study are included in the article/Supplementary Material, furtherinquiries can be directed to the corresponding author.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.

Author contributions

DB: data collection, data analysis, modelling, drafting the paper PP: conceptualization of the study, modelling, reviewing the paper YY: fund raising, conceptualization of the study, modelling, reviewing the paper, validation of results PD: crop simulation modelling MR: conceptualization of the study, livestock data generation, reviewing the paper MH: dairy data and scenario development, reviewing the paper JW: animal nutrition data generation, reviewing the paper AH: animal growth and breeding data, reviewing the paper YS: crop and agronomy data generation, reviewing the paper, and validation of the results.

Funding

Partial funding for this work came from the CGIAR Research Programs on Wheat (CRP-WHEAT) and Dryland Systems (CRP-DS) through the International Center for Agricultural Research in the Dry Areas (Grant Number 14044242).

Acknowledgments

The authors would also like to thank Samia Akroush, Hatem Cheikh M’hamed, Mohamed Annabi, Aden Aw-Hassan, Omar Hadi, Ayed Al-Abdallat, Jamal Abu El Enein, and Jamal Ayad for their contributions in data collection and sharing some ideas.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.986816/full#supplementary-material

Footnotes

¹Additional costs for raising the animals, such as veterinary fees or supplementary vitamins were not included because reliable data on these expenses were not available. Based on discussion with farmers in the region, it appears these expenses make up only a small fraction of total costs.

²While interest on loans is officially illegal in Jordan, banks often loan funds and are compensated for their services by charging the borrower fixed fees that vary with loan size. We approximate these fees with a rate of 0.5% per period.

³The Hashemite Kingdom of Jordan runs a fixed exchange rate with the U.S. dollar, where 1 JD is equal to approximately $1.41 USD.

⁴The simulations did not include the option to replant if germination failed. This occurred in 2.4% of all weather years. With germination failing due to lack of precipitation it is potentially likely replanting may also not be optimal given the drought conditions.

References

Ahmed, M., Hayat, R., Ahmad, M., ul-Hassan, M., Kheir, A. M. S., ul-Hassan, F., et al. (2022). Impact of climate change on dryland agricultural systems: A review of current status, potentials, and further work need. Int. J. Plant Prod. 16 (3), 341–363. doi:10.1007/s42106-022-00197-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Akroush, S., Yigezu, Y. A., and Abed Hadi, O. (2015). Profitability analysis of zero tillage among smallholder farm households in the Karak region of Jordan. ICARDA Working Paper#29. Available at: http://repo.mel.cgiar.org:8080/handle/20.500.11766/8384.

Google Scholar

Boussios, D., Preckel, P. V., Yigezu, Y. A., Dixit, P. N., Akroush, S., M'hamed, H. C., et al. (2019). Modeling producer responses with dynamic programming: A case for adaptive crop management. Agric. Econ. 50, 101–111. doi:10.1111/agec.12469

CrossRef Full Text | Google Scholar

Burt, O. R., and Allison, J. R. (1963). Farm management decisions with dynamic programming. J. Farm Econ. 45, 121–136. doi:10.2307/1235923

CrossRef Full Text | Google Scholar

Cocks, K. D. (1968). Discrete stochastic programming. Manag. Sci. 15, 72–79. doi:10.1287/mnsc.15.1.72

CrossRef Full Text | Google Scholar

Devkota, M., Singh, Y., Yigezu, Y. A., Bashour, I., Mussadek, R., and Mrabet, R. (2022). Conservation Agriculture in the drylands of the Middle East and North Africa (MENA) region: Past trend, current opportunities, challenges and future outlook. Adv. Agron. 172, 253–305. doi:10.1016/bs.agron.2021.11.001

CrossRef Full Text | Google Scholar

Djanibekov, U., and Villamor, G. B. (2017). Market-based instruments for risk-averse farmers: Rubber agroforest conservation in jambi province, Indonesia. Envir. Dev. Econ. 22 (2), 133–155. doi:10.1017/s1355770x16000310

CrossRef Full Text | Google Scholar

Dregne, H. E. (2002). Land degradation in the drylands. Arid Land Res. Manag. 16 (2), 99–132. doi:10.1080/153249802317304422

CrossRef Full Text | Google Scholar

El-Nazer, T., and McCarl, B. A. (1986). The choice of crop rotation: A modeling approach and case study. Am. J. Agric. Econ. 68, 127–136.

Google Scholar

El-Shater, T., Yigezu, Y. A., Mugera, A., Piggin, C., Haddad, A., Khalil, Y., et al. (2016). Does zero tillage improve the livelihoods of smallholder cropping farmers? J. Agric. Econ. 67 (1), 154–172. doi:10.1111/1477-9552.12133

CrossRef Full Text | Google Scholar

Emirhüseyinoğlu, G., and Ryan, S. M. (2020). Land use optimization for nutrient reduction under stochastic precipitation rates. Environ. Model. Softw. 123, 1364–8152. doi:10.1016/j.envsoft.2019.104527

CrossRef Full Text | Google Scholar

Engel, S., Palmer, C., Taschini, L., and Urech, S. (2015). Conservation payments under uncertainty. Land Econ. 91 (1), 36–56. doi:10.3368/le.91.1.36

CrossRef Full Text | Google Scholar

ERF (2014). “Harmonized household income and expenditure survey (HHIES). Economic research Forum (ERF),” in The hashemite kingdom of Jordan department of Statistics. (DOS).

Google Scholar

Fafchamps, M. (1993). Sequential labor decisions under uncertainty: An estimable household model of west-african farmers. Econometrica 61 (5), 1173–1197. doi:10.2307/2951497

CrossRef Full Text | Google Scholar

Fafchamps, M., Udry, C., and Czukas, K. (1998). Drought and saving in west Africa: Are livestock a buffer stock? J. Dev. Econ. 55 (2), 273–305. doi:10.1016/s0304-3878(98)00037-6

CrossRef Full Text | Google Scholar

Gibbons, J. M., Sparkes, D. L., Wilson, P., and Ramsden, S. J. (2005). Modelling optimal strategies for decreasing nitrate loss with variation in weather - a farm-level approach. Agric. Syst. 83 (2), 113–134. doi:10.1016/j.agsy.2004.02.010

CrossRef Full Text | Google Scholar

Goetz, S. J. (1992). A selectivity model of household food marketing behavior in sub‐saharan Africa. Am. J. Agric. Econ. 74 (2), 444–452. doi:10.2307/1242498

CrossRef Full Text | Google Scholar

Janssen, S., and van Ittersum, M. K. (2007). Assessing farm innovations and responses to policies: A review of bio-economic farm models. Agric. Syst. 94, 622–636. doi:10.1016/j.agsy.2007.03.001

CrossRef Full Text | Google Scholar

Jendoubi, D., Hossain, M. S., Giger, M., Tomićević-Dubljević, J., Ouessar, M., Liniger, H., et al. (2020). Local livelihoods and land users' perceptions of land degradation in northwest Tunisia. Environ. Dev. 33, 100507. ISSN 2211-4645. doi:10.1016/j.envdev.2020.100507

CrossRef Full Text | Google Scholar

Jones, R., Cacho, O., and Sinden, J. (2006). The importance of seasonal variability and tactical responses to risk on estimating the economic benefits of integrated weed management. Agric. Econ. 35, 245–256. doi:10.1111/j.1574-0862.2006.00159.x

CrossRef Full Text | Google Scholar

Keating, B. A., Carberry, P. S., Hammer, G. L., Probert, M. E., Robertson, M. J., Holzworth, D., et al. (2003). An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 18, 267–288. doi:10.1016/s1161-0301(02)00108-9

CrossRef Full Text | Google Scholar

Key, N., Sadoulet, E., and Janvry, A. D. (2000). Transactions costs and agricultural household supply response. Am. J. Agric. Econ. 82, 245–259. doi:10.1111/0002-9092.00022

CrossRef Full Text | Google Scholar

Maatman, A., Schweigman, C., Ruijs, A., and van Der Vlerk, M. H. (2002). Modeling farmers’ response to uncertain rainfall in Burkina Faso: A stochastic programming approach. Operations Res. 50, 399–414. doi:10.1287/opre.50.3.399.7749

CrossRef Full Text | Google Scholar

Maher, P., and Earnshaw, P. (2022). The flexible modelling framework for the met office unified model (Flex-UM, using UM 12.0 release). Geosci. Model Dev. 15, 1177–1194. doi:10.5194/gmd-15-1177-2022

CrossRef Full Text | Google Scholar

MEI@75 (2021). Agricultural technology in the Middle East: Sowing the seeds of the future. Available at: https://www.mei.edu/publications/agricultural-technology-middle-east-sowing-seeds-future.

Google Scholar

Niloofar, P., Lazarova-Molnar, S., Francis, D. P., Vulpe, A., Suciu, G., and Balanescu, M. (2020). Modeling and simulation for decision support in precision livestock farming. 2020 winter simulation conference. Orlando, FL, United States: WSC, 2601–2612. doi:10.1109/WSC48552.2020.9383975

CrossRef Full Text | Google Scholar

Piggin, C., Haddad, A., Khalil, Y., Loss, S., and Pala, M. (2015). Effects of tillage and time of sowing on bread wheat, chickpea, barley and lentil grown in rotation in rainfed systems in Syria. Field Crops Res. 173, 57–67. doi:10.1016/j.fcr.2014.12.014

CrossRef Full Text | Google Scholar

Rae, A. N. (1971a). An empirical application and evaluation of discrete stochastic programming in farm management. Am. J. Agric. Econ. 53 (4), 625–638. doi:10.2307/1237827

CrossRef Full Text | Google Scholar

Rae, A. N. (1971b). Stochastic programming, utility, and sequential decision problems in farm management. Am. J. Agric. Econ. 53 (3), 448–460. doi:10.2307/1238222

CrossRef Full Text | Google Scholar

Rosen, S., Murphy, K. M., and Scheinkman, J. A. (1993). “Cattle cycles,” in Working paper 4403 (Cambridge, MA, United States: National Bureau of Economic Research). doi:10.3386/w4403

CrossRef Full Text | Google Scholar

Rosenzweig, M. R., and Udry, C. (2014). Rainfall forecasts, weather, and wages over the agricultural production cycle. Am. Econ. Rev. 104, 278–283. doi:10.1257/aer.104.5.278

CrossRef Full Text | Google Scholar

Semenov, M. (2010). The use of multi-model ensembles from global climate models for impact assessments of climate change. Clim. Res. 41, 1–14. doi:10.3354/cr00836

CrossRef Full Text | Google Scholar

Sterk, G., Riksen, M., and Goossens, D. (2021). Dryland Degradation by wind erosion and its control. Ann. Arid Zone 41, 351–367.

Google Scholar

Taylor, A. M., Baker, T. G., and Preckel, P. V. (1993). “Applications of dynamic programming to agricultural decision problems,” in Applications of dynamic programming to agricultural decision problems. Editor C. R. Taylor (New York: CRC Press). doi:10.1201/9780429040917

CrossRef Full Text | Google Scholar

Teleken, J. T., Galvão, A. C., and Robazza, W. D. S. (2017). Comparing non-linear mathematical models to describe growth of different animals. Acta Sci. Anim. Sci. 39 (1), 73–81. doi:10.4025/actascianimsci.v39i1.31366

CrossRef Full Text | Google Scholar

Tessema, Y., Asafu-Adjaye, J., Rodriguez, D., Mallawaarachchi, T., and Shiferaw, B. (2015). A bio-economic analysis of the benefits of conservation agriculture: The case of smallholder farmers in Adami Tulu district, Ethiopia. Ecol. Econ. 120, 164–174. doi:10.1016/j.ecolecon.2015.10.020

CrossRef Full Text | Google Scholar

Upton, M. (1993). Livestock productivity assessment and modelling. Agric. Syst. 43 (4), 459–472. doi:10.1016/0308-521x(93)90034-y

CrossRef Full Text | Google Scholar

Van Kooten, G. C., Weisensel, W. P., and Chinthammit, D. (1990). Valuing trade-offs between net returns and stewardship practices: The case of soil conservation in saskatchewan. Am. J. Agric. Econ. 72, 104–113. doi:10.2307/1243149

CrossRef Full Text | Google Scholar

Yigezu, Y. A., El-Shater, T., Boughlala, M., Devkota, M., Mrabet, R., and Moussadek, R. (2021). Can an incremental approach be a better option in the dissemination of conservation agriculture? Some socio-economic justifications from the drylands of Morocco. Soil & Tillage Res. 212, 105067. doi:10.1016/j.still.2021.105067

CrossRef Full Text | Google Scholar