- 1College of Public Administration, Chongqing University, Chongqing, China
- 2China Institute for Development Planning, Tsinghua University, Beijing, China
- 3Collaborative Innovation Center for Local Government Governance at Chongqing University, Chongqing, China
- 4School of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing, China
- 5School of Cyberspace Security and Information Law, Chongqing University of Posts and Telecommunications, Chongqing, China
In the context of low-carbon globalization, green development has become the common pursuit of all countries and the theme of China’s development in the new era. Fine particulate matter (PM2.5) is one of the main challenges affecting air quality, and how to accurately predict PM2.5 plays a pivotal role in environmental governance. However, traditional data-driven approaches and deep learning methods for prediction rarely consider spatiotemporal features. Furthermore, different regions always have various implicit or hidden states, which have rarely been considered in the off-the-shelf model. To solve these problems, this study proposed a novel Spatial-Temporal Matrix Factorization Generative Adversarial Network (ST MFGAN) to capture spatiotemporal correlations and overcome the regional diversity problem at the same time. Specifically, Generative Adversarial Network (GAN) composed of graph Convolutional Network (GCN) and Long-Short-Term Memory (LSTM) network is used to generate a large amount of reliable spatiotemporal data, and matrix factorization network is used to decompose the vector output by GAN into multiple sub-networks. PM2.5 are finally combined and jointly predicted by the fusion layer. Extensive experiments show the superiority of the newly designed method.
1 Introduction
With the rapid development of China’s economy and the acceleration of urbanization process, the excessive emission of pollutants has caused severe pollution to the air and impedes the process of sustainable development seriously (Chen and Li, 2021; Dong et al., 2021). In many industrial cities, coal is the regions’ lifeblood. Meanwhile, road transportation and automobile transportation have become the main ways of transporting goods, which leads to air pollution to a certain extent. PM2.5 is the primary air pollutant, which turns out to be the focus of China’s haze governance at this stage. PM2.5 harms human health, which has been brought to the center of public attention (Xing et al., 2021). If PM2.5 can be accurately predicted, which will have important implications for environmental management and human health. The concentration of PM2.5 is affected by urban spatial morphology, land use layout, and meteorological factors (Ma et al., 2019). Long-time exposure to air pollution will increase the risk of cardiovascular and respiratory disease (Ma et al., 2020). To find solutions, the Chinese government has set up air quality monitoring stations in most cities, which can monitor PM2.5 and other air pollutant concentration in real-time. Based on observed data, many researchers employ various models to predict PM2.5, which can provide guidance for government management (Gu et al., 2019). The PM2.5 prediction methods fall into two categories: model-driven and data-driven methods. The model-driven methods particularly estimate the PM2.5 concentration by establishing mathematical and statistical models. The data-driven methods predict PM2.5 concentration by using neural networks, support vector regression (SVR), and other machine learning models.
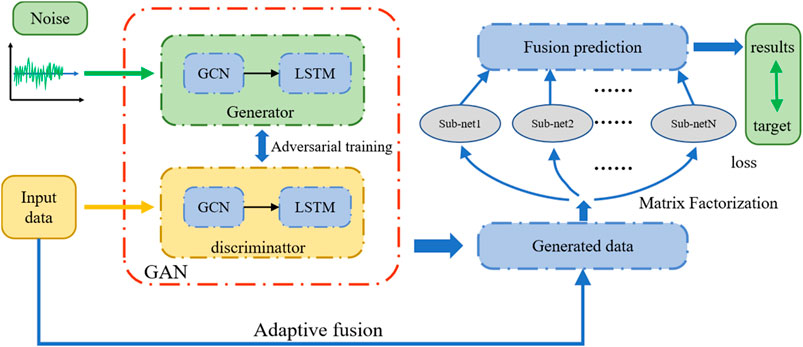
With the development of artificial intelligence and machine learning in recent years, methods such as artificial neural network (ANN) and SVR have been widely used in the prediction of air pollutant concentration. SVR model was employed to predict PM2.5 by using data from surrounding monitoring stations (Xiao et al., 2020). In Pak et al. (2020) research, A CNN-LSTM model was used to extract temporal and spatial features and predict PM2.5 of Beijing in China. However, there is currently rare work that consider the regional diversities. In different regions, the historical PM2.5 steady-state features of cities are usually different, and some cities follow the same pattern of the PM2.5 concentration (Du et al., 2021). There are three challenges in predicting PM2.5: spatial correlations, temporal correlations, and regional diversity. To cope with the challenges, this paper proposes a novel Spatial-Temporal Matrix Factorization Generative Adversarial Network called ST-MFGAN, which can capture spatiotemporal correlations and overcome regional diversity problems. Specifically, each component of GAN has a GCN-LSTM pipeline to capture spatiotemporal information. The output of the GAN is fed to dense layer and undergoes matrix decomposition to form multiple matrices. Each matrix is learned through an independent sub-net. These sub-net parameters will not interfere with each other and PM2.5 are finally combined and jointly predicted by the fusion layer. The main contributions of this paper are as follows:
1) In this paper, we propose a novel model, ST-MFGAN, to comprehensively consider spatiotemporal correlations and regional diversity. We design an ad-hoc predictor to achieve effectively prediction.
2) Most of PM2.5 prediction approaches do not adequately consider the spatiotemporal correlation within the datasets. In this paper, GAN is composed of GCN and LSTM, which can capture spatial information and temporal information to improve the performance of predicting PM2.5.
3) We verify our model and the other baselines in the PM2.5 prediction research line. Related results show that ST-MFGAN achieves a better performance compared with the existing models.
2 Related methods
2.1 GAN
GAN consists of two models: generator G and discriminator D, which are in a state of adversarial game. In the process of game (Goodfellow et al., 2014), generator plays the role of a liar, which can generate data similar to real data. The discriminator acts as a judge, distinguishing real data from generated data. G and D can be seen as players in two-player adversarial game. In theory, the discriminator and generator can achieve Nash equilibrium. In other words, the discriminator cannot distinguish between real data and generated data, the generator can generate data close to real data meanwhile. Based on this principle, the objective function V (G,D) of GAN is given as follows:
Where z represents random noise comes from the prior distribution, x samples from real data distribution, D(x) represents the probability that x come from the real data, and D [G(z)] is the probability that the input comes from the generated data rather than real data. In the training process of G, D [G(z)] tend to approach 1 as much as possible. In other words, G tries to minimize the objective function as much as possible. In the training process of D, D tries to maximize the objective function as much as possible. GANs have been gradually applied to prediction tasks recently due to admirable ability of feature extraction (Yoon et al., 2019), which has inspired a myriad of follow-ups to employ GAN to generation and prediction tasks. Considering that, employing GAN to PM2.5 prediction is appealing for this paper.
2.2 GNN
GNN has achieved state-of-the-art results on various graph-based learning tasks, such as a node or link classification. In recent studies, the mainstream of GNNs fall into Graph Convolutional Network (Kipf and Welling, 2016) and Graph attention network (Velickovic et al., 2017). Due to the powerful fitting abilities on non-Euclidean data, graph neural networks have been applied to fields such as social networks, knowledge graphs, molecular structures, and traffic networks. However, we focus on the variants of GNNs in the field of pollutant prediction in this paper.
2.3 LSTM
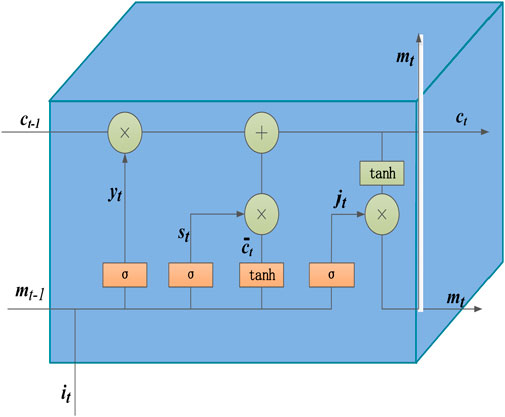
LSTM (Hochreiter and Schmidhuber, 1997) is a type of Recurrent Neural Network (RNN), which is designed to solve gradient explosion in RNN, and it is usually used for time series prediction. LSTM consists of three parts, namely the input gate, the output gate and the forget gate. The network structure of LSTM can be shown as Figure 1. LSTM is widely used to predict time series.
3 Prediction model via adversarial training
3.1 The establishment of PM2.5 prediction model via adversarial training
This paper proposes a PM2.5 prediction model based on GAN, named ST-MFGAN. The framework of ST-MFGAN can be constructed as Figure 2. The random noise is fed to the generator, and generator output data with spatiotemporal information similar to the real data. The real PM2.5 and generated PM2.5 concentration are fed to a dense layer. Then, a matrix factorization layer filters various regional hidden information in different sub-network. Finally, we use the fusion layer to utilize all the different hidden state information for collaborative prediction. When constructing the loss function of the generator, the MSE loss is added to original objective function of GAN, which can reduce the instability of GAN during training. The loss functions of the generator and the discriminator can be described as:
The loss function of the G consists of two parts, a and b are manually set hyperparameters, considering that the proportion of a and b should be the same, so a and b are both 0.5.
3.2 Modified GCN and LSTM for spatiotemporal information capturing
PM2.5 contains ammonium nitrate, which is easily decomposed when the temperature is high. Ammonium nitrate is also easily deliquescent, so temperature and humidity are closely correlated with PM2.5. The wind and vortex help the PM2.5 concentration in the air to spread horizontally and vertically, so the wind speed and vortex state are both related to PM2.5. Precipitation acts as a resistance to PM2.5 concentration, which will produce moisture removal and downward airflow. Therefore, precipitation can be also closely correlated with PM2.5 concentration. Based on the above analysis, this paper chooses time, temperature, humidity, wind speed, precipitation and other variables as input to predict the change of PM2.5 concentration. Assuming that the input matrix X = {x1, x2,…, xt}, X represents data at t time points, where x1, x2,…, xt represent time, temperature, humidity, wind speed, precipitation and vortex status at t time respectively. GCN and LSTM are added to the generator and discriminator of GAN due to strong feature extraction capabilities of them. This paper selects historical air data of different cities in the Beijing-Tianjin-Hebei region of China from the ERA5 datasets. Assuming that the input matrix
Here
Then, we can represent adjacency matrix as:
By this way, our modified GCN can be represent as:
And then the output of GCN is fed to LSTM. We perform spatiotemporal learning on the input data to GCN and LSTM and conduct adversarial training to generate data similar to real data.
3.3 Matrix factorization networks
Matrix factorization introduces a large number of parameters to learn the differences of different subregions. Each parameter subset learns independently and does not interfere with each other, which ensures the independence and reliability of the prediction of each region.Therefore, matrix factorization network is widely used in deep learning due to the advantage for spatio-temporal data in recent years (Wang and Ma, 2021). In order to predict PM2.5 more accurately, the real data
We suppose
3.4 Model summary
In this paper, ST-MFGAN is proposed to predict PM2.5. The generator and discriminator consist of GCN and LSTM, which can capture spatiotemporal correlations among the inputs and overcome the regional diversity problem. Matrix factorization networks is also used to make adaptive adjustments to the number of variable regions in this model, which can effectively reduce the interference between the parameters of each sub-network, and it can be used to predict PM2.5 more accurately compared to other models. In order to verify the effectiveness and superiority of the proposed method, comparative experiments and ablation experiments will be conducted in next section.
4 Experiment and result analysis
ERA5 dataset is used in this paper, and the historical air data of 13 cities in the Beijing-Tianjin-Hebei region are selected. It can make sense to choose this dataset since these cities are with more severe air pollution in China. Air data for the period 2015–2018 are selected from the data set of 13 cities in experiments. When dividing the data set, 3-year data from January 2015 to December 2017 is used for the training set, and data from January to December 2018 is selected for the testing set. To eliminate the dimensional influences between different indicators, we normalize all the features in the datasets, which is shown as:
Where
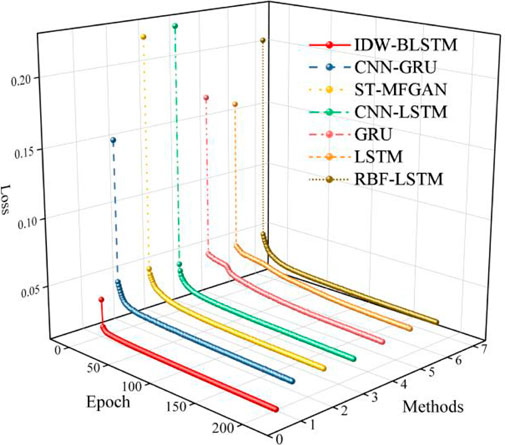
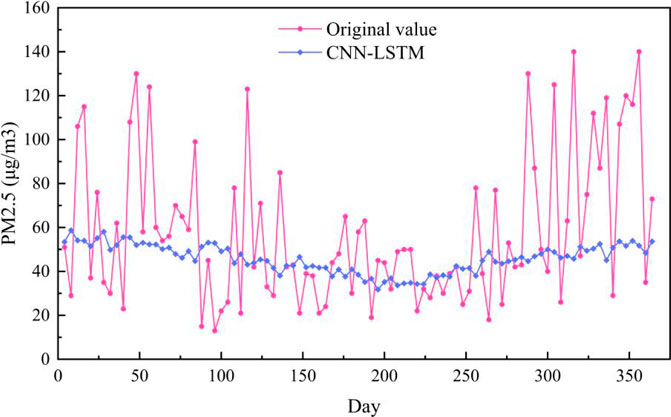
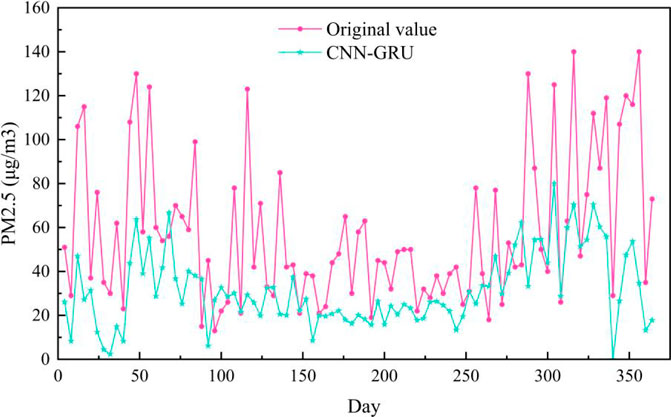
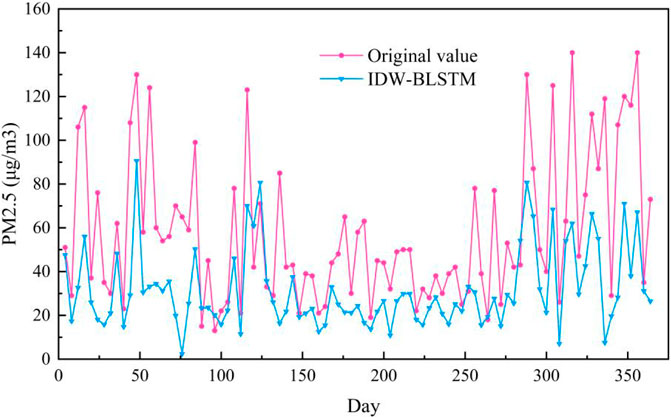
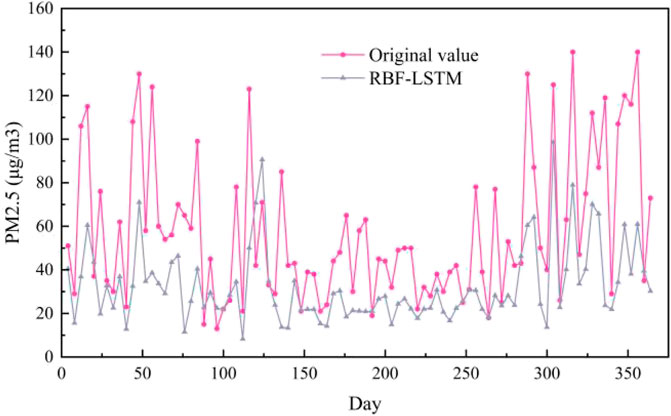
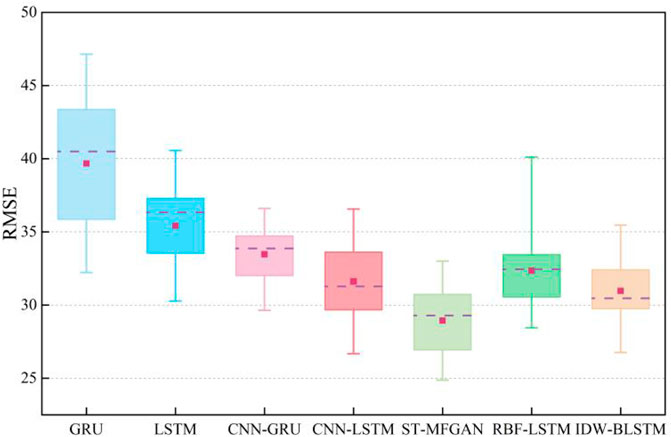
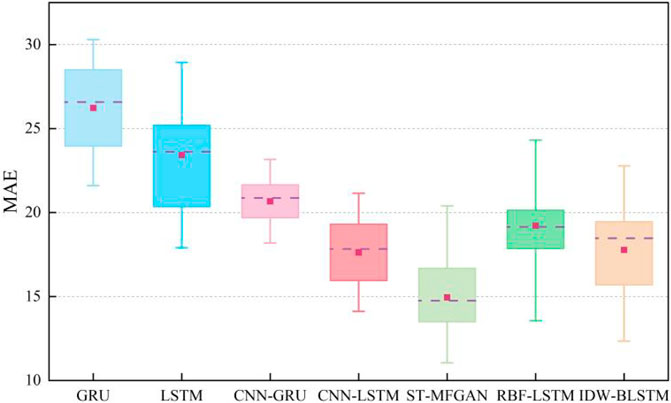
To verify the effectiveness and superiority of the proposed method, comparative experiments with other mainstream data-driven methods are conducted. We adopot six different models of GRU, LSTM, CNN-GRU, CNN-LSTM, IDW-LSTM, RBF-LSTM as baseline for this paper. GRU, LSTM, CNN-GRU, CNN-LSTM are the basic regression prediction models, which are widely used in PM2.5 prediction. IDW-LSTM is a methodology framework for PM2.5 prediction, which consists of inverse distance weighting and BLSTM (Ma et al., 2019). RBF-LSTM is proposed to forecast PM2.5 concentration, which consists of radial basis function and LSTM (Chen and Li, 2021). In the comparative experiments in this paper, the number of GRU layers of the GRU method is set to 2. In CNN-GRU, the number of CNN layers is set to 1, and the number of GRU layers is 2. The number of CNN layers in CNN-LSTM is 1, and the number of LSTM layers is 2. In IDW-LSTM, the number of BLSTM layers is 2. In LSTM and RBF-LSTM, the number of LSTM layers is 2. The training loss curves of seven models are shown in Figure 5. It can be seen from Figure 5, the loss of seven models do not decrease at the later stage of traing process, which indicates that all models are fully trained, which reflects the rigor and fairness of this paper to a certain extent. As can be seen from Figure 5, the loss of ST-MFGAN decreases fast during the training process and fluctuates less significantly in the later stages of training, which verifies that proposed model is stable during training. This can further indicate that proposed model can be better applied to predict PM2.5.
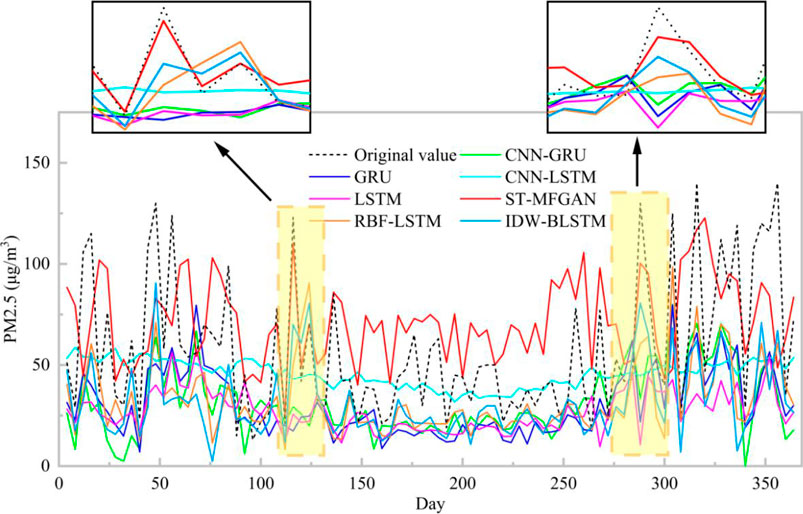
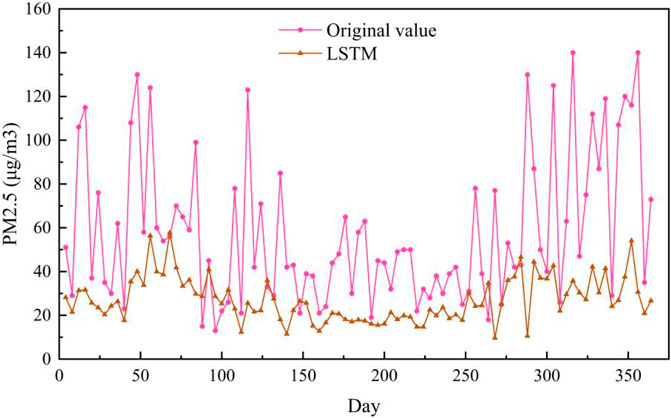
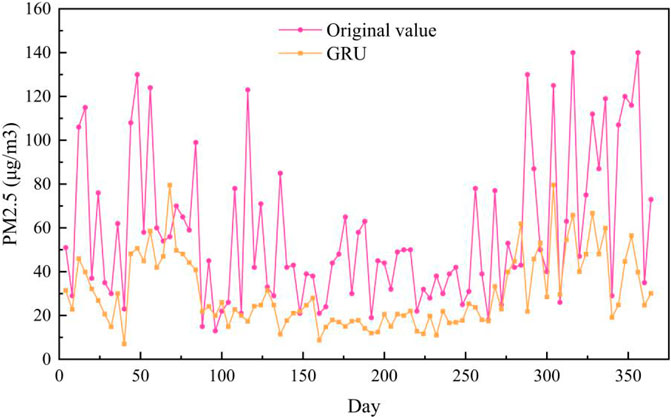
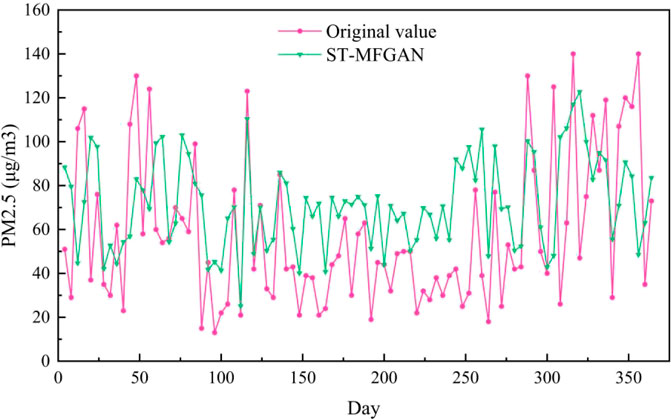
The PM2.5 prediction results on the Baoding test set are shown in Figure 6. As can be seen from Figure 6, the prediction curve of ST-MFGAN is closer to that of the actual PM2.5 compared with other models. Especially, when the real PM2.5 turn to be a brief peak, ST-MFGAN is more able to estimate the trend of PM2.5 and can predict more accurately than other models. As shown in Figures 7–13, the prediction effect of each method can be presented more clearly. The performance of ST-MFGAN is significantly better than other comparative models. In terms of the prediction performance, ST-MFGAN can predict the trend of PM2.5 more accurately.
In order to more intuitively describe the prediction accuracy of various methods, the root mean square error (RMSE) and mean absolute error (MAE) are adopted to evaluate the prediction performance of each model. The calculation of RMSE and MAE is defined as:
Where
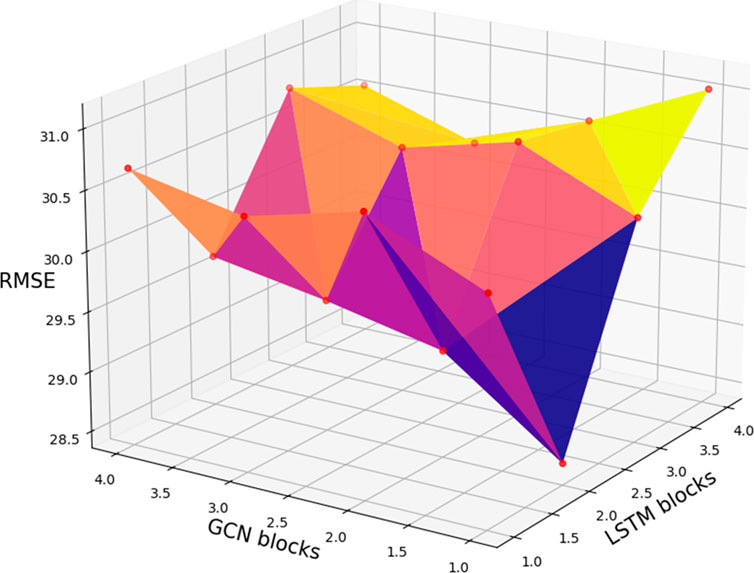
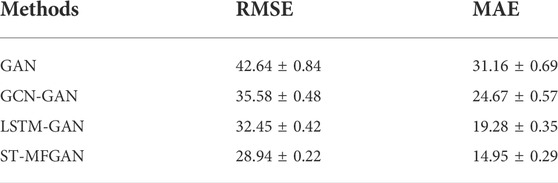
To further verify the validity of the model structure proposed in this paper, ablation experiments were conducted in this paper. We compare ST-MFGAN with the original GAN, GCN-GAN (GAN with generator of GCN), and LSTM-GAN (GAN with generator of LSTM), and experiments results are shown in Table 2.
It can be seen from the ablation experimental results that ST-MFGAN achieves the best prediction performance due to hitting lower RMSE and MAE, which further verifies the effectiveness of the model structure proposed in this paper.
5 Conclusion
This paper propose a PM2.5 prediction method based on ST-MFGAN. The generator and discriminator consist of GCN and LSTM, which can capture spatiotemporal correlations among the inputs compared with original GAN, and it can overcome the regional diversity problem. Matrix factorization networks are also used to make adaptive adjustments to the number of variable regions in this model. Compared with PM2.5 prediction methods based on LSTM, GRU, CNN-LSTM and CNN-GRU, IDW-LSTM, and RBF-LSTM, the method in this paper has a better prediction performance, which can be used in governing environment. It can be seen from the results of this paper that PM2.5 concentration changes periodically and is difficult to control. Therefore, the government needs to strengthen environmental management and introduces a series of powerful policies to control the concentration of PM2.5.
Although the PM2.5 prediction method of ST-MFGAN can effectively predict the concentration of PM2.5, there is still room for further improvement of this paper. Most studies on PM2.5 prediction use various meteorological variables to predict PM2.5. However, few studies currently take policy factors into account. Future research can take the policy into consideration, which may improve the forecasting effect of PM2.5. Compared with GRU, LSTM and other models, GAN may bring additional cost during the training process. Future research can focus on the study of lightweight GAN for PM2.5 prediction, which can reduce the number of parameters of the model so that GAN can be trained and predicted more quickly in the prediction task.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors contributed to this research. AZ completed the experiment of this paper and completed the writing of this article. SC provided ideological guidance for this research. FZ was an reviewer in editing this paper. XD also provided ideological guidance for this research. All authors approved this final manuscipt.
Funding
This work supported by Research Program supported by Fundamental Research Funds from the Central Universities (CN) (Nos. 2021CDJSKPT05, 2020CDJSK01WT07) and the National Natural Science Foundation of China (No. 72274026).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, Y. C., and Li, D. C. (2021). Selection of key features for PM2.5 prediction using a wavelet model and RBF-LSTM. Appl. Intell. (Dordr). 51, 2534–2555. doi:10.1007/s10489-020-02031-5
Dong, Z., Li, L., Lei, Y., Wu, S., Yan, D., and Chen, H. (2021). The economic loss of public health from PM2.5 pollution in the Fenwei Plain. Environ. Sci. Pollut. Res. 28, 2415–2425. doi:10.1007/s11356-020-10651-0
Du, P., Wang, J., Yang, W., and Niu, T. (2021). A novel hybrid fine particulate matter (pm2.5) forecasting and its further application system: Case studies in China. J. Forecast. 41, 64–85. doi:10.1002/for.2785
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative adversarial networks. Commun. ACM 3, 139–144. doi:10.1145/3422622
Gu, K., Qiao, J., and Li, X. (2019). Highly efficient picture-based prediction of PM2.5 concentration. IEEE Trans. Ind. Electron. 66, 3176–3184. doi:10.1109/TIE.2018.2840515
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735
Kipf, T. N., and Welling, M. (2016). Semi-supervised classification with graph convolutional networks. arXiv.
Ma, J., Ding, Y., Gan, V., Lin, C., and Wan, Z. (2019). Spatiotemporal prediction of PM2.5 concentrations at different time granularities using IDW-BLSTM. IEEE Access 7, 107897–107907. doi:10.1109/ACCESS.2019.2932445
Ma, J., Ding, Y., Jack, C., Cheng, P., Jiang, F., Gan, V. J. L., et al. (2020). A Lag-FLSTM deep learning network based on Bayesian Optimization for multi-sequential-variant PM2.5 prediction. Sustain. Cities Soc. 60, 102237. doi:10.1016/j.scs.2020.102237
Pak, U., Ma, J., Ryu, U., Ryom, K., Juhyok, U., Pak, K., et al. (2020). Deep learning-based PM2. 5 prediction considering the spatiotemporal correlations: A case study of beijing, China. Sci. Total Environ. 699, 133561. doi:10.1016/j.scitotenv.2019.07.367
Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., and Bengio, Y. (2017). Graph attention networks. arXiv.
Wang, Y., and Ma, X. K. (2021). Joint nonnegative matrix factorization and network embedding for graph co-clustering. Neurocomputing 462, 453–465. doi:10.1016/j.neucom.2021.08.014
Xiao, Y., Zhao, J., Liu, H., Wang, L., and Liu, J. (2020). Dynamic prediction of pm2.5 diffusion in urban residential areas in severely cold regions based on an improved urban canopy model. Sustain. Cities Soc. 62, 102352. doi:10.1016/j.scs.2020.102352
Xing, H., Wang, G., Liu, C., and Suo, M. (2021). Pm2.5 concentration modeling and prediction by using temperature-based deep belief network. Neural Netw. 133, 157–165. doi:10.1016/j.neunet.2020.10.013
Keywords: PM2.5, generative adversarial networks, matrix factorization, spatiotemporal prediction, environmental governance
Citation: Zhang A, Chen S, Zhao F and Dai X (2022) Good environmental governance: Predicting PM2.5 by using Spatiotemporal Matrix Factorization generative adversarial network. Front. Environ. Sci. 10:981268. doi: 10.3389/fenvs.2022.981268
Received: 30 June 2022; Accepted: 15 August 2022;
Published: 29 September 2022.
Edited by:
Juergen Pilz, University of Klagenfurt, AustriaReviewed by:
Gautam Kumar, San Jose State University, United StatesYanhu Chen, Beijing University of Posts and Telecommunications (BUPT), China
Copyright © 2022 Zhang, Chen, Zhao and Dai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sheng Chen, MjgxMjIwNDY1OUBxcS5jb20=
 An Zhang
An Zhang Sheng Chen
Sheng Chen Fen Zhao4
Fen Zhao4