- 1Department of Agricultural and Biological Engineering, University of Florida, Gainesville, FL, United States
- 2Department of Forest and Wildlife Ecology, University of Wisconsin-Madison, Madison, WI, United States
The relationship between nutrient cycling and water quality in mixed-use ecosystems is driven by interactions among biotic and abiotic processes. However, the underlying processes cannot always be directly observed or modeled at broad spatial scales. Numerous empirical studies have employed land use patterns, variations in watershed physiography or disturbance regimes to characterize nutrient export from mixed-use watersheds, but simultaneously disentangling the effects of such factors remains challenging and few models directly incorporate vegetation biochemistry. Here we use structural equation models (SEMs) to assess the relative influence of foliar chemical traits (derived from imaging spectroscopy), watershed physiography, and human land use on the water quality (summer baseflow nitrate-N and soluble reactive phosphorus concentration) in watersheds across the Upper Midwestern United States. We use an SEM to link water quality (stream nitrate-nitrogen and dissolved phosphorus) to foliar retention (AVIRIS-Classic derived foliar traits related to recalcitrance), watershed retention (wetland proportion, MODIS Tasseled Cap Wetness), runoff (agricultural and urban land use), and watershed leakiness (AVIRIS-Classic foliar nitrogen, nitrogen deposition). The SEMs confirmed that variables associated with foliar retention derived from imaging spectroscopy are negatively related to watershed leakiness (standardized path coefficient = −0.892) and positively to watershed retention (standardized path coefficient = 0.705), with features related to watershed retention and runoff exerting the strongest controls on water quality (standardized path coefficients of −0.270 and 0.331 respectively). Comparing forested and agricultural watersheds, we found significantly increased importance of foliar retention to watershed leakiness in forests compared to agriculture (standardized coefficients of −1.004 and −0.764 respectively), with measures of watershed retention more important to runoff and water quality in agricultural watersheds. The results illustrate the capacity of imaging spectroscopy to provide measures of foliar traits that influence nutrient cycling in watersheds. Ultimately, the results may help focus development and restoration policies towards building more resilient landscapes that take into consideration associations among functional traits of vegetation, physiography and climate.
Introduction
Stream water quality in mixed-use watersheds is a function of the interacting biotic and abiotic factors that control ecosystem-level nutrient cycling (Griffith 2002; Meador and Goldstein 2003; Buck et al., 2004; Ertaş et al., 2022). The forested and agricultural components of landscapes display inherently different nutrient cycling regimes, especially as consequence of anthropogenically mediated changes in ecosystem processes (e.g., nitrogen deposition, fertilizer use), soil properties (tillage), moisture regimes (irrigation) and broad-scale environmental changes related to climate (Schindler and Bayley 1993; Vitousek et al., 1997; Mosier 1998; Compton and Boone 2000). Nutrient management in mixed-use landscapes is important to the reduction of high nitrogen (N) and phosphorus (P) concentrations in streams that contribute to eutrophication and acidification of receiving waters and the loss of biological diversity and estuarine productivity, and present a public health concern (Vitousek et al., 1997; Friedland et al., 2021). Agricultural fertilization is the primary nonpoint source of nitrate-nitrogen (NO3-N) to receiving waters, but forest functional properties and disturbances to forests can also affect nutrient export, especially of nitrate-N (Townsend et al., 2004; K. N. Eshleman et al., 2009; Shortle et al., 2021). Like nitrate, streamwater phosphorus originates from a variety of sources, but in general is derived from nonpoint sources associated with agricultural and urban land use, and point sources associated with urbanization. Phosphorus is best predicted by urban and industrial activity in most cases and in some cases agriculture (Pieterse et al., 2003; Zampella et al., 2007; Coskun et al., 2008; Rosov et al., 2020).
The functional properties of vegetation affect nutrient dynamics at the watershed scale, even when decoupled from environmental factors such as N deposition and soil C: N ratios (Huang et al., 2011). The response of plants to nutrient availability depends on their physiology and climatic constraints on seasonal N availability (Arain et al., 2006; Seaton et al., 2019). Plant N availability and subsequent variations in local N cycling rates are also functions of competition within local species assemblages and the attendant differences in physiological trait adaptations (Reich et al., 1999; Reich et al., 2003; Huang et al., 2011). Therefore, it is notable that even within forested ecosystems, nutrient cycling rates can differ between deciduous and conifer dominated ecosystems (Aber and Driscoll 1997; Melvin et al., 2015), and may vary considerably within landscapes dominated by a single functional type (Smith et al., 2002). This is partly because of differences in foliar nitrogen and lignin/cellulose concentrations that characterize leaf lifespan (Wright et al., 2005; Shipley et al., 2006; Santiago 2007), influence soil C: N ratios (Ollinger et al., 2002) and, in combination with disturbance events (Eshleman et al., 2000; McNeil et al., 2007), may be strong controllers of nutrient cycling (Aber et al., 1991; Fortunel et al., 2009b; de Bello et al., 2010). Further, N output (or “leakage”) from forested ecosystems has also been linked to disturbance and land use legacies (Aber and Driscoll 1997; Chen et al., 2004; McNeil et al., 2008). For example (McNeil et al., 2007), demonstrated that N leakage from watersheds may be mediated by insect-related defoliation and could maintain N limitation in temperate forest ecosystems. Similar results have been obtained in the Hubbard Brook Experimental forest (Li et al., 2004) and the Chesapeake Bay watersheds (Eshleman et al., 2000; Townsend et al., 2004; Eshleman et al., 2009; Eshleman and Sabo 2016).
In most mixed land cover watersheds, agriculture is the most significant contributor of nutrients to receiving waters (Howarth et al., 1996; Carpenter et al., 1998; Howarth 1998; Hutchins et al., 2010; Roberts and Prince 2010). The major underlying factors are fertilizer application and land management practices (Mattikalli and Richards 1996; Cicek et al., 2010; Hutchins et al., 2010; Roberts and Prince 2010) and resultant direct nutrient runoff during rainfall events (Reay et al., 1992; McCarty et al., 2008; Morari et al., 2012). For pasture-dominated landscapes, N and P export has also been linked to subsidies from animal waste (Worrall and Burt 1999; Pieterse et al., 2003; Buck et al., 2004). Agricultural nutrient management thus forms an important part of water resources protection strategies (Shepard 2005) and it has been shown that even small improvements in agricultural practices can result in significant improvements in water quality indicators (Diebel et al., 2008; Diebel et al., 2009; Zimmerman et al., 2019).
Numerous studies have shown landscape-scale variables to be good predictors of aquatic habitat quality (Lyons et al., 1996; Fitzpatrick et al., 2001; Rooney and Bayley 2011) and have provided evidence of the importance of riparian zones for sustaining diverse fish communities in streams (Fennessy and Cronk 1997; Lowrance et al., 1997; Fitzpatrick et al., 2001; Meador and Goldstein 2003). A growing body of literature has empirically linked water quality in receiving waters with landcover associations (L. B. Johnson et al., 1997; Basnyat et al., 2000; Griffith et al., 2002; Buck et al., 2004; Stanley and Maxted 2008; Singh et al., 2013), but disentangling the relative influence of vegetation traits (as opposed to cover type), climate, disturbance and watershed physiography remains to be explored due to the complex and possibly nonlinear interactions between these factors.
Multispectral and hypertemporal satellite sensors have long been employed to generate land use and land cover maps, spatially explicit estimates of forest disturbance (Kennedy et al., 2010; Townsend et al., 2012; Soulard et al., 2017), and to derive parameters describing vegetation phenology (Reed et al., 1994; Stöckli et al., 2008; Schleip et al., 2009) that we hypothesize are related to water quality. Recent research has shown that spectroscopic methods can be used to characterize key plant functional traits such as foliar nitrogen (Townsend et al., 2003; Majeke et al., 2008; Martin et al., 2008; Singh et al., 2015; Wang et al., 2019), specific leaf area (SLA), foliar lignin and cellulose (Wright et al., 2002; Majeke et al., 2008; Kokaly et al., 2009; Dybzinski et al., 2013) and potentially δ15N concentrations (Kleinebecker et al., 2009; Elmore and Craine 2011; Singh et al., 2015) making it possible for these functional traits to be incorporated into analyses of the drivers of water quality. However, the interactions among these potential drivers have not been comprehensively evaluated, especially given the complexity of existing process models and the absence of data needed to quantify these traits across most regions. So, while a large body of research has linked the role of physiological trait associations (Santiago et al., 2004; Shipley et al., 2006; Fortunel et al., 2009a; de Bello et al., 2010), climatic factors (Fausey et al., 1995; Krysanova et al., 1998; Hall et al., 1999; Hu and Ou 2013), land use patterns (Basnyat et al., 2000; Griffith et al., 2002; Chen et al., 2007) and disturbance (Eshleman et al., 2000; Townsend et al., 2004; Eshleman et al., 2009) to nutrient cycling rates ranging from the stand to the watershed scale, the relative role of canopy foliar biochemical and structural traits remain to be explored due to lack of concurrent spatially-explicit data. A major objective of this research was to test how measurements of foliar traits derived from NASA’s Airborne Visible/Infrared Imaging Spectrometer (AVIRIS-Classic) relate to stream water nutrient export.
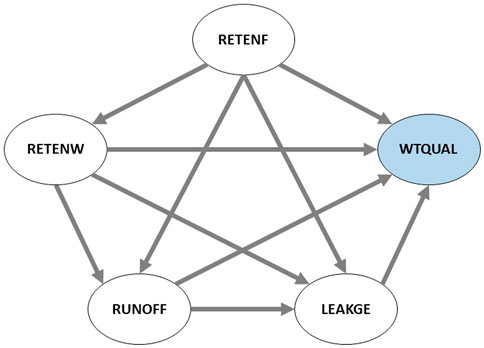
Here, we utilize a structural equation modeling approach to assess the relative influences of foliar biochemistry, watershed physiography and human land use patterns on water quality in watersheds across the Upper Midwestern United States (Figure 1). We explore the influence of four broad groups of variables on stream water quality: 1) nutrient retention due to foliar biochemistry, 2) nutrient retention due to watershed physiography, 3) an index of human activity (landscape composition dominated with urban and agricultural land use), and 4) indicators of watershed-scale nutrient ‘leakiness’. We hypothesize that: A) higher foliar recalcitrance has a direct positive effect on nutrient retention in watersheds and indirectly with overall water quality (i.e., lesser nutrient export), and is negatively correlated with indicators of watershed leakiness and indicators of human activity; B) indicators of watershed leakiness and high human activity have negative direct, influences on water quality (i.e., high nutrient export), as moderated indirectly by retention in watersheds and foliar recalcitrance. The structural model proposed is shown in Figure 2 with arrows pointing in the direction of hypothesized influence. Variables constituting the latent factors in Figure 2 are described in detail in the methods section.
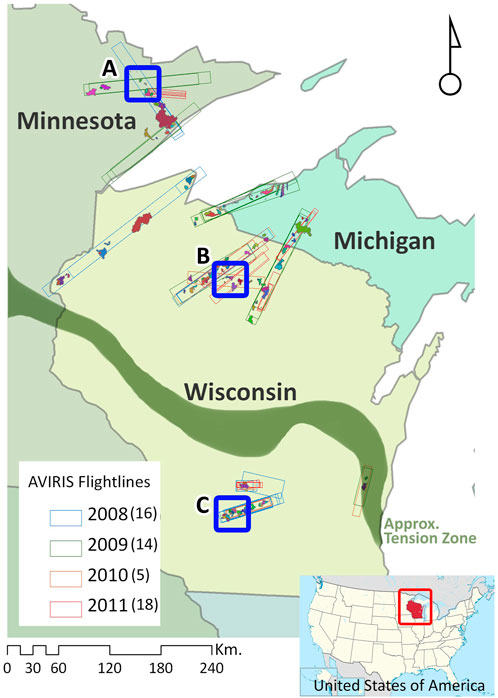
FIGURE 1. Study area. Sampled watersheds are overlaid on AVIRIS flightlines. Letters refer to locations of maps in Figure 5.
Data
Watersheds
Watersheds for this study were identified within 53 swaths that were imaged by AVIRIS-Classic between 2008 and 2011 in the upper Midwestern United States (Figure 1). Watersheds were selected to reflect the diversity in forest functional associations, landscape physiognomy and landcover composition. We selected first-through third-order watersheds from the NHD-plus database (NHDPlus 2010) that fell more than 90% within the AVIRIS swaths. NHD-plus stream layers intersected with selected watersheds were overlaid with TIGER (TIGER/Line 2011) road networks to identify ∼350 potential sampling locations. A total of 216 watersheds were selected in the field for sampling after screening for safe access and presence of water in the channel. Streams were sampled in 2010 and 2011, always within 1 year of AVIRIS-Classic acquisition, with 28 watersheds sampled in both years (Figure 1). Our sampling was limited to 2 years to correspond as closely as possible with AVIRIS overflights. Watershed sizes ranged from 9.8 ha to 7,685 ha with a median of 725 ha and mean of 1,123 ha (S.D. 1,329 ha, Supplementary Appendix Figure S1). Approximately 25% of watersheds are predominantly forested (>70% forest), around 13% of watersheds comprise at least 25% agricultural and pastoral use. There is a broad mix of wetlands across the state but predominantly in the forested north, The maximum proportion of urban landcover is 4%.
Water quality sampling
A total of 216 water samples from wadeable streams were obtained in the late summer (August-September) of 2010 and 2011, 5–50 m upstream from culverts depending on local accessibility. Streamwater samples were filtered on-site using 0.45 micron glass-fiber filters (Whatman Plc Piscataway, NJ), stored on ice in 60 ml Nalgene bottles (Nalge Nunc International Corporation, Rochester NY), and frozen until the chemical analyses were performed. Samples were analyzed for nitrate-N (NO3-N) and soluble reactive phosphorus (SRP) using protocols described in the Manual of analytical methods (WSLH 1993). Nitrate-N concentrations averaged 0.353 mg/L (0.0004–4.97 mg/L, median 0.042) and SRP concentrations averaged 0.0123 mg/L (Below detection limit −0.179 mg/L, median 0.0045). Distributions of both nitrate-N and SRP concentrations were strongly lognormal and were log-transformed prior to all analyses (Supplementary Appendix Figure S2).
Watershed characteristics
Broad indicators of watershed physiography (stream length, stream density) were obtained from NHD-plus stream network data (NHDPlus 2010) clipped to watershed boundaries obtained by terrain analysis of the National Elevation Dataset (Gesch et al., 2002) at field sampled locations. Average soil infiltration capacities for delineated watersheds were derived from the STATSGO database (Schwarz and Alexander 1995) by identifying major hydrologic soil groups, linking the hydrologic soil groups with infiltration capacities (NRCS 2007) and weighting by area within the respective watersheds. Contribution of groundwater to baseflow was obtained from Wolock (2003) and averaged within watersheds.
Climate and vegetation phenology
Daily precipitation and maximum and minimum temperatures were obtained from the DayMet database (Thornton et al., 2012), and averaged annually within each watershed to characterize an average climatological record for each watershed. Mean parameters of vegetation phenology for each watershed for the year sampled were obtained by fitting a double logistic model (Eq. 1) to NDVI time series obtained from the MODIS MOD09A1 product (500m, 8-day NDVI composites). Phenological parameters were obtained for each year and averaged over all pixels contained in each watershed, following Butt et al. (2011):
Where: a = minimum NDVI, b = max-min NDVI, ri = maximum rate of NDVI increase at start of season, SOS = start of season date (first inflection point), rd = maximum rate of NDVI decline at end of season, EOS = end of season date (second inflection point). Note that only SOS was used as a parameter as most sampling occurred during the middle of the growing season.
Landcover and foliar traits
Data on proportional landcover for each watershed were obtained from the National Land Cover Database (Fry et al., 2011). Maps of predicted foliar traits characterizing canopy biochemical (%N, %C, Lignin, Cellulose) and structural parameters (leaf mass per area, LMA) were obtained from results of concurrent AVIRIS campaigns (Singh et al., 2015) and averaged for each watershed. AVIRIS campaigns were conducted during the midsummer peak greenness period spanning 2008 through 2011 and measured −800 GB of imagery for this landscape. Imagery was acquired from NASA’s ER-2 platform at an altitude of ca. 14,000–20,000 m with pixel sizes ranging from 12 to 18 m.
Direct inputs and disturbance
In the absence of a continuous data record from Landsat (45% of all Landsat five and Landsat ETM + imagery was cloud contaminated in summer months), we employed disturbance indices (Healey et al., 2005) derived from the MOD09A1 product to characterize disturbance between the year of sampling and the previous year. Similar to other spatial products, averaged values of disturbance indices were assigned to each watershed for each year. Data on atmospheric nitrogen inputs to watersheds were obtained from the North American Nitrogen Deposition program (NADP 2014) for years corresponding to the sampling year and averaged within watershed boundaries.
Methods
PLS path models
Structural equation models (SEMs) are a set of statistical methods that aim to estimate a network of causal relationships (Vinzi et al., 2010b). Structural relationships are constructed as recursive linkages between (unmeasured) latent complex concepts, each measured through observable indicators. Overall, the intent is to study the complexity of a system using a causality concept among latent constructs (latent variables, LVs) while describing each LV by measured observations called manifest variables (MVs). The partial least squares (PLS) approach to SEMs, also known as path modeling (PLS-PM), represents an intersection of path analysis (Tukey 1964; Alwin and Hauser 1975; Vinzi et al., 2010b) and confirmatory factor analysis (Thurstone 1931). Proposed as a component-based alternative to covariance based structural equation modeling (CB-SEM) estimation procedures by Wold (Wold 1966), the PLS-PM technique iteratively solves for blocks of the measurement model in the first step (the relation of LVs to MVs), and proceeds with the estimation of the structural model (the interrelationships between LVs) in the second step. These steps are iterated until the aggregated residual error is minimized (Dijkstra 2010). The PLS-PM approach attempts to explain the residual variance of the latent and manifest variables rather than modeling the sample covariance matrix. As such, the PLS-PM approach relaxes strict distributional and sample size requirements of data when compared to covariance-based SEMs (Lohmoller 1989). In contrast to CB-SEM analyses, the PLS-PM approach allows for formative indicator constructs to be identified, i.e., situations when the manifest variables are supposed to cause changes in latent variables (as opposed to reflective indicators, in which the relationship is reversed). Confidence intervals for parameter estimates are finally obtained empirically by bootstrapping techniques. Details of PLS-PM are described in Vinzi et al. (2010a).
We defined five latent constructs (Figure 2) that represent a conceptual description of watershed function. These were: 1) nutrient retention due to foliar recalcitrance (RETENF), characterized by: carbon to nitrogen ratio, lignin to nitrogen ratio, fiber to cellulose ratio and leaf mass per unit area; 2) nutrient retention in wetlands (RETENW), characterized by: MODIS tasseled cap wetness index, percentage wetland landcover, percentage water area, stream length, groundwater contribution to baseflow, and soil infiltration capacity and mean phenological start of season date; 3) watershed nutrient ‘leakiness’ (LEAKGE) , characterized by: foliar N concentration, stream density, MODIS tasseled cap brightness index, total atmospheric N deposition, MODIS disturbance index, index of aridity (ratio of precipitation to potential evapotranspiration), proportion of area under coniferous forest and the composite terrain index derived from a digital elevation model (Gesch et al., 2002); 4) nutrient runoff from human dominated landcover (RUNOFF), characterized by: proportion of urban built up area, proportion of area under agriculture and pasture, and finally 5) water quality (WTQUAL), characterized by measured streamwater concentration of nitrate-N (NO3-N) and soluble reactive phosphorus (SRP). Table 1 presents the hypothesis associated with each variable, and Table 2 lists basic statistical information on all variables, and presents the hypothesis associated with each. In brief: for foliar retention (RETENF) we assume that the combination of high C: N ratios, high Nitrogen to Lignin ratios, high fiber to cellulose ratios, and high leaf LMA will in combination reduce nutrient exports from watersheds. For retention in watersheds (RETENW), a high tasseled cap wetness index, high proportion of wetland landcover, large proportion of water bodies, longer stream lengths, higher soil infiltration capacity, and an early start of season will reduce export. Note that we do not assign a hypothesis for baseflow contribution. For the potential for fertilizer-related subsidies from human dominated landcover (RUNOFF), we hypothesize that higher proportions of agricultural, urban (via lawns and golf courses), and pasture (via export from livestock operations) will cause higher exports. For watershed ‘leakiness’ (LEAKGE), we assume high foliar N concentrations (with higher N in cropland), higher stream density (i.e., shorter in-stream processing), higher tasseled cap brightness index (as an indicator of exposed soil), higher disturbance (derived from MODIS), higher aridity, and higher N subsidies from atmospheric deposition will cause higher exports, while larger proportions of coniferous landcover, and high values of the composite terrain index indicating wetlands or other lowlands areas will reduce nutrient export. For the inner model (Figure 3), we hypothesize that foliar retention (RETEN) will reduce nutrient export, especially in combination with forested and wetland landcover (RETENW). We hypothesize that higher proportion of agricultural and pastoral landcover (RUNOFF) will increase nutrient export but should be mediated by foliar retention and watershed retention. We hypothesize that watershed properties influencing nutrient leakage (LEAKGE) should increase export, especially in combination with agricultural land cover, but should also be mediated by foliar and wetland retention.
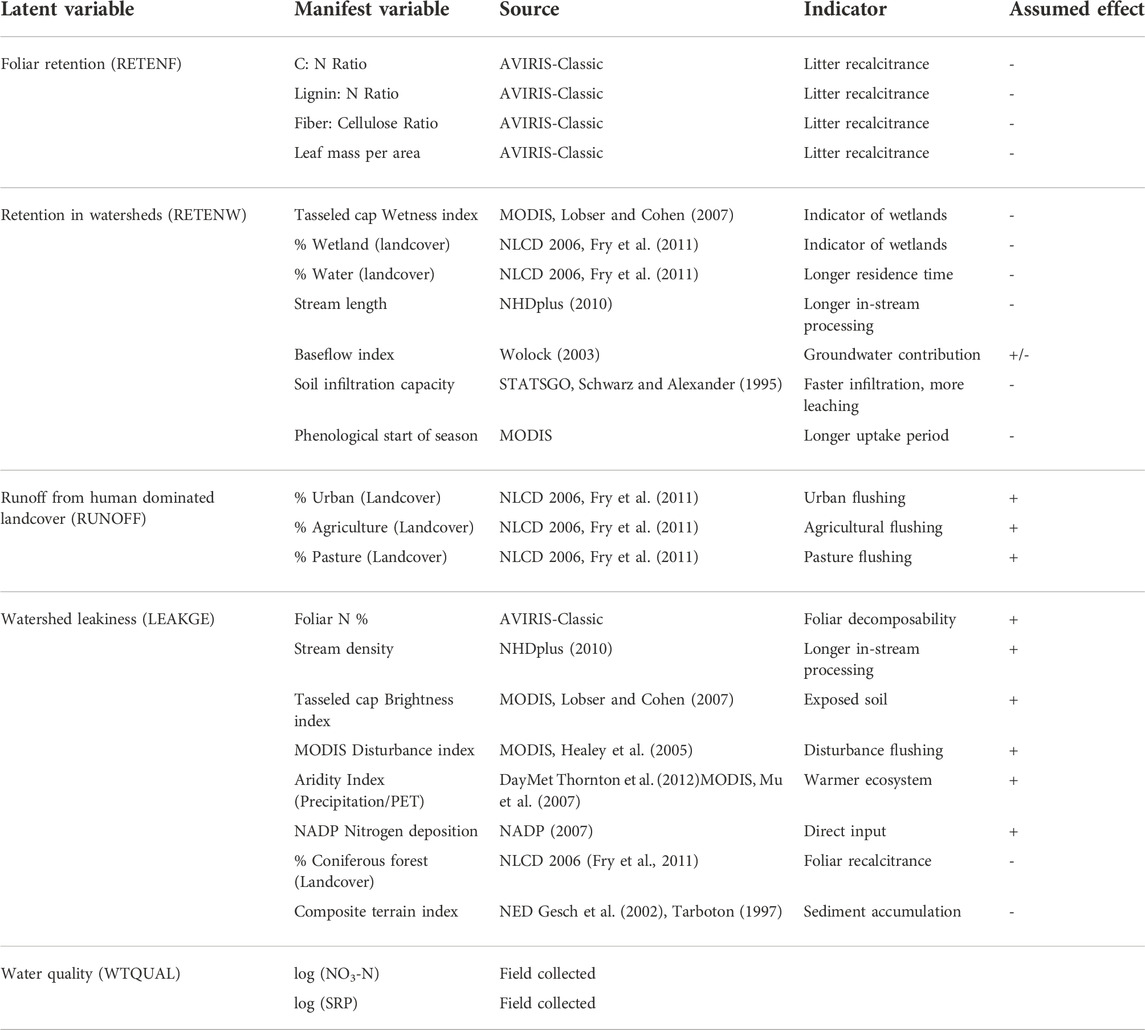
TABLE 1. Variables used in the study, sources, and basic hypotheses (±effect) associated with each; we consider an effect negative when it mitigates water quality indicators (i.e., reduces export), vice-versa for positive.
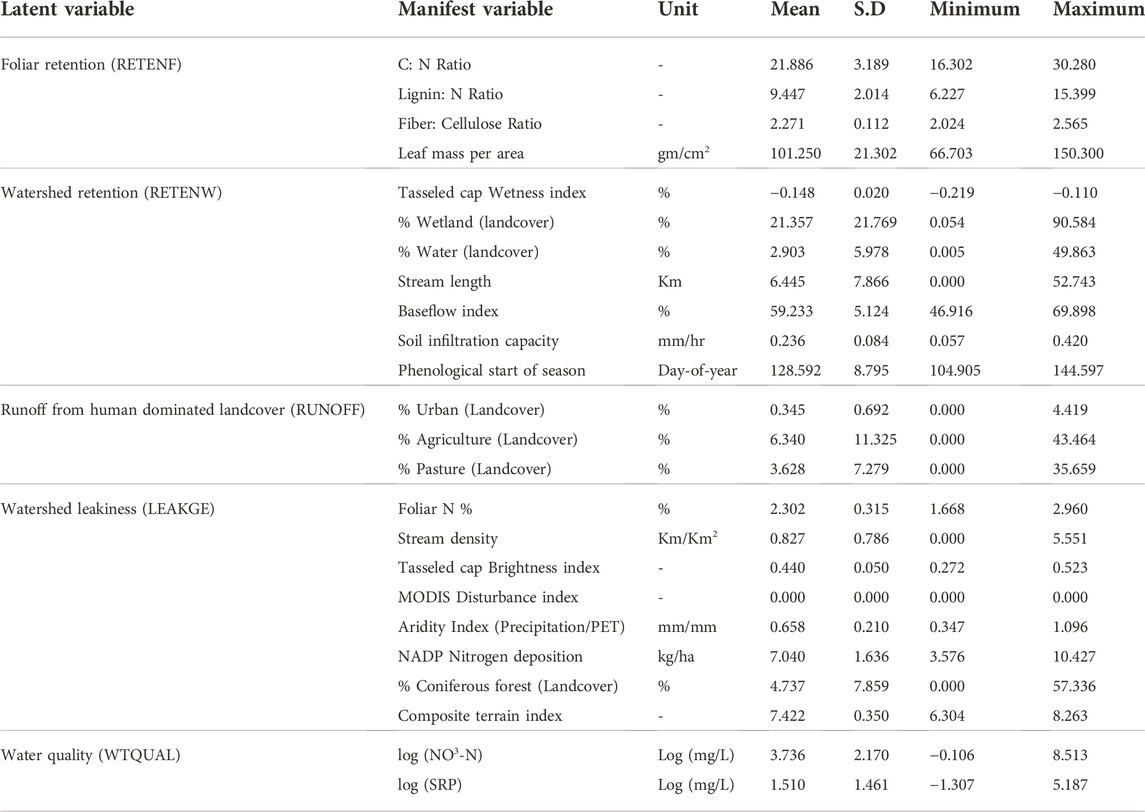
TABLE 2. Basic statistics of the variables used in the study; units, means, standard deviations and ranges are presented.

FIGURE 3. Fitted (reduced variable) structural model. Path colors denote whether the antecedent latent variable positively (blue) or negatively (red) effects the descendent latent variable. For example, RETENF increases RETENW, but decreases LEAKGE. Numbers adjacent to links denote standardized coefficient sizes. See Table 6 for significance levels.
We specified RETENF, RETENW, and LEAKGE as formative constructs (i.e., latent variables defined as being ‘caused’ by manifest variables), and RUNOFF and WTQUAL as reflective constructs (i.e., latent variables that ‘cause’ increases in manifest variables). We bootstrapped the model 500 times to obtain uncertainty estimates on all path coefficients. All analyses were conducted using the plspm package (Sanchez 2013) in R (R 2020).
Initial models were evaluated for specification appropriateness by inspecting measures of unidimensionality of the latent blocks. Unidimensionality metrics ensure satisfaction of the implicit assumption that manifest variables are better related to their own latent variable than others, and Kaiser’s rule that the first Eigenvalue of the correlation matrix should be higher than one while others are smaller. We used Dillon-Goldstein’s Rho (Chin 1998) and principal components analysis of each block to check for unidimensionalty following Vinzi et al. 2010a and Sanchez (Sanchez 2013). We also report the classical Cronbach’s alpha for each model construct. The model was termed suboptimal if it failed unidimensionality tests, namely if 1) the Dillon-Goldstein’s Rho was less than 0.7, and 2) if the first and second Eigenvectors were both higher than 1.0 (Kaiser’s rule). Model fits were further considered suboptimal if 3) the average communality index of a construct was less than 0.5 and 4) if the goodness-of-fit was less than 0.5. In brief, the communality index measures how much of the variability in a manifest variable is explained by the variability in its latent variable score (Vinzi et al., 2010b). The average communality of all MVs in a latent variable should be at least greater than 0.5. The goodness-of-fit statistic is simply the geometric mean of the average communality index and the average R2 of each latent variable.
To optimize the SEM, we 1) inspected the model outer correlation matrix to identify the manifest variables having higher correlations with latent constructs other than the ones they were initially assigned to, and 2) evaluated bootstrap confidence intervals of weights of under-performing manifest variables. We dropped those manifest variables that had low predictive power (non-significant path weights) and loaded highly on latent variables outside of their construct (high cross-loadings that did not make ecological sense, for example, if stream length were to load highly on foliar traits.) We report both the fully specified model and the final reduced model from this iterative process.
We conducted bootstrap tests with replacement to test whether nutrient cycling mechanisms differed between watersheds that were predominantly forested (>70% forest) and ones that were not. Note that this landscape is largely a matrix of farmland in south-central Wisconsin that sharply transitions to being largely forested north of the Tension Zone. Path coefficients were calculated in each resampling iteration and the standard error estimates were compared via a parametric t-test (Sanchez 2013).
Results
Unidimensionality tests indicated suboptimal fits in the fully specified model (Supplementary Table S2). Inspection of the outer correlation matrix revealed that multiple MVs loaded higher on other variables than the proposed construct indicating some amount of model miss-specification (Supplementary Table S1) and bootstrapped estimates of path weights (Supplementary Table S2) revealed that most, if not all, such MVs did not have significant path weights (p-value < 0.05). We iteratively dropped each non-significant MV and refit the model until all unidimensionality measures were satisfied (Table 3). After iteratively dropping non-significant manifest variables, we were left with two manifest variables in each construct (Table 4). The reduced model indicated an adequate fit with the Dillon-Goldstein’s Rho >0.7 for both reflective LVs (RUNOFF, WTQUAL, Table 3B). The reduced model also satisfied Kaiser’s rule (second Eigenvectors of all LVs less than 1.0; Table 3) and inspection of the outer correlation matrix confirmed the unidimensionality of the construct with every MV loading highly on its own LV (Table 4). Average communalities for all LVs were also greater than 0.5 (RETENF: 0.939, RETENW: 0.539, RUNOFF: 0.922, LEAKGE: 0.866, WTQUAL: 0.656). The reduced model had a higher goodness-of-fit (0.697) compared to the fully-specified model (0.536) (Table 3).
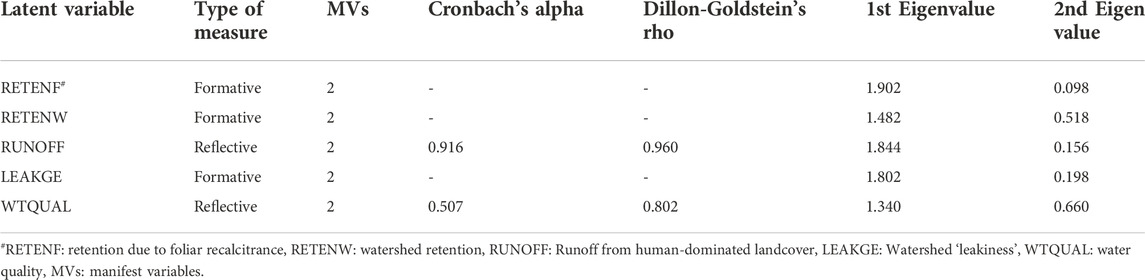
TABLE 3. Unidimensionality measures of the reduced-variable PLS path model. The model had a goodness-of-fit of 0.697.
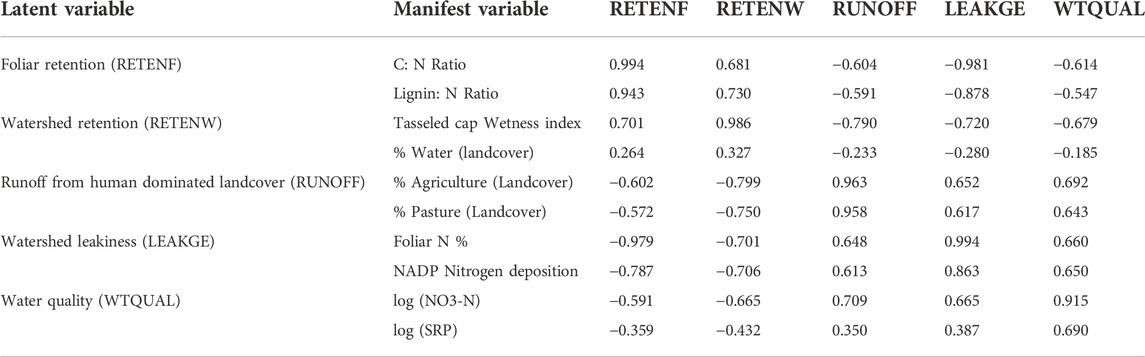
TABLE 4. Outer correlation matrix (correlations of manifest variables with latent variables) of the reduced variable model; shaded cells indicate latent variable blocks (in columns) associated with each manifest variable (in rows), numbers in bold typeface represent the maximum row-wise correlation of the manifest variable with latent variables.
The reduced model contained two manifest variables per each latent variable (Table 5). Nutrient retention due to foliar recalcitrance (RETENF) was best explained by foliar C: N ratios followed by foliar Lignin:N ratios. Retention in watersheds (RETENW) was best explained by the tasseled cap wetness index followed by proportional landcover classified as lakes. Runoff from human-dominated land use (RUNOFF) was equally well explained by proportional area under agriculture and pasture. Watershed ‘leakiness’ (LEAKGE) was best explained by foliar nitrogen concentration and atmospheric N deposition.
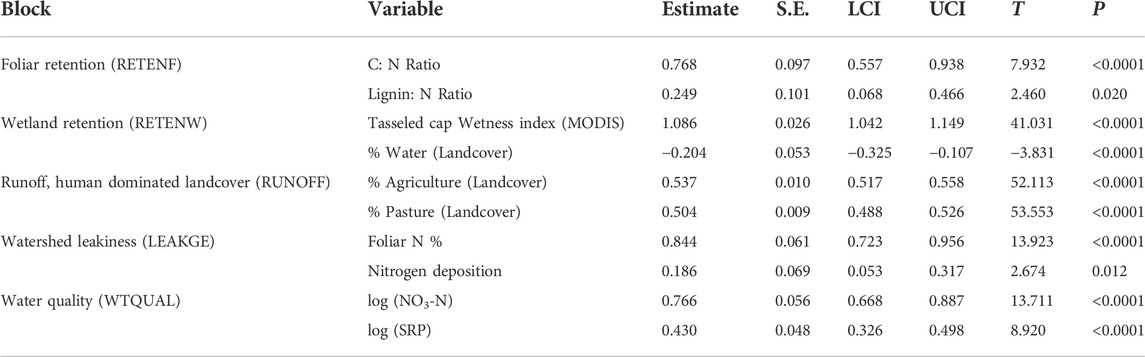
TABLE 5. Bootstrapped outer path weights (standardized coefficients of manifest variables on latent variables) for final reduced variable model. Path weights are presented as estimates from 500 bootstrap estimates, accompanied by interquartile confidence intervals (LCI, UCI), associated T statistics and P- values. All effects are significant at p < 0.05.
Individual inner model path coefficients estimated from the final model revealed that most of our hypotheses were supported by the proposed model (Table 6). The model indicated that foliar recalcitrance increased retention of nutrients in watersheds (RETENF → ↑RETENW; p < 0.0001) and decreased watershed leakiness (RETENF → ↓LEAKGE; p < 0.0001). Nutrient retention in watersheds reduced watershed-scale nutrient export (RETENW → ↓WTQUAL; p < 0.0001), runoff from human-dominated landcover (RETENW → ↓RUNOFF; p < 0.0001) and watershed leakiness (RETENW → ↓LEAKGE; p = 0.018). Runoff from human-dominated landcover increased watershed-scale nutrient export (RUNOFF → ↑WTQUAL; p < 0.0001). Direct loadings between other proposed linkages (Figure 3) had directions in agreement to proposed hypotheses but were not significant (all p > 0.05).
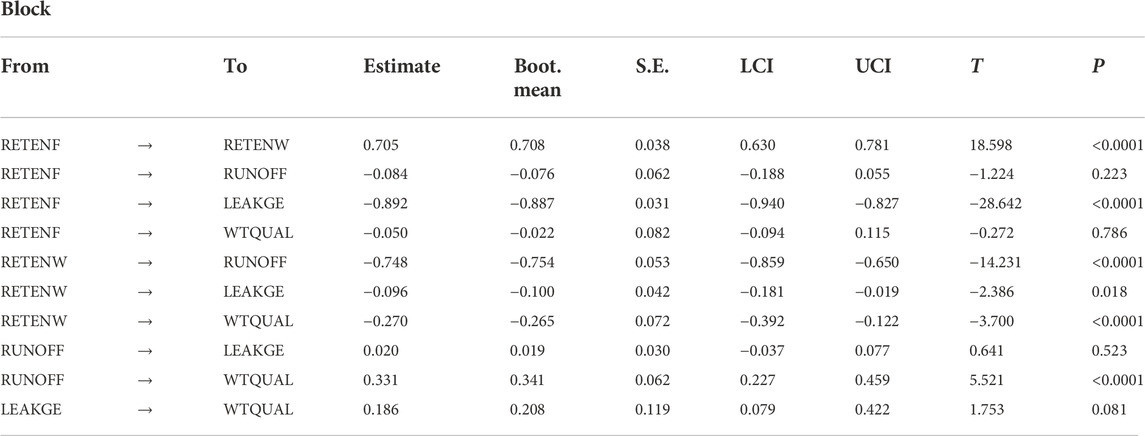
TABLE 6. Inner path coefficients of the final (reduced variable) model. Estimates denote whether an antecedent latent variable (‘From’ column) positively or negatively affects the descendent variable (‘To’ column). Path weights are presented as estimates from 500 bootstrap estimates, accompanied by interquartile confidence intervals (LCI, UCI), associated T statistics and P- values. Effects that are not significant (p < 0.05) are grayed out for clarity.
When paths were aggregated over all possible linkages (i.e., Total effects, Table 7), the model indicates that nutrient retention due to foliar retention had a significant effect on reducing watershed-scale nutrient export (RETENF → ↓WTQUAL; p < 0.0001), and reducing nutrient export from human-dominated landcover (RETENF → ↓RUNOFF; p < 0.0001). The model did not exhibit significant linkages between human-dominated land use patterns and watershed nutrient leakiness, or between watershed leakiness and water quality. Table 8 shows inner model fits that describe how well manifest variables described latent variables. Note the fit RETENF is not estimated because it does not have any antecedent latent variables.
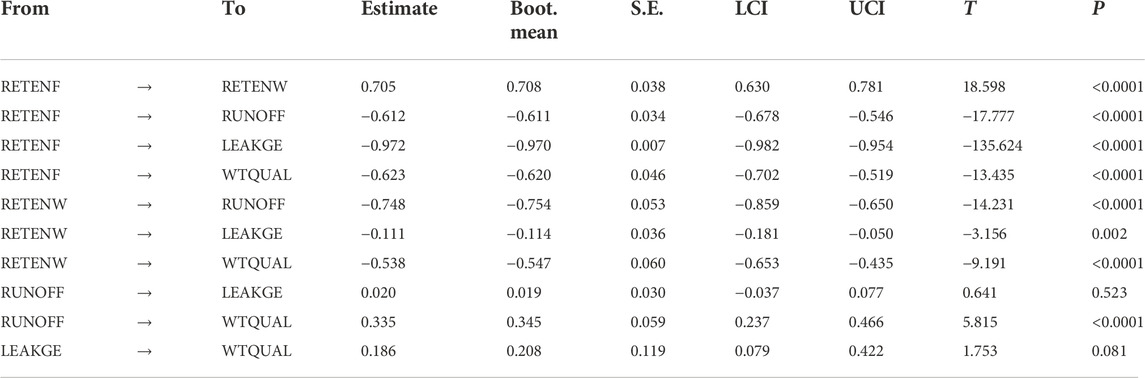
TABLE 7. Total effects of the final (reduced variable) model, estimates denote whether an antecedent latent variable (“From” column) positively or negatively affects the descendent variable (‘To’ column) while accounting for all paths connected through other latent variables (i.e., direct + indirect effects). Path weights are presented as estimates from 500 bootstrap estimates, accompanied by interquartile confidence intervals (LCI, UCI), associated T statistics and P- values. Effects that are not significant (p < 0.05) are grayed out for clarity.
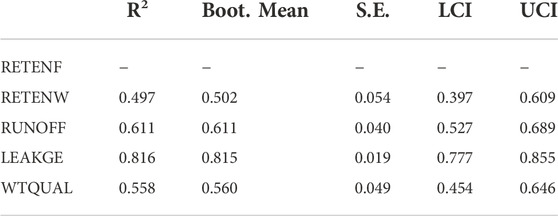
TABLE 8. Inner model fits. Coefficients of determination (R2) representing how well variation in latent variable is described by all antecedent latent variables. Bootstrap standard error estimates (S.E.), and associated interquartile confidence intervals (LCI, UCI) are also presented. Note that RETENF does not have any antecedent latent variables.
Comparing path coefficients between mostly forested (>70%) and other watersheds (Table 9; Figure 4), we found that nutrient retention due to foliar recalcitrance was the predominant factor mitigating nutrient leakage in forested watersheds (RETENF → ↓LEAKGE; p = 0.002). However, in other watersheds (dominated by agriculture in our study area), wetland retention played in more prominent role in ameliorating water quality directly (RETENW → ↓WTQUAL; p = 0.034) as well as through reduction of runoff (RETENW → ↓RUNOFF; p < 0.0001) and leakage (RETENW → ↓LEAKGE; p = 0.022).
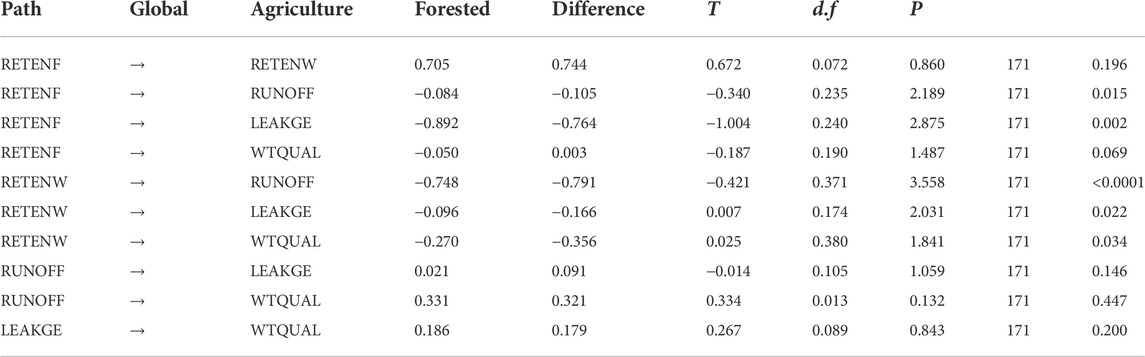
TABLE 9. Comparison of path coefficients between predominantly forested (>70% forested) and more agricultural watersheds. Estimates of Global path coefficients (‘Estimate’ column in Table 6) are presented along with differences, the bootstrap T-statistic of the difference (T), the degrees of freedom and the associated p-value. Comparisons that were not significant grayed out for clarity.
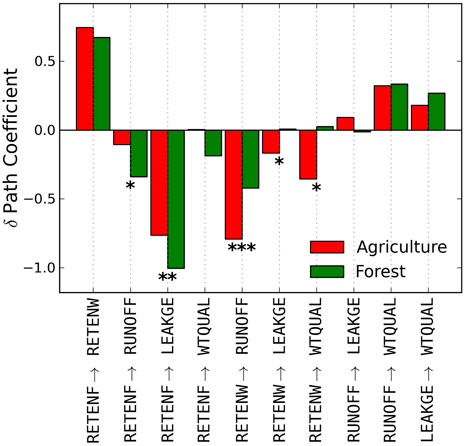
FIGURE 4. Comparison of inner path coefficients of models built for predominantly forested watersheds (>70% forested, green) vs. more agricultural ones (red). *p < 0.05, **p < 0.01, *p < 0.001.
Latent variable scores exhibited strong latitudinal gradients; foliar and watershed retention increased with latitude (RETENF*Latitude r = 0.83, RETENW*Latitude r = 0.74; both p < 0.0001) and runoff and watershed leakage declined (RUNOFF*Latitude r = −0.71, LEAKGE*Latitude = −0.91 respectively; both p < 0.0001), consequently translating to a large latitudinal gradient in water quality indices (WTQUAL*Latitude r = −0.71, p < 0.0001) that parallels agricultural land use patterns in the Upper Midwest (% [Agriculture + Pasture]*Latitude r = −0.72, p < 0.0001). Interestingly, this pattern is independent of the gradient in forest cover in surveyed watersheds (%Forest*Latitude r = 0.065, p = 0.387). These results show that foliar retention as derived from AVIRIS-Classic has a stronger relationship to ecosystem processes than traditionally used landscape variables such as percent land cover. Maps of latent variable scores derived from applying path weights to manifest variables show large amounts of spatial variation in projected litter recalcitrance between predominantly human dominated agriculture-woodlot landscapes (predicted low foliar recalcitrance Figure 5A), mixed-hardwood and wetland dominated forests (predicted moderate foliar recalcitrance Figure 5B) and mixed-coniferous wetland dominated landscapes (predicted high foliar recalcitrance Figure 5C) across the Midwest.
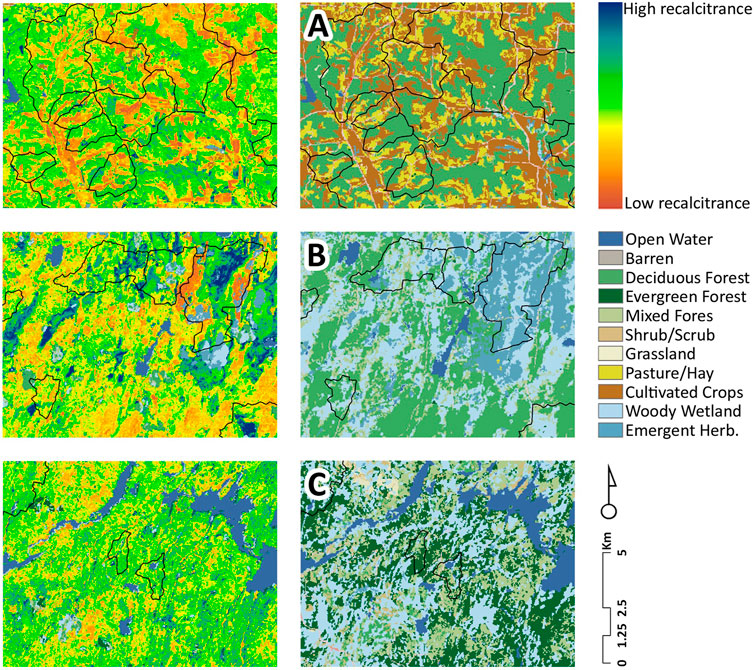
FIGURE 5. Maps of latent variable RETENF (nutrient retention due to foliar recalcitrance) derived by applying path weights (Estimate column, Table 5) to AVIRIS-derived maps of C: N ratio and lignin: N ratio. Brighter colors indicate projected low litter recalcitrance due to high litter quality. Panels on the right are land cover maps derived from NLCD 2006. Letters refer to location of sites in Figure 1. Polygons indicate watersheds used in the study.
Discussion
We explored the relative influence of canopy foliar traits, watershed physiography, and human land use patterns on measures of water quality in first-through third-order streams in the Upper Midwest, United states. We employed structural equation modeling to relate water quality measures (nitrate-N and soluble reactive phosphorus in stream water) with four broad latent variables: 1) nutrient retention due to foliar biochemistry, 2) nutrient retention due to watershed physiography, 3) an index of human activity (landscape composition dominated with urban and agricultural land use), and 4) indicators of watershed-scale nutrient ‘leakiness’. First, we found that higher foliar recalcitrance, as derived from AVIRIS-estimated C: N and lignin, had a direct positive effect on nutrient retention in watersheds and indirectly with overall water quality (i.e., lesser nutrient export), and was negatively correlated with indicators of watershed leakiness and indicators of human activity. Second, indicators of watershed leakiness, as derived from NADP deposition and AVIRIS-estimated %N, and high human activity (derived from NLCD land cover) had direct negative influences on water quality (i.e., high nutrient export) which could be moderated indirectly by retention in watersheds (Tasseled Cap wetness and water body cover) and foliar recalcitrance.
The comparison of structural models for mostly forested watersheds with agricultural watersheds showed that nutrient retention due to foliar recalcitrance was the major factor determining watershed nutrient leakiness in forested ecosystems (Table 9; Figure 4). This finding agrees with earlier studies that have associated recalcitrant foliar traits with reducing litter decomposability and affecting eventual nitrogen cycling rates in several ecosystems (Aber et al., 1991; Verchot et al., 2001; Fortunel et al., 2009a; Kazakou et al., 2009), especially ones with high rates of N deposition and disturbance.
Similarly, we found that indicators of wetland landcover mitigated nutrient export to streams. Importantly, the comparison of agricultural and forested watersheds (Table 9; Figure 4) revealed that watershed retention formed the most important factor mitigating runoff, leakage and eventual water quality in agricultural watersheds. Natural wetlands are known to be important sinks of nutrients (Howard Williams 1985; Johnston 1991; Uusi-Kamppa et al., 2000; Saunders and Kalff 2001), and have led to the proliferation of constructed wetlands for ameliorating water quality issues (Mitsch et al., 1995; Uusi-Kamppa et al., 2000; Mitsch et al., 2005; Vymazal 2007). While the MODIS wetness index was a strong predictor of nutrient retention in watersheds, proportional area mapped as wetlands (from NLCD 2006) was not. Indicators of human dominated land use also behaved as expected with higher proportional areas under agriculture and pastures indicating higher nutrient export to watersheds. Intensive agricultural (Allan et al., 1997; Johnes and Heathwaite 1997; Howarth 1998; Boesch et al., 2001; Hutchins et al., 2010) and animal feeding operations (Carpenter et al., 1998; Pieterse et al., 2003; Buck et al., 2004) have long been identified as detrimental to the water quality of receiving waters, and have attracted considerable attention for targeted management and establishment of total maximum daily loads (Reckhow et al., 2005; Migliaccio and Srivastava 2007; Srivastava et al., 2007; USEPA 2010). Indicators of nutrient leakage from watersheds, however, were not significant predictors of water quality (Table 6, 7). The leakage latent variable consisted of measures of foliar N concentration (possibly an indicator of fertilizer application and/or differential nutrient uptake by vegetation) and N deposition (direct inputs), both ostensibly strong predictors of nitrogen export (Aber and Driscoll 1997; Fenn and Poth 1999; Ollinger et al., 2002; Paerl et al., 2002). These effects may have been better captured by the latent vector for human land use (RUNOFF), which explicitly coded for patterns of agricultural cover types. Post-hoc tests revealed that this might also be an effect of the strong correlation of spatial N deposition patterns in the Upper Midwest with agricultural land use intensity (r = 0.66, p < 0.0001) and proportional land use under pasture (r = 0.55, p < 0.0001). As such, the results do not suggest that foliar N and N deposition are unrelated to water quality, only that patterns in these variables are weaker predictors than measures of land use.
Our findings are in general agreement with other studies conducted in the Upper Midwest in general and Wisconsin in particular (Fitzpatrick et al., 2001; Robertson et al., 2006; Rogers et al., 2009; Singh et al., 2013), but our work builds on these studies by incorporating measures related to the role of vegetation functional traits in watershed nutrient export. Our effort was made possible by recent developments in imaging spectroscopy technology (Ustin et al., 2004; Ollinger and Smith 2005; Kokaly et al., 2009; Singh et al., 2015; Wang et al., 2019) that enable landscape-scale estimation of foliar biochemical and morphological traits known to be strong drivers of ecosystem function and nutrient cycling (Reich et al., 1992; Shipley and Lechowicz 2000; Wright et al., 2004; Shipley et al., 2006). High foliar lignin to nitrogen ratios (Robinson and Jolidon 2005; Hobbie et al., 2007; Johnson et al., 2007) and leaf dry matter content (Garnier et al., 2004; Kazakou et al., 2006; Quested et al., 2007; Fortunel et al., 2009a; Fortunel et al., 2009b) slow litter decomposition rates, but linking measures of litter recalcitrance with landscape-scale processes has remained difficult. We demonstrate that information obtained from imaging spectrometry can be used to simultaneously link ecosystem characteristics such as foliar biochemistry with anthropogenic stressors such as land use patterns to assess landscape-scale responses of ecosystems to perturbations. Indeed, information obtained from imaging spectrometers is increasingly being used for assessing ecosystem attributes such as foliar biochemistry (Asner et al., 2007; Kokaly et al., 2009; Singh et al., 2015; Wang et al., 2019), nutrient cycling (Martin and Aber 1997; Ustin et al., 2004; Martin et al., 2008; Kokaly et al., 2009), invasive species (Lawrence et al., 2006; Underwood et al., 2006; He et al., 2011; Somers and Asner 2013) and mapping canopy fuels (Ha et al., 2006; Jia et al., 2006), and will be increasingly available to scientists and managers with data from missions such as PRISMA and HISUI, and planned missions such as EnMAP (Stuffler et al., 2007), CHIME and SBG. CHIME and SBG have potentially great potential, as these missions are intended to secure global coverage with biweekly or better repeat visits, enabling characterization of dynamics linkages between landscape or vegetation processes and water quality. As well, airborne programs such as the U.S. National Ecological Observatory Network’s (NEON) Airborne Observation Platform (Kampe et al., 2010) can be linked to ongoing aquatic sampling by NEON to further test relationships between watershed variables from imaging spectroscopy and aquatic response variables.
Land use and ecosystems link in multiple ways that influence water quality, although the connections may be indirect (Maloney and Weller 2011). Whereas it is relatively easy to monitor human-driven ecosystem stressors such as land use patterns as a basis to infer fertilizer application rates, the assessment of the role of landscape-scale, apparently unobservable determinants (e.g., decomposition rates) can be difficult. Our study provides a methodology that explicitly links measures of human land use, watershed physiography, ecosystem-wide nutrient subsidies and foliar biochemistry. This could facilitate a spatially explicit approach to targeting management interventions across large regions. We leverage the power of structural equation models to allow the formation of latent constructs that, although ‘unobservable’ in the strict sense, are based on measurements of ecosystem and anthropogenic indicators that have found wide empirical support in previous research and are used in guiding watershed management efforts worldwide.
Conclusion
Overall, we found that canopy foliar chemical and structural traits affected nutrient export across a broad region. These findings are made possible by the use of imaging spectroscopy data. Once such imagery becomes widely available, they will provide the basis for much more comprehensive assessments of the drivers of water quality at landscape and broader scales. Our results provide a potential framework to guide landscape management decisions such as designing nutrient conserving landscapes (Diebel et al., 2009). For example, ‘high leakage’ watersheds could be amended with strategically located wetlands or riparian buffers (Mitsch et al., 1995; Diebel et al., 2009; de Souza et al., 2013) when topographic modifications (e.g., grading) are not possible. Management agencies could target watersheds with varying amounts of disturbance regimes, soil properties and/or physiography (Smith et al., 1997; Brakebill and Preston 2003; Brakebill et al., 2010) by focusing on those factors that are controllable by either natural or management interventions in specific landscapes. For example, the comparisons in Figure 4 suggest that foliar traits play a larger role in mediating nutrient runoff and mitigating effects of N deposition in forests than in largely agricultural watersheds. In contrast, watershed retention (i.e., wetlands) may play a larger role in mitigating runoff and ameliorating effects of N deposition in agricultural compared to forested watersheds. Managing and monitoring ecosystems to ensure balanced delivery of multiple ecosystem services is a key challenge for applied ecology (de Bello et al., 2010). Our study provides a step in this direction: by identifying ecological associations in addition to landscape-scale physiographic and climatological variables, we enable insights into a range of drivers of water quality that may help focus development and restoration policies towards building more resilient landscapes. At the same time, utilizing recent advances in satellite and airborne imaging technologies may make this process more standardized and available to a broader audience of managers and stakeholders.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
AS and PT designed the study. AS collected field data, processed and analyzed imagery, conducted analyses, and wrote the initial manuscript. PT contributed to interpretation of the results, as well as writing, editing and proofreading the manuscript.
Funding
This work was conducted under NASA Terrestrial Ecology grant NNX08AN31G and Applied Sciences grant NNX09AO15G to PT, with additional support from NSF ASCEND Biology Integration Institute award DBI-2021898 and the NASA Surface Biology and Geology (SBG) mission through funding from CalTech Jet Propulsion Laboratory award 1673139.
Acknowledgments
The authors sincerely thank Steve Loheide, Eric Kruger, Mutlu Özdogan, Keith Eshleman, Brenden McNeil, Shawn Serbin, Clayton Kingdon and Bernard Isaacson for helpful discussions and field assistance that helped make this research possible. We also thank Emily Stanley for support in the analysis of stream water samples.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.974206/full#supplementary-material
References
Aber, J. D., and Driscoll, C. T. (1997). Effects of land use, climate variation, and N deposition on N cycling and C storage in northern hardwood forests. Glob. Biogeochem. Cycles 11, 639–648. doi:10.1029/97gb01366
Aber, J. D., Melillo, J. M., Nadelhoffer, K. J., Pastor, J., and Boone, R. D. (1991). “Factors controlling nitrogen cycling and nitrogen saturation in northern temperate forest ecosystems,” in Ecol Appl., 1, 303–315. doi:10.2307/1941759
Allan, J. D., Erickson, D. L., and Fay, J. (1997). The influence of catchment land use on stream integrity across multiple spatial scales. Freshw. Biol. 37, 149–161. doi:10.1046/j.1365-2427.1997.d01-546.x
Alwin, D. F., and Hauser, R. M. (1975). “The decomposition of effects in pathanalysis,” in American Sociological Review 40 (1), 37–47. doi:10.2307/2094445
Arain, M. A., Yuan, F., and Andrew Black, T. (2006). Soil–plant nitrogen cycling modulated carbon exchanges in a western temperate conifer forest in Canada. Agric. For. Meteorology 140 (1), 171–192. doi:10.1016/j.agrformet.2006.03.021
Asner, G. P., Knapp, D. E., Jones, M. O., and Martin, R. E. (2007). Carnegie airborne observatory: In-Flight fusion of hyperspectral imaging and waveform light detection and ranging (wLiDAR) for three-dimensional studies of ecosystems. J. Appl. Remote Sens. 1, 013536. doi:10.1117/1.2794018
Basnyat, P., Teeter, L. D., Lockaby, B. G., and Flynn, K. M. (2000). The use of Remote sensing and GIS in watershed level analyses of non-point source pollution problems. For. Ecol. Manag. 128, 65–73. doi:10.1016/s0378-1127(99)00273-x
Boesch, D. F., Brinsfield, R. B., and Magnien, R. E. (2001). Chesapeake Bay eutrophication: Scientific understanding, ecosystem restoration, and challenges for agriculture. J. Environ. Qual. 30, 303–320. doi:10.2134/jeq2001.302303x
Brakebill, J. W., Ator, S. W., and Schwarz, G. E. (2010). Sources of suspended-sediment flux in streams of the Chesapeake Bay watershed: A regional application of the sparrow Model1. JAWRA J. Am. Water Resour. Assoc. 46, 757–776. doi:10.1111/j.1752-1688.2010.00450.x
Brakebill, J. W., and Preston, S. D. (2003). A hydrologic network supporting spatially referenced regression modeling in the Chesapeake Bay watershed. Environ. Monit. Assess. 81, 73–84. doi:10.1023/a:1021356420864
Buck, O., Niyogi, D. K., and Townsend, C. R. (2004). Scale-dependence of land use effects on water quality of streams in agricultural catchments. Environ. Pollut. 130, 287–299. doi:10.1016/j.envpol.2003.10.018
Butt, B., Turner, M. D., Singh, A., and Brottem, L. (2011). Use of MODIS NDVI to evaluate changing latitudinal gradients of rangeland phenology in Sudano-Sahelian West Africa. Remote Sens. Environ. 115 (12), 3367–3376. doi:10.1016/j.rse.2011.08.001
Carpenter, S. R., Caraco, N. F., Correll, D. L., Howarth, R. W., Sharpley, A. N., and Smith, V. H. (1998). “Nonpoint pollution of surface waters with phosphorus and nitrogen,” in Ecological applications: A publication of the ecological society of America, 8, 559–568.
Chen, S., Hong, X., Harris, C. J., and Sharkey, P. M. (2004). Sparse modeling using orthogonal forward regression with PRESS statistic and regularization. IEEE Trans. Syst. Man. Cybern. B 34, 898–911. doi:10.1109/tsmcb.2003.817107
Chen, Z. Q., Hu, C. M., and Muller-Karger, F. (2007). Monitoring turbidity in tampa Bay using MODIS/aqua 250-M imagery. Remote Sens. Environ. 109, 207–220. doi:10.1016/j.rse.2006.12.019
Chin, W. W. (1998). “The partial least squares approach for structural equation modeling,” in Modern methods for business research. Editor G. A. Marcoulides (London: Lawrence Erlbaum Associates), 295–236.
Cicek, H., Sunohara, M., Wilkes, G., McNairn, B., Pick, F., Topp, E., et al. (2010). Using vegetation indices from satellite Remote sensing to assess corn and soybean response to controlled tile drainage. Agric. Water Manag. 98, 261–270. doi:10.1016/j.agwat.2010.08.019
Compton, J. E., and Boone, R. D. (2000). Long-term impacts of agriculture on soil carbon and nitrogen in new england forests. Ecology 81, 2314–2330. doi:10.1890/0012-9658(2000)081[2314:ltioao]2.0.co;2
Coskun, H. G., Tanik, A., Alganci, U., and Cigizoglu, H. K. (2008). Determination of environmental quality of a drinking water reservoir by Remote sensing, GIS and regression analysis. Water Air Soil Pollut. 194, 275–285. doi:10.1007/s11270-008-9716-x
de Bello, F., Lavorel, S., Diaz, S., Harrington, R., Cornelissen, J. H. C., Bardgett, R. D., et al. (2010). Towards an assessment of multiple ecosystem processes and services via functional traits. Biodivers. Conserv. 19, 2873–2893. doi:10.1007/s10531-010-9850-9
de Souza, A. L. T., Fonseca, D. G., Liborio, R. A., Tanaka, M. O., and Tanaka, M. O. (2013). Influence of riparian vegetation and forest structure on the water quality of rural low-order streams in SE Brazil. For. Ecol. Manag. 298, 12–18. doi:10.1016/j.foreco.2013.02.022
Diebel, M., Maxted, J., Robertson, D., Han, S., and Vander Zanden, M. (2009). Landscape planning for agricultural nonpoint source pollution reduction III: Assessing phosphorus and sediment reduction potential. Environ. Manag. 43, 69–83. doi:10.1007/s00267-008-9139-x
Diebel, M. W., Maxted, J. T., Nowak, P. J., and Vander Zanden, M. J. (2008). Landscape planning for agricultural nonpoint source pollution reduction I: A geographical allocation framework. Environ. Manag. 42, 789–802. doi:10.1007/s00267-008-9186-3
Dijkstra, T. K. (2010). “Latent variables and indices: Herman wold’s basic design and partial least squares,” in Handbook of partial least squares. Editors V. E. Vinzi, W. W. Chin, J. Henseler, and H. Wang (Berlin, Germany: Springer-Verlag), 23–46.
Dybzinski, R., Farrior, C. E., Ollinger, S., and Pacala, S. W. (2013). Interspecific vs intraspecific patterns in leaf nitrogen of forest trees across nitrogen availability gradients. New Phytol. 200, 112–121. doi:10.1111/nph.12353
Elmore, A. J., and Craine, J. M. (2011). Spectroscopic analysis of canopy nitrogen and nitrogen isotopes in managed pastures and hay land. IEEE Trans. Geosci. Remote Sens. 49, 2491–2498. doi:10.1109/tgrs.2011.2104964
Ertaş, A., Yorulmaz, B., and Sukatar, A. (2022). Comparative analysis of biotic indices for assessment of water quality of balaban stream in west anatolia, Turkey. Biologia 77, 721–730. doi:10.1007/s11756-021-00992-7
Eshleman, K. N., Gardner, R. H., Seagle, S. W., Castro, N. M., Fiscus, D. A., Webb, J. R., et al. (2000). Effects of disturbance on nitrogen export from forested lands of the Chesapeake Bay watershed. Environ. Monit. Assess. 63, 187–197. doi:10.1023/a:1006427401665
Eshleman, K. N., McNeil, B. E., and Townsend, P. A. (2009). Validation of a Remote sensing based index of forest disturbance using streamwater nitrogen data. Ecol. Indic. 9, 476–484. doi:10.1016/j.ecolind.2008.07.005
Eshleman, K. N., and Sabo, R. D. (2016). Declining nitrate-N yields in the upper potomac river basin: What is really driving progress under the Chesapeake Bay restoration? Atmos. Environ. 146, 280–289. doi:10.1016/j.atmosenv.2016.07.004
Fausey, N. R., Brown, L. C., Belcher, H. W., and Kanwar, R. S. (1995). Drainage and water-quality in great-lakes and corn-belt states. J. Irrig. Drain. Eng. 121, 283–288. doi:10.1061/(asce)0733-9437(1995)121:4(283)
Fenn, M. E., and Poth, M. A. (1999). Temporal and spatial trends in streamwater nitrate concentrations in the san bernardino mountains, southern California. J. Environ. Qual. 28, 822–836. doi:10.2134/jeq1999.00472425002800030013x
Fennessy, M. S., and Cronk, J. K. (1997). The effectiveness and restoration potential of riparian ecotones for the management of nonpoint source pollution, particularly nitrate. Crit. Rev. Environ. Sci. Technol. 27, 285–317. doi:10.1080/10643389709388502
Fitzpatrick, F. A., Scudder, B. C., Lenz, B. N., and Sullivan, D. J. (2001). Effects of multi-scale environmental characteristics on agricultural stream biota in eastern Wisconsin. J. Am. Water Resour. Assoc. 37, 1489–1507. doi:10.1111/j.1752-1688.2001.tb03655.x
Fortunel, C., Garnier, E., Joffre, R., Kazakou, E., Quested, H., Grigulis, K., et al. (2009a). Leaf traits capture the effects of land use changes and climate on litter decomposability of grasslands across europe. Ecology 90, 598–611. doi:10.1890/08-0418.1
Fortunel, C., Violle, C., Rourmet, C., Buatois, B., Navas, M. L., and Garnier, E. (2009b). Allocation strategies and seed traits are hardly affected by nitrogen supply in 18 species differing in successional status. Perspect. Plant Ecol. Evol. Syst. 11, 267–283. doi:10.1016/j.ppees.2009.04.003
Friedland, R., Macias, D., Cossarini, G., Daewel, U., Estournel, C., Garcia-Gorriz, E., et al. (2021). Effects of nutrient management scenarios on marine eutrophication indicators: A pan-European, multi-model assessment in support of the marine strategy framework directive. Front. Mar. Sci. 8. doi:10.3389/fmars.2021.596126
Fry, J. A., Xian, G. S., Jin, S., Dewitz, J., Homer, C. G., Yang, L., et al. (2011). “Completion of the 2011 national land cover database for the conterminous United States,” in Photogrammetric Engineering and Remote Sensing, 77 (9), 858–864.
Garnier, E., Cortez, J., Billes, G., Navas, M. L., Roumet, C., Debussche, M., et al. (2004). Plant functional markers capture ecosystem properties during secondary succession. Ecology 85, 2630–2637. doi:10.1890/03-0799
Gesch, D., Oimoen, M., Greenlee, S., Nelson, C., Steuck, M., and Tyler, D. (2002). The national elevation Dataset. Photogrammetric engineering and Remote sensing, 68 (1), 5-11. doi:10.3133/fs14899
Griffith, J. A. (2002). Geographic techniques and recent applications of Remote sensing to landscape-water quality studies. Water, Air, Soil Pollut. 138, 181–197. doi:10.1023/a:1015546915924
Griffith, J. A., Martinko, E. A., Whistler, J. L., and Price, K. P. (2002). “Interrelationships among landscapes, NDVI, and stream water quality in the US central plains,” in Ecological applications: A publication of the ecological society of America, 12, 1702–1718.
Ha, G. S. J., Burke, I. C., Kaufmann, M. R., Goetz, A. F. H., Kindel, B. C., and Pu, Y. F. (2006). Estimates of forest canopy fuel attributes using hyperspectral data. For. Ecol. Manag. 229, 27–38. doi:10.1016/j.foreco.2006.03.021
Hall, R. I., Leavitt, P. R., Quinlan, R., Dixit, A. S., and Smol, J. P. (1999). Effects of agriculture, urbanization, and climate on water quality in the northern great plains. Limnol. Oceanogr. 44, 739–756. doi:10.4319/lo.1999.44.3_part_2.0739
He, K. S., Rocchini, D., Neteler, M., and Nagendra, H. (2011). Benefits of hyperspectral Remote sensing for tracking plant invasions. Divers. Distributions 17, 381–392. doi:10.1111/j.1472-4642.2011.00761.x
Healey, S. P., Cohen, W. B., Yang, Z. Q., and Krankina, O. N. (2005). Comparison of tasseled cap-based Landsat data structures for use in forest disturbance detection. Remote Sens. Environ. 97, 301–310. doi:10.1016/j.rse.2005.05.009
Hobbie, S. E., Ogdahl, M., Chorover, J., Chadwick, O. A., Oleksyn, J., Zytkowiak, R., et al. (2007). Tree species effects on soil organic matter dynamics: The role of soil cation composition. Ecosystems 10, 999–1018. doi:10.1007/s10021-007-9073-4
Howard Williams, C. (1985). Cycling and retention of nitrogen and phosphorus in wetlands - a theoretical and applied perspective. Freshw. Biol. 15, 391–431. doi:10.1111/j.1365-2427.1985.tb00212.x
Howarth, R. W. (1998). An assessment of human influences on fluxes of nitrogen from the terrestrial landscape to the estuaries and continental shelves of the North atlantic ocean. Nutrient Cycl. Agroecosyst. 52, 213–223. doi:10.1023/a:1009784210657
Howarth, R. W., Billen, G., Swaney, D., Townsend, A., Jaworski, N., Lajtha, K., et al. (1996). Regional nitrogen budgets and riverine N&P fluxes for the drainages to the North atlantic ocean: Natural and human influences. Biogeochemistry 35, 75–139. doi:10.1007/bf02179825
Hu, X., and Ou, Y. (2013). Translating lake nutrient reference levels into nutrient criteria. Fresenius Environ. Bull. 22, 400–403.
Huang, S., Arain, M. A., Arora, V. K., Yuan, F. M., Brodeur, J., and Peichl, M. (2011). Analysis of nitrogen controls on carbon and water exchanges in a conifer forest using the CLASS-CTEMN+ model. Ecol. Model. 222, 3743–3760. doi:10.1016/j.ecolmodel.2011.09.008
Hutchins, M. G., Deflandre-Vlandas, A., Posen, P. E., Davies, H. N., and Neal, C. (2010). How do river nitrate concentrations respond to changes in land-use? A modelling case study of headwaters in the river derwent catchment, north yorkshire, UK. Environ. Model. Assess. (Dordr). 15, 93–109. doi:10.1007/s10666-009-9218-2
Jia, G. J., Burke, I. C., Goetz, A. F. H., Kaufmann, M. R., and Kindel, B. C. (2006). Assessing spatial patterns of forest fuel using AVIRIS data. Remote Sens. Environ. 102, 318–327. doi:10.1016/j.rse.2006.02.025
Johnes, P. J., and Heathwaite, A. L. (1997). Modelling the impact of land use change on water quality in agricultural catchments. Hydrol. Process. 11, 269–286. doi:10.1002/(sici)1099-1085(19970315)11:3<269:aid-hyp442>3.0.co;2-k
Johnson, J. M. F., Barbour, N. W., and Weyers, S. L. (2007). Chemical composition of crop biomass impacts its decomposition. Soil Sci. Soc. Am. J. 71, 155–162. doi:10.2136/sssaj2005.0419
Johnson, L. B., Richards, C., Host, G. E., and Arthur, J. W. (1997). Landscape influences on water chemistry in midwestern stream ecosystems. Freshw. Biol. 37, 193–208. – +. doi:10.1046/j.1365-2427.1997.d01-539.x
Johnston, C. A. (1991). Sediment and nutrient retention by fresh-water wetlands - effects on surface-water quality. Crit. Rev. Environ. Control 21, 491–565. doi:10.1080/10643389109388425
Kampe, T. U., Johnson, B. R., Kuester, M., and Keller, M. (2010). Neon: The first continental-scale ecological observatory with airborne Remote sensing of vegetation canopy biochemistry and structure. J. Appl. Remote Sens. 4, 043510. doi:10.1117/1.3361375
Kazakou, E., Vile, D., Shipley, B., Gallet, C., and Garnier, E. (2006). Co-variations in litter decomposition, leaf traits and plant growth in species from a mediterranean old-field succession. Funct. Ecol. 20, 21–30. doi:10.1111/j.1365-2435.2006.01080.x
Kazakou, E., Violle, C., Roumet, C., Pintor, C., Gimenez, O., and Garnier, E. (2009). Litter quality and decomposability of species from a mediterranean succession depend on leaf traits but not on nitrogen supply. Ann. Bot. 104, 1151–1161. doi:10.1093/aob/mcp202
Kennedy, R. E., Yang, Z. G., and Cohen, W. B. (2010). Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr - temporal segmentation algorithms. Remote Sens. Environ. 114, 2897–2910. doi:10.1016/j.rse.2010.07.008
Kleinebecker, T., Schmidt, S. R., Fritz, C., Smolders, A. J. P., and Holzel, N. (2009). Prediction of delta 13C and delta 15N in plant tissues with near-infrared reflectance spectroscopy. New Phytol. 184, 732–739. doi:10.1111/j.1469-8137.2009.02995.x
Kokaly, R. F., Asner, G. P., Ollinger, S. V., Martin, M. E., and Wessman, C. A. (2009). Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 113, S78–S91. doi:10.1016/j.rse.2008.10.018
Krysanova, V., Muller-Wohlfeil, D. I., and Becker, A. (1998). Development and test of a spatially distributed hydrological water quality model for mesoscale watersheds. Ecol. Model. 106, 261–289. doi:10.1016/s0304-3800(97)00204-4
Lawrence, R. L., Wood, S. D., and Sheley, R. L. (2006). Mapping invasive plants using hyperspectral imagery and breiman cutler classifications (RandomForest). Remote Sens. Environ. 100, 356–362. doi:10.1016/j.rse.2005.10.014
Li, X., Ambrose, R. B., and Araujo, R. (2004). Modeling mineral nitrogen export from a forest terrestrial ecosystem to streams. Trans. ASAE 47, 727–739. doi:10.13031/2013.16105
Lohmoller, J. B. (1989). Latent variable path modeling with partial least squares. Heidelberg: Physica.
Lowrance, R., Altier, L. S., Newbold, J. D., Schnabel, R. R., Groffman, P. M., Denver, J. M., et al. (1997). Water quality functions of riparian forest buffers in Chesapeake Bay watersheds. Environ. Manag. 21, 687–712. doi:10.1007/s002679900060
Lyons, John, Wang, Lizhu, and Simonson, Timothy D. (1996). Development and validation of an index of biotic integrity for coldwater streams in Wisconsin. North Am. J. Fish. Manag. 16, 241–256. doi:10.1577/1548-8675(1996)016<0241:davoai>2.3.co;2
Majeke, B., van Aardt, J. A. N., and Cho, M. A. (2008). Imaging spectroscopy of foliar biochemistry in forestry environments. South. For. a J. For. Sci. 70, 275–285. doi:10.2989/sf.2008.70.3.11.672
Maloney, K. O., and Weller, D. E. (2011). Anthropogenic disturbance and streams: Land use and land-use change affect stream ecosystems via multiple pathways. Freshw. Biol. 56, 611–626. doi:10.1111/j.1365-2427.2010.02522.x
Martin, M. E., and Aber, J. D. (1997). “High spectral resolution Remote sensing of forest canopy lignin, nitrogen, and ecosystem processes,” in Ecological applications: A publication of the ecological society of America, 7, 431–443.
Martin, M. E., Plourde, L. C., Ollinger, S. V., Smith, M. L., and McNeil, B. E. (2008). A generalizable method for Remote sensing of canopy nitrogen across a wide range of forest ecosystems. Remote Sens. Environ. 112, 3511–3519. doi:10.1016/j.rse.2008.04.008
Mattikalli, N. M., and Richards, K. S. (1996). Estimation of surface water quality changes in response to land use change: Application of the export coefficient model using Remote sensing and geographical information system. J. Environ. Manag. 48, 263–282. doi:10.1006/jema.1996.0077
McCarty, G. W., McConnell, L. L., Hapernan, C. J., Sadeghi, A., Graff, C., Hively, W. D., et al. (2008). Water quality and conservation practice effects in the choptank river watershed. J. Soil Water Conservation 63, 461–474. doi:10.2489/jswc.63.6.461
McNeil, B. E., de Beurs, K. M., Eshleman, K. N., Foster, J. R., and Townsend, P. A. (2007). Maintenance of ecosystem nitrogen limitation by ephemeral forest disturbance: An assessment using MODIS, Hyperion, and Landsat ETM+. Geophys. Res. Lett. 34, L19406. doi:10.1029/2007gl031387
McNeil, B. E., Read, J. M., Sullivan, T. J., McDonnell, T. C., Fernandez, I. J., and Driscoll, C. T. (2008). “The spatial pattern of nitrogen cycling in the adirondack park, New York,” in Ecological applications: A publication of the ecological society of America, 18, 438–452.
Meador, M. R., and Goldstein, R. M. (2003). Assessing water quality at large geographic scales: Relations among land use, water physicochemistry, riparian condition, and fish community structure. Environ. Manag. 31, 504–517. doi:10.1007/s00267-002-2805-5
Melvin, A. M., Mack, M. C., Johnstone, J. F., McGuire, A. D., Genet, H., and Schuur, E. A. G. (2015). Differences in ecosystem carbon distribution and nutrient cycling linked to forest tree species composition in a mid-successional boreal forest. Ecosystems 18 (8), 1472–1488. doi:10.1007/s10021-015-9912-7
Migliaccio, K. W., and Srivastava, P. (2007). Hydrologic components of watershed-scale models. Trans. Asabe 50, 1695–1703. doi:10.13031/2013.23955
Mitsch, W. J., Cronk, J. K., Wu, X. Y., Nairn, R. W., and Hey, D. L. (1995). “Phosphorus retention in constructed fresh-water riparian marshes,” in Ecological applications: A publication of the ecological society of America, 5, 830–845.
Mitsch, W. J., Zhang, L., Anderson, C. J., Altor, A. E., and Hernandez, M. E. (2005). Creating riverine wetlands: Ecological succession, nutrient retention, and pulsing effects. Ecol. Eng. 25, 510–527. doi:10.1016/j.ecoleng.2005.04.014
Morari, F., Lugato, E., Polese, R., Berti, A., and Giardini, L. (2012). Nitrate concentrations in groundwater under contrasting agricultural management practices in the low plains of Italy. Agric. Ecosyst. Environ. 147, 47–56. doi:10.1016/j.agee.2011.03.001
Mosier, A. R. (1998). Soil processes and global change. Biol. Fertil. Soils 27, 221–229. doi:10.1007/s003740050424
NADP (2014). “National atmospheric deposition program,” in NADP program office, Illinois state water survey, 2204 (Champaign: Griffith Dr.). IL 61820. Available Online at http://nadp.sws.uiuc.edu/ (Accessed August 2013).
NHDPlus (2010). Horizon systems, NHDPlus documentation, version1. Available Online at Http://www.horizon-Systems.com/nhdplus/documentation.php. (Accessed September 2012)
NRCS (2007). “Hydrologic soil groups,” Chapter 7, Part 630 Hydrology, National Engineering Handbook, US Department of Agriculture,” in Natural Resources Conservation Service, Washington DC.
Ollinger, S. V., Smith, M. L., Martin, M. E., Hallett, R. A., Goodale, C. L., and Aber, J. D. (2002). Regional variation in foliar chemistry and N cycling among forests of diverse history and composition. Ecology 83, 339–355. doi:10.2307/2680018
Ollinger, S. V., and Smith, M. L. (2005). Net primary production and canopy nitrogen in a temperate forest landscape: An analysis using imaging spectroscopy, modeling and field data. Ecosystems 8, 760–778. doi:10.1007/s10021-005-0079-5
Paerl, H. W., Dennis, R. L., and Whitall, D. R. (2002). Atmospheric deposition of nitrogen: Implications for nutrient over-enrichment of coastal waters. Estuaries 25, 677–693. doi:10.1007/bf02804899
Pieterse, N. M., Bleuten, W., and Jorgensen, S. E. (2003). Contribution of point sources and diffuse sources to nitrogen and phosphorus loads in lowland river tributaries. J. Hydrology 271, 213–225. doi:10.1016/s0022-1694(02)00350-5
Quested, H., Eriksson, O., Fortunel, C., and Garnier, E. (2007). Plant traits relate to whole-community litter quality and decomposition following land use change. Funct. Ecol. 21, 1016–1026. doi:10.1111/j.1365-2435.2007.01324.x
Reay, W. G., Gallagher, D. L., and Simmons, G. M. (1992). Groundwater discharge and its impact on surface-water quality in a Chesapeake Bay inlet. J. Am. Water Resour. Assoc. 28, 1121–1134. doi:10.1111/j.1752-1688.1992.tb04023.x
Reckhow, K. H., Arhonditsis, G. B., Kenney, M. A., Hauser, L., Tribo, J., Wu, C., et al. (2005). A predictive approach to nutrient criteria. Environ. Sci. Technol. 39, 2913–2919. doi:10.1021/es048584i
Reed, B. C., Brown, J. F., Vanderzee, D., Loveland, T. R., Merchant, J. W., and Ohlen, D. O. (1994). Measuring phenological variability from satellite imagery. J. Veg. Sci. 5, 703–714. doi:10.2307/3235884
Reich, P. B., Ellsworth, D. S., Walters, M. B., Vose, J. M., Gresham, C., Volin, J. C., et al. (1999). Generality of leaf trait relationships: A test across six biomes. Ecology 80, 1955–1969. doi:10.1890/0012-9658(1999)080[1955:goltra]2.0.co;2
Reich, P. B., Walters, M. B., and Ellsworth, D. S. (1992). Leaf life-span in relation to leaf, plant, and stand characteristics among diverse ecosystems. Ecol. Monogr. 62, 365–392. doi:10.2307/2937116
Reich, P. B., Wright, I. J., Cavender-Bares, J., Craine, J. M., Oleksyn, J., Westoby, M., et al. (2003). The evolution of plant functional variation: Traits, spectra, and strategies. Int. J. Plant Sci. 164, S143–S164. doi:10.1086/374368
Roberts, A. D., and Prince, S. D. (2010). Effects of urban and non-urban land cover on nitrogen and phosphorus runoff to Chesapeake Bay. Ecol. Indic. 10, 459–474. doi:10.1016/j.ecolind.2009.07.017
Robertson, D. M., Graczyk, D. J., Garrison, P. J., Wang, L., Laliberte, G., and Bannerman, R. (2006). Nutrient concentrations and their relations to biotic integrity of wadeable streams in Wisconsin. Middleton, WI: USGS Wisconsin Water Science Center.
Robinson, C. T., and Jolidon, C. (2005). Leaf breakdown and the ecosystem functioning of alpine streams. J. North Am. Benthol. Soc. 24, 495–507. doi:10.1899/04-100.1
Rogers, J. S., Potter, K. W., Hoffman, A. R., Hoopes, J. A., Wu, C. H., and Armstrong, D. E. (2009). Hydrologic and water quality functions of a disturbed wetland in an agricultural setting. JAWRA J. Am. Water Resour. Assoc. 45, 628–640. doi:10.1111/j.1752-1688.2009.00311.x
Rooney, R. C., and Bayley, S. E. (2011). Relative influence of local- and landscape-level habitat quality on aquatic plant diversity in shallow open-water wetlands in alberta’s boreal zone: Direct and indirect effects. Landsc. Ecol. 26, 1023–1034. doi:10.1007/s10980-011-9629-8
Rosov, K. A., Mallin, M. A., and Cahoon, L. B. (2020). Waste nutrients from U.S. Animal feeding operations: Regulations are inconsistent across states and inadequately assess nutrient export risk. J. Environ. Manag. 269, 110738. doi:10.1016/j.jenvman.2020.110738
Santiago, L. S. (2007). Extending the leaf economics spectrum to decomposition: Evidence from a tropical forest. Ecology 88, 1126–1131. doi:10.1890/06-1841
Santiago, L. S., Kitajima, K., Wright, S. J., and Mulkey, S. S. (2004). Coordinated changes in photosynthesis, water relations and leaf nutritional traits of canopy trees along a precipitation gradient in lowland tropical forest. Oecologia 139, 495–502. doi:10.1007/s00442-004-1542-2
Saunders, D. L., and Kalff, J. (2001). Nitrogen retention in wetlands, lakes and rivers. Hydrobiologia 443, 205–212. doi:10.1023/a:1017506914063
Schindler, D. W., and Bayley, S. E. (1993). The biosphere as an increasing sink for atmospheric carbon: Estimates from increased nitrogen depostion. Glob. Biogeochem. Cycles 7, 717–733. doi:10.1029/93gb02562
Schleip, C., Sparks, T. H., Estrella, N., and Menzel, A. (2009). Spatial variation in onset dates and trends in phenology across europe. Clim. Res. 39, 249–260. doi:10.3354/cr00830
Schwarz, G. E., and Alexander, R. B. (1995). “Soils data for the conterminous United States derived from the NRCS state soil geographic (STATSGO) data base,” in Open-file report Issue_Identification 95-449. 1.1 ed (Reston, VA: U.S. Geological Survey). http://water.usgs.gov/lookup/getspatial?ussoils.
Seaton, F. M., Jones, D. L., Creer, S., Paul, B. L., George, , Smart, S. M., et al. (2019). Plant and soil communities are associated with the response of soil water repellency to environmental stress. Sci. Total Environ. 687, 929–938. Available at: https://www.sciencedirect.com/science/article/pii/S0048969719326130. doi:10.1016/j.scitotenv.2019.06.052
Shepard, R. (2005). Nutrient management planning: Is it the answer to better management? J. Soil Water Conservation 60, 171–176.
Shipley, B., and Lechowicz, M. J. (2000). The functional Co-ordination of leaf morphology, nitrogen concentration, and gas exchange in 40 wetland species. Ecoscience 7, 183–194. doi:10.1080/11956860.2000.11682587
Shipley, B., Lechowicz, M. J., Wright, I., and Reich, P. B. (2006). Fundamental trade-offs generating the worldwide leaf economics spectrum. Ecology 87, 535–541. doi:10.1890/05-1051
Shortle, J., Ollikainen, M., and Iho, A. (2021). Water quality and agriculture: Economics and policy for nonpoint source water pollution. Springer International Publishing. Available at: https://link.springer.com/book/10.1007/978-3-030-47087-6#about-this-book.
Singh, A., Jakubowski, A. R., Chidister, I., and Townsend, P. A. (2013). A MODIS approach to predicting stream water quality in Wisconsin. Remote Sens. Environ. 128, 74–86. doi:10.1016/j.rse.2012.10.001
Singh, A., Serbin, S. P., McNeil, B. E., Kingdon, C. C., and Townsend, P. A. (2015). “Imaging spectroscopy algorithms for mapping canopy foliar chemical and morphological traits and their uncertainties,” in Ecological applications: A publication of the ecological society of America, 25, 2180–2197.8
Smith, M. L., Ollinger, S. V., Martin, M. E., Aber, J. D., Hallett, R. A., and Goodale, C. L. (2002). “Direct estimation of aboveground forest productivity through hyperspectral Remote sensing of canopy nitrogen,” in Ecological applications: A publication of the ecological society of America, 12, 1286–1302.
Smith, R. A., Schwarz, G. E., and Alexander, R. B. (1997). Regional interpretation of water-quality monitoring data. Water Resour. Res. 33, 2781–2798. doi:10.1029/97wr02171
Somers, B., and Asner, G. P. (2013). Multi-temporal hyperspectral mixture analysis and feature selection for invasive species mapping in rainforests. Remote Sens. Environ. 136, 14–27. doi:10.1016/j.rse.2013.04.006
Soulard, C. E., Acevedo, W., Cohen, W. B., Yang, Z, Stehman, S. V., and Taylor, J. L. (2017). Harmonization of forest disturbance datasets of the conterminous USA from 1986 to 2011. Environ. Monit. Assess. 189 (4), 170. doi:10.1007/s10661-017-5879-5
Srivastava, P., Migliaccio, K. W., and Simunek, J. (2007). Landscape models for simulating water quality at point, field, and watershed scales. Trans. Asabe 50, 1683–1693. doi:10.13031/2013.23961
Stanley, E. H., and Maxted, J. T. (2008). “Changes in the dissolved nitrogen pool across land cover gradients in Wisconsin streams,” in Ecological applications: A publication of the ecological society of America, 18, 1579–1590.
Stöckli, R., Rutishauser, T., Dragoni, D., O’Keefe, J., Thornton, P. E., Jolly, M., et al. (2008). Remote sensing data assimilation for a prognostic phenology model. J. Geophys. Res. 113. doi:10.1029/2008jg000781
Stuffler, T., Kaufmann, C., Hofer, S., Forster, K. P., Schreier, G., Mueller, A., et al. (2007). The EnMAP hyperspectral imager- an advanced optical payload for future applications in earth observation programmes. Acta Astronaut. 61, 115–120. doi:10.1016/j.actaastro.2007.01.033
Thornton, P. E., Thornton, M. M., Mayer, B. W., Wilhelmi, N., Wei, Y., and Cook, R. B. (2012). Daymet: Daily surface weather on a 1 Km grid for north America, 1980-2012. (Accessed August 2013). doi:10.3334/ORNLDAAC/Daymet_V2
Townsend, P. A., Eshleman, K. N., and Welcker, C. (2004). “Remote sensing of gypsy moth defoliation to assess variations in stream nitrogen concentrations,” in Ecological applications: A publication of the ecological society of America, 14, 504–516.
Townsend, P. A., Foster, J. R., Chastain, R. A., and Currie, W. S. (2003). Application of imaging spectroscopy to mapping canopy nitrogen in the forests of the central appalachian mountains using hyperion and AVIRIS. IEEE Trans. Geosci. Remote Sens. 41, 1347–1354. doi:10.1109/tgrs.2003.813205
Townsend, P. A., Singh, A., Foster, J. R., and Rehberg, N. J. (2012). A general Landsat model to predict canopy defoliation in broadleaf deciduous forests. Remote Sens. Environ. 119, 255–265. https://www.sciencedirect.com/science/article/pii/S0034425712000119. doi:10.1016/j.rse.2011.12.023
Tukey, J. W. (1964). “Causation, regression and path analysis,” in Statistics and mathematics in biology (Ne York: Hafner).
Underwood, E. C., Mulitsch, M. J., Greenberg, J. A., Whiting, M. L., Ustin, S. L., and Kefauver, S. C. (2006). Mapping invasive aquatic vegetation in the sacramento-san joaquin delta using hyperspectral imagery. Environ. Monit. Assess. 121, 47–64. doi:10.1007/s10661-005-9106-4
USEPA (2010). Chesapeake Bay total maximum daily load for nitrogen, phosphorus and sediment, executive summary. Annapolis, MD: US Environmental Protection Agency.
Ustin, S. L., Roberts, D. A., Gamon, J. A., Asner, G. P., and Green, R. O. (2004). Using imaging spectroscopy to study ecosystem processes and properties. Bioscience 54, 523–534. doi:10.1641/0006-3568(2004)054[0523:uistse]2.0.co;2
Uusi-Kamppa, J., Braskerud, B., Jansson, H., Syversen, N., and Uusitalo, R. (2000). Buffer zones and constructed wetlands as filters for agricultural phosphorus. J. Environ. Qual. 29, 151–158. doi:10.2134/jeq2000.00472425002900010019x
Verchot, L. V., Holmes, Z., Mulon, L., Groffman, P. M., and Lovett, G. M. (2001). Gross vs net rates of N mineralization and nitrification as indicators of functional differences between forest types. Soil Biol. Biochem. 33, 1889–1901. doi:10.1016/s0038-0717(01)00095-5
Vinzi, V. E., Chin, W. W., Henseler, J., and Wang, H. (2010a). “Handbook of partial least squares: Concepts, methods and applications,” in Springer handbooks of computational statistics (Berlin, Germany: Springer-Verlag), 813.
Vinzi, V. E., Trinchera, L., and Amato, S. (2010b). “PLS path modeling: From foundations to recent developments and open issues for model assessment and improvement,” in Handbook of partial least squares. Editors V. E. Vinzi, W. W. Chin, J. Henseler, and H. Wang (Berlin: Springer-Verlag), 47–82.
Vitousek, P. M., Aber, J. D., Howarth, R. W., Likens, G. E., Matson, P. A., Schindler, D. W., et al. (1997). “Human alteration of the global nitrogen cycle: Sources and consequences,” in Ecological applications: A publication of the ecological society of America, 7, 737–750.
Vymazal, Jan (2007). Removal of nutrients in various types of constructed wetlands. Sci. Total Environ. 380, 48–65. doi:10.1016/j.scitotenv.2006.09.014
Wang, Z., Townsend, P. A., and Schweiger, A. K. (2019). Mapping foliar functional traits and their uncertainties across three years in a grassland experiment. Remote Sens. Environ. 221, 405–416. https://www.sciencedirect.com/science/article/pii/S003442571830525X. doi:10.1016/j.rse.2018.11.016
Wold, H. (1966). “Estimation of principal component and related models by iterative least squares,” in Multivariate analysis. Editor P. R. Krishnaiah (New York: Academic Press), 391–420.
Wolock, D. M. (2003). Base-flow index grid for the conterminous United States.” U.S. Geological survey open-file report. Reston, Virginia: U.S. Geological Survey. http://water.usgs.gov/lookup/getspatial?bfi48grd.
Worrall, F., and Burt, T. P. (1999). The impact of land-use change on water quality at the catchment scale: The use of export coefficient and structural models. J. Hydrology 221, 75–90. doi:10.1016/s0022-1694(99)00084-0
Wright, I. J., Reich, P. B., Cornelissen, J. H. C., Falster, D. S., Garnier, E., Hikosaka, K., et al. (2005). Assessing the generality of global leaf trait relationships. New Phytol. 166, 485–496. doi:10.1111/j.1469-8137.2005.01349.x
Wright, I. J., Reich, P. B., Westoby, M., Ackerly, D. D., Baruch, Z., Bongers, F., et al. (2004). The worldwide leaf economics spectrum. Nature 428, 821–827. doi:10.1038/nature02403
Wright, I. J., Westoby, M., and Reich, P. B. (2002). Convergence towards higher leaf mass per area in dry and nutrient-poor habitats has different consequences for leaf life span. J. Ecol. 90, 534–543. doi:10.1046/j.1365-2745.2002.00689.x
WSLH (1993). “Manual of Analytical Methods. Environmental Science Section, Inorganic Chemistry Unit,” in Wisconsin State Laboratory of Hygiene, Madison, WI. [variously paged].
Zampella, R. A., Procopio, N. A., Lathrop, R. G., and Dow, C. L. (2007). Relationship of land-use/land-cover patterns and surface-water quality in the mullica river basin. J. Am. Water Resour. Assoc. 43, 594–604. doi:10.1111/j.1752-1688.2007.00045.x
Keywords: water quality, imaging spectroscopy, structural equation model, foliar traits, AVIRIS
Citation: Singh A and Townsend PA (2023) Influence of foliar traits, watershed physiography, and nutrient subsidies on stream water quality in the upper midwestern United States. Front. Environ. Sci. 10:974206. doi: 10.3389/fenvs.2022.974206
Received: 20 June 2022; Accepted: 08 November 2022;
Published: 17 March 2023.
Edited by:
Roozbeh Rajabi, Qom University of Technology, IranReviewed by:
Daniel Sousa, San Diego State University, United StatesRabin Bhattarai, University of Illinois at Urbana-Champaign, United States
Copyright © 2023 Singh and Townsend. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aditya Singh, YWRpdHlhMDFAdWZsLmVkdQ==
 Aditya Singh
Aditya Singh Philip A. Townsend2
Philip A. Townsend2