Application of feedback control to stomatal optimisation in a global land surface model

Accurate representations of stomatal conductance are required to predict the effects of climate change on terrestrial ecosystems. Stomatal optimisation theory, the idea that plants have evolved to maximise carbon gain under certain constraints, such as minimising water loss or preventing hydraulic damage, is a powerful approach to representing stomatal behaviour that bypasses the need to represent complex physiological processes. However, while their ability to replicate observed stomatal responses is promising, optimisation models often present practical problems for those trying to simulate the land surface. In particular, when realistic models of photosynthesis and more complex cost functions are used, closed-form solutions for the optimal stomatal conductance are often very difficult to find. As a result, implementing stomatal optimisation in land surface models currently relies either on simplifying approximations, that allow closed-form solutions to be found, or on numerical iteration which can be computationally expensive. Here we propose an alternative approach, using a method motivated by control theory that is computationally efficient and does not require simplifying approximations to be made to the underlying optimisation. Stomatal conductance is treated as the control variable in a simple closed-loop system and we use the Newton-Raphson method to track the time-varying maximum of the objective function. We compare the method to both numerical iteration and a semi-analytical approach by applying the methods to the SOX stomatal optimisation model at multiple sites across the Amazon rainforest. The feedback approach is able to more accurately replicate the results found by numerical iteration than the semi-analytical approach while maintaining improved computational efficiency.

1 Introduction

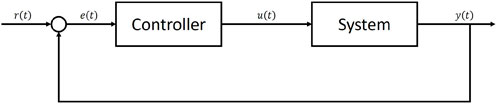
Stomata regulate gas exchange between leaf and atmosphere, balancing carbon gain required for growth, reproduction, and respiration, against the cost of losing excessive water through transpiration and the associated consequences for the plant hydraulic tissues (Cowan and Farquhar, 1977; Sperry et al., 2017). The dynamic behaviour of stomata has a strong influence over both the terrestrial carbon and water cycles (Sellers et al., 1996; Cox et al., 1999; Gedney et al., 2006). Combined with non-linear feedbacks between the land surface and atmosphere, small changes in stomatal responses to environmental change can cause large changes to future projections of the climate (Betts et al., 2004). As the frequency and severity of drought events increase across large parts of the globe (Hartmann et al., 2013; Marengo et al., 2018), the role that stomata play in regulating local and global climate is becoming ever more prominent, as plant water use strategies determine the survival of the vegetation in vulnerable ecosystems (Cox et al., 2000; Allen et al., 2010; Ponce-Campos et al., 2013; Anderegg et al., 2015; Hochberg et al., 2018). Despite this role, however, current land surface models (LSMs) often fail to accurately capture the response of vegetation to drought (Sitch et al., 2008; Powell et al., 2013; Ukkola et al., 2016; Restrepo-Coupe et al., 2017; Martínez-de la Torre et al., 2019). This reduces their ability to predict both short and long term changes to the land surface and interactions with the climate. Significant improvement to the representation of stomatal behaviour in LSMs is required to improve projections of future climate change and its impacts.Stomatal optimisation theory, the idea that plants are able to optimise carbon gain under certain physiological constraints, such as minimising water loss (Cowan and Farquhar, 1977) or preventing hydraulic damage (Sperry et al., 2017), is a powerful approach to representing stomatal behaviour that has seen renewed interest over recent years. Optimisation approaches offer encouraging results relative to observations (Anderegg et al., 2018; Eller et al., 2018, 2020; Venturas et al., 2018; Wang et al., 2019; Sabot et al., 2020; 2022a) while bypassing the need to represent complex and poorly understood physiological processes. The central concept is that stomata act to maximise carbon dioxide uptake for photosynthesis while simultaneously minimising the costs associated with excessive stomatal opening. These costs are typically expressed in terms of water loss, but may also be associated with non-hydrological processes such as in Prentice et al. (2014), where the optimisation model aims to minimise the carbon costs of transpiration and photosynthetic capacity. In optimisation models, an objective function, typically given by the difference between instantaneous carbon uptake and a cost function associated with water loss is maximised either instantaneously or over a finite period, resulting in an optimal stomatal conductance (Cowan and Farquhar, 1977; Wolf et al., 2016; Wang et al., 2020). Many of the observed behaviours of stomata to changes in climatic or edaphic conditions have been replicated by this approach (Buckley et al., 2017), making it an attractive option for those attempting to model plant behaviour. However, despite this promising ability to replicate observed stomatal responses, many global LSMs still use empirical representations of stomatal conductance such as the Leuning (1995) and Ball et al. (1987) models. The use of optimisation models, in particular for large scale and long term simulations is currently limited, in part due to the practical difficulties involved in solving for the optimal stomatal conductance (Buckley, 2017). Generally, closed-form analytical solutions are difficult or even impossible to find, in particular when sophisticated leaf photosynthesis models are used (e.g., Farquhar et al., 1980; Collatz et al., 1991). As a result, stomatal optimisation models are typically solved through numerical iteration. Unfortunately this can be impractical for large scale simulations of the climate where computational efficiency is desirable. Simplifying assumptions can sometimes be made about the functional form of either photosynthesis or the water loss cost equation that reduce the complexity of the problem, such that analytical solutions can be found (e.g., Medlyn et al., 2011; Eller et al., 2020). However, these simplifications are not always possible and can often misrepresent some of the fundamental assumptions in the model (Buckley et al., 2017; Sabot et al., 2022b). There is therefore a need for an alternative method to solve stomatal optimisation models that avoids the need for numerical iteration yet can still produce accurate solutions of the analytically optimal g_s.An area of promise that has yet to be extensively explored in the context of stomatal modelling is feedback control. A basic control problem consists of a system with an input and an output. The objective is to feed an input into the system that causes it to track some desired reference signal. In feedback control, measurements of the system output are compared against the reference signal through time, and the difference between them is used to design an input that is fed back into the system, guiding it is subsequent evolution through time (Figure 1). A simple example is the regulation of room temperature by a household boiler and thermostat (Franklin et al., 2011). Measurements of room temperature relative to the desired room temperature, which acts as the reference signal, provide information to the thermostat that allows the boiler to be turned on or off, maintaining the temperature of the house at, or near, the desired reference temperature. Feedback control methods have many applications across various fields of science and engineering, including, in particular, biological sciences (Cosentino and Bates, 2011) and generic optimisation problems (Hauswirth et al., 2021). Since the maximum of a function corresponds to a first derivative of zero, by setting the system output to be the first derivative of an objective function, and the reference signal to zero, we can reformulate the basic feedback control problem into an optimisation problem. This type of feedback optimisation is commonly applied in fields of engineering (e.g., Krishnamoorthy and Skogestad, 2022). Applying it to stomatal optimisation we can use the same methods to find a governing equation for the rate of change of stomatal conductance that causes the objective function to track the optimum through time. Such an effort could significantly increase the viability of stomatal optimisation models in LSMs, which in turn would improve our ability to capture responses of vegetation to changing water availability in the future.In this study we apply feedback optimisation techniques to the Stomatal Optimisation based on Xylem hydraulics (SOX) model (Eller et al., 2018, 2020). We implement SOX within the Joint United Kingdom Land Environment Simulator (JULES: Best et al., 2011; Clark et al., 2011) and use three different methods: numerical iteration; an approximate analytical solution; and feedback optimisation. We run JULES-SOX using these three approaches at four sites across the Amazon.

FIGURE 1

FIGURE 1. A basic feedback control system.

2 Methods

2.1 SOX

The Stomatal Optimisation based on Xylem hydraulics (SOX) model is a stomatal optimisation model designed to run within the JULES LSM (Best et al., 2011; Clark et al., 2011). Below we provide a brief introduction to the model, however, a full description and detailed evaluations of the model can be found in Eller et al. (2018) and Eller et al. (2020).SOX assumes that stomata act to maximise the instantaneous product of leaf photosynthesis (A) and the normalised xylem hydraulic conductance (K). The optimal stomatal conductance (g_s,opt) is found as the solution to the following equation:

$\frac{\partial \left(A\cdot K\right)}{\partial g_s}\left(g_{s,opt}\right)=0(1)$

The normalised xylem hydraulic conductance (K) is a function of leaf water potential (Ψ_l), which itself is a function of stomatal conductance. This K is given by the vulnerability curve (Eller et al., 2020):

$K\left(\mathrm{\Psi }\right)=\frac{1}{\left[1+{\left(\frac{\mathrm{\Psi }}{{\mathrm{\Psi }}_{50}}\right)}^a\right]}(2)$

where Ψ₅₀ is Ψ when K = 0.5 and the parameter a gives the shape of the vulnerability curve.Due to the complexity of the photosynthesis model used in JULES, and the functional form of the hydraulic conductivity equation used, a closed-form solution for g_s has not been found, and the model can only be solved by numerical iteration (Eller et al., 2018) or by simplifying some of its premises to produce a semi-analytical approximation (Eller et al., 2020).

2.2 Numerical iteration

The default method for solving the SOX model is by numerical iteration. An array of leaf internal carbon dioxide partial pressure (c_i) values is used to calculate the objective function, (J = A ⋅ K). The value of c_i that gives the greatest value of the objective function is then used to calculate the optimum stomatal conductance using the equilibrium diffusion equation:

$g_{s,opt}=\frac{A\left(c_{i,opt}\right)}{\left(c_a-c_{i,opt}\right)}(3)$

where c_a is atmospheric carbon dioxide partial pressure.The difference between the solution found by numerical iteration and the “true” solution depends on the number of different c_i values, or iterations used. For a sufficiently large number of iterations we can neglect differences between the numerical solution and the true analytical solution, and so for the remainder of this study we consider the solution found by numerical iteration to represent the true solution of the model. When SOX has been run using this method we refer to it as the “numerical version of SOX”.

2.3 Semi-analytical approximation

Eller et al. (2020) also present a semi-analytical approximation to SOX:

$g_{s,opt}=0.5\frac{\partial A}{\partial c_i}\left(\sqrt{\frac{4\xi }{\frac{\partial A}{\partial c_i}}+1}-1\right)(4)$

with

$\xi =\frac{2}{\frac{1}{K}\frac{\partial K}{\partial \psi }{r}_{p}1.6D}$

where ψ is leaf water potential; r_p is plant hydraulic resistance; and D is vapur pressure deficit.This is referred to as “semi-analytical” since it is not a true closed-form solution. For most realistic models of photosynthesis, including those typically used in JULES (Farquhar et al., 1980; Collatz et al., 1991), $\frac{\partial A}{\partial c_i}$ is not independent of g_s. Similarly, the cost function (K) in SOX depends on leaf water potential and therefore also on g_s. As a result the expression requires simplifying assumptions to be used. Eller et al. (2020) estimate both $\frac{\partial A}{\partial c_i}$ and $\frac{1}{K}\frac{\partial K}{\partial \psi }$ numerically, assuming both terms are constant with respect to g_s and within a model time-step. For the remainder of this study we refer to the combination of this semi-analytical expression and the approximations of the gradients of photosynthesis and the cost function as the “semi-analytical version of SOX”.

2.4 Applying feedback control to stomatal optimisation

A basic negative feedback control system consists of a system which takes a control input $(u\left(t\right))$ and produces an output $(y\left(t\right))$ (Figure 1). In the simplest case this output is given by a function of the input:

$y=F\left(u\left(t\right)\right)(5)$

The objective of feedback control is to design a governing equation for the input such that the output of the system tracks a reference signal $(r\left(t\right))$. This is achieved by measuring the error between the system output and the reference signal, e(t) = r(t) − y(t), and designing a controller that minimises this error through time, often with the additional objectives of minimising convergence time and overshoot, while maintaining stability.The aim of stomatal optimisation models is to maximise an instantaneous objective function (J). We want to control this objective function by varying stomatal conductance through time and hence stomatal conductance is our control variable:

$u\left(t\right)=g_s\left(t\right)(6)$

Setting the system output function (F) of our feedback problem to be the first derivative of the objective function:

$F\left(u\left(t\right)\right)=\frac{\partial J}{\partial g_s}\left(g_s\left(t\right)\right)(7)$

and setting the reference signal to zero:

$r\left(t\right)=0(8)$

we now have a feedback optimisation problem. The aim is to design a governing equation for the rate of change of stomatal conductance that guides our objective function towards its maximum, and can use methods from feedback control to do so.

2.4.1 Applying feedback control to SOX

To apply feedback control to SOX it is first convenient to non-dimensionalise the objective function by defining a maximum value for photosynthesis (A_max). The non-dimensional objective function is given by:

$\widehat{J}=\widehat{A}\cdot K(9)$

where

$\widehat{A}=\frac{A}{A_{\mathit{max}}}(10)$

We define A_max as the rate of photosynthesis when intercellular leaf CO₂ concentration is equal to atmospheric CO₂:

$A_{\mathit{max}}=A\left(c_i=c_a\right)(11)$

The cost function, K, in SOX is already normalised with respect to a maximum hydraulic conductance and so this is left unchanged.In order to apply the principle of feedback control, the objective function must be evaluated by the control variable. However, due to the co-limitation part of the photosynthesis model used in JULES it is not possible to rearrange A in terms of g_s. We therefore, re-formulate the control problem in terms of c_i using Fick’s Law (Eq. 3). In order to maintain non-dimensionality when differentiating the objective function, we differentiate with respect to the ratio intercellular leaf, to atmospheric CO₂ concentration:

$f_i=\frac{c_i}{c_a}(12)$

SOX (Eq. 1) is subsequently rewritten as:

$\frac{\partial \left(\widehat{A}\cdot K\right)}{\partial f_i}\left(f_{i,opt}\right)=0(13)$

The control variable is now f_i and its optimum value is tracked by the feedback system. The optimum c_i is found using Equation 12. As with the numerical iteration solution to SOX, the optimal stomatal conductance can be found from the optimal c_i value using the equilibrium diffusion equation (Eq. 3). Non-dimensionalising and reformulating SOX in this way does not alter the biological assumptions and has no effect on the optimum g_s, but they are implemented here to ensure that the objective function (Eq. 9) and the optimised variable (f_i) both occupy the range from zero to unity.We define the rate of change of f_i using a control equation analogous to the Newton-Raphson root finding algorithm:

$\frac{d{f}_i}{dt}=-{\left(\frac{{\partial }^2\widehat{J}}{\partial f_i^2}\right)}^{-1}\left(\frac{\partial \widehat{J}}{\partial f_i}\right)\left(1-\mathit{exp}\left\{-\frac{\mathrm{\Delta }t}{\tau }\right\}\right)(14)$

where τ is a tunable time-scale parameter representing the response time of the stomata (set to τ = 900 s by default), and the $1-\mathit{exp}\left\{-\frac{\mathrm{\Delta }t}{\tau }\right\}$ term accounts for model timesteps (Δt) which are non-negligible compared to τ.The derivatives for the Newton-Raphson increment are found by first expressing them in terms of $\widehat{A}$ and K:

$\frac{\partial \widehat{J}}{\partial f_i}=\widehat{A}\frac{\partial K}{\partial f_i}+K\frac{\partial \widehat{A}}{\partial f_i}(15)$

$\frac{{\partial }^2\widehat{J}}{\partial f_i^2}=\widehat{A}\frac{{\partial }^{2}K}{\partial f_i^2}+2\frac{\partial \widehat{A}}{\partial f_i}\frac{\partial K}{\partial f_i}+K\frac{{\partial }^2\widehat{A}}{\partial f_i^2}(16)$

The derivatives of $\widehat{A}$ and K are found numerically. It is possible to derive analytical derivatives for both $\widehat{A}$ and K which would allow an analytical calculation of the Newton-Raphson increment, however by using numerical derivatives we maintain greater generality as the photosynthesis model and cost function can be readily changed without requiring them to have analytical derivatives.

$\frac{\partial X}{\partial f_i}=\frac{X\left(f_i+h\right)-X\left(f_i-h\right)}{2h}(17)$

$\frac{{\partial }^{2}X}{\partial f_i^2}=\frac{X\left(f_i+h\right)-2X\left(f_i\right)+X\left(f_i-h\right)}{h^2}(18)$

where h is the numerical step-size in f_i (set equal to 0.0002), and variable X is either $\widehat{A}$ or K.

2.4.2 Additional constraints

The Newton-Raphson control equation is not sufficient by itself to track the optimum c_i. In addition to the above rate equation we implement three additional constraints.

The first is to limit the value of the second derivative of the objective function. The Newton-Raphson algorithm is not robust when the second derivative of the function being optimised changes sign anywhere within the optimisation domain (i.e. the function is not strictly convex or concave). In the case of attempting to maximise an objective function, this means that the method will break down if the second derivative becomes positive (the function is not concave). Unfortunately, the objective function in SOX is not strictly concave with respect to f_i for all environmental conditions, and the second derivative can become positive. To solve this, we set a maximum value for the second derivative that prevents it both approaching zero and becoming positive. We relate this limit to a maximum allowed rate of change in f_i:

${\left(\frac{{\partial }^2\widehat{J}}{\partial f_i^2}\right)}_{\mathit{max}}=-\left|\frac{{\widehat{J}}^{\prime }}{{\left(\frac{d{f}_i}{dt}\right)}_{\mathit{max}}dt}\right|(19)$

where ${\widehat{J}}^{\prime }=\frac{\partial \widehat{J}}{\partial f_i}$, and ${\left(\frac{d{f}_i}{dt}\right)}_{\mathit{max}}$ is a plant functional type (PFT) dependent parameter with default values of 1.67 × 10⁻⁴ s⁻¹ for C3 and 1.67 × 10⁻⁵ s⁻¹ for C4 respectively. These equate to a maximum allowed change in f_i of 0.15 and 0.015 per 15 minute time-step, for C3 and C4 plants respectively.The second is to set a condition for when leaf photosynthesis is limited by light and equal to zero. In this case the objective function is equal to zero for all values of f_i, resulting in a zero first derivative and rate of change of f_i. When photosynthesis is completely limited by light, there is no benefit for a plant to keep it is stomata open and so we implement the condition that when absorbed photosynthetically active radiation (APAR) is zero the rate of change of f_i is given by:

$\frac{d{f}_i}{dt}=-{\left(\frac{d{f}_i}{dt}\right)}_{\mathit{max}}\left(1-\mathit{exp}\left\{-\frac{\mathrm{\Delta }t}{\tau }\right\}\right)(20)$

Finally, the control variable, f_i, is kept within the range (0,1) i.e. intercellular leaf CO₂ concentration cannot drop below 0, and cannot exceed atmospheric CO₂ concentration.

2.5 An improved big leaf model within JULES

There are currently two options for canopy photosynthesis in JULES, both described fully in Clark et al. (2011). The first option is a big leaf approach, in which top of the canopy leaf photosynthesis is scaled to total canopy photosynthesis, using the assumption that both irradiance (I_par) and photosynthetic capacity (V_cmax) decline exponentially through the canopy, with the same rate of decay.The second approach is a multi-layer approach where gross photosynthesis is calculated for a number of equal increments of leaf area index (LAI) through the canopy, assuming again that both irradiance and photosynthetic capacity decay exponentially through the canopy, although with the option for these decay rates to differ. Mercado et al. (2007), along with discussion in Clark et al. (2011), demonstrate the superior performance of the multi-layer approach compared to the big-leaf approach, in particular it is ability to capture observed photosynthetic light responses, and diurnal cycles of GPP.For computational efficiency, it is beneficial for the feedback optimisation to be implemented as part of a big leaf approach, with just a single prognostic variable for the whole canopy. For this reason we present below a modified version of the big leaf approach that more accurately captures the light response and diurnal cycle of canopy photosynthesis.Photosynthesis in JULES uses the biochemistry of C₃ and C₄ photosynthesis from Collatz et al. (1991) and Collatz et al. (1992). Leaf photosynthesis is determined by three potentially-limiting rates:

1. Rubisco-limited rate (W_c)

$W_c=\left\{\begin{array}{cc}{V}_{\mathit{cmax}}\left(\frac{c_i-\mathrm{\Gamma }}{c_i+K_c\left(1+O_a/K_o\right)}\right)\hfill & {\text{for\hspace{0.17em}C}}_3\text{\hspace{0.17em}plants}\hfill \\ V_{\mathit{cmax}}\hfill & {\text{for\hspace{0.17em}C}}_4\text{\hspace{0.17em}plants}\hfill \end{array}\right.(21)$

where V_cmax (mol CO₂m⁻²s⁻¹) is the maximum rate of carboxylation of Rubisco, c_i (Pa) is the leaf internal carbon dioxide partial pressure, Γ (Pa) is the CO₂ compensation point in the ansence of mitochondrial respiration, O_a (Pa) is the partial pressure of atmospheric oxygen, and K_c and K_o (Pa) are the Michaelis-Menten parameters for CO₂ and O₂, respectively.

2. Light-limited rate (W_l)

$W_l=\left\{\begin{array}{cc}\alpha \left(1-\omega \right)I_{\mathit{par}}\left(\frac{c_i-\mathrm{\Gamma }}{c_i+2\mathrm{\Gamma }}\right)\hfill & {\text{for\hspace{0.17em}C}}_3\text{\hspace{0.17em}plants}\hfill \\ \alpha \left(1-\omega \right)I_{\mathit{par}}\hfill & {\text{for\hspace{0.17em}C}}_4\text{\hspace{0.17em}plants}\hfill \end{array}\right.(22)$

where α is the quantum efficiency of photosynthesis (mol CO₂mol⁻¹PAR), ω is the leaf scattering coefficient for PAR and I_par is the incident photosynthetically active radiation (PAR, mol m⁻²s⁻¹).

3. Rate of transport of photosynthetic products (in the case of C₃ plants) and PEPCarboxylase limitation (in the case of C₄ plants) (W_e)

$W_e=\left\{\begin{array}{cc}0.5V_{\mathit{cmax}}\hfill & {\text{for\hspace{0.17em}C}}_3\text{\hspace{0.17em}plants}\hfill \\ 2\times 10^4{V}_{\mathit{cmax}}\frac{c_i}{P_{*}}\hfill & {\text{for\hspace{0.17em}C}}_4\text{\hspace{0.17em}plants}\hfill \end{array}\right.(23)$

As in the original approach used in JULES and described in Clark et al. (2011), incident radiation attenuation through the canopy is assumed to follow Beer’s law:

$I_{\mathit{par}}\left(L\right)=I_0{e}^{-k_{\mathit{PAR}}L}(24)$

where I₀ is irradiance at the top of the canopy, k_PAR is a light extinction coefficient and L is the leaf area index through the canopy.Similarly, it is also assumed that photosynthetic capacity (V_cmax) varies through the canopy. Unlike the old big leaf approach, however, we assume a distinct extinction coefficient associated with the decline of Nitrogen through the canopy, similar to that used in the multi-layer canopy scheme also present in JULES:

$V_{\mathit{cmax}}=V_{cma{x}_0}{e}^{-k_{n}L}(25)$

where k_n is the decay coefficient of Nitrogen through the canopy with the default value of 0.2.We also introduce a decay of the quantum efficiency of photosynthesis (α) through the canopy to account for the decline of chlorophyll content through the canopy. The decay rate of α is assumed equal to that of V_cmax, since both depend on canopy Nitrogen.

$\alpha \left(L\right)={\alpha }_0{e}^{-k_{N}L}(26)$

where α₀ is the quantum efficiency of photosynthesis at the top of the canopy with the default value of 0.035.To scale to canopy photosynthesis, the three potentially-limiting rates are integrated over the canopy to find their respective canopy average values (denoted with a bar):

$\overline{W_c}=\frac{1}{L_c}{\int }_0^{L_c}{W}_{c}dL=W_{c_0}\frac{1-e^{-k_n{L}_c}}{k_n{L}_c}(27)$

$\overline{W_l}=\frac{1}{L_c}{\int }_0^{L_c}{W}_{l}dL=W_{l_0}\frac{1-e^{-\left(k_n+k_{\mathit{PAR}}\right)L_c}}{\left(k_n+k_{\mathit{PAR}}\right)L_c}(28)$

$\overline{W_e}=\frac{1}{L_c}{\int }_0^{L_c}{W}_{e}dL=W_{e_0}\frac{1-e^{-k_n{L}_c}}{k_n{L}_c}(29)$

Where $W_{c_0}$, $W_{l_0}$, and $W_{e_0}$ are the values of W_c, W_l and W_e at the top of the canopy respectively.Average gross canopy photosynthesis $(\bar{W})$ is then calculated as the smoothed minimum of these canopy average limiting rates. These are found as the smallest root of the following set of equations:

${\beta }_1{\overline{W_p}}^2-\overline{W_p}\left(\overline{W_c}+\overline{W_l}\right)+\overline{W_c}\overline{W_l}=0(30)$

${\beta }_2{\bar{W}}^2-\bar{W}\left(\overline{W_p}+\overline{W_e}\right)+\overline{W_p}\overline{W_e}=0(31)$

where $\overline{W_p}$ is the smoothed minimum of $\overline{W_c}$ and $\overline{W_l}$, and β₁ = 0.83 and β₂ = 0.93 are “co-limitation” coefficients.Finally total canopy gross photosynthesis is calculated by multiplying the average canopy photosynthesis by canopy LAI, with the same method also being used to calculate canopy respiration and stomatal conductance:

$W=\bar{W}{L}_c(32)$

In addition to the introduction of a vertical distribution in the quantum efficiency of photosynthesis (α), the new approach here differs from the original big-leaf approach in the order in which the co-limitation (Eq. 30 and Eq. 31) of the three potentially limiting rates is calculated, and the scaling of leaf to canopy photosynthesis. The original big leaf first calculates the co-limitation of the three rates at the top of the canopy leaf before scaling up to total canopy photosynthesis. Canopy photosynthesis is therefore rarely light-limited as top of the canopy leaves, which have the highest light conditions, determine the total canopy rate. The new approach instead performs co-limitation after each of the rates has been effectively scaled to the canopy. This better accounts for the contribution of lower canopy leaves that are typically shaded and therefore limited by incoming light.

2.6 JULES-SOX simulations

All three versions of SOX (numerical, feedback control and semi-analytical) were implemented into version 5.1 of the JULES LSM, along with the updated canopy photosynthesis scheme. The code for the feedback control version of JULES-SOX used in this study can be found at code. metoffice.gov.uk/svn/jules/main/branches/dev/simonjones/vn5.1_jules_SOX_feedback_control/. The revision at time of publication is 23887. Each version of JULES-SOX was then used to simulate plant function at four sites across the Amazon rainforest from the LBA network (Saleska et al., 2013). These sites include LBA-K34 Reserva Cuieiras, Manaus Brazil; LBA-K83 Tapajos National forest, Santarem Brazil; LBA-RJA Reserva Jaru; and LBA-K67 Tapajos National forest, Santarem Brazil. A summary of the environmental conditions at each site is given in the supplementary material (Supplementary Figure S1, S2). The simulations were spun up for 25 years and run on a 15 minute time-step. Driving data is provided from each site on an hourly basis and is linearly interpolated to 15 min by JULES. The simulation period for each site is as follows: K34–2003-01-01 04:00:00 to 2006-01-01 03:00:00; K83–2001-01-01 04:00:00 to 2004-01-01 03:00:00; RJA - 2000-01-01 04:00:00 to 2002-12-31 23:00:00; and K67–2002-01-01 02:00:00 to 2005-01-01 03:00:00. The parameters fitted in Eller et al. (2020) were used for SOX and are given in Supplementary Table S1.

2.7 Model evaluation

The aim of the study is to test the ability of feedback control to track the optimum solution of SOX found by numerical iteration. To do this we examine both predicted daily (24-h mean) grid-box gross primary productivity (GPP) and predicted daily stomatal transpiration from the feedback control approach and compare it against the same predictions from the numerical approach across all sites. We also compare predicted GPP and transpiration from the semi-analytical approximation against the numerical version of SOX, and present root mean square error (RMSE) values for both sets of comparisons. This allows us to then compare the ability of the feedback optimisation and semi-analytical versions to replicate the predictions made by the numerical version.We also compare the average diurnal cycle of predicted grid-box GPP, predicted grid-box transpiration, and predicted leaf water potential for each version of SOX at each site, in order investigate the ability of both the feedback control and semi-analytical approaches to represent the sub-daily behaviour of stomata predicted by SOX. We also assess the ability of JULES-SOX to capture observed sub-daily fluxes at each site and compare the average diurnal cycle of GPP predicted by each model to the equivalent cycle of observed GPP at each site, and across the same time period. We also compare the average diurnal cycle of transpiration to observations, although due to data availability this comparison is only made at site K67. Observations are taken from Saleska et al. (2013) and GPP and transpiration are taken as the “GEP_model” and “Fh20” variables respectively.Finally, an important part of the motivation behind the feedback control approach is that while the numerical version accurately represents the assumptions made within SOX it is computationally inefficient. So as well as evaluating each models ability to capture the assumptions made in SOX we also assess the computational efficiency of each method. We do this by presenting the total aggregate time taken to run all four sites, which provides a metric of the efficiency of each version.

3 Results

In general the feedback control approach was able to replicate the results from the numerical iteration approach more closely than the semi-analytical version of SOX (Figure 2 and Figure 3). With respect to predicted daily grid box GPP, the difference between the two approaches was relatively small, and both were able to replicate the result from the numerical version with reasonable accuracy (Figure 2). Non-etheless the root mean square error (RMSE) between predicted daily grid box GPP from the numerical version of SOX and the feedback control version of SOX (RMSE = 0.106) was lower than the RMSE between the numerical and semi-analytical versions (RMSE = 0.140) across all simulations (Figure 2). In contrast, there were more significant differences between the two approaches in terms of predicted daily grid-box stomatal transpiration (Figure 3) and canopy water potential (Figure 6). The feedback control version more closely matched the numerical solution, with a significantly lower RMSE value (RMSE = 29.4) for predicted transpiration compared to the semi-analytical version (RMSE = 264.4) (Figure 3). The semi-analytical version of SOX generally predicted larger values of transpiration compared with the numerical version (Figure 3). This was due to greater daily maxima in stomatal conductance, and therefore greater maxima in daily transpiration compared to the numerical and feedback control versions of SOX (Figure 5). The feedback control method generally predicted similar values of daily GPP relative to the numerical version, but there was a small bias towards lower values of daily GPP relative to the numerical version (Figure 2). This was mostly due to a lag in stomatal opening at dawn in the feedback control approach relative to the numerical version, resulting in overall lower average daily values (Figure 4).

FIGURE 2

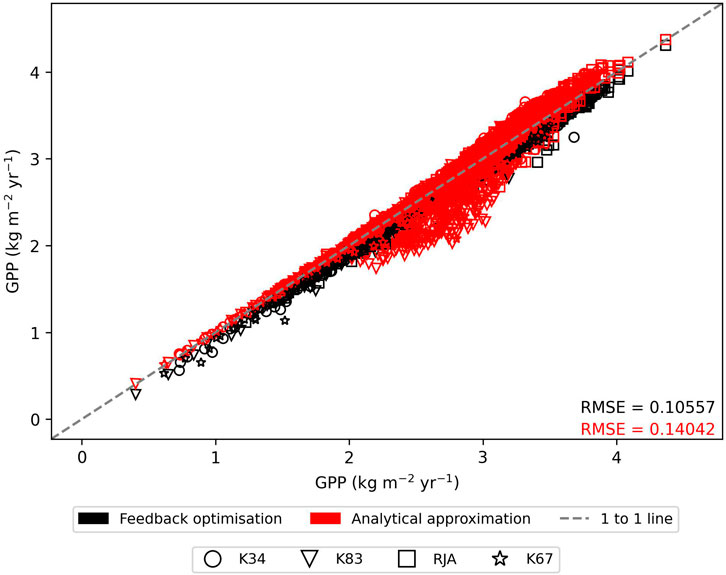
FIGURE 2. The comparison of predicted daily grid-box gross primary production (GPP, kg C m⁻² yr⁻¹) from the numerically solved version of JULES-SOX along the x axis against 1) feedback control version of JULES-SOX (black) and 2) the semi-analytical approximation of JULES-SOX (red) along the y-axis, across simulations from four sites in the Amazon rainforest. The sites are LBA-K34: Reserva Cuieiras, Manaus Brazil; LBA-K83: Tapajos National forest, Santarem Brazil; LBA-RJA: Reserva Jaru; LBA-K67: Tapajos National forest, Santarem Brazil. Root mean square error (RMSE) values between values predicted by the numerical version and the two other versions across all simulations are presented.

FIGURE 3

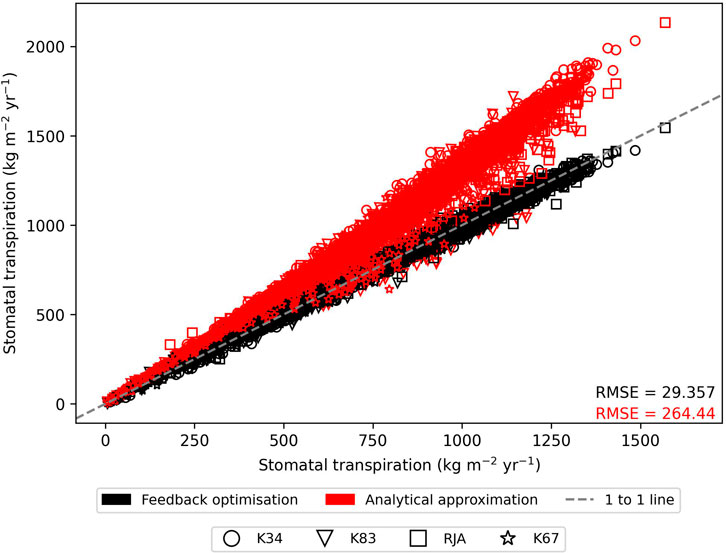
FIGURE 3. The comparison of predicted daily grid-box stomatal transpiration (kg H₂O m⁻²yr⁻¹) from the numerically solved version of JULES-SOX along the x axis against 1) feedback control version of JULES-SOX (black) and 2) the semi-analytical approximation of JULES-SOX (red) along the y-axis, across simulations from four sites in the Amazon rainforest. The sites are LBA-K34: Reserva Cuieiras, Manaus Brazil; LBA-K83: Tapajos National forest, Santarem Brazil; LBA-RJA: Reserva Jaru; LBA-K67: Tapajos National forest, Santarem Brazil. Root mean square error (RMSE) values between values predicted by the numerical version and the two other versions across all simulations are presented.

FIGURE 4

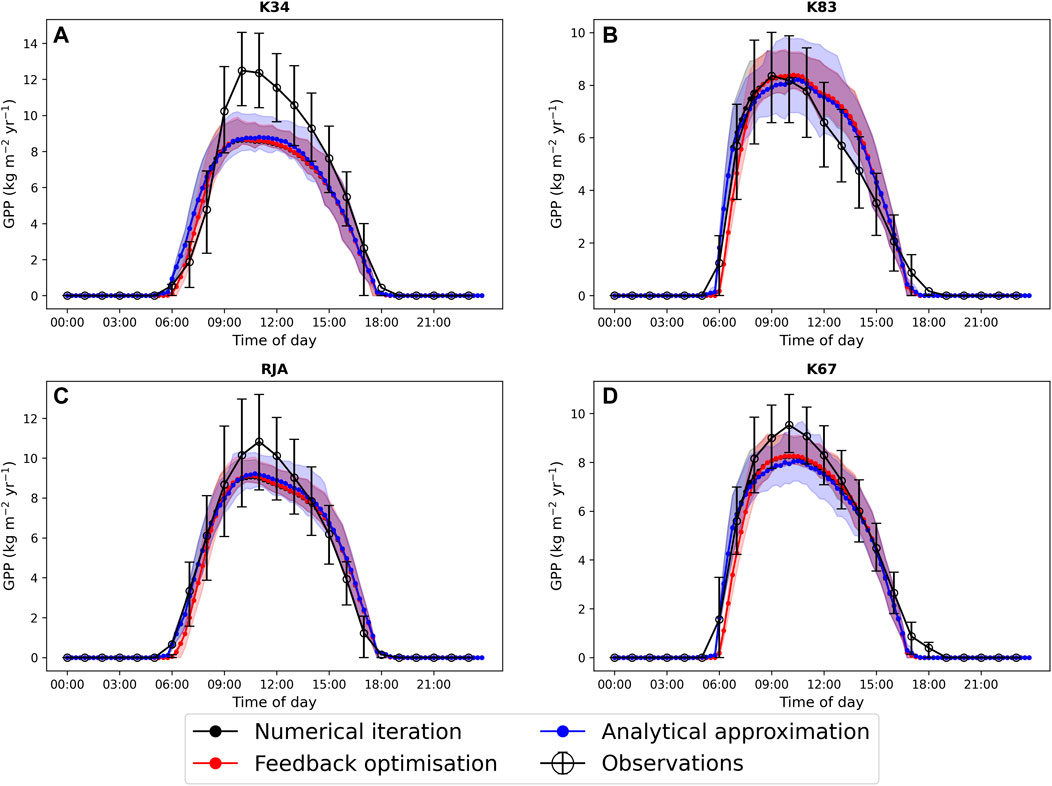
FIGURE 4. A comparison of the average diurnal cycle of predicted gross primary production (GPP, kg C m⁻²yr⁻¹) from JULES-SOX solved using three different methods (1. Numerical iteration (black), 2. Feedback control (red), 3. A semi-analytical approximation (blue))) and observed GPP at four sites in the Amazon rainforest. (A) LBA-K34 Reserva Cuieiras, Manaus Brazil; (B) LBA-K83 Tapajos National forest, Santarem Brazil; (C) LBA-RJA Reserva Jaru; (D) LBA-K67 Tapajos National forest, Santarem Brazil. Observed data is from Saleska et al. (2013). Error bars and shaded areas represent the 25% and 75% uncertainty percentiles.

All three approaches accurately captured the average diurnal cycle of observed GPP at each site, with the exception of the K34 site where the peak in daily GPP was underestimated by all three versions of the models (Figure 4). The similarity of the three versions of the model here is due to the weak dependence of the light-limited rate of photosynthesis (W_l, Eq. 22) on c_i and therefore g_s, which is most commonly the limiting rate in our new big leaf scheme. All three versions of JULES-SOX underestimated the amplitude of the average diurnal cycle of transpiration at the K67 site, but the semi-analytical version predicted greater daily maxima than the numerical and feedback control versions and was therefore closest to the observed values. The greater difference between the approaches in terms of predicted transpiration relative to predicted GPP is due to the greater dependence of transpiration on stomatal conductance than that of photosynthesis in the light-limited regime.

As expected, the numerical version of SOX was the least computationally efficient method. To run all four sites it took a combined time of 52 min and 52 s (3,172 s). The speed of the numerical version depends on the number of iterations used and the time taken of course reduces when fewer iterations are used, although at the cost of reduced accuracy. Both the semi-analytical and feedback control approaches were significantly faster, with total run times of 38 min and 4 s, and 25 min and 26 s respectively. The efficiency of the feedback control version could be improved further if instead of using the chain rule to calculate the derivatives of the Newton-Raphson increment, the derivatives are estimated directly using:

$\frac{\partial \widehat{J}}{\partial f_i}=\frac{\widehat{J}\left(f_i+h\right)-\widehat{J}\left(f_i-h\right)}{2h}(33)$

$\frac{{\partial }^2\widehat{J}}{\partial f_i^2}=\frac{\widehat{J}\left(f_i+h\right)-2\widehat{J}\left(f_i\right)+\widehat{J}\left(f_i-h\right)}{h^2}(34)$

This reduces the number of calculations required but results in a slightly less accurate estimate of the derivatives and so lowers the performance of the approach with respect to replicating the results of the numerical version.

4 Discussion

Accurately simulating stomatal behaviour is an important part of predicting climate change and its impacts in the future. Stomatal optimisation theory has shown promise as a relatively simple way to replicate observed stomatal responses, without the need for complex understanding of physiological processes. However, it is use in large scale simulations of the land surface has been limited due to the difficulties involved in solving for optimal stomatal conductance, with methods often compromising either on scientific accuracy, or on computational efficiency. Applying methods based in feedback control, we have demonstrated an alternative approach to solving stomatal optimisation models that may allow optimisation theory to be effectively implemented in LSMs and used in large scale modelling studies. Our approach significantly increases computational efficiency relative to numerical iteration while maintaining a close representation of the underlying assumptions made in the optimisation model.

One of the largest challenges facing stomatal optimisation models is defining the cost function associated with water loss (Wang et al., 2020). Plants may experience multiple different penalties for transpiring excessive water, including loss of hydraulic conductance through xylem cavitation (Tyree and Sperry, 1989; Martínez-Vilalta et al., 2014; Sperry and Love, 2015) and reduced cell turgor required for tissue expansion and growth (Hsiao, 1973; Cosgrove, 2014; Fricke, 2017). How to aggregate these potential costs into a single function is not currently clear (Wang et al., 2020). The ability to implement new assumptions into optimisation models and test them within the context of an LSM is therefore crucial to advancing stomatal optimisation models and improving predictions of stomatal behaviour in the future. Unlike the semi-analytical solution of SOX, the feedback control approach can in theory be applied to any realistic objective function, allowing new cost functions to be readily implemented into LSMs.

Plants in JULES have been reported to have a high sensitivity to drought events (Harper et al., 2016; Williams et al., 2018), due in part to the empirical ‘β-factor’ approach used to represent the effect of changes in soil moisture on canopy level photosynthesis (Cox et al., 1998; Clark et al., 2011). This sensitivity represents a significant component of simulating the response of vegetated ecosystems to drought and is a key source of error between model predictions and observations (Powell et al., 2013). Similarly, the response of stomata to changes in vapour pressure deficit (VPD) is traditionally controlled by the empirically derived relationship between intercellular leaf CO₂ and VPD from Jacobs (1994), as described in Best et al. (2011). Increases in VPD can reduce stomatal conductance and photosynthesis as the increased evaporative demand results in greater water loss through transpiration (Grossiord et al., 2020). Capturing this response is crucial for predicting the future of ecosystems across the globe as increasing VPD is a significant driver of tree mortality (Park Williams et al., 2013). The SOX model provides a theoretical basis that allows improved predictions of stomatal regulation during drought and periods of high VPD (Eller et al., 2018) that are more robust to changes in climate than the empirically derived responses. The semi-analytical approximation for SOX Eller et al. (2020) provides a means to implement stomatal optimisation into JULES that is computationally efficient and maintains some of the improved predictions of carbon and water fluxes. However, as we have shown here this approximation does not fully represent the assumptions made in SOX. In particular, the semi-analytical version often mischaracterises the sensitivity of stomata to VPD due to the linearisation of the vulnerability curve (Sabot et al., 2022b). Applying feedback control will allow SOX to be accurately and efficiently implemented into JULES while preserving the fundamental assumptions made in the model, and facilitate the implementation of alternative cost functions that may improve the capability of SOX to predict forest responses to extreme climate events such as drought, and increasing global VPD.

The feedback control approach is a promising alternative method for solving stomatal optimisation models. However, as can be seen in Figure 2–6, the method does not track the optimal solution perfectly. There are many potential reasons for this, including for example, numerical errors in the estimation of the objective function derivatives (indeed the tracking improves when analytical derivatives are used). A more scientifically interesting difference between the feedback control approach and the numerical solution can be seen when looking in particular at the average diurnal cycle of transpiration and leaf water potential at each of the four simulated sites (Figure 5). In particular, while the feedback method closely tracks the numerical solution throughout the middle of the day, there is a clear distinction between the two approaches at dawn when the stomata first open, as in general the feedback control approach tends to lag behind the optimal solution. This is because stomatal conductance (or more accurately f_i in this case) is now determined by a differential equation (Eq. 14), which introduces a time-scale into the rate of stomatal opening. The exact mechanisms that control the regulation of stomata are not well understood (Buckley, 2019). However, it is clear that physiological constraints related to the size, density and structure of stomata have a significant effect on the rate at which stomata can respond to changing environmental conditions (Lawson and Vialet-Chabrand, 2019). Observations show that these response times can be an order of magnitude or more slower than the response of photosynthesis (Lawson and Blatt, 2014; Lawson and Vialet-Chabrand, 2019), which decouples photosynthesis from stomatal conductance over short time-scales and can have important consequences for plant water use efficiency (Lawson and Blatt, 2014; Vialet-Chabrand et al., 2017; Eyland et al., 2021). Stomatal optimisation models do not intrinsically account for these physiological constraints and so implicitly assume that the rate of change of stomata is unbounded, although time-scales can be introduced using, for example, the “prognostic stomatal conductance” approach described by Sellers et al. (1996). In the absence of detailed understanding of the physiological mechanisms behind lagged stomatal regulation, the feedback approach presented here presents an efficient method for physiological constraints on stomatal opening to be accounted for, at least implicitly, and may help to bridge the gap between optimisation and mechanistic approaches, allowing more accurate predictions of sub-daily stomatal behaviour.

FIGURE 5

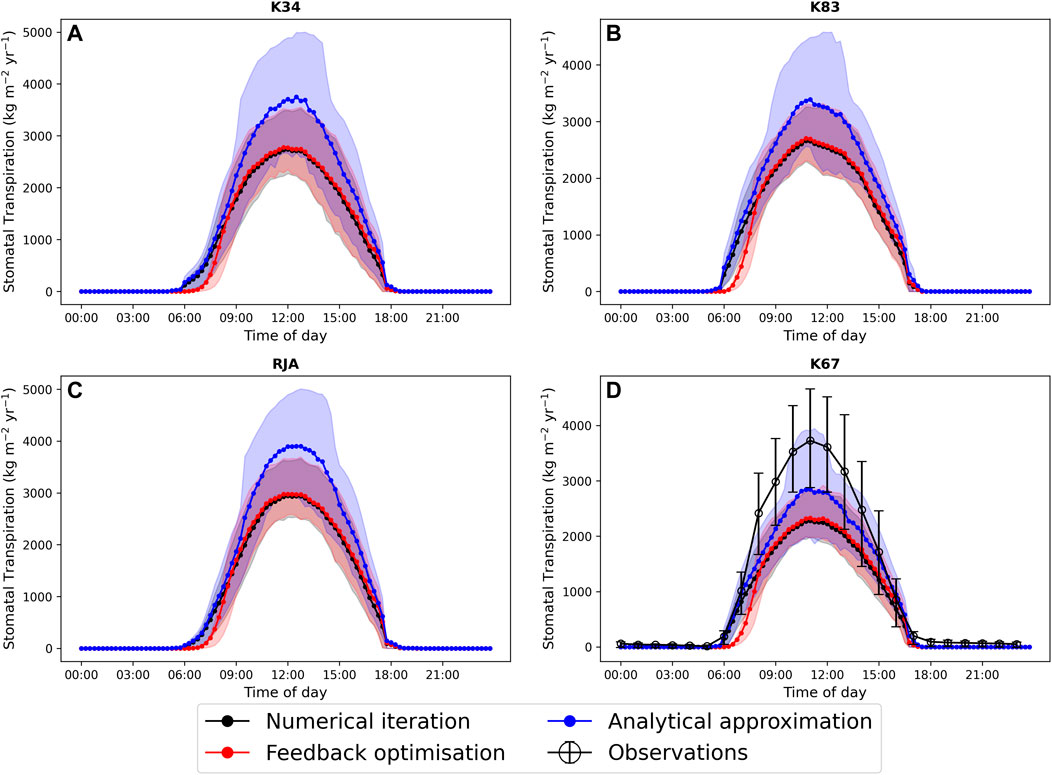
FIGURE 5. A comparison of the average diurnal cycle of predicted stomatal transpiration (kg H₂O m⁻²yr⁻¹) from JULES-SOX solved using three different methods (1. Numerical iteration (black), 2. Feedback control (red), 3. A semi-analytical approximation (blue))) and observed transpiration at four sites in the Amazon rainforest. (A) LBA-K34 Reserva Cuieiras, Manaus Brazil; (B) LBA-K83 Tapajos National forest, Santarem Brazil; (C) LBA-RJA Reserva Jaru; (D) LBA-K67 Tapajos National forest, Santarem Brazil. Observed data is from Saleska et al. (2013). Error bars and shaded areas represent the 25% and 75% uncertainty percentiles.

FIGURE 6

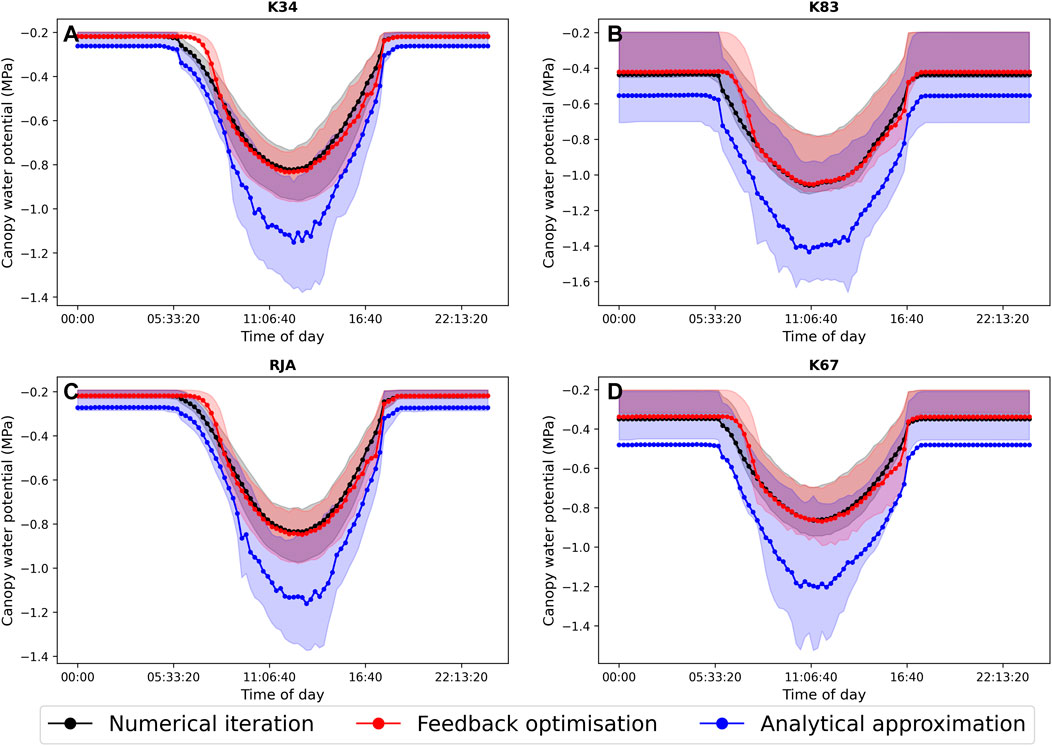
FIGURE 6. The average diurnal cycle of predicted canopy water potential (MPa) from JULES-SOX solved using three different methods (1. Numerical iteration (black), 2. Feedback control (red), 3. A semi-analytical approximation (blue)) at four sites in the Amazon rainforest. (A) LBA-K34 Reserva Cuieiras, Manaus Brazil; (B) LBA-K83 Tapajos National forest, Santarem Brazil; (C) LBA-RJA Reserva Jaru; (D) LBA-K67 Tapajos National forest, Santarem Brazil. Shaded areas represent the 25% and 75% uncertainty percentiles.

Feedback control has strong parallels with numerical optimisation (Hauswirth et al., 2021). These algorithms allow complex equations to be solved numerically and have been applied to stomatal optimisation models previously. For example, Anderegg et al. (2018) use the Newton-Raphson algorithm to solve their stomatal optimisation model for optimal stomatal conductance at each time-step. The difference between using a numerical solver in this way, and the feedback control approach we present here is that we do not use multiple iterations per time-step. Instead the Newton-Raphson algorithm determines the rate of change of f_i which is then solved through integration. It should be noted that this limits the feedback approach to simulations with relatively short time-steps, such as the 15 min time-step used here. The choice of the Newton-Raphson algorithm here was justified by our aim of replicating the numerical solution of SOX as closely as possible, as the Newton-Raphson algorithm typically has faster convergence than first order methods. However, despite the fast convergence of the Newton-Raphson algorithm and the relatively close tracking of the optimal solution by our implementation, its use requires additional constraints to be added to the model code that prevent the algorithm becoming unstable and producing unrealistic results. In particular, the algorithm is not robust when the objective function is not concave and the second derivative changes sign within the optimisation domain. This is the case in SOX where under certain environmental conditions the second derivative of the objective function can become positive. Our solution of artificially preventing the second derivative from approaching zero and ultimately changing sign, by giving it a maximum value appears to have been relatively successful here. However, we currently have no clear method for determining what this maximum value should be besides the tuning we have done. This may mean that our method is not robust for all sets of environmental conditions and future applications of feedback control to stomatal optimisation may use more robust methods such as the commonly used gradient ascent method. Feedback optimisation of non-concave/non-convex functions, in particular those that change through time, is an emerging field (Häberle et al., 2020; Ding et al., 2021) and further work is required to understand how these methods may be applicable to stomatal optimisation.

5 Conclusion

We present a feedback control based approach for tracking the optimum stomatal conductance predicted by stomatal optimisation models through time. We apply the approach to the SOX stomatal optimisation model, where it is able to accurately replicate predicted GPP, stomatal transpiration and leaf water potential found by numerical iteration. Feedback control represents a promising avenue for stomatal optimisation models that may allow them to be efficiently implemented into LSMs, improving the representation of stomatal behaviour in projections of global climate in the future.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1174.

Author contributions

PC suggested the feedback control approach. CE advised on implementing the approach in SOX. All authors contributed to the design of the study. SJ conducted the simulations and analysis. SJ wrote the first draft of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

The authors acknowledge funding from: CSSP Brazil project P109647 (“Brazilian ecosystem resilience in net-generation vegetation dynamics scheme”)—SJ; Human Frontier Science Program project RGP0016/2020 (“How plant heat stress will influence global warming this century”)—CE; European Research Council ECCLES project, grant agreement number 742472 (“Emergent constraints on climate-land feedbacks in the Earth System”)—PC.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.970266/full#supplementary-material

References

Allen, C. D., Macalady, A. K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., et al. (2010). A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 259, 660–684. Adaptation of Forests and Forest Management to Changing Climate. doi:10.1016/j.foreco.2009.09.001

CrossRef Full Text | Google Scholar

Anderegg, W. R. L., Flint, A., Huang, C.-y., Flint, L., Berry, J. A., Davis, F., et al. (2015). Tree mortality predicted from drought-induced vascular damage. Nat. Geosci. 8, 367–371. doi:10.1038/ngeo2400

CrossRef Full Text | Google Scholar

Anderegg, W. R. L., Wolf, A., Arango-Velez, A., Choat, B., Chmura, D. J., Jansen, S., et al. (2018). Woody plants optimise stomatal behaviour relative to hydraulic risk. Ecol. Lett. 21, 968–977. doi:10.1111/ele.12962

PubMed Abstract | CrossRef Full Text | Google Scholar

Ball, J. T., Woodrow, I. E., and Berry, J. A. (1987). A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. Dordrecht: Springer Netherlands, 221. doi:10.1007/978-94-017-0519-6_48

CrossRef Full Text | Google Scholar

Best, M. J., Pryor, M., Clark, D. B., Rooney, G. G., Essery, R. L. H., Ménard, C. B., et al. (2011). The joint UK land environment simulator (jules), model description - part 1: Energy and water fluxes. Geosci. Model Dev. 4, 677–699. doi:10.5194/gmd-4-677-2011

CrossRef Full Text | Google Scholar

Betts, R. A., Cox, P. M., Collins, M., Harris, P. P., Huntingford, C., and Jones, C. D. (2004). The role of ecosystem-atmosphere interactions in simulated amazonian precipitation decrease and forest dieback under global climate warming. Theor. Appl. Climatol. 78, 157–175. doi:10.1007/s00704-004-0050-y

CrossRef Full Text | Google Scholar

Buckley, T. N. (2019). How do stomata respond to water status? New Phytol. 224, 21–36. doi:10.1111/nph.15899

PubMed Abstract | CrossRef Full Text | Google Scholar

Buckley, T. N. (2017). Modeling stomatal conductance. Plant Physiol. 174, 572–582. doi:10.1104/pp.16.01772

PubMed Abstract | CrossRef Full Text | Google Scholar

Buckley, T. N., Sack, L., and Farquhar, G. D. (2017). Optimal plant water economy. Plant, Cell & Environ. 40, 881–896. doi:10.1111/pce.12823

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., et al. (2011). The joint UK land environment simulator (jules), model description - part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 4, 701–722. doi:10.5194/gmd-4-701-2011

CrossRef Full Text | Google Scholar

Collatz, G. J., Ball, J. T., Grivet, C., and Berry, J. A. (1991). Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorology 54, 107–136. doi:10.1016/0168-1923(91)90002-8

CrossRef Full Text | Google Scholar

Collatz, G. J., Ribas-Carbo, M., and Berry, J. A. (1992). Coupled photosynthesis-stomatal conductance model for leaves of c4 plants. Funct. Plant Biol. 19, 519–538. doi:10.1071/PP9920519

CrossRef Full Text | Google Scholar

Cosentino, C., and Bates, D. (2011). Feedback control in systems biology. Florida, United States: CRC Press.

Google Scholar

Cosgrove, D. J. (2014). Plant cell growth and elongation. United States: American Cancer Society. doi:10.1002/9780470015902.a0001688.pub2

CrossRef Full Text | Google Scholar

Cowan, I. R., and Farquhar, G. D. (1977). Stomatal function in relation to leaf metabolism and environment. Symp. Soc. Exp. Biol. 31, 471–505.

PubMed Abstract | Google Scholar

Cox, P., Betts, R. A., Jones, C., Spall, S. A., and Totterdell, I. J. (2000). Acceleration of global warming due to carbon-cycle feedbacks in a coupled climate model. Nature 408, 184–187. doi:10.1038/35041539

PubMed Abstract | CrossRef Full Text | Google Scholar

Cox, P., Huntingford, C., and Harding, R. (1998). A canopy conductance and photosynthesis model for use in a gcm land surface scheme. J. Hydrology 212-213, 79–94. doi:10.1016/S0022-1694(98)00203-0

CrossRef Full Text | Google Scholar

Cox, P. M., Betts, R. A., Bunton, C. B., Essery, R. L. H., Rowntree, P. R., and Smith, J. (1999). The impact of new land surface physics on the gcm simulation of climate and climate sensitivity. Clim. Dyn. 15, 183–203. doi:10.1007/s003820050276

CrossRef Full Text | Google Scholar

Ding, Y., Lavaei, J., and Arcak, M. (2021). Time-variation in online nonconvex optimization enables escaping from spurious local minima. IEEE Trans. Autom. Contr. 1, 1. doi:10.1109/TAC.2021.3135361

CrossRef Full Text | Google Scholar

Eller, C. B., Rowland, L., Mencuccini, M., Rosas, T., Williams, K., Harper, A., et al. (2020). Stomatal optimization based on xylem hydraulics (sox) improves land surface model simulation of vegetation responses to climate. New Phytol. 226, 1622–1637. doi:10.1111/nph.16419

PubMed Abstract | CrossRef Full Text | Google Scholar

Eller, C. B., Rowland, L., Oliveira, R. S., Bittencourt, P. R. L., Barros, F. V., da Costa, A. C. L., et al. (2018). Modelling tropical forest responses to drought and el niño with a stomatal optimization model based on xylem hydraulics. Phil. Trans. R. Soc. B 373, 20170315. doi:10.1098/rstb.2017.0315

PubMed Abstract | CrossRef Full Text | Google Scholar

Eyland, D., van Wesemael, J., Lawson, T., and Carpentier, S. (2021). The impact of slow stomatal kinetics on photosynthesis and water use efficiency under fluctuating light. Plant Physiol. 186, 998–1012. doi:10.1093/plphys/kiab114

PubMed Abstract | CrossRef Full Text | Google Scholar

Farquhar, G. D., von Caemmerer, S., and Berry, J. A. (1980). A biochemical model of photosynthetic co2 assimilation in leaves of c3 species. Planta 149, 78–90. doi:10.1007/BF00386231

PubMed Abstract | CrossRef Full Text | Google Scholar

Franklin, G., Powell, J., and Emami-Naeini, A. (2011). Feedback control of dynamic systems. London, United Kingdom: Pearson Education.

Google Scholar

Fricke, W. (2017). Turgor pressure. United States: American Cancer Society, 1–6. doi:10.1002/9780470015902.a0001687.pub2

CrossRef Full Text | Google Scholar

Gedney, N., Cox, P. M., Betts, R. A., Boucher, O., Huntingford, C., and Stott, P. A. (2006). Detection of a direct carbon dioxide effect in continental river runoff records. Nature 439, 835–838. doi:10.1038/nature04504

PubMed Abstract | CrossRef Full Text | Google Scholar

Grossiord, C., Buckley, T. N., Cernusak, L. A., Novick, K. A., Poulter, B., Siegwolf, R. T. W., et al. (2020). Plant responses to rising vapor pressure deficit. New Phytol. 226, 1550–1566. doi:10.1111/nph.16485

PubMed Abstract | CrossRef Full Text | Google Scholar

Häberle, V., Hauswirth, A., Ortmann, L., Bolognani, S., and Dörfler, F. (2020). Non-convex feedback optimization with input and output constraints. IEEE Control Syst. Lett. 1, 1. doi:10.1109/lcsys.2020.3002152

CrossRef Full Text | Google Scholar

Harper, A. B., Cox, P. M., Friedlingstein, P., Wiltshire, A. J., Jones, C. D., Sitch, S., et al. (2016). Improved representation of plant functional types and physiology in the joint UK land environment simulator (jules v4.2) using plant trait information. Geosci. Model Dev. 9, 2415–2440. doi:10.5194/gmd-9-2415-2016

CrossRef Full Text | Google Scholar

Hartmann, D., Klein Tank, A., Rusticucci, M., Alexander, L., Broönnimann, S., Charabi, Y., et al. (2013). Observations: Atmosphere and surface. Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press. book section 2. 159–254. doi:10.1017/CBO9781107415324.008

CrossRef Full Text | Google Scholar

Hauswirth, A., Bolognani, S., Hug, G., and Dörfler, F. (2021). Optimization algorithms as robust feedback controllers. arXiv. doi:10.48550/ARXIV.2103.11329

CrossRef Full Text | Google Scholar

Hochberg, U., Rockwell, F. E., Holbrook, N. M., and Cochard, H. (2018). Iso/anisohydry: A plant–environment interaction rather than a simple hydraulic trait. Trends Plant Sci. 23, 112–120. doi:10.1016/j.tplants.2017.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsiao, T. C. (1973). Plant responses to water stress. Annu. Rev. Plant Physiol. 24, 519–570. doi:10.1146/annurev.pp.24.060173.002511

CrossRef Full Text | Google Scholar

Jacobs, C. M. J. (1994). “Direct impact of atmospheric CO2 enrichment on regional transpiration,” (Netherlands: Wageningen Agricultural University). Ph.D. thesis.

Google Scholar

Krishnamoorthy, D., and Skogestad, S. (2022). Real-time optimization as a feedback control problem – A review. Comput. Chem. Eng. 161, 107723. doi:10.1016/j.compchemeng.2022.107723

CrossRef Full Text | Google Scholar

Lawson, T., and Blatt, M. R. (2014). Stomatal size, speed, and responsiveness impact on photosynthesis and water use efficiency. Plant Physiol. 164, 1556–1570. doi:10.1104/pp.114.237107

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawson, T., and Vialet-Chabrand, S. (2019). Speedy stomata, photosynthesis and plant water use efficiency. New Phytol. 221, 93–98. doi:10.1111/nph.15330

PubMed Abstract | CrossRef Full Text | Google Scholar

Leuning, R. (1995). A critical appraisal of a combined stomatal-photosynthesis model for c3 plants. Plant Cell Environ. 18, 339–355. doi:10.1111/j.1365-3040.1995.tb00370.x

CrossRef Full Text | Google Scholar

Marengo, J. A., Souza, C. M., Thonicke, K., Burton, C., Halladay, K., Betts, R. A., et al. (2018). Changes in climate and land use over the amazon region: Current and future variability and trends. Front. Earth Sci. (Lausanne). 6, 228. doi:10.3389/feart.2018.00228

CrossRef Full Text | Google Scholar

Martínez-de la Torre, A., Blyth, E. M., and Robinson, E. L. (2019). Evaluation of drydown processes in global land surface and hydrological models using flux tower evapotranspiration. Water 11, 356. doi:10.3390/w11020356

CrossRef Full Text | Google Scholar

Martínez-Vilalta, J., Poyatos, R., Aguadé, D., Retana, J., and Mencuccini, M. (2014). A new look at water transport regulation in plants. New Phytol. 204, 105–115. doi:10.1111/nph.12912

PubMed Abstract | CrossRef Full Text | Google Scholar

Medlyn, B. E., Duursma, R. A., Eamus, D., Ellsworth, D. S., Prentice, I. C., Barton, C. V. M., et al. (2011). Reconciling the optimal and empirical approaches to modelling stomatal conductance. Glob. Chang. Biol. 17, 2134–2144. doi:10.1111/j.1365-2486.2010.02375.x

CrossRef Full Text | Google Scholar

Mercado, L. M., Huntingford, C., Gash, J. H. C., Cox, P. M., and Jogireddy, V. (2007). Improving the representation of radiation interception and photosynthesis for climate model applications. Tellus B Chem. Phys. Meteorology 59, 553–565. doi:10.1111/j.1600-0889.2007.00256.x

CrossRef Full Text | Google Scholar

Park Williams, A., Allen, C. D., Macalady, A. K., Griffin, D., Woodhouse, C. A., Meko, D. M., et al. (2013). Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 3, 292–297. doi:10.1038/nclimate1693

CrossRef Full Text | Google Scholar

Ponce-Campos, G. E., Moran, M. S., Huete, A., Zhang, Y., Bresloff, C., Huxman, T. E., et al. (2013). Ecosystem resilience despite large-scale altered hydroclimatic conditions. Nature 494, 349–352. doi:10.1038/nature11836

PubMed Abstract | CrossRef Full Text | Google Scholar

Powell, T. L., Galbraith, D. R., Christoffersen, B. O., Harper, A., Imbuzeiro, H. M. A., Rowland, L., et al. (2013). Confronting model predictions of carbon fluxes with measurements of amazon forests subjected to experimental drought. New Phytol. 200, 350–365. doi:10.1111/nph.12390

PubMed Abstract | CrossRef Full Text | Google Scholar

Prentice, I. C., Dong, N., Gleason, S. M., Maire, V., and Wright, I. J. (2014). Balancing the costs of carbon gain and water transport: Testing a new theoretical framework for plant functional ecology. Ecol. Lett. 17, 82–91. doi:10.1111/ele.12211

PubMed Abstract | CrossRef Full Text | Google Scholar

Restrepo-Coupe, N., Levine, N. M., Christoffersen, B. O., Albert, L. P., Wu, J., Costa, M. H., et al. (2017). Do dynamic global vegetation models capture the seasonality of carbon fluxes in the amazon basin? A data-model intercomparison. Glob. Chang. Biol. 23, 191–208. doi:10.1111/gcb.13442

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabot, M. E. B., De Kauwe, M. G., Pitman, A. J., Ellsworth, D. S., Medlyn, B. E., Caldararu, S., et al. (2022a). Predicting resilience through the lens of competing adjustments to vegetation function. Plant, Cell & Environ. 45, 2744–2761. doi:10.1111/pce.14376

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabot, M. E. B., De Kauwe, M. G., Pitman, A. J., Medlyn, B. E., Ellsworth, D. S., Martin-StPaul, N. K., et al. (2022b). One stomatal model to rule them all? Toward improved representation of carbon and water exchange in global models. J. Adv. Model. Earth Syst. 14, e2021MS002761. doi:10.1029/2021ms002761

CrossRef Full Text | Google Scholar

Sabot, M. E. B., De Kauwe, M. G., Pitman, A. J., Medlyn, B. E., Verhoef, A., Ukkola, A. M., et al. (2020). Plant profit maximization improves predictions of European forest responses to drought. New Phytol. 226, 1638–1655. doi:10.1111/nph.16376

PubMed Abstract | CrossRef Full Text | Google Scholar

Saleska, S., Da Rocha, H., Huete, A., Nobre, A., Artaxo, P., and Shimabukuro, Y. (2013). Lba-eco cd-32 flux tower network data compilation, brazilian amazon. Version 1. 1999–2006. doi:10.3334/ORNLDAAC/1174

CrossRef Full Text | Google Scholar

Sellers, P. J., Bounoua, L., Collatz, G. J., Randall, D. A., Dazlich, D. A., Los, S. O., et al. (1996). Comparison of radiative and physiological effects of doubled atmospheric co₂ on climate. Science 271, 1402–1406. doi:10.1126/science.271.5254.1402

CrossRef Full Text | Google Scholar

Sitch, S., Huntingford, C., Gedney, N., Levy, P. E., Lomas, M., Piao, S. L., et al. (2008). Evaluation of the terrestrial carbon cycle, future plant geography and climate-carbon cycle feedbacks using five dynamic global vegetation models (dgvms). Glob. Chang. Biol. 14, 2015–2039. doi:10.1111/j.1365-2486.2008.01626.x

CrossRef Full Text | Google Scholar

Sperry, J. S., and Love, D. M. (2015). What plant hydraulics can tell us about responses to climate-change droughts. New Phytol. 207, 14–27. doi:10.1111/nph.13354

PubMed Abstract | CrossRef Full Text | Google Scholar

Sperry, J. S., Venturas, M. D., Anderegg, W. R. L., Mencuccini, M., Mackay, D. S., Wang, Y., et al. (2017). Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost. Plant, Cell & Environ. 40, 816–830. doi:10.1111/pce.12852

PubMed Abstract | CrossRef Full Text | Google Scholar

Tyree, M. T., and Sperry, J. S. (1989). Vulnerability of xylem to cavitation and embolism. Annu. Rev. Plant Physiol. Plant Mol. Biol. 40, 19–36. doi:10.1146/annurev.pp.40.060189.000315

CrossRef Full Text | Google Scholar

Ukkola, A. M., Kauwe, M. G. D., Pitman, A. J., Best, M. J., Abramowitz, G., Haverd, V., et al. (2016). Land surface models systematically overestimate the intensity, duration and magnitude of seasonal-scale evaporative droughts. Environ. Res. Lett. 11, 104012. doi:10.1088/1748-9326/11/10/104012

CrossRef Full Text | Google Scholar

Venturas, M. D., Sperry, J. S., Love, D. M., Frehner, E. H., Allred, M. G., Wang, Y., et al. (2018). A stomatal control model based on optimization of carbon gain versus hydraulic risk predicts aspen sapling responses to drought. New Phytol. 220, 836–850. doi:10.1111/nph.15333

PubMed Abstract | CrossRef Full Text | Google Scholar

Vialet-Chabrand, S. R., Matthews, J. S., McAusland, L., Blatt, M. R., Griffiths, H., and Lawson, T. (2017). Temporal dynamics of stomatal behavior: Modeling and implications for photosynthesis and water use. Plant Physiol. 174, 603–613. doi:10.1104/pp.17.00125

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Sperry, J. S., Anderegg, W. R. L., Venturas, M. D., and Trugman, A. T. (2020). A theoretical and empirical assessment of stomatal optimization modeling. New Phytol. 227, 311–325. doi:10.1111/nph.16572

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Sperry, J. S., Venturas, M. D., Trugman, A. T., Love, D. M., and Anderegg, W. R. L. (2019). The stomatal response to rising co2 concentration and drought is predicted by a hydraulic trait-based optimization model. Tree Physiol. 39, 1416–1427. doi:10.1093/treephys/tpz038

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, K. E., Harper, A. B., Huntingford, C., Mercado, L. M., Mathison, C. T., Falloon, P. D., et al. (2018). Revisiting the first islscp field experiment to evaluate water stress in julesv5.0. Geosci. Model Dev. Discuss. 1. doi:10.5194/gmd-2018-210

CrossRef Full Text | Google Scholar

Wolf, A., Anderegg, W. R. L., and Pacala, S. W. (2016). Optimal stomatal behavior with competition for water and risk of hydraulic impairment. Proc. Natl. Acad. Sci. U. S. A. 113, E7222–E7230. doi:10.1073/pnas.1615144113

PubMed Abstract | CrossRef Full Text | Google Scholar