Interactions between ecosystem services and land use in France: A spatial statistical analysis

The provision of ecosystem services (ESs) is driven by land use and biophysical conditions and is thus intrinsically linked to space. Large-scale ES models, developed to inform policy makers on ES drivers, do not usually consider spatial autocorrelation that could be inherent to the distribution of these ESs or to the modeling process. The objective of this study is to estimate the drivers of ecosystem services in France using statistical models and show how taking into account spatial autocorrelation improves the predictive quality of these models. We study six regulating ESs (habitat quality index, water retention index, topsoil organic matter, carbon storage, soil erosion control, and nitrogen oxide deposition velocity) and three provisioning ESs (crop production, grazing livestock density, and timber removal). For each of these ESs, we estimated and compared five spatial statistical models to investigate the best specification (using statistical tests and goodness-of-fit metrics). Our results show that (1) taking into account spatial autocorrelation improves the predictive accuracy of all ES models (ΔR² ranging from 0.13 to 0.58); (2) land use and biophysical variables (weather and soil texture) are significant drivers of most ESs; (3) forest was the most balanced land use for provision of a diversity of ESs compared to other land uses (agriculture, pasture, urban, and others); (4) Urban area is the worst land use for provision of most ESs. Our findings imply that further studies need to consider spatial autocorrelation of ESs in land use change and optimization scenario simulations.

1 Introduction

Land use and land cover are identified as being among the main factors driving the provision of ecosystem services (ESs) (Haines-Young et al., 2012; Lawler et al., 2014), i.e., the benefits that humans obtain from nature and ecosystems (Costanza et al., 2014). In recent decades, the main drivers of ES losses were land use change (Meyfroidt et al., 2022), agricultural and urban expansion into forests and other land uses (Benayas and Bullock, 2012; Zhang et al., 2018), and landscape fragmentation (Braat and De Groot, 2012). However, it is increasingly recognized that the design and implementation of well-informed land-use policies can promote ESs (Bennett et al., 2015), i.e., smoothen the trade-offs between regulating and maintaining ESs with provisioning ESs (e.g., biomass production for food, fuel, and fiber) (Fisher et al., 2009). These trade-offs are often very pronounced when it comes to mitigating and adapting to climate change and conserving biodiversity while achieving food security.

Modeling is a useful support for policy and decision-making as it can simulate the provision of ESs as a consequence of land use change, especially on a large scale (Accatino et al., 2019). Some studies focus on using mathematical equations to model the linkages between drivers and ES provision. We consider that drivers are those factors that affect the provision of ESs, e.g., land cover and land use (Bennett et al., 2009; Burkhard et al., 2012) These models, which are referred to as ecological production functions (Tallis et al., 2011), can be mechanistic or statistical. Mechanistic models translate into mathematical equations the chain of cause–effect relationships linking drivers to ES provision. An example of this type is the InVEST model (see Posner et al. (2016)), examples of whose applications can be found in Babbar et al. (2021); Daneshi et al. (2021). Statistical models are based on equations which do not necessarily have a biophysical meaning and whose parameters are estimated with data. Specifically, in the case of large-scale (single country to European scale) ES modeling, parameter estimations are performed using maps of drivers and ESs (Cord et al., 2017; Teillard et al., 2017; Accatino et al., 2019; Shi et al., 2021). With relationships (mechanistic or statistical) linking drivers to ESs, it is possible to run scenarios to explore what consequences changes in drivers have for ES provision (Seppelt et al., 2013; Kindu et al., 2018) or optimization scenarios to investigate the combinations of drivers that lead to maximization of one or more ESs (Pohjanmies et al., 2017; Accatino et al., 2019; Shi et al., 2021).

When it comes to modeling ES provision at large scales and with relatively coarse resolution, mechanistic models are often difficult to apply as they are often conceived for higher resolutions. Simple approaches at those scales can be based on matrices linking land use information to an expert-based score of ES provision (Burkhard et al., 2012). Other studies focus on multiple ESs at the same time, using statistical approaches for some and simple mechanistic models for others (Qiao et al., 2019). In contrast, statistical models of ESs can be built on the information provided in European-scale ES mapping projects (see Maes et al. (2011)). While the information provided by maps is static, it can be used for estimating statistical models in such a way that models can predict new map configurations in the case of future land use changes or in optimization exercises. When assessments are made with multiple ESs, it is advantageous to have a common spatial resolution and a common set of drivers being considered, with each ES having its own specific set of parameter values. However, although other studies already built statistical models at large scales from country (Teillard et al., 2017; Accatino et al., 2019; Shi et al., 2021) to global scale (Heck et al., 2018)) or focus on spatially explicit optimization (Wang et al., 2018), the spatial autocorrelation remains poorly taken into account in statistical ES models. In other words, the information about an ES in a certain spatial pixel might not be independent of the value of the same ES in neighboring pixels. There are different reasons for considering spatial autocorrelation. First, while multiple ESs are modeled together using the same spatial resolution, they are often based on data of different resolutions and different mapping techniques (Zulian et al., 2018). Considering spatial autocorrelation could serve to correct any bias that might come from bringing all data layers to a common resolution. Second, more and more studies advocate the need for a multiscale approach when making assessments involving multiple ecosystem services. Considering multiple scales is important because different ESs are based on phenomena involving different spatial ranges (Raudsepp-Hearne and Peterson, 2016; Wei et al., 2017), and spatial autocorrelation provides the possibility of considering wider spatial information. Third, as pointed out by Meyfroidt et al. (2022), certain land covers and uses might have spillovers, meaning that they influence land covers and uses and ES provision to a greater extent than their precise location. For example, it is recognized that urban land use might cause wider-scale negative effects on ES provision (Xu et al., 2017). Other studies already considered spatial autocorrelation using Moran’s I (Moran, 1950), but this was performed on some specific problems (not systematically on many ESs), such as the spatial autocorrelation related to urbanization (Zhang et al., 2018) or among ESs (Xu et al., 2017) (not between drivers and ESs).

In this study, we aim to estimate the drivers of ESs in France using spatial statistical models and explore the influence of spatial autocorrelation on the predictive accuracy of these models. We considered several spatial statistical specifications in which spatial autocorrelation was included in different ways. We then compared, via metrics, the performance of each model and identified the best performing model. Results of our analysis show that taking into account spatial autocorrelation increases the predictive accuracy of ES models. This can provide insights into the importance of the spatial information for each different ESs, and the estimated models could be used to simulate future scenarios.

2 Materials and methods

2.1 Data

We considered data layers for different ESs and driver sources available on a large (French to European) scale. As most of the data related to the whole of Europe, we considered only that part related to France. All the data layers were brought to a common resolution of 8 km × 8 km (see below for the respective resolutions of the data layers), with a total of 9571 spatial units in France¹. Some data were expressed in quantitative values (for example, soil organic carbon stocks), meaning that each spatial cell was assigned a continuous value. Other variables were expressed in classes: for example, the soil texture was divided into coarse, medium, medium-fine, and fine; land use is divided into several classes, such as permanent grassland and arable. For quantitative variables (ESs, temperature, precipitation, and slope), the up- or down-scaling process consisted of first intersecting the common resolution grid with that of the variable in question and then averaging the values per common grid cell. For categorical variables, we aggregated the areas per class, expressing, for each spatial unit, the proportion occupied by each class.

2.1.1 Ecosystem service data

ESs data were elaborated starting from the layers at 10 km² resolution provided by the Joint Research Center (see Maes et al. (2011) for a detailed description of the methodology and sources for each dataset). We considered six regulating ESs (habitat quality, water retention, topsoil organic matter concentration, carbon storage, soil erosion control, and NO_x deposition) and three provisioning ESs (crop production, grazing livestock density, and timber removal). All the ES data were expressed in quantitative values (Table 1).

TABLE 1

TABLE 1. Description and summary statistics of driver and ecosystem service variables.

The habitat quality index (HQI) denotes the richness in common bird species. It is dimensionless and represents the ratio between local common bird species richness and average species richness within a 500-km radius. This proxy is developed from the results of the species distribution model based on maximum entropy (Phillips et al., 2006) from the European Bird Census Council’s Atlas of European Breeding Birds data. The water retention index (WRI) represents the capacity of the ground to capture water and reduce runoff. This composite indicator is dimensionless and ranges from 0 (complete incapacity to retain water) to 10 (maximum soil retention capacity). It accounts for the presence of vegetation (for interception), the soil type and the presence of bedrock (for water-holding capacity and percolation), soil sealing, and topographic gradient. The topsoil organic matter content indicator (SOM) represents the concentration of organic matter in the upper 15 cm of the soil and is expressed as a percentage [%] of the dry fine earth fraction. The soil carbon storage indicator (CS) represents the capacity of ecosystems to contribute to climate change mitigation [100 tonC.ha⁻¹. Year⁻¹]. This indicator is based on the IPCC GPG Tier 1 approach which assigns default coefficients to different vegetation cover types regarding above-ground and below-ground biomass. The vegetation cover layer is based on the Global Land Cover 2000 project, which uses SPOT-VEGETATION satellite imagery for the year 2000. The NO_x deposition velocity indicator (NOX) represents the capacity of the vegetation layer to capture and remove air pollutants. This proxy takes into account the presence of pollutants (estimated with an air quality model) and the presence of vegetation, for which default deposition velocity parameters are given by Pistocchi (2008). The soil erosion control indicator (SEC) measures the capacity of the soil to limit erosion. This composite indicator ranges from 0 to 1 (1 meaning that the soil has a high capacity to control erosion) and considers rainfall intensity, soil type, slope, and vegetation type (forests and grasslands are the most efficient).

The crop production indicator (CROP) corresponds to the annual production of harvested crops [10³ tons. km⁻². year⁻¹ of dry matter]. This indicator is an output of the CAPRI model using input data from 2010 (Maes et al., 2015). The timber removal indicator (TIMB) is the quantity of timber removed from forests [10³ m³ km⁻². year⁻¹]. The indicator is derived Eurostat and data collected in 2010 (Maes et al., 2015). The grazing livestock density indicator (GLD) corresponds to the number of grazing animals (cattle, sheep, goats, etc.) in 2010 [10³ head. km⁻² of permanent grassland]. This indicator is an output of the CAPRI model using input data from 2010 (Maes et al., 2015).

2.1.2 Ecosystem service driver data

The drivers of ESs that we considered included land use and as biophysical (soil texture and slope) and weather (precipitation and temperature) variables (Table 1). The variables we considered were already used in other studies in the literature that estimate statistical models at the same scale (Accatino et al., 2019; Shi et al., 2021). Land use and land cover variables are, in particular, considered fundamental for ES prediction (Burkhard et al., 2012). While precipitation, temperature, and slope were expressed quantitatively, land use and soil texture were expressed qualitatively in terms of classes. Land cover data are obtained from the Corine Land Cover (CLC) dataset (EEA, 2019), at 100 m × 100 m resolution for the year 2012. Within each 8 km × 8 km square of the common resolution, we calculated the proportion (dimensionless, ranging from 0 to 1) of the surface area occupied by each class, namely, arable land (Ara), permanent grassland (PermGra), forest (For), urban areas (Urb), and other land use classes (e.g., wetlands, water bodies) (Oth). Correspondences between the classes used in this study and the CLC classes are provided in the Supplementary Material. Soil texture data were provided by the JRC (Panagos et al. (2012) – European soil database) at a resolution of 1 km × 1 km. Within each 8 km × 8 km square of the common resolution, we calculated the proportion (dimensionless, ranging from 0 to 1) of the surface area occupied by each soil texture class, namely, coarse (SoilTXT.C), medium (SoilTXT.M), medium-fine (SoilTXT.MF), and fine (SoilTXT.F). Slope (S) data were obtained from the GTOPO30 dataset, a Digital Elevation Model with a 30-arc-second resolution (approximately 1 km). In the model, we did not consider altitude because slope and altitude are highly correlated, and the slope was a better fit for the model. Temperature (T [°C]) and precipitation (P [mm]) data are obtained the E-OBS dataset managed by the Copernicus Climate Change Service at the 0.1° regular grid resolution (approximately 10 km). They correspond to the daily average values between 2015 and 2017.

2.1.3 Correlations between variables

Before proceeding to the modeling of the links between ESs and their divers, we constructed a correlation matrix between all the variables (ESs and drivers) using the Spearman correlation index ρ, which ranges from 1 (perfect negative correlation) to +1 (perfect positive correlation). In this study, correlations with an absolute value greater than 0.8 were considered strong (Figure 1).

FIGURE 1

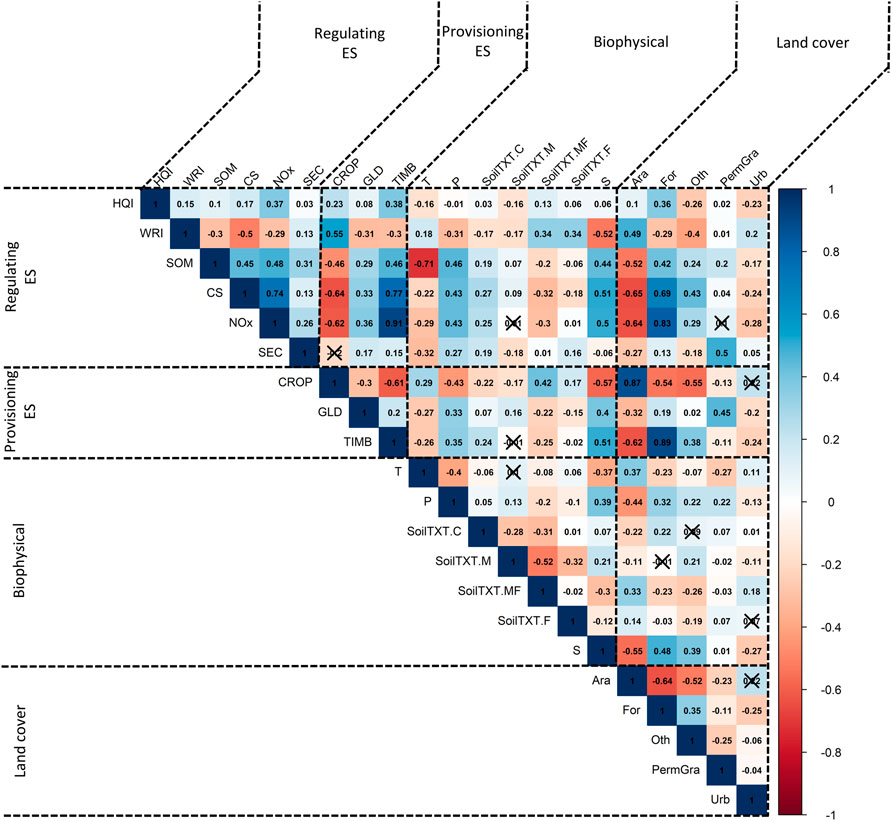
FIGURE 1. Correlation matrix between ecosystem services, biophysical variables, and land use area proportions at the scale of France using the Spearman method and with a significance level of 0.05. CROP stands for crop production; CS for carbon storage; HQI for habitat quality index; GLD for grazing livestock density; NOX for deposition velocity of nitrous oxide; SOM for topsoil organic matter concentration; SEC for soil erosion control; TIMB for timber removal; WRI for water retention index; S for slope; T for temperature; P for precipitation; Ara for arable land; For forest; Oth for wetlands and water bodies; PermGra for permanent grassland; Urb for urban areas; SoilTXT.C for the proportion of the area with coarse soil texture; SoilTXT.M for the proportion of the area with medium soil texture; SoilTXT.MF for the proportion of the area with medium fine soil texture; SoilTXT.F for the proportion of the area with fine soil texture.

These correlations provide useful information for the rest of the analysis, particularly on the following points: first, it allows checking carefully that the ESs considered are not highly correlated and that they do not capture the same phenomenon. We found that, with a few exceptions (e.g. TIMB and NOx, which are highly positively correlated), the correlations between ESs were low. Second, these correlations make it possible to verify the level of correlation between the drivers and thus avoid multicollinearity. Multicollinearity has the consequence of increasing the variance of the estimated parameters, so certain parameters may be insignificant even when a significant relationship exists between the variable to be explained and this driving variable. Moreover, parameters associated with two highly correlated driving variables can also have the wrong indication. In our case, we found fairly low levels of correlation between the driving variables. Finally, this matrix provides a preliminary idea of the links between the ESs and drivers. For example, forest land (respectively urban areas) is positively (negatively) correlated with the majority of ESs, as we showed in the models estimated in this study.

2.2 Statistical models and materials

2.2.1 Non-spatial statistical model

To be able to observe the effect of spatial autocorrelation on the modeling of ESs, we first proposed a non-spatial model that links ESs to drivers without considering spatial interactions among cells. This first model was called OLS, and the value ES_ij of the ES j (j = HQI, WRI, SOM, NOX, SEC, CROP, TIMB, GLD) in the cell i (i = 1 … , N) was modeled as follows:

$\mathit{log}\left(E{S}_{ij}\right)={\beta }_{LU}{\mathbf{L}\mathbf{U}}_i+{\beta }_{CL}{\mathbf{C}\mathbf{L}}_i+{\beta }_{SO}{\mathbf{S}\mathbf{O}}_i+{\epsilon }_{ij},(1)$

where ${\mathbf{L}\mathbf{U}}_{\mathbf{i}}={(Ar{a}_i,PermGr{a}_i,Fo{r}_i,Ur{b}_i,Ot{h}_i)}^T,{\mathbf{C}\mathbf{L}}_{\mathbf{i}}={(T_i,P_i)}^T$ and SO_i = (Txtc_i, SoilTXT.M_i, ${SoilTXT.M{F}_i,SoilTXT.F_i)}^T$ are vectors of land use proportions, weather, and soil variables, respectively, in each spatial unit i. β_LU, β_CL, and β_SO are unknown vectors of parameters to be estimated, and ɛ_ij are error terms identically and independently distributed. This model assumes that ESs are randomly distributed in space.

2.2.2 Spatial statistical models

The model in Eq. 1 assumes that the values of ESs are spatially independent across space, which is unlikely given the nature of the data. Omitting spatial dependence from a spatial data generating process could adversely affect the estimated model. It could suffer from bias in the regression coefficients, inconsistency, inefficiency, masking effects of spillovers, and prediction bias (Anselin, 1988).

2.2.2.1 Spatial autocorrelation

Relaxing the conventional assumption of independent observations in a cross-sectional setting requires that we provide a parsimonious way to specify structure for the spatial autocorrelation between the observations. In linear models, autocorrelation could be handled by inclusion of spatially lagged variables, which are weighted averages of the observations of “neighbors” of a given location. These spatially lagged variables could be dependent variables (spatial auto-regressive SAR models), driving variables (spatial cross-regressive SLX models), or error terms (SEM) or any combination of these options, which results in a range of spatial models (Elhorst, 2014). For example, the spatial Durbin model (SDM) is a combination of SAR and SLX and can be reduced to SEM (Lesage and Pace, 2009), while the spatial Durbin error model (SDEM) integrates all the elements of the SLX and the SEM. Finally, the general nesting spatial (GNS) model combines the SEM, SAR, and SLX models. Most empirical spatial econometrics studies in the literature focused mainly on two specifications: SAR and SEM, until the early 2000s (Elhorst, 2014).

There are many likely causes for the existence of spatial autocorrelation. For example, in the case of spatially correlated error terms (SEM), the source of spatial autocorrelation could be a data measurement problem; for instance, it can emerge from data measurement errors involving the spatial limits of the phenomena that differ from the boundaries used for the measurement. Another cause might be spatially correlated omitted variables. For example, LeSage and Pace (2009) provided motivation for regression models that include spatial autoregressive processes. This applies to our data, where the use of artificially constructed grids and differing scales could explain the existence of spatial autocorrelation (Anselin, 1988). In this study, we estimate five different spatial model specifications (Table 2).

TABLE 2

TABLE 2. Summary of the estimated spatial model specifications. W is the weight matrix, β are the estimated parameter vectors, LU are the proportions of land use area, CL are the weather variables, SO are the proportions of soil texture area, and ϵ are the error terms.

2.2.2.2 Weight matrix

Another central element of spatial analysis is the choice of the weight matrix W, which is the mathematical object that defines the assumed neighborhood structure to be used in this model. The weight matrix W is defined as a square matrix of order N, where N corresponds to the total number of grid cells. In this matrix, the term w_mn is equal to 1 if cells m and n are neighbors, and it is equal to 0 otherwise (Anselin, 1988). By convention, the diagonal elements of matrix W are zero (meaning that each cell is considered not to have spatial interaction with itself), and the rows are standardized such that their sum equals 1. A range of measures have been used in the literature to define such neighbor relationships, including contiguity (sharing a common geographical border) and distance criteria (distance bands or k − nearest neighbors) (Anselin, 1988). In this study, we considered different weight matrices (contiguity, distance bands, and k − nearest neighbors) in order to test the robustness of the results to the specification of the neighborhood definition. The estimation results were robust to the weight matrix specification; therefore, the study only presents the results of the queen contiguity-based spatial weight matrix (all cells surrounding a cell are considered neighbours, i.e., corners and edges).

2.2.2.3 Direct, indirect, and total impacts

Unlike classical linear models, the interpretation of spatial models requires the calculation of impact matrices because of the spillover effects on the driving variables (Elhorst, 2014). We give a brief definition of the elements present in each impact; see (LeSage and Pace, 2009) for details.

• Direct impact assesses the average change of an ES in cell i of a unit increase in the driving variable X. Therefore, it is similar to an estimated coefficient in simple linear regression.

• Indirect impact measures the average impact of an ES in cell i, if all observations except i have a unit increase in the driver variable X. In our case, the indirect impacts are the spatial spillovers from spatially lagged land use proportion variables.

• The total impact is the sum of both impacts.

2.2.3 Statistical spatial tests

Ignoring spatial effects in a model when they are present can have negative impacts on the estimators and their asymptotic properties. For example, if the data generation process is SAR and the lagged endogenous variable is ignored in the model specification, the OLS estimators will be biased and non-convergent. In the case of the SEM model, erroneously omitting a spatial autocorrelation error produces unbiased but inefficient estimators, and the statistical inference based on OLS is biased. Specification tests are important in this respect as they allow detecting the presence of spatial autocorrelation and choose the best model specification. There are different statistical tests in the literature, and here we present the Moran test and the Lagrange multiplier tests.

2.2.3.1 Moran Test

There are several procedures that can be used to statistically test the presence of spatial dependence against the null hypothesis (H₀) of spatial independence (Anselin, 1988). The most commonly used measure of spatial autocorrelation is Moran’s I (Moran, 1950) statistic, which indicates the degree of spatial association reflected in the data. When Moran’s test shows the existence of spatial autocorrelation, it can be taken into account in the statistical model in various ways by including spatially lagged variables, i.e., weighted averages of values of the “neighbors” of a given value (Anselin, 1988).

2.2.3.2 Lagrange Multiplier tests

Unlike Moran’s test, which detects a mis-specification problem but does not specify the form of the omitted autocorrelation, the Lagrange Multiplier (LM) tests can be used to choose the best spatial specification (Anselin, 1988) Robust forms are necessary (asymptotic adjustment) when both LM-Error and LM-Lag reject the hypothesis H₀ (Anselin et al., 1996).

2.2.3.3 Likelihood Ratio Tests

They are designed for nested models (constrained and non-constrained models) estimated by the maximum likelihood method. The constrained model is estimated under the constraint H₀ (here the hypothesis to test), and the unconstrained model is estimated without assuming H₀. If the hypothesis H₀ is rejected, this means that the unconstrained model is preferred. For more information, see Buse (1982).

2.2.4 Comparison of spatial models’ performances

For each ES, all the models (OLS, SAR, SEM, SLX, SDM, and SDEM) were estimated and their performance compared. The choice of the best performing model was based on three criteria: goodness-of-fit (R²), quality of prediction (RMSE), and statistical tests (Likelihood Ratio (LR) and Lagrange Multiplier (LM) tests proposed by Anselin (1988)). As there is no equivalent of R² for spatial models, in order to assess the goodness of fit of alternative spatial model specifications, we provided a pseudo-R² metric based on Nagelkerke (1991). We recall the classical definition of R² (see Nagelkerke (1991) for pseudo-R²) and RMSE

${\text{R}}^2=1-\frac{{\text{SS}}_{\text{res}}}{{\text{SS}}_{\text{tot}}}\text{,\hspace{0.17em}and\hspace{0.17em}}\text{RMSE}=\sqrt{\frac{1}{N}{\text{SS}}_{\text{res}}}(2)$

with SS_res the sum of squares of residuals, SS_tot the total sum of squares, and N the sample size. The closer R² (or pseudo R²) to 1, the more variability the model explains; the closer to 0 the RMSE, the better. RMSE gives an aggregated assessment of residuals (see Supplementary Figure S1). We also calculated the indirect and total impacts to take into account spatial spillover from spatially lagged land use proportion variables (LeSage and Pace, 2009).

3 Results

3.1 Spatial statistical tests

For the OLS model, we found the Moran’s I score significant for all ESs, meaning that the hypothesis H₀ of no spatial autocorrelation is rejected for all ESs (Table 3). In other words, for all the ESs, the value in a cell is dependent to some extent on the information from other spatially interacting cells. We found that both hypotheses of no spatially lagged dependent variable and no spatially autocorrelated error term are rejected at 1% significance for all models. The robust LM test results showed that both SAR and SEM specifications are not as relevant as the SDEM or SDM specifications for all ESs.

TABLE 3

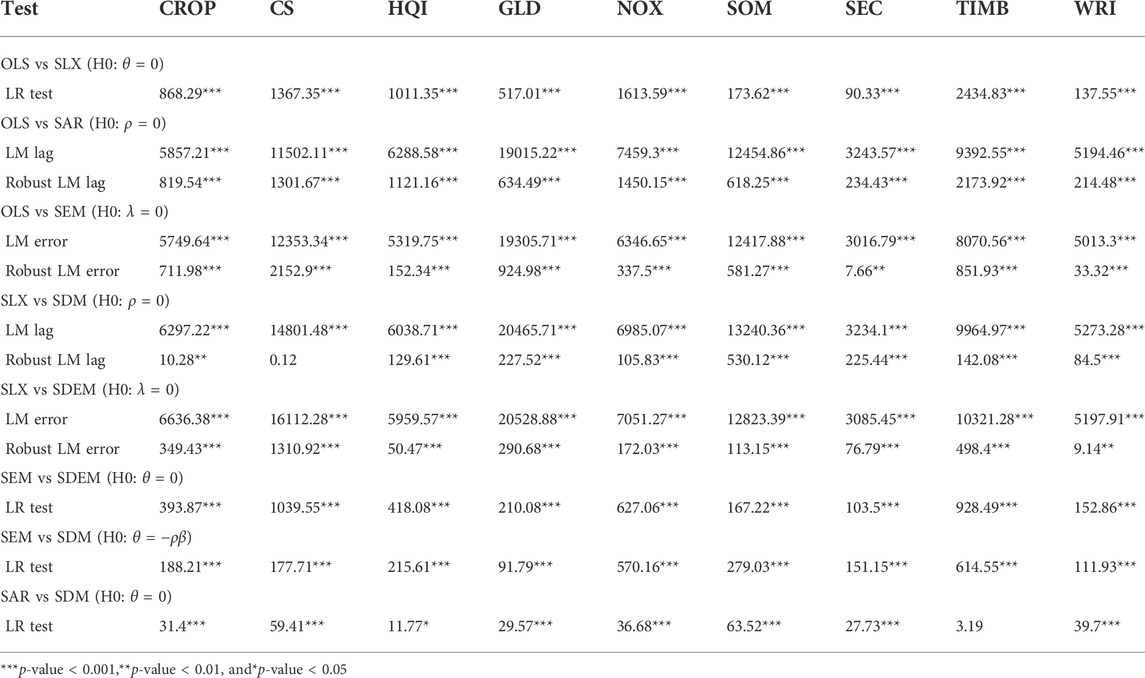
TABLE 3. Statistical tests (likelihood ratio (LR) and Lagrange Multiplier (LM)) between models (rows) per ecosystem service (column). We considered a non-spatial model (OLS), the spatial auto-regressive model (SAR), the spatial cross-regressive model (SLX), the spatial error model (SEM), the spatial Durbin model (SDM), and the spatial Durbin error model (SDEM). CROP stands for crop production; CS for carbon storage; HQI for habitat quality index; GLD for grazing livestock density; NOX for deposition velocity of nitrous oxide; SOM for topsoil organic matter concentration; SEC for soil erosion control; TIMB for timber removal; WRI for water retention index. It should be noted that the hypothesis H₀ depends on which models are compared. Each value of the statistical tests cannot be interpreted as such; only the significance of the statistical tests can be so interpreted.

3.2 Best performing model

Compared to the non-spatial model, taking into account spatial autocorrelation increases the R² criterion, i.e., the goodness-of-fit (see Table 4). The increases in R² were not the same for all the ESs. The highest gain in R² was observed for GLD, which went from a relatively poor explained variance (R² = 0.26) to a relatively high explained variance (R² = 0.84). For other ESs, the explained variance increased, with ΔR² ranging from 0.23 (NOX) to 0.27-0.28 (SOM and CS). We remark that, after including spatial autocorrelation, among the ESs strictly related to the presence of forest (CS, NOX, SOM, SEC, and TIMB), SEC had the lowest explained variance. SEC and WRI had low explained variance both for the OLS and SDEM models, although the performance improved with spatial autocorrelation included (R² < 0.50). The two ESs with the lowest gain in explained variance between OLS and SDEM were SEC and CROP, with the difference that CROP was already performing well with the OLS model, while SEC did not perform well with the SDEM model either. Both SEM and SDEM models gave very similar results in terms of prediction quality and goodness of fit, but results from SDEM models were slightly better for most ESs. To conclude, according to the criteria (R² and RMSE), the best specification for all ESs was the SDEM model (see the spatial distributions of ESs with this model compared to observations in Figure 2).

TABLE 4

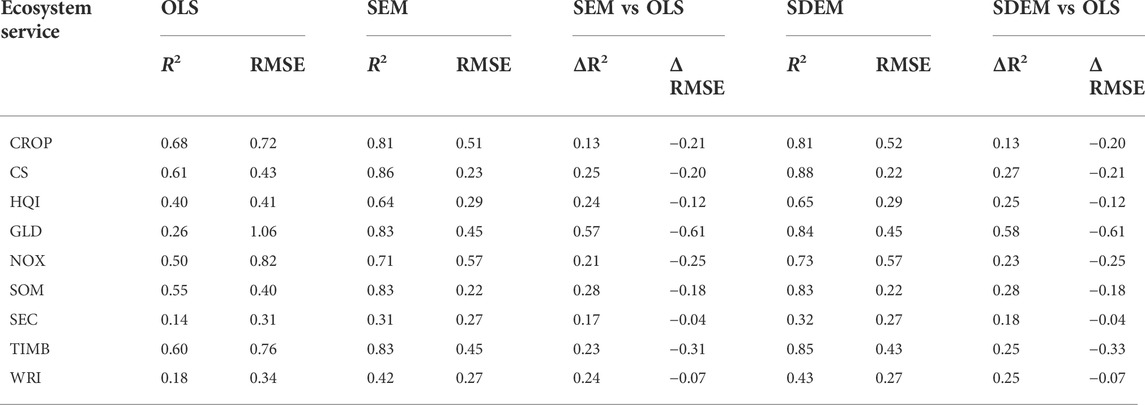
TABLE 4. Goodness-of-fit (R²) and prediction quality (RMSE) of the models (columns) per ecosystem service (rows). The models shown are a non-spatial model (OLS), the spatial error model (SEM), and the spatial Durbin error model (SDEM) as they showed the best performances with the Lagrange Multiplier test. We also show the difference in goodness-of-fit and prediction quality between the OLS model and spatial models (ΔR² and ΔRMSE). CROP stands for crop production; CS for carbon storage; HQI for habitat quality index; GLD for grazing livestock density; NOX for deposition velocity of nitrous oxide; SOM for topsoil organic matter concentration; SEC for soil erosion control; TIMB for timber removal; WRI for water retention index. We found that compared to OLS, R^2, and RMSE improved for all the spatial models.

FIGURE 2

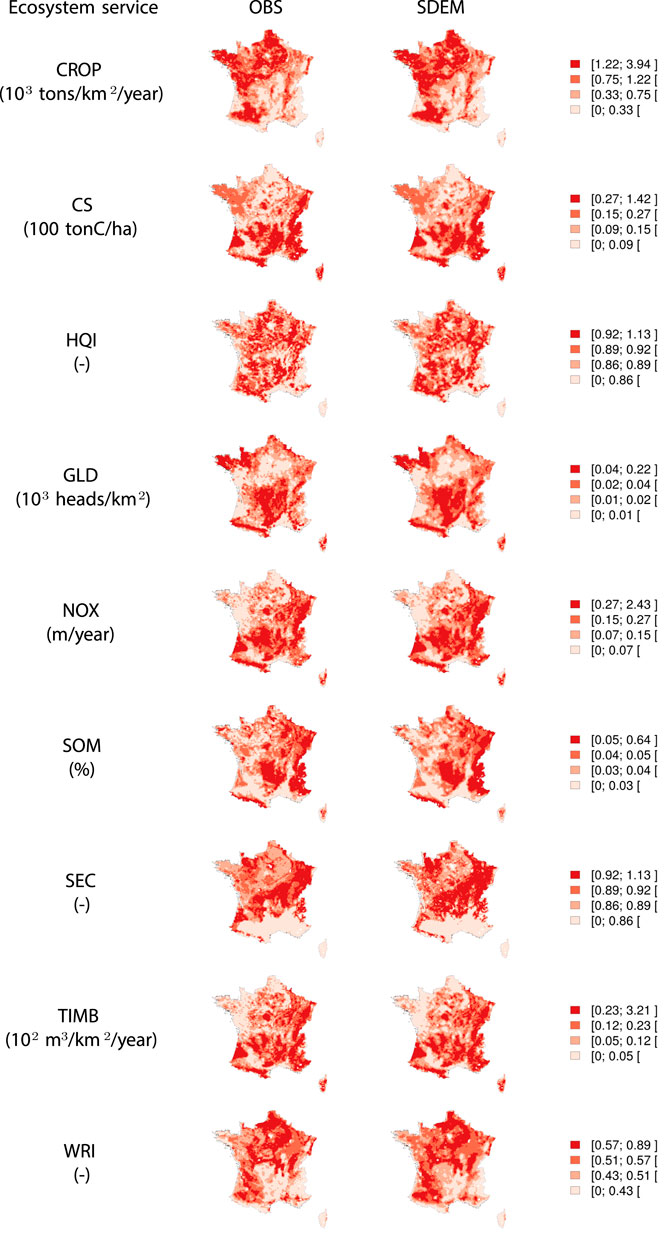
FIGURE 2. Spatial distributions of ecosystem services from observations (OBS) and from the spatial Durbin error model (SDEM). The color scale is unique for each ecosystem service. CROP stands for crop production; CS for carbon storage; HQI for habitat quality index; GLD for grazing livestock density; NOX for deposition velocity of nitrous oxide; SOM for topsoil organic matter concentration; SEC for soil erosion control; TIMB for timber removal; WRI for water retention index.

3.3 Significance of the impact of drivers

We showed that not all the drivers had the same impact on ES provision (see Figure 3 and Supplementary Table S2). Land use variables had significant impacts (positive or negative) on all ESs, with the exception of permanent grassland, for which the significance was weaker for GLD, SOM, SEC, and WRI (Figure 3). We found that forest was the land use that had the highest positive impacts on all ESs, except on CROP. On the contrary, urban land had the lowest negative impacts on all ESs, except on CROP. For CROP, arable land had the highest positive impact, while other land uses had the lowest negative impact. Permanent grassland showed non-significant impacts on GLD, WRI, and SOM. We also found that for arable land, other land uses, and urban land, all indirect impacts on ESs were significant, except with CROP (Supplementary Table S2). On the contrary, all other land uses had significant negative impacts on ESs related to forest (CS, NOX, SOM, SEC, and TIMB).

FIGURE 3

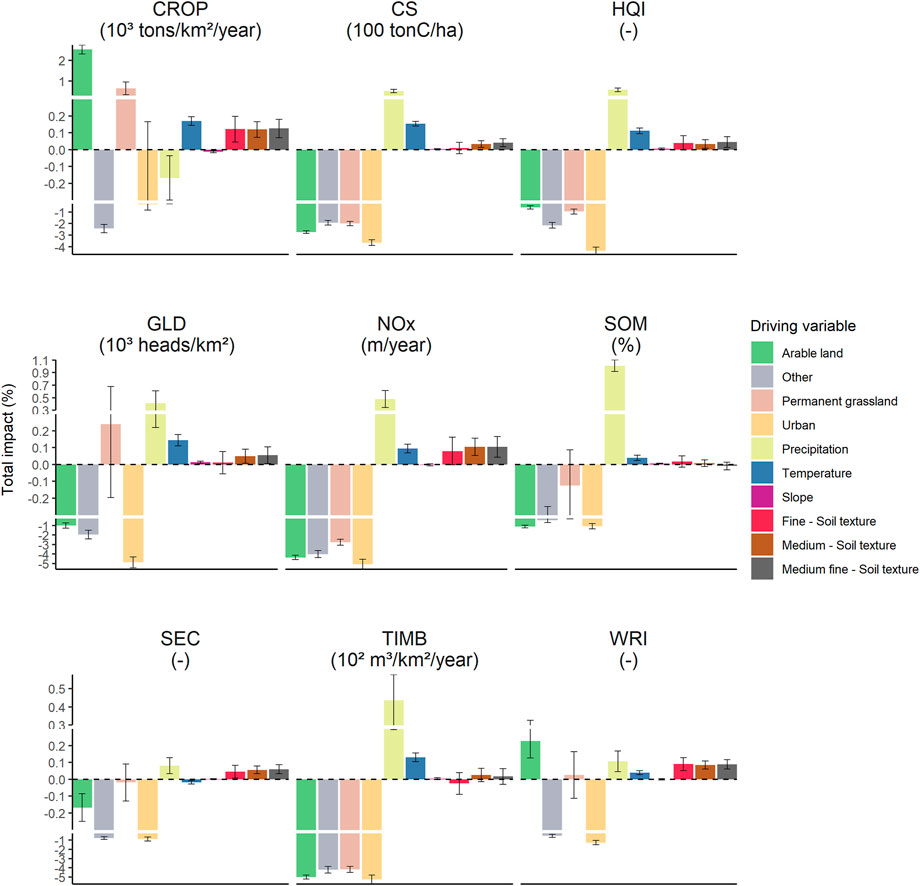
FIGURE 3. Total impacts of driving variables on ecosystem services with the spatial Durbin error model (SDEM). The total impact is the sum of direct and indirect impacts, and it corresponds to the relative variation (in %) of the ecosystem service in question when increasing the land use areapercentage (to the detriment of forest), the percentage of the soil texture area (to the detriment of the coarse soil texture), or the other biophysical variables by 1%. When the error bar (95% confidence interval of a normal distribution calculated from the estimated parameters and their standard deviations) overlaps the horizontal zero line, the impact of a driving variable on the ecosystem service is not statistically significant. CROP stands for crop production; CS for carbon storage; HQI for habitat quality index; GLD for grazing livestock density; NOX for deposition velocity of nitrous oxide; SOM for topsoil organic matter concentration; SEC for soil erosion control; TIMB for timber removal; WRI for water retention index.

We showed that weather drivers had significant impacts on all ESs, and the impact of precipitation was more significant on ESs than that of temperature. The impact of soil texture was also significant for most of the ESs, only slightly significant for HQI and GLD and not significant for SOM and TIMB. The soil-related driver that tended to show less significant impacts was SoilTXT.F. Slope has a significant impact on only some ESs, with for example, a negative impact on CROP and a positive impact on CS.

4 Discussion and conclusion

This study contributes to the large body of material empirically assessing relationships between land use and ESs on a large scale (see e.g., Burkhard et al. (2012); Accatino et al. (2019); Qiao et al. (2019); Shi et al. (2021)), with the specificity of taking into account spatial autocorrelation. We showed that taking into account spatial autocorrelation in large-scale ES statistical models allows us to significantly improve model fit and prediction accuracy (for example, we observed ΔR² ranging from 0.13 to 0.58). This is in agreement with other studies, stating that including spatial autocorrelation improves model fit and prediction accuracy (Record et al., 2013), while ignoring it can lead to inaccurate results (Kuhn, 2007). Importantly, the improvement in model prediction thanks to the inclusion of spatial autocorrelation was not the same for all the ESs. We also considered a set of drivers in addition to land use proportion variables, namely, weather (rainfall and temperature), soil texture, and topographical (slope) drivers. We found that in addition to land use, both weather variables had strong impacts on ES provision.

4.1 The importance of spatial autocorrelation in Statistical ecosystem services models

We demonstrated that including spatial autocorrelation is of fundamental importance for large-scale ES statistical models. Indeed, for all ESs, the Moran’s I measure of spatial autocorrelation was significant, and the performance, in terms of explained variance, was better with models, including spatial autocorrelation (especially the SDEM model, the best performing among all the models explored) than with the non-spatial model. However, the improvements in explained variance obtained with the inclusion of spatial autocorrelation were different among ESs. The importance of considering spatial autocorrelation, as well as the differences observed across different ESs, finds confirmation in other studies that implemented Moran’s I (Xu et al., 2017; Zhang et al., 2018; Zheng et al., 2020). Some ESs already performed well without spatial autocorrelation included, while other ESs did not achieve satisfactory performances even with spatial autocorrelation included.

Grazing livestock density showed the highest increase in explained variance with the inclusion of spatial autocorrelation (R² = 0.26 in the OLS model and R² = 0.84 in the SDEM model). This means that a single cell with a high percentage of permanent grassland in a cell group does not imply only extensive ruminant (grazing) livestock in that cell. However, a cell group with several cells with a high percentage of permanent grassland indicates a region of predominantly extensive ruminant (grazing) livestock. Similarly, for habitat quality index, a high percentage of forest in one cell does not necessarily imply a high value, while a high percentage of forest in several cells in a group does, showing the importance of resource continuity (see Schellhorn et al. (2015)). For permanent grasslands and for forests, spatial continuity on the scale of several hundred km² respectively better explains ruminant density and habitat quality for common birds. For the habitat quality index, the inclusion of spatial autocorrelation improved the predictive capacity of the model, and this is widely acknowledged in biodiversity statistical modeling (Dormann et al., 2007). Thus, including spatial characteristics in the statistical model referring to this ES certainly provides more information necessary for prediction of the ES.

Some ESs already performed well when spatial autocorrelation was not considered. This was the case when the provision of an ES is not subject to spatially explicit interactions, and it is strongly dependent on one land use. Among those investigated, the ESs with these characteristics are crop production (related to agricultural land) as well as carbon storage, topsoil organic matter, and timber removal (related to forest). Among the ESs related to forest, carbon storage and topsoil organic matter gained more explained variance than timber removal when moving from the OLS to the SDEM model. This might be due to the different data sets used (carbon storage and topsoil organic matter rely on older data) and from the fact that carbon storage and soil organic matter also rely, albeit to a lesser extent, on other land cover types and not only on forest land use. Following the expert-based assessment matrix proposed by Burkhard et al. (2012), crop production is indeed strongly dependent on agricultural land, timber removal is strongly dependent on forest, while carbon storage and topsoil organic matter are dependent on a wider spectrum of land use types.

Water retention index and soil erosion control showed the worst performance with both the OLS and SDEM models. Following Maes et al. (2011), the indicators used to represent these two ESs are based on cross-referencing between (at least) two layers. For example, the map of the water retention index ES is obtained via a model that takes into account much information (Pistocchi, 2008). The concept of cross-referencing data layers is not captured in the statistical models in our study. The same logic is also present for nitrogen oxide deposition: the map of this ES is obtained by cross-referencing the presence of forest with air pollution (calculated using a model). The factors determining air pollution are not included in our statistical models. Improvements to the prediction of these ESs can be obtained by including interrelations among drivers and by using machine learning techniques (see e.g., Willcock et al. (2018)).

To sum up, analysis of and comparison between different ESs made it possible to understand why including spatial autocorrelation is important in large-scale ES models. Our analysis suggests some possible reasons for this. First, the ES itself (or its index) might be based on some spatially explicit processes, i.e., the process leading to ES provision might involve spatially explicit dynamics (Pan et al., 2019) or it requires a certain degree of resource continuity (Schellhorn et al., 2015). Second, the indicator used for representing the ES might include spatial information. This is the case for grazing livestock density and habitat quality, whose performances improve when moving from OLS to SDEM. There are also other ESs, not included in this study, based on marked spatial processes, for example, pollination is based on the proximity between pollinator habitat and pollination-dependent crops (Zulian et al., 2013). Third, including spatial autocorrelation can serve to correct some distortions intrinsic to the data. This is why crop production improves its performance when spatial characteristics are included, even though the process is not spatially explicit. It is important to note that in analyses (see Shi et al. (2021)) that bring together data from different sources, resolutions, methods, and years, it is important to come to a common resolution for all the ESs and the drivers. Another source of distortion might arise from the resolution in itself, as argued by Grêt-Regamey et al. (2015): the choice of resolution might lead to biased estimations. Specifically, it is difficult to capture ESs having a non-clustered and scattered resolution if the resolution is too coarse. Distortions created by the choice of spatial resolution can at least be mitigated with the inclusion of spatial autocorrelation.

4.2 Considering non-land-use-related drivers

Our analysis confirmed the importance of considering land use variables as main drivers of the large-scale provision of ESs. This was also recognized in other studies (Tallis et al., 2011; Burkhard et al., 2012; Accatino et al., 2019). Our results find coherence with other studies (see e.g., Burkhard et al. (2012)), and we also found that urban land use has a negative impact on all ESs, as confirmed by other studies (Montoya-Tangarife et al., 2017; Xu et al., 2017). However, we also showed that weather, soil, and topographic drivers have their importance and should be considered in ESs modeling. Weather variables were found to have strongly significant impacts on all the ESs and soil variables on most of them. Indeed, these variables contribute to ESs either directly or indirectly, acting as drivers for the land uses providing the ESs. Soil texture was not found significant for grazing livestock density and habitat quality, as neither ES is directly related to soil properties, while it was found strongly significant for water retention and soil erosion control (except for SoilTXT.F), both strongly related to soil structure. Soil texture also played a role in crop production, as identified by previous research (Zwetsloot et al., 2021).

4.3 Limits

For a comprehensive assessment of the links between ESs and land use in France, several other drivers should also be taken into consideration. For example, the type of cropping system (organic farming vs. conventional farming, for example) on arable land since it determines, for example, productivity or the stock of organic matter in the soil (Marriott and Wander, 2006). Taking such a determinant into account would undoubtedly help improve the statistical quality of different models. Different possible land uses within arable land could also be detailed, e.g., heterogeneous agricultural practices and crop diversification that could have a higher stock of organic matter in the soil, better provision of ESs, for the same level of productivity than permanent crops or annual crops (Beillouin et al., 2021). In both cases, the refinement would require more data.

4.4 Perspectives

Our framework could be applied in different contexts, and several remaining questions could be considered in future work. First, simulations could be performed to study the impacts on ESs of changes in drivers. Indeed, our statistical models allow the estimation of how ESs will be modified when one or many drivers change. This could, for example, be used to estimate the impact of climate change on ESs using future climate scenarios to provide the value of weather variables included in our models. Second, a possible application is to simulate the impacts of public policies such as a tax on deforestation or a subsidy to maintain forests. To perform this, we need to develop a land use model that will link land uses to their drivers, such as the economic rents associated with each use (Chakir and Lungarska, 2017; Lungarska and Chakir, 2018). Our analysis is a first step for further research that sheds new light on the important question of ES preservation and enhancement in a context of growing tensions between social, environmental, and economic challenges.

Data availability statement

The raw data are available from the sources listed in the article, and preprocessed data are available upon request from the corresponding author.

Author contributions

All co-authors contributed equally to the research leading to this manuscript. IM and CP contributed equally as junior researchers, and FA and RC contributed equally as senior researchers.

Funding

The research leading to these results received funding from l’Agence National de la Recherche within the STIMUL (Scenarios Towards Integrating Multi-scale Land use tools) flagship project as part of the “Investments d’Avenir” Programme (LabEx BASC; ANR-11-LABX-0034) as well as Programme CLAND (ANR-16-CONV-0003). The French Agence Nationale de la Recherche is not accountable for the content of this research.

Author disclaimer

The authors are solely responsible for any omissions or deficiencies.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.954655/full#supplementary-material

Footnotes

¹This 8-km resolution grid corresponds to the regular grid used in the SAFRAN model. For more information see https://www.umr-cnrm.fr/spip.php?article788&lang=en

References

Accatino, F., Tonda, A., Dross, C., Léger, F., and Tichit, M. (2019). Trade-offs and synergies between livestock production and other ecosystem services. Agric. Syst. 168, 58–72. doi:10.1016/j.agsy.2018.08.002

CrossRef Full Text | Google Scholar

Anselin, L., Bera, A. K., Florax, R., and Yoon, M. J. (1996). Simple diagnostic tests for spatial dependence. Regional Sci. Urban Econ. 26 (1), 77–104. doi:10.1016/0166-0462(95)02111-6

CrossRef Full Text | Google Scholar

Anselin, L. (1988). Spatial econometrics : Methods and models. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Babbar, D., Areendran, G., Sahana, M., Sarma, K., Raj, K., and Sivadas, A. (2021). Assessment and prediction of carbon sequestration using markov chain and invest model in sariska tiger reserve, India. J. Clean. Prod. 278, 123333. doi:10.1016/j.jclepro.2020.123333

CrossRef Full Text | Google Scholar

Beillouin, D., Ben-Ari, T., Malézieux, E., Seufert, V., and Makowski, D. (2021). Positive but variable effects of crop diversification on biodiversity and ecosystem services. Glob. Chang. Biol. 27, 4697–4710. doi:10.1111/gcb.15747

PubMed Abstract | CrossRef Full Text | Google Scholar

Benayas, J. M. R., and Bullock, J. M. (2012). Restoration of biodiversity and ecosystem services on agricultural land. Ecosystems 15 (6), 883–899. doi:10.1007/s10021-012-9552-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, E. M., Cramer, W., Begossi, A., Cundill, G., Díaz, S., Egoh, B. N., et al. (2015). Linking biodiversity, ecosystem services, and human well-being: Three challenges for designing research for sustainability. Curr. Opin. Environ. Sustain. 14, 76–85. doi:10.1016/j.cosust.2015.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, E. M., Peterson, G. D., and Gordon, L. J. (2009). Understanding relationships among multiple ecosystem services. Ecol. Lett. 12 (12), 1394–1404. doi:10.1111/j.1461-0248.2009.01387.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Braat, L. C., and De Groot, R. (2012). The ecosystem services agenda: Bridging the worlds of natural science and economics, conservation and development, and public and private policy. Ecosyst. Serv. 1 (1), 4–15. doi:10.1016/j.ecoser.2012.07.011

CrossRef Full Text | Google Scholar

Burkhard, B., Kroll, F., Nedkov, S., and Müller, F. (2012). Mapping ecosystem service supply, demand and budgets. Ecol. Indic. 21, 17–29. Challenges of sustaining natural capital and ecosystem services. doi:10.1016/j.ecolind.2011.06.019

CrossRef Full Text | Google Scholar

Buse, A. (1982). The likelihood ratio, wald, and Lagrange multiplier tests: An expository note. Am. Statistician 36 (3), 153–157. doi:10.2307/2683166

CrossRef Full Text | Google Scholar

Chakir, R., and Lungarska, A. (2017). Agricultural rent in land-use models: comparison of frequently used proxies. Spat. Econ. Anal. 12 (2-3), 279–303. doi:10.1080/17421772.2017.1273542

CrossRef Full Text | Google Scholar

Cord, A. F., Bartkowski, B., Beckmann, M., Dittrich, A., Hermans-Neumann, K., Kaim, A., et al. (2017). Towards systematic analyses of ecosystem service trade-offs and synergies: Main concepts, methods and the road ahead. Ecosyst. Serv. 28, 264–272. SI:Servicing ES-EcoSummit16. doi:10.1016/j.ecoser.2017.07.012

CrossRef Full Text | Google Scholar

Costanza, R., De Groot, R., Sutton, P., Van der Ploeg, S., Anderson, S. J., Kubiszewski, I., et al. (2014). Changes in the global value of ecosystem services. Glob. Environ. change 26, 152–158. doi:10.1016/j.gloenvcha.2014.04.002

CrossRef Full Text | Google Scholar

Daneshi, A., Brouwer, R., Najafinejad, A., Panahi, M., Zarandian, A., and Maghsood, F. F. (2021). Modelling the impacts of climate and land use change on water security in a semi-arid forested watershed using invest. J. Hydrology 593, 125621. doi:10.1016/j.jhydrol.2020.125621

CrossRef Full Text | Google Scholar

Dormann, C. F., McPherson, M. J., Araújo, B. M., Bivand, R., Bolliger, J., Carl, G., et al. (2007). Methods to account for spatial autocorrelation in the analysis of species distributional data: a review. Ecography 30 (5), 609–628. doi:10.1111/j.2007.0906-7590.05171.x

CrossRef Full Text | Google Scholar

EEA, E. E. A. (2019). Corine land cover (CLC) 2012, version 20. Available at: http://land.copernicus.eu/pan-european/corine-land-cover/clc-2012/view.

Google Scholar

Elhorst, J. P. (2014). Spatial econometrics: From cross-sectional data to spatial panels, 479. Springer. doi:10.1007/978-3-642-40340-8

CrossRef Full Text | Google Scholar

Fisher, B., Turner, R. K., and Morling, P. (2009). Defining and classifying ecosystem services for decision making. Ecol. Econ. 68 (3), 643–653. doi:10.1016/j.ecolecon.2008.09.014

CrossRef Full Text | Google Scholar

Grêt-Regamey, A., Weibel, B., Bagstad, K. J., Ferrari, M., Geneletti, D., Klug, H., et al. (2015). On the effects of scale for ecosystem services mapping. PLOS ONE 9 (12), 1–26.

Google Scholar

Haines-Young, R., Potschin, M., and Kienast, F. (2012). Indicators of ecosystem service potential at European scales: mapping marginal changes and trade-offs. Ecol. Indic. 21, 39–53. doi:10.1016/j.ecolind.2011.09.004

CrossRef Full Text | Google Scholar

Heck, V., Gerten, D., Lucht, W., and Popp, A. (2018). Biomass-based negative emissions difficult to reconcile with planetary boundaries. Nat. Clim. Chang. 8 (2), 151–155. doi:10.1038/s41558-017-0064-y

CrossRef Full Text | Google Scholar

Kindu, M., Schneider, T., Döllerer, M., Teketay, D., and Knoke, T. (2018). Scenario modelling of land use/land cover changes in munessa-shashemene landscape of the ethiopian highlands. Sci. Total Environ. 622, 534–546. doi:10.1016/j.scitotenv.2017.11.338

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuhn, I. (2007). Incorporating spatial autocorrelation may invert observed patterns. Biodivers. Lett. 13, 66–69.

Google Scholar

Lawler, J. J., Lewis, D. J., Nelson, E., Plantinga, A. J., Polasky, S., Withey, J. C., et al. (2014). Projected land-use change impacts on ecosystem services in the United States. Proc. Natl. Acad. Sci. U. S. A. 111 (20), 7492–7497. doi:10.1073/pnas.1405557111

PubMed Abstract | CrossRef Full Text | Google Scholar

LeSage, J., and Pace, R. (2009). Introduction to spatial econometrics. Boca Raton FL: CRC Press.

Google Scholar

Lungarska, A., and Chakir, R. (2018). Climate-induced land use change in France: Impacts of agricultural adaptation and climate change mitigation. Ecol. Econ. 147, 134–154. doi:10.1016/j.ecolecon.2017.12.030

CrossRef Full Text | Google Scholar

Maes, J., Fabrega, N., Zulian, G., Barbosa, A., Vizcaino, P., Ivits, E., et al. (2015). “Mapping and assessment of ecosystems and their services: Trends in ecosystems and ecosystem services in the European Union between 2000 and 2010,” in Publications office of the European Union, Luxembourg. Institute for Environment and Sustainability. Available at: https://ec.europa.eu/JRC.

Google Scholar

Maes, J., Paracchini, M., and Zulian, G. (2011). “A European assessment of the provision of ecosystem services–towards an atlas of ecosystem services,” in Jrc scientific and technical reports european commission, joint research centre (Ispra(VA), Italy: Institute for Environment and Sustainability).

Google Scholar

Marriott, E. E., and Wander, M. M. (2006). Total and labile soil organic matter in organic and conventional farming systems. Soil Sci. Soc. Am. J. 70 (3), 950–959. eprint: Available at: https://onlinelibrary.wiley.com/doi/pdf/10.2136/sssaj2005.0241.

CrossRef Full Text | Google Scholar

Meyfroidt, P., de Bremond, A., Ryan, C. M., Archer, E., Aspinall, R., Chhabra, A., et al. (2022). Ten facts about land systems for sustainability. Proc. Natl. Acad. Sci. U. S. A. 119 (7), e2109217118. doi:10.1073/pnas.2109217118

PubMed Abstract | CrossRef Full Text | Google Scholar

Montoya-Tangarife, C., De La Barrera, F., Salazar, A., and Inostroza, L. (2017). Monitoring the effects of land cover change on the supply of ecosystem services in an urban region: A study of santiago-valparaíso, chile. PloS one 12 (11), e0188117. doi:10.1371/journal.pone.0188117

PubMed Abstract | CrossRef Full Text | Google Scholar

Moran, P. A. P. (1950). Notes on continuous stochastic phenomena. Biometrika 37 (1/2), 17–23. doi:10.2307/2332142

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagelkerke, N. J. D. (1991). A note on a general definition of the coefficient of determination. Biometrika 78 (3), 691–692. doi:10.1093/biomet/78.3.691

CrossRef Full Text | Google Scholar

Pan, H., Zhang, L., Cong, C., Deal, B., and Wang, Y. (2019). A dynamic and spatially explicit modeling approach to identify the ecosystem service implications of complex urban systems interactions. Ecol. Indic. 102, 426–436. doi:10.1016/j.ecolind.2019.02.059

CrossRef Full Text | Google Scholar

Panagos, P., Van Liedekerke, M., Jones, A., and Montanarella, L. (2012). European soil data centre: Response to European policy support and public data requirements. Land Use Policy 29 (2), 329–338. doi:10.1016/j.landusepol.2011.07.003

CrossRef Full Text | Google Scholar

Phillips, S. J., Anderson, R. P., and Schapire, R. E. (2006). Maximum entropy modeling of species geographic distributions. Ecol. Model. 190 (3), 231–259. doi:10.1016/j.ecolmodel.2005.03.026

CrossRef Full Text | Google Scholar

Pistocchi, A. (2008). A gis-based approach for modeling the fate and transport of pollutants in Europe. Environ. Sci. Technol. 42 (10), 3640–3647. PMID: 18546702. doi:10.1021/es071548+

PubMed Abstract | CrossRef Full Text | Google Scholar

Pohjanmies, T., Eyvindson, K., Triviño, M., and Mönkkönen, M. (2017). More is more? Forest management allocation at different spatial scales to mitigate conflicts between ecosystem services. Landsc. Ecol. 32 (12), 2337–2349. doi:10.1007/s10980-017-0572-1

CrossRef Full Text | Google Scholar

Posner, S., Verutes, G., Koh, I., Denu, D., and Ricketts, T. (2016). Global use of ecosystem service models. Ecosyst. Serv. 17, 131–141. doi:10.1016/j.ecoser.2015.12.003

CrossRef Full Text | Google Scholar

Qiao, X., Gu, Y., Zou, C., Xu, D., Wang, L., Ye, X., et al. (2019). Temporal variation and spatial scale dependency of the trade-offs and synergies among multiple ecosystem services in the taihu lake basin of china. Sci. Total Environ. 651, 218–229. doi:10.1016/j.scitotenv.2018.09.135

PubMed Abstract | CrossRef Full Text | Google Scholar

Raudsepp-Hearne, C., and Peterson, G. D. (2016). Scale and ecosystem services: How do observation, management, and analysis shift with scale—lessons from Québec. Ecol. Soc. 21 (3), art16. doi:10.5751/es-08605-210316

CrossRef Full Text | Google Scholar

Record, S., Fitzpatrick, M. C., Finley, A. O., Veloz, S., and Ellison, A. M. (2013). Should species distribution models account for spatial autocorrelation? a test of model projections across eight millennia of climate change. Glob. Ecol. Biogeogr. 22, 760–771. doi:10.1111/geb.12017

CrossRef Full Text | Google Scholar

Schellhorn, N. A., Gagic, V., and Bommarco, R. (2015). Time will tell: Resource continuity bolsters ecosystem services. Trends Ecol. Evol. 30 (9), 524–530. doi:10.1016/j.tree.2015.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Seppelt, R., Lautenbach, S., and Volk, M. (2013). Identifying trade-offs between ecosystem services, land use, and biodiversity: a plea for combining scenario analysis and optimization on different spatial scales. Curr. Opin. Environ. Sustain. 5 (5), 458–463. doi:10.1016/j.cosust.2013.05.002

CrossRef Full Text | Google Scholar

Shi, Y., Pinsard, C., and Accatino, F. (2021). Land sharing strategies for addressing the trade-off between carbon storage and crop production in France. Reg. Environ. Change 21 (4), 92. doi:10.1007/s10113-021-01818-7

CrossRef Full Text | Google Scholar

Tallis, H., Ricketts, T. H., Daily, G. C., and Polasky, S. (2011). Natural capital: Theory and practice of mapping ecosystem services. Oxford University Press.

Google Scholar

Teillard, F., Doyen, L., Dross, C., Jiguet, F., and Tichit, M. (2017). Optimal allocations of agricultural intensity reveal win-no loss solutions for food production and biodiversity. Reg. Environ. Change 17 (5), 1397–1408. doi:10.1007/s10113-016-0947-x

CrossRef Full Text | Google Scholar

Wang, Y., Li, X., Zhang, Q., Li, J., and Zhou, X. (2018). Projections of future land use changes: Multiple scenarios-based impacts analysis on ecosystem services for wuhan city, china. Ecol. Indic. 94, 430–445. doi:10.1016/j.ecolind.2018.06.047

CrossRef Full Text | Google Scholar

Wei, H., Fan, W., Wang, X., Lu, N., Dong, X., Zhao, Y., et al. (2017). Integrating supply and social demand in ecosystem services assessment: A review. Ecosyst. Serv. 25, 15–27. doi:10.1016/j.ecoser.2017.03.017

CrossRef Full Text | Google Scholar

Willcock, S., Martínez-López, J., Hooftman, D. A., Bagstad, K. J., Balbi, S., Marzo, A., et al. (2018). Machine learning for ecosystem services. Ecosyst. Serv. 33, 165–174. doi:10.1016/j.ecoser.2018.04.004

CrossRef Full Text | Google Scholar

Xu, S., Liu, Y., Wang, X., and Zhang, G. (2017). Scale effect on spatial patterns of ecosystem services and associations among them in semi-arid area: A case study in ningxia hui autonomous region, china. Sci. Total Environ. 598, 297–306. doi:10.1016/j.scitotenv.2017.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Y., Zhang, Y., Liu, Y., Zhang, G., and Chen, Y. (2018). On the spatial relationship between ecosystem services and urbanization: A case study in wuhan, china. Sci. total Environ. 637, 780–790. doi:10.1016/j.scitotenv.2018.04.396

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, D., Wang, Y., Hao, S., Xu, W., Lv, L., and Yu, S. (2020). Spatial-temporal variation and tradeoffs/synergies analysis on multiple ecosystem services: A case study in the three-river headwaters region of china. Ecol. Indic. 116, 106494. doi:10.1016/j.ecolind.2020.106494

CrossRef Full Text | Google Scholar

Zulian, G., Maes, J., and Paracchini, M. L. (2013). Linking land cover data and crop yields for mapping and assessment of pollination services in Europe. Land 2 (3), 472–492. doi:10.3390/land2030472

CrossRef Full Text | Google Scholar

Zulian, G., Stange, E., Woods, H., Carvalho, L., Dick, J., Andrews, C., et al. (2018). Practical application of spatial ecosystem service models to aid decision support. Ecosyst. Serv. 29, 465–480. doi:10.1016/j.ecoser.2017.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Zwetsloot, M. J., van Leeuwen, J., Hemerik, L., Martens, H., Simo Josa, I., Van de Broek, M., et al. (2021). Soil multifunctionality: Synergies and trade-offs across European climatic zones and land uses. Eur. J. Soil Sci. 72 (4), 1640–1654. doi:10.1111/ejss.13051

CrossRef Full Text | Google Scholar