Impacts of Industrial Agglomeration and Energy Intensity on Industrial Eco-Efficiency-Analysis Based on Spatial Correlation and Mediating Effect

As a measuring tool of industrial sustainable development, industrial eco-efficiency works as a link between economic benefit and environmental pressure. Industrial agglomeration and energy have always been considered an important influence factor on industrial eco-efficiency. The Chinese government is facing the challenge of reaching a Carbon Peak by the 2060s, within this context, it is critically important to explore the relationship between industrial agglomeration and industrial eco-efficiency, moreover, energy intensity may play a key role between them, which should not be ignored. Therefore, based on the STIRPAT model, this paper constructs a spatial autocorrelation model (SAC model) to analyze the provincial panel dataset from 2009 to 2018, and it is found that: First, the industrial agglomeration has an inverted N-shaped relationship with industrial eco-efficiency, and industrial eco-efficiency indeed have a positive spatial spillover effect. Second, energy intensity plays a mediating role, industrial agglomeration would affect industrial eco-efficiency through energy intensity. Therefore, it is suggested that the government should introduce differentiated industrial agglomeration policies as well as energy-saving policies. In addition, this paper suggests that policymakers should adhere to consistent industrial sustainable development policies.

1 Introduction

China’s industry acts as a crucial driving force for China’s economic development (Popescu et al., 2016). In 2021, China’s GDP exceeded 114.36 trillion yuan, ranking second in the world. The industrial added value reached 45.09 trillion yuan, accounting for 39.4% of GDP, with a growth rate of 8.2% over the previous year (Statistical Bulletin on National Economic and Social Development, 2022).

However, if we look into energy consumption and industrial emissions in China since the reform and opening-up, it is found that the industrial economic growth caused serious environmental problems simultaneously. Energy consumption increased by 9 times, and industrial emissions increased by 15 times from 1978 to 2020 (World Bank Data, 2020), which inferred that the rapid development of industry has brought excessive energy consumption and industrial emissions (Liu et al., 2021). According to the Environmental Performance Index (EPI) report released by Yale University and Columbia University in 2018, China’s EPI score in 2020 was 37.3, ranking 120th out of 180 countries (2020 EPI Results, 2021), indicating that China’s environmental problems continue to worsen (Li et al., 2021b). On 22 September 2020, China committed at the 75th Session of the United Nations General Assembly: It will strive to reach its carbon emission peak by 2030 and realize carbon neutrality by the 2060s (Wang et al., 2021). This means that the Chinese government will face greater challenges in saving energy and reducing industrial emissions in the future (Lin and Zhu, 2019; Li et al., 2021b). Within this context, how to realize the sustainable development of China’s industry has been a topic worth investigating deeply (Cai and Hu, 2022; Li and Wang, 2022; Yang et al., 2022).

Sustainable industrial development is an abstract concept that needs to be evaluated. Industrial eco-efficiency (hereinafter referred to as IEE) works as an evaluating tool, linking both economic benefit and environmental performance (Wang et al., 2011). Additionally, IEE has a significant advantage in quantifying the level of sustainable development and in explaining micro and macroeconomic issues (UNESCAP, 2009).

Meanwhile, more scholars adopt spatial economics to explain economic problems recently. Because each region’s economic activity is not isolated but closely related, which infers there may be a spatial correlation. Therefore, this paper believes that it is necessary to study whether IEE is influenced by surrounding areas, and explore whether IEE has a spatial spillover effect, to provide some policy suggestions for the decision-makers.

Driven by the industrial policies of the Chinese government, industrial enterprises begin to agglomerate in the regions with locational advantages and carry out compact production activities to reduce costs. Industrial agglomeration gradually changes the industrial structure and spatial distribution, which would affect regional industrial output and industrial emissions (Li et al., 2021c). Marshall (1890) propose that industrial agglomeration originated from the externality of the economy, Coase, (1960) and Henderson, (2003) further explain the causes and modes of agglomeration. Theoretically, industrial agglomeration is considered to have two basic effects: economies of scale and the crowding effect (Moomaw, 1981; Beeson, 1987; Ciccone, 2002, Yang et al., 2021). On the one hand, due to factors such as economies of scale, learning theory, and labor pooling, industrial agglomeration can improve economic benefits and reduce environmental pressure. On the other hand, a large number of enterprises concentrated in a limited space may reduce economic benefits and increase environmental pressure, which is not conducive to IEE. It can be observed that the final influence of industrial agglomeration on IEE depends on which effect plays a dominant role, so there may be a complex relationship between IEE and agglomeration.

Meanwhile, China’s energy consumption has always been a prominent issue. In 2020, China’s GDP ranked second among G20 countries, but its energy consumption per unit of GDP ranked the third lowest, illustrating that China’s energy utilization problem is still very serious (International Energy Agency, 2020). Many scholars believe that industrial agglomeration will directly affect energy intensity (Shi and Shen, 2013; Liu et al., 2017; Cao et al., 2022; Zheng and Lin, 2018; Wang et al., 2020). First, economies of scale of industrial agglomeration will promote enterprises to achieve intensive energy use, and improve energy efficiency. Second, the crowding effect may also lead to excessive competition for limited energy resources, and the energy consumption of industrial clusters becomes higher than that of other areas.

In addition, energy intensity also plays a critical role in improving IEE. Reducing energy intensity is conducive to decreasing environmental pressure, so improving energy utilization efficiency has positive significance to IEE. Many studies argue that industrial agglomeration is directly related to energy intensity or energy efficiency (Lei et al., 2017; Li and Hong, 2017; Liu and Jin, 2019; Zhang and Wang, 2019; Yang et al., 2022). Therefore, the influence of industrial agglomeration on IEE may be realized by influencing energy intensity. IEE, industrial agglomeration, and energy intensity are all of great importance for the realization of carbon neutrality and carbon peak commitment of the Chinese government at the macro level, as well as for the improvement of people’s welfare and environmental quality at the micro-level, therefore the in-depth study of IEE has essential practical significance.

2 Literature Review

The impact of industrial agglomeration on IEE is the theme of this study, so we review the literature related to industrial agglomeration and environmental performance or eco-efficiency. Some researchers propose that industrial agglomeration will increase the level of environmental pollution and reduce IEE. Dong et al. (2020) believe that industrial agglomeration has a positive impact on pollution agglomeration at the provincial level, and this impact is stronger in the northern and eastern regions, but weaker in the western regions.

Hong et al. (2020) conclude that industrial agglomeration could decrease pollution. Li J. et al. (2021) reveal the link between high-tech industrial agglomeration and Green Total Factor Productivity (GTFP) and argue that industrial agglomeration is positively correlated with GTFP. Other academic researchers also verify that the impact of industrial agglomeration is not monotonous by adding quadratic and cubic terms into the model. Shao et al. (2019) believe that economic agglomeration had an N-shape relationship with carbon emissions, and Chen et al. (2020) deem that the relationship between agglomeration and IEE is U-shaped. Guo et al. (2020) come to a consistent conclusion with the above viewpoint in investigating the sustainable industrial development in Northeast China from 2003 to 2016.

In addition, more and more studies have applied spatial autocorrelation theory to the study of industrial agglomeration and eco-efficiency (Ge et al., 2021; Han et al., 2022). According to Tobler’s First Law, “Everything is related to everything else, but the things that are near are more closely related” (Tobler, 1970), which means that regional economic behaviors have spatial effects on geography. Due to the lack of independence among spatial data, spatial autocorrelation is a common phenomenon (Fujita et al., 2000). Subsequently, spatial econometrics has been widely used to explain various economic phenomena with spatial correlation (Elhorst, 2014), and many important theoretical and practical achievements are made in IEE and industrial agglomeration (Chen et al., 2020; Ge et al., 2022).

Based on the previous research, it can be found that industrial agglomeration could promote IEE through two mechanisms: The first is labor pooling (Overman and Puga, 2010). Labor agglomeration is conducive to improving labor quality, providing enterprises with better human resources, and increasing economic benefit. The second is knowledge spillover (Feldman, 1999). The gathering of enterprises connected with production activities is conducive to the spillover of knowledge and technology, which generates scale effect, reduces energy consumption and industrial emissions, and finally improves IEE.

The above mechanisms result from the external economy of industrial agglomeration, meanwhile, there is also external diseconomy in industrial agglomeration. Due to intensive production in a limited space, industrial emissions may increase, which may have a negative impact on IEE, so industrial agglomeration might have a nonlinear impact on the economy and environment. Therefore, this paper proposes the first research hypothesis in this study:

Hypotheses 1: Industrial agglomeration has a nonlinear effect on IEE, and there is a spatial spillover.

Previous studies have argued that agglomeration has a direct impact on energy intensity, and generally there are three types of conclusions. First, the positive externality of industrial agglomeration can reduce energy intensity. Wang and Chen (2010) point out that industrial agglomeration could improve energy efficiency, and industrial agglomeration will increase energy intensity. Chen F. (2016) holds that manufacturing industrial agglomeration increased China’s energy intensity as a whole. Shi and Shen (2013) analyze the economic agglomeration of 30 provinces in China from 1998 to 2010 and find that economic agglomeration first inhibits and then promotes energy efficiency. Ji and Zhao (2016) check the inverted U-shaped relationship between industrial agglomeration and energy efficiency of 20 subsectors in China’s manufacturing industry from 2002 to 2012. They contend that energy efficiency will decrease at a low agglomeration level, and increase at a high agglomeration level.

It is generally agreed that energy intensity would increase environmental pollution and reduce IEE. Li and Hong (2017) assert that energy intensity can increase environmental pollution, and there is a positive spatial correlation. Zhang and Wang (2019) study the haze pollution of 29 provinces in China from 2001 to 2015. It is certificated that the energy utilization efficiency could reduce haze pollution, and there is a negative spatial correlation. Lei et al. (2017) demonstrate the positive relationship between energy intensity and environmental pollution.

From the previous studies on industrial agglomeration and energy intensity, it can be inferred that industrial agglomeration, energy intensity and IEE are closely related. Industrial agglomeration may promote energy intensive utilization through sharing and learning mechanisms (Chatman and Noland, 2011), thus energy intensity decrease. As mentioned above, researchers put forward different conclusions about the effect of industrial agglomeration on energy by empirical analysis, so the relationship between them may also be nonlinear. There is a consensus that energy intensity inhibits IEE because energy consumption is an important source of environmental stress.

It is not hard to see that energy intensity may play a key role in the impact of industrial agglomeration on IEE. Industrial agglomeration may affect IEE through energy intensity, this mechanism mainly considers that energy intensity will directly affect the environmental input in IEE’s indicator, the scale effect of industrial agglomeration may reduce energy intensity and improve IEE. In view of this, we propose the second hypothesis of this study:

Hypotheses 2: Energy intensity plays a mediating role between industrial agglomeration and IEE.

It is found that previous studies more focus on regional eco-efficiency, but rarely on industrial eco-efficiency specifically, and the research objectives are always limited to the industrial agglomeration effect, and there is little literature discussing in which way industrial agglomeration influences IEE. In general, some researchers are more interested in the connection between industrial agglomeration and IEE, or industrial agglomeration and energy, but rare literature puts them into one research framework.

Therefore, the contribution of this paper is to explore the nonlinear impact of industrial agglomeration on industrial eco-efficiency from the perspective of spatial correlation and introduce energy intensity into the research framework as the mediating variable, to further discuss the mechanism of industrial agglomeration on IEE. This study could enrich the theory of industrial sustainable development, and have practical significance for the government to formulate industrial and energy policies, not only for Chinese industry but also for other developing countries facing the same industrial sustainable problems.

The rest of this article is organized as follows: The second section is the literature review. The third section is the methodology, including evaluation of IEE, model setting, variables description, and data sources, The fourth section is empirical results analysis, including IEE evaluation result, spatial regression, robustness test, and mediation effect test. The fifth section is the conclusion.

3 Methodology

3.1 IEE Evaluation by Super-DEA Method

“Eco-efficiency” is proposed by Schaltegger and Sturm (1990), which is defined as the ratio of economic output to environmental impact. At the Earth Summit held in Rio de Janeiro in 1992, the World Business Council for Sustainable Development (WBCSD) explain the eco-efficiency by the following:

$Eco-Efficiency=\frac{products and services value}{environmental load} (1)$

DEA model is widely adopted in efficiency measurement, and it is very suitable for the situation in which Decision Making Units (DMUs) have multiple input and output indices (Guo and Xu, 2016; Yuan et al., 2017). On this basis, the Super-DEA model is applied for evaluation in this paper, due to two significant advantages compared to the general DEA model. Firstly, the Super-efficiency DEA can further distinguish the difference between those effective DMUs, secondly, the data truncation problem can be avoided. Suppose an evaluation system has n DMUs, and each DMU_j is composed of m input indices and s output indices. Input vector X_j and Output vector Y_j are stated following Eq. 2, and Eq. 3:

$Input vector:X_j={(x_{1j},x_{2j},\dots x_{mj})}^T (2)$

$Output vector:Y_j={(y_{1j},y_{2j},\dots y_{sj})}^T (3)$

And the linear programming of the super-efficiency DEA model is expressed by the following:

$\begin{array}{l}min[\theta - \epsilon ({\displaystyle \sum }_{i=1}^m{S}_i^{-}+{\displaystyle \sum }_{r=1}^s{S}_r^{+})] \\ s.t.{\displaystyle \sum }_{\begin{array}{c}j=1\\ j\ne k\end{array}}^n{X}_{ij}{\lambda }_j+S_i^{-}\mathrm{⩽}\theta X_0\\ {\displaystyle \sum }_{\begin{array}{c}j=1\\ j\ne k\end{array}}^n{Y}_{rj}{\lambda }_j-S_r^{+}=Y_0\\ {\lambda }_j\mathrm{⩾}0,S_r^{+}\mathrm{⩾}0,S_i^{-}\mathrm{⩽}0\\ i=\mathrm{1,2}\dots ,m\\ j=\mathrm{1,2}\dots ,n\\ r=\mathrm{1,2}\dots ,s\end{array}(4)$

where X represents the input index, Y represents the output index of DMU_j, θ represents technical efficiency, and λ represents the matrix. $S_i^{-}$ represents input slacks, and $S_r^{+}$ represents output slacks.

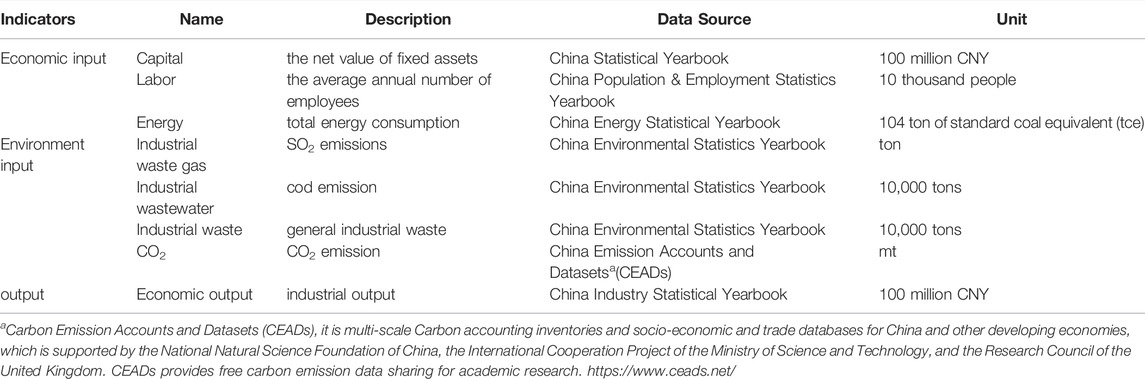
For the input-output indicator setting, we refer to the method in previous literature (Chen L., 2016; Wang et al., 2016; Yang, 2020), which treats capital and labor as economic input, energy and industrial emissions as environmental input, industrial output as economic outputs. Some indicators such as ammonia nitrogen emissions or industrial soot dust are deleted, because official statistics are not available now (Yuan and Zhang, 2017; Zhou et al., 2020).

Finally, this study employs Super-efficiency slack-based measurement (SBM) DEA method to evaluate IEE, the input-output indicators of IEE in this paper are set as shown in Table 1.

TABLE 1

TABLE 1. Variables Description in super-efficiency DEA Model.

3.2 Empirical Model Setting

STIRPAT model is widely adopted to examine the impact factors of environmental pressure (York et al., 2003). Therefore, this paper expands the model by introducing industrial agglomeration as an explanatory variable, and other control variables to check the impact of industrial agglomeration on IEE and constructs the econometric model as the model (5):

$ie{e}_{it}={\beta }_{1}ag{g}_{it}+{\beta }_{2}ag{g}_{it}^2+{\beta }_{3}ag{g}_{it}^3+{\beta }_{4}ener{g}_{it}+Z_{it}+{\epsilon }_{it} (5)$

where i represents province, t represents the year, iee represents industrial eco-efficiency measured by the super-efficiency DEA method, agg represents industrial agglomeration, energ represents energy intensity, and Z_it represents a series of control variables such as industrial structure, environmental regulation, and technological level. ε_it represents the error term. Considering that industrial agglomeration may have a nonlinear impact on IEE, the quadratic term and the cubic term of agg are introduced into the model.

Based on the previous literature, it is proved that industrial agglomeration has a strong spatial correlation with eco-efficiency (Yu et al., 2018a; Wang and Yang, 2019; Li et al., 2020). Since the general panel regression model may lead to biased estimates, this paper takes spatial correlation factors into account in empirical analysis, and the spatial panel regression model can better analyze the impact of industrial agglomeration on IEE.

The most significant feature of spatial econometrics compared with traditional econometrics is setting a spatial weight matrix, which explains spatial correlation by adjacent, geographic distance, or economic distance. This paper adopts the three common spatial weight matrices, the inverted geographic distance square matrix (W01) (Fan and Zhou, 2018) for the main regression model, the economic distance weight matrix (W02) (Wang et al., 2019) and the economic geography weight matrix (W03) (Chen et al., 2020) for robustness test, which are constructed as follows:

$W01=\{\begin{array}{c}\frac{1}{d_{ij}^2} i\ne j\\ 0 i=j\end{array},d_{ij} is the dis\tan ce between 2 areas(6)$

$W02=\{\begin{array}{c}\frac{1}{\left|\overline{E_i}-\overline{E_j}\right|} i\ne j\\ 0 i=j\end{array} , \overline{E} is the average GDP (7)$

$W03=\{\begin{array}{c}\frac{\overline{(E_i}\ast \overline{E_j)}}{d_{ij}^2} i\ne j\\ 0 i=j\end{array},\overline{E} is the average GDP, d_{ij} is the distance between 2 areas(8)$

The first step of adopting the spatial econometric model is to determine whether this study is suitable for the spatial econometric method. Generally, it is to judge whether there is a spatial correlation by the Moran’s Index (Anselin, 2019), which is calculated as following (9), where Y denotes IEE in this paper.

$I=\frac{n}{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^n{W}_{ij}}\ast \frac{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^n{W}_{ij}\left(Y_i-\overline{Y}\right)\left(Y_j-\overline{Y}\right)}{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2} (9)$

$\overline{Y}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{Y}_i$

When Moran’s index is significantly positive, it indicates that variables are positively spatial correlated; when Moran’s index is significantly negative, it means that there is a negative spatial correlation. If Moran’s index is not significant, it illustrates that the variables have no obvious spatial correlation, then it is not necessary to adopt the spatial econometric method for research.

Based on the model 5, Spatial Autocorrelation Model (SAC) (Halleck Vega and Elhorst, 2015) is constructed in this paper to study the impact of industrial agglomeration on IEE. The specific model is set as the model (10):

$ie{e}_{it}={\beta }_0{W}_{ij}ie{e}_{it}+{\beta }_{1}ag{g}_{it}+{\beta }_{2}ag{g}_{it}^2+{\beta }_{3}ag{g}_{it}^3+{\beta }_{4}ener{g}_{it}+Z_{it}+{\epsilon }_{it}(10)$

${\epsilon }_{it}=\lambda W_{ij}{\epsilon }_{it}+\nu$

The second research hypothesis in this paper is that industrial agglomeration affected the IEE through energy intensity, in order to test whether energy intensity is a mediator variable, referring to Baron and Kenny (1986), the mediating effect was tested as the following:

$DV=d_{1}IV+e_1(11)$

$MV=d_{2}IV+e_2(12)$

$DV=d_{3}IV+d_{4}MV+e_3(13)$

Model (11) indicates that explanatory variables affect the explained variables, there may be mediating effect if d₁ is significant. However, to prove that there is a mediating effect, the following tests are needed. Model (12) explains the impact of explanatory variables on the mediating variables, and Model (13) represents the influence of the mediating variables and explanatory variables on the explained variables. If the coefficients d₂ and d₄ are both significant, therefore the mediation effect is verified.

In fact, the Model (13) has been already certificated through the SAC model (10) in the first research hypothesis. Based on the second hypothesis of this paper, the mediating model is constructed taking IEE as the explained variable, energy intensity as the mediator, industrial agglomeration as the explanatory variable, and other control variables. The specific mediation effect is verified by the model (14) and model (15):

$ie{e}_{it}={\alpha }_0{W}_{ij}ie{e}_{it}+{\alpha }_{1}ag{g}_{it}+{\alpha }_{2}ag{g}_{it}^2+{\alpha }_{3}ag{g}_{it}^3+Z_{it}+{\epsilon }_{it}(14)$

${\epsilon }_{it}=\lambda W_{ij}{\epsilon }_{it}+\nu$

$ener{g}_{it}={\eta }_0{W}_{ij}ener{g}_{it}+{\eta }_{1}ag{g}_{it}+{\eta }_{2}ag{g}_{it}^2+Z_{it}+{\epsilon }_{it}(15)$

${\epsilon }_{it}=\lambda W_{ij}{\epsilon }_{it}+\nu$

3.3 Variables Description

The explained variable is IEE (iee), which is calculated by the super DEA method in the previous step. The core explanatory variables of this paper are industrial agglomeration (agg) and energy consumption (energ). According to Yan and He (2019), the level of industrial agglomeration can be expressed by the location entropy of employment, which can better describe the distribution characteristics of industrial agglomeration. The industrial agglomeration index can be calculated by the following Eq. 16.

$AG{G}_{it}=\frac{L_{it}/L_t}{Q_{it}/Q_t}(16)$

where L refers to industrial employment of i province in t year, Q refers to the total employment of i province in t year. As stated in the theory of agglomeration (Krugman, 1991), industrial agglomeration may lead to economies of scale and a crowding effect. Since the influence of industrial agglomeration on IEE may be nonlinear, the quadratic and cubic terms of industrial agglomeration are introduced into the model.

Energy intensity (energ) acts as a mediating variable in this study, which is measured by the proportion of power consumption in regional GDP (Yuan et al., 2020). The higher the energy intensity per unit of output means the higher the energy consumption, which would decrease IEE, so the expected sign is negative.

There are five control variables in this model, namely, 1) Human Resources (edu). Human resources are expressed by the average schooling years of the urban population (Peng and Li, 2015). Human capital could improve eco-efficiency through technological innovation and environmental protection awareness, so the sign of the expected variable is positive. 2) Level of industrialization (indus). It is expressed by the share of the industrial added value in GDP (Yu et al., 2018b). The higher the industrial added value per unit of GDP, the more industrial output, so the expected sign is positive. 3) Population density (lnpopul). Population density is calculated by the ratio of the total population to the administrative area at the end of the year, and takes the natural logarithm form into the model (Wang et al., 2019). Areas with a large population have abundant labor resources, which is conducive to enterprises employing more professional labor and improving industrial output value. The expected sign is positive. 4) Environmental Regulation (lnregul). It is calculated by the proportion of total investment in pollution control in GDP (Yuan, 2018). Theoretically, the government raises the threshold of environmental regulation to diminish the emission of enterprises and promote eco-efficiency, so the expected sign is positive. 5) Technological Innovation (lnpaten). It is expressed as the number of approved patents filed per 10,000 people (Zhang et al., 2021). Technological innovation is an important driver of economic development, as well as an important way to promote clean production and reduce pollution. The expected sign is positive.

3.4 Data Sources

The above data are obtained from the China Statistical Yearbook, China Environmental Statistical Yearbook, China Industrial Statistical Yearbook, China Employment Statistical Yearbook, Economy Prediction System (EPS) database, China Economic Network, Provincial Statistical Yearbook, and official data released by the National Bureau of Statistics. In order to reduce the impact of inflation, the currency data has been deflated on basis of 2009. Some missing data were supplemented by linear interpolation. The research object of this paper is provinces and municipalities in mainland China. Due to statistical data missing in Tibet, the data set is composed of panel data of 30 provinces from 2009 to 2018 as shown in Table 2, which lists the name, description, unit, symbol, and expected sign of all variables.

TABLE 2

TABLE 2. Variable description.

4 Empirical Results Analysis

4.1 The IEE Evaluation Results

Table 3 shows the evaluation results of regional IEE, it can be found that there are significant regional disparities in IEE in China. From 2009 to 2018, the mean of IEE in five provinces exceed 1, including Beijing, Tianjin, Shanghai, Jiangsu, and Guangdong, and the efficiency ranking of these effective provinces could be also observed, indicating that it is more scientific to adopt super-efficiency DEA to measure IEE. From the mean of IEE, Beijing has the highest IEE during this period, as the political and economic center of China, the government attaches great importance to improving its environmental quality, such as transforming the previous state-owned industrial park to be the venue of the Winter Olympic Games (Deng et al., 2020), these policies are conducive to improve the IEE. Meanwhile, IEE values in nine provinces are less than 0.3, including Inner Mongolia, Heilongjiang, Gansu, Yunnan, Guizhou, Shanxi, Qinghai, Xinjiang, and Ningxia, which means that there has great potential for improvement of IEE. The provinces with lower IEE are mainly distributed in the western region of China, which might be related to the level of economic development and industrialization (Zhang et al., 2017).

TABLE 3

TABLE 3. Regional IEE from 2009 to 2018.

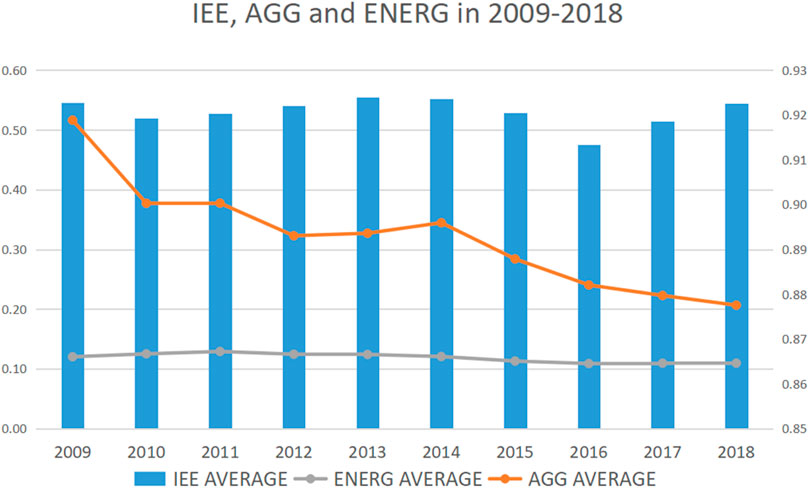
Figure 1 displays the average level of China’s IEE, industrial agglomeration, and energy intensity from 2009 to 2018. It can be seen that the average level of national IEE fluctuates slightly in some years during the study period, but is relatively stable in the range of 0.48–0.55, indicating that the regional IEE level is relatively low on the whole. Industrial agglomeration has been in an obvious downward trend during this period, which may be related to the industrial policies implemented by the Chinese government, including transferring some industries to central and western regions to alleviate excessive industrial concentration in eastern China and narrow the imbalance in regional industrial development.

FIGURE 1

FIGURE 1. IEE, industrial agglomeration and energy intensity from 2009–2018.

4.2 Spatial Regression

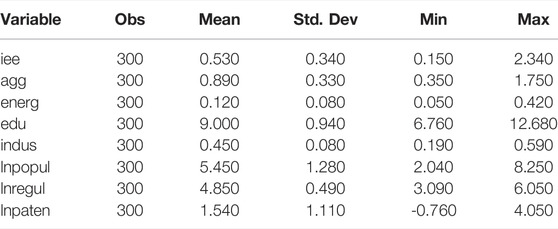
The descriptive statistics, multicollinearity, and correlation analysis of each variable are given in Tables 4, 5. It can be seen that each variable has no outliers and there are no completely unrelated variables or serious multicollinearity (VIF is less than 5), so the data set is relatively stable.

TABLE 4

TABLE 4. Descriptive Statistics.

TABLE 5

TABLE 5. Pairwise correlations and VIF.

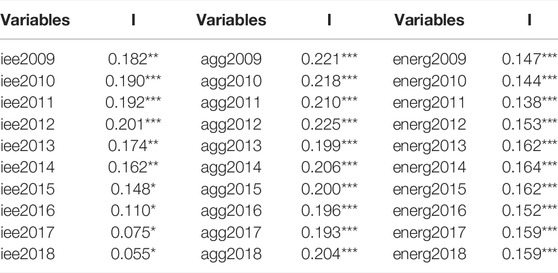
As noted earlier, Moran Index is used to measure whether variables have a spatial correlation. Table 6 lists the Moran Index of IEE, industrial agglomeration, and energy intensity. It can be found that these variables show spatial positive correlation in all years, so it is reasonable and feasible to construct the spatial econometric model in this study.

TABLE 6

TABLE 6. Moran Index.

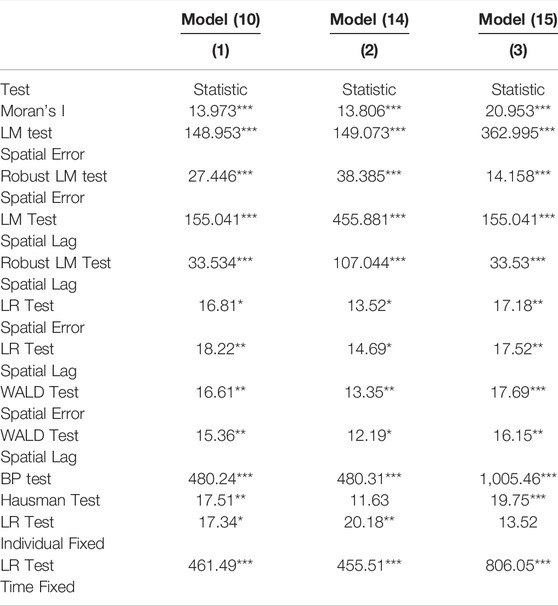
The specific spatial econometric model (10) is diagnosed by the LM, LR, and WALD test as shown in Column (1) of Table 7. The Robust LM Error and Robust Lag statistics were all significant at a significance level of 10%, indicating that SAR and SEM could not accurately reflect the spatial relationship between industrial agglomeration and IEE. According to the results of the BP test, Hausman test, and LR test, it is necessary to analyze the relationship between IEE and industrial agglomeration with individual and time both fixed effects.

TABLE 7

TABLE 7. LM test, LR, WALD, BP, HAUSMAN test results.

Table 8 lists the SAC model regression results of industrial agglomeration effects on IEE, as well as the non-spatial OLS model, fixed effects panel, and Spatial Durbin Model (SDM model) regression results for comparison, the results illustrate that the spatial model considering the fixed effects and spatial correlation is more suitable than that of the former two, with more reliable estimation. Furthermore, according to Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) (Yu et al., 2018a), it can be found that the SAC model has better goodness of fit compared with the SDM model, which also proves that the setting of SAC model in this study is reasonable (Li and Guo, 2019).

TABLE 8

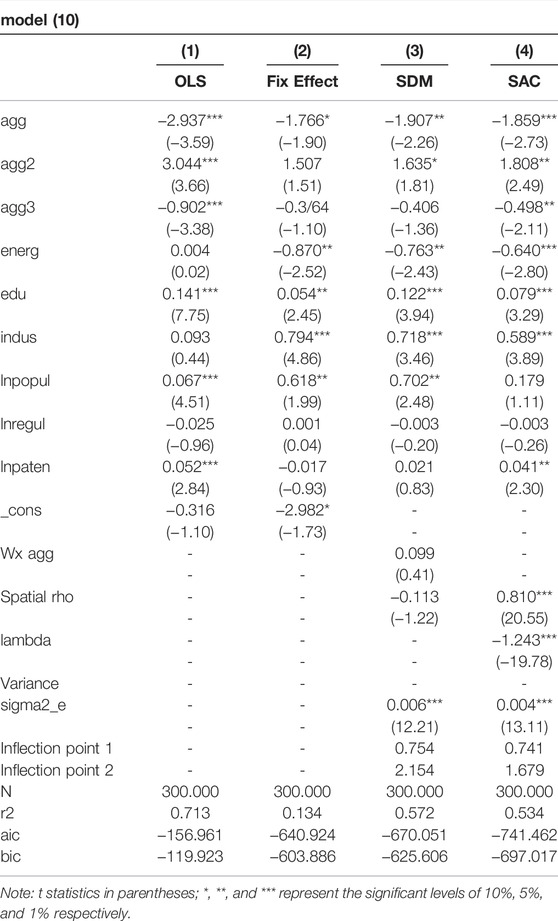
TABLE 8. Regression results of non-spatial OLS model, non-spatial fixed effect panel model, SDM model, and SAC model.

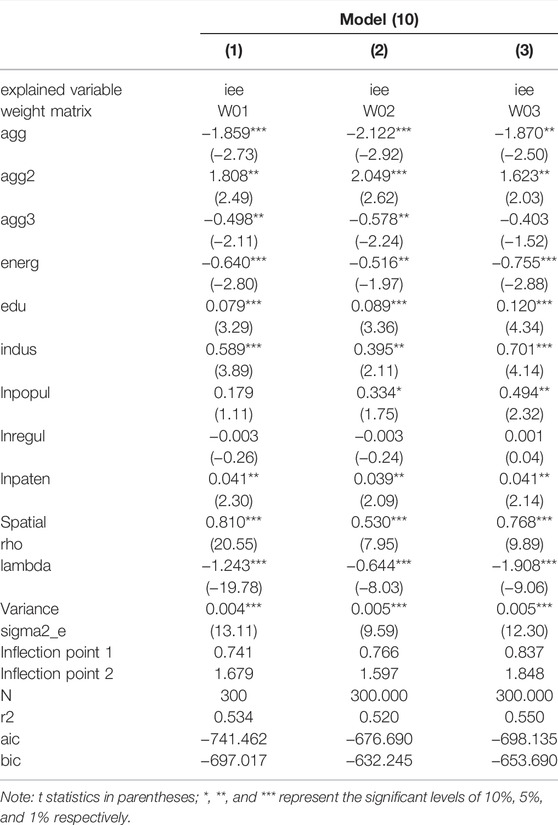
It is observed from the empirical results of the spatial SAC model that the spatial error coefficient is significantly positive, indicating that IEE has a positive spatial correlation. The coefficient of the cubic term of the industrial agglomeration is negative, the quadratic term is positive, and the primary term is negative, which all pass the 5% significance test, revealing that the relationship between the industrial agglomeration and IEE is inverted N-shaped. Specifically, there are two inflection points in the inverted N-shaped curve, which means that in different stages of industrial agglomeration, its impact on IEE is inhibiting first, then promoting, and inhibiting again.

When the level of industrial agglomeration is lower than the first inflection point (agg<0.741), industrial agglomeration could hinder IEE. In the initial stage of industrial agglomeration, enterprises may only simply gather in geographical locations, enterprises enter industrial parks or industrial zones to get preferential policies from the government. However, the weak connections and associations among enterprises make it difficult to create knowledge spillover and economies of scale. However, the concentrated production in limited space increase industrial emissions, so the IEE would decrease.

According to the average industrial agglomeration index from 2009 to 2018 shown in Table 9, there are 11 provinces with industrial agglomeration on the left of the first inflection point, including Beijing, Inner Mongolia, Heilongjiang, Guangxi, Hainan, Guizhou, Yunnan, Shaanxi, Gansu, Ningxia, and Xinjiang. Except for Beijing as the political center, and Inner Mongolia and Heilongjiang as traditional heavy industry bases in northeast China, the other eight provinces are located in western China with a relatively backward industrial level. This result is consistent with the regional imbalance of China’s current industrial development.

TABLE 9

TABLE 9. Average Industrial Aggregation (2009–2018).

When the level of industrial agglomeration is between the first inflection point and the second inflection point (0.741<agg<1.679), industrial agglomeration could improve IEE. The main reason is that industrial agglomeration has developed from the simple concentration into deeper cooperation with upstream and downstream enterprises in the industrial chain, the government provides more infrastructure, as well as preferential policies, therefore quality and scale of the industry agglomeration are both improved, therefore economies of scale become greater than the crowding effect, the IEE would increase.

There are 18 provinces with an industrial agglomeration level between the first and second inflection points, including Tianjin, Hebei, Shanxi, Liaoning, Jilin, Shanghai, Jiangsu, Anhui, Fujian, Jiangxi, Shandong, Henan, Hubei, Hunan, Guangdong, Chongqing, Sichuan, and Qinghai. These provinces are mainly distributed in eastern and central China, indicating that industry in these regions has been developing rapidly in the 40 years of reform and opening-up, and the improvement of industrial agglomeration has a positive impact on IEE.

When the industrial agglomeration level exceeds the second inflection point (agg>1.679), industrial agglomeration will again hinder IEE. As the environmental capacity for industrial agglomeration is limited, excessive industrial concentration may result in huge energy consumption and pollution emissions, and continuously rising production costs. Economies of scale can no longer make up for the negative impact brought by the crowding effect, thus industrial agglomeration will lead to the decline of IEE.

As shown in Table 9, industrial agglomeration in Zhejiang province is on the right side of the second inflection point, illustrating that excessive industrial agglomeration level has hindered IEE. Should also be noticed at the same time, the industrial agglomeration levels in three provinces including Jiangsu, Guangdong, and Fujian are next to the second inflection point, which represent the highest level of China’s industrial development. It can be inferred that these developed eastern regions are already very close to the limit of local environmental capacity, if we continue to blindly expand industrial agglomeration in these regions, IEE will decline ultimately. The results also reflect the fact that excessive industrial agglomeration in some eastern developed provinces has already led to environmental degradation.

Energy intensity is negative and significant at the 1% significance level. This indicates that high energy intensity would increase energy consumption and hinder IEE, which is the same as the expected symbol, this may be due to inadequate energy utilization, high energy consumption per unit output leads to the decline of IEE. (Fisher-Vanden et al., 2004).

Regression analysis of other control variables is as follows:1) Human Resources (edu). The coefficient of human resources is positive at 1% significance level, in line with the expected sign. This shows that human resources play a positive role in promoting IEE because human resources determine the quality of labor force input. 2) Industrialization level (indus). The coefficient of industrialization passes the 1% significance test, illustrating a high industrial output value, which is beneficial to IEE. 3) Population Scale (lnpopul). The coefficient of population density is positive but not significant, which may result from large energy demand and industrial emissions in areas with large populations. 4) Environmental regulation (lnregul). The coefficient of environmental regulation is negative but not significant, indicating that environmental regulation has not played a positive role. The possible reason is that the environmental regulation increases the compliance cost of enterprises, and the higher production cost leads to the decline of IEE. 5) Technological innovation (lnpaten). The coefficient of technological innovation is positive at the 5% significance level, indicating that technological innovation could improve IEE. The possible reason is that technological progress emphasizes the innovation of emission reduction and clean production technology.

4.3 Robustness Test

To further test the reliability of the empirical results, this paper conducts a robustness test by different spatial weight matrices, which are the economic distance matrix (W02) and the economic geography matrix (W03). Columns (1)-(3) in Table 10 show the regression results of IEE under three spatial weight matrices. It can be observed that the coefficients of the primary term, quadratic term, and cubic term of industrial agglomeration are respectively negative, positive, and negative, most of them pass the 5% significance test, which is consistent with the previous conclusion and verifies again that the relationship between industrial agglomeration and IEE is inverted N-shaped. Meanwhile, the coefficient of spatial correlation is positive at different significance levels, which proves that IEE indeed has a spatial spillover effect. The above results check the robustness of the core conclusion of this study, therefore, the first research hypothesis of this paper has been verified.

TABLE 10

TABLE 10. Robustness test result.

4.4 Mediation Effect Test

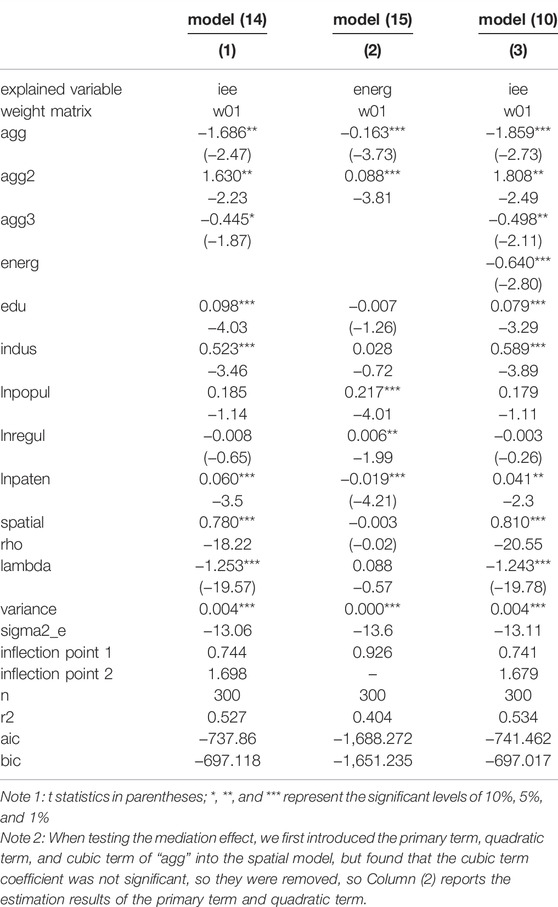
The diagnosis test result of the model (14) and model (15) are shown in Columns (1)–-(2) of Table 7, indicating that the SAC model with both fixed effects should be selected for the mediation model. In order to show the mediation effect more clearly, we listed the regression results of model (14) (15) and model (10) in Table 11. Column (1) of Table 11 gives the regression result from the model (14), it is found that the correlation coefficients of the primary term, secondary term, and tertiary term of industrial agglomeration are negative, positive, and negative respectively, and which pass the significance test at different levels, indicating that industrial agglomeration has an obvious influence on IEE, and their relationship is inverted N-shape. Moreover, this empirical result remains robust and reliable under the different weight matrices. Column (2) of Table 11 reports the regression result of the model (15), it can be illustrated that the correlation coefficients of the primary and secondary terms of industrial agglomeration are positive and negative respectively, and both significant at different levels, indicating that industrial agglomeration has a significant U-shaped impact on energy intensity. When industrial agglomeration is lower than the inflection point (agg = 0.926), it can reduce energy consumption, but when it is higher than the inflection point, it will increase energy consumption. Therefore, the result verifies the second hypothesis of this paper, energy intensity acts as mediating role between the industrial agglomeration and IEE.

TABLE 11

TABLE 11. Mediating effect test result.

5 Conclusion

This paper analyzes the spatial correlation of IEE by panel data of 30 provinces in China and constructs the SAC model to investigate the complex impact of industrial agglomeration on IEE. The main conclusions are as follows:

The relationship between industrial agglomeration and IEE is inverted N- shaped. In the initial stage of industrial agglomeration, it is difficult to generate economies of scale, therefore it hinders IEE. When industrial agglomeration develops to a relatively mature stage, the economies of scale exceed the crowding effect, industrial agglomeration can promote IEE. This non-linear relationship between them has also been confirmed in previous studies (Cheng et al., 2019; Guo et al., 2020). Furthermore, this study found that when industrial agglomeration overexpands, it again hinders IEE. Therefore, the level of industrial agglomeration should be controlled at the second inflection point. And the result shows that IEE indeed has a positive spatial spillover effect, IEE in one region will be affected by IEE in neighboring areas. Moreover, this study reveals that energy intensity plays a mediating role in the impact of industrial agglomeration on Deindustrialize agglomeration can affect IEE by influencing energy intensity, which was not involved in previous studies, as far as we know. The above conclusions are significant under different spatial weight matrices, so the core conclusion is reliable.

Based on the above conclusion, we propose the following suggestions:

First, industrial agglomeration policies should be differentiated according to the stage of regional industrial agglomeration. In terms of China’s industrial agglomeration, there are 11 provinces to the left of the first inflection point, most of which are located in western China. This result indicates that industrial agglomeration is still in the early stage of development, so these regions should improve the level of industrial agglomeration on the premise of protecting the environment and promoting more regions to cross the first inflection point. The government should introduce preferential policies to encourage enterprises’ industrial cooperation, provide better infrastructure and public resources, and therefore give full play to economies of scale to improve IEE. At the same time, there are 18 provinces between the first and second inflection points, mainly located in the eastern and central regions, illustrating the rapid industrial development in these provinces, and industrial agglomeration will continue to improve. However, the level of industrial agglomeration should be controlled before the second inflection point, and more attention to improving the quality of industrial agglomeration. The government should strictly restrict the entry of projects with high energy consumption and high pollution into industrial parks or industrial zones through environmental regulations, and eliminate the existing backward industries. The government can also introduce other preferential policies to improve IEE, including human resources, technological innovation, and industrial structure optimization.

Second, due to the existence of the spatial spillover effect, it is verified that the Chinese government’s regional integration industrial policy is reasonable and scientific, which needs to adhere to in the future, such as the Yangtze River Delta Economic Belt, Beijing-Tianjin-Hebei Economic Zone, and Pearl River Delta Economic Zone in eastern China. A collaborative mechanism should be established to improve IEE, and decision-makers should formulate industrial strategies from long-term interests, and achieve a “win-win” effect between economic interests and environmental interests. It is found that the energy intensity plays a mediation role between industrial agglomeration and IEE, industrial agglomeration affects energy intensity directly, so the government should give priority to energy-saving policies to improve energy efficiency.

Finally, it is suggested to formulate differentiated industrial agglomeration policies and energy policies according to the different stages of industrial agglomeration, so as to promote regional industrial economy in favor of sustainable development. This study found that energy intensity has a significant mediating effect in the process of industrial agglomeration affecting IEE, so the government is suggested to pay full attention to the role of energy conservation policy when promoting sustainable industrial development. Since industrial agglomeration has been proved to have a non-linear relationship with energy intensity, the government is suggested to set appropriate emission reduction targets according to the level of industrial agglomeration. Industrial agglomeration policy should coordinate with energy conservation policy, to make industrial agglomeration and energy intensity play positive effects on IEE simultaneously.

The limitation of this study lies in the availability of industrial emissions data and the lack of unified measurement for CO₂ emissions, resulting in the limited sample capacity. The future research direction is to find the latest scientific input and output indicators to measure IEE and to expand panel data to counties and cities for further grouping analysis.

In the context of the current global COVID-19, the sustainable development of the industry faces more uncertainties and challenges, including economic policies (Işık et al., 2020), the risk of SMEs closing down (Eggers, 2020), the increase in enterprise costs, the decline of labor efficiency, the challenge of environmental quality (Ahmad et al., 2021; Isik et al., 2021), energy supply and other aspects, all of which might have a significant impact on IEE, so they could be considered into the study of industrial sustainable development in the future.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

CZ: empirical research, HH: research direction, JY: conclusion and policy, DW: theoretical basis, JC: literature review, XM: research framework, QZ: data collection.

Funding

This research was funded by the Ministry of Science and Technology of China under Grant 2020AAA0108400, in part by the National Social Science Fund of China Grant 19BJY106, in part by the National Natural Science Foundation of China under Grant 71825007, in part by the Strategic Priority Research Program of CAS under Grant XDA2302020.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank CEADs for data sharing, and thanks for the joint efforts of all team members, which realized the current research results.

References

Ahmad, M., Işık, C., Jabeen, G., Ali, T., Ozturk, I., and Atchike, D. W. (2021). Heterogeneous Links Among Urban Concentration, Non-renewable Energy Use Intensity, Economic Development, and Environmental Emissions across Regional Development Levels. Sci. Total Environ. 765, 144527. doi:10.1016/j.scitotenv.2020.144527

PubMed Abstract | CrossRef Full Text | Google Scholar

Anselin, L. (2019). “The Moran Scatterplot as an ESDA Tool to Assess Local Instability in Spatial Association,” in Spatial Analytical Perspectives on GIS (London: Routledge), 111–126. doi:10.1201/9780203739051-8

CrossRef Full Text | Google Scholar

Baron, R. M., and Kenny, D. A. (1986). The Moderator-Mediator Variable Distinction in Social Psychological Research: Conceptual, Strategic, and Statistical Considerations. J. Personality Soc. Psychol. 51, 1173–1182. doi:10.1037/0022-3514.51.6.1173

PubMed Abstract | CrossRef Full Text | Google Scholar

Beeson, P. (1987). Total Factor Productivity Growth and Agglomeration Economies in Manufacturing, 1959-73*. J. Reg. Sci. 27, 183–199. doi:10.1111/j.1467-9787.1987.tb01154.x

CrossRef Full Text | Google Scholar

Cai, Y., and Hu, Z. (2022). Industrial Agglomeration and Industrial SO2 Emissions in China's 285 Cities: Evidence from Multiple Agglomeration Types. J. Clean. Prod. 353, 131675. doi:10.1016/j.jclepro.2022.131675

CrossRef Full Text | Google Scholar

Chatman, D. G., and Noland, R. B. (2011). Do Public Transport Improvements Increase Agglomeration Economies? A Review of Literature and an Agenda for Research. Transp. Rev. 31, 725–742. doi:10.1080/01441647.2011.587908

CrossRef Full Text | Google Scholar

Chen, C., Sun, Y., Lan, Q., and Jiang, F. (2020). Impacts of Industrial Agglomeration on Pollution and Ecological Efficiency-A Spatial Econometric Analysis Based on a Big Panel Dataset of China's 259 Cities. J. Clean. Prod. 258, 120721. doi:10.1016/j.jclepro.2020.120721

CrossRef Full Text | Google Scholar

Chen, F. (2016a). The Influence of Industrial Agglomeration on the Energy Consumption Intensity-Based on Provincial Panel Data in China. Soft Sci. 30, 112–116.

Google Scholar

Chen, L. (2016b). Estimation of China’s Industrial Ecological Efficiency Based on Non-radial BM-DEA Model. Stat. Decis., 57–59. doi:10.13546/j.cnki.tjyjc.2016.22.015

CrossRef Full Text | Google Scholar

Cheng, Y., Shao, T., Lai, H., Shen, M., and Li, Y. (2019). Total-Factor Eco-Efficiency and its Influencing Factors in the Yangtze River Delta Urban. Int. J. Environ. Res. Public Health.

Google Scholar

Ciccone, A. (2002). Agglomeration Effects in Europe. Eur. Econ. Rev. Sci. Cit. Index (SSCI) 46, 213–227. doi:10.1016/S0014-2921(00)00099-4WE

CrossRef Full Text | Google Scholar

Coase, R. H. (1960). The Problem of Social Cost. J. Law Econ. 3, 13–44. doi:10.1002/9780470752135.ch1

CrossRef Full Text | Google Scholar

Deng, H., Mancini, M., Zhang, L., and Bonino, M. (2020). Beijing 2022 between Urban Renovation and Olympic Sporting Legacy: the Case of Shougang. Mov. Sport Sci/Sci Mot., 53–65. doi:10.1051/sm/2019040

CrossRef Full Text | Google Scholar

Dong, F., Wang, Y., Zheng, L., Li, J., and Xie, S. (2020). Can Industrial Agglomeration Promote Pollution Agglomeration? Evidence from China. J. Clean. Prod. 246, 118960. doi:10.1016/j.jclepro.2019.118960

CrossRef Full Text | Google Scholar

Eggers, F. (2020). Masters of Disasters? Challenges and Opportunities for SMEs in Times of Crisis. J. Bus. Res. 116, 199–208. doi:10.1016/j.jbusres.2020.05.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Elhorst, J. P. (2014). Spatial Econometrics: From Cross-Sectional Data to Spatial Panels. Heidelberg: Springer.

Google Scholar

EPI Results (2021). EPI Results. Available at: https://epi.yale.edu/epi-results/2020/component/epi (Accessed December 23, 2021).

Google Scholar

Fan, Z., and Zhou, S. (2018). The Effect of New Urbanization on Economic Growth—Research Based on the Dynamic Panel Data Models with Spatial Errors. J. Appl. Stat. Manag. 27, 14–154.

Google Scholar

Feldman, M. P. (1999). The New Economics of Innovation, Spillovers and Agglomeration: Areview of Empirical Studies. Econ. Innovation New Technol. 8, 5–25. doi:10.1080/10438599900000002

CrossRef Full Text | Google Scholar

Fisher-Vanden, K., Jefferson, G. H., Liu, H., and Tao, Q. (2004). What Is Driving China's Decline in Energy Intensity? Resour. Energy Econ. 26, 77–97. doi:10.1016/j.reseneeco.2003.07.002

CrossRef Full Text | Google Scholar

Ge, T., Hao, X., and Li, J. (2021). Effects of Public Participation on Environmental Governance in China: A Spatial Durbin Econometric Analysis. J. Clean. Prod. 321, 129042. doi:10.1016/j.jclepro.2021.129042

CrossRef Full Text | Google Scholar

Ge, T., Ma, L., and Wang, C. (2022). Spatial Effect of Economic Growth Targets on CO2 Emissions: Evidence from Prefectural-Level Cities in China. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.857225

CrossRef Full Text | Google Scholar

Guo, L., and Xu, S. (2016). Industrial Eco-Efficiency with the Integration Super Efficiency DEA: The Central Six Provinces 2003-2013 Data as an Example. Econ. Geogr. 36, 116–121.

Google Scholar

Guo, Y., Tong, L., and Mei, L. (2020). The Effect of Industrial Agglomeration on Green Development Efficiency in Northeast China since the Revitalization. J. Clean. Prod. 258, 120584. doi:10.1016/j.jclepro.2020.120584

CrossRef Full Text | Google Scholar

Halleck Vega, S., and Elhorst, J. P. (2015). The Slx Model. J. Regional Sci. 55, 339–363. doi:10.1111/jors.12188

CrossRef Full Text | Google Scholar

Han, C.-Y., Gu, Z.-L., and Yang, H. (2022). Investigate the Effects of Industrial Agglomeration on Nitrogen Dioxide Pollution Using Spatial Panel Durbin and Panel Threshold Models. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.844479

CrossRef Full Text | Google Scholar

Henderson, J. V. (2003). Marshall's Scale Economies. J. Urban Econ. 53, 1–28. doi:10.1016/S0094-1190(02)00505-3

CrossRef Full Text | Google Scholar

Holmes, T. J., Fujita, M., Krugman, P., and Venables, A. J. (2000). The Spatial Economy: Cities, Regions, and International Trade. South. Econ. J. 67, 491–493. doi:10.2307/1061487

CrossRef Full Text | Google Scholar

Hong, Y., Lyu, X., Chen, Y., and Li, W. (2020). Industrial Agglomeration Externalities, Local Governments' Competition and Environmental Pollution: Evidence from Chinese Prefecture-Level Cities. J. Clean. Prod. 277, 123455. doi:10.1016/j.jclepro.2020.123455

CrossRef Full Text | Google Scholar

International Energy Agency (2020). International Energy Agency. Available at: https://www.iea.org/.

Google Scholar

Isik, C., Ongan, S., Ozdemir, D., Ahmad, M., Irfan, M., Alvarado, R., et al. (2021). The Increases and Decreases of the Environment Kuznets Curve (EKC) for 8 OECD Countries. Environ. Sci. Pollut. Res. 28, 28535–28543. doi:10.1007/s11356-021-12637-y

CrossRef Full Text | Google Scholar

Işık, C., Sirakaya-Turk, E., and Ongan, S. (2020). Testing the Efficacy of the Economic Policy Uncertainty Index on Tourism Demand in USMCA: Theory and Evidence. Tour. Econ. 26, 1344–1357. doi:10.1177/1354816619888346

CrossRef Full Text | Google Scholar

Ji, Y., and Zhao, N. (2016). Is Industrial Agglomeration Beneficial to Improve Energy Efficiency?-A Threshold Regression Model Test Based on the Degree of Industrial Agglomeration and the Level of Opening up. J. BEIJING Inst. Technol. Soc. Sci. Ed. 18, 19–27.

Google Scholar

Krugman, P. (1991). Increasing Returns and Economic Geography. J. Political Econ. 99, 483–499. Available at: https://pr.princeton.edu/pictures/g-k/krugman/krugman-increasing_returns_1991.pdf. doi:10.1086/261763

CrossRef Full Text | Google Scholar

Lei, H., Wang, H., and Zhu, M. (2017). Industrial Agglomeration,Energy Consumption and Environmental Pollution. J. Ind. Technol. Econ., 58–64.

Google Scholar

Li, J., Xia, M., and Yuan, Q. (2021a). Research on Influence of Specialized Agglomeration High-Tech Industry on Green Total and Diversified Agglomeration of Factor Productivity. J. Stat. Inf. 36, 42–50.

Google Scholar

Li, L., and Hong, X. (2017). Spatial Effects of Energy-Related Carbon Emissions and Environmental Pollution -STIRPAT Durbin Model Based on Energy Intensity and Technology Progress. J. Ind. Technol. Econ., 65–72.

Google Scholar

Li, X., Hu, Z., and Cao, J. (2021b). The Impact of Carbon Market Pilots on Air Pollution: Evidence from China. Environ. Sci. Pollut. Res. 28, 62274–62291. doi:10.1007/s11356-021-14995-z

CrossRef Full Text | Google Scholar

Li, X., and Wang, D. (2022). Does Transfer Payments Promote Low‐Carbon Development of Resource‐Exhausted Cities in China? Earth's Future 10. doi:10.1029/2021EF002339

CrossRef Full Text | Google Scholar

Li, X., Zhu, X., Li, J., and Gu, C. (2021c). Influence of Different Industrial Agglomeration Modes on Eco-Efficiency in China. Ijerph 18, 13139. doi:10.3390/ijerph182413139

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., and Guo, X. (2019). The Effect and Mechanism of Financial Development on Urban Total Factor Productivity. Inq. Into Econ. Issues, 162–172.

Google Scholar

Li, Z., Hu, M., and Zhou, N. (2020). The Spatial Pattern and Influencing Factors of Industrial Eco-Efficiency in Chinese Prefecture-Level Cities. Econ. Geogr. 38, 126–134. doi:10.16110/j.cnki.issn2095-3151.2020.06.016

CrossRef Full Text | Google Scholar

Lin, B., and Zhu, J. (2019). Impact of Energy Saving and Emission Reduction Policy on Urban Sustainable Development: Empirical Evidence from China. Appl. Energy 239, 12–22. doi:10.1016/j.apenergy.2019.01.166

CrossRef Full Text | Google Scholar

Liu, J., Cheng, Z., and Zhang, H. (2017). Does Industrial Agglomeration Promote the Increase of Energy Efficiency in China? J. Clean. Prod. 164, 30–37. doi:10.1016/j.jclepro.2017.06.179

CrossRef Full Text | Google Scholar

Liu, X., Zhao, T., Chang, C.-T., and Fu, C. J. (2021). China's Renewable Energy Strategy and Industrial Adjustment Policy. Renew. Energy 170, 1382–1395. doi:10.1016/j.renene.2021.02.045

CrossRef Full Text | Google Scholar

Liu, Y., and Jin, S. (2019). Temporal and Spatial Evolution Characteristics and Influencing Factors of Energy Consumption Carbon Emissions in Six Provinces of Central China. Econ. Geogr. 39, 182–191.

Google Scholar

Marshall, A. (1890). Principles of Economics. Macmillan London.

Google Scholar

Moomaw, R. L. (1981). Productivity and City Size: A Critique of the Evidence. Q. J. Econ. 96, 675–688. Science Citation Index (SSCI). doi:10.2307/1880747WE-Social

CrossRef Full Text | Google Scholar

Overman, H. G., and Puga, D. (2010). “Labor Pooling as a Source of Agglomeration: An Empirical Investigation,” in Agglomeration Economics (University of Chicago Press), 133–150.

Google Scholar

Peng, X., and Li, B. (2015). Trade Openness, FDI and Green Transformation of Chinese Industry: An Empirical Analysis Based on Dynamic Threshold Model Using Panel Data. J. Int. Trade, 166–176. doi:10.13510/j.cnki.jit.2015.01.016

CrossRef Full Text | Google Scholar

Popescu, G. H., Nica, E., Nicolăescu, E., and Lăzăroiu, G. (2016). China’s Steel Industry as a Driving Force for Economic Growth and International Competitiveness. Metalurgija 55, 123–126.

Google Scholar

Schaltegger, S., and Sturm, A. (2014). Ökologische Rationalität. Kognit. Menschen Tieren 44, 79–104. doi:10.1515/9783110368901.79

CrossRef Full Text | Google Scholar

Shao, S., Zhang, K., and Dou, J. (2019). Effects of Economic Agglomeration on Energy Saving and Emission Reduction: Theory and Empirical Evidence from China. Manage. World, 36–61. doi:10.19744/j.cnki.11-1235/f.2019.0005

CrossRef Full Text | Google Scholar

Shi, B., and Shen, K. (2013). The Government Intervention, the Economic Agglomeration and the Energy Efficiency Shi. Manage. World 84, 487–492. doi:10.19744/j.cnki.11-1235/f.2013.10.002

CrossRef Full Text | Google Scholar

Statistical Bulletin on National Economic and Social Development (2022). stats.gov. Available at: http://www.stats.gov.cn/tjsj/zxfb/202202/t20220227_1827960.html.

Google Scholar

Tobler, W. R. (1970). A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 46, 234. doi:10.2307/143141

CrossRef Full Text | Google Scholar

UNESCAP (2009). Eco-Efficiency Indicators: Measuring Resource-Use Efficiency and the Impact of Economic Activities on the Environment. Available at: https://hdl.handle.net/20.500.12870/1598

Google Scholar

Wang, H., and Chen, Y. (2010). Industrial Agglomeration and Industrial Energy Efficiency: Empirical Analyses Based on 25 Industries in China. J. Financ. Econ. 36, 69–79.

Google Scholar

Wang, H., and Yang, J. (2019). Total-factor Industrial Eco-Efficiency and its Influencing Factors in China: A Spatial Panel Data Approach. J. Clean. Prod. 227, 263–271. doi:10.1016/j.jclepro.2019.04.119

CrossRef Full Text | Google Scholar

Wang, J., Yu, C. W., and Cao, S.-J. (2021). Technology Pathway of Efficient and Climate-Friendly Cooling in Buildings: Towards Carbon Neutrality. Indoor Built Environ. 30, 1307–1311. doi:10.1177/1420326x211027365

CrossRef Full Text | Google Scholar

Wang, K., Zhang, C., and Meng, X. (2016). Study on the Heterogeneity of China’s Regional Industrial Eco-Efficiency from the Perspective of Environmental Pressure. Sci. Technol. Manag. Res., 242–247.

Google Scholar

Wang, N., Zhu, Y., and Yang, T. (2020). The Impact of Transportation Infrastructure and Industrial Agglomeration on Energy Efficiency: Evidence from China's Industrial Sectors. J. Clean. Prod. 244, 118708. doi:10.1016/j.jclepro.2019.118708

CrossRef Full Text | Google Scholar

Wang, Y., Liu, J., Hansson, L., Zhang, K., and Wang, R. (2011). Implementing Stricter Environmental Regulation to Enhance Eco-Efficiency and Sustainability: a Case Study of Shandong Province's Pulp and Paper Industry, China. J. Clean. Prod. 19, 303–310. doi:10.1016/j.jclepro.2010.11.006

CrossRef Full Text | Google Scholar

Wang, Y., Zhao, T., Wang, J., Guo, F., Kan, X., and Yuan, R. (2019). Spatial Analysis on Carbon Emission Abatement Capacity at Provincial Level in China from 1997 to 2014: An Empirical Study Based on SDM Model. Atmos. Pollut. Res. 10, 97–104. doi:10.1016/j.apr.2018.06.003

CrossRef Full Text | Google Scholar

World Bank Data (2020). World Bank Data. Available at: https://data.worldbank.org/indicator/NE.CON.TOTL.CD?locations=CN.

Google Scholar

Yan, C., and He, H. (2019). Agglomeration of Productive Service Industry, Fiscal Decentralization and Prefectural Industrial Ecological Efficiency. Rev. Econ. Manag., 92–107.

Google Scholar

Yang, C. (2020). Spatio-temporal Difference and Convergence of Industrial Eco-Efficiency in China. Macroeconomics 106–137. doi:10.16304/j.cnki.11-3952/f.2020.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, H., Xu, X., and Zhang, F. (2022). Industrial Co-agglomeration, Green Technological Innovation, and Total Factor Energy Efficiency. Environ. Sci. Pollut. Res. doi:10.1007/s11356-022-20078-4

CrossRef Full Text | Google Scholar

York, R., Rosa, E. A., and Dietz, T. (2003). STIRPAT, IPAT and ImPACT: Analytic Tools for Unpacking the Driving Forces of Environmental Impacts. Ecol. Econ. 46, 351–365. doi:10.1016/S0921-8009(03)00188-5

CrossRef Full Text | Google Scholar

Yu, Y., Huang, J., and Zhang, N. (2018a). Industrial Eco-Efficiency, Regional Disparity, and Spatial Convergence of China's Regions. J. Clean. Prod. 204, 872–887. doi:10.1016/j.jclepro.2018.09.054

CrossRef Full Text | Google Scholar

Yu, Y., Zhang, Y., and Miao, X. (2018b). Impacts of Dynamic Agglomeration Externalities on Eco-Efficiency: Empirical Evidence from China. Ijerph 15, 2304. doi:10.3390/ijerph15102304

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, B. (2018). Innovation-driven Chinese Industrial Green Total Factor Productivity under Environmental Regulation. Ind. Econ. Res., 101–113. doi:10.7498/aps.51.2804

CrossRef Full Text | Google Scholar

Yuan, B., Ren, S., and Chen, X. (2017). Can Environmental Regulation Promote the Coordinated Development of Economy and Environment in China's Manufacturing Industry?-A Panel Data Analysis of 28 Sub-sectors. J. Clean. Prod. 149, 11–24. doi:10.1016/j.jclepro.2017.02.065

CrossRef Full Text | Google Scholar

Yuan, B., and Zhang, K. (2017). Can the “Unlocked” Institution Release the Vitality of Manufacturing Green Development? — Evidence from the Panel Data Analysis of 28 Industries from 2003 to 2014. East China Econ. Manag. 31, 104–111.

Google Scholar

Yuan, H., Feng, Y., Lee, C.-C., and Cen, Y. (2020). How Does Manufacturing Agglomeration Affect Green Economic Efficiency? Energy Econ. 92, 104944. doi:10.1016/j.eneco.2020.104944

CrossRef Full Text | Google Scholar

Zhang, H., Yuan, P., and Zhu, Z. (2021). City Population Size, Industrial Agglomeration and CO2 Emission in Chinese Prefectures. China Environ. Sci. 41, 2459–2470. doi:10.19674/j.cnki.issn1000-6923.2021.0260

CrossRef Full Text | Google Scholar

Zhang, J., Liu, Y., Chang, Y., and Zhang, L. (2017). Industrial Eco-Efficiency in China: A Provincial Quantification Using Three-Stage Data Envelopment Analysis. J. Clean. Prod. 143, 238–249. doi:10.1016/j.jclepro.2016.12.123

CrossRef Full Text | Google Scholar

Zhang, X., and Wang, J. (2019). The Spatial Effect of Region Energy Efficiency on Haze Pollution-Empirical Analysis Based on the Spatial Durbin Model. China Environ. Sci. 39, 1371–1379.

Google Scholar

Zheng, Q., and Lin, B. (2018). Impact of Industrial Agglomeration on Energy Efficiency in China's Paper Industry. J. Clean. Prod. 184, 1072–1080. doi:10.1016/j.jclepro.2018.03.016

CrossRef Full Text | Google Scholar

Zhou, Y., Liu, Z., Liu, S., Chen, M., Zhang, X., and Wang, Y. (2020). Analysis of Industrial Eco-Efficiency and its Influencing Factors in China. Clean. Techn Environ. Policy 22, 2023–2038. doi:10.1007/s10098-020-01943-7

CrossRef Full Text | Google Scholar